Abstract
Nowadays, the systems for visual information processing are significantly extending their application field. Moreover, an unsolved problem for such systems is that the classification procedure has often-conflicting requirements for performance and classification reliability. Therefore, the goal of the article is to develop the wavelet method for classifying the systems for visual information processing by evaluating the performance and informativeness of the adopted classification solutions. This method of classification uses the Haar wavelet functions with training and calculates the ranges of changes in the coefficients of the separating surfaces. The authors proposed to select the ranges of changes in these coefficients by employing the Shannon entropy formula for measuring the information content. A case study proved that such a method will significantly increase the speed of detecting the intervals of coefficient values. In addition, this enables us to justify the choice of the width of the ranges for the change of coefficients, solving the contradiction between the performance and reliability of the classifier.
1. Introduction
The application field of visual information processing systems and/or non-stationary periodic signals is actively expanding at present [1,2,3,4,5]. For example, such systems are in demand in technical diagnostics, in quality management, in traffic control, in many military fields, in fields related to decision support in medicine, security, and so on. Visual information processing in such systems investigates physical processes and phenomena that are unambiguously described by random signals or images. In particular, this applies to the tasks of remote parameter control of stationary and moving control objects [3], as well as the remote sensing and tracking of objects in different backgrounds [4], object counting, and product manufacturing control [5].
The modern approach to the creation of such systems involves extensive use of computer information technology (IT). The implementation of such an approach involves adaptation to a specific application of existing IT. Such an adaptation is based on a pragmatic approach; that is, an effort to achieve the goal with the minimum values of the procedures parameters sufficient to make the right decision.
An important computational procedure in the above systems is the classification procedure [6]. The development of actual IT often requires training the classifier on new datasets. Such datasets may have a small volume; clusters of data may overlap in the feature space [2,6,7]. In addition, when a system is functioning, the data for classification may be distorted in shape (scale, shift, rotation) and with an increased level of noise due to changes in capture conditions [1,2,4,5,6].
In such a situation, the quality and/or efficiency of decisions made in the system may decrease [4]. However, increasing the dataset for training the classifier by measurements (e.g., when researching new drug methods in medicine, security methods in military applications, etc.) can reduce the speed of training such systems.
Increasing the set of images and/or signals under study based on known augmentation methods [8,9] with unknown parameters of noise distribution laws and/or shape distortions may not acheive the required values of quality and efficiency of such systems within the limits of acceptable resource intensity.
In such cases, it is necessary to choose a classification method and its parameters. However, when making such a choice for a particular applied task, it is often difficult to implement a systematic pragmatic approach, taking into account the information sufficiency. Such an approach, as a rule, requires a quantitative assessment of the effectiveness and/or quality of the investigated classifiers variants. For most classification methods, the implementation of such an approach requires a large number of experiments, i.e., up to a complete enumeration of parameter variants.
Classification training enables us to calculate the coefficients that determine the shape of the surfaces and separate classes in the feature space. Tasks traditionally solved in the system (pattern recognition, clustering, and finding informative features) often differ in the fact that their solution algorithms contain objective functions defined implicitly by measuring their parameters. The classification problem also belongs to this category of problems.
Classifier training is often complicated by the high level of noise in the training sample data. The quality functional is not explicitly known and may have a multi-extremal surface (this is due to the complex shape of clusters) and be noisy, especially when the analysis is performed on small datasets.
The existing classification methods in systems for visual information processing are usually based on optimization techniques, determining the direction of search for an extremum of the objective function using the first derivative. Such methods include the following: steepest descent, gradient, Gauss-Seidel, Rosenbrock, Powell, and Southwell [10]. Under the above conditions, these methods have a low reliability and (often) do not meet the requirements of practice since they find local extrema only. This can also occur due to different levels of noise in the data during the training of the classifier and in the working mode of classification. In addition, the quantity of objects and the variance of their parameters in the class may be different during the training of the classifier. Such peculiarities may appear in classification with a complex form of clusters.
A number of References are devoted to determining the quality of information technologies and systems based on them. In particular, in [11], the main components of systems quality in terms of the information component—syntactic, semantic, and pragmatic—are highlighted as well as the features of information quality for healthcare, energy, and transport devices. The methodology assumes the presence of 16 attributes, which are used to assess the quality of systems. A similar approach is also implemented in other studies [12,13].
When designing systems for visual information processing, the required performance must be ensured. In addition, an important direction is the creation of adaptive systems, i.e., those capable of changing their parameters depending on changing surveillance conditions. Moreover, it is necessary to achieve the coordination of the characteristics for the individual procedures of the system. At the same time, some authors [14] state that estimating the parameters of individual procedures when assessing the quality of new or adapted-to-the-applied-task information technologies is a labor-intensive process.
To solve such problems by successively coordinating the characteristic procedures, the multicriteria decision analysis (MCDA) can be considered as a legitimate solution [15]. It is also called multi the object optimization (MOO) or post Pareto optimization (PPO) [16]. For this purpose, a wide range of methods has been developed [17]. In practice, approximate methods for solving MCDA problems are also used [18]. Among them, one can single out the main criterion method and the linear convolution method [19]. At the same time, the application of the main criterion method is limited due to the difficulties associated with the choice of the main criterion and limitations [20]. The linear convolution method requires the determination of the weight coefficients necessary to combine partial objective functionals [21]. Experts formulate requirements for speed and classification reliability in different ways in different application areas; that is, the methods of both groups can require additional information from experts in order to formulate and solve various types of constrained scalar optimization problems.
To solve a problem by matching the characteristics of individual procedures, a number of studies suggest using the well-known Shannon entropy formula to measure the information content [22]. For example, such an approach has been proposed for choosing the procedures for segmentation [23,24], clustering [25], and classification [26,27,28,29].
The authors have previously developed a classification method using Haar’s wavelet transform (WT) and hyperbolic WT with improved noise immunity and reduced error [30,31]. In this case, the error in determining the extremum of the objective function during processing with the Haar WT can be high (due to the asymmetry of the objective function). It has been shown that this error can be reduced by processing with the hyperbolic WT.
In [30], the classification, determining the coefficients of separating surfaces using multistage processing by the Haar WF and hyperbolic WFs, was described. Such an approach enabled us to obtain a set of the nested intervals for these coefficients. However, due to such complex processing, its performance is low.
Therefore, the goal of this article is to develop an improved wavelet method for classifying the systems for visual information processing by evaluating the performance and informativeness of the adopted classification solutions and employing the Shannon entropy formula for measuring the information content.
2. Materials and Methods
The classification consists in assigning the presented objects to one class by comparing their parameters. It is based on the compactness hypothesis—the assumption that objects of the same class are similar in terms of parameter values. In the classification, we search for the minimum of the functional over the vector of coefficients . The probability of incorrect classification was estimated as the ratio of the number of incorrectly recognized objects to the total number of objects in the sample. These coefficients define the type of surface separating the classes in the parameter space. At the first stage (during training the classifier), the separating surface is constructed by training samples of known classes; at the second stage (in the “working” mode), the class of the object under study is determined.
Depending on which dataset is provided for research (for pragmatic reasons), three possible approaches to classification in a system for visual information processing can be considered.
- If the parameters of the general population are known, it is recommended to carry out a point estimation of the coefficient values separating the classes of surfaces;
- If random sample data with a known type of distribution law with unknown parameters are presented, it is recommended to carry out interval estimates of these coefficient values;
- If the law of distribution is unknown, we suggest using the iterative method of intelligent data analysis—in particular, the method of classification with WT. This method enables us to select areas where the value of the coefficient is located, at which the necessary values of reliability and performance are achieved during the training of the classifier, as well as the adaptation of the system parameters using the Shannon entropy formula.
When training the classifier, the class of separating surfaces is set after the formation of the training sample of parameters. After that the following functional is formulated—, with —the method of searching the extremum of this functional has to be selected. For this purpose, authors chose the WT-based method, employing the WT property as equal to zero at the optimum point [32]. The WT has this property if real wavelets are used as base ones in the form of odd symmetric functions that have compact or efficient support. At the same time, the WT enables us to search efficiently for the extremum of objective functions for the “ravine” type, and it has high noise immunity (compared to the differentiation operation). The Haar wavelet function is also characterized by low computational complexity. The impulse response of the Haar wavelet function (WF) is shown in Figure 1a. The illustration of the estimation of the trend towards an extremum is given in Figure 1b.
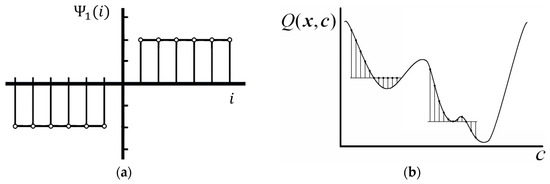
Figure 1.
Features of the search for WT-based extremum: WF Haar impulse response (a)’ fragment of the objective function (b).
At the stage of classification with training, the coefficients of the ranges of the separating surfaces between classes are determined using Haar WT:
where is the functional that depends on the vector of coefficients for separating surfaces and measurement data ; is the step; is the iteration number (order); and is the start number. In (1),
determines the direction of movement to the extremum, where
In (3), is the carrier length of WF at -th start; is the sampling interval; is that Haar WF at -th start; is the dimension of the parameter vector.
According to (1), the iterative scheme is similar to the iterative scheme for finding a first-order optimum. In the last one, the direction of movement to an extremum is determined using a finite-difference estimate of the derivative (Figure 2a,b).
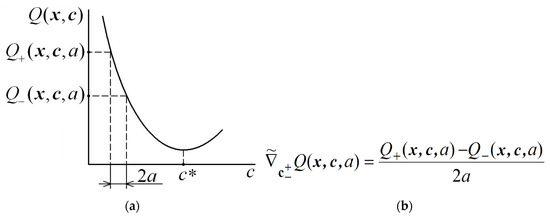
Figure 2.
Specific features of extremum search with gradient estimation: fragment of objective function (a); gradient estimation (b).
To estimate the direction of search for the optimum in (2), the symmetric and nonstationary Haar WF were selected (see Figure 1). This enables us to use the integral character of WT, as well as to identify the segment of the objective function where the global extremum is located. Changing the WF carrier length in the subsequent steps of the search allows us to reduce the error of extremum determination inside the segment of the objective function found in the previous steps (to narrow the interval).
Determination of the variation range of the separating surfaces coefficients is based on Haar WT optimization with initial data: —start error; —error of coefficient value; —error in determining the coefficient range.
Step 1. Setting: —initial approximation to the optimum coordinate; —step; —WF sampling step; —WF carrier length of the first start ; —the step of changing the length of in determining the value ranges of coefficients (in this article = 1); start number ; iteration number ;
Step 2. According to (2), the direction of search is estimated for the start . At , for this, a weighted sum with WF is used. The carrier length for WF is determined by analyzing the objective. The integral character of such WT enables us to reduce the sensitivity to local extrema and allocate a segment of the objective function and determine the range of change for its coordinates with a low error;
At this step, the sign of the estimate by (3) is checked. If the sign changes, then a number of nested ranges for extremum coordinate changes are determined. The maximum range is determined at the start— c —by the length of the WF carrier for the first start, , in the subsequent processing steps with the WF carrier length, which varies as ;
Step 3. The range of the coefficient value is searched using (1);
Step 4. If the condition is satisfied at the iteration : , then the search at the current start ends, otherwise— and go to step 2;
Step 5. If and the coefficient value found at the -th step differs from the result of the start by no more than , then the algorithm is ended. In the opposite case (or ), the start number is increased . In particular, having , the WF is represented by , and at , the search direction is evaluated by discrete differentiation (see Figure 1) and the jump to Step 2 is performed.
When the sign changes, a number of nested ranges of extremum coordinate changes are defined. In classification, these are the ranges of coefficient values for the segments separating the classes in the feature space. The maximum range is defined with the maximum length of the WF carrier; the other ranges are defined with increasingly shorter lengths of the WF carrier.
3. Case Study
The effect of the interval width changing for the coefficient of the separating surface on the relative value of the average risk was investigated. The sample was synthesized artificially to study the capabilities of the method for the simplest case: linearly separable classes.
The authors illustrate the classification method using the example of separating objects in the feature space into two classes for clarity. The article considers a rather simple case: the division by a straight-line segment, when only two coefficients are calculated. According to this, the research was conducted with variance in two classes of 70 objects-values of parameters (features) per each, separated into the two-dimensional feature space by the segment .
Such a situation can occur when the dispersion of classes in the operating mode increases due to changes in operating conditions. A similar result can be obtained if the classifier is trained based on a small sample of data.
The article investigates a method that allows us to determine a set of nested ranges for coefficient values. In this case, the classes of patterns in the feature space can be divided not by a segment, but by a “range”. Next, the situation is investigated when classes of patterns become less compact in the working mode of classification due to an increase of dispersion. If the pattern comes into the range, it is difficult to determine which class it belongs to. The classification error is also registered when the pattern belongs to the wrong class. Thus, the influence of the “range” width and variance on the classification result is evaluated.
Figure 3 shows the result of division in the two-dimensional space of the parameter features, X1, X2 by three intervals: 1, 2, 3. The result was obtained by studying the influence of changing —relative mean-square deviation (RMSD)—in the working mode of classification.
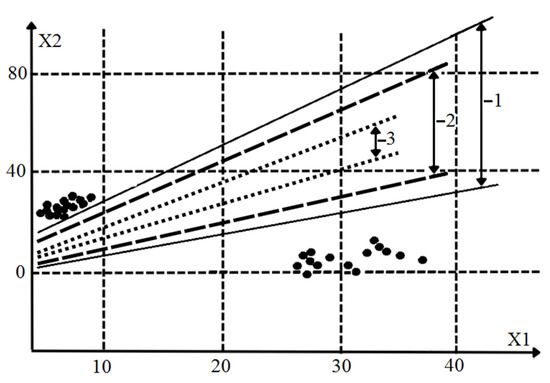
Figure 3.
The result of separating the two classes by three intervals: having a first interval (1); the second interval (2); and the third one (3).
Here, , where and are the RMSDs in classes in working mode and “teaching” mode, respectively; is the distance between the centers of the classes for the training sample; , where represents a width of coefficient interval ; , where is a probability of wrong classification and is a probability of hitting the interval correspondingly.
Based on the research results, it can be concluded that with the relative interval width and (Table 1, column 2), the amount of the relative value of the average risk is practically equal to one. That is, for further research, and the choice of system parameters for a given increase of noise in the data, an interval of this width can be selected without loss of reliability.

Table 1.
Dependence of the relative average risk on for different RMSDs of parameters in the classes in the classification working mode.
To estimate the time consumption depending on classification error and speed, the authors conducted a second series of experiments. Here, the time for determining the ranges for coefficients was validated experimentally using the example of two classes for 15 values of parameter features per each class. When classifying, the search for the minimum of the functional was performed. The functional in this case is the probability of the incorrect classification over the vector of coefficients . The probability of incorrect classification was estimated as the ratio of the number of incorrectly recognized objects to the total number of objects in the sample. The classes were divided in a two-dimensional feature space by the segment . When calculating for given values of error and the training step , one range for and two ranges for were obtained. The time (by timer) when determining the range for the coefficients and was, respectively, 0.08 s and 0.1 s.
The step was selected for the further research. During calculation, the one range for the class and seven nested ranges for the class are obtained. Figure 3 shows the result of separating these two classes with the help of at (a line 1 in Figure 3), (a line 2 in Figure 3), and (a line 3 in Figure 3). Range detection time for was 0.23 s, and for was 13.1 s.
Based on results above, we may conclude firstly that reducing the parameter γ enables us to determine a greater number of ranges. At the same time, time costs can increase by more than two orders of magnitude. However, obtaining a set of ranges when debugging the classification method allows us to evaluate the relationship between the parameter γ, the error δ1, and the classification performance.
Secondly, we may conclude that the time for determining the set of nested ranges for coefficients depends on the variance in the training sample at the training mode and the variance in the working mode of classification. Moreover, for the widest range, it can be less by several times than for subsequent ranges.
To evaluate the classifier parameters in terms of pragmatic sufficiency, we propose to carry out the definition of the classification efficiency indicator based on the statistical approach using the Shannon entropy formula for measuring the information content. For this purpose, the following designations were employed:
—the priori probability distribution for occurrence of a class of objects;
—the probability distribution of deciding whether objects belong to the appropriate class;
—the conditional probability distribution for occurrence of the object under the condition that the classifier makes a decision .
Then, the information measure [33]:
Usage of (4) is complicated by the difficulty of calculating the conditional probabilities . Therefore, the symmetry property of information measure is employed for calculations . The probability distributions can be found using the matrix data:
Since the priori probabilities are unknown, we assume . For an ideal classifier, the maximum possible amount of information , and for arbitrary ,
To compare different classification procedures, we introduce an indicator of classification efficiency:
Then, we estimated the indicator for two classes with 15 parameter features each. Those two classes were separated using at and the «exact» value of , determined with an error of 0.001.
Note that in determining the parameters (6), the following probabilities were calculated: —the probability of correctly classifying an object into class 1; —the probability of correctly classifying an object into class 2; —the probability of correctly classifying an object of class 1 into class 2; —the probability of correctly classifying an object of class 2 into class 1. Some of the objects fall into the “range” because of increasing variance in the classes. As the result, the informativity of indicator decreases.
The results of the investigation are represented in Table 2.

Table 2.
Assessment of classification.
The “widest” range of coefficient values was selected for the investigation. However, as can be seen from Table 2, changes of indicator are considerably close. Therefore, if requirements to the system performance are high, then classification in the above example can be made by choosing the coefficient value from the range in order to increase the procedure productivity.
For example, when adapting existing IT to new application tasks in a system for visual information processing, it is often necessary to carry out an identification procedure (determination of parameter features). This procedure may require reducing the dimensionality of the feature space. In such a reduction, the classification is performed repeatedly, increasing the set of features consistently in order to ensure the required reliability. To improve the performance of the initial and intermediate stages of classification and enhance the visualization of the result, we can recommend using classification based on the Haar WT with the definition of the classification efficiency indicator .
4. Discussion
This article is a significant extension of [30] with further details regarding classification by training and determining a set of nested coefficient value ranges for separating surfaces with a reduced number of coefficient ranges using the Haar WT only. Moreover, by choosing the search parameters—error = 0.1 and interval = 0.7—one range is obtained for and two ranges for . This reduced the time taken determining the coefficient ranges and as 0.08 s and 0.1 s, respectively.
Thus, the proposed method enables us to increase the performance of determining sets of coefficient value intervals during the training of the classifier, which is verified by the results of experimental investigations.
In addition, the authors proposed the use of the Shannon entropy estimates to increase the performance of the procedure for reducing the feature space for identification. Moreover, the evaluation of intermediate classification results is simplified by visualizing the dependence of informativeness and avoiding the estimates of systems efficiency in the multidimensional space [11,12,13].
Summarizing, the main advantage of the proposed method over that proposed in [28] is the defining of the set of intervals where the value of coefficients is located, which are separating the classes of surfaces with the higher performance. At the same time, we note that the performance in the applied task depends on the size of the training sample and the location, which, along with the compactness of data clusters in the feature space, determine the form of the objective function.
In addition, the number of intervals (and the performance, respectively) is related to the choice of error and interval . However, this kind of research is usually carried out when selecting classification methods and/or adapting them to the new application areas.
The authors plan to expand the application area of the proposed method for the analysis and processing of non-stationary periodic biomedical signals, such as electrocardiogram signals [34], because the methods selected for classification in this application area have high requirements for both noise immunity and efficiency, as well as operational efficiency.
5. Conclusions
The authors proposed an improved method of classification by training and determining the set of the nested coefficient value ranges for separating surfaces using the Haar WT with the reduced number of coefficient ranges and superior performance. To estimate the informativeness, the performance, average classification risk, and Shannon entropy were evaluated.
It was experimentally proven that when dividing the training sample into two classes, the time for determining one range was reduced to 0.1 s, which is more than two times faster than in existing methods.
In addition, the results of the study confirmed that the time spent determining the entire set of nested ranges of coefficients depends on the ratio of the variance in the data sample for the training mode and the variance in the working mode of classification. Thus, for the widest range, it can be several times less than for subsequent ranges.
It is shown that the values of the efficiency indicator for the classification procedure for the test sample differ by units of percent when it is investigated using the informativeness estimation. Therefore, if the requirements to the performance of the system for visual information processing are high, the classification can be run by choosing the value of the coefficient from the range based on pragmatic considerations.
Thus, the proposed method, firstly, can be applied to select the parameters of the classifier at the debugging stage, taking into account the required level of reliability and informativeness. Secondly, it can be recommended for use in a wide range of applied systems for visual information processing.
Moreover, wavelet transform methods are one of the promising approaches to analyzing signals containing areas of non-stationarity and intervals of either slowly changing or jumping changes or high-frequency pulsations. Therefore, the proposed method can find wide application in the processing of medical signals and images, in the non-destructive control and monitoring of vibrodiagnostics of machines and equipment, and in steganographic systems of data transmission and protection. It can also be applied in many areas of physics, including molecular dynamics, astrophysics, seismic geophysics, optics, and quantum mechanics.
As a direction for further applied research, we expect future researchers to employ the proposed wavelet method of effective surface separation for the optimal selection of training samples when using machine-learning methods to increase the accuracy and speed of processing and classifying large streams of data (images) during the real-time analysis of physical processes.
Author Contributions
Conceptualization, G.S.; methodology, G.S. and A.S.; software, G.S. and N.V.; validation, G.S. and N.V.; formal analysis, A.S. and B.R.; investigation, G.S. and N.V.; writing—original draft preparation, G.S.; writing—review and editing, W.H., G.S., A.S., L.Y., B.R. and A.M.; visualization, G.S. and N.V.; supervision, A.S.; project administration, A.S.; funding acquisition, all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant No. 61772180, the Key R & D plan of Hubei Province (2020BHB004, 2020BAB012).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaur, S.; Singla, J.; Nkenyereye, L.; Jha, S.; Prashar, D.; Joshi, G.P.; El-Sappagh, S.; Islam, M.D.S.; Islam, S.M.R. Medical diagnostic systems using artificial intelligence (AI) algorithms: Principles and perspectives. IEEE Access 2020, 8, 228049–228069. [Google Scholar] [CrossRef]
- Rzecki, K. Classification algorithm for person identification and gesture recognition based on hand gestures with small training sets. Sensors 2020, 20, 7279. [Google Scholar] [CrossRef]
- Chemerys, O.; Bushma, O.; Lytvyn, O.; Belotserkovsky, A.; Belotserkovsky, P. Network of Autonomous Units for the Complex Technological Objects Reliable Monitoring. In Reliability Engineering and Computational Intelligence; Springer: Cham, Switzerland, 2021; Volume 976, pp. 261–274. [Google Scholar] [CrossRef]
- Yuan, C.; Liu, Z.; Zhang, Y. Aerial images-based forest fire detection for firefighting using optical remote sensing techniques and unmanned aerial vehicles. J. Intell. Robot. Syst. 2017, 88, 635–654. [Google Scholar] [CrossRef]
- Zhao, W.; Gurudu, S.; Taheri, S.; Ghosh, S.; Sathiaseelan, M.A.; Asadizanjani, N. PCB component detection using computer vision for hardware assurance. Big Data Cogn. Comput. 2022, 6, 39. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: New York, NY, USA, 2018; p. 1168. [Google Scholar]
- Bhatia, S.; Sharma, M.; Bhatia, K.K.; Das, P. Opinion target extraction with sentiment analysis. Int. J. Comput. 2018, 17, 136–142. [Google Scholar] [CrossRef]
- Frid-Adar, M.; Diamant, I.; Klang, E.; Amitai, M.; Goldberger, J.; Greenspan, H. GAN-based synthetic medical image augmentation for increased CNN performance in liver lesion classification. Neurocomputing 2018, 321, 321–331. [Google Scholar] [CrossRef]
- Bayer, M.; Kaufhold, M.A.; Reuter, C. A survey on data augmentation for text classification. ACM Comput. Surv. 2023, 55, 1–39. [Google Scholar] [CrossRef]
- Li, B.; Ong, Y.S.; Le, M.N.; Goh, C.K. Memetic Gradient Search. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, 1–6 June 2008. [Google Scholar] [CrossRef]
- Stawowy, M.; Duer, S.; Paś, J.; Wawrzyński, W. Determining information quality in ICT systems. Energies 2021, 14, 5549. [Google Scholar] [CrossRef]
- Firmani, D.; Mecella, M.; Scannapieco, M.; Batini, C. On the meaningfulness of “big data” quality. Data Sci. Eng. 2016, 1, 6–20. [Google Scholar] [CrossRef]
- Laranjeiro, N.; Soydemir, S.N.; Bernardino, J. A Survey on Data Quality: Classifying Poor Data. In Proceedings of the 2015 IEEE 21st Pacific Rim International Symposium on Dependable Computing (PRDC), Zhangjiajie, China, 18–20 November 2015. [Google Scholar] [CrossRef]
- Bychkova, S.M.; Makarova, N.N.; Zhidkova, E.A. Measurement of information in the subsystem of internal control of the controlling system of organizations of the agro-industrial complex. Enterp. Sustain. 2018, 6, 35–43. [Google Scholar] [CrossRef]
- Ceballos, B.; Lamata, M.T.; Pelta, D.A. A comparative analysis of multi-criteria decision-making methods. Prog. Artif. Intell. 2016, 5, 315–322. [Google Scholar] [CrossRef]
- Smedberg, H.; Barrera-Diaz, C.A.; Nourmohammadi, A.; Bandaru, S.; Ng, A.H. Knowledge-Driven Multi-Objective Optimization for Reconfigurable Manufacturing Systems. Math. Comput. Appl. 2022, 27, 106. [Google Scholar] [CrossRef]
- Wątróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Zioło, M. Generalised framework for multi-criteria method selection. Omega 2019, 86, 107–124. [Google Scholar] [CrossRef]
- Herzel, A.; Ruzika, S.; Thielen, C. Approximation Methods for Multiobjective Optimization Problems: A Survey. Inf. J. Comput. 2021, 33, 1284–1299. [Google Scholar] [CrossRef]
- Kondruk, N.; Malyar, M. Dimensionality Reduction of the Criterion Space in Some Optimization Problems. In Proceedings of the II International Scientific Symposium “Intelligent Solutions” (IntSol-2021), Kyiv/Uzhhorod, Ukraine, 28–30 September 2021; Available online: http://surl.li/gpjro (accessed on 17 December 2022).
- Ribeiro, R.; Romão, E.L.; Luz, E.; Gomes, J.H.; Costa, S. Optimization of the resistance spot welding process of 22MnB5-galvannealed steel using response surface methodology and global criterion method based on principal components analysis. Metals 2020, 10, 1338. [Google Scholar] [CrossRef]
- Kasimbeyli, R.; Ozturk, Z.K.; Kasimbeyli, N.; Yalcin, G.D.; Erdem, B.I. Comparison of some scalarization methods in multiobjective optimization: Comparison of scalarization methods. Bull. Malays. Math. Sci. Soc. 2019, 42, 1875–1905. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Sys. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Qian, K.; Tian, L.; Liu, Y.; Wen, X.; Bao, J. Image robust recognition based on feature-entropy-oriented differential fusion capsule network. Appl. Intell. 2021, 51, 1108–1117. [Google Scholar] [CrossRef]
- Altameemi, H.G.A.; Alani, A.A.; Asmael, A.A.A.; Al-Obaidi, M.A.A. Competent Hybrid Digital Image Watermarking Technique Based on Daubechies Wavelet and Block Bitmap Modification. Int. J. Comput. 2022, 21, 303–310. [Google Scholar] [CrossRef]
- Hyde, R.; Hossaini, R.; Leeson, A.A. Cluster-based analysis of multi-model climate ensembles. Geosci. Model Dev. 2018, 11, 2033–2048. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Cantwell, G.T.; Young, J.G. Improved mutual information measure for clustering, classification, and community detection. Phys. Rev. E 2020, 101, 042304. [Google Scholar] [CrossRef] [PubMed]
- Orenes, Y.; Rabasa, A.; Rodriguez-Sala, J.J.; Sanchez-Soriano, J. Benchmarking Analysis of the Accuracy of Classification Methods Related to Entropy. Entropy 2021, 23, 850. [Google Scholar] [CrossRef]
- Aggrawal, C.C. Data Classification. In Data Mining; Springer: Cham, Switzerland, 2015; pp. 285–344. [Google Scholar] [CrossRef]
- Paliy, I.; Sachenko, A.; Koval, V.; Kurylyak, Y. Approach to Face Recognition Using Neural Networks. In Proceedings of the 2005 IEEE Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, Sofia, Bulgaria, 5–7 September 2005. [Google Scholar] [CrossRef]
- Babilunga, O.; Krylov, V.; Shcherbakova, G. Method of classification with training on the wavelet transformation base. Electrotech. Comput. Syst. 2015, 19, 231–234. Available online: http://dspace.opu.ua/jspui/bitstream/123456789/1344/1/231-234.pdf (accessed on 17 December 2022). [CrossRef]
- Shcherbakova, G.; Krylov, V.; Abakumov, V.; Brovkov, V.; Kozina, Y. Sub Gradient Iterative Method for Neural Networks Training. In Proceedings of the 6th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems, Prague, Czech Republic, 15–17 September 2011. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Z.; Shi, Z.; Zhang, X.; Liu, C. Application and Optimization of Wavelet Transform Filter for North-Seeking Gyroscope Sensor Exposed to Vibration. Sensors 2019, 19, 3624. [Google Scholar] [CrossRef] [PubMed]
- Anisimov, B.V.; Kurganov, V.D.; Zlobin, V.K. Raspoznavanie I Tsifrovaya Obrabotka Zobrazhenii [The Recognition and the Digital Imaging]; Vysshaya Shkola: Moskow, Russia, 1993; 295p. (In Russian) [Google Scholar]
- Srinivas, M.; Basil, T.; Mohan, C.K. Adaptive learning based heartbeat classification. Bio-Med. Mater. Eng. 2015, 26, 49–55. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).