Soil Deformation Investigation of a Piled-Raft Foundation Pit Under-Crossed by a Super-Large Diameter Shield Tunnel
Abstract
1. Introduction
2. Methods
2.1. Engineering Background
2.2. Establishment of Numerical Model
3. Results
3.1. Model Validation
3.2. Different Grouting Schemes
3.3. Different Backfill Thickness
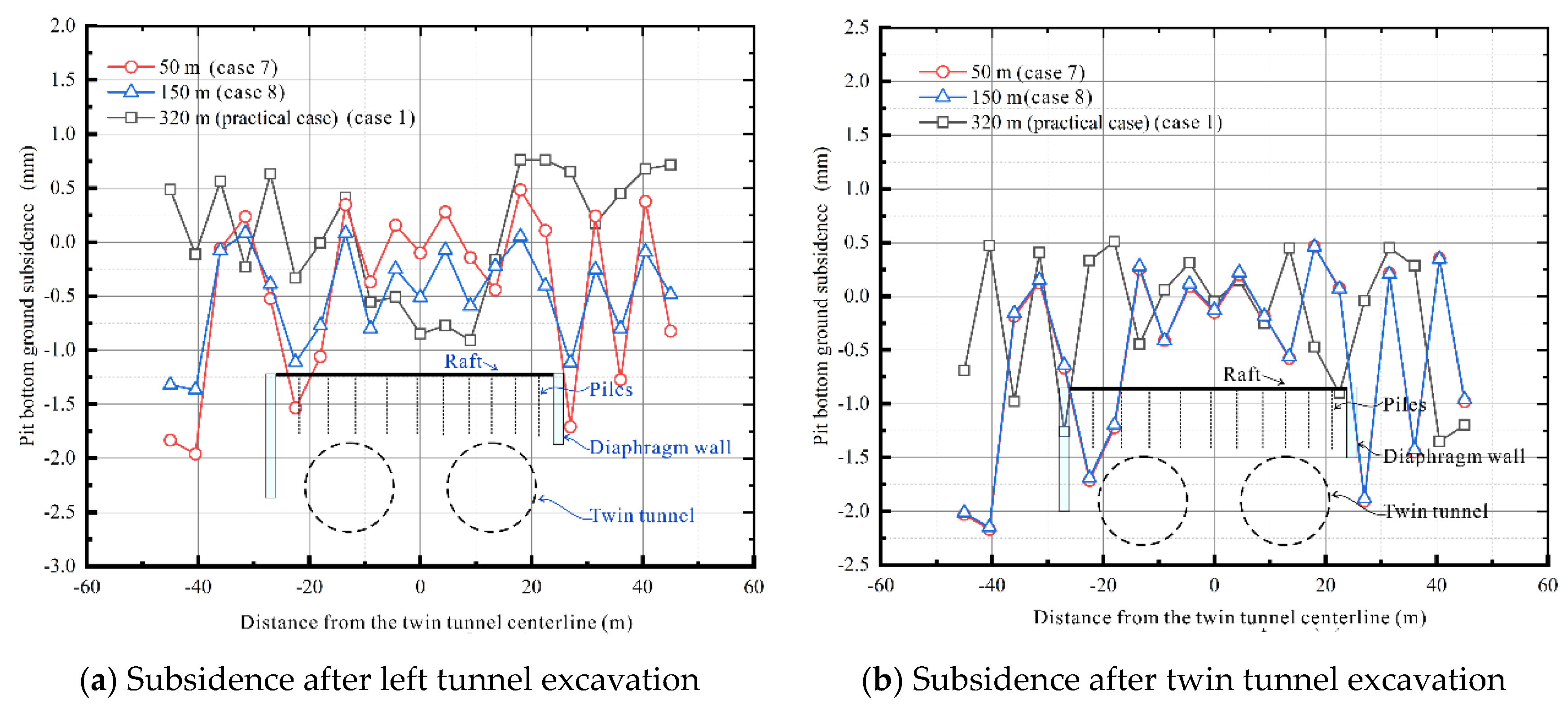
3.4. Different Distance between Shield Machines
4. Discussion
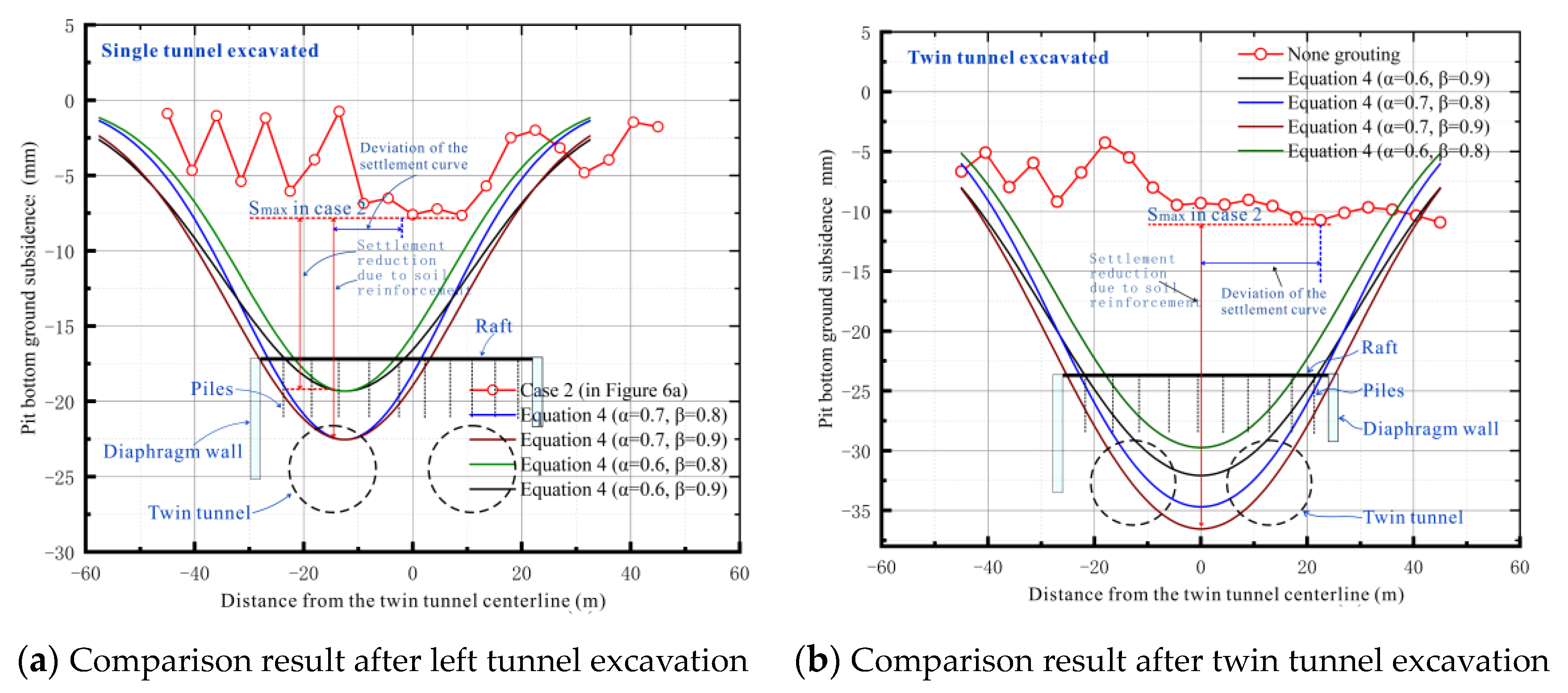
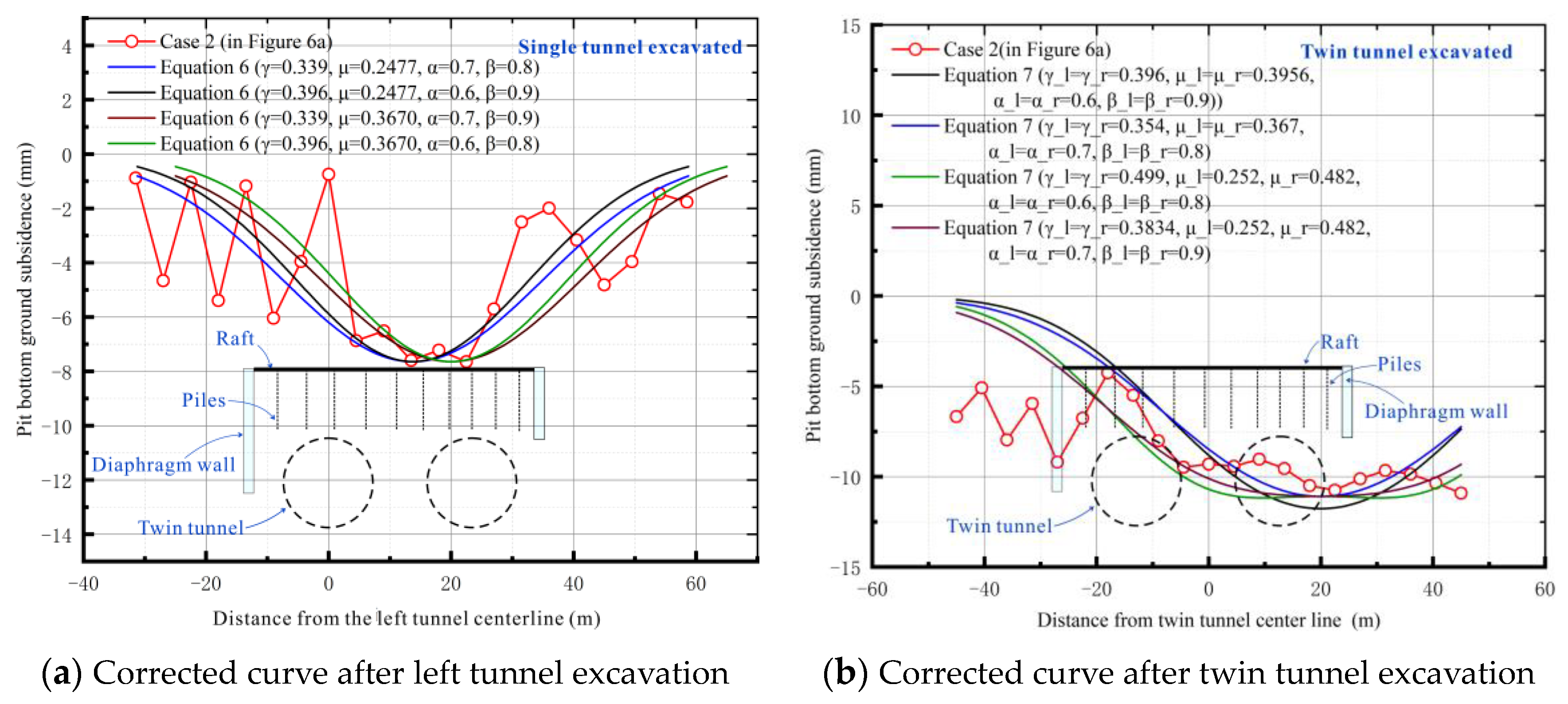
4.1. Influence of Load Characteristics on Settlement Curve
4.2. Limitations and Prospects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kouroussis, G.; Vogiatzis, K.; Kassomenos, P. Special issue on impact on the urban environment and the quality of life from the construction and operation of lrt (light rapid transit) systems preface. Sci. Total Environ. 2016, 568, 1275. [Google Scholar] [CrossRef]
- Cui, X.; Ye, M.; Yan, Z. Performance of a foundation pit supported by bored piles and steel struts: A case study. Soils Found. 2018, 58, 1016–1027. [Google Scholar] [CrossRef]
- Wang, J. Super-large diameter shield tunneling technologies in China in recent decade. Tunn. Constr. 2017, 37, 330. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=JSSD201703014&DbName=CJFQ2017 (accessed on 30 March 2017). (In Chinese).
- Chakeri, H.; Ozcelik, Y.; Unver, B. Effects of important factors on surface settlement prediction for metro tunnel excavated by EPB. Tunn. Undergr. Space Technol. 2013, 36, 14–23. [Google Scholar] [CrossRef]
- Zhu, C. Control of surface settlement by considering shield tunneling technology. KSCE J. Civ. Eng. 2017, 21, 2896–2907. [Google Scholar] [CrossRef]
- Lai, J.; Zhou, H.; Wang, K.e.; Qiu, J.; Wang, L.; Wang, J.; Feng, Z. Shield-driven induced ground surface and Ming Dynasty city wall settlement of Xi’an metro. Tunn. Undergr. Space Technol. 2020, 97, 103220. [Google Scholar] [CrossRef]
- Lin, X.T.; Chen, R.P.; Wu, H.N.; Cheng, H.Z. Deformation behaviors of existing tunnels caused by shield tunneling undercrossing with oblique angle. Tunn. Undergr. Space Technol. 2019, 89, 78–90. [Google Scholar] [CrossRef]
- Ou, C.Y.; Hsieh, P.G.; Chiou, D.C. Characteristics of ground surface settlement during excavation. Can. Geotech. J. 1993, 30, 758–767. [Google Scholar] [CrossRef]
- Song, Z.; Tian, X.; Zhang, Y. A New Modified Peck Formula for Predicting the Surface Settlement Based on Stochastic Medium Theory. Adv. Civ. Eng. 2019, 2019, 7328190. [Google Scholar] [CrossRef]
- Fang, Y.S.; Lin, J.S.; Su, C.S. An estimation of ground settlement due to shield tunnelling by the Peck–Fujita method. Can. Geotech. J. 1994, 31, 431–443. [Google Scholar] [CrossRef]
- Suwansawat, S.; Einstein, H.H. Artificial neural networks for predicting the maximum surface settlement caused by EPB shield tunneling. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2006, 21, 133–150. [Google Scholar] [CrossRef]
- Jallow, A.; Ou, C.Y.; Lim, A. Three-dimensional numerical study of long-term settlement induced in shield tunneling. Tunn. Undergr. Space Technol. 2019, 88, 221–236. [Google Scholar] [CrossRef]
- Jin, D.; Shen, X.; Yuan, D. Theoretical analysis of three-dimensional ground displacements induced by shield tunneling. Appl. Math. Model. 2019, 79, 85–105. [Google Scholar] [CrossRef]
- Fang, K.; Yang, Z.; Jiang, Y.; Sun, Z.; Wang, Z. Surface subsidence characteristics of fully overlapping tunnels constructed using tunnel boring machine in a clay stratum. Comput. Geotech. 2020, 125, 103679. [Google Scholar] [CrossRef]
- Zhang, N.; Zhou, A.; Pan, Y.; Shen, S.-L. Measurement and prediction of tunnelling-induced ground settlement in karst region by using expanding deep learning method. Measurement 2021, 183, 109700. [Google Scholar] [CrossRef]
- Zhang, K.; Lyu, H.-M.; Shen, S.-L.; Zhou, A.; Yin, Z.-Y. Evolutionary hybrid neural network approach to predict shield tunneling-induced ground settlements. Tunn. Undergr. Space Technol. 2020, 106, 103594. [Google Scholar] [CrossRef]
- Shi, J.; Fu, Z.; Guo, W. Investigation of geometric effects on three-dimensional tunnel deformation mechanisms due to basement excavation. Comput. Geotech. 2019, 106, 108–116. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, D.W.; Yang, C.; Zhang, Q.B. Long-term performance of metro tunnels induced by adjacent large deep excavation and protective measures in Nanjing silty clay. Tunn. Undergr. Space Technol. 2020, 95, 103147. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Shi, J.; Mašín, D.; Sun, H.; Lei, G.H. Influence of sand density and retaining wall stiffness on three-dimensional responses of tunnel to basement excavation. Can. Geotech. J. 2015, 52, 1811–1829. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, G.; Jiang, C. The study for longitudinal deformation of adjacent shield tunnel due to foundation pit excavation with consideration of the retaining structure deformation. Symmetry 2020, 12, 2103. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, X.; Chen, Y.; Chen, L. Numerical parametric study of countermeasures to alleviate basement excavation effects on an existing tunnel. Tunn. Undergr. Space Technol. 2018, 72, 145–153. [Google Scholar] [CrossRef]
- Li, M.G.; Chen, J.J.; Wang, J.H.; Zhu, Y.F. Comparative study of construction methods for deep excavations above shield tunnels. Tunn. Undergr. Space Technol. 2018, 71, 329–339. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, G.; Lin, X.; Xia, C.; Wei, X. Transverse Force Analysis of Adjacent Shield Tunnel Caused by Foundation Pit Excavation Considering Deformation of Retaining Structures. Symmetry 2021, 13, 1478. [Google Scholar] [CrossRef]
- Wei, G.; Hu, L.W.; Chen, K.L. Numerical Simulation of Effect of Foundation Pit Excavation on Underlain Shield Tunnel. Appl. Mech. Mater. 2014, 580–583, 1001–1007. [Google Scholar] [CrossRef]
- Qiu, J.; Jiang, J.; Zhou, X.; Zhang, Y.; Pan, Y. Analytical solution for evaluating deformation response of existing metro tunnel due to excavation of adjacent foundation pit. J. Cent. South Univ. 2021, 28, 1888–1900. [Google Scholar] [CrossRef]
- Lu, N.; Kaya, M. Power Law for Elastic Moduli of Unsaturated Soil. J. Geotech. Geoenviron. Eng. 2014, 140, 46–56. [Google Scholar] [CrossRef]
- Oliver-Denzil, S.; Taylor, M.A.; Farshid, V. Statistical distributions of wave velocities and elastic moduli in near-surface unsaturated soils. Soil Dyn. Earthq. Eng. 2022, 157, 107247. [Google Scholar] [CrossRef]
- Ghorbani, J.; Airey, D.W. Modelling stress-induced anisotropy in multi-phase granular soils. Comput. Mech. 2021, 67, 497–521. [Google Scholar] [CrossRef]
- Fang, Y.; Jian, C.; Dariusz, W.; Nikolaos, N.; Ran, Y.; Yi, H. Subsurface Settlements of Shield Tunneling Predicted by 2D and 3D Constitutive Models considering Non-coaxiality and Soil Anisotropy: A Case Study. Can. Geotech. J. 2022, 59, 424–440. [Google Scholar] [CrossRef]
- Gong, X.N. Design Manual for Deep Foundation Pit Construction; China Building Industry Press: Beijing, China, 2017; 134p, ISBN 978-7-112-20808-1. (In Chinese) [Google Scholar]
- Yao, A.; Zhao, Q.; Guan, J.; Liu, F.; Su, N. Improvement of Peck formula based on Beijing underground subway tunnel construction. Chin. J. Undergr. Space Eng. 2010, 6, 789–793. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=BASE201004024&DbName=CJFQ2010 (accessed on 5 May 2023). (In Chinese).
- Wei, G. Prediction of soil settlement caused by double-line parallel shield tunnel construction. Disaster Adv. 2013, 6, 23–27. [Google Scholar]
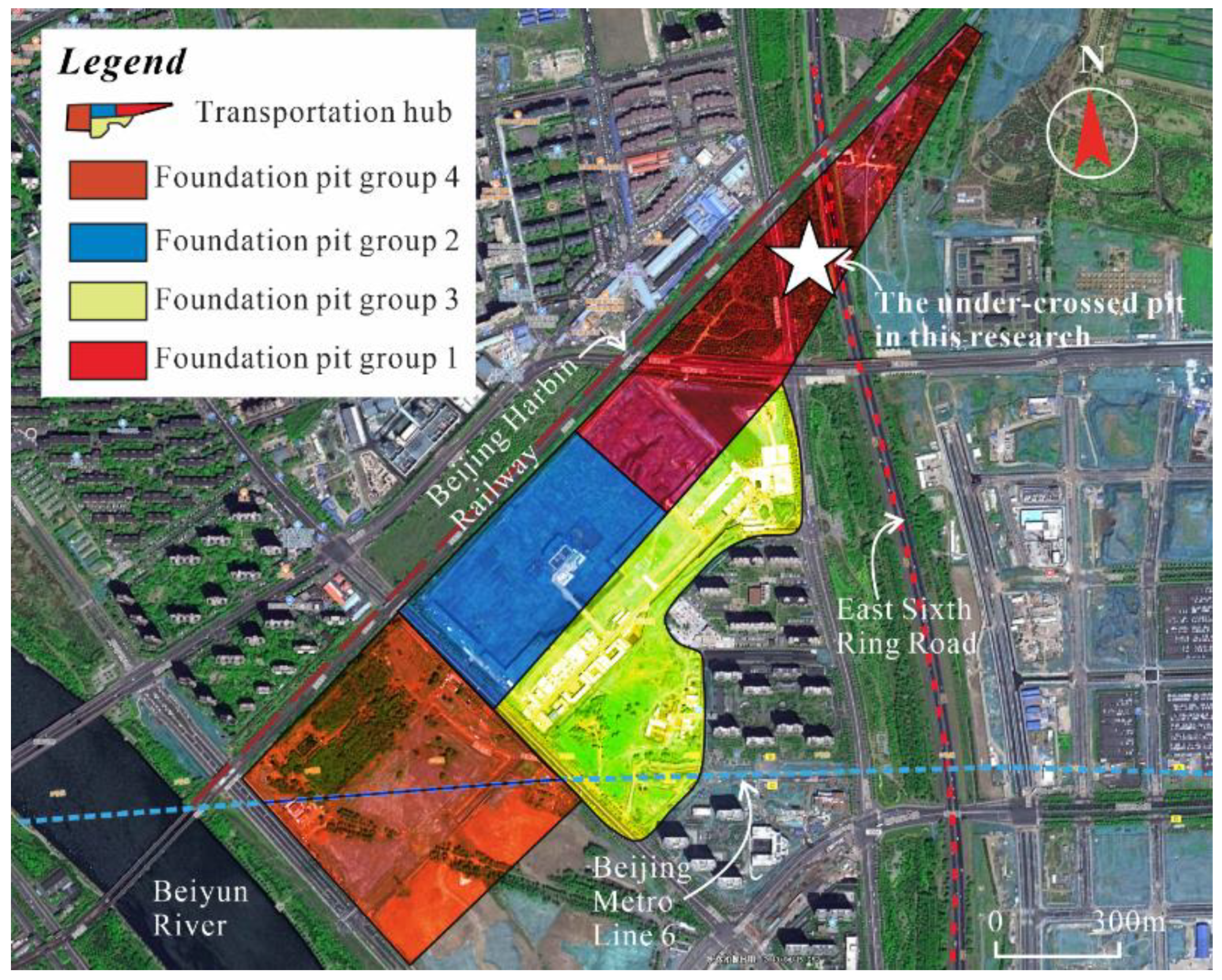


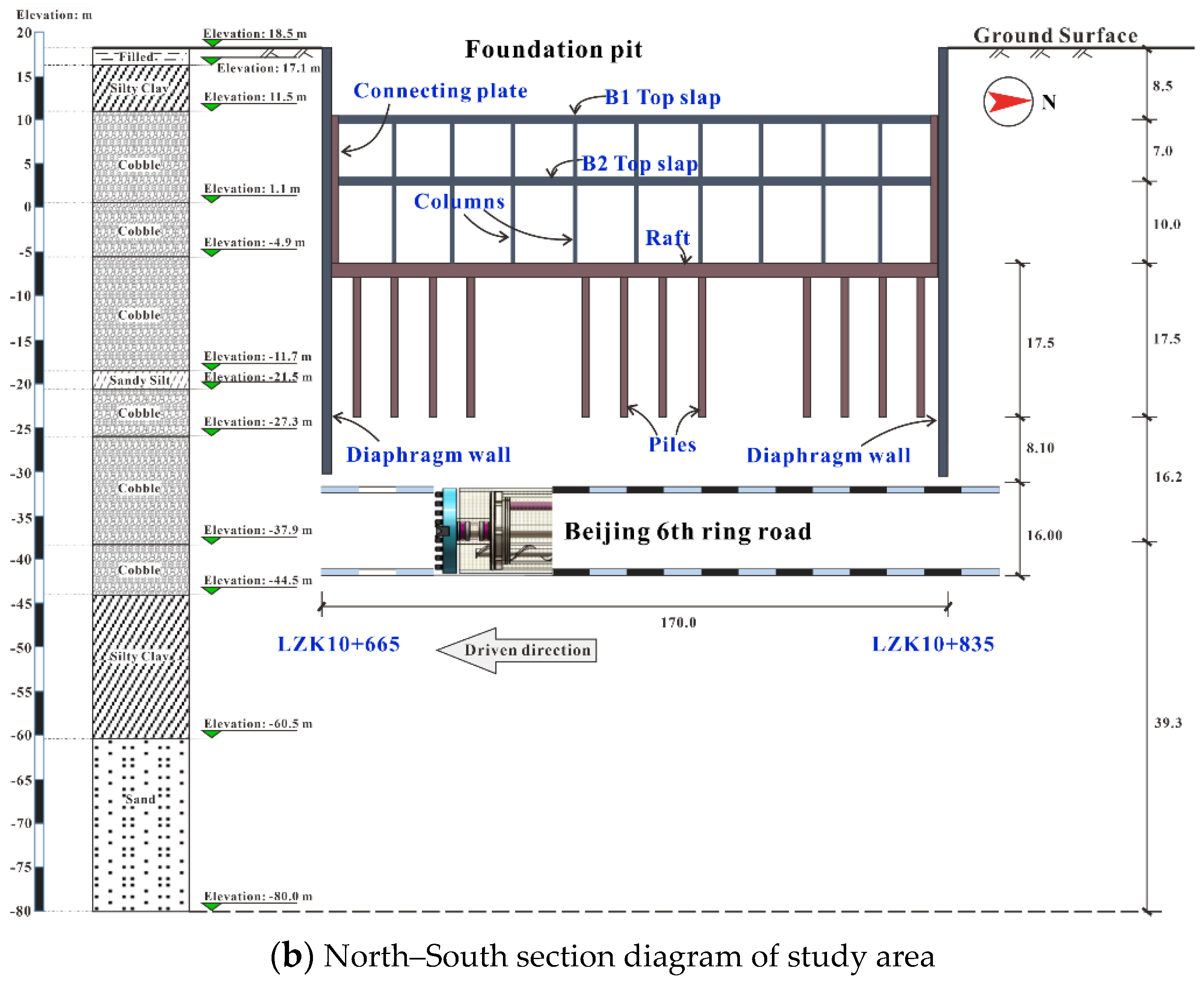
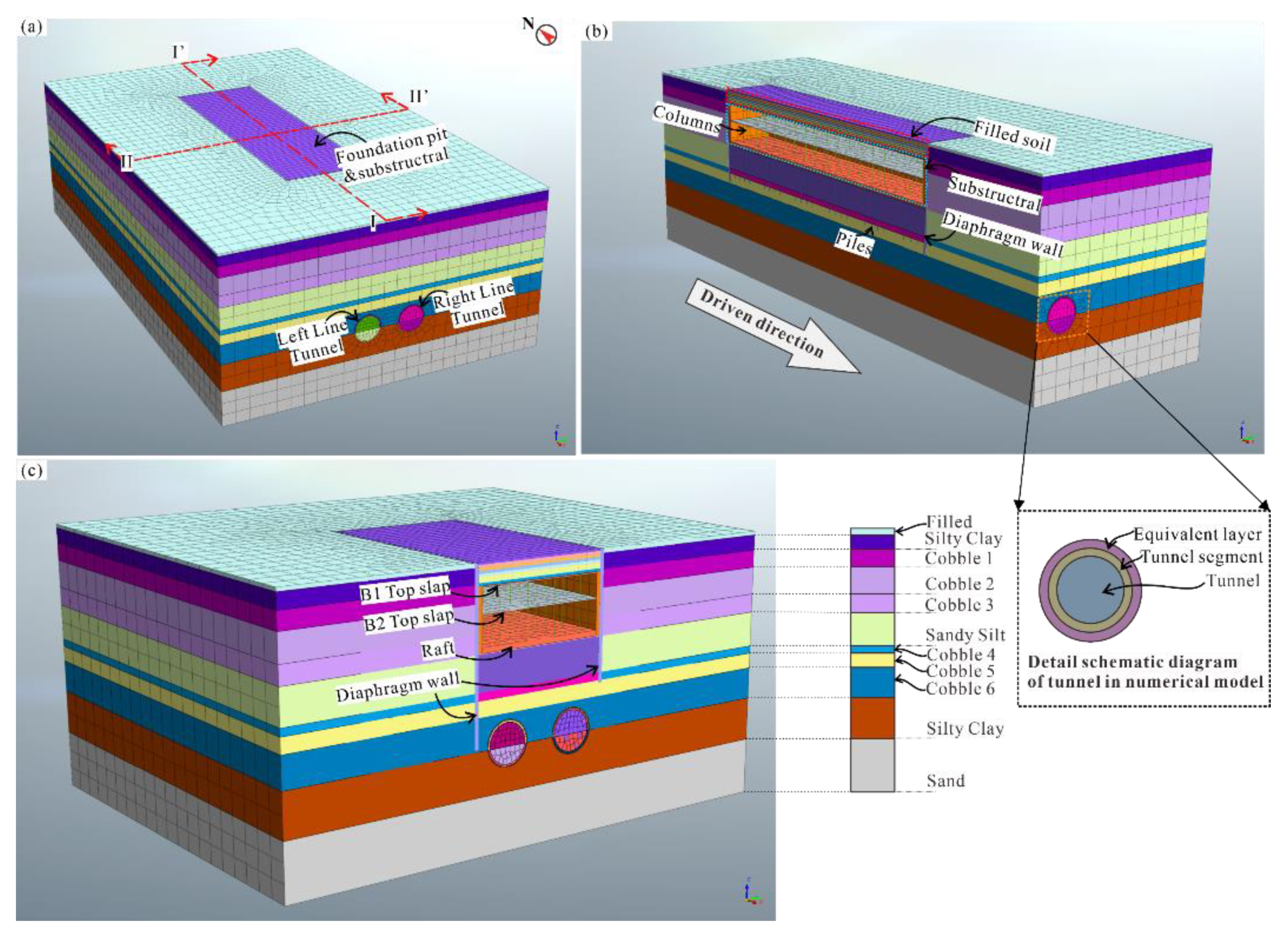


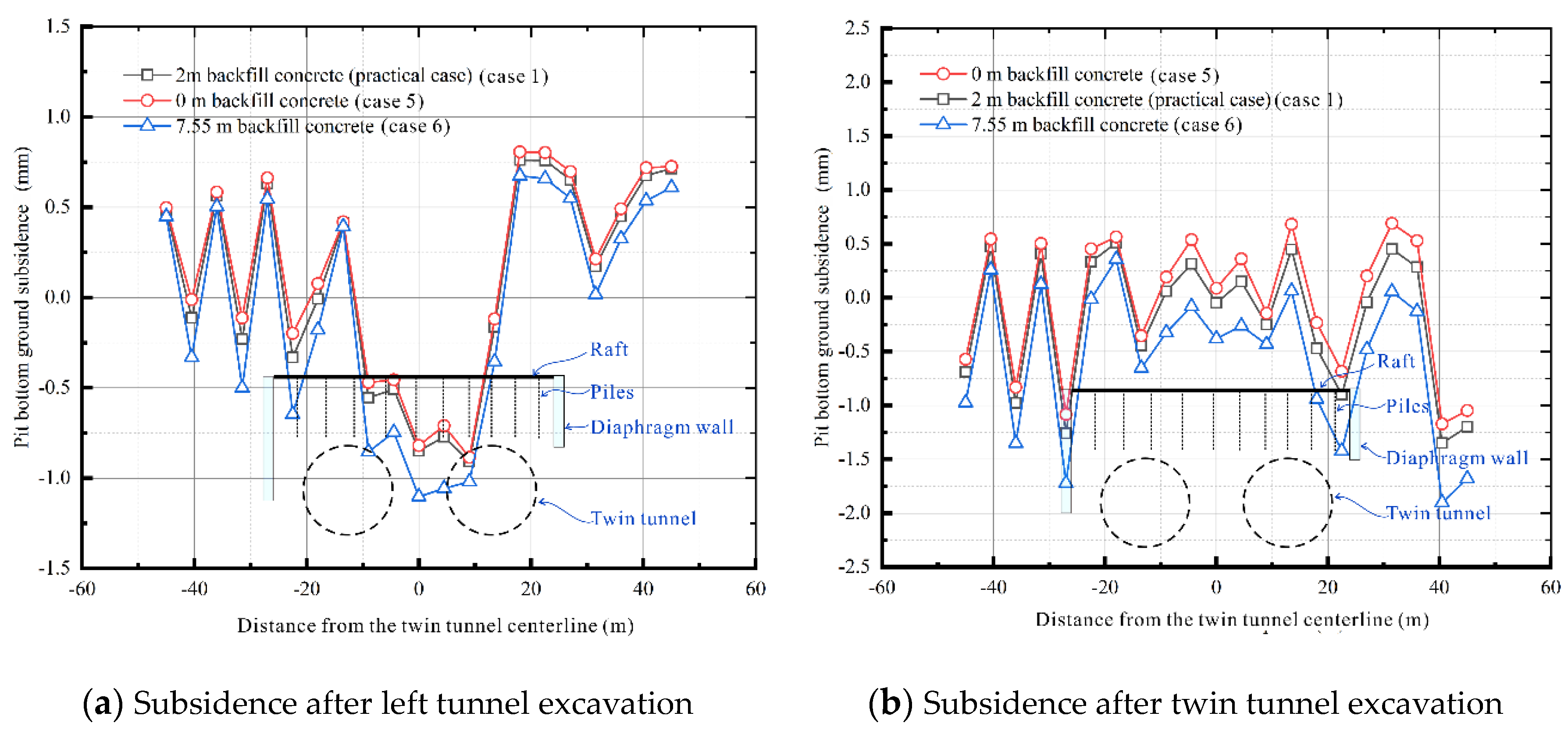

| Soil Layer | Height/m | Specific Weight/(kNꞏm−3) | Poisson Ratio | Elastic Modulus/MPa | Cohesion/kPa | Friction Angel/(°) |
|---|---|---|---|---|---|---|
| Filled | 1.4 | 18.1 | 0.34 | 8.39 | 0 | 10 |
| Silty clay | 5.6 | 18.6 | 0.28 | 23.47 | 18.9 | 22.9 |
| Cobble 1 | 10.4 | 18.6 | 0.28 | 24.94 | 0 | 34.5 |
| Cobble 2 | 6 | 19.9 | 0.28 | 27.25 | 0 | 34.3 |
| Cobble 3 | 13.8 | 19.9 | 0.25 | 40 | 4.5 | 32 |
| Sandy silt | 2.8 | 19.9 | 0.27 | 55 | 0 | 34 |
| Cobble 4 | 5.8 | 19.2 | 0.28 | 55 | 0 | 34 |
| Cobble 5 | 10.6 | 19.9 | 0.25 | 70 | 0 | 35 |
| Cobble 6 | 6.6 | 19.7 | 0.28 | 90 | 0 | 36 |
| Silty clay | 16 | 19.3 | 0.28 | 66.67 | 52.7 | 17.7 |
| Sand | 19.5 | 19.9 | 0.25 | 100 | 0 | 36 |
| Type of Components | Elastic Modulus/MPa | Poisson Ratio | Specific Weight/(kNꞏm−3) |
|---|---|---|---|
| Diaphragm walls | 32,500 | 0.3 | 23.9 |
| Connecting plates | 30,000 | 0.3 | 23.7 |
| Columns | 34,500 | 0.3 | 24.2 |
| Floor slabs | 30,000 | 0.3 | 23.7 |
| Piles | 31,500 | 0.3 | 23.8 |
| Tunnel segments | 36,000 | 0.2 | 24.3 |
| Synchronous grouting slurry | 120 | 0.2 | 24 |
| Back wall grouting layer | 380 | 0.2 | 21 |
| Backfilling lightweight concrete | 20,000 | 0.2 | 13 |
| Construction Methods | Synchronous Grouting | Backwall Grouting | Backfill Thickness | Distance between Shield Machines | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 m | 2 m | 7.55 m | 50 m | 150 m | 320 m | ||||
| Practical case/Case 1 | ◯ | ◯ | ◯ | ◯ | |||||
| Grouting | Case 2 | ◯ | ◯ | ◯ | |||||
| Case 3 | ◯ | ◯ | ◯ | ||||||
| Case 4 | ◯ | ◯ | |||||||
| Backfilled | Case 5 | ◯ | ◯ | ◯ | ◯ | ||||
| Case 6 | ◯ | ◯ | ◯ | ◯ | |||||
| Distance | Case 7 | ◯ | ◯ | ◯ | ◯ | ||||
| Case 8 | ◯ | ◯ | ◯ | ◯ | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Li, Y.; Yao, A.; Gao, X.; Li, H. Soil Deformation Investigation of a Piled-Raft Foundation Pit Under-Crossed by a Super-Large Diameter Shield Tunnel. Appl. Sci. 2023, 13, 5774. https://doi.org/10.3390/app13095774
Jiang Y, Li Y, Yao A, Gao X, Li H. Soil Deformation Investigation of a Piled-Raft Foundation Pit Under-Crossed by a Super-Large Diameter Shield Tunnel. Applied Sciences. 2023; 13(9):5774. https://doi.org/10.3390/app13095774
Chicago/Turabian StyleJiang, Yue, Yanlin Li, Aijun Yao, Xiangzhi Gao, and Hui Li. 2023. "Soil Deformation Investigation of a Piled-Raft Foundation Pit Under-Crossed by a Super-Large Diameter Shield Tunnel" Applied Sciences 13, no. 9: 5774. https://doi.org/10.3390/app13095774
APA StyleJiang, Y., Li, Y., Yao, A., Gao, X., & Li, H. (2023). Soil Deformation Investigation of a Piled-Raft Foundation Pit Under-Crossed by a Super-Large Diameter Shield Tunnel. Applied Sciences, 13(9), 5774. https://doi.org/10.3390/app13095774






