Stability and Distribution of Rock Slope under Asymmetric Excavation
Abstract
1. Introduction
2. Mining Analysis of Fushun West Open Pit
2.1. Distribution of Rock Strata and Structure in Fushun West Open Pit and Its Surrounding Area
2.2. Rock Mechanics Parameters and Slope Stability Analysis Method
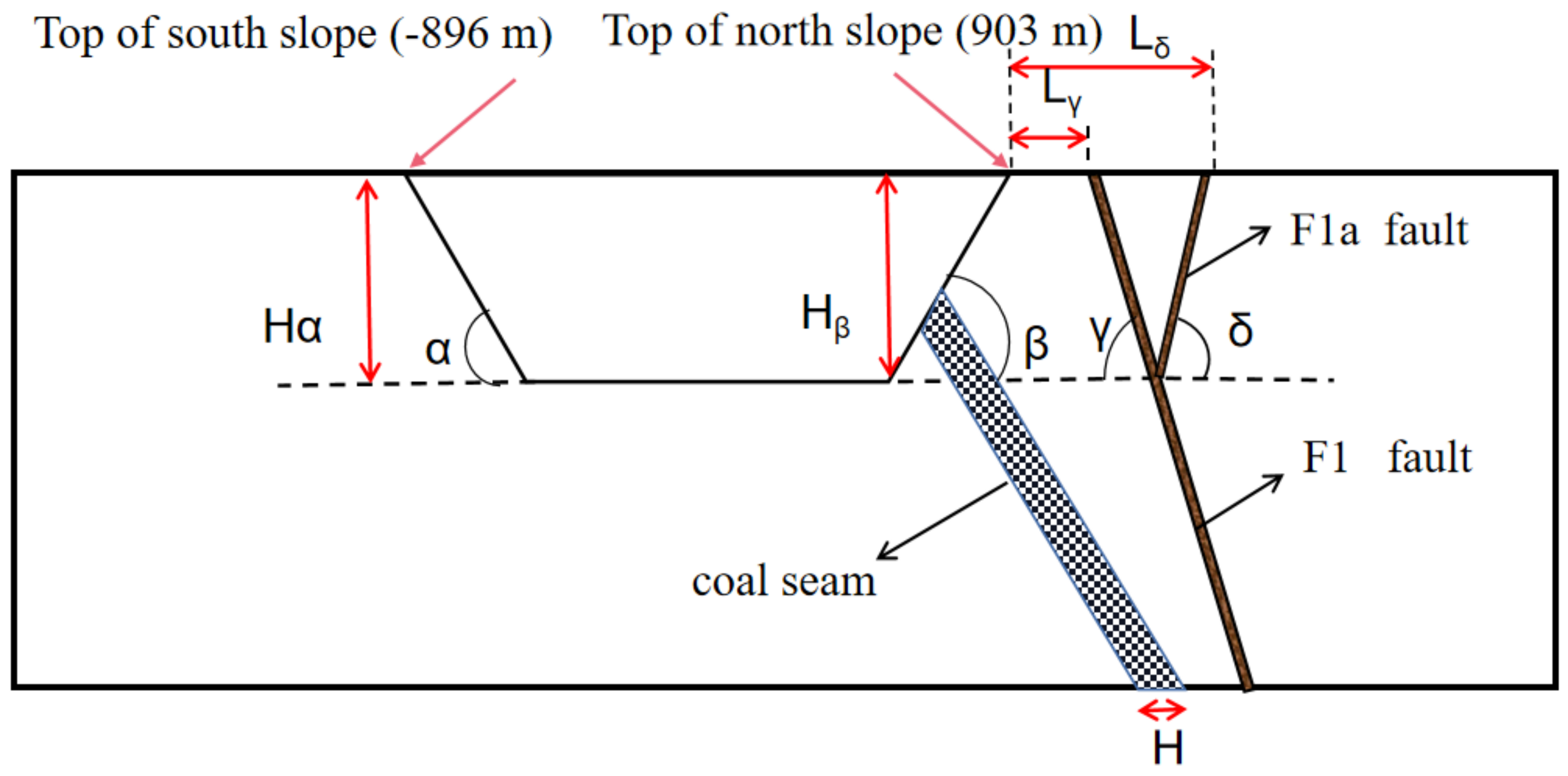
2.3. Asymmetric Excavation and Fault Impact Analysis
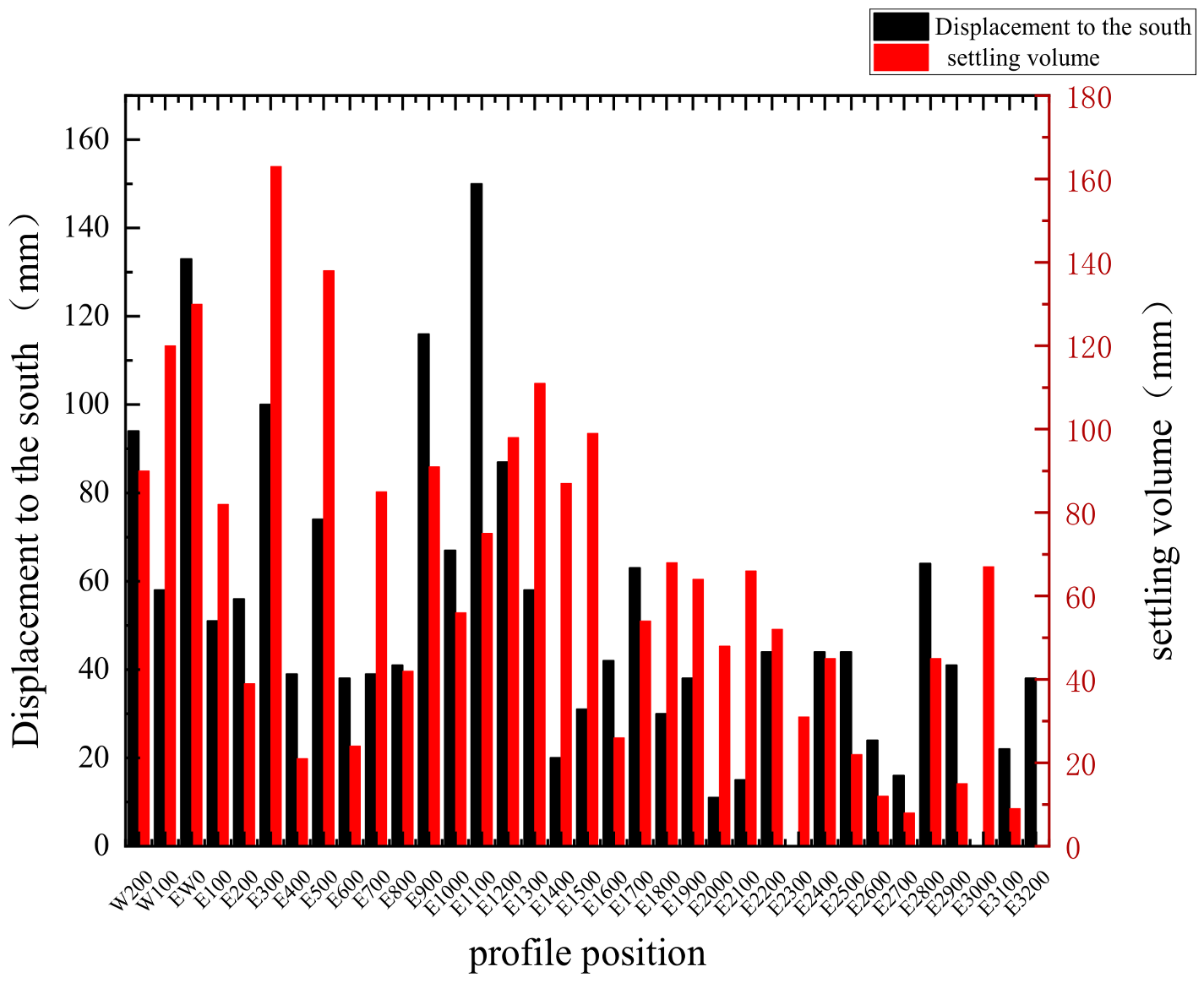
2.4. Division of Slope Influence Zone
3. Study on the Stability of a Rock Slope and Its Influence Area Distribution
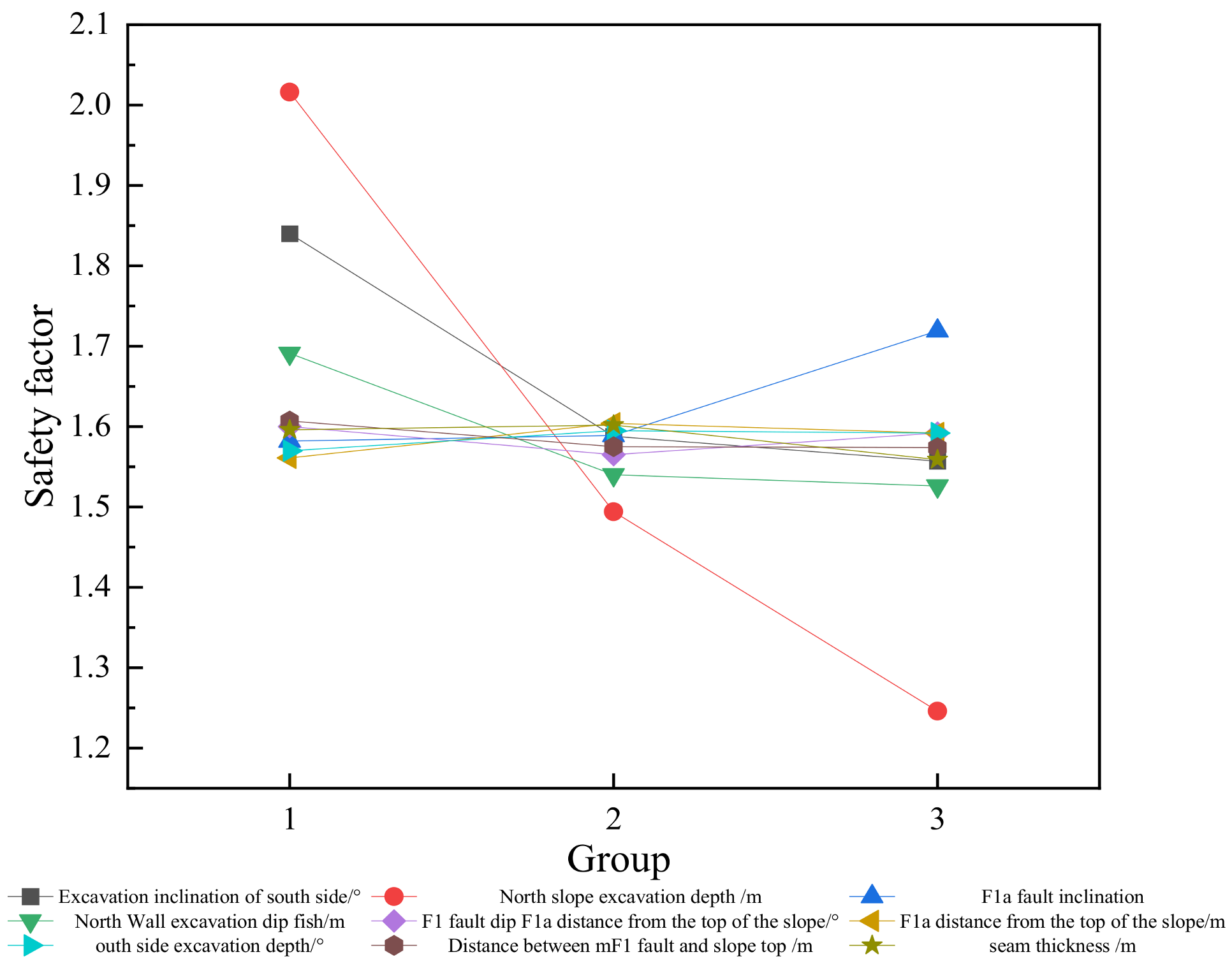
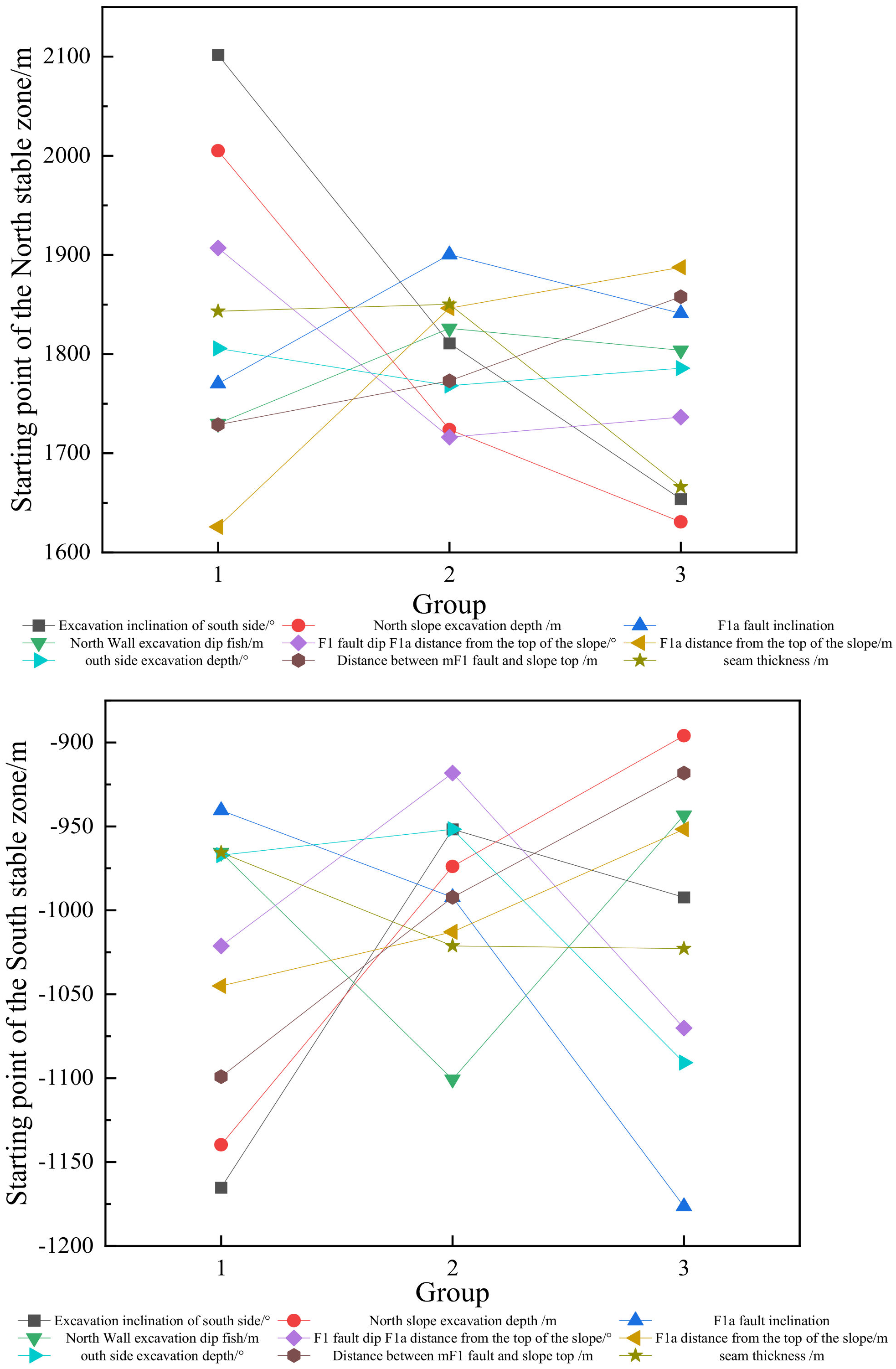
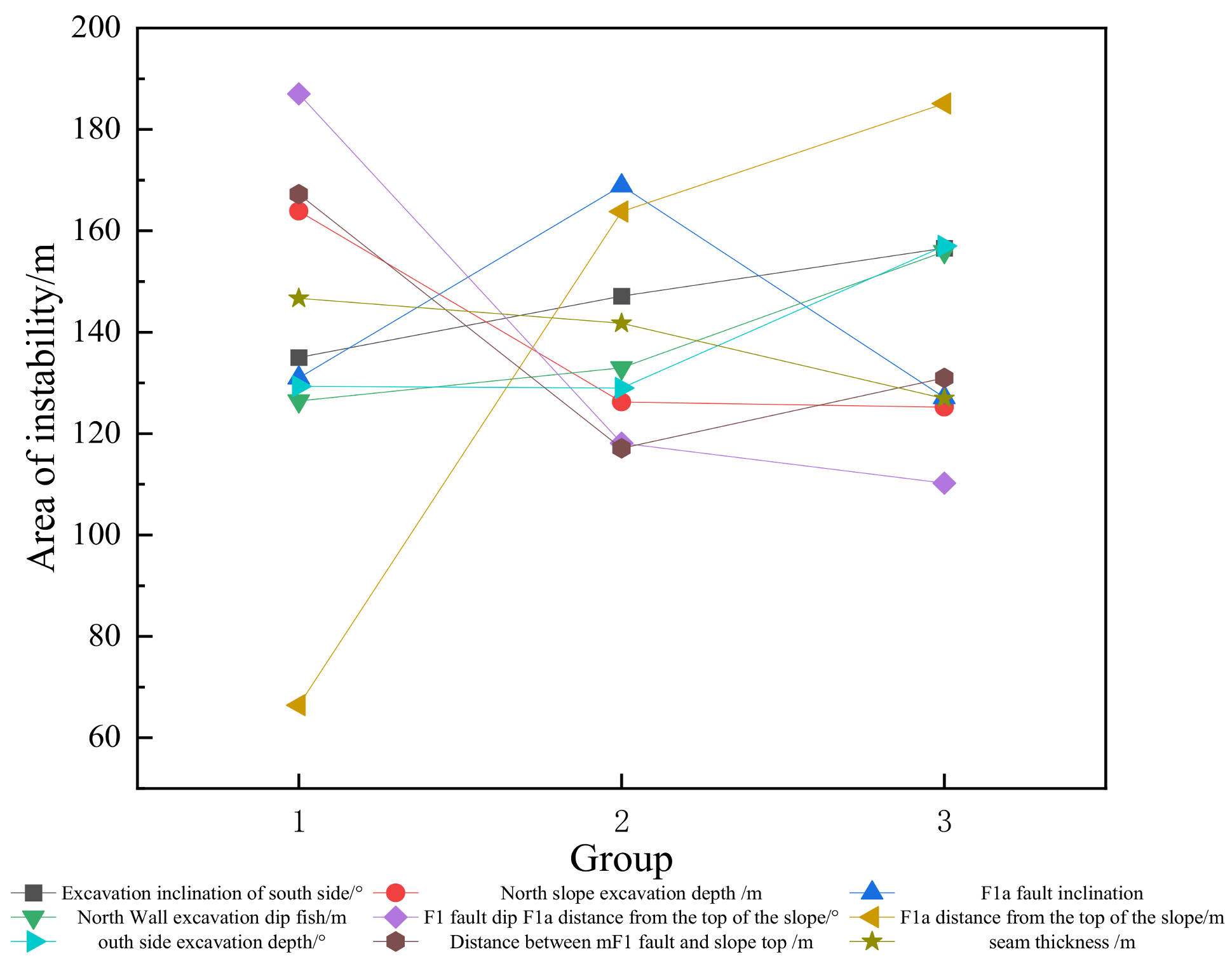
3.1. Scheme Design and Experimental Results
3.2. Range Analysis
3.3. Analysis of Variance
4. Discussion
- Although this paper studied the influence of open-pit mining design and geological structure on the stability of an open-pit slope and the scope of the surrounding influence zone with an orthogonal experiment, it did not discuss the influence mechanisms of these nine factors, which will require similar model experiments in the future.
- Open-pit mines are located in special geographical locations. There are large numbers of geological structures around, and open-pit mining is a long process. In the numerical analysis, the Mohr–Coulomb constitutive model adopted in this paper did not consider the creep effect caused by time to the geological structure around the open pit. In a subsequent study, the author will use a constitutive equation that is consistent with the creep effect of shallow strata to analyze the safety factor and the range of the stable zone of the open-pit slope under asymmetric unloading.
5. Conclusions
- Due to the influence of the surrounding geological structure, the significant influencing factors affecting the initial position of the south slope were mainly the excavation dip angle and excavation depth of the north slope, and the influence of the excavation dip angle of the north slope was greater than that of the excavation depth of the south slope. When controlling the scope of the stable zone of the south surface, the excavation depth should not exceed 450 m.
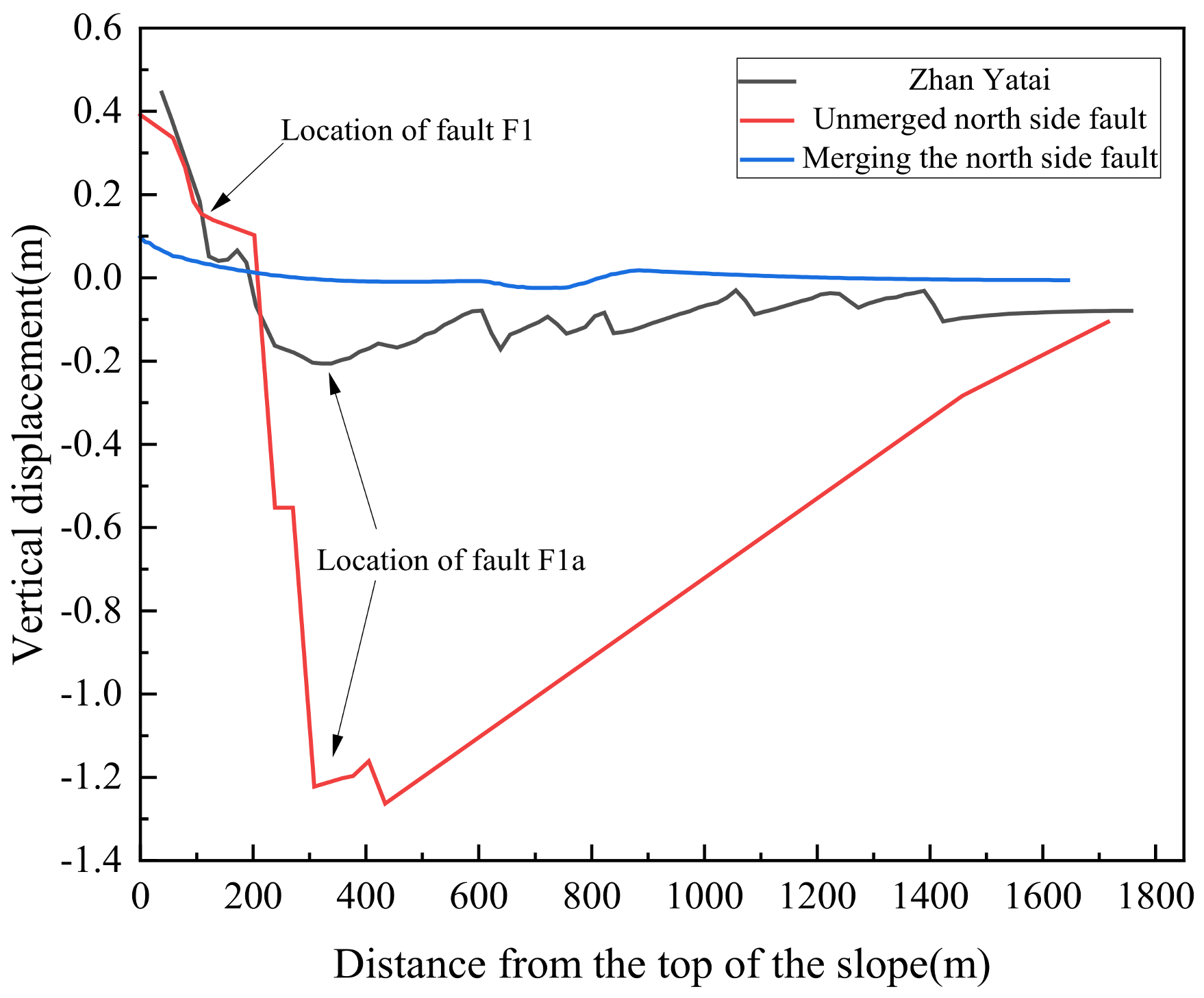
- With an increase in the distance between the F1 fault and the top of the slope, the range of the unstable area on the north side of the open-pit mine gradually expanded, while with an increase in the F1 fault dip angle, the range of the unstable area gradually decreased. In the process of open-pit mining, the range of the unstable area in an area containing a reverse fault can be reduced by reducing the distance between the fault and the top of the slope and selecting a position with a fault dip angle less than 60° for excavation construction.
- The significant influencing factor of the safety factor was the mode of open-pit mining, and the influencing order was as follows: north slope > south slope > north slope > south slope. With increases in the excavation inclinations of the north slope and south slope, the safety factor decreased greatly. The safety factor of the south slope should be designed to be less than 35°, and the safety factor of the north slope should be designed to be less than 30°.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, Z.; Liu, X.; Wang, L.-G.; Wang, Y. Study on slope deformation, failure and sliding law under excavation in Fushun West Open Pit. Met. Mine 2021, 2, 190–199. [Google Scholar] [CrossRef]
- Guo, H. The slope instability mode in Montenegro and failure mechanism study. Open-Air Min. Technol. 2021, 36, 25–28. [Google Scholar] [CrossRef]
- Wang, S.-Z.; Wang, J.-A.; Zhou, J.-X. Study on reinforced structural system of buildings in the affected area of open-pit slope. Min. Res. Dev. 2023, 2001, 147–153. [Google Scholar] [CrossRef]
- Li, Q. Coal ecotype strip mining theory and technology system and its application. J. Coal Sci. 2023, 1–18. [Google Scholar] [CrossRef]
- Bravo-Zapata, M.F.; Muñoz, E.; Lapeña-Mañero, P.; Montenegro-Cooper, J.M.; King, R.W. Analysis of the Influence of Geomechanical Parameters and Geometry on Slope Stability in Granitic Residual Soils. Appl. Sci. 2022, 12, 5574. [Google Scholar] [CrossRef]
- Hu, B.; Hu, Q.; Liu, Y.; Tao, G. Research on the Improvement of Granite Residual Soil Caused by Fly Ash and Its Slope Stability under Rainfall Conditions. Appl. Sci. 2024, 14, 3734. [Google Scholar] [CrossRef]
- Wei, S.-W.; Lv, S.; Jiang, J.-J.; Cai, D.-G.; Cui, Z.-D. Similarity Model Test on Rainfall Scouring Mechanism of High-Speed Railway Subgrade Slope. Appl. Sci. 2024, 14, 244. [Google Scholar] [CrossRef]
- Wang, B.; Wang, S. Shear Strength Analysis and Slope Stability Study of Straight Root Herbaceous Root Soil Composite. Appl. Sci. 2023, 13, 12632. [Google Scholar] [CrossRef]
- Tang, J.; Chen, D. Effect of Drying–Wetting Cycle and Vibration on Strength Properties of Granite Residual Soil. Appl. Sci. 2024, 14, 458. [Google Scholar] [CrossRef]
- Qu, M.; Dang, F. Numerical Analysis of Instability Mechanism of a High Slope under Excavation Unloading and Rainfall. Appl. Sci. 2022, 12, 7990. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, R.; Chang, J.; Chen, X.; Zheng, Y.; Wu, R.; Jiang, X.-Y. Research on the analysis method of block-bending compound topping-failure of antidip rock slope. Chin. J. Rock Mech. Eng. 2023, 42, 1482–1496. [Google Scholar] [CrossRef]
- Vick, L.M.; Böhme, M.; Rouyet, L.; Bergh, S.G.; Corner, G.D.; Lauknes, T.R. Structurally controlled rock slope deformation in northern Norway. Landslides 2020, 17, 1745–1776. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, W.; Ning, Y.; Xiao, H.; Xie, W. Analytical method of stability analyses of toppling rock slopes subjected to flexural toppling failure damage. Eur. J. Environ. Civ. Eng. 2023, 27, 2373–2387. [Google Scholar] [CrossRef]
- Haghgouei, H.; Kargar, A.R.; Amini, M.; Esmaeili, K. An analytical solution for analysis of toppling-slumping failure in rock slopes. Eng. Geol. 2020, 265, 105396. [Google Scholar] [CrossRef]
- Shuheng, Z.; Yinjun, M. Research on the influence of weak interlayer in open-pit slope on stability. Adv. Civ. Eng. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Zheng, D.; Pan, Y.; Wang, Q.; Zhou, H.; Zheng, H.; Li, D. Evolutionary mechanisms of deep-seated toppling deformation of rock slope under different free-face conditions. Environ. Earth Sci. 2023, 82, 221. [Google Scholar] [CrossRef]
- Zhang, B.; Jiang, Y.; Zhang, J.; Liu, Z.; Wang, W. Upper limit analysis of three-dimensional rock slope stability under different saturation. Chin. J. Civ. Eng. 2023, 56, 78–90. [Google Scholar] [CrossRef]
- Gao, A.; Wang, J.; Li, F.; Xie, J. Analysis of building damage location characteristics around the West open pit Mine. J. China Coal Soc. 2021, 46, 1320–1330. [Google Scholar] [CrossRef]
- Tian, H.; Kong, Z. Influence of Rainfall Intensity and Slope on the Slope Erosion of Longling Completely Weathered Granite. Appl. Sci. 2023, 13, 5295. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, A.; Wu, Z.; Zhu, A.; Li, L.; Tu, F. Stability of gently inclined bedding rock slope with weak interlayers based on cusp mutation theory. J. Henan Polytech. Univ. (Nat. Sci. Ed.) 2022, 41, 188–195. [Google Scholar] [CrossRef]
- Jin, P.; Shen, L.; Han, X.; Guo, J.; Wang, M. Spatial and temporal distribution characteristics and influencing factors of geological hazards in the West Open Pit Mine in Fushun, Liaoning Province. Chin. J. Geol. Hazards Prev. 2022, 33, 68–76. [Google Scholar] [CrossRef]
- Tian, Y.; Wu, Y.; Wang, H.; Li, H.; He, L.; Zhao, H. A Theory of Slope Shear Scouring and the Failure Mechanism of PFC3D on a Gangue Slope. Appl. Sci. 2023, 13, 5066. [Google Scholar] [CrossRef]
- Zhan, Y. Activation mechanism and long-term mechanical behavior of the Northern Slope fault zone in Fushun West Open Pit Mine. Ph.D. Thesis, Beijing University of Science and Technology, Beijing, China, 2022. [Google Scholar] [CrossRef]
- Jia, H.-J.; Ding, S.-F.; Shi, Z.-Z. Approximate weighted kernel k-means algorithm for solving large-scale spectral clustering. J. Softw. 2015, 2001, 2836–2846. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, C.; Zhang, H. Improved K-means algorithm based on density Canopy. Knowl. -Based Syst. 2018, 145, 289–297. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y. Research and Application of spatial projection in K-means algorithm. Comput. Eng. Appl. 2020, 56, 200–204. [Google Scholar]
- Zhai, Q.; Zhou, Y.; Song, Q.; Wang, J.; Meng, Z.; Zhang, Y.L. Application of dimensionality reduction and clustering algorithm in tobacco similarity analysis. Front. Data Comput. 2021, 112–121. [Google Scholar]
- Shen, H.; Kong, Y.; Pang, J. Orthogonal test on strength of ceramic-based hybrid fiber concrete. J. Yangtze River Sci. Res. Inst. 2021, 38, 144–148. [Google Scholar]
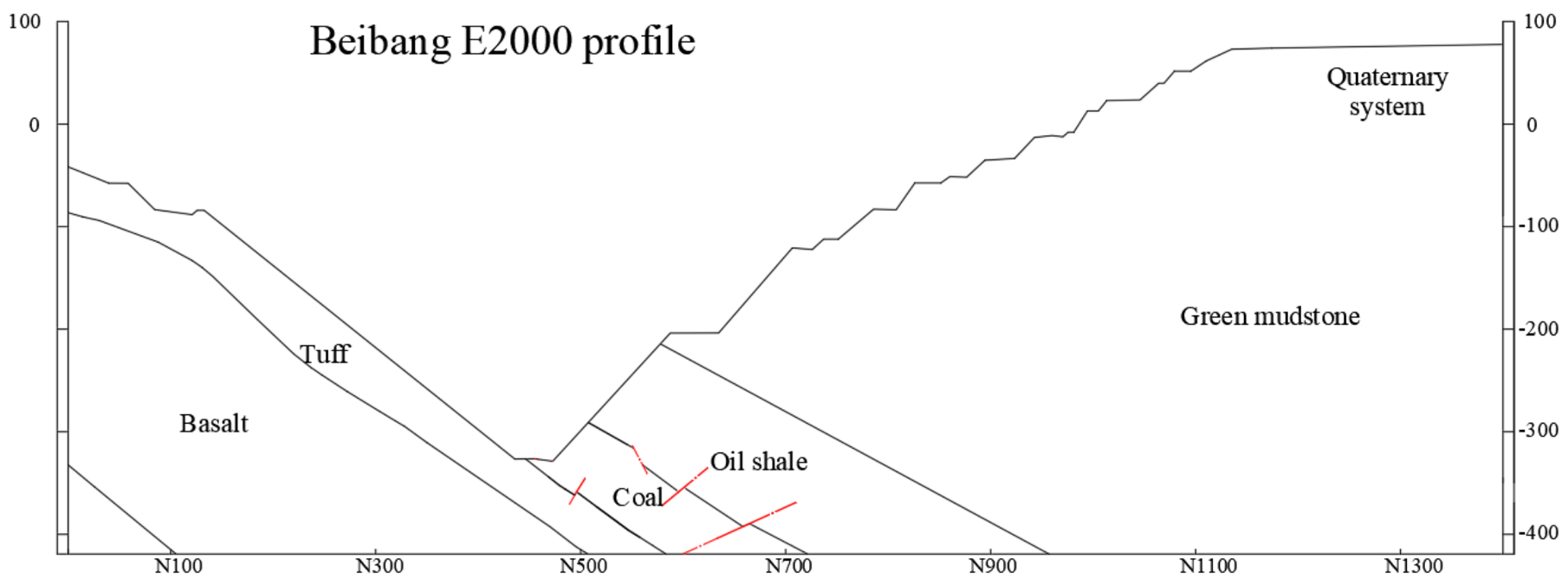
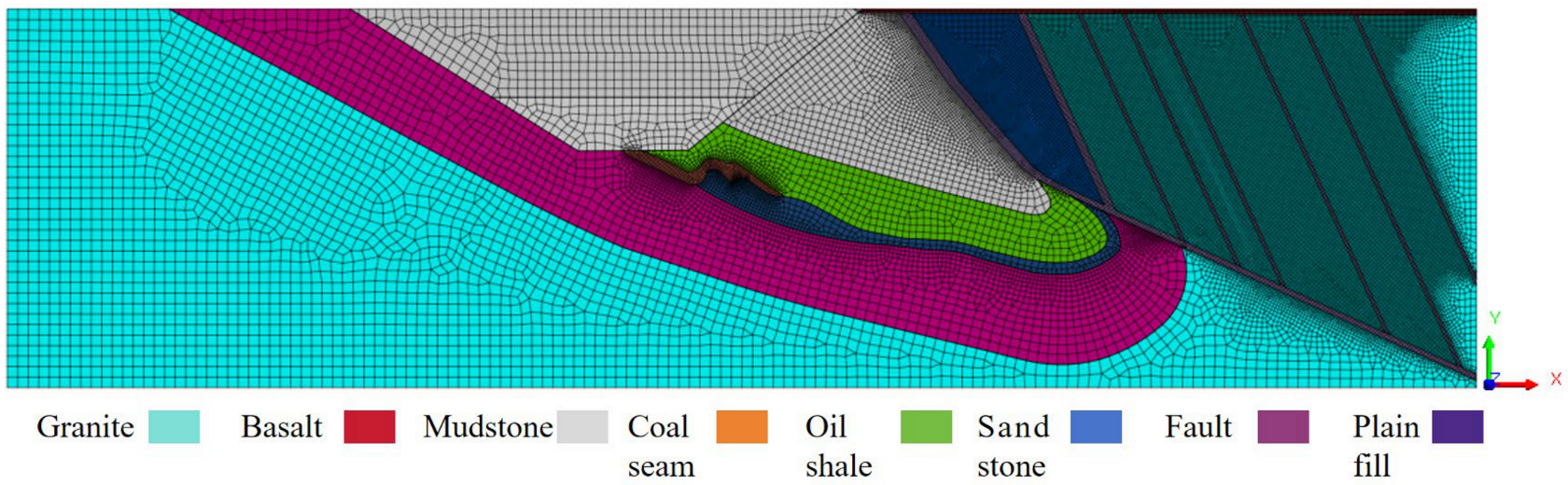


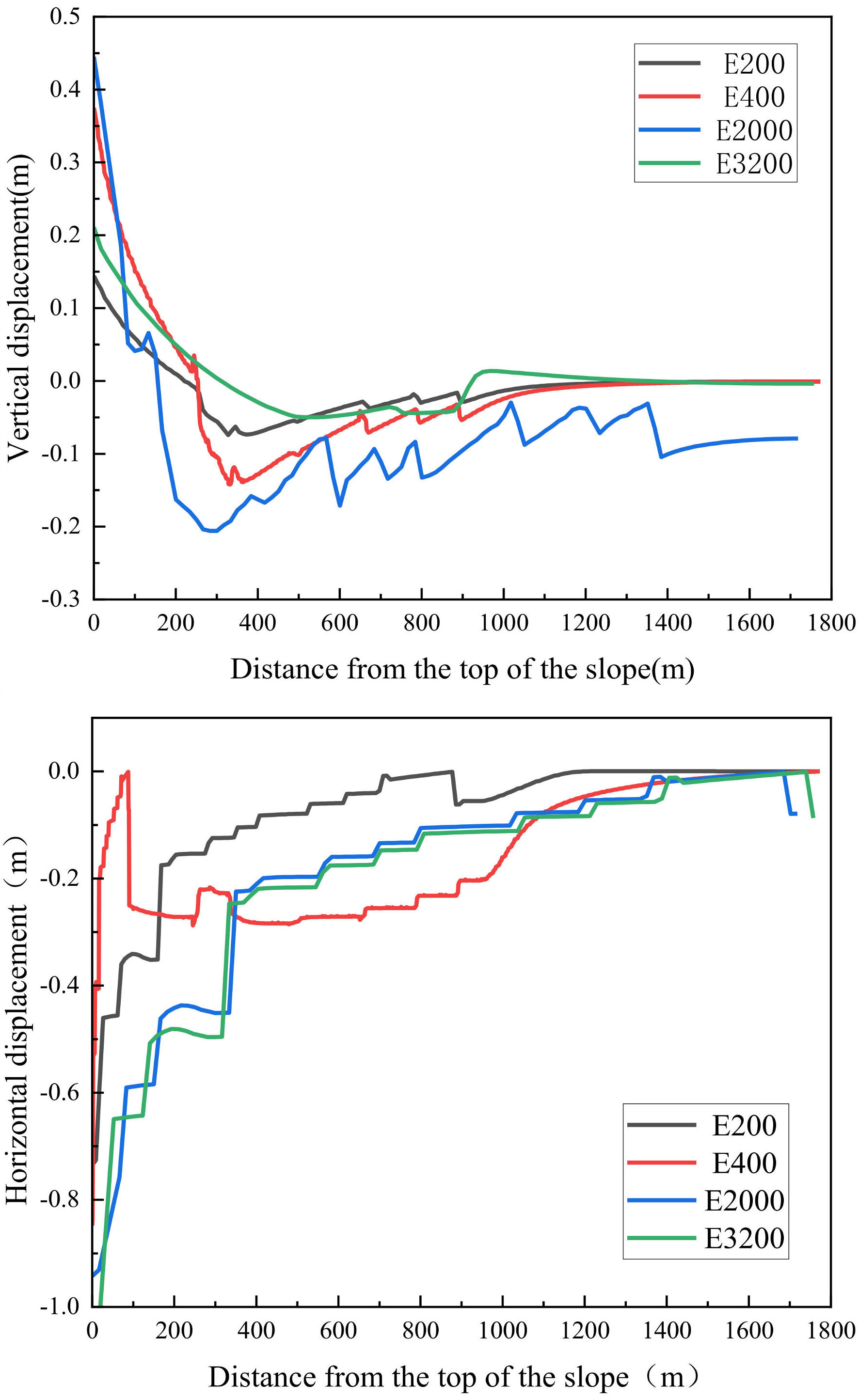
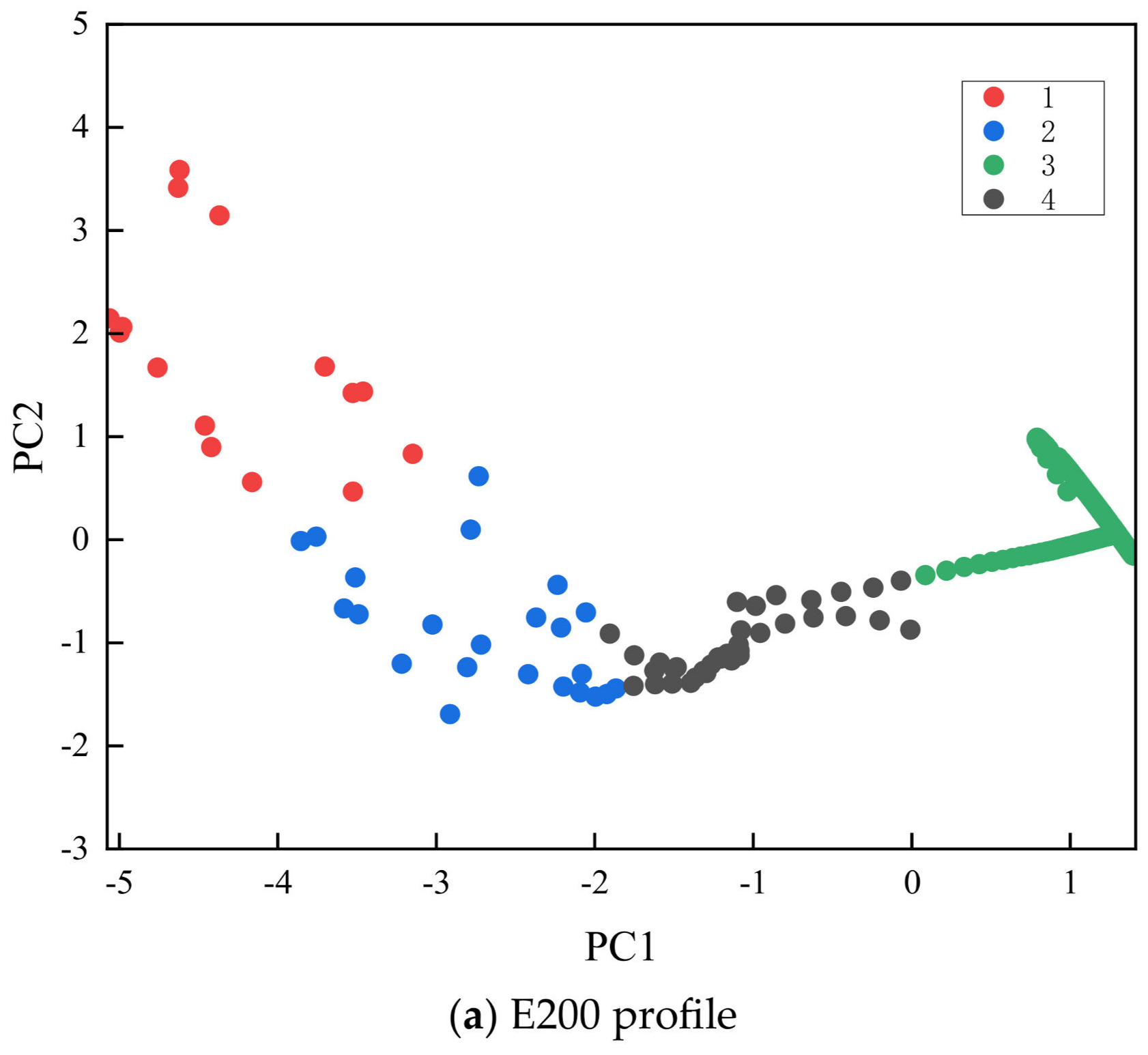
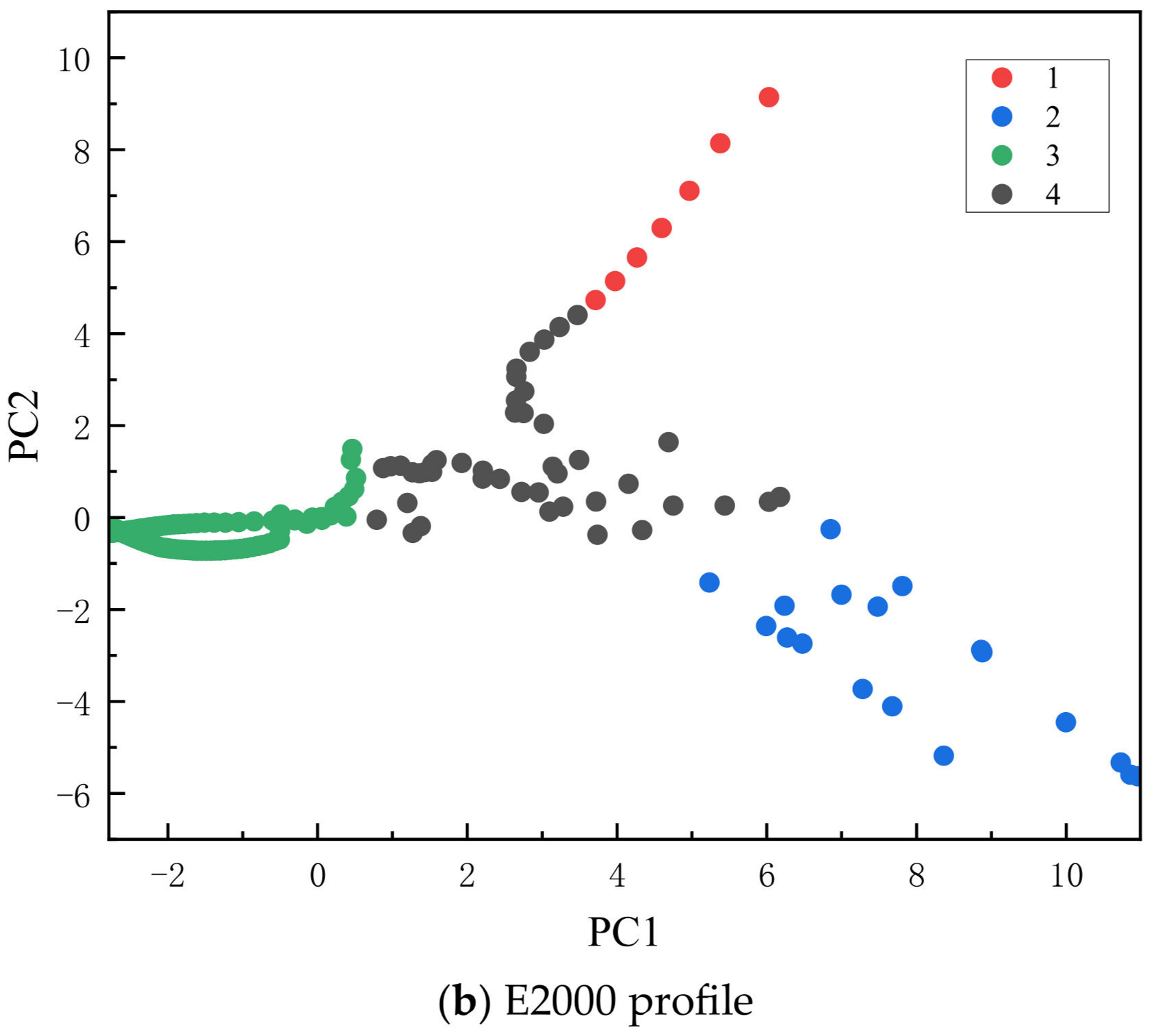
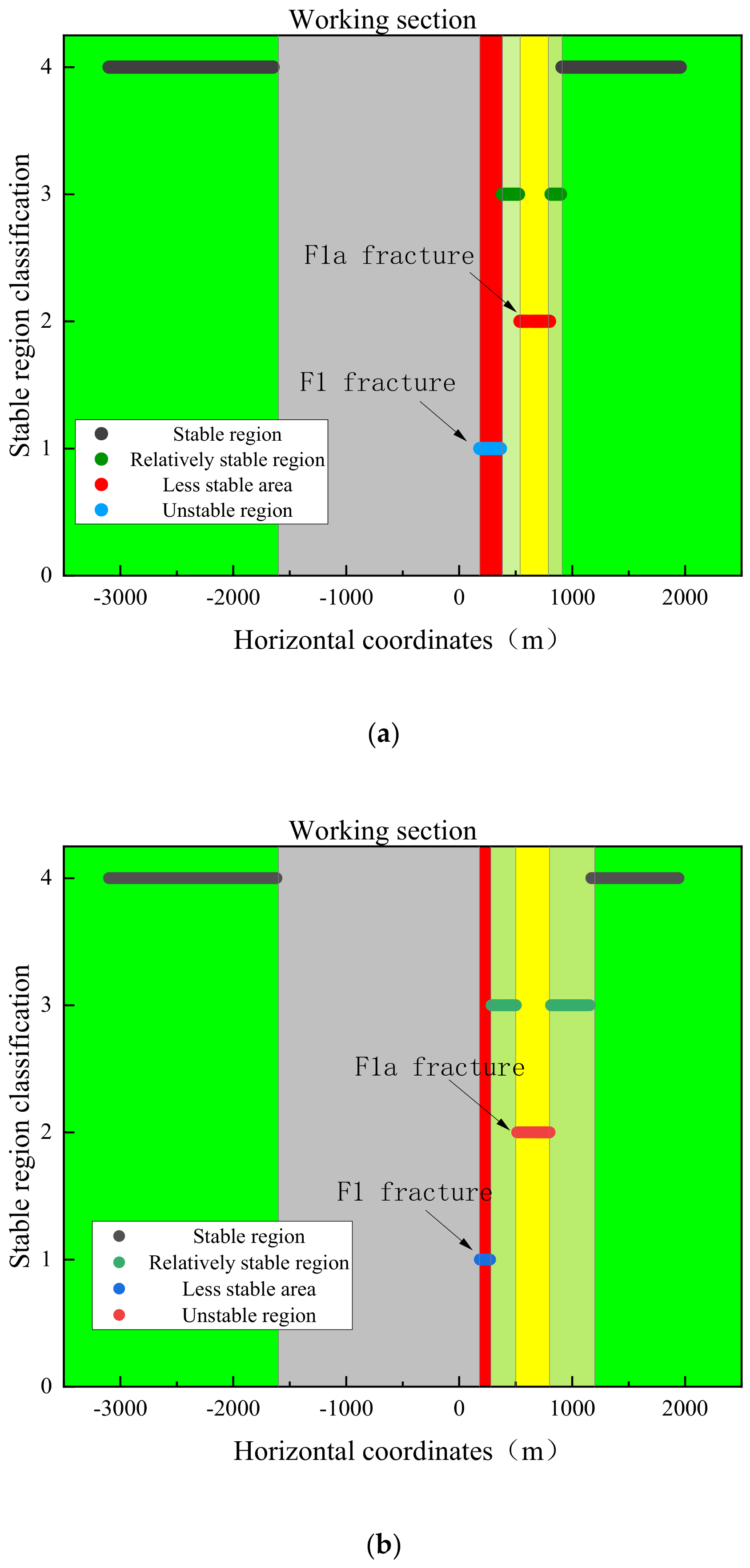
| Formation | Elastic Modulus (GPa) | Density (g/cm3) | Cohesion (Mpa) | Friction Angle (°) | Poisson’s Ratio | Tensile Strength (Mpa) |
|---|---|---|---|---|---|---|
| Plain fill | 0.2 | 1.8 | 0.1 | 20 | 0.29 | 0 |
| Marlstone | 12 | 1.6 | 1.1 | 30 | 0.27 | 3 |
| Granitic gneiss | 30 | 2.74 | 0.24 | 54 | 0.23 | 5 |
| Basalt | 25 | 2.7 | 0.25 | 48 | 0.23 | 2.5 |
| Tuff | 0.32 | 2.35 | 0.18 | 32 | 0.36 | 0.26 |
| Coal seam | 0.22 | 1.3 | 0.28 | 15 | 0.36 | 0.24 |
| Kerogen shale | 2.8 | 1.8 | 0.6 | 30 | 0.29 | 1.8 |
| Green mudstone | 1.6 | 2.25 | 0.5 | 25 | 0.32 | 0.22 |
| Cretaceous sandstone | 2.8 | 2.3 | 0.58 | 29 | 0.25 | 1.8 |
| Faultage | 0.1 | 1.8 | 0.13 | 7 | 0.4 | 0.22 |
| Property | South Slope of Excavation (°) | North Slope of Excavation (°) | South-Side Excavation Depth (m) | North-Side Excavation Depth (m) | F1 Fault Dip (°) | F1 Distance from the Top of the Slope (m) | F1a Fault Dip (°) | F1a Distance from the Top of the Slope (m) | |
|---|---|---|---|---|---|---|---|---|---|
| Profile | |||||||||
| E200 | 25 | 30 | 300 | 450 | 50 | 160 | 75 | 300 | |
| E400 | 25 | 50 | 400 | 450 | 45 | 80 | 75 | 200 | |
| E2000 | 45 | 45 | 400 | 400 | 55 | 0 | 65 | 400 | |
| E3200 | 35 | 50 | 500 | 550 | 55 | 160 | 75 | 300 | |
| Level of Factor | South Slope of Excavation (α) (°) | North Slope of Excavation (β) (°) | South-Side Excavation Depth (Hα) (m) | North-Side Excavation Depth (Hβ) (m) | F1 Fault Dip (γ) (°) | F1 Distance from the Top of the Slope (Lγ) (m) | F1a Fault Dip (δ) (°) | F1a Distance from the Top of the Slope (Hδ) (m) | Thickness of Coal Seam (H) (m) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 25 | 30 | 300 | 350 | 45 | 0 | 65 | 300 | 50 |
| 2 | 35 | 40 | 400 | 450 | 50 | 80 | 70 | 400 | 100 |
| 3 | 45 | 50 | 500 | 550 | 55 | 160 | 75 | 500 | 150 |
| Group | Starting Point of the South Stable Zone (m) | The Width of the Unstable Zone (m) | Starting Point of the North Stable Zone (m) | Safety Factor |
|---|---|---|---|---|
| 1 | −1096 | 138 | 3040 | 2.1 |
| 2 | −1096 | 133 | 3035 | 1.975 |
| 3 | −896 | 107 | 2809 | 2.016 |
| 4 | −896 | 160 | 2862 | 1.55 |
| 5 | −1597 | 25 | 3428 | 1.453 |
| 6 | −896 | 156 | 2858 | 1.538 |
| 7 | −896 | 105 | 2807 | 1.376 |
| 8 | −896 | 236 | 2938 | 1.25 |
| 9 | −896 | 50 | 2752 | 1.15 |
| 10 | −1322 | 105 | 3233 | 2.152 |
| 11 | −1397 | 228 | 3431 | 2 |
| 12 | −896 | 50 | 2752 | 1.919 |
| 13 | −896 | 75 | 2777 | 1.594 |
| 14 | −896 | 130 | 2832 | 1.438 |
| 15 | −896 | 210 | 2912 | 1.507 |
| 16 | -896 | 165 | 2867 | 1.438 |
| 17 | −896 | 100 | 2802 | 1.203 |
| 18 | −896 | 156 | 2858 | 1.138 |
| 19 | −896 | 210 | 2912 | 2.052 |
| 20 | −1336 | 50 | 3192 | 1.92 |
| 21 | −1322 | 454 | 3582 | 2.013 |
| 22 | −896 | 130 | 2832 | 1.6 |
| 23 | −896 | 190 | 2892 | 1.413 |
| 24 | −896 | 60 | 2762 | 1.355 |
| 25 | −896 | 50 | 2752 | 1.355 |
| 26 | −896 | 105 | 2807 | 1.204 |
| 27 | −896 | 160 | 2862 | 1.1 |
| Factor | South Slope of Excavation | North Slope of Excavation | South-Side Excavation Depth | North-Side Excavation Depth | F1 Fault Dip | F1 Distance from the Top of the Slope | F1a Fault Dip | F1a Distance from the Top of the Slope | Thickness of Coal seam |
|---|---|---|---|---|---|---|---|---|---|
| Safety factor | 0.283 | 0.770 | 0.137 | 0.165 | 0.036 | 0.043 | 0.025 | 0.033 | 0.044 |
| South side, hold steady | 213.56 | 243.67 | 236.00 | 157.33 | 151.89 | 93.33 | 139.11 | 180.89 | 57.22 |
| North side, hold steady | 448.00 | 374.33 | 130.11 | 96.11 | 190.89 | 261.67 | 37.56 | 129.00 | 184.11 |
| Range of instability | 21.56 | 38.67 | 41.78 | 29.44 | 76.78 | 118.67 | 28.00 | 50.11 | 19.78 |
| Target Parameter | Source of Variation | Class III Sum of Squares | Mean Square | F | Significance |
|---|---|---|---|---|---|
| Safety factor | Excavation inclination on south side | 0.011 | 0.006 | 2.263 | 0.000 |
| North slope of excavation | 2.783 | 1.391 | 568.030 | 0.000 | |
| South-side excavation depth | 0.000 | 0.000 | 0.044 | 0.958 | |
| Excavation depth on the north side | 0.150 | 0.075 | 30.694 | 0.000 | |
| F1 fault dip | 0.006 | 0.003 | 1.273 | 0.331 | |
| F1 distance from the top of the slope | 0.009 | 0.004 | 1.789 | 0.228 | |
| F1a fault dip | 0.003 | 0.002 | 0.698 | 0.526 | |
| F1a distance from the top of the slope | 0.006 | 0.003 | 1.298 | 0.325 | |
| Seam thickness | 0.010 | 0.005 | 2.044 | 0.192 | |
| South side, hold steady | Excavation inclination on south side | 3304.519 | 1652.259 | 0.088 | 0.093 |
| North slope of excavation | 278,767.185 | 139,383.5 | 7.461 | 0.001 | |
| South-side excavation depth | 853,99.407 | 42,699.70 | 2.286 | 0.002 | |
| Excavation depth on the north side | 130,507.852 | 65,253.92 | 3.493 | 0.081 | |
| F1 fault dip | 108,208.074 | 54,104.03 | 2.896 | 0.113 | |
| F1 distance from the top of the slope | 40,471.185 | 20,235.59 | 1.083 | 0.383 | |
| F1a fault dip | 104,651.630 | 52,325.81 | 2.801 | 0.120 | |
| F1a distance from the top of the slope | 148,866.074 | 74,433.03 | 3.984 | 0.063 | |
| Seam thickness | 191,26.741 | 9563.370 | 0.512 | 0.618 | |
| North side, hold steady | Excavation inclination on south side | 261,609.185 | 130,804.5 | 4.688 | 0.000 |
| North slope of excavation | 683,643.185 | 341,821.5 | 12.251 | 0.001 | |
| South-side excavation depth | 204,758.296 | 102,379.1 | 3.669 | 0.074 | |
| Excavation depth on the north side | 45,606.741 | 22,803.37 | 0.817 | 0.475 | |
| F1 fault dip | 197,923.852 | 98,961.92 | 3.547 | 0.032 | |
| F1 distance from the top of the slope | 356,293.407 | 178,146.7 | 6.385 | 0.028 | |
| F1a fault dip | 63,55.852 | 31,77.926 | 0.114 | 0.894 | |
| F1a distance from the top of the slope | 77,378.741 | 38,689.37 | 1.387 | 0.045 | |
| Seam thickness | 195,829.407 | 97,914.70 | 3.509 | 0.081 | |
| Range of instability | Excavation inclination on south side | 5088.222 | 2544.111 | 0.534 | 0.606 |
| North slope of excavation | 8744.667 | 4372.333 | 0.918 | 0.092 | |
| South-side excavation depth | 13,601.556 | 6800.778 | 1.428 | 0.295 | |
| Excavation depth on the north side | 4301.556 | 2150.778 | .451 | 0.652 | |
| F1 fault dip | 32,108.222 | 16,054.11 | 3.370 | 0.001 | |
| F1 distance from the top of the slope | 72,032.000 | 36,016.00 | 7.560 | 0.000 | |
| F1a fault dip | 4648.667 | 2324.333 | 0.488 | 0.631 | |
| F1a distance from the top of the slope | 12,048.222 | 6024.111 | 1.265 | 0.133 | |
| Seam thickness | 1910.222 | 955.111 | 0.200 | 0.822 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Xiang, P.; Shen, H.; Ji, H.; Quan, D.; Wang, W. Stability and Distribution of Rock Slope under Asymmetric Excavation. Appl. Sci. 2024, 14, 4384. https://doi.org/10.3390/app14114384
Li M, Xiang P, Shen H, Ji H, Quan D, Wang W. Stability and Distribution of Rock Slope under Asymmetric Excavation. Applied Sciences. 2024; 14(11):4384. https://doi.org/10.3390/app14114384
Chicago/Turabian StyleLi, Ming, Peng Xiang, Hengxiang Shen, Hongguang Ji, Daolu Quan, and Wensheng Wang. 2024. "Stability and Distribution of Rock Slope under Asymmetric Excavation" Applied Sciences 14, no. 11: 4384. https://doi.org/10.3390/app14114384
APA StyleLi, M., Xiang, P., Shen, H., Ji, H., Quan, D., & Wang, W. (2024). Stability and Distribution of Rock Slope under Asymmetric Excavation. Applied Sciences, 14(11), 4384. https://doi.org/10.3390/app14114384






