Abstract
In this article, to further improve the accuracy and speed of grasp detection for unknown objects, a new omni-dimensional dynamic convolution grasp detection network (ODGNet) is proposed. The ODGNet includes two key designs. Firstly, it integrates omni-dimensional dynamic convolution to enhance the feature extraction of the graspable region. Secondly, it employs a grasping region feature enhancement fusion module to refine the features of the graspable region and promote the separation of the graspable region from the background. The ODGNet attained an accuracy of 98.4% and 97.8% on the image-wise and object-wise subsets of the Cornell dataset, respectively. Moreover, the ODGNet’s detection speed can reach 50 fps. A comparison with previous algorithms shows that the ODGNet not only improves the grasp detection accuracy, but also satisfies the requirement of real-time grasping. The grasping experiments in the simulation environment verify the effectiveness of the proposed algorithm.
1. Introduction
With the development of artificial intelligence technology, the potential applications of robotic grasping have shifted from traditional industrial environments to a variety of unstructured scenarios, such as medical assistance, disaster relief and rescue, and family services [1]. In traditional industrial environments, the targets are known objects with fixed shapes and sizes, so the robot only needs to grasp them with a specific grasping configuration. However, in unstructured scenarios, the targets are often unknown objects with unfixed shapes and sizes and with different types. For these unknown objects, there still exist numerous challenges in generating the corresponding grasping configurations quickly and accurately [2].
In order to accurately describe a grasping pose, Jiang et al. [3] proposed the rectangular grasping representation method, which significantly contributed to subsequent research. Lenz et al. [4] developed two fully connected neural networks to identify the optimal grasping rectangle from a pool of potential grasp rectangle candidates. Redmon et al. [5] and Kumra et al. [6] subsequently integrated the convolutional neural network architecture into the grasp detection model. Although all the aforementioned methods initially produce a series of grasping rectangles and subsequently select the optimal one, none achieve very high grasp detection accuracy. To improve the grasp detection accuracy, Zhou et al. [7] introduced the method of target detection into grasp detection. However, its detection speed is excessively slow. To enhance the grasp detection speed, Morrison et al. [8] devised a lightweight fully convolutional neural network. This network directly predicts the grasp quality, grasp angle, and grasp width of each pixel, resulting in the final grasp configuration. Yu et al. [9] and Yan et al. [10] improved the network model on this basis, and both the detection speed and the detection accuracy are greatly improved. However, the aforementioned methods merely stack a few convolution layers during the feature extraction stage, failing to adequately extract features. Also, there is no use of multi-scale features to enhance the grasping features. Additionally, the segmentation of graspable and non-graspable regions is inadequate, often resulting in incorrect grasping configurations.
In order to solve the above problems and further improve the accuracy and speed of grasp detection, this article proposes the grasp detection network ODGNet. The network introduces omni-dimensional dynamic convolution (ODConv) [11] into the feature extraction stage to enhance the feature extraction capability of the grasping region; at the same time, the Shuffle Attention (SA) [12] module and the ODConv are used to form a grasping region feature enhancement and fusion (GRFEF) module, which enhances the feature learning ability of the grasping region, and suppresses the non-grasping region features; during feature reconstruction, the primary pixel features in the feature extraction part are fused with the advanced semantic features to further enhance the feature expression ability of the grasping region. The experimental results from the Cornell dataset [6] demonstrate that the algorithm presented in this paper outperforms in both grasp detection accuracy and detection speed. Moreover, the grasp detection performance with the multi-object dataset [13] surpasses that of the comparative method. Additionally, the simulated grasping experiments validate the efficacy of the proposed method.
The specific contributions of this paper are as follows:
- A novel grasp detection network, ODGNet, is proposed, which can output the object’s corresponding grasp configuration by inputting the RGB-D image;
- The ODGNet firstly introduces ODConv to enhance the feature extraction ability of the grasping region; secondly, a GRFEF module is designed, which enhances the feature learning ability of the grasping region and suppresses the non-grasping region features; finally, the multi-scale features are used to improve the grasp detection accuracy;
- The ODGNet was trained and tested on the Cornell dataset and also tested on the multi-object dataset. The test results show that it delivers good detection results for both single and multiple objects;
- Robot grasping experiments were carried out in a simulation environment, and the results demonstrate the feasibility and effectiveness of the proposed method.
The remainder of this article is organized as follows: Section 2 presents related work on robot grasp detection, omni-dimensional dynamic convolution, and attention mechanisms; Section 3 describes the grasp detection problem and the proposed method; Section 4 provides detailed experimental validation; and Section 5 summarizes the article and looks at future research directions.
2. Related Work
2.1. Deep Learning Methods for Robotic Grasp Detection
With the increasing number of potential applications of robots, robot grasp detection methods are also evolving. Grasp detection methods are divided into analytical and data-driven methods [2]. The analytical method is to analyze the physical models of the robot and the object, and calculate the appropriate grasping position according to the kinematics and dynamics equations. And the analytical method usually has to satisfy the principles of force closure and form closure [14]. In real scenarios, accurate physical models are difficult to obtain, which makes the method difficult to implement. A data-driven method refers to the use of a priori knowledge of object grasping to predict the grasping postures of an object [15]. Traditional data-driven methods usually require manually building a knowledge library for grasping, which contains the correspondence between the object features and the grasping postures. Traditional data-driven methods are good at predicting the grasping postures of known and similar objects, but cannot predict the grasping postures of unknown objects.
The data-driven method based on deep learning can automatically extract the features of the grasping region and establish the mapping relationship between the features of the grasping regions and the grasping postures through deep neural networks. The deep learning-based grasp detection method is able to predict the grasping posture of the unknown objects. The deep learning-based grasp detection method was first proposed in [4], which obtains the optimal grasping posture from many candidates through two cascaded deep networks. Pinto et al. [16] used AlexNet [17] to sample and evaluate a large number of grasping candidates. Mahler et al. [18] proposed the Grasp Quality Convolutional Neural Network, which iteratively performs multiple rounds of sampling and evaluation for grasping candidates. The above methods are slow to detect because a large number of candidates need to be evaluated.
In [8], Morrison et al. proposed a lightweight fully convolutional network, GGCNN, which takes a depth image as the input and outputs three grasping parameter maps, including a grasping quality map, a grasping angle map, and a grasping width map. This method can generate grasping configurations end-to-end, and the grasping parameter map representation method has been used in subsequent studies. After that, Morrison et al. [19] introduced the Multi-View Pickup Controller to improve the grasp detection accuracy. Kumra et al. [20] introduced a multilayer residual module into the GGCNN, constituting the Generative Residual Convolutional Neural Network (GR-ConvNet), which enhances the depth of the network, resulting in enhanced network generalization, and the detection accuracy on the Cornell dataset reached 97.7%. In [21], Yu et al. introduced the SE-ResNet module into the UNet architecture to constitute SE-ResUNet, which further improved the detection accuracy. In [9], Yu et al. used Selective Kernel Convolution to enhance the usage of multi-scale features. In [22], Geng et al. designed a hierarchical multi-scale feature fusion module and an Inverted Shuffle Residual module to further improve the detection accuracy.
In addition to using CNNs to design grasp detection networks, Wang et al. [23] were the first to introduce the Transformer architecture into grasp detection networks, obtaining TF-Grasp. Due to the powerful self-attention mechanism, TF-Grasp can acquire both global and local information, and obtains a 97.99% grasp detection accuracy on the Cornell dataset. Zhang et al. [24] used a hierarchical Transformer as an encoder and a CNN based on the channel attention mechanism as a decoder, and also achieved good detection results. Although most of the networks constructed based on Transformer have a higher accuracy of grasp detection than those based on the CNN architecture, their detection speed is relatively slow and difficult to deploy, so the current grasp detection networks are still based on the CNN architecture.
2.2. Omni-Dimensional Dynamic Convolution
With the proposal of LeNet [25], convolutional neural networks have become the basis of various network architectures and have driven the development of deep learning. The current convolutional neural network architecture is widely used in the fields of computer vision and natural language processing, specifically including target detection, image segmentation, grasp detection, speech recognition, and other related application scenarios. In modern convolutional neural network architectures, each convolutional layer has only one static convolutional kernel applied to all the input features. To achieve a better network model performance, it is common practice to stack more convolutional layers according to a specific structure or to use an attention mechanism. However, this approach still treats the convolutional kernel parameters as fixed values. In contrast, dynamic convolution applies the attention mechanism to n convolutional kernels in order to use different linear combinations of n kernels for different input features [11].
The idea of dynamic convolution was first introduced by Yang et al. [26] in Conditionally Parameterized Convolutions (CondConv); they proposed the computation of the parameters of the convolution kernel from the attention function of the input features. Later, Chen et al. [27] proposed dynamic convolution (DyConv), in which they improved the attention mechanism and facilitated the learning of the attention model by constraining the attention output based on CondConv. The above dynamic convolution methods, although they can significantly improve the performance of the model, only endow the dynamic properties of the convolution kernel in the dimension of the number of convolution kernels, ignoring the spatial size, the number of input channels, and the number of output channels of each convolution kernel in the space of the convolution kernels. Therefore, Li et al. [11] proposed omni-dimensional dynamic convolution, which utilizes a novel multi-dimensional attention mechanism and a parallel strategy to learn the attention parameters of the convolution kernel in each convolutional layer along the four dimensions of the kernel space. Thanks to its multidimensional attention mechanism, even ODConv with only one convolutional kernel exhibits a better performance than CondConv and DyConv networks with multiple convolutional kernels.
2.3. Attention Mechanisms
In the field of computer vision, the attention mechanism is widely used. The attention mechanism is similar to the working mechanism of the human visual system, which makes the network pay more attention to the important features and ignore the unnecessary ones by weighting the input features.
Squeeze-and-Excitation (SE) networks [28] emphasize valid feature channels and suppress invalid feature channels by establishing relationships between the channels of input features and the weighting each channel. ECANet [29] replaces the two fully connected layers in SE with a 1 × 1 convolution, which not only avoids dimensionality reduction, but also achieves cross-channel interaction with fewer parameters. The above two attention mechanisms only consider the interactions between channels, and do not consider the spatial dimensionality of the features. CBAM [30] and DANet [31] use both the channel attention mechanism and the spatial attention mechanism. CBAM uses the channel attention mechanism and the spatial attention mechanism serially, while DANet uses the channel attention mechanism and the spatial attention mechanism in parallel. These two attention mechanisms greatly enhance the effective information of the input features, and the model performance is greatly improved, but their number of parameters also increases substantially compared to the channel attention mechanism. Therefore, Zhang et al. [12] address this problem by proposing the Shuffle Attention module, which uses Shuffle Units to effectively combine channel attention and spatial attention. Specifically, the SA module first groups the input features into multiple sub-features by channel dimension; then, for each sub-feature, a Shuffle Unit is used to compute the feature dependencies in the channel and spatial dimensions; finally, all the sub-features are concatenated in the channel dimension, and channel shuffle is used to achieve information interaction between the different sub-features. The SA module is efficient and effective. Therefore, we chose to use the SA mechanism to build the GRFEF module.
3. Method
3.1. Grasp Representation
In this paper, we study the planar grasp detection problem. The target object is placed on a plane. Firstly, the RGB-D image of the target object is captured by a depth camera, and then the image is fed into the grasp detection network after certain preprocessing steps, and finally, the network outputs the object’s grasping configuration, which guides the parallel gripper to perform grasping. The focus of planar grasp detection is to predict the grasp configuration information from the input image.
The classical grasp representation method is proposed in [4], which describes a grasp posture by an oriented rectangle. A grasp posture is represented as , where denotes the coordinates of the center point of the grasp rectangular box; denotes the angle of the grasp rectangular box positively to the x-axis; denotes the opening width of the gripper jaws; and denotes the width of the fingers of the gripper jaws, depending on the gripper jaw type used.
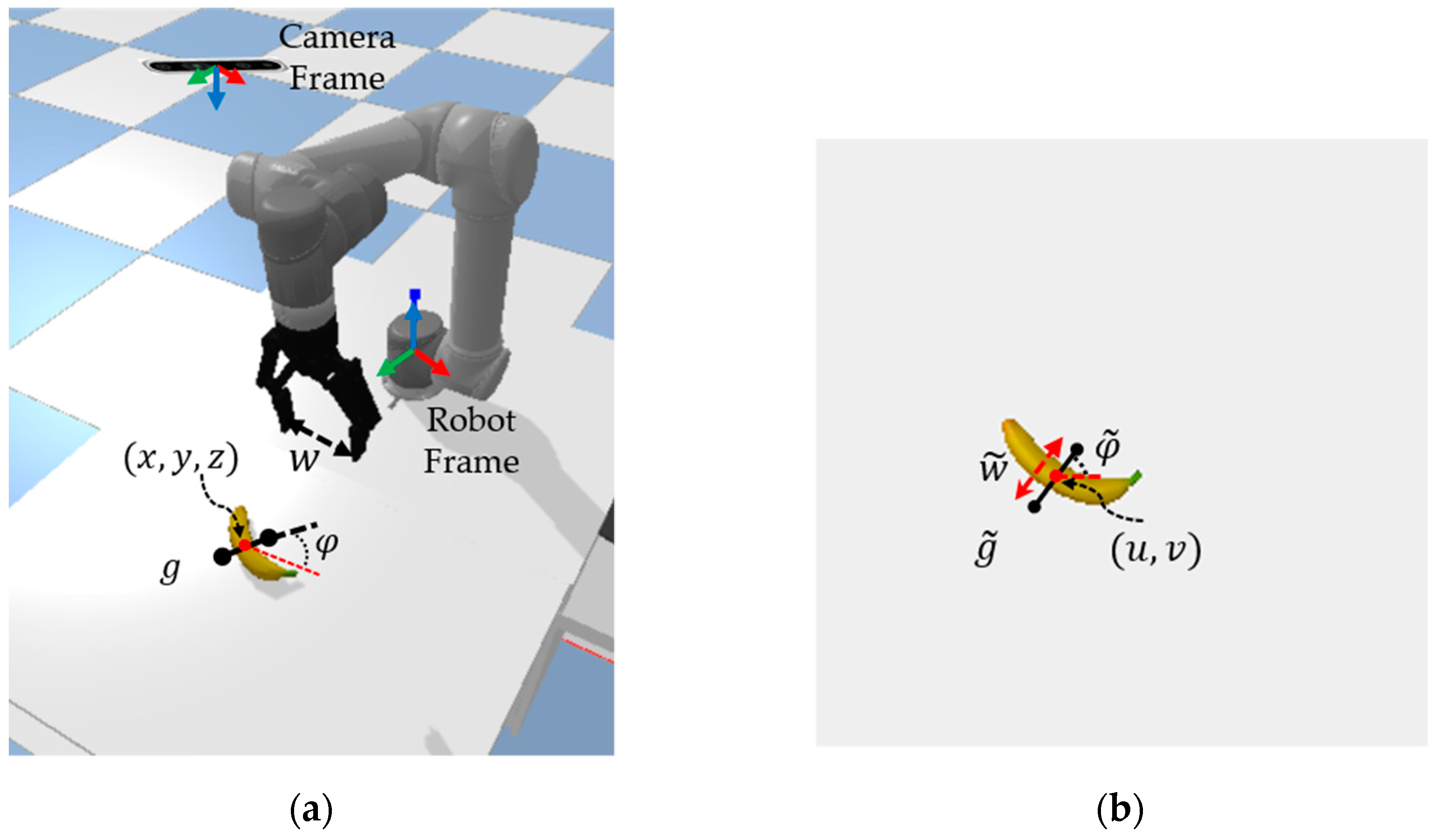
However, the rectangle representation method does not consider the grasping quality of each grasp rectangle, and also, , as a known variable, can be ignored. Therefore, a new grasp representation was proposed in [8], as shown in Figure 1a, defining the grasp configuration of the gripper in the robot coordinate system as
where is the position of the grasp centre point of the jaws, is the angle of rotation of the jaws, is the opening width of the jaws, and is the quality score of this grasp.
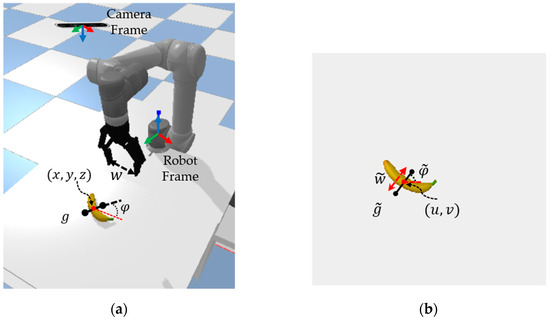
Figure 1.
Grasping configurations of the same object in different coordinate systems. (a) Grasping configuration in robot coordinate system. (b) Grasping configuration in pixel coordinate system.
In reality, grasp detection will not directly obtain the grasping configuration in the robot coordinate system, but will first obtain the grasping configuration in the pixel coordinate system. Shown in Figure 1b is the grasping configuration in the pixel coordinate system, denoted as
where is the centre position of the grasp in the pixel coordinate system; is the angle with the horizontal axis of the pixel coordinate system, which takes the range of ; is the width of the grasp in the pixel coordinate system, which takes the range of , where represents the maximum opening width of the jaws; and denotes the quality of this grasp, which takes the range of . The higher the value of is, the higher the success rate of this grasp.
Finally, the grasping configuration in the pixel coordinate system can be transformed into the grasping configuration in the robot coordinate system according to the corresponding transformation matrix:
where is the transformation matrix that transforms from the camera coordinate system to the robot coordinate system and is the transformation matrix that transforms from the pixel coordinate system to the camera coordinate system.
In order to achieve an end-to-end grasp detection network, it is necessary to predict the grasp configuration of each pixel point in the image. We define a set of grasp configurations corresponding to all pixel points in an image as three grasp parameter maps , where represent the grasp quality map, the grasp angle map, and the grasp width map, respectively. The value of each pixel point in the three maps represents the value of and at that point, respectively. Once the input image has gone through the grasp detection network to obtain the grasp parameter maps , the optimal grasp configuration can be determined by finding the extreme value point in the grasp quality map , denoted as
The optimal grasp configuration in the pixel coordinate system is subsequently transformed into the grasp configuration in the robot coordinate system by Equation (3).
Most of the current grasp datasets are labelled with grasp rectangles, and in order to use these datasets for training, the rectangle labels need to be transformed into the form of grasp parameter maps first. Specifically, we set the pixel values corresponding to all grasping rectangle regions to 1 and the rest to 0, thus generating a grasping quality map . Similarly, we set the pixel values corresponding to the grasping rectangle regions to the corresponding grasping angle and grasping width values, thus generating a grasping angle map and a grasping width map . Considering that the rectangle contains not only the object but also part of the background, the central third of the grasp rectangle is cropped out as the mentioned grasp rectangle area.
3.2. Network Architecture
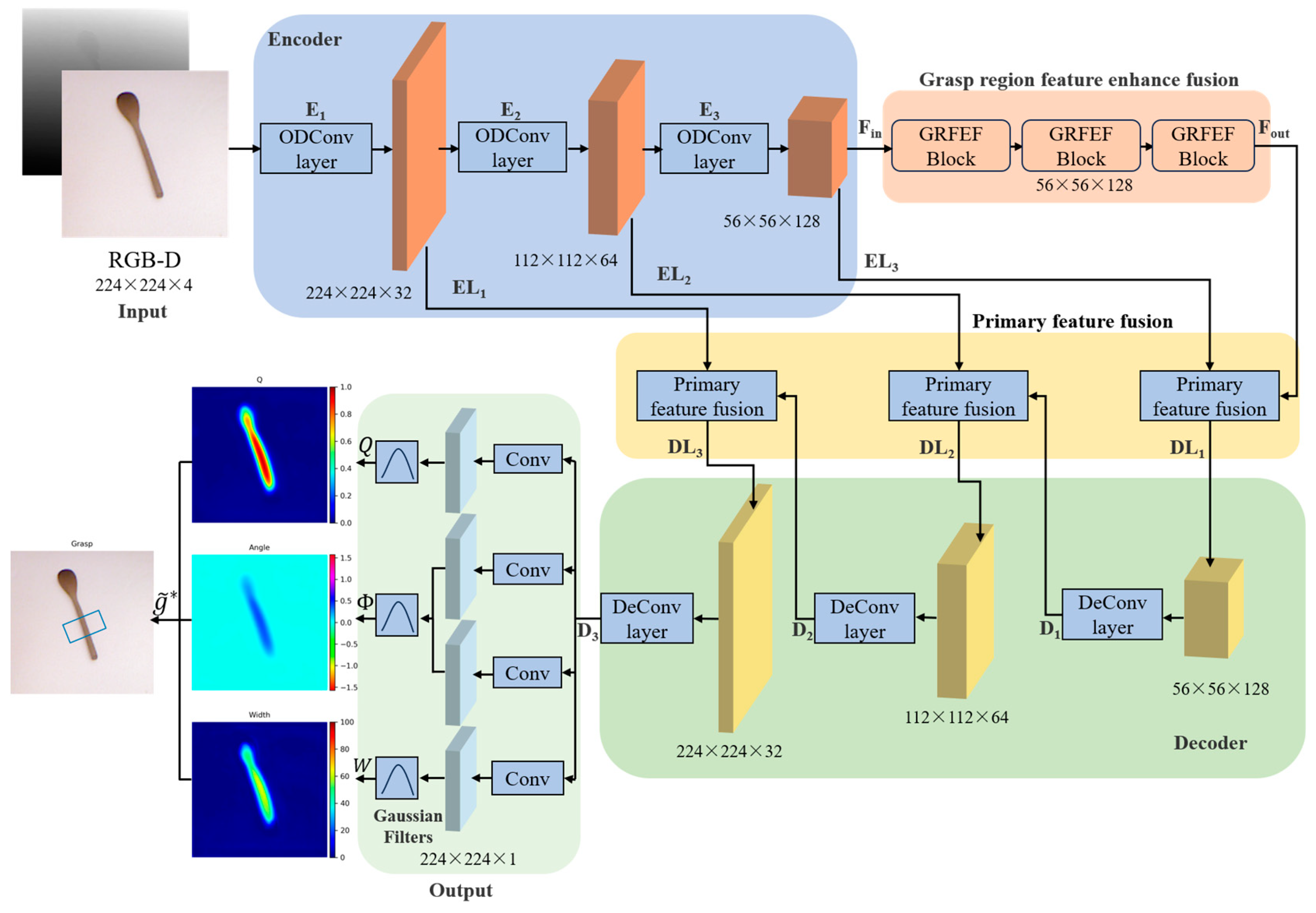
The overall architecture of the ODGNet is shown in Figure 2. It consists of an input layer, an encoder, a grasping region enhancement fusion layer, a primary feature fusion layer, a decoder, and an output layer. In the input layer, the input data are multimodal data consisting of RGB images and depth images, where the dimensions of the input RGB image are 224 × 224 × 3 and the shape of the input depth image is 224 × 224 × 1. Aiming to make full use of the information of the RGB image and the depth image, we concatenate the RGB image and the depth image in the channel dimension to obtain the RGB-D image, which have the dimensions 224 × 224 × 4.
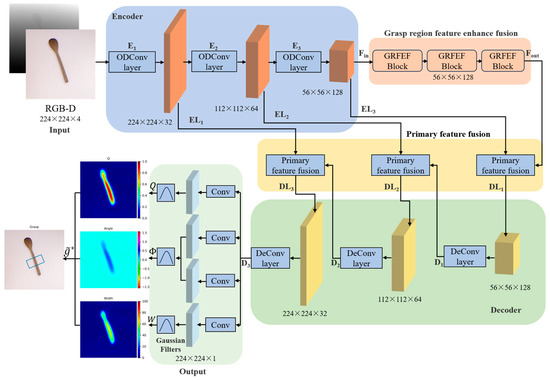
Figure 2.
Overall architecture of ODGNet.
The encoder consists of three omni-dimensional dynamic convolution layers for feature extraction; the size of the convolution kernel for the first omni-dimensional dynamic convolution is 9 × 9, and the size of the convolution kernel for the second and third omni-dimensional dynamic convolution is 4 × 4.
After going through the encoder, a feature map Fin with the dimensions 56 × 56 × 128 is obtained. In the grasping region feature enhancement fusion stage, three successive GRFEF modules are passed. On the one hand, this enhances the ability of the network to learn the features of the grasping region, and on the other hand, it suppresses the features of the non-grasping region, and outputs the 56 × 56 × 128 feature map Fout.
In the feature reconstruction stage, the primary pixel features of the encoder are fused with the high-level semantic features of the decoder through the primary feature fusion layer. This further improves the grasping region feature representation. Afterwards, the size of the feature map is restored to the input image size by transposed convolution, and the feature map D3 with the dimensions 224 × 224 × 32 is output.
Finally, in the output layer, the reconstructed feature D3 is used as the input to output the grasping quality map , the grasping angle map , and the grasping width map . The final grasp was obtained through three grasping maps.
3.2.1. Omni-Dimensional Dynamic Convolutional Layer
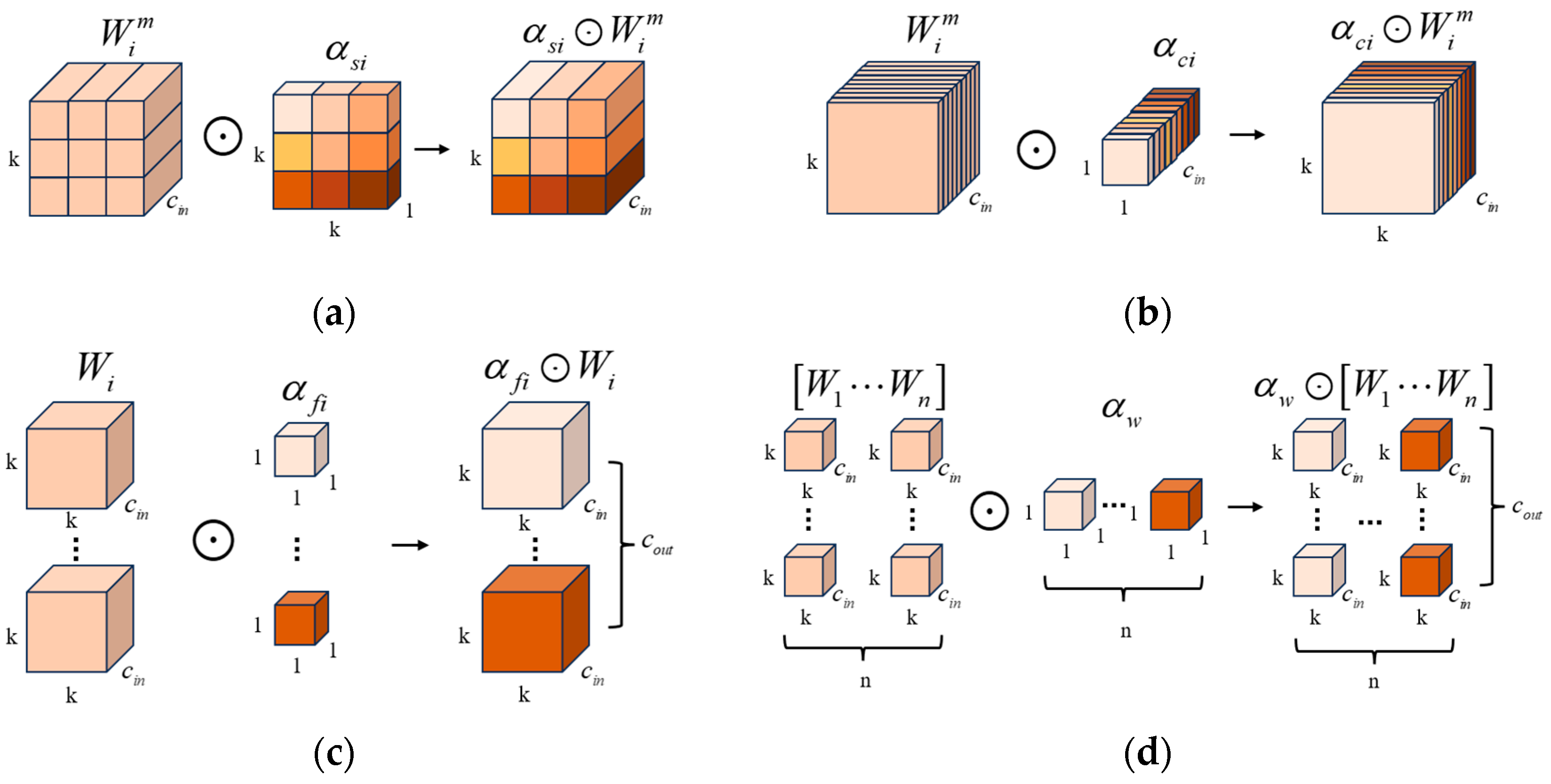
In the feature extraction stage of the encoder, omni-dimensional dynamic convolution is introduced in this paper in order to improve the feature extraction capability. The core idea of ODConv is to transform fixed convolutional kernel parameters into learnable dynamic parameters that can be adapted to different input features. ODConv is a dynamic convolution that utilizes a multidimensional attention mechanism to learn the four complementary attention types of the convolution kernel along the four dimensions of the kernel space in a parallel manner [11]. It is defined as follows:
where denotes the input features and denotes the output features; denotes the ith convolutional kernel; denote the attention weights computed along the dimension of the number of convolution kernels, the dimension of the output channel, the dimension of the input channel, and the dimension of the kernel space for , respectively; is the Hadamard product [32], representing the multiplication of the matrix elements at the corresponding positions and denoting multiplication operations in different dimensions along the kernel space; denotes a convolution operation. Figure 3 illustrates the process of Hadamard product operations for the four attention weights with the convolution kernel in ODConv.
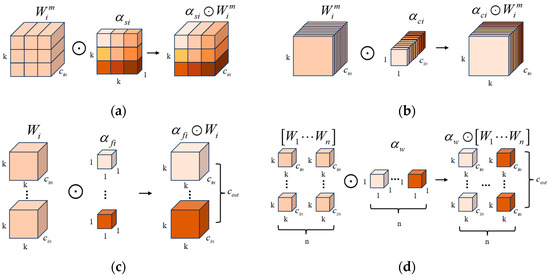
Figure 3.
Illustration of Hadamard product operations for the four attention weights with the convolution kernel in ODConv. (a) Hadamard product along the spatial dimension; (b) Hadamard product along the input channel dimension; (c) Hadamard product along the output channel dimension; (d) Hadamard product along the convolution kernel dimension.
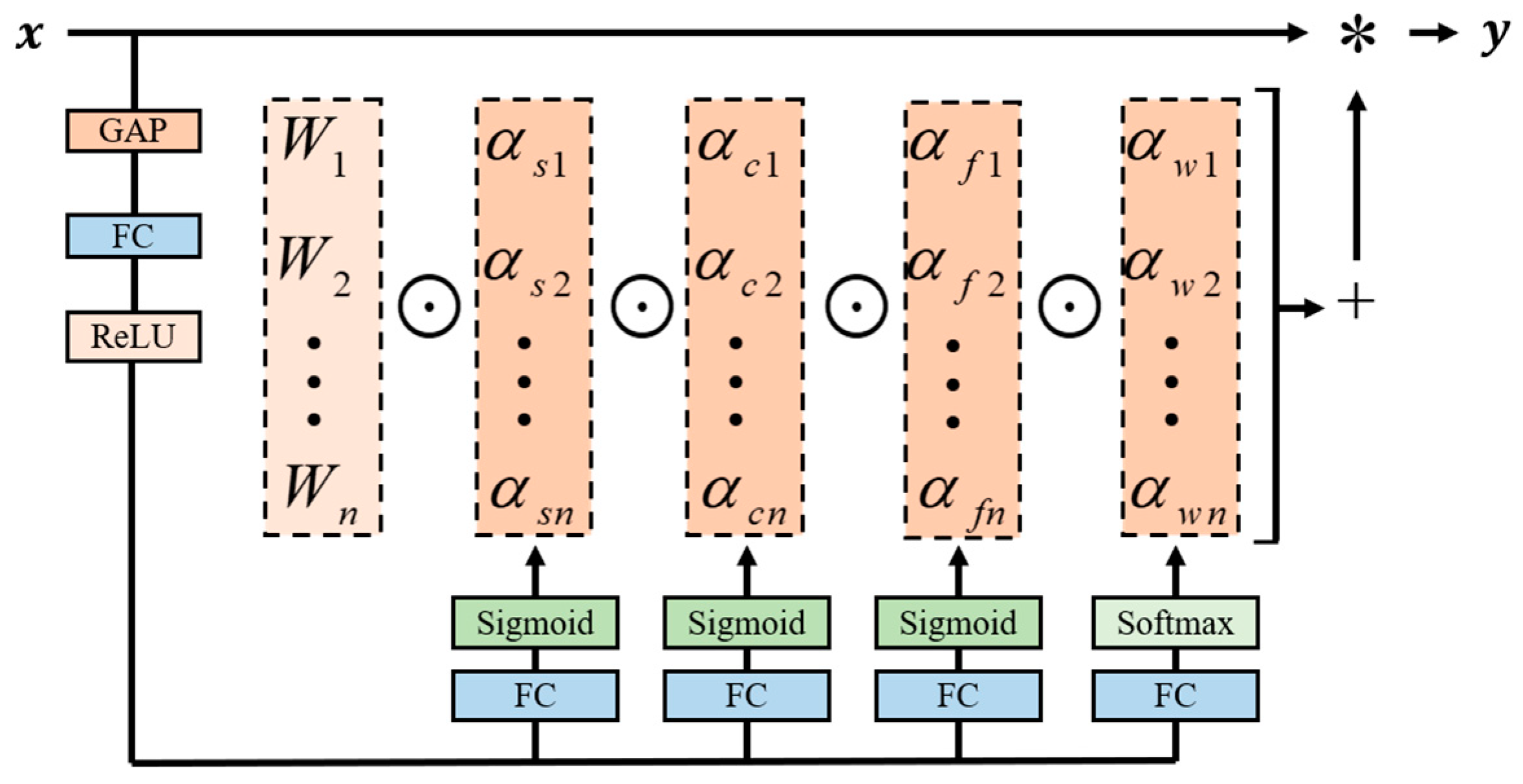
The four attention weights are computed with the multi-head attention module . The multi-head attention module is shown in Figure 4. Firstly, the input x is subjected to channel-wise Global Average Pooling (GAP) to obtain the feature vector with the length of . Then, the feature vector is mapped to a low-dimensional space by a fully connected (FC) layer and ReLu activation function to reduce the complexity of the model. Finally, the normalized attention parameters () are generated by fully connected layers and softmax or Sigmoid functions in the four branching heads.
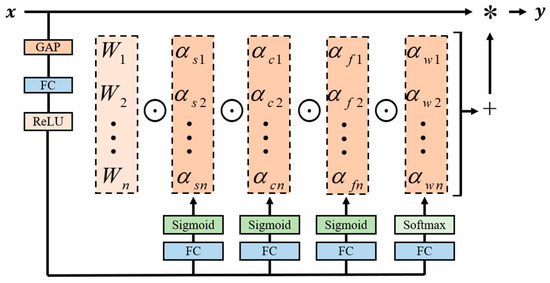
Figure 4.
The structure of omni-dimensional dynamic convolution.
Omni-dimensional dynamic convolution utilizes this multidimensional attention mechanism and a parallel strategy to learn the complementary attention of the convolutional kernels of all four dimensions of the convolutional layer along the kernel space, which can significantly enhance the feature extraction capability of the basic convolutional operations. In this paper, feature extraction of the input image is performed by three consecutive omni-dimensional dynamic convolutional layers, each of which contains an omni-dimensional dynamic convolution with four kernels, a batch normalization operation, and a ReLu activation function.
3.2.2. Grasping Region Feature Enhancement Fusion Module
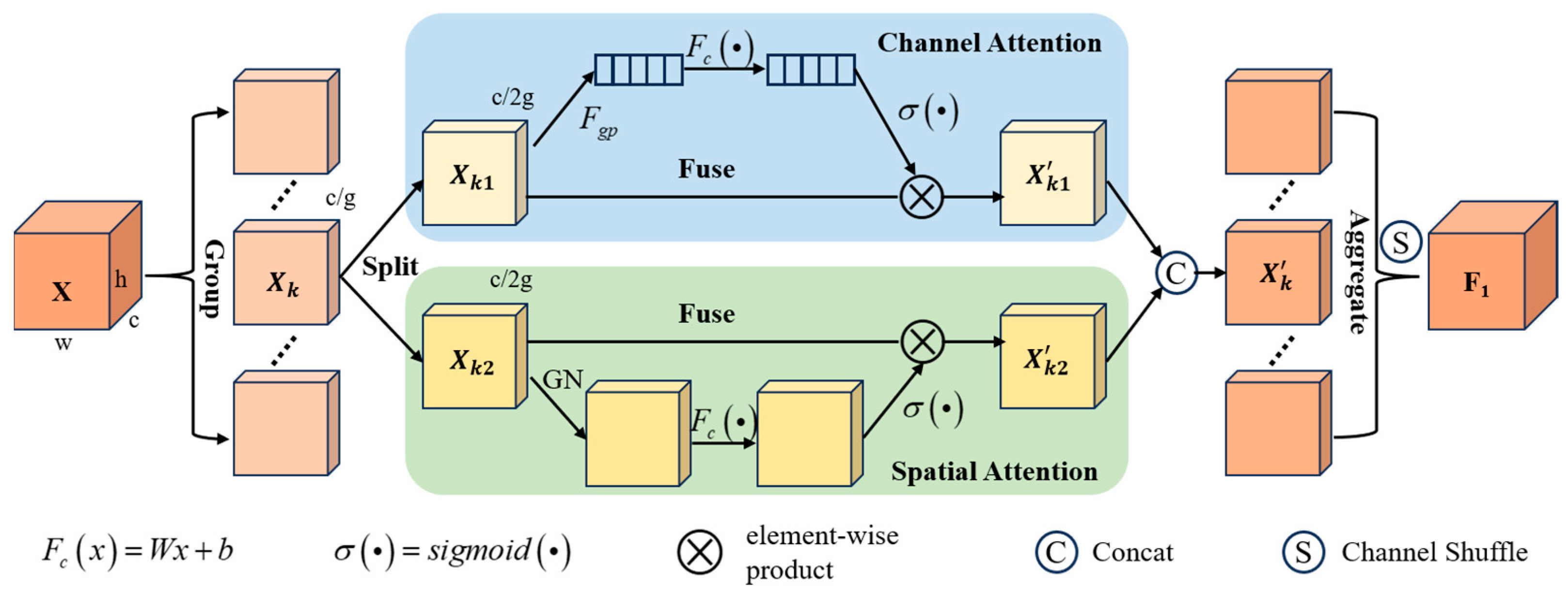
In the feature fusion stage, in order to further enhance the expression ability of the grasping region and solve the problem of non-consistency between the grasping region and the full view of the object, a grasping region feature enhancement fusion (GRFEF) module is proposed. As shown in Figure 5, this module consists of two ordinary convolutions, one omni-dimensional dynamic convolution and the SA module, which enhances the expression ability of the grasping region features through this two-branch feature fusion.

Figure 5.
The structure of GRFEF module.
On the one hand, the deep feature X is sequentially subjected to ordinary 3 × 3 convolution, 3 × 3 omni-dimensional dynamic convolution, and ordinary 3 × 3 convolution to obtain the feature F2; on the other hand, the feature X is passed through the SA module to obtain the feature F1; finally, the feature F1 and F2 are directly added and the feature Y is output through the ReLu activation function.
The design of Shuffle Attention (SA) incorporates the ideas of group convolution, spatial attention mechanisms, channel attention mechanisms, and ShuffleNetV2 [33]. As shown in Figure 6, in the SA module, the input feature map is first divided into g groups along the channel dimension, denoted as ; this part corresponds to the group part of Figure 6. Then, it is further divided into two sub-features along the channel dimension, denoted as . Sub-feature passes through the channel attention branch to obtain the dependencies between different channels. Sub-feature passes through the spatial attention branch to obtain the spatial dependencies between features. The channel attention branch first performs global averaging pooling (GAP) to obtain the feature vectors :
and then obtains the channel attention weights through the Sigmoid activation function after linear transformation:
where .
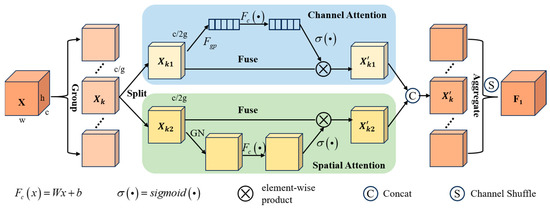
Figure 6.
The structure of SA module.
The spatial attention branch will first perform Group Norm (GN), and then, after linear transformation, the spatial attention weights are obtained by Sigmoid activation function, expressed as follows:
where .
After that, the results of the two types of attention are concatenated in the channel dimension., i.e., . Finally, the channel shuffle operation is used to ensure the interaction between the sub-features of each group.
3.2.3. Primary Feature Fusion Module
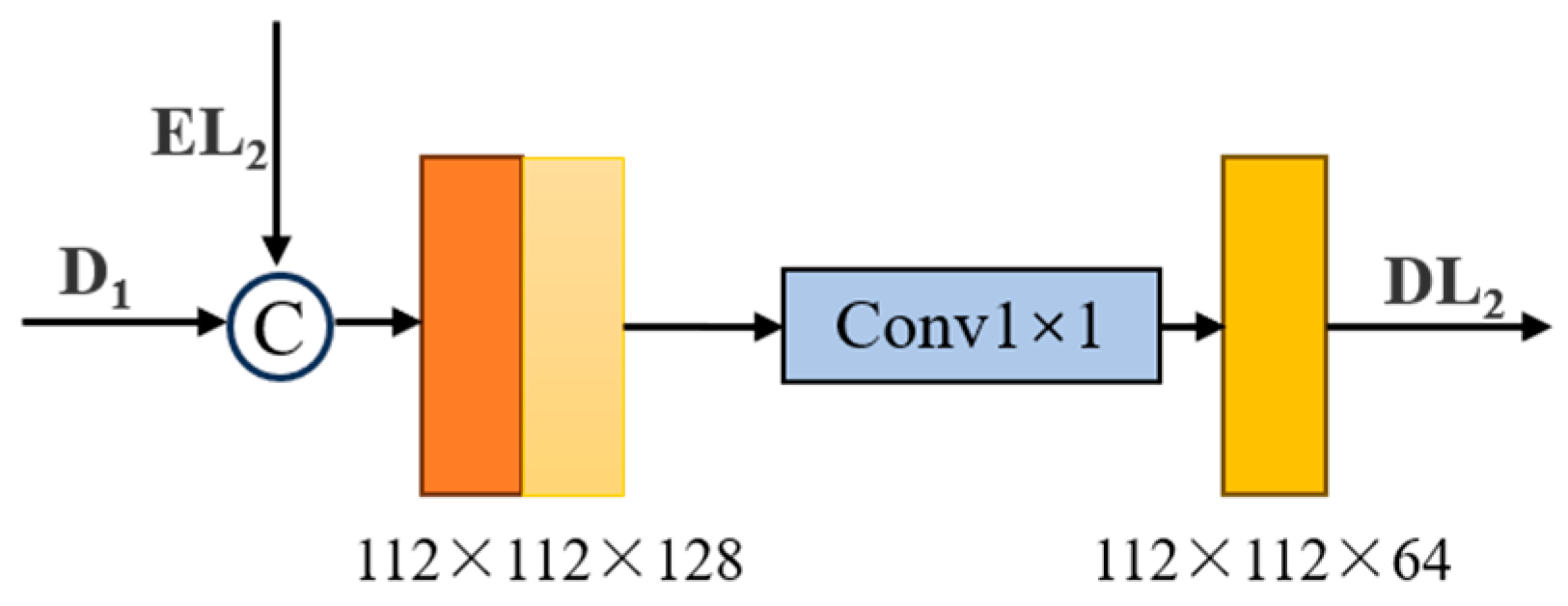
In general, the primary feature of convolutional neural networks retains more accurate location information, while the advanced feature contains stronger semantic information. For grasp detection, both location and semantic information are important. Inspired by the feature pyramid network [34], this paper proposes a module for primary feature fusion. The expressive ability of the grasping region is enhanced by fusing the high-resolution, semantically weak features down-sampled by the encoder with the low-resolution, semantically strong features up-sampled by the decoder. This is illustrated here in conjunction with the fusion of the down-sampled second layer features with the up-sampled second layer features. As shown in Figure 7, firstly, the feature EL1 of the down-sampling part is concatenated with the feature D1 of the up-sampling part in the channel dimension, the number of channels is doubled, then, the number of channels is restored to its original size by a 1 × 1 common convolution, and finally, the obtained feature DL2 is fed into the next layer of the transposed convolution for the next step of up-sampling. The expression of the grasping region is further enhanced by three sequential primary feature fusion modules.
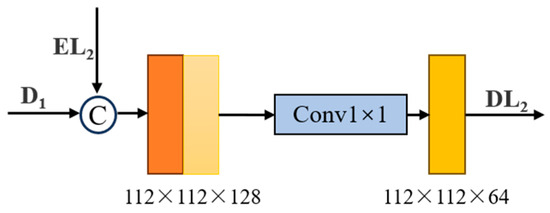
Figure 7.
The structure of the second primary feature fusion module.
3.2.4. Output Processing Module
The feature D3 is obtained after the feature reconstruction of the decoder. Then, D3 is used as input and passed through four 1 × 1 convolutions in parallel to obtain four grasping parameter maps, which are grasping quality map , grasping angle map and , and grasping width map . The grasping angle maps are decomposed into and . can be solved by the following equation:
In order to improve the success rate of grasping, this paper uses a 2D Gaussian kernel to smooth the grasping parameter maps [35]. It makes the distribution of grasping points more uniform, so that the best grasping configuration can be obtained. The 2D Gaussian kernel expression is given below:
where . Once the smoothed grasping parameter map is obtained, the final grasping configuration can be obtained according to Equation (4).
3.3. Loss Function
The purpose of a grasp detection network is to predict a set of grasp parameter maps from a set of input images . For a dataset consisting of objects and rectangle labels, their rectangle labels are processed to obtain the corresponding grasping parameter map . The goal when training the grasp detection network is to minimize the difference between and . In this paper, we use smooth L1 [36] as the loss function and the complete loss function can be expressed as
where is
Considering the different roles of grasping quality, grasping angle, and grasping width, the remaining two parameters are generally determined based on the grasping quality. Therefore, adding weights to the losses corresponding to these four parameters, the total loss function is further expressed as
where are the smooth L1 loss functions of , respectively, and are the weights of , respectively. Here, .
4. Experimental Validation
In order to verify the performance of the ODGNet, in this section, firstly, the ODGNet is trained and tested on the Cornell dataset and compared with the results of the previous algorithms; secondly, in order to test the ability of the multi-object grasp detection, grasp detection experiments are conducted on the multi-object dataset; then, in order to test the contribution of each module to the algorithm, the relevant ablation experiments are conducted; and lastly, the grasping experiments are carried out in a simulation environment.
4.1. Dataset Preprocessing
The Cornell dataset is widely used for the training of grasp detection algorithms. It consists of 885 RGB images with a resolution of 640 × 480, their corresponding depth images, and their grasp labels. Due to the small amount of data in the Cornell dataset, data enhancement is required to increase the training data. The first step is image cropping. The cropped image not only satisfies the input requirements but also saves computational resources. In this paper, the method used is to crop the image based on the center of the grasping rectangle rather than the center of the source image, which allows the target object to be able to appear at different locations in the cropped image. The size of the cropped image is 224 × 224. The second step is image rotation, where the cropped image is randomly rotated to allow for a wider range of object grasping angles. After a series of data enhancement operations, the training data are greatly expanded, which helps to improve the model performance.
4.2. Training Details
The ODGNet is trained on an NVIDIA GPU RTX 3080 with 10 GB memory. The computer system is ubuntu 18.04 with Cuda 11.1. The deep learning framework is PyTorch 2.0 with python 3.8. The optimizer uses Ranger with the initial learning rate set to 0.0005 and the batch size set to 8. A total of 50 epochs are trained on the Cornell grasp dataset and each epoch contains 1000 batches. A proportion of 90% of the dataset is set as the training set and the remaining 10% is used as the test set. For the training set, 90% is used for training and 10% is used for validation.
4.3. Evaluation Metric
The grasp evaluation metrics are evaluated according to grasp rectangles, so the grasp configuration map needs to be converted into grasp rectangles at first. The grasping configuration is considered effective when the following two conditions are satisfied [8,9].
- (1)
- The Jaccard index between the predicted grasping rectangle and the ground truth of grasping rectangle is greater than 0.25, expressed as
- (2)
- The variance between the predicted grasp angle and the ground truth of grasp angle is less than 30°, expressed as
4.4. Experimental Results and Analysis
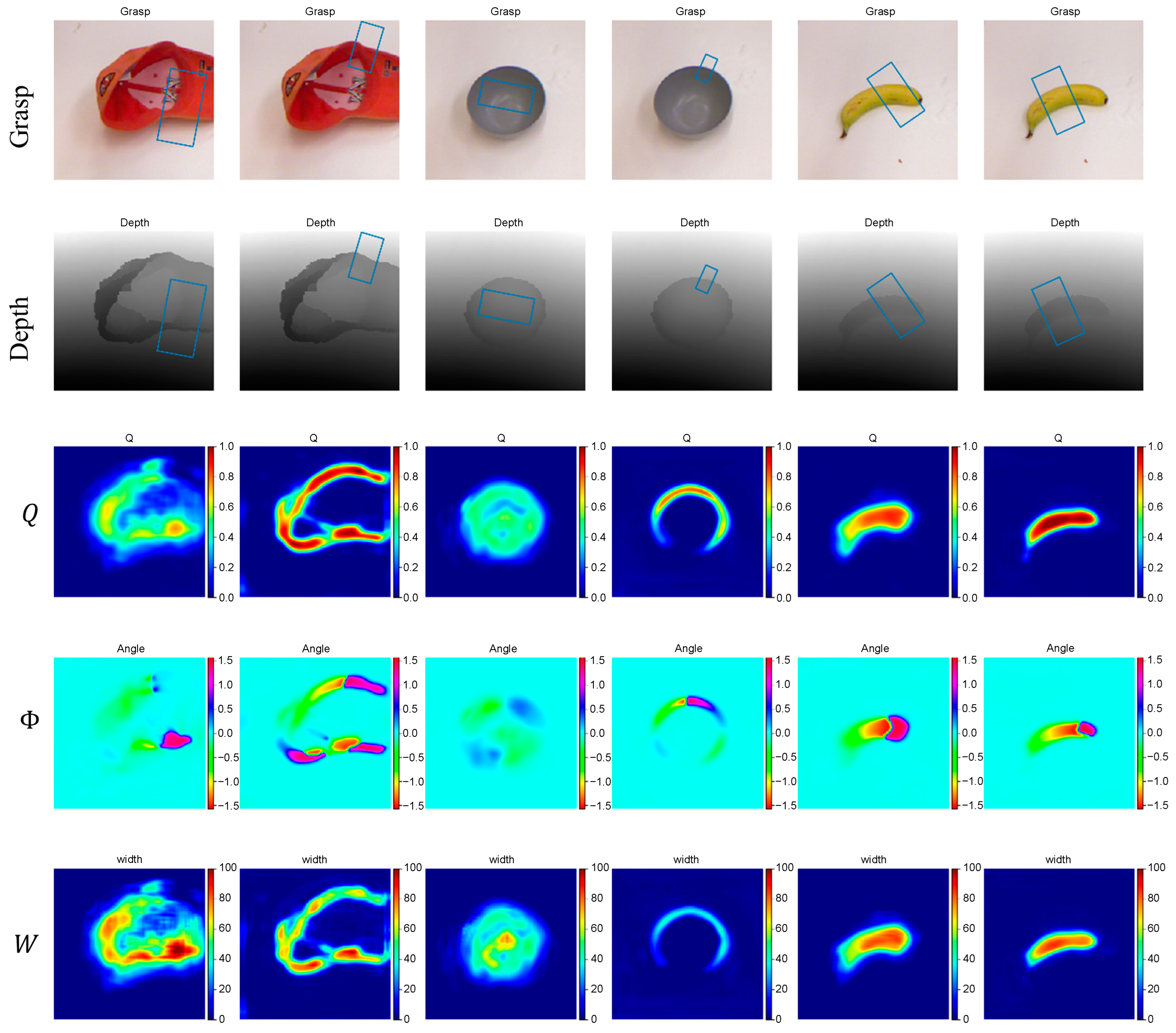
The ODGNet is trained and tested on the Cornell dataset with RGB-D as the input, and the results of this network for grasp detection on the Cornell dataset are shown in Figure 8. In Figure 8, from top to bottom, each row is, in turn, the TOP-3 predicted grasping rectangular boxes in the color image, the TOP-3 predicted grasping rectangular boxes in the depth image, the grasping quality map , the grasping angle map , and the grasping width map .

Figure 8.
Grasp detection results with the Cornell dataset.
TOP-3 predicted grasping refers to finding three local extreme points from the grasping quality map . And then, three grasping rectangular boxes are generated based on these three points, the grasping angle map, and the grasping width map. Since some of the grasping quality maps only have two extreme points, only two grasping rectangular boxes are generated.
As can be seen from the grasp quality map in Figure 8, the grasping region is well predicted and the grasp quality score of the background is almost 0, indicating that ODGNet can separate the grasping region from the background well. From the predicted grasping rectangular boxes for each object, it is clear that our method exhibits excellent grasping adaptability for all shapes of objects.
4.4.1. Comparison Experiments on Cornell Dataset
To facilitate a comprehensive comparison of the performance of our model with those in related studies, the Cornell dataset was split using the image-wise split (IW) and object-wise split (OW) methods [8,9]:
- (1)
- IW: All images in the Cornell dataset are randomly divided into a training set and a test set. The objects in the test set may have been seen in the training set, but with different positions and orientations. The purpose of splitting by image is to test the network’s grasp detection ability for the same object but at different placement positions.
- (2)
- OW: All the images in the Cornell dataset are divided into training and test sets by object category, and the images of the objects that have been used in the training set are not used again in the test set. Its purpose is to test the network’s grasp detection ability for the unknown objects.
Shown in Table 1 is a comparison of the detection results among the different methods using the Cornell dataset with the IW and OW splitting modes. From Table 1, it can be seen that compared with some existing methods, the ODGNet not only achieves the best detection accuracy of 98.4% in the IW splitting mode, but also achieves the best performance of 97.8% in the OW splitting mode, which indicates that the detection of unknown objects is extremely effective. Moreover, the detection speed of a single image is 21 ms, which fully satisfies the requirement of real-time grasp detection.

Table 1.
Comparison of results on the Cornell dataset.
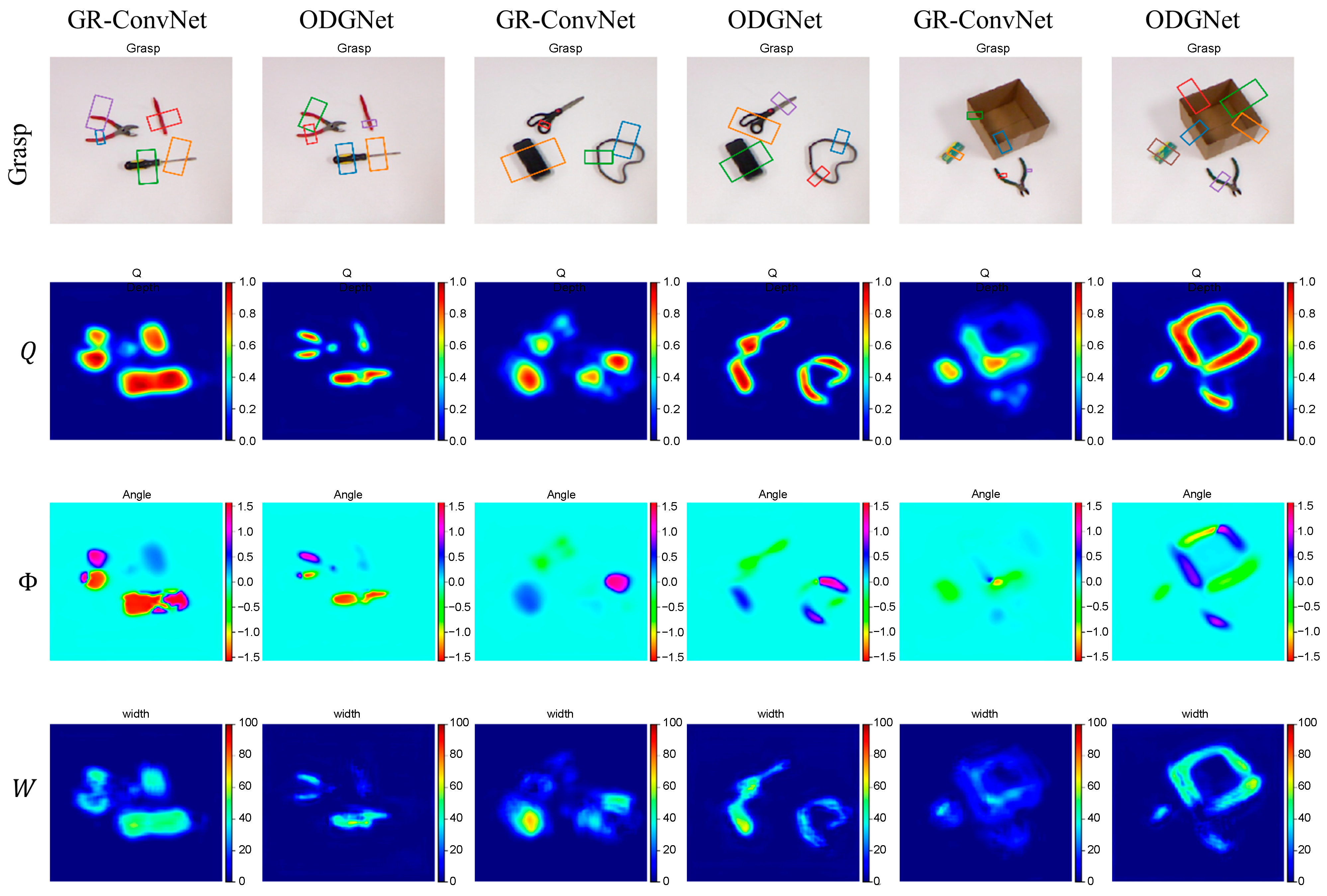
In order to gain a more intuitive understanding of the detection effect of ODGNet on the Cornell dataset, this paper chooses the GR-ConvNet algorithm, for which a very good grasp detection effect has been reported in recent years, for comparison. In Figure 9, the grasp detection results of the ODGNet algorithm and GR-ConvNet algorithm on the Cornell dataset are shown.
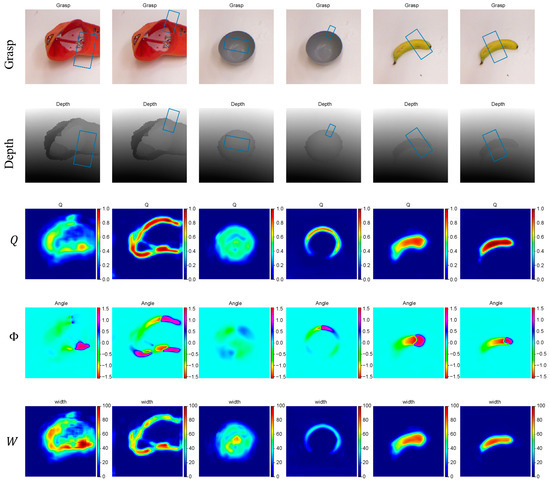
Figure 9.
Comparison of grasp detection results on the Cornell dataset.
In Figure 9, the first object detected is a red hat. From the grasping quality map and grasping width map generated by GR-ConvNet, its predicted grasping region is distributed along the edge of the hat, and the overall trend is correct. However, its score for the whole grasping region is very low, and it cannot obtain good grasp detection results. In contrast, the ODGNet algorithm predicts the grasp quality map with a score close to 1 for the edge of the hat, which predicts the grasping region very well. The second object is a bowl, whose graspable region should be the edge of the bowl, and the interior of the bowl is not graspable. However, the GR-ConvNet algorithm generates a grasp quality map that treats all regions of the bowl as graspable regions, which in turn generates grasp rectangles that are also located in the interior of the bowl. The ODGNet algorithm, on the other hand, accurately predicts the edge grasping regions. For these two objects, they clearly exhibit the characteristic of inconsistency between the graspable region and the full view of the object. The GR-ConvNet algorithm only extracts the features by ordinary convolution and does not use the attention mechanism, so it has an insufficient learning ability for the relationship between the graspable region and the full view of the object. On the contrary, the ODGNet algorithm introduces ODConv to enhance the feature extraction ability of the grasping region, and, at the same time, introduces the attention mechanism to construct the feature enhancement fusion module of the grasping region, which strengthens the feature learning ability of the graspable region. The last object is a banana; comparing the grasping quality maps of the two algorithms, the GR-ConvNet algorithm predicts a significantly wider distribution and lower scores of grasping regions, with poor grasping results. Considering that the algorithm does not use multi-scale features, it is not capable of learning enough grasping features for objects of different scales.
In order to evaluate the robustness of ODGNet more rigorously, the Jaccard index was modified. The experiments were conducted at Jaccard index values of 0.25, 0.30, 0.35, and 0.40, respectively, and the corresponding detection results are shown in Table 2. From Table 2, it can be seen that the detection accuracy of both algorithms decreases with the increase in the Jaccard index, but the accuracy of ODGNet decreases more slowly, and the detection accuracy of ODGNet is above 91% both with the IW subset and OW subset. This proves that the proposed method is more robust.

Table 2.
Comparison of accuracy at different Jaccard indices.
4.4.2. Experiments on Multi-Object Dataset
In order to evaluate the effectiveness of ODGNet for grasp detection in the clutter scenes, it was tested on a multi-object dataset [13]. The multi-object dataset consists of 97 RGB-D images, each containing at least three objects, each labelled using multiple rectangular boxes, and each object is previously unseen. The GR-ConvNet algorithm is also used as a comparison group, and the specific detection results are shown in Figure 10.
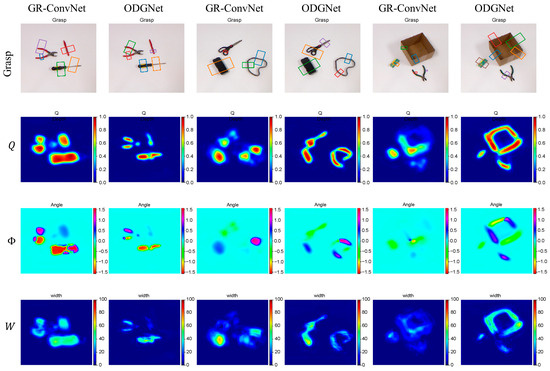
Figure 10.
Comparison of grasp detection results on multi-object datasets.
In Figure 10, there are three scenes. For the GR-ConvNet, in the first scene, although it generates some better grasping rectangles, its grasping area is too large in the grasping quality map; in the second and third scenes, the GR-ConvNet does not generate suitable grasping rectangles for some objects, the grasping quality scores are too low in the grasping quality maps, and the grasping regions of the objects are not extracted.
For ODGNet, on the one hand, since ODGNet utilizes multi-scale features, in the first scene, the generated grasping regions are accurate and suitable in size; on the other hand, since ODGNet uses ODConv and the attention mechanism, which enhance the feature extraction capability and the localization of the graspable regions, the graspable regions of all the objects are predicted well and good grasping configurations are generated in the second and third scenes.
4.4.3. Ablation Experiments
In order to verify the role of each module in the ODGNet, ablation experiments are conducted. In the ablation experiments, the ODConv is replaced by ordinary convolution, the SA module is replaced by a shorting module, and the primary feature fusion module is directly removed. The ablation results are shown in Table 3. The results show that the ODConv and SA module contribute the most to the network, and the primary feature fusion module utilizes multi-scale features to further improve the detection accuracy.

Table 3.
Results of ablation experiments on the Cornell dataset.
4.4.4. Experiments in the Simulation Environment
We used the PyBullet simulation platform to build a grasping environment with the UR5 robotic arm, and selected 10 common objects in YCB [38] as the objects to be grasped. The grasping experiment was divided into two scenarios: a single-object grasping scenario and a multi-object grasping scenario, and the positions of the objects in each scenario were randomly generated, and the experimental process is shown in Figure 11. In each of the two scenarios, we performed 250 grasping tasks and counted the number of successful tasks.

Figure 11.
Experimental process of single-object and multi-object grasping in the simulation environment.
We conducted the same experiments with the GR-ConvNet algorithm, and the experimental results are shown in Table 4. In Table 4, the ODGNet has a higher grasping success rate than the GR-ConvNet in two grasping scenarios, and the grasping success rate in the two grasping scenarios are above 90%. The results show that ODGNet has excellent grasp detection performance even in unstructured scenes with multiple objects.

Table 4.
Grasping results in the simulation environment.
The above experiments can show that the ODGNet can perform fast and accurate grasp detection for unknown objects. The experimental results with the Cornell dataset and multi-object dataset show that the ODConv in ODGNet enhances the ability of feature extraction, the GRFEF module enhances the ability of feature learning for the graspable region, and the primary feature fusion module enhances the ability to utilize multi-scale features. The ablation experiment proves that each module contributes to the ODGNet accordingly, and the simulation grasping experiment proves the effectiveness of the proposed method.
5. Conclusions
In this paper, we propose a novel grasp detection network called ODGNet. This network can efficiently and accurately predict the optimal grasping configuration from input RGB-D images. Benefiting from the ODConv and GRFEF modules, the ODGNet achieves a better grasp detection performance with the Cornell dataset and multi-object dataset. In the simulated grasping experiments, our method achieved a grasp success rate of 95.2% for single objects and 90.4% for multiple objects. In conclusion, our method exhibits a higher detection accuracy and faster detection speed for potential application industries such as tidying up the home environment and grasping various workpieces. Future work will focus on improving the grasp detection of multiple objects in complex environments, as well as studying the extension of the algorithm to three-finger grippers and multi-finger grippers.
Author Contributions
Conceptualization, X.K. and B.T.; methodology, B.T.; software, B.T.; validation, X.K. and B.T.; formal analysis, B.T.; investigation, B.T.; resources, X.K.; data curation, B.T.; writing—original draft preparation, B.T.; writing—review and editing, X.K.; visualization, B.T.; supervision, X.K.; project administration, X.K.; funding acquisition, X.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China: Design and Development of High Performance Marine Electric Field Sensor, grant number 2022YFC3104001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ODConv | Omni-dimensional dynamic convolution |
| ODGNet | Omni-dimensional dynamic convolution grasp detection network |
| SA | Shuffle Attention |
| GRFEF | Grasping region feature enhancement and fusion |
| GR-ConvNet | Generative Residual Convolutional Neural Network |
| GAP | Global Average Pooling |
| FC | Fully connected |
References
- Du, G.; Wang, K.; Lian, S.; Zhao, K. Vision-Based Robotic Grasping from Object Localization, Object Pose Estimation to Grasp Estimation for Parallel Grippers: A Review. Artif. Intell. Rev. 2021, 54, 1677–1734. [Google Scholar] [CrossRef]
- Dong, M.; Zhang, J. A Review of Robotic Grasp Detection Technology. Robotica 2023, 41, 3846–3885. [Google Scholar] [CrossRef]
- Jiang, Y.; Moseson, S.; Saxena, A. Efficient Grasping from RGBD Images: Learning Using a New Rectangle Representation. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3304–3311. [Google Scholar]
- Lenz, I.; Lee, H.; Saxena, A. Deep Learning for Detecting Robotic Grasps. Int. J. Robot. Res. 2015, 34, 705–724. [Google Scholar] [CrossRef]
- Redmon, J.; Angelova, A. Real-Time Grasp Detection Using Convolutional Neural Networks. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Washington, DC, USA, 26–30 May 2015; pp. 1316–1322. [Google Scholar]
- Kumra, S.; Kanan, C. Robotic Grasp Detection Using Deep Convolutional Neural Networks. arXiv 2017, arXiv:1611.08036. Available online: https://arxiv.org/abs/1611.08036v3 (accessed on 13 April 2024).
- Zhou, X.; Lan, X.; Zhang, H.; Tian, Z.; Zhang, Y.; Zheng, N. Fully Convolutional Grasp Detection Network with Oriented Anchor Box. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7223–7230. [Google Scholar]
- Morrison, D.; Corke, P.; Leitner, J. Closing the Loop for Robotic Grasping: A Real-Time, Generative Grasp Synthesis Approach 2018. arXiv 2018, arXiv:1804.05172. [Google Scholar]
- Yu, S.; Zhai, D.-H.; Xia, Y. SKGNet: Robotic Grasp Detection With Selective Kernel Convolution. IEEE Trans. Autom. Sci. Eng. 2022, 20, 2241–2252. [Google Scholar] [CrossRef]
- Yan, S.; Zhang, L. CR-Net: Robot Grasping Detection Method Integrating Convolutional Block Attention Module and Residual Module. IET Comput. Vis. 2024, 18, 420–433. [Google Scholar] [CrossRef]
- Li, C.; Zhou, A.; Yao, A. Omni-Dimensional Dynamic Convolution. arXiv 2022, arXiv:2209.07947. [Google Scholar]
- Zhang, Q.-L.; Yang, Y.-B. SA-Net: Shuffle Attention for Deep Convolutional Neural Networks. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 2235–2239. [Google Scholar]
- Chu, F.-J.; Xu, R.; Vela, P.A. Real-World Multiobject, Multigrasp Detection. IEEE Robot. Autom. Lett. 2018, 3, 3355–3362. [Google Scholar] [CrossRef]
- Bicchi, A. Hands for Dexterous Manipulation and Robust Grasping: A Difficult Road toward Simplicity. IEEE Trans. Robot. Autom. 2000, 16, 652–662. [Google Scholar] [CrossRef]
- Bohg, J.; Morales, A.; Asfour, T.; Kragic, D. Data-Driven Grasp Synthesis—A Survey. IEEE Trans. Robot. 2014, 30, 289–309. [Google Scholar] [CrossRef]
- Pinto, L.; Gupta, A. Supersizing Self-Supervision: Learning to Grasp from 50K Tries and 700 Robot Hours. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3406–3413. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, Nevada, 3–6 December 2012; Volume 25. [Google Scholar]
- Mahler, J.; Liang, J.; Niyaz, S.; Laskey, M.; Doan, R.; Liu, X.; Aparicio, J.; Goldberg, K. Dex-Net 2.0: Deep Learning to Plan Robust Grasps with Synthetic Point Clouds and Analytic Grasp Metrics. arXiv 2017, arXiv:1703.09312. [Google Scholar] [CrossRef]
- Morrison, D.; Corke, P.; Leitner, J. Learning Robust, Real-Time, Reactive Robotic Grasping. Int. J. Robot. Res. 2020, 39, 183–201. [Google Scholar] [CrossRef]
- Kumra, S.; Joshi, S.; Sahin, F. Antipodal Robotic Grasping Using Generative Residual Convolutional Neural Network. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 19–25 October 2020; pp. 9626–9633. [Google Scholar]
- Yu, S.; Zhai, D.-H.; Xia, Y.; Wu, H.; Liao, J. SE-ResUNet: A Novel Robotic Grasp Detection Method. IEEE Robot. Autom. Lett. 2022, 7, 5238–5245. [Google Scholar] [CrossRef]
- Geng, W.; Cao, Z.; Guan, P.; Jing, F.; Tan, M.; Yu, J. Grasp Detection with Hierarchical Multi-Scale Feature Fusion and Inverted Shuffle Residual. Tsinghua Sci. Technol. 2024, 29, 244–256. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, Z.; Kan, Z. When Transformer Meets Robotic Grasping: Exploits Context for Efficient Grasp Detection. IEEE Robot. Autom. Lett. 2022, 7, 8170–8177. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, X. Bilateral Cross-Modal Fusion Network for Robot Grasp Detection. Sensors 2023, 23, 3340. [Google Scholar] [CrossRef] [PubMed]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Yang, B.; Bender, G.; Le, Q.V.; Ngiam, J. CondConv: Conditionally Parameterized Convolutions for Efficient Inference. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Chen, Y.; Dai, X.; Liu, M.; Chen, D.; Yuan, L.; Liu, Z. Dynamic Convolution: Attention Over Convolution Kernels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11030–11039. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual Attention Network for Scene Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Davis, C. The Norm of the Schur Product Operation. Numer. Math. 1962, 4, 343–344. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, X.; Zheng, H.-T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 116–131. [Google Scholar]
- Lin, T.-Y.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, Hawaii, 21–26 June 2017; pp. 2117–2125. [Google Scholar]
- Johns, E.; Leutenegger, S.; Davison, A.J. Deep Learning a Grasp Function for Grasping under Gripper Pose Uncertainty. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 4461–4468. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Asif, U.; Tang, J.; Harrer, S. GraspNet: An Efficient Convolutional Neural Network for Real-Time Grasp Detection for Low-Powered Devices. In Proceedings of the International Joint Conferences on Artificial Intelligence, Stockholm, Sweden, 13 July 2018. [Google Scholar]
- Calli, B.; Singh, A.; Bruce, J.; Walsman, A.; Konolige, K.; Srinivasa, S.; Abbeel, P.; Dollar, A.M. Yale-CMU-Berkeley Dataset for Robotic Manipulation Research. Int. J. Robot. Res. 2017, 36, 261–268. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).