Flutter of a Plate at High Supersonic Speeds
Abstract
:1. Introduction
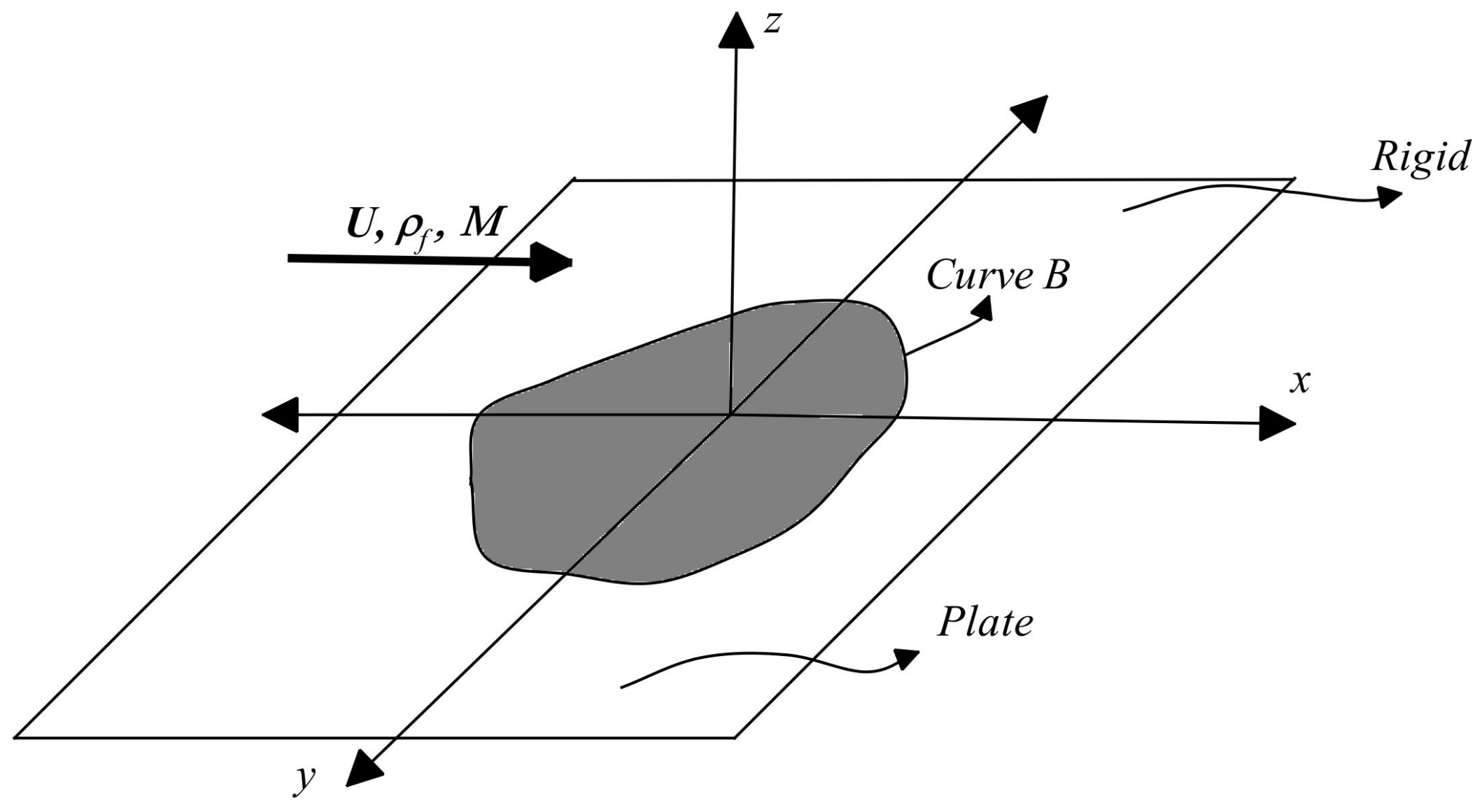
2. General Formulation
3. Piston Theory Approximation
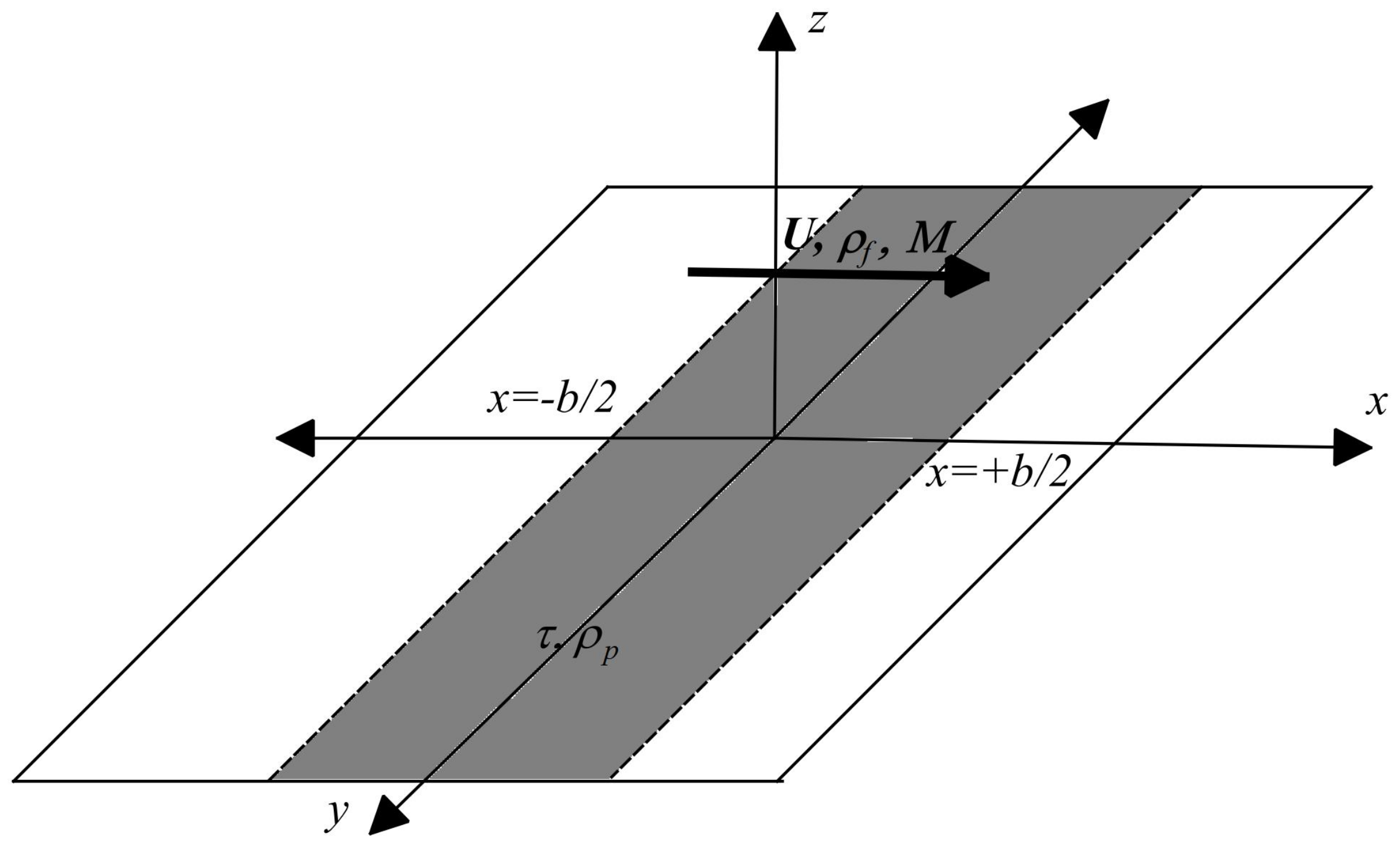
4. Infinite Strip Plate
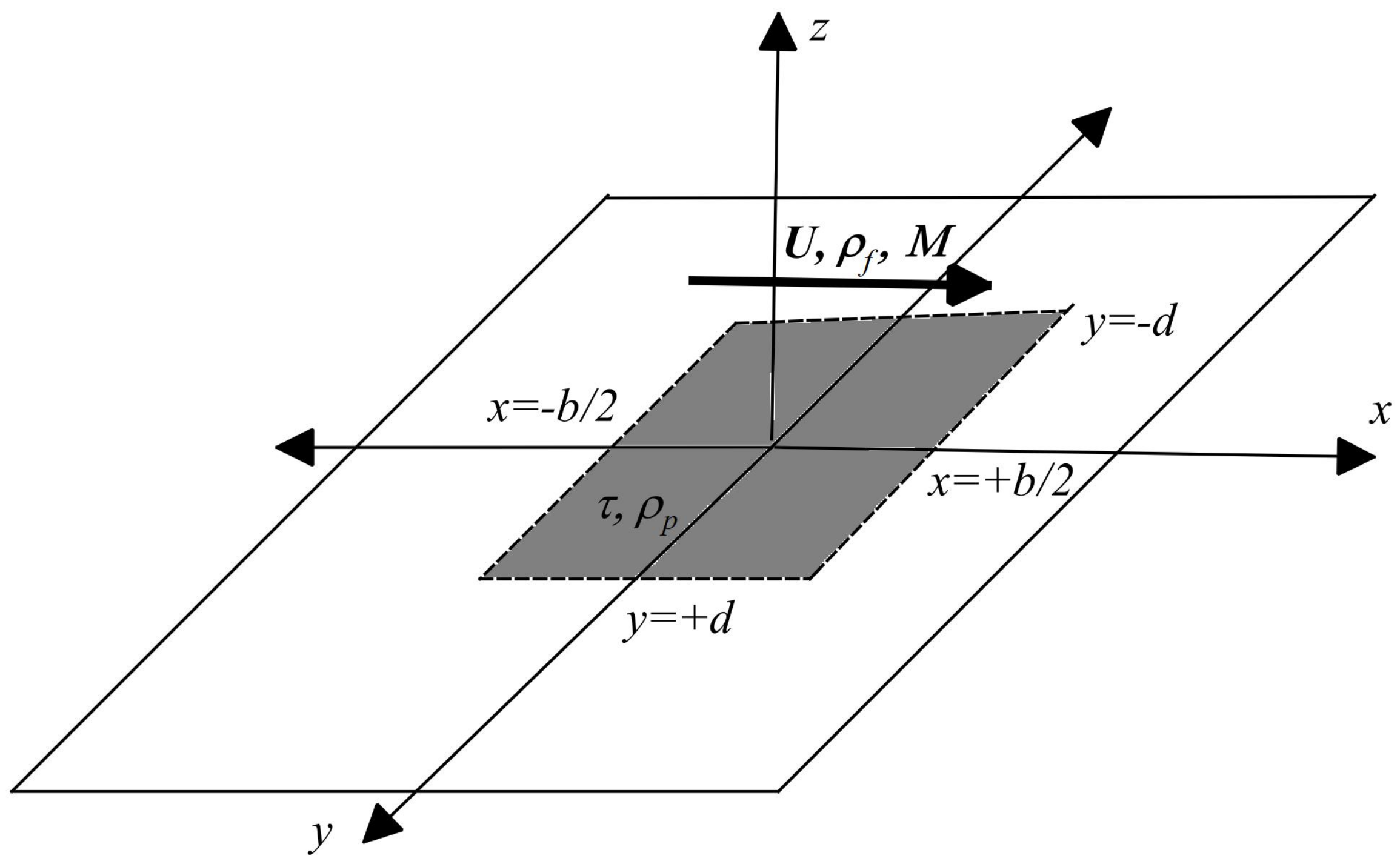
5. Rectangular Plate
6. Analytical Solution
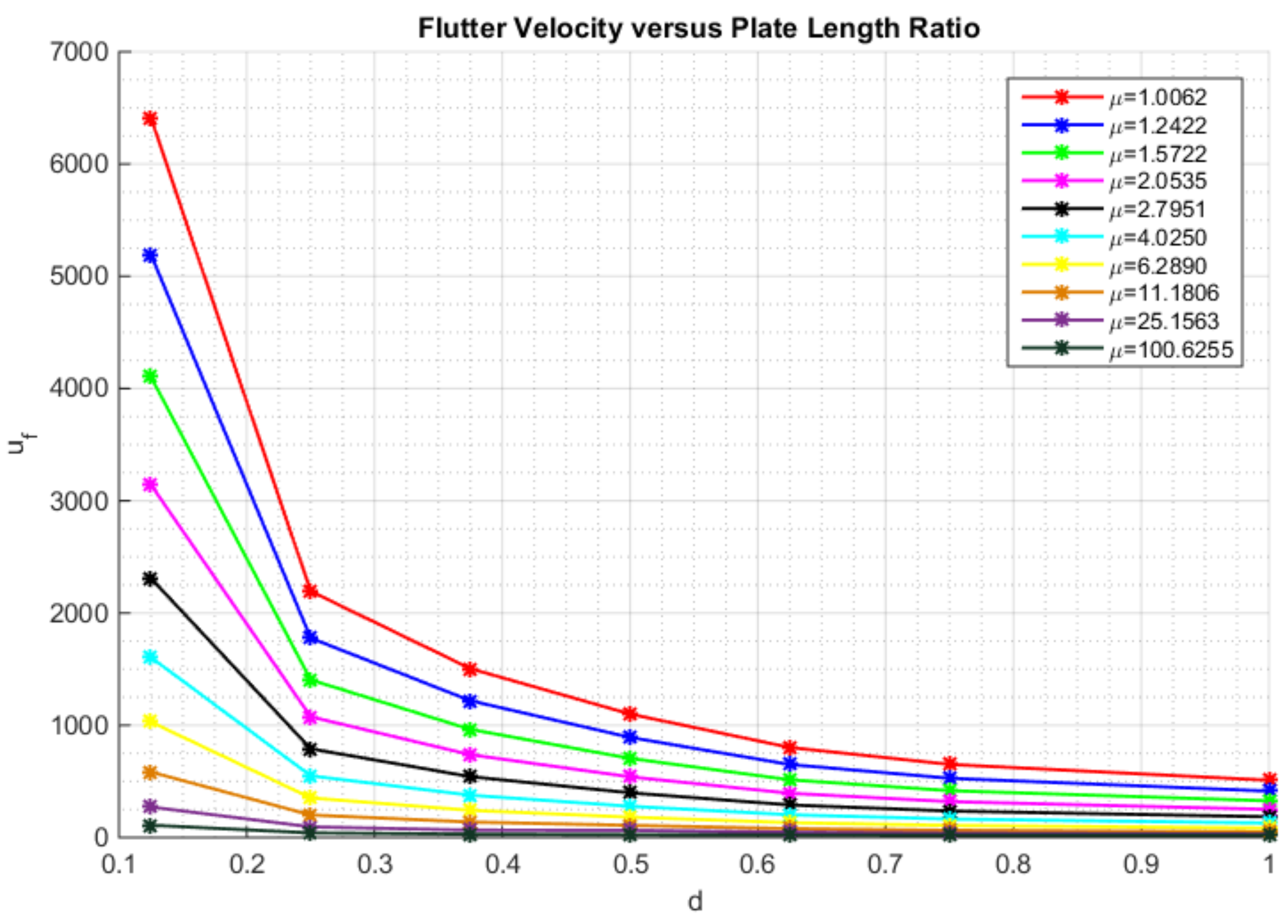
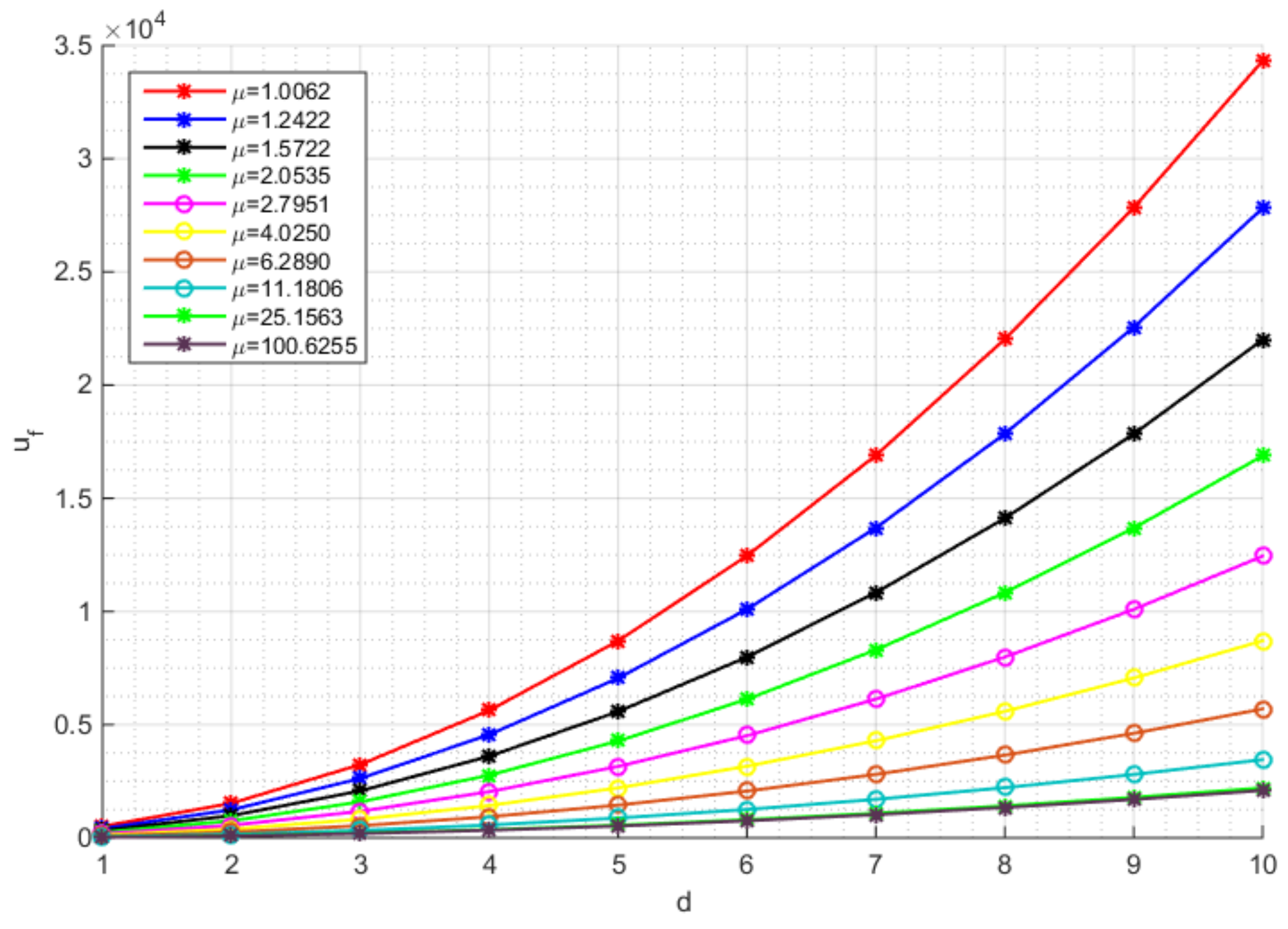
7. Results and Discussion
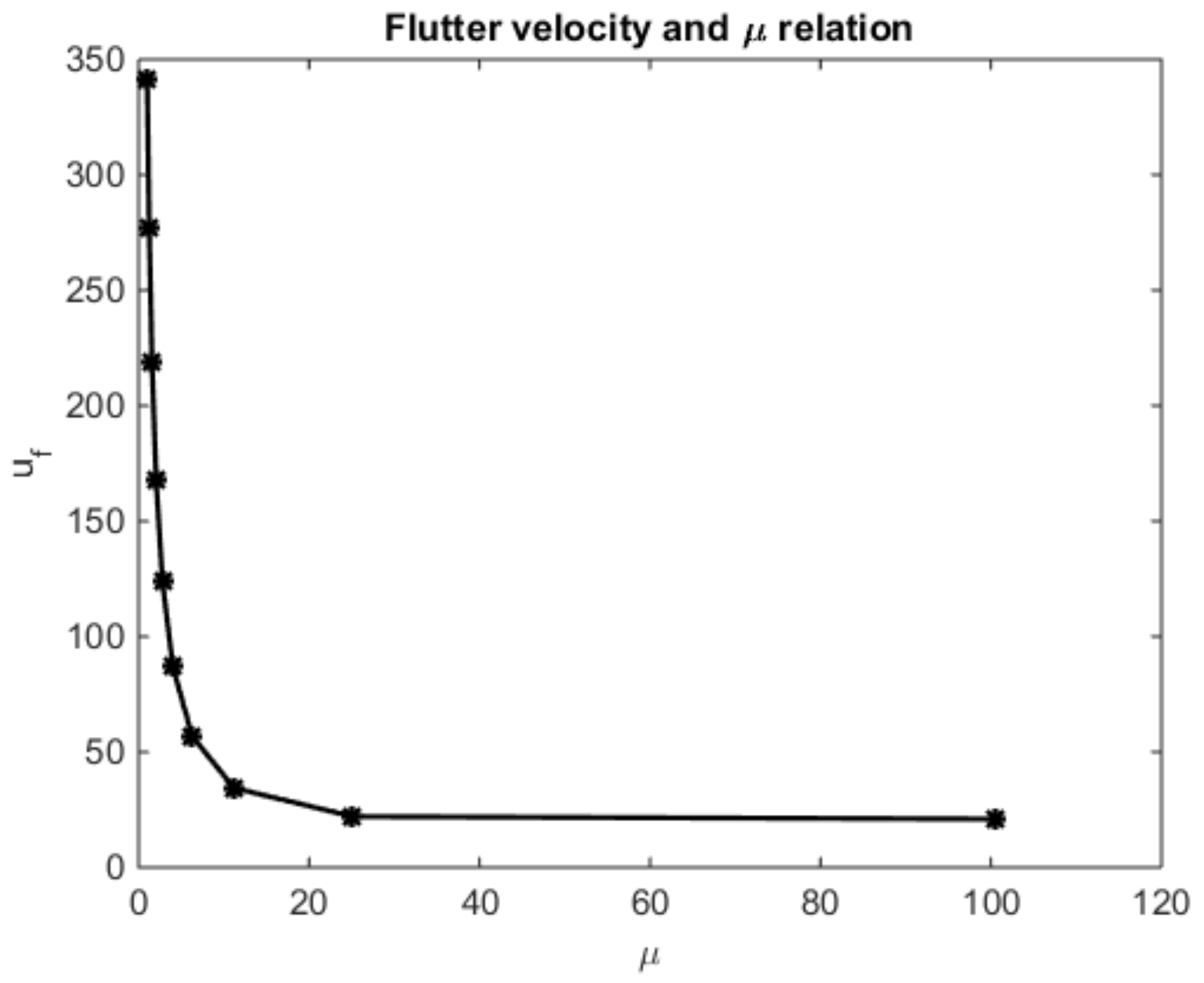
7.1. Infinite Strip
7.2. Rectangular Plate
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Definition |
| E | Young’s modulus |
| Thickness of plate | |
| b | Length of plate |
| d | Width of plate |
| Density of plate | |
| w | Displacement of plate |
| Poisson’s ratio | |
| U | Velocity of the fluid |
| Density of the fluid | |
| M | Mach number |
| Mass ratio | |
| Dimensionless sound velocity | |
| Base function | |
| R | Residual |
| N | Number of collocation points |
| Dimensionless flutter velocity |
References
- Bisplinghoff, R.L.; Ashley, H.; Halfman, R.L. Aeroelasticity. In Dover Books on Aeronautical Engineering Series; Dover Publications: New York, NY, USA, 1996. [Google Scholar]
- Dowell, E.H.; Crawley, E.F.; Curtiss, H.C.; Peters, D.A.; Scanlan, R.H.; Sisto, F. A Modern Course in Aeroelasticity; Springer Science and Business Media: Dordrecht, The Netherlands, 1995. [Google Scholar]
- AGARD. Manual on Aeroelasticity; Report No: 578; NATO: Washington, DC, USA, 1971. [Google Scholar]
- Erol, U.; Sule, K. Vibrations of an Infinite Plate Placed in a Circular Channel Containing Fluid Flow. Aircr. Eng. Aerosp. Technol. 2010, 81, 533–535. [Google Scholar]
- Epureanu, B.I.; Yin, S.H. Identification of damage in an aeroelastic system based on attractor deformations. Comput. Struct. 2004, 82, 2743–2751. [Google Scholar] [CrossRef]
- Vedeneev, V.V. Panel flutter at low supersonic speeds. J. Fluids Struct. 2012, 29, 79–96. [Google Scholar] [CrossRef]
- Dowell, E.H. Flutter of infinitely Long Plates and Shells. Part 1: Plate. AIAA J. 1966, 4, 1370–1377. [Google Scholar] [CrossRef]
- Durak, B. Theoretical Investigation of Fluid-Elastic Body Interactions in Shell Structures. Ph.D. Thesis, Istanbul University, Istanbul, Türkiye, 2018. [Google Scholar]
- Kapkin, S.; Demir, M.S.; Kaya, M.O.; Uzal, E. Flutter of a Membrane in a Stagnation Flow. J. Appl. Fluid Mech. 2019, 12, 981–985. [Google Scholar] [CrossRef]
- Uzal, E.; Korbahti, B. Vibration control of an elastic strip by a singular force. Sadhana 2010, 35, 233–240. [Google Scholar] [CrossRef]
- Uzal, E.; Korbahti, B. Vibrations of an Anisotropic Plate Under Fluid Flow in a Channel. J. Vib. Control 2007, 13, 1191–1204. [Google Scholar]
- Sezgin, A.; Krstic, M. Boundary Backstepping Control of Flow-Induced Vibrations of a Membrane at High Mach Numbers. J. Dyn. Syst. Meas. Control 2015, 137, 081003-1. [Google Scholar] [CrossRef]
- Tubaldi, E.; Alijani, F.; Amabili, M. Non-linear vibrations and stability of a periodically supported rectangular plate in axial flow. Int. J. Non-Linear Mech. 2014, 66, 54–65. [Google Scholar] [CrossRef]
- Li, W.L. Vibration analysis of rectangular plates with general elastic boundary supports. J. Sound Vib. 2018, 422, 15–33. [Google Scholar] [CrossRef]
- Lin, T.R.; Zhang, K. An analytical study of the free and forced vibration response of a ribbed plate with free boundary conditions. J. Sound Vib. 2004, 273, 619–635. [Google Scholar] [CrossRef]
- Liu, C.; Xie, C.; Meng, Y.; Bai, L. Experimental and Numerical Flutter Analysis Using Local Piston Theory with Viscous Correction. Aerospace 2023, 10, 870. [Google Scholar] [CrossRef]
- Ashley, H.; Zartarian, G. Piston Theory-A New Aerodynamic Tool for the Aeroelastician. J. Aeronaut. Sci. 1956, 23, 1109–1118. [Google Scholar] [CrossRef]
- Eisenberger, M.; Deutsch, A. Solution of thin rectangular plate vibrations for all combinations of boundary conditions. J. Sound Vib. 2019, 452, 1–12. [Google Scholar] [CrossRef]
- Shitov, S.; Vedeneev, V. Flutter of rectangular simply supported plates at low supersonic speeds. J. Fluids Struct. 2017, 69, 154–173. [Google Scholar] [CrossRef]
- Vedeneev, V. Flutter of a Wide Strip Plate in a Supersonic Gas Flow. Fluid Dyn. 2005, 40, 805–817. [Google Scholar] [CrossRef]
- Yao, G.; Liu, D. Aeroelastic stability analysis of a pyrotechnic separation plate in subsonic airflow. Appl. Math. Model. 2022, 107, 574–590. [Google Scholar] [CrossRef]
- Tang, D.; Dowell, E.H. Limit cycle oscillations of two-dimensional panels in low subsonic flow. Int. J. Non-Linear Mech. 2002, 37, 1199–1209. [Google Scholar] [CrossRef]
- Cho, D.S.; Kim, B.H.; Kim, J.H.; Vladimir, N.; Choi, T.M. Forced vibration analysis of arbitrarily constrained rectangular plates and stiffened panels using the assumed mode method. Thin-Walled Struct. 2015, 90, 182–190. [Google Scholar] [CrossRef]
- Tenenbaum, J.; Eisenberger, M. Analytic solution of rectangular plate buckling with rotationally restrained and free edges. Thin-Walled Struct. 2020, 157, 106979. [Google Scholar] [CrossRef]
- Dowell, E.H.; Hall, K.C. Modeling of Fluid-Structure Iteration. Annu. Rev. Fluid Mech. 2001, 33, 445–490. [Google Scholar] [CrossRef]
- Bortoli, A.L.D. Aeroelastic analysis of panels in compressible flows. J. Fluids Struct. 2005, 20, 189–195. [Google Scholar] [CrossRef]
- Morrison, D.D.; Riley, J.D.; Zancanaro, J.F. Multiple shooting method for two-point boundary value problems. Commun. ACM 1962, 5, 613–614. [Google Scholar] [CrossRef]
- Osborne, M.R. On shooting methods for boundary value problems. J. Math. Anal. Appl. 1969, 27, 417–433. [Google Scholar] [CrossRef]
- Fang, L.; Vandewalle, S.; Meyers, J. An SQP-based multiple shooting algorithm for large-scale PDE-constrained optimal control problems. J. Comput. Phys. 2023, 477, 111927. [Google Scholar] [CrossRef]
- Sylvester, M.A.; Baker, B.E. Some Experimental Studies of Panle Flutter at Mach Number 1.3; National Advisory Committee for Aeronautics Technical Note; NACA TN 3914; NACA: Washington, DC, USA, 1957; Volume 3914. [Google Scholar]
| Number of Collocation Points | (Non-Dimensional Flutter Velocity) |
|---|---|
| 8 | 90.9697280425894 |
| 10 | 91.1667370035824 |
| 12 | 91.1563146276537 |
| 14 | 91.1564970192325 |
| Collocation Method | Analytical Results | |||
|---|---|---|---|---|
| Before Flutter | After Flutter | Before Flutter | After Flutter | |
| 1.006255 | 358.920571 | 359.571969 | 359.467520 | 359.571969 |
| 1.242290 | 291.097486 | 291.372886 | 291.315280 | 291.372886 |
| 1.572273 | 230.265262 | 230.461233 | 230.377137 | 230.461233 |
| 2.053581 | 176.682416 | 176.762617 | 176.671744 | 176.762617 |
| 2.795152 | 130.248788 | 130.299136 | 130.23840 | 130.299136 |
| 4.025020 | 90.6746705 | 91.1957893 | 91.156960 | 91.195789 |
| 6.289093 | 59.2604927 | 59.6428185 | 59.604512 | 59.642818 |
| 11.18061 | 36.0023423 | 36.1616447 | 36.111424 | 36.161644 |
| Material | Experimental Result | Theory |
|---|---|---|
| Steel | 254.7695 (panels with tension, clamped front and rear) | 263.5333 |
| Steel | 254.7695 (buckled panels, clamped front and rear) | 263.5333 |
| Brass | No flutter (panels with tension, clamped front and rear) | 919.6203 |
| Aluminum | No flutter (buckled panels, clamped on four edges) | 397.2558 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sezgin, A.; Durak, B.; Sayın, A.; Yildiz, H.; Ozer, H.O.; Sakman, L.E.; Kapkin, S.; Uzal, E. Flutter of a Plate at High Supersonic Speeds. Appl. Sci. 2024, 14, 4892. https://doi.org/10.3390/app14114892
Sezgin A, Durak B, Sayın A, Yildiz H, Ozer HO, Sakman LE, Kapkin S, Uzal E. Flutter of a Plate at High Supersonic Speeds. Applied Sciences. 2024; 14(11):4892. https://doi.org/10.3390/app14114892
Chicago/Turabian StyleSezgin, Aziz, Birkan Durak, Alaattin Sayın, Huseyin Yildiz, Hasan Omur Ozer, Lutfi Emir Sakman, Sule Kapkin, and Erol Uzal. 2024. "Flutter of a Plate at High Supersonic Speeds" Applied Sciences 14, no. 11: 4892. https://doi.org/10.3390/app14114892
APA StyleSezgin, A., Durak, B., Sayın, A., Yildiz, H., Ozer, H. O., Sakman, L. E., Kapkin, S., & Uzal, E. (2024). Flutter of a Plate at High Supersonic Speeds. Applied Sciences, 14(11), 4892. https://doi.org/10.3390/app14114892







