Dynamic Instability Investigation of the Automotive Driveshaft’s Forced Torsional Vibration Using the Asymptotic Method
Abstract
Featured Application
Abstract
1. Introduction
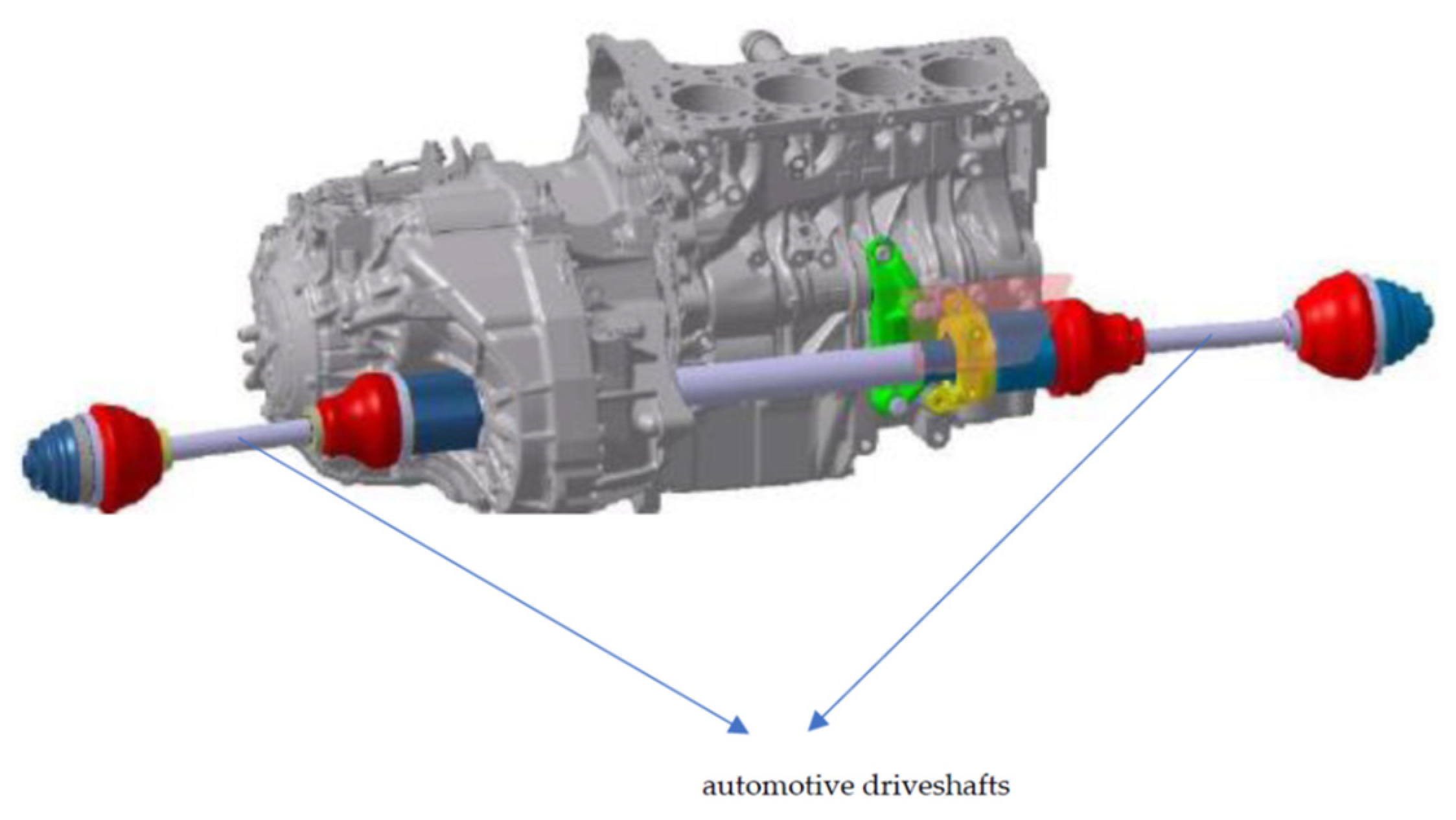
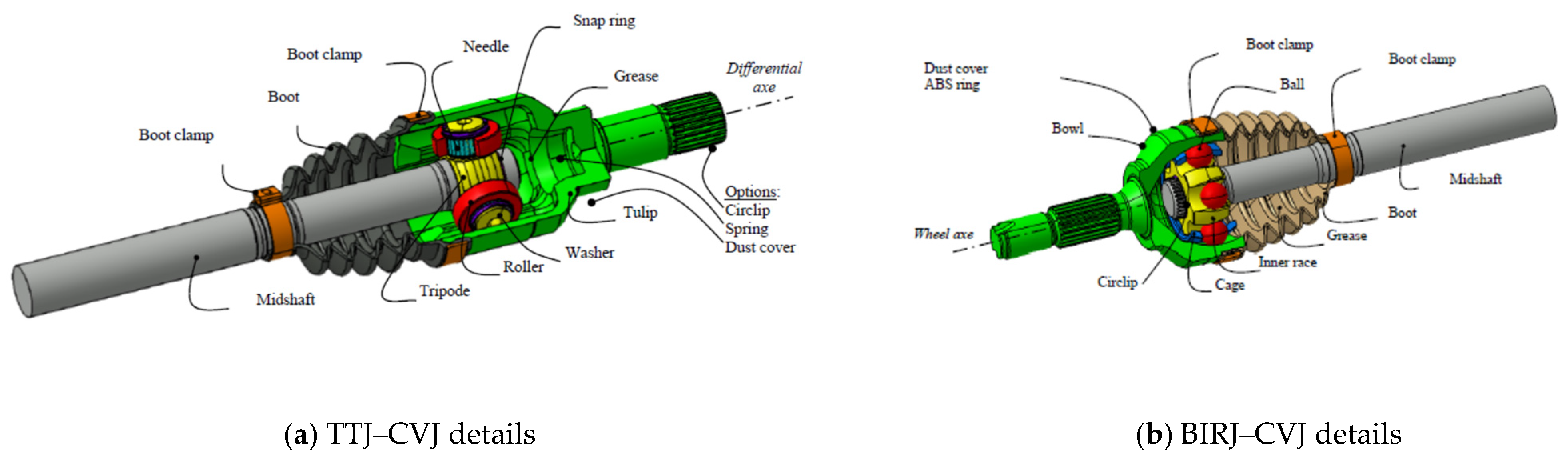
- the AD–MA (automotive’s driveshaft-middle ax),
- the tripod linked with tulip and assembled using splines on the middle ax,
- the tulip’s bell (TB),
- the tulip ax (TA), assembled with splines in the geared box.
- the AD–MA,
- the inner race (IR) assembled with splines on the AD–MA,
- the BB (bowl’s bell) linked with IR through balls,
- the BA (bowl’s ax) linked to the SW (steering wheel) with splines.
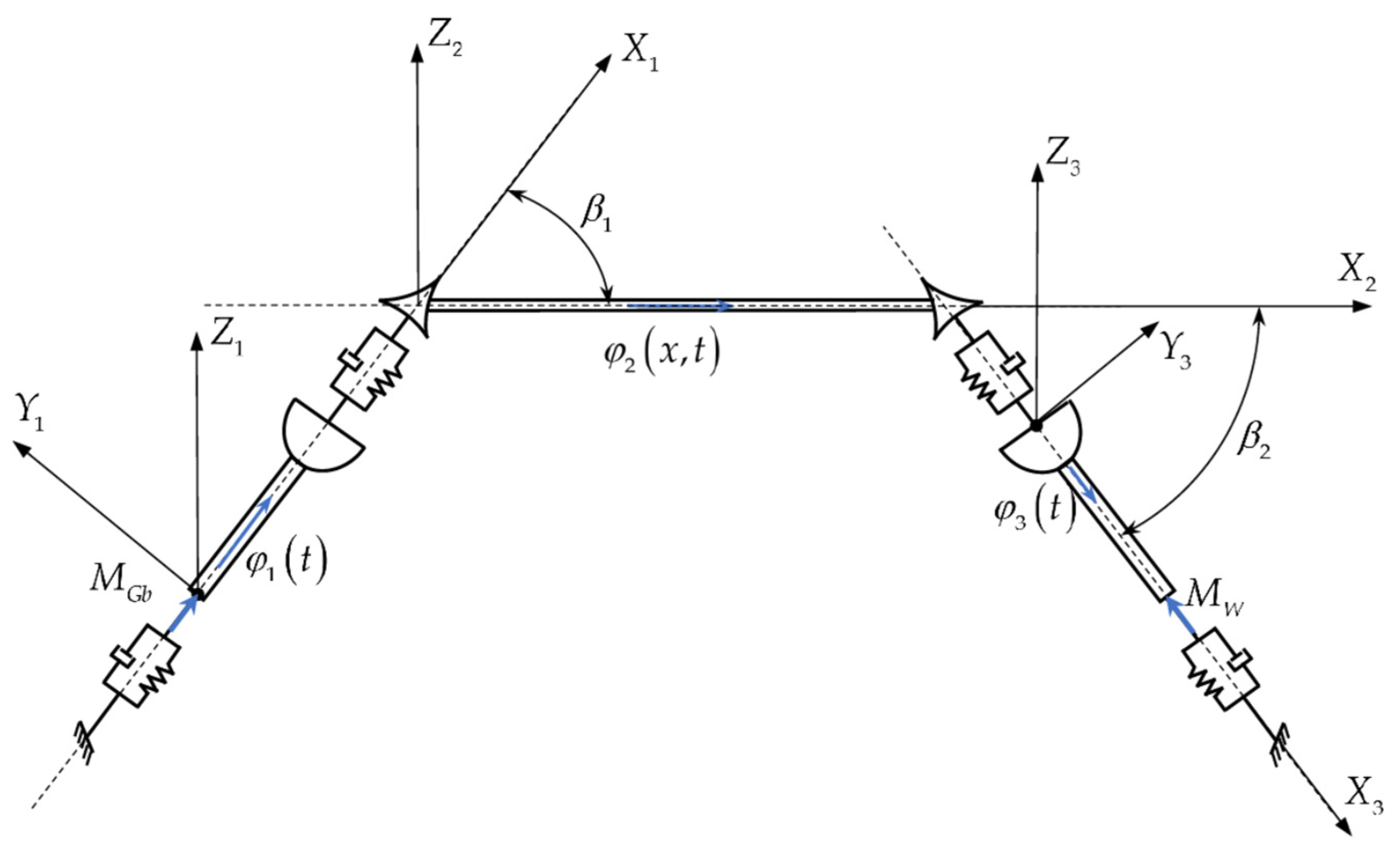
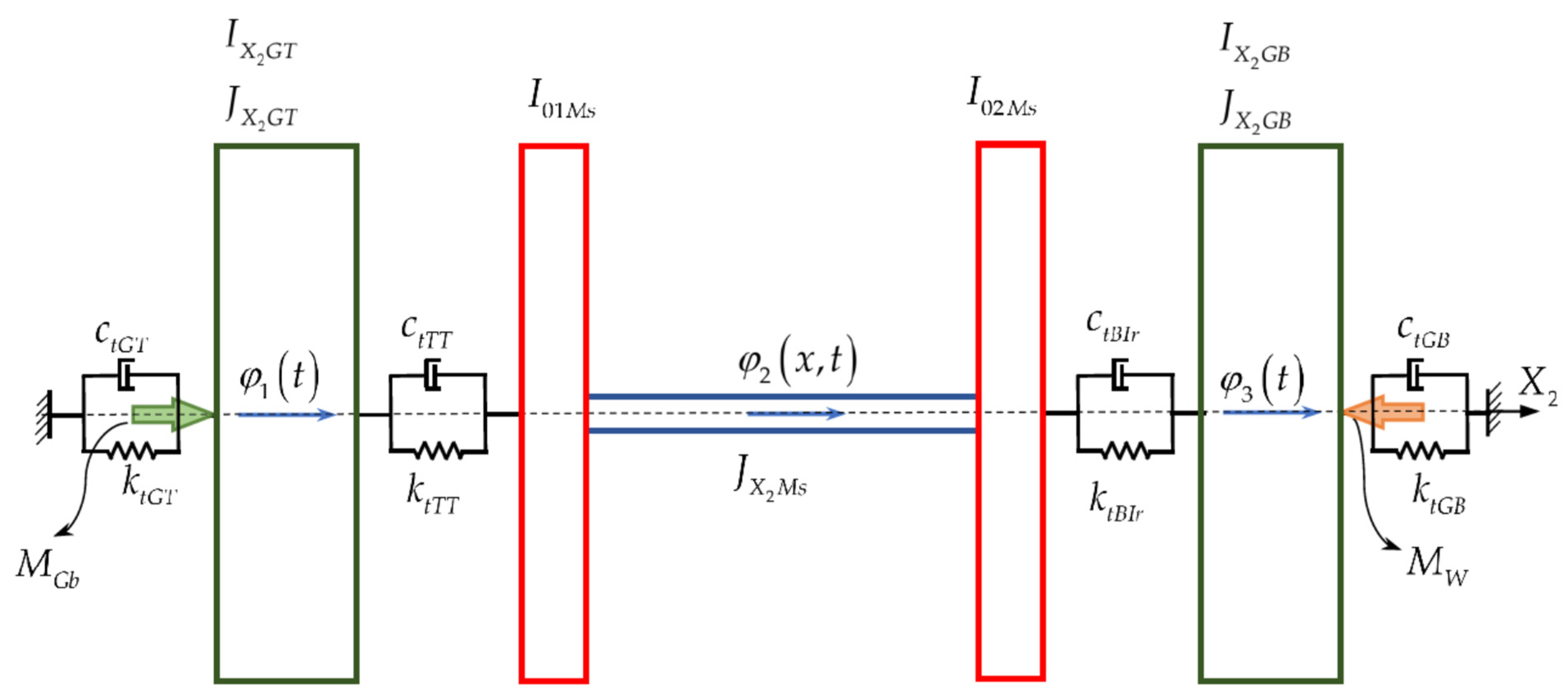
2. The Analysis of DMADFTV
- −
- attached to the GT (global tulip: TB and TA), having a rigid rotation with around axis ,
- −
- attached to the MA, having a rigid rotation with around axis ,
- −
- attached to the GB (global bowl: BB and BA), having a rigid rotation with around axis , while is the angle between the longitudinal directions of the GT and the MA regarding the axis , , and is the angle between the longitudinal directions of the GB and the MA regarding the axis , . The angle between the longitudinal directions of the GT and the MA regarding the axis , is given by the internal length of the trucks inside the TB, the external diameter of the MA, and the internal diameter of the TB (see Figure 5a), conforming to the designer calculus [27] (pp. 214–230). The angle between the longitudinal directions of the GB and the MA regarding the axis is given by the internal length of the trucks inside the IR, the external diameter of the MA, and the internal diameter of the BB (see Figure 5b), conforming to the designer calculus [27] (pp. 153–208).
3. The Equations of ADFTV and the Mathematical Solutions of FOAM
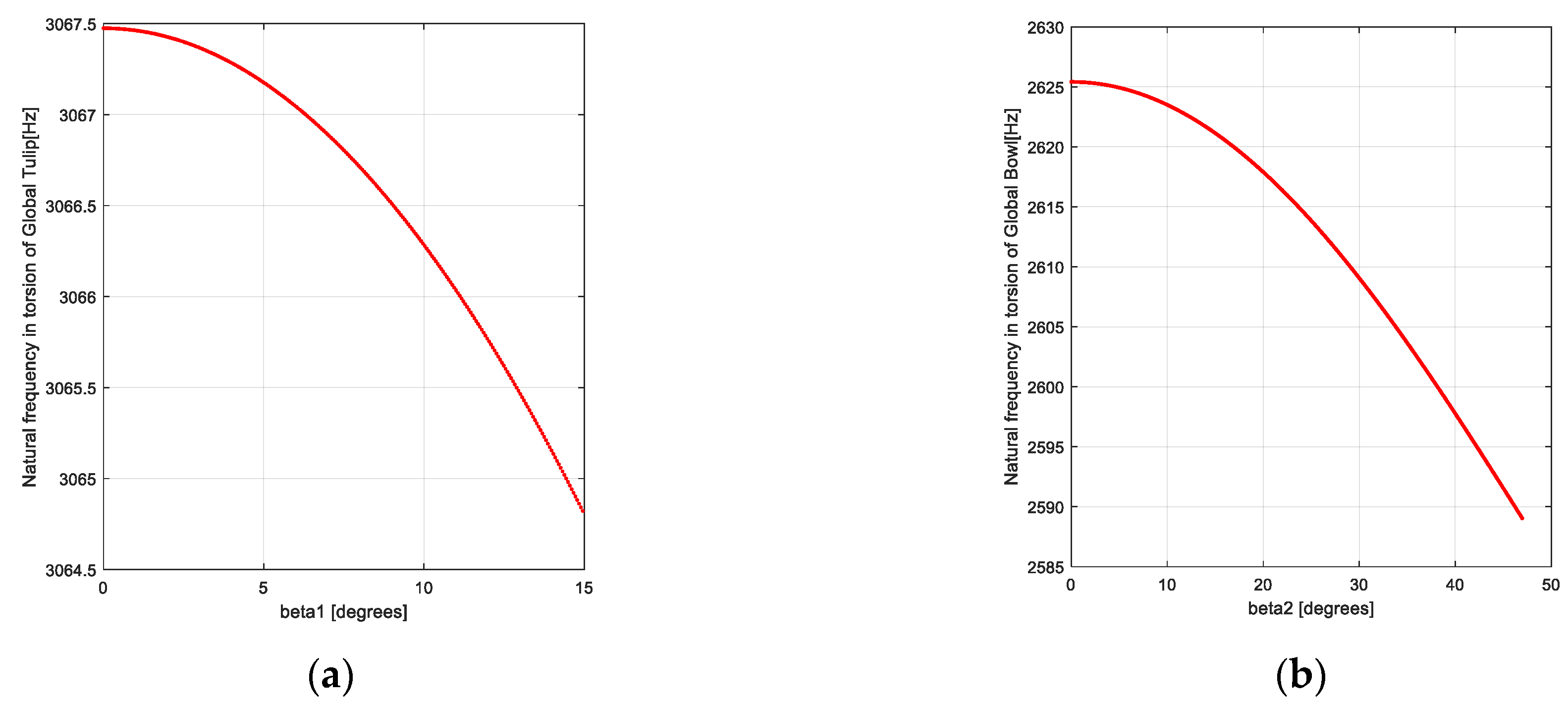
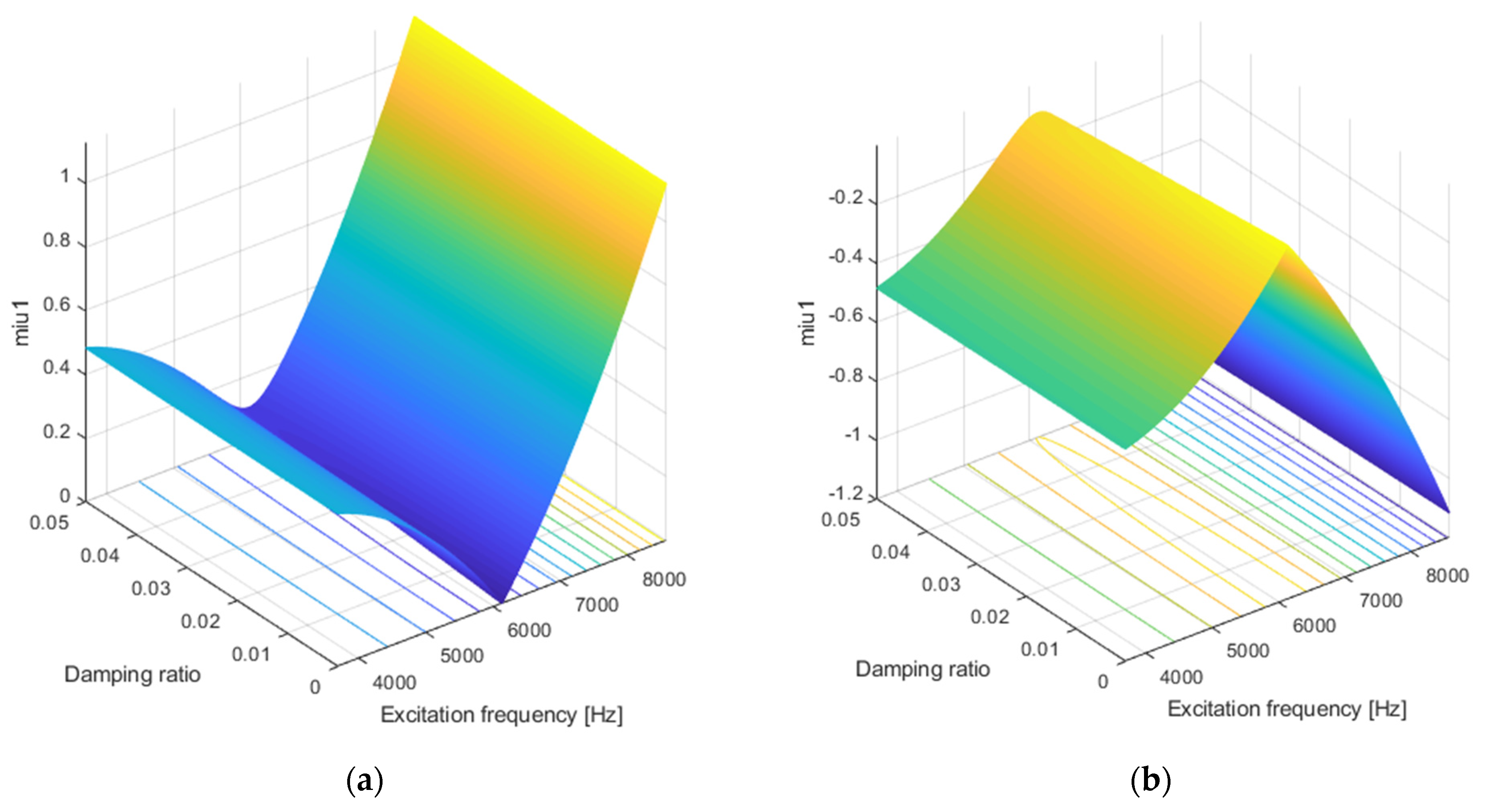
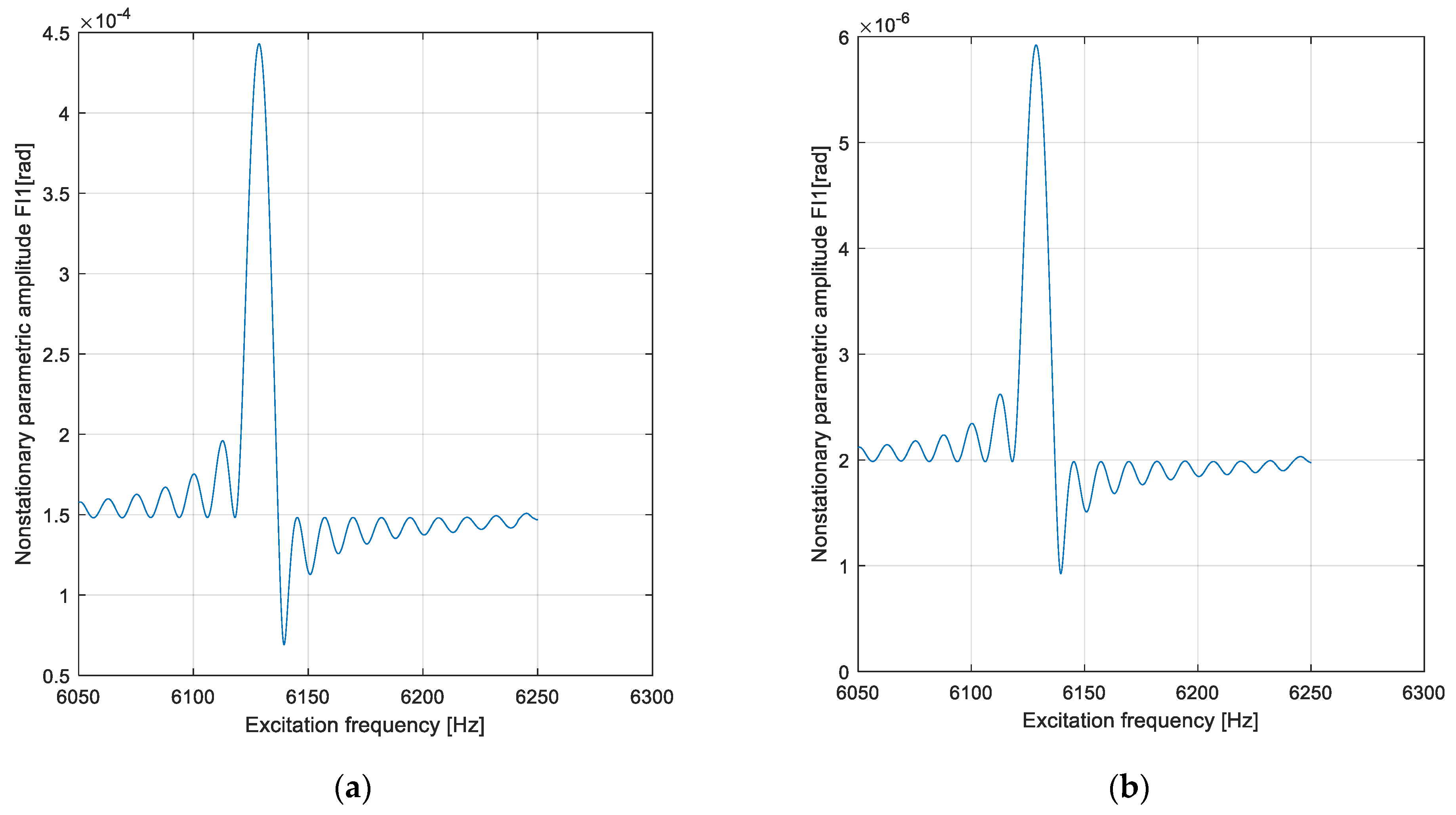
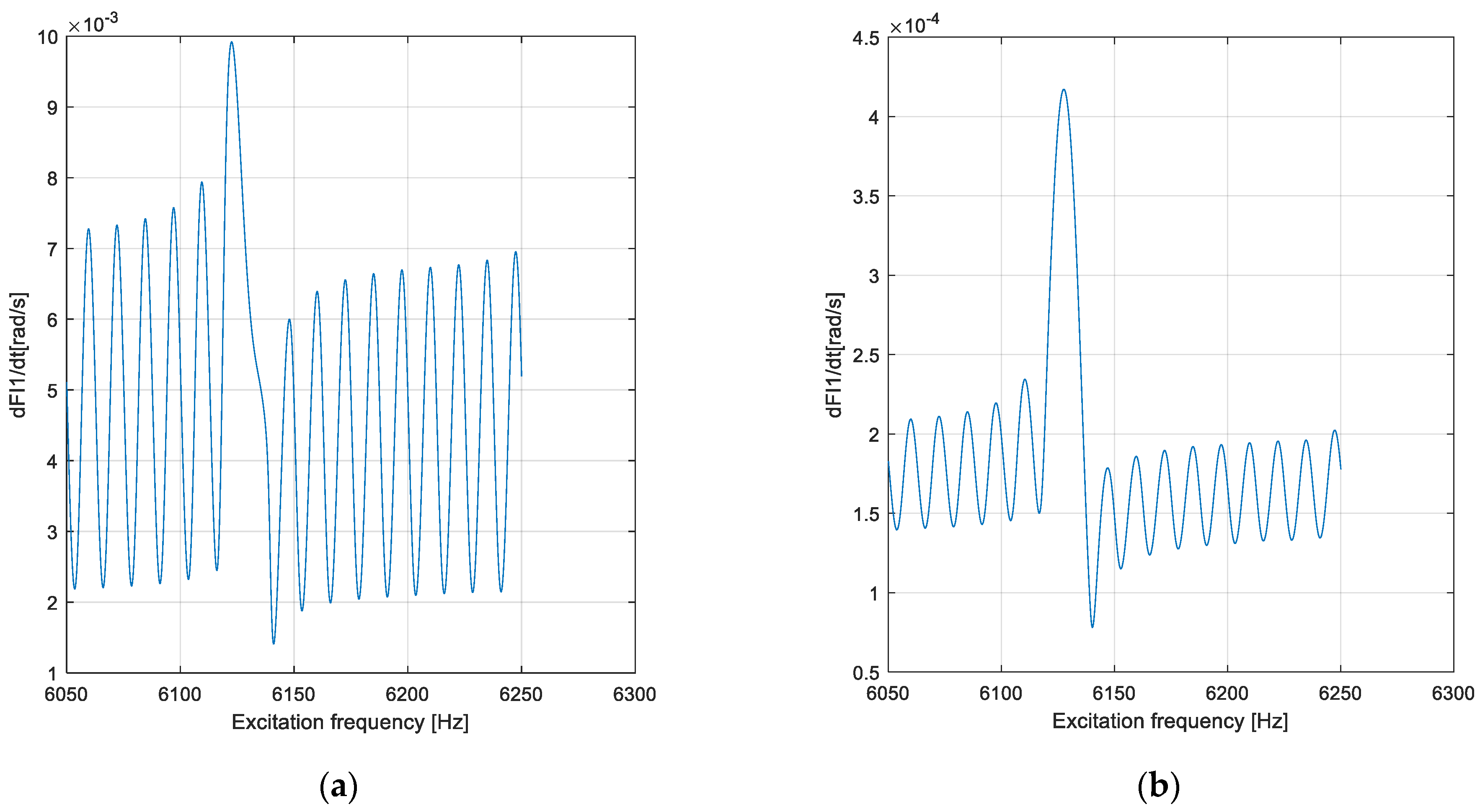
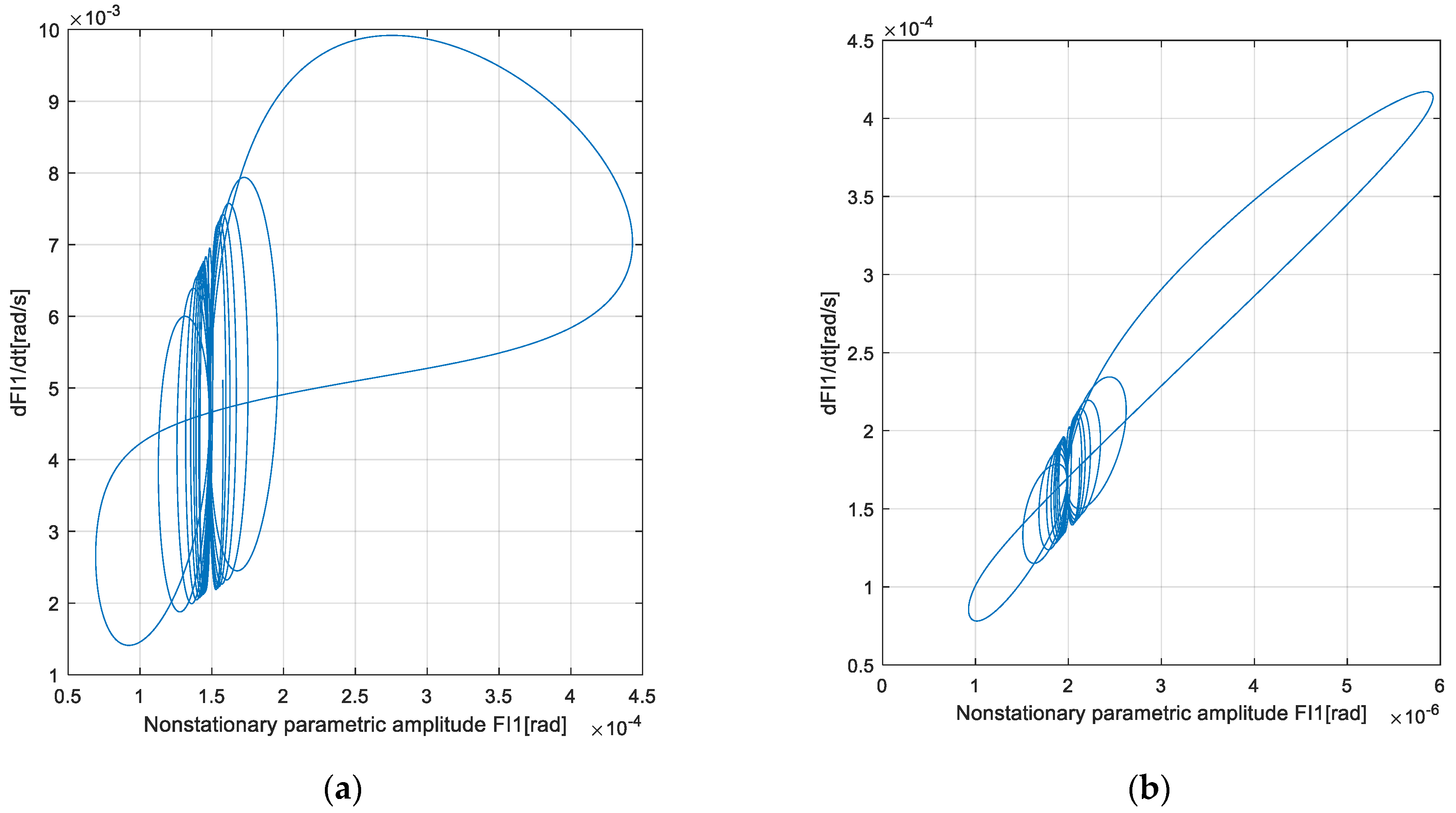
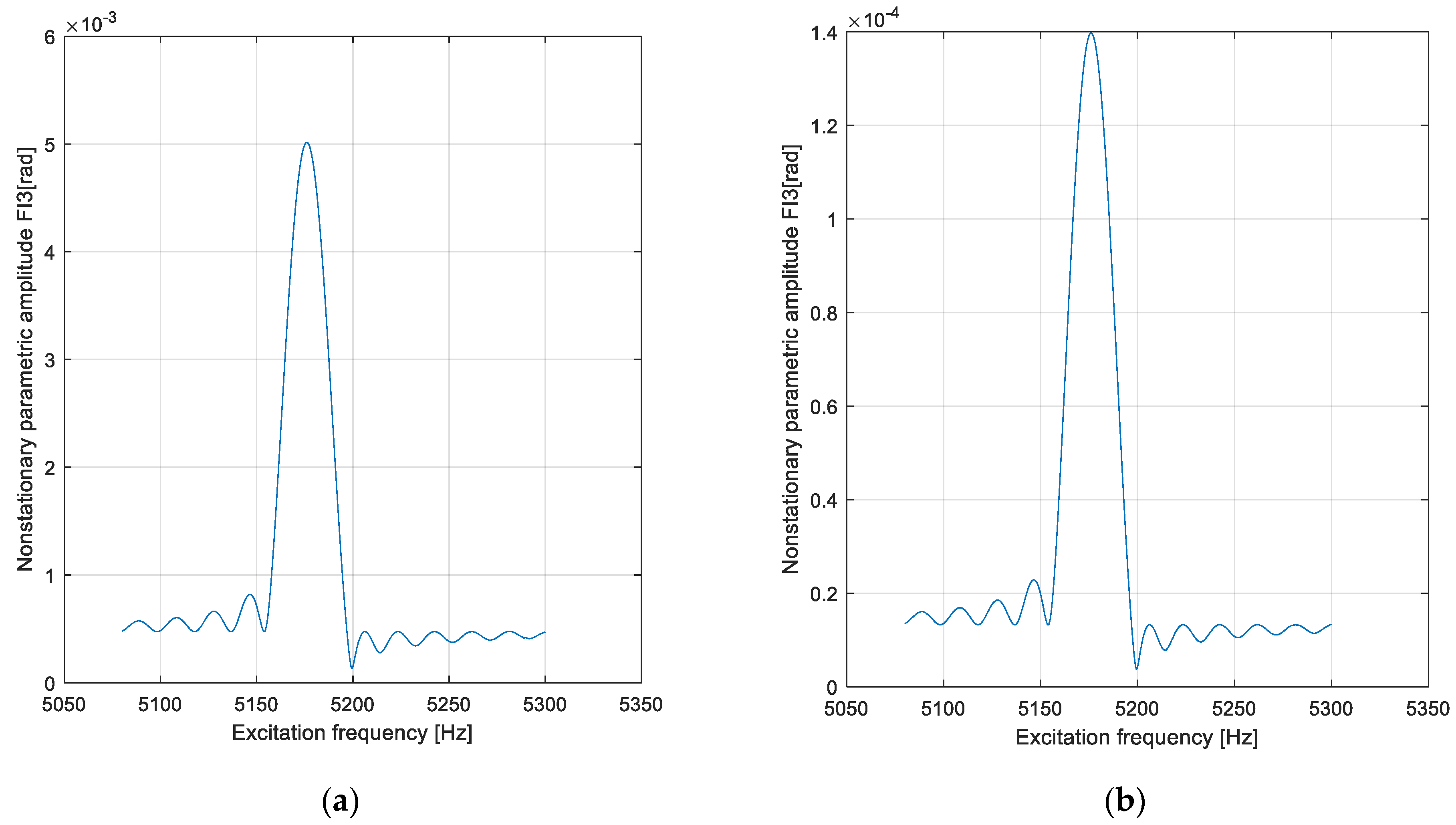
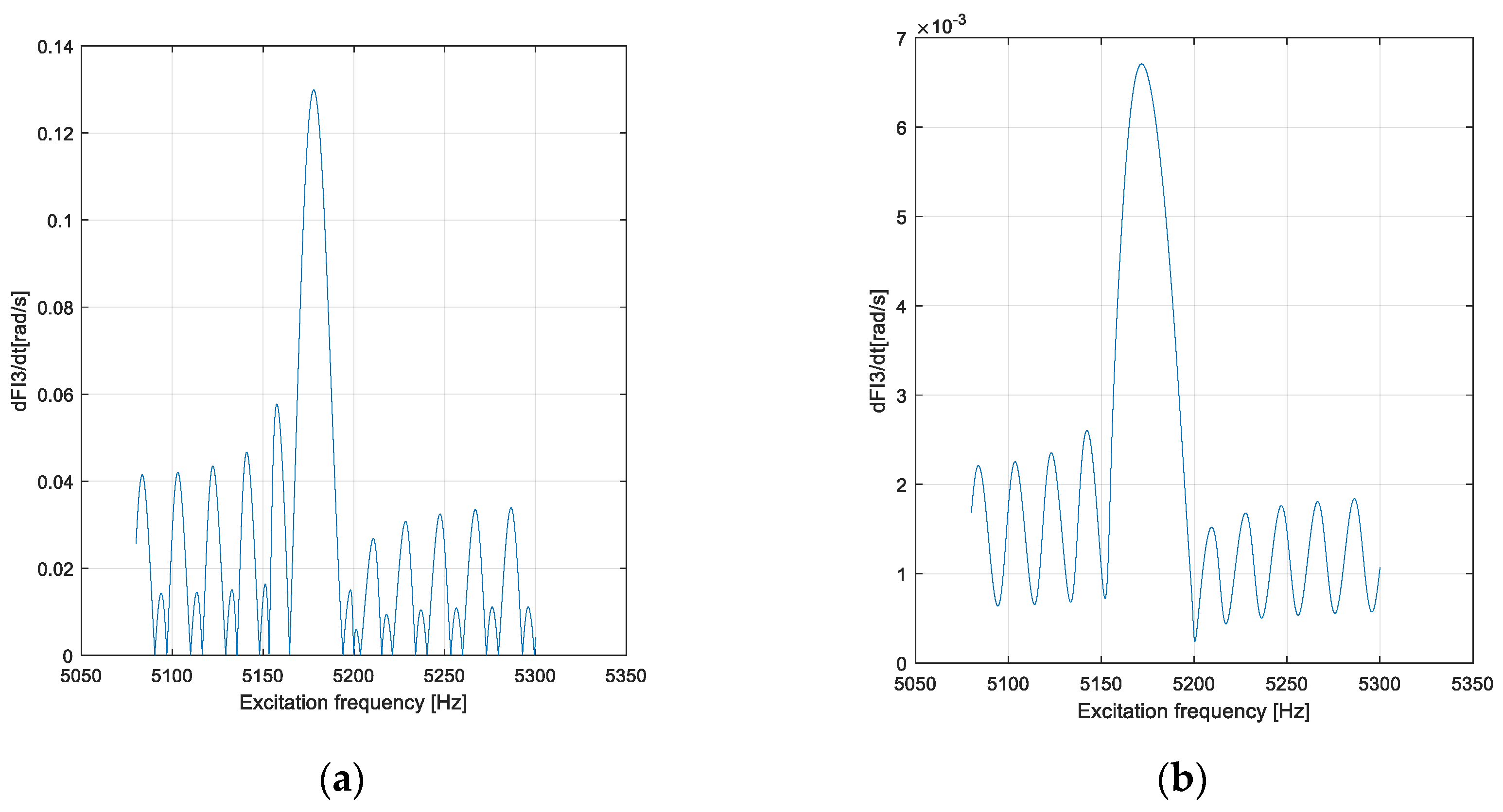
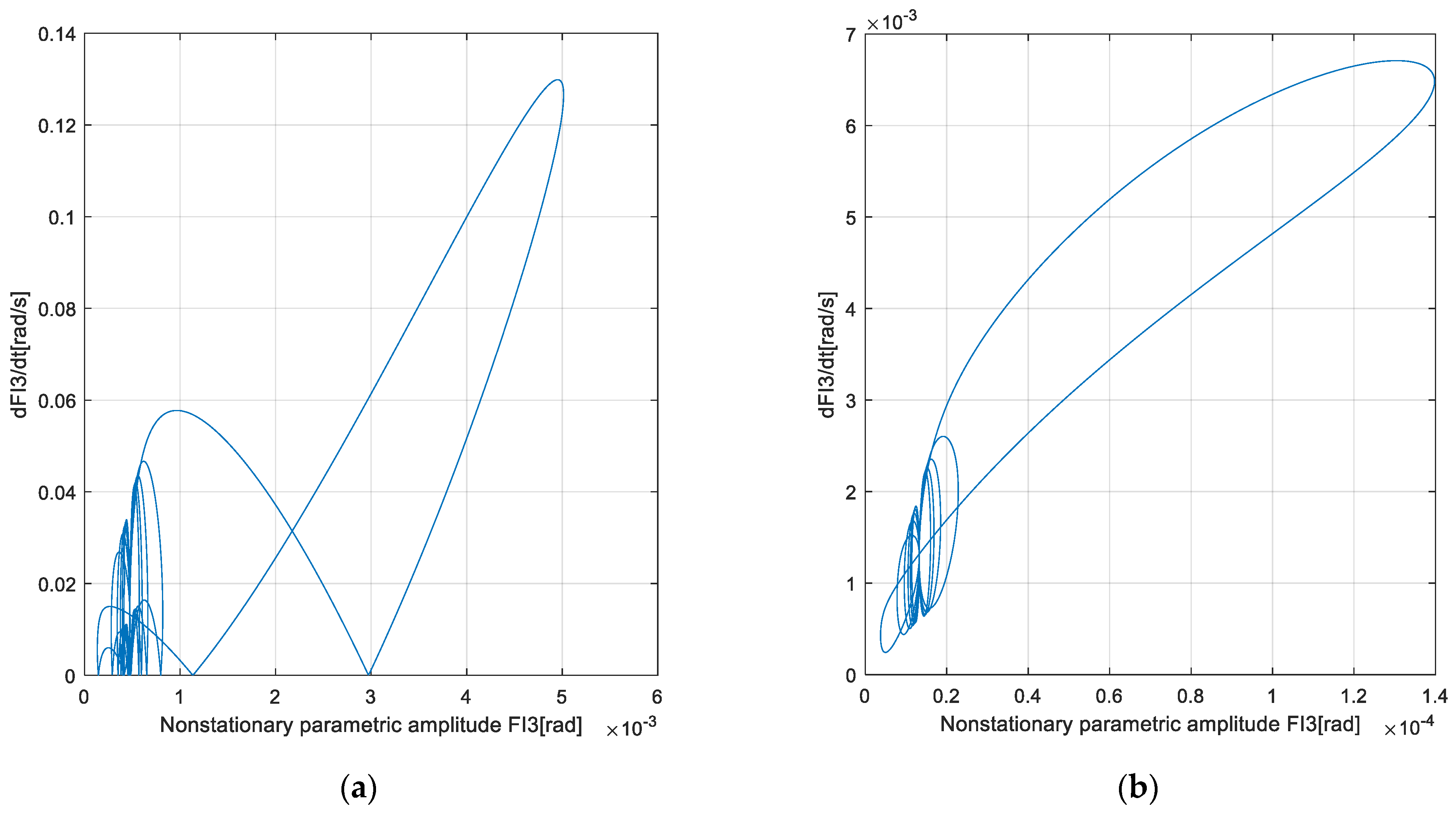
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| The List of Mathematical Symbols in Appendix A and Appendix B | |
| variable coefficients in Equation (A13)-Appendix B, and Equations (4) and (7), | |
| variable coefficients in Equation (A14)-Appendix B, and Equations (5) and (8), | |
| uniform speed of the torsional wave, | |
| damping coefficient of the BIRJ in torsion, | |
| damping coefficient of the GB in torsion, | |
| damping coefficient of the GT in torsion, | |
| damping coefficient of the TTJ in torsion, | |
| diameter of the BA, | |
| diameter of the TA, | |
| distance from the BB’s CM to the centroid of the inner race, | |
| distance from the TB’s CM to the centroid of the tripod, | |
| diameter of the middle ax, | |
| torsional stiffness of the BA, | |
| torsional stiffness of the TA, | |
| torsional stiffness of the BB, | |
| torsional stiffness of the TB, | |
| torsional stiffness of the GB, | |
| torsional stiffness of the GT, | |
| torsional stiffness of the BIRJ, | |
| torsional stiffness of the TTJ, | |
| non-dimensional coefficient of the ADGN induced by BIRJ’s quasi-isometry mentioned in [2,4], | |
| non-dimensional coefficient of the ADGN induced by TTJ’s quasi-isometry mentioned in [2,4], | |
| variable coefficients in Equation (A15)-Appendix B, | |
| variable coefficients in Equation (A16)-Appendix B, | |
| G | transversal elasticity modulus, |
| AIMM of the GB, | |
| AIMM of the GT, | |
| principal AIGMs of the inner race, | |
| AIMM of the tripod, | |
| AIMM of the inner race, | |
| AIGM of the uniform middle ax (midshaft) as a bar/tube, | |
| AIGM of the bowl’s ax, | |
| AIGM of the tulip’s ax, | |
| AIGM of the GB, | |
| AIGM of the GT, | |
| AIGM of the BB, | |
| AIGM of the TB, | |
| , | principal AIGMs of the BB, |
| , | principal AIGMs of the TB, |
| principal AIGMs of the tripod, | |
| AIGM of the inner race, | |
| AIGM of the tripod, | |
| length of the BA, | |
| length of the BB, | |
| length of the TA, | |
| length of the inner race, | |
| length of the MA, | |
| length of the TB, | |
| length of the tripod, | |
| rayon of the coupling torsion for the link BB–inner race, | |
| rayon of the coupling torsion for the link TB–tripod, | |
| cross-section area of BB, | |
| cross-section area of TB, | |
| , | variable coefficients in Equation (A15)-Appendix B, and Equations (7) and (9), |
| , | variable coefficients in Equation (A16)-Appendix B, and Equations (8) and (10), |
| AIGM nonuniformity of the BB, | |
| AIGM’s nonuniformity of the TB, | |
| AIMM’s nonuniformity of the GB, | |
| AIMM’s nonuniformity of the GT, | |
| logarithmic decrement of the AD’s material, | |
| AD’s material density. | |
| Nomenclature of Acronyms and Abbreviations | |
| ADE | automotive driveshaft’s elements [28], |
| ADFTV | automotive driveshaft’s forced torsional vibration [1,28], |
| ADGN | automotive driveshaft’s geometric nonuniformity, in the isometric sense [2,4], mathematically defined by Equation (A11) in Appendix B [4], |
| ADKN | automotive driveshaft’s kinematic nonuniformity, in the isometric sense [2,4], |
| ADL | automotive drive line, |
| AD-MA | automotive driveshaft-middle ax [1,28], |
| AIGM | axial inertial geometric moment [1], |
| AIMM | axial inertial mass moment [1], |
| AM | asymptotic method [31], |
| AMA | asymptotic method approach [31], |
| APPR | the area of principal parametric resonance, mathematically defined by Equation (11), [26] (p. 341), [6,32], |
| BA | bowl’s ax [1,4], |
| BB | bowl’s bell [1,4], |
| BIRJ | bowl-inner race joint [1,28], |
| CM | center mass, |
| CVJ | constant velocity joint [1,4,28], |
| DIBF | dynamic instability boundary frontiers [26,32], |
| DOF | degrees of freedom, |
| DMADFTV | the dynamic model for the automotive driveshaft’s forced torsional vibration, |
| DSOE | differential system of equations, |
| FOAM | first-order asymptotic method [31], |
| HBM | harmonic balance method [1,31], |
| ICSM | inertial characteristics for the spinning movements [1], |
| INP-AD | isometry nonuniformity properties of AD [2,4], |
| IR | inner race (of the GB) [28], |
| KCC | Kosambi–Cartan–Chern theory [20,21,22,23,24,25], |
| LFB | logarithmic frequency balayage [31,32], |
| LHS | left-hand side, |
| MA | middle ax [1,28], |
| NA | nonlinear amplitude [26,31,32], |
| NFTV | nonstationary forced torsional vibrations [26,31,32], |
| NPA | nonlinear phase angle [26,31,32], |
| NSA | nonstationary spectral amplitude [26,31,32], |
| NSVA | nonstationary spectral velocity amplitude [26,31,32], |
| RHS | right-hand side, |
| SA | spectral amplitude [26,31,32], |
| SOR | sweep of rate [26,31], |
| SUV | sport utility vehicle, |
| SVA | spectral velocity amplitude [26,31,32], |
| SSA | Six Sigma Approach [12], |
| SW | steering wheel, |
| TA | tulip’s ax [1,28], |
| TB | tulip’s bell [1,28], |
| TTJ | tulip–tripod joint [1,28], |
| VAHP | variational approach of Hamilton’s principle [29] (pp. 272–295). |
Appendix A. Relations of AIGM, AIMM, Stiffness, Damping Coefficients of TA, GT, Tripod, MA, IR, BA, GB, and the Coefficients in the Mathematical Procedure of AM
Appendix B. Mathematical Expressions of the Terms and Coefficients in Paragraph 3
References
- Bugaru, M.; Vasile, A. A Physically Consistent Model for forced Torsional Vibrations of Automotive Driveshafts. Computation 2022, 10, 10. [Google Scholar] [CrossRef]
- Duditza, F.; Diaconescu, D. Zur Kinematik und Dynamik von Tripode-Gelenkgetrieben. Konstruction 1975, 27, 335–341. [Google Scholar]
- Grünwald, B. Theory, Computation and Design of Internal Combustion Engines for Automotive; Didactic &Pedagogical Publishing House: Bucharest, Romania, 1980. [Google Scholar]
- Bugaru, M.; Vasile, A. Nonuniformity of Isometric Properties of Automotive Driveshafts. Computation 2021, 9, 145. [Google Scholar] [CrossRef]
- Steinwede, J. Design of a Homokinetic Joint for Use in Bent Axis Axial Piston Motors. Ph.D. Thesis, Aachen University, Aachen, Germany, 25 November 2020. [Google Scholar] [CrossRef]
- Mazzei, A.J.; Scott, R.A. Principal Parametric Resonance Zones of a Rotating Rigid Shaft Driven through a Universal Joint. J. Sound Vib. 2001, 244, 555–562. [Google Scholar] [CrossRef][Green Version]
- Browne, M.; Palazzolo, A. Super harmonic nonlinear lateral vibrations of a segmented driveline incorporating a tuned damper excited by a non-constant velocity joints. J. Sound Vib. 2008, 323, 334–351. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, J.; Xia, F. Modeling and Analysis of Amplitude-Frequency Characteristics of Torsional Vibration for Automotive Powertrain. Shock Vib. 2020, 2020, 6403413. [Google Scholar] [CrossRef]
- Idehara, S.J.; Flach, F.L.; Lemes, D. Modeling of nonlinear torsional vibration of automotive powertrain. J. Vib. Control 2018, 24, 1774–1786. [Google Scholar] [CrossRef]
- Feng, H.; Rakheja, S.; Shangguan, W.B. Analysis and optimization for generated axial force of a driveshaft system with interval of uncertainty. Struct. Multidiscip. Optim. 2021, 63, 197–210. [Google Scholar] [CrossRef]
- Tiberiu-Petrescu, F.I.T.; Petrescu, R.V.V. The structure, geometry, and kinematics of a universal joint. Indep. J. Man Agement Prod. 2019, 10, 1713–1724. [Google Scholar] [CrossRef]
- Ertürka, A.T.; Karabayb, S.; Baynalc, K.; Korkutd, T. Vibration Noise Harshness of a Light Truck Driveshaft, Analysis and Improvement with Six Sigma Approach. Acta Phys. Pol. A 2017, 131, 477–480. [Google Scholar] [CrossRef]
- Kamalakkannan, B. Modelling and Simulation of Vehicle Kinematics and Dynamics. Master’s Thesis, Halmstad University, Halmstad, Sweden, 13 January 2017. [Google Scholar]
- Kishore, M.; Keerthi, J.; Kumar, V. Design and Analysis of Drive Shaft of an Automobile. Int. J. Eng. Trends Technol. 2016, 38, 291–296. [Google Scholar] [CrossRef]
- Shao, K.; Zheng, J.; Huang, K.; Qiu, M.; Sun, Z. Robust model referenced control for vehicle rollover prevention with time-varying speed. Int. J. Veh. Des. 2021, 85, 48–68. [Google Scholar] [CrossRef]
- Deng, B.; Zhao, H.; Shao, K.; Li, W.; Yin, A. Hierarchical Synchronization Control Strategy of Active Rear Axle Independent Steering System. Appl. Sci. 2020, 10, 3537. [Google Scholar] [CrossRef]
- Farshidianfar, A.; Ebrahimi, M.; Rahnejat, H.; Menday, M.T.; Moavenian, M. Optimization of the high-frequency torsional vibration of vehicle driveline systems using genetic algorithms. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2002, 216, 249–262. [Google Scholar] [CrossRef]
- Komorska, I.; Puchalski, A. On-board diagnostics of mechanical defects of the vehicle drive system based on the vibration signal reference model. J. Vibroeng. 2013, 15, 450–458, ISSN 1392-8716. [Google Scholar]
- Alugongo, A.A. Parametric Vibration of a Cardan Shaft and Sensitivity Analysis. In Proceedings of the World Congress on Engineering and Computer Science 2018 Vol II WCECS, San Francisco, CA, USA, 23–25 October 2018; Available online: https://www.google.com/search?client=firefox-b-d&q=Parametric+Vibration+of+a+Cardan+Shaft+and+Sensitivity+Analysis+Alfayo+A.+Alugong (accessed on 19 March 2024).
- Böhmer, C.G.; Harko, T.; Sabau, S.V. Jacoby stability analysis of dynamical systems-Applications in Gravitation and Cosmology. Adv. Theor. Math. Phys. 2012, 16, 1145–1196. [Google Scholar] [CrossRef]
- Harko, T.; Ho, C.Y.; Leung, C.S.; Yip, S. Jacobi stability analysis of the Lorenz system. Int. J. Geom. Methods Mod. Phys. 2015, 12, 1550081. [Google Scholar] [CrossRef]
- Wang, F.; Liu, T.; Kuznetsov, N.V.; Wei, Z. Jacobi Stability Analysis and the Onset of Chaos in a Two-Degree-of-Freedom Mechanical System. Int. J. Bifurc. Chaos 2021, 31, 2150075. [Google Scholar] [CrossRef]
- Blaga, C.; Blaga, P.A.; Harko, T. Jacobi Stability Analysis of the Classical Restricted Three Body Problem. Rom. Astron. J. 2021, 31, 101–112. [Google Scholar] [CrossRef]
- Mallikarjun, K.Y.; Narasimhamurthy, S.K. Finsler Spaces and their applications to Field Theory. Differ. Geom. Dyn. Syst. 2019, 21, 97–105. [Google Scholar]
- Roy, S.; Ray, A.; Chowdhury, A.R. Kosambi-Cartan-Chern(KCC) Perspective on Chaos: Unveiling Hidden Attractors in Nonlinear Autonomous Systems. Phys. Rev. E 2024, 109, 044205. [Google Scholar] [CrossRef] [PubMed]
- Deciu, E.; Bugaru, M.; Dragomirescu, C. Nonlinear Vibrations with Applications in Mechanical Engineering; Romanian Academy Publishing House: Bucharest, Romania, 2002; ISBN 973-27-0911-1. [Google Scholar]
- Seherr-Thoss, H.C.; Schmelz, F.; Aucktor, E. Designing Joints and Driveshafts. In Universal Joints and Driveshafts, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 109–248. [Google Scholar]
- Bugaru, M.; Chereches, T.; Trana, E.; Gheorghian, S.; Homotescu, T.N. Theoretical model of the dynamic interaction between wagon train and continuous rail. WSEAS Trans. Math. 2006, 5, 374–378. [Google Scholar]
- Rao, S.S. Torsional Vibrations of Shafts. In Vibration of Continuous System; John Wiley & Sons: Hoboken, NJ, USA, 2007; pp. 272–316. ISBN 978-0-471-77171-5. [Google Scholar]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Mitropolskii, Y.A. Problems of the Asymptotic Theory of Nonstationary Vibrations; Izdatel’stovo Nauka: Moscow, Russia, 1965. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bugaru, M.; Vasile, O. Dynamic Instability Investigation of the Automotive Driveshaft’s Forced Torsional Vibration Using the Asymptotic Method. Appl. Sci. 2024, 14, 7681. https://doi.org/10.3390/app14177681
Bugaru M, Vasile O. Dynamic Instability Investigation of the Automotive Driveshaft’s Forced Torsional Vibration Using the Asymptotic Method. Applied Sciences. 2024; 14(17):7681. https://doi.org/10.3390/app14177681
Chicago/Turabian StyleBugaru, Mihai, and Ovidiu Vasile. 2024. "Dynamic Instability Investigation of the Automotive Driveshaft’s Forced Torsional Vibration Using the Asymptotic Method" Applied Sciences 14, no. 17: 7681. https://doi.org/10.3390/app14177681
APA StyleBugaru, M., & Vasile, O. (2024). Dynamic Instability Investigation of the Automotive Driveshaft’s Forced Torsional Vibration Using the Asymptotic Method. Applied Sciences, 14(17), 7681. https://doi.org/10.3390/app14177681






