Solar Sail-Based Mars-Synchronous Displaced Orbits for Remote Sensing Applications
Abstract
:1. Introduction
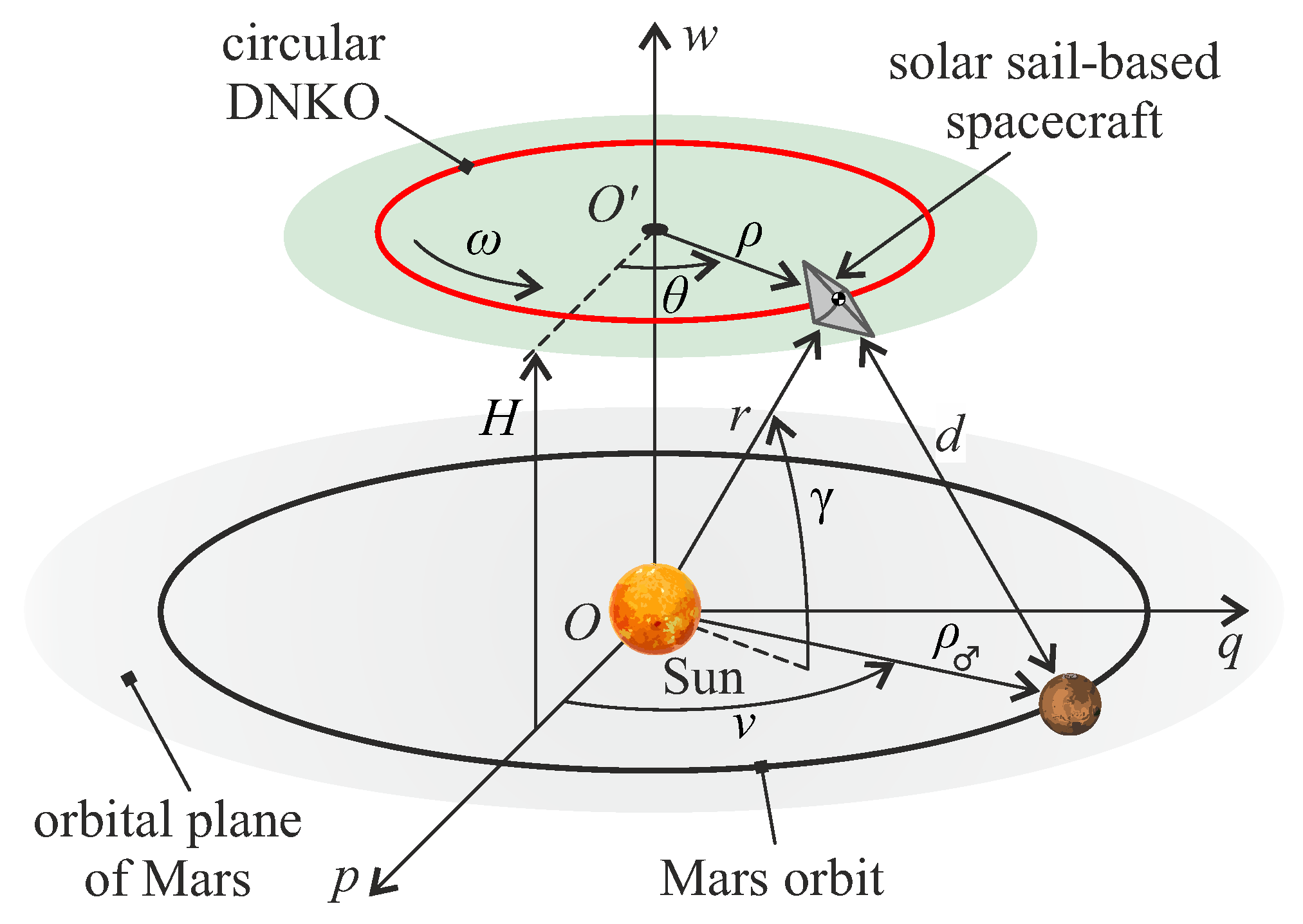
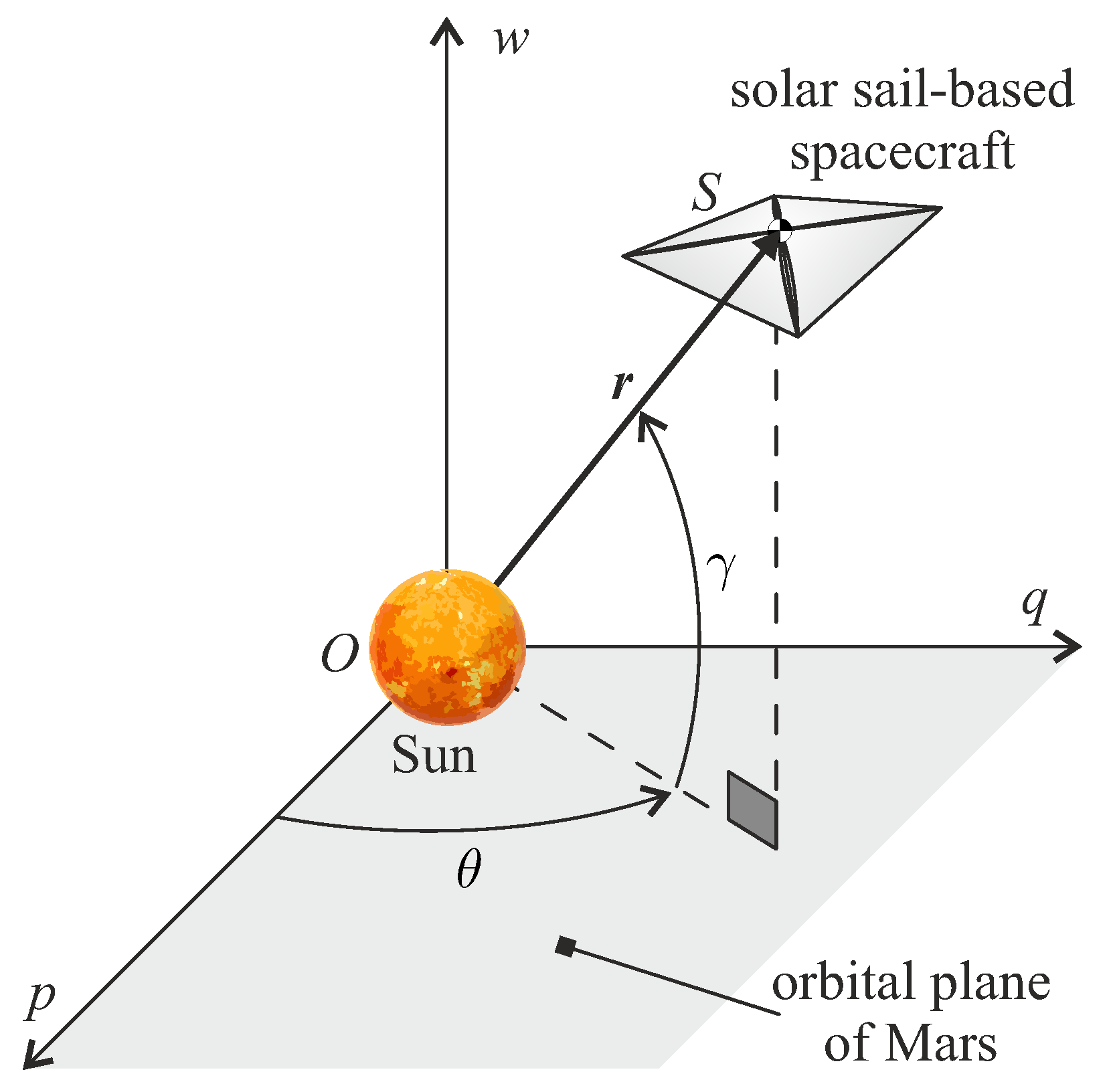
2. Mathematical Preliminaries
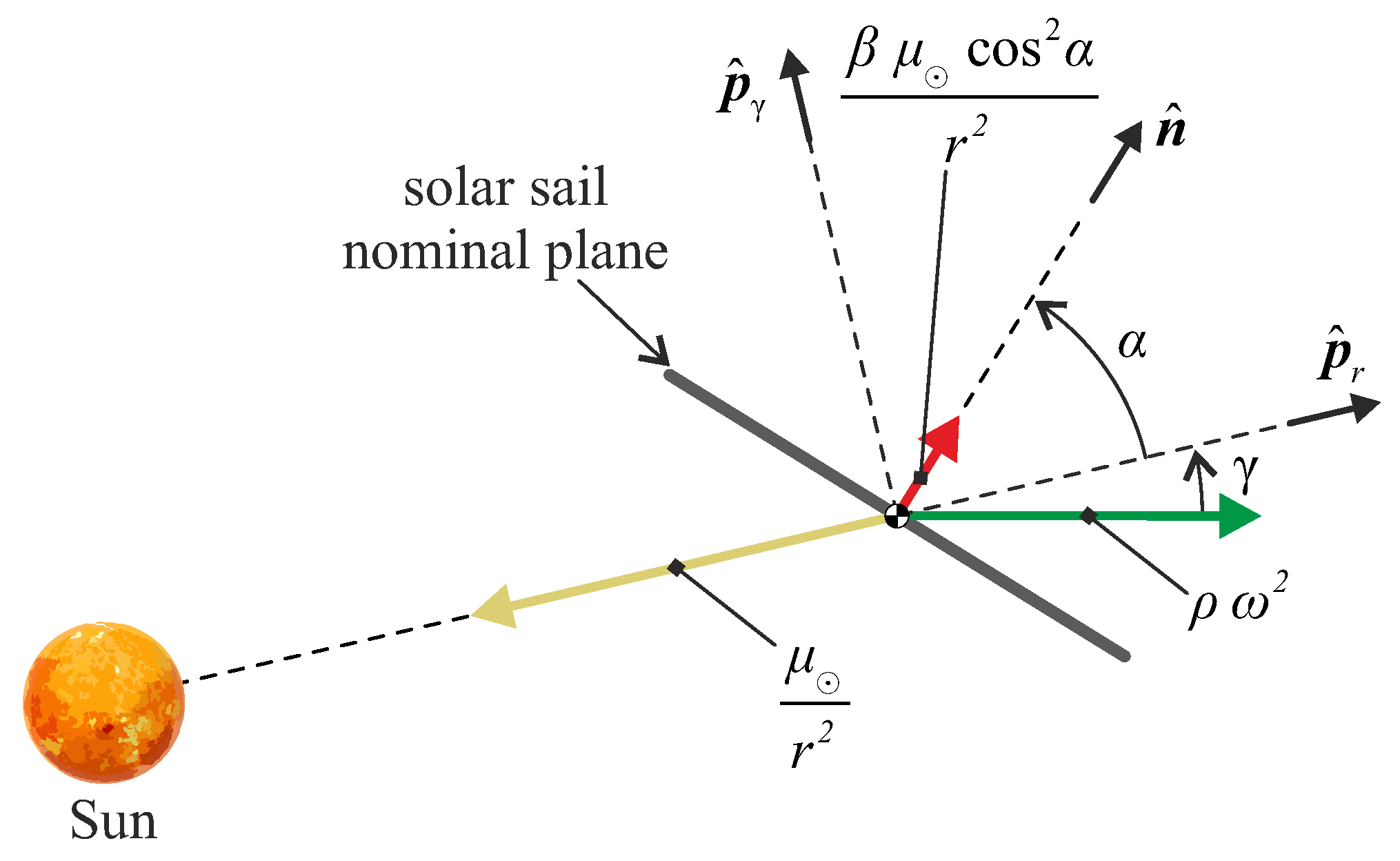
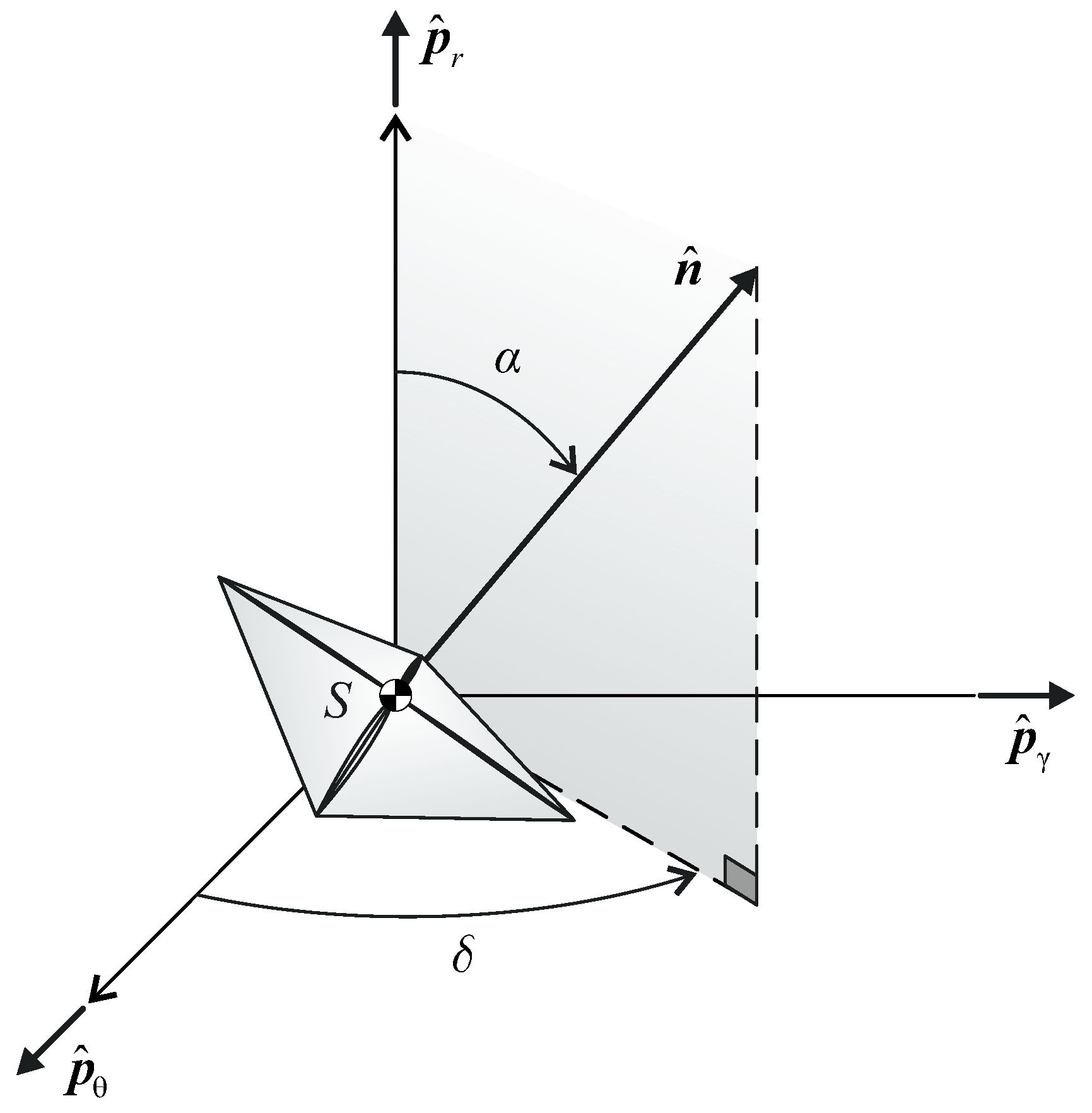
2.1. Thrust Vector Model of an Ideal Solar Sail
2.2. Sail Performance Required to Maintain a Circular DNKO
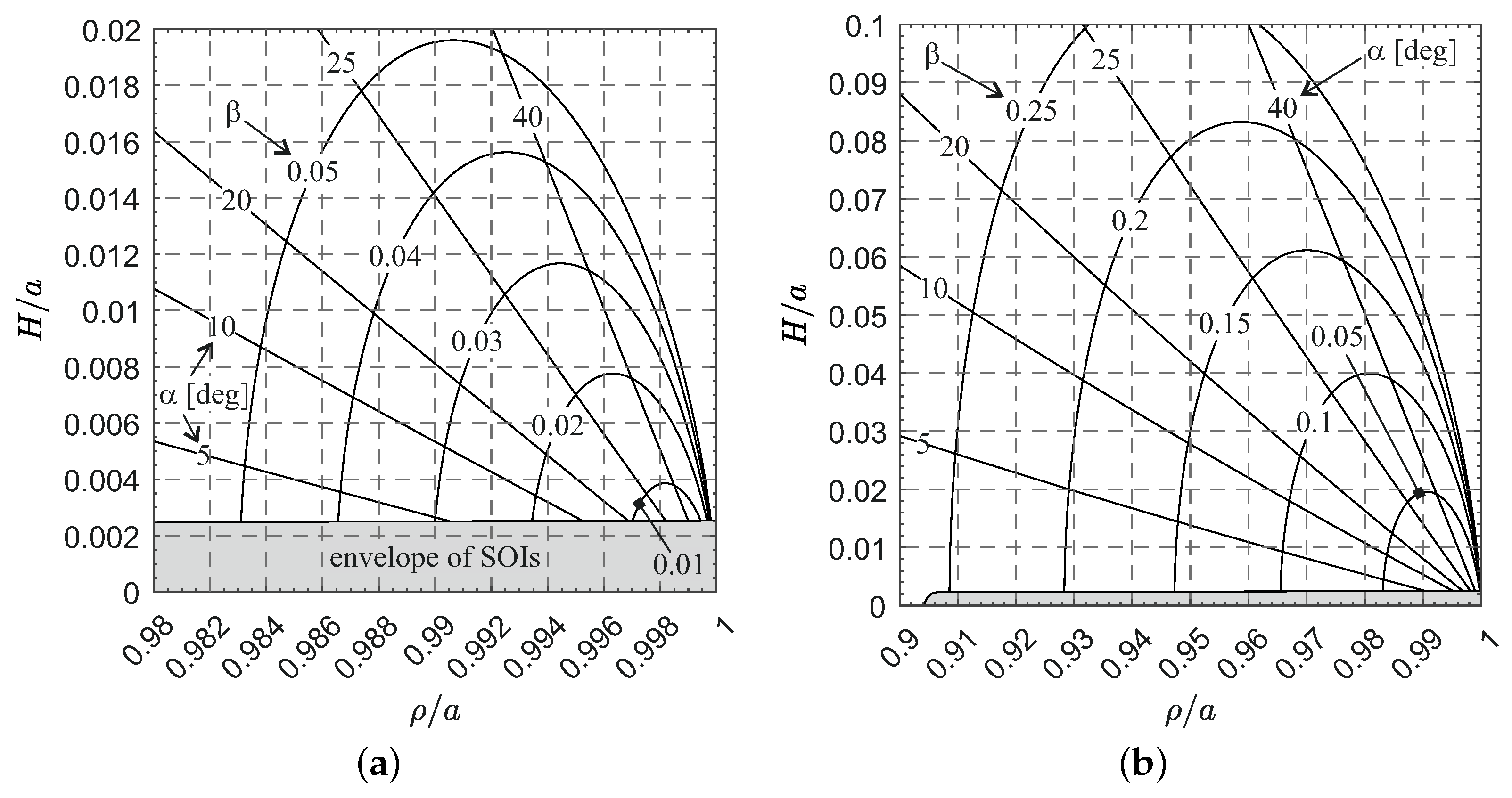
3. Numerical Results
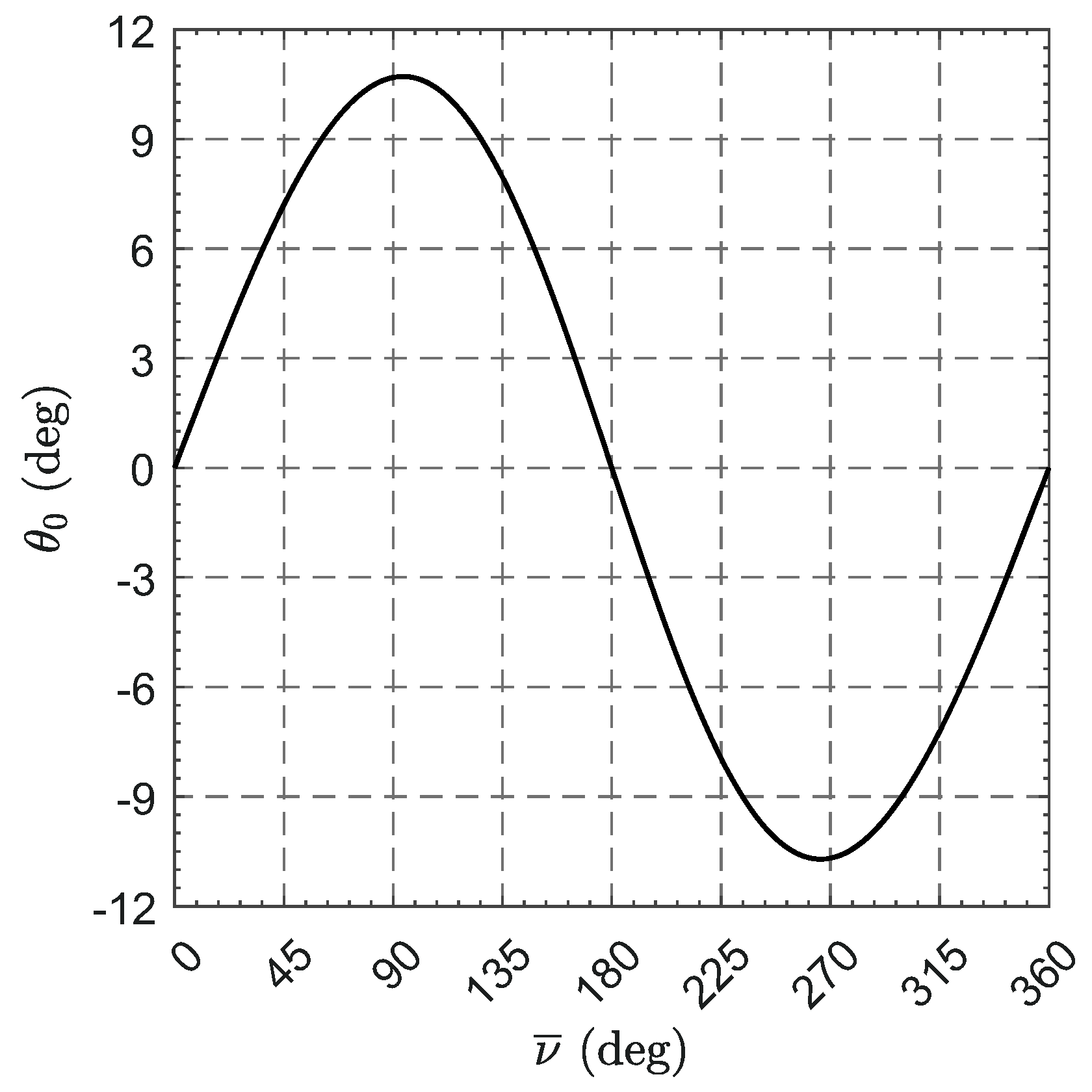
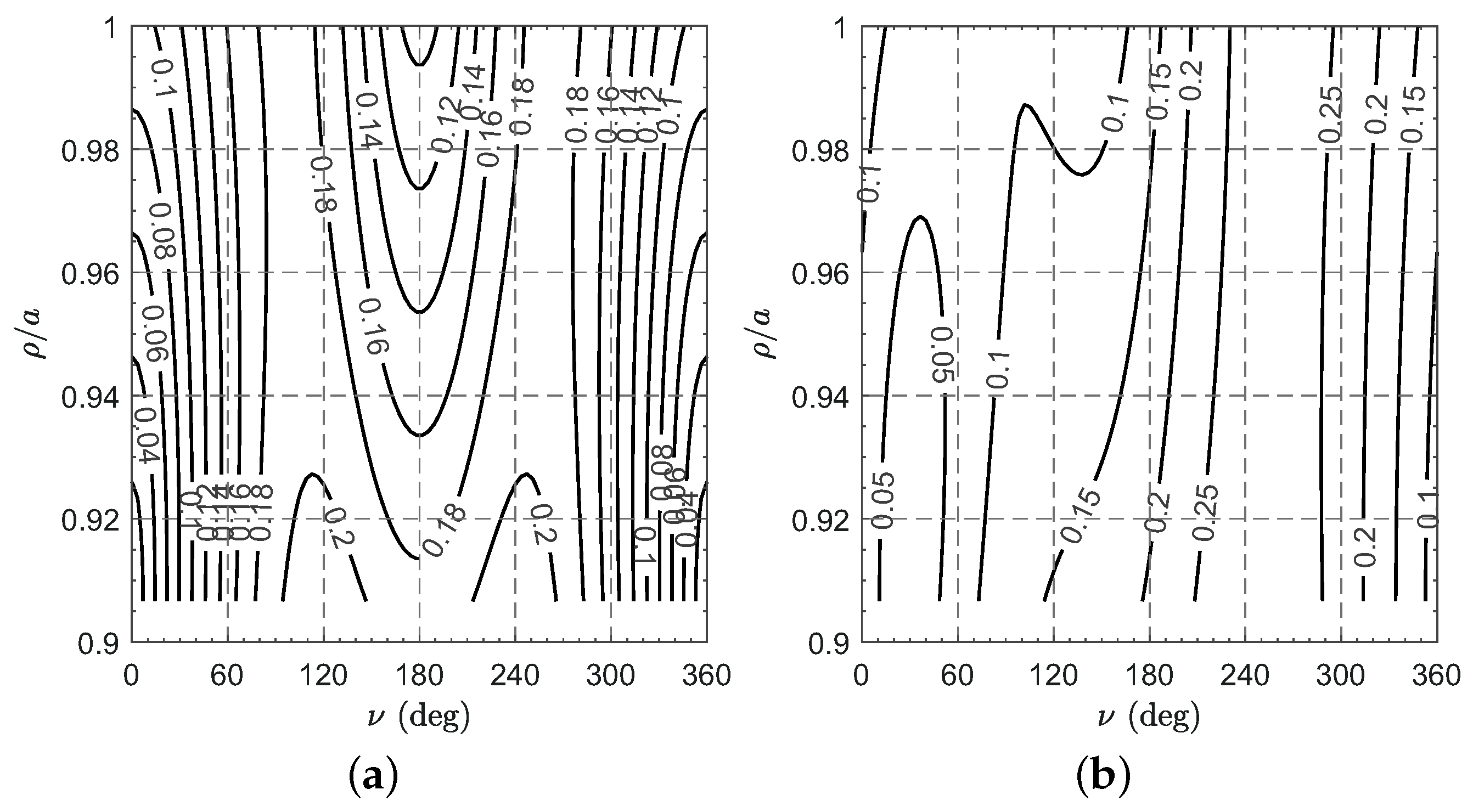
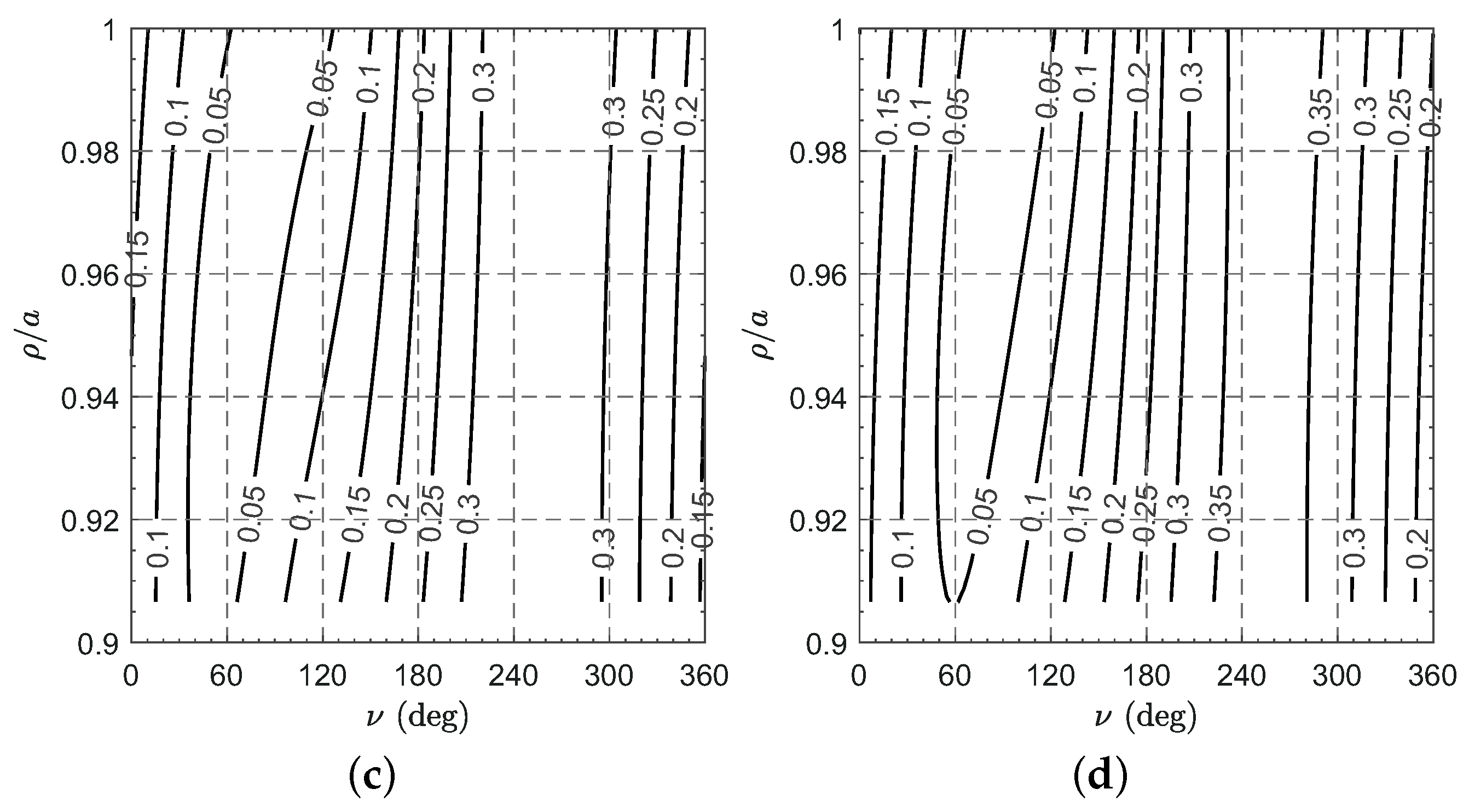
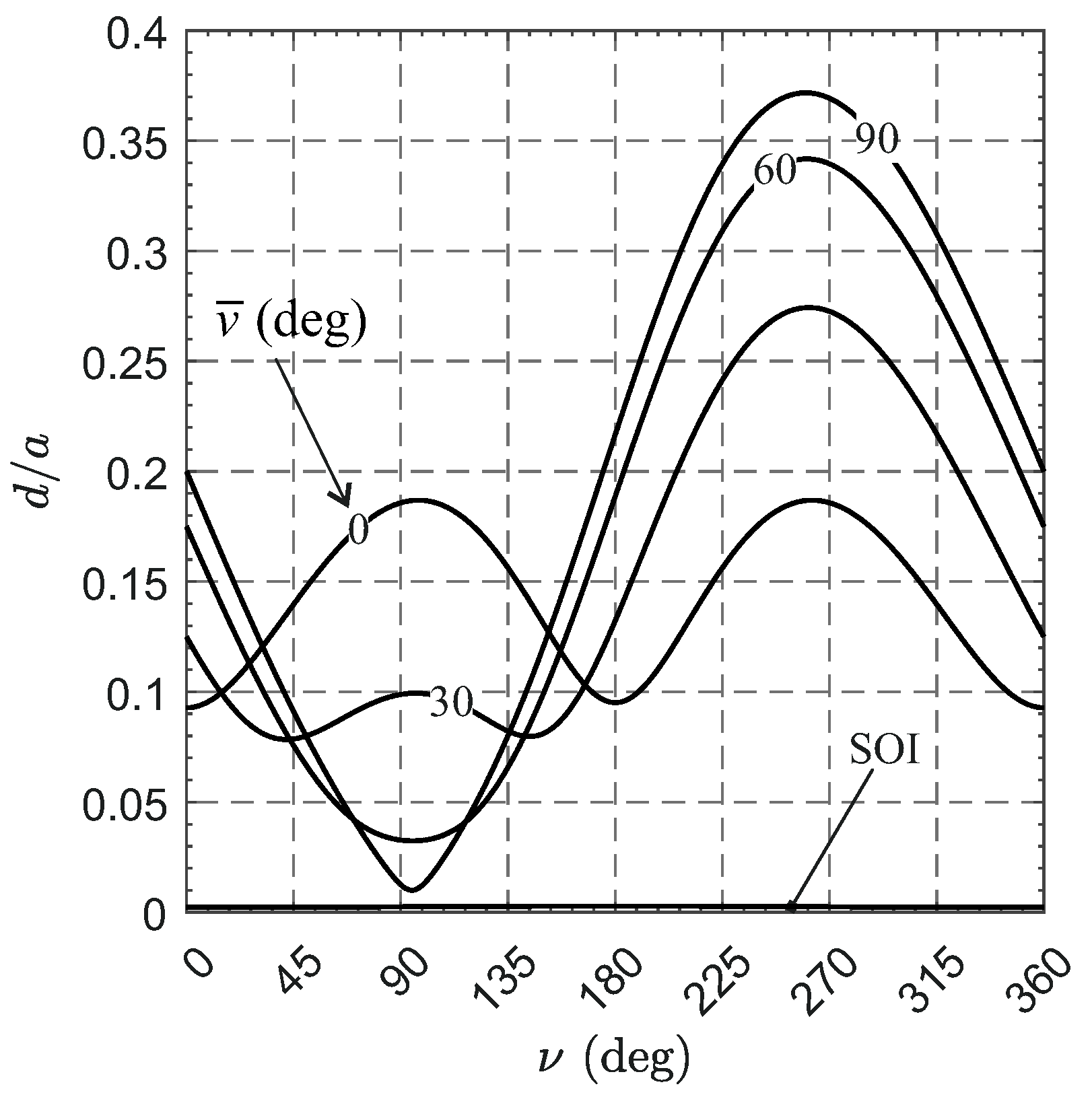
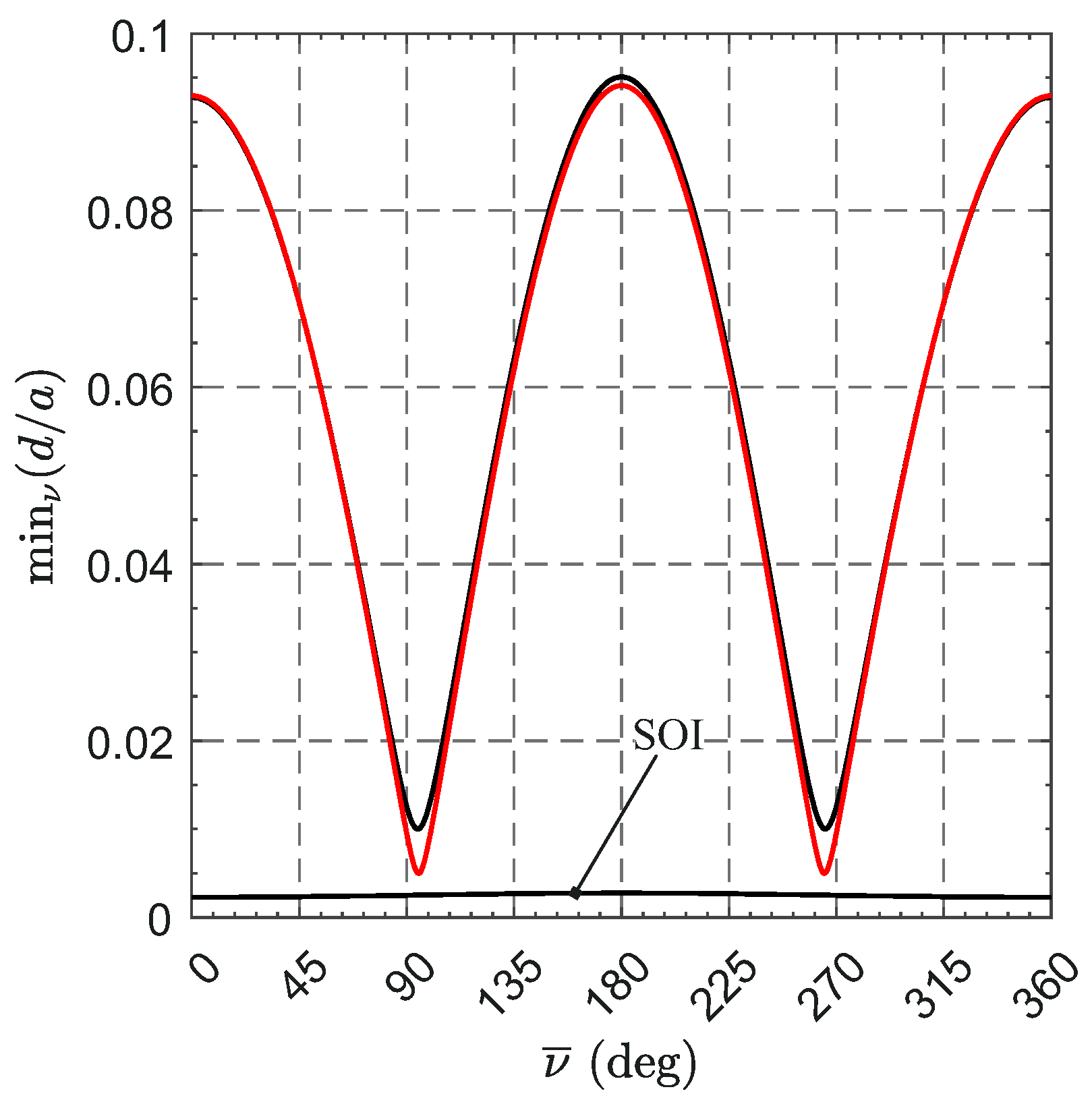
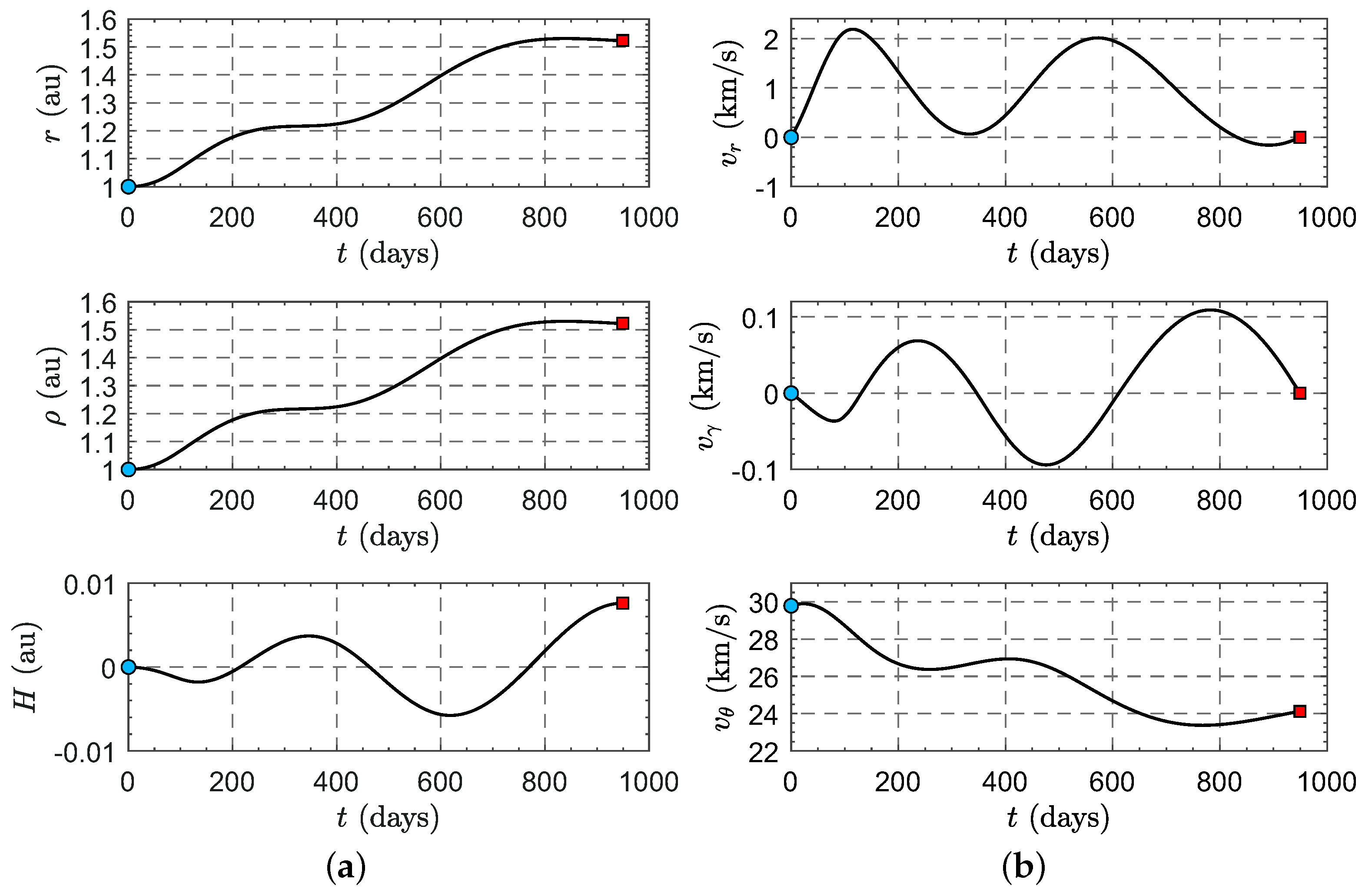
3.1. Evaluation of the Mars-Spacecraft Distance
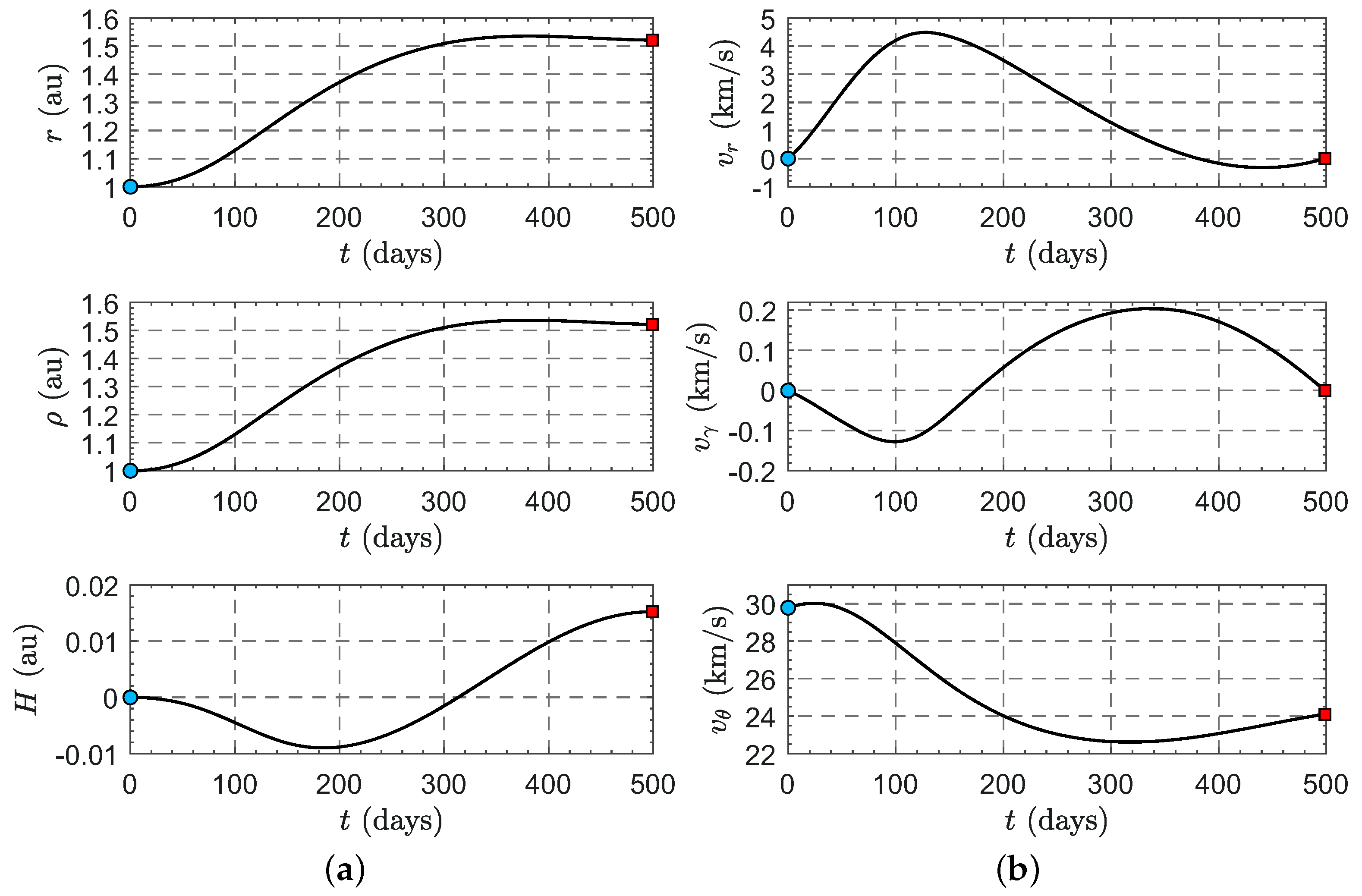
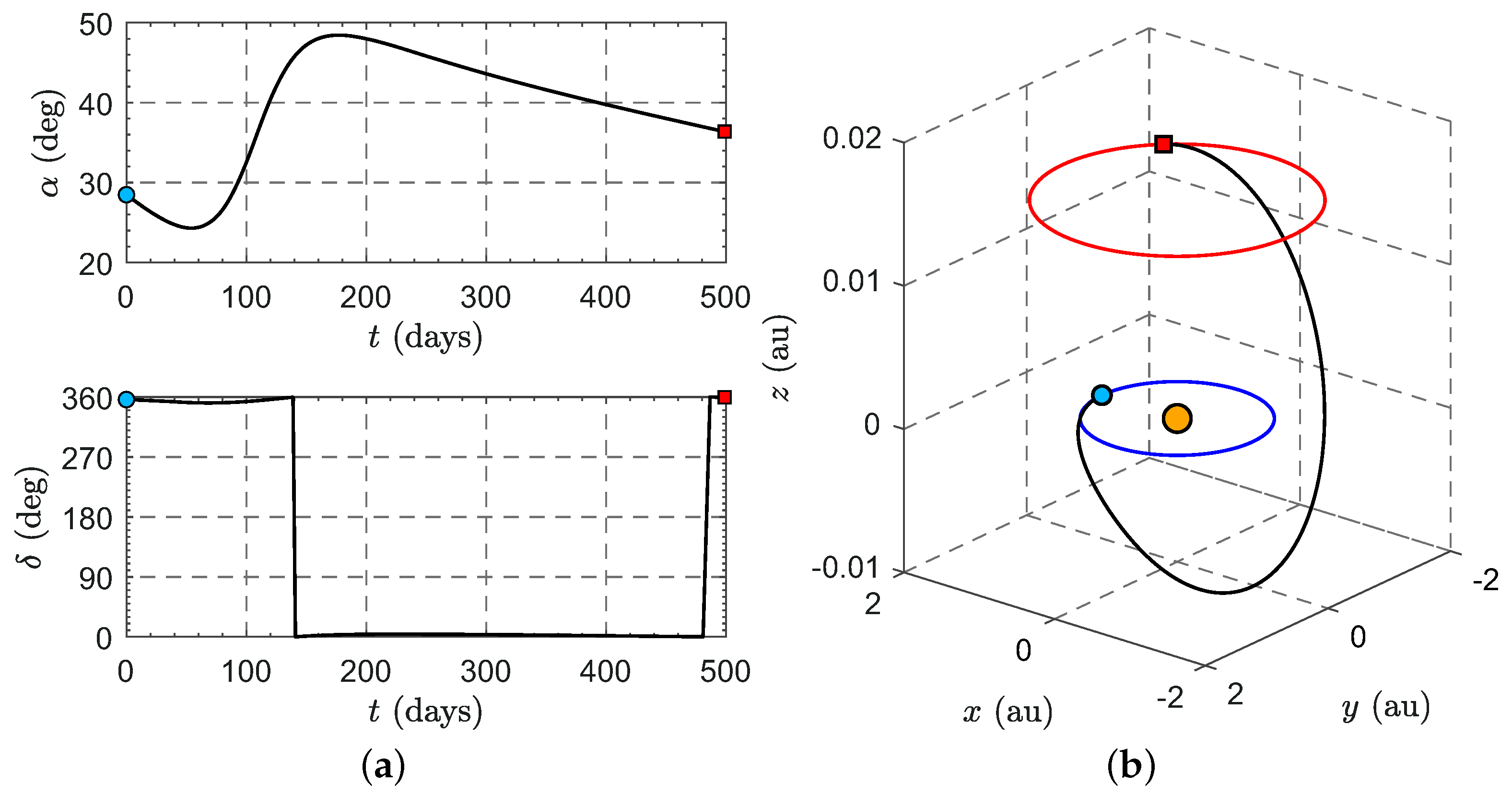
4. Preliminary Study of the Heliocentric Transfer Trajectory
Mission Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations and Symbols
| ACS3 | Advanced Composite Solar Sail System |
| DNKO | displaced non-Keplerian orbit |
| Notation | |
| a | semimajor axis of Mars heliocentric orbit [au] |
| A | sail surface (reference) area [m2] |
| propulsive acceleration vector [mm/s2] | |
| radial component of the propulsive acceleration vector [mm/s2] | |
| azimuthal component of the propulsive acceleration vector [mm/s2] | |
| normal component of the propulsive acceleration vector [mm/s2] | |
| c | speed of light in vacuum [km/s] |
| d | Mars-spacecraft distance [au] |
| e | eccentricity of Mars heliocentric orbit |
| E | eccentric anomaly [deg] |
| H | displacement between Mars heliocentric orbital plane and the DNKO [au] |
| solar constant [W/m2] | |
| J | performance index [days] |
| unit vector of the Mars orbital angular momentum | |
| m | total spacecraft mass [kg] |
| unit vector normal to the sail nominal plane | |
| O | Sun’s center of mass |
| center of the circular DNKO | |
| radial unit vector | |
| azimuthal unit vector | |
| normal unit vector | |
| axes of the reference frame | |
| r | Sun-spacecraft distance [au] |
| Sun-spacecraft (position) vector [au] | |
| reference distance [] | |
| S | spacecraft center of mass |
| t | time [days] |
| perifocal reference frame | |
| spherical reference frame | |
| radial component of spacecraft inertial velocity [km/s] | |
| azimuthal component of spacecraft inertial velocity [km/s] | |
| normal component of spacecraft inertial velocity [km/s] | |
| sail cone angle [deg] | |
| sail lightness number | |
| elevation angle [deg] | |
| clock angle [deg] | |
| azimuthal angle [deg] | |
| Sun’s gravitational parameter [km3/s2] | |
| true anomaly [deg] | |
| radius of the circular DNKO [au] | |
| angular offset between the spacecraft and Mars [deg] | |
| Mars mean motion [deg/day] | |
| Subscripts | |
| i | start of the transfer |
| f | end of the transfer |
| 0 | start of the observation phase |
| ♂ | of Mars |
| Superscripts | |
| · | derivative with respect to time |
| − | reference value |
References
- Fu, B.; Sperber, E.; Eke, F. Solar sail technology—A state of the art review. Prog. Aerosp. Sci. 2016, 86, 1–19. [Google Scholar] [CrossRef]
- Gong, S.; Macdonald, M. Review on solar sail technology. Astrodynamics 2019, 3, 93–125. [Google Scholar] [CrossRef]
- Zhao, P.; Wu, C.; Li, Y. Design and application of solar sailing: A review on key technologies. Chin. J. Aeronaut. 2023, 36, 125–144. [Google Scholar] [CrossRef]
- Firuzi, S.; Gong, S. Refractive sail and its applications in solar sailing. Aerosp. Sci. Technol. 2018, 77, 362–372. [Google Scholar] [CrossRef]
- Bassetto, M.; Caruso, A.; Quarta, A.A.; Mengali, G. Optimal Steering Law of Refractive Sail. Adv. Space Res. 2021, 67, 2855–2864. [Google Scholar] [CrossRef]
- Swartzlander, G.A., Jr. Radiation pressure on a diffractive sailcraft. J. Opt. Soc. Am. B Opt. Phys. 2017, 34, C25–C30. [Google Scholar] [CrossRef]
- Swartzlander, G.A., Jr. Flying on a rainbow: A solar-driven diffractive sailcraft. J. Br. Interplanet. Soc. 2018, 71, 130–132. [Google Scholar]
- Dubill, A.L.; Swartzlander, G.A., Jr. Circumnavigating the Sun with diffractive solar sails. Acta Astronaut. 2021, 187, 190–195. [Google Scholar] [CrossRef]
- Forward, R.L. Statite—A spacecraft that does not orbit. J. Spacecr. Rockets 1991, 28, 606–611. [Google Scholar] [CrossRef]
- McKay, R.J.; MacDonald, M.; Biggs, J.; McInnes, C. Survey of highly-non-Keplerian orbits with low-thrust propulsion. J. Guid. Control Dyn. 2011, 34, 645–666. [Google Scholar] [CrossRef]
- McInnes, C.R. Dynamics, stability, and control of displaced non-Keplerian orbits. J. Guid. Control Dyn. 1998, 21, 799–805. [Google Scholar] [CrossRef]
- Bookless, J.; McInnes, C.R. Dynamics and control of displaced periodic orbits using solar-sail propulsion. J. Guid. Control Dyn. 2006, 29, 527–537. [Google Scholar] [CrossRef]
- McInnes, C.R. Displaced non-Keplerian orbits using impulsive thrust. Celest. Mech. Dyn. Astron. 2011, 110, 199–215. [Google Scholar] [CrossRef]
- Caruso, A.; Mengali, G.; Quarta, A.A. Elliptic displaced orbit approximation with equally spaced impulses. J. Guid. Control Dyn. 2019, 42, 411–415. [Google Scholar] [CrossRef]
- de Almeida Junior, A.K.; Prado, A.F.B.d.A.; Yokoyama, T.; Sanchez, D.M. Searching for orbits to observe the poles of celestial bodies. Adv. Space Res. 2020, 66, 2378–2401. [Google Scholar] [CrossRef]
- McInnes, C.R. Solar Sailing: Technology, Dynamics and Mission Applications; Springer: Berlin/Heidelberg, Germany, 1999; pp. 171–196. [Google Scholar] [CrossRef]
- West, J.L. The GeoStorm warning mission: Enhanced opportunities based on new technology. Adv. Astronaut. Sci. 2005, 119, 29–42. [Google Scholar]
- Boni, L.; Bassetto, M.; Niccolai, L.; Mengali, G.; Quarta, A.A.; Circi, C.; Pellegrini, R.C.; Cavallini, E. Structural response of Helianthus solar sail during attitude maneuvers. Aerosp. Sci. Technol. 2023, 133, 1–9. [Google Scholar] [CrossRef]
- Gong, S.; Li, J. Solar sail heliocentric elliptic displaced orbits. J. Guid. Control Dyn. 2014, 37, 2021–2025. [Google Scholar] [CrossRef]
- Gong, S.; Li, J. Spin-stabilized solar sail for displaced solar orbits. Aerosp. Sci. Technol. 2014, 32, 188–199. [Google Scholar] [CrossRef]
- Song, M.; He, X.; He, D. Displaced orbits for solar sail equipped with reflectance control devices in Hill’s restricted three-body problem with oblateness. Astrophy. Space Sci. 2016, 361, 1–7. [Google Scholar] [CrossRef]
- Gong, S.; Baoyin, H.; Li, J. Relative orbit design and control of formation around displaced solar orbits. Aerosp. Sci. Technol. 2008, 12, 195–201. [Google Scholar] [CrossRef]
- Ceriotti, M.; McInnes, C.R.; Diedrich, B.L. The pole-sitter mission concept: An overview of recent developments and possible future applications. In Proceedings of the 62nd International Astronautical Congress (IAC), Cape Town, South Africa, 3–7 October 2011. [Google Scholar]
- Ceriotti, M.; Heiligers, J.; McInnes, C.R. Trajectory and spacecraft design for a pole-sitter mission. J. Spacecr. Rockets 2014, 51, 311–326. [Google Scholar] [CrossRef]
- Heiligers, J.; Scheeres, D.J. Solar-sail orbital motion about asteroids and binary asteroid systems. J. Guid. Control Dyn. 2018, 41, 1947–1962. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Mengali, G. Magnetic sail-based displaced non-Keplerian orbits. Aerosp. Sci. Technol. 2019, 92, 363–372. [Google Scholar] [CrossRef]
- Bassetto, M.; Mengali, G.; Quarta, A.A. Diffractive sail-based displaced orbits for high-latitude environment monitoring. Remote Sens. 2023, 15, 5626. [Google Scholar] [CrossRef]
- Zubrin, R.M.; Andrews, D.G. Magnetic sails and interplanetary travel. J. Spacecr. Rockets 1991, 28, 197–203. [Google Scholar] [CrossRef]
- Andrews, D.G.; Zubrin, R.M. Magnetic sails and interstellar travel. J. Br. Interplanet. Soc. 1990, 43, 265–272. [Google Scholar]
- Zubrin, R.M. The use of magnetic sails to escape from low Earth orbit. J. Br. Interplanet. Soc. 1992, 46, 3–10. [Google Scholar] [CrossRef]
- Sengupta, P.; Vadali, S.R.; Alfriend, K.T. Satellite Orbit Design and Maintenance for Terrestrial Coverage. J. Spacecr. Rockets 2010, 47, 177–187. [Google Scholar] [CrossRef]
- Vendl, J.K.; Holzinger, M.J. Cislunar Periodic Orbit Analysis for Persistent Space Object Detection Capability. J. Spacecr. Rockets 2021, 58, 1174–1185. [Google Scholar] [CrossRef]
- Alvarado, K.I.; Singh, S.K. Exploration and Maintenance of Homeomorphic Orbit Revs in the Elliptic Restricted Three-Body Problem. Aerospace 2024, 11, 407. [Google Scholar] [CrossRef]
- MacDonald, M.; McKay, R.J.; Vasile, M.; De Frescheville, F.; Biggs, J.D.; McInnes, C.R. Low-thrust-enabled highly-non-Keplerian orbits in support of future Mars exploration. J. Guid. Control Dyn. 2011, 34, 1396–1411. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Bassetto, M. Optimal solar sail transfers to circular Earth-synchronous displaced orbits. Astrodynamics 2020, 4, 193–204. [Google Scholar] [CrossRef]
- Oguri, K.; Lantoine, G.; Sweetser, T.H. Robust Solar Sail Trajectory Design under Uncertainty with Application to NEA Scout Mission. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Campbell, B.A. Factoring Thrust Uncertainty into Solar Sail Performance Validation. In Proceedings of the 6th International Symposium on Space Sailing, New York, NY, USA, 5–9 June 2023. [Google Scholar]
- Wang, W.; Mengali, G.; Quarta, A.A.; Baoyin, H. Spacecraft Relative Motion Control Near an Asteroid with Uncertainties: A Lyapunov Redesign Approach. IEEE Trans. Aerosp. Electron. Syst. 2024, in press. [CrossRef]
- Wright, J.L. Space Sailing; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Dachwald, B.; Mengali, G.; Quarta, A.A.; Macdonald, M. Parametric model and optimal control of solar sails with optical degradation. J. Guid. Control Dyn. 2006, 29, 1170–1178. [Google Scholar] [CrossRef]
- Dachwald, B.; Macdonald, M.; McInnes, C.R.; Mengali, G.; Quarta, A.A. Impact of optical degradation on solar sail mission performance. J. Spacecr. Rockets 2007, 44, 740–749. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Mengali, G.; Cipolla, V. Trajectory analysis of a Sun-facing solar sail with optical degradation. J. Guid. Control Dyn. 2020, 43, 1727–1732. [Google Scholar] [CrossRef]
- Bate, R.R.; Mueller, D.D.; White, J.E. Fundamentals of Astrodynamics; Dover Publications: New York, NY, USA, 1971; Chapter 2; pp. 53–55. [Google Scholar]
- Spencer, D.A.; Betts, B.; Bellardo, J.M.; Diaz, A.; Plante, B.; Mansell, J.R. The LightSail 2 solar sailing technology demonstration. Adv. Space Res. 2021, 67, 2878–2889. [Google Scholar] [CrossRef]
- McNutt, L.; Johnson, L.; Kahn, P.; Castillo-Rogez, J.; Frick, A. Near-Earth Asteroid (NEA) Scout. In Proceedings of the AIAA SPACE 2014 Conference and Exposition, San Diego, CA, USA, 4–7 August 2014. [Google Scholar] [CrossRef]
- Lockett, T.R.; Castillo-Rogez, J.; Johnson, L.; Matus, J.; Lightholder, J.; Marinan, A.; Few, A. Near-Earth Asteroid Scout Flight Mission. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 20–29. [Google Scholar] [CrossRef]
- Wilkie, W.K.; Fernandez, J.M.; Stohlman, O.R.; Schneider, N.R.; Dean, G.D.; Kang, J.H.; Warren, J.E.; Cook, S.M.; Brown, P.L.; Denkins, T.C.; et al. An overview of the NASA Advanced Composite Solar Sail (ACS3) technology demonstration project. In Proceedings of the AIAA Scitech Forum, Virtual Event, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- Wie, B. Thrust vector control analysis and design for solar-sail spacecraft. J. Spacecr. Rockets 2007, 44, 545–557. [Google Scholar] [CrossRef]
- Ross, I.M. A Primer on Pontryagin’s Principle in Optimal Control; Collegiate Publishers: San Francisco, CA, USA, 2015; Chapter 2; pp. 127–129. ISBN 9780984357116. [Google Scholar]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Yang, W.Y.; Cao, W.; Kim, J.; Park, K.W.; Park, H.H.; Joung, J.; Ro, J.S.; Hong, C.H.; Im, T. Applied Numerical Methods Using MATLAB; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020; Chapters 3 and 6; pp. 166–172, 312. [Google Scholar]
- Quarta, A.A. Fast initialization of the indirect optimization problem in the solar sail circle-to-circle orbit transfer. Aerosp. Sci. Technol. 2024, 147, 109058. [Google Scholar] [CrossRef]
- Quarta, A.A. Initial costate approximation for rapid orbit raising with very low propulsive acceleration. Appl. Sci. 2024, 14, 1124. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassetto, M.; Quarta, A.A. Solar Sail-Based Mars-Synchronous Displaced Orbits for Remote Sensing Applications. Appl. Sci. 2024, 14, 5001. https://doi.org/10.3390/app14125001
Bassetto M, Quarta AA. Solar Sail-Based Mars-Synchronous Displaced Orbits for Remote Sensing Applications. Applied Sciences. 2024; 14(12):5001. https://doi.org/10.3390/app14125001
Chicago/Turabian StyleBassetto, Marco, and Alessandro A. Quarta. 2024. "Solar Sail-Based Mars-Synchronous Displaced Orbits for Remote Sensing Applications" Applied Sciences 14, no. 12: 5001. https://doi.org/10.3390/app14125001





