Water Impermeability of Self-Compacting Fly-Ash-Containing Concrete
Abstract
1. Introduction
- By “wet spot”;
- By filtration coefficient;
- By penetration depth of water under pressure;
- By air permeability.
2. Materials and Methods
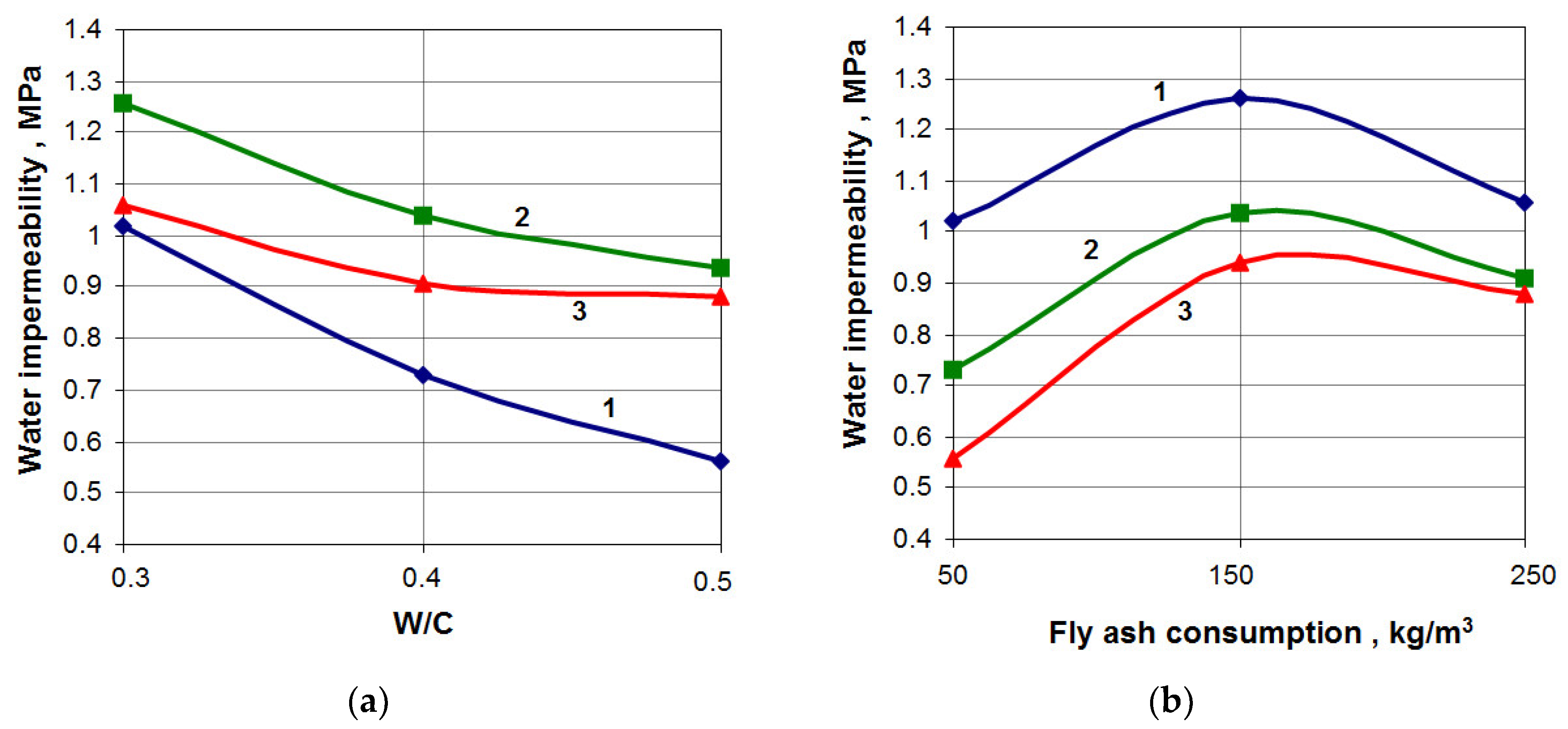
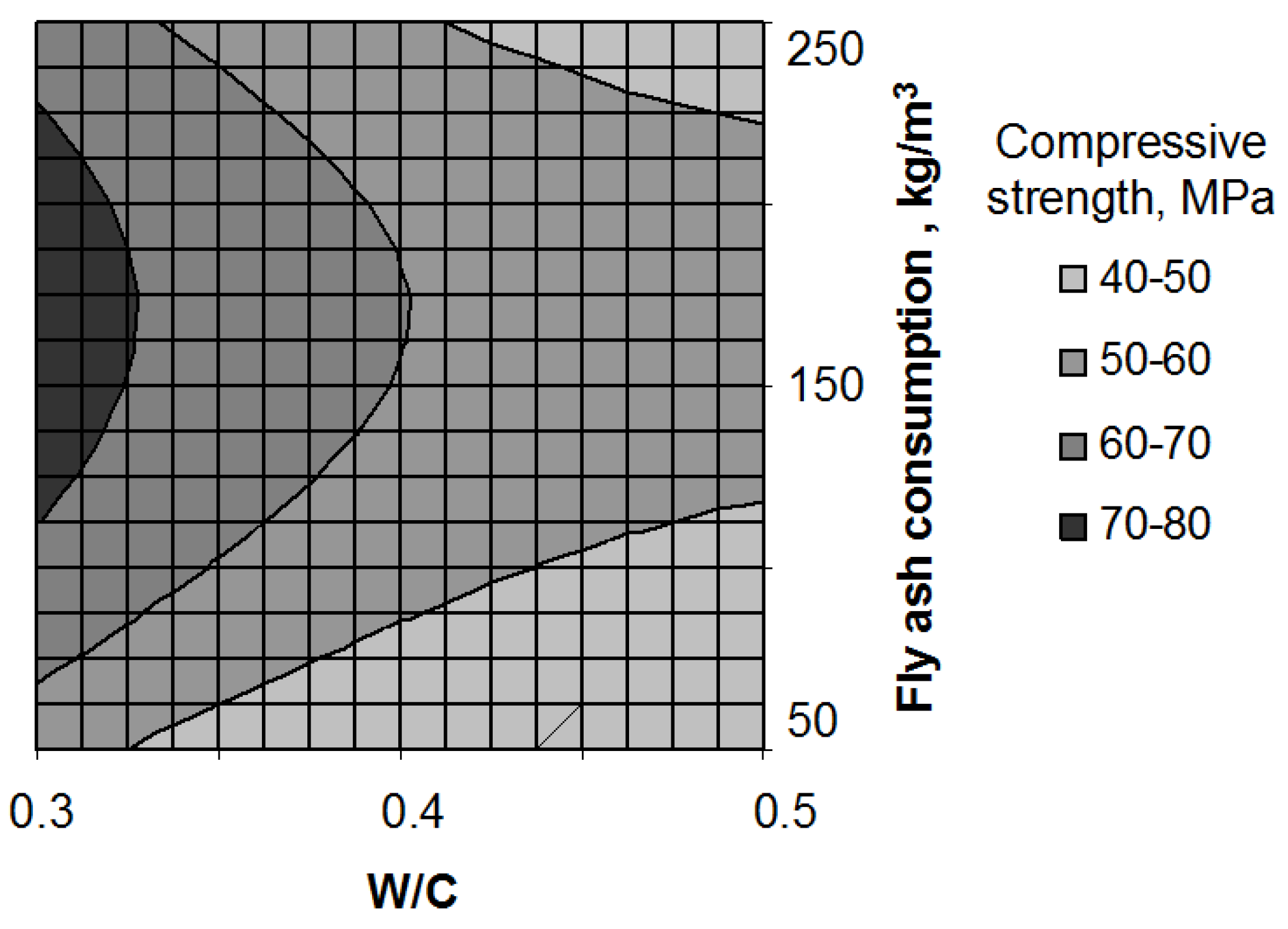
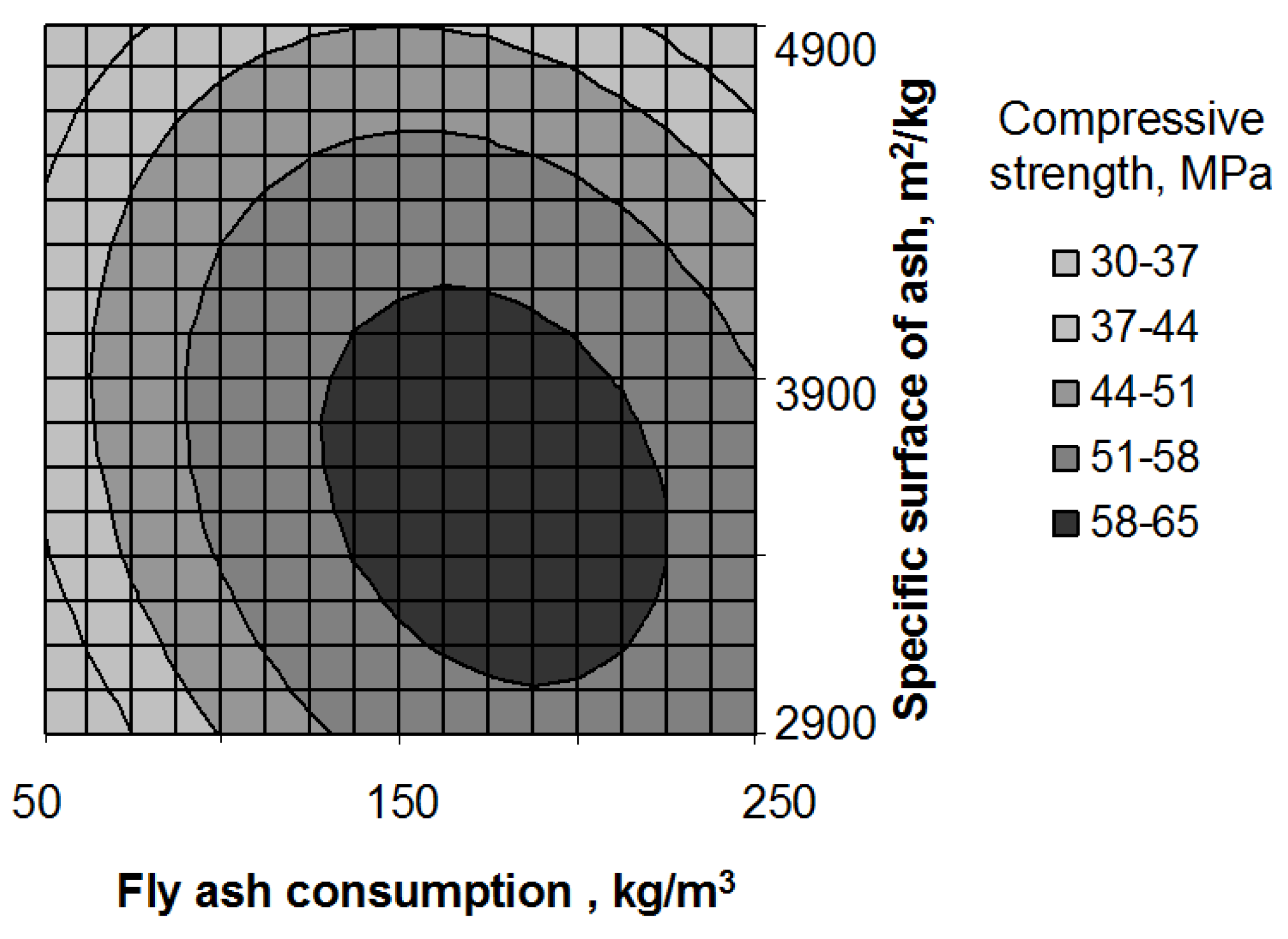
3. Results and Discussion
4. Conclusions
- The results of the experiments showed the possibility of reducing cement consumption up to 20–23% by adding the optimal amount of fly ash to the composition of self-compacting concrete while ensuring the required strength.
- Additional grinding of the ash to the optimum specific surface area allows for additional savings in cement of 8–10%.
- For compositions of self-compacting concrete containing fly ash additive with different specific surface areas, a set of experimental/statistical models of mixture water separation, strength, and water impermeability of concrete was obtained.
- Analysis of the obtained models allowed us to obtain quantitative estimates of the influence of the main technological factors and their interactions on the studied properties of self-compacted concrete.
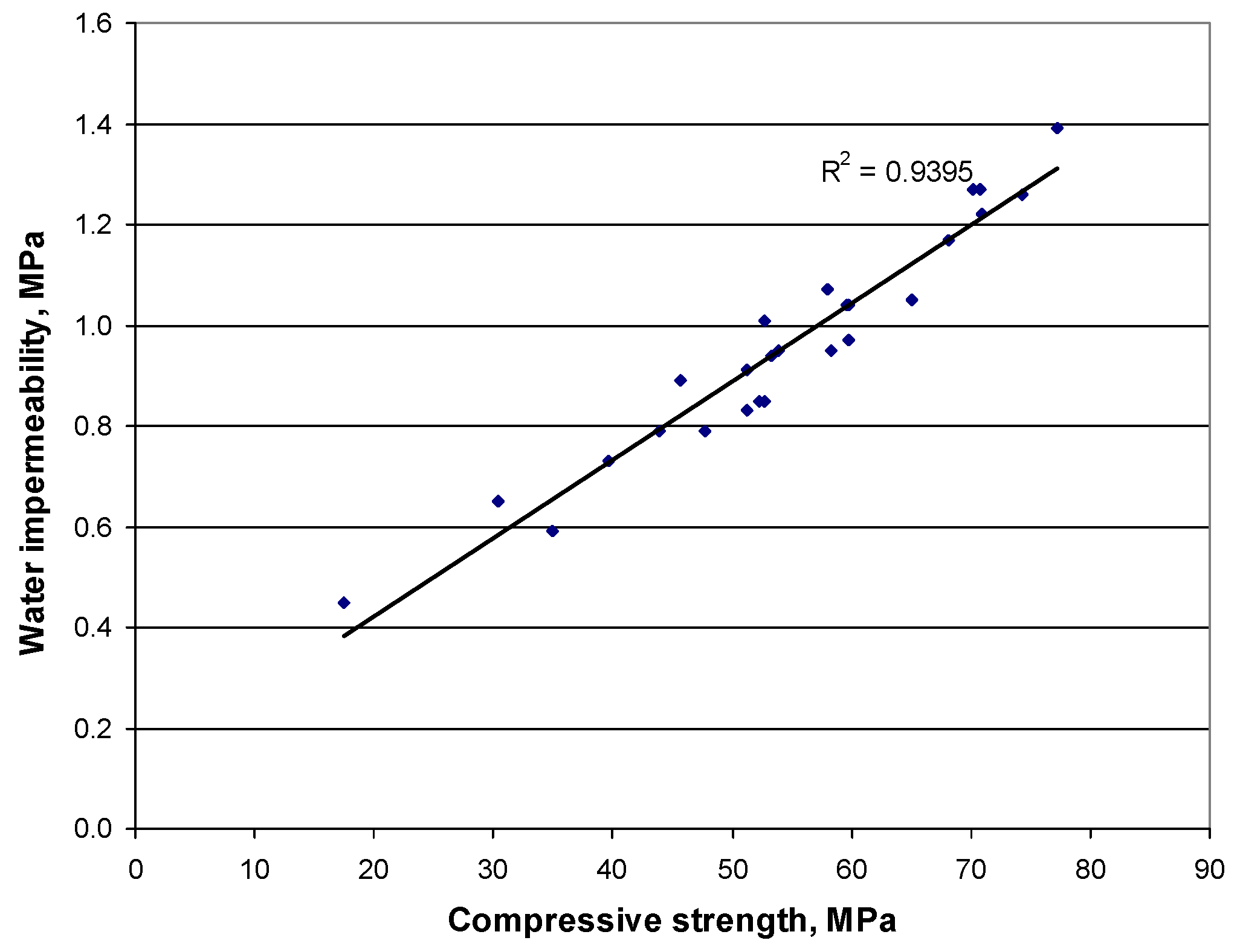
- A high level of correlation between the impermeability and strength of concrete was established, which allowed us to propose an empirical equation for predicting impermeability. Experimental verification showed the possibility of using this equation to predict water resistance with sufficient accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yunusova, F.; Muslimov, T. Water Impermeability of Hydraulic Concrete Based with Thermal Power Plant Waste Substrate. IOP Conf. Ser. Mater. Sci. Eng. 2020, 883, 012044. [Google Scholar] [CrossRef]
- Muhammad, N.Z.; Keyvanfar, A.; Muhd, M.Z.; Shafaghat, A.; Mirza, J. Waterproof Performance of Concrete: A Critical Review on Implemented Approaches. Constr. Build. Mater. 2015, 101, 80–90. [Google Scholar] [CrossRef]
- Skutnik, Z.; Sobolewski, M.; Koda, E. An Experimental Assessment of the Water Permeability of Concrete with a Superplasticizer and Admixtures. Materials 2020, 13, 5624. [Google Scholar] [CrossRef]
- Dvorkin, L.; Nwaubani, S.; Dvorkin, O. Construction Materials; Nova Science: Hauppauge, NY, USA, 2010. [Google Scholar]
- Phung, Q.T.; Maes, N.; De Schutter, G.; Jacques, D.; Ye, G. Determination of Water Permeability of Cementitious Materials Using a Controlled Constant Flow Method. Constr. Build. Mater. 2013, 47, 1488–1496. [Google Scholar] [CrossRef]
- Kameche, Z.A.; Ghomari, F.; Choinska, M.; Khelidj, A. Assessment of Liquid Water and Gas Permeabilities of Partially Saturated Ordinary Concrete. Constr. Build. Mater. 2014, 65, 551–565. [Google Scholar] [CrossRef]
- Dvorkin, L. The Main Properties of Cement Concretes: Monograph. Palmarium Academic Publishing: London, UK, 2019. [Google Scholar]
- Neville, A.M. Properties of Concrete; Pearson: London, UK, 2011; ISBN 9780273755807. [Google Scholar]
- Powers, T. Structure and Physical Properties of Hardened Portland Cement Paste. J. Am. Ceram. Soc. 1958, 41, 1–6. [Google Scholar] [CrossRef]
- Stolnikov, V.V. Studies on Hydraulic Concrete; Gosenergoizdat: Moscow, Russia, 1962; p. 330. [Google Scholar]
- Stolnikov, V.V. Design and Construction of High Dams. Energia 1972, 144. [Google Scholar]
- Zhang, H. Building Materials in Civil Engineering; Woodhead Publishing Series in Civil and Structural Engineering; Elsevier Science: Amsterdam, The Netherlands, 2011; ISBN 9781845699567. [Google Scholar]
- Li, X.; Xu, Q.; Chen, S. An Experimental and Numerical Study on Water Permeability of Concrete. Constr. Build. Mater. 2016, 105, 503–510. [Google Scholar] [CrossRef]
- Nyame, B.K.; Illston, J.M. Relationships between Permeability and Pore Structure of Hardened Cement Paste. Mag. Concr. Res. 1981, 33, 139–146. [Google Scholar] [CrossRef]
- Dvorkin, O.; Dvorkin, L. Basics of Concrete Science: Optimum Design of Concrete Mixtures, Kindle ed.; Amazon: Seattle, WA, USA, 2012. [Google Scholar]
- Sizov, V. To the Question of Concrete Water Permeability Prediction. Concr. Reinf. Concr. 1996, 6, 8–11. [Google Scholar]
- Stark, J.; Wicht, B.; F.A. Finger—Institut für Baustoffkunde der Bauhaus—Universität Weimar. Dauerhaftigkeit von Beton: Der Baustoff als Werkstoff; Mit 42 … Tabellen; BauPraxis Series; Birkhäuser: Basel, Switzerland, 2001; ISBN 9783764363444. [Google Scholar]
- Wang, F.H.; Li, S. Effect of Silica Fume on Workability and Water Impermeability of Concrete. Appl. Mech. Mater. 2012, 238, 157–160. [Google Scholar] [CrossRef]
- Egorochkina, I.; Shlyakhova, E. Reduction of Permeability of Fine-Grained Concrete. In Networked Control Systems for Connected and Automated Vehicles. NN 2022; Lecture Notes in Networks and Systems; Springer: Cham, Siwitzerland, 2023; pp. 1623–1631. [Google Scholar]
- EN 12350-8:2019; Testing Fresh Concrete—Part 8: Self-Compacting Concrete—Slump-Flow Test. British Standards Institution: London, UK, 2019.
- EN 480-4:2005; Admixtures for Concrete, Mortar and Grout—Test Methods—Part 4: Determination of Bleeding of Concrete. British Standards Institution: London, UK, 2005.
- EN 12390-3:2019; Testing Hardened Concrete—Part 3: Compressive Strength of Test Specimens. British Standards Institution: London, UK, 2019.
- Montgomery, D.C. Design and Analysis of Experiments, 5th ed.; Wiley: Hoboken, NJ, USA, 2000; ISBN 9788126510481. [Google Scholar]
- Dvorkin, L.; Dvorkin, O.; Ribakov, Y. Mathematical Experiments Planning in Concrete Technology; Mathematics Research Developments; Nova Science Publishers: Hauppauge, NY, USA, 2012; ISBN 9781621002833. [Google Scholar]
- Rathbone, R.; Majors, R. Techniques for Measuring Ammonia in Fly Ash, Mortar, and Concrete. 2003. Available online: https://p2infohouse.org/ref/45/44826.pdf (accessed on 1 May 2024).
- Zhang, P.; Li, D.; Qiao, Y.; Zhang, S.; Sun, C.; Zhao, T. Effect of Air Entrainment on the Mechanical Properties, Chloride Migration, and Microstructure of Ordinary Concrete and Fly Ash Concrete. J. Mater. Civ. Eng. 2018, 30. [Google Scholar] [CrossRef]
- De Schutter, G.; Bartos, P.; Domone, P.; Gibbs, J. Self-Compacting Concrete; Whittles Publishing: Dunbeath, UK, 2008; ISBN 978-1904445-30-2. [Google Scholar]



| SiO2 | Al2O3 | Fe2O3 | CaO | MgO | R2O (Na2O + K2O) | L.O.I |
|---|---|---|---|---|---|---|
| 56.91 | 22.68 | 9.60 | 3.61 | 1.65 | 1.66 | 3.85 |
| Factors | Levels of Variation | Interval | |||
|---|---|---|---|---|---|
| Natural | Coded | −1 | 0 | +1 | |
| Water–cement ratio, W/C | X1 | 0.3 | 0.4 | 0.5 | 0.1 |
| Water consumption, kg/m3 | X2 | 170 | 180 | 190 | 10 |
| Sand content in the volume of sand and aggregate (r) | X3 | 0.34 | 0.41 | 0.48 | 0.07 |
| Fly ash consumption (D), kg/m3 | X4 | 50 | 150 | 250 | 100 |
| Specific surface area of ash (S), m2/kg | X5 | 290 | 390 | 490 | 100 |
| No. | Planning Matrix | Concrete Compositions | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Water Consumption, kg/m3 | Cement Consumption, kg/m3 | r | D, kg/m3 | S, m2/kg | ||||||
| X1 | X2 | X3 | X4 | X5 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 190 | 380 | 0.48 | 250 | 490 |
| 2 | −1 | −1 | 1 | 1 | 1 | 170 | 567 | 0.34 | 50 | 290 |
| 3 | −1 | 1 | −1 | −1 | −1 | 190 | 633 | 0.34 | 50 | 290 |
| 4 | 1 | −1 | −1 | −1 | −1 | 170 | 340 | 0.48 | 250 | 490 |
| 5 | −1 | 1 | −1 | 1 | 1 | 190 | 633 | 0.34 | 50 | 290 |
| 6 | 1 | −1 | −1 | 1 | 1 | 170 | 340 | 0.48 | 250 | 490 |
| 7 | 1 | 1 | 1 | −1 | −1 | 190 | 380 | 0.48 | 250 | 490 |
| 8 | −1 | −1 | 1 | −1 | −1 | 170 | 567 | 0.34 | 50 | 290 |
| 9 | −1 | 1 | 1 | 1 | −1 | 190 | 633 | 0.34 | 50 | 290 |
| 10 | 1 | −1 | 1 | 1 | −1 | 170 | 340 | 0.48 | 250 | 490 |
| 11 | 1 | 1 | −1 | −1 | 1 | 190 | 380 | 0.48 | 250 | 490 |
| 12 | −1 | −1 | −1 | −1 | 1 | 170 | 567 | 0.34 | 50 | 290 |
| 13 | −1 | 1 | 1 | −1 | 1 | 190 | 633 | 0.34 | 50 | 290 |
| 14 | 1 | −1 | 1 | −1 | 1 | 170 | 340 | 0.48 | 250 | 490 |
| 15 | 1 | 1 | −1 | 1 | −1 | 190 | 380 | 0.48 | 250 | 490 |
| 16 | −1 | −1 | −1 | 1 | −1 | 170 | 567 | 0.34 | 50 | 290 |
| 17 | 1 | 0 | 0 | 0 | 0 | 180 | 360 | 0.48 | 250 | 490 |
| 18 | −1 | 0 | 0 | 0 | 0 | 180 | 600 | 0.34 | 50 | 290 |
| 19 | 0 | 1 | 0 | 0 | 0 | 190 | 475 | 0.41 | 150 | 390 |
| 20 | 0 | −1 | 0 | 0 | 0 | 170 | 425 | 0.41 | 150 | 390 |
| 21 | 0 | 0 | 1 | 0 | 0 | 180 | 450 | 0.41 | 150 | 390 |
| 22 | 0 | 0 | −1 | 0 | 0 | 180 | 450 | 0.41 | 150 | 390 |
| 23 | 0 | 0 | 0 | 1 | 0 | 180 | 450 | 0.41 | 150 | 390 |
| 24 | 0 | 0 | 0 | −1 | 0 | 180 | 450 | 0.41 | 150 | 390 |
| 25 | 0 | 0 | 0 | 0 | 1 | 180 | 450 | 0.41 | 150 | 390 |
| 26 | 0 | 0 | 0 | 0 | −1 | 180 | 450 | 0.41 | 150 | 390 |
| 27 | 0 | 0 | 0 | 0 | 0 | 180 | 450 | 0.41 | 150 | 390 |
| No. | Planning Matrix | Water Separation of Concrete Mix, g/L | Compressive Strength, MPa | Water Impermeability, MPa | ||||
|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 0.13 | 34.9 | 0.59 |
| 2 | −1 | −1 | 1 | 1 | 1 | 0.83 | 58.0 | 1.07 |
| 3 | −1 | 1 | −1 | −1 | −1 | 1.93 | 59.8 | 0.97 |
| 4 | 1 | −1 | −1 | −1 | −1 | 0.43 | 52.7 | 1.01 |
| 5 | −1 | 1 | −1 | 1 | 1 | 0.41 | 70.1 | 1.27 |
| 6 | 1 | −1 | −1 | 1 | 1 | 0.47 | 51.3 | 0.83 |
| 7 | 1 | 1 | 1 | −1 | −1 | 5.09 | 30.3 | 0.65 |
| 8 | −1 | −1 | 1 | −1 | −1 | 2.47 | 65.1 | 1.05 |
| 9 | −1 | 1 | 1 | 1 | −1 | 2.89 | 70.8 | 1.27 |
| 10 | 1 | −1 | 1 | 1 | −1 | 0.71 | 47.7 | 0.79 |
| 11 | 1 | 1 | −1 | −1 | 1 | 0.01 | 45.6 | 0.89 |
| 12 | −1 | −1 | −1 | −1 | 1 | 0.67 | 52.7 | 0.85 |
| 13 | −1 | 1 | 1 | −1 | 1 | 3.65 | 52.3 | 0.85 |
| 14 | 1 | −1 | 1 | −1 | 1 | 0.39 | 17.5 | 0.45 |
| 15 | 1 | 1 | −1 | 1 | −1 | 0.13 | 58.3 | 0.95 |
| 16 | −1 | −1 | −1 | 1 | −1 | 0.11 | 77.2 | 1.39 |
| 17 | 1 | 0 | 0 | 0 | 0 | 0.27 | 53.3 | 0.94 |
| 18 | −1 | 0 | 0 | 0 | 0 | 0.97 | 74.3 | 1.26 |
| 19 | 0 | 1 | 0 | 0 | 0 | 1.28 | 68.1 | 1.17 |
| 20 | 0 | −1 | 0 | 0 | 0 | 0.26 | 68.1 | 1.17 |
| 21 | 0 | 0 | 1 | 0 | 0 | 2.09 | 59.6 | 1.04 |
| 22 | 0 | 0 | −1 | 0 | 0 | 0.59 | 71.0 | 1.22 |
| 23 | 0 | 0 | 0 | 1 | 0 | 0.06 | 51.3 | 0.91 |
| 24 | 0 | 0 | 0 | −1 | 0 | 1.18 | 39.7 | 0.73 |
| 25 | 0 | 0 | 0 | 0 | 1 | 0.55 | 43.9 | 0.79 |
| 26 | 0 | 0 | 0 | 0 | −1 | 1.45 | 53.9 | 0.95 |
| 27 | 0 | 0 | 0 | 0 | 0 | 0.77 | 59.7 | 1.04 |
| Properties | Mathematical (Polynomial) Models | |
|---|---|---|
| Water impermeability (W, MPa) | (6) | |
| Compressive strength, (fc, MPa) | (7) | |
| Water separation (WS, g/L) | (8) | |
| No. | Compressive Strength, MPa | Experimental Water Impermeability Value, MPa | Calculated Water Impermeability Value by Equation (9), MPa | Accuracy, % |
|---|---|---|---|---|
| 1 | 33.8 | 0.65 | 0.63 | −2.6 |
| 2 | 57.6 | 0.92 | 1.00 | 8.3 |
| 3 | 60.1 | 0.99 | 1.04 | 4.6 |
| 4 | 54.0 | 1.01 | 0.95 | −6.2 |
| 5 | 70.2 | 1.11 | 1.20 | 7.2 |
| 6 | 53.9 | 0.85 | 0.95 | 10.4 |
| 7 | 28.9 | 0.57 | 0.56 | −2.9 |
| 8 | 65.5 | 1.19 | 1.13 | −5.6 |
| 9 | 68.9 | 1.13 | 1.18 | 3.9 |
| 10 | 48.2 | 0.94 | 0.86 | −9.1 |
| Average | ±6.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dvorkin, L.; Bordiuzhenko, O.; Mierzwiński, D.; Tracz, T.; Sitarz, M. Water Impermeability of Self-Compacting Fly-Ash-Containing Concrete. Appl. Sci. 2024, 14, 5373. https://doi.org/10.3390/app14135373
Dvorkin L, Bordiuzhenko O, Mierzwiński D, Tracz T, Sitarz M. Water Impermeability of Self-Compacting Fly-Ash-Containing Concrete. Applied Sciences. 2024; 14(13):5373. https://doi.org/10.3390/app14135373
Chicago/Turabian StyleDvorkin, Leonid, Oleh Bordiuzhenko, Dariusz Mierzwiński, Tomasz Tracz, and Mateusz Sitarz. 2024. "Water Impermeability of Self-Compacting Fly-Ash-Containing Concrete" Applied Sciences 14, no. 13: 5373. https://doi.org/10.3390/app14135373
APA StyleDvorkin, L., Bordiuzhenko, O., Mierzwiński, D., Tracz, T., & Sitarz, M. (2024). Water Impermeability of Self-Compacting Fly-Ash-Containing Concrete. Applied Sciences, 14(13), 5373. https://doi.org/10.3390/app14135373








