Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges
Abstract
:1. Introduction

2. Modeling of Stay Cable
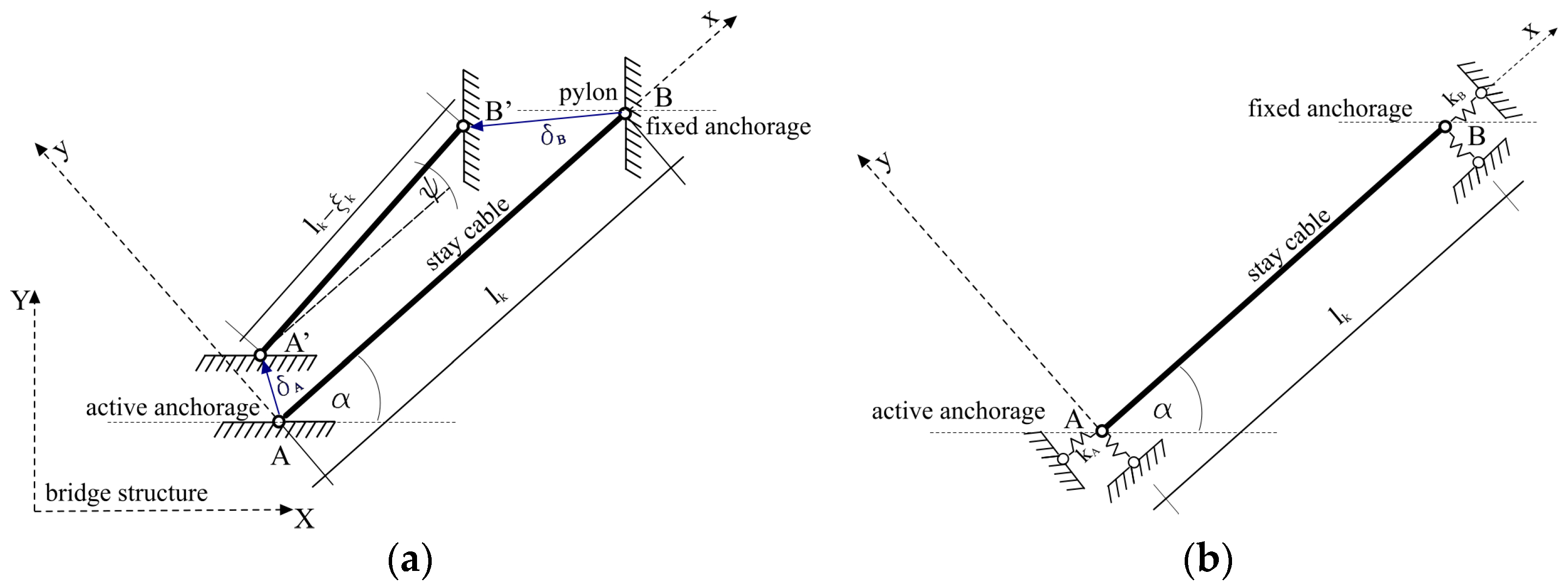

3. Algorithms for Calculation
3.1. Strand Tensioning in Single Cycle
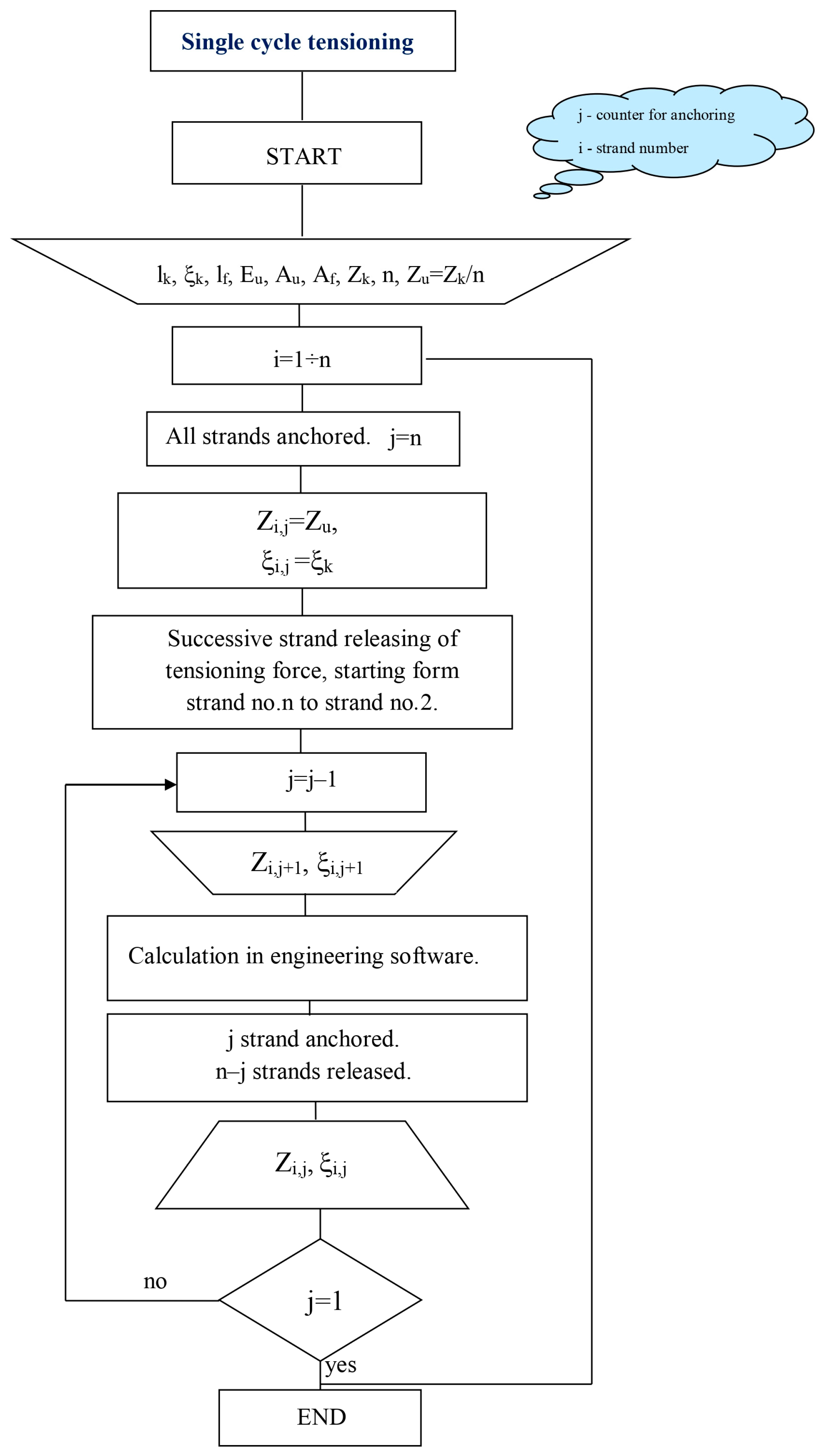
3.2. Partial Tensioning of Strands over Multiple Cycles
3.2.1. First Cycle (c = 1)
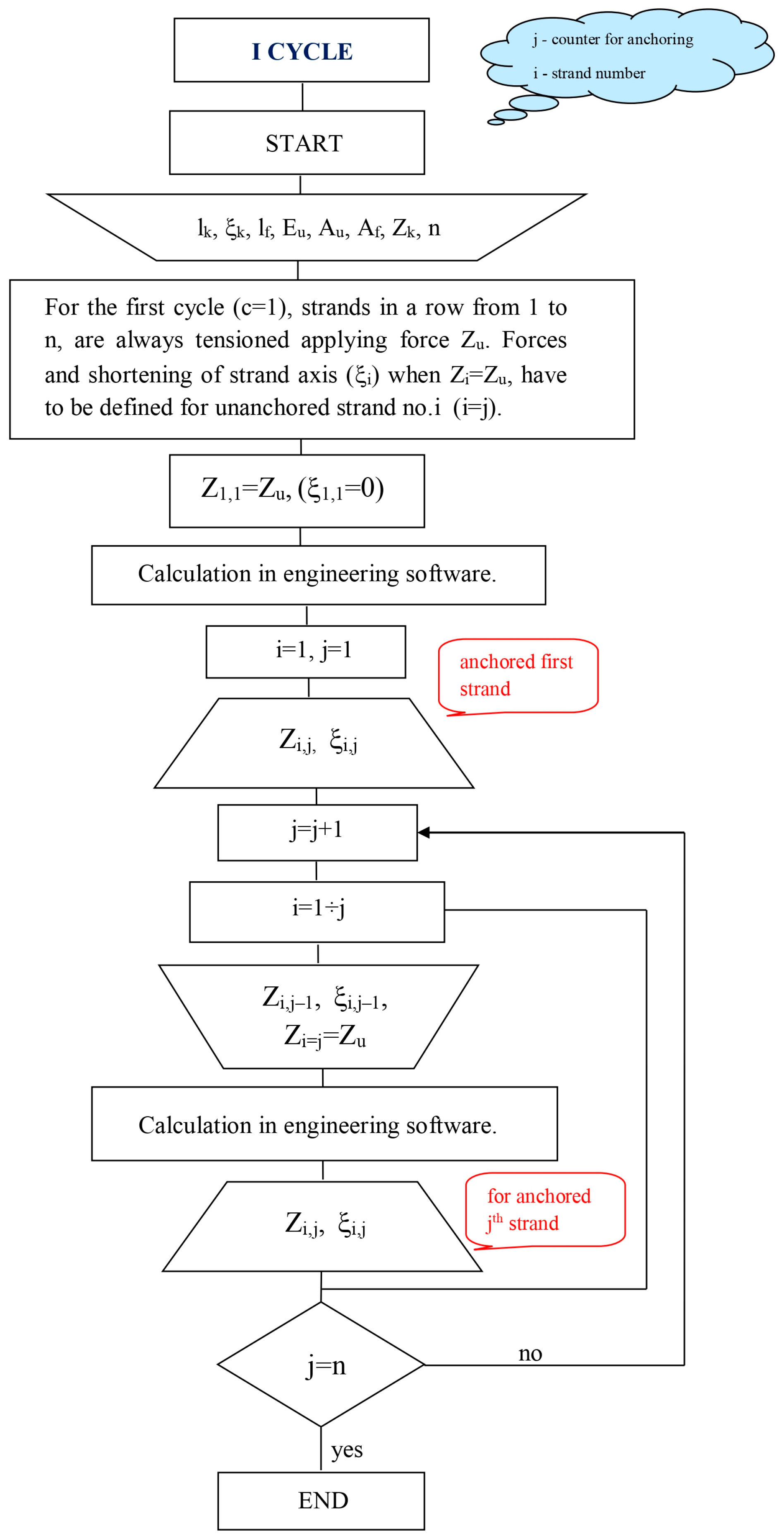
3.2.2. Subsequent (Higher) Cycles (c > 1)
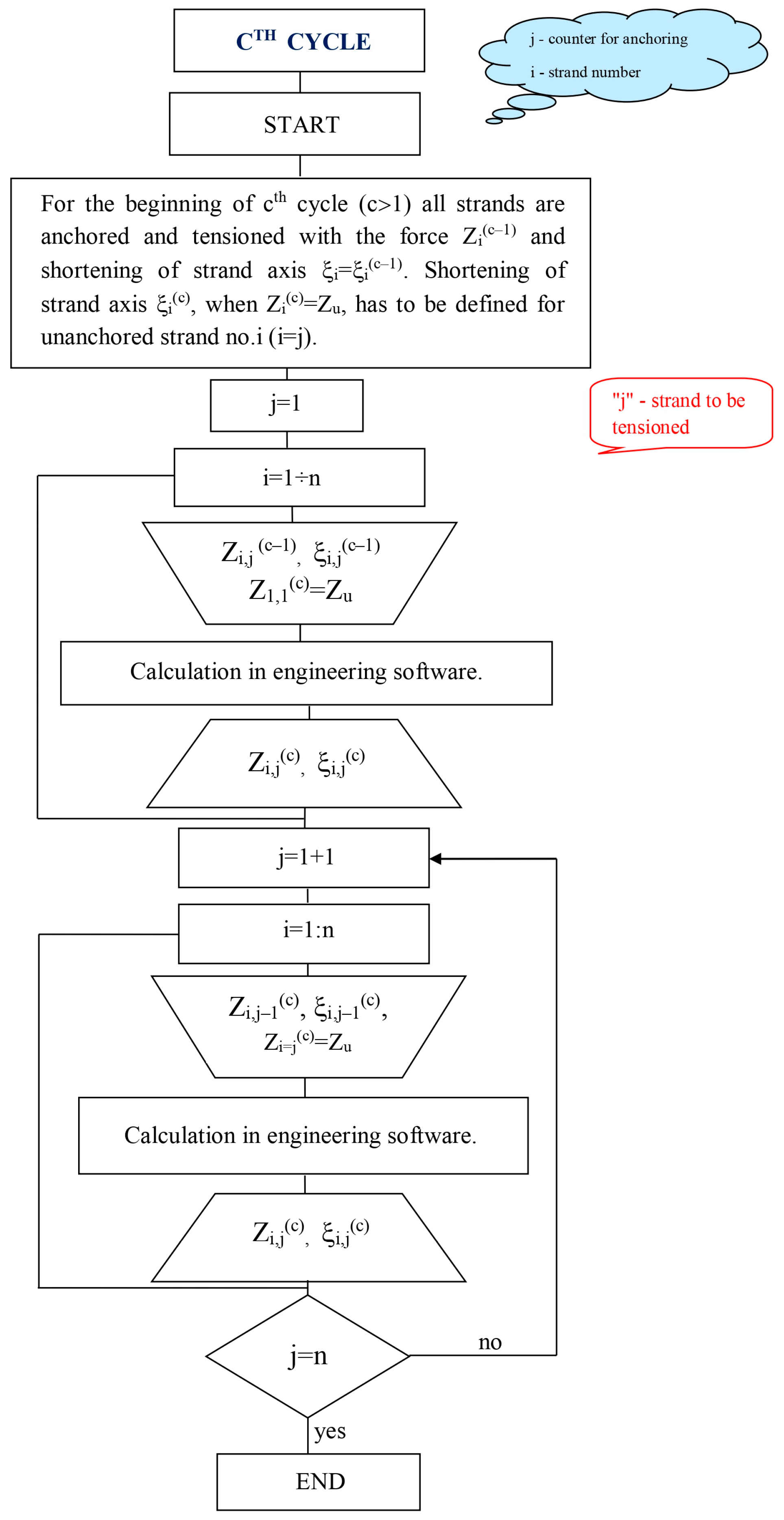
4. Numerical Example
5. Results
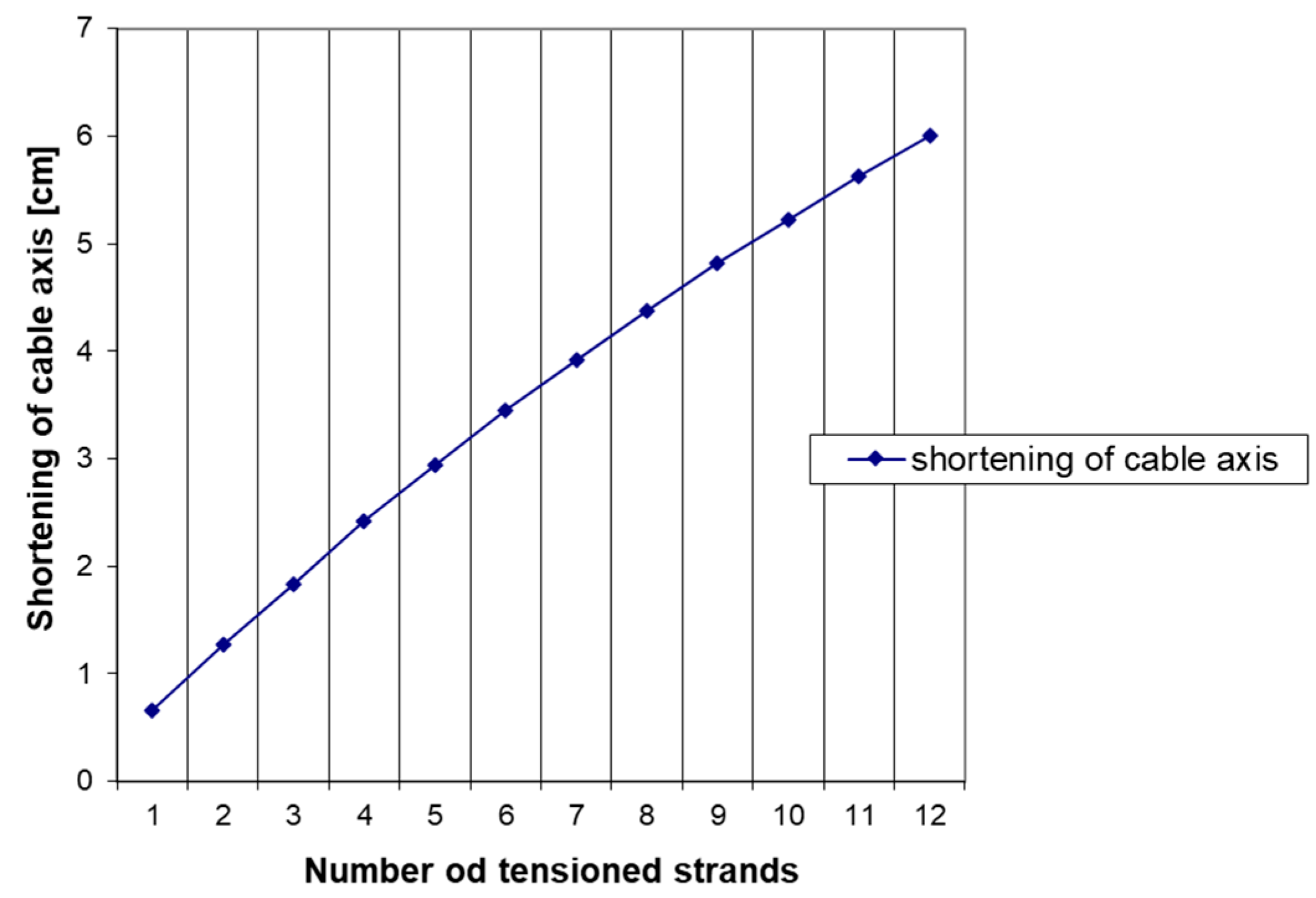
5.1. Single-Cycle Tensioning of Strands
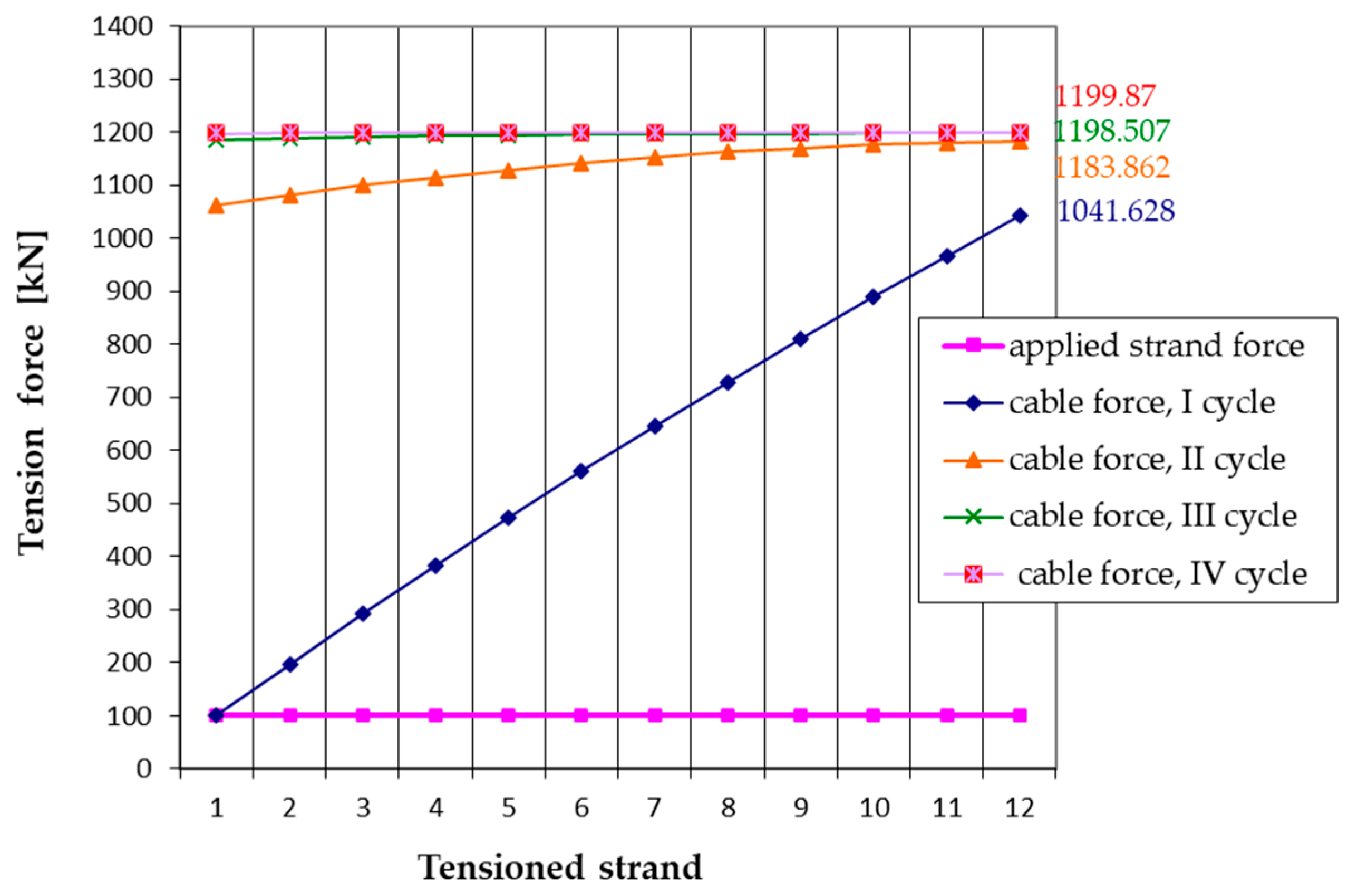
5.2. Multi-Cycle Tensioning of Strands
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Wang, S.; Huang, K.; Zhong, J.; Cheng, H. Research on Dynamic Response of a Single-Tower Cable-Stayed Bridge with Successive Cable Breaks Based on a 3D Index. Appl. Sci. 2023, 13, 9197. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, J.Y.; Cao, M.S.; Damjanovic, D.; Ostachowicz, W. Identification of instantaneous tension of bridge cables from dynamic responses: Strict algorithm and applications. Mech. Syst. Signal Process. 2020, 142, 106729. [Google Scholar] [CrossRef]
- Podolny, W., Jr.; Asce, M.; Fleming, J.F. Historical Development of Cable-Stayed Bridges. J. Struct. Div. 1972, 98. [Google Scholar] [CrossRef]
- Gimsing, N.J.; Georgiakis, C.T. Cable Supported Bridges Concept and Design, 3rd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Walther, R.; Houriet, B.; Isler, W.; Moia, P.; Klein, J.F. Cable Stayed Bridges, 2nd ed.; Thomas Telford Publishing: London, UK, 1999. [Google Scholar]
- Huang, D.; Chen, W. Cable Structures in Bridge Engineering. J. Bridge Eng. 2019, 24, 02019001. [Google Scholar] [CrossRef]
- Wilson, J.C.; Gravelle, W. Modelling of a cable-stayed bridge for dynamic analysis. Earthq. Eng. Struct. Dyn. 1991, 20, 707–721. [Google Scholar] [CrossRef]
- Wang, P.H.; Tang, T.Y.; Zheng, H.N. Analysis of cable-stayed bridges during construction by cantilever methods. Comput. Struct. 2004, 82, 329–346. [Google Scholar] [CrossRef]
- Shen, G.; Macdonald, J.; Coules, H.E. Nonlinear cable-deck interaction vibrations of cable-stayed bridges. J. Sound Vib. 2023, 544, 117428. [Google Scholar] [CrossRef]
- Fragassa, C.; Minak, G.; Pavlovic, A. Measuring deformations in the telescopic boom under static and dynamic load conditions. Facta Univ. Ser. Mech. Eng. 2020, 18, 315–328. [Google Scholar] [CrossRef]
- Cho, S.; Lynch, J.P.; Lee, J.J.; Yun, C.B. Development of an Automated Wireless Tension Force Estimation System for Cable-stayed Bridges. J. Intell. Mater. Syst. Struct. 2010, 21, 361–367. [Google Scholar] [CrossRef]
- Wang, P.H.; Tseng, T.C.; Yang, C.G. Initial shape of cable-stayed bridges. Comput. Struct. 1993, 47, 111–123. [Google Scholar] [CrossRef]
- Chen, D.W.; Au, F.T.K.; Tham, L.G.; Lee, P.K.K. Determination of initial cable forces in prestressed concrete cable-stayed bridges for given design deck profiles using the force equilibrium method. Comput. Struct. 2000, 74, 1–9. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, Z.; Li, M.; Fu, N. Cable Force Optimization of Cable-Stayed Bridge Based on Multiobjective Particle Swarm Optimization Algorithm with Mutation Operation and the Influence Matrix. Appl. Sci. 2023, 13, 2611. [Google Scholar] [CrossRef]
- Martins, A.M.; Simões, L.M.; Negrão, J.H. Optimization of cable-stayed bridges: A literature survey. Adv. Eng. Softw. 2020, 149, 102829. [Google Scholar] [CrossRef]
- Xiao, F.; Hulsey, J.L.; Chen, G.S.; Xiang, Y. Optimal static strain sensor placement for truss bridges. Int. J. Distrib. Sens. Netw. 2017, 13. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The Current Development of Structural Health Monitoring for Bridges: A Review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Xiao, F.; Hulsey, J.L.; Balasubramanian, R. Fiber optic health monitoring and temperature behavior of bridge in cold region. Struct. Control Health Monit. 2017, 24, e2020. [Google Scholar] [CrossRef]
- Suangga, M.; Hidayat, I.; Celine, J. Temperature effect on cable tension forces of cable-stayed bridge. IOP Conf. Ser. Earth Environ. Sci. 2018, 195, 012009. [Google Scholar] [CrossRef]
- Xiao, F.; Sun, H.; Mao, Y.; Chen, G.S. Damage identification of large-scale space truss structures based on stiffness separation method. Structures 2023, 53, 109–118. [Google Scholar] [CrossRef]
- Hou, S.; Dong, B.; Wang, H.; Wu, G. Inspection of surface defects on stay cables using a robot and transfer learning. Autom. Constr. 2020, 119, 103382. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Xiao, Z.; Liu, L. A tensioning control method for stay cables with super large tonnage cable force. Int. J. Struct. Integr. 2024, 15, 613–630. [Google Scholar] [CrossRef]
- Li, T.; Liu, Z. An improved continuum model for determining the behavior of suspension bridges during construction. Autom. Constr. 2021, 127, 103715. [Google Scholar] [CrossRef]
- Spasojević Šurdilović, M. Modeling and Sterss and Starin Analysis of Cable-Stayed Bridges during the Phase Formation of the Structaral System Using Temporary Supports. Master’s Thesis, Faculty of Civil Engineering and Architecture, University of Niš, Niš, Serbia, 2007. (In Serbian). [Google Scholar]
- Spasojević Šurdilović, M.; Spasojević, A.; Spasojević, N. Specifična problematika projektovanja i izvođenja pešačkog mosta preko reke Nišave u Nišu. In Proceedings of the Third International Scientific-Expert Conference, GNP 2010, Žabljak, Montenegro, 15–19 February 2010; Volume 1, pp. 643–648. (In Serbian). [Google Scholar]
- Spasojević Šurdilović, M.; Spasojević, A.; Stojić, D. Modelling of a bridge stay cable for individual strand tensioning. Građevinar 2014, 66, 549–554. [Google Scholar] [CrossRef]
- Freyssinet Commercial Brochure. Freyssinet HD Stay Cable. Available online: www.freyssinet.com (accessed on 20 March 2024).
- El Shenawy, E.A. Form Finding for Cable-Stayed and Extradosed Bridges. Ph.D. Thesis, Technischen Universität Berlin, Berlin, Germany, 2013. [Google Scholar]
- Spasojević Šurdilović, M.; Spasojević, A. Analytical solutions for determining tension force in strands of bridge stay-cable in isotension procedure. In Proceedings of the International Conference Innovation as a Function of Engineering Development-IDE 2011, Nis, Serbia, 25–26 November 2011; pp. 319–324. [Google Scholar]
- He, W.Y.; Meng, F.C.; Ren, W.X. Cable force estimation of cables with small sag considering inclination angle effect. Adv. Bridge Eng. 2021, 2, 15. [Google Scholar] [CrossRef]
- Croce, P. Non-linear behavior of heavy stays. Int. J. Solids Struct. 2013, 50, 1093–1107. [Google Scholar] [CrossRef]
- Feng, X.H.; Zhu, Z.Q.; He, X.Q. Geometrical Nonlinear Analysis for Multi-Parameters of Four Tower Cable-Stayed Bridge Based on The Bar Element Model. In Proceedings of the International Conference on Structural, Mechanical and Materials Engineering (ICSMME 2015), Dalian, China, 6–8 November 2015. [Google Scholar]
- Irvine, H.M. Free vibration of inclined cables. ASCE J. Struct. Div. 1978, 104, 343–347. [Google Scholar] [CrossRef]
- Hajdin, N.; Michaltsos, G.T.; Konstantakopulus, T.G. About the equivalent elastic modulus of elasticity of cables of cable-stayed bridges. Facta Univ. 1998, 1, 569–575. [Google Scholar]
- Wang, L.-Z.; Guo, Z.; Yuan, F. Quasi-static three-dimensional analysis of suction anchor mooring system. Ocean Eng. 2010, 37, 1127–1138. [Google Scholar] [CrossRef]
- Ernst, J.H. Der E-modul von seilen under berücksichtigung des durchhanges. Bauing 1965, 40, 52–55. (In German) [Google Scholar]
- The Centre for Structures and Prestressing–IMS Institute. Available online: https://institutims.rs/ (accessed on 9 June 2024).
- Stanković, M.; Đorđević, Đ. Stress, Software System for Static Calculation of Engineering Structures; Trion Computers: Niš, Serbia, 1991. (In Serbian) [Google Scholar]
- Spasojević Šurdilović, M.; Spasojević, A. Analytical Solutions for Deformations of Bridge Stay Cables. Proc. Fac. Civ. Eng. Archit. Niš 2010, 25, 207–214. (In Serbian) [Google Scholar]


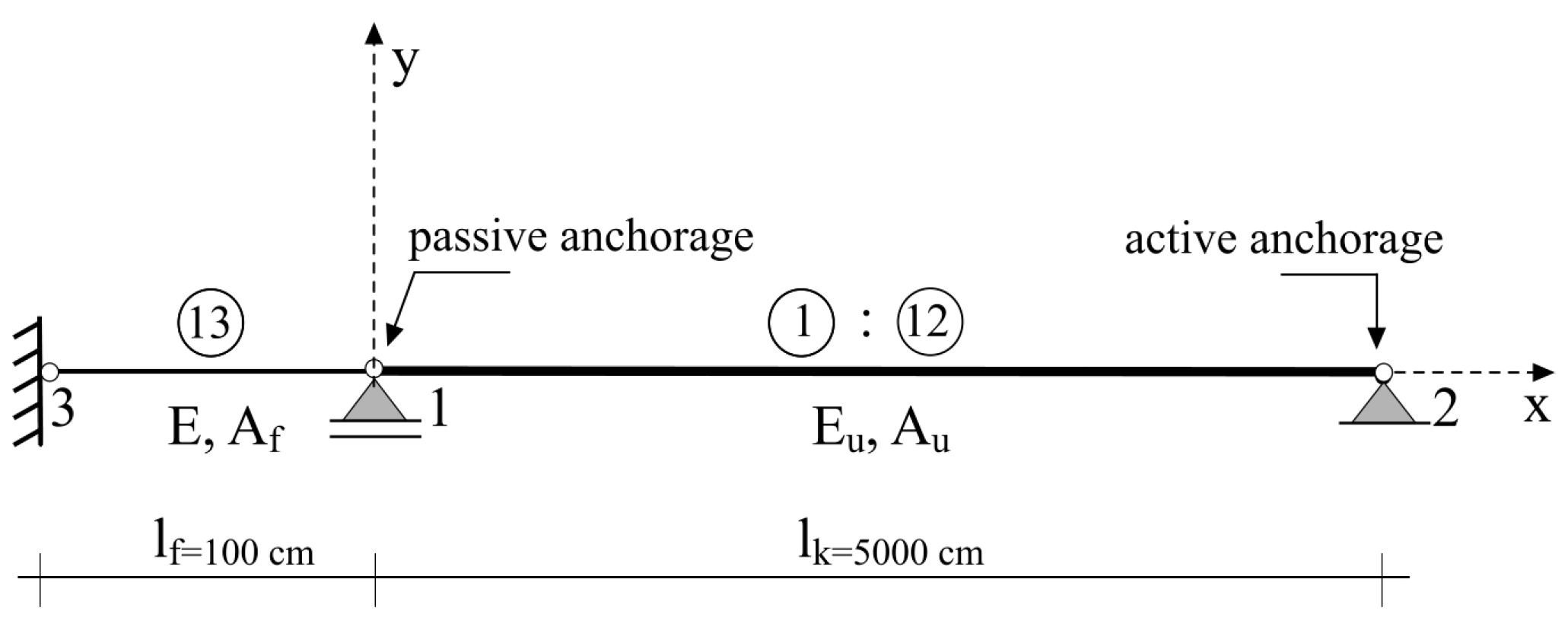


| Characteristic | Symbol | Value |
|---|---|---|
| Diameter (steel) | d | 15.7 mm |
| Total diameter (steel + grease + HDPE) | D | 19.1 mm |
| Area of strand (steel) | Au | 150 mm2 |
| Strand mass (steel + grease + HDPE) | ms | 1.29 kg/m |
| Relaxation class | - | 2 (low relaxation level: <2.5%) |
| Characteristic tensile strength | fpk | 1860 N/mm2 |
| Characteristic failure force | Fpk = Au · fpk | 279 kN |
| Characteristic value of yield force at which permanent 0.1% elongation occurs | Fp 0.1 | 246 kN |
| Allowed force in strand (for considered case) | 0.45 Fpk | 12.55 kN |
| Modulus of elasticity | E | 1.94 (±0.01) × 105 MPa |
| Property | Symbol | Value |
|---|---|---|
| External diameter of pipe | dp | 110 mm (Ddp = +1.0 mm) |
| Pipe wall thickness | s | 6.6 mm (Ds= +0.9 mm) |
| Mass of the HDPE pipe | mp | 2.166 kg/m1 |
| Strand | Tension Force in Strand Zi * [kN] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 131.26 | 127.633 | 124.201 | 120.948 | 117.862 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 |
| 2 | 127.633 | 124.201 | 120.948 | 117.862 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | |
| 3 | 124.201 | 120.948 | 117.862 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | ||
| 4 | 120.948 | 117.862 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | |||
| 5 | 117.862 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | ||||
| 6 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | |||||
| 7 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | ||||||
| 8 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | |||||||
| 9 | 106.946 | 104.526 | 102.213 | 100 | ||||||||
| 10 | 104.526 | 102.213 | 100 | |||||||||
| 11 | 102.213 | 100 | ||||||||||
| 12 | 100 | |||||||||||
| Zki [kN] ** | 131.26 | 255.266 | 372.603 | 483.792 | 589.31 | 689.574 | 784.973 | 875.848 | 962.514 | 1045.26 | 1124.34 | 1200 |
| ξki [cm] *** | 0.6563 | 1.2763 | 1.8630 | 2.4190 | 2.9465 | 3.4479 | 3.9249 | 4.3792 | 4.8126 | 5.2263 | 5.6217 | 6.000 |
| Strand (i) | Zu [kN] | Zi(c) * [kN] | |||
|---|---|---|---|---|---|
| Zi(1) | Zi(2) | Zi(3) | Zi(4) | ||
| 1 | 100 | 72.457 | 96.450 | 99.620 | 99.967 |
| 2 | 100 | 75.299 | 97.010 | 99.716 | 99.975 |
| 3 | 100 | 78.062 | 97.521 | 99.773 | 99.980 |
| 4 | 100 | 80.751 | 97.984 | 99.822 | 99.985 |
| 5 | 100 | 83.370 | 98.400 | 99.863 | 99.988 |
| 6 | 100 | 85.922 | 98.768 | 99.897 | 99.991 |
| 7 | 100 | 88.410 | 99.089 | 99.925 | 99.993 |
| 8 | 100 | 90.838 | 99.364 | 99.947 | 99.995 |
| 9 | 100 | 93.208 | 99.592 | 99.965 | 99.997 |
| 10 | 100 | 95.524 | 99.774 | 99.979 | 100 |
| 11 | 100 | 97.787 | 99.910 | 100 | 100 |
| 12 | 100 | 100 | 100 | 100 | 100 |
| Zk(c) [kN] ** | 1041.628 | 1183.862 | 1198.507 | 1199.870 | |
| ξk(c) [cm] *** | 5.208 | 5.920 | 5.993 | 6.000 | |
| γk(c) **** | 86.8% | 98.66% | 99.88% | 100% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spasojević Šurdilović, M.; Živković, S.; Turnić, D. Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges. Appl. Sci. 2024, 14, 5410. https://doi.org/10.3390/app14135410
Spasojević Šurdilović M, Živković S, Turnić D. Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges. Applied Sciences. 2024; 14(13):5410. https://doi.org/10.3390/app14135410
Chicago/Turabian StyleSpasojević Šurdilović, Marija, Srđan Živković, and Dragana Turnić. 2024. "Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges" Applied Sciences 14, no. 13: 5410. https://doi.org/10.3390/app14135410
APA StyleSpasojević Šurdilović, M., Živković, S., & Turnić, D. (2024). Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges. Applied Sciences, 14(13), 5410. https://doi.org/10.3390/app14135410








