Convergence-Related Serviceability Limit States of Segmental Tunnel Rings: Lessons Learned from Structural Analysis of Real-Scale Tests
Abstract
:1. Introduction
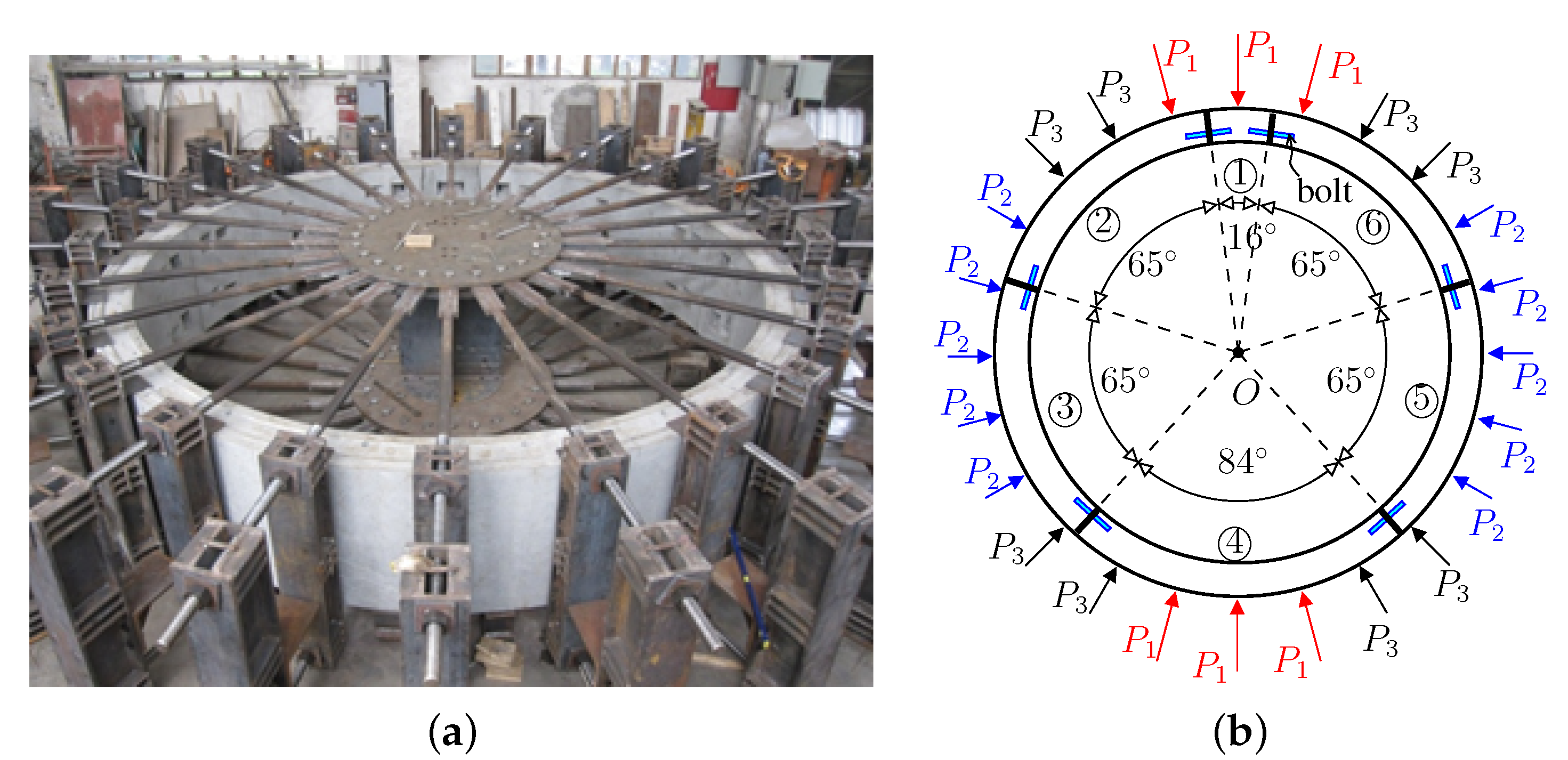
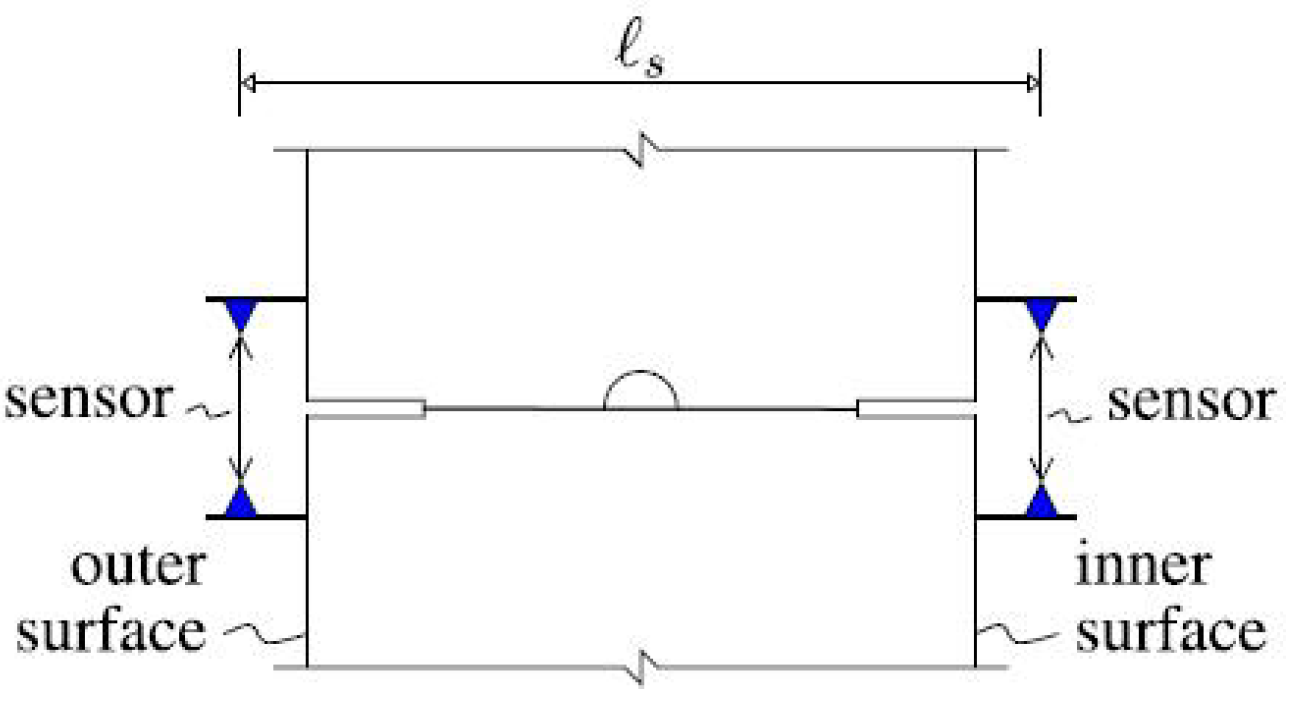
2. Experimental Data from Real-Scale Tests on Segmental Tunnel Linings
3. Hybrid Analysis
3.1. Transfer Relations
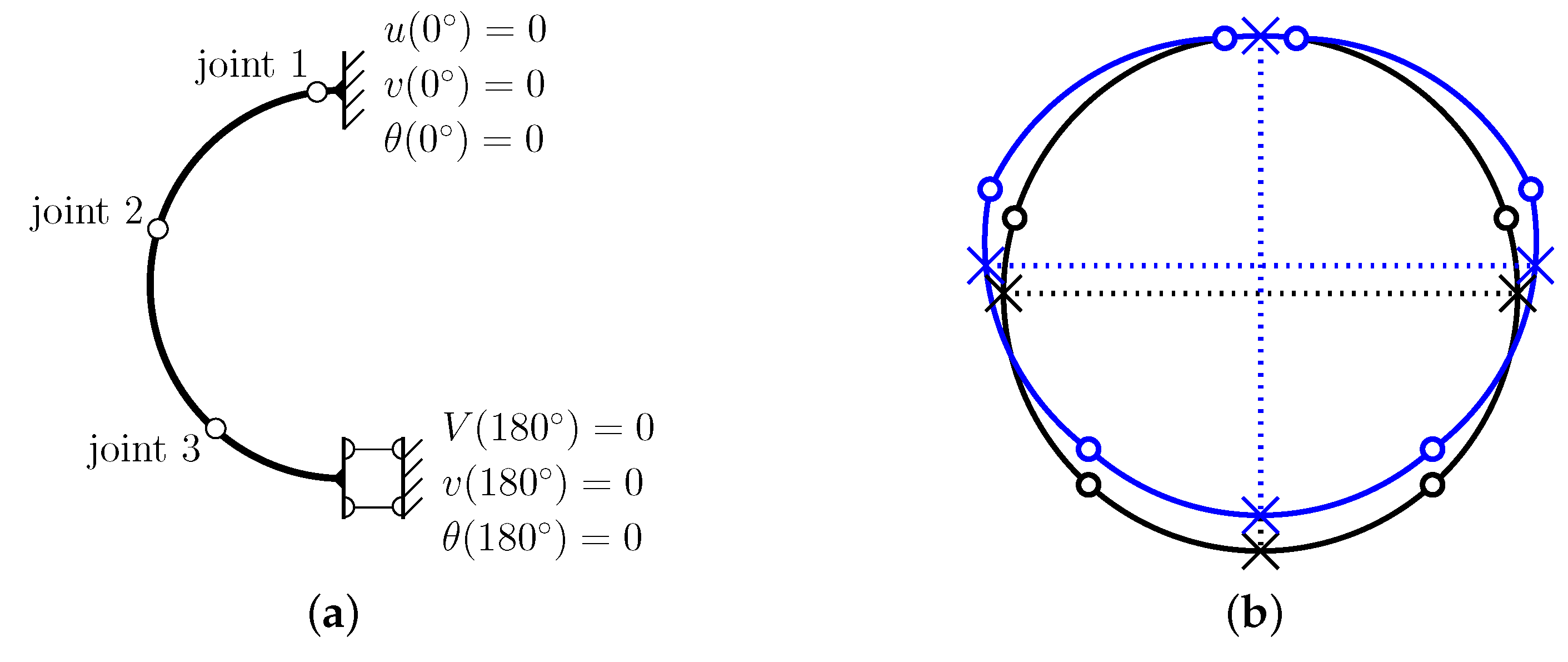
3.2. Strategy for Symmetric Rigid-Body Displacements
3.3. Symmetric Model of Rigid-Body Displacements
4. Extended Hybrid Method
4.1. Application of the Hybrid Method Using the Strategy of Symmetric Rigid-Body Displacements
4.2. Improved Strategy of Symmetric Rigid-Body Displacements
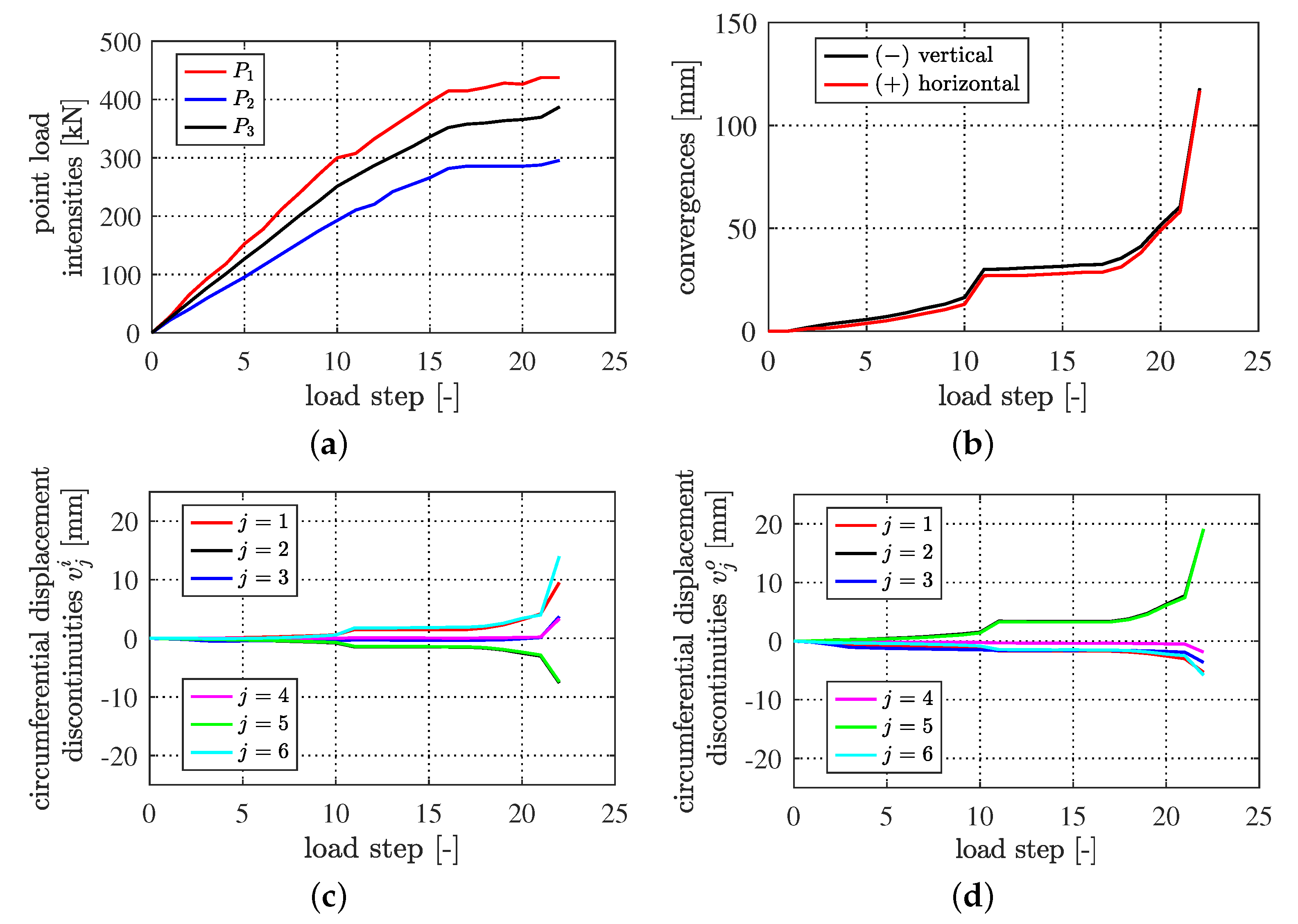
4.3. Presentation and Discussion of Results
5. Conclusions
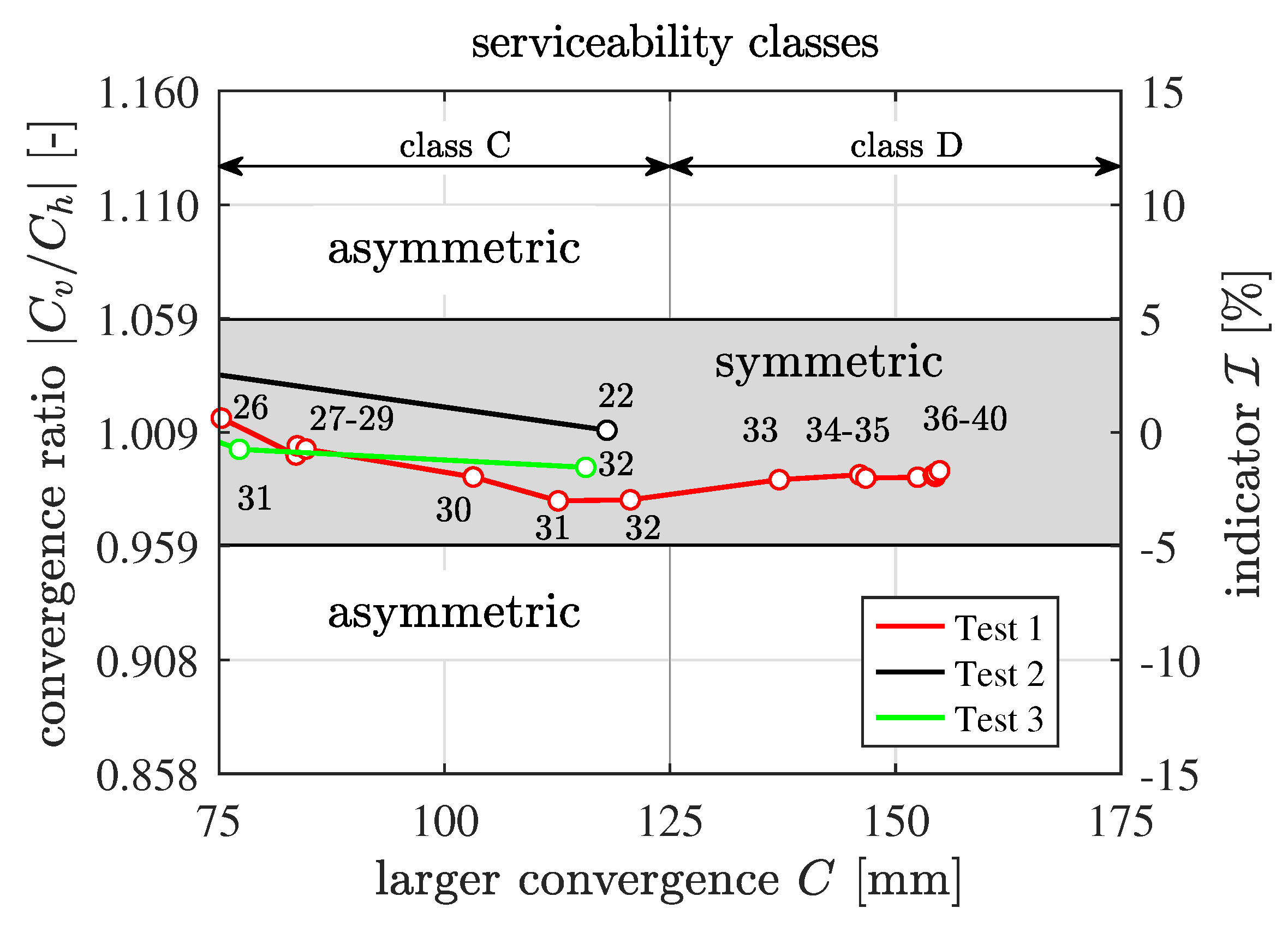
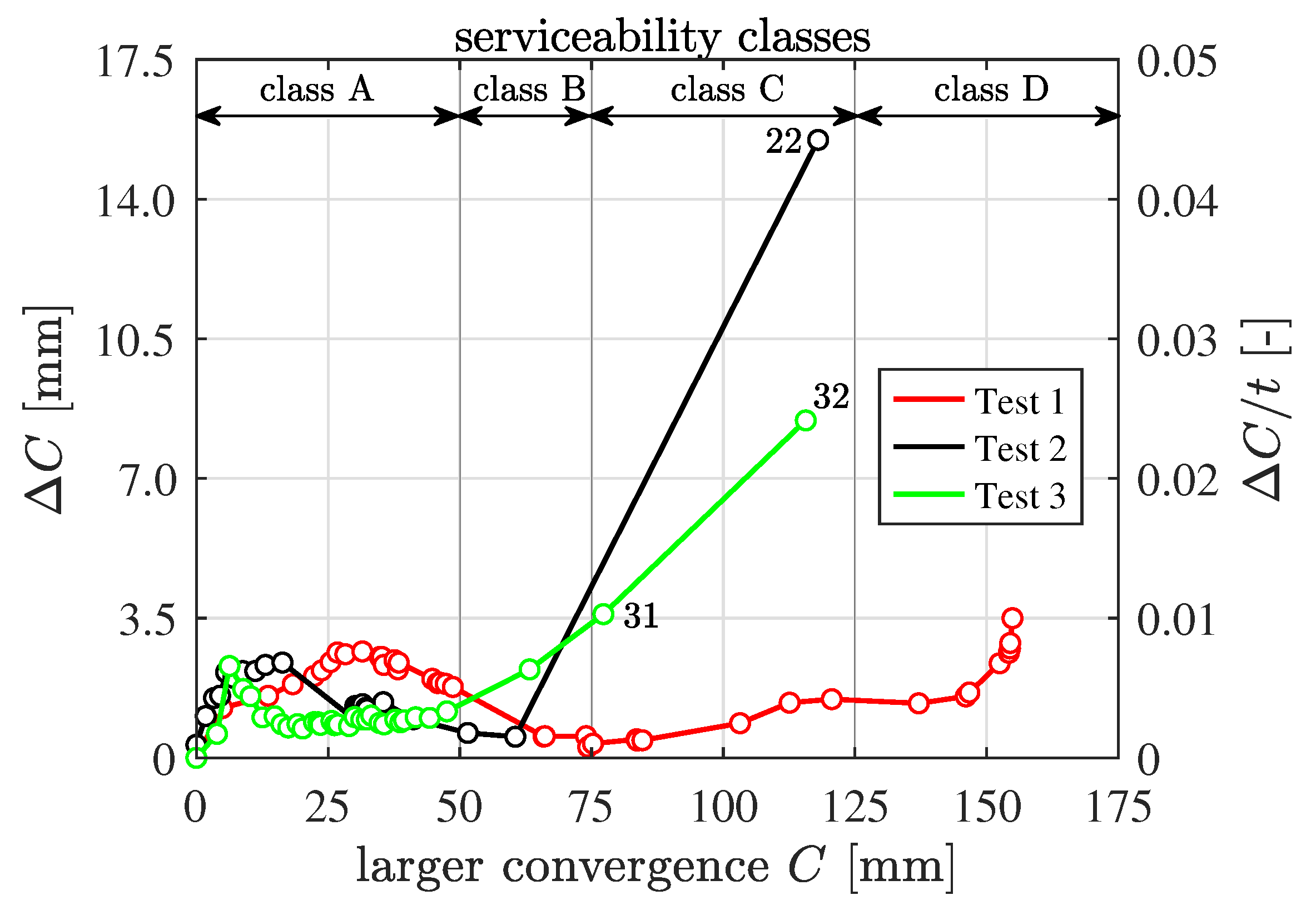
- The structural analysis of segmental tunnel rings can be categorized into only three classes: Class A is the category of asymmetric problems [13]. Class B includes symmetric problems without sudden failures at the joints during the loading process [35], and Class C is the category of symmetric problems with some sudden failures, such as concrete spalling, at the segmental interfaces.
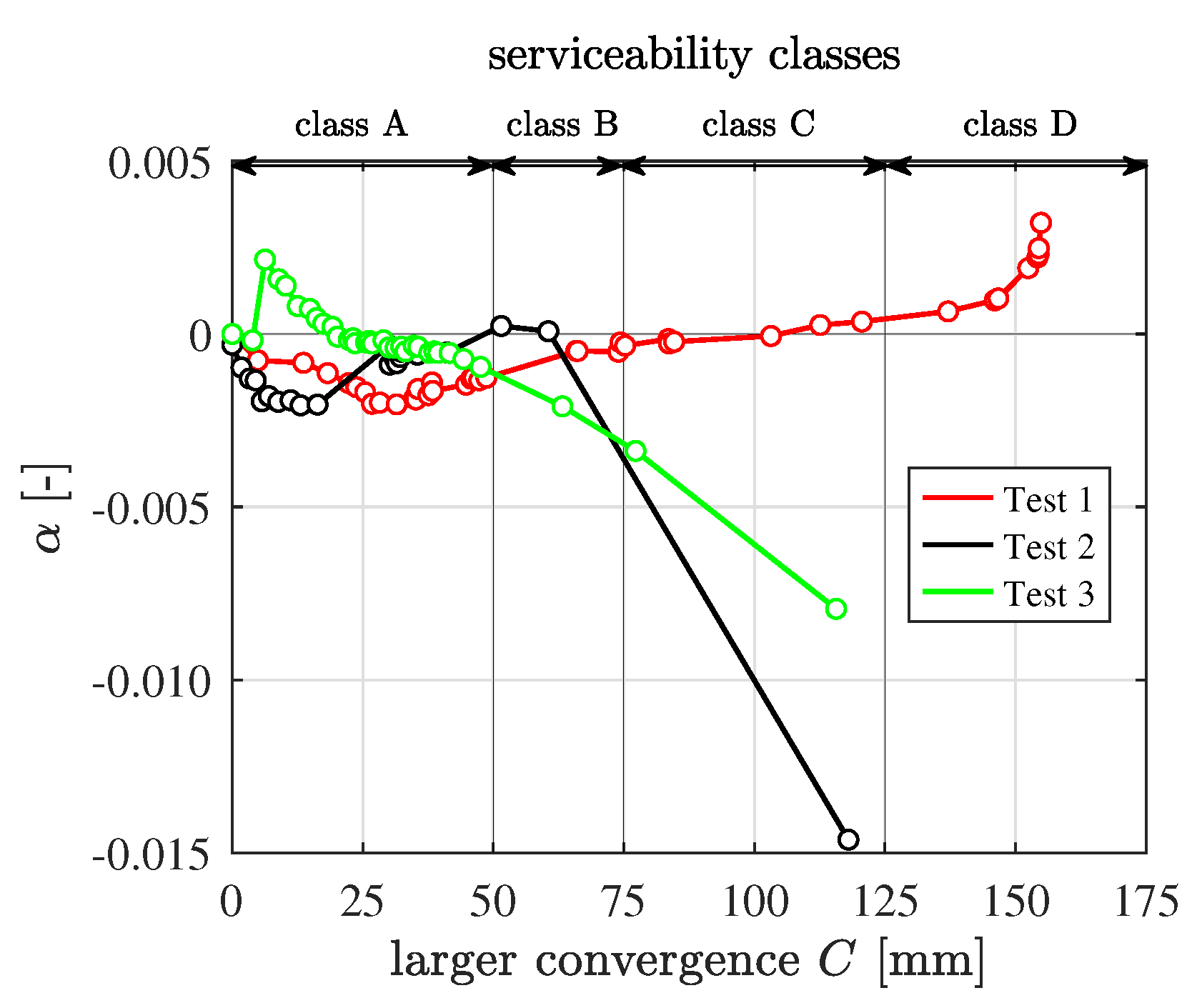
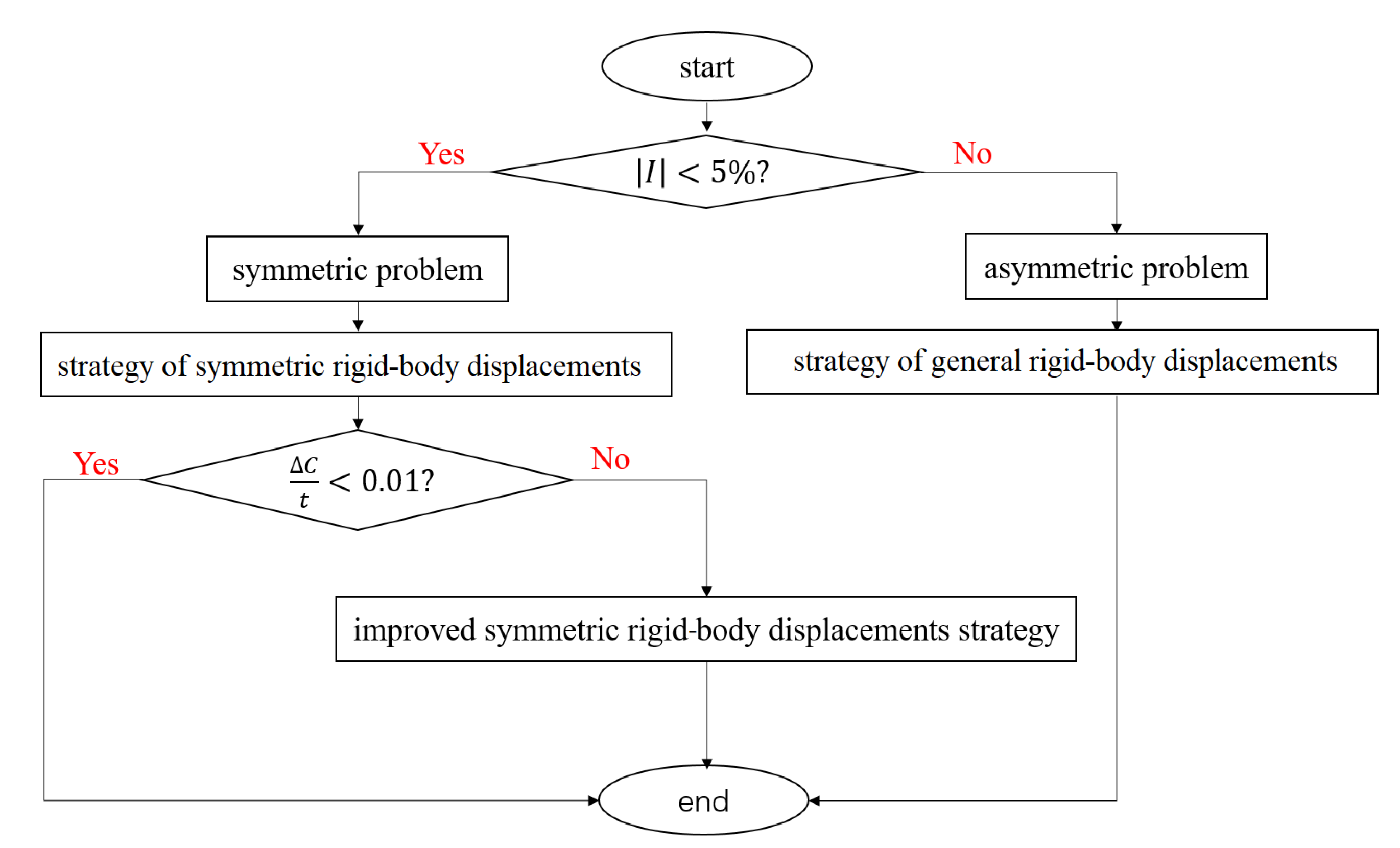
- An efficient analysis procedure was proposed in this paper. With the help of , the analysis problem was, at first, categorized as an asymmetric or a symmetric problem. For the asymmetric problems, the strategy of general rigid-body displacements was employed. For the symmetric problems, the strategy of symmetric rigid-body displacements was used. The accuracy of the simulations of the symmetric problems was checked by . If it was found to be unacceptable, the improved strategy of symmetric rigid-body displacements was used.
- The reason for the difference between Class A and Class B is different from the reason for the treatment as an asymmetric problem, characterized by the development of the asymmetric structural behavior in a progressive and subtle fashion [13]. The third class of problems is characterized by the development of the deformations in a sudden fashion.
- When convergence-related serviceability class C is reached, the stress state or the failure states of the interfaces need to be checked carefully. Local failure results in a rapid increase in structural deformations. Serviceability class D will then be reached soon.
- It is suggested that, upon the attainment of convergence-related serviceability class C and the detection of local failure at segmental interfaces, the strengthening of the structure should be considered at serviceability class C rather than only at serviceability class D, i.e., at the SLS.
- If the tunnel is located in an aggressive environment and the cracking at the outer surface is not acceptable, the definition of the convergence-related SLS should be stricter. In this case, should be set equal to rather than to .
- The accuracy of the extended hybrid method was validated by means of monitoring the data collected during full-scale testing. In the future, it will be interesting to equip real tunnels with advanced monitoring techniques that enable the collection of similar data, and to use these data for the further validation of the applicability of the method presented.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, C.T.; Sun, C.W.; Duann, S.W.; Hwang, R.N. Response of a Taipei Rapid Transit System (TRTS) tunnel to adjacent excavation. Tunn. Undergr. Space Technol. 2001, 16, 151–158. [Google Scholar] [CrossRef]
- Avanaki, M.J. Effects of hybrid steel fiber reinforced composites on structural performance of segmental linings subjected to TBM jacks. Struct. Concr. 2019, 6, 1909–1925. [Google Scholar] [CrossRef]
- Li, X.; Lin, X.; Zhu, H.; Wang, X.; Liu, Z. Condition assessment of shield tunnel using a new indicator: The tunnel serviceability index. Tunn. Undergr. Space Technol. 2017, 67, 98–106. [Google Scholar] [CrossRef]
- Sun, W.; Han, F.; Zhang, Y.; Zhang, W.; Zhang, R.; Su, W. Experimental assessment of structural responses of tunnels under the groundwater level fluctuation. Tunn. Undergr. Space Technol. 2023, 137, 105138–105153. [Google Scholar] [CrossRef]
- Gong, W.; Juang, C.H.; Huang, H.; Zhang, J.; Luo, Z. Improved analytical model for circumferential behavior of jointed shield tunnels considering the longitudinal differential settlement. Tunn. Undergr. Space Technol. 2015, 45, 153–165. [Google Scholar] [CrossRef]
- British Tunnelling Society. Tunnel Lining Design Guide; Thomas Telford: London, UK, 2004. [Google Scholar]
- German Tunnelling Committee. Recommendations for the Design, Production and Installation of Segmental Rings; German Tunnelling Committee: Cologne, Germany, 2013. [Google Scholar]
- GB50157; Code for Design of Metro. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2013.
- DGJ08-11-99; Shanghai Foundation Design Code. Shanghai Construction Committee: Shanghai, China, 1999.
- Peck, R. Deep excavations and tunneling in soft ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, August 1969. [Google Scholar]
- Carpio, F.; Peña, F.; Galván, A. Recommended deformation limits for the structural design of segmental tunnels built in soft soil. Tunn. Undergr. Space Technol. 2019, 90, 264–276. [Google Scholar] [CrossRef]
- DG/TJ08-2123-2013; Code for Structural Appraisal of Shield Tunnel. Shanghai Municipal Commission of City Development and Transport: Shanghai, China, 2013.
- Jiang, Z.; Liu, X.; Schlappal, T.; Zhang, J.; Mang, H.A.; Pichler, B.L. Asymmetric serviceability limit states of symmetrically loaded segmental tunnel rings: Hybrid analysis of real-scale tests. Tunn. Undergr. Space Technol. 2021, 113, 103832. [Google Scholar] [CrossRef]
- Chang, C.T.; Wang, M.J.; Chang, C.T. Repair of displaced shield tunnel of the Taipei rapid transit system. Tunn. Undergr. Space Technol. 2001, 15, 167–173. [Google Scholar] [CrossRef]
- Kiriyama, K.; Kakizaki, M.; Takabayashi, T.; Hirosawa, N.; Takeuchi, T.; Hajohta, H. Structure and construction examples of tunnel reinforcement method using thin steel panels. Nippon. Steel Tech. Rep. 2005, 92, 45–50. [Google Scholar]
- Gu, C. Structural reinforcement technology for deformed tunnels. Shield Tunn. Technol. 2013, 1, 21–25. [Google Scholar]
- Moss, N. London underground monitoring: Recent experience and future requirements. In Proceedings of the First International Workshop on Monitoring and Inspection of Metro Tunnel, Tongji University, Shanghai, China, 26–28 May 2014. [Google Scholar]
- Kontogianni, V.; Stiros, S. Tunnel deformation during excavation—A kinematic approach based on geodetic observations. Field Meas. Geomech. 2003, 1, 189–193. [Google Scholar]
- Kontogianni, V.; Stiros, S. Induced deformation during tunnel excavation: Evidence from geodetic monitoring. Eng. Geol. 2005, 79, 115–126. [Google Scholar] [CrossRef]
- Barla, G.B.; Bonini, M.; Debernardi, D. Time dependent deformations in squeezing tunnels. In Proceedings of the 12th International Conference of International Association for Computer Methods and Advances in Geomechanics, Goa, India, 1–6 October 2008. [Google Scholar]
- Stiros, S.; Kontogianni, V. Mean deformation tensor and mean deformation ellipse of an excavated tunnel section. Int. J. Rock Mech. Min. Sci. 2009, 46, 1306–1314. [Google Scholar] [CrossRef]
- Nakai, T.; Maruki, Y.; Ryu, M.; Ohnishi, Y.; Nishiyama, S.; Tatebe, T.; Komae, M. Support design of river crossing tunnel using keyblock concept and its validation by monitoring of the countermeasure by digital photogrammetry. Tunn. Undergr. Space Technol. 2004, 19, 440–441. [Google Scholar]
- Hashimoto, T.; Koyama, Y.; Yingyongrattanakul, N.; Kayukawa, K.; Sugimoto, M. Applications of the New Deformation Meter for Monitoring Tunnel Lining Deformation. In Proceedings of the International Symposium on Underground Excavation and Tunnelling, Bangkok, Thailand, 15–16 May 2006. [Google Scholar]
- Yu, Q.; Jiang, G.; Chao, Z.; Fu, S.; Shang, Y.; Yang, X. Deformation monitoring system of tunnel rocks with innovative broken-ray videometrics. In Proceedings of the ICEM: International Conference on Experimental Mechanics, Nanjing, China, 8–12 November 2008. [Google Scholar]
- Kavvadas, M. Monitoring ground deformation in tunnelling: Current practice in transportation tunnels. Eng. Geol. 2005, 79, 93–113. [Google Scholar] [CrossRef]
- Shan, J.; Toth, C.K. Topographic Laser Ranging and Scanning: Principles and Processing. In Scanning Principles and Processing; CRS Press: Boca Raton, FL, USA, 2014; pp. 215–234. [Google Scholar]
- Gosliga, R.V.; Lindenbergh, R.; Pfeifer, N. Deformation analysis of a bored tunnel by means of terrestrial laser scanning. Image Eng. Vis. Metrol. ISPRS Comm. 2006, 36, 167–172. [Google Scholar]
- Jaboyedoff, M.; Demers, D.; Locat, J.; Locat, A.; Turmel, D. Use of terrestrial laser scanning for the characterization of retrogressive landslides in sensitive clay and rotational landslides in river banks. Rev. Can. Gotechnique 2009, 46, 1379–1390. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Fernandez-Steeger, T.M.; Wiatr, T.; Rodrigues, D.; Azzam, R. Use of terrestrial laser scanning for engineering geological applications on volcanic rock slopes—An example from Madeira island (Portugal). Nat. Hazards Earth Syst. Sci. 2011, 11, 807–817. [Google Scholar] [CrossRef]
- Abellan, A.; Vilaplana, J.M.; Calvet, J.; García-Sellés, D.; Asensio, E. Rockfall monitoring by Terrestrial Laser Scanning—Case study of the basaltic rock face at Castellfollit de la Roca (Catalonia, Spain). Nat. Hazards Earth Syst. Sci. 2011, 11, 829–841. [Google Scholar] [CrossRef]
- Granitzer, A.N.; Tschuchnigg, F. Numerical Analysis of Segmental Tunnel Linings employing a Hybrid Modeling Approach. Comput. Eng. Phys. Model. 2021, 4, 1–18. [Google Scholar]
- Sun, W.; Zhang, W.; Goh, A.T.C.; Zhang, R. Experimental and computational analysis of hydraulic behavior in shallow buried structures in sand. Gondwana Res. 2023, 124, 339–350. [Google Scholar] [CrossRef]
- Zhang, Y.; Karlovek, J.; Liu, X. Identification method for internal forces of segmental tunnel linings via the combination of laser scanning and hybrid structural analysis. Sensors 2022, 22, 2421. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.L.; Vida, C.; Yuan, Y.; Hellmich, C.; Mang, H.A.; Pichler, B. A hybrid analysis method for displacement-monitored segmented circular tunnel rings. Eng. Struct. 2017, 148, 839–856. [Google Scholar] [CrossRef]
- Zhang, J.L.; Mang, H.A.; Liu, X.; Yuan, Y.; Pichler, B. On a nonlinear hybrid method for multiscale analysis of a bearing capacity test on a real-scale segmental tunnel ring. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1343–1372. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Bai, Y.; Yuan, Y.; Mang, H.A. Experimental investigation of the ultimate bearing capacity of continuously jointed segmental tunnel linings. Struct. Infrastruct. Eng. 2016, 12, 1364–1379. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, Z.; Yuan, Y.; Mang, H.A. Experimental investigation of the ultimate bearing capacity of deformed segmental tunnel linings strengthened by epoxy-bonded steel plates. Struct. Infrastruct. Eng. 2018, 14, 685–700. [Google Scholar] [CrossRef]


| class | A | B | C | D |
| serviceability | excellent | good | endangered | violated |
| criterion |
| class | A | B | C | D |
| serviceability | excellent | good | endangered | violated |
| criterion |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Liu, X.; Mang, H.A.; Zhang, J.; Pichler, B. Convergence-Related Serviceability Limit States of Segmental Tunnel Rings: Lessons Learned from Structural Analysis of Real-Scale Tests. Appl. Sci. 2024, 14, 5483. https://doi.org/10.3390/app14135483
Jiang Z, Liu X, Mang HA, Zhang J, Pichler B. Convergence-Related Serviceability Limit States of Segmental Tunnel Rings: Lessons Learned from Structural Analysis of Real-Scale Tests. Applied Sciences. 2024; 14(13):5483. https://doi.org/10.3390/app14135483
Chicago/Turabian StyleJiang, Zijie, Xian Liu, Herbert A. Mang, Jiaolong Zhang, and Bernhard Pichler. 2024. "Convergence-Related Serviceability Limit States of Segmental Tunnel Rings: Lessons Learned from Structural Analysis of Real-Scale Tests" Applied Sciences 14, no. 13: 5483. https://doi.org/10.3390/app14135483
APA StyleJiang, Z., Liu, X., Mang, H. A., Zhang, J., & Pichler, B. (2024). Convergence-Related Serviceability Limit States of Segmental Tunnel Rings: Lessons Learned from Structural Analysis of Real-Scale Tests. Applied Sciences, 14(13), 5483. https://doi.org/10.3390/app14135483






