Development Models of Stoichiometric Thermodynamic Equilibrium for Predicting Gas Composition from Biomass Gasification: Correction Factors for Reaction Equilibrium Constants
Abstract
:1. Introduction
2. Modeling
2.1. Basis Model
2.2. Energy Balance
2.3. Cold Gasification Efficiency
2.4. Simulated Model
2.5. Correction Factors
3. Methods and Materials
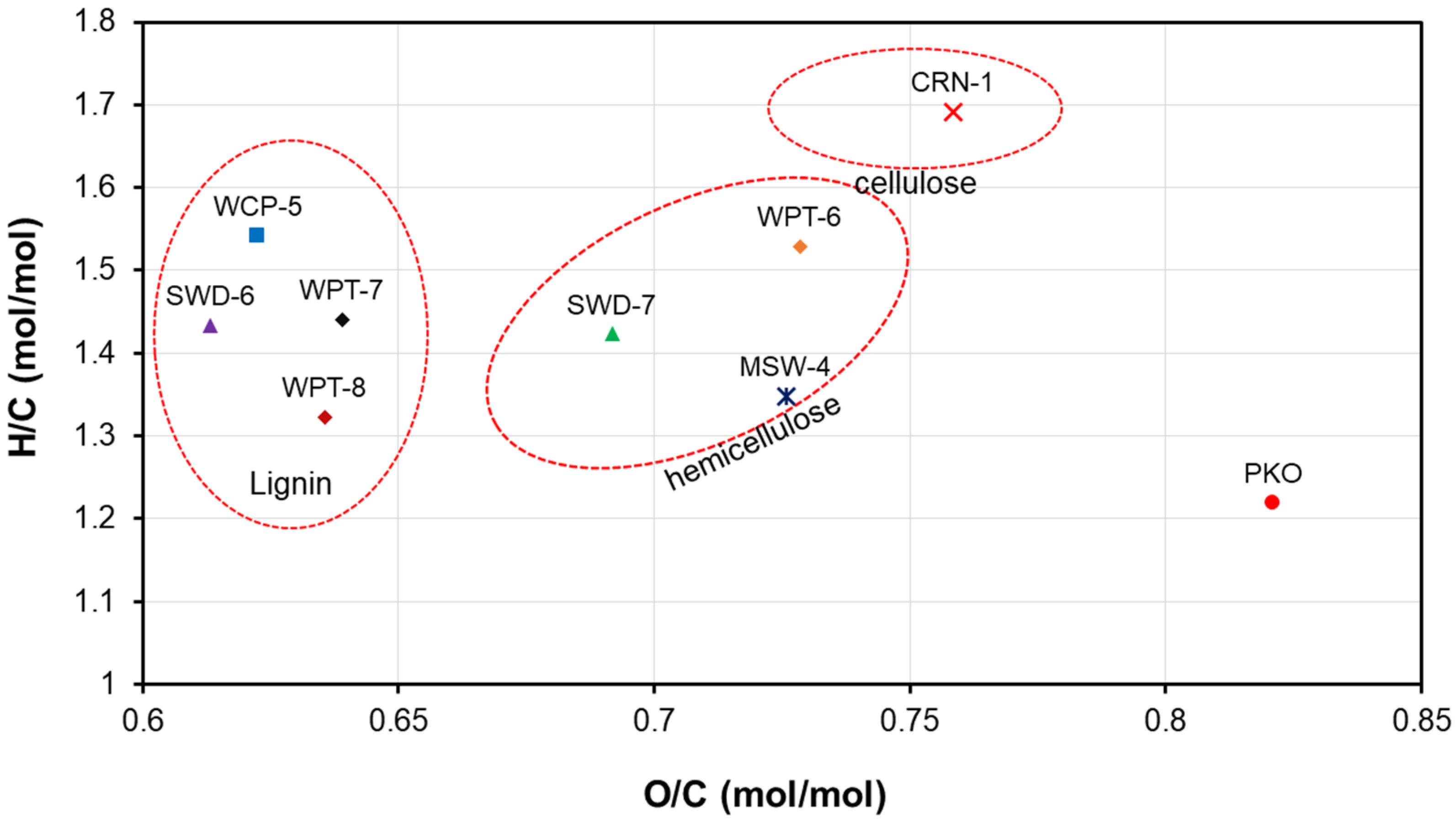
3.1. Biomass and Operating Data
3.2. Model Validation and Accuracy
3.3. Algorithm of the Model Development
4. Results and Discussion
4.1. Correction Factors and New Empirical Correlation for the Equilibrium Constant
4.2. Simulation, Validation, and Accuracy of the Composition of Producer Gas Using the Developed Stoichiometric Models
4.3. Empirical Correlation between Independent and Dependent Variables in Biomass Gasification
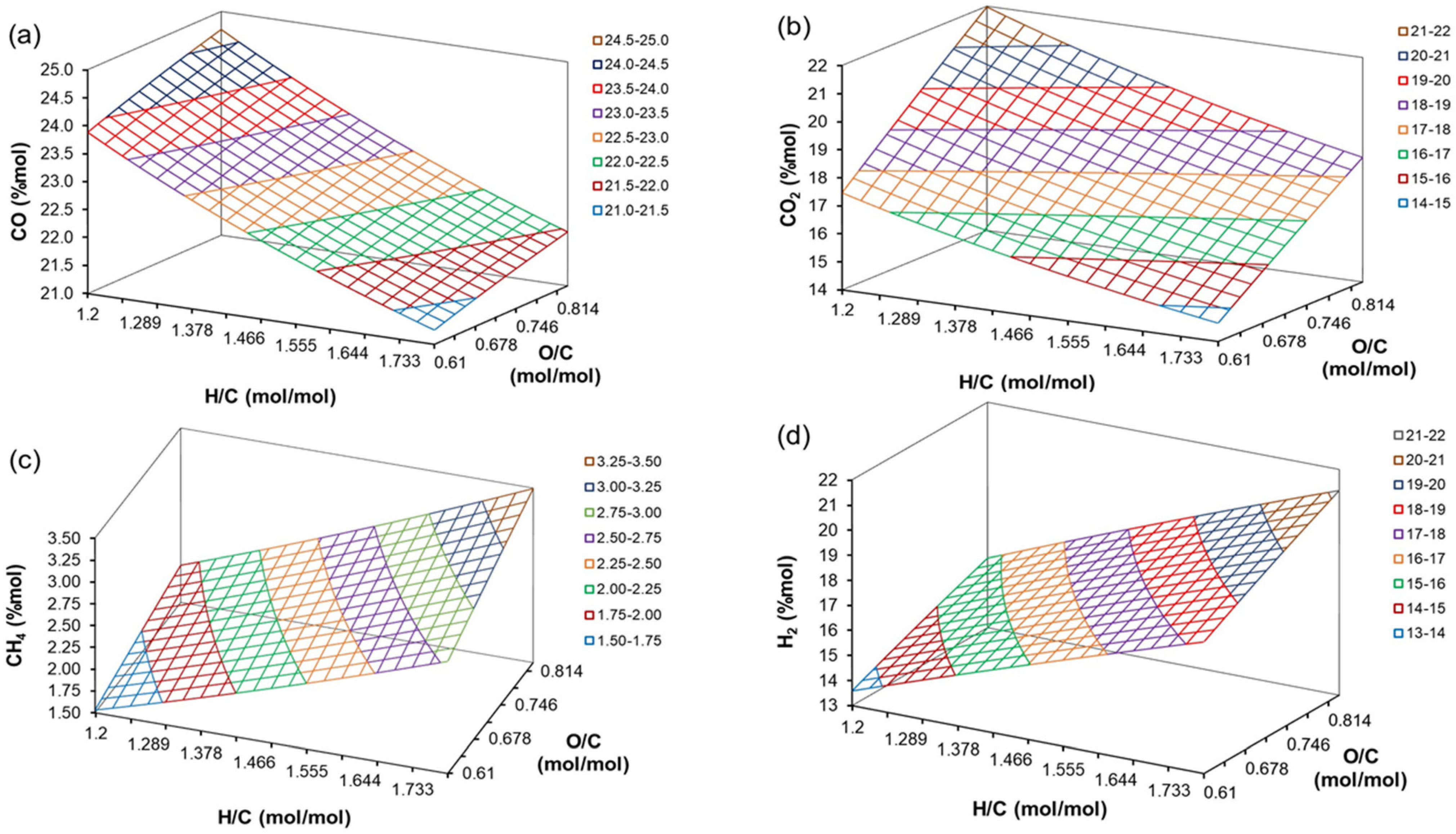
4.4. The Effect of H/C, O/C, ER, and T on Producer Gas Composition
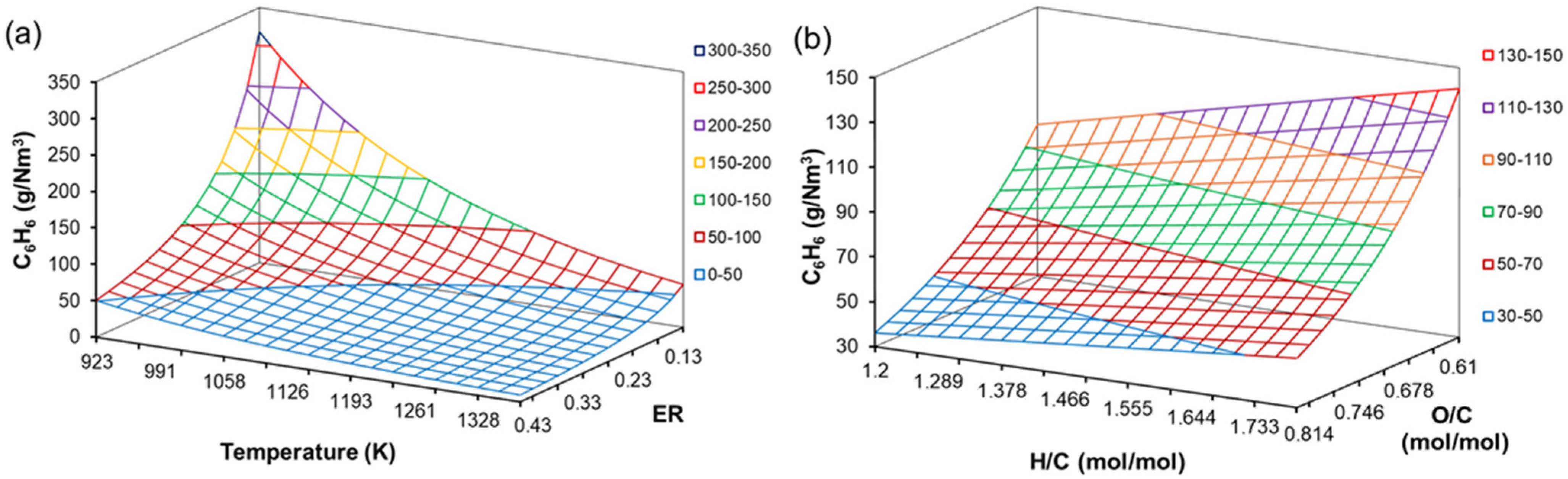
4.5. Effect of H/C, O/C, ER and T on Tar Content
4.6. Effect of H/C, O/C, ER, and T on LHV-Gas
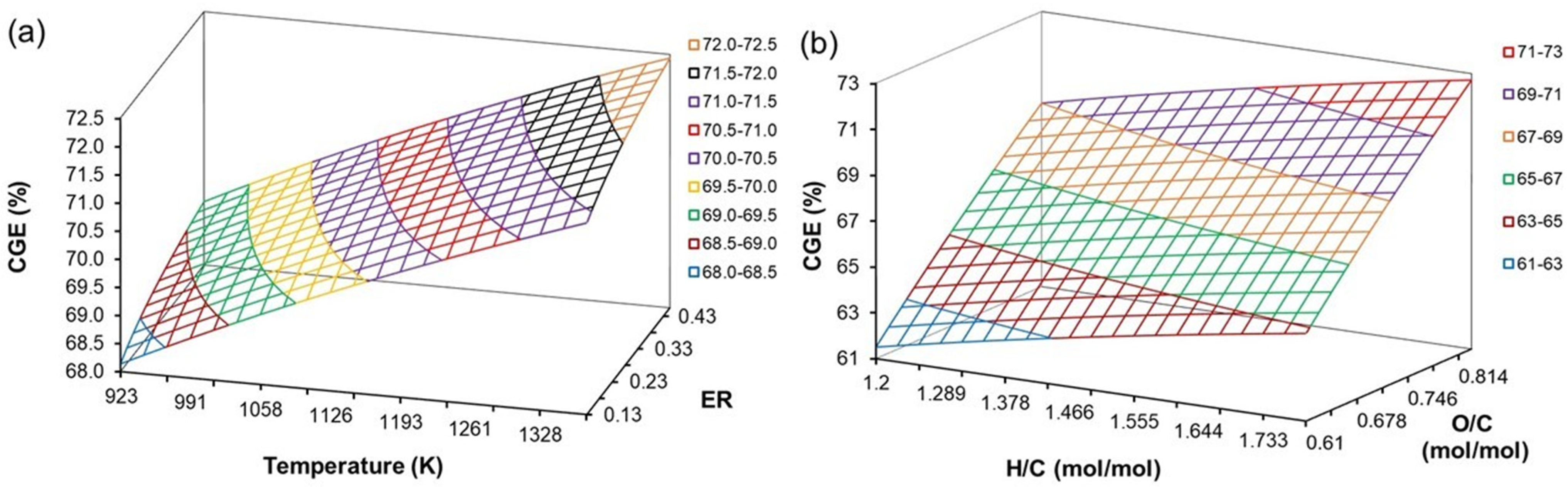
4.7. Effect of H/C, O/C, ER, and T on CGE
5. Conclusions
- All models can predict the composition of the producer gas with an RMSE of less than 3.5%.
- All models can predict the concentration of tar (C6H6) in gas producers through using steam reforming reactions in the modeling process.
- Only three models (M1D, M2C, and M3C) out of 24 models showed high accuracy in predicting CO, CO2, H2, and N2 gas concentration.
- Model M2C can be further used to develop empirical correlations that include H/C, O/C, and N/C.
- The empirical correlation models have power function equations that include biomass content and gasification operating parameters (H/C, O/C, N/C, ER, and T) as the input variables.
- The empirical correlations estimated the composition of CO, CO2, CH4, H2, and tar content (C6H6), LHV, and CGE with R2 of prediction of each composition was 0.9815, 0.9931, 0.9960, 0.9354, 0.8634, 0.9950, and 0.8423, respectively. These results confirmed that the inclusion of H/C, O/C, and N/C into the models makes the models more reliable.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Situmorang, Y.A.; Zhao, Z.; Yoshida, A.; Abudula, A.; Guan, G. Small-Scale Biomass Gasification Systems for Power Generation (<200 kW Class): A Review. Renew. Sustain. Energy Rev. 2020, 117, 109486. [Google Scholar] [CrossRef]
- Suparmin, P.; Nurhasanah, R.; Hendri, H.; Ridwan, M. Biomass for Dual-Fuel Syngas Diesel Power Plants. Part I: The Effect of Preheating on Characteristics of the Syngas Gasification of Municipal Solid Waste and Wood Pellets. Arab. J. Basic. Appl. Sci. 2023, 30, 378–392. [Google Scholar] [CrossRef]
- Silva, I.P.; Lima, R.M.A.; Silva, G.F.; Ruzene, D.S.; Silva, D.P. Thermodynamic Equilibrium Model Based on Stoichiometric Method for Biomass Gasification: A Review of Model Modifications. Renew. Sustain. Energy Rev. 2019, 114, 109305. [Google Scholar] [CrossRef]
- Sudarmanta, B.; Sampurno; Dwiyantoro, B.A.; Gemilang, S.E.; Putra, A.B.K. Performance Characterization of Waste to Electric Prototype Uses a Dual Fuel Diesel Engine and a Multi-Stage Downdraft Gasification Reactor. Mater. Sci. Forum 2019, 964, 80–87. [Google Scholar] [CrossRef]
- Silva, I.P.; Lima, R.M.A.; Santana, H.E.P.; Silva, G.F.; Ruzene, D.S.; Silva, D.P. Development of a Semi-Empirical Model for Woody Biomass Gasification Based on Stoichiometric Thermodynamic Equilibrium Model. Energy 2022, 241, 122894. [Google Scholar] [CrossRef]
- Loha, C.; Gu, S.; De Wilde, J.; Mahanta, P.; Chatterjee, P.K. Advances in Mathematical Modelling of Fluidized Bed Gasification. Renew. Sustain. Energy Rev. 2014, 40, 688–715. [Google Scholar] [CrossRef]
- Safarian, S.; Unnþórsson, R.; Richter, C. A Review of Biomass Gasification Modelling. Renew. Sustain. Energy Rev. 2019, 110, 378–391. [Google Scholar] [CrossRef]
- Molino, A.; Larocca, V.; Chianese, S.; Musmarra, D. Biofuels Production by Biomass Gasification: A Review. Energies 2018, 11, 811. [Google Scholar] [CrossRef]
- Safarian, S.; Unnthorsson, R.; Richter, C. The Equivalence of Stoichiometric and Non-Stoichiometric Methods for Modeling Gasification and Other Reaction Equilibria. Renew. Sustain. Energy Rev. 2020, 131, 109982. [Google Scholar] [CrossRef]
- Watson, J.; Zhang, Y.; Si, B.; Chen, W.T.; de Souza, R. Gasification of Biowaste: A Critical Review and Outlooks. Renew. Sustain. Energy Rev. 2018, 83, 1–17. [Google Scholar] [CrossRef]
- Ibrahim, A.; Veremieiev, S.; Gaskell, P.H. An Advanced, Comprehensive Thermochemical Equilibrium Model of a Downdraft Biomass Gasifier. Renew. Energy 2022, 194, 912–925. [Google Scholar] [CrossRef]
- Kaydouh, M.N.; El Hassan, N. Thermodynamic Simulation of the Co-Gasification of Biomass and Plastic Waste for Hydrogen-Rich Syngas Production. Results Eng. 2022, 16, 100771. [Google Scholar] [CrossRef]
- Samadi, S.H.; Ghobadian, B.; Nosrati, M. Prediction and Estimation of Biomass Energy from Agricultural Residues Using Air Gasification Technology in Iran. Renew. Energy 2020, 149, 1077–1091. [Google Scholar] [CrossRef]
- Said, M.S.M.; Ghani, W.A.W.A.K.; Tan, H.B.; Ng, D.K.S. Prediction and Optimisation of Syngas Production from Air Gasification of Napier Grass via Stoichiometric Equilibrium Model. Energy Convers. Manag. X 2021, 10, 100057. [Google Scholar] [CrossRef]
- Ayub, H.M.U.; Park, S.J.; Binns, M. Biomass to Syngas: Modified Stoichiometric Thermodynamic Models for Downdraft Biomass Gasification. Energies 2020, 13, 5383. [Google Scholar] [CrossRef]
- Kushwah, A.; Reina, T.R.; Short, M. Modelling Approaches for Biomass Gasifiers: A Comprehensive Overview. Sci. Total Environ. 2022, 834, 155243. [Google Scholar] [CrossRef] [PubMed]
- Valderrama Rios, M.L.; González, A.M.; Lora, E.E.S.; Almazán del Olmo, O.A. Reduction of Tar Generated during Biomass Gasification: A Review. Biomass Bioenergy 2018, 108, 345–370. [Google Scholar] [CrossRef]
- Janajreh, I.; Adeyemi, I.; Raza, S.S.; Ghenai, C. A Review of Recent Developments and Future Prospects in Gasification Systems and Their Modelling. Renew. Sustain. Energy Rev. 2021, 138, 110505. [Google Scholar] [CrossRef]
- Susastriawan, A.A.P.; Saptoadi, H. Purnomo Small-Scale Downdraft Gasifiers for Biomass Gasification: A Review. Renew. Sustain. Energy Rev. 2017, 76, 989–1003. [Google Scholar] [CrossRef]
- Aydin, E.S.; Yucel, O.; Sadikoglu, H. Development of a Semi-Empirical Equilibrium Model for Downdraft Gasification Systems. Energy 2017, 130, 86–98. [Google Scholar] [CrossRef]
- Gagliano, A.; Nocera, F.; Patania, F.; Bruno, M.; Castaldo, D.G. A Robust Numerical Model for Characterizing the Syngas Composition in a Downdraft Gasification Process. Comptes Rendus Chim. 2016, 19, 441–449. [Google Scholar] [CrossRef]
- Basu, P. Biomass Gasification, Pyrolysis, and Torrefacion. Practical Design and Theory, 2nd ed.; Academic Press: London, UK, 2013. [Google Scholar]
- Shayan, E.; Zare, V.; Mirzaee, I. Hydrogen Production from Biomass Gasification; a Theoretical Comparison of Using Different Gasification Agents. Energy Convers. Manag. 2018, 159, 30–41. [Google Scholar] [CrossRef]
- Zainal, Z.A.; Ali, R.; Lean, C.H.; Seetharamu, K.N. Prediction of Performance of a Downdraft Gasifier Using Equilibrium Modeling for Different Biomass Materials. Energy Convers. Manag. 2001, 42, 1499–1515. [Google Scholar] [CrossRef]
- Eri, Q.; Wu, W.; Zhao, X. Numerical Investigation of the Air-Steam Biomass Gasification Process Based on Thermodynamic Equilibrium Model. Energies 2017, 10, 2163. [Google Scholar] [CrossRef]
- Liao, L.; Zheng, J.; Li, C.; Liu, R.; Zhang, Y. Thermodynamic Modelling Modification and Experimental Validation of Entrained-Flow Gasification of Biomass. J. Energy Inst. 2022, 103, 160–168. [Google Scholar] [CrossRef]
- Pradhan, P.; Arora, A.; Mahajani, S.M. A Semi-Empirical Approach towards Predicting Producer Gas Composition in Biomass Gasification. Bioresour. Technol. 2019, 272, 535–544. [Google Scholar] [CrossRef] [PubMed]
- Gopan, G.; Hauchhum, L.; Pattanayak, S.; Kalita, P.; Krishnan, R. Prediction of Species Concentration in Syngas Produced through Gasification of Different Bamboo Biomasses: A Numerical Approach. Int. J. Energy Environ. Eng. 2022, 13, 1383–1394. [Google Scholar] [CrossRef]
- Loha, C.; Chattopadhyay, H.; Chatterjee, P.K. Energy Generation from Fluidized Bed Gasification of Rice Husk. J. Renew. Sustain. Energy 2013, 5, 043111. [Google Scholar] [CrossRef]
- Ferreira, S.; Monteiro, E.; Calado, L.; Silva, V.; Brito, P.; Vilarinho, C. Experimental and Modelling Analysis of Brewers’ Spent Grains Gasification in a Downdraft Reactor. Energies 2019, 12, 4413. [Google Scholar] [CrossRef]
- Park, S.W.; Lee, J.S.; Yang, W.S.; Alam, M.T.; Seo, Y.C. A Comparative Study of the Gasification of Solid Refuse Fuel in Downdraft Fixed Bed and Bubbling Fluidized Bed Reactors. Waste Biomass Valorization 2020, 11, 2345–2356. [Google Scholar] [CrossRef]
- Guo, F.; Dong, Y.; Dong, L.; Guo, C. Effect of Design and Operating Parameters on the Gasification Process of Biomass in a Downdraft Fixed Bed: An Experimental Study. Int. J. Hydrogen Energy 2014, 39, 5625–5633. [Google Scholar] [CrossRef]
- Lim, Y.I.; Lee, U. Do Quasi-Equilibrium Thermodynamic Model with Empirical Equations for Air-Steam Biomass Gasification in Fluidized-Beds. Fuel Process. Technol. 2014, 128, 199–210. [Google Scholar] [CrossRef]
- Mendiburu, A.Z.; Carvalho, J.A.; Coronado, C.J.R. Thermochemical Equilibrium Modelling of Biomass Downdraft Gasifier: Stoichiometric Models. Energy 2014, 66, 189–201. [Google Scholar] [CrossRef]
- Ayub, H.M.U.; Qyyum, M.A.; Qadeer, K.; Binns, M.; Tawfik, A.; Lee, M. Robustness Enhancement of Biomass Steam Gasification Thermodynamic Models for Biohydrogen Production: Introducing New Correction Factors. J. Clean Prod. 2021, 321, 128954. [Google Scholar] [CrossRef]
- Rodriguez-Alejandro, D.A.; Nam, H.; Maglinao, A.L.; Capareda, S.C.; Aguilera-Alvarado, A.F. Development of a Modified Equilibrium Model for Biomass Pilot-Scale Fluidized Bed Gasifier Performance Predictions. Energy 2016, 115, 1092–1108. [Google Scholar] [CrossRef]
- Fu, Q.; Huang, Y.; Niu, M.; Yang, G.; Shao, Z. Experimental and Predicted Approaches for Biomass Gasification with Enriched Air-Steam in a Fluidised Bed. Waste Manag. Res. 2014, 32, 988–996. [Google Scholar] [CrossRef]
- Vonk, G.; Piriou, B.; Felipe Dos Santos, P.; Wolbert, D.; Vaïtilingom, G. Comparative Analysis of Wood and Solid Recovered Fuels Gasification in a Downdraft Fixed Bed Reactor. Waste Manag. 2019, 85, 106–120. [Google Scholar] [CrossRef]
- Kardaś, D.; Kluska, J.; Kazimierski, P. The Course and Effects of Syngas Production from Beechwood and RDF in Updraft Reactor in the Light of Experimental Tests and Numerical Calculations. Therm. Sci. Eng. Prog. 2018, 8, 136–144. [Google Scholar] [CrossRef]
- Saleh, A.R.; Sudarmanta, B.; Fansuri, H.; Muraza, O. Improved Municipal Solid Waste Gasification Efficiency Using a Modified Downdraft Gasifier with Variations of Air Input and Preheated Air Temperature. Energy Fuels 2019, 33, 11049–11056. [Google Scholar] [CrossRef]
- Erlich, C.; Fransson, T.H. Downdraft Gasification of Pellets Made of Wood, Palm-Oil Residues Respective Bagasse: Experimental Study. Appl. Energy 2011, 88, 899–908. [Google Scholar] [CrossRef]
- Atnaw, S.M.; Sulaiman, S.A.; Yusup, S. Syngas Production from Downdraft Gasification of Oil Palm Fronds. Energy 2013, 61, 491–501. [Google Scholar] [CrossRef]
- Atnaw, S.M.; Kueh, S.C.; Sulaiman, S.A. Study on Tar Generated from Downdraft Gasification of Oil Palm Fronds. Sci. World J. 2014, 2014, 497830. [Google Scholar] [CrossRef] [PubMed]
- Ariffin, M.A.; Wan Mahmood, W.M.F.; Harun, Z.; Mohamed, R. Medium-Scale Gasification of Oil Palm Empty Fruit Bunch for Power Generation. J. Mater. Cycles Waste Manag. 2017, 19, 1244–1252. [Google Scholar] [CrossRef]
- Subramanian, P.; Sampathrajan, A.; Venkatachalam, P. Fluidized Bed Gasification of Select Granular Biomaterials. Bioresour. Technol. 2011, 102, 1914–1920. [Google Scholar] [CrossRef] [PubMed]
- Ghassemi, H.; Shahsavan-Markadeh, R. Effects of Various Operational Parameters on Biomass Gasification Process; A Modified Equilibrium Model. Energy Convers Manag. 2014, 79, 18–24. [Google Scholar] [CrossRef]
- Thamavithya, M.; Jarungthammachote, S.; Dutta, A.; Basu, P. Experimental Study on Sawdust Gasification in a Spout-Fluid Bed Reactor. Int. J. Energy Res. 2012, 36, 204–217. [Google Scholar] [CrossRef]
- Sreejith, C.C.; Muraleedharan, C.; Arun, P. Performance Prediction of Fluidised Bed Gasification of Biomass Using Experimental Data-Based Simulation Models. Biomass Convers Biorefin. 2013, 3, 283–304. [Google Scholar] [CrossRef]
- Simone, M.; Barontini, F.; Nicolella, C.; Tognotti, L. Gasification of Pelletized Biomass in a Pilot Scale Downdraft Gasifier. Bioresour. Technol. 2012, 116, 403–412. [Google Scholar] [CrossRef]
- Olgun, H.; Ozdogan, S.; Yinesor, G. Results with a Bench Scale Downdraft Biomass Gasifier for Agricultural and Forestry Residues. Biomass Bioenergy 2011, 35, 572–580. [Google Scholar] [CrossRef]
- Svishchev, D.A.; Kozlov, A.N.; Donskoy, I.G.; Ryzhkov, A.F. A Semi-Empirical Approach to the Thermodynamic Analysis of Downdraft Gasification. Fuel 2016, 168, 91–106. [Google Scholar] [CrossRef]
- Kashyap, P.V.; Pulla, R.H.; Sharma, A.K.; Sharma, P.K. Development of a Non-Stoichiometric Equilibrium Model of Downdraft Gasifier. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 1–19. [Google Scholar] [CrossRef]
- Bandara, J.C.; Jaiswal, R.; Nielsen, H.K.; Moldestad, B.M.E.; Eikeland, M.S. Air Gasification of Wood Chips, Wood Pellets and Grass Pellets in a Bubbling Fluidized Bed Reactor. Energy 2021, 233, 121149. [Google Scholar] [CrossRef]
- Gunarathne, D.S.; Mueller, A.; Fleck, S.; Kolb, T.; Chmielewski, J.K.; Yang, W.; Blasiak, W. Gasification Characteristics of Steam Exploded Biomass in an Updraft Pilot Scale Gasifier. Energy 2014, 71, 496–506. [Google Scholar] [CrossRef]
- Campoy, M.; Gómez-Barea, A.; Ollero, P.; Nilsson, S. Gasification of Wastes in a Pilot Fluidized Bed Gasifier. Fuel Process. Technol. 2014, 121, 63–69. [Google Scholar] [CrossRef]
- Galindo, A.L.; Lora, E.S.; Andrade, R.V.; Giraldo, S.Y.; Jaén, R.L.; Cobas, V.M. Biomass Gasification in a Downdraft Gasifier with a Two-Stage Air Supply: Effect of Operating Conditions on Gas Quality. Biomass Bioenergy 2014, 61, 236–244. [Google Scholar] [CrossRef]
- Arun, K.; Venkata Ramanan, M.; Mohanasutan, S. Comparative Studies and Analysis on Gasification of Coconut Shells and Corn Cobs in a Perforated Fixed Bed Downdraft Reactor by Admitting Air through Equally Spaced Conduits. Biomass Convers Biorefin. 2020, 12, 1257–1269. [Google Scholar] [CrossRef]
- Rupesh, S.; Muraleedharan, C.; Arun, P. A Comparative Study on Gaseous Fuel Generation Capability of Biomass Materials by Thermo-Chemical Gasification Using Stoichiometric Quasi-Steady-State Model. Int. J. Energy Environ. Eng. 2015, 6, 375–384. [Google Scholar] [CrossRef]
- Rupesh, S.; Muraleedharan, C.; Arun, P. Energy and Exergy Analysis of Syngas Production from Different Biomasses through Air-Steam Gasification. Front. Energy 2020, 14, 607–619. [Google Scholar] [CrossRef]
- Huang, H.J.; Ramaswamy, S. Modeling Biomass Gasification Using Thermodynamic Equilibrium Approach. In Applied Biochemistry and Biotechnology; Springer: Berlin/Heidelberg, Germany, 2009; Volume 154, pp. 193–204. [Google Scholar]
- Pio, D.T.; Tarelho, L.A.C. Empirical and Chemical Equilibrium Modelling for Prediction of Biomass Gasification Products in Bubbling Fluidized Beds. Energy 2020, 202, 117654. [Google Scholar] [CrossRef]
- Buragohain, B.; Mahanta, P.; Moholkar, V.S. Performance Correlations for Biomass Gasifiers Using Semi-Equilibrium Non-Stoichiometric Thermodynamic Models. Int. J. Energy Res. 2012, 36, 590–618. [Google Scholar] [CrossRef]
- Chen, G.; Jamro, I.A.; Samo, S.R.; Wenga, T.; Baloch, H.A.; Yan, B.; Ma, W. Hydrogen-Rich Syngas Production from Municipal Solid Waste Gasification through the Application of Central Composite Design: An Optimization Study. Int. J. Hydrogen Energy 2020, 45, 33260–33273. [Google Scholar] [CrossRef]
- Zhang, Y.; Wan, L.; Guan, J.; Xiong, Q.; Zhang, S.; Jin, X. A Review on Biomass Gasification: Effect of Main Parameters on Char Generation and Reaction. Energy Fuels 2020, 34, 13438–13455. [Google Scholar] [CrossRef]
- Ramos, A.; Monteiro, E.; Rouboa, A. Numerical Approaches and Comprehensive Models for Gasification Process: A Review. Renew. Sustain. Energy Rev. 2019, 110, 188–206. [Google Scholar] [CrossRef]
- Shahbaz, M.; Al-Ansari, T.; Inayat, M.; Sulaiman, S.A.; Parthasarathy, P.; McKay, G. A Critical Review on the Influence of Process Parameters in Catalytic Co-Gasification: Current Performance and Challenges for a Future Prospectus. Renew. Sustain. Energy Rev. 2020, 134, 110382. [Google Scholar] [CrossRef]
- Guangul, F.M.; Sulaiman, S.A.; Ramli, A. Study of the Effects of Operating Factors on the Resulting Producer Gas of Oil Palm Fronds Gasification with a Single Throat Downdraft Gasifier. Renew. Energy 2014, 72, 271–283. [Google Scholar] [CrossRef]
- Arun, K.; Venkata Ramanan, M.; Sai Ganesh, S. Stoichiometric Equilibrium Modelling of Corn Cob Gasification and Validation Using Experimental Analysis. Energy Fuels 2016, 30, 7435–7442. [Google Scholar] [CrossRef]
- Raheem, A.; Zhao, M.; Dastyar, W.; Channa, A.Q.; Ji, G.; Zhang, Y. Parametric Gasification Process of Sugarcane Bagasse for Syngas Production. Int. J. Hydrogen Energy 2019, 44, 16234–16247. [Google Scholar] [CrossRef]
- Susastriawan, A.A.P.; Saptoadi, H. Purnomo Design and Experimental Study of Pilot Scale Throat-Less Downdraft Gasifier Fed by Rice Husk and Wood Sawdust. Int. J. Sustain. Energy 2018, 37, 873–885. [Google Scholar] [CrossRef]
- Zhang, Z.; Pang, S. Experimental Investigation of Tar Formation and Producer Gas Composition in Biomass Steam Gasification in a 100 kW Dual Fluidised Bed Gasifier. Renew. Energy 2019, 132, 416–424. [Google Scholar] [CrossRef]
- Trinh, T.H.; Uemura, Y. A Theoretical Equation Preseting Slope in Van Krevelen Diagram for Biomass Pyrolysis. Platform 2019, 3, 57–64. [Google Scholar] [CrossRef]
- Gai, C.; Dong, Y. Experimental Study on Non-Woody Biomass Gasification in a Downdraft Gasifier. Int. J. Hydrogen Energy 2012, 37, 4935–4944. [Google Scholar] [CrossRef]
- Omar, M.M.; Munir, A.; Ahmad, M.; Tanveer, A. Downdraft Gasifier Structure and Process Improvement for High Quality and Quantity Producer Gas Production. J. Energy Inst. 2018, 91, 1034–1044. [Google Scholar] [CrossRef]
- Tauqir, W.; Zubair, M.; Nazir, H. Parametric Analysis of a Steady State Equilibrium-Based Biomass Gasification Model for Syngas and Biochar Production and Heat Generation. Energy Convers Manag. 2019, 199, 111954. [Google Scholar] [CrossRef]
- Indrawan, N.; Kumar, A.; Kumar, S. Recent Advances in Power Generation Through Biomass and Municipal Solid Waste Gasification. In Energy, Environment, and Sustainability; Springer Nature: Berlin/Heidelberg, Germany, 2018; pp. 369–401. [Google Scholar] [CrossRef]
- Cao, Y.; Bai, Y.; Du, J. Study on Gasification Characteristics of Pine Sawdust Using Olivine as in-Bed Material for Combustible Gas Production. J. Energy Inst. 2021, 96, 168–172. [Google Scholar] [CrossRef]
- Saleh, A.R.; Sudarmanta, B.; Fansuri, H.; Muraza, O. Syngas Production from Municipal Solid Waste with a Reduced Tar Yield by Three-Stages of Air Inlet to a Downdraft Gasifier. Fuel 2020, 263, 116509. [Google Scholar] [CrossRef]
- Aydin, E.S.; Yucel, O.; Sadikoglu, H. Experimental Study on Hydrogen-Rich Syngas Production via Gasification of Pine Cone Particles and Wood Pellets in a Fixed Bed Downdraft Gasifier. Int. J. Hydrogen Energy 2019, 44, 17389–17396. [Google Scholar] [CrossRef]
- Kirsanovs, V.; Blumberga, D.; Veidenbergs, I.; Rochas, C.; Vigants, E.; Vigants, G. Experimental Investigation of Downdraft Gasifier at Various Conditions. Energy Procedia 2017, 128, 332–338. [Google Scholar] [CrossRef]
- Mhilu, C.F. Modeling Performance of High-Temperature Biomass Gasification Process. ISRN Chem. Eng. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Ariffin, M.A.; Wan Mahmood, W.M.F.; Mohamed, R.; Mohd Nor, M.T. Performance of Oil Palm Kernel Shell Gasification Using a Medium-Scale Downdraft Gasifier. Int. J. Green Energy 2016, 13, 513–520. [Google Scholar] [CrossRef]
- Zaman, S.A.; Roy, D.; Ghosh, S. Process Modelling and Optimization for Biomass Steam-Gasification Employing Response Surface Methodology. Biomass Bioenergy 2020, 143, 105847. [Google Scholar] [CrossRef]
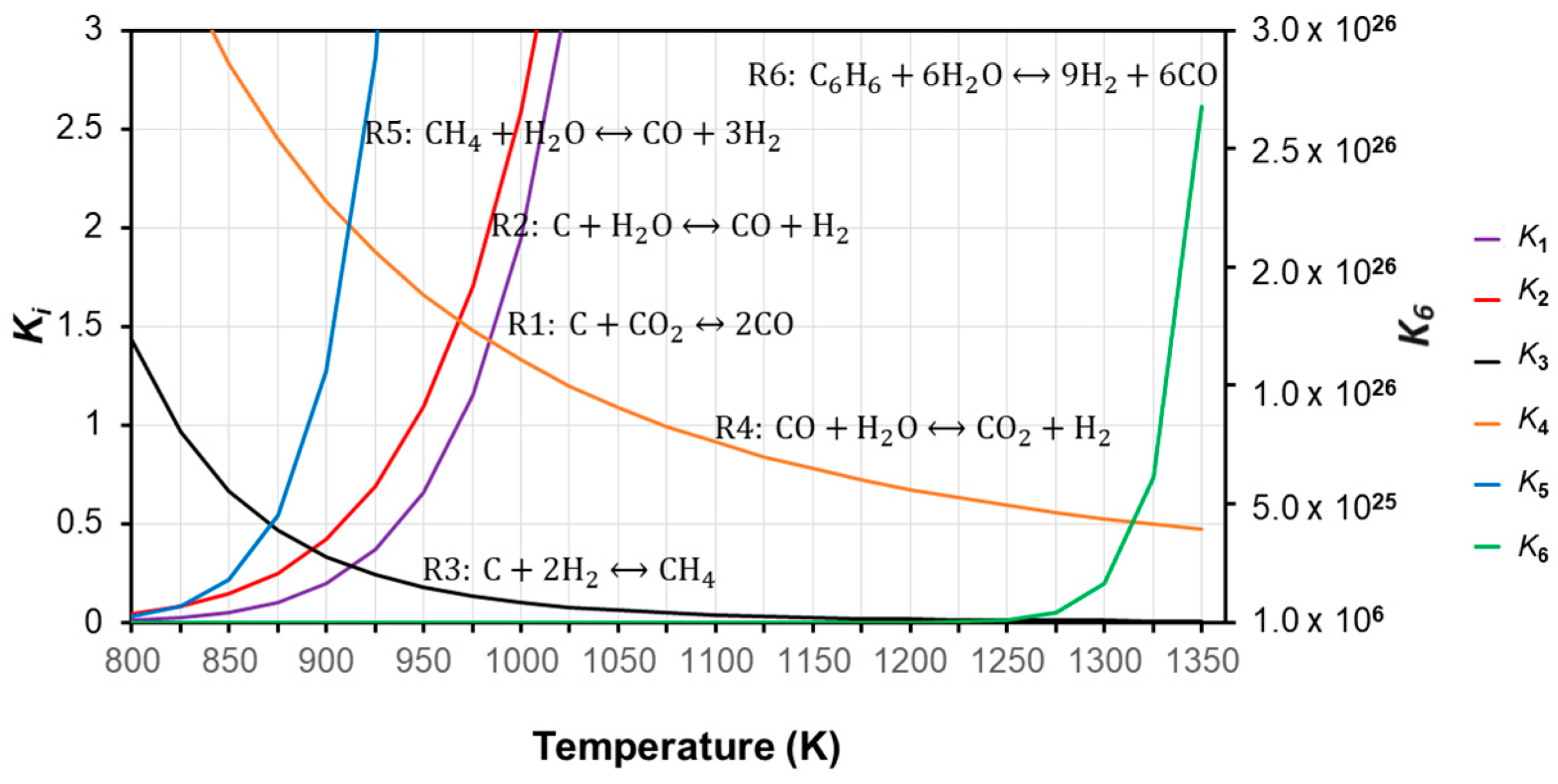
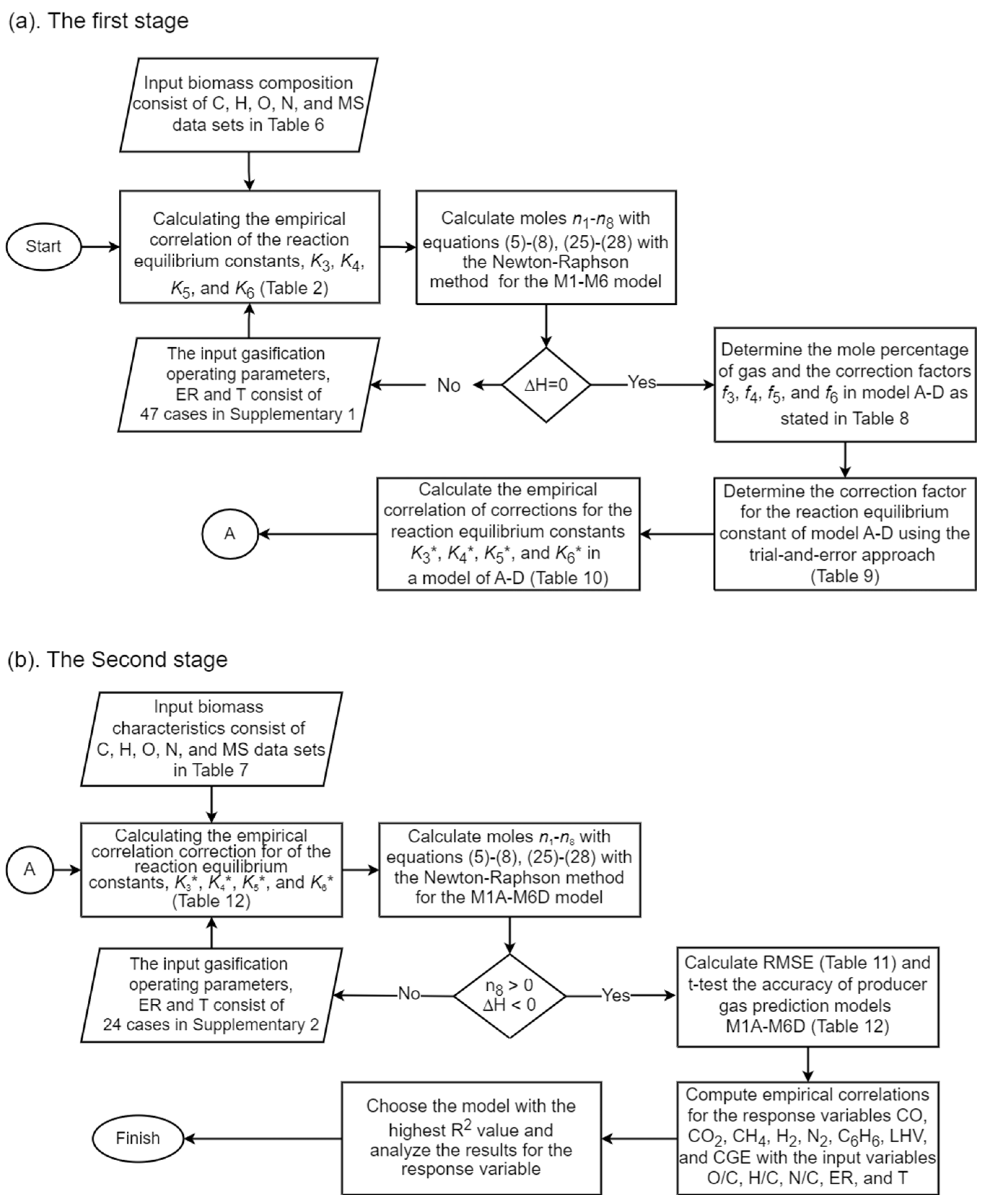
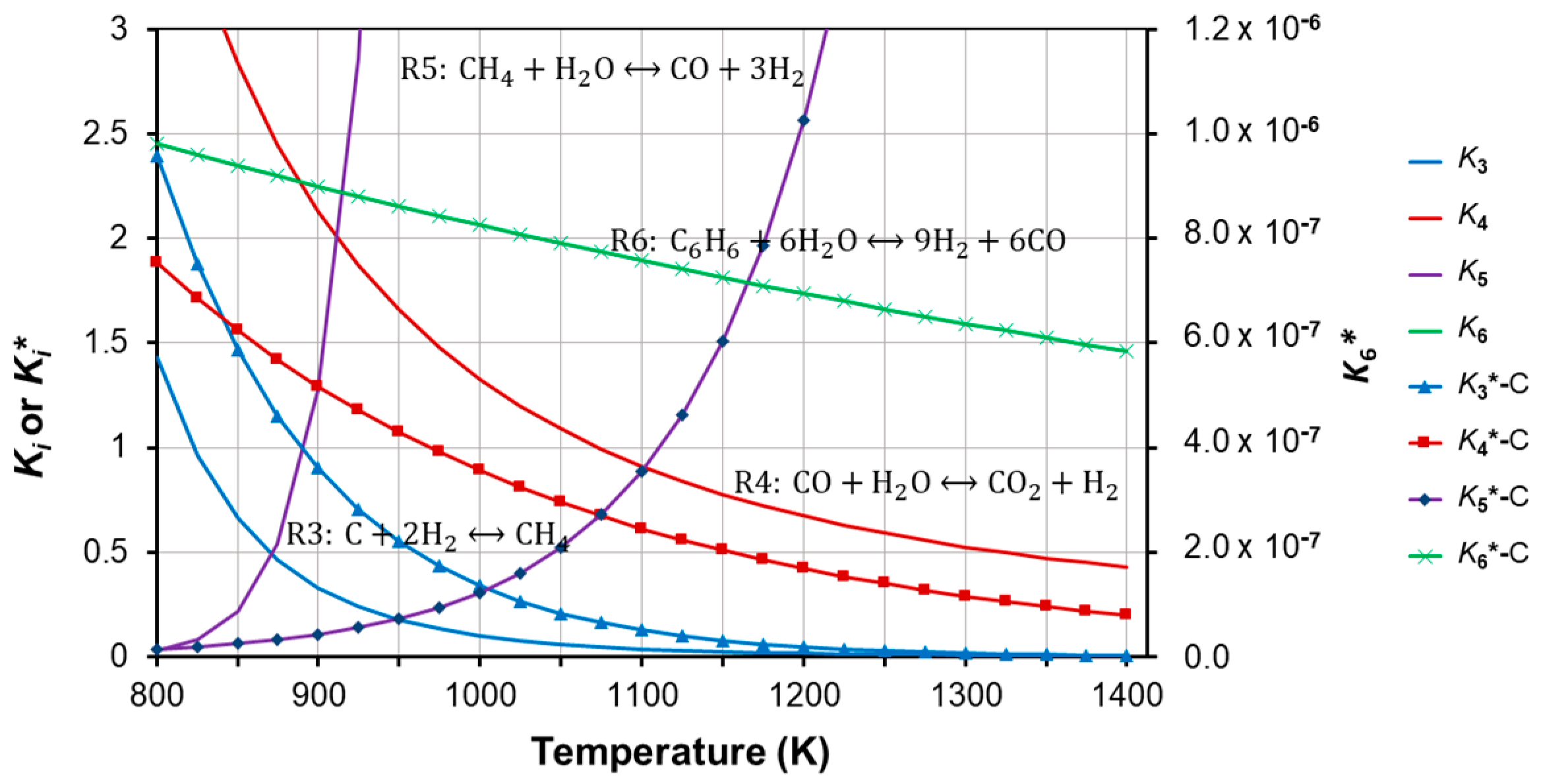
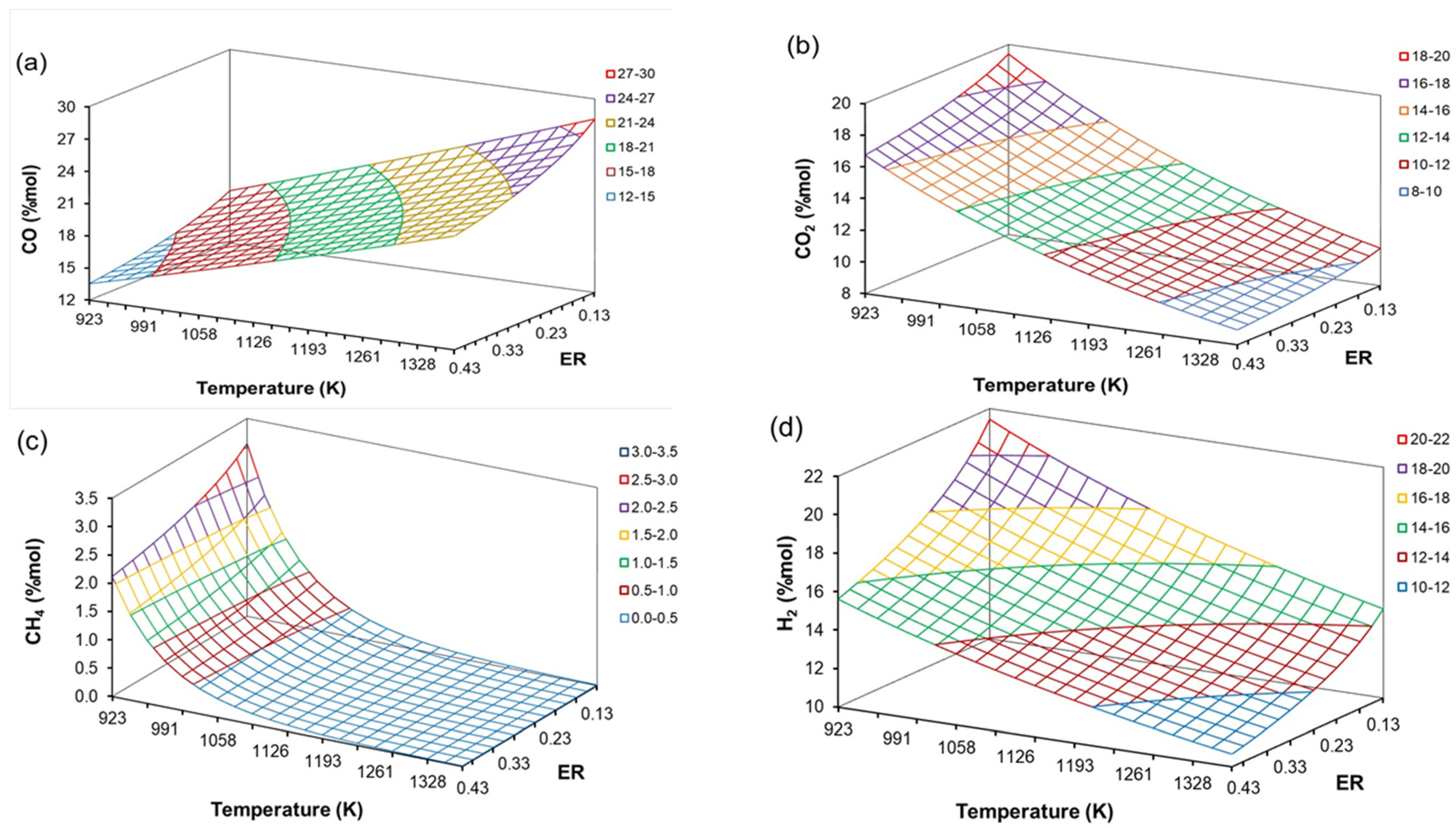

| Coefficient | CO | CO2 | CH4 | H2O | C6H6 |
|---|---|---|---|---|---|
| −110.541 | −393.546 | −74.851 | −241.845 | 82.927 | |
| a’ | 5.619 × 10−3 | −1.949 × 10−2 | −4.620 × 10−2 | −8.95 × 10−3 | −0.1824 |
| b’ | −1.19 × 10−5 | 3.122 × 10−5 | 1.13 × 10−5 | −3.672 × 10−6 | 1.903 × 10−4 |
| c’ | 6.383 × 10−9 | −2.448 × 10−8 | 1.319 × 10−8 | 5.209 × 10−9 | −8.67 × 10−8 |
| d’ | −1.846 × 10−12 | 6.946 × 10−12 | −6.647 × 10−12 | −1.478 × 10−12 | 1.208 × 10−11 |
| e’ | −4.891 × 102 | −4.891 × 1022 | −4.891 × 102 | 0.0 | −2.935 × 103 |
| f’ | 0.86841 | 5.270 | 14.11 | 2.868 | 49.50 |
| g’ | −6.131 × 10−2 | −0.1207 | −0.2234 | −1.722 × 10−2 | −0.9787 |
| Coefficient | ||||||
|---|---|---|---|---|---|---|
| 54.08108 | 7.16594 | 60.51782 | −46.91514 | −53.35188 | −13.57183 | |
| 0.00398 | −0.00062 | 0.00798 | −0.00460 | −0.00860 | −0.01459 | |
| −23,462.56 | −15,661.36 | 5341.56 | 7801.20 | −21,002.92 | −81,609.84 | |
| −4.83331 | 1.45729 | −10.88627 | 6.29061 | 12.34356 | 20.99726 | |
| −7.865 × 10−7 | −3.409 × 10−8 | −1.098 × 10−6 | 7.524 × 10−7 | 1.064 × 10−6 | 1.573 × 10−6 | |
| 241,923.75 | 36,765.58 | 162,197.73 | −205,158.18 | −125,432.15 | 285,399.51 | |
| -adj | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Product | (kJ/kmol) | a | b | c | d | T(K) |
|---|---|---|---|---|---|---|
| CO | −110,541 | 28.16 | 1.675 × 10−3 | 5.372 × 10−6 | −2.222 × 10−9 | 273–1800 |
| CO2 | −393,546 | 22.26 | 5.981 × 10−2 | −3.501 × 10−5 | −7.447 × 10−9 | 273–1800 |
| CH4 | −74,851 | 19.89 | 5.024 × 10−2 | 1.269 × 10−5 | −1.101 × 10−8 | 273–1800 |
| H2 | 0 | 29.11 | −1.916 × 10−3 | 4.004 × 10−6 | −8.704 × 10−10 | 273–1800 |
| H2O | −241,845 | 32.24 | 1.923 × 10−3 | 1.055 × 10−5 | −3.595 × 10−9 | 273–1800 |
| N2 | 0 | 28.9 | −1.571 × 10−3 | 8.081 × 10−6 | −2.873 × 10−9 | 273–1800 |
| C6H6 | 82,927 | −36.22 | 0.4848 | −3.157 × 10−4 | 7.762 × 10−8 | 273–1800 |
| Models | Moles of Carbon C (n7) | Reactions Used | Equation Used | ||
|---|---|---|---|---|---|
| M1 | Ignored | R3 | R4 | R5 | (5)–(8); (25)–(27) |
| M2 | Ignored | R3 | R4 | R6 | (5)–(8); (25); (26); (28) |
| M3 | Ignored | R4 | R5 | R6 | (5)–(8); (26)–(28) |
| M4 | Empirical correlation | R3 | R4 | R5 | (5)–(8); (25)–(27) |
| M5 | Empirical correlation | R3 | R4 | R6 | (5)–(8); (25); (26); (28) |
| M6 | Empirical correlation | R4 | R5 | R6 | (5)–(8); (26)–(28) |
| Correction Factors | ||||
|---|---|---|---|---|
| Biomass | Ultimate Analysis (% wt) | Proximate Analysis (% wt) | HHV (MJ/kg) | Case Number | Reference | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | H | O | N | S | VM | FC | Ash | MS | ||||
| Municipal solid waste | 50.40 | 5.70 | 41.70 | 2.20 | 0.00 | 75.80 | 17.00 | 1.30 | 5.90 | 19.939 | 5 | [38] |
| Municipal solid waste | 58.10 | 6.50 | 31.40 | 2.60 | 0.60 | 62.80 | 24.80 | 12.40 | 11.7 | 24.5 | 2 | [39] |
| Municipal solid waste | 47.26 | 6.70 | 45.54 | 0.49 | 0.01 | 65.78 | 20.19 | 4.21 | 9.82 | 19.589 | 2 | [40] |
| Palm kernel oil | 49.80 | 6.50 | 38.20 | 0.80 | 0.12 | N/A | N/A | 8.40 | 11.00 | 20.917 | 3 | [41] |
| Palm kernel oil | 42.40 | 5.80 | 48.20 | 3.60 | 0.00 | 76.35 | 11.50 | 3.40 | 8.75 | 16.526 | 4 | [42] |
| Palm kernel oil | 44.58 | 4.53 | 48.80 | 0.71 | 0.07 | 83.50 | 15.20 | 1.30 | 16.00 | 15.824 | 1 | [43] |
| Palm kernel oil | 42.08 | 7.00 | 49.90 | 0.99 | 0.00 | 83.00 | 9.00 | 3.00 | 5.00 | 17.700 | 1 | [44] |
| Rice husk | 47.18 | 3.60 | 48.20 | 1.01 | 0.12 | 73.40 | 20.60 | 6.00 | 13.63 | 15.599 | 2 | [45] |
| Rice husk | 38.92 | 5.10 | 53.89 | 2.17 | 0.12 | 63.80 | 16.87 | 19.33 | 8.1 | 13.596 | 1 | [46] |
| Sawdust | 49.15 | 5.74 | 44.31 | 0.81 | 0.00 | 68.01 | 13.02 | 0.89 | 18 | 19.309 | 2 | [47] |
| Sawdust | 51.73 | 6.00 | 41.48 | 0.62 | 0.00 | 70.30 | 15.10 | 3.30 | 11.20 | 20.761 | 2 | [48] |
| Sawdust | 48.91 | 5.80 | 45.11 | 0.18 | 0.00 | 80.63 | 17.27 | 2.10 | 0.00 | 19.197 | 1 | [49] |
| Sawdust | 50.40 | 6.60 | 39.67 | 0.90 | 0.48 | 84.34 | 13.74 | 1.92 | 9.82 | 21.264 | 3 | [37] |
| Woodchips | 45.60 | 5.90 | 48.40 | 1.00 | 0.00 | 77.50 | 12.30 | 1.50 | 8.80 | 17.820 | 2 | [50] |
| Woodchips | 49.20 | 5.50 | 45.20 | 0.10 | 0.00 | 78.10 | 14.70 | 0.40 | 6.80 | 18.973 | 4 | [51] |
| Woodchips | 49.22 | 6.06 | 43.21 | 0.13 | 0.08 | 78.10 | 14.70 | 1.69 | 8 | 19.826 | 3 | [52] |
| Wood pellets | 50.00 | 6.00 | 42.60 | 3.19 | 0.00 | 77.80 | 14.00 | 0.30 | 7.9 | 20.065 | 1 | [53] |
| Wood pellets | 52.60 | 5.80 | 40.60 | 0.10 | 0.00 | 76.80 | 22.30 | 0.90 | 4.2 | 20.978 | 1 | [54] |
| Wood pellets | 49.80 | 5.80 | 42.20 | 2.00 | 0.06 | 81.00 | 18.40 | 0.70 | 6.30 | 19.817 | 3 | [55] |
| Wood pellets | 50.70 | 6.90 | 42.40 | 0.30 | 0.18 | N/A | N/A | 0.39 | 7.50 | 21.451 | 4 | [20] |
| Total | 20 | 47 | ||||||||||
| Biomass | Ultimate Analysis (% wt) | Proximate Analysis (% wt) | HHV (MJ/kg) | Case Number | Reference | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | H | O | N | S | VM | FC | Ash | MS | ||||
| Woodchips | 50.60 | 6.50 | 42.00 | 0.20 | 0.10 | 72.40 | 19.20 | 0.70 | 7.70 | 20.973 | 4 | [20] |
| Wood pellets | 46.78 | 5.96 | 45.44 | 0.32 | 0.09 | 83.01 | 15.66 | 1.34 | 12.23 | 18.631 | 5 | [56] |
| Sawdust | 51.33 | 6.13 | 41.97 | 0.12 | 0.02 | 77.76 | 20.44 | 1.80 | 9.3 | 20.765 | 2 | [45] |
| Corn | 44.70 | 6.30 | 45.20 | 1.20 | 0.09 | 66.30 | 16.60 | 2.40 | 14.7 | 18.295 | 4 | [57] |
| Wood pellets | 49.80 | 5.80 | 42.20 | 2.00 | 0.06 | 81.00 | 18.40 | 0.70 | 6.30 | 19.817 | 3 | [55] |
| Palm kernel oil | 44.58 | 4.53 | 48.80 | 0.71 | 0.07 | 83.50 | 15.20 | 1.30 | 16.00 | 15.824 | 1 | [43] |
| Sawdust | 48.91 | 5.80 | 45.11 | 0.18 | 0.00 | 80.63 | 17.27 | 2.10 | 0.00 | 19.197 | 1 | [49] |
| Wood pellets | 50.00 | 6.00 | 42.60 | 3.19 | 0.00 | 77.80 | 14.00 | 0.30 | 7.9 | 20.065 | 2 | [53] |
| Municipal solid waste | 46.30 | 5.20 | 44.80 | 2.90 | 0.86 | 47.00 | 8.50 | 0.00 | 14.30 | 17.701 | 2 | [55] |
| Total | 9 | 24 | ||||||||||
| Factor Model | Correction Factor | |||
|---|---|---|---|---|
| A | 14.7690 | 3.5143 | 0.0924 | 0.0092 |
| B | 66.4224 | 1.3221 | 0.0904 | 0.0513 |
| C | 33.9060 | 1.5202 | 0.0602 | 0.0054 |
| D | 305.3084 | 1.2181 | 0.0364 | 0.3595 |
| Factor Model | ||||
|---|---|---|---|---|
| A | ||||
| B | ||||
| C | ||||
| D |
| Factor Models | Coefficient and R2-adj | ||||
|---|---|---|---|---|---|
| A | a0 | 4289.2370 | 46.2788 | 1.1535 × 10−5 | 2.0959 × 10−6 |
| a1 | −0.009770 | −0.003742 | 0.010617 | −0.000864 | |
| R2-adj | 0.9817 | 0.9725 | 0.9803 | 0.9998 | |
| B | a0 | 6246.2697 | 36.2444 | 1.1279 × 10−5 | 2.5967 × 10−6 |
| a1 | −0.009770 | −0.003742 | 0.010617 | −0.000864 | |
| R2-adj | 0.9817 | 0.9725 | 0.9803 | 0.9998 | |
| C | a0 | 5939.6868 | 37.5318 | 7.5092 × 10−6 | 1.9585 × 10−6 |
| a1 | −0.009770 | −0.003742 | 0.010617 | −0.000864 | |
| R2-adj | 0.9817 | 0.9725 | 0.9803 | 0.9998 | |
| D | a0 | 10,289.1435 | 35.5092 | 4.5442 × 10−6 | 3.3126 × 10−6 |
| a1 | −0.00977 | −0.00374 | 0.0106166 | −0.000864 | |
| R2-adj | 0.9817 | 0.9725 | 0.9803 | 0.9998 |
| Model | A | B | C | D | Original Model | |
|---|---|---|---|---|---|---|
| ΔH (kJ/kmol) | M1 | −17,658 | −9759 | −17,603 | −15,742 | 66,247 |
| M2 | −16,135 | −13,498 | −14,367 | −13,001 | 10,270 | |
| M3 | −16,144 | −13,483 | −14,389 | −13,175 | 8787 | |
| M4 | −18,142 | −14,542 | −20,843 | −18,112 | 69,783 | |
| M5 | −20,304 | −17,526 | −18,397 | −17,199 | 1013 | |
| M6 | −20,564 | −17,711 | −20,050 | −17,642 | 1680 | |
| C6H6 (%mol) | M1 | 1.691 | 1.245 | 1.746 | 1.700 | −1.743 |
| M2 | 1.652 | 1.542 | 1.599 | 1.450 | 0.000 | |
| M3 | 2.835 | 1.556 | 1.578 | 1.412 | 0.029 | |
| M4 | 1.073 | 1.550 | 1.093 | 0.984 | −2.268 | |
| M5 | 1.094 | 0.998 | 1.045 | 0.908 | 0.024 | |
| M6 | 1.099 | 1.018 | 1.028 | 0.885 | 0.000 | |
| RMSE (%) | M1 | 2.906 | 3.374 | 2.752 | 2.867 | 14.270 |
| M2 | 2.834 | 2.684 | 2.675 | 2.667 | 6.989 | |
| M3 | 2.838 | 2.684 | 2.659 | 2.657 | 6.940 | |
| M4 | 3.094 | 2.351 | 2.862 | 2.803 | 14.647 | |
| M5 | 2.965 | 2.740 | 2.755 | 2.694 | 7.095 | |
| M6 | 2.947 | 2.764 | 2.747 | 2.697 | 6.713 |
| Model | CO (%vol) | CO2 (%vol) | CH4 (%vol) | H2 (%vol) | N2 (%vol) | t-Stat CO | t-Stat CO2 | t-Stat CH4 | t-Stat H2 | t-Stat N2 |
|---|---|---|---|---|---|---|---|---|---|---|
| M1O | 36.190 | 2.159 | 0.395 | 28.362 | 34.637 | |||||
| M1A | 17.399 | 13.998 | 0.261 | 14.985 | 51.666 | −0.943 | 2.960 | −8.836 | 2.829 | −1.827 |
| M1B | 20.736 | 11.913 | 0.458 | 16.110 | 49.539 | 4.787 | −0.373 | −7.995 | 5.045 | −4.460 |
| M1C | 18.065 | 13.486 | 0.313 | 14.031 | 52.358 | 0.214 | 2.145 | −8.631 | 0.882 | −0.956 |
| M1D | 18.582 | 13.332 | 0.528 | 13.903 | 51.956 | 1.043 | 1.816 | −7.694 | 0.525 | −1.408 |
| M2O | 25.002 | 9.124 | 0.307 | 21.165 | 44.403 | |||||
| M2A | 17.489 | 13.926 | 0.311 | 14.920 | 51.702 | −0.877 | 2.857 | −8.707 | 2.756 | −1.742 |
| M2B | 19.121 | 12.804 | 0.389 | 14.505 | 51.639 | 2.329 | 1.051 | −8.431 | 1.954 | −1.834 |
| M2C | 18.710 | 13.071 | 0.360 | 14.424 | 51.835 | 1.519 | 1.478 | −8.516 | 1.765 | −1.590 |
| M2D | 19.448 | 12.633 | 0.611 | 14.418 | 51.440 | 3.015 | 0.774 | −7.183 | 1.817 | −2.078 |
| M3O | 24.924 | 9.133 | 0.363 | 21.511 | 44.040 | |||||
| M3A | 17.764 | 14.190 | 0.321 | 15.164 | 52.562 | −0.359 | 3.252 | −8.725 | 3.231 | −0.683 |
| M3B | 19.120 | 12.785 | 0.323 | 14.543 | 51.673 | 2.348 | 1.022 | −8.760 | 2.037 | −1.811 |
| M3C | 18.727 | 13.077 | 0.443 | 14.357 | 51.819 | 1.560 | 1.494 | −8.111 | 1.635 | −1.605 |
| M3D | 19.461 | 12.656 | 0.761 | 14.302 | 51.408 | 3.049 | 0.807 | −6.087 | 1.563 | −2.105 |
| M4O | 36.402 | 1.747 | 0.386 | 29.540 | 34.193 | |||||
| M4A | 17.144 | 13.802 | 0.320 | 16.189 | 51.471 | −1.374 | 2.610 | −8.678 | 5.173 | −1.983 |
| M4B | 20.152 | 12.021 | 0.582 | 17.405 | 49.162 | 4.071 | −0.191 | −7.144 | 7.348 | −4.523 |
| M4C | 17.598 | 13.364 | 0.386 | 15.061 | 52.498 | −0.541 | 1.840 | −8.259 | 3.137 | −0.771 |
| M4D | 18.344 | 12.949 | 0.634 | 15.036 | 52.054 | 0.635 | 1.220 | −6.885 | 3.139 | −1.328 |
| M5O | 24.520 | 9.061 | 0.273 | 21.994 | 44.128 | |||||
| M5A | 16.741 | 13.951 | 0.344 | 15.496 | 52.374 | −2.267 | 2.905 | −8.589 | 3.832 | −0.889 |
| M5B | 18.366 | 12.829 | 0.416 | 15.021 | 52.371 | 0.803 | 1.091 | −8.229 | 2.962 | −0.898 |
| M5C | 17.966 | 13.089 | 0.393 | 14.971 | 52.537 | 0.045 | 1.512 | −8.342 | 2.835 | −0.694 |
| M5D | 18.645 | 12.697 | 0.659 | 14.898 | 52.193 | 1.336 | 0.871 | −6.761 | 2.836 | −1.110 |
| M6O | 23.943 | 9.367 | 0.160 | 21.743 | 44.763 | |||||
| M6A | 16.744 | 13.944 | 0.320 | 15.517 | 52.375 | −1.473 | 2.658 | −8.919 | 3.770 | −1.147 |
| M6B | 18.370 | 12.807 | 0.322 | 15.101 | 52.382 | 1.630 | 0.837 | −8.910 | 2.975 | −1.155 |
| M6C | 18.130 | 13.287 | 0.436 | 14.952 | 52.167 | 0.295 | 1.979 | −8.405 | 3.055 | −1.197 |
| M6D | 18.653 | 12.711 | 0.754 | 14.823 | 52.174 | 2.216 | 0.678 | −6.041 | 2.615 | −1.402 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suparmin, P.; Nelwan, L.O.; Mardjan, S.S.; Purwanti, N. Development Models of Stoichiometric Thermodynamic Equilibrium for Predicting Gas Composition from Biomass Gasification: Correction Factors for Reaction Equilibrium Constants. Appl. Sci. 2024, 14, 5880. https://doi.org/10.3390/app14135880
Suparmin P, Nelwan LO, Mardjan SS, Purwanti N. Development Models of Stoichiometric Thermodynamic Equilibrium for Predicting Gas Composition from Biomass Gasification: Correction Factors for Reaction Equilibrium Constants. Applied Sciences. 2024; 14(13):5880. https://doi.org/10.3390/app14135880
Chicago/Turabian StyleSuparmin, Prayudi, Leopold Oscar Nelwan, Sutrisno S. Mardjan, and Nanik Purwanti. 2024. "Development Models of Stoichiometric Thermodynamic Equilibrium for Predicting Gas Composition from Biomass Gasification: Correction Factors for Reaction Equilibrium Constants" Applied Sciences 14, no. 13: 5880. https://doi.org/10.3390/app14135880
APA StyleSuparmin, P., Nelwan, L. O., Mardjan, S. S., & Purwanti, N. (2024). Development Models of Stoichiometric Thermodynamic Equilibrium for Predicting Gas Composition from Biomass Gasification: Correction Factors for Reaction Equilibrium Constants. Applied Sciences, 14(13), 5880. https://doi.org/10.3390/app14135880





