Study on the Vibration Effects of Cyclic Blasting on Bridge Structures under Construction
Abstract
:1. Introduction
2. Overview of the Zhanma Tian Tunnel Project
3. Numerical Simulation and Analysis of Blasting Vibration
3.1. Model Overview
3.1.1. Construction of the Finite Element Model
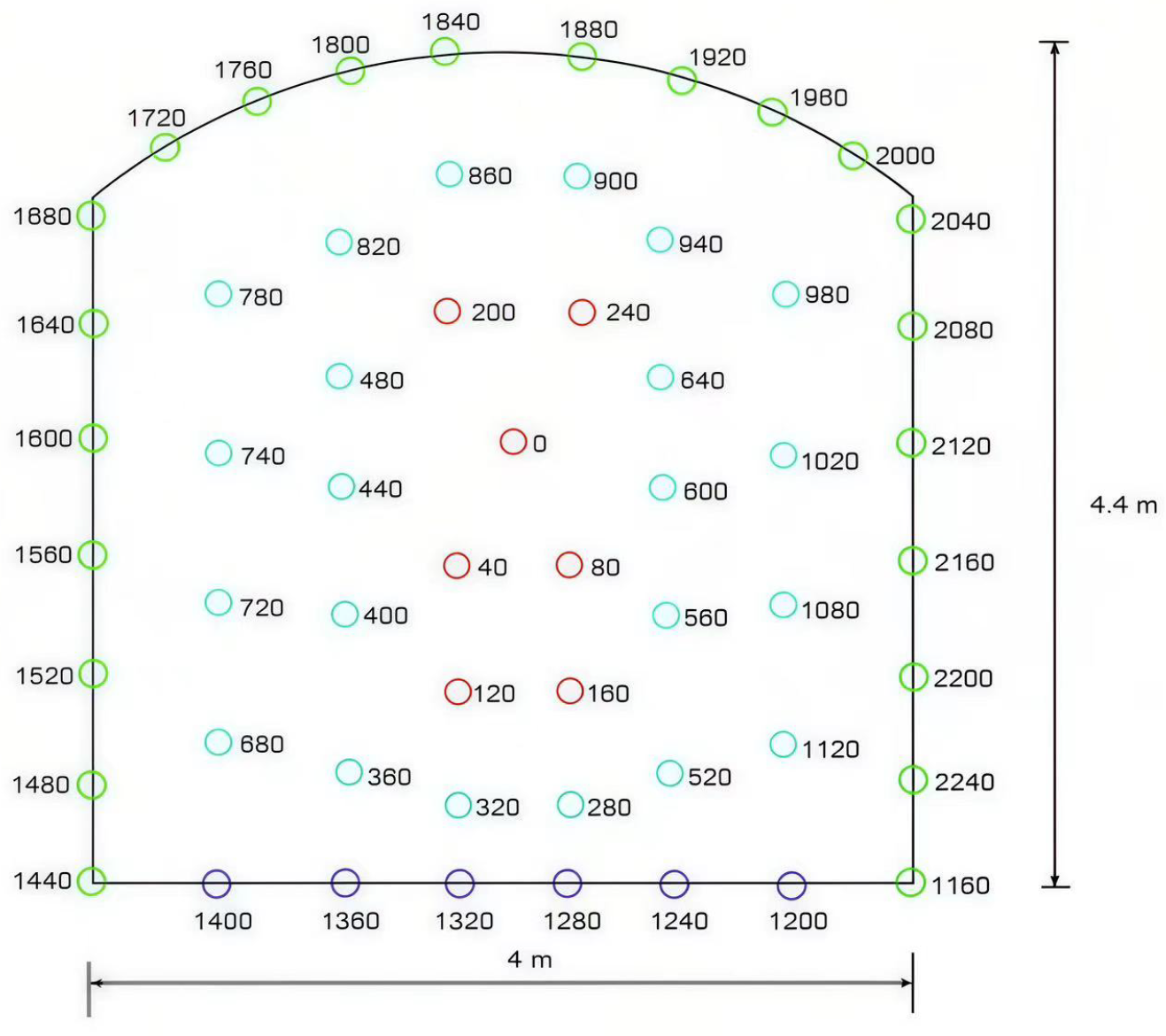
3.1.2. Arrangement of Blast Vibration Monitoring Points
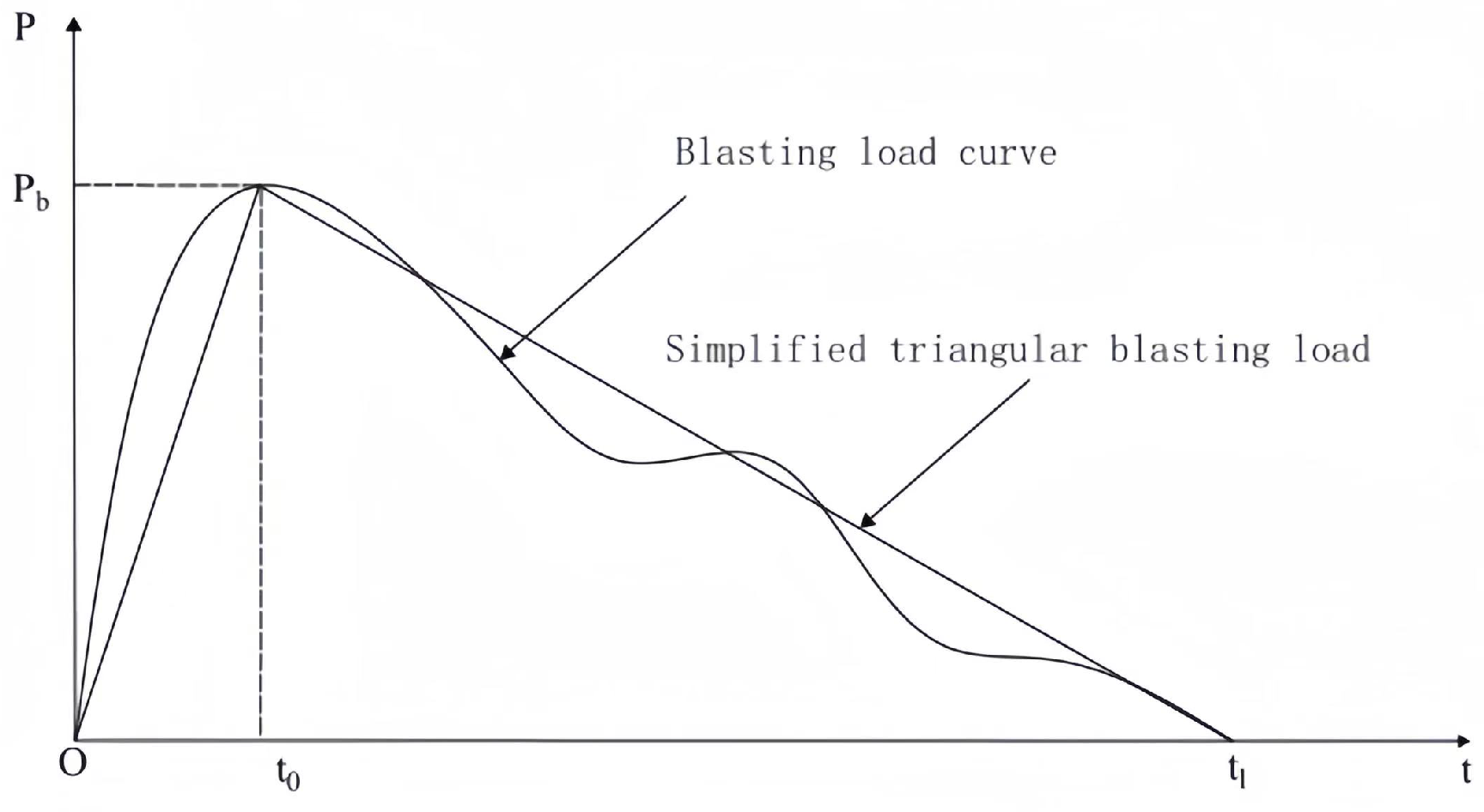
3.2. Blasting Vibration Load
3.3. Comparative Analysis of Numerical Simulation Results
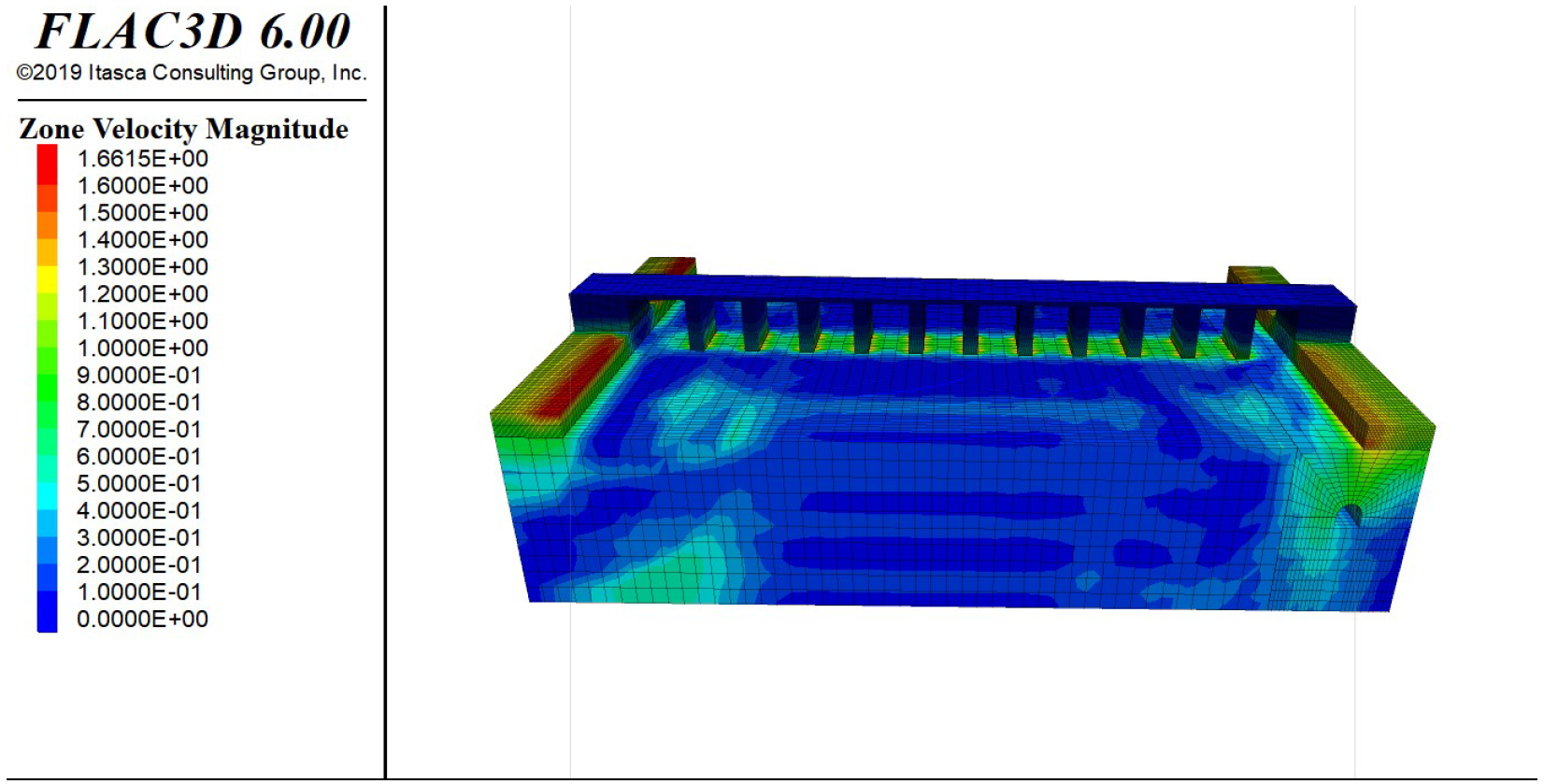
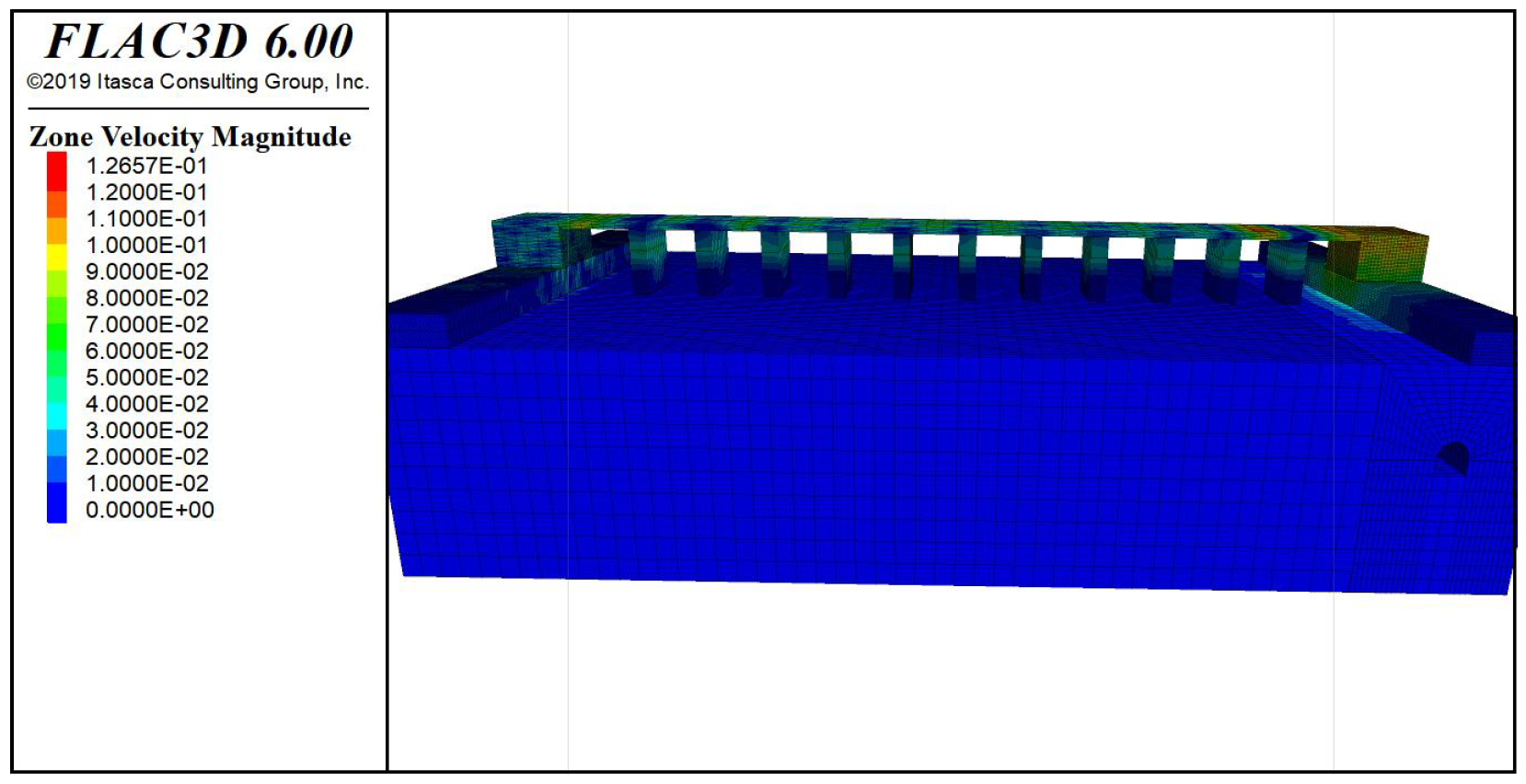
3.3.1. Stress Cloud Map Analysis of the Bridge Model under Vibration Caused by Circular Blasting
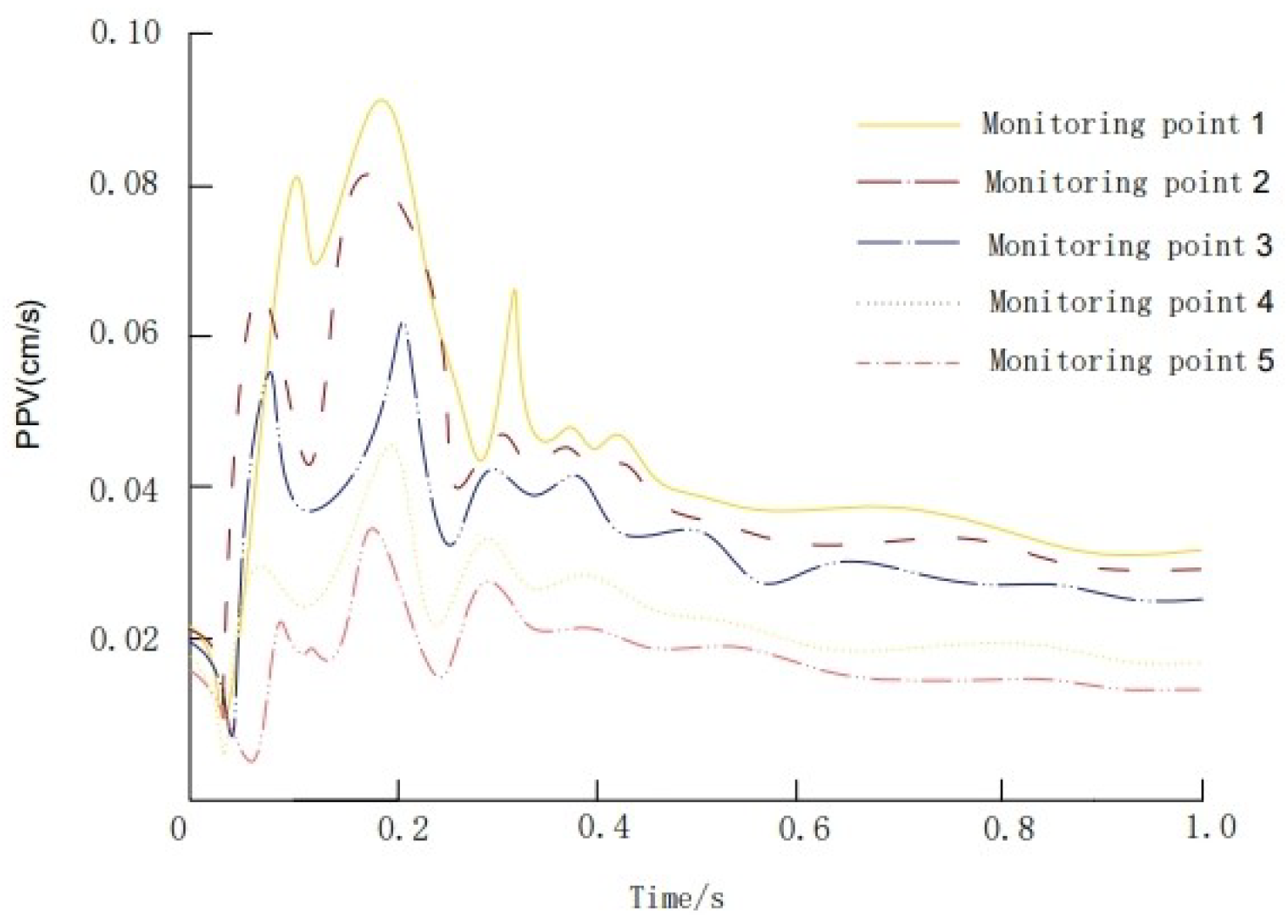
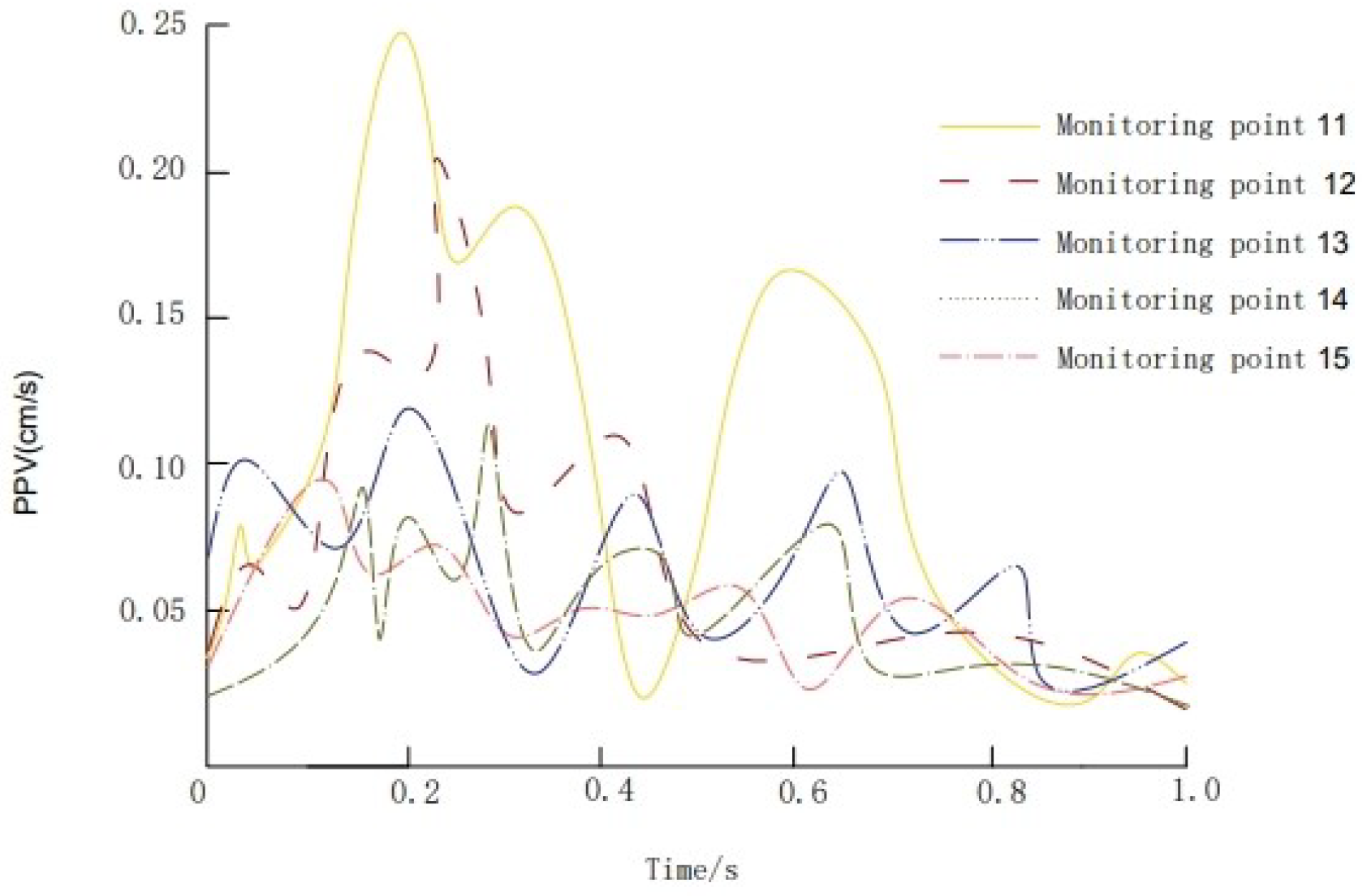
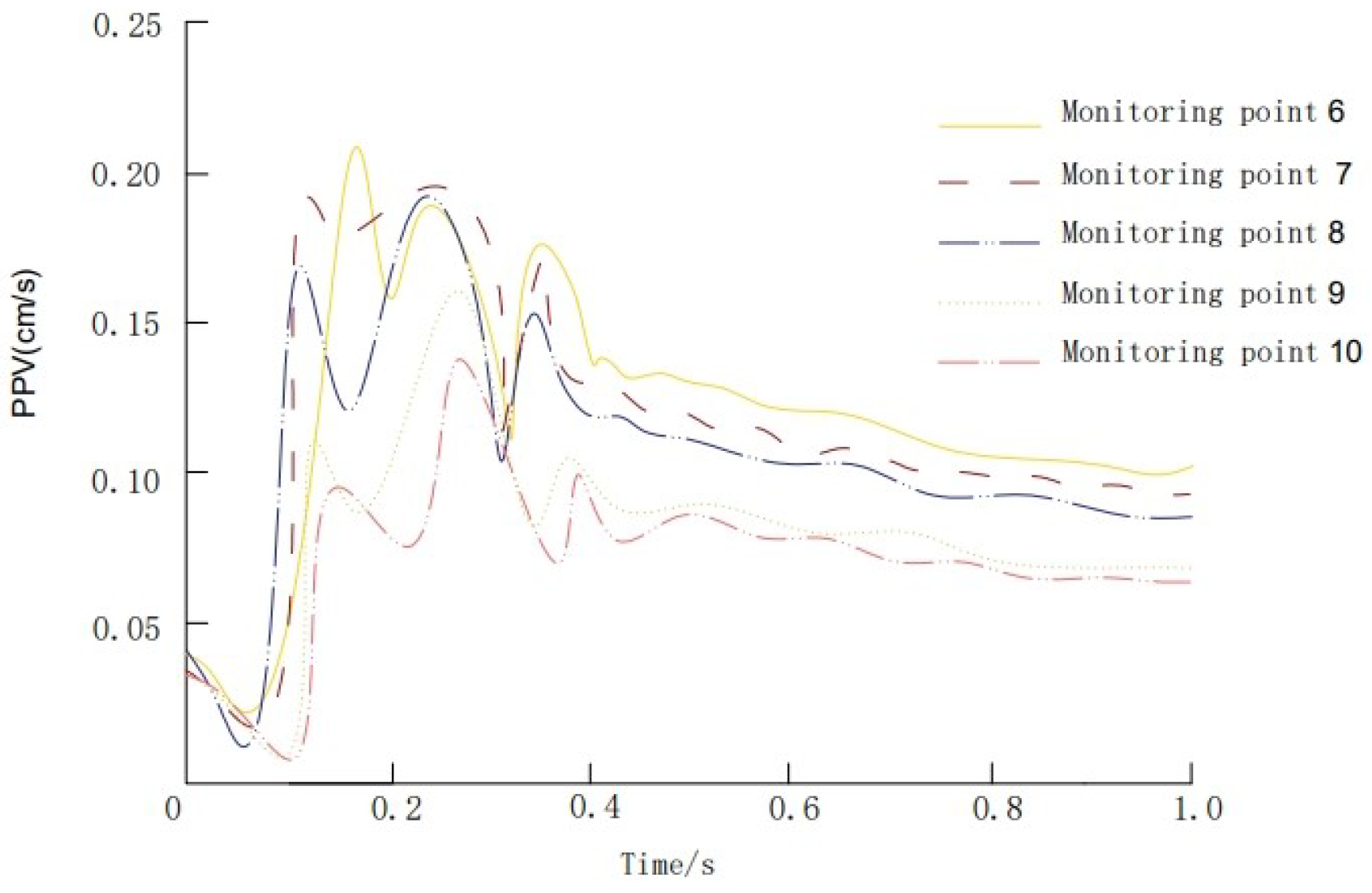
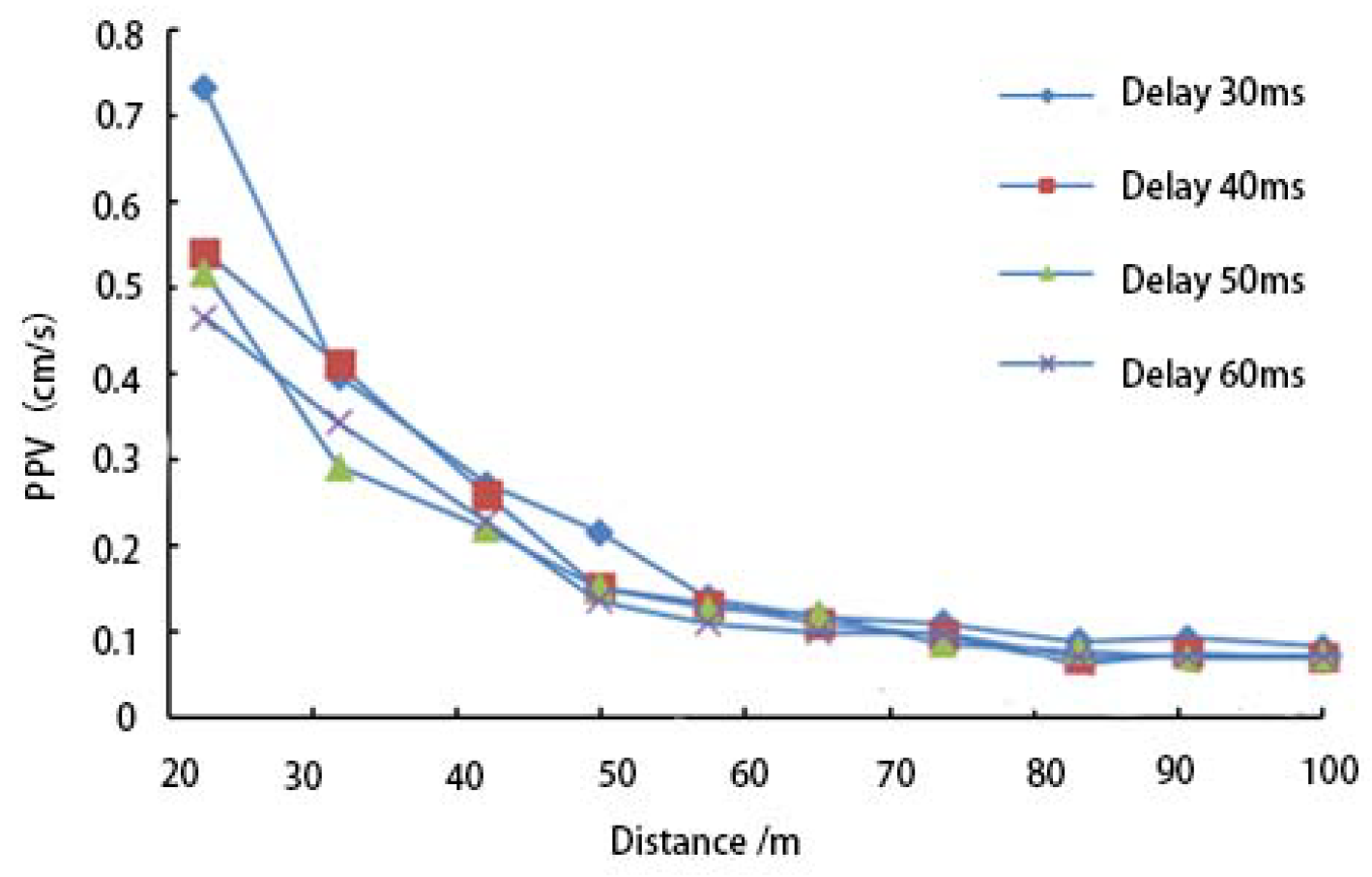
3.3.2. Analysis of the Measured Vibration Velocity of the Bridge under Blasting Conditions
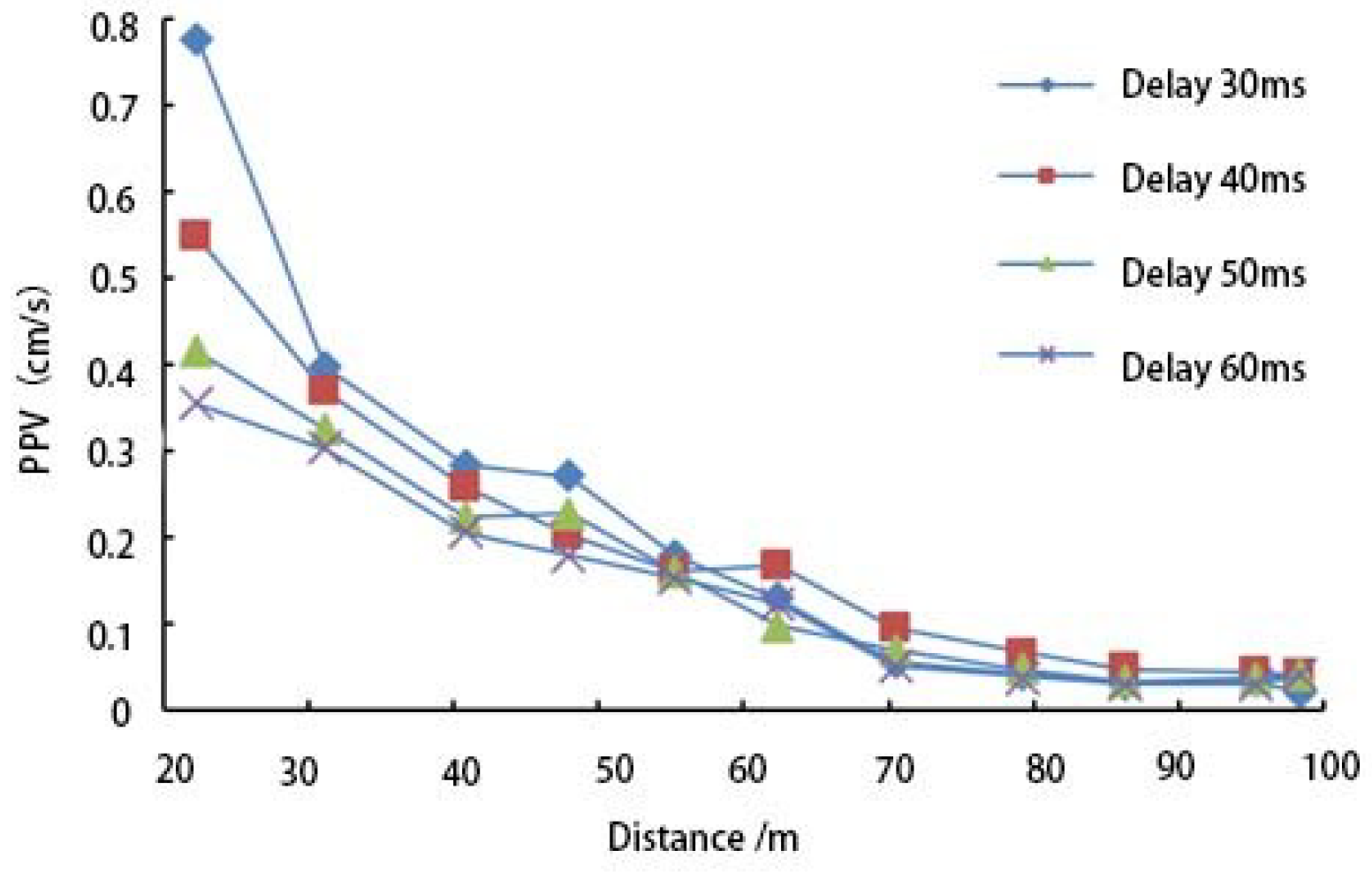
3.3.3. Analysis of Simulated Blasting Vibration Velocity of the Bridge
4. Effect and Optimization of Multiple Blasting Vibrations on Bridges under Construction
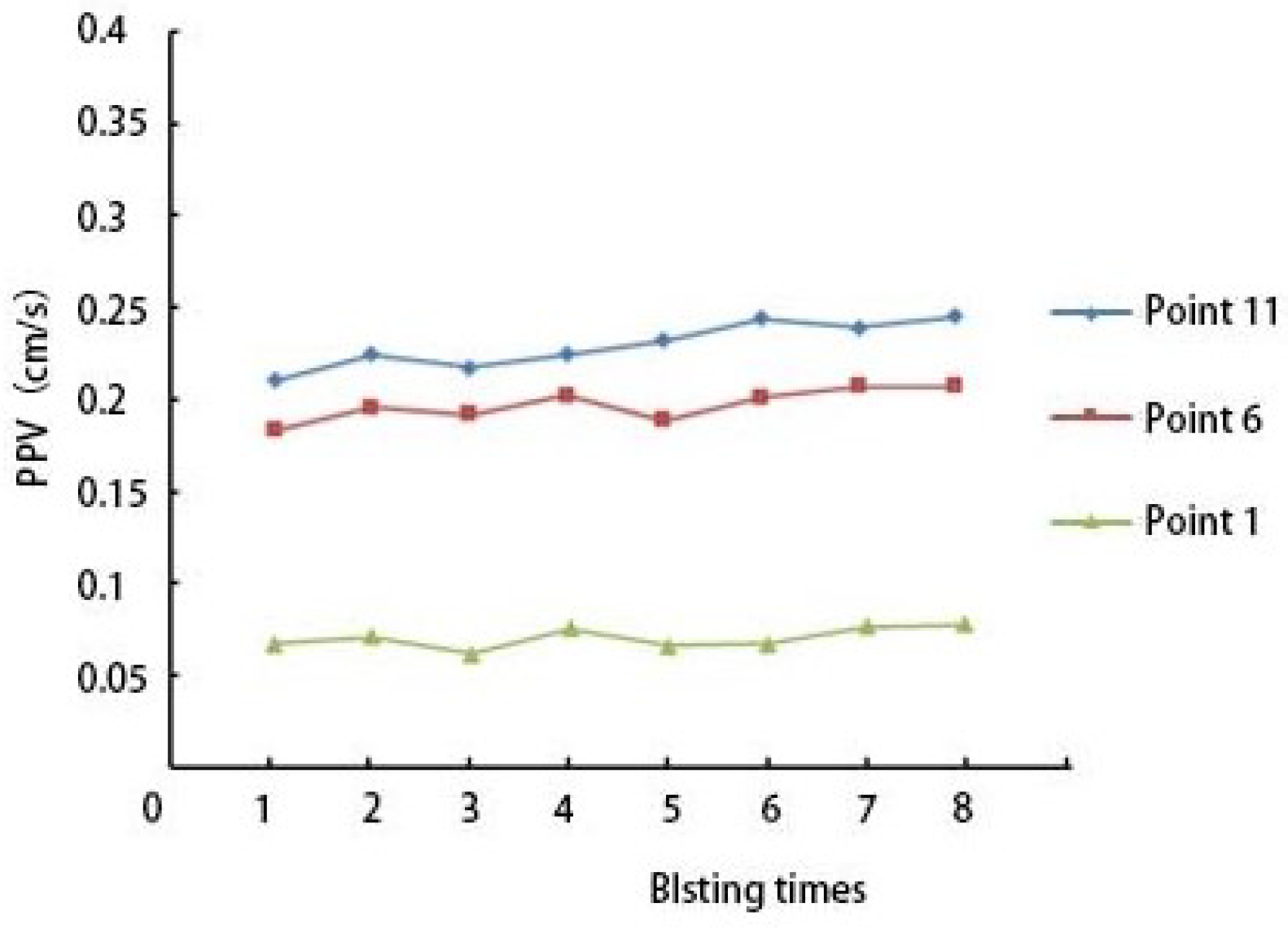
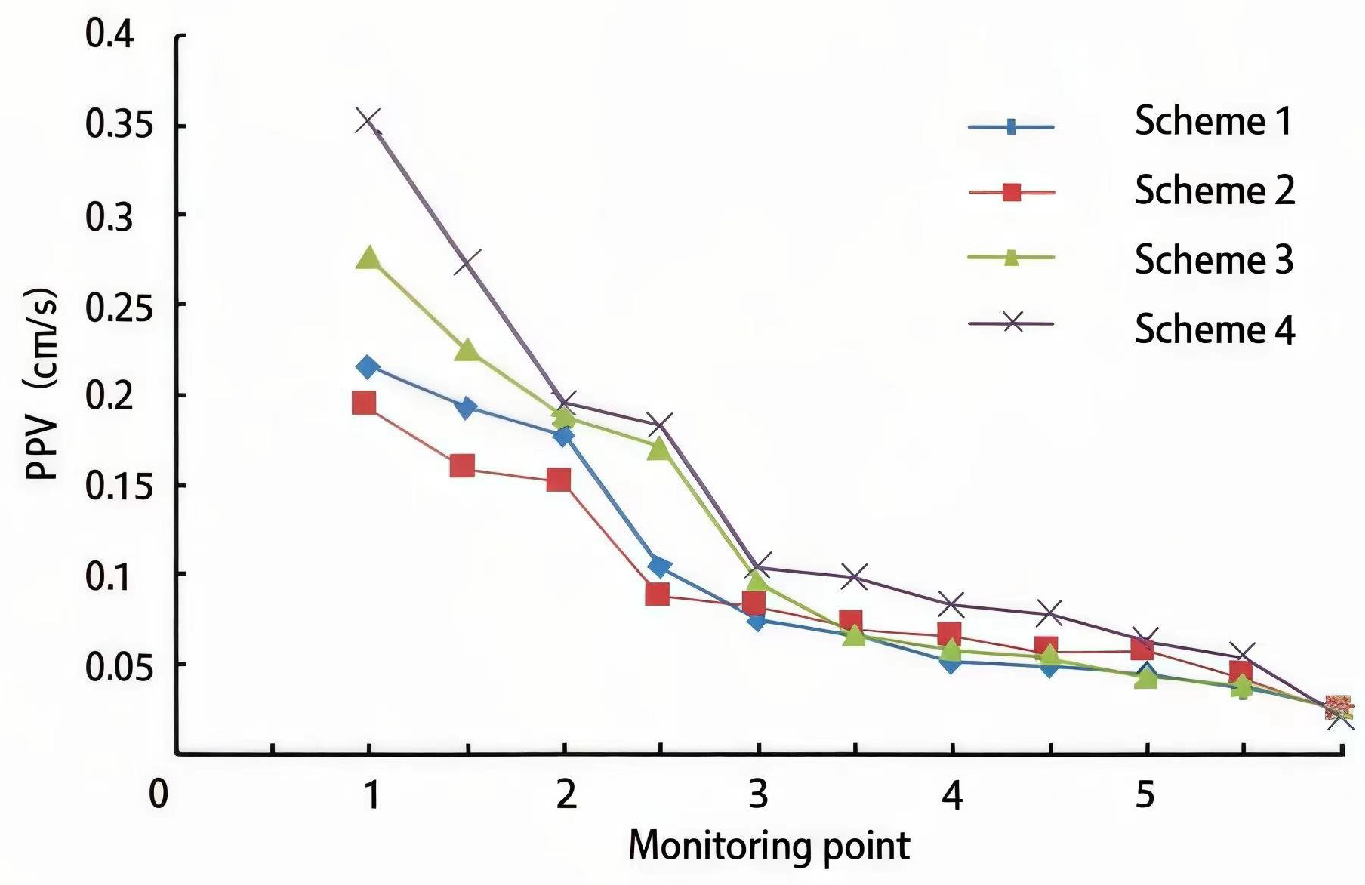
4.1. Relationship between Blasting Vibration Velocity and Blasting Frequency of Bridge Structures
4.2. Optimization and Analysis of Blasting Vibration Scheme
5. Discussion
5.1. Implications of Findings
5.2. Limitations of the Study
5.3. Directions for Future Research
6. Conclusions
- The results show that vibration velocity decreases more rapidly at the bridge deck than at the pier base with increasing distance from the tunnel.
- Peak vibration velocities were recorded at 0.235 cm/s for the bridge deck and 0.081 cm/s for the pier base, with a predicted 0.209 cm/s at the middle column.
- The peak vibration velocity induced by blasting remains within safe limits, and regression analysis indicates that eight daily blasting cycles do not compromise the safety of bridge structures 43 m away.
- The optimized blasting scheme is Scheme 2, with a hole depth of 1.9 m, a linear charge density of 0.33 kg/t, and a blasting delay of 50 ms, making it the optimal blasting scheme for this project. This scheme ensures both construction efficiency and compliance with safety standards.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, G.; Feng, X.-T.; Jiang, Q.; Yao, Z.; Li, S. In situ observation of spalling process of intact rock mass at large cavern excavation. Eng. Geol. 2017, 226, 52–69. [Google Scholar] [CrossRef]
- Wang, S.; Sloan, S.; Sheng, D.; Tang, C. Numerical analysis of the failure process around a circular opening in rock. Comput. Geotech. 2012, 39, 8–16. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, L.; Chen, S.; Sun, J.; Yang, J. The spatiotemporal distribution law of microseismic events and rockburst characteristics of the deeply buried tunnel group. Energies 2018, 11, 3257. [Google Scholar] [CrossRef]
- Li, H.; Shu, D. Influential factors analysis of blasting vibration attenuation law. J. Wuhan. Univ. Technol. 2005, 38, 79–82. [Google Scholar]
- Ma, G.; Hao, H.; Zhou, Y. Assessment of structure damage to blasting induced ground motions. Eng. Struct. 2000, 22, 1378–1389. [Google Scholar] [CrossRef]
- Lu, W.B.; Luo, Y.; Chen, M.; Shu, D.Q. An introduction to chinese safety regulations for blasting vibration. Environ. Earth. Sci. 2012, 67, 1951–1959. [Google Scholar] [CrossRef]
- Bayraktar, A.; Altunişik, A.C.; Özcan, M. Safety assessment of structures for near-field blast-induced ground excitations using operational modal analysis. Soil. Dyn. Earthq. Eng. 2012, 39, 23–36. [Google Scholar] [CrossRef]
- Bayraktar, A.; Türker, T.; Altunişik, A.C.; Sevim, B. Evaluation of blast effects on reinforced concrete buildings considering operational modal analysis results. Soil. Dyn. Earthq. Eng. 2010, 30, 310–319. [Google Scholar] [CrossRef]
- Dhakal, R.P.; Pan, T.-C. Response characteristics of structures subjected to blasting-induced ground motion. Int. J. Impact Eng. 2003, 28, 813–828. [Google Scholar] [CrossRef]
- Li, B.; Rong, H.-C.; Pan, T.-C. Drift-controlled design of reinforced concrete frame structures under distant blast conditions—Part i: Theoretical basis. Int. J. Impact. Eng. 2007, 34, 743–754. [Google Scholar] [CrossRef]
- Li, B.; Rong, H.-C.; Pan, T.-C. Drift-controlled design of reinforced concrete frame structures under distant blast conditions—Part ii: Implementation and evaluation. Int. J. Impact. Eng. 2007, 34, 755–770. [Google Scholar] [CrossRef]
- Ramulu, M.; Chakraborty, A.; Sitharam, T. Damage assessment of basaltic rock mass due to repeated blasting in a railway tunnelling project—A case study. Tunn. Undergr. Sp. Technol. 2009, 24, 208–221. [Google Scholar] [CrossRef]
- Huo, X.S.; Wong, L.U. Experimental study of early-age behavior of high performance concrete deck slabs under different curing methods. Constr. Build. Mater. Ater. 2006, 20, 1049–1056. [Google Scholar] [CrossRef]
- Wang, Z.W.; Li, X.B.; Peng, K.; Xie, J.F. Impact of blasting parameters on vibration signal spectrum: Determination and statistical evidence. Tunn. Undergr. Sp. Technol. 2015, 48, 94–100. [Google Scholar] [CrossRef]
- He, R.; Jiang, N.; Li, D.W.; Qi, J.F. Dynamic response characteristic of building structure under blasting vibration of underneath tunnel. Shock. Vib. 2022, 2022, 9980665. [Google Scholar] [CrossRef]
- Guan, X.; Yang, N.; Zhang, W.; Li, M.; Liu, Z.; Wang, X.; Zhang, S. Vibration response and failure modes analysis of the temporary support structure under blasting excavation of tunnels. Eng. Fail. Anal. 2022, 136, 106188. [Google Scholar] [CrossRef]
- Deng, X.; Wang, J.; Wang, R.; Liu, Q. Influence of blasting vibrations generated by tunnel construction on an existing road. Int. J. Civ. Eng. 2020, 18, 1381–1393. [Google Scholar] [CrossRef]
- Yue, H.Z.; Yu, C.; Li, H.B.; Zhou, C.B.; Chen, S.H.; Shao, Z.S. The Effect of Blast-Hole Arrangement, Delay Time, and Decoupling Charge on Rock Damage and Vibration Attenuation in Multihole Blasting. Shock. Vib. 2022, 2022, 2110160. [Google Scholar] [CrossRef]
- He, L.; Kong, D.; Lei, Z. Research on vibration propagation law and dynamic effect of bench blasting. Mathematics 2022, 10, 2951. [Google Scholar] [CrossRef]
- Chen, F.; He, G.; Dong, S.; Zhao, S.; Shi, L.; Liu, X.; Zhang, B.; Qi, N.; Deng, S.; Zhang, J. Space-time effect prediction of blasting vibration based on intelligent automatic blasting vibration monitoring system. Appl. Sci. 2021, 12, 12. [Google Scholar] [CrossRef]
- Dai, C.; Sui, H.; Ma, C. Study on the vibration effect of short footage blasting load on surrounding rock-support structure of tunnel. Shock. Vib. 2020, 2020, 8829349. [Google Scholar] [CrossRef]
- Lai, J.; Wang, K. Vibration response characteristics of the cross tunnel structure. Shock. Vib. 2016, 2016, 9524206. [Google Scholar] [CrossRef]
- Huang, D.; Cui, S.; Li, X. Wavelet packet analysis of blasting vibration signal of mountain tunnel. Soil. Dyn. Earthq. Eng. 2019, 117, 72–80. [Google Scholar] [CrossRef]
- Wan, S.; Huang, J.; Luo, Y.; Li, X.; Pu, Q. Research on cumulative damage characteristics of rock anchor beam concrete supporting structure by blasting vibration of underground powerhouse. Shock. Vib. 2021, 2021, 8887713. [Google Scholar] [CrossRef]
- Yao, Q.; Yang, X.G.; Chen, X.Z.; Li, H.T. Numerical simulation of dynamic response of large underground powerhouse subjected to blasting vibration. J. Vib. Control. 2014, 33, 66–76. [Google Scholar]
- Geniş, M. Assessment of the dynamic stability of the portals of the dorukhan tunnel using numerical analysis. Int. J. Rock. Mech. Min. 2010, 47, 1231–1241. [Google Scholar] [CrossRef]
- Zhu, B.; Jiang, N.; Zhou, C.; Luo, X.; Li, H.; Chang, X.; Xia, Y. Dynamic interaction of the pipe-soil subject to underground blasting excavation vibration in an urban soil-rock stratum. Tunn. Undergr. Sp. Technol. 2022, 129, 104700. [Google Scholar] [CrossRef]
- Li, J.; Hao, H. A simplified numerical method for blast induced structural response analysis. Int. J. Prot. Struct. 2014, 5, 323–348. [Google Scholar] [CrossRef]
- Li, Z.; Wu, S.; Cheng, Z.; Jiang, Y. Numerical investigation of the dynamic responses and damage of linings subjected to violent gas explosions inside highway tunnels. Shock. Vib. 2018, 2018, 2792043. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Li, D.; Wu, L.; Gao, W.; Zhou, H. Numerical simulation of the effect of empty hole between adjacent blast holes in the perforation process of blasting. J. Intell. Fuzzy. Syst. 2019, 37, 3137–3148. [Google Scholar] [CrossRef]









| Material | Density/(g/cm3) | Elastic Modulus/MPa | Poisson’s Ratio | Tensile Stress/MPa |
|---|---|---|---|---|
| Dolomite | 2.8 | 60 | 0.25 | 80,250 |
| Reinforced concrete | 2.48 | 25.525 | 0.2 | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, Y.; Chi, E. Study on the Vibration Effects of Cyclic Blasting on Bridge Structures under Construction. Appl. Sci. 2024, 14, 5940. https://doi.org/10.3390/app14135940
Che Y, Chi E. Study on the Vibration Effects of Cyclic Blasting on Bridge Structures under Construction. Applied Sciences. 2024; 14(13):5940. https://doi.org/10.3390/app14135940
Chicago/Turabian StyleChe, Yunhao, and Enan Chi. 2024. "Study on the Vibration Effects of Cyclic Blasting on Bridge Structures under Construction" Applied Sciences 14, no. 13: 5940. https://doi.org/10.3390/app14135940
APA StyleChe, Y., & Chi, E. (2024). Study on the Vibration Effects of Cyclic Blasting on Bridge Structures under Construction. Applied Sciences, 14(13), 5940. https://doi.org/10.3390/app14135940









