Research on the Reasonable Width of Coal Pillar Driving along Goaf under Thick Hard Roof
Abstract
:1. Introduction
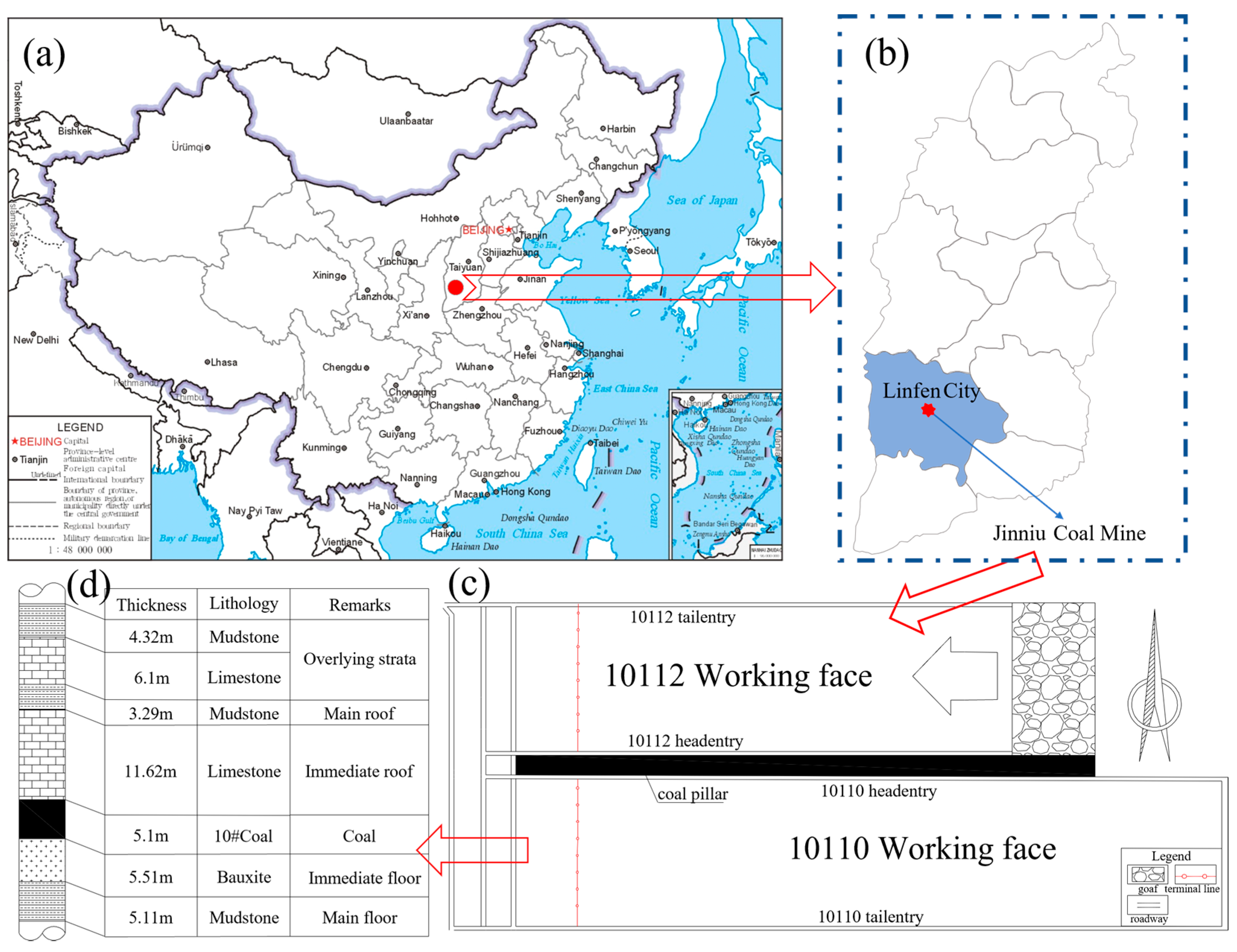
2. Project Overview
3. Method
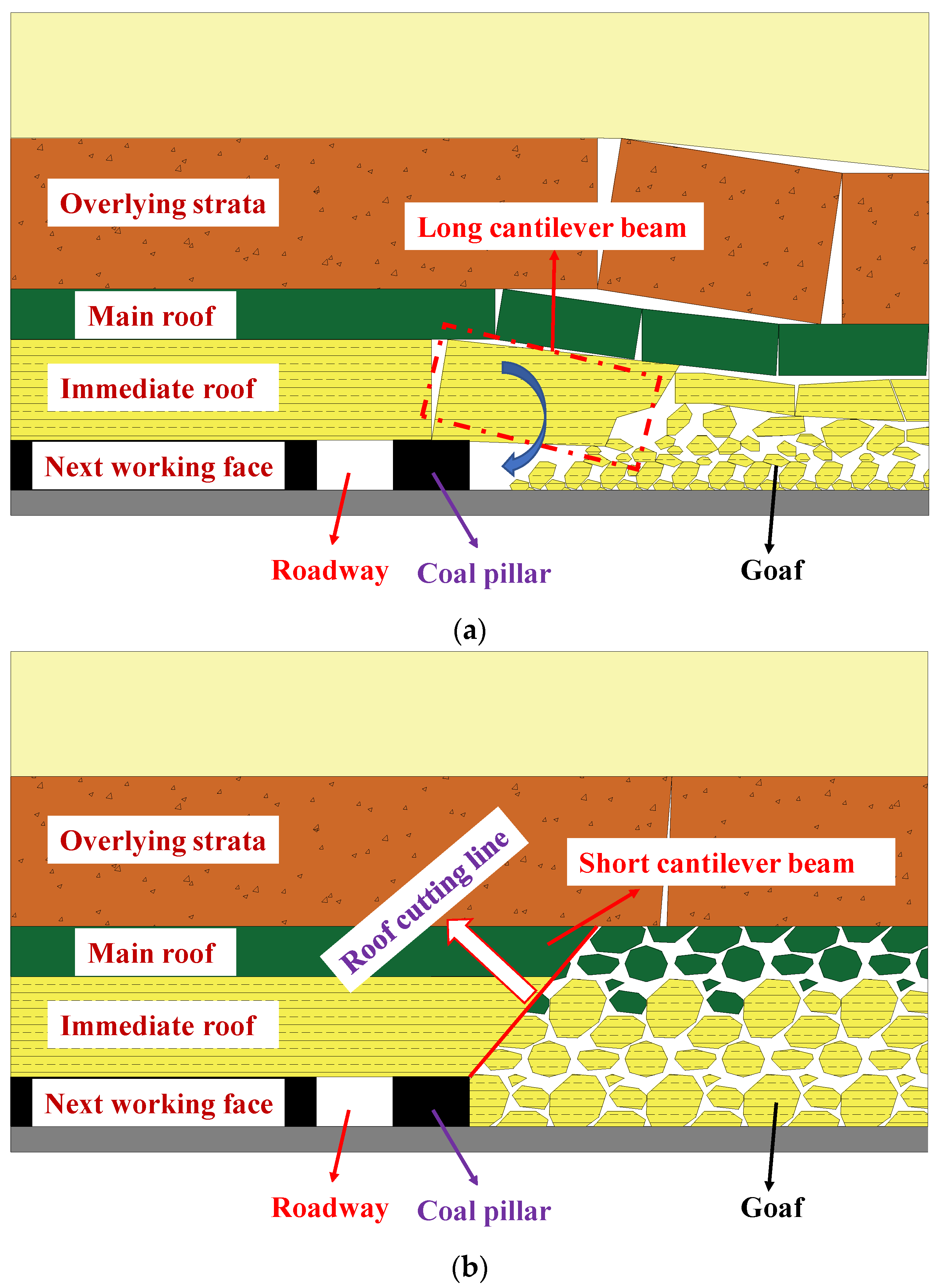
3.1. Analysis of Roof Cutting Pressure Relief in the Goaf
3.2. Theoretical Calculation of the Parameters of the Roof Cutting Pressure Relief
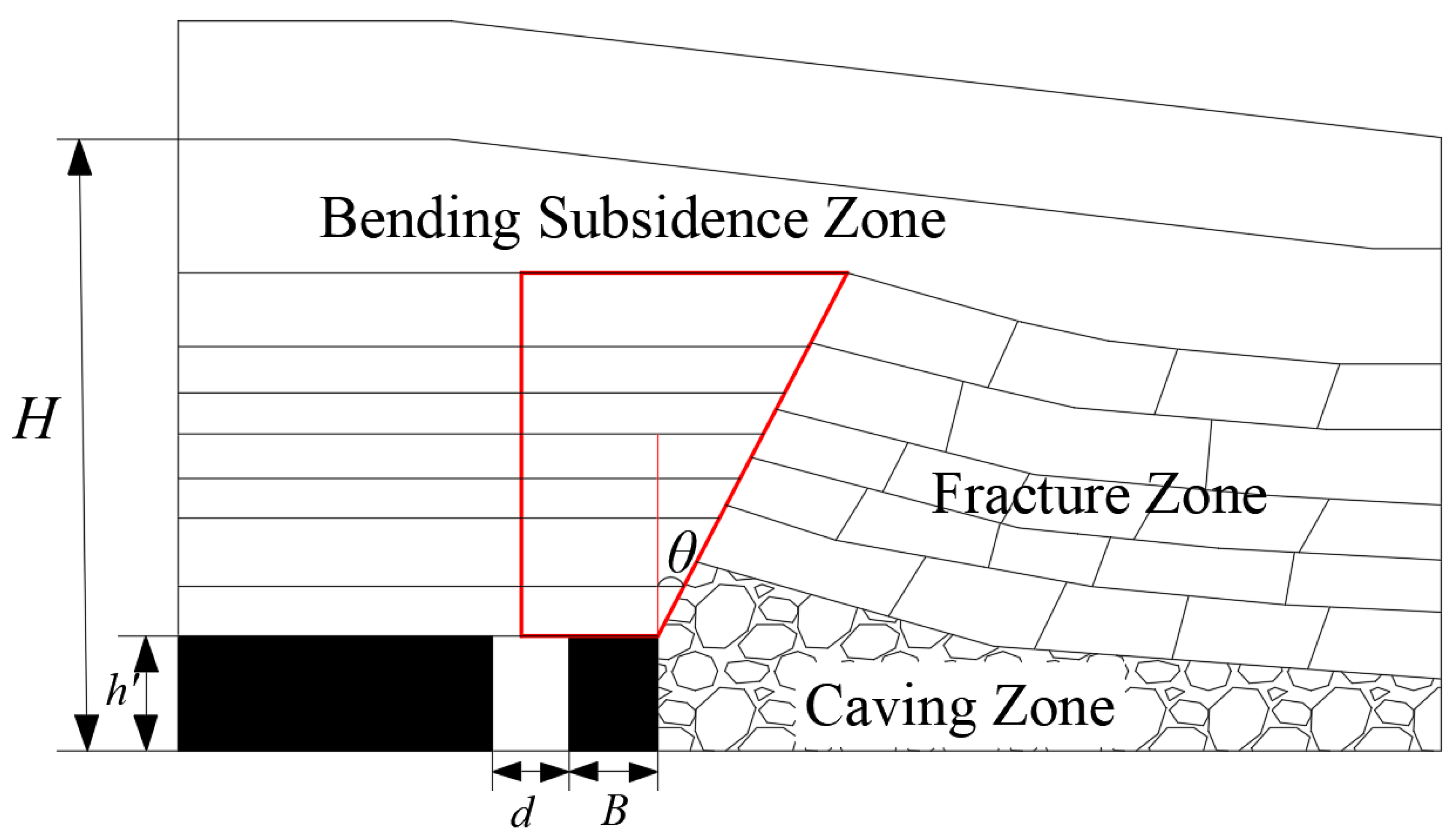
3.2.1. Theoretical Calculation of Roof Cutting Depth
3.2.2. Theoretical Calculation of Roof Cutting Angle
3.3. Theoretical Calculation of Coal Pillar Width under Thick Hard Roof
3.4. Numerical Simulation Program
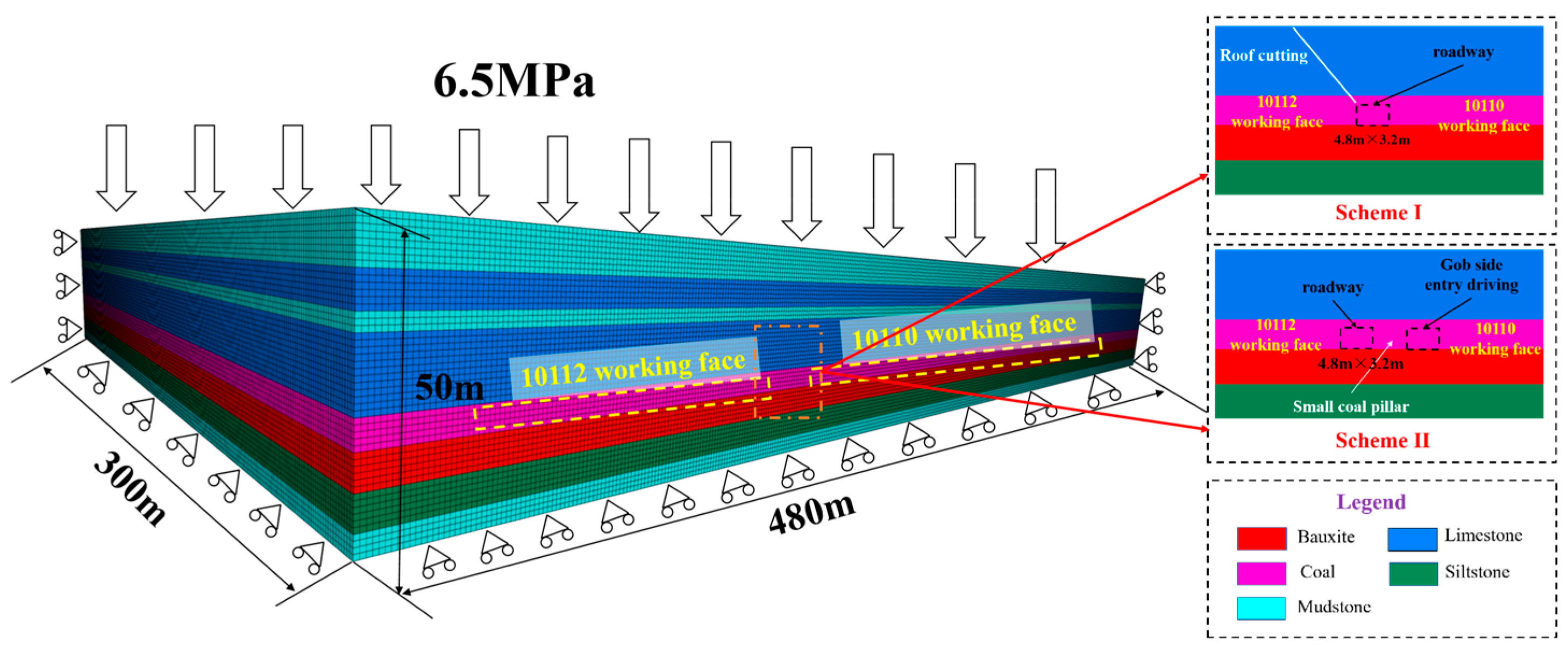
3.4.1. Establishment of Numerical Model
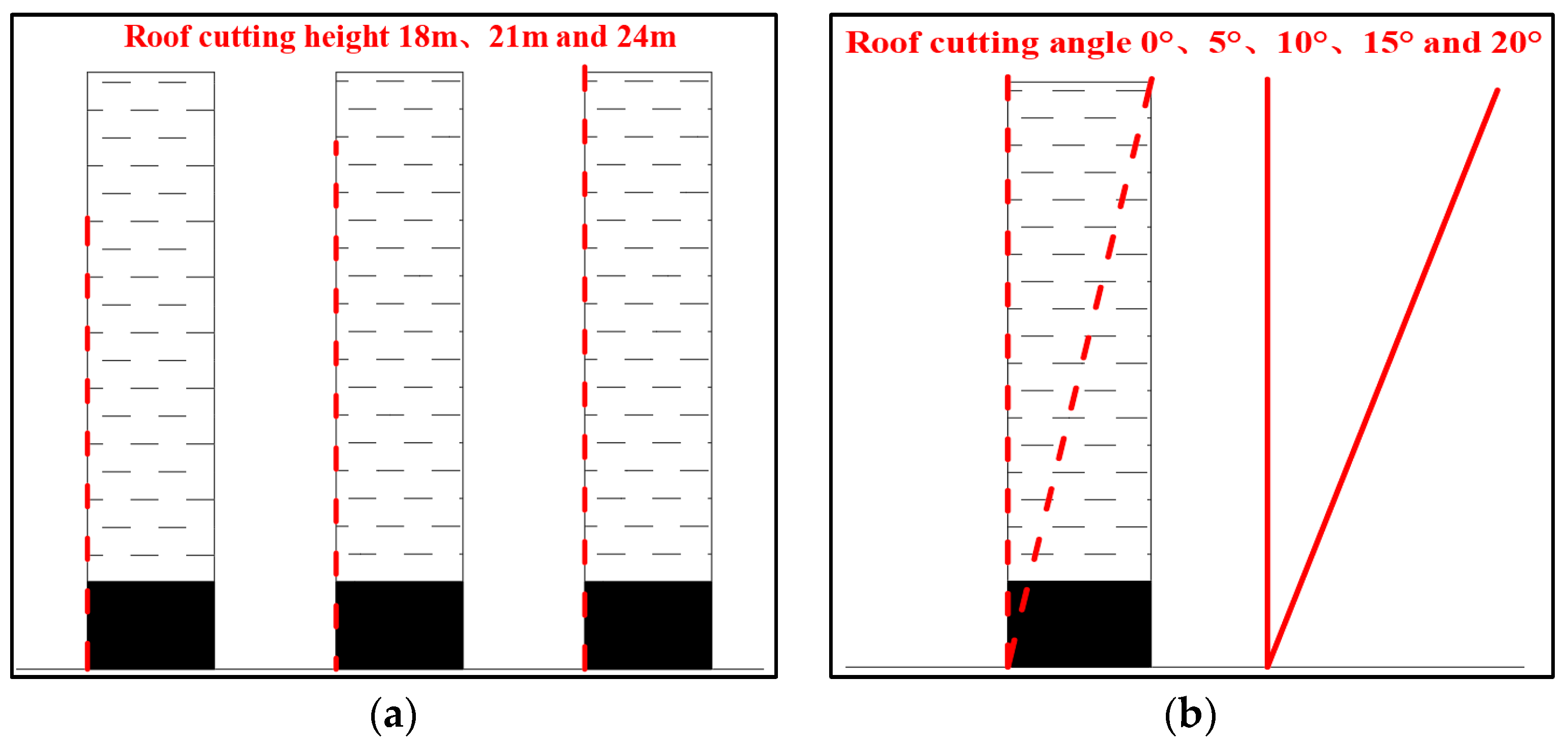
3.4.2. Numerical Simulation Scheme
4. Results and Discussion
4.1. Numerical Simulation of Roof Cutting Parameters
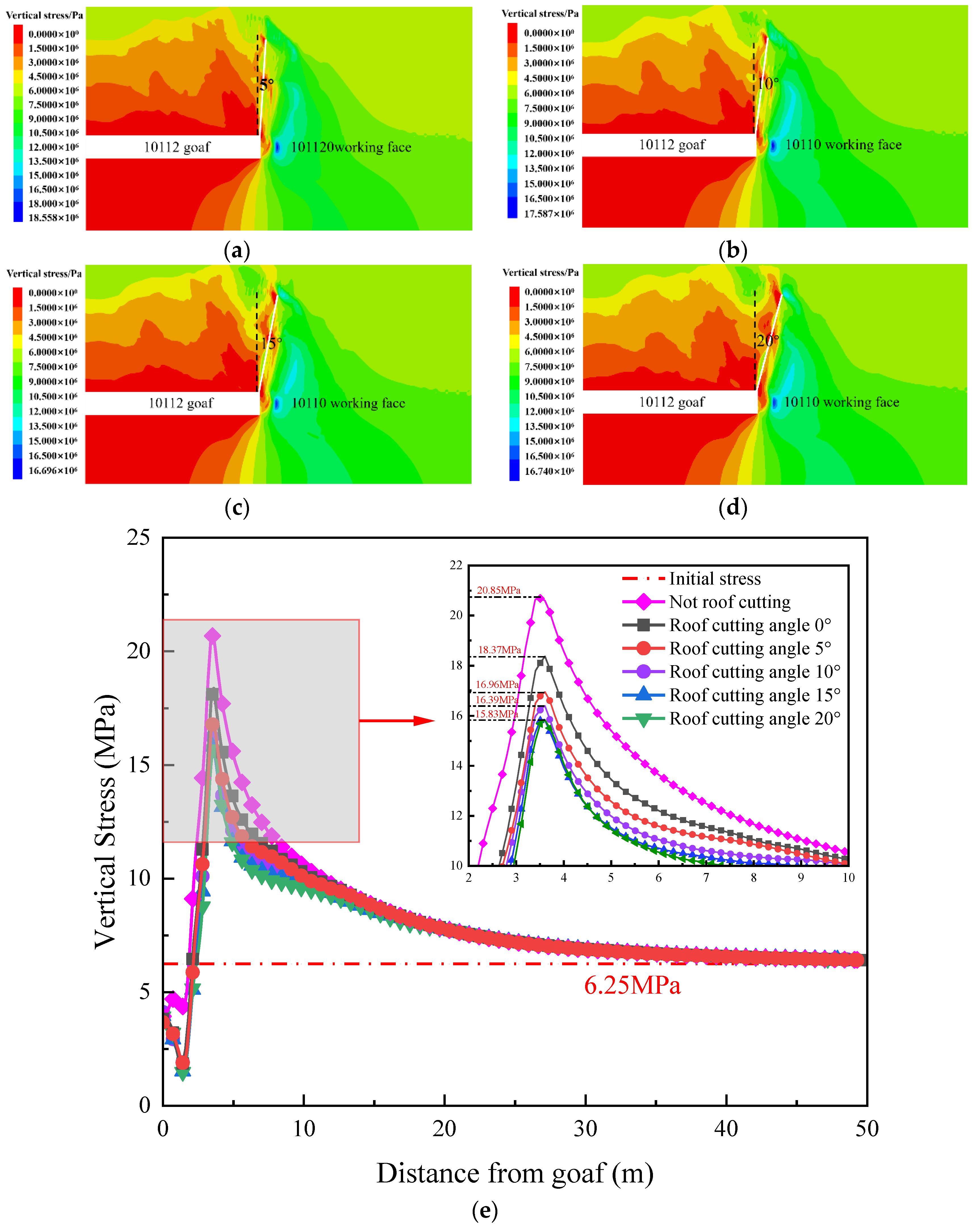
4.1.1. Stress Distribution along Goaf under Different Roof Cutting Heights
4.1.2. Stress Distribution along Goaf under Different Roof-Cutting Angles
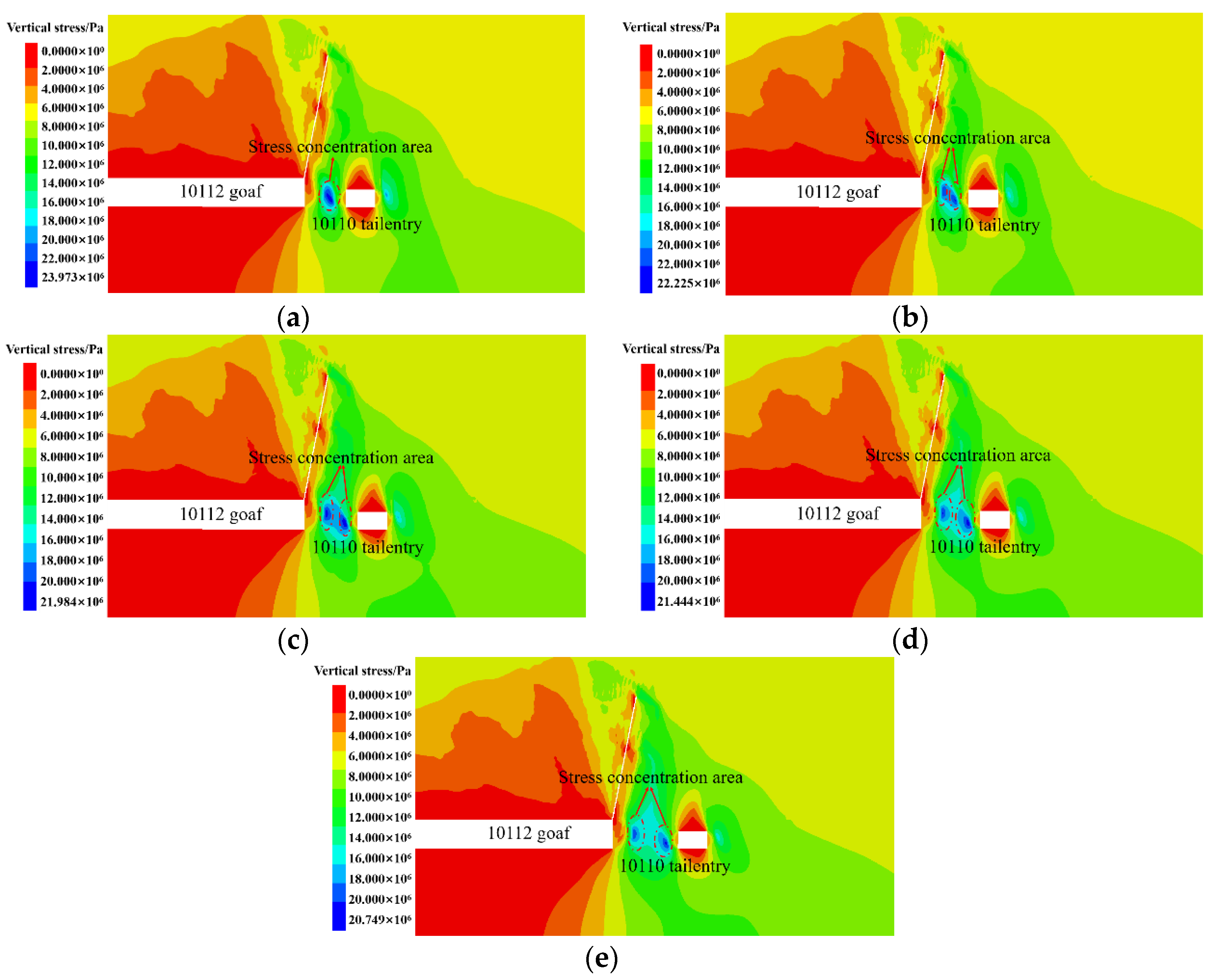
4.2. Numerical Simulation Analysis of Coal Pillar Width
4.2.1. Characteristics of the Stress Distribution along the Goaf
4.2.2. Characteristics of the Displacement Distribution along Goaf
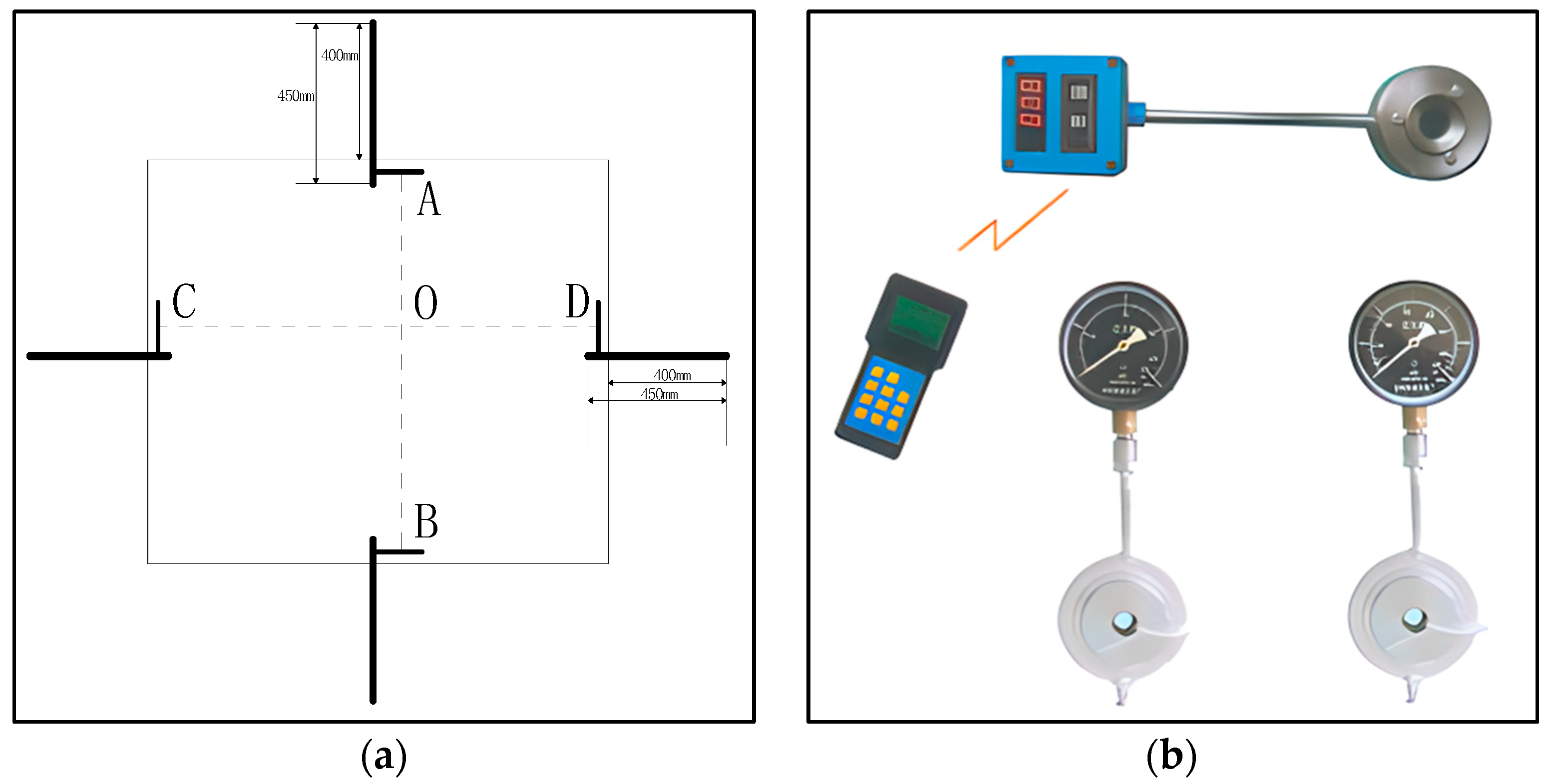
4.3. On-Site Industrial Experiments
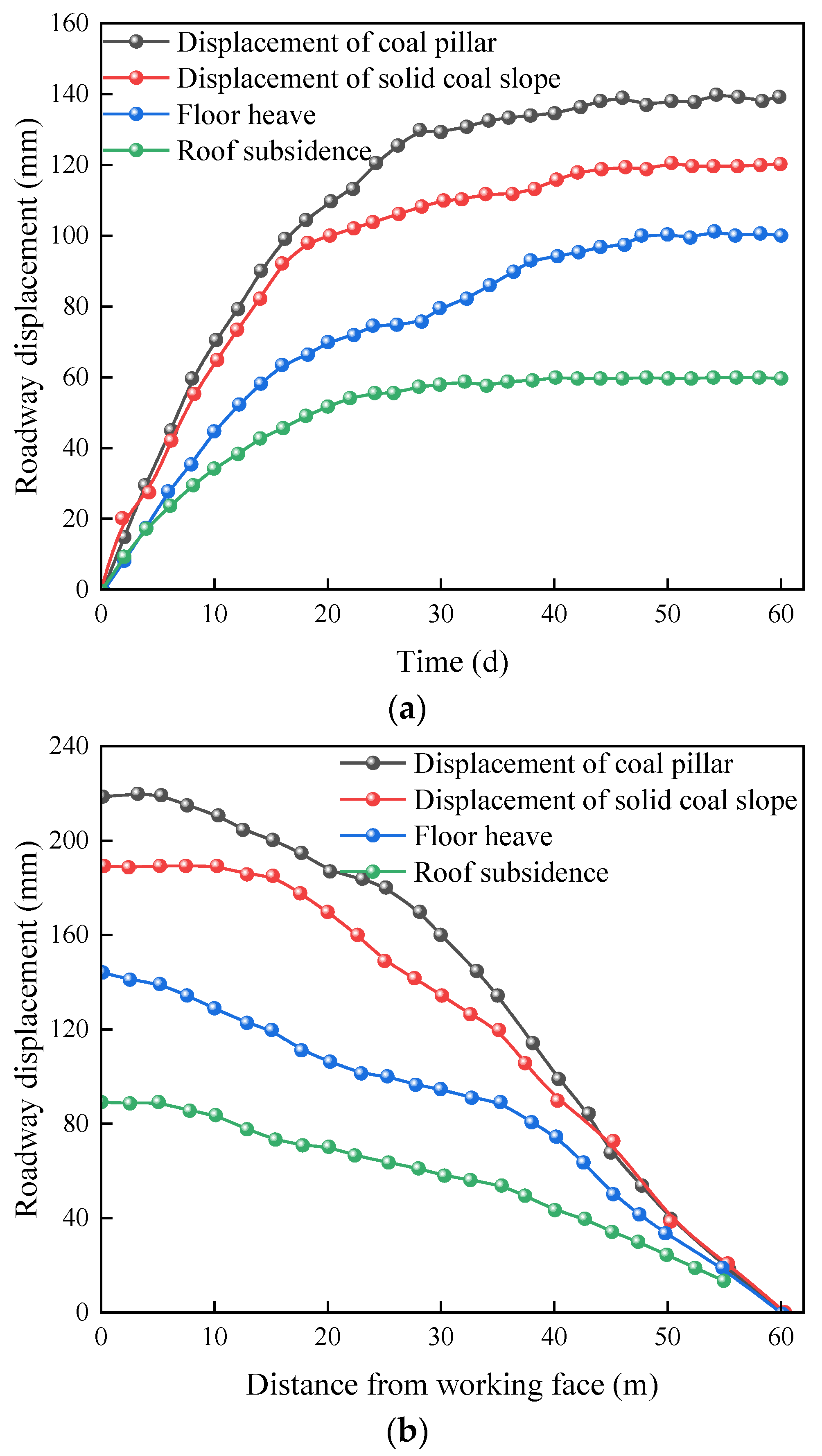
4.3.1. Roadway Surface Displacement Observation Result
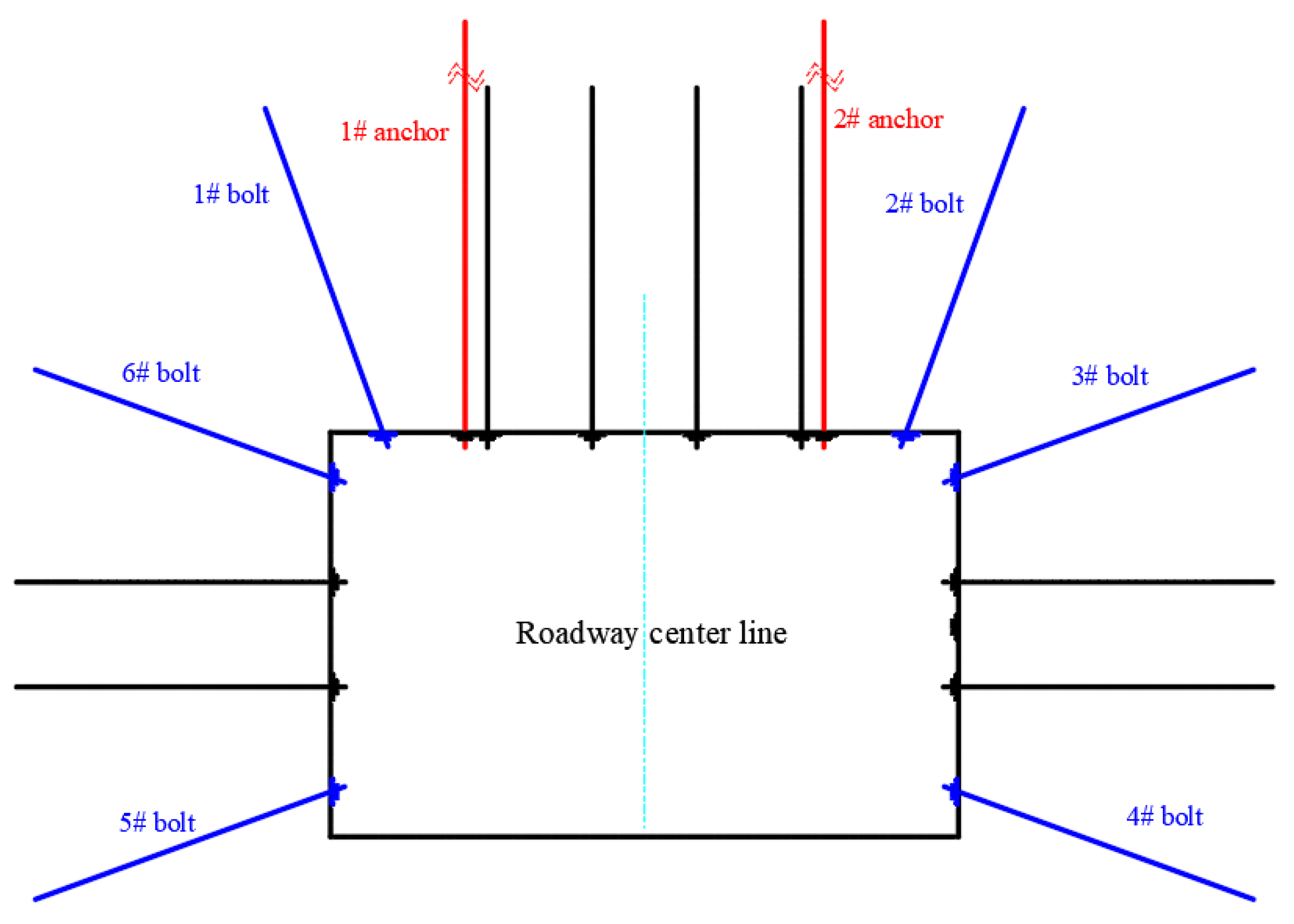
4.3.2. Anchor (Bolt) Stress Monitoring Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, W.; Deng, K.; Zou, Y. Research status and main issues of strip mining in China. Coal Sci. Technol. 2004, 32, 7–11. [Google Scholar]
- Cong, L.; Weng, M.; Qin, Z.; Feng, M. Instability mechanism and prevention of wide coal pillar with three strong stress disturbances under hard roof. J. China Coal Soc. 2022, 47, 125–134. [Google Scholar]
- Hao, R. Determination of reasonable size of coal pillar in longwall face. Shanxi Coking Coal Sci. Technol. 2012, 36, 20–22+29. [Google Scholar]
- Huang, Q.; Qian, M.; Shi, P. Structural analysis of cyclic pressurization of old roofs in shallow buried coal seams. J. China Coal Soc. 1999, 581–585. [Google Scholar]
- Dong, S.; Li, W. Influence analysis of principal stress deflection on fault stability based on theory of internal and external stress fields. Saf. Coal Mines 2021, 52, 213–219. [Google Scholar]
- Song, Z.; Hao, J.; Shi, Y.; Tang, J.; Liu, J. An overview of connotation and development of practical ground pressure control theory. J. Shandong Univ. Sci. Technol. (Nat. Sci.) 2019, 38, 1–15. [Google Scholar]
- Jia, X.; Zhai, Y. A review of the theory and practice of thin-sheet mine pressure in quarries. Mine Press. Roof Manag. 1999, 22–25, 238. [Google Scholar]
- Jia, X.; Li, H.; Wang, Q.; Jia, R. Application of thin-slab mining pressure theory to roof coal workings. J. Taiyuan Univ. Technol. 1999, 30, 179–183. [Google Scholar]
- Ma, R. Research on Reasonable Narrow Width of Coal Pillar for Decompression and Anticlimbing along the Hollow Tunnel. Master’s Thesis, Guizhou University, Guiyang, China, 2021. [Google Scholar]
- Zhan, Z. Study on Reasonable Reserved Coal Pillar Width for Gob Side Entry Driving by Roof Cutting and Pressure Relief in Selian No.2 Mine. Master’s Thesis, Anhui University of Technology, Ma’anshan City, China, 2021. [Google Scholar]
- Bo, J.; Wang, W.; Hou, C.; Huang, H. Research on the control mechanism and support technology of the perimeter rock in the open-cut tunnel. J. China Coal Soc. 2000, 478–481. [Google Scholar] [CrossRef]
- Xu, L.; Li, M.W.; Guo, L.; Xiao, T.Q.; Liu, H.L.; Elmo, D. Critical parameters and engineering applications of cut-through critical layer depressurization along a hollow tunnel. J. Min. Saf. Eng. 2023, 40, 91–100. [Google Scholar]
- Yang, Z.; Liu, C.; Tang, S.; Dou, L.; Cao, J. Rock burst mechanism analysis in an advanced segment of gob-side entry under different dip angles of the seam and prevention technology. Int. J. Min. Sci. Technol. 2018, 28, 891–899. [Google Scholar] [CrossRef]
- Zha, W.; Shi, H.; Liu, S.; Kang, C. Surrounding rock control of gob-side entry driving with narrow coal pillar and roadway side sealing technology in Yangliu Coal Mine. Int. J. Min. Sci. Technol. 2017, 27, 819–823. [Google Scholar] [CrossRef]
- Xu, C.; Yuan, L.; Cheng, Y.; Wang, K.; Zhou, A.; Shu, L. Square-form structure failure model of mining-affected hard rock strata: Theoretical derivation, application and verification. Environ. Earth Sci. 2016, 75, 1180. [Google Scholar] [CrossRef]
- Chen, B.; Liu, C.; Wang, B. A case study of the periodic fracture control of a thick-hard roof based on deep-hole pre-splitting blasting. Energy Explor. Exploit. 2022, 40, 279–301. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, C.; Yetilmezsoy, K.; Zhang, B.; Zhang, S. Fractural structure of thick hard roof stratum using long beam theory and numerical modeling. Environ. Earth Sci. 2017, 76, 751. [Google Scholar] [CrossRef]
- Bu, Q.; Tu, M.; Zhang, X.; Zhang, M.; Zhao, Q. Analysis of Energy Accumulation and Dispersion Evolution of a Thick Hard Roof and Dynamic Load Response of the Hydraulic Support in a Large Space Stope. Front. Earth Sci. 2022, 10, 884361. [Google Scholar] [CrossRef]
- Li, J.; Fu, B.; Zhang, H.; Zhao, Q.; Bu, Q. Study on Fracture Behavior of Directly Covered Thick Hard Roof Based on Bearing Capacity of Supports. Appl. Sci. 2023, 13, 2546. [Google Scholar] [CrossRef]
- Yu, M.; Zuo, J.; Sun, Y.; Mi, C.; Li, Z. Investigation on fracture models and ground pressure distribution of thick hard rock strata including weak interlayer. Int. J. Min. Sci. Technol. 2022, 32, 137–153. [Google Scholar] [CrossRef]
- Guo, Y.; Lu, C.; He, Z.; Song, J. Numerical and Field Investigations of Tremors Induced by Thick-Hard Strata Fracture. Appl. Sci. 2022, 12, 11151. [Google Scholar] [CrossRef]
- Ju, F.; Xiao, M.; He, Z.; Ning, P.; Huang, P. Study on Fracture and Stress Evolution Characteristics of Ultra-Thick Hard Sandstone Roof in the Fully Mechanized Mining Face with Large Mining Height: A Case Study of Xiaojihan Coal Mine in Western China. Adv. Civ. Eng. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Huo, B.; Meng, F.; Li, T.; Song, Z.; Jin, J.; Huang, Y. Research on small coal pillar protection technology for consolidation face of multi-layer hard roof and extra thick coal seam. Coal Sci. Technol. 2024, 52, 13–23. [Google Scholar] [CrossRef]
- Qin, D.; Chang, Z.; Xia, Z. Experiment Study on the Mechanical Behavior and Acoustic Emission Response of Thick and Hard Sandstone Roof in Xinjiang Mining Area. Adv. Civ. Eng. 2024, 2024, 1–12. [Google Scholar] [CrossRef]
- Hu, B.; Wu, Y.; Yu, Y.; Xie, P.; Wen, H.; Zhang, H. Numerical study on the dynamic pressure control for self-forming roadways using CHRCT in thin coal seams with thick and hard roofs. Energy Explor. Exploit. 2024. [Google Scholar] [CrossRef]
- Li, C.; Xin, D.; Liu, Y.; Chen, T. A Case Study on Strong Strata Behaviors Mechanism of Mining Reserved Roadway and Its Prevention Techniques. Processes 2023, 11, 1341. [Google Scholar] [CrossRef]
- Zhu, J.; Li, W.; Teng, B.; Liu, Y. Failure characteristics of thick hard roof stratum under hydraulic pre-splitting and its application in a coal mine, Dongsheng mining area. Environ. Earth Sci. 2024, 83, 153. [Google Scholar] [CrossRef]
- Li, Z.; Qi, C.; Gao, R.; Yu, B.; Zhu, Y.; Zhang, H.; Zhang, J. Simulation Study and Engineering Application of Weakening Mine Pressure Behavior in Stope through Ground Fracturing Thick and Hard Rock Strata. Appl. Sci. 2024, 14, 415. [Google Scholar] [CrossRef]
- Wang, M.; Xu, Y.; Xu, Q.; Shan, C.; Li, Z.; Nan, H.; Li, Y.; Liu, H.; Chu, T. Stability control of overburden and coal pillars in the gob-side entry under dynamic pressure. Int. J. Rock Mech. Min. 2023, 170, 105490. [Google Scholar] [CrossRef]
- Zhao, J. A study on reasonable width of coal pillar for protecting the roadway along the hollow digging roadway in the working face with hard roof island. Coal Technol. 2022, 41, 71–75. [Google Scholar]
- Shan, C.; Qi, S.; Xie, G.; Qin, J.; Li, Y.; Huang, P.; Zhang, Q.; Ren, G. Study on Multi-scale strength and Control of Coal Pillar in Gob Side Entry of Fully Mechanized Top Coal Caving Face in “Double Hard’ Seam. Coal Technol. 2023, 42, 63–68. [Google Scholar]
- Hou, C.; Li, X. Stability principles of large and small structures in the perimeter rock of a generalized open cut. J. China Coal Soc. 2001, 1–7. [Google Scholar]
- Feng, Z. Review of the “Control of Surrounding Rock in Chinese Coal Mining Quarries”. Mine Pressure and Roof Management. 1995. [Google Scholar]
- Hou, C.; Ma, N. Discussion on the stress and limit equilibrium zones of coal body in two gangs of coal seam roadway. J. China Coal Soc. 1989, 4, 21–29. [Google Scholar]
- Kumar, A.; Kumar, R.; Singh, A.K.; Ram, S.; Singh, P.K.; Singh, R. Numerical modelling-based pillar strength estimation for an increased height of extraction. Arab. J. Geosci. 2017, 10, 411. [Google Scholar] [CrossRef]
- Holland, C.T. The Strength of Coal in Mine Pillars. In Proceedings of the 6th U.S Symposium on Rock Mechanics (USRMS), Rolla, MI, USA, 28–30 October 1964. ARMA-64-450. [Google Scholar]
- Salamon, A.; Munro, M. A study of the strength of coal pillars. J. S. Afr. Inst. Min. Metall. 1967, 68, 55–67. [Google Scholar]
- Bieniawski, Z.T. The point-load test in geotechnical practice. Eng. Geol. 1975, 9, 1–11. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, J.; Wang, C.; Sun, C.; Xu, C.; Song, Z.; Su, Y. Mechanism of gob-pillar interaction for subcritical panels and its application. Chin. J. Rock. Mech. Eng. 2017, 36, 1185–1200. [Google Scholar]
- Cheng, H.; Lu, D.; Wang, E. Theoretical analysis and calculate on the thickness of the medium thickness seam nether roof. Hebei Coal 2011, 16–17. [Google Scholar] [CrossRef]
- Fu, F. Research on the technology of cutting top and unloading pressure of small coal pillar in medium-thickness coal seam. Shanxi Chem. Ind. 2023, 43, 141–143. [Google Scholar]
- Gaddy, F.L. A Study of the Ultimate Strength of Coal as Related to the Absolute Size of the Cubical Specimens Tested; Virginia Polytechnic Institute: Blacksburg, VA, USA, 1956. [Google Scholar]
- Zhang, Y. Research and Application of Reserved Narrow Coal Pillar Roof Cutting and Pressure Relief. Technol. Qingyun Coal Ind. Shandong Coal Sci. Technol. 2023, 41, 27–31. [Google Scholar]





| Immediate Roof Lithology | Compressive Strength/MPa | ||
|---|---|---|---|
| hard | >40 | 2.1 | 16 |
| medium hard | 20–40 | 4.7 | 19 |
| weak | <20 | 6.2 | 32 |
| Rock Quality of the Roof of the Working Face | Fracture Zone Height H/m | Lateral Support Angle (°) |
|---|---|---|
| stiff | 30 | |
| medium-hard | 20 | |
| flabby | 10 |
| Layer | Modulus of Elasticity E/GPa | Poisson’s Ratio | Internal Friction Angle f/° | Cohesion C/MPa | Tensile Strength t/MPa |
|---|---|---|---|---|---|
| mudstone | 1.77 | 0.2 | 25.3 | 6.3 | 0.58 |
| limestone | 6.5 | 0.32 | 25.3 | 11.2 | 5.7 |
| coal | 6.4 | 0.31 | 22.8 | 2.7 | 0.49 |
| bauxite | 14.2 | 0.23 | 25.3 | 6.3 | 2.53 |
| siltstone | 3.34 | 0.23 | 42 | 3.2 | 1.29 |
| Program | 1 | 2 | 3 | 4 | 5 |
| Width of coal pillar/m | 7 | 8 | 9 | 10 | 11 |
| Width of Coal Pillar/m | Peak Vertical Stress/MPa | Stress Concentration Factor | ||
|---|---|---|---|---|
| Coal Pillar | Solid Coal Slope | Coal Pillar | Solid Coal Slope | |
| 7 | 23.04 | 18.74 | 3.69 | 3.00 |
| 8 | 20.05 | 17.14 | 3.21 | 2.74 |
| 9 | 19.98 | 16.10 | 3.20 | 2.58 |
| 10 | 19.34 | 16.07 | 3.09 | 2.57 |
| 11 | 19.20 | 15.65 | 3.07 | 2.50 |
| Width of Coal Pillar/m | Roof Subsidence/mm | Floor Heave/mm | Roof and Floor Approach/mm | Coal Pillar/mm | Solid Coal Slope/mm | Approach of Two Sides/mm |
|---|---|---|---|---|---|---|
| 7 | 159.94 | 70.30 | 230.24 | 165.63 | 68.55 | 234.18 |
| 8 | 141.60 | 62.50 | 204.10 | 123.43 | 62.30 | 185.73 |
| 9 | 120.00 | 57.90 | 177.90 | 103.46 | 57.28 | 160.74 |
| 10 | 114.47 | 54.77 | 170.23 | 89.55 | 47.82 | 137.47 |
| 11 | 106.93 | 52.68 | 159.61 | 80.99 | 43.66 | 124.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, W.; Xu, D.; Han, Z.; Zhang, H. Research on the Reasonable Width of Coal Pillar Driving along Goaf under Thick Hard Roof. Appl. Sci. 2024, 14, 6381. https://doi.org/10.3390/app14146381
Gu W, Xu D, Han Z, Zhang H. Research on the Reasonable Width of Coal Pillar Driving along Goaf under Thick Hard Roof. Applied Sciences. 2024; 14(14):6381. https://doi.org/10.3390/app14146381
Chicago/Turabian StyleGu, Wei, Dalong Xu, Zhenfei Han, and Hao Zhang. 2024. "Research on the Reasonable Width of Coal Pillar Driving along Goaf under Thick Hard Roof" Applied Sciences 14, no. 14: 6381. https://doi.org/10.3390/app14146381
APA StyleGu, W., Xu, D., Han, Z., & Zhang, H. (2024). Research on the Reasonable Width of Coal Pillar Driving along Goaf under Thick Hard Roof. Applied Sciences, 14(14), 6381. https://doi.org/10.3390/app14146381





