Comparison between an Adaptive Gain Scheduling Control Strategy and a Fuzzy Multimodel Intelligent Control Applied to the Speed Control of Non-Holonomic Robots
Abstract
:1. Introduction
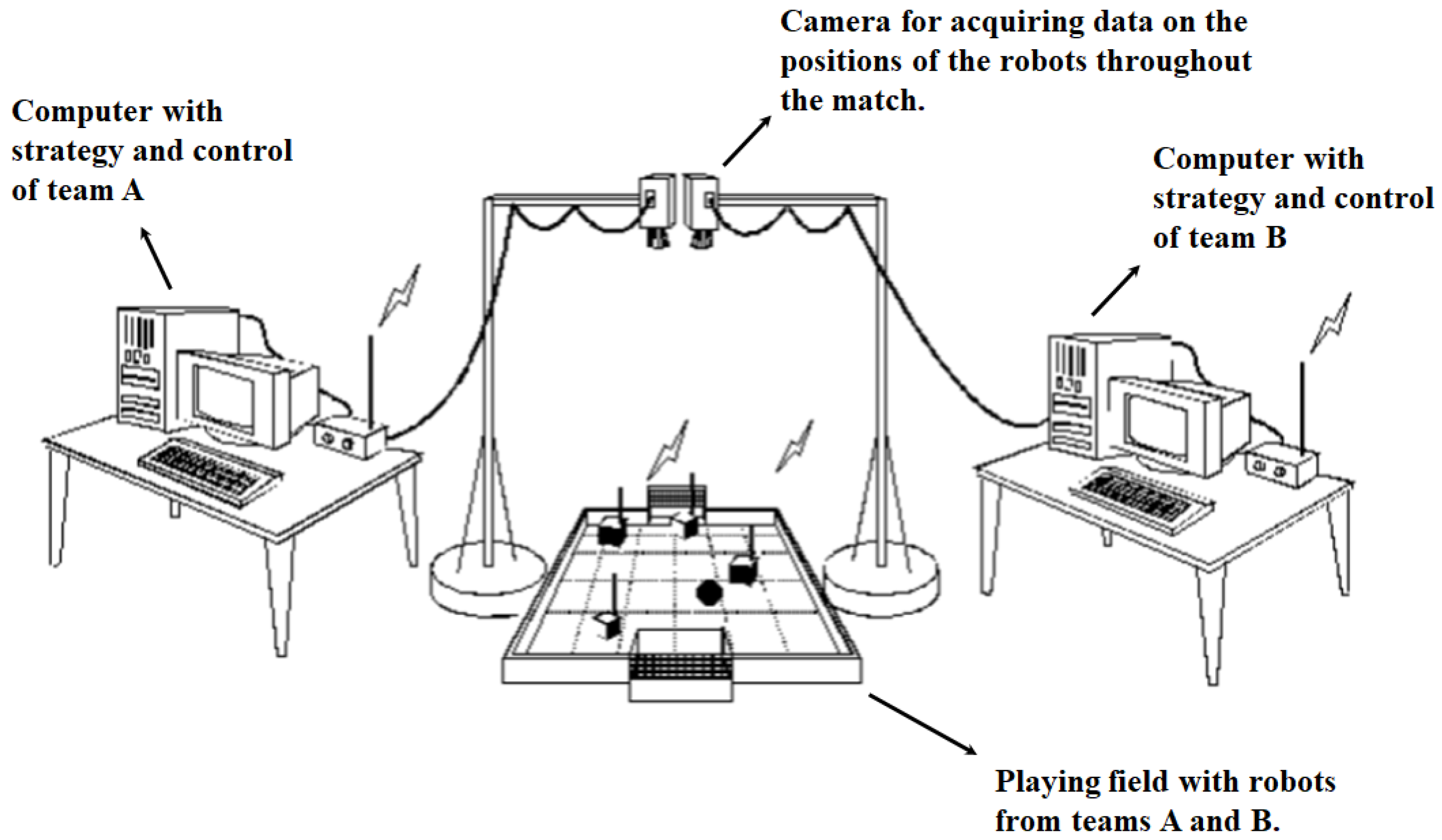
2. Structure of the Competitions
2.1. Computer Vision
2.2. Communication and Triggering
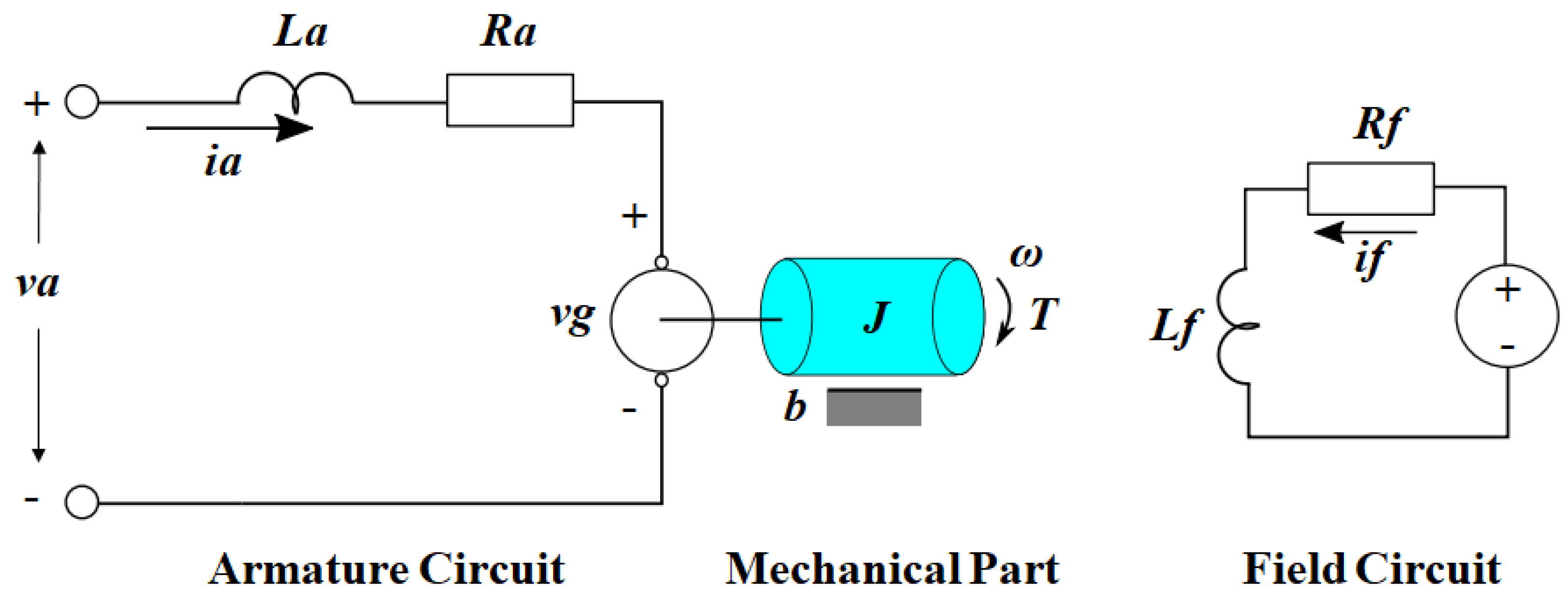
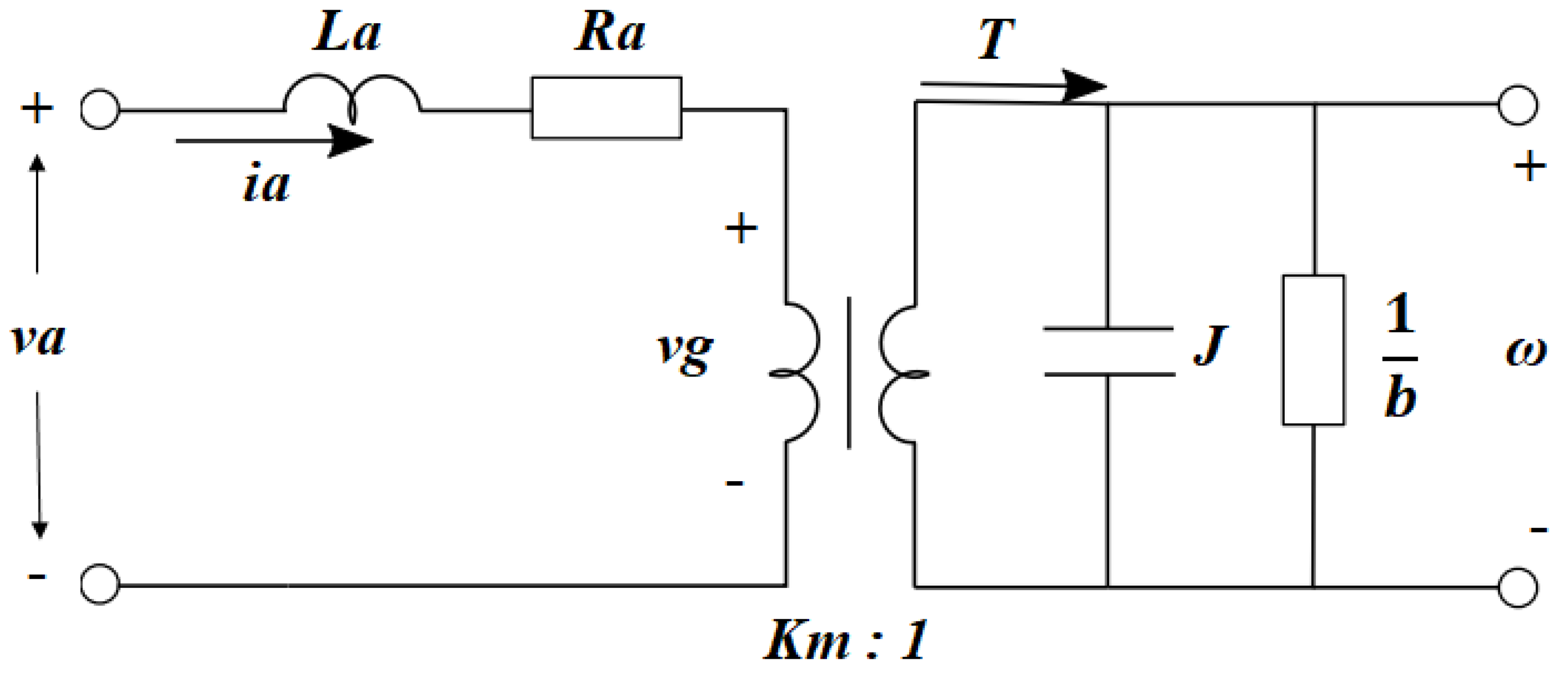
3. DC Motor Mathematical Modeling
- Armature winding: it is located in the rotating part of the DC motor (rotor) and is responsible for producing the torque that moves it and the output voltage when in generator mode.
- Field winding: this is a fixed part that is responsible for the constant magnetic flux passing through the armature; in small DC motors, such as those used in this work, the field winding is often replaced by placing permanent magnets around the armature, which are responsible for generating a constant magnetic field.
- Commutator: It keeps the armature current circulating in the same direction, causing the torque to maintain its direction for a constant input voltage.
- Brushes: these are where the armature winding contacts the power supply.
4. Control Strategies
4.1. Local Discrete PI Controllers
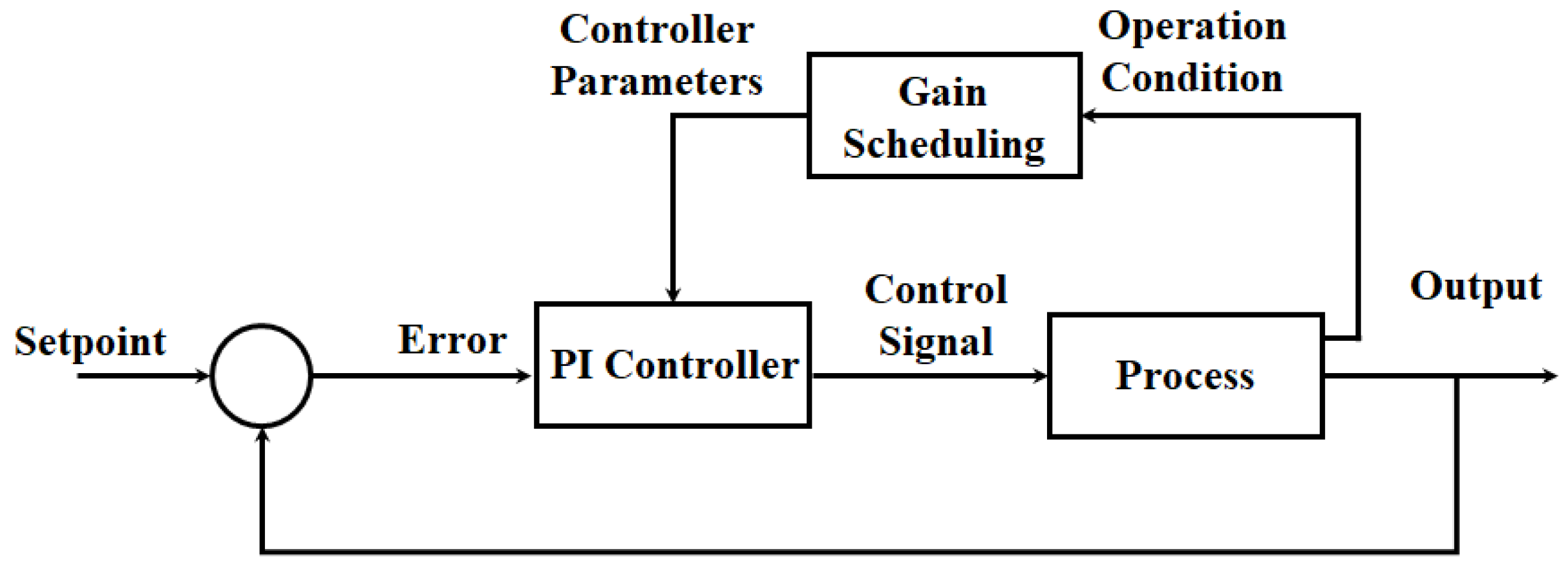
4.2. Gain Scheduling Control
- Obtain a valid representation or approximation of the nonlinear system for each operating point and perform its linearization;
- Apply linear control techniques to develop a controller that meets the needs of the linearized system;
- Choose the architecture of the gain scheduler (rules used in transitions);
- Validate the performance of the controller.
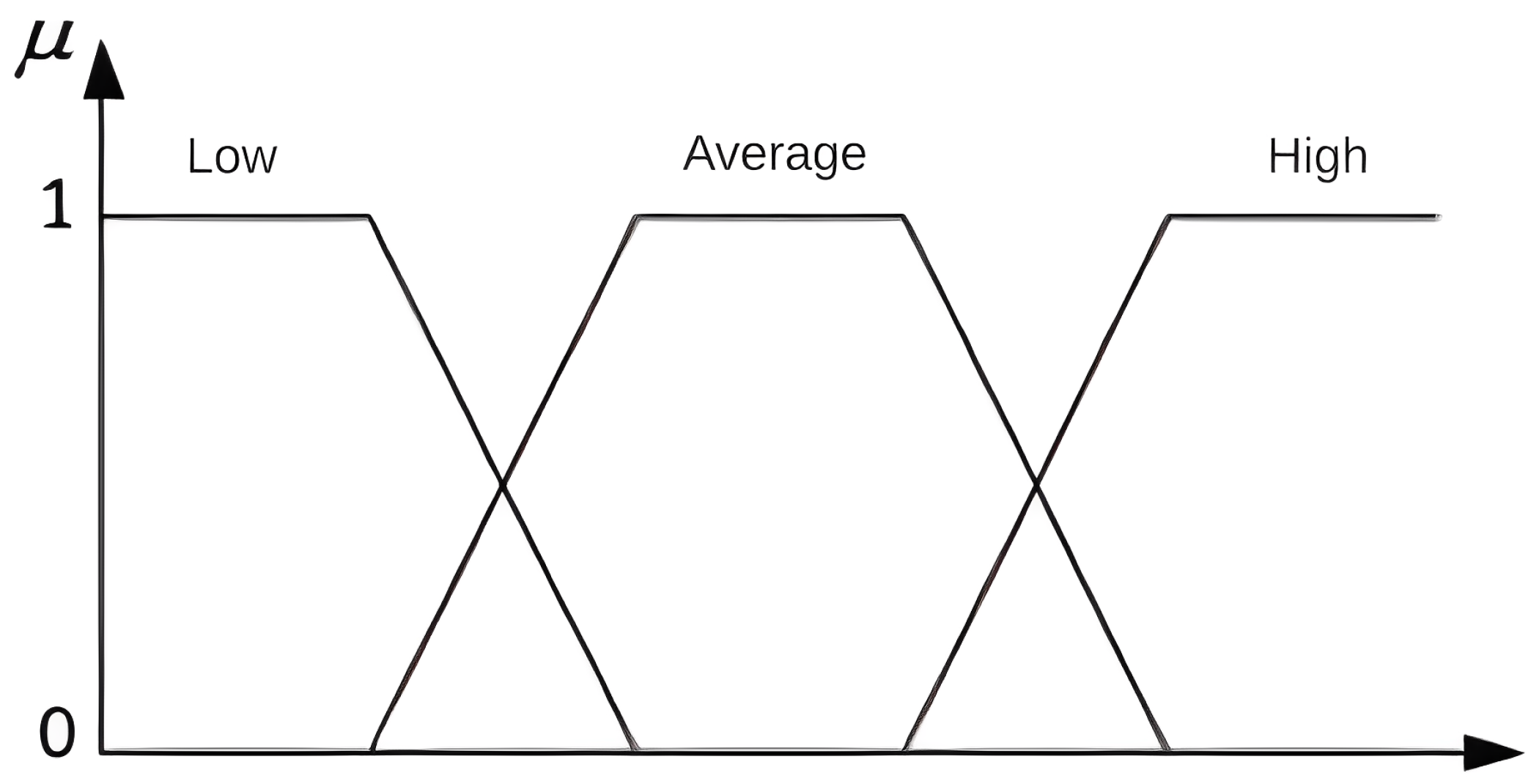
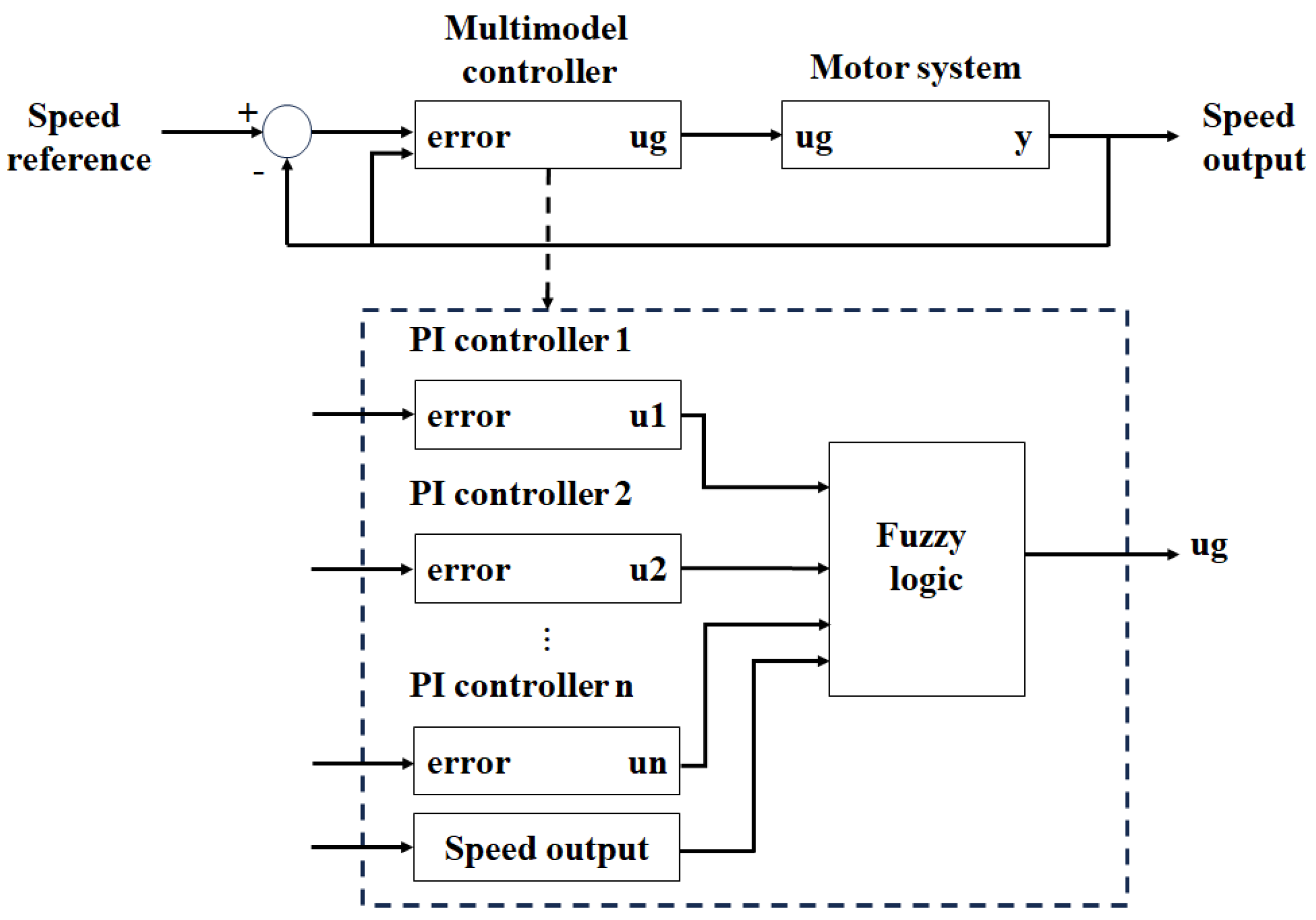
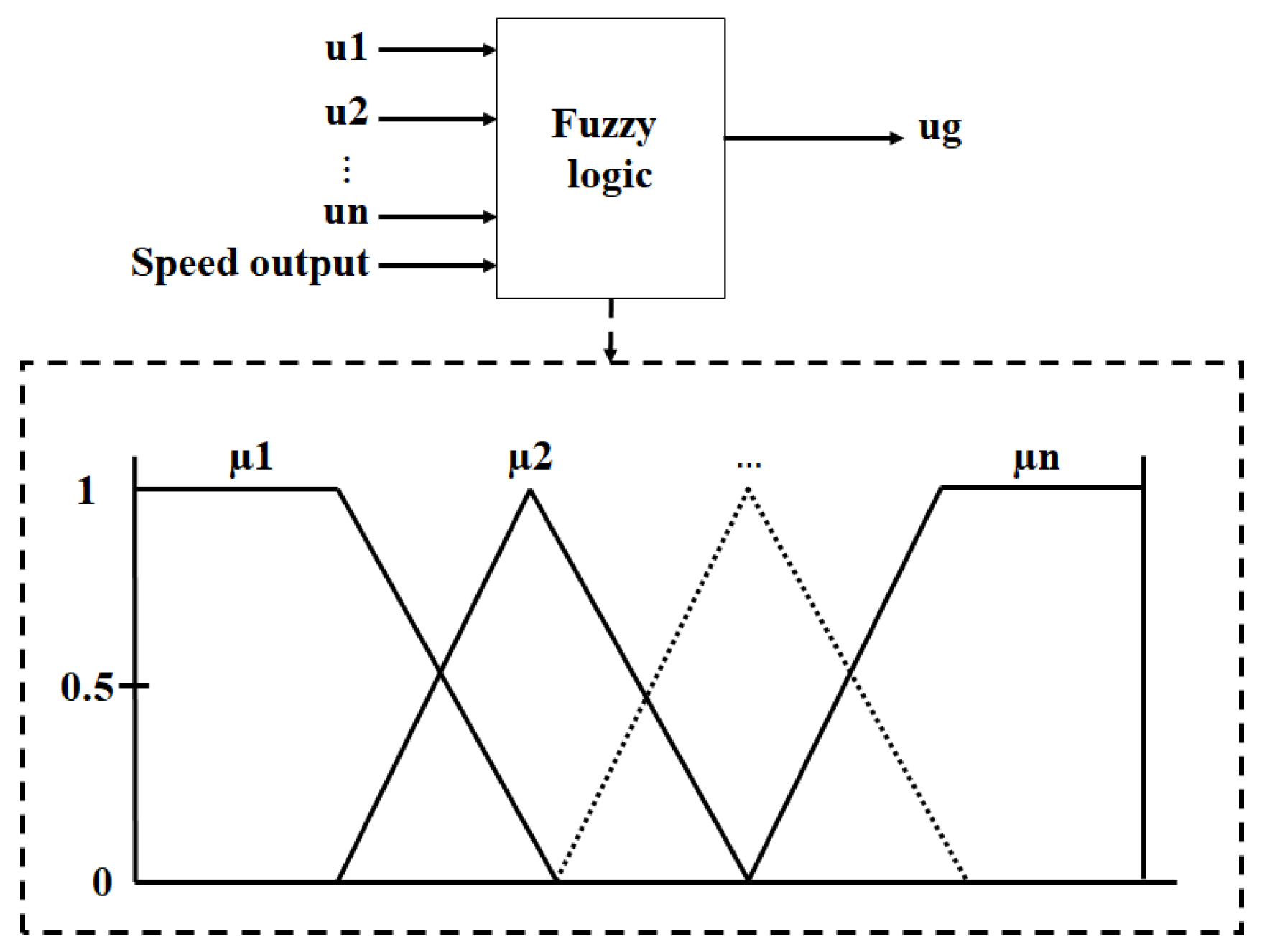
4.3. Fuzzy Multimodel Control
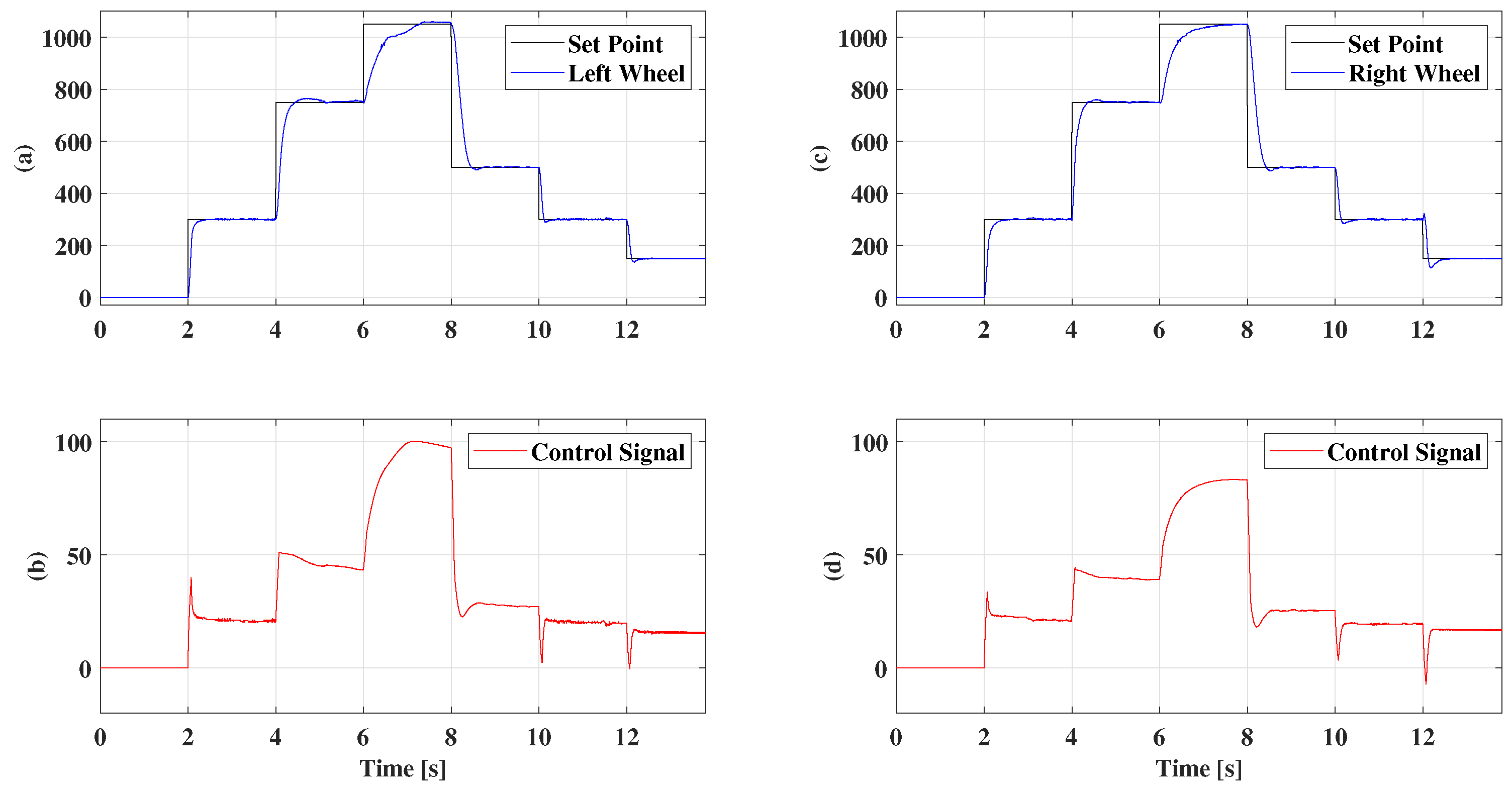
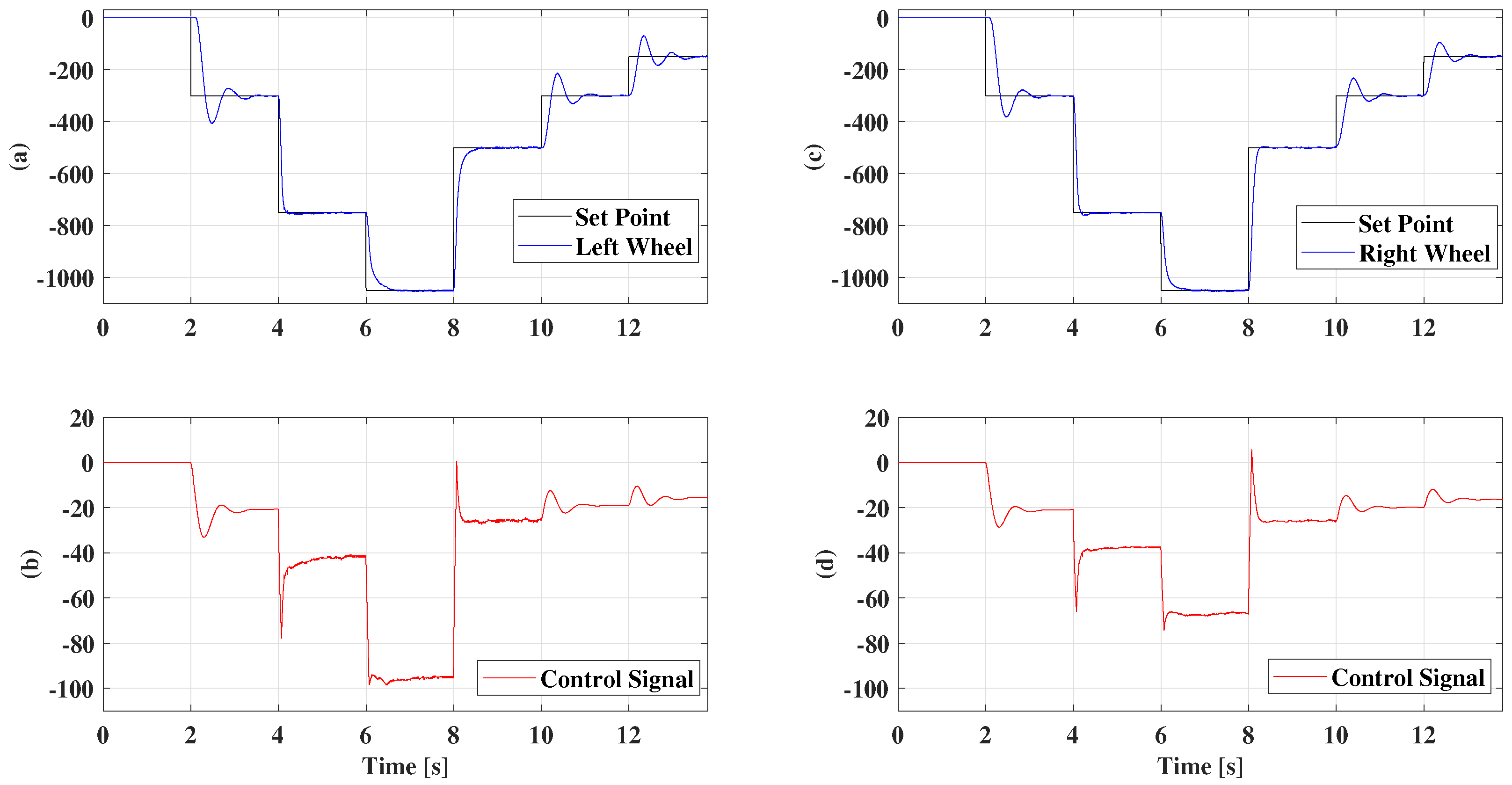
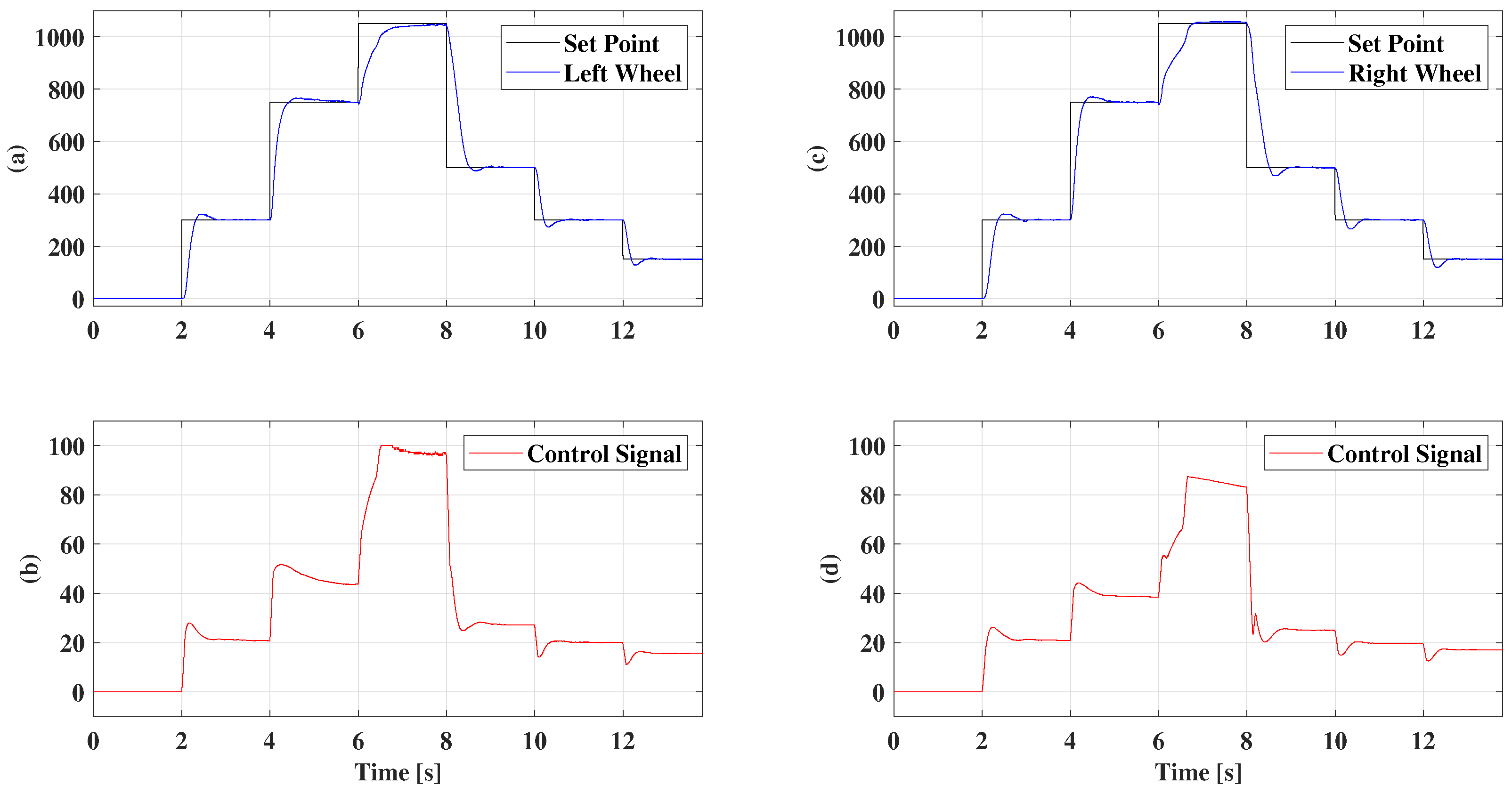
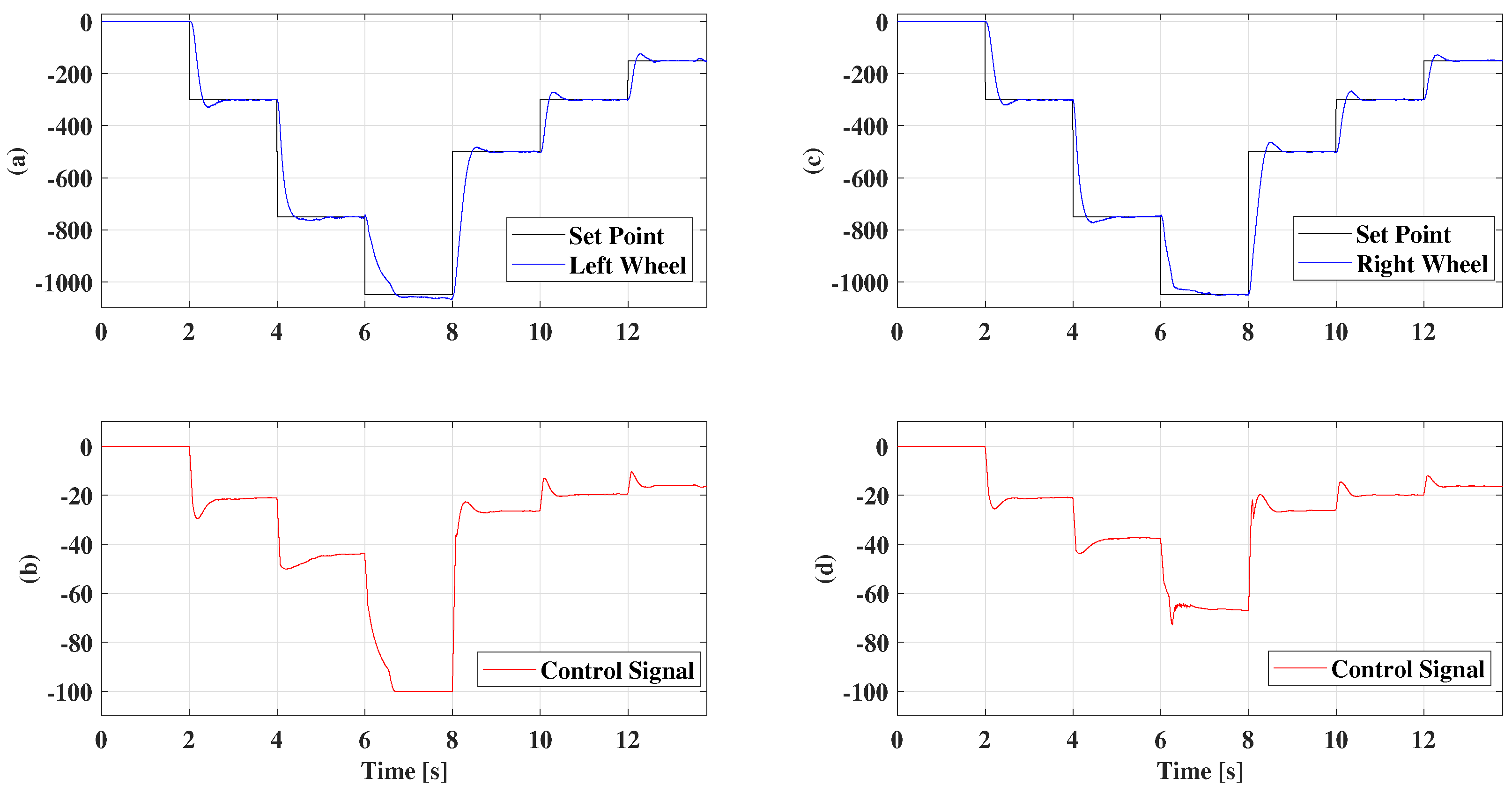
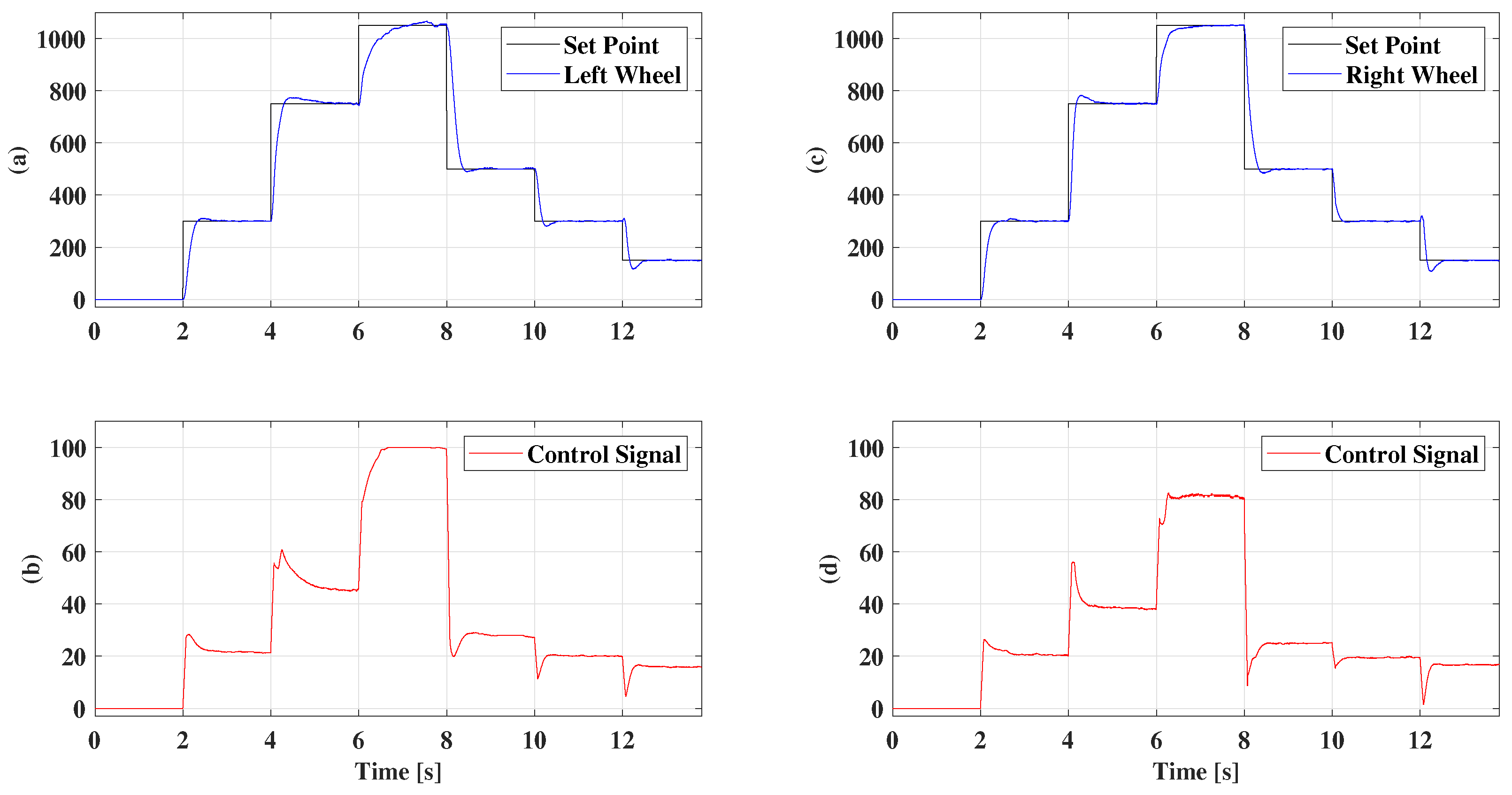
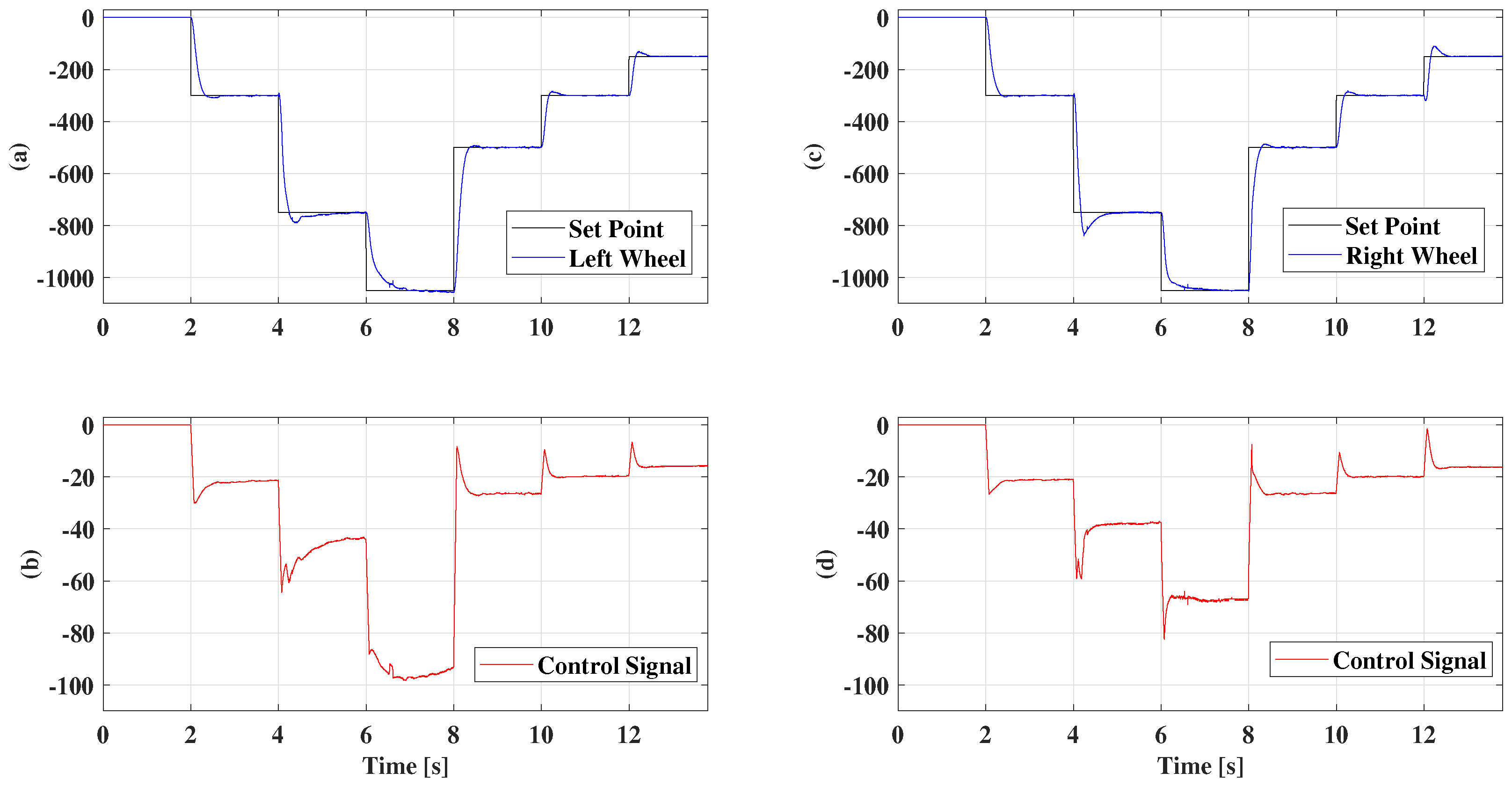
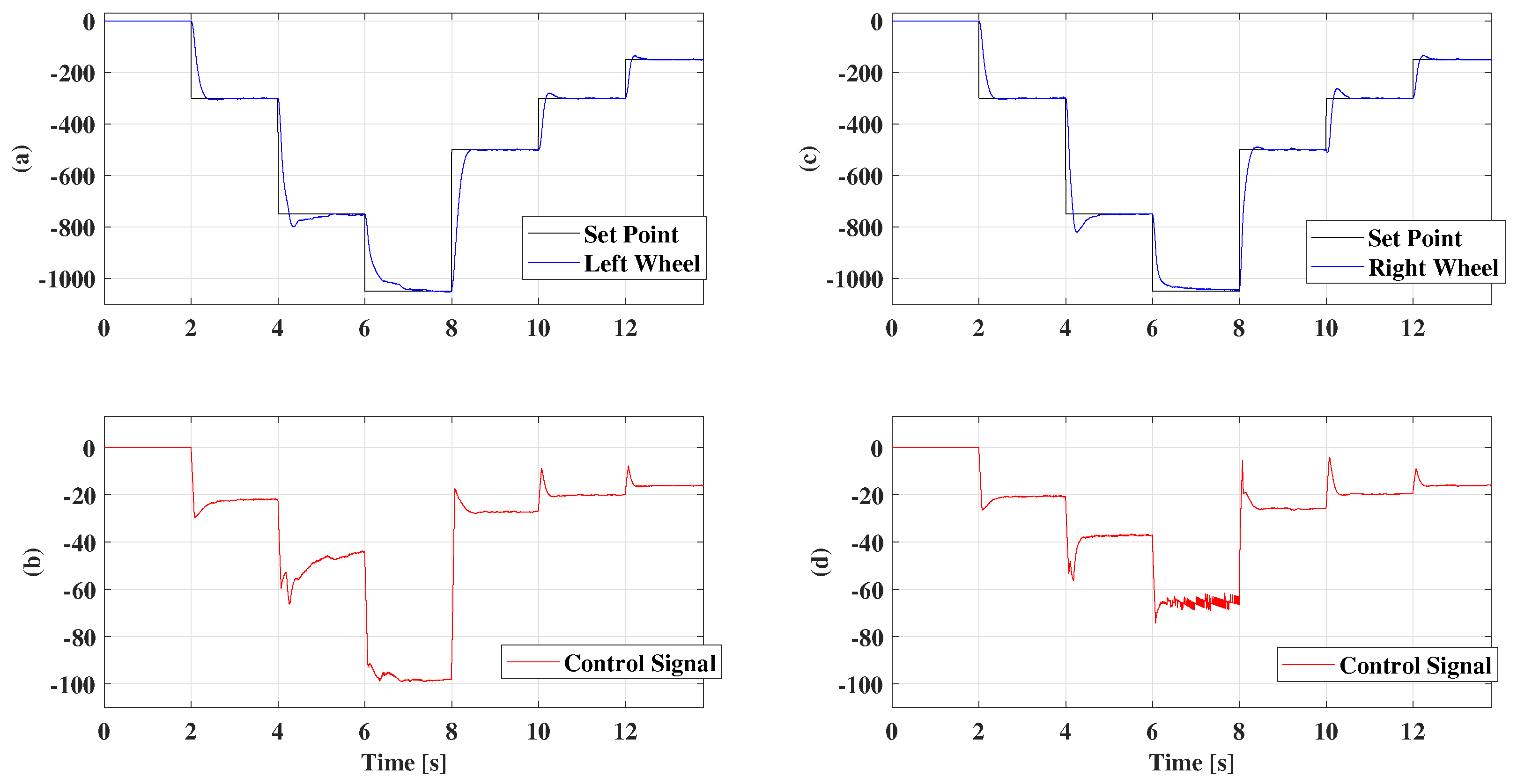
5. Results
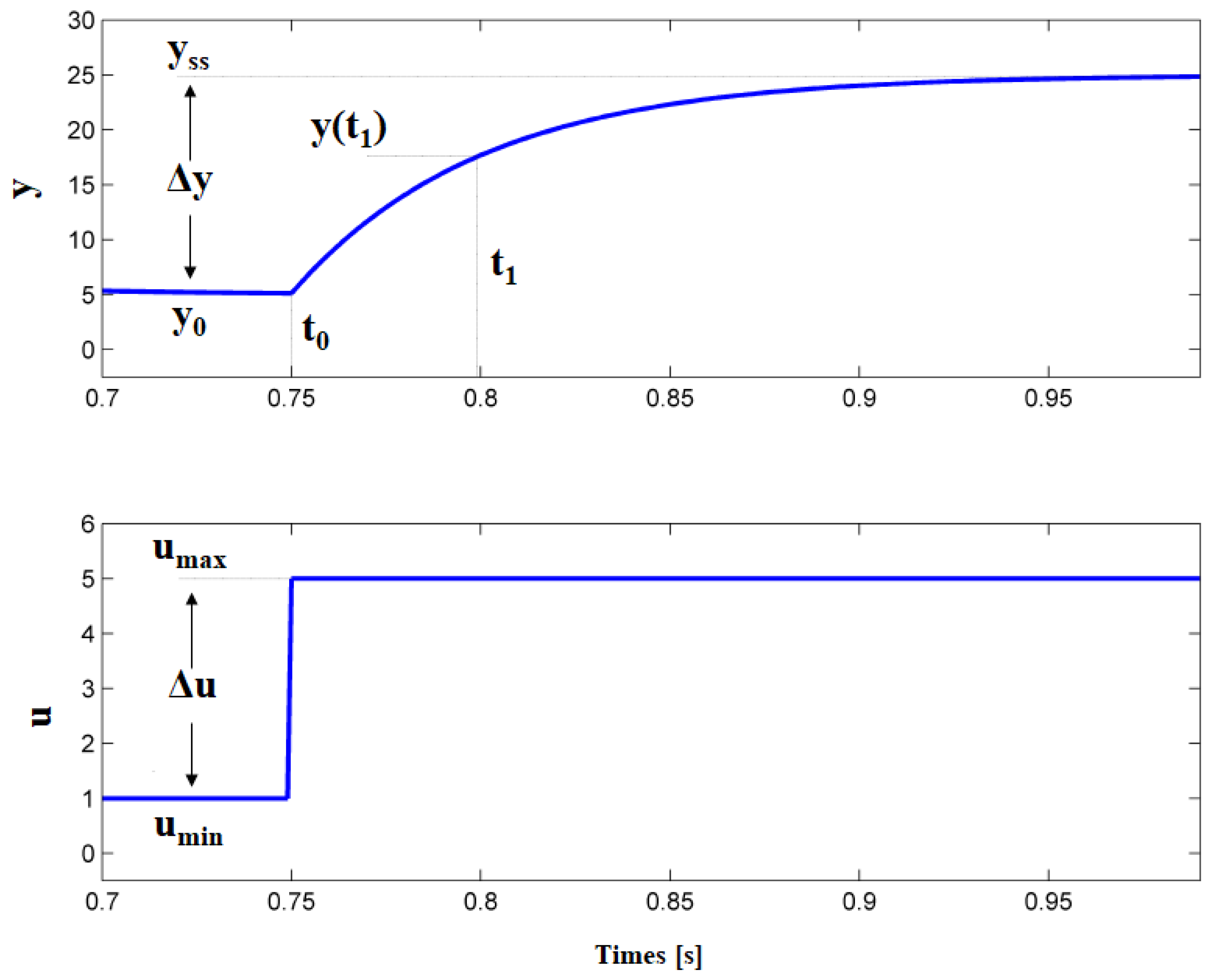
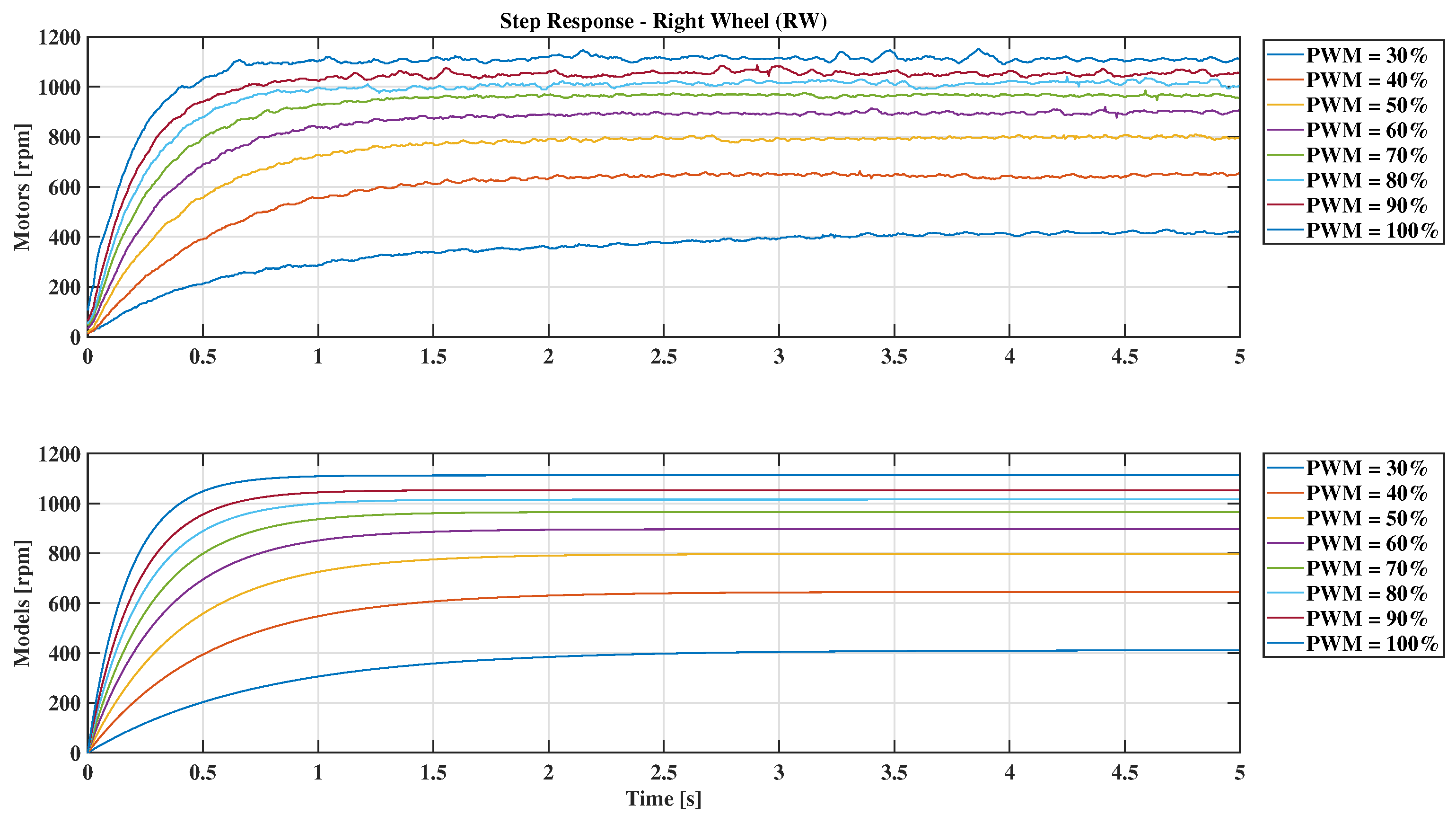
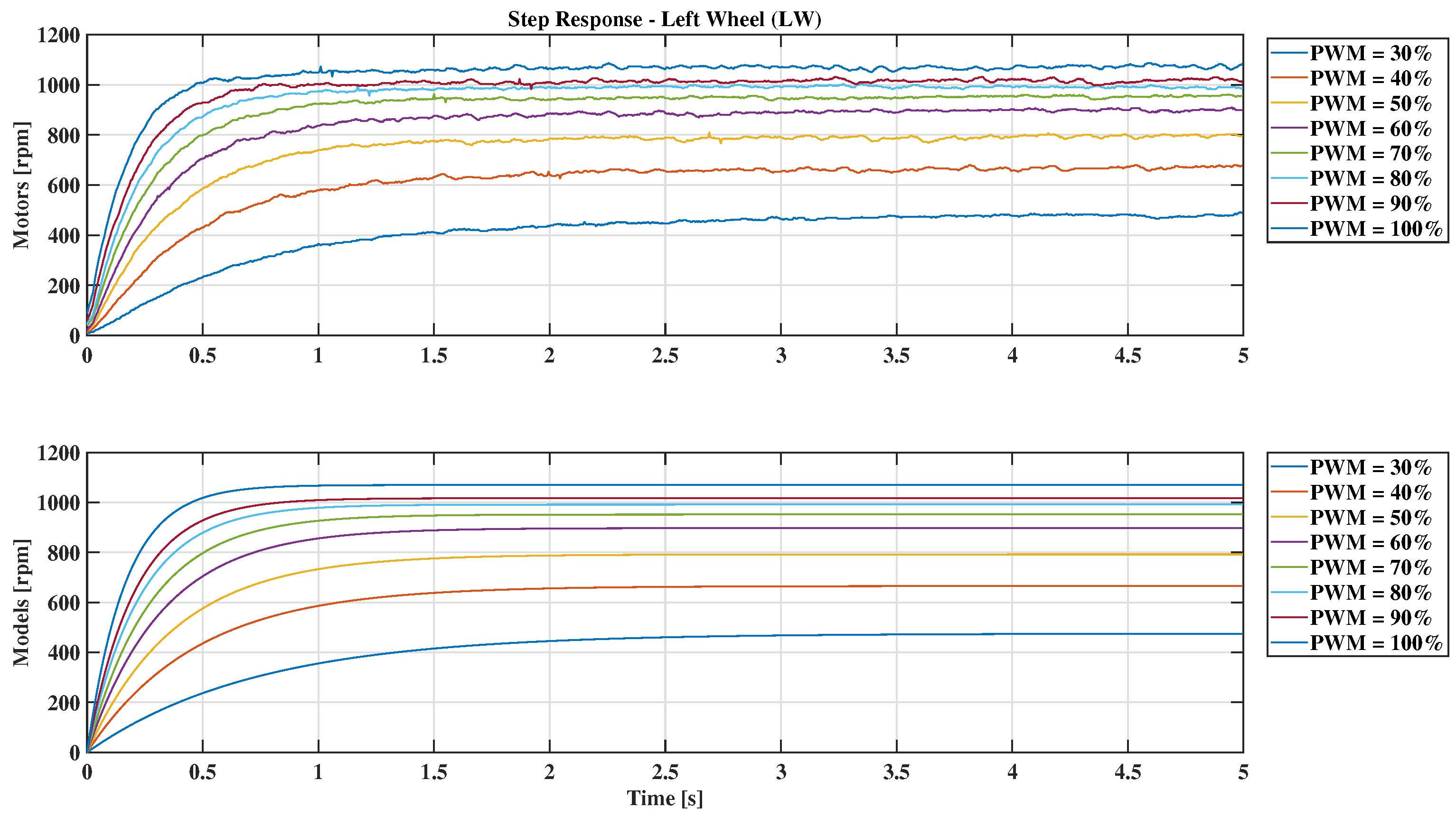
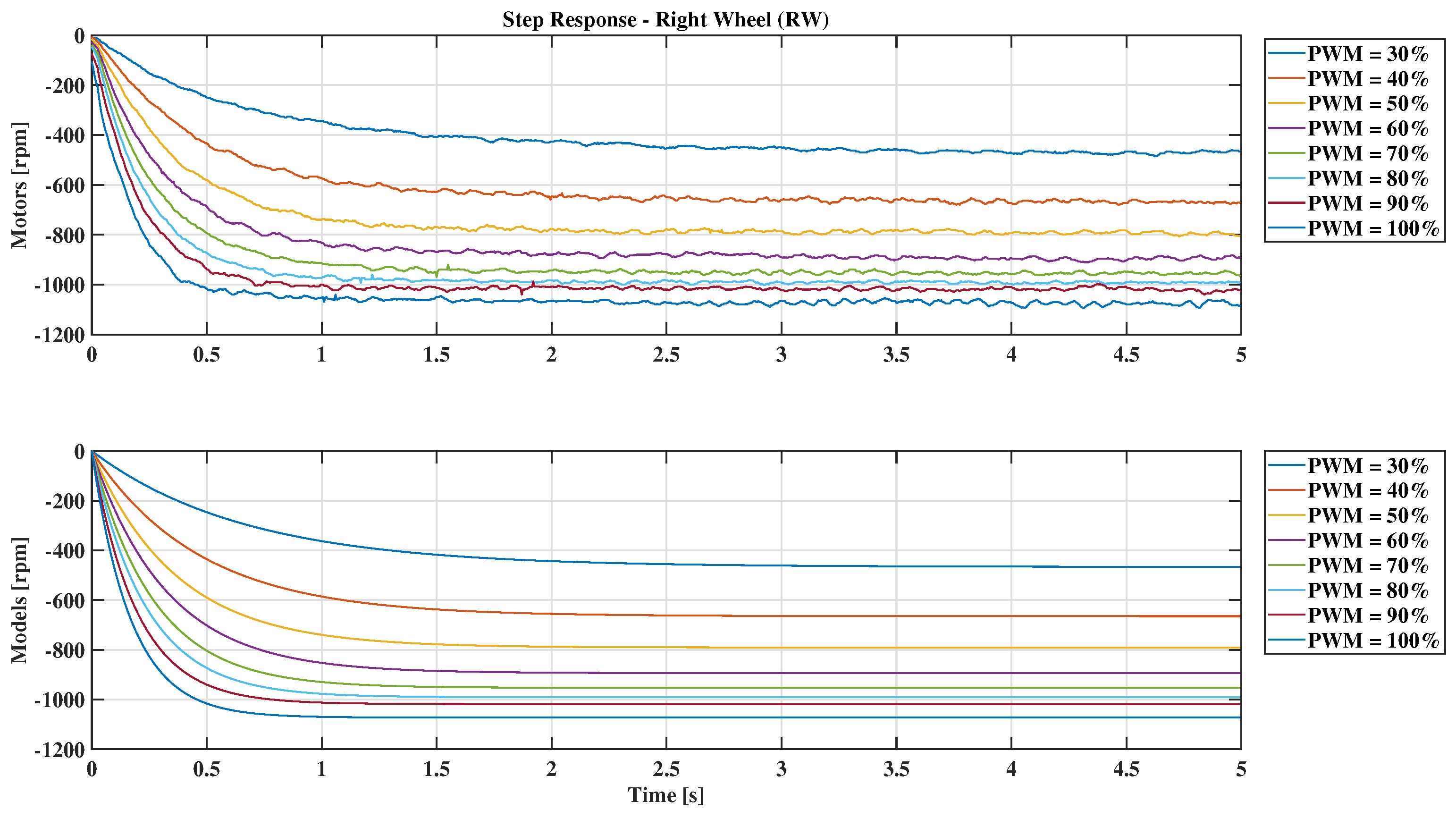
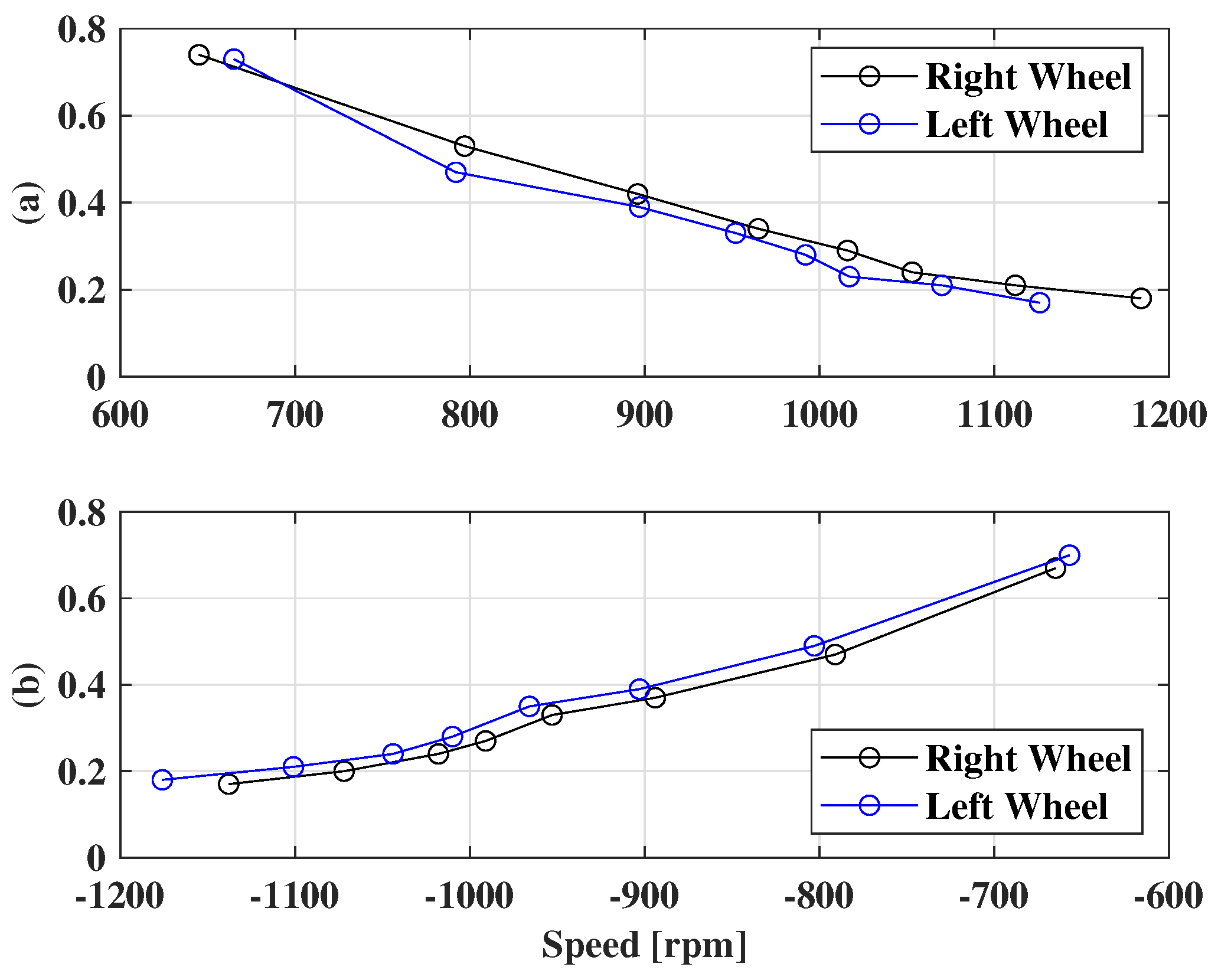
5.1. Local Models and PI Controllers
5.2. Gain Scheduling
5.3. Fuzzy Multimodel Control with Two Models
5.4. Fuzzy Multimodel Control with Three Models
5.5. Fuzzy Multimodel Control with 4 Models
5.6. Performance Criteria
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Niku, S.B. Introduction to Robotics: Analysis, Control, Applications; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Siegwart, R.; Nourbakhsh, I.R.; Scaramuzza, D. Introduction to Autonomous Mobile Robots; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Bruzzone, L.; Nodehi, S.E.; Fanghella, P. Tracked locomotion systems for ground mobile robots: A review. Machines 2022, 10, 648. [Google Scholar] [CrossRef]
- Sun, W.; Tang, S.; Gao, H.; Zhao, J. Two timescale tracking control of nonholonomic wheeled mobile robots. IEEE Trans. Control Syst. Technol. 2016, 24, 2059–2069. [Google Scholar] [CrossRef]
- Rubio, F.; Valero, F.; Llopis-Albert, C. A review of mobile robots: Concepts, methods, theoretical framework, and applications. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419839596. [Google Scholar] [CrossRef]
- De Wit, C.C.; Sordalen, O. Exponential stabilization of mobile robots with nonholonomic constraints. In Proceedings of the [1991] 30th IEEE Conference on Decision and Control, Brighton, UK, 11–13 December 1991; IEEE: Piscataway, NJ, USA, 1991; pp. 692–697. [Google Scholar]
- Chen, Z.; Liu, Y.; He, W.; Qiao, H.; Ji, H. Adaptive-neural-network-based trajectory tracking control for a nonholonomic wheeled mobile robot with velocity constraints. IEEE Trans. Ind. Electron. 2020, 68, 5057–5067. [Google Scholar] [CrossRef]
- Bie, H.; Li, P.; Chen, F.; Ghaderpour, E. An Observer-Based Type-3 Fuzzy Control for Non-Holonomic Wheeled Robots. Symmetry 2023, 15, 1354. [Google Scholar] [CrossRef]
- Cen, H.; Singh, B.K. Nonholonomic wheeled mobile robot trajectory tracking control based on improved sliding mode variable structure. Wirel. Commun. Mob. Comput. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Akande, T.; Alabi, O.; Ajagbe, S. A deep learning-based CAE approach for simulating 3D vehicle wheels under real-world conditions. Artif. Intell. Appl. 2024. [Google Scholar] [CrossRef]
- Sani, M.; Hably, A.; Robu, B.; Dumon, J.; Meslem, N. Real-time Dynamic Obstacle Avoidance for a Non-holonomic Mobile Robot. In Proceedings of the 2023 IEEE 32nd International Symposium on Industrial Electronics (ISIE), Helsinki/Espoo, Finland, 19–21 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Zin, T.P.; Nyein, A.K. DC Gear-Motor Position control for 3-DOF Articulated Painting Robot arm. In Proceedings of the International Conference on Science and Technology for Sustainable Development, Yangon, Myanmar, 7 August 2019. [Google Scholar]
- Cook, M.D.; Bonniwell, J.L.; Rodriguez, L.A.; Williams, D.W.; Pribbernow, J. Low-cost dc motor system for teaching automatic controls. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4283–4288. [Google Scholar]
- Sands, T. Control of DC motors to guide unmanned underwater vehicles. Appl. Sci. 2021, 11, 2144. [Google Scholar] [CrossRef]
- Saá-Tapia, F.; Mayorga-Miranda, L.; Ayala-Chauvin, M.; Domènech-Mestres, C. Control System Test Platform for a DC Motor. In Proceedings of the International Conference on Human-Computer Interaction, Virtual, 26 June–1 July 2022; Springer: Cham, Switzerland, 2022; pp. 675–682. [Google Scholar]
- Bhatta, B.; Salim, G.; Borra, V.; Li, F.X. Low-Cost DC Motor Control System Experiments for Engineering Students. In Proceedings of the 2023 ASEE Annual Conference & Exposition, Baltimore, MD, USA, 25 June 2023. [Google Scholar]
- Westenskow, D.R. Fundamentals of feedback control: PID, fuzzy logic, and neural networks. J. Clin. Anesth. 1997, 9, 33S–35S. [Google Scholar] [CrossRef]
- Sami, S.S.; Obaid, Z.A.; Muhssin, M.T.; Hussain, A.N. Detailed modelling and simulation of different DC motor types for research and educational purposes. Int. J. Power Electron. Drive Syst. 2021, 12, 703–714. [Google Scholar] [CrossRef]
- Khan, H.; Khatoon, S.; Gaur, P.; Abbas, M.; Saleel, C.A.; Khan, S.A. Speed Control of Wheeled Mobile Robot by Nature-Inspired Social Spider Algorithm-Based PID Controller. Processes 2023, 11, 1202. [Google Scholar] [CrossRef]
- Astrom, K.; Hagglund, T. PID Controllers: Theory, Design, and Tuning; Instrument Society of America: Research Triangle Park, NC, USA, 2011. [Google Scholar]
- Cabré, T.P.; Vela, A.S.; Ribes, M.T.; Blanc, J.M.; Pablo, J.R.; Sancho, F.C. Didactic platform for DC motor speed and position control in Z-plane. ISA Trans. 2021, 118, 116–132. [Google Scholar] [CrossRef] [PubMed]
- Foss, B.A.; Johansen, T.A.; Sørensen, A.V. Nonlinear predictive control using local models—Applied to a batch fermentation process. Control Eng. Pract. 1995, 3, 389–396. [Google Scholar] [CrossRef]
- Murray-Smith, R.; Johansen, T. Multiple Model Approaches to Nonlinear Modelling and Control; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Zeng, W.; Jiang, Q.; Liu, Y.; Xie, J.; Yu, T. A multi-level fuzzy switching control method based on fuzzy multi-model and its application for PWR core power control. Prog. Nucl. Energy 2021, 138, 103743. [Google Scholar] [CrossRef]
- Bensafia, Y.; Boukra, T.; Khettab, K. Fractionalized PID Control in Multi-model Approach: A New Tool for Detection and Diagnosis Faults of DC Motor. Prz. Elektrotechniczny 2023, 99, 45. [Google Scholar] [CrossRef]
- Qu, S.; He, T.; Zhu, G. Model-Assisted Online Optimization of Gain-Scheduled PID Control Using NSGA-II Iterative Genetic Algorithm. Appl. Sci. 2023, 13, 6444. [Google Scholar] [CrossRef]
- Sadati, N.; Talasaz, A. Robust fuzzy multimodel control using variable structure system. In Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems, Singapore, 1–3 December 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 1, pp. 497–502. [Google Scholar]
- Camacho, O.; Iglesias, E.; Herrera, M.; Aboukheir, H. Fuzzy logic-based control: From fundamentals to applications. Rev. Digit. Novasinergia 2021, 4, 6–37. [Google Scholar]
- Helali, R.G.M. An Exploratory Study of Factors Affecting Research Productivity in Higher Educational Institutes Using Regression and Deep Learning Techniques. Artif. Intell. Appl. 2023. [Google Scholar] [CrossRef]
- Solc, F.; Honzik, B. Modelling and control of a soccer robot. In Proceedings of the 7th International Workshop on Advanced Motion Control, Maribor, Slovenia, 3–5 July 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 506–509. [Google Scholar]
- Siregar, S.; Ibrahim, I.; Sani, M.I.; Sari, M.I. Design of Computer Vision Based Ball Detection System on Wheeled Robot Soccer. In Proceedings of the International Conference on Control, Electronics, Renewable Energy and Communications, Bandung, Indonesia, 5–7 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 46–49. [Google Scholar]
- Vázquez-Hurtado, C.; Rodriguez-Padilla, C. Adapting a Very Small Size Soccer (VSSS) competition for learning robotics in virtual teaching. In Proceedings of the IEEE Global Engineering Education Conference, Tunis, Tunisia, 28–31 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 553–558. [Google Scholar]
- Pal, S.; Roy, A.; Shivakumara, P.; Pal, U. Adapting a swin transformer for license plate number and text detection in drone images. Artif. Intell. Appl. 2023, 1, 145–154. [Google Scholar] [CrossRef]
- Okuyama, I.; Maximo, M.; Afonso, R. Minimum-time trajectory planning for a differential drive mobile robot considering non-slipping constraints. J. Control. Autom. Electr. Syst. 2021, 32, 120–131. [Google Scholar] [CrossRef]
- Hilal, M.; ALRikabi, H.; Aljazaery, I.A. A Control System of DC Motor Speed: Systematic Review: A Control System of DC Motor Speed: Systematic Review. Wasit J. Comput. Math. Sci. 2023, 2, 93–111. [Google Scholar]
- Adewusi, S. Modeling and parameter identification of a DC motor using constraint optimization technique. IOSR J. Mech. Civ. Eng. (IOSR-JMCE) 2016, 13, 46–56. [Google Scholar]
- Menaka, S.; Patilkulkarni, S. DC Motor System Identification and Speed Control Using dSPACE Tools. In Smart Sensors Measurement and Instrumentation: Select Proceedings of CISCON 2021; Springer: Berlin/Heidelberg, Germany, 2023; pp. 115–128. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Sistemas de Controle para Engenharia; Bookman Editora: São Paulo, Brazil, 2013. [Google Scholar]
- Phillips, C.L.; Nagle, H.T.; Chakrabortty, A. Digital Control System Analysis and Design; Prentice Hall: Englewood Cliffs, NJ, USA, 1990; Volume 2. [Google Scholar]
- Rugh, W.J.; Shamma, J.S. Research on gain scheduling. Automatica 2000, 36, 1401–1425. [Google Scholar] [CrossRef]
- Han, J.; Shan, X.; Liu, H.; Xiao, J.; Huang, T. Fuzzy gain scheduling PID control of a hybrid robot based on dynamic characteristics. Mech. Mach. Theory 2023, 184, 105283. [Google Scholar] [CrossRef]
- Åström, K.J.; Wittenmark, B. Adaptive Control; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Leith, D.J.; Leithead, W.E. Survey of gain-scheduling analysis and design. Int. J. Control 2000, 73, 1001–1025. [Google Scholar] [CrossRef]
- Boufrioua, H.; Boukhezzar, B. Gain Scheduling: A Short Review. In Proceedings of the 2022 2nd International Conference on Advanced Electrical Engineering (ICAEE), Constantine, Algeria, 29–31 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Chen, G.; Joo, Y.H. Fuzzy control systems: An introduction. In Encyclopedia of Artificial Intelligence; IGI Global: Pennsylvania, PA, USA, 2009; pp. 688–695. [Google Scholar]
- Belman-Flores, J.M.; Rodríguez-Valderrama, D.A.; Ledesma, S.; García-Pabón, J.J.; Hernández, D.; Pardo-Cely, D.M. A review on applications of fuzzy logic control for refrigeration systems. Appl. Sci. 2022, 12, 1302. [Google Scholar] [CrossRef]
- Khoi, P.B. Application of fuzzy logic in the robot control for mechanical processing. Vietnam. J. Sci. Technol. 2023, 61, 531–569. [Google Scholar]
- Fan, Y.; An, Y.; Wang, W.; Yang, C. TS fuzzy adaptive control based on small gain approach for an uncertain robot manipulators. Int. J. Fuzzy Syst. 2020, 22, 930–942. [Google Scholar] [CrossRef]
- Awad, N.; Lasheen, A.; Elnaggar, M.; Kamel, A. Model predictive control with fuzzy logic switching for path tracking of autonomous vehicles. ISA Trans. 2022, 129, 193–205. [Google Scholar] [CrossRef]





| Positive Direction | ||||||
|---|---|---|---|---|---|---|
| PWM Step (%) | RW Model | Kp | Ki | LW Model | Kp | Ki |
| 30 | 0.754 | 4.85 | 0.643 | 4.14 | ||
| 40 | 0.446 | 2.98 | 0.377 | 2.56 | ||
| 50 | 0.340 | 2.36 | 0.313 | 2.20 | ||
| 60 | 0.280 | 2.04 | 0.269 | 1.97 | ||
| 70 | 0.248 | 1.88 | 0.240 | 1.84 | ||
| 80 | 0.215 | 1.72 | 0.208 | 1.69 | ||
| 90 | 0.194 | 1.64 | 0.194 | 1.66 | ||
| 100 | 0.156 | 1.44 | 0.147 | 1.41 | ||
| Negative Direction | ||||||
| PWM Step (%) | RW Model | Kp | Ki | LW Model | Kp | Ki |
| 30 | 0.680 | 3.19 | 0.643 | 3.62 | ||
| 40 | 0.377 | 2.11 | 0.400 | 2.22 | ||
| 50 | 0.294 | 1.72 | 0.313 | 1.81 | ||
| 60 | 0.271 | 1.63 | 0.289 | 1.71 | ||
| 70 | 0.234 | 1.49 | 0.242 | 1.52 | ||
| 80 | 0.214 | 1.42 | 0.216 | 1.43 | ||
| 90 | 0.180 | 1.30 | 0.196 | 1.36 | ||
| 100 | 0.154 | 1.19 | 0.157 | 1.20 | ||
| PWM (%) | Right Wheel (rpm) | Left Wheel (rpm) | ||
|---|---|---|---|---|
| Positive | Negative | Positive | Negative | |
| 30 | 645 | −665 | 665 | −657 |
| 40 | 797 | −791 | 792 | −803 |
| 50 | 896 | −894 | 897 | −903 |
| 60 | 965 | −953 | 952 | −966 |
| 70 | 1016 | −991 | 992 | −1010 |
| 80 | 1053 | −1018 | 1017 | −1044 |
| 90 | 1112 | −1072 | 1070 | −1101 |
| 100 | 1184 | −1138 | 1126 | −1176 |
| Right Wheel | ||||
|---|---|---|---|---|
| Positive Direction | Negative Direction | |||
| ISE | ITAE | ISE | ITAE | |
| Gain Scheduling | ||||
| Multimodel Control: 2 Models | ||||
| Multimodel Control: 3 Models | ||||
| Multimodel Control: 4 Models | ||||
| Left Wheel | ||||
|---|---|---|---|---|
| Positive Direction | Negative Direction | |||
| ISE | ITAE | ISE | ITAE | |
| Gain Scheduling | ||||
| Multimodel Control: 2 Models | ||||
| Multimodel Control: 3 Models | ||||
| Multimodel Control: 4 Models | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miquelanti, M.G.; Pugliese, L.F.; Silva, W.W.A.G.; Braga, R.A.S.; Monte-Mor, J.A. Comparison between an Adaptive Gain Scheduling Control Strategy and a Fuzzy Multimodel Intelligent Control Applied to the Speed Control of Non-Holonomic Robots. Appl. Sci. 2024, 14, 6675. https://doi.org/10.3390/app14156675
Miquelanti MG, Pugliese LF, Silva WWAG, Braga RAS, Monte-Mor JA. Comparison between an Adaptive Gain Scheduling Control Strategy and a Fuzzy Multimodel Intelligent Control Applied to the Speed Control of Non-Holonomic Robots. Applied Sciences. 2024; 14(15):6675. https://doi.org/10.3390/app14156675
Chicago/Turabian StyleMiquelanti, Mateus G., Luiz F. Pugliese, Waner W. A. G. Silva, Rodrigo A. S. Braga, and Juliano A. Monte-Mor. 2024. "Comparison between an Adaptive Gain Scheduling Control Strategy and a Fuzzy Multimodel Intelligent Control Applied to the Speed Control of Non-Holonomic Robots" Applied Sciences 14, no. 15: 6675. https://doi.org/10.3390/app14156675
APA StyleMiquelanti, M. G., Pugliese, L. F., Silva, W. W. A. G., Braga, R. A. S., & Monte-Mor, J. A. (2024). Comparison between an Adaptive Gain Scheduling Control Strategy and a Fuzzy Multimodel Intelligent Control Applied to the Speed Control of Non-Holonomic Robots. Applied Sciences, 14(15), 6675. https://doi.org/10.3390/app14156675






