Research on the Dynamic Response Characteristics of the Propulsion Shaft System with an On-Shaft Generator in Ships
Abstract
:1. Introduction
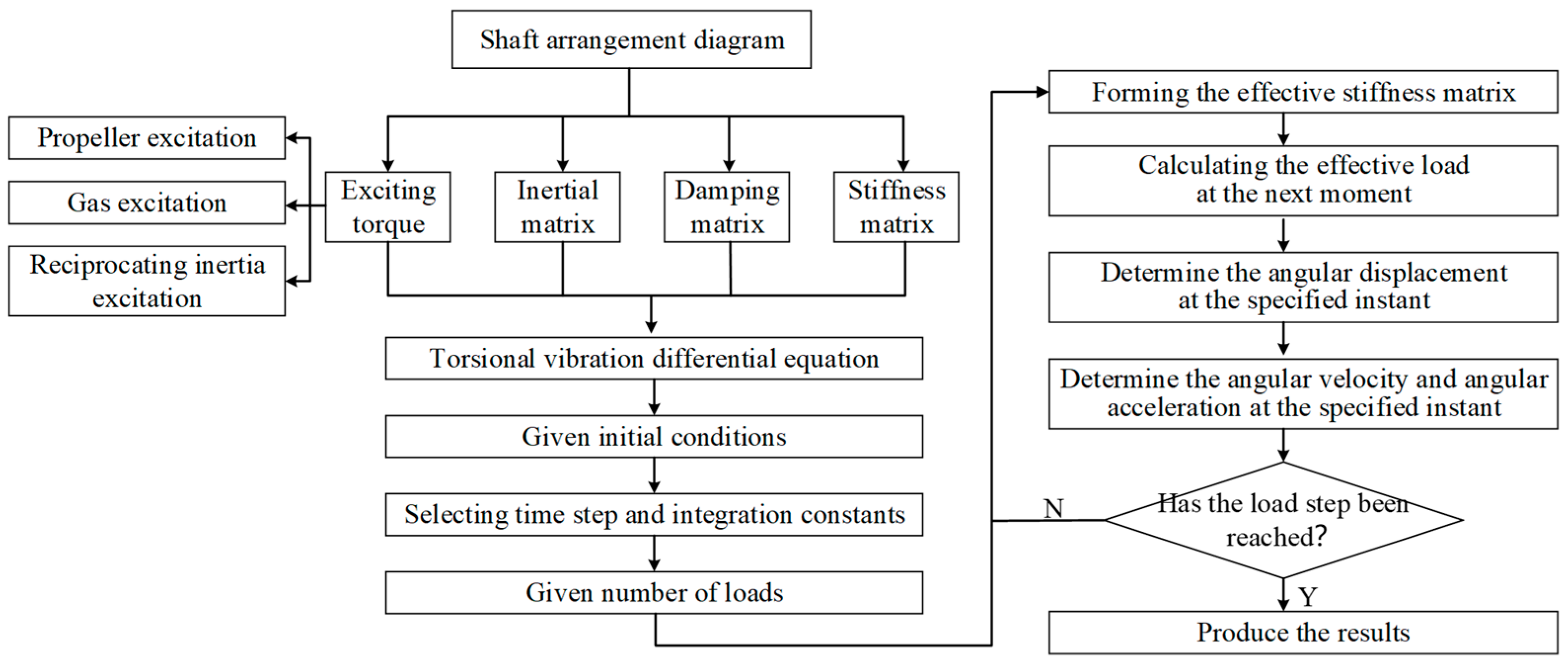
2. Transient Calculation Theory
2.1. Transient Calculation Model
2.2. Research on Dynamic Response Methods
3. Transient Response Simulation
3.1. Main Calculation Parameters
3.2. Simulation Modeling
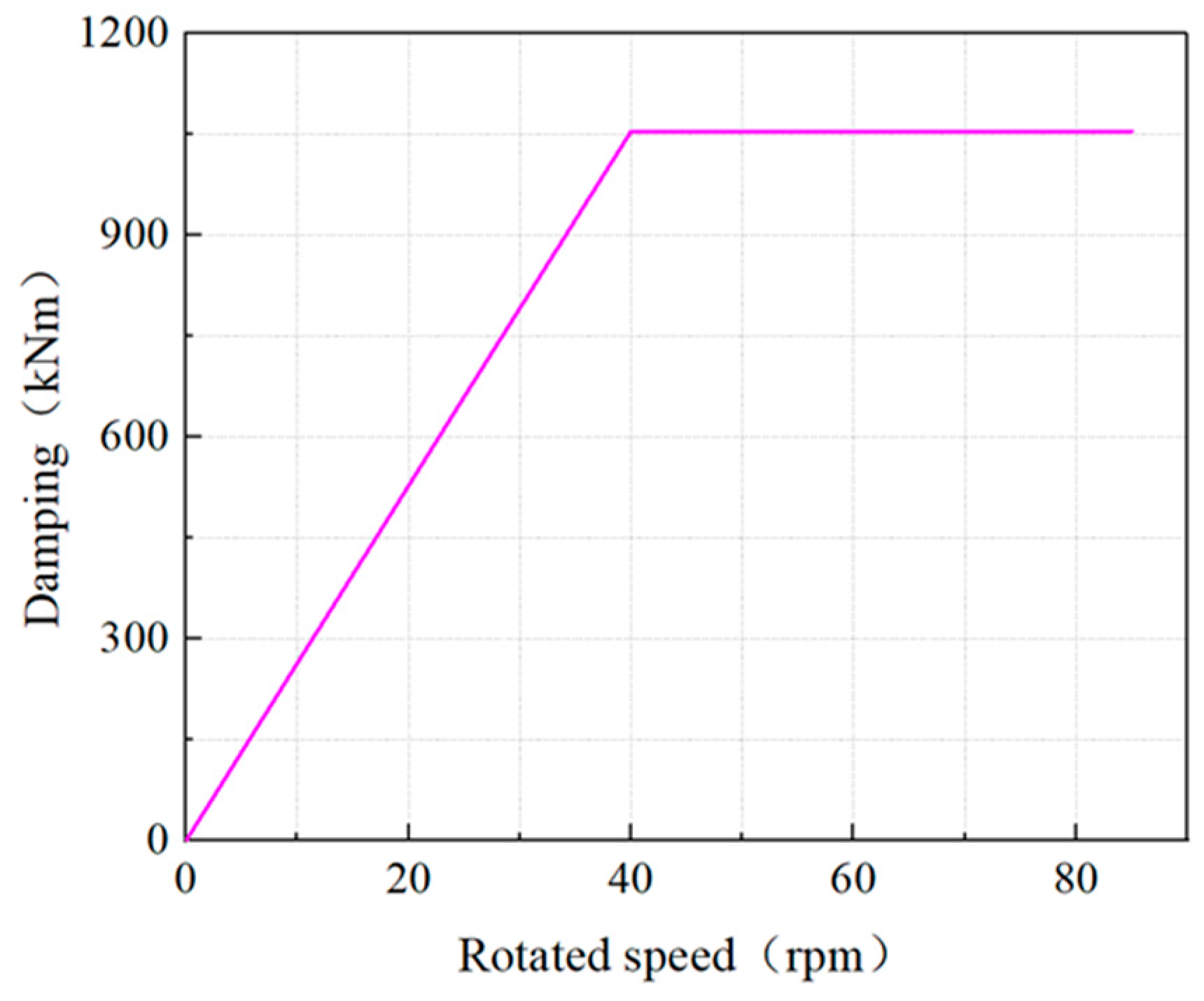
3.3. Research on Incentive and Damping Parameters
3.3.1. Transient Excitation Calculation
3.3.2. Transient Damping Calculation
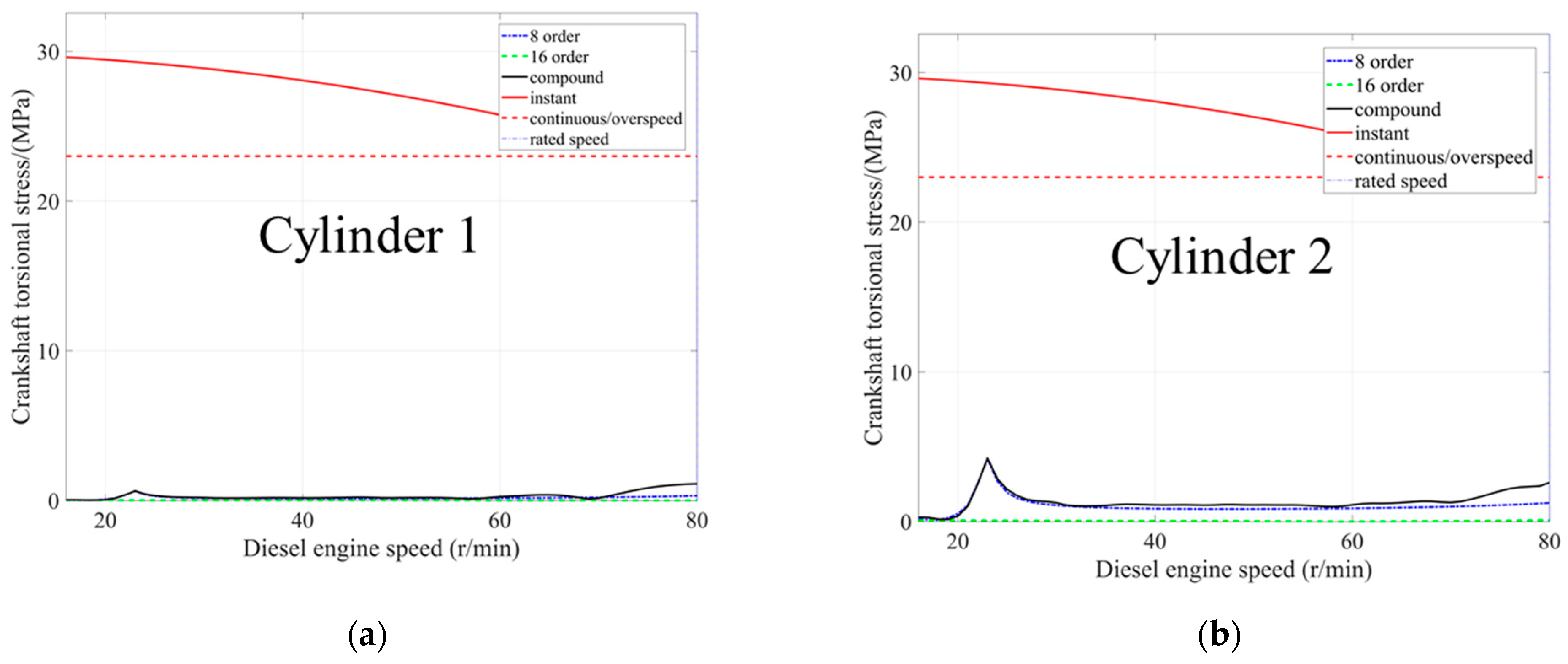
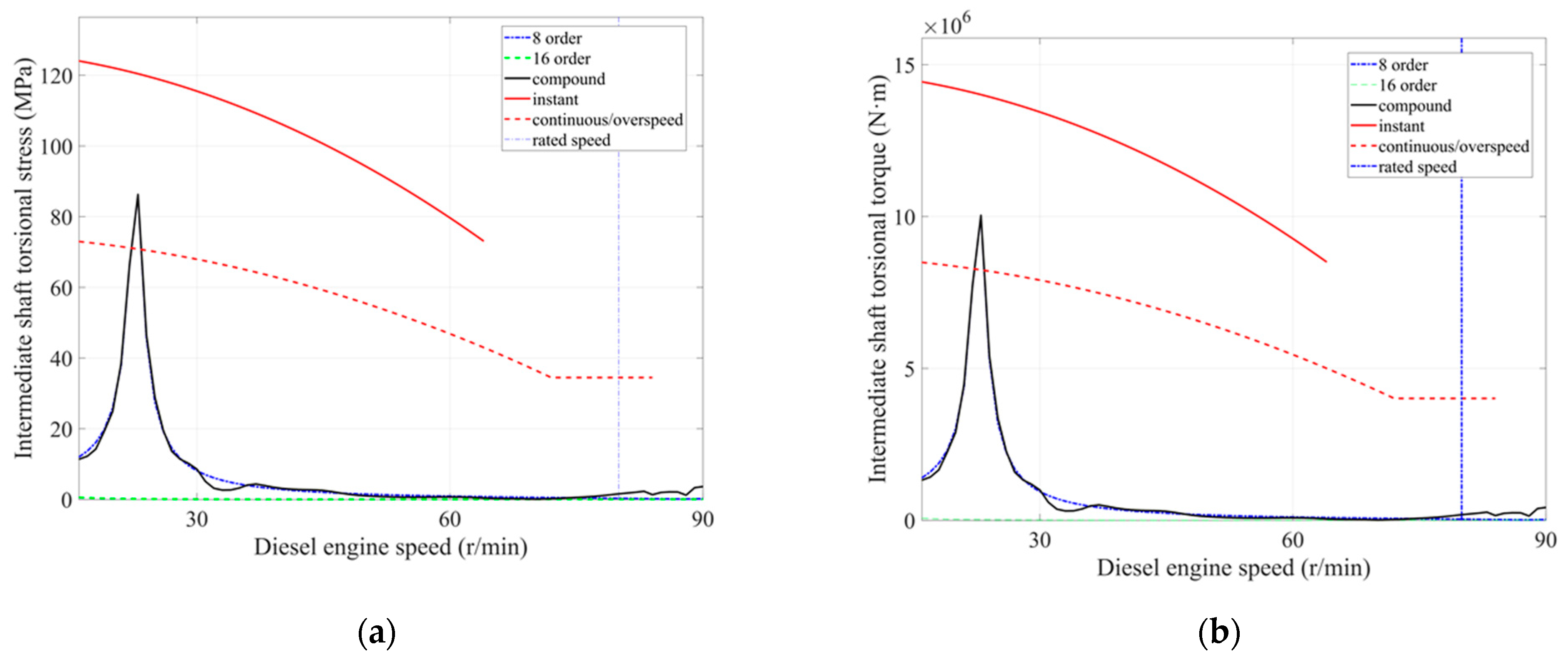
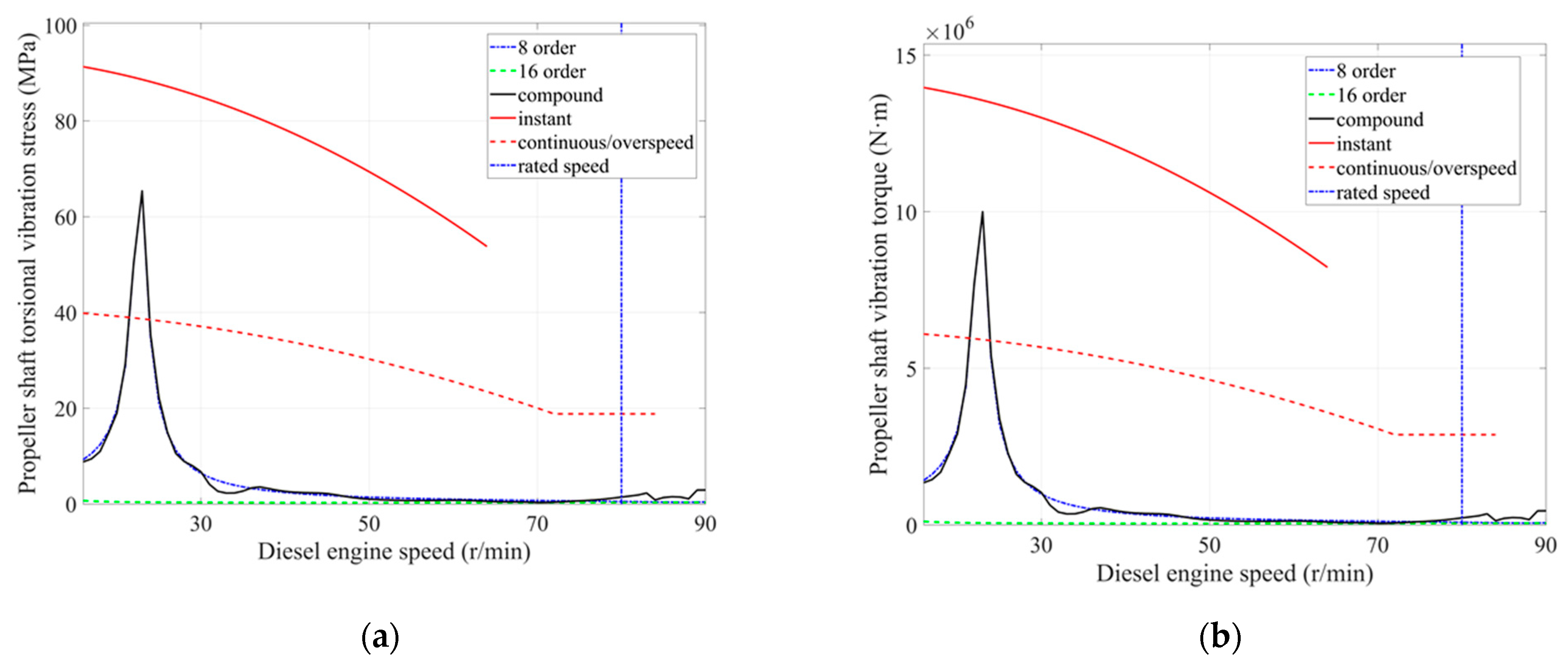
3.4. Simulation Result Analysis
4. Real Ship Experimental Verification
4.1. Experimental Equipment
4.2. Experimental System Layout and Parameter Setting
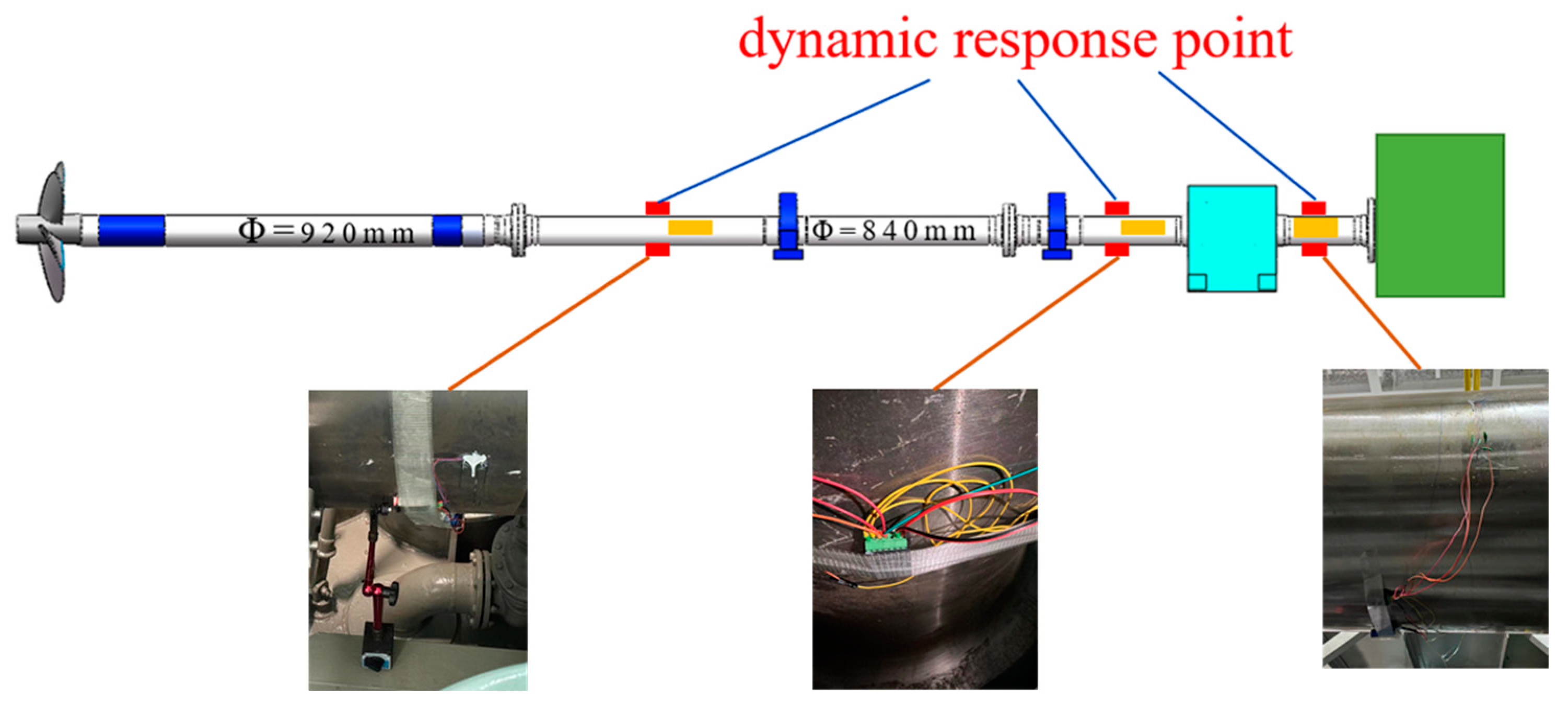
4.2.1. Experimental Point Layout
4.2.2. Experimental Measurement
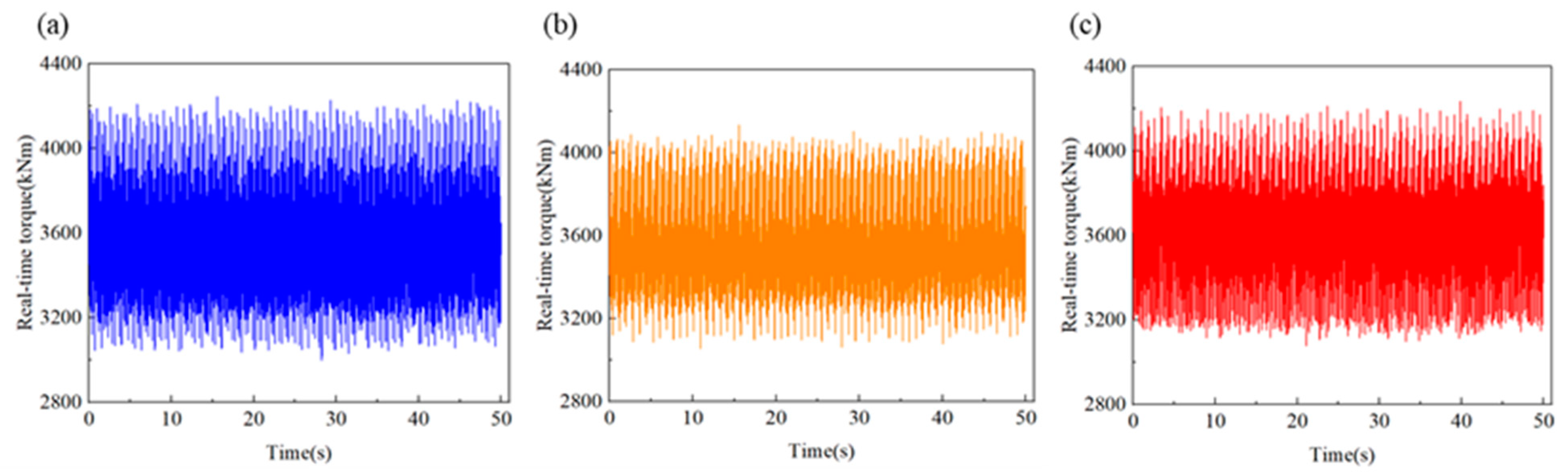
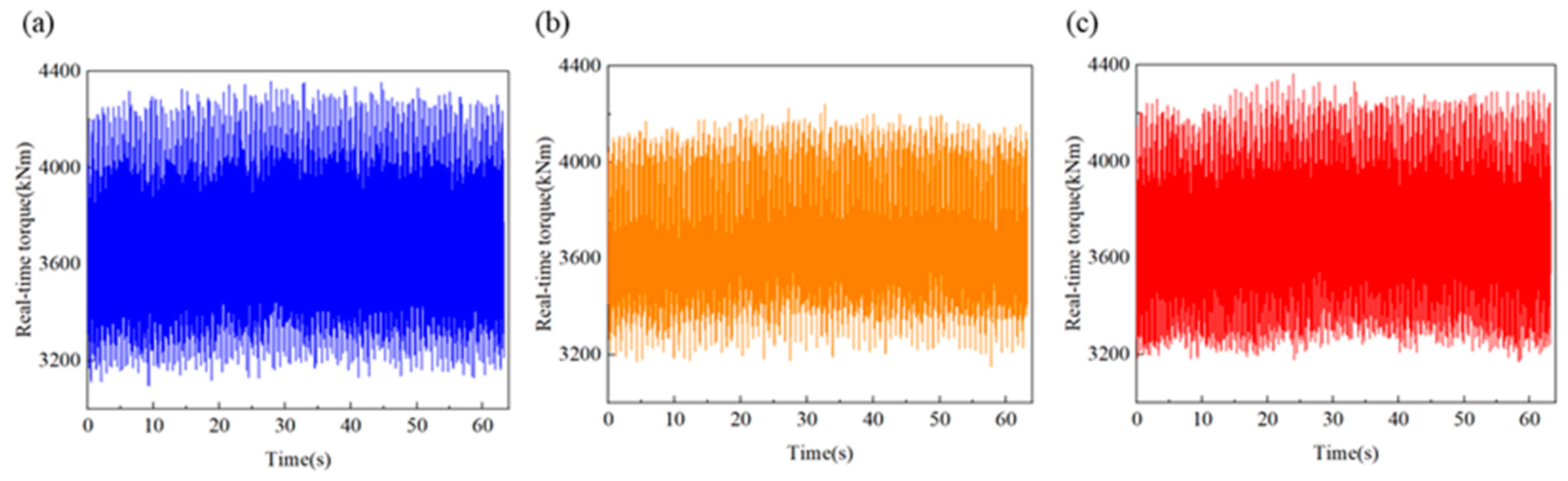
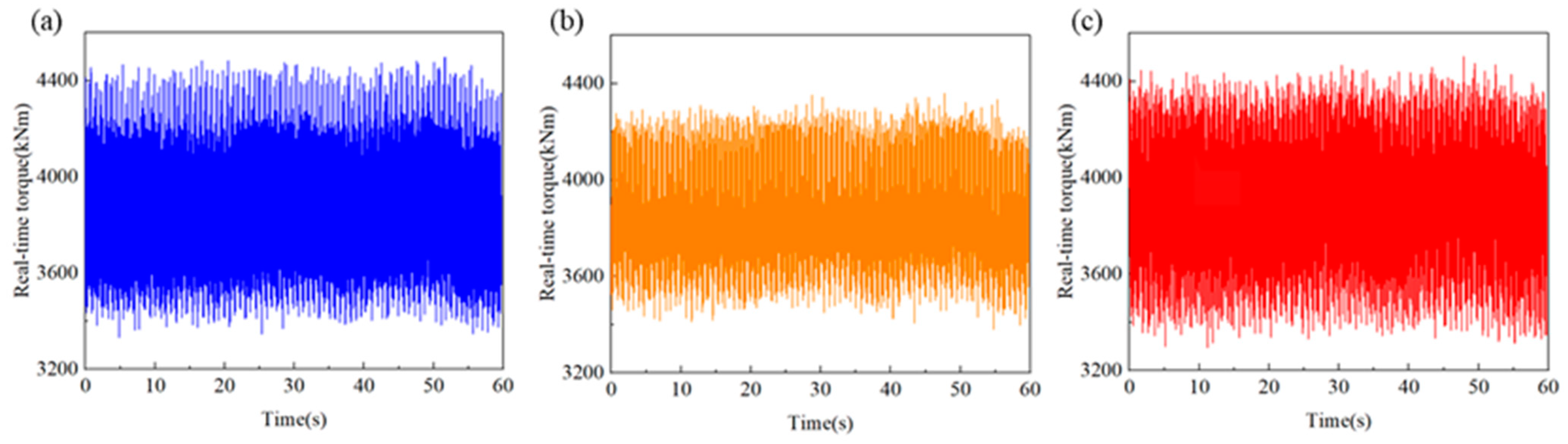
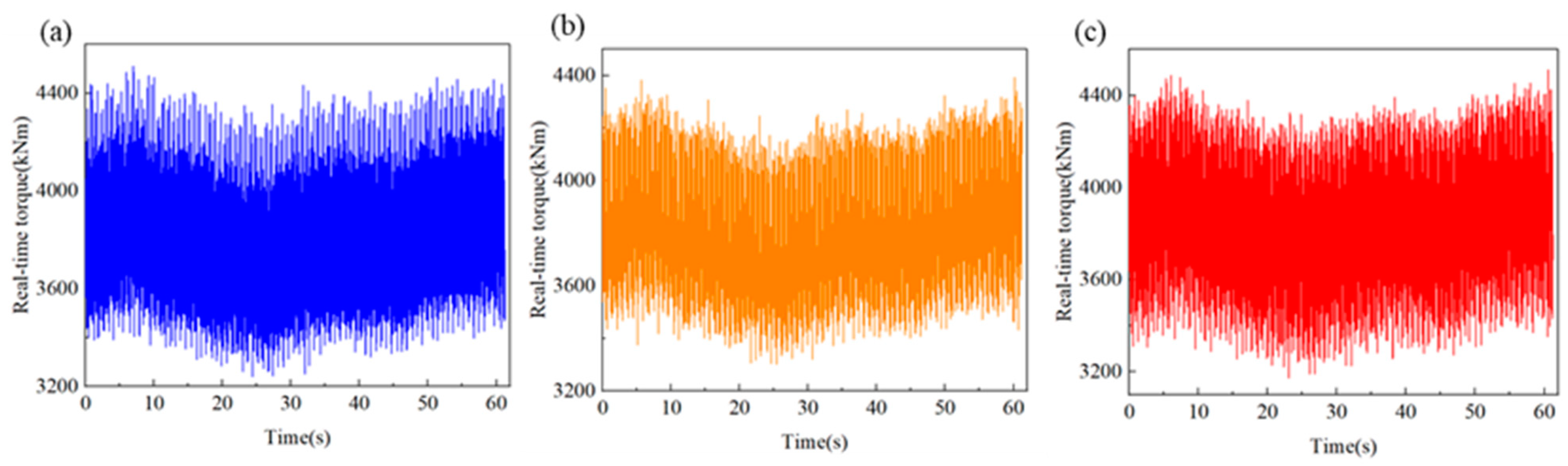
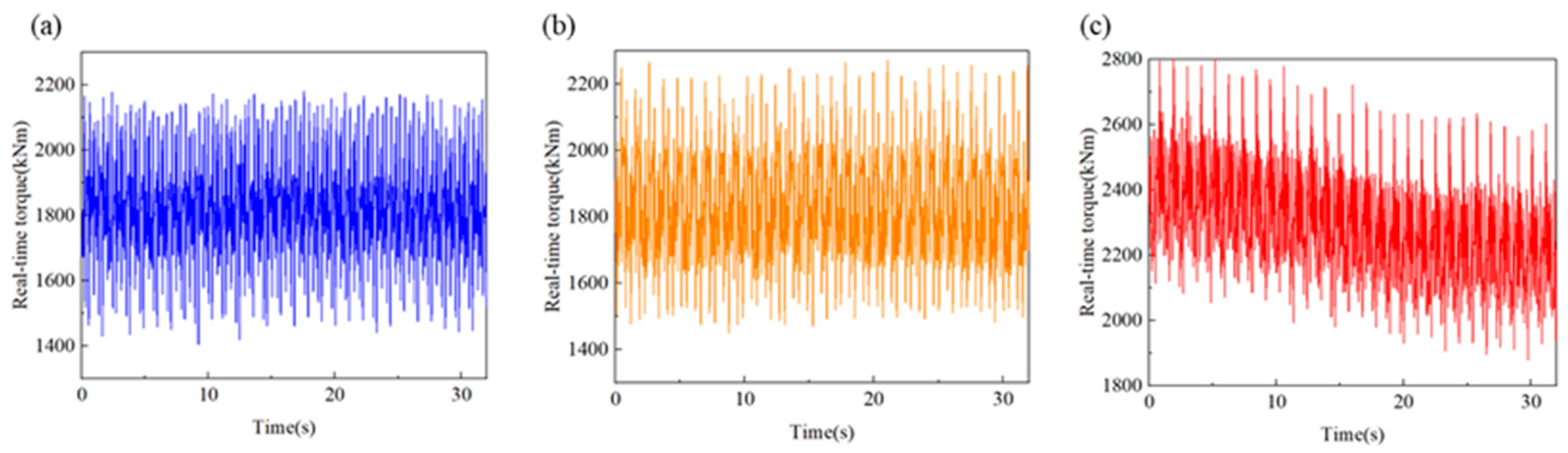
4.3. Experimental Result Analysis
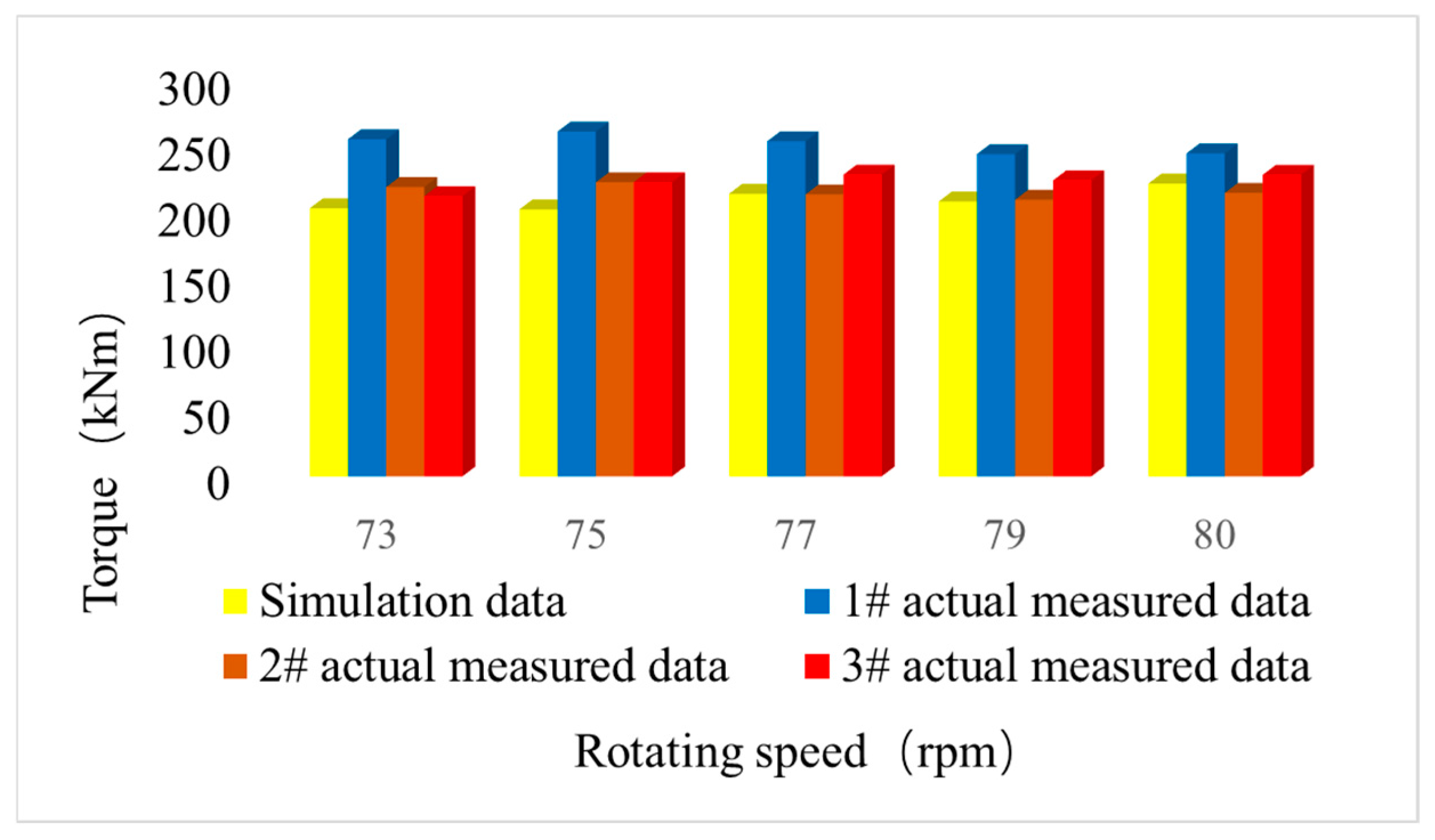
4.4. Simulation and Experimental Result Comparison Analysis
5. Conclusions
- (a)
- After the installation of the shaft-driven generator with or without bearing support, the measured torque at the pre- and post-generator measurement points in the propulsion shaft system is less than 10% different from the results of dynamic response simulation calculations, confirming the consistency between simulation results and actual ship experimental results. This further verifies the accuracy of the lumped-parameter system theoretical model of the propulsion shaft system with the shaft-driven generator.
- (b)
- Based on the actual ship experimental data, the theoretical calculation model is further calibrated, and the empirical coefficients in the calculation formula for the diesel engine excitation are revised to improve the accuracy of the simulation calculations.
- (c)
- Under normal operating conditions, the measured torque results at different measurement points are far less than the continuous allowable torque of 4.01 × 106 N·m and the instantaneous torque. This confirms that the installation of the shaft-driven generator without bearing support has a minimal impact on the dynamic response of the propulsion shaft system. The dynamic torque amplitude is within the allowable range, further indicating that the propulsion shaft system with the shaft-driven generator without bearing support can safely operate within the working speed range. This provides theoretical and experimental support for the future installation of the propulsion shaft system with the shaft-driven generator without bearing support.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, D.; Yu, J. Transient and Unstable Torsional Vibrations on a 4-Stroke Marine Diesel Engine. In Proceedings of the Internal Combustion Engine Division Spring Technical Conference, Salzburg, Austria, 11–14 May 2003. [Google Scholar]
- Manngård, M.; Koene, I.; Lund, W.; Haikonen, S.; Fagerholm, F.; Wilczek, M.; Toivonen, H. Torque estimation in marine propulsion systems. Mech. Syst. Signal Proc. 2022, 172, 108969. [Google Scholar] [CrossRef]
- Liao, P. Research and Software Development on Transient Torsional Vibration of Typical Propulsion Shaft Systems of Ships in Ice Areas. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2018. [Google Scholar]
- Li, J. Analysis and Research on Torsional Vibration of Propulsion Shafting of Ships Sailing in Ice Areas. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2016. [Google Scholar]
- Firouzi, J.; Ghassemi, H.; Shadmani, M. Analytical model for coupled torsional-longitudinal vibrations of marine propeller shafting system considering blade characteristics. Appl. Math. Model. 2021, 94, 737–756. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, R.; Wang, M. Research on the Marine Shafting Torsional Vibration with Gears Transmission. Int. J. Eng. Ind. 2012, 3, 99–111. [Google Scholar]
- Polić, D.; Ehlers, S.; Æsøy, V. Propeller torque load and propeller shaft torque response correlation during ice-propeller interaction. J. Mar. Sci. Appl. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Polić, D.; Æsøy, V.; Ehlers, S. Transient simulation of the propulsion machinery system operating in ice–modeling approach. Ocean Eng. 2016, 124, 437–449. [Google Scholar] [CrossRef]
- Zhao, F. Research on Random Excitation Response of Ship Propulsion Shafting Based on Non-Parametric Modeling. Master’s Thesis, Dalian Maritime University, Dalian, China, 2023. [Google Scholar]
- Zambon, A.; Moro, L. Torsional vibration analysis of diesel driven propulsion systems: The case of a polar-class vessel. Ocean Eng. 2022, 245, 110330. [Google Scholar] [CrossRef]
- Zambon, A.; Moro, L.; Oldford, D. Impact of different characteristics of the ice–propeller interaction torque on the torsional vibration response of a Polar-Class shaftline. Ocean Eng. 2022, 266, 112630. [Google Scholar] [CrossRef]
- Zambon, A.; Moro, L.; Kennedy, A.; Oldford, D. Torsional vibrations of Polar-Class shaftlines: Correlating ice–propeller interaction torque to sea ice thickness. Ocean Eng. 2023, 267, 113250. [Google Scholar] [CrossRef]
- Shen, X. Research on Torsional Vibration Characteristics of High-Power Complex Propulsion Shafting. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2013. [Google Scholar]
- Yang, Y.; Tang, W.; Ma, J. Optimal design for a VLCC propulsion system based on torsional vibration analysis. Procedia Eng. 2011, 15, 5378–5383. [Google Scholar] [CrossRef]
- Huang, G. Research on Simulation Method and Application of Shaft Torsional Vibration. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2016. [Google Scholar]
- Senjanović, I.; Ančić, I.; Magazinović, G.; Alujević, N.; Vladimir, N.; Cho, D. Validation of analytical methods for the estimation of the torsional vibrations of ship power transmission systems. Ocean Eng. 2019, 184, 107–120. [Google Scholar] [CrossRef]
- Senjanović, I.; Hadžić, N.; Murawski, L.; Vladimir, N.; Alujević, N.; Cho, D. Analytical procedures for torsional vibration analysis of ship power transmission system. Eng. Struct. 2019, 178, 227–244. [Google Scholar] [CrossRef]
- Batrak, Y.; Serdjuchenko, A.; Tarasenko, A. Calculation of Torsional Vibration Responses in Propulsion Shafting System Caused by Ice Impacts. In Proceedings of the Torsional Vibration Symposium, Salzburg, Austria, 21–23 May 2014. [Google Scholar]
- Batrak, Y.; Serdjuchenko, A.; Tarasenko, A. Calculation of propulsion shafting transient torsional vibration induced by ice Impacts on the Propeller Blades. In Proceedings of the WMTC, Saint-Petersburg, Russia, 29 May–1 June 2012. [Google Scholar]
- Batrak, Y. Ice induced propulsion shafting torsional vibration analysis issues and case studies. In Proceedings of the Torsional Vibration Symposium, Salzburg, Austria, 8–9 June 2017. [Google Scholar]
- Hu, Y. Design and Development of Three-Dimensional Analysis Platform for Ship Shafting. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2019. [Google Scholar]
- Vlahopoulos, N.; Zhao, X. An investigation of power flow in the mid-frequency range for systems of co-linear beams based on a hybrid finite element formulation. J. Sound Vibr. 2001, 242, 445–473. [Google Scholar] [CrossRef]
- Bulut, G. Dynamic stability analysis of torsional vibrations of a shaft system connected by a Hooke’s joint through a continuous system model. J. Sound Vibr. 2014, 333, 3691–3701. [Google Scholar] [CrossRef]
- Turhan, Ö.; Bulut, G. Linearly coupled shaft torsional and blade-bending vibrations in multi-stage rotor-blade systems. J. Sound Vibr. 2006, 296, 292–318. [Google Scholar] [CrossRef]
- Murawski, L.; Charchalis, A. Simplified method of torsional vibration calculation of marine power transmission system. Mar. Struct. 2014, 39, 335–349. [Google Scholar] [CrossRef]
- Murawski, L. Shaft line alignment analysis taking ship construction flexibility and deformations into consideration. Mar. Struct. 2015, 18, 62–84. [Google Scholar] [CrossRef]
- Buchacz, A. Introduction to synthesis of the torsional vibrating discrete-continuous mechatronic systems by means of the hypergraphs and structural numbers method. J. Vibroeng. 2012, 14, 514–519. [Google Scholar]
- Han, H.; Lee, K. Experimental verification for lateral-torsional coupled vibration of the propulsion shaft system in a ship. Eng. Fract. Mech. 2019, 104, 758–771. [Google Scholar] [CrossRef]
- Han, H.; Lee, K.; Park, S. Parametric study to identify the cause of high torsional vibration of the propulsion shaft in the ship. Eng. Fail. Anal. 2016, 59, 334–346. [Google Scholar] [CrossRef]
- Han, H.; Lee, K.; Park, S. Estimate of the fatigue life of the propulsion shaft from torsional vibration measurement and the linear damage summation law in ships. Ocean Eng. 2015, 107, 212–221. [Google Scholar] [CrossRef]
- Wang, Q.; Ying, Q.; Yang, S. Internal Combustion Engine Shafting Torsional Vibration, 1st ed.; Dalian University of Technology Press: Dalian, China, 1991; pp. 75–102. [Google Scholar]
- ICAS. International Association of Classification Societies: Polar Class Draft Technical Background Note for Shafting [S]; IACS: Kolkata, India, 2016. [Google Scholar]
- Siddique, M.F.; Ahmad, Z.; Ullah, N.; Kim, J. A Hybrid Deep Learning Approach: Integrating Short-Time Fourier Transform and Continuous Wavelet Transform for Improved Pipeline Leak Detection. Sensors 2023, 23, 8079. [Google Scholar] [CrossRef] [PubMed]
- Siddique, M.F.; Ahmad, Z.; Ullah, N.; Kim, J. Pipeline leak diagnosis based on leak-augmented scalograms and deep learning. Eng. Appl. Comp. Fluid. 2023, 17, 2225577. [Google Scholar] [CrossRef]




| Equipment | Parameter | Equipment | Parameter | ||
|---|---|---|---|---|---|
| main engine | model | 8G95ME-C | propeller | moment of inertia | 498,093 kgm2 |
| maximum continuous output power | 45,300 kW | mass | 80,105 kg | ||
| maximum continuous speed | 80 r/min | number of blades | 5 | ||
| number of cylinders | 8 | diameter | 10.1 m | ||
| cylinder bore diameter | 950 mm | vibration damper | model | Geislinger D260/GU | |
| firing order | 1-8-3-4-7-2-5-6 | torsional stiffness | 71 MNm/rad | ||
| piston stroke | 3460 mm | instantaneous elastic torque | 1150 kNm | ||
| flywheel | mass | 9331 kg | continuous elastic torque | 768 kNm | |
| moment of inertia | 35,000 kgm2 | mass | 11,200 kg | ||
| System Component | Inertia (kgm2) | System Component (MNm/rad) | Outer Diameter (mm) | Inner Diameter (mm) | Internal Damping (Nms/rad) | Damping Coefficient | Damping Factor |
|---|---|---|---|---|---|---|---|
| damper | 9890 | 71.0 | - | 0 | 155,000 | 0 | 0 |
| TVD | 5572 | 7812.5 | 1220 | 0 | 0 | 0.005 | 0 |
| cylinder | 91,505 | 6172.8 | 1220 | 0 | 0 | 0.005 | 0.0085 |
| cylinder | 91,505 | 6211.2 | 1220 | 0 | 0 | 0.005 | 0.0085 |
| cylinder | 91,505 | 6060.6 | 1220 | 0 | 0 | 0.005 | 0.0085 |
| cylinder | 91,505 | 9090.9 | 1220 | 0 | 0 | 0.005 | 0.0085 |
| camshaft drive | 18,833 | 9090.9 | 1220 | 0 | 0 | 0.005 | 0.0085 |
| cylinder | 91,505 | 6060.6 | 1220 | 0 | 0 | 0.005 | 0.0085 |
| cylinder | 91,505 | 6172.8 | 1220 | 0 | 0 | 0.005 | 0.0085 |
| cylinder | 91,505 | 6410.3 | 1220 | 0 | 0 | 0.005 | 0.0085 |
| cylinder | 91,505 | 9708.7 | 1220 | 0 | 0 | 0.005 | 0.0085 |
| thrust bearing | 13,385 | 14,925.4 | 1240 | 200 | 0 | 0 | 0.0085 |
| turn + rotor1 | 37,843 | 1280.4 | 840 | 0 | 0 | 0 | 0.005 |
| rotor1 + rotor2 | 28,551 | 703.2 | 840 | 0 | 0 | 0 | 0 |
| rotor2 + I/S | 5748 | 279.3 | 840 | 0 | 0 | 0 | 0 |
| I/S + P/S | 7917 | 407.8 | 920 | 0 | 0 | 0 | 0 |
| P/S + prop | 502,256 | - | - | 0 | 0 | 0 | 0 |
| No. | Experimental Parameter | Parameter Setting |
|---|---|---|
| 1 | sampling frequency | 1 kHz |
| 2 | strain range | 3189 με |
| 3 | bridge circuit | mode 6 |
| 4 | bridge voltage | 3 V |
| 5 | strain gauge resistance | 350 Ω |
| 6 | sensitivity coefficient | 2.09 |
| 7 | the outer diameter of the measurement shaft | 840 mm |
| 8 | elastic modulus | 206 GPa |
| 9 | Poisson ratio | 0.28 |
| Dynamic Torque | Torque Amplitude (kNm) | Torque Difference Ratio (%) |
|---|---|---|
| simulation torque | 153.48 | - |
| the midpoint of intermediate shaft torque | 154.26 | 0.06 |
| rear end of motor torque | 161.17 | 4.77 |
| the front end of the motor torque | 145.42 | 5.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Zhou, R.; Ma, Z.; Wang, J.; Ding, L. Research on the Dynamic Response Characteristics of the Propulsion Shaft System with an On-Shaft Generator in Ships. Appl. Sci. 2024, 14, 6769. https://doi.org/10.3390/app14156769
Guo Y, Zhou R, Ma Z, Wang J, Ding L. Research on the Dynamic Response Characteristics of the Propulsion Shaft System with an On-Shaft Generator in Ships. Applied Sciences. 2024; 14(15):6769. https://doi.org/10.3390/app14156769
Chicago/Turabian StyleGuo, Yukuo, Ruiping Zhou, Zhaozhao Ma, Jianzheng Wang, and Longqi Ding. 2024. "Research on the Dynamic Response Characteristics of the Propulsion Shaft System with an On-Shaft Generator in Ships" Applied Sciences 14, no. 15: 6769. https://doi.org/10.3390/app14156769
APA StyleGuo, Y., Zhou, R., Ma, Z., Wang, J., & Ding, L. (2024). Research on the Dynamic Response Characteristics of the Propulsion Shaft System with an On-Shaft Generator in Ships. Applied Sciences, 14(15), 6769. https://doi.org/10.3390/app14156769







