Location and Capacity Optimization of Waste Recycling Centers: Mathematical Models and Numerical Experiments

Abstract

With rapid urbanization growth, considerable amounts of construction waste are generated on an annual basis, posing significant economic and environmental challenges worldwide. Re-cycling construction waste is a sustainable way for waste disposal, leading to the necessity of meticulous planning of recycling centers. A well-designed plan for constructing recycling centers can effectively improve the recycling rate of construction waste while minimizing investment. This paper formulates a two-stage stochastic model for planning recycling centers with the objective of maximizing the recycling rate under different scenarios. This study comprehensively considers various uncertain factors, such as the amount of construction waste generated and the demand for recycled materials. A case study of Guangzhou is used for validation, which demonstrates the effectiveness of the developed model in planning recycling center construction. The comparison between the proposed model and a conventional mean value model shows the importance of accounting for uncertainties. Specifically, the derived results indicate that 7% more construction waste is recycled with the same investment in constructing recycling centers. Additionally, via a sensitivity analysis, valuable managerial insights on investing resources in recycling center construction are provided to decision makers. Ultimately, the research findings are expected to enhance the recycling rate of construction waste, thereby contributing to sustainable industry development.

1. Introduction

Construction waste comprises surplus materials from the spheres of construction, renovation, and demolition. They encompass, but are not limited to, activities such as land excavation, civil and building construction, site clearance, demolition processes, roadwork, and building renovation [1,2]. In 2022 alone, approximately 8.6 million tons of construction waste will be generated globally from various construction-related tasks [3]. Numerous countries worldwide, including the U.S., U.K., Spain, India, and China, are confronted with huge construction waste generation [4,5]. For instance, China, propelled by rapid urbanization, accounts for a substantial amount of construction waste, approximately 30–40% of the annual global construction waste estimates [6,7]. The generation of excessive construction waste leads to significant economic and environmental problems that cannot be ignored, e.g., natural resource overconsumption and soil contamination, resulting in serious negative health effects [8,9]. Generally, construction waste is treated at disposal sites such as landfills or recycling centers. However, in current practice, only 5% of the construction waste generated is recycled [10], indicating that landfills are still the most commonly used approach for disposing of construction waste. Depositing construction waste into designated landfill cells or areas within the landfills requires a fair amount of land resources to deal with the escalating amounts of construction waste [4]. Moreover, construction waste landfills cause land depletion and deterioration [11,12], solid waste exacerbation, as well as dust and gas emissions [13]. The presence of toxic materials in construction waste, such as asbestos and volatile organic compounds [12,14], constitutes the potential contamination of soil and water through erosion induced by rainfall. Recycling is widely perceived as an effective countermeasure to mitigate the economic and environmental challenges of landfills. The recycling of construction waste produces one of the most crucial raw materials for construction, i.e., recycled aggregates. When utilized effectively, recycled concrete aggregate exhibits commensurable mechanical and durability performances to conventional concrete but at a reduced cost [15,16]. Additionally, the conventional way of producing construction materials usually entails huge energy consumption and greenhouse gas emissions, directly contributing to environmental degradation and global warming. Conversely, products manufactured from recycled waste are a more sustainable alternative, as they reduce the need for raw resource extraction, minimize energy consumption, and lower greenhouse gas emissions [17,18].

Although it has been reported that 90% of construction waste can be recycled [5], most of the construction waste is still disposed of in landfills. Having that said, extensive studies have highlighted various factors contributing to the ineffective recycling of construction waste, along with recommendations to enhance recycling rates. Primarily, the volume of waste significantly exceeds the capacity of recycling centers, highlighting the inadequate number of such facilities [19,20]. Therefore, a well-designed plan for recycling centers can effectively improve the recycling rate of construction waste [21]. Nevertheless, the planning of these centers calls for complex decisions revolving around considerations of waste generation, transportation, and land use. High costs of land acquisition and imprecise estimation of waste quantities are the two main hindrances to construction waste recycling initiatives [19]. Additionally, the uncertain demand for recycled materials constitutes a critical factor influencing recycling rates as well [22]. Ignoring these uncertainties in construction waste management can lead to the inefficient use of substantial government investments in recycling centers [23,24]. Consequently, the plan for recycling centers should meticulously consider the quantities of construction waste generated and the demand for recycled materials across multiple scenarios [25]. Despite the importance of this endeavor, minimal studies have analyzed the plan of recycling centers within the context of stochastic scenarios, specifically addressing the uncertainties in both the supply of construction waste and demand for recycled materials.

The selection of site location and the determination of maximum processing capacity are pivotal decisions in the planning of recycling centers, which should be undertaken amidst varying degrees of uncertainty. Meanwhile, further investigation of governmental investment influencing the success of construction waste recycling is in great need. This study aims to design a plan for the construction of recycling centers to improve the recycling rate of construction waste with limited investments. Specifically, the objectives are to: (1) formulate a two-stage stochastic model that comprehensively considers recycling center planning with the stochastic scenarios of construction waste generation and recycled product demand; (2) validate the proposed model through a real-world case based on Guangzhou data and compare the optimal solutions with those derived by a mean value model; and (3) conduct a sensitivity analysis to demonstrate the impact of the construction waste management budget on the recycling rate, which can help stakeholders make more informed construction decisions.

The rest of this paper is structured as follows: Section 2 reviews and discusses related literature. Our two-stage model is formulated in Section 3. Computational experiments are conducted in Section 4. Finally, Section 5 summarizes our conclusions on construction waste management.

2. Literature Review

Owing to the increasing generation of construction waste and the adverse effects caused by landfills, both the government and the public have shown dedication to improving the recycling rate of construction waste [26]. Extensive studies have analyzed the challenges of construction waste recycling and offered recommendations for improving the recycling rate. Zhang et al. [27] adapted the waste hierarchy to explore construction waste practices in the EU, leading to the discovery of a direct correlation between landfilling restrictions and high recycling rates. By comparing construction waste management in the USA and China, Aslam et al. [4] revealed information about construction waste management policies, challenges, and other facts in the construction sector. The study concluded that suitable utilization of recycled materials enables the generation of financial income, leading to a stronger economy and environmental benefits. Meanwhile, Ulubeyli et al. [23] gave a full picture of management issues with recycling plants, which illustrated the lack of recycling plants encountered in many countries around the world, such as Brazil [28], Turkey [23], and China [19]. Additionally, the location and processing capacity of recycling plants should be carefully considered, as the cost of transportation and the initial investment play a decisive role in management. Taking China as a case study, Ma et al. [19] successfully demonstrated that inaccurate estimation of waste quantity poses threats to the recycling process and thus provided mitigatory measures by tightening the regulation on small-scale construction projects to counter the impact of uncertain factors. Most of these studies emphasized the importance of construction waste recycling center planning, governmental investment, and the imperative to account for uncertainties present in construction waste management.

Numerous studies affiliated with construction waste facility planning are outlined in Table 1. “NA” in the “Objective(s)” column indicates that the studies did not specify a mathematical optimization objective. These studies approached the investigated problem using two tools: evaluation techniques and mathematical programming. Among them, the most commonly used evaluation tool was the Analytical Hierarchy Process (AHP). Ding et al. [29] innovatively combined the AHP-Entropy approach with Geographic Information Systems (GISs) to categorize potential landfills into three levels. In addition, hybrid decision tools, including AHP, GIS, Monte Carlo simulation, and Technique for Order of Preference by Similarity to Ideal Solution, were provided for ranking the potential facility sites [30]. Another evaluation tool used was the stakeholder network. A qualitative questionnaire was administered to propose a new integration of the network, assisting in the decision-making process for selecting recycling centers [31]. However, both AHP and stakeholder networks may pose certain limitations, such as the uncertainty of the scale or the loss of information due to the reliability of less quantitative data [32]. Therefore, it can only cater to general planning, while the actual influence and construction details still need to be considered. On the other hand, mathematical programming methods, which are more quantitative, have the potential to address this issue. Mixed integer linear programming (MILP) models attracted significant attention during the early days. For instance, Galan et al. [33] identified the locations and capacity of the transfer stations and recycling plants by formulating a MILP model. Considering the recycling network design requires lengthy and tedious planning, Pan et al. [21] deployed the multi-objective, multi-period MILP model to determine the optimal locations and the expansion strategy for construction waste recycling centers. However, methods based on AHP and MILP always assumed the research environment was certain, overlooking the uncertainty in construction waste management that impacts the planning of recycling initiatives [25].

Heuristic algorithms are widely used to solve strategic and operational planning problems in various industries [34,35,36]. When compared to multi-objective MILP models, they can efficiently solve multi-objective problems and overcome the discontinuity of objective and constraint functions [37,38].However, they require complex parameter settings and incur high computational costs. The swarm algorithm and GA-PSO algorithm were successfully applied to balance various objectives but failed to optimize the capacity of recycling centers in uncertain situations [39,40,41]. From a lifecycle perspective, Atta and Bakhoum employed lifecycle assessment (LCA) to identify eco-friendly candidate locations for recycling centers [42]. This method is effective for optimizing environmental objectives; however, it does not align with the government’s focus on recycling rates [40,41].

Table 1. Summary of the existing literature.

Studies	Facility Planning Methods	Objective (s)	Uncertain Factors Considered	Deciding the Optimal Capacity
[29]	AHP	NA	No	No
[30]	AHP	NA	No	No
[31]	Stakeholder network	Provide high-value recycled material	No	No
[33]	MILP	Minimize the total costs	No	No
[21]	MILP	Maximize the recycling rate; Maximize the profits of recycling firms; Minimize the costs of contractors for disposing of CDW	No	Yes
[40]	Swarm algorithm	Minimize environmental impact; Minimize total costs	No	Yes
[39]	Swarm algorithm	Minimize total costs	Demand for goods	No
[41]	GA-PSO algorithm	Minimize total costs	No	No
[42]	LCA	Minimize environmental impact	All input data	No
Yang and Chen (2020) [26]	RO	Minimize total costs	Construction waste generation	No
[43]	RO	Minimize total costs	Construction waste generation; Transportation cost	No
[25]	RO	Minimize total costs	Construction waste generation; Demand for recycled construction material	No
[44]	RO	Minimize total costs	Construction waste generation	No
[45]	RO	Minimize total costs	Construction waste generation	No
[46]	SO	Maximize the expected profit	Construction waste generation; Recycling rate in recycling facility	No

Table 1. Summary of the existing literature.

Studies	Facility Planning Methods	Objective (s)	Uncertain Factors Considered	Deciding the Optimal Capacity
[29]	AHP	NA	No	No
[30]	AHP	NA	No	No
[31]	Stakeholder network	Provide high-value recycled material	No	No
[33]	MILP	Minimize the total costs	No	No
[21]	MILP	Maximize the recycling rate; Maximize the profits of recycling firms; Minimize the costs of contractors for disposing of CDW	No	Yes
[40]	Swarm algorithm	Minimize environmental impact; Minimize total costs	No	Yes
[39]	Swarm algorithm	Minimize total costs	Demand for goods	No
[41]	GA-PSO algorithm	Minimize total costs	No	No
[42]	LCA	Minimize environmental impact	All input data	No
Yang and Chen (2020) [26]	RO	Minimize total costs	Construction waste generation	No
[43]	RO	Minimize total costs	Construction waste generation; Transportation cost	No
[25]	RO	Minimize total costs	Construction waste generation; Demand for recycled construction material	No
[44]	RO	Minimize total costs	Construction waste generation	No
[45]	RO	Minimize total costs	Construction waste generation	No
[46]	SO	Maximize the expected profit	Construction waste generation; Recycling rate in recycling facility	No

Robust optimization (RO) methods were applied in solving the site selection problems under uncertain factors. By setting the maximum disturbance thresholds for the uncertainty factors, the robust methods guarantee the decision-maker against stochastic uncertainty [47]. This is proven by Yang and Chen [26], Jahangiri et al. [44], and Wu et al. [45], where they proposed a robust optimization model for designing a construction recycling network that not only accounted for the numbers, locations, and capacities of sorting and processing facilities but also the quantities of construction waste allocated between them. Ultimately, this model emphasized the adaptation of facility capacities as a way to counteract supply uncertainty. Notably, the influence of transportation costs on the recycling rate was also factored in. Likewise, Li et al. [43] explored two uncertainties (waste generation and transportation costs) to determine optimal facility locations that can minimize the total costs. With the same optimal objective, another robust method was used to develop the facility location model, taking into consideration supply and demand uncertainties [25]. This approach aligns the model more closely with the realities of the construction industry, helping decisionmakers choose better locations. However, robust optimization methods always take into account the worst possible scenarios, leading to potentially substantial investments by decision makers to attain the objective function [25].

Stochastic optimization (SO) provides an alternative mathematical programming method to deal with uncertainty in construction waste management. This method is proven highly versatile by its wide application in many uncertain location problems, e.g., warehouses [48], electronic equipment [49], and distribution centers [50]. In the topic related to construction waste facility planning, Saif et al. [46] developed a two-stage stochastic model for a reverse logistics network tailored to cope with the uncertainty of the supply and quality of the materials, aiming to achieve maximum profits by selling recycled materials. Primarily, the operational status of recycling centers was denoted by binary variables; however, these variables did not capture the optimal area or capacity of these facilities.

In summary, existing methods were unable to optimize the capacity and location of recycling centers in uncertain situations. Evaluation tools such as AHP and stakeholder network plans were relatively simple to operate, but due to their reliance on less quantitative data, they were not capable of handling uncertainty about construction waste or optimizing the capacity of recycling centers. MILP and heuristic algorithms solved multi-objective problems in construction management, but they considered uncertainty in a rather limited manner, focusing primarily on the demand for recycled material. RO methods protected decision makers against stochastic uncertainty by considering the worst possible scenarios. This approach often required substantial investments to achieve the objective function. Additionally, the objectives of optimization focused on minimizing total costs or environmental impact; however, the impacts of government interventions and understanding the strategies remained a noticeable gap. The government, whose objective is to maximize the waste recycling rate, plays an important role in construction waste management [17]. Thus, from a governmental perspective, particularly on its strategies and impacts, they remain relatively underexplored.

3. Problem Description and Model Formulation

This study focuses on the problem of an uncertain supply of construction waste and fluctuating demand for recycled materials to optimally determine the capacities and locations of recycling centers. Section 3.1 first presents a detailed problem statement, while a two-stage stochastic programming model is formulated in Section 3.2.

3.1. Problem Statement

Consider a region with $S$ construction sites where the demolition of existing buildings takes place (indexed by $s$, $s=1,\dots ,S$), resulting in the generation of construction waste. Generally, waste generated will be disposed of through landfilling, wherein it is collected and transported to designated landfill sites. Given that many resourceful materials can be recycled from waste and reused in new projects, the regional government is now planning to select from $R$ candidate locations to establish waste recycling centers (indexed by $r$). The maximum area that can be used to establish recycling centers at location $r$ is known as $a_r$. The constructed area of the recycling center at location $r$, denoted by ${\alpha }_r$ (to be determined), should be no greater than $a_r$. The capacity of the recycling center at location $r$ is $e^1{\alpha }_r$ ton, where $e^1$ is a coefficient representing the waste handling capacity per unit area of recycling centers (ton/m²). The construction waste can be delivered either to landfill sites or to recycling centers (if established) for disposal. If the waste is delivered to a landfill site, it will be directly landfilled. However, if the waste is delivered to recycling centers, it will be sorted and reused. Denote $e^2$ as a conversion rate of waste to materials, i.e., $e^2$ tons of building materials can be recycled from one ton of construction waste. Subsequently, the recycled materials will then be sold to $S^{\prime }$ construction sites of new projects for reutilization to foster a sustainable cycle. Additionally, $s$ is used to index the construction site requiring recycled materials, where $s=S+1,\dots ,S+S^{\prime }$. The objective of the government is to maximize waste recycling, i.e., the weight of recycled building materials delivered to construction sites for reusing, subject to a predetermined cost threshold $C^{max}$. Specifically, the unit cost of establishing a recycling center at location $r$ per square meter (including land acquisition and construction costs) is denoted as $C_r^1$. The transportation cost between the construction site $s$ and recycling center $r$ is denoted by $C_{s,r}^2$. If $s=1,\dots ,S$, it indicates the cost of delivering one ton of construction waste from a construction site $s$ to a recycling center $r$; if $s=S+1,\dots ,S+S^{\prime }$, it indicates the cost of delivering one ton of recycled materials from a recycling center $r$ to a construction site $s$. Therefore, the total costs used to establish the recycling centers and transport waste and materials should be no greater than $C^{max}$.

As site selection for recycling centers is a long-term decision, we shall comprehensively account for the stochastic amount of construction waste generated from demolition activities and the stochastic amount of building materials necessitated by future projects. Consider $\Omega$ scenarios (indexed by $\omega$), each with a possibility of $p_{\omega }$, and ${\sum }_{\omega =1}^{\Omega }{p}_{\omega }=1$. The stochastic parameter $V_{s,\omega }$ is used to indicate the weight of construction waste generated by the construction site $s=1,\dots ,S$ or the weight of recycled building materials required by the construction site $s=S+1,\dots ,S+S^{\prime }$ in each scenario $\omega$. The uncertainty of parameter $V_{s,\omega }$ leads to the formulation of the investigated problem as a two-stage stochastic program. In the first stage, the government decides the establishment of recycling centers (i.e., variable ${\alpha }_r$). In the second stage, the government observes the realization of $V_{s,\omega }$ and further decides (1) the weight of construction waste delivered from construction site $s$ to recycling center $r$ in scenario $\omega$, denoted by ${\beta }_{s,r,\omega }$ ($s=1,\dots ,S)$; (2) the weight of recycled building materials from recycling center $r$ to construction site $s$ in scenario $\omega$, denoted by ${\beta }_{s,r,\omega }$ ($s=S+1,\dots ,S+S^{\prime }$); (3) the weight of construction waste delivered from construction site $s$ to landfill site in scenario $\omega$, denoted by ${\gamma }_{s,\omega }$ ($s=1,\dots ,S)$.

3.2. Model Formulation

According to the analysis of the investigated problem, it can be formulated into a two-stage stochastic programming model. This study focuses on two underlying assumptions: (1) this paper only considers recyclable construction waste, while non-recyclable waste will still be disposed of via landfilling; and (2) there is no upper limit on the capacity of a landfill site because all construction waste is delivered to the landfill site prior to the establishment of recycling centers. The notation used in this paper is listed as follows:

• Indices:

• $r$: index for the location of the recycling center
• $s$: index for the construction site
• $\omega$: index for the scenario

• Parameters:

• $R$: the number of candidate locations for establishing recycling centers
• $S$: the number of construction sites that generate construction waste ($s=1,\dots ,S$)
• $S^{\prime }$: the number of construction sites that require recycled building materials ($s=S+1,\dots ,S+S^{\prime }$)
• $\Omega$: the number of scenarios
• $a_r$: the maximum area of the recycling center at location $r$
• $e^1$: the waste handling capacity per unit area of recycling centers
• $e^2$: the weight of building materials recycled per ton of construction waste
• $C_r^1$: the unit cost of establishing a recycling center at a location $r$
• $C_{s,r}^2$: the unit cost of delivering one ton of construction waste from the construction site $s=1,\dots ,S$ to the recycling center $r$ or the unit cost of delivering one ton of recycled materials from the recycling center $r$ to the construction site $s=S+1,\dots ,S+S^{\prime }$ (CNY/ton)
• $C_s^3$: the unit cost of delivering one ton of construction waste from the construction site $s=1,\dots ,S$ to the landfill site (CNY/ton)
• $C^{max}$: the maximum total costs
• $p_{\omega }$: the possibility of scenario $\omega$
• $V_{s,\omega }$: the weight of construction waste generated by the construction site $s=1,\dots ,S$ or the weight of recycled building materials required by the construction site $s=S+1,\dots ,S+S^{\prime }$ in scenario $\omega$

• Variables:

• ${\alpha }_r$: continuous, the constructed area of the recycling center at location $r=1,\dots ,R$
• ${\beta }_{s,r,\omega }$: continuous, the weight of construction waste delivered from construction site $s=1,\dots ,S$ to recycling center $r$ or the weight of recycled building materials from recycling center $r$ to construction site $s=S+1,\dots ,S+S^{\prime }$ in scenario $\omega$
• ${\gamma }_{s,\omega }$: continuous, the weight of construction waste delivered from the construction site $s=1,\dots ,S$ to the landfill site in the scenario $\omega$

• Mathematical model:

Based on the above definition of indices, parameters, and variables, a two-stage stochastic programming model is formulated as follows.

$$\begin{array}{}\mathrm{(1)}& \left[\mathbf{M}1\right] \mathrm{Maximize}{\sum }_{\omega =1}^{\mathsf{\Omega }}{p}_{\omega }{\sum }_{r=1}^R{\sum }_{s=S+1}^{S+S^{\prime }}{\beta }_{s,r,\omega }\hfill & \mathrm{(2)}& \mathrm{s}.\mathrm{t}. {\gamma }_{s,\omega }+{\sum }_{r=1}^R{\beta }_{s,r,\omega }=V_{s,\omega }\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=1,\dots ,S, \omega =1,\dots ,\mathsf{\Omega }\mathrm{(3)}& {\sum }_{s=1}^S{\beta }_{s,r,\omega }\le e^1{\alpha }_r\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall r=1,\dots ,R,\omega =1,\dots ,\mathsf{\Omega }\mathrm{(4)}& e^2{\sum }_{s=1}^S{\beta }_{s,r,\omega }\ge {\sum }_{s=S+1}^{S+S^{\prime }}{\beta }_{s,r,\omega }\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall r=1,\dots ,R,\omega =1,\dots ,\mathsf{\Omega }\mathrm{(5)}& {\sum }_{r=1}^R{\beta }_{s,r,\omega }\le V_{s,\omega }\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=S+1,\dots ,S+S^{\prime },\omega =1,\dots ,\mathsf{\Omega }\mathrm{(6)}& {\sum }_{r=1}^R\left(C_r^1{\alpha }_r+{\sum }_{s=1}^{S+S^{\prime }}{C}_{s,r}^2{\beta }_{s,r,\omega }\right)+{\sum }_{s=1}^S{C}_s^3{\gamma }_{s,\omega }\le C^{max}& \hfill \hspace{0.5em}\forall \omega =1,\dots ,\mathsf{\Omega }\mathrm{(7)}& 0\le {\alpha }_r\le a_r\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall r=1,\dots ,R\mathrm{(8)}& {\beta }_{s,r,\omega }\ge 0\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=1,\dots ,S+S^{\prime },r=1,\dots ,R,\omega =1,\dots ,\mathsf{\Omega }\mathrm{(9)}& {\gamma }_{s,\omega }\ge 0\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=1,\dots ,S, \omega =1,\dots ,\mathsf{\Omega }\end{array}$$

Objective (1) maximizes the weight of building materials recycled from construction waste and delivered to construction sites that require recycled building materials. Constraints (2) indicate that all the construction waste generated by each construction site is delivered either to landfill sites or to recycling centers in all scenarios. Constraints (3) guarantee that the total weight of construction waste delivered from all $S$ construction sites to each recycling center $r$ should not exceed the waste handling capacity of the recycling center in all scenarios. Constraints (4) ensure that the total weight of building materials delivered from each recycling center $r$ to all $S^{\prime }$ construction sites should not exceed the maximum weight of building materials that can be recycled from construction waste in all scenarios. Constraints (5) require that the weight of building materials delivered from all recycling centers to each construction site $s=S+1,\dots ,S+S^{\prime }$ should not exceed the weight of recycled building materials required by the construction site. Constraints (6) set an upper limit on the total expenses, covering land acquisition, building recycling centers, and transporting construction waste and recycled materials. Constraints (7)–(9) define the domains of the decision variables.

4. Computational Experiments

After completing the problem description, we then proceed to utilize the data from Guangzhou to illustrate the functionality of our proposed two-stage stochastic programming model. Based on the 10-year statistical data on the volume of construction waste generated in Guangzhou (from 2010 to 2019) [51], evidently, the city has shown a continuous growth trend in construction waste generation. As urbanization progresses in Guangzhou, the volume of construction waste generated continues to rise annually. This escalating trend raises concerns about the capacity of existing disposal facilities to handle the upward trajectory of construction waste. In light of this challenge, there is a pressing obligation to explore the establishment of additional construction waste recycling centers in Guangzhou. Stochastic optimization is leveraged for the planning of new construction waste recycling centers. Furthermore, this section underscores the importance of accounting for the stochastic nature of construction waste generation and the demand for recycled materials in waste management. By juxtaposing the model against a mean value model, this study demonstrates the efficacy of incorporating these uncertainties. Additionally, a sensitivity analysis is conducted to evaluate the impact of governmental investment in waste disposal on the recycling rate of construction waste. This endeavor enables the government to be furnished with valuable insights for budgetary decision-making in the planning of new recycling centers.

4.1. Experimental Setting

Our case study interprets the data primarily from two reliable sources. Firstly, official documents related to the location of identified potential construction waste recycling facilities and landfill sites, land use costs, the amount of construction waste generated, and the demand for materials recycled from construction waste are collected. Secondly, relevant literature provided supplementary information about the transportation costs, disposal fees of landfills, and construction costs of recycling centers (including land use costs and equipment fees). The above-mentioned can be further referred to in

Table 2. Relevant official documents and literature.

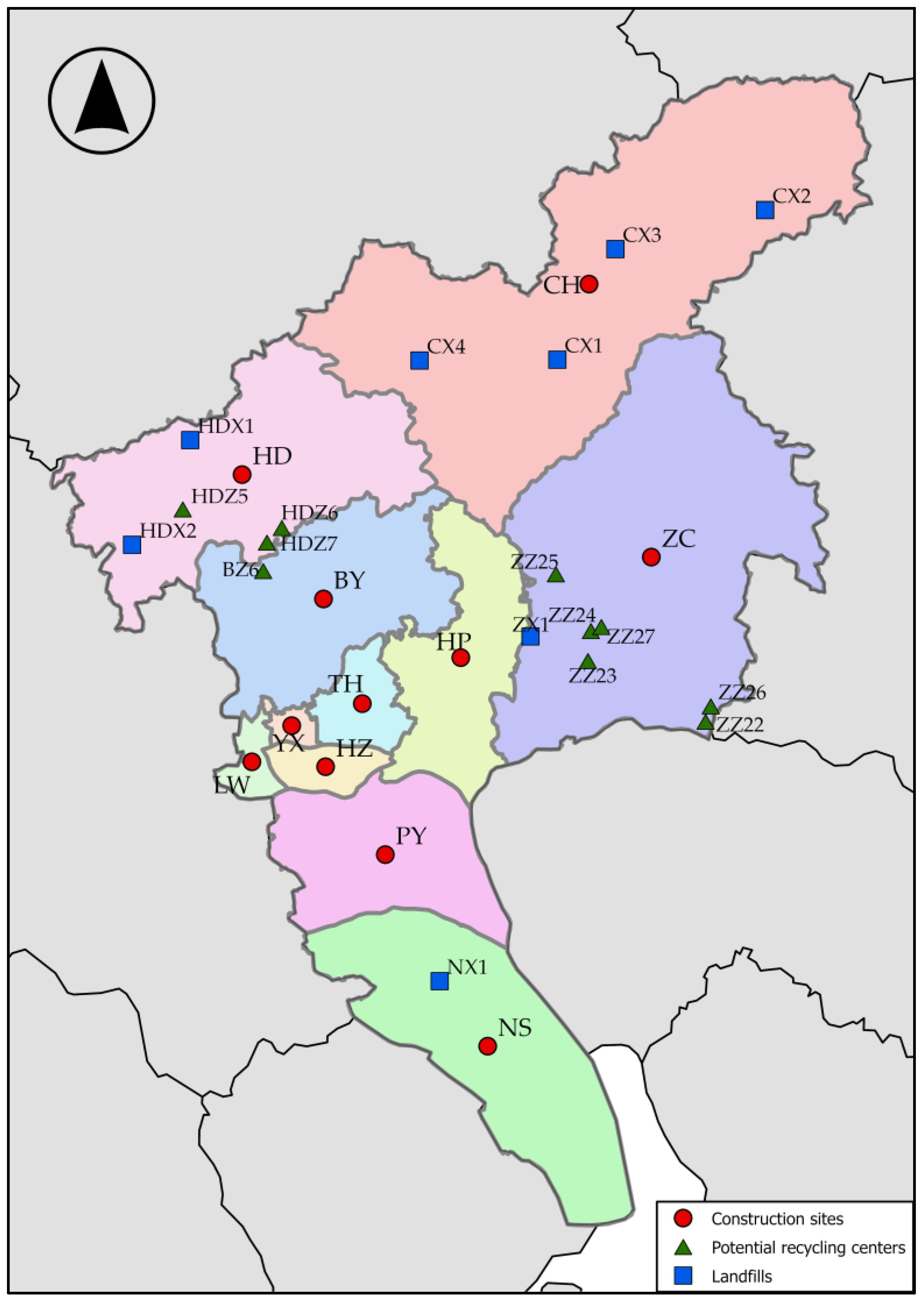
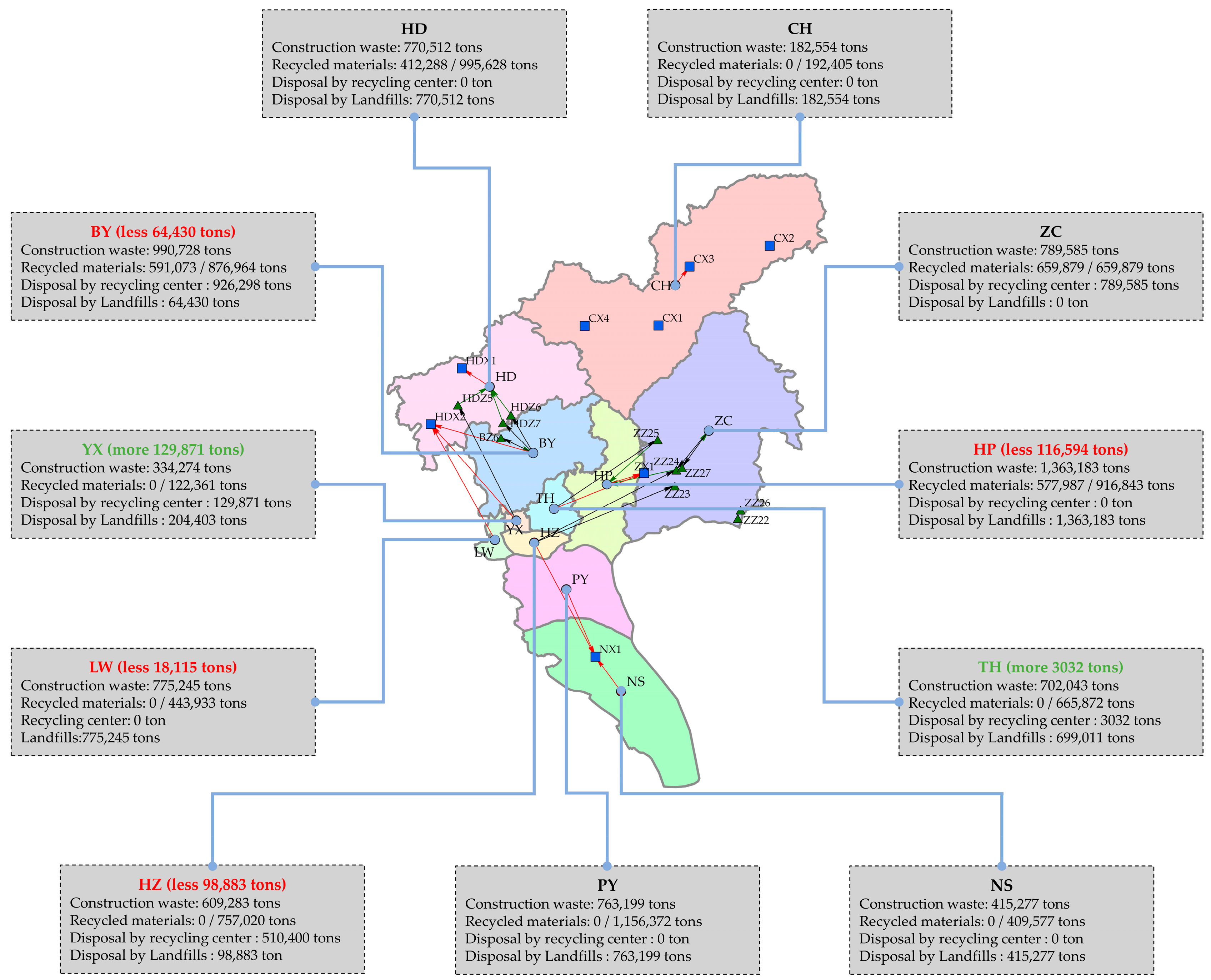
No.	Name of the Official Documents or Literature	Related Inputs
1	Layout Planning of Construction Waste Disposal Facilities in Guangzhou (from 2021 to 2035) [51]	$R$, $S$, $S^{\prime }$, $a_r$, $e^1$, $C_r^1$, $C_{s,r}^2$, and $V_{s,\omega }$
2	Technical Standard for Construction and Demolition Waste Treatment (CJJ/T134-2019) [52]	$e^2$
3	2023 Guangzhou State-owned Construction Land Benchmark Land Value Land Level Scope and Price [53]	$C_r^1$
4	UK Waste Classification Scheme [54]	$e^1$
5	Cost-benefit analysis of demolition waste management via agent-based modeling: A case study in Shenzhen [55]	$C_{s,r}^2$ and $C_s^3$
6	Evaluation of the economic feasibility for the recycling of construction and demolition waste in China—The case of Chongqing [56]	$C_r^1$

. Do note that a total of 20 scenarios are considered in this study, each with an equal probability of occurrence, i.e., $\Omega =20$ and $p_{\omega }={\displaystyle \frac{1}{\Omega }}=0.05$.

First, we introduce the data regarding construction waste recycling centers. Here, the data related to parameters $R$, $a_r$, $e^1$, $e^2$, and $C_r^1$ are introduced. According to the Guangzhou Municipal Planning and Natural Resources Bureau’s website [51], there are ten potential locations for the establishment of construction waste treatment plants. Therefore, $R=10$. The values of the expected maximum construction area $a_r$ are shown in

Table 3. Basic information about recycling centers.

Recycling Center ID	The Maximum Area of the Recycling Center (m2)	Land Price Class	Land Cost (CNY/m2)	Total Cost (CNY/m2)
HDZ5	4392.00	6	655	1415.58
HDZ6	6665.00	5	975	1735.58
HDZ7	3619.60	4	1317	2077.58
BZ6	21,041.00	5	975	1735.58
ZZ22	27,573.60	6	655	1415.58
ZZ23	10,242.00	6	655	1415.58
ZZ24	30,221.60	7	470	1230.58
ZZ25	12,096.90	6	655	1415.58
ZZ26	132,471.50	6	655	1415.58
ZZ27	7925.50	7	470	1230.58

Notes: (1) The column “land price class” refers to the eight categories of state-owned construction land prices determined by the Guangzhou Municipal Planning and Natural Resources Bureau based on the location of the land. Each category corresponds to a different price. (2) The figures in the column “Total costs” are calculated by summing the corresponding land cost and a construction cost of 760.58 CNY/m².

, while the geographic locations are shown in Figure 1. Subsequently, the Guangzhou Municipal Planning and Natural Resources Bureau releases information on the processing capacity and area of the 37 existing recycling plants for construction waste [51]. The computation of construction waste volume per unit area for recycling centers involves determining the average of the existing recycling plants, with the exception of a single recycling center that is operating below full capacity. The average value is calculated as 405.85 m²/m³, derived from the density of construction waste, which is established at 1.2 tons/m² [54]. Subsequently, the value of $e^1$ is calculated by:

$$e^1={\displaystyle \frac{1.2\times \mathrm{10,000}}{405.85}}\approx 29.57 \mathrm{t}/{\mathrm{m}}^2.$$

According to the Technical Standard for Construction and Demolition Waste Treatment [52], the minimum resource utilization rate for construction waste should not be less than 95%. Therefore, it is assumed that 95% of the construction waste will be recycled, i.e., $e^2=0.95$.

The initial capital cost of constructing a recycling center consists of two key elements: land costs, construction costs, and equipment fees. In terms of land expenses, the Guangzhou Municipal Planning and Natural Resources Bureau allocates average land prices specifically for construction purposes in a myriad of areas [53]. The land use costs can be determined according to the geographical position of the potential recycling treatment plants. In terms of the fee for construction and equipment, a medium-scale recycling facility with a maximum waste recycling capacity of 200,000 tons per year requires EUR6,353,120 (about USD6,799,109) [56]. Given the average exchange rate of 1:7.6425 between the Euro and the Chinese Yuan in 2023 [57], the value of $e^2$ is calculated by:

$${\displaystyle \frac{\mathrm{653,120}\times e^1}{\mathrm{200,000}}}=99.52 \mathrm{€}=760.58 \mathrm{CNY}.$$

Following that, the two components of costs (land cost, construction cost, and equipment fee) are summed up to obtain $C_r^1$, as shown in Table 3.

Then, we introduce the data regarding the construction site. Here, the data related to parameters $S$, $S^{\prime }$, and $V_{s,\omega }$ are introduced. Guangzhou comprises 11 municipal regions, such as Yuexiu District, Baiyun District, and Tianhe District. For simplicity, this study considers all construction sites within each municipal region as a single construction site positioned in the center of the municipal region, i.e., $S=S^{\prime }=11$. This assumption possesses minimal impact on the optimal solutions, as the construction sites within an administrative district are generally close in proximity, thereby exerting little influence on transportation costs.

For the generation of construction waste and the demand for recycled material, the Guangzhou Municipal Planning and Natural Resources Bureau has projected the average generation of construction and demolition waste for the next 15 years across 11 districts [51]. They have devised four methods for construction waste disposal, namely sorting center recycling, onsite soil backfilling within the urban area, comprehensive utilization, and direct landfilling, along with the anticipated quantities of construction waste to be disposed of for each method. Notably, the reuse process at the sorting center primarily involves manual filtration and shipment of valuable construction waste materials, such as paper, scrap, rebar, and formwork, to respective secondary markets [21]. Conversely, onsite soil backfilling refers to the transportation of excavated soil to low-lying areas for filling purposes. These two methods predominantly emphasize the reuse of construction waste, with limited involvement in recycling. Hence, this study regards the expected volume of construction waste to be processed through comprehensive utilization and direct landfilling as the actual generation of construction waste.

The aforementioned amount of construction waste is to be handled jointly by ten potential recycling plants and existing disposal facilities in Guangzhou. Furthermore, the currently available disposal facilities for construction waste in Guangzhou are essentially capable of meeting the past five years’ production of construction waste [51]. Based on the production of construction waste in 2019 [51], the annual processing capacity of existing disposal facilities is estimated. From there, the amount of construction waste is adjusted according to the proportion of construction waste generated at each construction site each year. Finally, the total amount of construction waste that needs to be handled by the newly constructed recycling plants can be determined.

During the construction phase of building projects, typically, the quantity of construction waste generated amounts to approximately 10–20% of the total raw material input for the project, with an assumed median value of 15% [51]. Following this, this study calculates the demand for recycled materials based on the projected quantities of construction waste produced by newly constructed buildings in each district. Subsequently, by subtracting the production capacity of existing recycling plants from the proportionate demand for construction waste raw materials across worksites, we are able to get the volume of recycled building materials required by construction sites, as shown in

Table 4. The predictive weight of construction waste generated or recycled building materials required by construction sites of $V_s$.

Construction Site ID	The Weight of Construction Waste Generated (ton)	The Weight of Recycled Building Materials Required (ton)
YX	288,200	510,171
LW	675,960	2,276,147
TH	796,480	3,374,977
HZ	708,710	3,296,489
BY	1033,590	3,688,928
PY	898,660	4,630,783
HP	1,147,560	4,513,051
HD	848,880	4,042,124
NS	463,740	1,844,464
ZC	771,590	3,061,026
CH	226,630	745,634

. This study benchmarks the forecasted values and randomly generates the values of $V_{s,\omega }$, $s=S+1,\dots ,S+S^{\prime }$, $\omega =1,\dots ,\mathsf{\Omega }$, within the range of 80–120% of the forecasted values for the construction of 20 different scenarios.

Then, we introduce the data regarding transportation and disposal costs. The geographic locations of construction sites, potential recycling centers, and landfill sites are shown in Figure 1. The distance between these facilities and construction sites is calculated using Euclidean distance, and the transportation cost of 1 ton of construction waste is 3.5 CNY per kilometer [55]. $C_{s,r}^2$ is presented in

Table 5. The cost of transporting 1 ton construction waste between construction sites to recycling centers.

CNY/ton	YX	LW	TH	HZ	BY	PY	HP	HD	NS	ZC	CH
HDZ5	116.37	125.77	127.19	141.43	80.30	192.21	151.51	32.78	296.47	226.37	222.36
HDZ6	95.10	113.30	92.95	116.64	39.79	164.48	106.32	31.49	267.68	178.17	187.53
HDZ7	88.81	105.65	90.08	111.38	38.60	160.25	108.47	34.19	264.02	184.91	197.47
BZ6	75.70	92.00	79.76	98.84	32.11	148.35	103.84	46.72	252.43	186.67	207.55
ZZ22	199.19	219.30	165.43	184.29	192.82	167.06	121.60	251.99	188.08	82.47	215.98
ZZ23	145.92	168.93	110.57	136.25	130.47	134.92	61.17	188.35	191.28	57.87	179.51
ZZ24	151.01	174.93	115.51	143.51	129.44	146.16	63.98	183.32	205.53	45.38	165.17
ZZ25	146.47	171.87	112.11	144.44	112.39	157.73	61.02	157.94	228.93	46.54	138.95
ZZ26	201.91	222.56	167.73	187.78	193.13	172.29	122.44	250.87	195.60	76.42	209.56
ZZ27	156.38	180.31	120.88	148.86	134.21	151.00	69.29	187.15	208.67	40.76	163.34

.

Before the establishment of recycling centers, all construction waste was disposed of via landfilling, thereby indicating that existing landfills could accommodate the construction waste generated entirely in Guangzhou. To alleviate transportation costs, construction waste from construction sites that is unable to be transported to recycling plants will be directed to the nearest landfills. A processing fee of 30 CNY/ton of construction waste is imposed. Thus, the total cost, denoted as $C_s^3$, comprises both processing and transportation expenses (refer to

Table 6. The disposal cost of 1 ton construction waste in landfills.

CNY/ton	YX	LW	TH	HZ	BY	PY	HP	HD	NS	ZC	CH
CX1	246.46	271.89	219.22	254.23	190.21	280.67	179.71	190.91	360.21	134.50	69.14
CX2	365.07	390.88	334.92	369.54	311.71	387.97	288.85	310.76	451.51	204.34	121.50
CX3	305.59	330.84	278.82	313.82	247.98	339.76	238.71	238.87	416.14	177.97	50.93
CX4	214.94	238.09	196.28	229.38	152.84	266.80	173.31	131.05	359.74	175.59	119.02
HDX1	174.93	186.69	180.71	199.21	129.26	249.32	196.46	59.85	353.53	258.45	235.26
HDX2	145.62	148.76	164.25	171.19	125.54	221.87	196.96	92.63	324.92	279.61	282.12
NX1	171.71	168.69	168.07	146.54	221.44	96.12	185.30	290.50	68.84	257.20	371.03
ZX1	152.56	176.94	117.13	146.74	131.18	155.69	65.08	188.75	227.40	99.38	200.59
Minimum price	145.62	148.76	117.13	146.54	125.54	96.12	65.08	59.85	68.84	99.38	50.93

).

4.2. Experimental Results

After setting the experimental parameters, CPLEX is used to solve the proposed two-stage stochastic programming model. The derived results indicate that the total amount of construction waste generated by 11 worksites every year is 7,827,582 tons on average, and the overall demand for recycled materials every year is 7,117,667 tons on average in the 20 scenarios. With the adjusted maximum total budget, $C^{max}$, of 886 million CNY, the optimal results about the constructed area of the recycling center at the ten candidate locations, ${\alpha }_r$, are shown in

Table 7. The planned construction area of recycled centers at 10 locations.

Recycling Center ID	The Optimal Area (m2)	The Maximum Area (m2)
HDZ5	4392.0	4392.0
HDZ6	6665.5	6665.0
HDZ7	3619.6	3619.6
BZ6	21,041.0	21,041.0
ZZ22	0.0	27,573.6
ZZ23	10,242.0	10,242.0
ZZ24	29,255.7	30,221.6
ZZ25	2228.7	12,096.9
ZZ26	0.0	132,471.5
ZZ27	7923.0	7923.0

. For variables concerning the weight of construction waste transported from construction sites to recycling centers and landfills, apparently, the results vary across scenarios. Here, we solely present one scenario for demonstration purposes, as depicted in Figure 2. The locations of construction sites, recycling centers, and landfills are annotated using the same notation as shown in Figure 1. Transportation routes for construction waste from construction sites to recycling centers are indicated with black arrow lines. Meanwhile, red arrow lines represent the routes for transporting recycled materials from construction sites to landfills. Concurrently, the routes for moving recycling materials between recycling centers and construction sites are denoted by green arrow lines. The term “recycled material” indicates a supply-demand ratio: 412,288/995,628 tons. Here, 412,288 tons represent the actual amount of recycled materials received by the construction site, whereas 995,628 tons denote the total demand for recycled materials.

According to Figure 2 and Table 7, it is evident that the recycling centers HDZ5, HDZ6, HDZ7, BZ6, ZZ23, and ZZ27 are scheduled for complete construction. ZZ25 is designated for partial construction, while the construction of ZZ22 and ZZ26 is not recommended. In this scenario, the cumulative volume of construction waste recycled totals 2,398,089 tons. To demonstrate the superiority of our model, this study has conducted comparative experiments to further evaluate the impact of incorporating the parameter of uncertainty in the decision-making process.

4.2.1. Mean Value Problem

Should decision makers neglect the uncertain amount of construction waste and the uncertain demand for recycled materials, they may opt for the mean values of parameters in all possible scenarios as deterministic parameters. The plan for the size and location of recycling centers can be obtained by solving the following model [M2]:

• Newly defined parameters:

• $V_s^{avg}$: the average weight of construction waste generated by the construction site $s=1,\dots ,S$ or the average weight of recycled building materials required by the construction site $s=S+1,\dots ,S+S^{\prime }$ of all scenarios

• Newly defined variables:

• ${\beta }_{s,r}^{avg}$: continuous, the weight of construction waste delivered from the construction site $s=1,\dots ,S$ to recycling center $r$ or the weight of recycled building materials from recycling center $r$ to construction site $s=S+1,\dots ,S+S^{\prime }$
• ${\gamma }_s^{avg}$: continuous, the weight of construction waste delivered from the construction site $s=1,\dots ,S$ to the landfill site

• Mathematical model:

$$\begin{array}{}\mathrm{(10)}& \left[\mathbf{M}2\right] \mathrm{Maximize}{\sum }_{r=1}^R{\sum }_{s=S+1}^{S+S^{\prime }}{\beta }_{s,r}^{avg}\hfill & & \mathsf{s}.\mathsf{t}. \mathrm{Constraints} \left(7\right)\hfill & \mathrm{(11)}& { \gamma }_s^{avg}+{\sum }_{r=1}^R{\beta }_{s,r}^{avg}=V_s^{avg}\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=1,\dots ,S\mathrm{(12)}& {\sum }_{s=1}^S{\beta }_{s,r}^{avg}\le e^1{\alpha }_r\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall r=1,\dots ,R\mathrm{(13)}& e^2{\sum }_{s=1}^S{\beta }_{s,r}^{avg}\ge {\sum }_{s=S+1}^{S+S^{\prime }}{\beta }_{s,r}^{avg}\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall r=1,\dots ,R\mathrm{(14)}& {\sum }_{r=1}^R{\beta }_{s,r}^{avg}\le V_s^{avg}\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=S+1,\dots ,S+S^{\prime }\mathrm{(15)}& {\sum }_{r=1}^R\left(C_r^1{\alpha }_r+{\sum }_{s=1}^{S+S^{\prime }}{C}_{s,r}^2{\beta }_{s,r}^{avg}\right)+{\sum }_{s=1}^S{C}_s^3{\gamma }_s^{avg}\le C^{max}\hfill & \mathrm{(16)}& {\beta }_{s,r}^{avg}\ge 0\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=1,\dots ,S+S^{\prime },r=1,\dots ,R\mathrm{(17)}& {\gamma }_s^{avg}\ge 0\hfill & \hfill \forall s=1,\dots ,S\end{array}$$

By solving [M2], we can also obtain the optimal value of ${\alpha }_r$, denoted as ${\alpha }_r^{**}$.

4.2.2. Comparative Results

Next, a comparative analysis is conducted between the optimal results by solving [M1], denoted as ${\alpha }_r^{*}$ and [M2], denoted as ${\alpha }_r^{**}$. This comparative analysis is narrated through a meticulously designed process, articulated in the following steps:

(1)

[M1] is solved to obtain the optimal solution, ${\alpha }_r^{*}$, alongside the corresponding optimal objective value, ${\overline{z}}^{*}$.

(2)

Subsequently, [M2] is resolved to determine the solution, ${\alpha }_r^{**}$. For each scenario $\omega =1,\dots ,\mathsf{\Omega }$, the comparison model [M3] is then solved to obtain the objective value specific to each scenario. Following the acquisition of objective values across all scenarios, we compute the mean objective value, ${\overline{z}}^{**}$, serving as a critical measure for assessing model performance under varied conditions.

(3)

The final stage of our analysis involves a comprehensive comparison between the objective values ${\overline{z}}^{*}$ and ${\overline{z}}^{**}$.

The mathematical model [M3] is presented as follows:

• Newly defined parameters:

• ${\alpha }_r^{act}$: the optimal value of ${\alpha }_r$ by solving the model [M2] (i.e., ${\alpha }_r^{**}$)
• $V_s^{act}$: the weight of construction waste generated by the construction site $s=1,\dots ,S$ or the weight of recycled building materials required by the construction site $s=S+1,\dots ,S+S^{\prime }$

• Newly defined variables:

• ${\beta }_{s,r}^{act}$: continuous, the weight of construction waste delivered from the construction site $s=1,\dots ,S$ to the recycling center $r$ or the weight of recycled building materials from the recycling center $r$ to the construction site $s=S+1,\dots ,S+S^{\prime }$
• ${\gamma }_s^{act}$: continuous, the weight of construction waste delivered from the construction site $s=1,\dots ,S$ to the landfill site

• Mathematical model:

$$\begin{array}{}\mathrm{(18)}& \left[\mathbf{M}3\right] \mathrm{Maximize}{\sum }_{r=1}^R{\sum }_{s=S+1}^{S+S^{\prime }}{\beta }_{s,r}^{act}\hfill & \mathrm{(19)}& \mathrm{s}.\mathrm{t}. {\gamma }_s^{act}+{\sum }_{r=1}^R{\beta }_{s,r}^{act}=V_s^{act}\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=1,\dots ,S\mathrm{(20)}& {\sum }_{s=1}^S{\beta }_{s,r}^{act}\le e^1{\alpha }_r^{act}\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall r=1,\dots ,R\mathrm{(21)}& e^2{\sum }_{s=1}^S{\beta }_{s,r}^{act}\ge {\sum }_{s=S+1}^{S+S^{\prime }}{\beta }_{s,r}^{act}\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall r=1,\dots ,R\mathrm{(22)}& {\sum }_{r=1}^R{\beta }_{s,r}^{act}\le V_s^{act}\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=S+1,\dots ,S+S^{\prime }\mathrm{(23)}& {\sum }_{r=1}^R\left(C_r^1{\alpha }_r^{act}+{\sum }_{s=1}^{S+S^{\prime }}{C}_{s,r}^2{\beta }_{s,r}^{act}\right)+{\sum }_{s=1}^S{C}_s^3{\gamma }_s^{act}\le C^{max}\hfill & \mathrm{(24)}& {\beta }_{s,r}^{act}\ge 0\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=1,\dots ,S+S^{\prime },r=1,\dots ,R\mathrm{(25)}& {\gamma }_s^{act}\ge 0\hfill & \hfill \hspace{0.5em}\hspace{0.5em}\forall s=1,\dots ,S\end{array}$$

The algorithmic framework for comparing the solutions derived by deterministic programming is presented in Algorithm 1.

By solving [M2], we obtain the optimal results about ${\alpha }_r^{**}$, as outlined in

Table 8. The planned constructed area of recycled centers at 10 locations from [M2].

Recycling Center ID	The Optimal Area (m2)	The Maximum Area (m2)
HDZ5	4392.0	4392.0
HDZ6	6665.5	6665.0
HDZ7	3619.6	3619.6
BZ6	21,041.0	21,041.0
ZZ22	0	27,573.6
ZZ23	10,242.0	10,242.0
ZZ24	25,798.0	30,221.6
ZZ25	102.5	12,096.9
ZZ26	0	132,471.5
ZZ27	7923.0	7923.0

. Additionally, we engage the same scenario in Section 4.2 and solve [M3] for optimal illustration. Figure 3 illustrates the recycling plan formulated by model [M3], which does not account for uncertainties in construction waste management. The red font indicates that less construction waste is recycled at a construction site compared to model [M1], while the green font signifies more recycling. Specifically, the red label “BY (less 64,430 tons)” denotes that model [M3] recycles 64,430 tons less than model [M1] at the BY construction site. A notable improvement is observed when compared to the results solved by [M1]. In the plan derived by [M3], approximately 2,241,227 tons of construction waste are recycled. This figure is about 7% lower than the results achieved by [M1]. Figure 4 compares the relative values of recycled construction waste managed by [M1] and [M3]. We assume that all amounts of recycled construction waste solved by [M3] are standardized to 0.5, with the maximum relative value set to 1. To substantiate the superiority of [M1], we conduct tests using 100 sets of stochastic numbers ranging from 80% to 120%, reflecting variations in the volume of construction waste and the demand for recycled materials. The results consistently show that the recycling rates achieved by [M1] surpass those of [M3].

Algorithm 1: Calculating the optimality gap of the solutions derived by deterministic and stochastic programming
1:	Input: ${\alpha }_r^{**}$ and all other deterministic parameters
2:	Output: ${\overline{z}}^{**}$
3:	${\overline{z}}^{**}\leftarrow 0$
4:	For $r=1,\dots ,R$
5:	$\hspace{0.17em}{\alpha }_r^{act}\leftarrow {\alpha }_r^{**}$
6:	End for
7:	For $\omega =1,\dots ,\mathsf{\Omega }$
8:	For $s=1,\dots ,S+S^{\prime }$
9:	$\hspace{0.17em} \hspace{0.17em}{V}_s^{act}\leftarrow V_{s,\omega }$
10:	End for
11:	Solve model [M3] and define $z$ as the optimal objective value of [M3]
12:	$\hspace{0.17em}{\overline{z}}^{**}\leftarrow {\overline{z}}^{**}+z$
13:	End for
14:	${\overline{z}}^{**}\leftarrow {\displaystyle \frac{{\overline{z}}^{**}}{\mathsf{\Omega }}}$

4.3. Sensitivity Analysis

In this section, a sensitivity analysis is conducted considering the government’s investment to evaluate its impact on the recycling rate. Do note that the recycling rate is defined as:

$$\mathrm{Recycling} \mathrm{rate}={\displaystyle \frac{\mathrm{Total} \mathrm{amount}\mathrm{of} \mathrm{construction} \mathrm{waste} \mathrm{recycled} }{\mathrm{Total} \mathrm{a}\mathrm{mount} \mathrm{of} \mathrm{construction} \mathrm{waste} \mathrm{generated}}}$$

Figure 5 shows the results of the sensitivity analysis, where the value of the investment ranges from 800 to 2500 million CNY with a step size of 50 million CNY. Each marker represents the observed recycling rate percentage, corresponding to specific investment levels. When the investment is set at 800 million CNY, no generated construction waste is recycled. The recycling rate exhibits a positive trajectory in conjunction with increasing investment. The maximum recycling rate observed reaches 92.72% (indicated by the red dashed line in Figure 5), which is achievable beyond an investment level of 22.5 billion CNY. A red marker indicates that when the amount of investment equates to the disposal of construction waste to landfills, the recycling rate is 31.90%.

4.4. Summary of Results and Managerial Insights

The comparison between our two-stage stochastic model and the mean value model for the planning of establishing recycling centers shows that our model achieves a higher recycling rate. The sensitivity of the optimal recycling rate of construction waste to total disposal costs provides crucial insights for the government, which allows them to optimize the locations and sizing of recycling centers based on investment levels.

First, the uncertainty associated with the generation and demand of construction waste significantly influences waste management strategies. Failure to reckon with these uncertainties may lead to decision makers devising suboptimal plans, resulting in inefficient investment usage and limited material recycling efforts. Notably, when managed with a total expenditure of 886 million CNY, the two-stage stochastic model enables the recycling of over 32,110 tons more construction waste than the mean value method.

Second, the sensitivity analysis emphasizes the cost-effectiveness of constructing a recycling center for construction waste as compared to direct landfill disposal, provided that proper site planning is implemented. Additionally, computational models reveal that if construction waste is solely disposed of via landfill, the associated cost would amount to approximately 886 million CNY. Conversely, an initial investment of the same magnitude can achieve a recycling rate of 31.90%. This clearly suggests that some recycling facilities are already operational, and further reductions in investment do not preclude recycling endeavors. The recycling centers built are in locations with convenient access to construction sites, which indirectly emphasizes the importance of transportation costs. Thus, these facilities are well-planned, as evidently, the cost of recycling construction waste proves lower than disposing of it in a landfill.

Third, an examination of investment variability reveals rapid changes in recycling rates occurring between 800 and 900 million CNY. This observation demonstrates a clear positive correlation between increased financial investment in waste management and enhanced recycling efficacy. Consequently, it is imperative for decision makers to thoroughly consider recycling objectives and adjust budget allocations accordingly to optimize outcomes in waste management strategies.

When the total investment surpasses a certain threshold, additional increments do not augment the volume of construction waste recycled. This plateau indicates that the capacity of the planned recycling centers has been maximized. Under the circumstances of an ample budget, the planning of additional recycling centers should be considered. This rate plateau is visually represented by a horizontal dashed line extending from the point where the maximum recycling rate begins to where it first occurs, delineating the fact that beyond the threshold, additional investment does not result in improved recycling rates. Decision makers are encouraged to consider the establishment of additional recycling facilities once the budget exceeds this established threshold.

5. Conclusions

The uncertainties in construction waste generation and the demand for recycled materials are two of the key factors in the planning of recycling centers. To deal with these uncertainties, this paper designs a two-stage stochastic model aiming at maximizing the recycling rate of construction waste and conducting a sensitivity analysis to further reveal the correlation between recycling rate and investment. The proposed model is compared with the mean value decision model through a case study in Guangzhou. The contributions of this paper can be encapsulated into two key domains: (1) This study addresses the limitations of traditional plans for constructing recycling centers, which often fail to determine the optimal location and capacity under conditions of uncertainty. Our comparison of the proposed model with the mean value model, using a real-world case study from Guangzhou, demonstrates that our model attains a commendatory recycling rate. (2) From the perspective of decision makers aiming to maximize recycling rates, this study conducts a sensitivity analysis to evaluate how the construction waste management budget influences recycling rates. The analysis reveals that transportation costs significantly influence the planning of recycling center development, underscoring the need for strategic budget allocation to enhance recycling efficiency.

All in all, this paper proposes several potential enhancements for the current recycling centers. Principally, diagram theory regarding the optimal plan for facility locations, e.g., Voronoi diagrams [58,59], can be compared with the two-stage stochastic model. The differences between diagram theory and mathematical methods in the optimal location plan for construction waste management warrant further research. Furthermore, integrating active building information modeling (BIM) into waste management strategies could provide a comprehensive perspective. Active BIM, incorporating optimization methods for quantitative mathematical analysis and the Internet of Things, has been employed to enhance the efficiency of working facilities and construction plans [60,61]. The recycling process involves multiple stages and the storage of construction waste that cannot be processed immediately. Active BIM optimizes the placement and processing sequences of construction waste, enhancing overall efficiency.