On-Site Sensor Sensitivity Adjustment Technique for a Maintenance-Free Heat Flow Monitoring in Building Systems
Abstract
1. Introduction
2. Materials and Methods
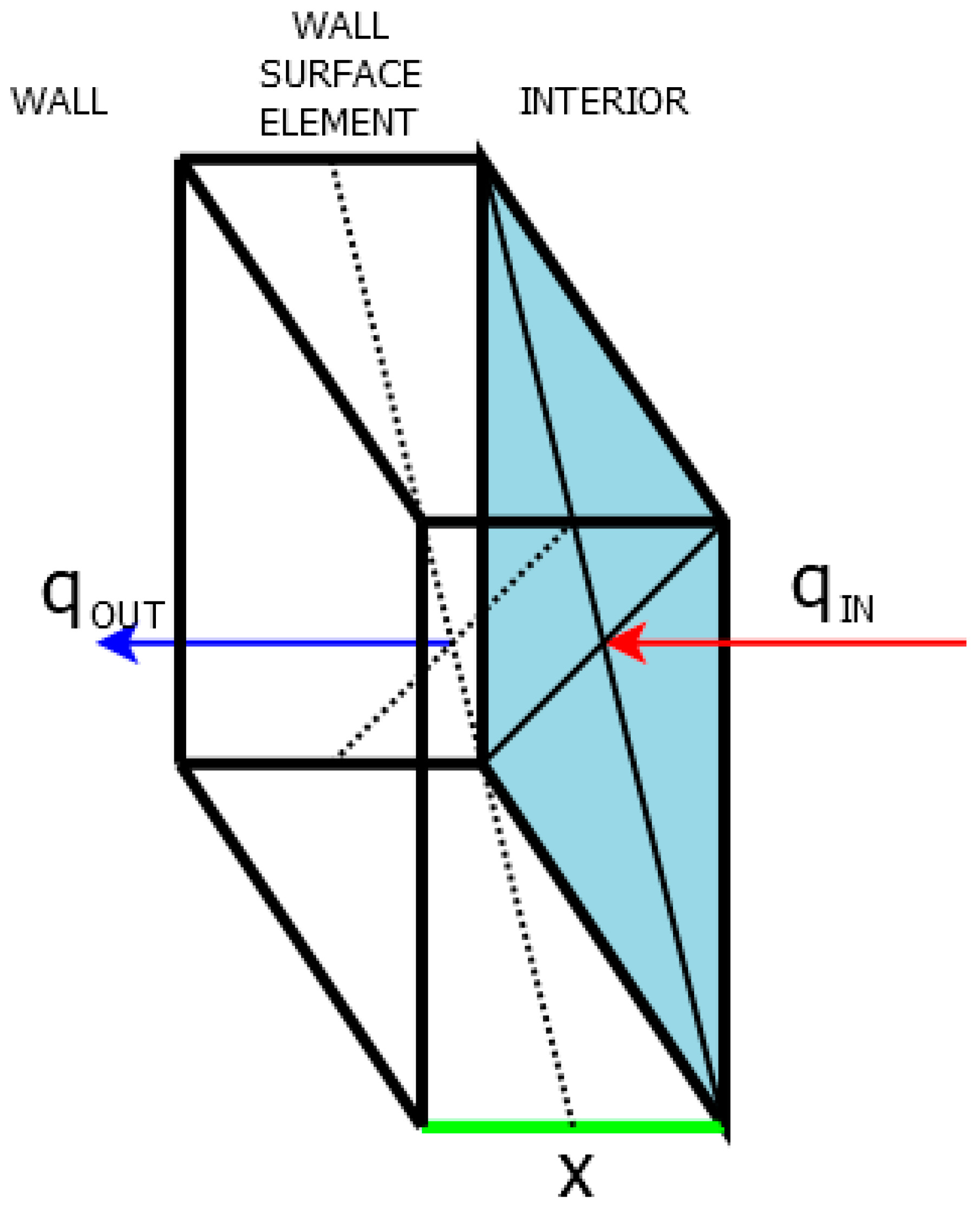
2.1. Theoretical Background
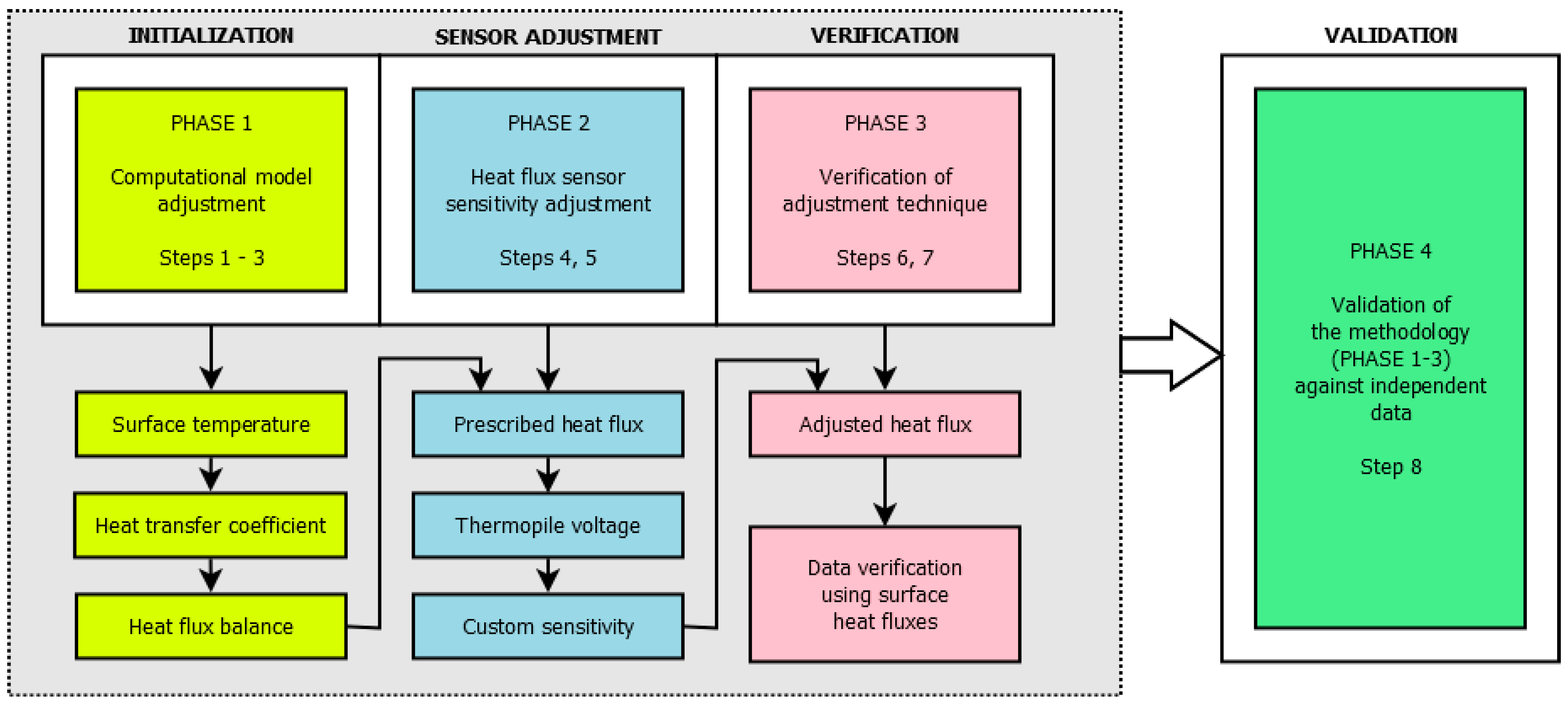
2.2. Design of the Adaptive Self-Adjustment Procedure
- Heat transfer coefficient α of the computational model is optimized by fitting the simulated surface temperature, Ts,sim(t), to that determined experimentally, Ts,exp (t);
- Heat flux from the interior to the wall surface, qIN(t), is calculated from the experimental data using Equation (2) and the optimized heat transfer coefficient α from the previous step;
- Heat flux from the wall surface element to the wall, qOUT(t), is calculated from the computational data using Equation (3) and compared with qIN(t) from the previous step to validate the setup and accuracy of the computational model;
- qIN(t) and qOUT(t) are averaged to form a new variable, qREF(t), having a sufficient robustness as it combines both experimental and computational outputs;
- Sensitivity of heat flux sensors (thermopiles) is adjusted using raw U(t) (voltage) data and q(t) from the previous step and custom sensitivity function S is identified for each thermopile;
- Raw data provided by the heat flux sensors in the period are adopted and transformed into heat flux using S function from the previous step;
- The heat flux obtained in the previous step is compared with experimentally and computationally derived data to verify the adjusted sensitivity;
- The verified heat flux obtained in the previous step is validated against the reference heat flux obtained from an independent sensor.
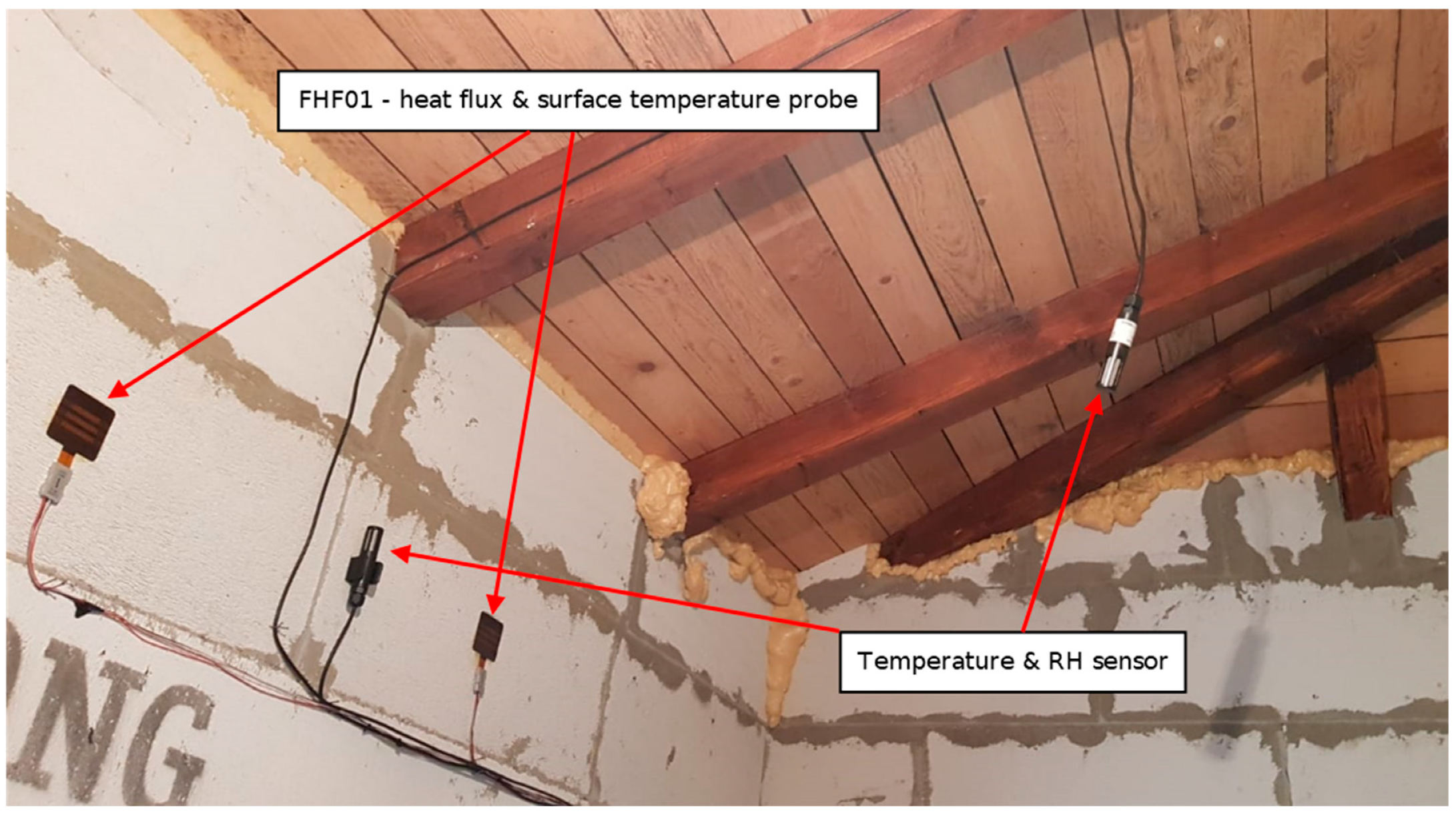
2.3. Self-Adjustment Procedure in Real Conditions
2.4. Validation of the Proposed Self-Adjustment Approach
3. Results
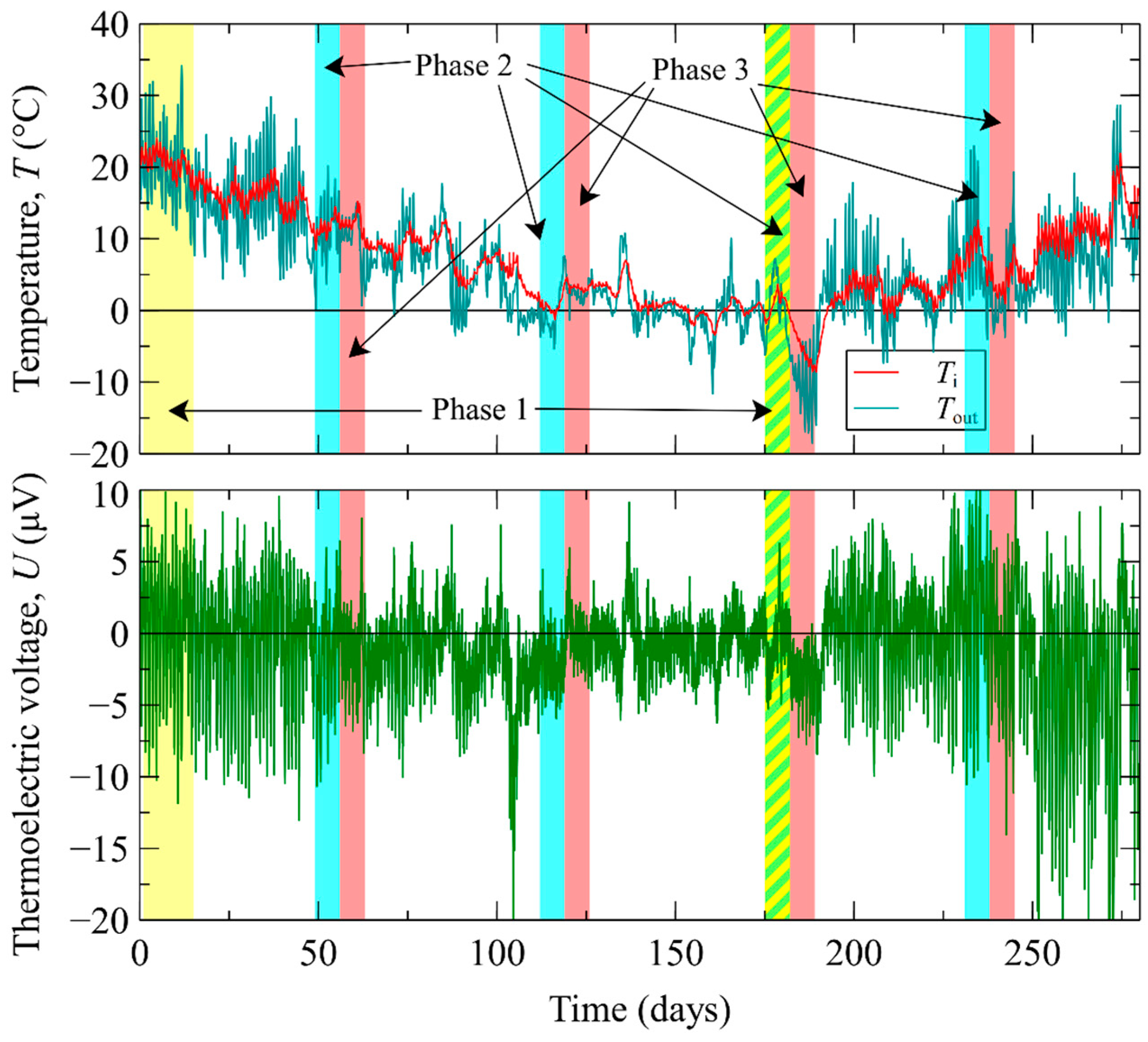
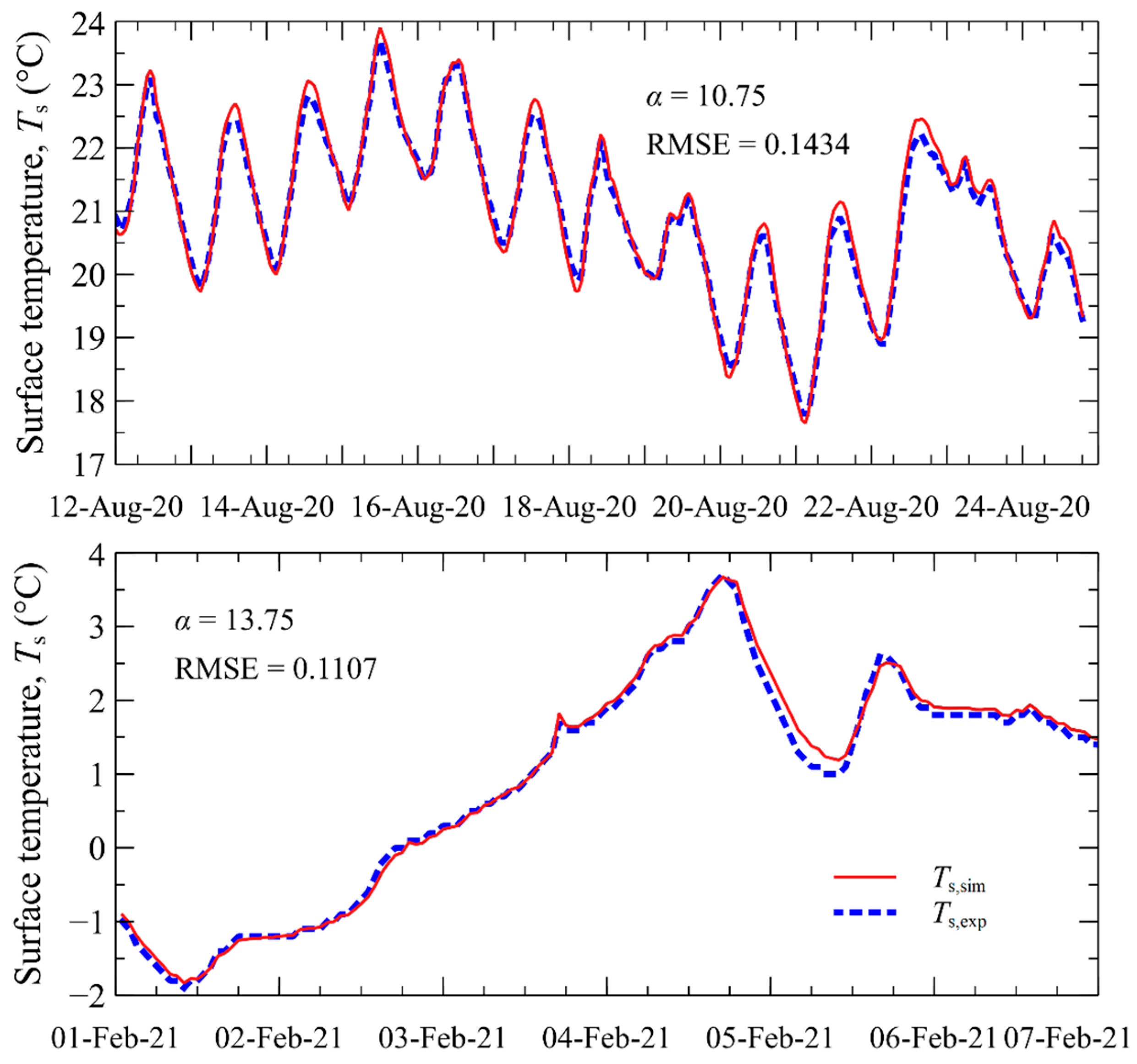
3.1. Phase 1—Initialization
3.2. Phase 2—Sensor Sensitivity Adjustment
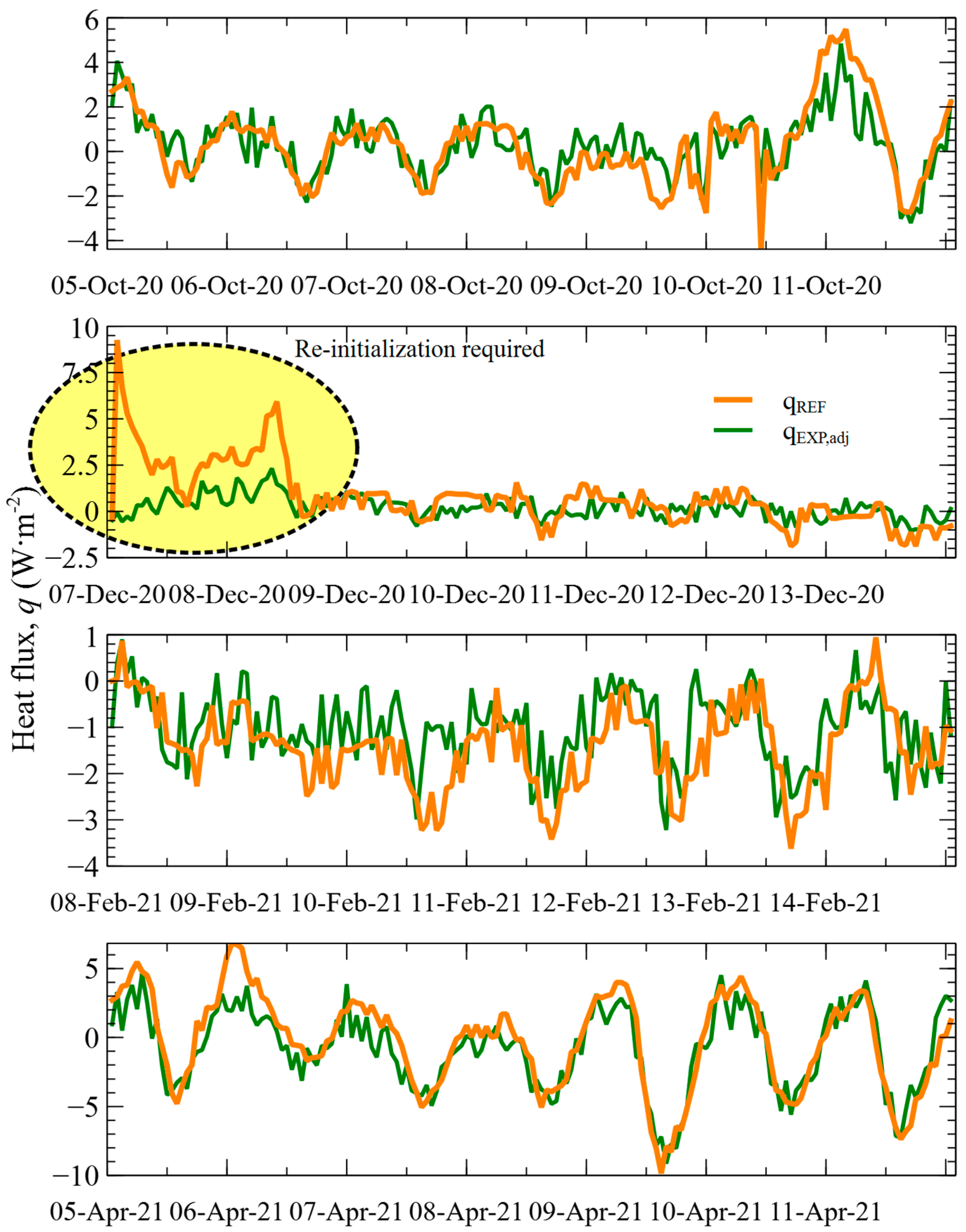
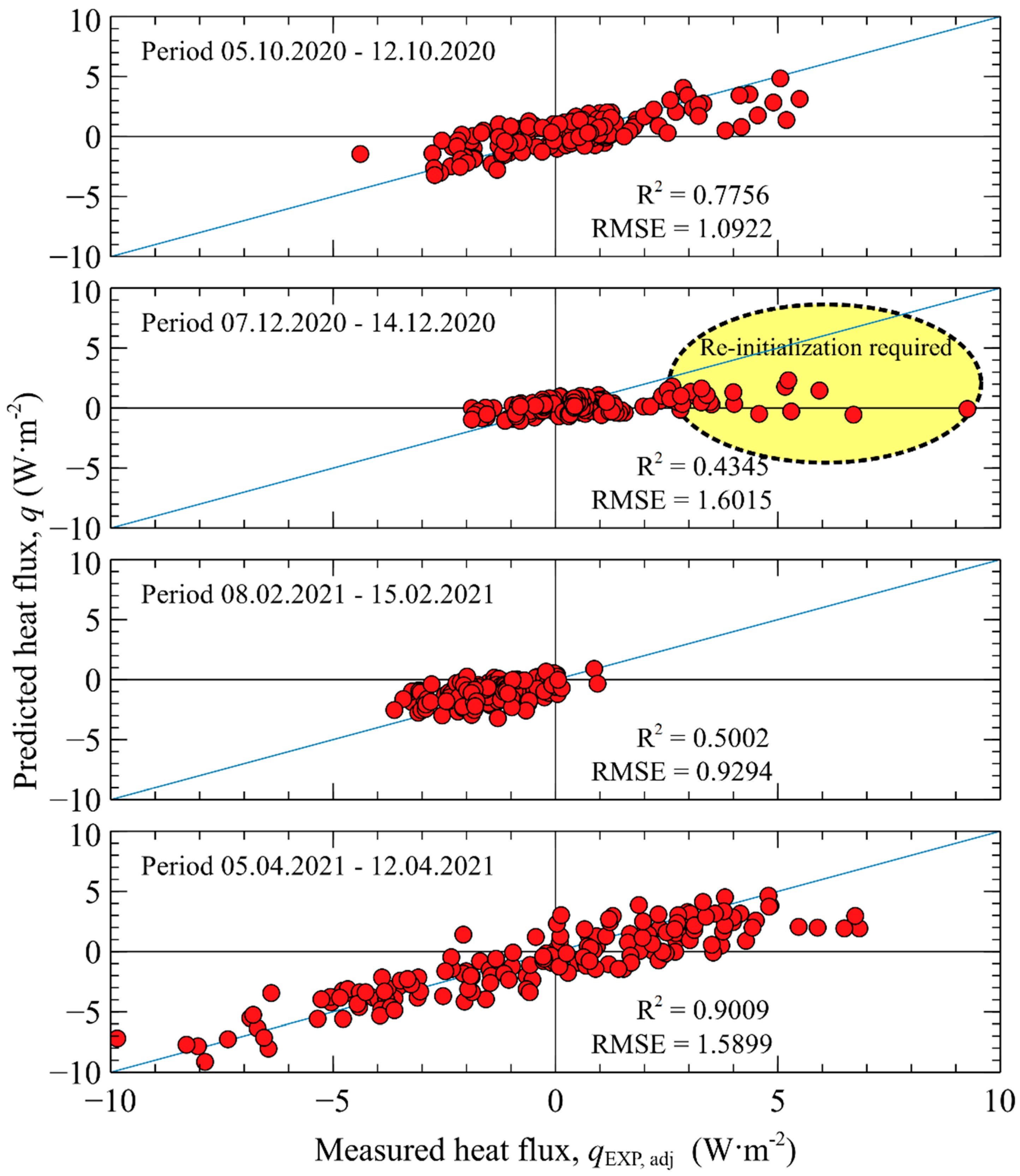
3.3. Phase 3—Sensor Performance Verification
3.4. Validation of the Self-Adjustment Technique
4. Discussion
5. Conclusions
- Factory calibration of heat flux sensors is not always sufficient as the real experimental conditions may differ from those effective during the calibration. Also, some errors may arise from the type of installation of the heat flux sensors which can subsequently affect the sensitivity of the sensor.
- Continuous monitoring of heat flow sensor performance and silent checking of their accuracy allows the proposed technique to be applied instantaneously during the ongoing experiment without interfering with experimental apparatus or taking technological breaks required for sensor manipulation or replacement.
- The proposed approach is suitable for both short-term and long-term heat flux measurements while bringing an entirely new potential for maintenance-free applications. However, a qualified decision on sensor sensitivity re-adjustment or re-initialization of the computational model running in the background is crucial to ensure high accuracy of the method.
- The principles of the adaptive re-adjustments of heat flux sensor performance allow for their integration into automatic systems and smart HVAC technologies to efficiently control the indoor environment and thermal comfort of residential buildings based on real-time performance data.
- Although the validation was performed with sufficient accuracy, the additional testing would be beneficial to include various conditions, surface materials, or different kinds of probes. Such a complex validation should be considered an essential precondition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Chen, Y. Transient Heat Flow Calculation for Multilayer Constructions Using a Frequency-Domain Regression Method. Build. Environ. 2003, 38, 45–61. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, X.; Medina, M.A. Calculation of Transient Phase Change Heat Transfer through Building Envelopes: An Improved Enthalpy Model and Error Analysis. Energy Build. 2020, 209, 109673. [Google Scholar] [CrossRef]
- Fu, T.; Zong, A.; Zhang, Y.; Wang, H.S. A Method to Measure Heat Flux in Convection Using Gardon Gauge. Appl. Therm. Eng. 2016, 108, 1357–1361. [Google Scholar] [CrossRef]
- Purpura, C.; Trifoni, E.; Petrella, O.; Marciano, L.; Musto, M.; Rotondo, G. Gardon Gauge Heat Flux Sensor Verification by New Working Facility. Measurement 2019, 134, 245–252. [Google Scholar] [CrossRef]
- Gardon, R. An Instrument for the Direct Measurement of Intense Thermal Radiation. Rev. Sci. Instrum. 2004, 24, 366. [Google Scholar] [CrossRef]
- Kidd, C.T.; Nelson, C.G. How the Schmidt-Boelter Gage Really Works. In Proceedings of the 41st International Instrumentation Symposium, Aurora, CO, USA, 7–11 May 1995. [Google Scholar]
- Kidd, C.T.; Adams, J.C. Fast-Response Heat-Flux Sensor for Measurement Commonality in Hypersonic Wind Tunnels. J. Spacecr. Rockets 2012, 38, 719–729. [Google Scholar] [CrossRef]
- Lam, C.S.; Weckman, E.J.; Lam, C.S.; Weckman, E.J. Steady-State Heat Flux Measurements in Radiative and Mixed Radiative–Convective Environments. Fire Mater. 2009, 33, 303–321. [Google Scholar] [CrossRef]
- Mocikat, H.; Herwig, H. Heat Transfer Measurements with Surface Mounted Foil-Sensors in an Active Mode: A Comprehensive Review and a New Design. Sensors 2009, 9, 3011–3032. [Google Scholar] [CrossRef]
- Lakatos, Á.; Kovács, Z. Comparison of Thermal Insulation Performance of Vacuum Insulation Panels with EPS Protection Layers Measured with Different Methods. Energy Build. 2021, 236, 110771. [Google Scholar] [CrossRef]
- Ballestrín, J.; Estrada, C.A.; Rodríguez-Alonso, M.; Pérez-Rábago, C.; Langley, L.W.; Barnes, A. Heat Flux Sensors: Calorimeters or Radiometers? Solar Energy 2006, 80, 1314–1320. [Google Scholar] [CrossRef]
- Sharkov, A.V.; Korablev, V.A.; Nekrasov, A.S.; Minkin, D.A.; Fadeeva, S.V. A Radiometer for Measuring High-Intensity Heat Flux Density and a Method of Calibrating It. Meas. Tech. 2012, 54, 1276–1279. [Google Scholar] [CrossRef]
- Childs, P.R.N.; Greenwood, J.R.; Long, C.A. Heat Flux Measurement Techniques. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 1999, 213, 655–677. [Google Scholar] [CrossRef]
- Nakos, J. Description of Heat Flux Measurement Methods Used in Hydrocarbon and Propellant Fuel Fires at Sandia; Sandia National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 2010. [Google Scholar]
- Levinson, R.; Chen, S.; Ferrari, C.; Berdahl, P.; Slack, J. Methods and Instrumentation to Measure the Effective Solar Reflectance of Fluorescent Cool Surfaces. Energy Build. 2017, 152, 752–765. [Google Scholar] [CrossRef]
- ASTM C177-19; Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Guarded-Hot-Plate Apparatus. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM C518-17; Standard Test Method for Steady-State Thermal Transmission Properties by Means of the Heat Flow Meter Apparatus. ASTM International: West Conshohocken, PA, USA, 2017.
- Lakatos, Á.; Csík, A.; Csarnovics, I. Experimental Verification of Thermal Properties of the Aerogel Blanket. Case Stud. Therm. Eng. 2021, 25, 100966. [Google Scholar] [CrossRef]
- ASTM C1130-21; Standard Practice for Calibration of Thin Heat Flux Transducers. ASTM International: West Conshohocken, PA, USA, 2021.
- ASTM C1363-19; Standard Test Method for Thermal Performance of Building Materials and Envelope Assemblies by Means of a Hot Box Apparatus. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM C1114-06; Standard Test Method for Steady-State Thermal Transmission Properties by Means of the Thin-Heater Apparatus. ASTM International: West Conshohocken, PA, USA, 2019.
- ISO 8302:1991; Thermal Insulation—Determination of Steady-State Thermal Resistance and Related Properties—Guarded Hot Plate Apparatus. Technical Committee: ISO/TC 163; International Organization for Standardization: Geneve, Switzerland, 1991.
- ASTM C1046-95R21; Standard Practice for In-Situ Measurement of Heat Flux and Temperature on Building Envelope Components. ASTM International: West Conshohocken, PA, USA, 2021.
- ASTM C1155-95R21; Standard Practice for Determining Thermal Resistance of Building Envelope Components from the In-Situ Data. ASTM International: West Conshohocken, PA, USA, 2021.
- Zarr, R.R.; Martinez-Fuentes, V.; Filliben, J.J.; Dougherty, B.P. Calibration of Thin Heat Flux Sensors for Building Applications Using ASTM C 1130. J. Test. Eval. 2001, 29, 293–300. [Google Scholar] [CrossRef]
- HFP01SC Brochure HFP01SC Self-Calibrating Heat Flux Sensor Brochure. Available online: www.hukseflux.com (accessed on 17 April 2022).
- FHF04SC Brochure FHF04SC Self-Calibrating Heat Flux Sensor with Integrated Heater Brochure. Available online: www.hukseflux.com (accessed on 17 April 2022).
- Info; huksefluxcom FHF05 Series Heat Flux Sensors User Manual. Available online: www.hukseflux.com (accessed on 18 July 2024).
- Maděra, J.; Kočí, V.; Kočí, J.; Černý, R. Physical and Mathematical Models of Hygrothermal Processes in Historical Building Envelopes. AIP Conf. Proc. 2017, 1906, 140003. [Google Scholar] [CrossRef]
- Maděra, J.; Kočí, J.; Kočí, V.; Kruis, J. Parallel Modeling of Hygrothermal Performance of External Wall Made of Highly Perforated Bricks. Adv. Eng. Softw. 2017, 113, 47–53. [Google Scholar] [CrossRef]
- Kočí, V.; Jerman, M.; Pavlík, Z.; Maděra, J.; Žák, J.; Černý, R. Interior Thermal Insulation Systems Based on Wood Fiberboards: Experimental Analysis and Computational Assessment of Hygrothermal and Energy Performance in the Central European Climate. Energy Build. 2020, 222, 110093. [Google Scholar] [CrossRef]
- Künzel, H.M. Simultaneous Heat and Moisture Transport in Building Components: One-and Two-Dimensional Calculation Using Simple Parameters; Fraunhofer IRB Verlag Suttgart; IRB-Verlag: Stuttgart, Germany, 1995. [Google Scholar]
- Jerman, M.; Keppert, M.; Výborný, J.; Černý, R. Hygric, Thermal and Durability Properties of Autoclaved Aerated Concrete. Constr. Build. Mater. 2013, 41, 352–359. [Google Scholar] [CrossRef]
- Kočí, V.; Maděra, J.; Jerman, M.; Žumár, J.; Koňáková, D.; Čáchová, M.; Vejmelková, E.; Reiterman, P.; Černý, R. Application of Waste Ceramic Dust as a Ready-to-Use Replacement of Cement in Lime-Cement Plasters: An Environmental-Friendly and Energy-Efficient Solution. Clean. Technol. Environ. Policy 2016, 18, 1725–1733. [Google Scholar] [CrossRef]
- User Manual FHF01, Hukseflux Thermal Sensors. Available online: https://www.hukseflux.com/uploads/product-documents/FHF01_manual_v2006.pdf (accessed on 14 December 2021).
- User Manual HFP01 & HFP03, Heat Flux Plate/Heat Flux Sensor, Hukseflux Thermal Sensors. Available online: https://www.hukseflux.com/uploads/product-documents/HFP01_HFP03_manual_v1721.pdf (accessed on 14 December 2021).
- Info; huksefluxcom Self-Calibrating Heat Flux Sensor TM Hukseflux Thermal Sensors. HFP01SC User Manual Self-Calibrating Heat Flux Sensor TM Hukseflux Thermal Sensors. Available online: www.hukseflux.com (accessed on 5 April 2022).
- Maffulli, R.; He, L. Wall Temperature Effects on Heat Transfer Coefficient for High-Pressure Turbines. J. Propuls. Power 2014, 30, 1080–1090. [Google Scholar] [CrossRef]
- Janssen, H. Dependence of Heat Transfer Coefficients on the Wall Temperature Shape and Consequences for the Calculation of Overall Heat Transfer Coefficients for Heat Exchangers. Heat Transf. Coeff. 1996, 31, 153–161. [Google Scholar] [CrossRef]
- Yu, Y.; Li, H. Virtual In-Situ Calibration Method in Building Systems. Autom. Constr. 2015, 59, 59–67. [Google Scholar] [CrossRef]
- Bychkovskiy, V.; Megerian, S.; Estrin, D.; Potkonjak, M. A Collaborative Approach to In-Place Sensor Calibration. Lect. Notes Comput. Sci. 2003, 2634, 301–316. [Google Scholar] [CrossRef]
- Dulev, V.; Ermishin, S.; Khoteev, N.; Lopatin, A.; Shabanov, P.; Menshikov, A.; Startsev, A. Automated Measuring System Designed to Calibrate Measuring Devices Using Virtual Standards® Technology. In Proceedings of the AUTOTESTCON, San Antonio, TX, USA, 20–23 September 2004; pp. 158–164. [Google Scholar] [CrossRef]
- Sapozhnikov, S.Z.; Mityakov, V.Y.; Mityakov, A.V.; Pokhodun, A.I.; Sokolov, N.A.; Matveev, M.S. The Calibration of Gradient Heat Flux Sensors. Meas. Tech. 2012, 54, 1155–1159. [Google Scholar] [CrossRef]
- Sharkov, A.V.; Korablev, V.A.; Makarov, D.S.; Minkin, D.A.; Nekrasov, A.S.; Gordeichik, A.A. Measurement of High-Density Heat Flux Using an Automated Installation. Meas. Tech. 2016, 59, 67–69. [Google Scholar] [CrossRef]
- Zhang, J.; Mei, G.; Bao, T.; Yan, L.E. An Experimental Study on Thermal Analyses of Crushed-Rock Layers with Single-Size Aggregates. Cold Reg. Sci. Technol. 2019, 160, 110–118. [Google Scholar] [CrossRef]
- Ha, T.-T.; Feuillet, V.; Waeytens, J.; Zibouche, K.; Peiffer, L.; Garcia, Y.; le Sant, V.; Bouchie, R.; Koenen, A.; Monchau, J.-P.; et al. Measurement Prototype for Fast Estimation of Building Wall Thermal Resistance under Controlled and Natural Environmental Conditions. Energy Build. 2022, 268, 112166. [Google Scholar] [CrossRef]
- Chihab, Y.; Bouferra, R.; Garoum, M.; Essaleh, M.; Laaroussi, N. Thermal Inertia and Energy Efficiency Enhancements of Hollow Clay Bricks Integrated with Phase Change Materials. J. Build. Eng. 2022, 53, 104569. [Google Scholar] [CrossRef]
- Al-Absi, Z.A.; Hafizal, M.I.M.; Ismail, M. Experimental Study on the Thermal Performance of PCM-Based Panels Developed for Exterior Finishes of Building Walls. J. Build. Eng. 2022, 52, 104379. [Google Scholar] [CrossRef]
- Balocco, C.; Pierucci, G.; de Lucia, M. An Experimental Method for Building Energy Need Evaluation at Real Operative Conditions. A Case Study Validation. Energy Build. 2022, 266, 112114. [Google Scholar] [CrossRef]
- Briga-Sá, A.; Leitão, D.; Boaventura-Cunha, J.; Martins, F.F. Trombe Wall Thermal Performance: Data Mining Techniques for Indoor Temperatures and Heat Flux Forecasting. Energy Build. 2021, 252, 111407. [Google Scholar] [CrossRef]
- Stella, P.; Personne, E. Effects of Conventional, Extensive and Semi-Intensive Green Roofs on Building Conductive Heat Fluxes and Surface Temperatures in Winter in Paris. Build. Environ. 2021, 205, 108202. [Google Scholar] [CrossRef]
- Rincón-Casado, A.; Jara, E.Á.R.; Pardo, A.R.; Lissén, J.M.S.; Flor, F.J.S. de la Reducing the Cooling Energy Demand by Optimizing the Airflow Distribution in a Ventilated Roof: Numerical Study for an Existing Residential Building and Applicability Map. Appl. Sci. 2024, 14, 6596. [Google Scholar] [CrossRef]
- Santos, P.; Abrantes, D.; Lopes, P.; Moga, L. The Relevance of Surface Resistances on the Conductive Thermal Resistance of Lightweight Steel-Framed Walls: A Numerical Simulation Study. Appl. Sci. 2024, 14, 3748. [Google Scholar] [CrossRef]
- Küheylan, C.D.; Özkan, D.B. Experimental and Theoretical Study of Heat Transfer in a Chilled Ceiling System. Appl. Sci. 2024, 14, 5908. [Google Scholar] [CrossRef]
- Harangozó, J.; Tureková, I.; Marková, I.; Hašková, A.; Králik, R. Study of the Influence of Heat Flow on the Time to Ignition of Spruce and Beech Wood. Appl. Sci. 2024, 14, 4237. [Google Scholar] [CrossRef]







| Parameter | AAC | Ext. Plaster | |
|---|---|---|---|
| Simulation | ρv (kg·m−3) | 500 | 1244 |
| ρ (kg·m−3) | 2206 | 2415 | |
| ψ (–) | 0.31 | 0.34 | |
| λ (W·m−1·K−1) | 0.12 | 0.28 | |
| c (J·kg−1·K−1) | 1050 | 1054 | |
| Boundary conditions | Determined experimentally | ||
| Experiment | Wall orientation | North | |
| Wall thickness | 500 mm | ||
| Exterior plaster thickness | 10 mm | ||
| Description | Period | |
|---|---|---|
| Phase 1 | Initialization 1 | 11 August 2020–24 August 2020 |
| Initialization 2 | 1 February 2021–7 February 2021 | |
| Phase 2 | Sensor adjustment 1 | 28 September 2020–4 October 2020 |
| Sensor adjustment 2 | 31 November 2020–6 December 2020 | |
| Sensor adjustment 3 | 1 February 2021–7 February 2021 | |
| Sensor adjustment 4 | 29 March 2021–4 April 2021 | |
| Phase 3 | Performance verification 1 | 5 October 2020–12 October 2020 |
| Performance verification 2 | 7 December 2020–14 December 2020 | |
| Performance verification 3 | 8 February 2021–15 February 2021 | |
| Performance verification 4 | 5 April 2021–12 April 2021 | |
| Phase 4 | Validation | 1 March 2022–17 March 2022 |
| Period | A (W·V−1·m−2) | B (W·m−2) | RMSE |
|---|---|---|---|
| 28 September 2020–4 October 2020 | 0.4880 | 0.8915 | 1.078 |
| 30 November 2020–6 December 2020 | 0.3412 | 0.2712 | 0.888 |
| 1 February 2021–7 February 2021 | 0.4570 | 0.3482 | 0.889 |
| 29 March 2021–4 April 2021 | 0.6468 | −0.0156 | 1.270 |
| USC (mV) | Ucurrent (mV) | Rcurrent (Ω) | Rheater (Ω) | Aheater (m2) | SSC (V·m2·W−1) | |
|---|---|---|---|---|---|---|
| 1 | 3.012 | 0.596 | 10 | 99.2 ± 1.0 | (3885 ± 136) × 10−6 | (60.34 ± 2.41) × 10−6 |
| 2 | 2.958 | 0.594 | 10 | 99.2 ± 1.0 | (3885 ± 136) × 10−6 | (65.69 ± 2.63) × 10−6 |
| 3 | 2.925 | 0.592 | 10 | 99.2 ± 1.0 | (3885 ± 136) × 10−6 | (65.42 ± 2.62) × 10−6 |
| 4 | 2.938 | 0.593 | 10 | 99.2 ± 1.0 | (3885 ± 136) × 10−6 | (65.46 ± 2.62) × 10−6 |
| 5 | 2.859 | 0.588 | 10 | 99.2 ± 1.0 | (3885 ± 136) × 10−6 | (64.66 ± 2.59) × 10−6 |
| SSC = (64.31 ± 2.57) × 10−6 V·m2·W−1 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kočí, J.; Maděra, J.; Černý, R. On-Site Sensor Sensitivity Adjustment Technique for a Maintenance-Free Heat Flow Monitoring in Building Systems. Appl. Sci. 2024, 14, 7323. https://doi.org/10.3390/app14167323
Kočí J, Maděra J, Černý R. On-Site Sensor Sensitivity Adjustment Technique for a Maintenance-Free Heat Flow Monitoring in Building Systems. Applied Sciences. 2024; 14(16):7323. https://doi.org/10.3390/app14167323
Chicago/Turabian StyleKočí, Jan, Jiří Maděra, and Robert Černý. 2024. "On-Site Sensor Sensitivity Adjustment Technique for a Maintenance-Free Heat Flow Monitoring in Building Systems" Applied Sciences 14, no. 16: 7323. https://doi.org/10.3390/app14167323
APA StyleKočí, J., Maděra, J., & Černý, R. (2024). On-Site Sensor Sensitivity Adjustment Technique for a Maintenance-Free Heat Flow Monitoring in Building Systems. Applied Sciences, 14(16), 7323. https://doi.org/10.3390/app14167323







