Analytical Investigation of the Effects of Additional Load Mass on the Fundamental Frequency of Pedestrian Beam Bridges
Abstract
:1. Introduction
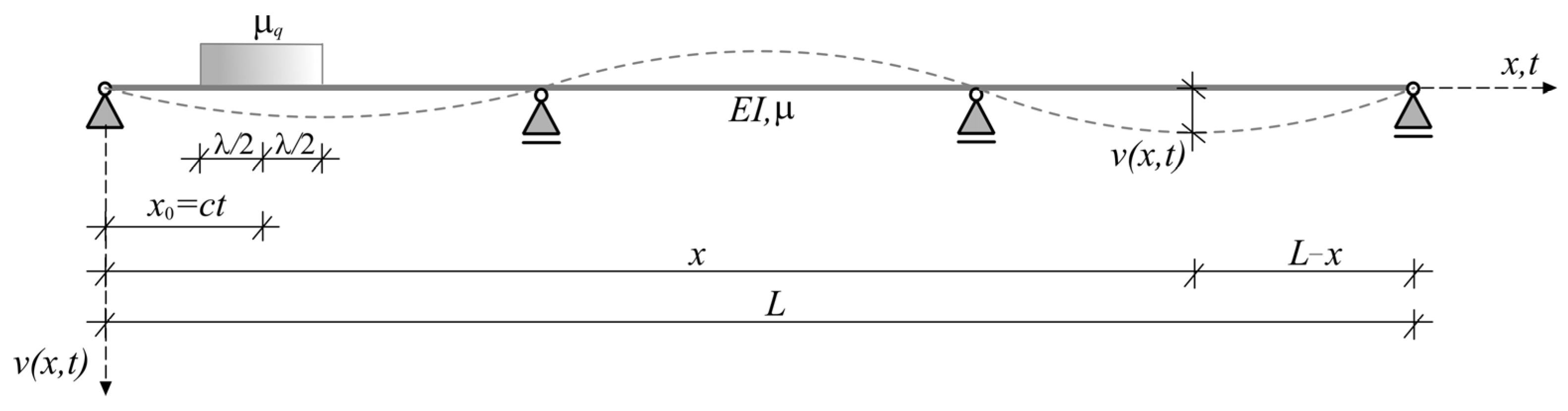
2. Problem Statement
3. Analytical Solutions for Beams with One, Two, and Three Equal Spans
- The eigenmode shape function for mode r, which satisfies boundary conditions:
- Natural frequency of the r-th mode:
- Generalized mass of the r-th mode:
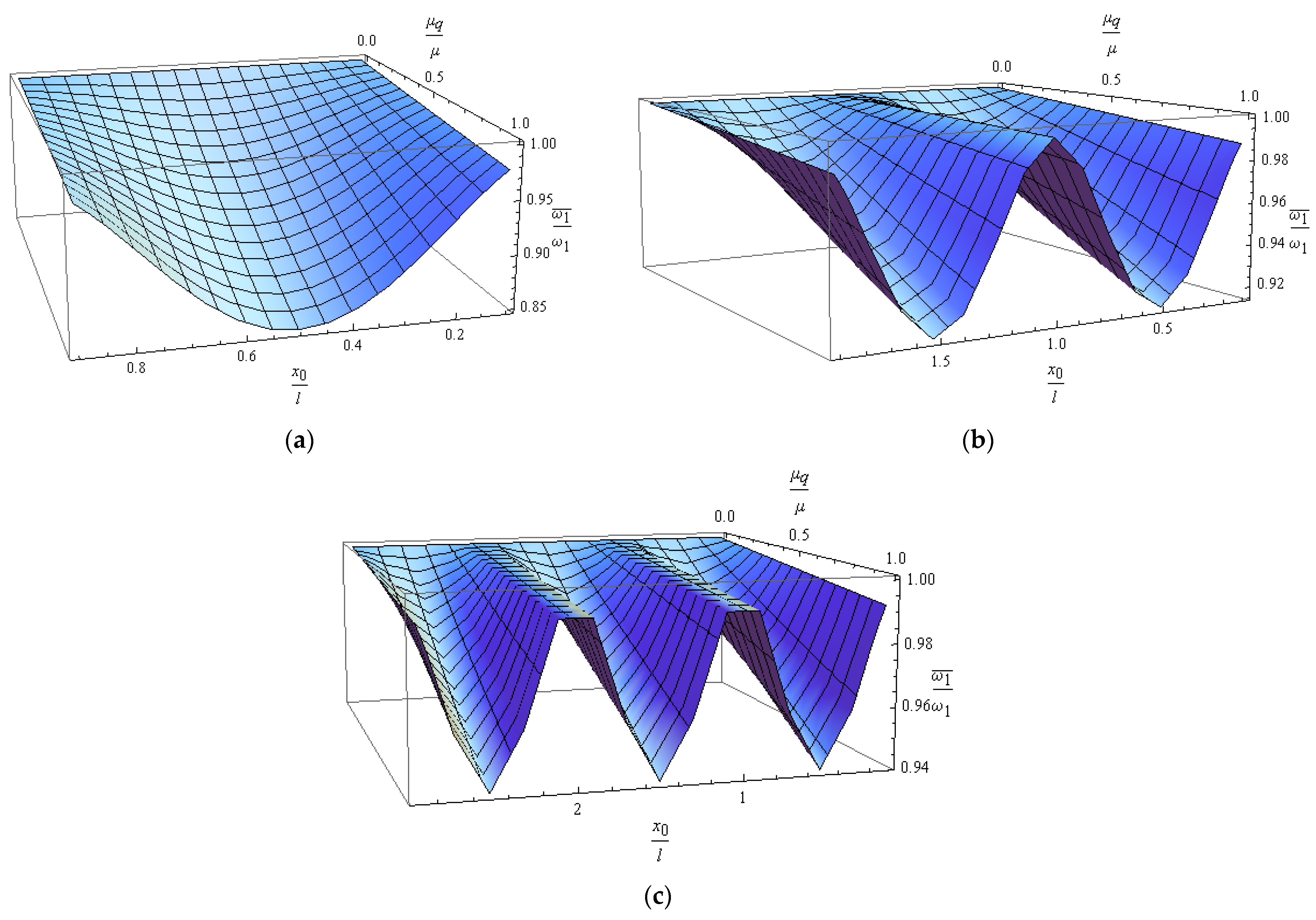
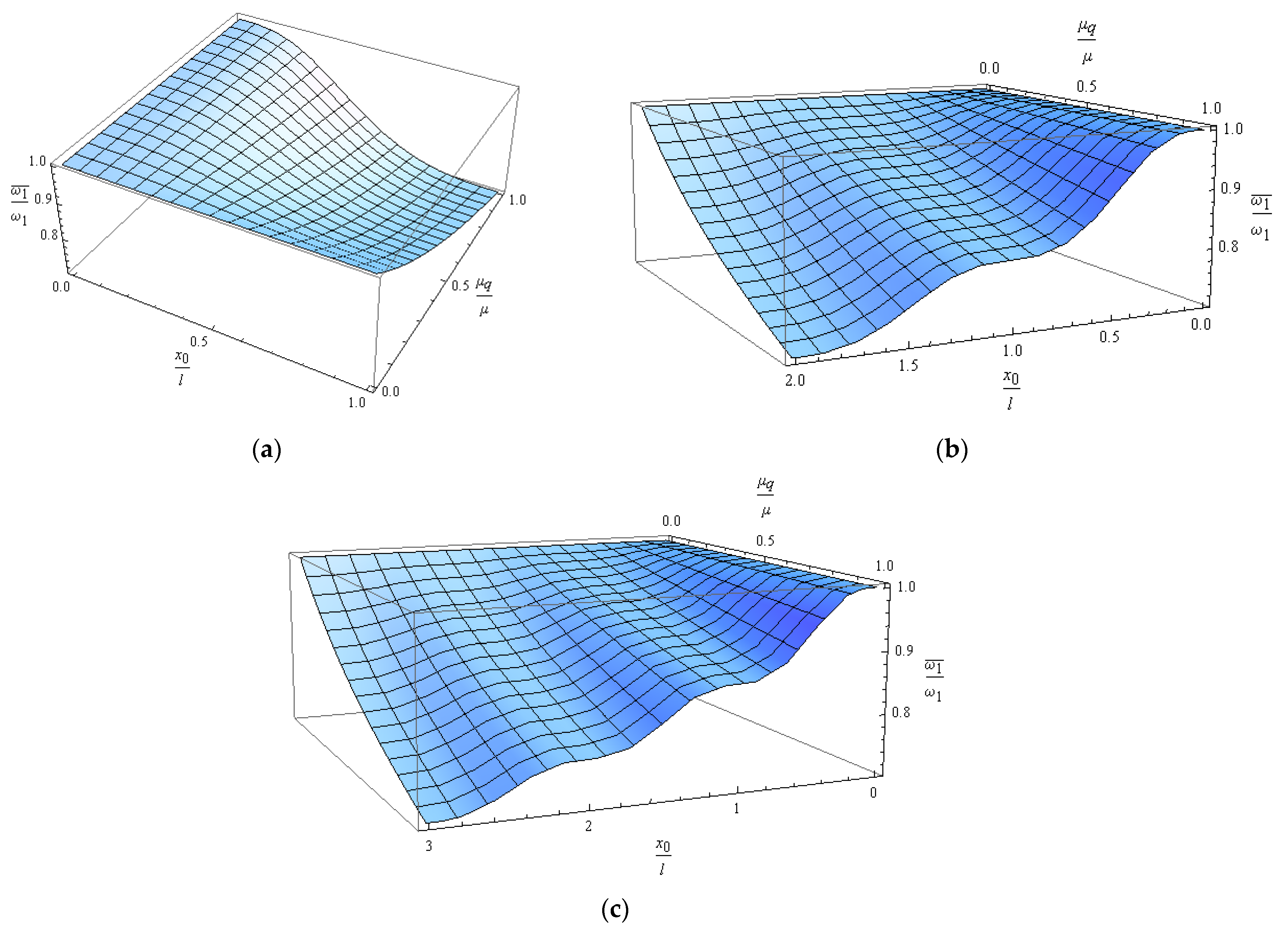
3.1. Influence of Additional Mass over Length λ
3.2. Influence of the Arrival of a Uniformly Distributed Mass
3.3. Influence of Concentrated Mass
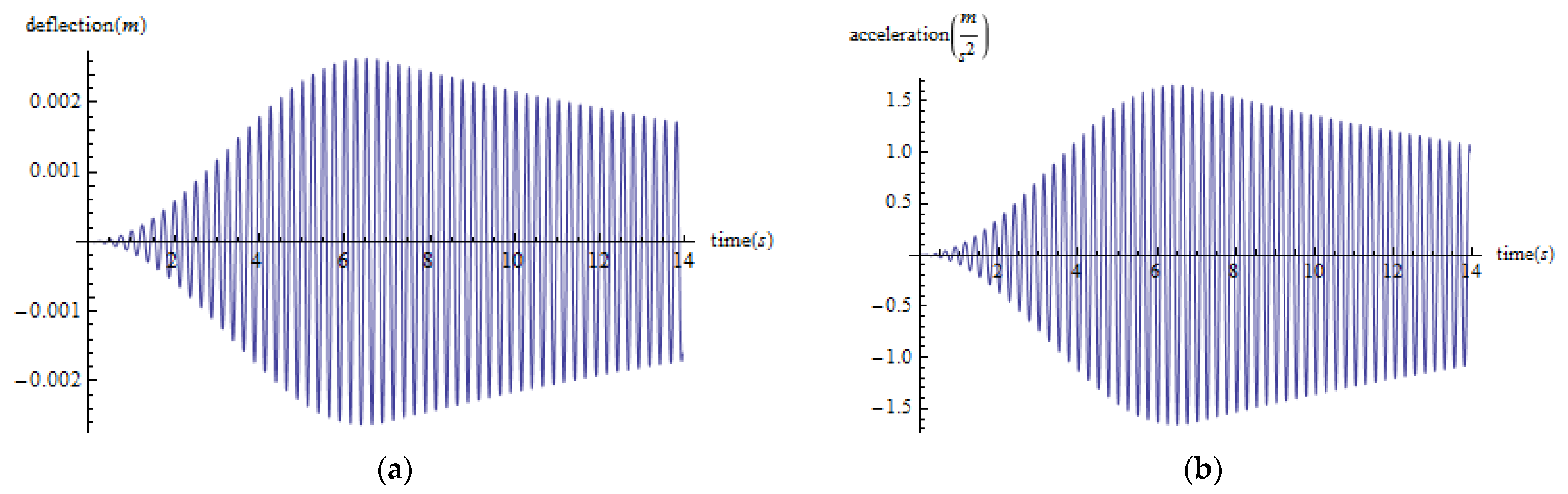
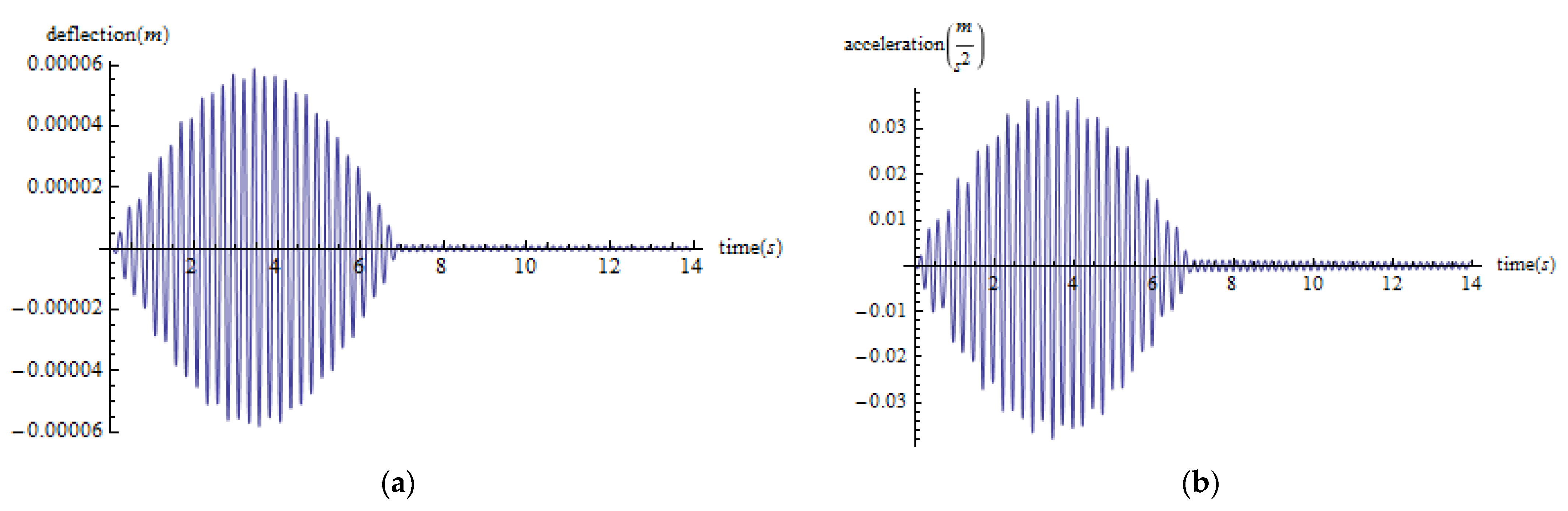
4. Application Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Archibald, P.; Fanning, J.P.; Pavic, A. Interactive horizontal load model for pedestrians crossing footbridges. Bridge Struct.–Assesment Des. Constr. 2005, 1, 169–176. [Google Scholar] [CrossRef]
- Shahabpoor, E.; Pavic, A.; Racic, V.; Zivanovic, S. Effect of group walking traffic on dynamic properties of pedestrian structures. J. Sound Vib. 2017, 387, 207–225. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, D.; Wang, Z.; Huang, S.; He, Y. Pedestrian-induced footbridge vibration response based on a simple beam analytical method. Adv. Bridge Eng. 2022, 3, 3. [Google Scholar] [CrossRef]
- Han, J.; Wang, H.; Liu, Y. Vibration analysis of a floor system based on probabilistic human-induced force model. Eng. Mech. 2014, 31, 81–87. [Google Scholar] [CrossRef]
- Dallard, P.; Fitzpatrick, A.J.; Flint, A.; Le Bourva, S.; Low, A.; Ridsdill-Smith, R.M.; Willford, M. The London Millennium Footbridge. Struct. Eng. 2001, 79, 17–33. [Google Scholar]
- Strogatz, S.H.; Abrams, D.M.; McRobie, A.; Eckhardt, B.; Ott, E. Crowded synchrony on the Millennium Bridge. Nature 2005, 438, 43–44. [Google Scholar] [CrossRef]
- Ingólfsson, E.; Georgakis, C.; Jönsson, J. Pedestrian-induced lateral vibrations of footbridges: A literature review. Eng. Struct. 2012, 45, 21–52. [Google Scholar] [CrossRef]
- Blekherman, A.N. Autoparametric Resonance in a Pedestrian Steel Arch Bridge: Solferino Bridge, Paris. J. Bridge Eng. 2007, 12, 669–676. [Google Scholar] [CrossRef]
- Ricciardelli, F.; Demartino, C. Design of footbridges against pedestrian-induced vibrations. J. Bridge Eng. 2016, 21, C4015003. [Google Scholar] [CrossRef]
- De Luca, A.; Bauer, M.; Pinto, M.; Malsch, E. Vibration analysis of footbridges: An overview of the current practice. In Proceedings of the 14th International Conference on Vibration Engineering and Technology of Machinery VETOMAC XIV, Lisbon, Portugal, 10–13 September 2018. [Google Scholar]
- EN 1991-2; Eurocode 1: Actions on Structures–Part 2: Traffic Loads on Bridges. European Committee for Standardization (CEN): Brussels, Belgium, 2003.
- EN 1990; Eurocode–Basis of Structural Design. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
- AASHTO. LRFD Guide Specifications for the Design of Pedestrian Bridges, 2nd ed.; With 2015 Interim Revisions; American Association of State Highway and Transport Officials: Washington, DC, USA, 2009. [Google Scholar]
- Sétra. Footbridges-Assessment of Vibrational Behaviour of Footbridges under Pedestrian Loading. Technical Guide EQ-SETRA–06-ED17–FR+ENG; Service D’études Techniques des Routes et Autoroutes (Sétra): Paris, France, 2006. [Google Scholar]
- FIB. Guidelines for the Design of Footbridges. Bulletin 32; Fédération Internationale du Béton: Lausanne, Switzerland, 2005. [Google Scholar]
- Fairley, T.E.; Griffin, M.J. The apparent mass of the seated human body: Vertical vibration. J. Biomech. 1989, 22, 81–94. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Griffin, M.J. Mathematical models for the apparent masses of standing subjects exposed to vertical whole-body vibration. J. Sound Vib. 2003, 260, 431–451. [Google Scholar] [CrossRef]
- Zheng, G.; Qiu, Y.; Griffin, M.J. Vertical and dual-axis vibration of the seated human body: Nonlinearity, cross-axis coupling, and associations between resonances in transmissibility and apparent mass. J. Sound Vib. 2012, 331, 5880–5894. [Google Scholar] [CrossRef]
- Sun, C.; Liu, C.; Zheng, X.; Wu, J.; Wang, Z.; Qiu, Y. An analytical model of seated human body exposed to combined fore-aft, lateral, and vertical vibration verified with experimental modal analysis. Mech. Syst. Signal Process. 2023, 200, 110527. [Google Scholar] [CrossRef]
- Fouli, M.; Camara, A. Human–structure interaction effects on lightweight footbridges with tuned mass dampers. Structures 2024, 62, 106263. [Google Scholar] [CrossRef]
- Colmenares, D.; Costa, G.; Civera, M.; Surace, C.; Karoumi, R. Quantification of the human–structure interaction effect through full-scale dynamic testing: The Folke Bernadotte Bridge. Structures 2023, 55, 2249–2265. [Google Scholar] [CrossRef]
- Gallegos-Calderón, C.; Naranjo-Pérez, J.; Díaz, I.M.; Goicolea, J.M. Identification of a Human-Structure Interaction Model on an Ultra-Lightweight FRP Footbridge. Appl. Sci. 2021, 11, 6654. [Google Scholar] [CrossRef]
- Zivanovic, S.; Pavic, A.; Reynolds, P. Vibration serviceability of footbridge under human-induced excitation: A literature review. J. Sound Vib. 2005, 279, 1–74. [Google Scholar] [CrossRef]
- Racic, V.; Pavic, A.; Brownjohn, J.M.W. Experimental identification and analytical modelling of human walking forces: Literature review. J. Sound Vib. 2009, 326, 1–49. [Google Scholar] [CrossRef]
- Shahabpoor, E.; Pavic, A.; Racic, V. Interaction between Walking Humans and Structures in Vertical Direction: A Literature Review. Shock Vib. 2016, 2016, 3430285. [Google Scholar] [CrossRef]
- Garinei, A. Vibrations of simple beam-like modelled bridge under harmonic moving loads. Int. J. Eng. Sci. 2006, 44, 778–787. [Google Scholar] [CrossRef]
- Stăncioiu, D.; James, S.; Ouyang, H.; Mottershead, J.E. Experimental model of a mass travelling on a continuous beam. J. Phys. Conf. Ser. 2009, 181, 012084. [Google Scholar] [CrossRef]
- Karimi, A.H.; Ziaei-Rad, S. Vibration analysis of a beam with moving support subjected to a moving mass travelling with constant and variable speed. Commun. Nonlinear Sci. Numer. Simul. 2015, 29, 372–390. [Google Scholar] [CrossRef]
- Mashaly, E.-S.; Ebrahim, T.M.; Abou-Elfath, H.; Ebrahim, O.A. Evaluating the vertical vibration response of footbridges using a response spectrum approach. Alex. Eng. J. 2013, 52, 419–424. [Google Scholar] [CrossRef]
- Heinemeyer, C.; Butz, C.; Keil, A.; Schlaich, M.; Goldbeck, A.; Trometor, S.; Lukic, M.; Chabrolin, B.; Lemaire, A.; Martin, P.-O.; et al. Design of Lightweight Footbridges for Human Induced Vibrations; Sedlacek, G., Heinemeyer, C., Butz, C., Geradin, M., Eds.; JRC Scientific and Technical Reports; European Commission: Luxembourg, 2009. [Google Scholar]
- Ellis, B.R.; Ji, T. Human-structure interaction in vertical vibration. Proc. Inst. Civ. Eng.-Struct. Build. 1997, 122, 1–9. [Google Scholar] [CrossRef]
- Maraveas, C.; Fasoulakis, Z.C.; Tsavdaridis, K.D. A Review of Human Induced Vibrations on Footbridges. Am. J. Eng. Appl. Sci. 2015, 8, 422–433. [Google Scholar] [CrossRef]
- Sachse, R. The Influence of Human Occupants on the Dynamic Properties of Slender Structures. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2002. [Google Scholar]
- Gao, Y.A.; Yang, Q.S. A theoretical treatment of crowd-structure interaction. Int. J. Struct. Stab. Dyn. 2018, 18, 1871001. [Google Scholar] [CrossRef]
- Busca, G.; Cappellini, A.; Manzoni, S.; Tarabini, M.; Vanali, M. Quantification of changes in modal parameters due presence of passive people on a slender structure. J. Sound Vib. 2014, 333, 5641–5652. [Google Scholar] [CrossRef]
- Yang, J.P.; Su, Z.; Yau, J.D.; Yang, D.S. Investigation of Spatial-Varying Frequencies Concerning Effects of Moving Mass on a Beam. Int. J. Struct. Stab. Dyn. 2023, 23, 2340002. [Google Scholar] [CrossRef]
- O’Sullivan, D.; Caprani, C.; Keogh, J. The Response of a Footbridge to Pedestrians Carrying Additional Mass. In Proceedings of the Bridge and Concrete Research Ireland (BCRI) Conference, Dublin, Ireland, 6–7 September 2012. [Google Scholar]
- Bergenudd, J.; Battini, J.-M.; Crocetti, R. Dynamic analysis of pedestrian timber truss bridge at three construction stages. Structures 2024, 59, 1005763. [Google Scholar] [CrossRef]
- Dallali, E.G.; Dey, P. Evaluation of the Equivalent Moving Force Model for Lightweight Aluminum Footbridges in Simulating the Bridge Response under a Single-Pedestrian Walking Load. Eng. Proc. 2023, 43, 22. [Google Scholar] [CrossRef]
- Tian, R.; Yang, X.; Zhang, Q.; Guo, X. Vibration reduction in beam bridge under moving loads using nonlinear smooth and discontinuous oscillator. Adv. Mech. Eng. 2016, 8, 1–12. [Google Scholar] [CrossRef]
- Li, J.; Liu, X. Human-Induced Vibration Analysis and Reduction Design for Super Long Span Pedestrian Arch Bridges with Tuned Mass Dampers. Appl. Sci. 2023, 13, 8263. [Google Scholar] [CrossRef]
- Manolis, G.D.; Dadoulis, G.I. Passive Control in a Continuous Beam under a Traveling Heavy Mass: Dynamic Response and Experimental Verification. Sensors 2024, 24, 573. [Google Scholar] [CrossRef] [PubMed]
- Spasojević-Šurdilović, M. Analiza graničnog stanja upotrebljivosti pešačkih mostova u pogledu vibracija indukovanih pešacima. Ph.D. Thesis, University of Niš, Niš, Serbia, 2013. [Google Scholar]
- Brčić, V. Dinamika Konstrukcija, 2nd ed.; Građevinska knjiga: Belgrade, Serbia, 1981. [Google Scholar]
- Blanchard, J.; Davies, B.L.; Smith, J.W. Design criteria and analysis for dynamic loading of footbridges. In Proceedings of the Symopsium on Dynamic Behaviour of Bridges at the Transport and Road Research Laboratory, Crowthorne, Berkshire, England, 19 May 1977. [Google Scholar]
- BS 5400-2; Steel, Concrete and Composite Bridges–Part 2: Specification for Loads. British Standards Institution (BSI): London, UK, 1978.
- SRPS EN 1991-2/NA:2019; Eurocode 1–Actions on Structures–Part 2: Traffic Loads on Bridges–National Annex. Institute for Standardization of Serbia (ISS): Belgrade, Serbia, 2019.


| Dynamic Model of the Bridge | Circular Frequency |
|---|---|
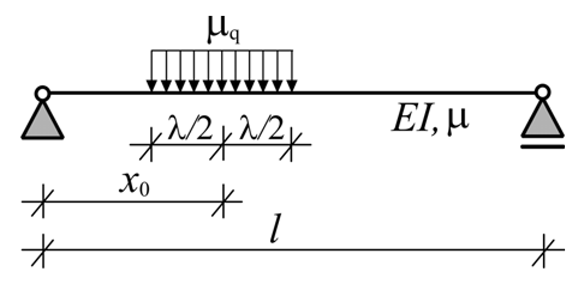 | |
 | |
 |
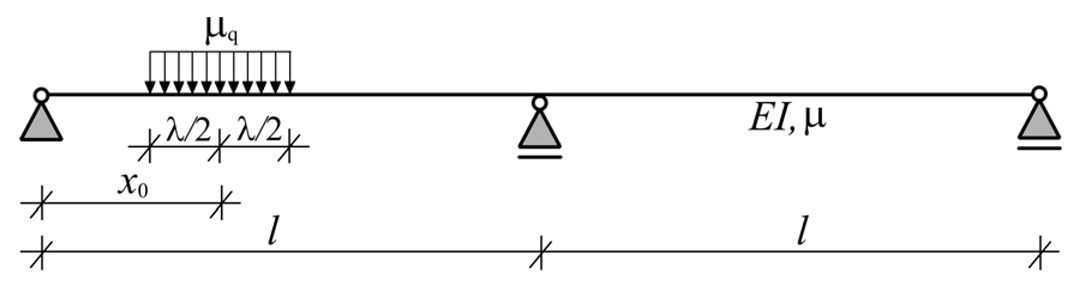
| Dynamic Model of the Bridge | Circular Frequency |
|---|---|
 | |
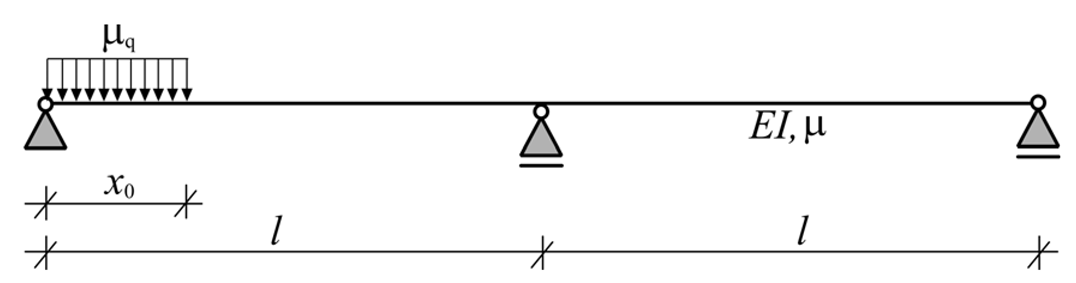 | |
 |
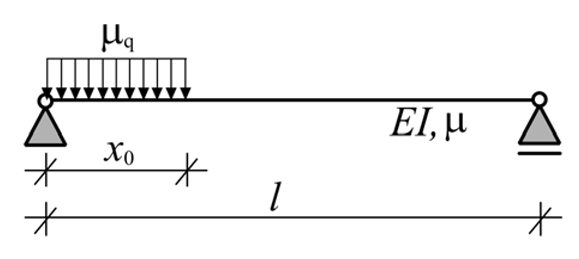
| Dynamic Model of the Bridge | Circular Frequency |
|---|---|
 | |
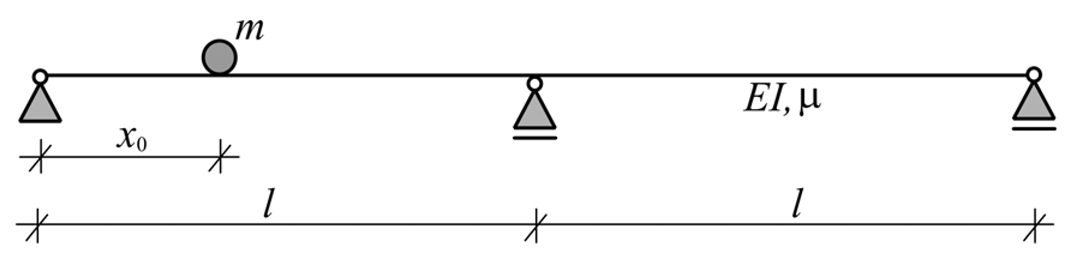 | |
 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spasojević Šurdilović, M.; Zorić, A.; Živković, S.; Turnić, D. Analytical Investigation of the Effects of Additional Load Mass on the Fundamental Frequency of Pedestrian Beam Bridges. Appl. Sci. 2024, 14, 7369. https://doi.org/10.3390/app14167369
Spasojević Šurdilović M, Zorić A, Živković S, Turnić D. Analytical Investigation of the Effects of Additional Load Mass on the Fundamental Frequency of Pedestrian Beam Bridges. Applied Sciences. 2024; 14(16):7369. https://doi.org/10.3390/app14167369
Chicago/Turabian StyleSpasojević Šurdilović, Marija, Andrija Zorić, Srđan Živković, and Dragana Turnić. 2024. "Analytical Investigation of the Effects of Additional Load Mass on the Fundamental Frequency of Pedestrian Beam Bridges" Applied Sciences 14, no. 16: 7369. https://doi.org/10.3390/app14167369







