Allocation and Sizing of DSTATCOM with Renewable Energy Systems and Load Uncertainty Using Enhanced Gray Wolf Optimization
Abstract
1. Introduction
- Introducing a new method for the optimal allocation and sizing of DSTATCOMs in radial distribution systems.
- Incorporating the uncertainty associated with load fluctuations and renewable energy generation into the DSTATCOM allocation and sizing process.
2. Problem Formulation
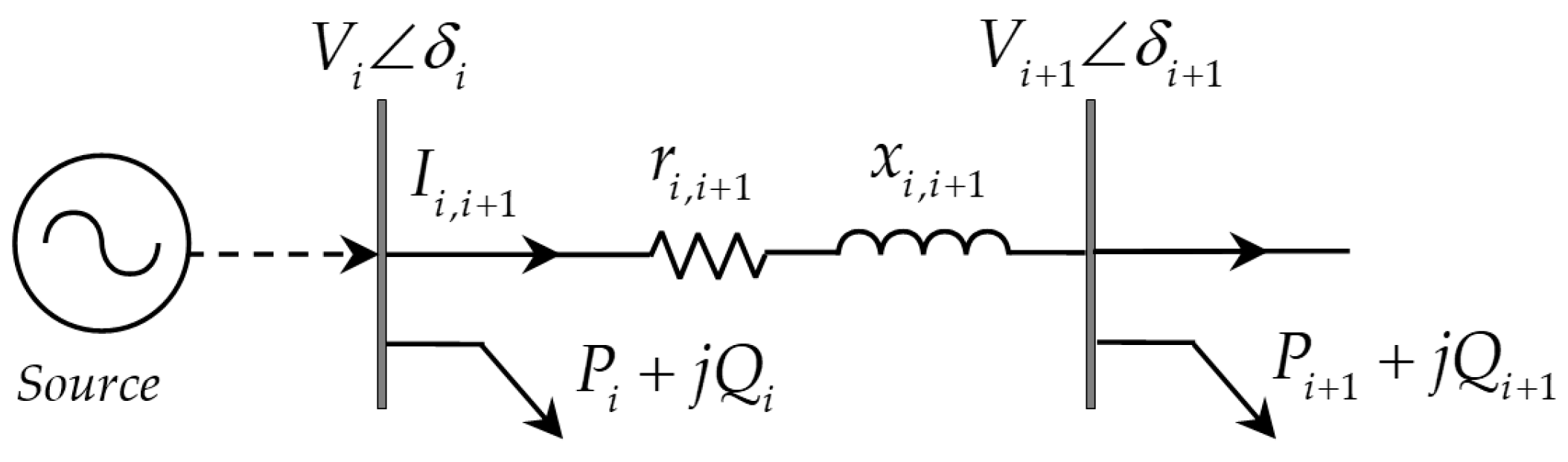
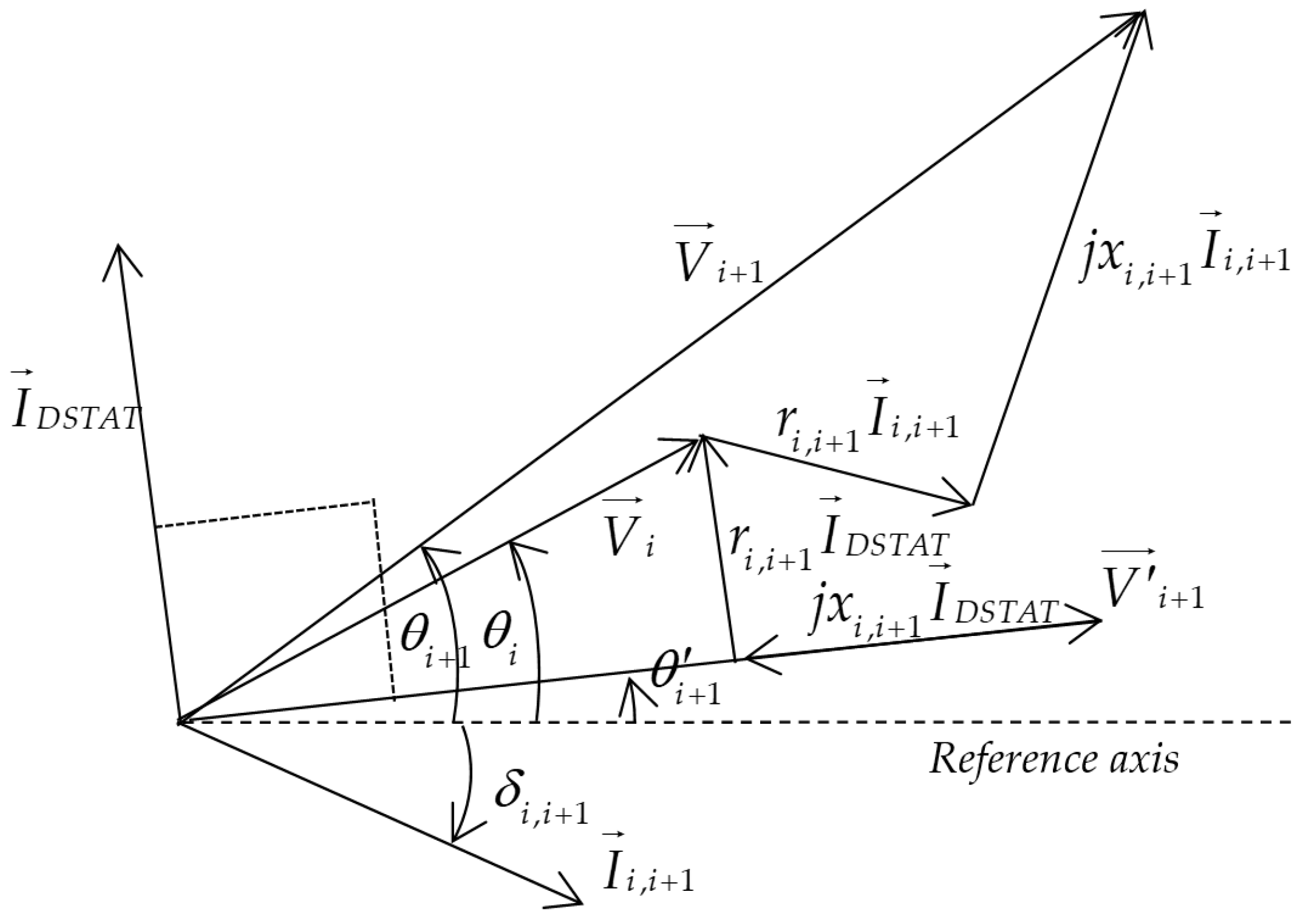
2.1. Modeling of DSTATCOM
2.2. Voltage Stability Index (VSI)
2.3. DSTATCOM-Integrated Load Flow Steps
- Step 1: Preparation—Read system data, including the system’s topology, bus characteristics, branch parameters, load consumption values, and DSTATCOM data, along with its operating constraints.
- Step 2: Initialization—Assume a flat voltage profile as the starting point for the initial voltages and set the first iteration, denoted as , to 0.
- Step 3: Nodal Current Calculation—Calculate the injected current at each load bus using the assumed known voltage, with the following equation:
- Step 4: Adding Current Injected by the DSTATCOM—For each bus where the DSTATCOM is connected, calculate the current it injects using Equation (4). Then, add this calculated current to the previously injected current on the same bus.
- Step 5: Backward Sweep—Starting with the last-ordered branch, the current flowing between the node and its preceding node is determined using the BIBC (branch-current to bus-current) matrix [16], as follows:
- Step 6: Forward Sweep—The node voltages are updated iteratively, starting from the root bus, in accordance with the following equation:
- Step 7: Convergence Check—Repeat Step 5 and Step 6 until the difference in voltage magnitudes between successive iterations at each node falls below a predefined tolerance limit, as follows:
- Step 8: Displaying Results—Using the converged voltages, calculate the branch currents with Ohm’s and Kirchhoff’s laws. Compute the active power losses in each branch and sum them to calculate the total losses.
3. Renewable Energy Resource Modeling
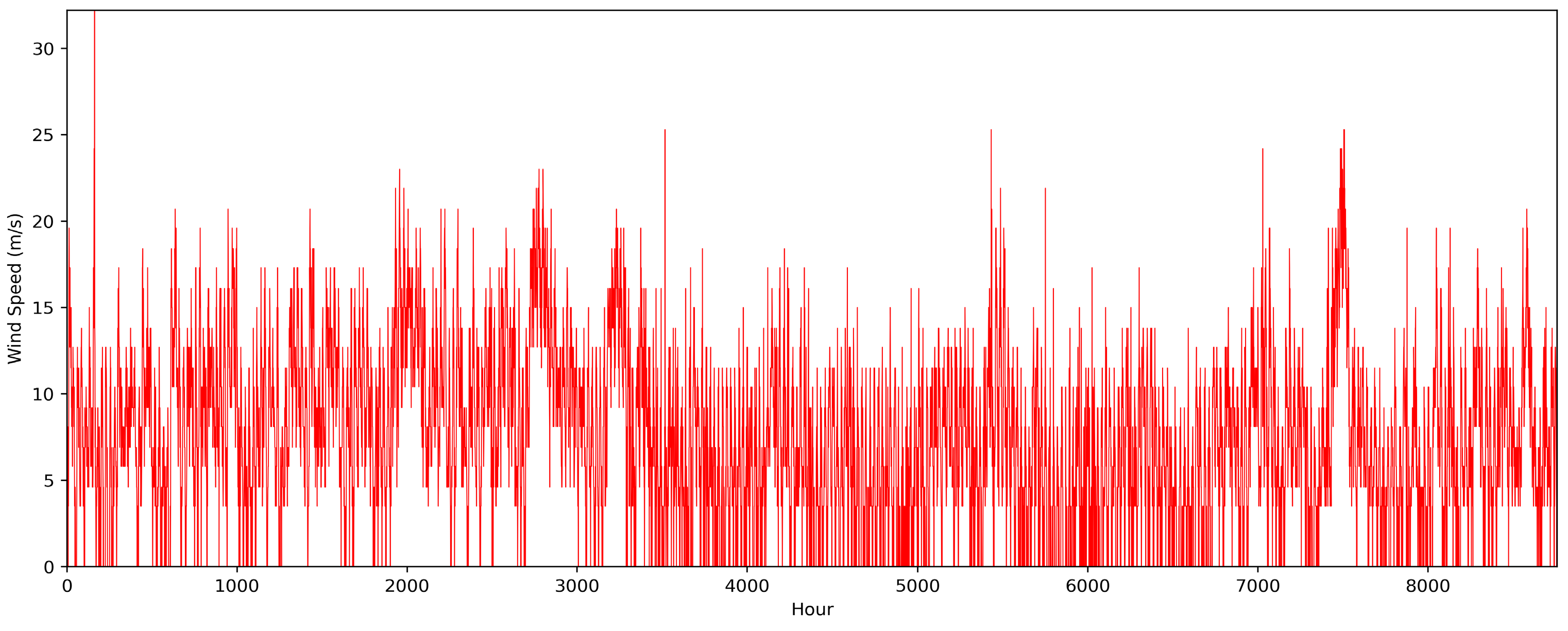
3.1. Wind Power Generators
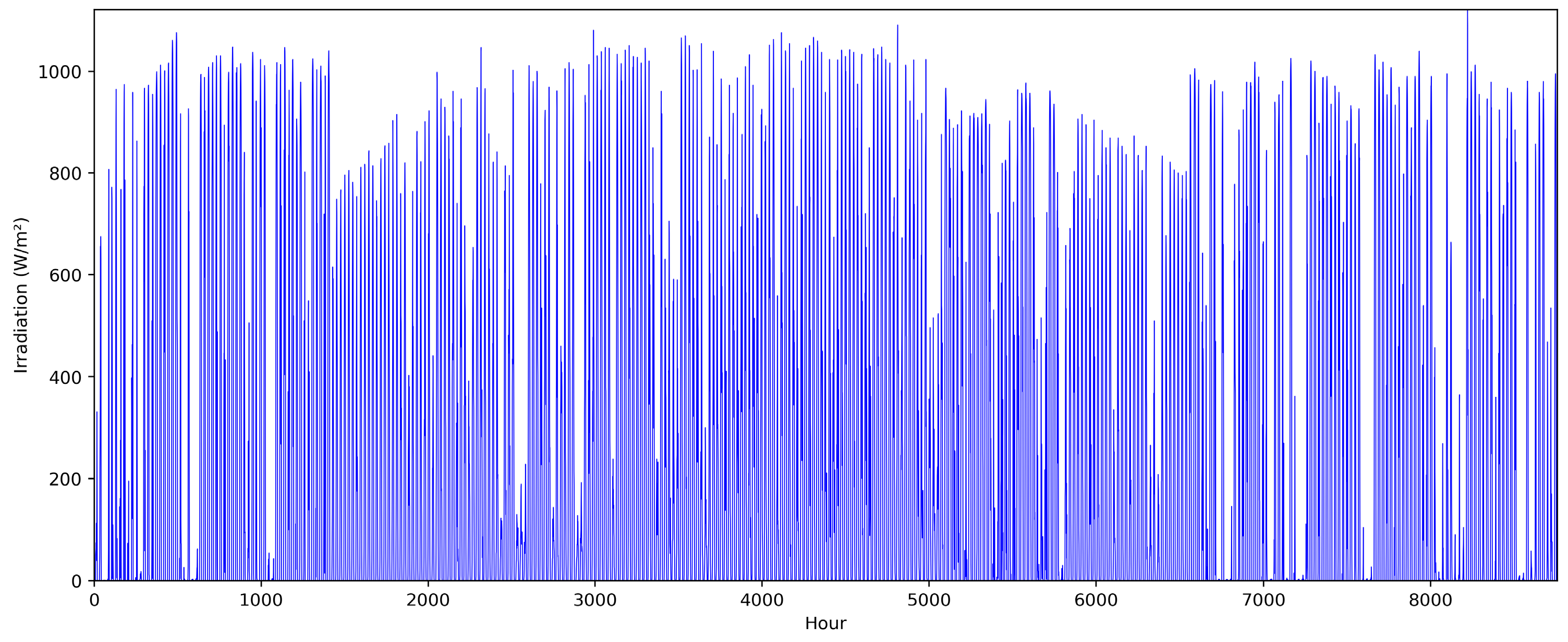
3.2. Solar Power Generators
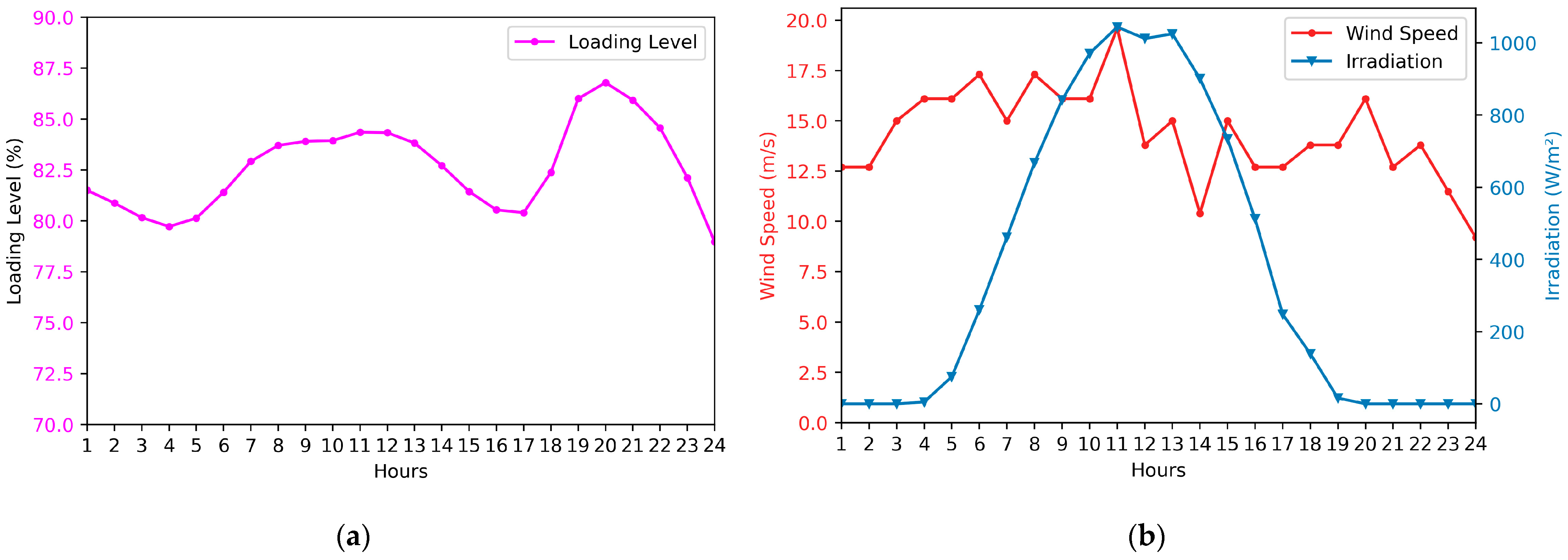
3.3. Fast Scenario Reduction Method
- Step 1:
- Scenario Generation—Start by generating a large set of scenarios using methods like Monte Carlo simulations, historical data, or other suitable techniques. Organize these scenarios into a matrix, denoted as , where each row represents a scenario containing the loading level , the irradiance , and the wind speed , as follows:
- Step 2:
- Additionally, initialize the probability of each scenario to , where represents the total number of scenarios.
- Step 3:
- Distance Calculation—Calculate distances between each pair of scenarios and , using an appropriate measure to form a distance matrix. In this paper, the Euclidean distance with the 2-norm is adopted, and can be expressed as follows:
- Step 4:
- Scenarios Merging—Identify the pair of scenarios and that have the smallest Euclidean distance, as calculated in Step 2. Merge these two scenarios into a single representative scenario, often by taking the weighted average, based on their probabilities. The new scenario’s values for loading, irradiance, and wind speed can be computed as:
- Step 5:
- Termination Check—Determine if the stopping criterion has been met (e.g., by reaching a predefined tolerance level or desired number of scenarios ); otherwise, return to Step 2.
4. Improved Gray Wolf Optimization
5. Application of I-GWO to the Proposed Problem
5.1. Problem Formulation
- The first term in Equation (43) aims to maximize the TACS by minimizing both power loss costs and DSTATCOMs costs.
- The second term in Equation (43) aims to improve the voltage profile by reducing the voltage deviation .
- Power Flow Equations: The net active and reactive powers must be equal to zero, and the node voltage equation must be satisfied at each bus:
- 2.
- Branch flow limits: The current in each branch of the distribution system must not surpass the maximum permissible current limit , as expressed by:
5.2. Constraint Handling
5.3. Algorithm Steps
- Step 1:
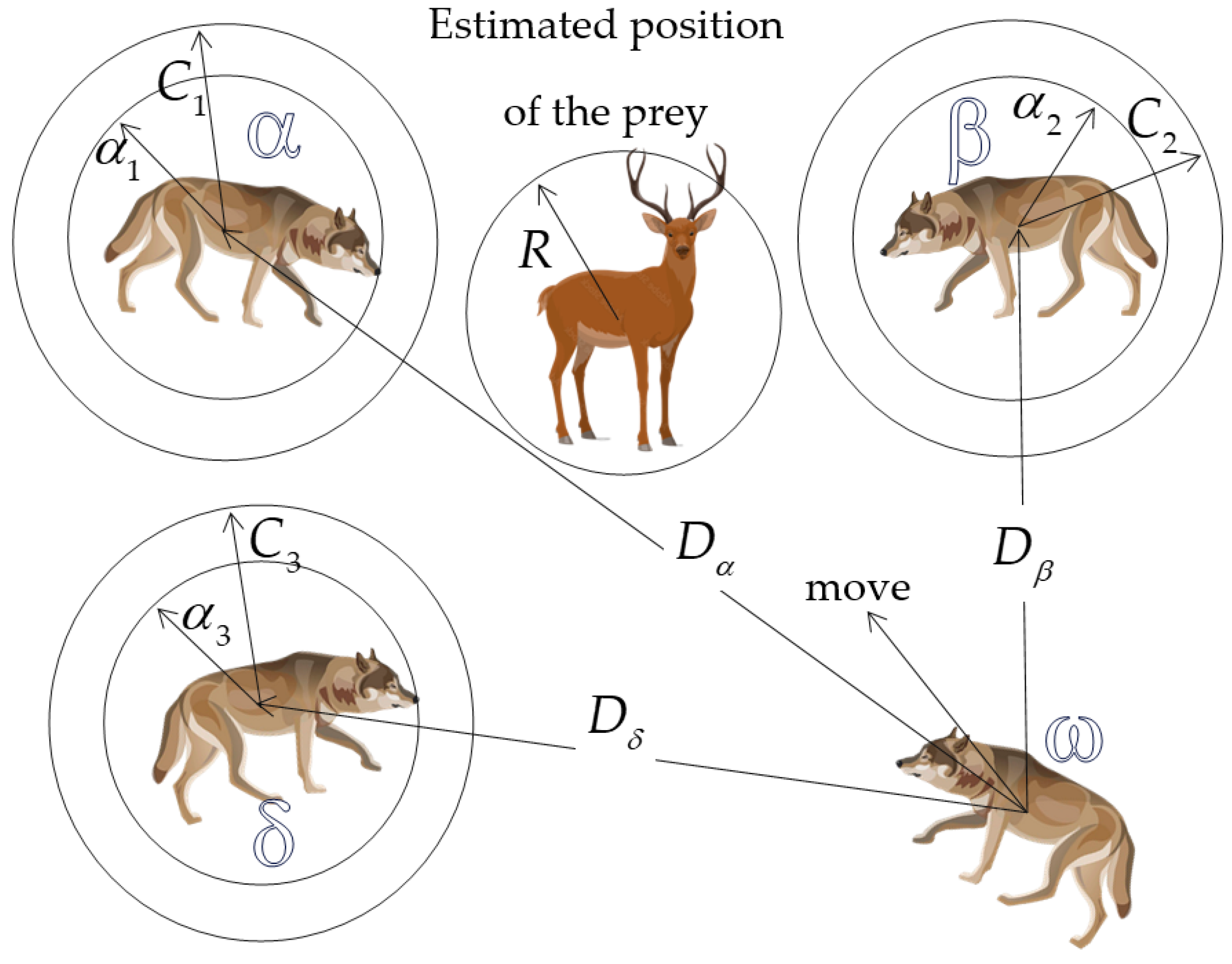
- Initialization—Generate an initial population of gray wolves (solutions). Each individual (wolf) corresponds to the location and size of the DSTATCOM within the power network, as illustrated in Figure 9.
- Step 2:
- Evaluation—Execute the load flow analysis using the forward-backward sweep algorithm for each search agent (wolf). Obtain the active power losses and then calculate the fitness of each wolf in the population using Equation (49).
- Step 3:
- Wolf Ranking—The wolves are sorted based on their fitness levels. From this ranking, the top three wolves are identified. The fittest wolf is designated as the alpha (α), followed by the beta (β) as the second-fittest, and the delta (δ) as the third-fittest. All other wolves in the ranking after these three are considered omegas (ω).
- Step 4:
- Position Updating—Update the positions of the beta and delta wolves relative to the alpha wolf using Equation (35) for approaching and attacking. The omegas update their positions in relation to all three dominant wolves (alpha, beta, and delta), according to Equation (36).
- Step 5:
- Convergence Check—Calculate the fitness of all wolves using Equation (49), then update their positions. Check if a stopping criterion is met, such as a maximum number of iterations, a minimum error requirement, or another convergence indicator. If the stopping criterion is not satisfied, return to Step 2, and continue the iterations.
- Step 6:
- Solution Extraction—Once convergence is achieved or the stopping criterion is met, the alpha wolf’s position represents the optimal solution (or a near-optimal solution) to the problem.
6. Simulation Results and Discussion
- Scenario (1): This scenario did not consider the presence of renewable generations and assumed a fixed load demand.
- Scenario (2): This scenario considered the presence of renewable energies located at predefined positions, also considering uncertain generation and load uncertainty.
6.1. Scenario (1)
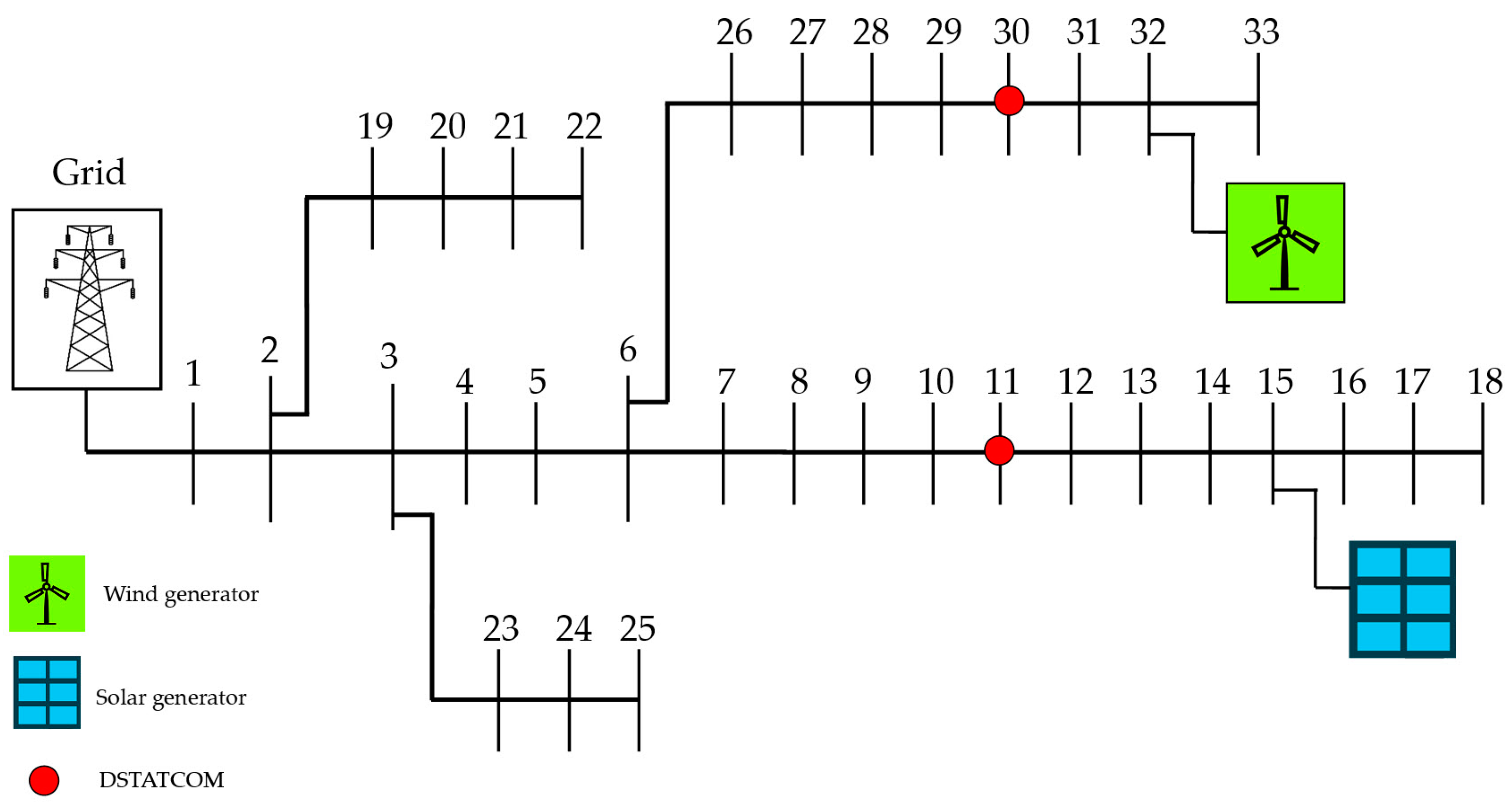
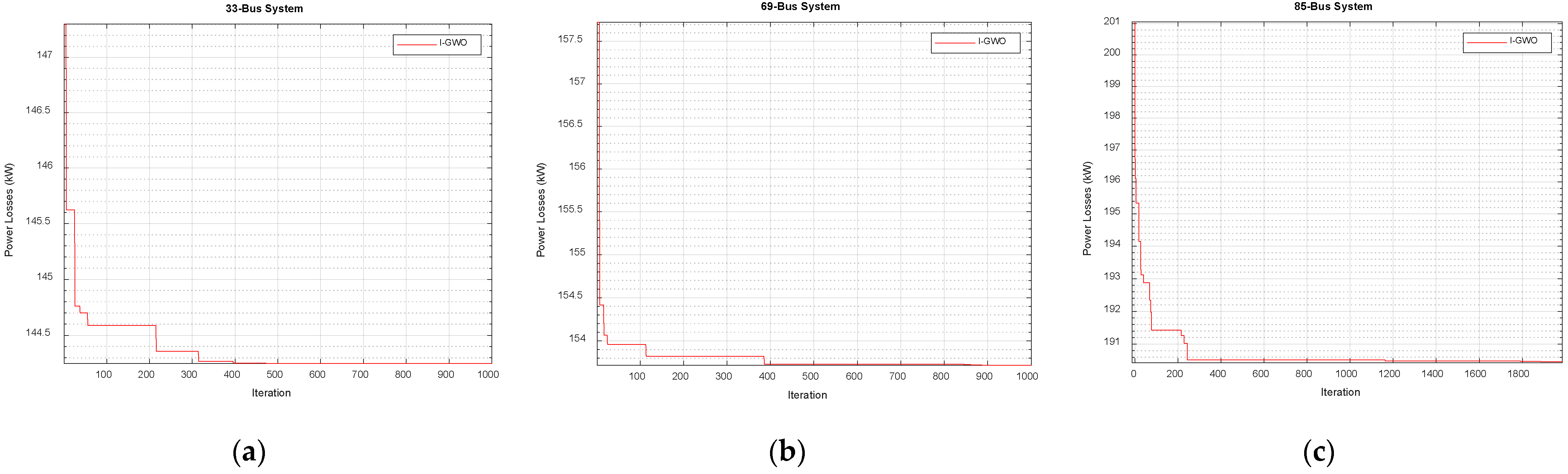
6.1.1. The 33-Bus Test System
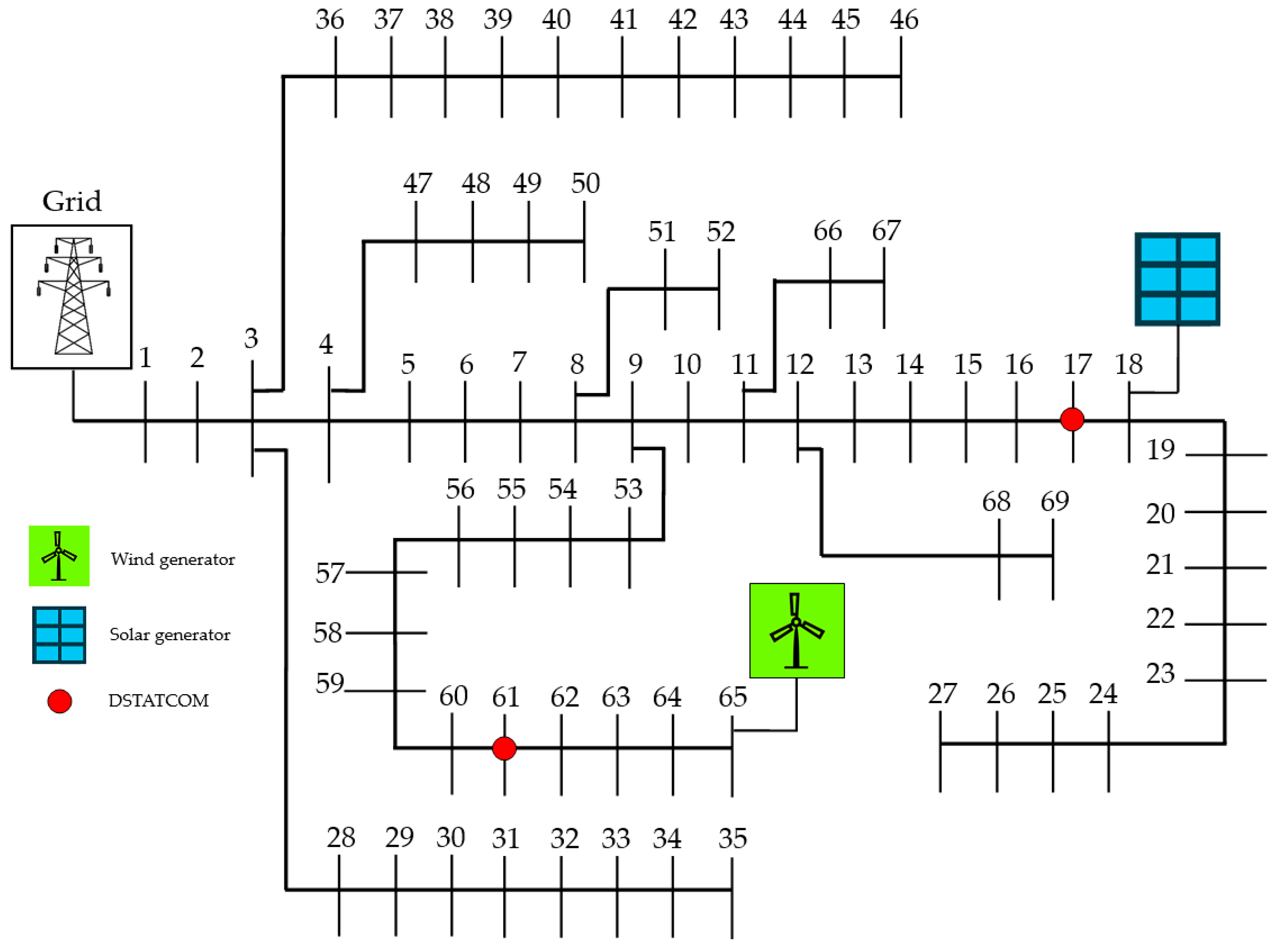
6.1.2. IEEE 69-Bus Test System
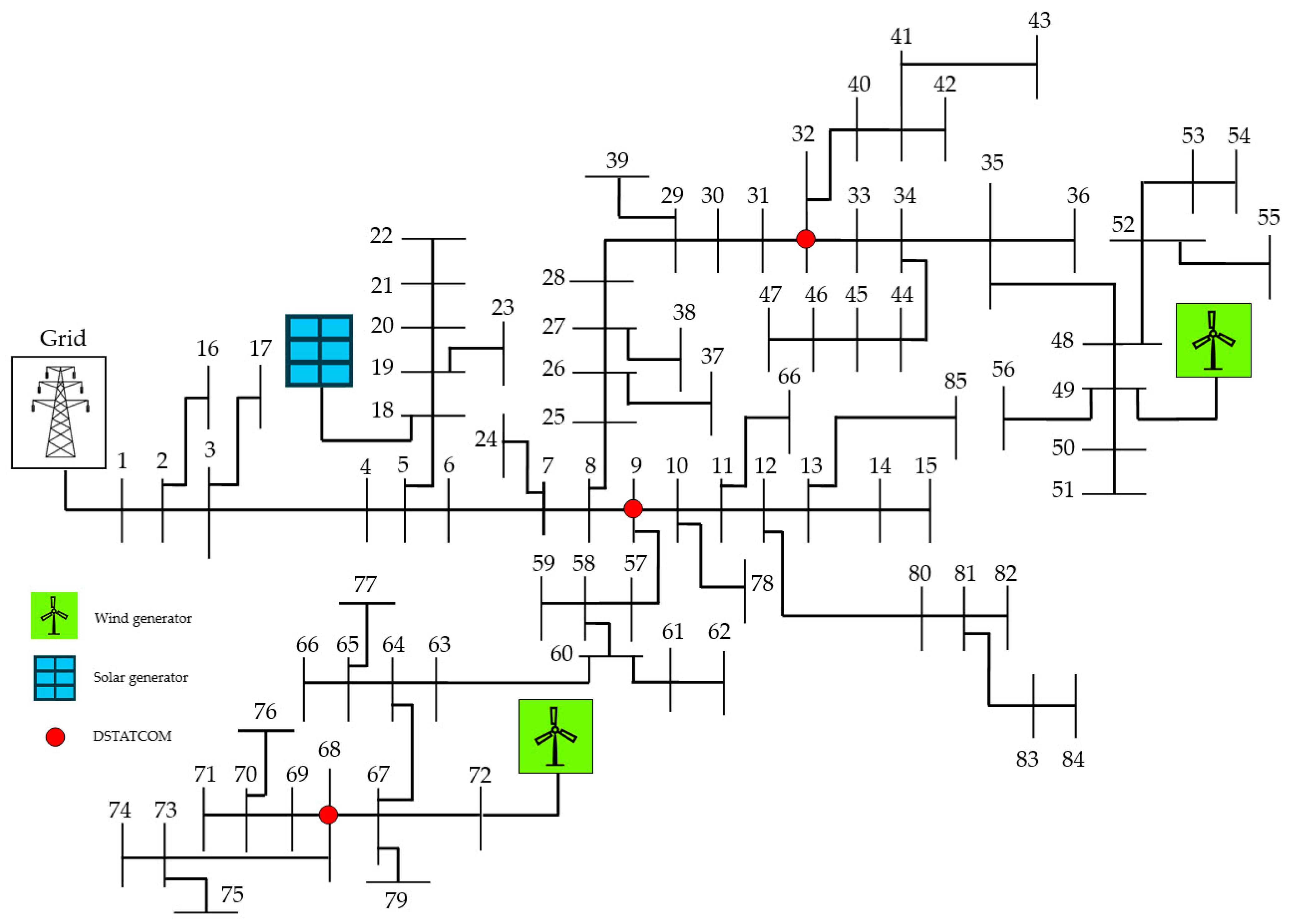
6.1.3. IEEE 85-Bus Test System
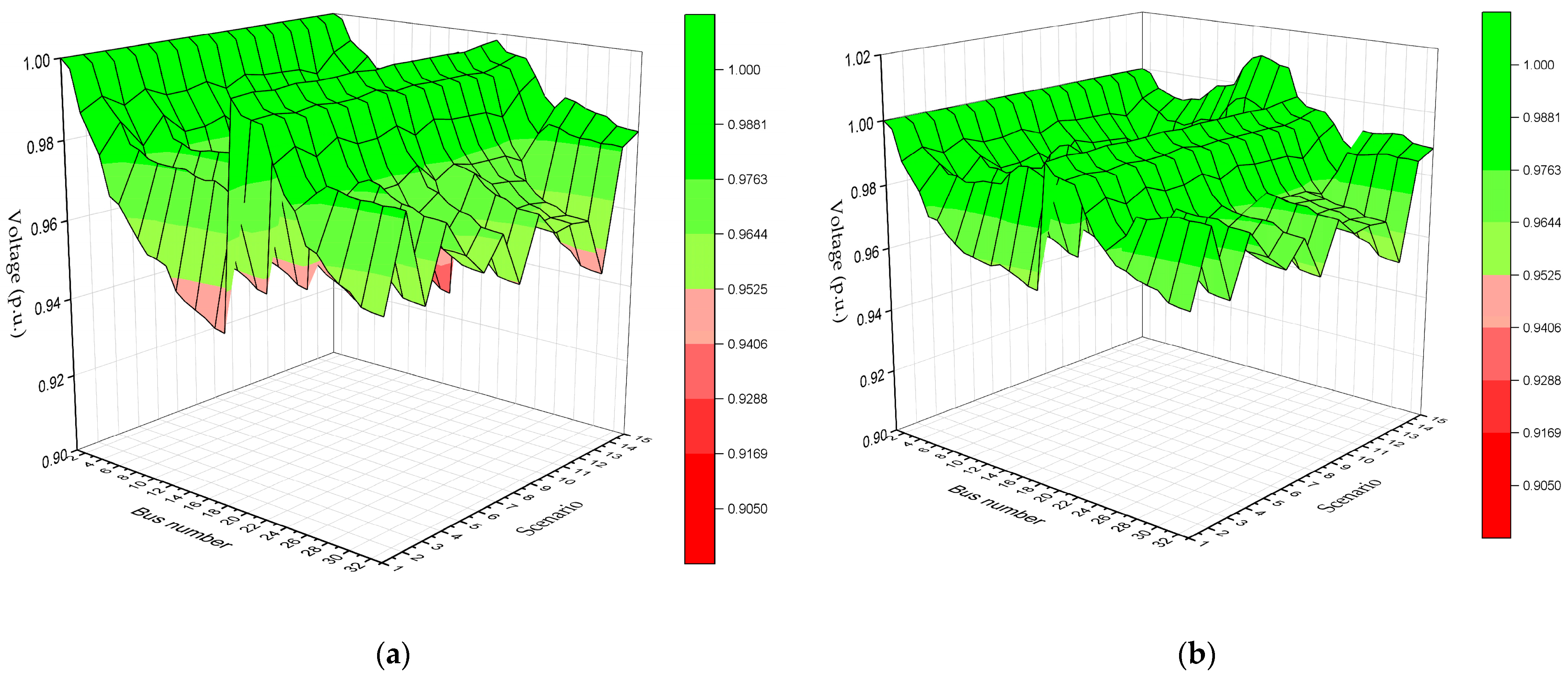
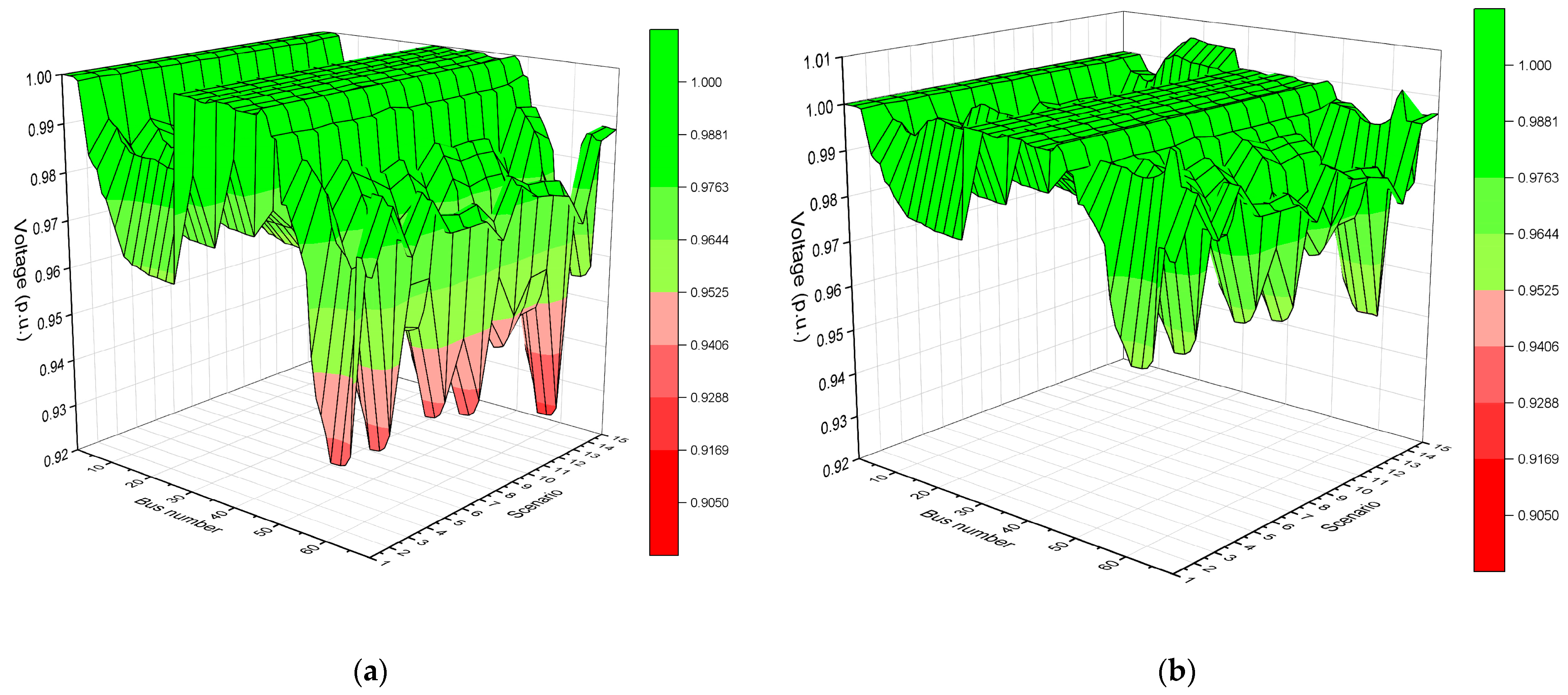
6.2. Scenario (2)
6.3. Comparative Analysis
7. Conclusions
Further Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Bus | Load at the Receiving End | Branch Data | ||||
|---|---|---|---|---|---|---|
| Send | Receive | PL (kW) | QL (kVAr) | R (Ω) | X (Ω) | Imax (A) |
| 1 | 2 | 100 | 60 | 0.0922 | 0.0470 | 400 |
| 2 | 3 | 90 | 40 | 0.4930 | 0.2510 | 400 |
| 3 | 4 | 120 | 80 | 0.3661 | 0.1864 | 400 |
| 4 | 5 | 60 | 30 | 0.3811 | 0.1941 | 400 |
| 5 | 6 | 60 | 20 | 0.8190 | 0.7070 | 400 |
| 6 | 7 | 200 | 100 | 0.1872 | 0.6188 | 300 |
| 7 | 8 | 200 | 100 | 1.7117 | 1.2357 | 300 |
| 8 | 9 | 60 | 20 | 1.0299 | 0.7400 | 200 |
| 9 | 10 | 60 | 20 | 1.0440 | 0.7400 | 200 |
| 10 | 11 | 45 | 30 | 0.1967 | 0.0651 | 200 |
| 11 | 12 | 60 | 35 | 0.3744 | 0.1237 | 200 |
| 12 | 13 | 60 | 35 | 1.4680 | 1.1549 | 200 |
| 13 | 14 | 120 | 80 | 0.5416 | 0.7129 | 200 |
| 14 | 15 | 60 | 10 | 0.5909 | 0.5260 | 200 |
| 15 | 16 | 60 | 20 | 0.7462 | 0.5449 | 200 |
| 16 | 17 | 60 | 20 | 1.2889 | 1.7210 | 200 |
| 17 | 18 | 90 | 40 | 0.7320 | 0.5739 | 200 |
| 2 | 19 | 90 | 40 | 0.1640 | 0.1564 | 200 |
| 19 | 20 | 90 | 40 | 1.5042 | 1.3555 | 200 |
| 20 | 21 | 90 | 40 | 0.4095 | 0.4784 | 200 |
| 21 | 22 | 90 | 40 | 0.7089 | 0.9373 | 200 |
| 3 | 23 | 90 | 50 | 0.4512 | 0.3084 | 200 |
| 23 | 24 | 420 | 200 | 0.8980 | 0.7091 | 200 |
| 24 | 25 | 420 | 200 | 0.8959 | 0.7010 | 200 |
| 6 | 26 | 60 | 25 | 0.2031 | 0.1034 | 300 |
| 26 | 27 | 60 | 25 | 0.2842 | 0.1447 | 300 |
| 27 | 28 | 60 | 20 | 1.0589 | 0.9338 | 300 |
| 28 | 29 | 120 | 70 | 0.8043 | 0.7006 | 200 |
| 29 | 30 | 200 | 600 | 0.5074 | 0.2585 | 200 |
| 30 | 31 | 150 | 70 | 0.9745 | 0.9629 | 200 |
| 31 | 32 | 210 | 100 | 0.3105 | 0.3619 | 200 |
| 32 | 33 | 60 | 40 | 0.3411 | 0.5302 | 200 |
| Type | Bus | (MW) | (m/s) | (m/s) | (m/s) | (MW) | (W/m²) | (W/m²) |
|---|---|---|---|---|---|---|---|---|
| WTG | 32 | 0.6 | 3 | 26 | 15 | |||
| PVG | 15 | 0.6 | 1000 | 150 |
Appendix B
| Bus | Load at the Receiving End | Branch Data | ||||
|---|---|---|---|---|---|---|
| Send | Receive | PL (kW) | QL (kVAr) | R (Ω) | X (Ω) | Imax (A) |
| 1 | 2 | 0 | 0 | 0.0005 | 0.0012 | 400 |
| 2 | 3 | 0 | 0 | 0.0005 | 0.0012 | 400 |
| 3 | 4 | 0 | 0 | 0.0015 | 0.0036 | 400 |
| 4 | 5 | 0 | 0 | 0.0251 | 0.0294 | 400 |
| 5 | 6 | 2.6 | 2.2 | 0.3660 | 0.1864 | 400 |
| 6 | 7 | 40.4 | 30 | 0.3811 | 0.1941 | 400 |
| 7 | 8 | 75 | 54 | 0.0922 | 0.0470 | 400 |
| 8 | 9 | 30 | 22 | 0.0493 | 0.0257 | 400 |
| 9 | 10 | 28 | 19 | 0.8190 | 0.2707 | 400 |
| 10 | 11 | 145 | 104 | 0.1872 | 0.0619 | 200 |
| 11 | 12 | 145 | 104 | 0.7114 | 0.2351 | 200 |
| 12 | 13 | 8 | 5 | 1.0300 | 0.3400 | 200 |
| 13 | 14 | 8 | 5.5 | 1.0440 | 0.3450 | 200 |
| 14 | 15 | 0 | 0 | 1.0580 | 0.3496 | 200 |
| 15 | 16 | 45.5 | 30 | 0.1966 | 0.0650 | 200 |
| 16 | 17 | 60 | 35 | 0.3744 | 0.1238 | 200 |
| 17 | 18 | 60 | 35 | 0.0047 | 0.0016 | 200 |
| 18 | 19 | 0 | 0 | 0.3276 | 0.1083 | 200 |
| 19 | 20 | 1 | 0.6 | 0.2106 | 0.0696 | 200 |
| 20 | 21 | 114 | 81 | 0.3416 | 0.1129 | 200 |
| 21 | 22 | 5 | 3.5 | 0.0140 | 0.0046 | 200 |
| 22 | 23 | 0 | 0 | 0.1591 | 0.0526 | 200 |
| 23 | 24 | 28 | 20 | 0.3463 | 0.1145 | 200 |
| 24 | 25 | 0 | 0 | 0.7488 | 0.2475 | 200 |
| 25 | 26 | 14 | 10 | 0.3089 | 0.1021 | 200 |
| 26 | 27 | 14 | 10 | 0.1732 | 0.0572 | 200 |
| 3 | 28 | 26 | 18.6 | 0.0044 | 0.0108 | 200 |
| 28 | 29 | 26 | 18.6 | 0.0640 | 0.1565 | 200 |
| 29 | 30 | 0 | 0 | 0.3978 | 0.1315 | 200 |
| 30 | 31 | 0 | 0 | 0.0702 | 0.0232 | 200 |
| 31 | 32 | 0 | 0 | 0.3510 | 0.1160 | 200 |
| 32 | 33 | 14 | 10 | 0.8390 | 0.2816 | 200 |
| 33 | 34 | 19.5 | 14 | 1.7080 | 0.5646 | 200 |
| 34 | 35 | 6 | 4 | 1.4740 | 0.4873 | 200 |
| 3 | 36 | 26 | 18.55 | 0.0044 | 0.0108 | 200 |
| 36 | 37 | 26 | 18.55 | 0.0640 | 0.1565 | 200 |
| 37 | 38 | 0 | 0 | 0.1053 | 0.1230 | 200 |
| 38 | 39 | 24 | 17 | 0.0304 | 0.0355 | 200 |
| 39 | 40 | 24 | 17 | 0.0018 | 0.0021 | 200 |
| 40 | 41 | 1.2 | 1 | 0.7283 | 0.8509 | 200 |
| 41 | 42 | 0 | 0 | 0.3100 | 0.3623 | 200 |
| 42 | 43 | 6 | 4.3 | 0.0410 | 0.0478 | 200 |
| 43 | 44 | 0 | 0 | 0.0092 | 0.0116 | 200 |
| 44 | 45 | 39.22 | 26.3 | 0.1089 | 0.1373 | 200 |
| 45 | 46 | 39.22 | 26.3 | 0.0009 | 0.0012 | 200 |
| 4 | 47 | 0 | 0 | 0.0034 | 0.0084 | 300 |
| 47 | 48 | 79 | 56.4 | 0.0851 | 0.2083 | 300 |
| 48 | 49 | 384.7 | 274 | 0.2898 | 0.7091 | 300 |
| 49 | 50 | 384.7 | 274 | 0.0822 | 0.2011 | 300 |
| 8 | 51 | 40.5 | 28.3 | 0.0928 | 0.0473 | 300 |
| 51 | 52 | 3.6 | 2.7 | 0.3319 | 0.1114 | 200 |
| 9 | 53 | 4.35 | 3.5 | 0.1740 | 0.0886 | 300 |
| 53 | 54 | 26.4 | 19 | 0.2030 | 0.1034 | 300 |
| 54 | 55 | 26 | 17.2 | 0.2842 | 0.1447 | 300 |
| 55 | 56 | 0 | 0 | 0.2813 | 0.1433 | 300 |
| 56 | 57 | 0 | 0 | 1.5900 | 0.5337 | 300 |
| 57 | 58 | 0 | 0 | 0.7837 | 0.2630 | 300 |
| 58 | 59 | 100 | 72 | 0.3042 | 0.1006 | 300 |
| 59 | 60 | 0 | 0 | 0.3861 | 0.1172 | 300 |
| 60 | 61 | 1244 | 888 | 0.5075 | 0.2585 | 300 |
| 61 | 62 | 32 | 23 | 0.0974 | 0.0496 | 300 |
| 62 | 63 | 0 | 0 | 0.1450 | 0.0738 | 300 |
| 63 | 64 | 227 | 162 | 0.7105 | 0.3619 | 300 |
| 64 | 65 | 59 | 42 | 1.0410 | 0.5302 | 300 |
| 11 | 66 | 18 | 13 | 0.2012 | 0.0611 | 200 |
| 66 | 67 | 18 | 13 | 0.0047 | 0.0014 | 200 |
| 12 | 68 | 28 | 20 | 0.7394 | 0.2444 | 200 |
| 68 | 69 | 28 | 20 | 0.0047 | 0.0016 | 200 |
| Type | Bus | (MW) | (m/s) | (m/s) | (m/s) | (MW) | (W/m²) | (W/m²) |
|---|---|---|---|---|---|---|---|---|
| WTG | 65 | 1.5 | 3 | 26 | 15 | |||
| PVG | 18 | 0.5 | 1000 | 150 |
Appendix C
| Bus | Load at the Receiving End | Branch Data | ||||
|---|---|---|---|---|---|---|
| Send | Receive | PL (kW) | QL (kVAr) | R (Ω) | X (Ω) | Imax (A) |
| 1 | 2 | 0.1080 | 0.0750 | 0 | 0 | 130 |
| 2 | 3 | 0.1630 | 0.1120 | 0 | 0 | 130 |
| 3 | 4 | 0.2170 | 0.1490 | 56 | 57.13 | 130 |
| 4 | 5 | 0.1080 | 0.0740 | 0 | 0 | 130 |
| 5 | 6 | 0.4350 | 0.2980 | 35.29 | 36 | 130 |
| 6 | 7 | 0.2720 | 0.1860 | 0 | 0 | 130 |
| 7 | 8 | 1.1970 | 0.8200 | 35.29 | 36 | 130 |
| 8 | 9 | 0.1080 | 0.0740 | 0 | 0 | 130 |
| 9 | 10 | 0.5980 | 0.4100 | 0 | 0 | 130 |
| 10 | 11 | 0.5440 | 0.3730 | 56 | 57.13 | 130 |
| 11 | 12 | 0.5440 | 0.3730 | 0 | 0 | 130 |
| 12 | 13 | 0.5980 | 0.4100 | 0 | 0 | 130 |
| 13 | 14 | 0.2720 | 0.1860 | 35.29 | 36 | 130 |
| 14 | 15 | 0.3260 | 0.2230 | 35.29 | 36 | 130 |
| 2 | 16 | 0.7280 | 0.3020 | 35.29 | 36 | 130 |
| 3 | 17 | 0.4550 | 0.1890 | 112 | 114.26 | 130 |
| 5 | 18 | 0.8200 | 0.3400 | 56 | 57.13 | 130 |
| 18 | 19 | 0.6370 | 0.2640 | 56 | 57.13 | 130 |
| 19 | 20 | 0.4550 | 0.1890 | 35.29 | 36 | 130 |
| 20 | 21 | 0.8190 | 0.3400 | 35.29 | 36 | 130 |
| 21 | 22 | 1.5480 | 0.6420 | 35.29 | 36 | 130 |
| 19 | 23 | 0.1820 | 0.0750 | 56 | 57.13 | 130 |
| 7 | 24 | 0.9100 | 0.3780 | 35.29 | 36 | 130 |
| 8 | 25 | 0.4550 | 0.1890 | 35.29 | 36 | 130 |
| 25 | 26 | 0.3640 | 0.1510 | 56 | 57.13 | 130 |
| 26 | 27 | 0.5460 | 0.2260 | 0 | 0 | 130 |
| 27 | 28 | 0.2730 | 0.1130 | 56 | 57.13 | 130 |
| 28 | 29 | 0.5460 | 0.2260 | 0 | 0 | 130 |
| 29 | 30 | 0.5460 | 0.2260 | 35.29 | 36 | 130 |
| 30 | 31 | 0.2730 | 0.1130 | 35.29 | 36 | 130 |
| 31 | 32 | 0.1820 | 0.0750 | 0 | 0 | 130 |
| 32 | 33 | 0.1820 | 0.0750 | 14 | 14.28 | 130 |
| 33 | 34 | 0.8190 | 0.3400 | 0 | 0 | 130 |
| 34 | 35 | 0.6370 | 0.2640 | 0 | 0 | 130 |
| 35 | 36 | 0.1820 | 0.0750 | 35.29 | 36 | 130 |
| 26 | 37 | 0.3640 | 0.1510 | 56 | 57.13 | 130 |
| 27 | 38 | 1.0020 | 0.4160 | 56 | 57.13 | 130 |
| 29 | 39 | 0.5460 | 0.2260 | 56 | 57.13 | 130 |
| 32 | 40 | 0.4550 | 0.1890 | 35.29 | 36 | 130 |
| 40 | 41 | 1.0020 | 0.4160 | 0 | 0 | 130 |
| 41 | 42 | 0.2730 | 0.1130 | 35.29 | 36 | 130 |
| 41 | 43 | 0.4550 | 0.1890 | 35.29 | 36 | 130 |
| 34 | 44 | 1.0020 | 0.4160 | 35.29 | 36 | 130 |
| 44 | 45 | 0.9110 | 0.3780 | 35.29 | 36 | 130 |
| 45 | 46 | 0.9110 | 0.3780 | 35.29 | 36 | 130 |
| 46 | 47 | 0.5460 | 0.2260 | 14 | 14.28 | 130 |
| 35 | 48 | 0.6370 | 0.2640 | 0 | 0 | 130 |
| 48 | 49 | 0.1820 | 0.0750 | 0 | 0 | 130 |
| 49 | 50 | 0.3640 | 0.1510 | 36.29 | 37.02 | 130 |
| 50 | 51 | 0.4550 | 0.1890 | 56 | 57.13 | 130 |
| 48 | 52 | 1.3660 | 0.5670 | 0 | 0 | 130 |
| 52 | 53 | 0.4550 | 0.1890 | 35.29 | 36 | 130 |
| 53 | 54 | 0.5460 | 0.2260 | 56 | 57.13 | 130 |
| 52 | 55 | 0.5460 | 0.2260 | 56 | 57.13 | 130 |
| 49 | 56 | 0.5460 | 0.2260 | 14 | 14.28 | 130 |
| 9 | 57 | 0.2730 | 0.1130 | 56 | 57.13 | 130 |
| 57 | 58 | 0.8190 | 0.3400 | 0 | 0 | 130 |
| 58 | 59 | 0.1820 | 0.0750 | 56 | 57.13 | 130 |
| 58 | 60 | 0.5460 | 0.2260 | 56 | 57.13 | 130 |
| 60 | 61 | 0.7280 | 0.3020 | 56 | 57.13 | 130 |
| 61 | 62 | 1.0020 | 0.4150 | 56 | 57.13 | 130 |
| 60 | 63 | 0.1820 | 0.0750 | 14 | 14.28 | 130 |
| 63 | 64 | 0.7280 | 0.3020 | 0 | 0 | 130 |
| 64 | 65 | 0.1820 | 0.0750 | 0 | 0 | 130 |
| 65 | 66 | 0.1820 | 0.0750 | 56 | 57.13 | 130 |
| 64 | 67 | 0.4550 | 0.1890 | 0 | 0 | 130 |
| 67 | 68 | 0.9100 | 0.3780 | 0 | 0 | 130 |
| 68 | 69 | 1.0920 | 0.4530 | 56 | 57.13 | 130 |
| 69 | 70 | 0.4550 | 0.1890 | 0 | 0 | 130 |
| 70 | 71 | 0.5460 | 0.2260 | 35.29 | 36 | 130 |
| 67 | 72 | 0.1820 | 0.0750 | 56 | 57.13 | 130 |
| 68 | 73 | 1.1840 | 0.4910 | 0 | 0 | 130 |
| 73 | 74 | 0.2730 | 0.1130 | 56 | 57.13 | 130 |
| 73 | 75 | 1.0020 | 0.4160 | 35.29 | 36 | 130 |
| 70 | 76 | 0.5460 | 0.2260 | 56 | 57.13 | 130 |
| 65 | 77 | 0.0910 | 0.0370 | 14 | 14.28 | 130 |
| 10 | 78 | 0.6370 | 0.2640 | 56 | 57.13 | 130 |
| 67 | 79 | 0.5460 | 0.2260 | 35.29 | 36 | 130 |
| 12 | 80 | 0.7280 | 0.3020 | 56 | 57.13 | 130 |
| 80 | 81 | 0.3640 | 0.1510 | 0 | 0 | 130 |
| 81 | 82 | 0.0910 | 0.0370 | 56 | 57.13 | 130 |
| 81 | 83 | 1.0920 | 0.4530 | 35.29 | 36 | 130 |
| 83 | 84 | 1.0020 | 0.4160 | 14 | 14.28 | 130 |
| 13 | 85 | 0.8190 | 0.3400 | 35.29 | 36 | 130 |
| Type | Bus | (MW) | (m/s) | (m/s) | (m/s) | (MW) | (W/m²) | (W/m²) |
|---|---|---|---|---|---|---|---|---|
| WTG | 49 | 1.0 | 3 | 26 | 15 | |||
| WTG | 72 | 1.5 | 3 | 26 | 15 | |||
| PVG | 18 | 0.5 | 1000 | 150 |
Appendix D
References
- Mohammedi, R.D.; Mosbah, M.; Hellal, A.; Arif, S. An efficient BBO algorithm for optimal allocation and sizing of shunt capacitors in radial distribution networks. In Proceedings of the 2015 4th International Conference on Electrical Engineering (ICEE), Boumerdes, Algeria, 13–15 December 2015; pp. 1–5. [Google Scholar]
- Mosbah, M.; Mohammedi, R.D.; Arif, S.; Hellal, A. Optimal of shunt capacitor placement and size in Algerian distribution network using particle swarm optimization. In Proceedings of the 2016 8th International Conference on Modelling, Identification and Control (ICMIC), Boumerdes, Algeria, 15–17 November 2016; pp. 192–197. [Google Scholar]
- Jazebi, S.; Hosseinian, S.H.; Vahidi, B. DSTATCOM allocation in distribution networks considering reconfiguration using differential evolution algorithm. Energy Convers. Manag. 2011, 52, 2777–2783. [Google Scholar] [CrossRef]
- Devi, S.; Geethanjali, M. Optimal location and sizing determination of Distributed Generation and DSTATCOM using Particle Swarm Optimization algorithm. Int. J. Electr. Power Energy Syst. 2014, 62, 562–570. [Google Scholar] [CrossRef]
- Castiblanco-Pérez, C.M.; Toro-Rodríguez, D.E.; Montoya, O.D.; Giral-Ramírez, D.A. Optimal Placement and Sizing of D-STATCOM in Radial and Meshed Distribution Networks Using a Discrete-Continuous Version of the Genetic Algorithm. Electronics 2021, 10, 1452. [Google Scholar] [CrossRef]
- Taher, S.A.; Afsari, S.A. Optimal location and sizing of DSTATCOM in distribution systems by immune algorithm. Int. J. Electr. Power Energy Syst. 2014, 60, 34–44. [Google Scholar] [CrossRef]
- Thangaraj, Y.; Kuppan, R. Multi-objective simultaneous placement of DG and DSTATCOM using novel lightning search algorithm. J. Appl. Res. Technol. 2017, 15, 477–491. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Ravi, K.; Devabalaji, K.R. DSTATCOM allocation in distribution networks considering load variations using bat algorithm. Ain Shams Eng. J. 2017, 8, 391–403. [Google Scholar] [CrossRef]
- Devabalaji, K.R.; Ravi, K. Optimal size and siting of multiple DG and DSTATCOM in radial distribution system using Bacterial Foraging Optimization Algorithm. Ain Shams Eng. J. 2016, 7, 959–971. [Google Scholar] [CrossRef]
- Kaliaperumal Rukmani, D.; Thangaraj, Y.; Subramaniam, U.; Ramachandran, S.; Madurai Elavarasan, R.; Das, N.; Baringo, L.; Imran Abdul Rasheed, M. A New Approach to Optimal Location and Sizing of DSTATCOM in Radial Distribution Networks Using Bio-Inspired Cuckoo Search Algorithm. Energies 2020, 13, 4615. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Jurado, F. Optimal allocation of distribution static compensators using a developed multi-objective sine cosine approach. Comput. Electr. Eng. 2020, 85, 106671. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Dash, S.K.; Mishra, S.; Abdelaziz, A.Y. A Critical Analysis of Modeling Aspects of D-STATCOMs for Optimal Reactive Power Compensation in Power Distribution Networks. Energies 2022, 15, 6908. [Google Scholar] [CrossRef]
- Chakravorty, M.; Das, D. Voltage stability analysis of radial distribution networks. Int. J. Electr. Power Energy Syst. 2001, 23, 129–135. [Google Scholar] [CrossRef]
- Kawambwa, S.; Mwifunyi, R.; Mnyanghwalo, D.; Hamisi, N.; Kalinga, E.; Mvungi, N. An improved backward/forward sweep power flow method based on network tree depth for radial distribution systems. J. Electr. Syst. Inf. Technol. 2021, 8, 7. [Google Scholar] [CrossRef]
- Hassan, M.H.; Kamel, S.; Hussien, A.G. Optimal power flow analysis considering renewable energy resources uncertainty based on an improved wild horse optimizer. IET Gener. Transm. Distrib. 2023, 17, 3582–3606. [Google Scholar] [CrossRef]
- Ali, Z.M.; Diaaeldin, I.M.; HE Abdel Aleem, S.; El-Rafei, A.; Abdelaziz, A.Y.; Jurado, F. Scenario-Based Network Reconfiguration and Renewable Energy Resources Integration in Large-Scale Distribution Systems Considering Parameters Uncertainty. Mathematics 2021, 9, 26. [Google Scholar] [CrossRef]
- Dupačová, J.; Gröwe-Kuska, N.; Römisch, W. Scenario reduction in stochastic programming. Math. Program. 2003, 95, 493–511. [Google Scholar] [CrossRef]
- Mohammedi, R.D.; Mosbah, M.; Kouzou, A. Multi-Objective Optimal Scheduling for Adrar Power System including Wind Power Generation. Electroteh. Electron. Autom. 2018, 66, 102–109. [Google Scholar]
- Mohammedi, R.D.; Zine, R.; Mosbah, M.; Arif, S. Optimum network reconfiguration using grey wolf optimizer. TELKOMNIKA (Telecommun. Comput. Electron. Control) 2018, 16, 2428–2435. [Google Scholar] [CrossRef]
- Mirjalili, S. Improved Grey Wolf Optimizer (I-GWO). Available online: https://www.mathworks.com/matlabcentral/fileexchange/81253 (accessed on 22 August 2023).
- Shahryari, E.; Shayeghi, H.; Moradzadeh, M. Probabilistic and Multi-Objective Placement of D-STATCOM in Distribution Systems Considering Load Uncertainty. Electr. Power Compon. Syst. 2018, 46, 27–42. [Google Scholar] [CrossRef]
- Rahimi, I.; Gandomi, A.H.; Chen, F.; Mezura-Montes, E. A Review on Constraint Handling Techniques for Population-based Algorithms: From single-objective to multi-objective optimization. Arch. Comput. Methods Eng. 2023, 30, 2181–2209. [Google Scholar] [CrossRef]
- Dolatabadi, S.H.; Ghorbanian, M.; Siano, P.; Hatziargyriou, N.D. An Enhanced IEEE 33 Bus Benchmark Test System for Distribution System Studies. IEEE Trans. Power Syst. 2021, 36, 2565–2572. [Google Scholar] [CrossRef]
- Khodabakhshian, A.; Andishgar, M.H. Simultaneous placement and sizing of DGs and shunt capacitors in distribution systems by using IMDE algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 599–607. [Google Scholar] [CrossRef]
- Prakash, D.B.; Lakshminarayana, C. Optimal siting of capacitors in radial distribution network using Whale Optimization Algorithm. Alex. Eng. J. 2017, 56, 499–509. [Google Scholar] [CrossRef]




| Scenario | Loading Level (%) | Solar Irradiance (W/m2) | Wind Speed (m/s) | Probability τs |
|---|---|---|---|---|
| 1 | 93.310 | 18 | 5.8 | 0.044 |
| 2 | 96.237 | 770 | 13.8 | 0.037 |
| 3 | 101.527 | 366 | 6.9 | 0.034 |
| 4 | 96.254 | 955 | 10.4 | 0.041 |
| 5 | 101.270 | 190 | 11.5 | 0.040 |
| 6 | 100.379 | 555 | 6.9 | 0.029 |
| 7 | 85.263 | 1 | 6.9 | 0.258 |
| 8 | 101.718 | 91 | 6.9 | 0.062 |
| 9 | 101.425 | 859 | 10.4 | 0.044 |
| 10 | 103.318 | 664 | 9.2 | 0.037 |
| 11 | 103.181 | 460 | 10.4 | 0.037 |
| 12 | 102.005 | 269 | 10.4 | 0.039 |
| 13 | 93.310 | 18 | 5.8 | 0.044 |
| 14 | 96.237 | 770 | 13.8 | 0.037 |
| 15 | 101.527 | 366 | 6.9 | 0.034 |
| Test System | 33-Bus | 69-Bus | 85-Bus | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of DSTATCOMs | Single | Two | Three | Single | Two | Three | Single | Two | Three |
| Population Size | 100 | 200 | 400 | 200 | 500 | 800 | 400 | 800 | 1000 |
| Max Iterations of I-GWO | 500 | 1000 | 2000 | 500 | 1000 | 2000 | 500 | 1000 | 2000 |
| Range | [0, 2] | [0, 2] | [0, 2] | [0, 2] | [0, 2] | [0, 2] | [0, 2] | [0, 2] | [0, 2] |
| Max Iteration of Load Flow | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| Tolerance of Load Flow | 10−5 | 10−5 | 10−5 | 10−5 | 10−5 | 10−5 | 10−5 | 10−5 | 10−5 |
| Outputs | Base Case | Number of DSTATCOMs | ||
|---|---|---|---|---|
| Single | Two | Three | ||
| Optimal size (kVAr) and location | 1850.00 (30) | 699.58 (14) 1386.89 (30) | 953.38 (7) 477.22 (14) 1044.78 (30) | |
| Ploss (kW) | 202.68 | 153.27 | 144.23 | 141.31 |
| % Reduction in Ploss | 24.37 | 28.84 | 30.28 | |
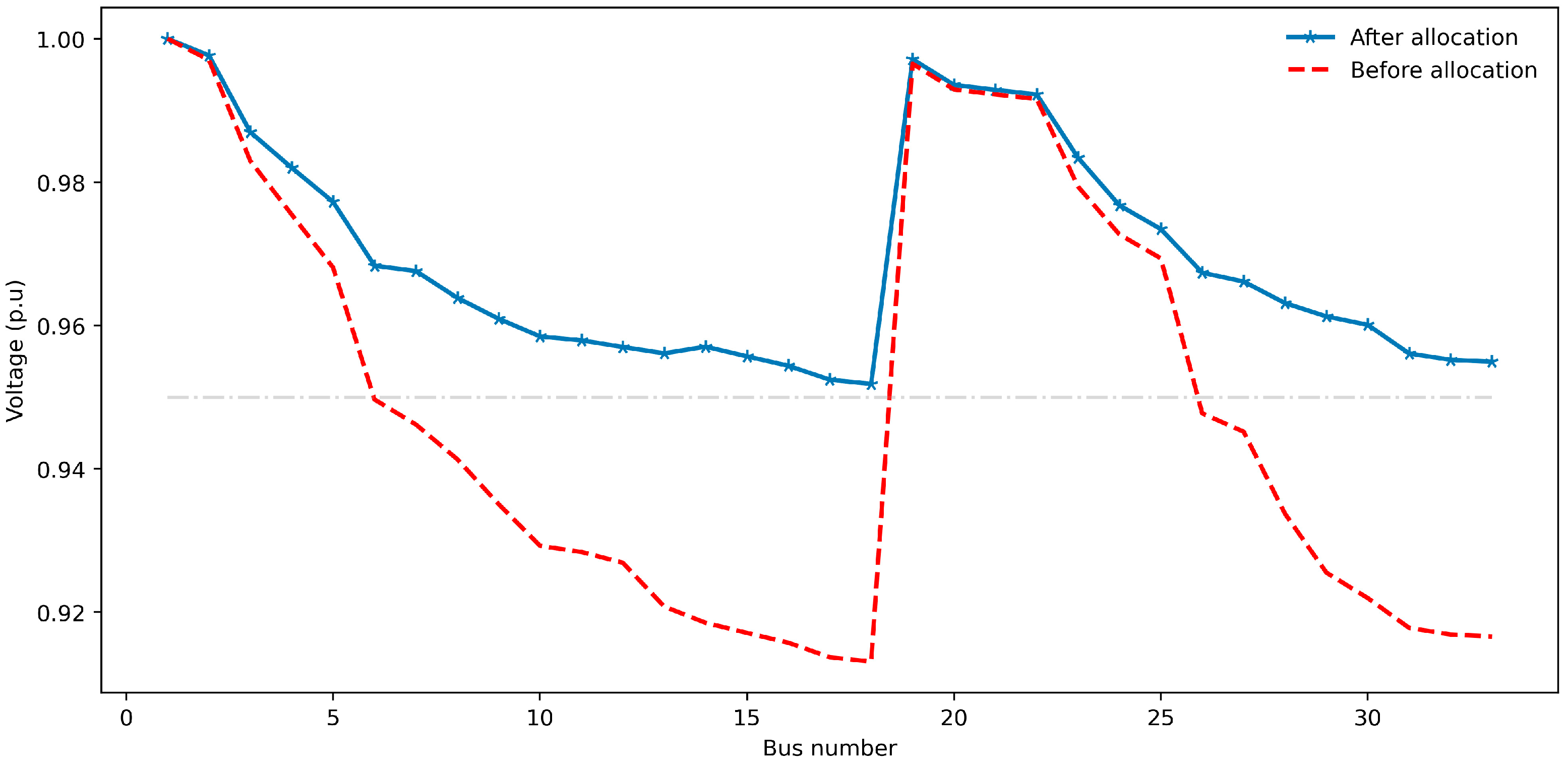
| Vmin (p.u.) | 0.91309 | 0.93031 | 0.95184 | 0.95324 |
| VSImin (p.u.) | 0.69511 | 0.74904 | 0.82083 | 0.82567 |
| Cost of loss (USD/yr) | 106,526.61 | 80,561.00 | 75,806.05 | 74,275.08 |
| Cost of DSTATCOMs (USD/yr) | 9812.33 | 11,066.52 | 13,129.36 | |
| TACS (USD/yr) | 16,153.27 | 19,654.05 | 19,121.17 | |
| Outputs | Base Case | Number of DSTATCOMs | ||
|---|---|---|---|---|
| Single | Two | Three | ||
| Optimal size (kVAr) and location | 1850 (61) | 556.34 (17) 1474.55 (61) | 820.24 (9) 500.03 (17) 1351.73 (61) | |
| Ploss (kW) | 224.99 | 158.49 | 153.73 | 154.12 |
| % Reduction in Ploss | 29.56 | 31.67 | 31.50 | |
| Vmin (p.u.) | 0.90919 | 0.93665 | 0.95144 | 0.95219 |
| VSImin (p.u.) | 0.68331 | 0.76968 | 0.81947 | 0.82205 |
| Cost of loss (USD/yr) | 118,254.41 | 83,301.84 | 80,798.93 | 81,006.31 |
| Cost of DSTATCOMs (USD/yr) | 9812.33 | 10,771.76 | 14,172.17 | |
| TACS (USD/yr) | 25,140.24 | 26,683.72 | 23,075.93 | |
| Outputs | Base Case | Number of DSTATCOMs | ||
|---|---|---|---|---|
| Single | Two | Three | ||
| Optimal size (kVAr) and location | 2150 (32) | 2150.00 (9) 1286.23 (32) | 1929.15 (8) 896.70 (34) 727.25 (67) | |
| Ploss (kW) | 316.19 | 229.11 | 200.08 | 190.51 |
| % Reduction in Ploss | 32.12 | 36.72 | 39.75 | |
| Vmin (p.u.) | 0.87129 | 0.93176 | 0.95219 | 0.95304 |
| VSImin (p.u.) | 0.57631 | 0.75373 | 0.82171 | 0.82499 |
| Cost of loss (USD/yr) | 166,189.63 | 120,419.81 | 105,163.24 | 100,131.51 |
| Cost of DSTATCOMs (USD/yr) | 11,403.52 | 18,225.65 | 18,845.46 | |
| TACS (USD/yr) | 34,366.30 | 42,800.74 | 47,212.50 | |
| Outputs | 33-Bus | 69-Bus | 85-Bus | |||
|---|---|---|---|---|---|---|
| Without DSTATCOMs | With DSTATCOMs | Without DSTATCOMs | With DSTATCOMs | Without DSTATCOMs | With DSTATCOMs | |
| Optimal size (kVAr) and location | 696.15 (11) 1309.73 (30) | 653.78 (17) 1459.28 (61) | 1133.36 (9) 1073.75 (32) 468.16 (68) | |||
| Ploss (kW) | 135.84 | 55.17 | 124.08 | 48.74 | 171.75 | 64.66 |
| % Reduction in Ploss | 59.39 | 58.18 | 62.35 | |||
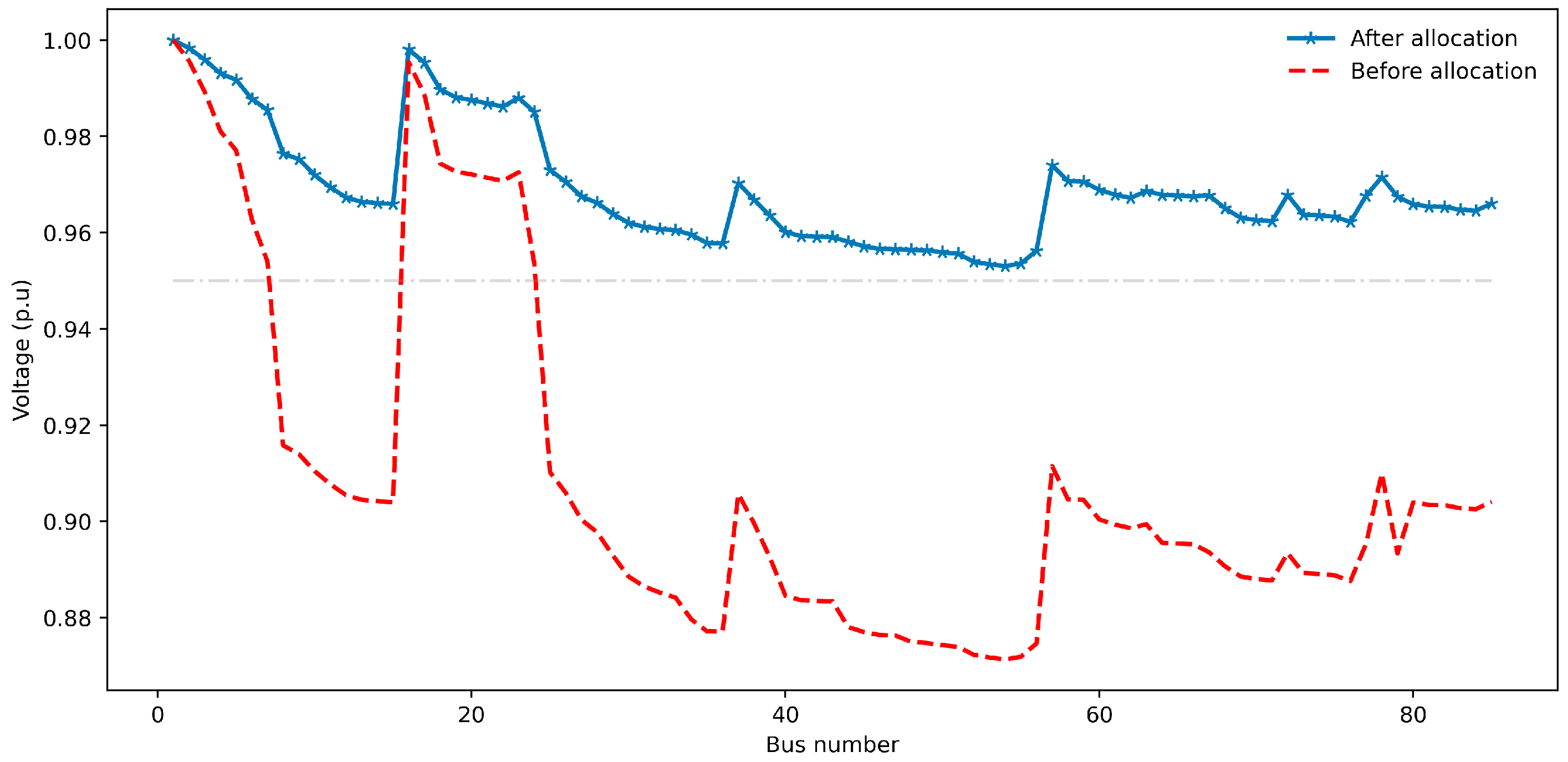
| Vmin (p.u.) | 0.91109 | 0.95211 | 0.92155 | 0.95195 | 0.89245 | 0.95098 |
| VSImin (p.u.) | 0.68904 | 0.81178 | 0.72124 | 0.81493 | 0.63436 | 0.79202 |
| Cost of loss (USD/yr) | 71,396.33 | 48,123.80 | 65,214.82 | 32,567.67 | 90,271.13 | 37,289.27 |
| Cost of DSTATCOMs (USD/yr) | 10,639.09 | 11,207.57 | 14,189.55 | |||
| TACS (USD/yr) | 12,633.44 | 17,472.80 | 38,792.32 | |||
| Outputs | BFOA [9] | MOPSO [11] | LSA [7] | MOSCA [11] | Proposed Approach |
|---|---|---|---|---|---|
| Optimal size (kVAr) and location | 632.00 (12) 487.00 (28) 550.00 (31) | 679.21 (16) 549.50 (29) 722.03 (30) | 341 (14) 516 (24) 1013 (30) | 733.41 (8) 410.26 (16) 1029.04 (30) | 400.72 (13) 554.87 (24) 1089.27 (30) |
| Ploss (kW) | 144.38 | 152.44 | 138.35 | 150.27 | 132.16 |
| Vmin (p.u.) | 0.92400 | 0.95120 | 0.93010 | 0.9517 | 0.93774 |
| VSImin (p.u.) | 0.72280 | 0.81600 | 0.74230 | 0.81900 | 0.77327 |
| Outputs | CSA [10] | MOPSO [11] | LSA [7] | MOSCA [11] | Proposed Approach |
|---|---|---|---|---|---|
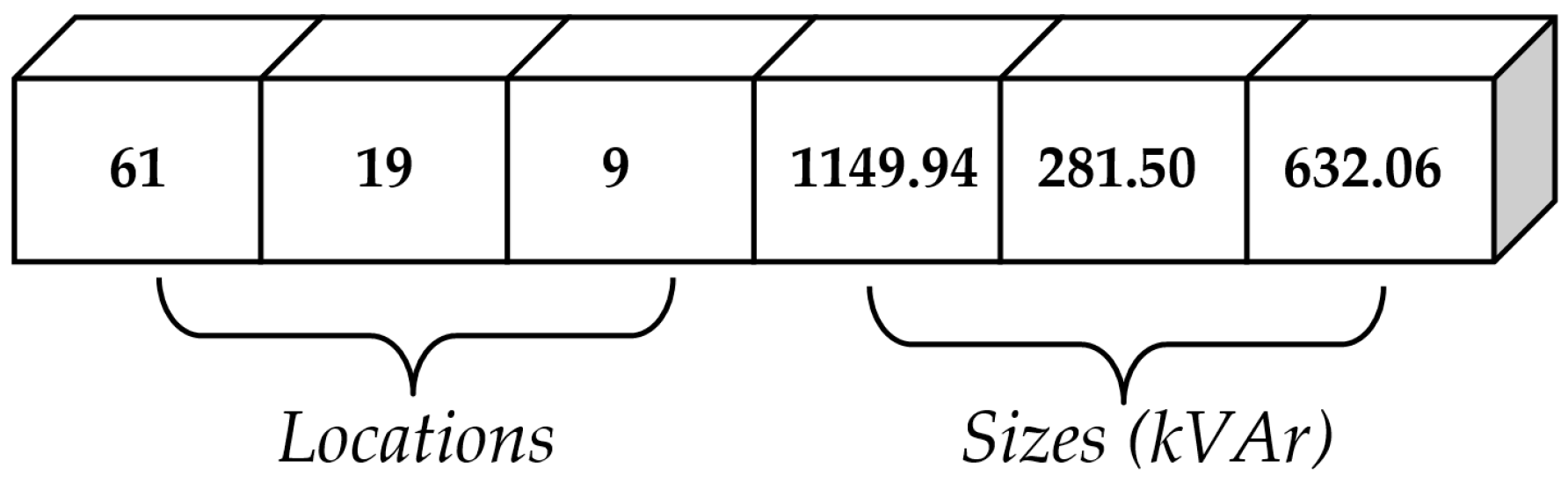
| Optimal size (kVAr) and location | 350.00 (25) 230.00 (18) 1170.00 (61) | 906.40 (53) 846.50 (56) 1135.30 (62) | 374.00 (11) 240.00 (18) 1217.00 (61) | 226.60 (25) 1078.70 (62) 226.60 (63) | 632.06 (9) 281.50 (19) 1149.94 (61) |
| Ploss (kW) | 158.85 | 159.42 | 145.16 | 158.75 | 146.02 |
| Vmin (p.u.) | 0.93010 | 0.93660 | 0.93110 | 0.93890 | 0.92984 |
| VSImin (p.u.) | 0.74280 | 0.77120 | 0.74460 | 0.77700 | 0.74753 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammedi, R.D.; Kouzou, A.; Mosbah, M.; Souli, A.; Rodriguez, J.; Abdelrahem, M. Allocation and Sizing of DSTATCOM with Renewable Energy Systems and Load Uncertainty Using Enhanced Gray Wolf Optimization. Appl. Sci. 2024, 14, 556. https://doi.org/10.3390/app14020556
Mohammedi RD, Kouzou A, Mosbah M, Souli A, Rodriguez J, Abdelrahem M. Allocation and Sizing of DSTATCOM with Renewable Energy Systems and Load Uncertainty Using Enhanced Gray Wolf Optimization. Applied Sciences. 2024; 14(2):556. https://doi.org/10.3390/app14020556
Chicago/Turabian StyleMohammedi, Ridha Djamel, Abdellah Kouzou, Mustafa Mosbah, Aissa Souli, Jose Rodriguez, and Mohamed Abdelrahem. 2024. "Allocation and Sizing of DSTATCOM with Renewable Energy Systems and Load Uncertainty Using Enhanced Gray Wolf Optimization" Applied Sciences 14, no. 2: 556. https://doi.org/10.3390/app14020556
APA StyleMohammedi, R. D., Kouzou, A., Mosbah, M., Souli, A., Rodriguez, J., & Abdelrahem, M. (2024). Allocation and Sizing of DSTATCOM with Renewable Energy Systems and Load Uncertainty Using Enhanced Gray Wolf Optimization. Applied Sciences, 14(2), 556. https://doi.org/10.3390/app14020556









