An Efficient Code for the Multi-Material Topology Optimization of 2D/3D Continuum Structures Written in Matlab
Abstract
1. Introduction
2. The Formulation of the Multi-Material Topology Optimization Problem
2.1. Design Variable
2.2. Filtering and Projection
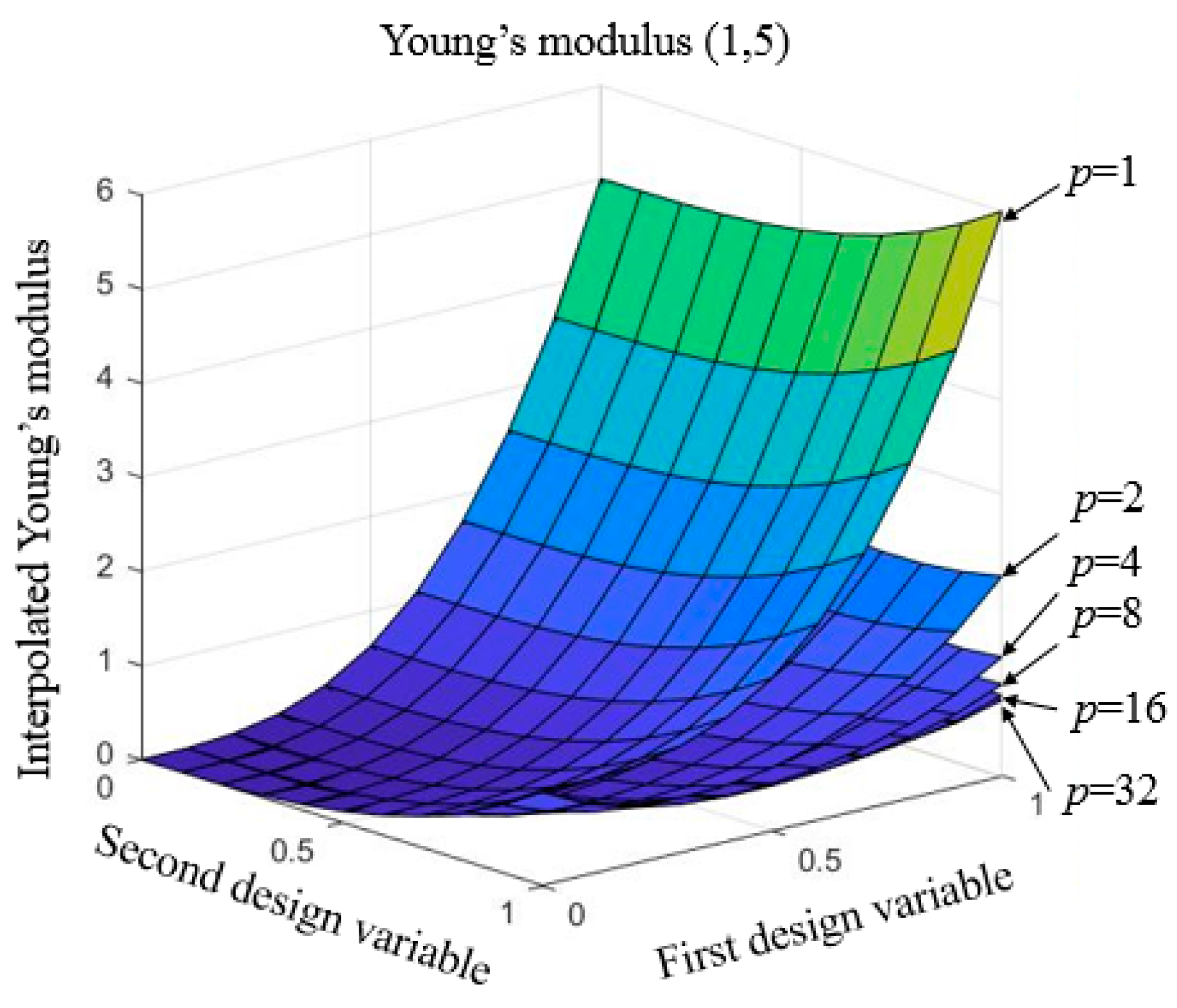
2.3. The Mapping-Based Interpolation Function for Multi-Materials
2.4. Optimization Model
2.5. Sensitivity Analysis
3. Matlab Implementation
3.1. Parameter Setting (Lines 1–10)
3.2. Predefined (Lines 1–42)
3.3. Initialization (Lines 43–53)
3.4. Iterative Solution (Lines 54–137)
3.5. Image Display (Lines 138–145)
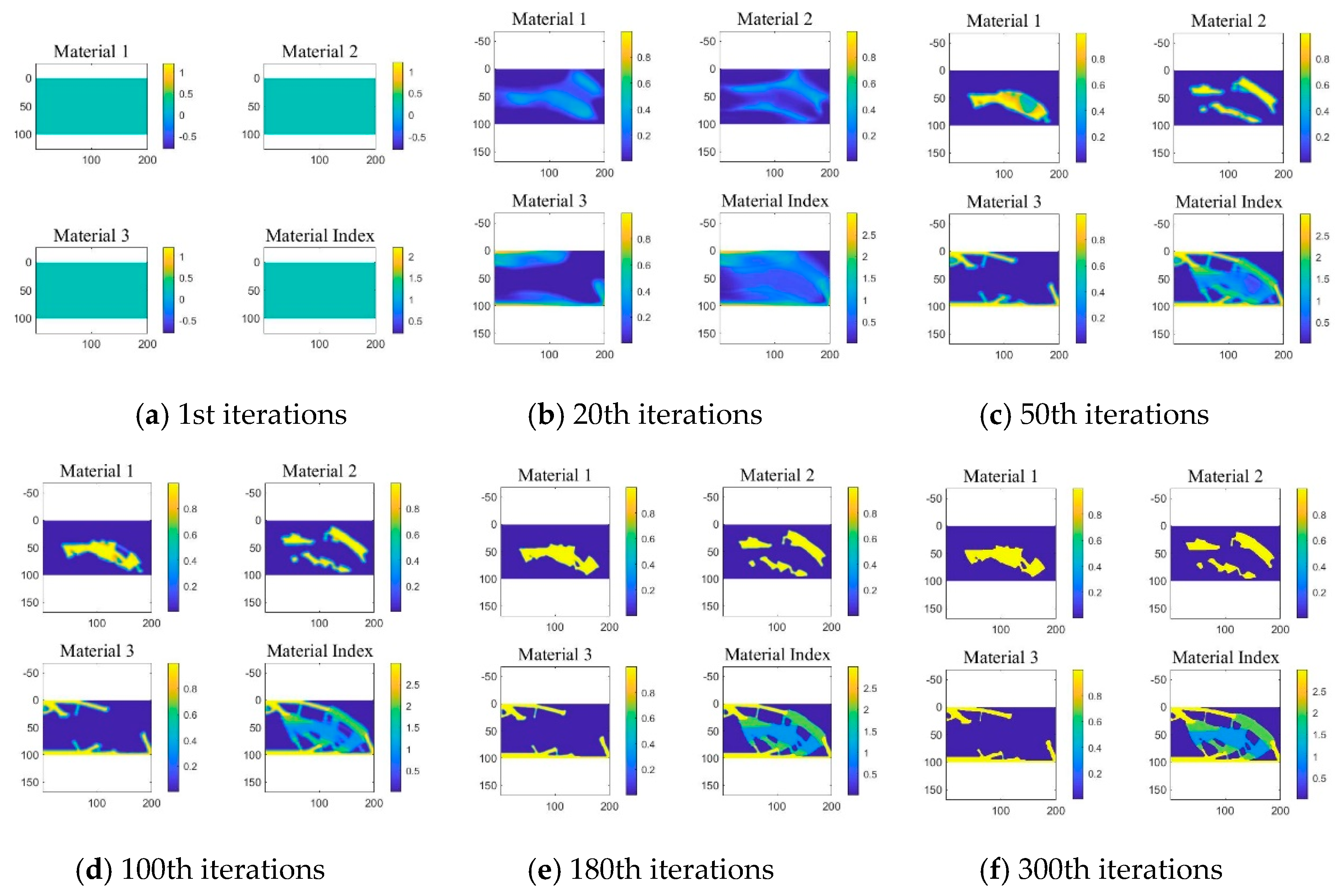
3.6. Visualization of the Optimization Procedure
4. Numerical Examples
4.1. Example 1: The Number of Materials
4.2. Example 2: Different Values of Parameter p for the P-Norm
5. Extension to 3D
5.1. 3D Matlab Implementation
5.2. 3D Numerical Examples
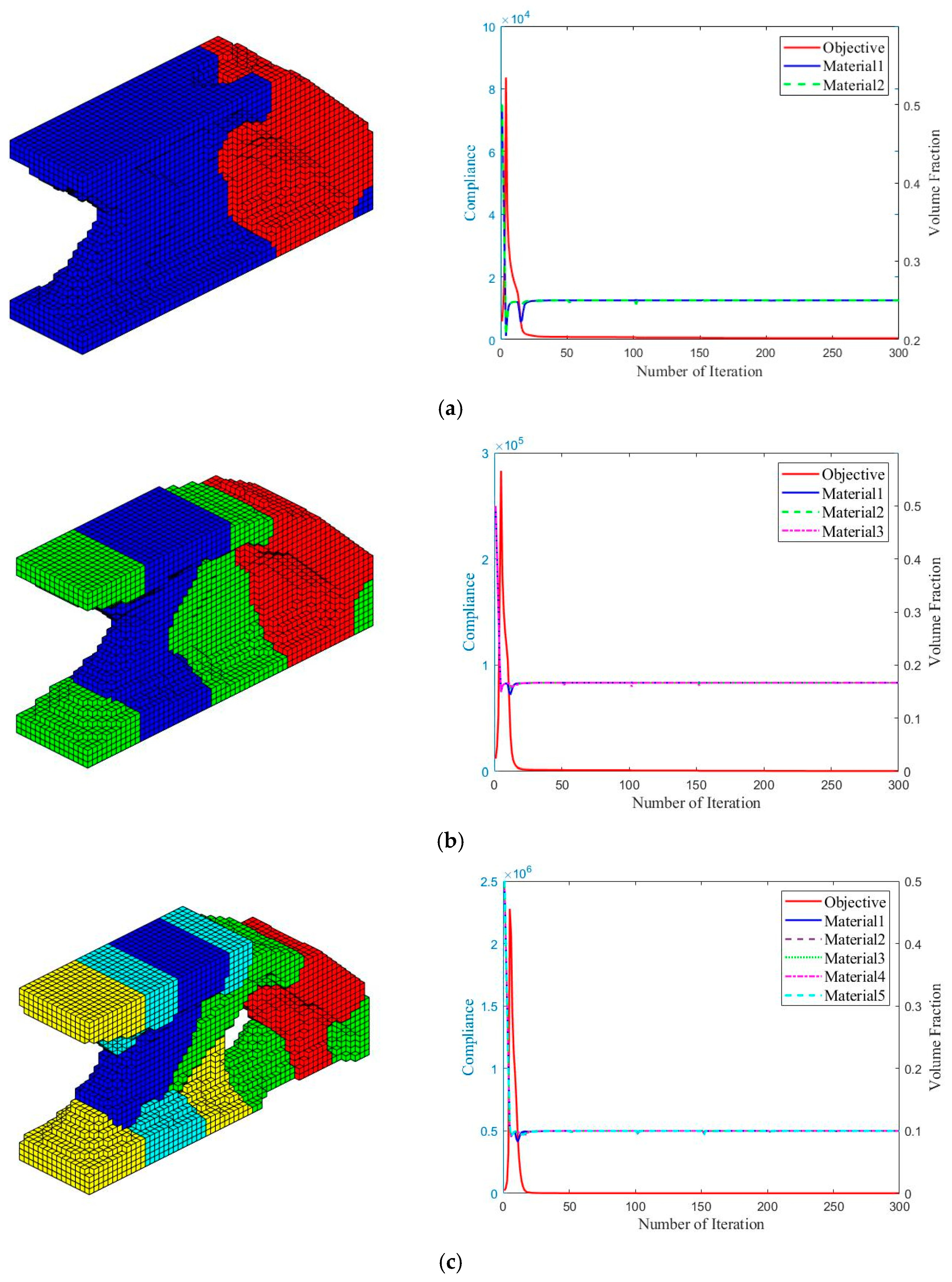
5.2.1. Example 1: The Number of Materials
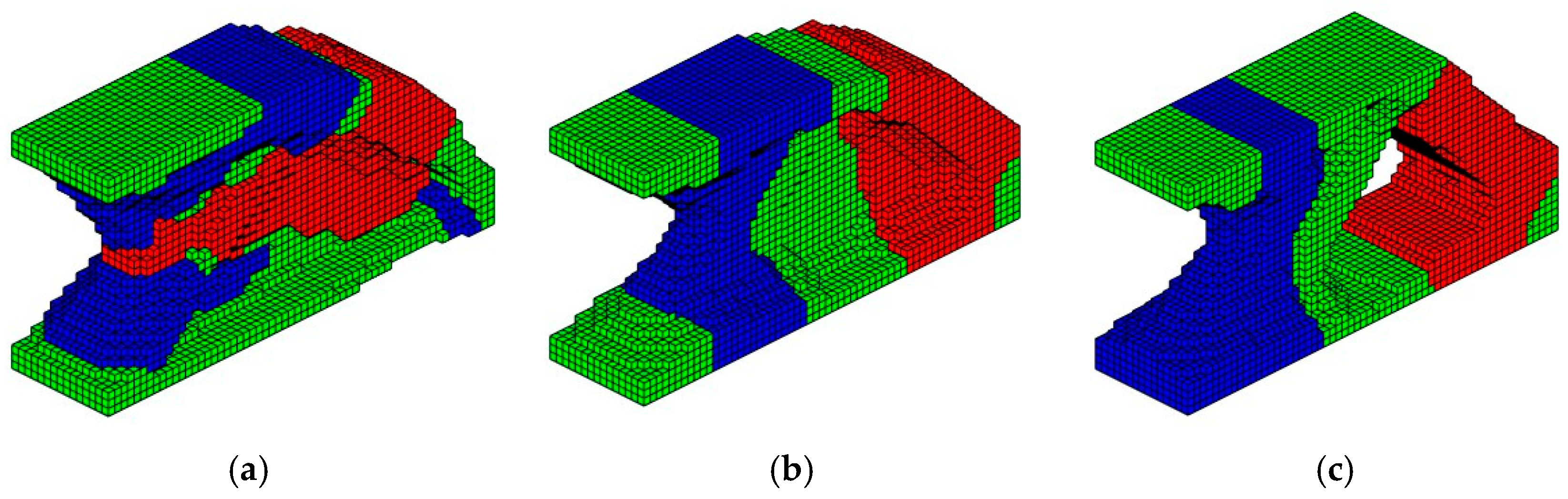
5.2.2. Example 2: Different Filter Radii
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SIMP | Solid Isotropic Material with Penalization |
| DMO | Discrete Material Optimization |
| RAMP | Rational Approximation of Material Properties |
| SFP | Shape Function Parameterization |
| GSM | Ground Structure Method |
Appendix A. Multimaterial2d.m
- 1 %% LOOP PARAMETERS
- 2 clear;
- 3 NumIter = 300;delta=1e-9;
- 4 nelx=200; nely=100;
- 5 penal=3; rmin=5; NMaterial=3;
- 6 NCON=NMaterial; NDV=nelx*nely*NMaterial; NDV3=nelx*nely;
- 7 movelimit=0.1; beta = 1;
- 8 %% MATERIAL PROPERTIES
- 9 par.E(1)=1; par.E(2)=2; par.E(3)=5;
- 10 nu = 0.3;
- 11 %% PREPARE FINITE ELEMENT ANALYSIS
- 12 A11 = [12 3 -6 -3; 3 12 3 0; -6 3 12 -3; -3 0 -3 12];
- 13 A12 = [-6 -3 0 3; -3 -6 -3 -6; 0 -3 -6 3; 3 -6 3 -6];
- 14 B11 = [-4 3 -2 9; 3 -4 -9 4; -2 -9 -4 -3; 9 4 -3 -4];
- 15 B12 = [ 2 -3 4 -9; -3 2 9 -2; 4 9 2 3; -9 -2 3 2];
- 16 lk = 1/(1-nu^2)/24*([A11 A12;A12’ A11]+nu*[B11 B12;B12’ B11]);
- 17 nodenrs = reshape(1:(1+nelx)*(1+nely),1+nely,1+nelx);
- 18 edofVec = reshape(2*nodenrs(1:end-1,1:end-1)+1,nelx*nely,1);
- 19 edofMat = repmat(edofVec,1,8)+repmat([0 1 2*nely+[2 3 0 1] -2 -1],nelx*nely,1);
- 20 iK = reshape(kron(edofMat,ones(8,1))’,64*nelx*nely,1);
- 21 jK = reshape(kron(edofMat,ones(1,8))’,64*nelx*nely,1);
- 22 %% PREPARE FILTER
- 23 iH = ones(nelx*nely*(2*(ceil(rmin)-1)+1)^2,1);
- 24 jH = ones(size(iH));
- 25 sH = zeros(size(iH));
- 26 k = 0;
- 27 for i1 = 1:nelx
- 28 for j1 = 1:nely
- 29 e1 = (i1-1)*nely+j1;
- 30 for i2 = max(i1-(ceil(rmin)-1),1):min(i1+(ceil(rmin)-1),nelx)
- 31 for j2 = max(j1-(ceil(rmin)-1),1):min(j1+(ceil(rmin)-1),nely)
- 32 e2 = (i2-1)*nely+j2;
- 33 k = k+1;
- 34 iH(k) = e1;
- 35 jH(k) = e2;
- 36 sH(k) = max(0,rmin-sqrt((i1-i2)^2+(j1-j2)^2));
- 37 end
- 38 end
- 39 end
- 40 end
- 41 H = sparse(iH,jH,sH);
- 42 Hs = sum(H,2);
- 43 %% INITIALIZE ITERATION
- 44 loopbeta=0;
- 45 x=ones(NDV,1)*0.5;
- 46 for i=0:NMaterial-1
- 47 xTilde(1:nely,1:nelx,i+1)=reshape(x(1+i*NDV3:NDV3+i*NDV3),nely,nelx);
- 48 end
- 49 xPhys = (tanh(beta*0.5) + tanh(beta*(xTilde-0.5)))/(tanh(beta*0.5) + tanh(beta*(1-0.5)));
- 50 %% MMA PARAMETER INITIALIZE
- 51 a0=0; a=zeros(NCON,1);cc=1.0e6*ones(NCON,1); d=0*ones(NCON,1);
- 52 xmin=1e-3*ones(NDV,1); xmax=1*ones(NDV,1);
- 53 xold=x; xolder=xold;low=0; upp=1;
- 54 %% START ITERATION
- 55 for iter=1:NumIter
- 56 loopbeta=loopbeta+1;
- 57 %% FE-ANALYSIS
- 58 [KE0] = lk; p=6;
- 59 for i=1:NMaterial
- 60 KE(:,:,i)=par.E(i)*KE0;
- 61 end
- 62 KE_test=zeros(64,nely*nelx); g=zeros(NMaterial,1);
- 63 r1=xPhys(:,:,1); r2=xPhys(:,:,2); r3=xPhys(:,:,3);
- 64 for j=1:NMaterial
- 65 post_x(1:nely,1:nelx,j)=(xPhys(:,:,j).*(r1.^p + r2.^p + r3.^p ).^(1/p))./(r1 + r2 + r3 + delta);
- 66 dr(1:nely,1:nelx,j)=(post_x(1:nely,1:nelx,j)).^penal;
- 67 KE_test=reshape(KE(:,:,j),64,1)*reshape(dr(1:nely,1:nelx,j),1,nely*nelx)+KE_test;
- 68 g(j)=sum((sum(xPhys(:,:,j))’));
- 69 end
- 70 sK = reshape(KE_test,64*nelx*nely,1);
- 71 K = sparse(iK,jK,sK); K = (K+K’)/2;
- 72 %% DEFINE LOADS AND SUPPORTS (HALF MBB-BEAM)
- 73 F = sparse(2*(nely+1)*(nelx+1),1); U = zeros(2*(nely+1)*(nelx+1),1);
- 74 F(2,1) = -0.1;
- 75 fixeddofs = union([1:2:2*(nely+1)],[2*(nelx+1)*(nely+1)]);
- 76 alldofs = [1:2*(nely+1)*(nelx+1)];
- 77 freedofs = setdiff(alldofs,fixeddofs);
- 78 %% SOLVING
- 79 U(freedofs,:) = K(freedofs,freedofs)\F(freedofs,:);
- 80 U(fixeddofs,:)= 0;
- 81 c=F’*U;
- 82 %% SENSITIVITY ANALYSIS
- 83 dc=zeros(nely,nelx,NMaterial);
- 84 dgdx_test=zeros(NMaterial,nely*nelx*NMaterial);
- 85 KES=reshape(sum(U(edofMat)*KE0.*U(edofMat),2),nely,nelx);
- 86 for n=1:NMaterial
- 87 for m=1:NMaterial
- 88 if m==n
- 89 dmdrn(1:nely,1:nelx,m)=penal.*post_x(1:nely,1:nelx,m).^(penal -1).*...
- 90 ((r1.^p + r2.^p + r3.^p).^(1/p)./(r1 + r2 + r3 + delta) -(xPhys(:,:,m).*(r1.^p + r2.^p + r3.^p).^(1/p))./(r1 + r2 + r3 + delta).^2 + (xPhys(:,:,m).*xPhys(:,:,n).^(p -1).*(r1.^p + r2.^p + r3.^p).^(1/p -1))./(r1 + r2 + r3 + delta));
- 91 mass_dmdrn=1;
- 92 else
- 93 dmdrn(1:nely,1:nelx,m)=penal.*post_x(1:nely,1:nelx,m).^(penal -1).*...
- 94 (((xPhys(:,:,m).*xPhys(:,:,n).^(p -1).*(r1.^p + r2.^p + r3.^p).^(1/p -1))./(r1 + r2 + r3 + delta)- (xPhys(:,:,m).*(r1.^p + r2.^p + r3.^p).^(1/p))./(r1 + r2 + r3 + delta).^2));
- 95 mass_dmdrn=0;
- 96 end
- 97 dgdx_test(m,1+(n-1)*NDV3:NDV3+NDV3*(n-1))=repmat(mass_dmdrn,1,nelx*nely);
- 98 end
- 99 dc(:,:,n)=-dmdrn(:,:,1).*KES.*par.E(1)-dmdrn(:,:,2).*KES.*par.E(2)-dmdrn(:,:,3).*KES.*par.E(3);
- 100 end
- 101 %% FILTERING/MODIFICATION OF SENSITIVITIES
- 102 filtereddc=[];dfdx=[];
- 103 for i=1:NMaterial
- 104 dxx = beta* (1-tanh(beta*(xTilde-0.5)).*tanh(beta*(xTilde-0.5)))/(tanh(beta*0.5) + tanh(beta*(1-0.5)));
- 105 [filtereddc(:,:,i)] = H*(reshape(dc(:,:,i).*dxx(:,:,i),NDV3,1)./Hs);
- 106 dfdx=[dfdx;filtereddc(:,:,i)];
- 107 g(i)=(g(i)/NDV3-0.5/3)*1;
- 108 dgdx1=(dgdx_test(i,:)/NDV3)*1;
- 109 for j=0:NMaterial-1
- 110 dgdx2=reshape(dgdx1(:,1+j*NDV3:NDV3+j*NDV3),nely,nelx);
- 111 dgdx(i,1+j*NDV3:NDV3+j*NDV3) = H*(reshape(dgdx2(:,:).*dxx(:,:,i),NDV3,1)./Hs);
- 112 end
- 113 end
- 114 %% OPTIMALITY CRITERIA UPDATE OF DESIGN VARIABLES AND PHYSICAL DENSITIES
- 115 f=c*1e2; dfdx=dfdx*1e2; cons(iter,1)=g(1);cons(iter,2)=g(2);cons(iter,3)=g(3);
- 116 for j=1:length(x)
- 117 xmin(j)=max(1e-3,x(j)-movelimit); xmax(j)=min(1,x(j)+movelimit);
- 118 end
- 119 %% MMA OPTIZATION
- 120 [xnew, y, z, lamda, ksi, eta, mu, zeta, s, low, upp] = ...
- 121 mmasub(NCON,length(x), iter, ...
- 122 x, xmin, xmax, xold, xolder, ...
- 123 f, (dfdx), g, dgdx, low, upp, a0, a, cc, d);
- 124 %% PRINT RESULTS
- 125 disp(sprintf(‘Iter.:%3d Obj.: %8.4e max constraint: %6.3e’, iter, f,max(g)))
- 126 %% UPDATE PARAMETER
- 127 change=norm(abs(xnew-x));
- 128 xolder=xold; xold=x; x = xnew;
- 129 for i=0:NMaterial-1
- 130 xTilde(1:nely,1:nelx,i+1) = reshape((H*xnew(1+i*NDV3:NDV3+i*NDV3,:))./Hs,nely,nelx);
- 131 end
- 132 xPhys = (tanh(beta*0.5) + tanh(beta*(xTilde-0.5)))/(tanh(beta*0.5) + tanh(beta*(1-0.5)));
- 133 if beta < 100 && (loopbeta >= 50)
- 134 beta = 2*beta;loopbeta = 0;
- 135 fprintf(‘Parameter beta increased to %g.\n’,beta);
- 136 end
- 137 end
- 138 %% PLOT DENSITIES
- 139 xx=post_x(:,:,1);
- 140 for i=2:NMaterial
- 141 xx=xx+i*post_x(:,:,i);
- 142 end
- 143 imagesc(xx); axis equal; axis off;colorbar; hold on;
- 144 plot([0 nelx nelx 0 0]+0.5,[0 0 nely nely 0]+0.5,‘k’);axis([-1 nelx+1 -1 nely+1])
- 145 saveas(figure(1),‘result.png’);
Appendix B. Multimaterial3d.m
- 1 %% LOOP PARAMETERS
- 2 clear;
- 3 NumIter = 300;delta=1e-9;
- 4 nelx=60; nely=30; nelz = 15;
- 5 penal=3; rmin=5; NMaterial=3;
- 6 NDV=nelx*nely*nelz*NMaterial; NDV3=nelx*nely*nelz;
- 7 movelimit=0.1; beta =1;
- 8 %% MATERIAL PROPERTIES
- 9 par.E(1)=1; par.E(2)=2; par.E(3)=5;
- 10 nu = 0.3;
- 11 %% USER-DEFINED LOAD DOFs
- 12 il = nelx; jl = 0; kl = 0:nelz;
- 13 loadnid = kl*(nelx+1)*(nely+1)+il*(nely+1)+(nely+1-jl);
- 14 loaddof = 3*loadnid(:) - 1;
- 15 %% USER-DEFINED SUPPORT FIXED DOFs
- 16 [jf,kf] = meshgrid(1:nely+1,1:nelz+1);
- 17 fixednid = (kf-1)*(nely+1)*(nelx+1)+jf;
- 18 fixeddofs = [3*fixednid(:); 3*fixednid(:)-1; 3*fixednid(:)-2];
- 19 %% DEFINE LOADS AND SUPPORTS (HALF MBB-BEAM)
- 20 nele = nelx*nely*nelz;
- 21 ndof=3*(nelx+1)*(nely+1)*(nelz+1);
- 22 F=sparse(loaddof,1,-1,ndof,1);
- 23 U=zeros(ndof,1);
- 24 freedofs=setdiff(1:ndof,fixeddofs);
- 25 %% PREPARE FINITE ELEMENT ANALYSIS
- 26 ke=1/(1+nu)/(2*nu-1)/144 *([-32;-6;-6;8;6;6;10;6;3;-4;-6;-3;-4;-3;-6;10;3;6;8;3;3;4;-3;-3;-32;-6;-6;-4;-3;6;10;3;6;8;6;-3;-4;-6;-3;4;-3;3;8;3;...
- 27 3;10;6;-32;-6;-3;-4;-3;-3;4;-3;-6;-4;6;6;8;6;3;10;3;3;8;3;6;10;-32;6;6; -4;6;3;10;-6;-3;10;-3;-6;-4;3;6;4;3;3;8;-3;-3;-32;-6;-6;8;6;-6;10;3;3;4;...
- 28 -3;3;-4;-6;-3;10;6;-3;8;3;-32;3;-6;-4;3;-3;4;-6;3;10;-6;6;8;-3;6;10;-3;3;8;-32;-6;6;8;6;-6;8;3;-3;4;-3;3;-4;-3;6;10;3;-6;-32;6;-6;-4;3;3;8;-3;...
- 29 3;10;-6;-3;-4;6;-3;4;3;-32;6;3;-4;-3;-3;8;-3;-6;10;-6;-6;8;-6;-3;10;-32;6;-6;4;3;-3;8;-3;3;10;-3;6;-4;3;-6;-32;6;-3;10;-6;-3;8;-3;3;4;3;3;-4;6;...
- 30 -32;3;-6;10;3;-3;8;6;-3;10;6;-6;8;-32;-6;6;8;6;-6;10;6;-3;-4;-6;3;-32;6;-6;-4;3;6;10;-3;6;8;-6;-32;6;3;-4;3;3;4;3;6;-4;-32;6;-6;-4;6;-3;10;-6;3;...
- 31 -32;6;-6;8;-6;-6;10;-3;-32;-3;6;-4;-3;3;4;-32;-6;-6;8;6;6;-32;-6;-6;-4; -3;-32;-6;-3;-4;-32;6;6;-32;-6;-32]+nu*[48;0;0;0;-24;-24;-12;0;-12;0;...
- 32 24;0;0;0;24;-12;-12;0;-12;0;0;-12;12;12;48;0;24;0;0;0;-12;-12;-24;0;-24;0;0;24;12;-12;12;0;-12;0;-12;-12;0;48;24;0;0;12;12;-12;0;24;0;-24;-24;0;...
- 33 0;-12;-12;0;0;-12;-12;0;-12;48;0;0;0;-24;0;-12;0;12;-12;12;0;0;0;-24; -12;-12;-12;-12;0;0;48;0;24;0;-24;0;-12;-12;-12;-12;12;0;0;24;12;-12;0;...
- 34 0;-12;0;48;0;24;0;-12;12;-12;0;-12;-12;24;-24;0;12;0;-12;0;0;-12;48;0;0;0;-24;24;-12;0;0;-12;12;-12;0;0;-24;-12;-12;0;48;0;24;0;0;0;-12;0;-12;...
- 35 -12;0;0;0;-24;12;-12;-12;48;-24;0;0;0;0;-12;12;0;-12;24;24;0;0;12;-12;48;0;0;-12;-12;12;-12;0;0;-12;12;0;0;0;24;48;0;12;-12;0;0;-12;0;-12;-12;...
- 36 -12;0;0;-24;48;-12;0;-12;0;0;-12;0;12;-12;-24;24;0;48;0;0;0;-24;24;-12;0;12;0;24;0;48;0;24;0;0;0;-12;12;-24;0;24;48;-24;0;0;-12;-12;-12;0;-24;...
- 37 0;48;0;0;0;-24;0;-12;0;-12;48;0;24;0;24;0;-12;12;48;0;-24;0;12;-12;-12;48;0;0;0;-24;-24;48;0;24;0;0;48;24;0;0;48;0;0;48;0;48]);
- 38 lk(tril(ones(24))==1)=ke’;
- 39 lk = reshape(lk,24,24 );
- 40 lk =lk + lk’- diag( diag( lk ) );
- 41 Num_node = (1+nely)*(1+nelx)*(1+nelz);
- 42 nodenrs = reshape(1:Num_node,1+nely,1+nelx,1+nelz);
- 43 edofVec = reshape(3*nodenrs(1:end-1,1:end-1,1:end-1)+1,nelx*nely*nelz,1);
- 44 edofMat = repmat(edofVec,1,24)+ repmat([0 1 2 3*nely + [3 4 5 0 1 2] -3 -2 -1 3*(nely+1)*(nelx+1)+[0 1 2 3*nely + [3 4 5 0 1 2] -3 -2 -1]],nele,1);
- 45 iK = reshape(kron(edofMat,ones(24,1))’,24*24*nele,1);
- 46 jK = reshape(kron(edofMat,ones(1,24))’,24*24*nele,1);
- 47 %% PREPARE FILTER
- 48 iH = ones(nele*(2*(ceil(rmin)-1)+1)^2,1);jH = ones(size(iH));sH = zeros(size(iH));
- 49 k = 0;
- 50 for k1 = 1:nelz
- 51 for i1 = 1:nelx
- 52 for j1 = 1:nely
- 53 e1 = (k1-1)*nelx*nely + (i1-1)*nely+j1;
- 54 for k2 = max(k1-(ceil(rmin)-1),1):min(k1+(ceil(rmin)-1),nelz)
- 55 for i2 = max(i1-(ceil(rmin)-1),1):min(i1+(ceil(rmin)-1),nelx)
- 56 for j2 = max(j1-(ceil(rmin)-1),1):min(j1+(ceil(rmin)-1),nely)
- 57 e2 = (k2-1)*nelx*nely + (i2-1)*nely+j2;
- 58 k = k+1;
- 59 iH(k) = e1;
- 60 jH(k) = e2;
- 61 sH(k) = max(0,rmin-sqrt((i1-i2)^2+(j1-j2)^2+(k1-k2)^2));
- 62 end
- 63 end
- 64 end
- 65 end
- 66 end
- 67 end
- 68 H = sparse(iH,jH,sH);
- 69 Hs = sum(H,2);
- 70 %% INITIALIZE ITERATION
- 71 loopbeta=0;
- 72 x=ones(NDV,1)*0.5;
- 73 for i=0:NMaterial-1
- 74 xTilde(1:nely,1:nelx,1:nelz,i+1)=reshape(x(1+i*NDV3:NDV3+i*NDV3),nely,nelx,nelz);
- 75 end
- 76 xPhys = (tanh(beta*0.5) + tanh(beta*(xTilde-0.5)))/(tanh(beta*0.5) + tanh(beta*(1-0.5)));
- 77 %% MMA PARAMETER INITIALIZE
- 78 a0=0; a=zeros(NMaterial,1);cc=1.0e6*ones(NMaterial,1); d=0*ones(NMaterial,1);
- 79 xmin=1e-3*ones(NDV,1); xmax=1*ones(NDV,1);
- 80 xold=x; xolder=xold;low=0; upp=1;
- 81 %% START ITERATION
- 82 for iter=1:NumIter
- 83 loopbeta=loopbeta+1;
- 84 %% FE-ANALYSIS
- 85 KE0=lk; p=6;
- 86 for i=1:NMaterial
- 87 KE(:,:,i)=par.E(i)*KE0;
- 88 end
- 89 KE_test=zeros(24*24,nely*nelx*nelz); g=zeros(NMaterial,1);
- 90 r1=xPhys(:,:,:,1); r2=xPhys(:,:,:,2); r3=xPhys(:,:,:,3);
- 91 for j=1:NMaterial
- 92 post_x(1:nely,1:nelx,1:nelz,j)=(xPhys(:,:,:,j).*(r1.^p + r2.^p + r3.^p ).^(1/p))./(r1 + r2 + r3+delta);
- 93 dr(1:nely,1:nelx,1:nelz,j)=(post_x(1:nely,1:nelx,1:nelz,j)).^penal;
- 94 KE_test=reshape(KE(:,:,j),24*24,1)*reshape(dr(:,:,:,j),1,nely*nelx*nelz)+KE_test;
- 95 g(j)=sum(sum(sum(xPhys(:,:,:,j))));
- 96 end
- 97 sK = reshape(KE_test,24*24*nelx*nely*nelz,1);
- 98 K = sparse(iK,jK,sK);
- 99 K = (K+K’)/2;
- 100 %% SOLVING
- 101 U(freedofs,:) = K(freedofs,freedofs)\F(freedofs,:);
- 102 U(fixeddofs,:)= 0;
- 103 c=F’*U;
- 104 %% COMPUTE SENSITIVITIES
- 105 dc=zeros(nely,nelx,nelz,NMaterial);
- 106 dgdx_test=zeros(NMaterial,nely*nelx*nelz*NMaterial);
- 107 KES=reshape(sum(U(edofMat)*KE0.*U(edofMat),2),[nely,nelx,nelz]);
- 108 for n=1:NMaterial
- 109 for m=1:NMaterial
- 110 if m==n
- 111 drmdn(1:nely,1:nelx,1:nelz,m)=penal.*post_x(1:nely,1:nelx,1:nelz,m).^(penal -1).*...
- 112 ((r1.^p + r2.^p + r3.^p).^(1/p)./(r1 + r2 + r3+delta) - (xPhys(:,:,:,m).*(r1.^p + r2.^p + r3.^p).^(1/p))./(r1 + r2 + r3+delta).^2 + (xPhys(:,:,:,m).*xPhys(:,:,:,n).^(p - 1).*(r1.^p + r2.^p + r3.^p).^(1/p - 1))./(r1 + r2 + r3+delta));
- 113 mass_drmdn=1;
- 114 else
- 115 drmdn(1:nely,1:nelx,1:nelz,m)=penal.*post_x(1:nely,1:nelx,1:nelz,m).^(penal - 1).*...
- 116 (((xPhys(:,:,:,m).*xPhys(:,:,:,n).^(p - 1).*(r1.^p + r2.^p + r3.^p).^(1/p - 1))./(r1 + r2 + r3+delta)- (xPhys(:,:,:,m).*(r1.^p + r2.^p + r3.^p).^(1/p))./(r1 + r2 + r3+delta).^2));
- 117 mass_drmdn=0;
- 118 end
- 119 dgdx_test(m,1+(n-1)*NDV3:NDV3+NDV3*(n-1))=repmat(mass_drmdn,1,nelx*nely*nelz);
- 120 end
- 121 dc(:,:,:,n)=-drmdn(:,:,:,1).*KES.*par.E(1)-drmdn(:,:,:,2).*KES.*par.E(2)-drmdn(:,:,:,3).*KES.*par.E(3);
- 122 end
- 123 %% FILTERING/MODIFICATION OF SENSITIVITIES
- 124 filtereddc=[];dfdx=[];
- 125 for i=1:NMaterial
- 126 dxx = beta * (1-tanh(beta*(xTilde-0.5)).*tanh(beta*(xTilde-0.5)))/(tanh(beta*0.5) + tanh(beta*(1-0.5)));
- 127 [filtereddc(:,:,:,i)]= H*(reshape(dc(:,:,:,i).*dxx(:,:,:,i),NDV3,1)./Hs);
- 128 dfdx=[dfdx;filtereddc(:,:,:,i)];
- 129 g(i)=(g(i)/NDV3-0.5/NMaterial)*1;
- 130 dgdx1=(dgdx_test(i,:)/NDV3)*1;
- 131 for j=0:NMaterial-1
- 132 dgdx2=reshape(dgdx1(:,1+j*NDV3:NDV3+j*NDV3),nely,nelx,nelz);
- 133 dgdx(i,1+j*NDV3:NDV3+j*NDV3)=H*(reshape(dgdx2(:,:,:).*dxx(:,:,:,i),NDV3,1)./Hs);
- 134 end
- 135 end
- 136 %% OPTIMALITY CRITERIA UPDATE OF DESIGN VARIABLES AND PHYSICAL DENSITIES
- 137 for j=1:length(x)
- 138 xmin(j)=max(1e-3,x(j)-movelimit); xmax(j)=min(1,x(j)+movelimit);
- 139 end
- 140 %% MMA OPTIZATION
- 141 [xnew, y, z, lamda, ksi, eta, mu, zeta, s, low, upp] = ...
- 142 mmasub(NMaterial,length(x), iter, ...
- 143 x, xmin, xmax, xold, xolder, ...
- 144 c, (dfdx), g*1e4, dgdx*1e4, low, upp, a0, a, cc, d);
- 145 %% PRINT RESULTS
- 146 disp(sprintf(‘Iter.:%3d Obj.: %8.4e max constraint: %6.3e’, iter,c ,max(g)))
- 147 %% UPDATE PARAMETER
- 148 change=norm(abs(xnew-x));
- 149 xolder=xold; xold=x; x = xnew;
- 150 for i=0:NMaterial-1
- 151 xTilde(1:nely,1:nelx,1:nelz,i+1)= reshape((H*xnew(1+i*NDV3:NDV3+i*NDV3,:))./Hs,nely,nelx,nelz);
- 152 end
- 153 xPhys = (tanh(beta*0.5) + tanh(beta*(xTilde-0.5)))/(tanh(beta*0.5) + tanh(beta*(1-0.5)));
- 154 if beta < 100 && (loopbeta >= 50)
- 155 beta = 2*beta;loopbeta = 0;
- 156 end
- 157 %% PLOT CURRENT MULTI-MATERIAL DENSITIES
- 158 figure(1);
- 159 subplot(2,2,1); display_3D(post_x,1,NMaterial);axis equal; hold on;title(‘Material 1’)
- 160 subplot(2,2,2); display_3D(post_x,2,NMaterial);axis equal; hold on;title(‘Material 2’)
- 161 subplot(2,2,3); display_3D(post_x,3,NMaterial);axis equal; hold on;title(‘Material 3’)
- 162 subplot(2,2,4); display_3D(post_x,4,NMaterial);axis equal; hold on;title(‘Material Index’)
- 163 end
- 164 %% PLOT DENSITIES
- 165 close all;
- 166 display_3D(post_x, NMaterial+1,NMaterial);axis equal; hold on;
- 167 %% 3D TOPOLOGY DISPLAY FUNCTION
- 168 function display_3D(post_x,NMat,Tolnmaterial)
- 169 if NMat<Tolnmaterial+1
- 170 NM=NMat;Nn=NMat;
- 171 else
- 172 NM=NMat-1;Nn=1;
- 173 end
- 174 for Nm=Nn:NM
- 175 [nely,nelx,nelz] = size(post_x(:,:,:,Nm));
- 176 hx = 1; hy = 1; hz = 1;
- 177 face = [1 2 3 4; 2 6 7 3; 4 3 7 8; 1 5 8 4; 1 2 6 5; 5 6 7 8];
- 178 for k = 1:nelz
- 179 z = (k-1)*hz;
- 180 for i = 1:nelx
- 181 x = (i-1)*hx;
- 182 for j = 1:nely
- 183 y = nely*hy - (j-1)*hy;
- 184 if (post_x(j,i,k,Nm) >0.5)
- 185 vert = [x y z; x y-hx z; x+hx y-hx z; x+hx y z; x y z+hx;x y-hx z+hx; x+hx y-hx z+hx;x+hx y z+hx];
- 186 vert(:,[2 3]) = vert(:,[3 2]); vert(:,2,:) = -vert(:,2,:);
- 187 if Nm==1
- 188 patch(‘Faces’,face,’Vertices’,vert,’FaceColor’,’r’);
- 189 elseif Nm==2
- 190 patch(‘Faces’,face,’Vertices’,vert,’FaceColor’,’b’);
- 191 elseif Nm==3
- 192 patch(‘Faces’,face,’Vertices’,vert,’FaceColor’,’g’);
- 193 end
- 194 end
- 195 end
- 196 end
- 197 end
- 198 end
- 199 axis equal; axis tight; axis off; box on; view([-45,30]); hold on;
- 200 end
References
- Huang, X.; Li, W. A new multi-material topology optimization algorithm and selection of candidate materials. Comput. Methods Appl. Mech. Eng. 2021, 386, 114114. [Google Scholar] [CrossRef]
- Liu, W.; Yoon, G.H.; Yi, B.; Choi, H.; Yang, Y. Controlling wave propagation in one-dimensional structures through topology optimization. Comput. Struct. 2020, 241, 106368. [Google Scholar] [CrossRef]
- Yang, X.; Li, M. Discrete multi-material topology optimization under total mass constraint. Comput.-Aided Des. 2018, 102, 182–192. [Google Scholar] [CrossRef]
- Bohrer, R.; Kim, I.Y. Multi-material topology optimization considering isotropic and anisotropic materials combination. Struct. Multidisc. Optim. 2021, 64, 1567–1583. [Google Scholar] [CrossRef]
- Liu, B.; Huang, X.; Cui, Y. Topology optimization of multi-material structures with explicitly graded interfaces. Comput. Methods Appl. Mech. Eng. 2022, 398, 115166. [Google Scholar] [CrossRef]
- Chandrasekhar, A.; Suresh, K. Multi-Material Topology Optimization Using Neural Networks. Comput.-Aided Des. 2021, 136, 103017. [Google Scholar] [CrossRef]
- Zhang, X.S.; Paulino, G.H.; Ramos, A.S. Multi-material topology optimization with multiple volume constraints: A general approach applied to ground structures with material nonlinearity. Struct. Multidisc. Optim. 2018, 57, 161–182. [Google Scholar] [CrossRef]
- Shah, V.; Pamwar, M.; Sangha, B.; Kim, I.Y. Multi-material topology optimization considering natural frequency constraint. Eng. Comput. 2022, 39, 2604–2629. [Google Scholar] [CrossRef]
- Sigmund, O.; Torquato, S. Design of materials with extreme thermal expansion using a three-phase topology optimization method. J. Mech. Phys. Solids 1997, 45, 1037–1067. [Google Scholar] [CrossRef]
- Hvejsel, C.F.; Lund, E. Material interpolation schemes for unified topology and multi-material optimization. Struct. Multidisc. Optim. 2011, 43, 811–825. [Google Scholar] [CrossRef]
- Stegmann, J.; Lund, E. Discrete material optimization of general composite shell structures. Int. J. Numer. Meth. Eng. 2005, 62, 2009–2027. [Google Scholar] [CrossRef]
- Gao, T.; Zhang, W. A mass constraint formulation for structural topology optimization with multiphase materials. Int. J. Numer. Meth. Eng. 2011, 88, 774–796. [Google Scholar] [CrossRef]
- Bruyneel, M. SFP—A new parameterization based on shape functions for optimal material selection: Application to conventional composite plies. Struct. Multidisc. Optim. 2011, 43, 17–27. [Google Scholar] [CrossRef]
- Yin, L.; Ananthasuresh, G.K. Topology optimization of compliant mechanisms with multiple materials using a peak function material interpolation scheme. Struct. Multidiscip. Optim. 2001, 23, 49–62. [Google Scholar] [CrossRef]
- Zuo, W.; Saitou, K. Multi-material topology optimization using ordered SIMP interpolation. Struct. Multidiscip. Optim. 2017, 55, 477–491. [Google Scholar] [CrossRef]
- Yi, B.; Yoon, G.H.; Zheng, R.; Liu, L.; Li, D.; Peng, X. A unified material interpolation for topology optimization of multi-materials. Comput. Struct. 2023, 282, 107041. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 line topology optimization code written in Matlab. Struct. Multidisc. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidisc. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef]
- Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef]
- Ferrari, F.; Sigmund, O. A new generation 99 line Matlab code for compliance topology optimization and its extension to 3D. Struct. Multidiscip. Optim. 2020, 62, 2211–2228. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.-M. A further review of ESO type methods for topology optimization. Struct. Multidiscip. Optim. 2010, 41, 671–683. [Google Scholar] [CrossRef]
- Challis, V.J. A discrete level-set topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2010, 41, 453–464. [Google Scholar] [CrossRef]
- Wei, P.; Li, Z.; Li, X.; Wang, M.Y. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions. Struct. Multidiscip. Optim. 2018, 58, 831–849. [Google Scholar] [CrossRef]
- Zhang, W.; Yuan, J.; Zhang, J.; Guo, X. A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model. Struct. Multidiscip. Optim. 2016, 53, 1243–1260. [Google Scholar] [CrossRef]
- Du, Z.; Cui, T.; Liu, C.; Zhang, W.; Guo, Y.; Guo, X. An efficient and easy-to-extend Matlab code of the Moving Morphable Component (MMC) method for three-dimensional topology optimization. Struct. Multidiscip. Optim. 2022, 65, 158. [Google Scholar] [CrossRef]
- Xia, L.; Breitkopf, P. Design of materials using topology optimization and energy-based homogenization approach in Matlab. Struct. Multidiscip. Optim. 2015, 52, 1229–1241. [Google Scholar] [CrossRef]
- Dong, G.; Tang, Y.; Zhao, Y.F. A 149 Line Homogenization Code for Three-Dimensional Cellular Materials Written in matlab. J. Eng. Mater. Technol. 2019, 141, 011005. [Google Scholar] [CrossRef]
- Liu, P.; Yan, Y.; Zhang, X.; Luo, Y. A MATLAB code for the material-field series-expansion topology optimization method. Front. Mech. Eng. 2021, 16, 607–622. [Google Scholar] [CrossRef]
- Tavakoli, R.; Mohseni, S.M. Alternating active-phase algorithm for multimaterial topology optimization problems: A 115-line MATLAB implementation. Struct. Multidiscip. Optim. 2014, 49, 621–642. [Google Scholar] [CrossRef]
- Sanders, E.D.; Pereira, A.; Aguiló, M.A.; Paulino, G.H. PolyMat: An efficient Matlab code for multi-material topology optimization. Struct. Multidiscip. Optim. 2018, 58, 2727–2759. [Google Scholar] [CrossRef]
- Gangl, P. A multi-material topology optimization algorithm based on the topological derivative. Comput. Methods Appl. Mech. Eng. 2020, 366, 113090. [Google Scholar] [CrossRef]
- Wang, F.; Lazarov, B.S.; Sigmund, O. On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 767–784. [Google Scholar] [CrossRef]
- Xu, S.; Cai, Y.; Cheng, G. Volume preserving nonlinear density filter based on heaviside functions. Struct. Multidiscip. Optim. 2010, 41, 495–505. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Numer. Meth. Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, R.; Yi, B.; Peng, X.; Yoon, G.-H. An Efficient Code for the Multi-Material Topology Optimization of 2D/3D Continuum Structures Written in Matlab. Appl. Sci. 2024, 14, 657. https://doi.org/10.3390/app14020657
Zheng R, Yi B, Peng X, Yoon G-H. An Efficient Code for the Multi-Material Topology Optimization of 2D/3D Continuum Structures Written in Matlab. Applied Sciences. 2024; 14(2):657. https://doi.org/10.3390/app14020657
Chicago/Turabian StyleZheng, Ran, Bing Yi, Xiang Peng, and Gil-Ho Yoon. 2024. "An Efficient Code for the Multi-Material Topology Optimization of 2D/3D Continuum Structures Written in Matlab" Applied Sciences 14, no. 2: 657. https://doi.org/10.3390/app14020657
APA StyleZheng, R., Yi, B., Peng, X., & Yoon, G.-H. (2024). An Efficient Code for the Multi-Material Topology Optimization of 2D/3D Continuum Structures Written in Matlab. Applied Sciences, 14(2), 657. https://doi.org/10.3390/app14020657







