A Coordinated Bidding Strategy of Wind Power Producers and DR Aggregators Using a Cooperative Game Approach
Abstract
1. Introduction
- Considering the complementary characteristics of wind power and DR resources, an appropriate coordinated bidding strategy using cooperative game theory is developed. Compared to existing studies on coordinated trading strategy for wind power and other resources, as proposed in this paper, wind power and DR resources can strategically perform regulation provision by taking advantage of their complementary characteristics.
- Based on cooperative game theory, WPPs and DRAs form a coalition and strategically bid in both energy and regulation markets to achieve maximum benefits. Then, two different profit allocation methods are deployed to reasonably allocate the additional profits of the coalition to each player.
- Uncertainties associated with wind outputs and DR are considered and represented by multiple scenarios. The conditional value-at-risk (CVaR) is employed to quantify the risks attributed to collaborative bidding decisions.
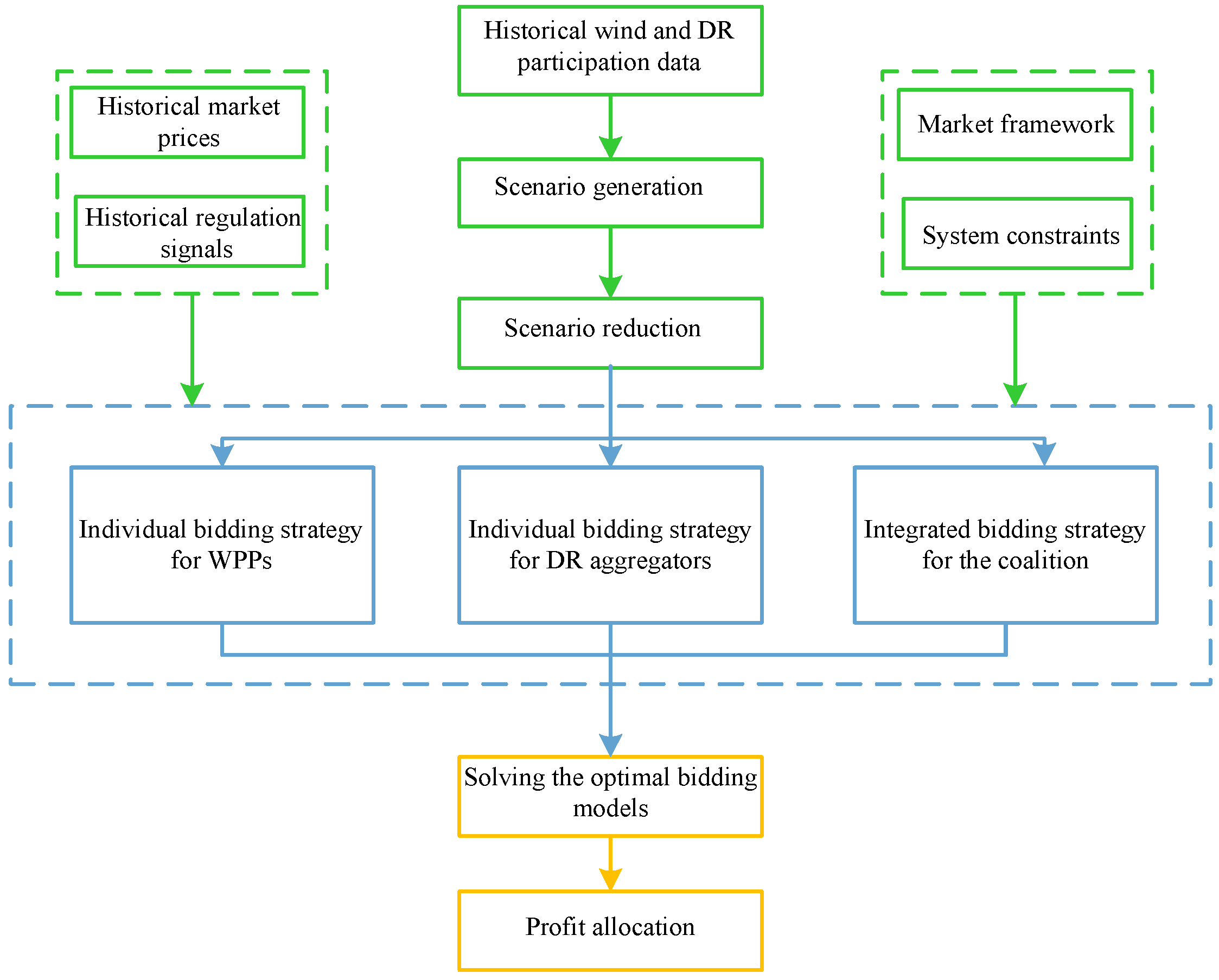
2. Problem Description
2.1. Complementary Characteristics of Wind and DR Resources
2.2. Cooperation Scheme of Wind Power and DR Resource
2.3. DR Modeling
2.4. Uncertainty Modeling
3. Mathematical Formulation
3.1. Individual Bidding Strategies for a WPP
3.2. Individual Bidding Strategies for a DR Aggregator
3.3. Integrated Bidding Strategies for Coordinated Wind-DR Power Plant
- (1)
- In the coalition, we assume that the WPP provides low-priced energy to the DR aggregator. The benefit received by the WPP equals the purchase cost of DR aggregators. Therefore, within the coalition, the energy provided by a WPP to a DR aggregator is free. In return, DR aggregators can offer DR capacity for mitigating wind output imbalances caused by forecasting errors. Similarly, within the coalition, the DR capacity provided by the DR aggregator to the WPP is free.
- (2)
- As described in Section 2, wind power and DR resources are complementary when providing frequency regulation. Therefore, through the coordinated bidding strategy, the coalition can optimize the operation states of wind generation and DR resources to respond to regulation signals more economically.
3.4. Cooperative Game-Theory Profit Allocation Method
3.4.1. Nucleolus-Based Method
3.4.2. Shapley-Value Method
4. Case Study
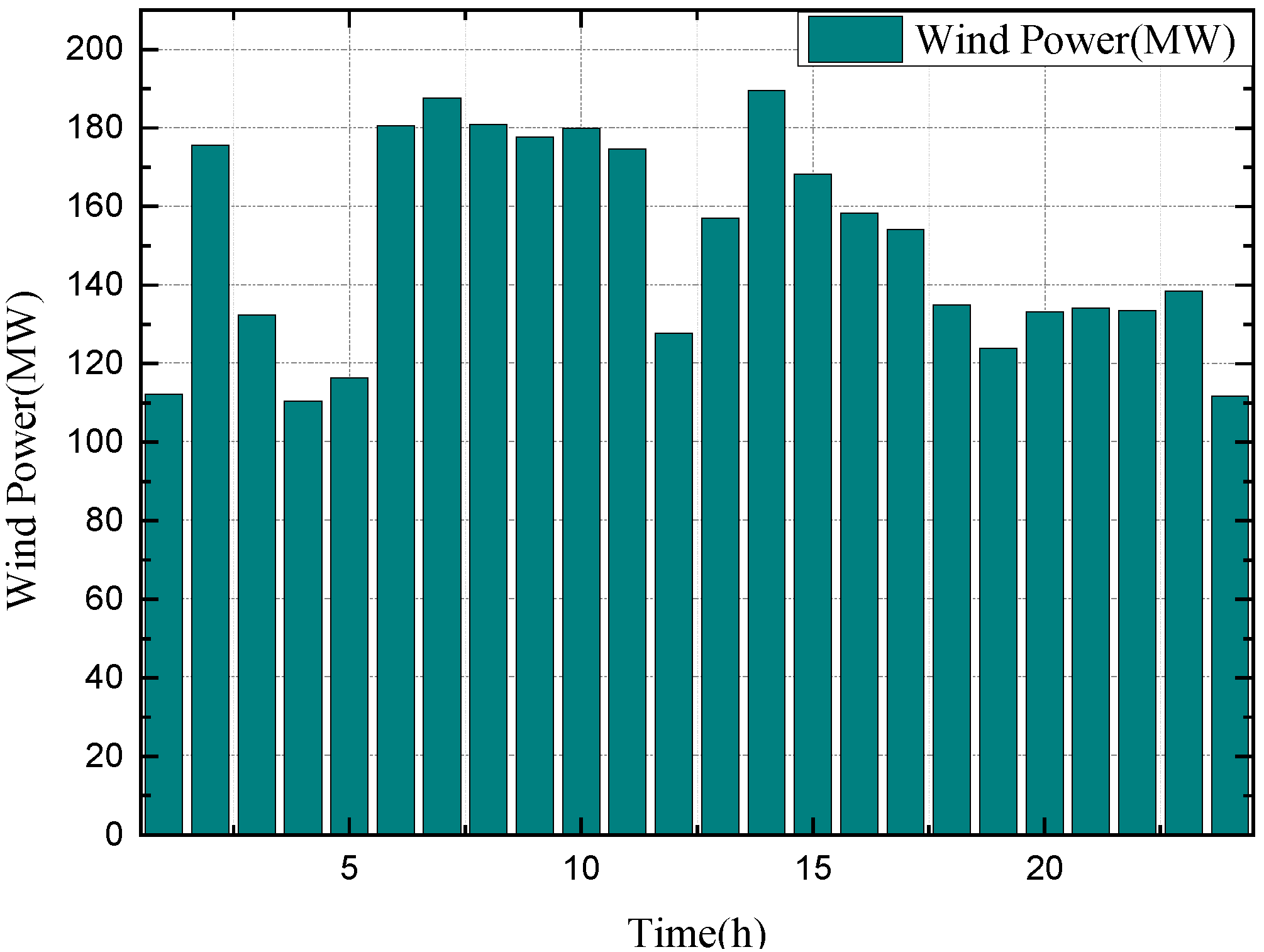
4.1. Data
4.2. Bidding Results
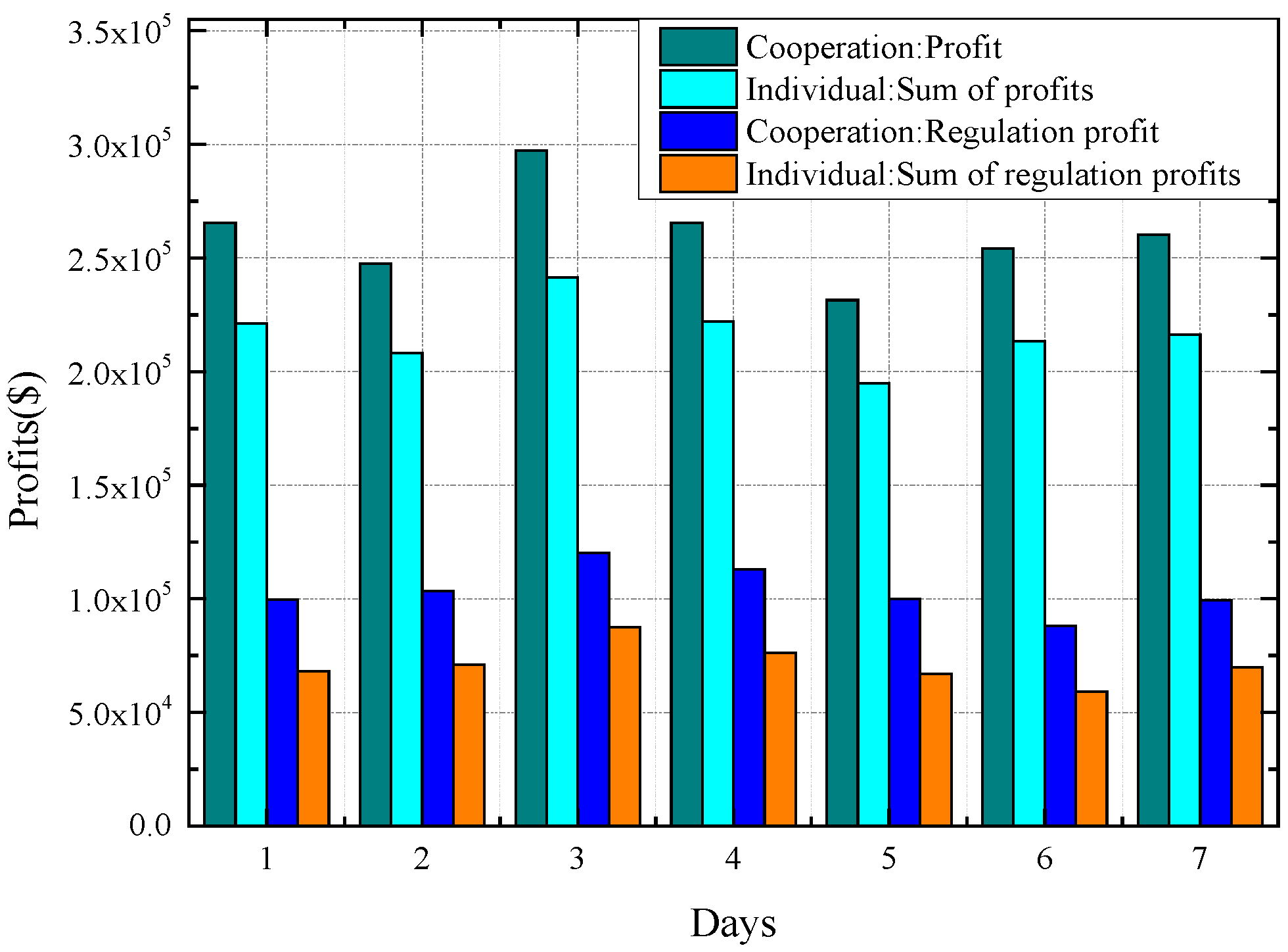
4.3. Three-Player Game
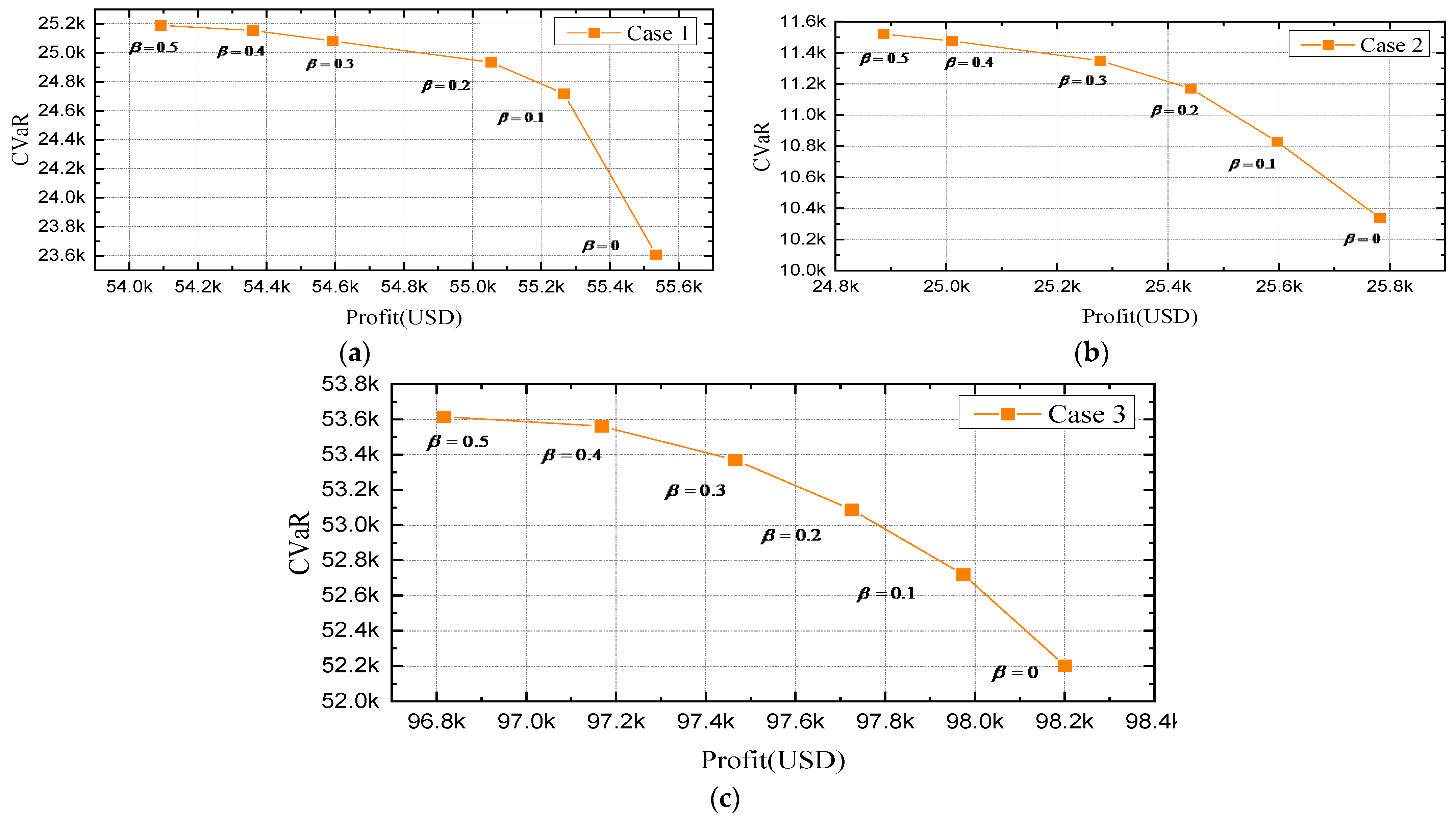
4.4. Impact of Risk Management
5. Discussions and Conclusions
5.1. Integrated Discussion of Results
- A cooperative framework is proposed for wind power and DR resources, aiming to explore their complementary characteristics in the provision of frequency regulation. Furthermore, leveraging these complementary attributes, an optimal bidding strategy is developed for WPPs and DR aggregators. Notably, the coalition formed between WPP 1 and the DRA results in a significant increase in total profit by 5.0%, when compared to a scenario where the DRA operates without the participation of wind power producers;
- CVaR is deployed to control the revenue volatility associated with uncertainties. The results of the case study demonstrate that as β increases, the CVaR rises and the market revenue declines. Specifically, in Case S2 (where β ranges from 0 to 0.5), CVaR increases by 6.7%, resulting in a revenue reduction from USD 55,534.5 to USD 54,029. Similarly, in Case S4, CVaR rises by 11.4%, leading to a 3.47% decline in revenue;
- The coordinated bidding strategy can bring higher benefits for both WPPs and DR aggregators. The results show that the proposed trading scheme results in the highest market benefits in both two-player and three-player games. In addition, the regulation-related profits become a larger fraction of the overall profits. Specifically, in Case S6, the coalition achieved market profits with 46.54% from frequency regulation and 5.9% from energy imbalance, highlighting the significant contribution of regulation-related activities to the total earnings.
5.2. Future Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kang, W.; Guan, Y.; Arbab-Zavar, B.; Guerrero, J.M. Distributed Event-Triggered Secondary Frequency Regulation by Sharing HESS Power in Microgrids. IEEE Trans. Smart Grid 2024, 15, 3375–3389. [Google Scholar] [CrossRef]
- Ding, Z.; Yuan, K.; Qi, J.; Wang, Y.; Hu, J.; Zhang, K. Robust and cost-efficient coordinated primary frequency control of wind power and demand response based on their complementary regulation characteristics. IEEE Trans. Smart Grid 2022, 13, 4436–4448. [Google Scholar] [CrossRef]
- Li, L.; Zhu, D.; Zou, X.; Hu, J.; Kang, Y.; Guerrero, J.M. Review of frequency regulation requirements for wind power plants in international grid codes. Renew. Sustain. Energy Rev. 2023, 187, 113731. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, X.; Deng, X.; Huang, Y.; Li, C.; Wu, J. Bidding strategy for wind power and Large-scale electric vehicles participating in Day-ahead energy and frequency regulation market. Appl. Energy 2023, 341, 121063. [Google Scholar] [CrossRef]
- Schledorn, A.; Junker, R.G.; Guericke, D.; Madsen, H.; Dominković, D.F. Frigg: Soft-linking energy system and demand response models. Appl. Energy 2022, 317, 119074. [Google Scholar] [CrossRef]
- Federal Energy Regulatory Commission (FERC). FERC Order 755: Frequency Regulation Compensation in the Organized Wholesale Power Markets; Federal Energy Regulatory Commission (FERC): Washington, DC, USA, 2011.
- National Development and Reform Commission of China, National Energy Administration of China. Notice on Further Improving the Trading Mechanism of Electric Power Market Transaction. 2018. Available online: https://www.ndrc.gov.cn/fzggw/jgsj/yxj/sjdt/201807/t20180718_986995.html (accessed on 14 November 2024). (In Chinese)
- Sarnaduti, B.; Adil, K.; Hamid, O.; Mads, A. Optimal frequency regulation using packetized energy management. IEEE Trans. Smart Grid 2022, 14, 341–353. [Google Scholar]
- Yang, C.; Du, X.; Xu, D.; Tang, J.; Lin, X.; Xie, K.; Li, W. Optimal bidding strategy of renewable-based virtual power plant in the day-ahead market. IEEE Trans. Power Energy Syst. 2023, 144, 108557. [Google Scholar] [CrossRef]
- Mehdi, F.; Kate, S. The impact of various carbon reduction policies on green flowshop scheduling. Appl. Energy 2019, 249, 300–315. [Google Scholar]
- Pannell, D.J.; Alston, J.M.; Jeffrey, S.; Buckley, Y.M.; Vesk, P.; Rhodes, J.R.; McDonald-Madden, E.; Nally, S.; Goucher, G.; Thamo, T. Policy-oriented environmental research: What is it worth? Environ. Sci. Policy 2018, 86, 64–71. [Google Scholar] [CrossRef]
- Agheb, S.; Tan, X.; Sun, B.; Tsang, D.H. Contract Design for Aggregating, Trading, and Distributing Reserves in Demand-Side Frequency Regulation. IEEE Trans. Ind. Inf. 2017, 14, 2539–2549. [Google Scholar] [CrossRef]
- Tavakoli, A.; Negnevitsky, M.; Nguyen, D.T.; Muttaqi, K.M. Energy exchange between electric vehicle load and wind generating utilities. IEEE Trans. Power Syst. 2015, 31, 1248–1258. [Google Scholar] [CrossRef]
- Yingchao, D.; Cong, W.; Hongli, Z.; Xiaojun, Z. A novel multi-objective optimization framework for optimal integrated energy system planning with demand response under multiple uncertainties. Inf. Sci. 2024, 663, 120252. [Google Scholar]
- Vrettos, E.; Oldewurtel, F.; Andersson, G. Robust energy-constrained frequency reserves from aggregations of commercial buildings. IEEE Trans. Power Syst. 2016, 31, 4272–4285. [Google Scholar] [CrossRef]
- Zhan, S.; Hou, P.; Enevoldsen, P.; Yang, G.; Zhu, J.; Eichman, J.; Jacobson, M.Z. Co-optimized trading of hybrid wind power plant with retired EV batteries in energy and reserve markets under uncertainties. Int. J. Electr. Power Energy Syst. 2020, 117, 105631. [Google Scholar] [CrossRef]
- Chen, X.; Wang, C.; Wu, Q.; Dong, X.; Yang, M.; He, S.; Liang, J. Optimal operation of integrated energy system considering dynamic heat-gas characteristics and uncertain wind power. Energy 2020, 198, 117270. [Google Scholar] [CrossRef]
- Zhang, R.; Jiang, T.; Li, F.; Li, G.; Chen, H.; Li, X. Coordinated Bidding Strategy of Wind Farms and Power-to-Gas Facilities using a Cooperative Game Approach. IEEE Trans. Sustain. Energy 2020, 11, 2545–2555. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, M.; Wang, J.; Du, E.; Zhang, N.; Li, G. Profit-sharing mechanism for aggregation of wind farms and concentrating solar power. IEEE Trans. Sustain. Energy 2020, 11, 2606–2616. [Google Scholar] [CrossRef]
- GAMS/SCENRED Documentation. 2024. Available online: http://www.gams.com/docs/document.htm (accessed on 14 November 2024).
- PJM—Markets and Operations, Data Miner. 2024. Available online: https://dataminer2.pjm.com (accessed on 14 November 2024).
- PJM Market Demand Response Programs. 2024. Available online: https://www.pjm.com/markets-and-operations/demand-response.aspx (accessed on 14 November 2024).





| Case | Bidding Entity | Bidding Scenarios | Market(s) Involved |
|---|---|---|---|
| Case 1 | WPP 1 without DR aggregators | S1 | Energy market |
| S2 | Energy and frequency regulation markets | ||
| Case 2 | DRA without wind power producers | S3 | Energy market |
| S4 | Energy and frequency regulation markets | ||
| Case 3 | Coalition of WPP 1 and DRA | S5 | Energy market |
| S6 | Energy and frequency regulation markets |
| Player | Uncoordinated Profits (USD) | Nucleolus-Based Method | Shapley-Value Method | ||
|---|---|---|---|---|---|
| Profit (USD) | Surplus Profit (USD) | Profit (USD) | Surplus Profit (USD) | ||
| WPP 1 | 55,534.5 | 57,563.95 | 2029.45 | 57,563.95 | 2029.45 |
| DRA | 25,782 | 27,811.45 | 2029.45 | 27,811.45 | 2029.45 |
| Player | Uncoordinated Profits (USD) | Nucleolus-Based Method | Shapley-Value Method | ||
|---|---|---|---|---|---|
| Profit (USD) | Surplus Profit (USD) | Profit (USD) | Surplus Profit (USD) | ||
| WPP 1 | 55,534.5 | 58,579 | 3044.6 | 58,375.0 | 2840.5 |
| WPP2 | 38,683.0 | 41,078 | 2394.7 | 41,199.0 | 2516.0 |
| DRA | 25,782.0 | 28,253 | 2471.2 | 28,336.0 | 2554.0 |
| Total | 119,999.5 | 127,910.0 | 7910.5 | 127,910.0 | 7910.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, X.; Zheng, S.; Chen, H.; Bi, W. A Coordinated Bidding Strategy of Wind Power Producers and DR Aggregators Using a Cooperative Game Approach. Appl. Sci. 2024, 14, 10699. https://doi.org/10.3390/app142210699
Dai X, Zheng S, Chen H, Bi W. A Coordinated Bidding Strategy of Wind Power Producers and DR Aggregators Using a Cooperative Game Approach. Applied Sciences. 2024; 14(22):10699. https://doi.org/10.3390/app142210699
Chicago/Turabian StyleDai, Xuemei, Shiyuan Zheng, Haoran Chen, and Wenjun Bi. 2024. "A Coordinated Bidding Strategy of Wind Power Producers and DR Aggregators Using a Cooperative Game Approach" Applied Sciences 14, no. 22: 10699. https://doi.org/10.3390/app142210699
APA StyleDai, X., Zheng, S., Chen, H., & Bi, W. (2024). A Coordinated Bidding Strategy of Wind Power Producers and DR Aggregators Using a Cooperative Game Approach. Applied Sciences, 14(22), 10699. https://doi.org/10.3390/app142210699





