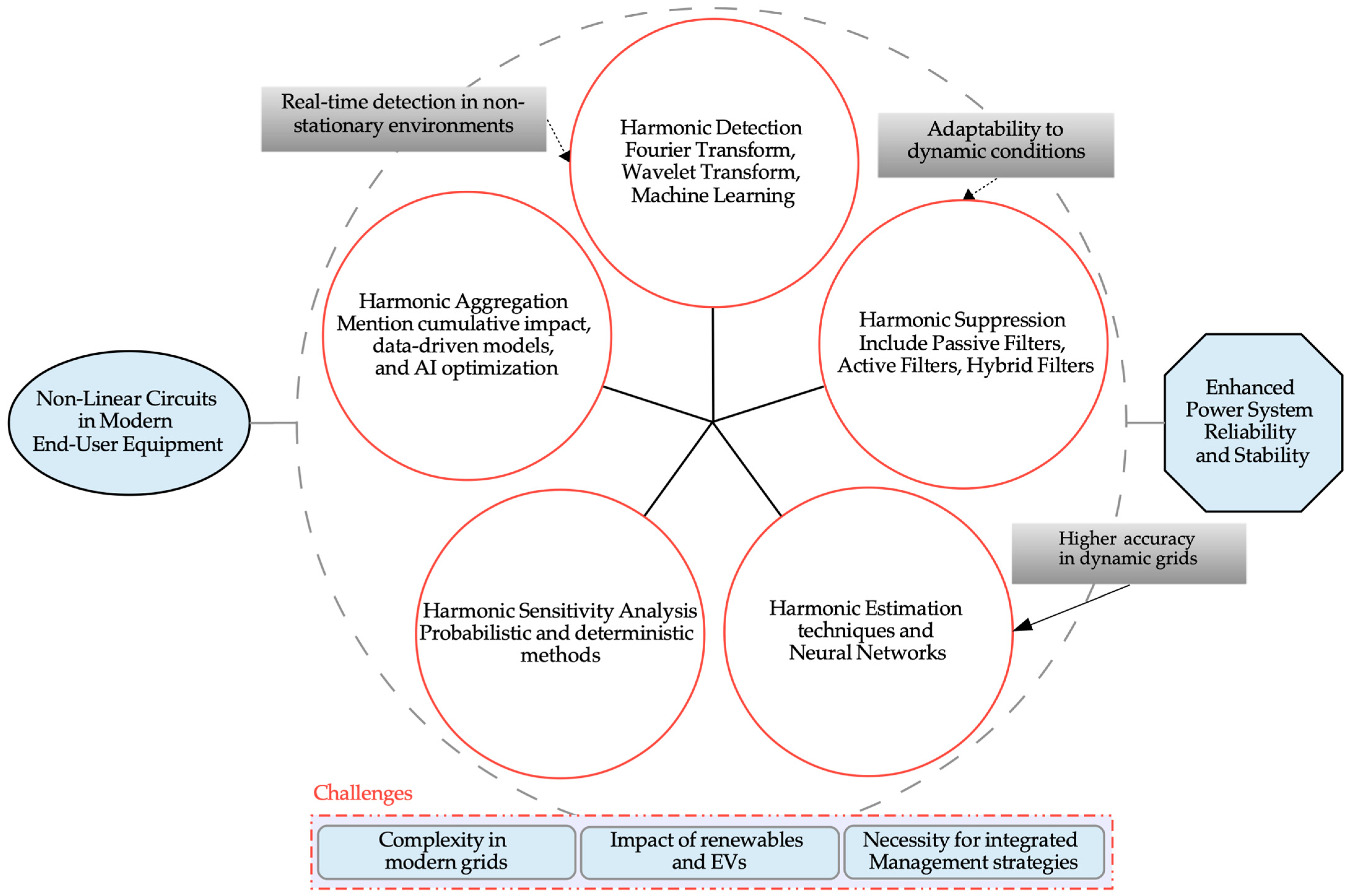
A Review of Harmonic Detection, Suppression, Aggregation, and Estimation Techniques
Abstract
1. Introduction
2. Harmonic Detection Principles and Methods
2.1. Discrete Fourier Transform
2.2. Based on 3-φ Instantaneous Reactive Power
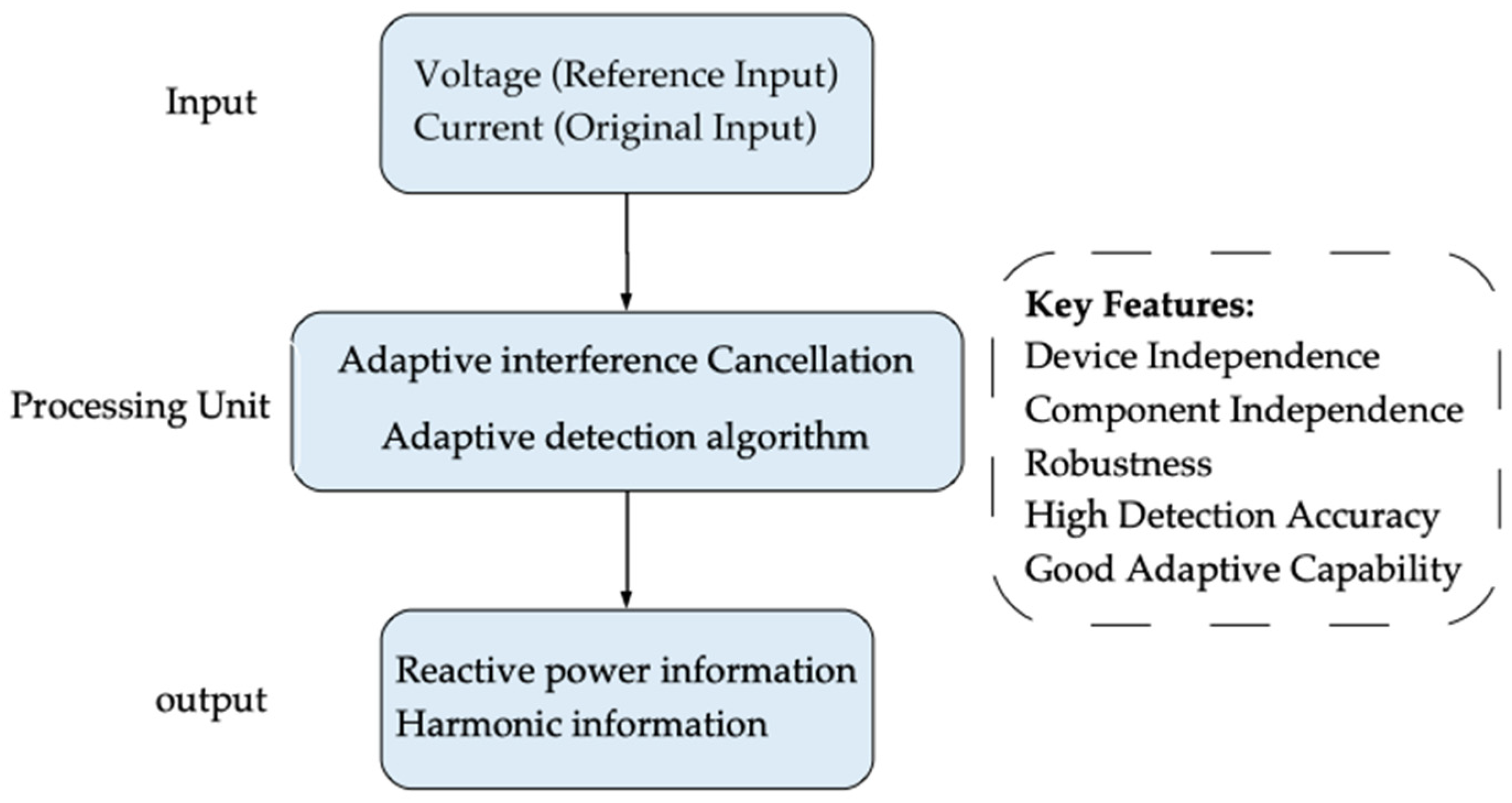
2.3. Adaptive Detection Method
2.4. Detection Based on Wavelet Analysis
2.5. Neural Network (NN) Based Method
3. Harmonic Suppression Methods
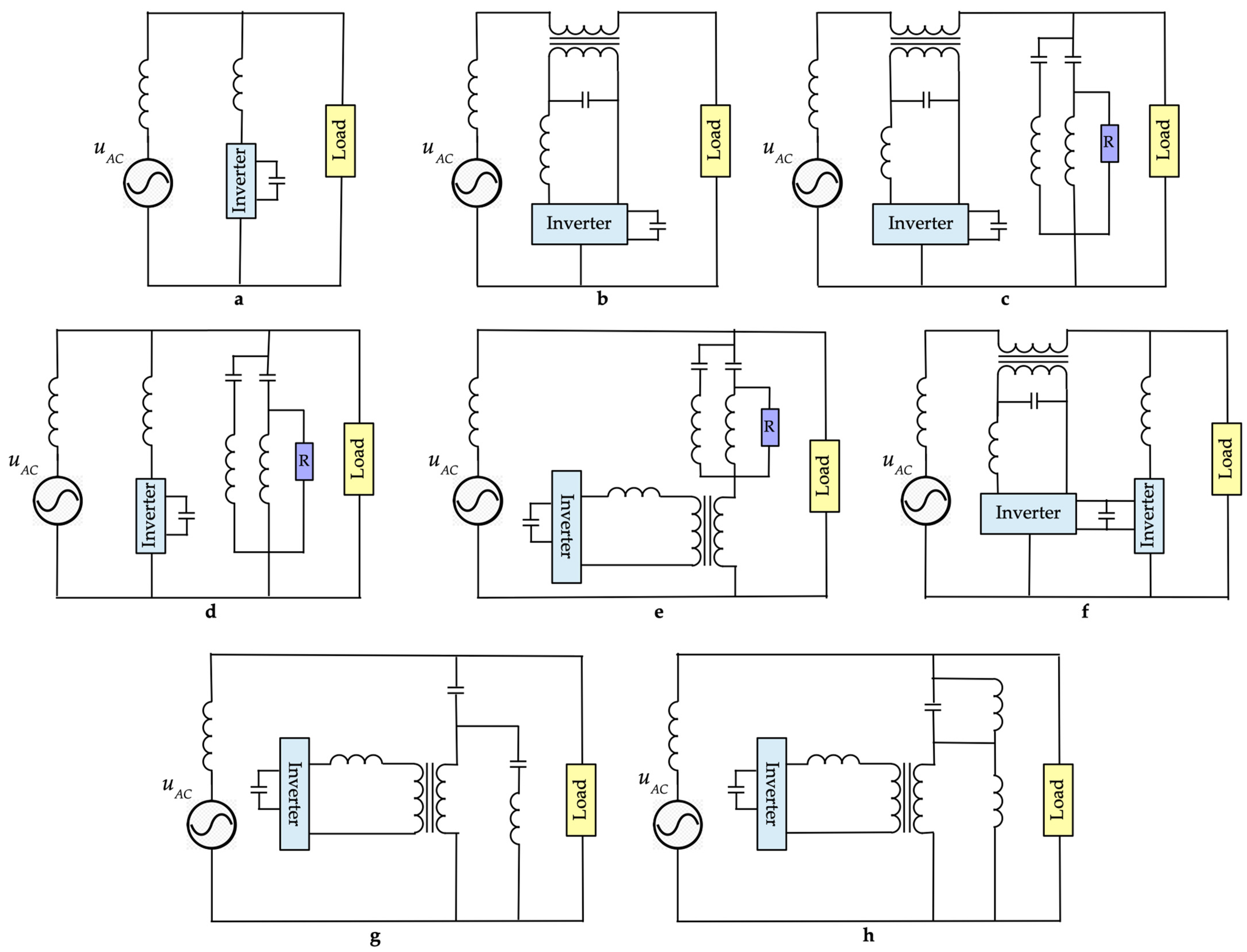
3.1. Passive Power Filter
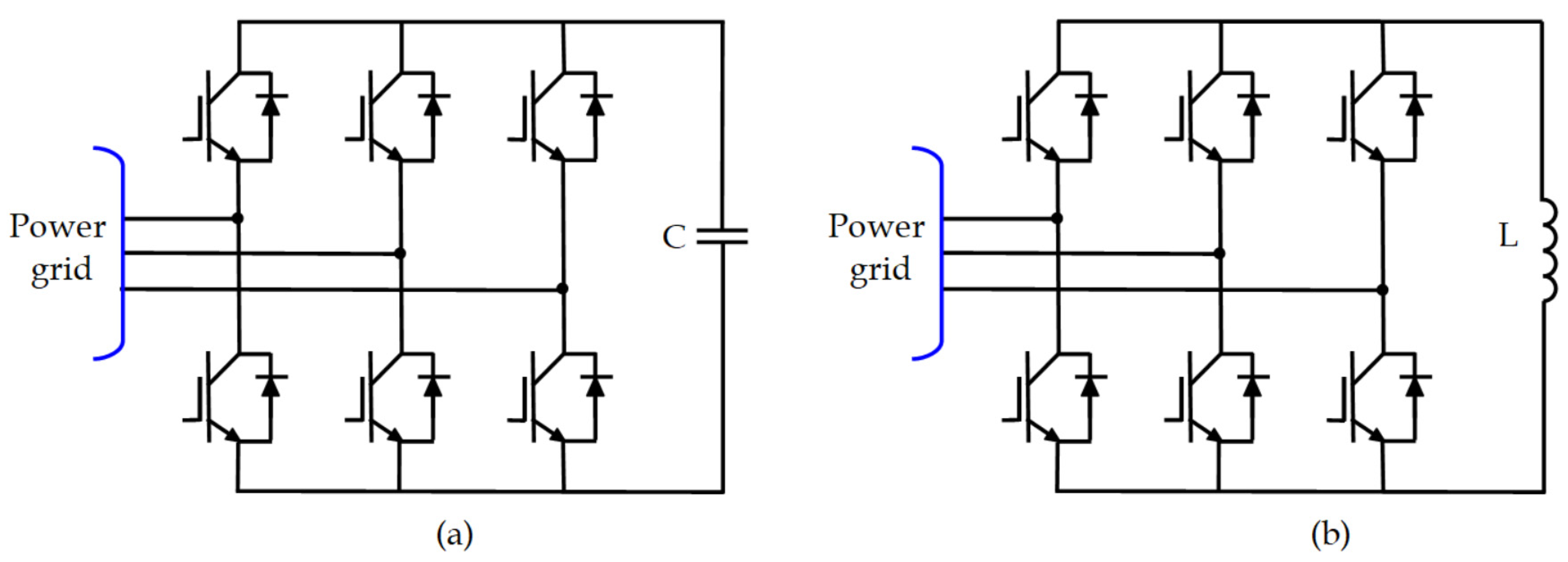
3.2. Active Power Filter
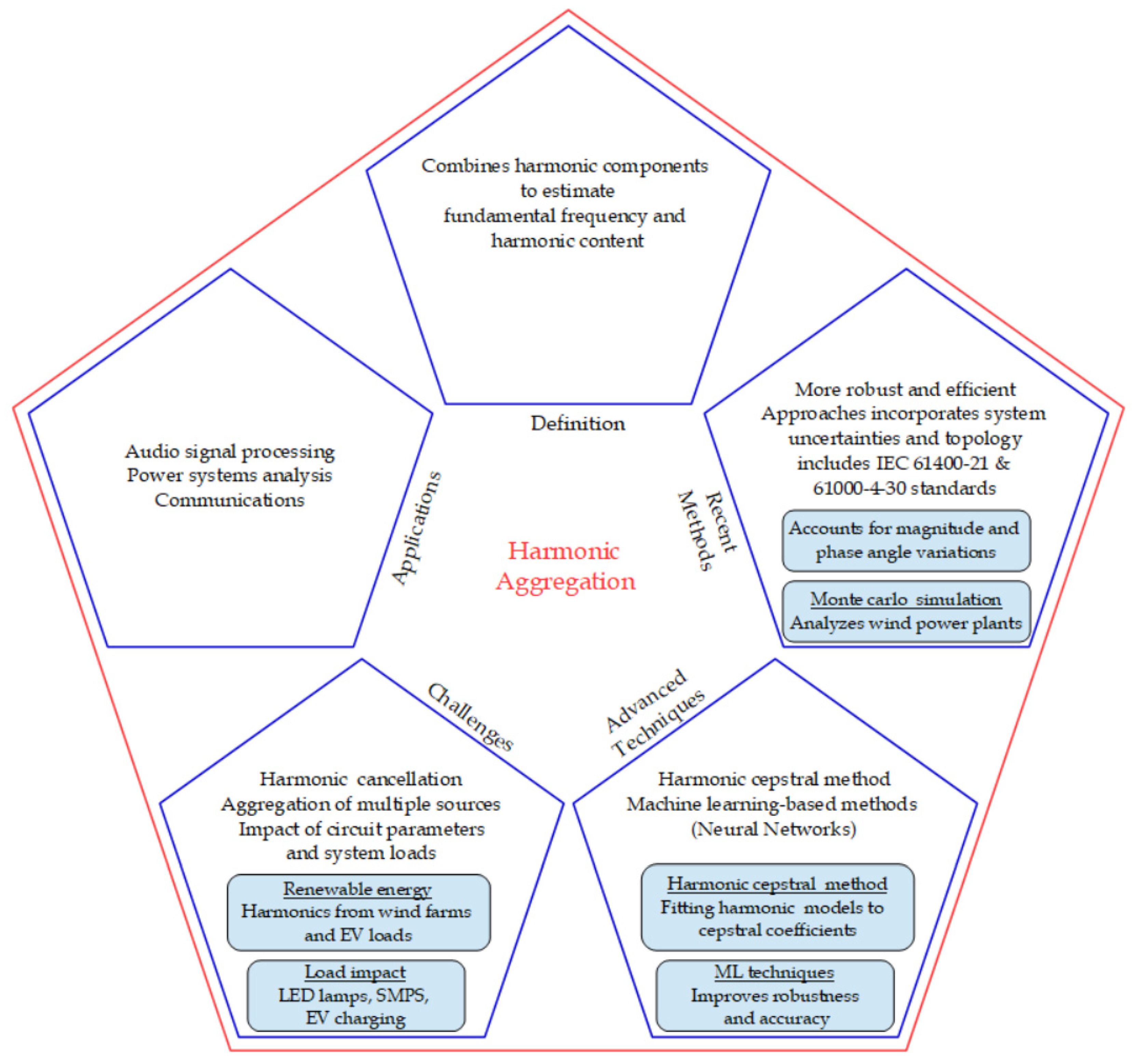
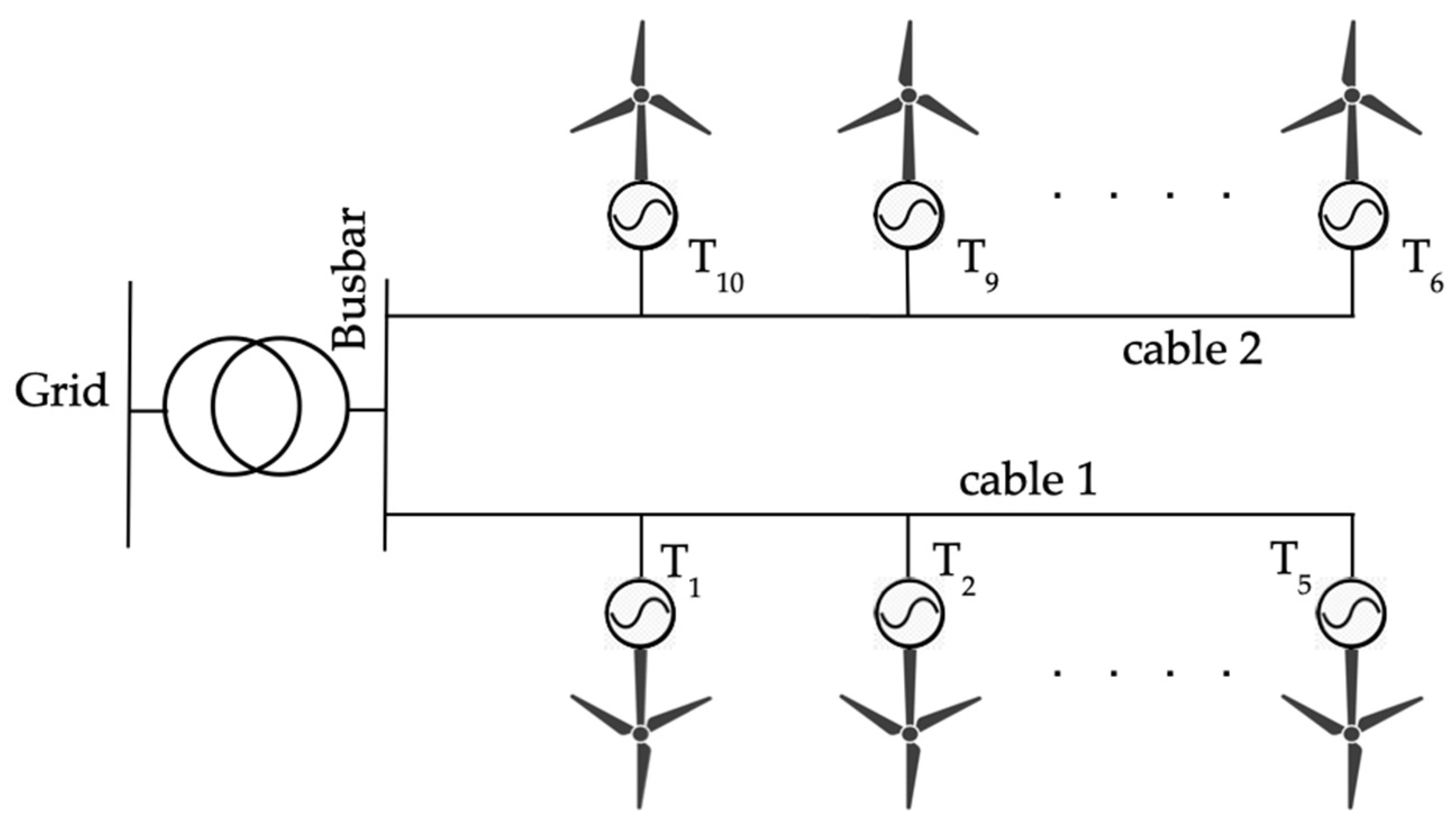
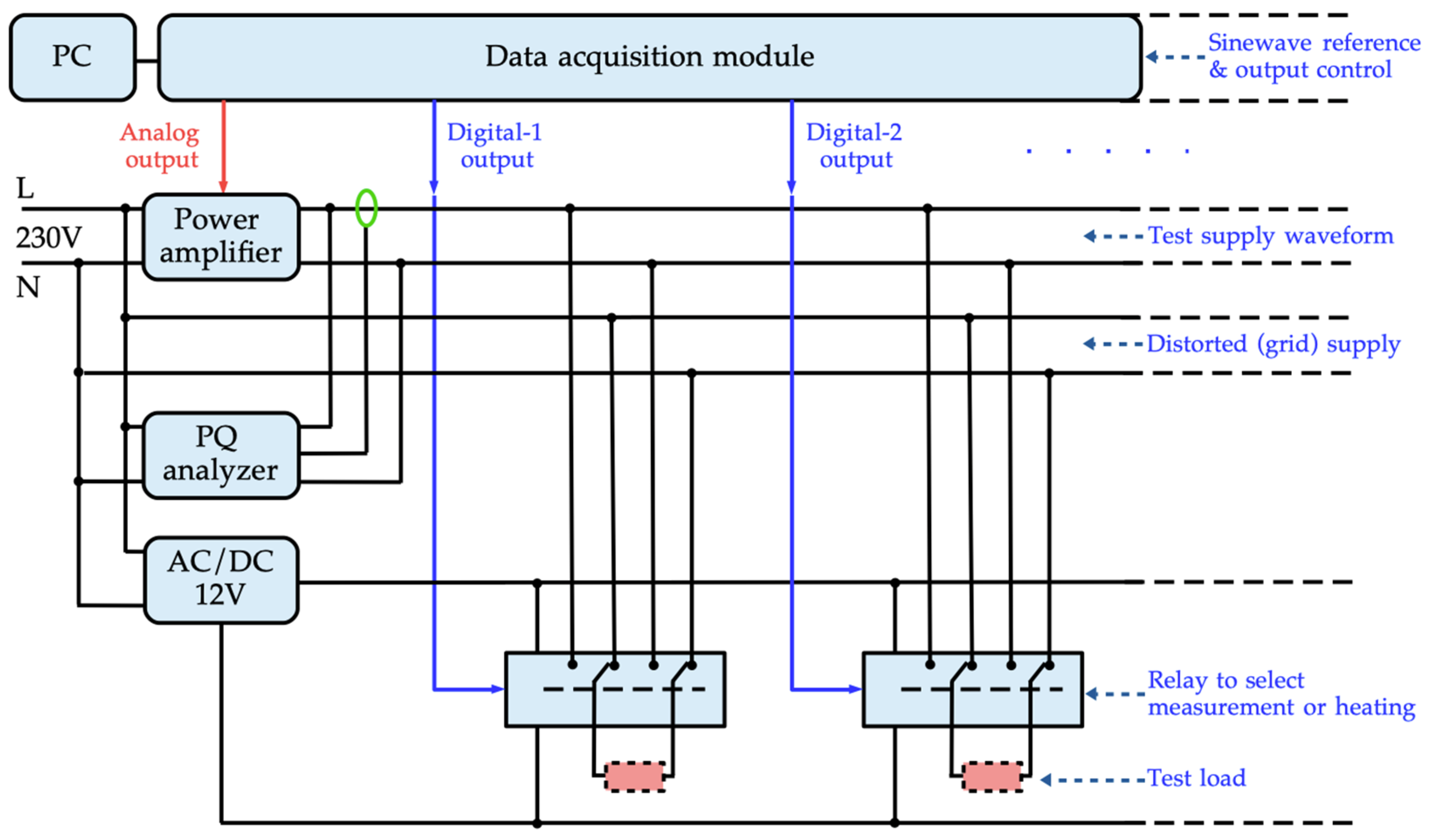
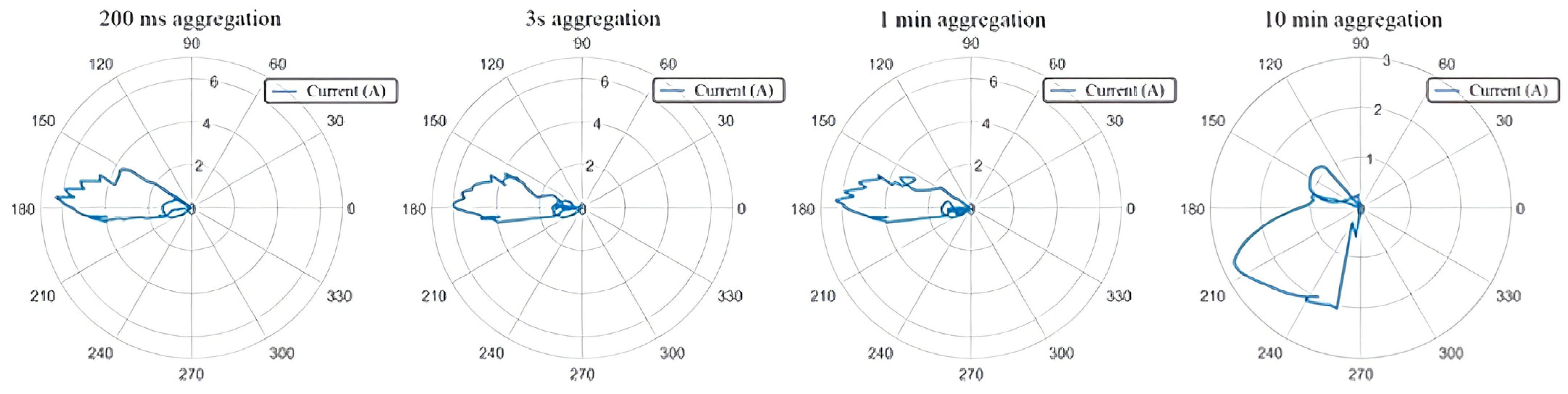
4. Harmonic Aggregation
5. Harmonic Estimation Models
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C.S.; Bai, Z.X.; Xiao, X.Y.; Liu, Y.M.; Zhang, Y. Research of Harmonic Distortion Power for Harmonic Source Detection. In Proceedings of the 2016 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 126–129. [Google Scholar] [CrossRef]
- Iqbal, M.N.; Kütt, L.; Asad, B.; Shabbir, N.; Rasheed, I. Time-Dependent Variations in Current Harmonic Emission by LED Lamps in the Low-Voltage Network. Electr. Eng. 2021, 103, 1525–1539. [Google Scholar] [CrossRef]
- Rakpenthai, C.; Uatrongjit, S.; Watson, N.R.; Premrudeepreechacharn, S. On Harmonic State Estimation of Power System with Uncertain Network Parameters. IEEE Trans. Power Syst. 2013, 28, 4829–4838. [Google Scholar] [CrossRef]
- Yang, J.Z.; Yu, C.S.; Liu, C.W. A New Method for Power Signal Harmonic Analysis. IEEE Trans. Power Deliv. 2005, 20, 1235–1239. [Google Scholar] [CrossRef]
- Frigo, G.; Derviskadic, A.; Pegoraro, P.A.; Muscas, C.; Paolone, M. Harmonic Phasor Measurements in Real-World PMU-Based Acquisitions. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019. [Google Scholar] [CrossRef]
- Wright, P.S.; Christensen, A.E.; Davis, P.N.; Lippert, T. Multiple-Site Amplitude and Phase Measurements of Harmonics for Analysis of Harmonic Propagation on Bornholm Island. IEEE Trans. Instrum. Meas. 2017, 66, 1176–1183. [Google Scholar] [CrossRef]
- Sardar, M.U.; Vaimann, T.; Kutt, L.; Kallaste, A.; Asad, B.; Kudelina, K.; Akbar, S. Analysis of Common Mode and Rapidly Varying Voltage Profile on Stator Current Harmonics of an Inverter-Fed Induction Motor. In Proceedings of the 2023 IEEE 64th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Online, 9–11 October 2023. [Google Scholar] [CrossRef]
- Sardar, M.U.; Kütt, L.; Kudelina, K. Characterization of High-Frequency Impedance- Based Models for Transient Terminal Overvoltage Estimation in Cable-Fed Motor Drive Systems. In Proceedings of the 2024 International Conference on Electrical Machines (ICEM), Torino, Italy, 1–4 September 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Shabbir, N.; Kütt, L.; Jarkovoi, M.; Iqbal, M.N.; Rassõlkin, A.; Daniel, K. An Overview of Measurement Standards for Power Quality. Agron. Res. 2021, 19, 944–960. [Google Scholar] [CrossRef]
- An, B.; Li, Y.; Liu, F.; Xie, B.; Hu, S.; Wang, P.; Zhang, Z.; Luo, L.; Cao, Y. An Asymmetrical Connection Balance Transformer-Based Hybrid Railway Power Conditioning System with Cost-Function Optimization. IEEE Trans. Transp. Electrif. 2018, 4, 577–590. [Google Scholar] [CrossRef]
- Chen, J.; Hu, H.; Ge, Y.; Wang, K.; He, Z.Y. Techno-Economic Model-Based Capacity Design Approach for Railway Power Conditioner-Based Energy Storage System. IEEE Trans. Ind. Electron. 2022, 69, 4730–4741. [Google Scholar] [CrossRef]
- Davis, E.J.; Emanuel, A.E.; Pileggi, D.J. Closure to Discussion of “Harmonic Pollution Metering: Theoretical Considerations”. IEEE Trans. Power Deliv. 2000, 15, 1353–1354. [Google Scholar] [CrossRef]
- Shabbir, N.; Kütt, L.; Asad, B.; Jawad, M.; Iqbal, M.N.; Daniel, K. Spectrum Analysis for Condition Monitoring and Fault Diagnosis of Ventilation Motor: A Case Study. Energies 2021, 14, 2001. [Google Scholar] [CrossRef]
- Duffey, C.K.; Stratford, R.P. Update of Harmonic Standard IEEE-519—IEEE Recommended Practices and Requirements for Harmonic Control in Electric Power Systems. IEEE Ind. Appl. Soc. 1989, 25, 1618–1624. [Google Scholar] [CrossRef]
- Iqbal, M.N.; Kütt, L.; Daniel, K.; Shabbir, N.; Amjad, A.; Awan, A.W.; Ali, M. Inaccuracies and Uncertainties for Harmonic Estimation in Distribution Networks. Sustainability 2024, 16, 6523. [Google Scholar] [CrossRef]
- Soares, V.; Verdelho, P.; Marques, G.D. An Instantaneous Active and Reactive Current Component Method for Active Filters. IEEE Trans. Power Electron. 2000, 15, 660–669. [Google Scholar] [CrossRef]
- Baccarelli, P.; Burghignoli, P.; Frezza, F.; Galli, A.; Lampariello, P.; Lovat, G.; Paulotto, S.; Member, S.S.; Galli, A.; Lampariello, P.; et al. Fundamental Modal Properties of Surface Waves on Metamaterial Grounded Slabs. IEEE Trans. Microw. Theory Tech. 2005, 53, 1431–1441. [Google Scholar] [CrossRef]
- Moeini, A.; Zhao, H.; Wang, S. A Current-Reference-Based Selective Harmonic Current Mitigation PWM Technique to Improve the Performance of Cascaded H-Bridge Multilevel Active Rectifiers. IEEE Trans. Ind. Electron. 2018, 65, 727–737. [Google Scholar] [CrossRef]
- Wilkinson, W.A.; Cox, M.D. Discrete Wavelet Analysis of Power System Transients. IEEE Trans. Power Syst. 1996, 11, 2038–2044. [Google Scholar] [CrossRef]
- Shabbir, N.; Kutt, L.; Jawad, M.; Iqbal, M.N.; Ghahfarokhi, P.S. Forecasting of Energy Consumption and Production Using Recurrent Neural Networks. Adv. Electr. Electron. Eng. 2020, 18, 190–197. [Google Scholar] [CrossRef]
- Cichocki, A. Artificial Neural Networks for Real-Time Estimation of Basic Waveforms of Voltages and Currents. IEEE Trans. Power Syst. 1994, 9, 612–618. [Google Scholar] [CrossRef]
- Hu, Y.; Zhu, Z.-Q.; Liu, K. Current Control for Dual Three-Phase Permanent Magnet Synchronous Motors Accounting for Current Unbalance and Harmonics. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 272–284. [Google Scholar] [CrossRef]
- Gao, X.; Liao, L.-Z. A New One-Layer Neural Network for Linear and Quadratic Programming. IEEE Trans. Neural Netw. 2010, 21, 918–929. [Google Scholar] [CrossRef]
- Zhu, X.; Shen, C.; Ren, X. Harmonic Detection Method Using APFFT and Neural Network. In Proceedings of the 2013 5th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2013. [Google Scholar] [CrossRef]
- Hu, Y.; Shao, Y.; Yang, R.; Chen, G. Current Harmonic Suppression for Grid-Connected VSG Based on Virtual Harmonic Impedance. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Republic of Korea, 27–30 May 2019; Volume 3, pp. 2022–2026. [Google Scholar] [CrossRef]
- Rong, S.; Xu, M.; Chen, X.; Liu, Z.; Su, H.; Li, H. Research on Optimal Virtual Impedance Harmonic Suppression Method for Grid-Connected Inverter. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 585–591. [Google Scholar] [CrossRef]
- Beres, R.N.; Wang, X.; Liserre, M.; Blaabjerg, F.; Bak, C.L. A Review of Passive Power Filters for Three-Phase Grid-Connected Voltage-Source Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 54–69. [Google Scholar] [CrossRef]
- Dekka, A.R.; Beig, A.R.; Poshtan, M. Comparison of Passive and Active Power Filters in Oil Drilling Rigs. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011; pp. 470–475. [Google Scholar] [CrossRef]
- Shakeri, S.; Esmaeili, S.; Hossein, M.; Koochi, R. Passive Harmonic Filter Design Considering Voltage Sag Performance-Applicable to Large Industries. IEEE Trans. Power Deliv. 2022, 37, 1714–1722. [Google Scholar] [CrossRef]
- Rizk, G.; Salameh, S.; Kanaan, H.Y.; Rachid, E.A. Design of Passive Power Filters for a Three-Phase Semi-Controlled Rectifier with Typical Loads. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; pp. 590–595. [Google Scholar] [CrossRef]
- Kedra, B. Comparison of an Active and Hybrid Power Filter Devices. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 556–560. [Google Scholar] [CrossRef]
- Alhuwaishel, F.M.; Morsy, A.S.; Enjeti, P.N. A New Active Output Filter (AOF) for Variable Speed Constant Frequency (VSCF) Power System in Aerospace Applications. IEEE Trans. Power Electron. 2018, 33, 1087–1093. [Google Scholar] [CrossRef]
- Wang, L.; Lam, C.S.; Wong, M.C. Unbalanced Control Strategy for a Thyristor-Controlled LC-Coupling Hybrid Active Power Filter in Three-Phase Three-Wire Systems. IEEE Trans. Power Electron. 2017, 32, 1056–1069. [Google Scholar] [CrossRef]
- Grady, W.M.; Samotyj, M.J.; Noyola, A.H. Survey of Active Power Line Conditioning Mehtodologies. IEEE Trans. Power Deliv. 1990, 5, 1536–1542. [Google Scholar] [CrossRef]
- El-Habrouk, M.; Darwish, M.K.; Mehta, P. Active Power Filters: A Review. IEEE Proc. Electric Power Appl. 2000, 147, 403–413. [Google Scholar] [CrossRef]
- Xie, N.; Xu, Q.; Zeng, J.; Liu, X.; Zhang, W.; Zhang, C. Noval Hybrid Control Method for APF Based on PI and FRC. J. Eng. 2019, 2019, 3002–3006. [Google Scholar] [CrossRef]
- Kim, S.; Enjeti, P.N. A New Hybrid Active Power Filter (APF) Topology. IEEE Trans. Power Electron. 2002, 17, 48–54. [Google Scholar] [CrossRef]
- Chen, Z.; Blaabjerg, F.; Pedersen, J.K. A Hybrid Compensation System with an Active Filter and Distributed Passive Filters in Power Systems with Dispersed Generation. In Proceedings of the IEEE 34th Annual Conference on Power Electronics Specialist, Acapulco, Mexico, 15–19 June 2003; Volume 2, pp. 767–772. [Google Scholar] [CrossRef]
- Peng, F.Z.; Akagi, H.; Nabae, A. A New Approach to Harmonic Compensation in Power Systems A Combined System of Shunt Passive and Series Active Filters. IEEE Trans. Ind. Appl. 1990, 26, 983–989. [Google Scholar] [CrossRef]
- Chen, Z.; Geng, X.; Yin, F. A Harmonic Suppression Method Based on Fractional Lower Order Statistics for Power System. IEEE Trans. Ind. Electron. 2016, 63, 3745–3755. [Google Scholar] [CrossRef]
- Chan, K. Technical and Performance Aspects of a Dynamic Voltage Restorer. In Proceedings of the IEE Half Day Colloquium on Dynamic Voltage Restorers—Replacing Those Missing Cycles (Digest No. 1998/189), Glasgow, UK, 11 February 1998. [Google Scholar] [CrossRef]
- Tu, C.; Guo, Q.; Jiang, F.; Chen, C.; Li, X.; Xiao, F.; Gao, J. Dynamic Voltage Restorer With an Improved Strategy to Voltage Sag Compensation and Energy Self-Recovery. CPSS Trans. Power Electron. Appl. 2019, 4, 219–229. [Google Scholar] [CrossRef]
- Daniel, K.; Kütt, L.; Iqbal, M.N.; Shabbir, N.; Ur Rehman, A.; Shafiq, M.; Hamam, H. Current Harmonic Aggregation Cases for Contemporary Loads. Energies 2022, 15, 437. [Google Scholar] [CrossRef]
- Medeiros, F.; Brasil, D.C.; Marques, C.A.G.; Duque, C.A.; Ribeiro, P.F. Considerations on the Aggregation of Harmonics Produced by Large Wind Farms. In Proceedings of the 2012 IEEE 15th International Conference on Harmonics and Quality of Power, Hong Kong, China, 17–20 June 2012; pp. 364–369. [Google Scholar] [CrossRef]
- IEC 61400-21-1:2019; Wind Energy Generation Systems: Measurement & Electrical Characteristics—Wind Turbines. IEC International Electrotechnical Commission: Geneva, Switzerland, 2019.
- David, J.; Robinson, D.; Elphick, S. Aggregation of Multiple Inverter-Based Harmonic Sources within a Renewable Energy Generation Plant. In Proceedings of the 2022 20th International Conference on Harmonics & Quality of Power (ICHQP), Naples, Italy, 29 May–1 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Collin, A.J.; Cresswell, C.E.; Djokić, S.Ž. Harmonic Cancellation of Modern Switch-Mode Power Supply Load. In Proceedings of the 14th International Conference on Harmonics and Quality of Power—ICHQP 2010, Bergamo, Italy, 26–29 September 2010. [Google Scholar] [CrossRef]
- Larose, C.; Gagnon, R.; Prud’Homme, P.; Fecteau, M.; Asmine, M. Type-III Wind Power Plant Harmonic Emissions: Field Measurements and Aggregation Guidelines for Adequate Representation of Harmonics. IEEE Trans. Sustain. Energy 2013, 4, 797–804. [Google Scholar] [CrossRef]
- Yang, K.; Bollen, M.H.J.; Larsson, E.O.A. Wind Power Harmonic Aggregation of Multiple Turbines in Power Bins. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 723–727. [Google Scholar] [CrossRef]
- Blanco, A.M.; Meyer, J.; Schegner, P. Aggregation Characteristic of Low-Order Harmonic Currents in Residential Low-Voltage Networks. In Proceedings of the 2017 IEEE Manchester PowerTech, Powertech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Blanco, A.M.; Yanchenko, S.; Meyer, J.; Schegner, P. The Impact of Supply Voltage Distortion on the Harmonic Current Emission of Non-Linear Loads. DYNA 2015, 82, 150–159. [Google Scholar] [CrossRef]
- Iqbal, M.N.N.; Lauri, K.; Kütt, L.; Asad, B.; Shabbir, N. Impact of Cable Impedance on the Harmonic Emission of LED Lamps. In Proceedings of the 2020 21st International Scientific Conference on Electric Power Engineering (EPE), Prague, Czech Republic, 19–21 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Naveed Iqbal, M.; Jarkovoi, M.; Kutt, L.; Shabbir, N. Impact of LED Thermal Stability to Household Lighting Harmonic Load Current Modeling. In Proceedings of the 2019 Electric Power Quality and Supply Reliability Conference (PQ) & 2019 Symposium on Electrical Engineering and Mechatronics (SEEM), Kärdla, Estonia, 12–15 June 2019. [Google Scholar] [CrossRef]
- Jarkovoi, M.; Naveed Iqbal, M.; Kutt, L. Analysis of Harmonic Current Stability and Summation of LED Lamps. In Proceedings of the 2019 Electric Power Quality and Supply Reliability Conference (PQ) & 2019 Symposium on Electrical Engineering and Mechatronics (SEEM), Kärdla, Estonia, 12–15 June 2019; pp. 1–8. [Google Scholar] [CrossRef]
- IEC 61000-4-30; 2003 Electromagnetic Compatibility (EMC) Part 4-30: Testing and Measurement Techniques Power Quality Measurement Methods. IEC International Electrotechnical Commission: Geneva, Switzerland, 2003.
- Peterson, B.; Blanco, A.M.; Rens, J.; Meyer, J.; Botha, G.; Desmet, J. Impact of Aggregation Interval on Harmonic Phase Angle Measurements. In Proceedings of the 2018 IEEE 9th International Workshop on Applied Measurements for Power Systems (AMPS), Bologna, Italy, 26–28 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Foskolos, G.; Lundengard, K. The Impact of Aggregation Interval on Current Harmonic Simulation of Aggregated Electric Vehicle Loads. In Proceedings of the 2020 19th International Conference on Harmonics and Quality of Power (ICHQP), Dubai, United Arab Emirates, 6–7 July 2020. [Google Scholar] [CrossRef]
- Lennerhag, O.; Bollen, M.H.J. A Stochastic Aggregate Harmonic Load Model. IEEE Trans. Power Deliv. 2020, 35, 2127–2135. [Google Scholar] [CrossRef]
- Trelles-Molina, D.; Rosado-Romero, R.A.; Ortuno-Gonzalez, D.A.; Fernandez, E. Extension on IEC 61000-3-6’s General Summation Law to Estimate Harmonic Current at PCC Based on Probability Distribution. IEEE Lett. Electromagn. Compat. Pract. Appl. 2022, 4, 36–39. [Google Scholar] [CrossRef]
- Morfi, V.; Degottex, G.; Mouchtaris, A. A Computationally Efficient Refinement of the Fundamental Frequency Estimate for the Adaptive Harmonic Model. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 1478–1482. [Google Scholar] [CrossRef]
- Olga, P.; Alexey, P.; Natalia, S. Application of Parametric DFT in Cepstral Method for Scales Bases Identification. In Proceedings of the 2020 22th International Conference on Digital Signal Processing and its Applications (DSPA), Moscow, Russia, 25–27 March 2020. [Google Scholar] [CrossRef]
- Taghvaie, A.; Warnakulasuriya, T.; Kumar, D.; Zare, F.; Sharma, R.; Vilathgamuwa, D.M. A Comprehensive Review of Harmonic Issues and Estimation Techniques in Power System Networks Based on Traditional and Artificial Intelligence/Machine Learning. IEEE Access 2023, 11, 31417–31442. [Google Scholar] [CrossRef]
- de Oliveira, R.A.; Bollen, M.H.J. Deep Learning for Power Quality. Electr. Power Syst. Res. 2023, 214, 108887. [Google Scholar] [CrossRef]
- Lobos, T.; Leonowicz, Z.; Rezmer, J. Harmonics and Interharmonics Estimation Using Advanced Signal Processing Methods. In Proceedings of the Ninth International Conference on Harmonics and Quality of Power. Proceedings (Cat. No.00EX441), Orlando, FL, USA, 1–4 October 2000; Volume 1, pp. 335–340. [Google Scholar] [CrossRef]
- Yu, K.K.C.; Watson, N.R.; Arrillaga, J. An Adaptive Kalman Filter for Dynamic Harmonic State Estimation and Harmonic Injection Tracking. IEEE Trans. Power Deliv. 2005, 20, 1577–1584. [Google Scholar] [CrossRef]
- Wu, C.; Magaña, M.E.; Cotilla-Sánchez, E. Dynamic Frequency and Amplitude Estimation for Three-Phase Unbalanced Power Systems Using the Unscented Kalman Filter. IEEE Trans. Instrum. Meas. 2019, 68, 3387–3395. [Google Scholar] [CrossRef]
- Zhou, N.; Wang, J.; Wang, Q.; Wei, N. Measurement-Based Harmonic Modeling of an Electric Vehicle Charging Station Using a Three-Phase Uncontrolled Rectifier. IEEE Trans. Smart Grid 2015, 6, 1332–1340. [Google Scholar] [CrossRef]
- Rodriguez Maldonado, J. Total Harmonic Distortion Estimation, Minimization Inter Harmonic Amplitude and Expanding Bands Rejection in TKF Filters. IEEE Lat. Am. Trans. 2016, 14, 652–656. [Google Scholar] [CrossRef]
- Sezgin, E.; Göl, M.; Salor, Ö. State-Estimation-Based Determination of Harmonic Current Contributions of Iron and Steel Plants Supplied from PCC. IEEE Trans. Ind. Appl. 2016, 52, 2654–2663. [Google Scholar] [CrossRef]
- Dai, Z.; Lin, W.; Lin, H. Estimation of Single-Phase Grid Voltage Parameters with Zero Steady-State Error. IEEE Trans. Power Electron. 2016, 31, 3867–3879. [Google Scholar] [CrossRef]
- Dai, Z.; Lin, W. Adaptive Estimation of Three-Phase Grid Voltage Parameters under Unbalanced Faults and Harmonic Disturbances. IEEE Trans. Power Electron. 2017, 32, 5613–5627. [Google Scholar] [CrossRef]
- Carta, D.; Muscas, C.; Pegoraro, P.A.; Sulis, S. Identification and Estimation of Harmonic Sources Based on Compressive Sensing. IEEE Trans. Instrum. Meas. 2019, 68, 95–104. [Google Scholar] [CrossRef]
- Esparza, M.; Segundo, J.; Gurrola-Corral, C.; Visairo-Cruz, N.; Barcenas, E.; Barocio, E. Parameter Estimation of a Grid-Connected VSC Using the Extended Harmonic Domain. IEEE Trans. Ind. Electron. 2019, 66, 6044–6054. [Google Scholar] [CrossRef]
- Dobrovolný, P.; Vandersteen, G.; Wambacq, P.; Donnay, S. Analysis and Compact Behavioral Modeling of Nonlinear Distortion in Analog Communication Circuits. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2003, 22, 1215–1227. [Google Scholar] [CrossRef]
- Baxevanakis, D.; Sotiriadis, P.P. A General Time-Domain Method for Harmonic Distortion Estimation in CMOS Circuits. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2021, 40, 157–170. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; De La O Serna, J.A. Dynamic Phasor and Frequency Estimates through Maximally Flat Differentiators. IEEE Trans. Instrum. Meas. 2010, 59, 1803–1811. [Google Scholar] [CrossRef]
- Zecevic, Z.; Krstajic, B. Dynamic Harmonic Phasor Estimation by Adaptive Taylor-Based Bandpass Filter. IEEE Trans. Instrum. Meas. 2021, 70, 6500509. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Wang, Q.; Wang, F.; Huang, S. Dynamic Harmonic Synchrophasor Estimator Based on Sinc Interpolation Functions. IEEE Trans. Instrum. Meas. 2019, 68, 3054–3065. [Google Scholar] [CrossRef]
- Xiao, X.; Li, Z.; Wang, Y.; Zhou, Y. A Practical Approach to Estimate Harmonic Distortions in Residential Distribution System. IEEE Trans. Power Deliv. 2021, 36, 1418–1427. [Google Scholar] [CrossRef]
- Son, K.J.; An, G.S.; Nam, K.D.; Chang, T.G. An Advanced Frequency Estimation Algorithm Based on Analytic Compensation of Effects of Dominant Harmonic in Power Systems. IEEE Access 2021, 9, 146568–146577. [Google Scholar] [CrossRef]
- Yaghoobi, J.; Zare, F.; Rehman, T.; Rathnayake, H. Analysis of High Frequency Harmonics in Distribution Networks: 9-150 KHz. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, VIC, Australia, 13–15 February 2019; pp. 1229–1234. [Google Scholar] [CrossRef]
- Rathnayake, H.; Khajeh, K.G.; Zare, F.; Sharma, R. Harmonic Analysis of Grid-Tied Active Front End Inverters for the Frequency Range of 0-9 Khz in Distribution Networks: Addressing Future Regulations. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, VIC, Australia, 13–15 February 2019; pp. 446–451. [Google Scholar] [CrossRef]
- Moradi, A.; Yaghoobi, J.; Zare, F. A Precise Model of DC-Link Current in Adjustable Speed Drives for the Harmonic Analysis of Electrical Networks. IEEE Access 2022, 10, 45663–45676. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, G.; Xu, W.; Mayordomo, J.G. A Harmonically Coupled Admittance Matrix Model for AC/DC Converters. IEEE Trans. Power Syst. 2007, 22, 1574–1582. [Google Scholar] [CrossRef]
- Savoor, R.; Meier-Hellstern, K. Estimating the Frequency Coupling Matrix From Network Measurements. IEEE Trans. Control Netw. Syst. 2020, 7, 353–388. [Google Scholar] [CrossRef]
- Yadav, J.; Vasudevan, K.; Meyer, J.; Kumar, D. Frequency Coupling Matrix Model of a Three-Phase Variable Frequency Drive. IEEE Trans. Ind. Appl. 2022, 58, 3652–3663. [Google Scholar] [CrossRef]
- Daniel, K.; Kütt, L.; Iqbal, M.N.; Shabbir, N.; Parker, M.; Jarkovoi, M. Waveform Variation Defined Model for Harmonic Current Emissions Including Cross-Order Supply Voltage Harmonics Influence. IEEE Access 2023, 11, 42276–42289. [Google Scholar] [CrossRef]
- Yi, C.; Wang, H.; Zhou, Q.; Hu, Q.; Zhou, P.; Lin, J. An Adaptive Harmonic Product Spectrum for Rotating Machinery Fault Diagnosis. IEEE Trans. Instrum. Meas. 2023, 72, 3500612. [Google Scholar]
- Bi, G.; Zhang, G.; Wang, G.; Wang, Q.; Hu, Y.; Xu, D. Adaptive Iterative Learning Control-Based Rotor Position Harmonic Error Suppression Method for Sensorless PMSM Drives. IEEE Trans. Ind. Electron. 2022, 69, 10870–10881. [Google Scholar] [CrossRef]
- Sun, W.; So, H.C.; Chen, Y.; Huang, L.T.; Huang, L. Approximate Subspace-Based Iterative Adaptive Approach for Fast Two-Dimensional Spectral Estimation. IEEE Trans. Signal Process. 2014, 62, 3220–3231. [Google Scholar] [CrossRef]
- Iqbal, M.N.; Kütt, L.; Daniel, K.; Jarkovoi, M.; Asad, B.; Shabbir, N. Bivariate Stochastic Model of Current Harmonic Analysis in the Low Voltage Distribution Grid. Proc. Est. Acad. Sci. 2021, 70, 190–206. [Google Scholar] [CrossRef]
- Iqbal, M.N.; Kutt, L.; Shabbir, N.; Asad, B. Comparison of Current Harmonic Emission by Different Lighting Technologies. In Proceedings of the 2020 IEEE 61th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 5–7 November 2020; pp. 1–5. [Google Scholar] [CrossRef]


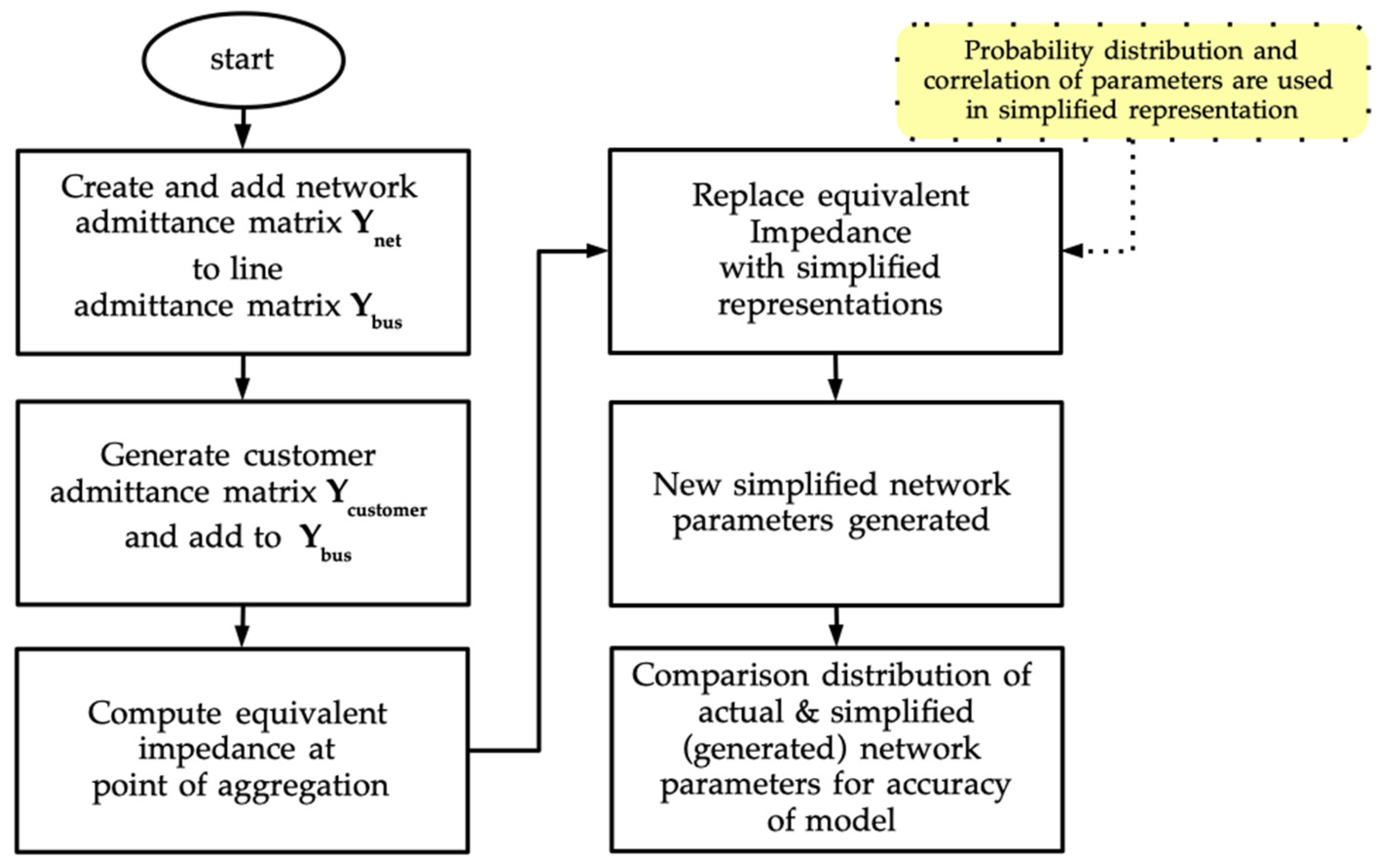
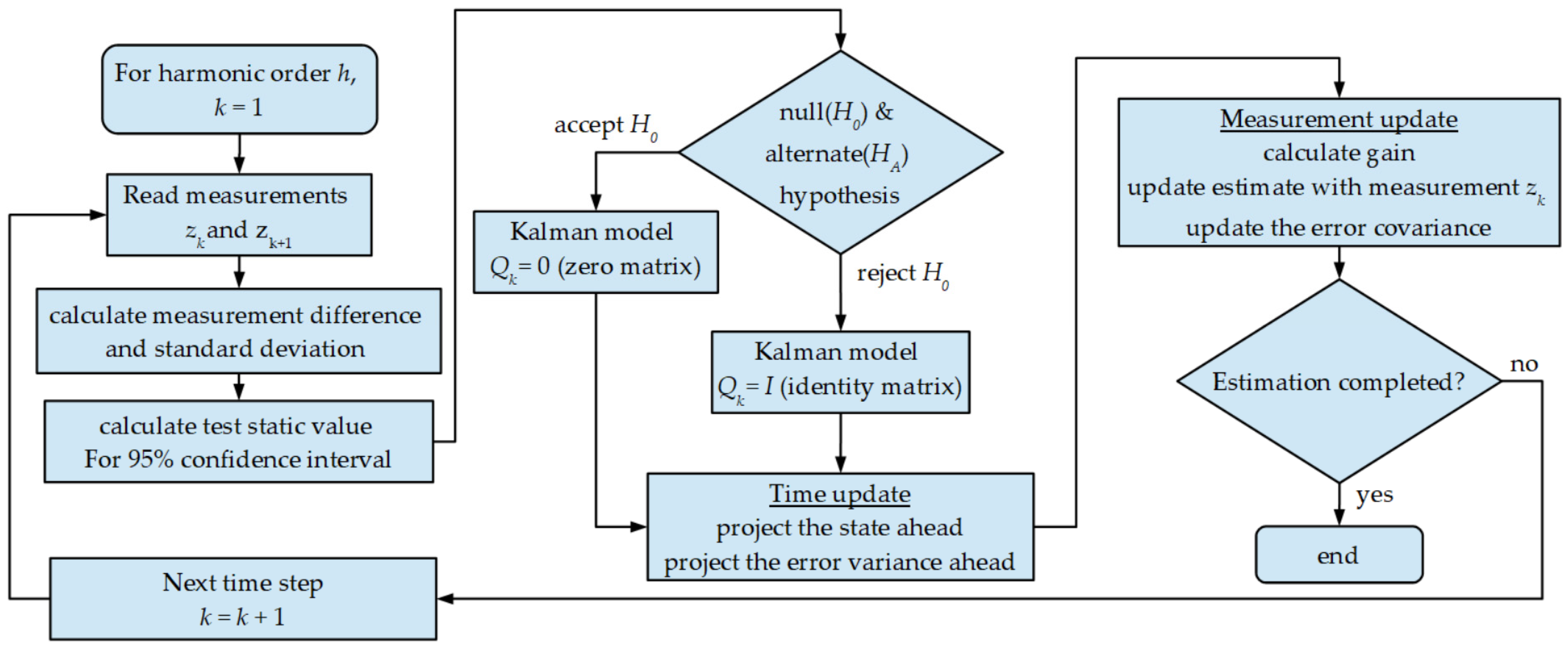

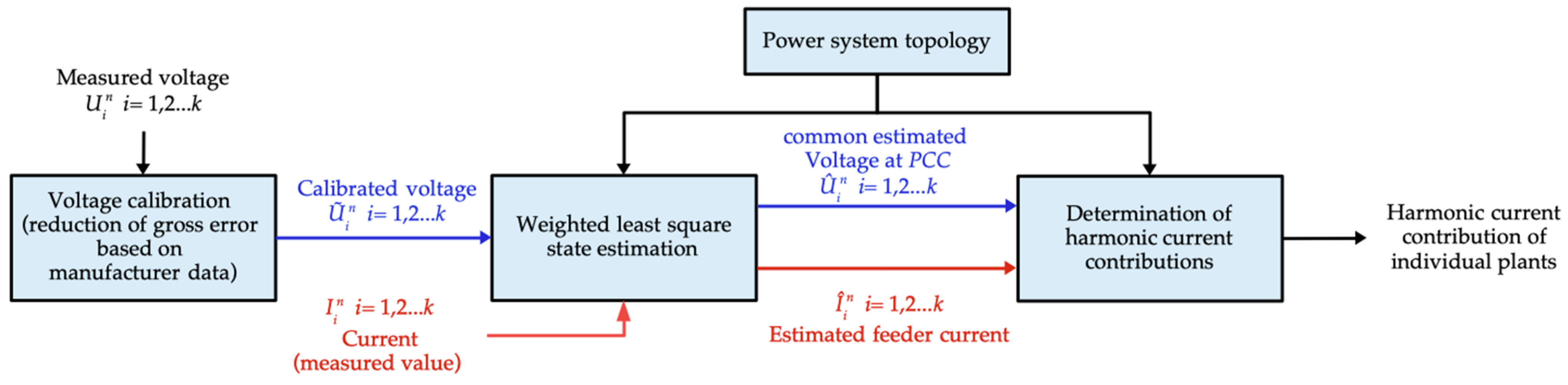
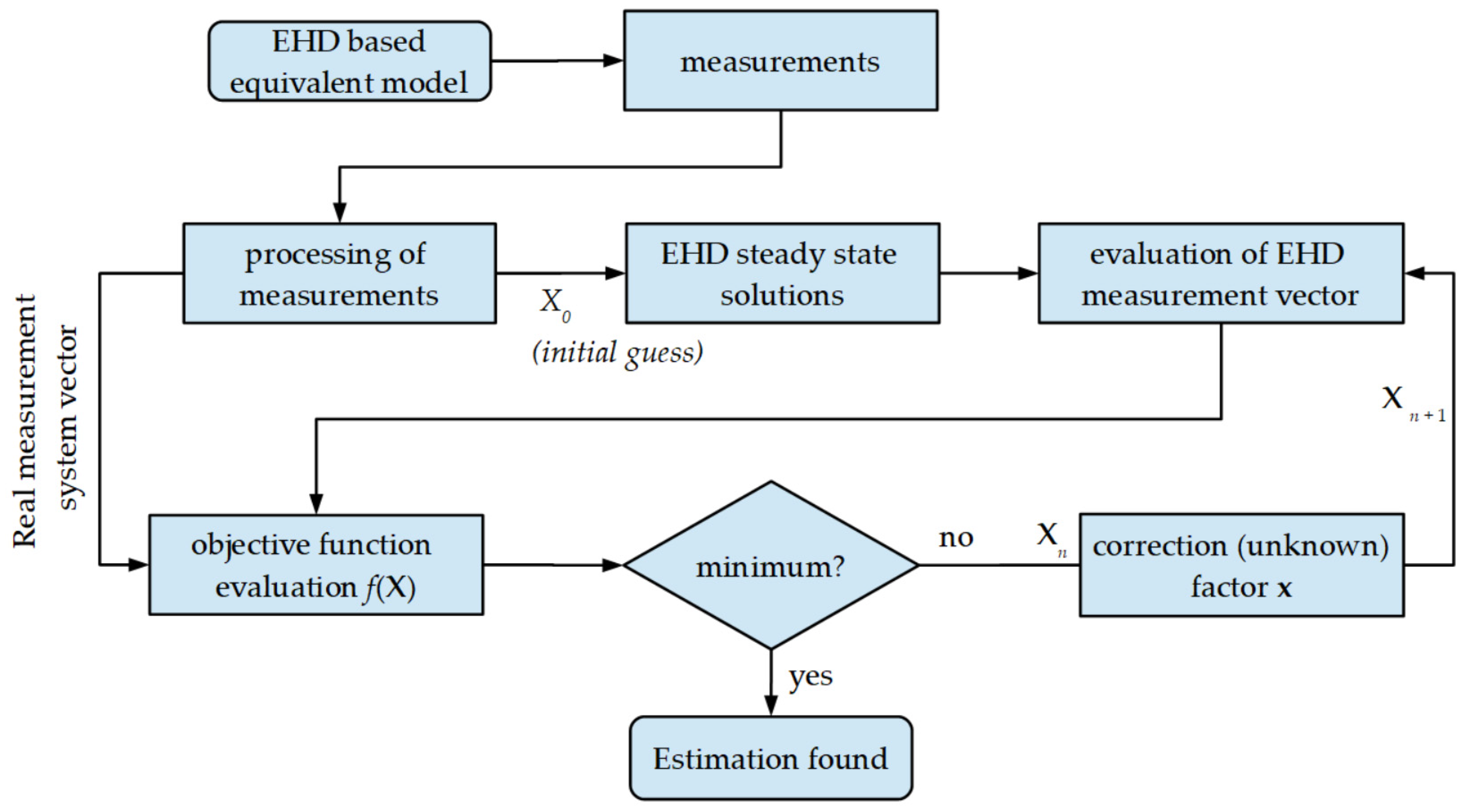
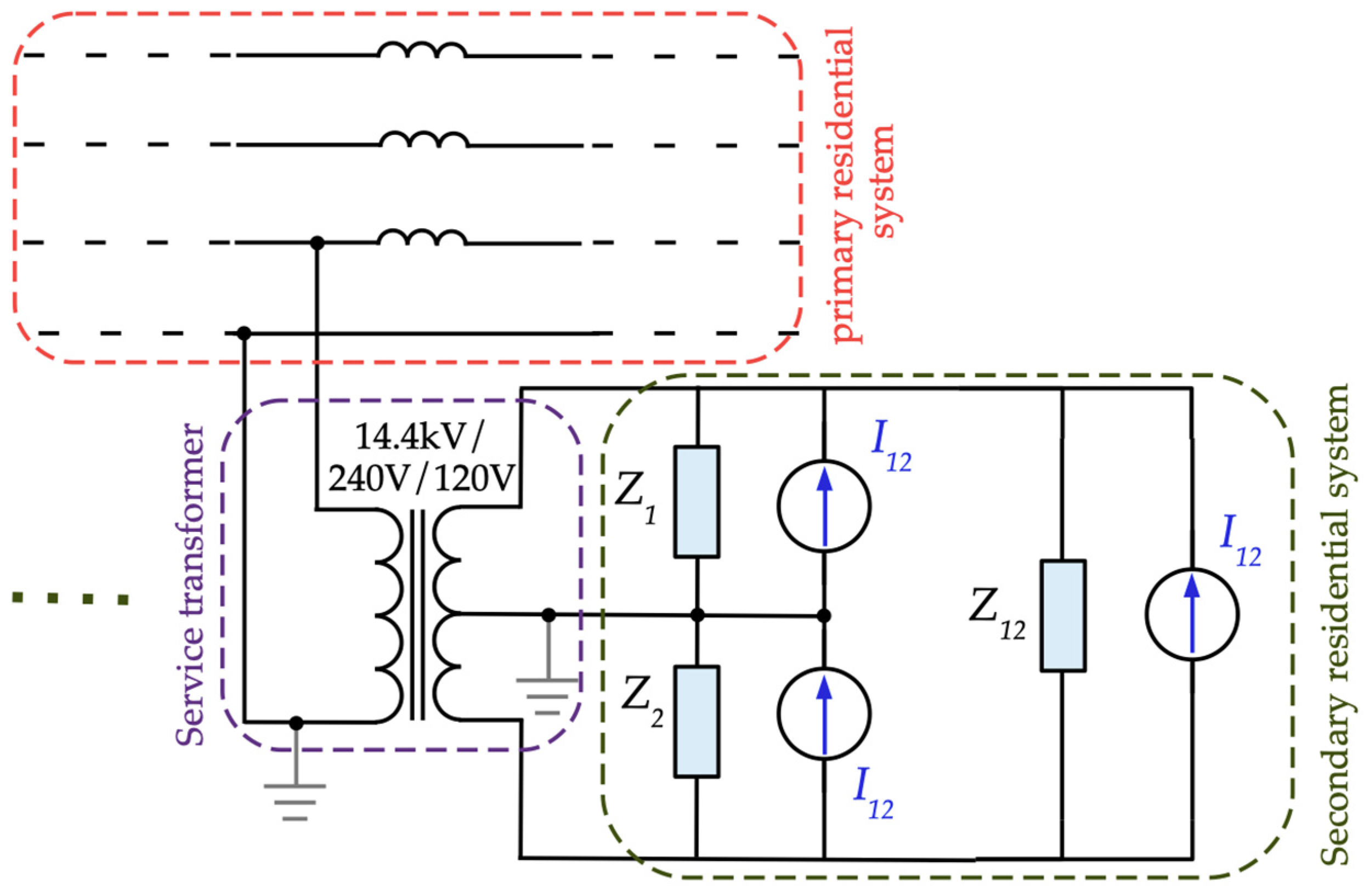
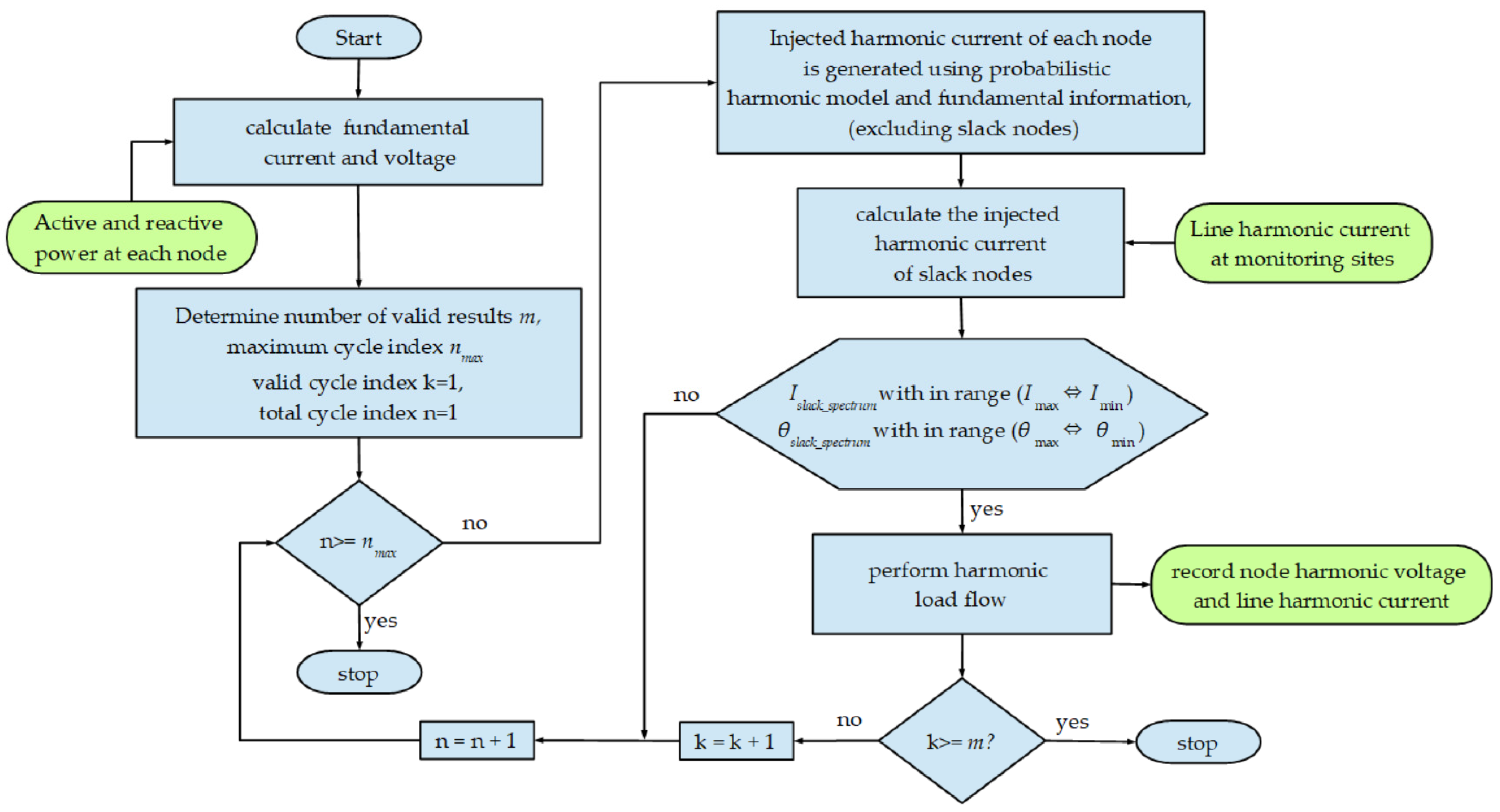

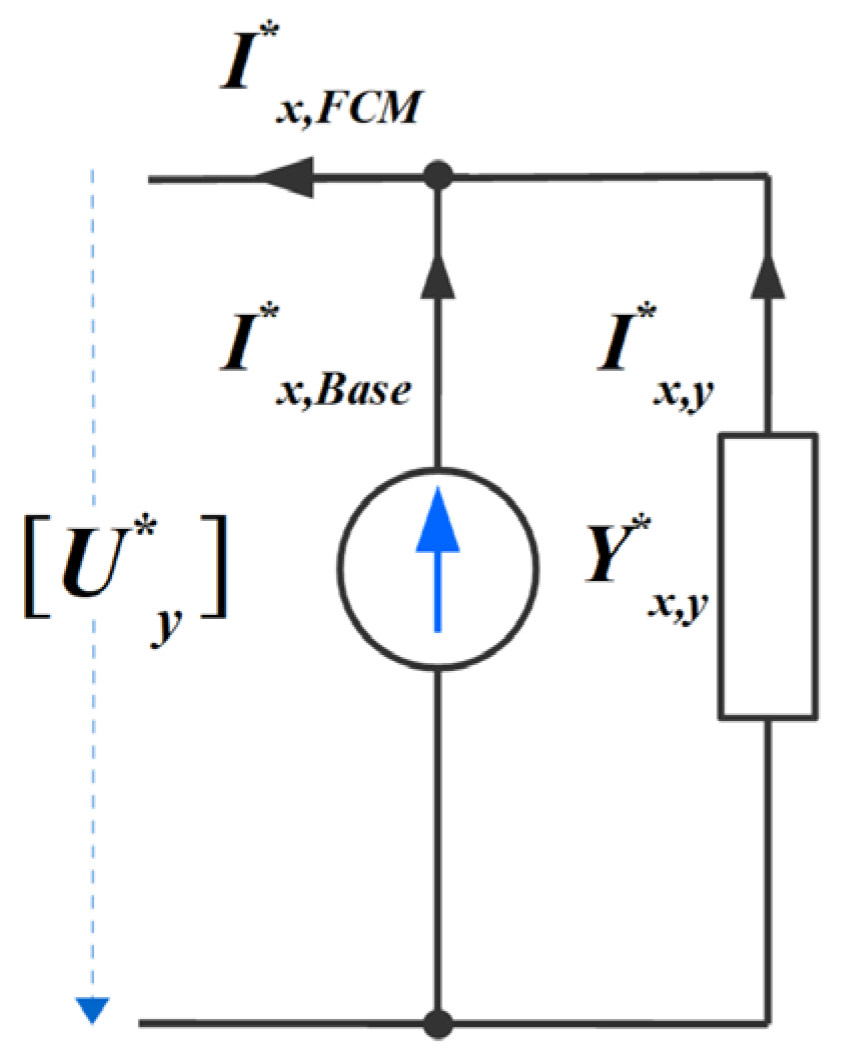

| Method | Ref. | Advantage | Disadvantage | Applications |
|---|---|---|---|---|
| Fourier Transform | [13,14] | Widely used, decomposes signals into frequencies | Not suitable for time-varying or non-stationary signals | Power systems with steady-state harmonics |
| Wavelet Transform | [13,19] | Analyzes non-stationary signals, time-varying frequency | Complex, spectrum leakage, band aliasing | Dynamic systems, transient analysis |
| Adaptive Detection Method | [16,17,18] | Independent of component parameters, high accuracy | Complex parameter adjustment, dependent on circuit components | Detection in variable grid voltage |
| Neural Network-Based Method | [20,21,22,23,24] | Adaptive, can learn from data | Computationally intensive, requires large datasets | Advanced AI-driven detection models |
| Method | Ref. | Advantage | Disadvantage | Applications |
|---|---|---|---|---|
| Passive Filters | [27,28,29,30] | Low-cost, simple implementation | Performance affected by system frequency changes | Common in industrial power systems |
| Active Power Filters (APF) | [31,32,33,34,35] | Suppresses dynamic harmonics, compensates reactive power | High hardware cost, complex circuit design | High-performance grid systems |
| Hybrid Filters (Passive + Active PF) | [36,37,38,39] | Balances cost and performance | Slight impact on device capacity | Modern power systems with budget constraints |
| Dynamic Voltage Restorer (DVR) | [41,42] | Compensates for voltage sags/swells, mitigates harmonic distortion | Expensive and complex | Grid systems with voltage fluctuation issues |
| Method | Ref. | Advantage | Disadvantage | Applications |
|---|---|---|---|---|
| Arithmetic Summation | [54] | Simple to implement | Does not account for phase variations | Harmonic assessment in simple systems |
| Monte Carlo Simulation | [50] | Accounts for randomness and variability | Computationally intensive | Large-scale harmonic studies, renewable energy integration |
| IEC 61400-Series Methodology | [55,56,57,58,59] | Widely adopted standard | Induces errors in summation | Wind farms and renewable energy grid integration |
| Machine Learning Approaches | [62,63] | High accuracy, can adapt to complex systems | Requires training, computationally intensive | Advanced grid systems with variable sources |
| Method | Ref. | Advantage | Disadvantage | Applications |
|---|---|---|---|---|
| Prony Method | [64] | Accurate in estimating harmonic parameters, effective in noisy environments | Requires high computational resources, not efficient for real-time use | Harmonic estimation in industrial converters |
| Min-Norm Method | [64] | Provides better accuracy than Fourier in some cases | Limited by its dependence on frequency precision | Harmonic detection in systems with precise frequency requirements |
| Adaptive Kalman Filter (AKF) | [65] | Adaptive, handles dynamic harmonic states, noise covariance is dynamic | Complex, high computational cost, can estimate limited harmonics | Dynamic systems with fluctuating grid voltage and harmonic distortion |
| Unscented Kalman Filter (UKF) | [66] | High accuracy in tracking grid waveform changes, handles frequency and amplitude variations. | Limited harmonic estimation capacity, computationally expensive | Unbalanced three-phase power systems with dynamic harmonic content |
| State-Estimation-Based Method | [69] | Eliminates need for expensive equipment, accurate even without synchronized measurements | May struggle with high-frequency harmonics, complex model tuning | Large-scale industrial power systems like iron and steel plants |
| Compressive Sensing Harmonics Detector (CSHD) | [72] | Efficient, reduces the number of necessary measurements | May be less effective in high variability environments | Identifying and estimating principal pollution sources in distribution grids |
| Taylor–Kalman–Fourier (TKF) Filter | [68] | Reduces total harmonic distortion (THD), accurate with dynamic components | Complexity in implementation, sensitive to tuning parameters | Estimating dynamic harmonic content in power systems |
| Flat-Top FIR Filter (Harmonic Phasor Estimation) | [76] | Accurate under nominal frequency conditions, computationally efficient | May produce errors under frequency deviations | Embedded systems with fixed harmonic frequencies |
| Time-Domain Harmonic Distortion Estimation | [75] | Compact modeling of harmonic distortion in circuits | Limited to specific circuit types | Estimating harmonic distortion in CMOS circuits |
| Dynamic Harmonic Phasor Estimation (HPE) | [81] | High accuracy with harmonic modulation, zero-error under nominal conditions | Complex mathematical modeling, limited flexibility | Systems with variable harmonic frequencies, improving estimation accuracy |
| Norton Coupled Model | [91] | Effective for estimating harmonics in nonlinear loads | Requires detailed component-level data | Nonlinear loads in distribution networks |
| Frequency Coupling Matrix (FCM) Model | [84,85,86] | Can estimate harmonic currents and voltages in complex systems, includes harmonic interactions | Sensitive to variations in grid impedance, complex parameter tuning | Harmonic analysis in AC/DC converters and multi-frequency grid systems |
| Fourier-based Estimation | [92] | Widely used, fast computations | Inaccurate for non-stationary signals | Stationary power systems with constant harmonics |
| Waveform Variation Defined Model (WVDM) | [87] | Models cross-order supply voltage harmonics influence, precise with low-order harmonics | Complex to implement, requires empirical validation | Estimating harmonic current emissions in residential systems |
| Harmonic Product Spectrum (HPS), Harmonic Sum Spectrum (HSS) | [88,89] | Simple to implement, computationally efficient | Sensitive to noise and distortions | Used in signal processing where speed is prioritized |
| Iterative Adaptive Harmonic Estimation (IAHE) | [89,90] | More accurate in noisy/distorted environments, robust in challenging conditions | Computationally intensive, more complex to implement | Suitable for accurate harmonic estimation in noisy conditions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daniel, K.; Kütt, L.; Iqbal, M.N.; Shabbir, N.; Raja, H.A.; Sardar, M.U. A Review of Harmonic Detection, Suppression, Aggregation, and Estimation Techniques. Appl. Sci. 2024, 14, 10966. https://doi.org/10.3390/app142310966
Daniel K, Kütt L, Iqbal MN, Shabbir N, Raja HA, Sardar MU. A Review of Harmonic Detection, Suppression, Aggregation, and Estimation Techniques. Applied Sciences. 2024; 14(23):10966. https://doi.org/10.3390/app142310966
Chicago/Turabian StyleDaniel, Kamran, Lauri Kütt, Muhammad Naveed Iqbal, Noman Shabbir, Hadi Ashraf Raja, and Muhammad Usman Sardar. 2024. "A Review of Harmonic Detection, Suppression, Aggregation, and Estimation Techniques" Applied Sciences 14, no. 23: 10966. https://doi.org/10.3390/app142310966
APA StyleDaniel, K., Kütt, L., Iqbal, M. N., Shabbir, N., Raja, H. A., & Sardar, M. U. (2024). A Review of Harmonic Detection, Suppression, Aggregation, and Estimation Techniques. Applied Sciences, 14(23), 10966. https://doi.org/10.3390/app142310966










