Experimental and Numerical Investigations of Flat Approach Slab–Soil Interaction in Jointless Bridge
Abstract
:1. Introduction
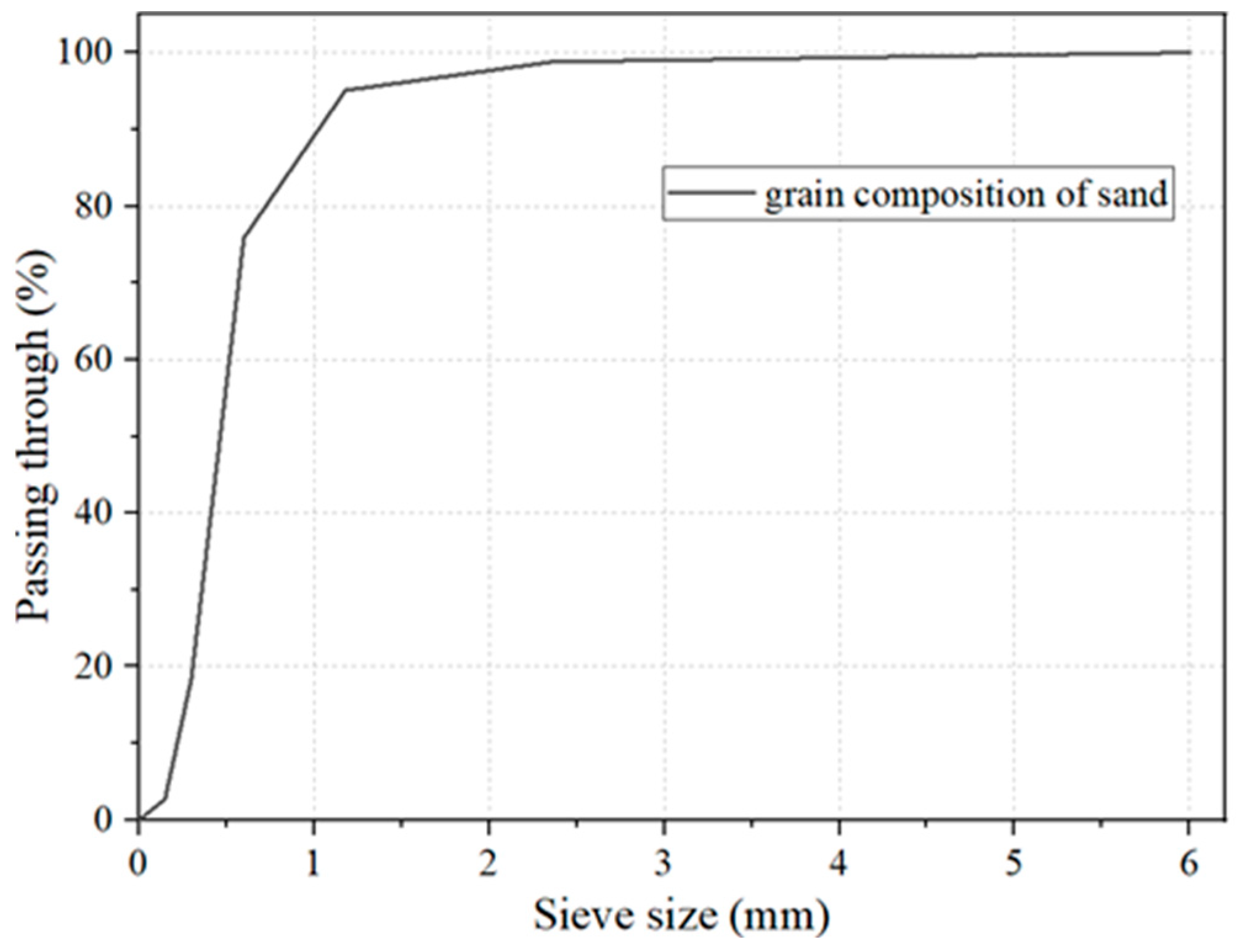
2. Experimental Test
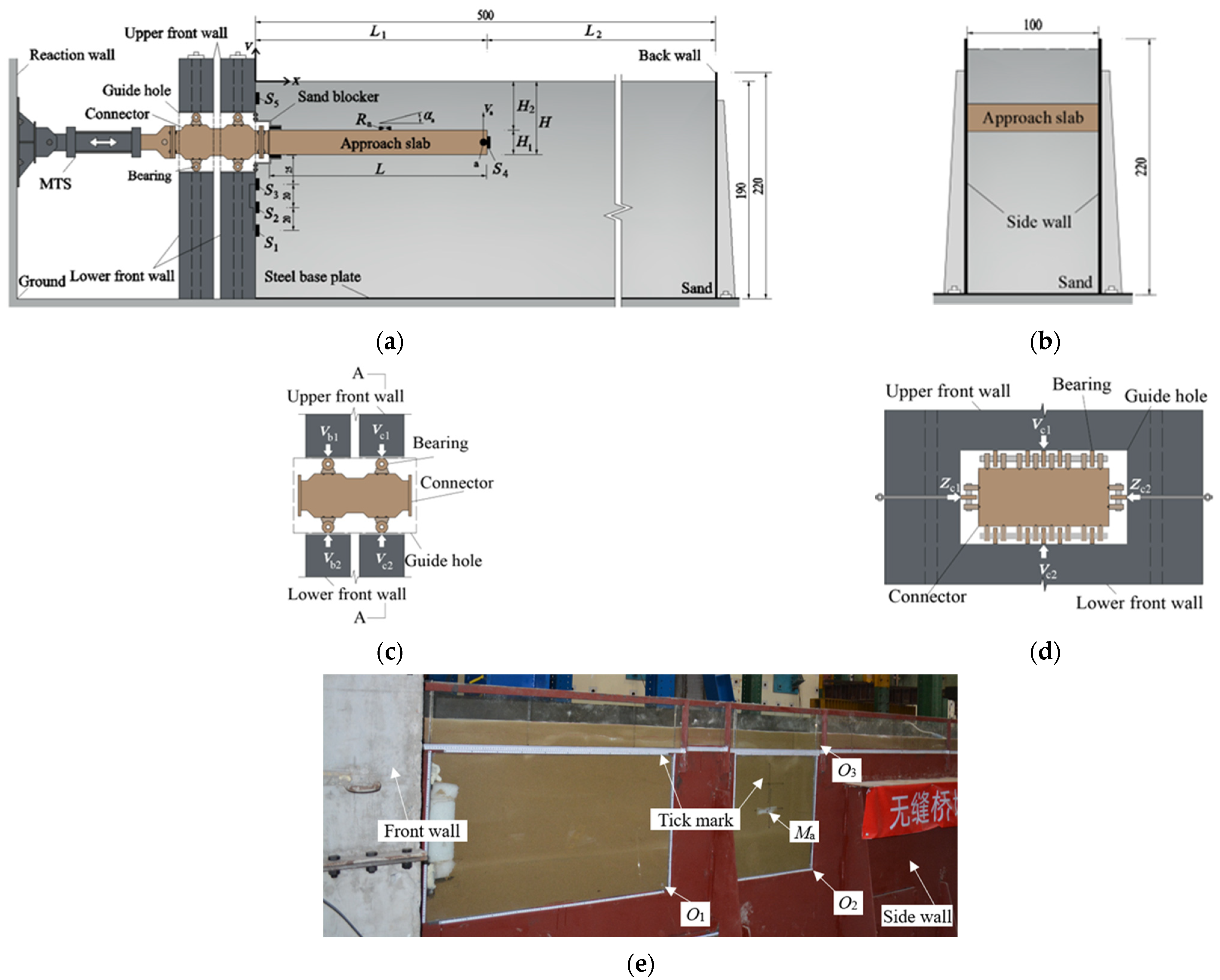
2.1. Specimen Design and Fabrication
2.2. Soil Container Design and Fabrication
2.3. Test Cases and Set-Up
2.4. Instrument Setup
2.5. Experimental Results
2.5.1. Specimen Movement
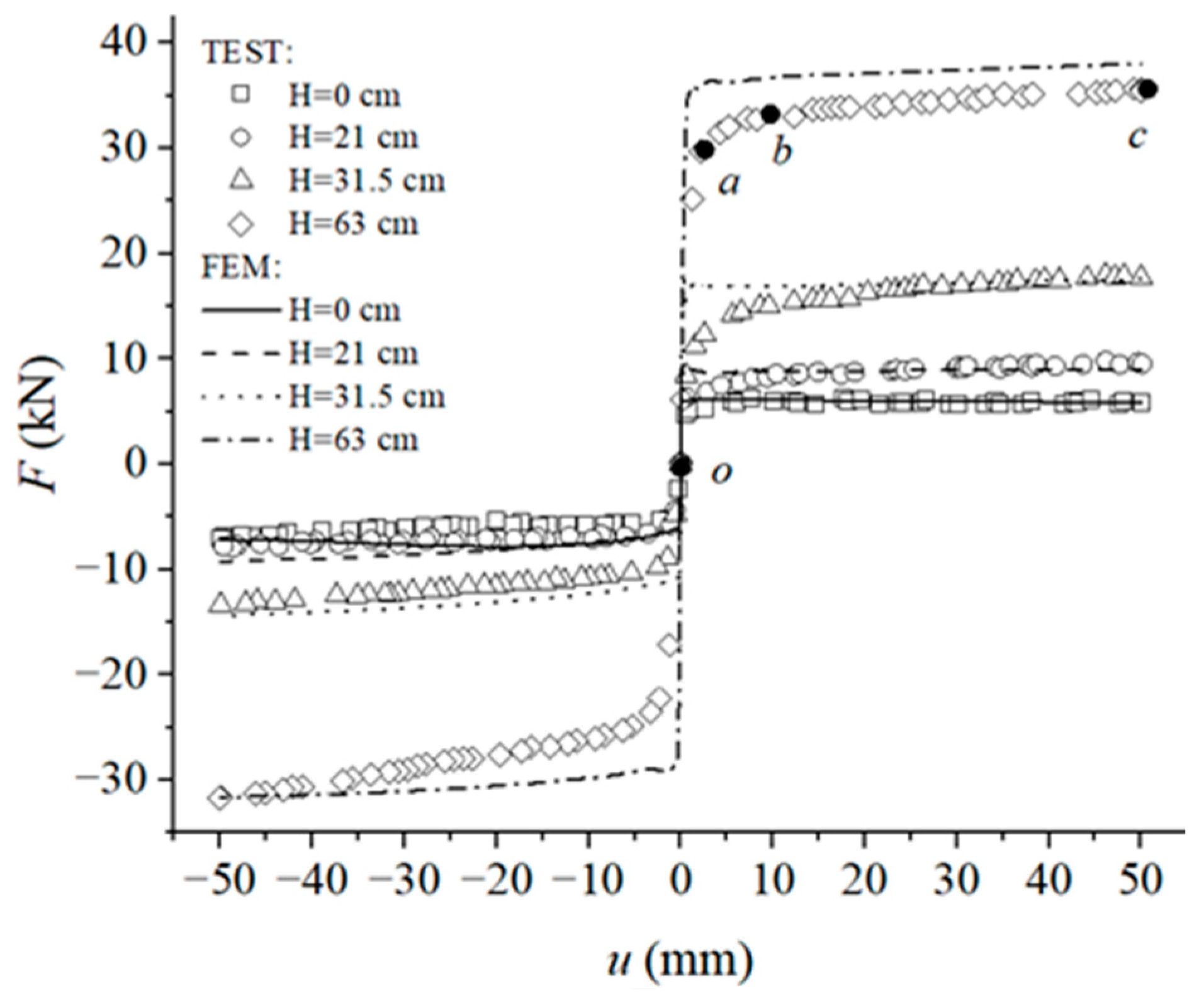
2.5.2. Load–Displacement Curve
- Elastic stage oa: when u is less than ua, F and u exhibit a linear relationship. The sand is in an elastic state, and the stiffness of the curve is k.
- Elastoplastic stage ab: when u is between ua and ub, the internal stress of the sand is redistributed, and some soil particles slip relatively. The sand enters a plastic state, and the k gradually decreases.
- Failure stage bc: when u is larger than ub, the sand in the plastic state gradually forms a slip surface. With a rapid increase in u, F increases slightly. The stiffness of the curve decreases to l. The value of Fu at point c is the ultimate load.
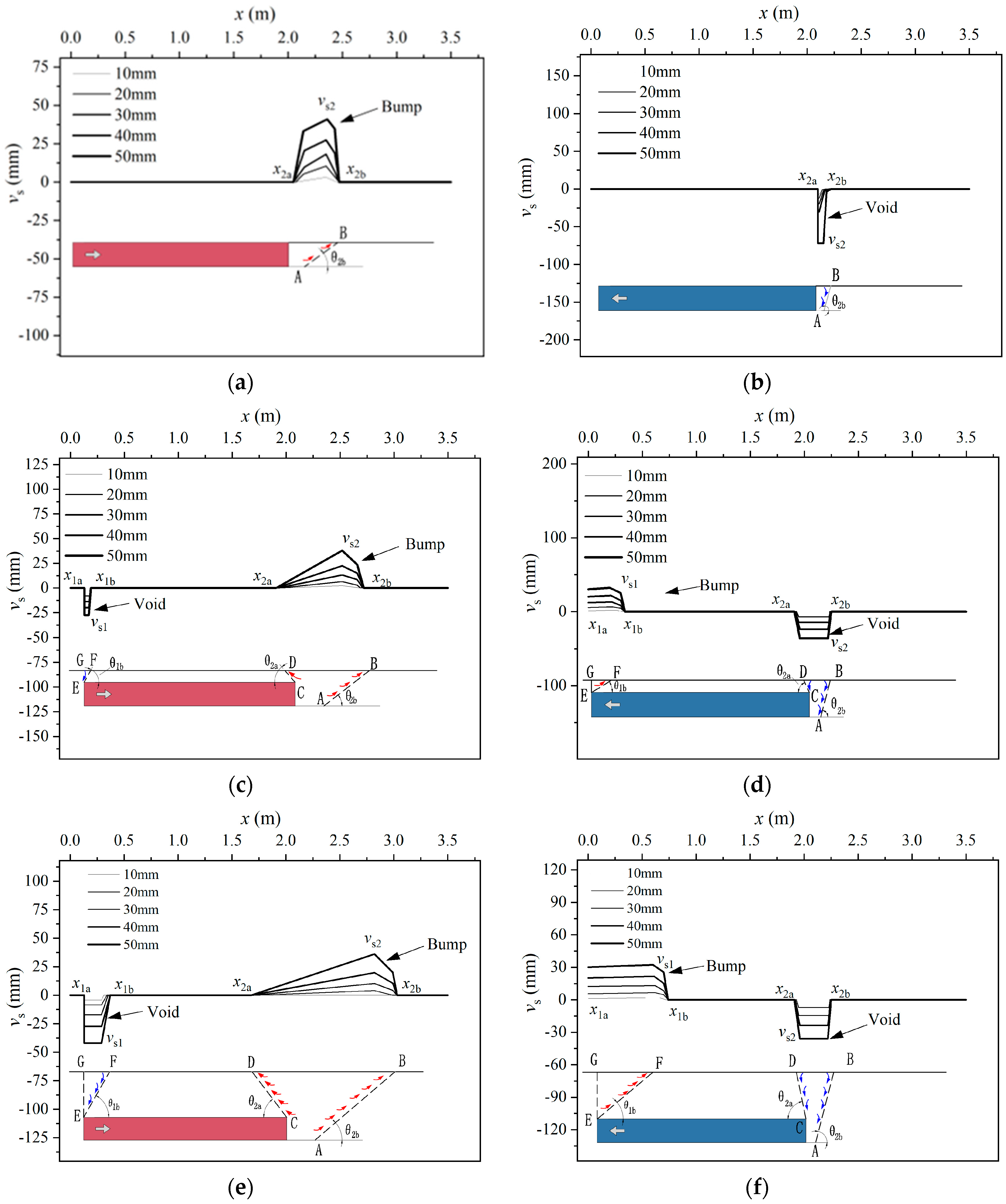
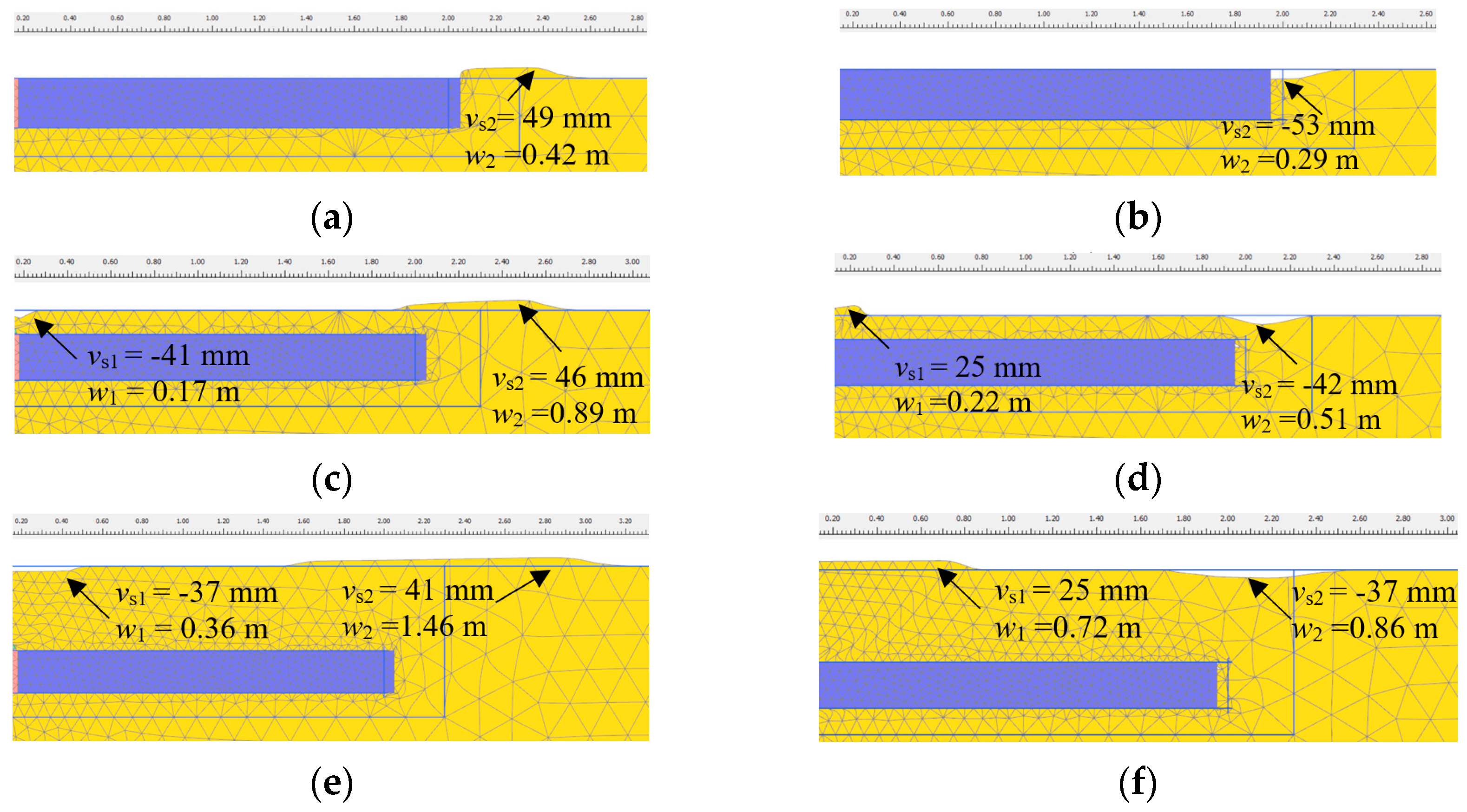
2.5.3. Sand Deformation
- Elastic stage
- Elastoplastic stage
- Failure stage
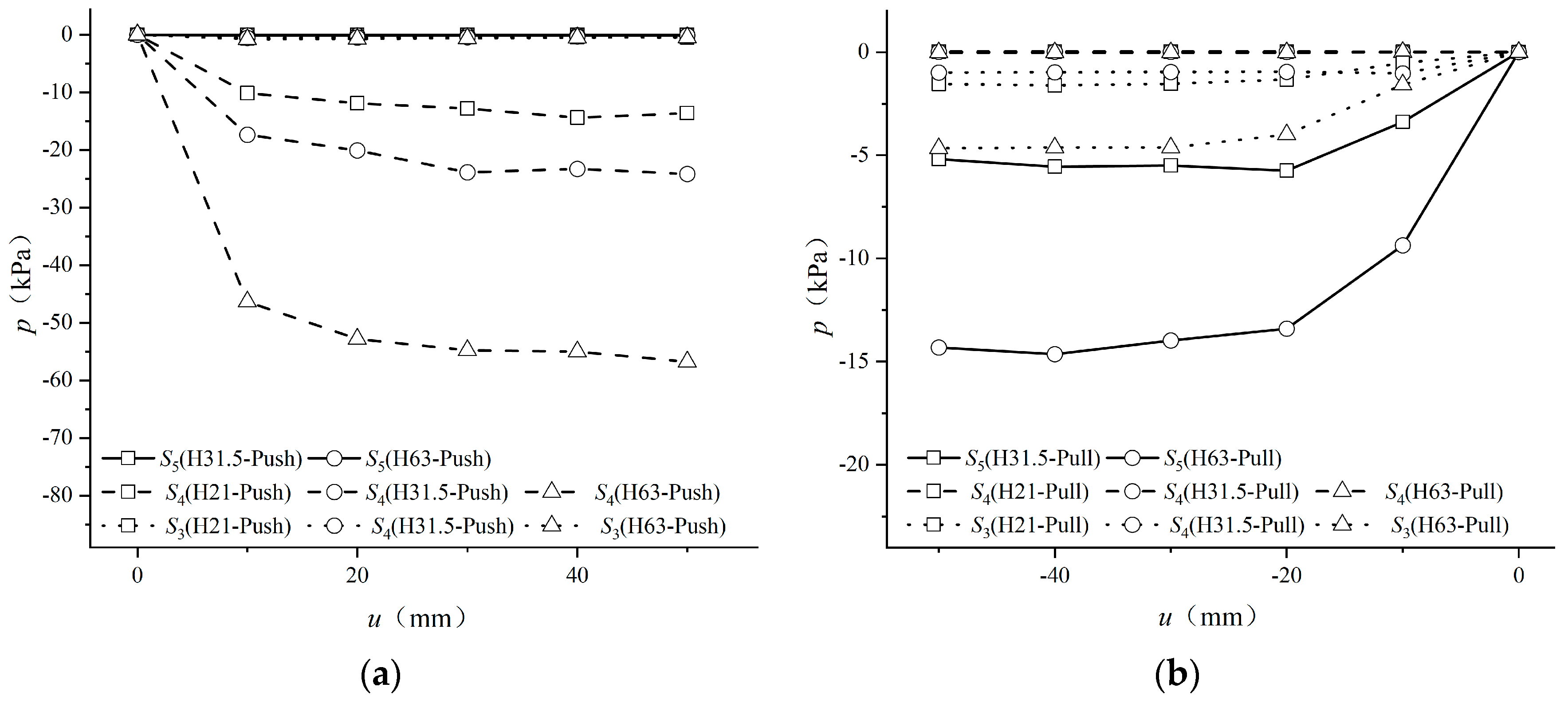
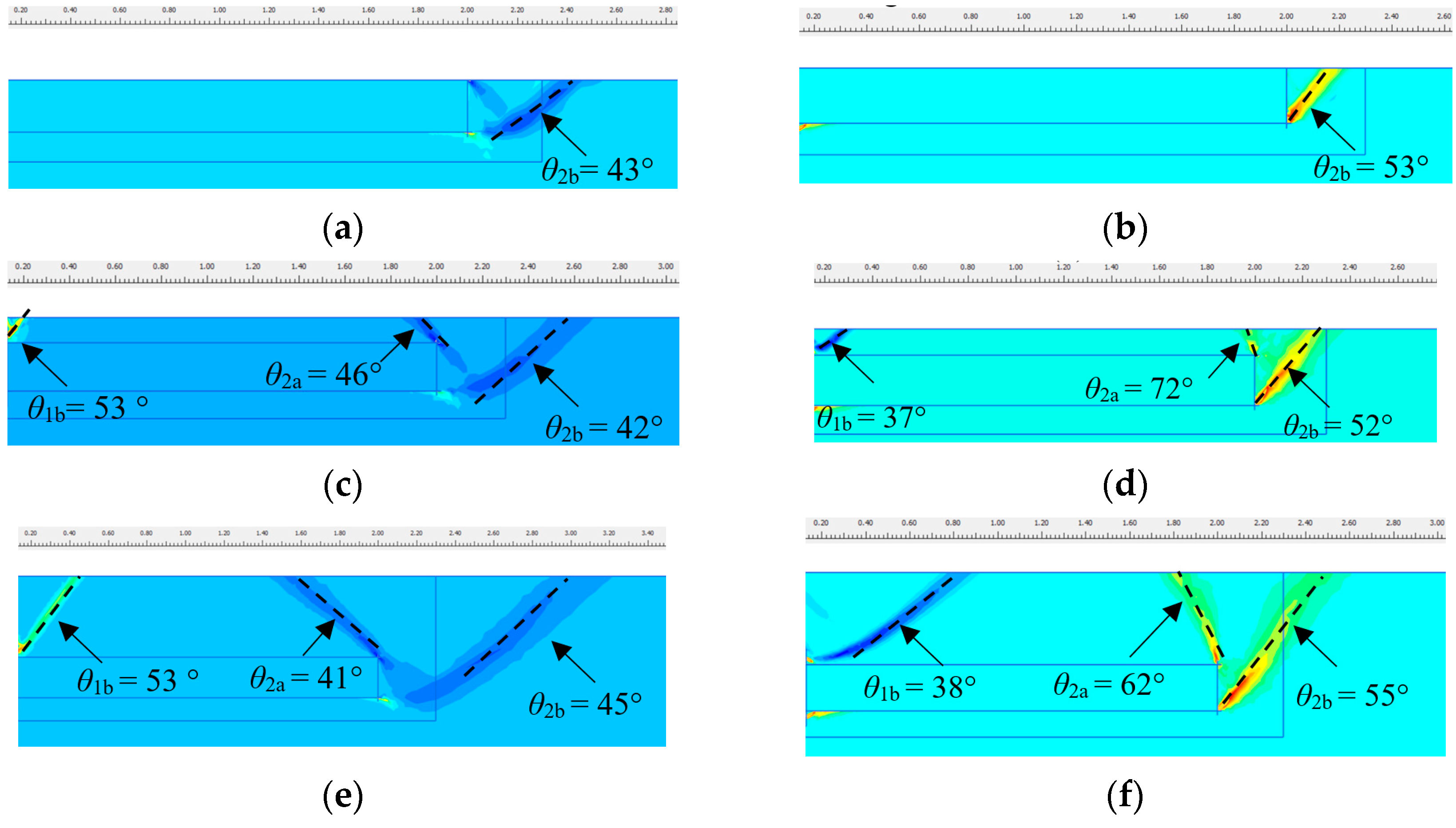
2.5.4. Earth Pressure
3. Finite Element Simulation and Verification
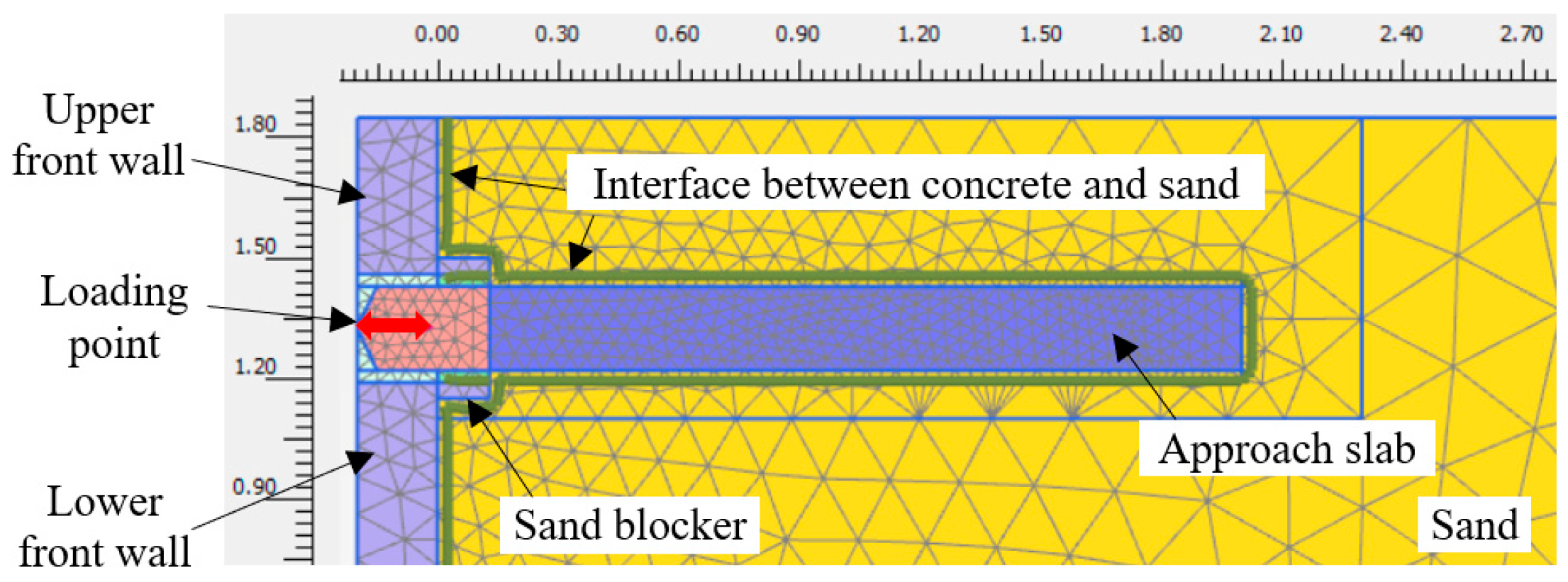
3.1. Finite Element Model Simulation
3.1.1. Model Introduction
3.1.2. Material Properties
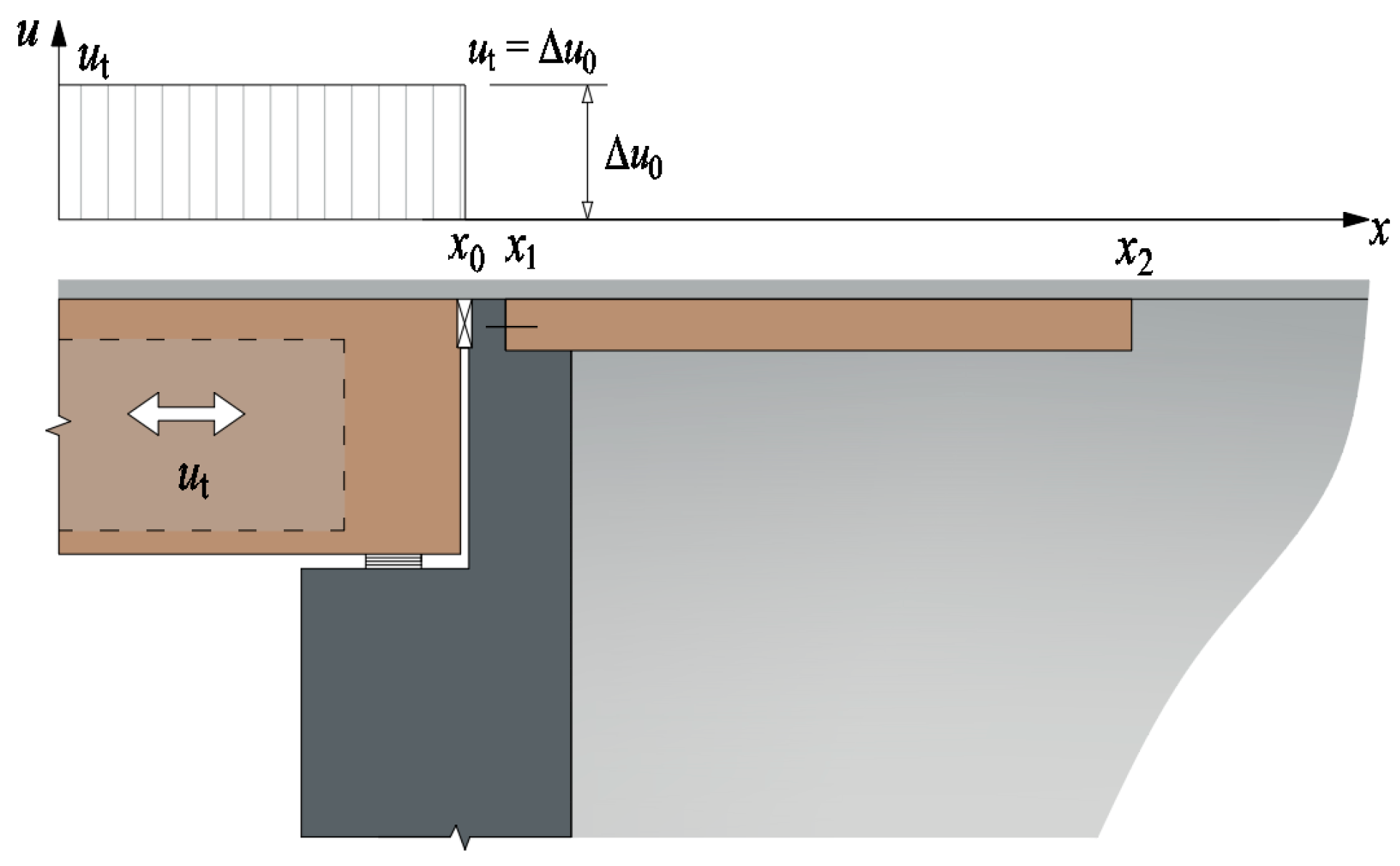
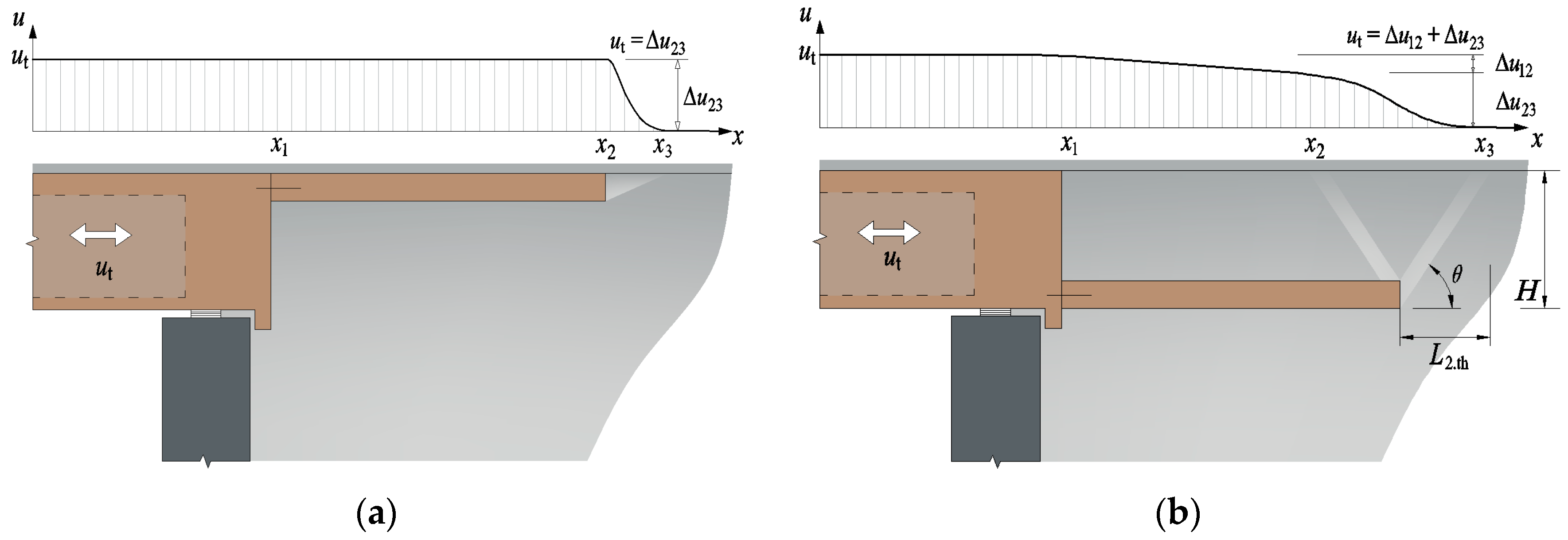
3.1.3. Boundary Conditions
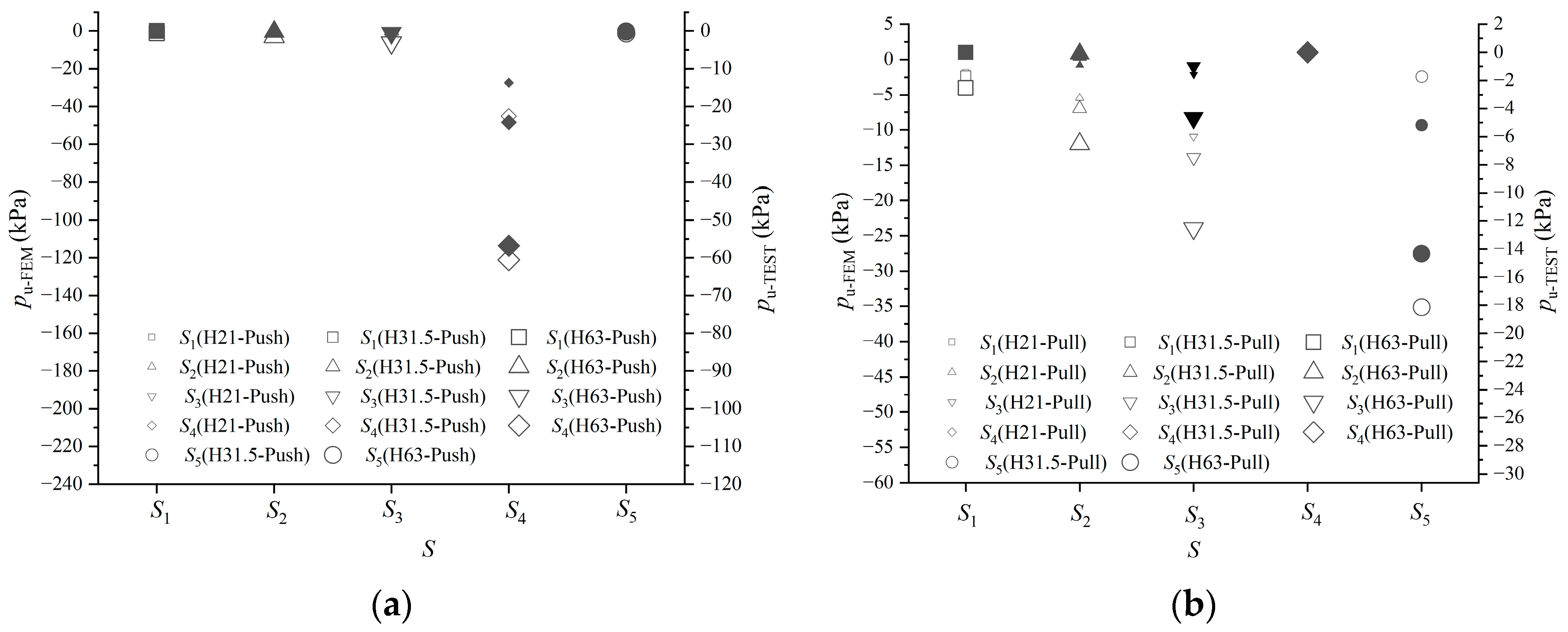
3.2. Finite Element Model Verification
3.2.1. Specimen Movement
3.2.2. Load–Displacement Curve
3.2.3. Sand Deformation
3.2.4. Earth Pressure
4. Mechanism Analysis of FASSI
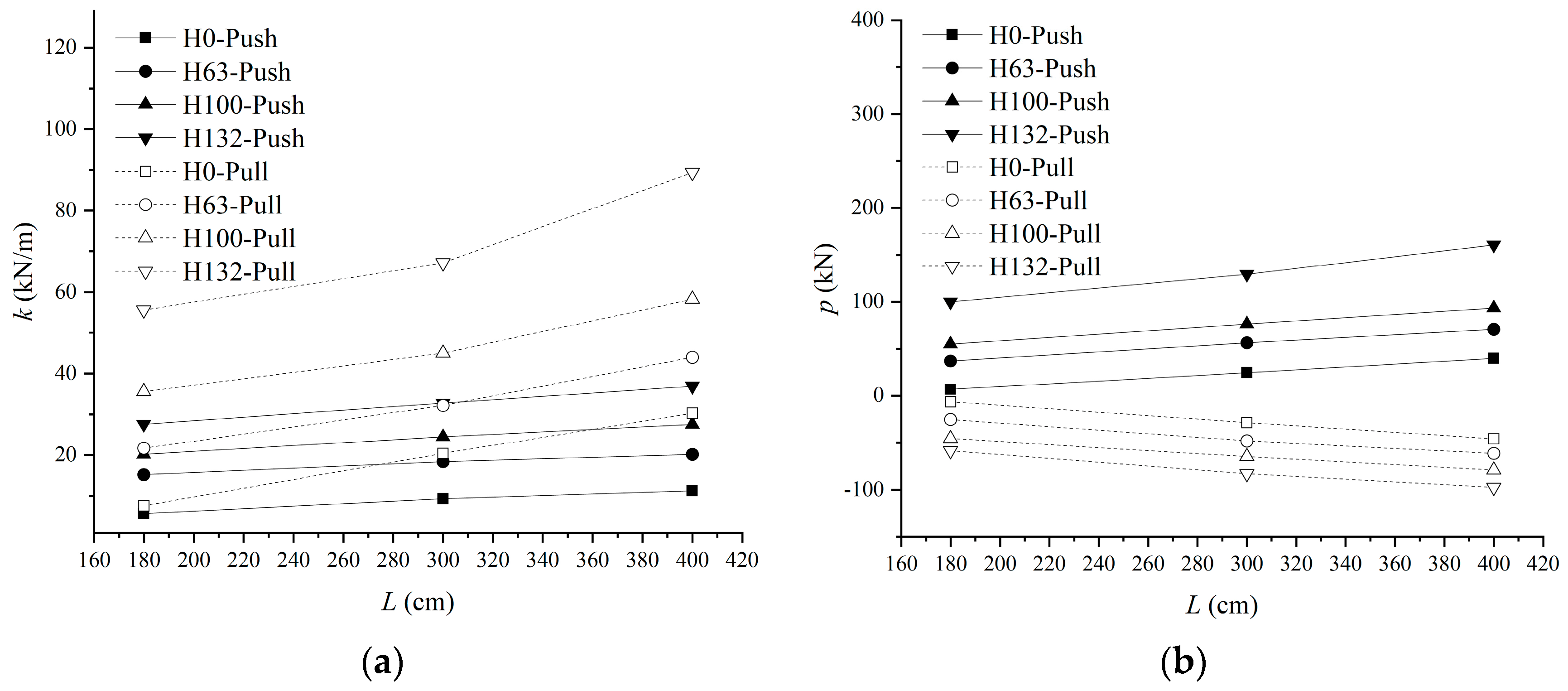
4.1. Parametric Analysis
4.2. Load–Displacement Curve
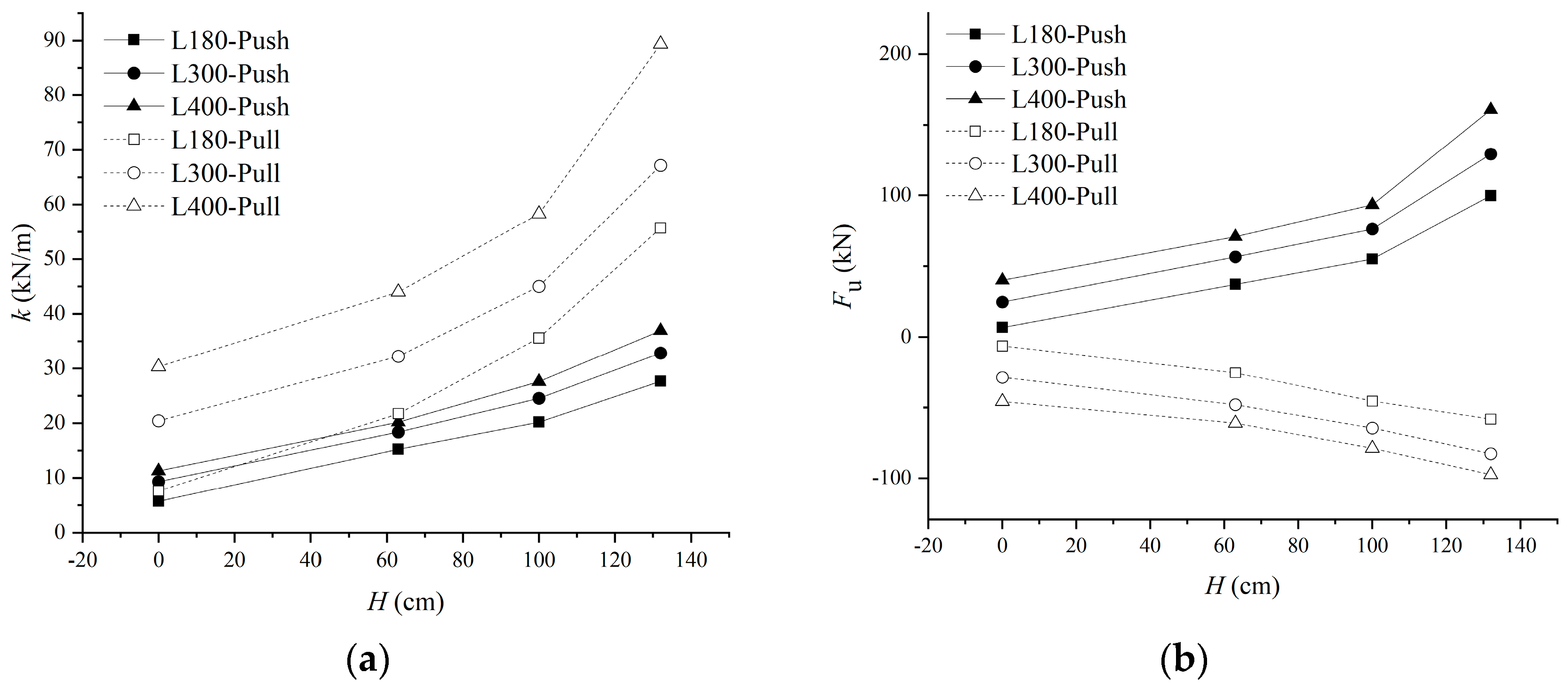
4.2.1. Influence of Embedded Depth
4.2.2. Influence of Slab Length
4.3. Sand Deformation
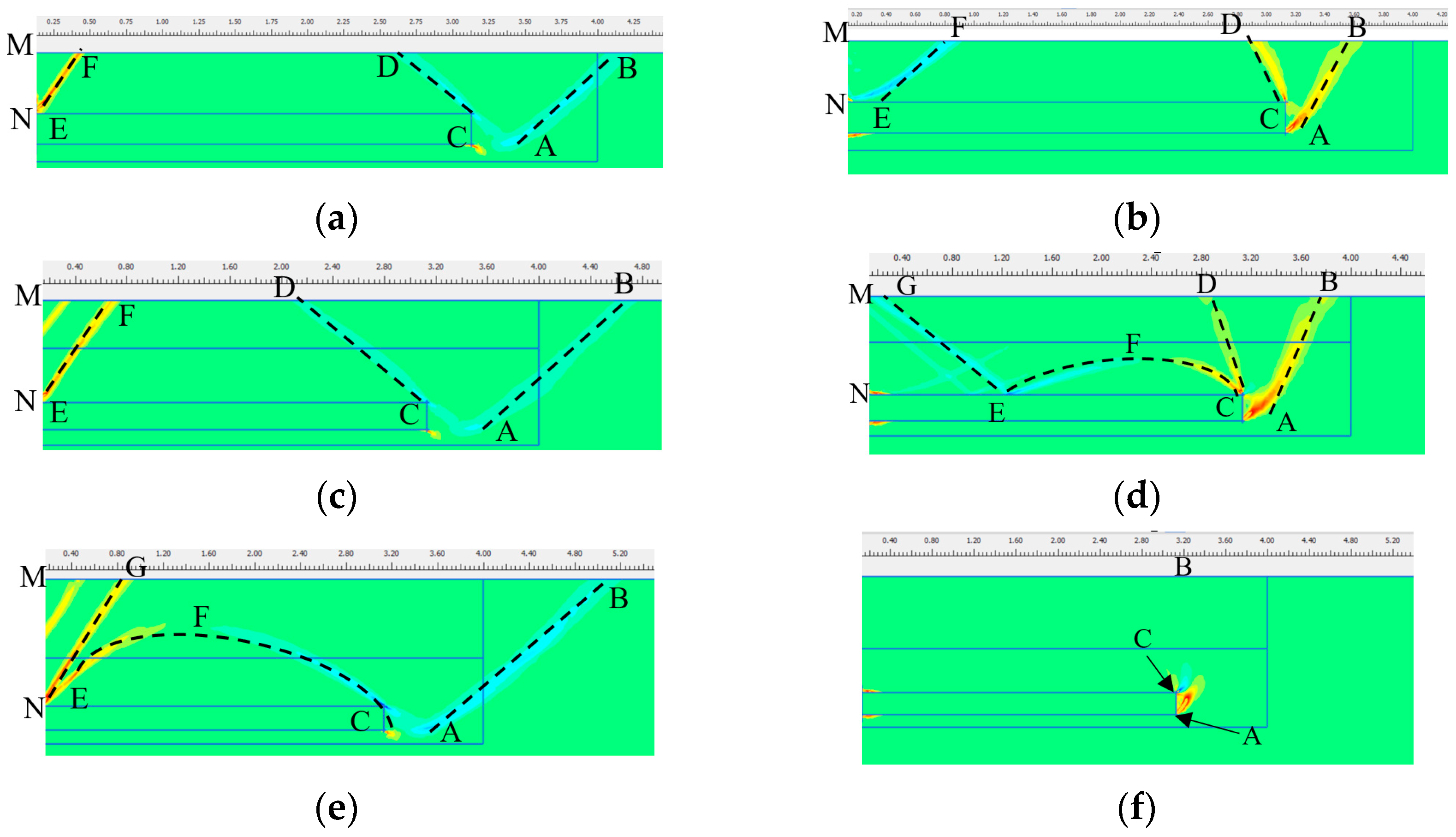
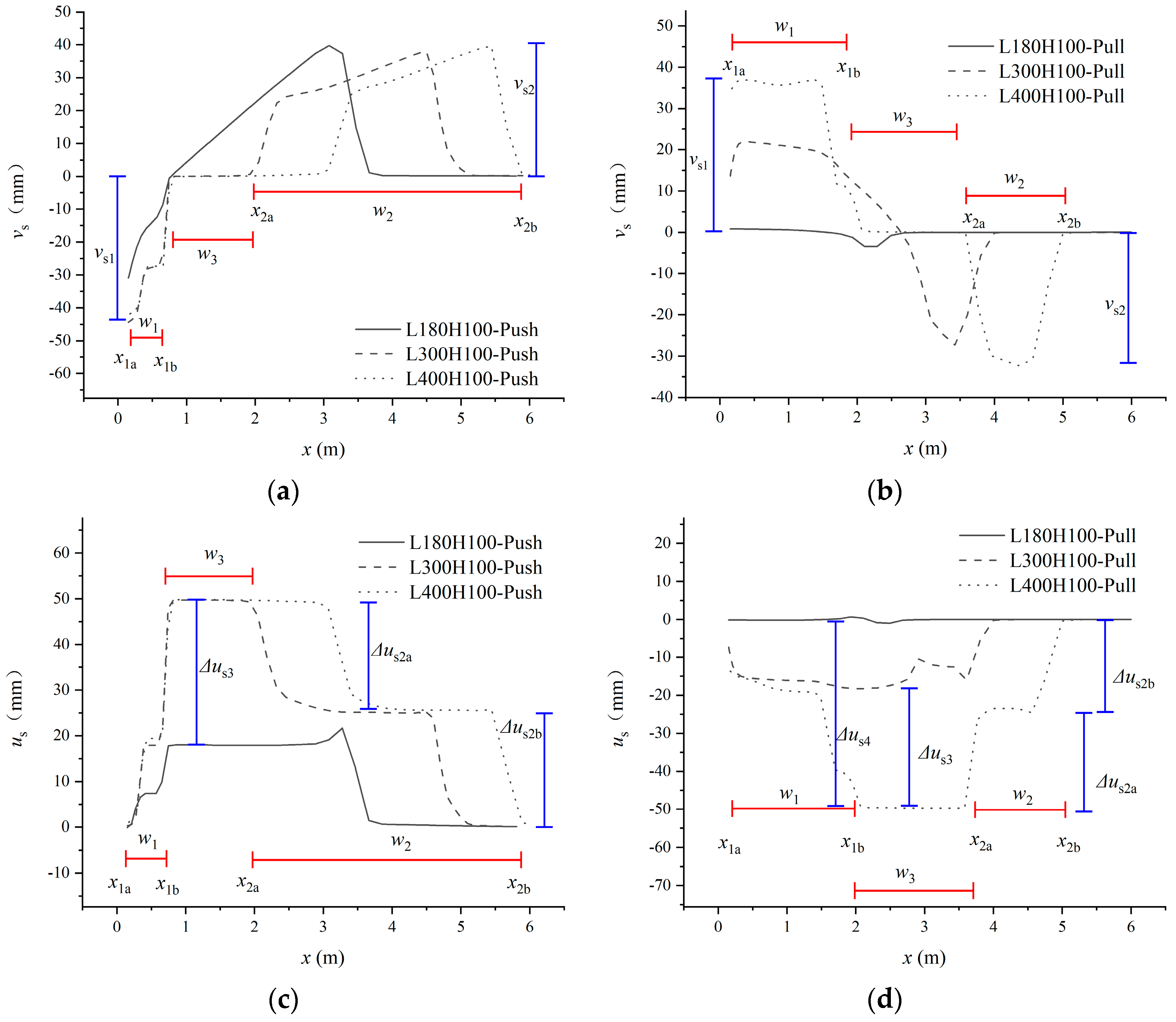
4.3.1. Influence of Embedded Depth
- Under push displacement:
- Under pull displacement:
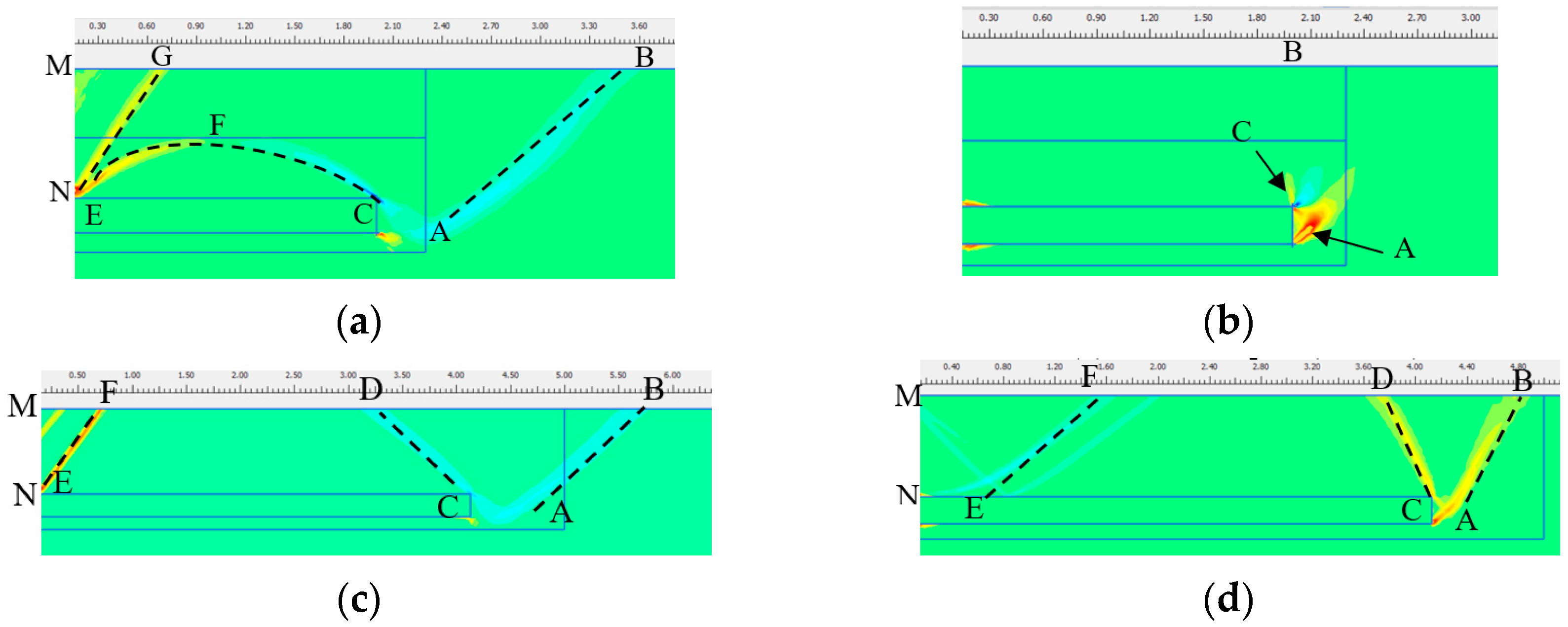
4.3.2. Influence of Slab Length
- Under push displacement:
- Under pull displacement:
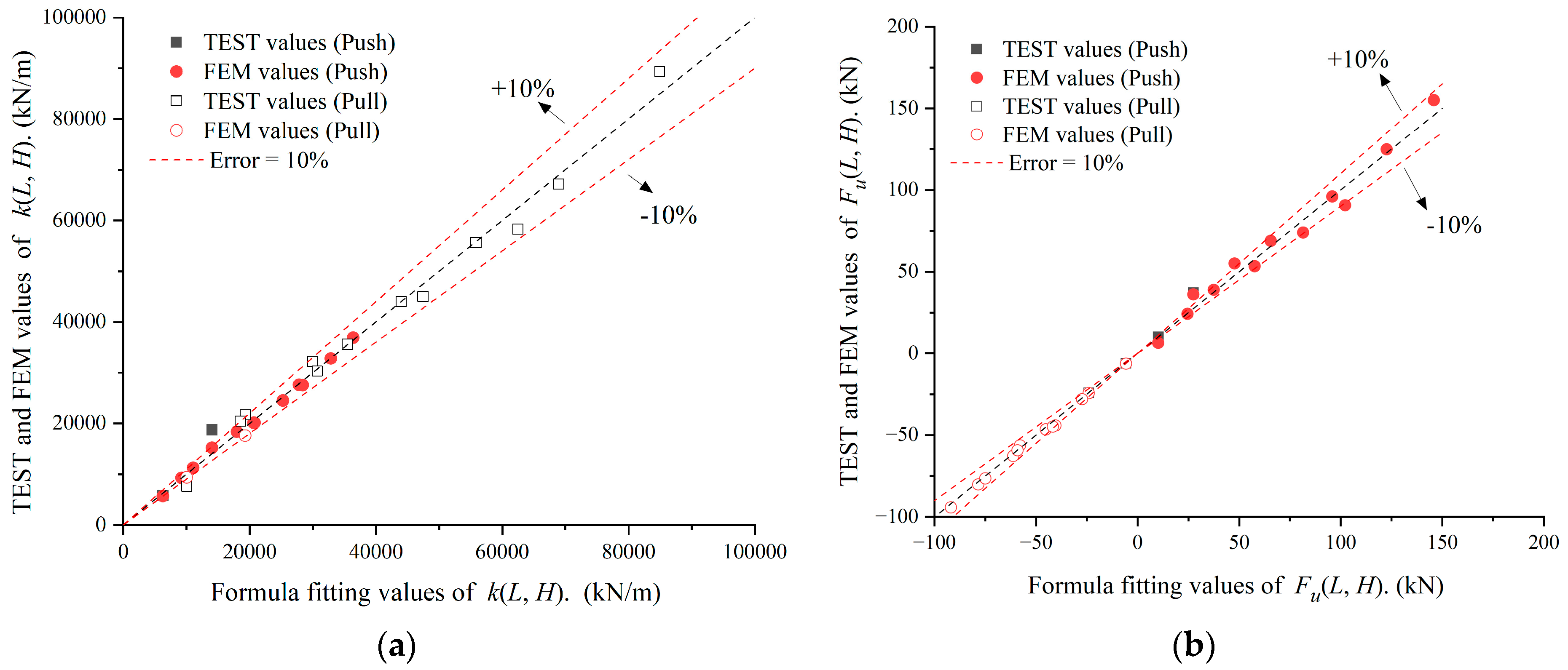
5. Simplified Calculation Formula for Load–Displacement Curve
6. Conclusions
- The load–displacement curves of FASSI under push or pull displacement can be divided into three stages: the elastic stage, the elastoplastic stage, and the failure stage. In the elastic stage, the longitudinal displacement of a FAS can be absorbed by the sand and no obvious cracks or deformations can be observed on the sand surface. In the elastoplastic stage, part of the sand enters the plastic deformation stage, and bumps and voids can be observed on the sand surface. In the failure stage, a through-going shear slip surface is formed, leading to an overall shear failure of the sand.
- Under push displacement, the sand at the distal end of the approach slab is in a passive state and uplifted to form a bump due to compression; the sand at the proximal end of the approach slab is in an active state and subsides to form a void due to tension. Under pull displacement, the deformations of the sand at the distal and proximal ends of the approach slab are opposite to those under pull displacement. The pavement deformation can be reduced with an increase in the embedded depth, which could reduce the risk of pavement settlement and cracking.
- With an increase in the embedded depth or slab length, the stiffness and ultimate load of the load–displacement curves of FASSI increase under push displacement, the stiffness increases and the ultimate load decreases under pull displacement.
- The longitudinal displacement transfer mode and vertical deformation distribution mode of FASSI are affected by the embedded depth and slab length. With an increase in the embedded depth or a decrease in the slab length, the sand deformation on its surface decreases, which is beneficial for avoiding pavement crack risks and improving pavement evenness.
- A simplified calculation formula that can be used to predict the load–displacement curves of FASSI based on a bilinear function model was proposed by considering the embedded depth and slab length as the parameters. The functions for the embedded depth and slab length were obtained through three-dimensional surface fitting.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, G. Structural Behavior of Integral Abutment Bridge Approach Slabs. Ph.D. Dissertation, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2023. [Google Scholar]
- Aloisio, A.; Pelliciari, M.; Xue, J.; Fragiacomo, M.; Briseghella, B. Effect of Pre-Hole Filled with High-Damping Material on the Inelastic Response Spectrum of Integral Abutment Bridges. J. Earthq. Eng. 2023, 27, 3319–3340. [Google Scholar] [CrossRef]
- Hassan, M.S.K.; Liyanapathirana, D.S.; Fuentes, W.; Leo, C.J.; Hu, P. A review of soil deformation and lateral pressure ratcheting phenomena in integral abutment bridges. Transp. Geotech. 2024, 49, 101388. [Google Scholar] [CrossRef]
- White, D.; Sritharan, S.; Suleiman, M.T.; Chetlur, S. Identification of the Best Practices for Design, Construction, and Repair of Bridge Approaches; No. CTRE Project 02-118; Iowa Department of Transportation: Ames, IA, USA, 2005. [Google Scholar]
- White, D.J.; Mekkawy, M.M.; Sritharan, S.; Suleiman, M.T. “Underlying” causes for settlement of bridge approach pavement systems. J. Perform. Constr. Facil. 2007, 21, 273–282. [Google Scholar] [CrossRef]
- Ahmad, I.; Shokouhian, M. Promoting Sustainable Green Infrastructure: Experimental and Numerical Investigation of Concrete Reinforced with Recycled Steel Fibers. Arch. Adv. Eng. Sci. 2024, 1–13. [Google Scholar] [CrossRef]
- Erarslan, N.; Şen, B. The Analysis of Liquefaction Potential and Post-Liquefaction Deformations at a Highway Bridge Crossing. Arch. Adv. Eng. Sci. 2023, 1–9. [Google Scholar] [CrossRef]
- Xue, J.; Aloisio, A.; Lin, Y.; Fragiacomo, M.; Briseghella, B. Optimum design of piles with pre-hole filled with high-damping material: Experimental tests and analytical modelling. Soil Dyn. Earthq. Eng. 2021, 151, 106995. [Google Scholar] [CrossRef]
- Hoppe, E.; Weakley, K.; Thompson, P. Jointless Bridge Design at the Virginia Department of Transportation. Transp. Res. Procedia 2016, 14, 3943–3952. [Google Scholar] [CrossRef]
- Breña, S.F.; Bonczar, C.H.; Civjan, S.A.; DeJong, J.T.; Crovo, D.S. Evaluation of seasonal and yearly behavior of an integral abutment bridge. J. Bridge Eng. 2007, 12, 296–305. [Google Scholar] [CrossRef]
- Prakash, B.; Tiwari, A.K.; Dash, S.R.; Patra, S. Structural evaluation and performance based optimization of approach slab design for mitigating bridge approach settlement through an Indian case study. Structures 2024, 60, 105864. [Google Scholar] [CrossRef]
- Arockiasamy, M.; Butrieng, N.; Sivakumar, M. State-of-the-Art of Integral Abutment Bridges: Design and Practice. J. Bridge Eng. 2004, 9, 497–506. [Google Scholar] [CrossRef]
- Wasserman, E.P. Integral abutment design (practices in the United States). In Proceedings of the 1st US-Italy Seismic Bridge Workshop, Pavia, Italy, 18–20 April 2007. [Google Scholar]
- Connal, J. Integral abutment bridges: Australian and US practice. In Proceedings of the Austroads Bridge Conference, Hobart, Australia, 19–24 May 2004. No. AP-G79/04. [Google Scholar]
- Ala, N. Seamless Bridge System for the US Practice. Ph.D. Dissertation, University of Nebraska-Lincoln, Lincoln, NE, USA, 2011. [Google Scholar]
- Puppala, A.J.; Saride, S.; Archeewa, E.; Hoyos, L.R.; Nazarian, S. Recommendations for Design, Construction, and Maintenance of Bridge Approach Slabs: Synthesis Report. 2009. Available online: https://library.ctr.utexas.edu/hostedpdfs/uta/0-6022-1.pdf (accessed on 10 December 2024).
- Xia, Y.; Cheng, Y. Research on differential settlement characteristics of high fill embankment on expressway. Highw. Eng. 2019, 4, 268–273. [Google Scholar]
- Akiyama, H.; Kajikawa, Y. Fundamentally Structural Characteristics of Integral Bridges. Ph.D. Dissertation, Kanzawa University, Kanazawa, Japan, 2008. [Google Scholar]
- Hoppe, E.J. Guidelines For the Use, Design, and Construction of Bridge Approach Slabs; Virginia Department of Transportation: Richmond, VA, USA, 1999. [Google Scholar]
- Kunin, J.; Alampalli, S. Integral Abutment Bridges: Current Practice in United States and Canada. J. Perform. Constr. Facil. 2000, 14, 104–111. [Google Scholar] [CrossRef]
- Tabatabai, H.; Oesterle, R.G.; Lawson, T.J. Jointless Bridges, Experimental Research and Field Studies; Report Submitted to the Federal Highway Administration: Washington, DC, USA, 2005; Volume I. [Google Scholar]
- Maruri, R.F.; Petro, S.H. Integral Abutments and Jointless Bridges (IAJB) 2004 Survey Summary; Federal Highway Administration West Virginia Department of Transportation: Washington, DC, USA, 2005. [Google Scholar]
- Lin, Z.; Peng, D. Influence of Approach Plate on Mechanical Performance of Bridges Without Expansion Joints. In Proceedings of the 13th National Conference on Structural Engineering, Vancouver, BC, Canada, 1–6 August 2004; Volume II. [Google Scholar]
- Xue, J.Q.; Tang, Y.F.; Briseghella, B.; Huang, F.Y.; Nuti, C. Experimental Study on SSI of Flat Buried Approach Slab in Jointless Bridge. In Bridge Maintenance, Safety, Management, Life-Cycle Sustainability and Innovations; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Briseghella, B.; Tang, Y.F.; Xue, J.Q.; Chen, B.C.; Huang, F.Y. Review of research on approach slabs in jointless bridges. J. Fuzhou Univ. (Nat. Sci. Ed.) 2021, 49, 209–216. [Google Scholar]
- Prakash, B.; Tiwari, A.K.; Dash, S.R. Bridge Approach Settlement and its Mitigation Schemes: A Review. Transp. Res. Rec. J. Transp. Res. Board 2024, 2678, 660–689. [Google Scholar] [CrossRef]
- Reza, F. Synthesis of Bridge Approach Panels Best Practices; No. MN/RC 2013-09. 2013. Available online: https://mdl.mndot.gov/_flysystem/fedora/2023-01/201309.pdf (accessed on 10 December 2024).
- Ala, N.; Azizinamini, A. Proposed design provisions for a seamless bridge system: Cases of flexible and jointed pavements. J. Bridge Eng. 2016, 21, 04015045. [Google Scholar] [CrossRef]
- Lu, Q.; Li, M.; Gunaratne, M.; Xin, C.; Hoque, M.; Rajalingola, M. Best Practices for Construction and Repair of Bridge Approaches and Departures. 2018. Available online: https://rosap.ntl.bts.gov/view/dot/35511 (accessed on 10 December 2024).
- White, H.; Pétursson, H.; Collin, P. Integral abutment bridges: The European way. Pract. Period. Struct. Des. Constr. 2010, 15, 201–208. [Google Scholar] [CrossRef]
- Wendner, R.; Strauss, A. Inclined Approach Slab Solution for Jointless Bridges: Performance Assessment of the Soil-Structure Interaction. J. Perform. Constr. Facil. 2015, 29, 04014045. [Google Scholar] [CrossRef]
- Phares, B.M.; Faris, A.S.; Greimann, L.; Bierwagen, D. Integral bridge abutment to approach slab connection. J. Bridge Eng. 2013, 18, 179–181. [Google Scholar] [CrossRef]
- Tang, Y.; Briseghella, B.; Xue, J.; Zhang, P.; Huang, F. Research on friction between grade flat approach slab and sliding material in jointless bridges. In Proceedings of the 20th Congress of IABSE, New York, NY, USA, 4–6 September 2019; The Evolving. Metropolis-Report. International Association for Bridge and Structural Engineering (IABSE): Zurich, Switzerland, 2019; pp. 959–963. [Google Scholar]
- Jin, X. Design and Experimental Research on a New Fully Jointless Bridge System. Ph.D. Dissertation, Hunan University, Changsha, China.
- Jin, X.; Shao, X. A study of fully jointless bridge-approach system with semi-integral abutment. J. Civ. Eng. 2009, 9, 68–73. [Google Scholar]
- Burdet, O.; Einpaul, J.; Muttoni, A. Experimental Investigation of Soil-structure Interaction for the Transition Slabs of Integral Bridges. Struct. Concr. 2016, 16, 470–479. [Google Scholar] [CrossRef]
- D’Amato, M.; Laterza, M.; Casamassima, V.I.T.O. Seismic performance evaluation of a multi-span existing masonry arch bridge. Open Civ. Eng. J. 2017, 11, 1191–1207. [Google Scholar] [CrossRef]
- Rota, M.; Pecker, A.; Bolognini, D.; Pinho, R. A methodology for seismic vulnerability of masonry arch bridge walls. J. Earthq. Eng. 2005, 9, 331–353. [Google Scholar] [CrossRef]
- Fahnestock, L.A.; Chee, M.; Liu, G.; Kode, U.; LaFave, J.M. Synthesis of Bridge Approach Slab Behavior, Design, and Construction Practice. Pract. Period. Struct. Des. Constr. 2023, 27, 04022032. [Google Scholar] [CrossRef]
- Abo El-Khier, M.; Morcous, G. Design and Detailing of Bridge Approach Slabs: Cast-in-Place and Precast Concrete Options. In Sustainable Issues in Infrastructure Engineering: The Official 2020 Publication of the Soil-Structure Interaction Group in Egypt (SSIGE); Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 193–206. [Google Scholar]
- Tang, Y.; Briseghella, B.; Xue, J.; Huang, F.; Chen, B.; Nuti, C. Numerical Analysis of the Mechanical Behaviors of Girders in Jointless Bridge Considering the Grade Flat Approach Slab. In Life-Cycle Civil Engineering: Innovation, Theory and Practice; CRC Press: Boca Raton, FL, USA, 2021; pp. 1486–1491. [Google Scholar]
- Slavinska, O.; Andriy, B.; Ihor, K.; Oleksandr, D. Estimation of the Service Life of Approach Slabs of Road Bridges Based on the Statistical Modeling Method. Tehnički Glasnik 2024, 18, 618–625. [Google Scholar] [CrossRef]
- Fu, R.H.; Briseghella, B.; Xue, J.-Q.; Aloisio, A.; Lin, Y.-B.; Nuti, C. Experimental and Finite Element Analyses of Laterally Loaded RC Piles with Pre-Hole Filled by Various Filling Materials in IABs. Eng. Struct. 2022, 272, 114991. [Google Scholar] [CrossRef]
- Lombardi, D.; Bhattacharya, S.; Scarpa, F.; Bianchi, M. Dynamic Response of a Geotechnical Rigid Model Container with Absorbing Boundaries. Soil Dyn. Earthq. Eng. 2015, 69, 46–56. [Google Scholar] [CrossRef]
- Dreier, D. Interaction Sol-Structure Dans Le Domaine Des Ponts Intégraux; EPFL: Lausanne, Switzerland, 2010. [Google Scholar]
- GB50021-2001; Code for Geotechnical Investigation. Ministry of Construction of the People’s Republic of China: Beijing, China, 2002.
- White, H.L. Integral Abutment Bridges: Comparison of Current Practice Between European Countries and the United States. In Proceedings of the Transportation Research Board Annual Meeting, Washington, DC, USA, 13–17 January 2008. [Google Scholar]
- Yan, M. Study on the Influence of Moisture Content on the Quasi-cohesion of Sandy Soil and Its Engineering Application. Master’s Thesis, Chang’an University, Xi’an, China, 2019. [Google Scholar]
- Li, G. Advanced Soil Mechanics; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Cui, D. Research on Apparent Cohesion of Unsaturated Sandy Soil. North. Commun. 2014, 2, 86–87. [Google Scholar]
- Movahedifar, M.; Bolouri, J. An Investigation on the Effect of Cyclic Displacement on the Integral Bridge Abutment. J. Civ. Eng. Manag. 2014, 20, 256–269. [Google Scholar] [CrossRef]
- Ooi, P.S.K.; Lin, X.; Hamada, H.S. Numerical Study of an Integral Abutment Bridge Supported on Drilled Shafts. J. Bridge Eng. 2010, 15, 19–31. [Google Scholar] [CrossRef]
- Abdel-Fattah, M.T.; Abdel-Fattah, T.T. Behavior of Integral Frame Abutment Bridges Due to Cyclic Thermal Loading: Nonlinear Finite-Element Analysis. J. Bridge Eng. 2019, 24, 04019031.1–04019031.15. [Google Scholar] [CrossRef]
- Bolton, M.D. Discussion: The Strength and Dilatancy of Sands. Geotechnique 1987, 36, 219–226. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J.; Broere, W.; Waterman, D. Plaxis 2D, version 9.0; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Potyondy, J.G. Skin Friction between Various Soils and Construction Materials. Géotechnique 1961, 11, 339–353. [Google Scholar] [CrossRef]







| H (cm) | Loading Direction | Test Cases | a | b | c | k (kN/mm) | l (kN/mm) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| ua (mm) | Fa (kN) | ub (mm) | Fb (kN) | uc (mm) | Fu (kN) | |||||
| 0 | Push | H0-Push | 0.52 | 4.81 | 1.52 | 5 | 50 | 5.85 | 9.25 | 0.02 |
| 21 | H21-Push | 0.61 | 6.36 | 3.38 | 7.2 | 50 | 9.51 | 10.43 | 0.05 | |
| 31.5 | H31.5-Push | 0.75 | 8.43 | 6.42 | 15.3 | 50 | 17.71 | 11.24 | 0.06 | |
| 63 | H63-Push | 1.42 | 26.41 | 8.74 | 35.5 | 50 | 35.62 | 18.60 | 0.00 | |
| 0 | Pull | H0-Pull | −0.45 | −2.73 | −2.45 | −5.1 | −50 | −6.75 | 6.07 | 0.03 |
| 21 | H21-Pull | −0.56 | −3.84 | −2.58 | −7 | −50 | −7.82 | 6.86 | 0.02 | |
| 31.5 | H31.5-Pull | −1.21 | −8.74 | −3.66 | −10.3 | −50 | −13.35 | 7.22 | 0.07 | |
| 63 | H63-Pull | −1.41 | −18.12 | −5.27 | −18.6 | −50 | −31.7 | 12.85 | 0.29 | |
| Parameters | x1a | x1b | w1 | vs1 | x2a | x2b | w2 | vs2 | θ1b | θ2a | θ2b |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Units | m | mm | m | mm | ° | ||||||
| H21-Push | / | / | / | / | 2.05 | 2.47 | 0.42 | 40 | / | / | 36 |
| H31.5-Push | 0.13 | 0.19 | 0.06 | −55 | 1.91 | 2.74 | 0.83 | 38 | 71 | 53 | 39 |
| H63-Push | 0.12 | 0.39 | 0.27 | −42 | 1.67 | 3.04 | 1.36 | 36 | 70 | 49 | 38 |
| H21-Pull | / | / | / | / | 2.10 | 2.23 | 0.13 | −72 | / | / | 74 |
| H31.5-Pull | 0.00 | 0.32 | 0.32 | 18 | 1.94 | 2.19 | 0.24 | −38 | 35 | 78 | 76 |
| H63-Pull | 0.00 | 0.82 | 0.82 | 15 | 1.90 | 2.26 | 0.35 | −35 | 32 | 65 | 77 |
| Loading Direction | L (cm) | H (cm) | Labels | k (kN/mm) | Fu (kN) |
|---|---|---|---|---|---|
| Push | 180 | 0 | L180H0-Push | 5.68 | 6.65 |
| 63 | L180H63-Push | 15.21 | 37.17 | ||
| 100 | L180H100-Push | 20.15 | 55.06 | ||
| 132 | L180H132-Push | 27.63 | 99.71 | ||
| 300 | 0 | L300H0-Push | 9.29 | 24.70 | |
| 63 | L300H63-Push | 18.37 | 56.60 | ||
| 100 | L300H100-Push | 24.51 | 76.21 | ||
| 132 | L300H132-Push | 32.80 | 129.24 | ||
| 400 | 0 | L400H0-Push | 11.26 | 40.09 | |
| 63 | L400H63-Push | 20.16 | 70.88 | ||
| 100 | L400H100-Push | 27.58 | 93.25 | ||
| 132 | L400H132-Push | 36.92 | 160.77 | ||
| Pull | 180 | 0 | L180H0-Pull | 7.58 | −6.45 |
| 63 | L180H63-Pull | 21.69 | −25.28 | ||
| 100 | L180H100-Pull | 35.58 | −45.53 | ||
| 132 | L180H132-Pull | 55.66 | −58.33 | ||
| 300 | 0 | L300H0-Pull | 20.41 | −28.66 | |
| 63 | L300H63-Pull | 32.21 | −48.03 | ||
| 100 | L300H100-Pull | 45.01 | −64.62 | ||
| 132 | L300H132-Pull | 67.16 | −82.73 | ||
| 400 | 0 | L400H0-Pull | 30.29 | −45.82 | |
| 63 | L400H63-Pull | 43.99 | −61.14 | ||
| 100 | L400H100-Pull | 58.29 | −78.88 | ||
| 132 | L400H132-Pull | 89.37 | −97.46 |
| Loading Direction | L | H | VDM | vs1 | vs2 | LDM | Δus2a | Δus2b | Δus3 | Δus4 |
|---|---|---|---|---|---|---|---|---|---|---|
| cm | mm | mm | ||||||||
| Push | 180 | 63 | VDM1a | −28 | 41 | LDM1a | −24 | −26 | / | / |
| 180 | 100 | VDM2a | −27 | 40 | LDM2a | / | −18 | −32 | / | |
| 180 | 132 | VDM2a | −27 | 39 | LDM2a | / | −12 | −38 | / | |
| 300 | 63 | VDM1a | −28 | 42 | LDM1a | −24 | −26 | / | / | |
| 300 | 100 | VDM1a | −45 | 38 | LDM1a | −25 | −25 | / | / | |
| 300 | 132 | VDM2a | −40 | 36 | LDM2a | / | −21 | −29 | / | |
| 400 | 63 | VDM1a | −28 | 40 | LDM1a | −24 | −26 | / | / | |
| 400 | 100 | VDM1a | −42 | 39 | LDM1a | −25 | −25 | / | / | |
| 400 | 132 | VDM1a | −43 | 35 | LDM1a | −24 | −26 | / | / | |
| Pull | 180 | 63 | VDM2b | 41 | −35 | LDM2b | 5 | 15 | 30 | / |
| 180 | 100 | VDM3b | 1 | −3 | LDM3b | / | 1 | / | 49 | |
| 180 | 132 | VDM3b | 1 | −2 | LDM3b | / | 1 | / | 49 | |
| 300 | 63 | VDM1b | 41 | −36 | LDM1b | 27 | 23 | / | / | |
| 300 | 100 | VDM2b | 23 | −27 | LDM2b | 6 | 12 | 32 | / | |
| 300 | 132 | VDM3b | −1 | −2 | LDM3b | / | 1 | / | 49 | |
| 400 | 63 | VDM1b | 41 | −35 | LDM1b | 25 | 25 | / | / | |
| 400 | 100 | VDM1b | 36 | −32 | LDM1b | 27 | 23 | / | / | |
| 400 | 132 | VDM2b | 9 | −12 | LDM2b | 3 | 5 | 42 | / | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Briseghella, B.; Xue, J.; Nuti, C.; Huang, F. Experimental and Numerical Investigations of Flat Approach Slab–Soil Interaction in Jointless Bridge. Appl. Sci. 2024, 14, 11726. https://doi.org/10.3390/app142411726
Tang Y, Briseghella B, Xue J, Nuti C, Huang F. Experimental and Numerical Investigations of Flat Approach Slab–Soil Interaction in Jointless Bridge. Applied Sciences. 2024; 14(24):11726. https://doi.org/10.3390/app142411726
Chicago/Turabian StyleTang, Yufeng, Bruno Briseghella, Junqing Xue, Camillo Nuti, and Fuyun Huang. 2024. "Experimental and Numerical Investigations of Flat Approach Slab–Soil Interaction in Jointless Bridge" Applied Sciences 14, no. 24: 11726. https://doi.org/10.3390/app142411726
APA StyleTang, Y., Briseghella, B., Xue, J., Nuti, C., & Huang, F. (2024). Experimental and Numerical Investigations of Flat Approach Slab–Soil Interaction in Jointless Bridge. Applied Sciences, 14(24), 11726. https://doi.org/10.3390/app142411726









