A Theoretical Method for Calculating the Internal Contact Pressure of Parallel Wire Cable during Fretting Wear
Abstract
1. Introduction
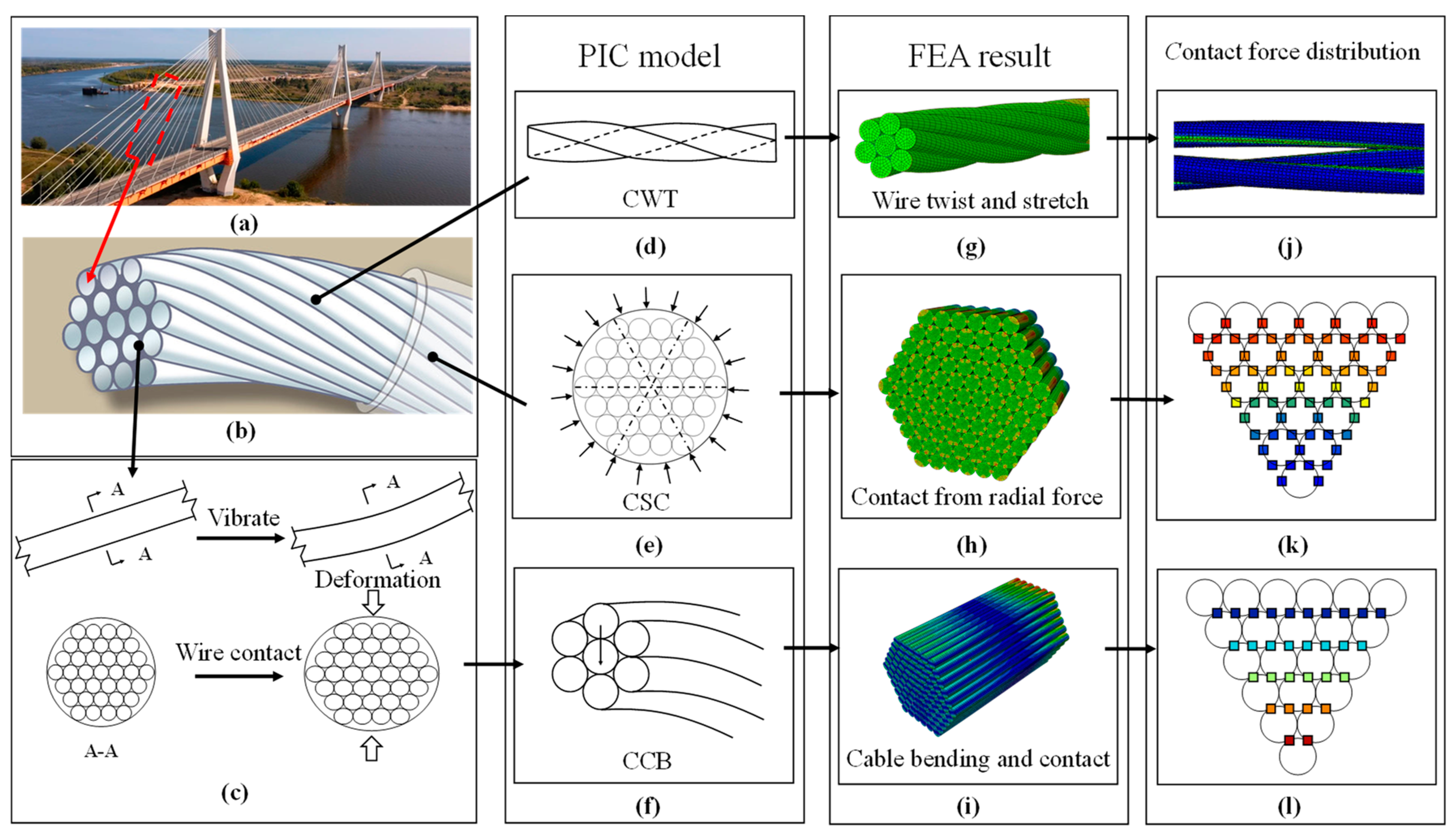
2. Theoretical Derivation of PIC Model
- Contact pressure caused by wire twisting (CWT): contact pressure generated by the twisting of parallel wires during the manufacturing process;
- Contact pressure caused by sheath compression (CSC): constriction due to external radial forces, such as sheath and clamp;
- Contact pressure caused by cable bending (CCB): contact of wires in different layers caused by the bending during the operation stage.
2.1. Basic Rules in Theoretical Derivation of PIC Model
- Tight contact is maintained between the wires.
- Only the twisting effect of the wires is considered, disregarding torsion resulting from tension.
- The radial force generated by sheath compression is uniform.
- Wire deformation adheres to the assumption of a flat cross-section, neglecting shear deformation arising from wire bending.
2.2. Contact Pressure Caused by Wire Twisting
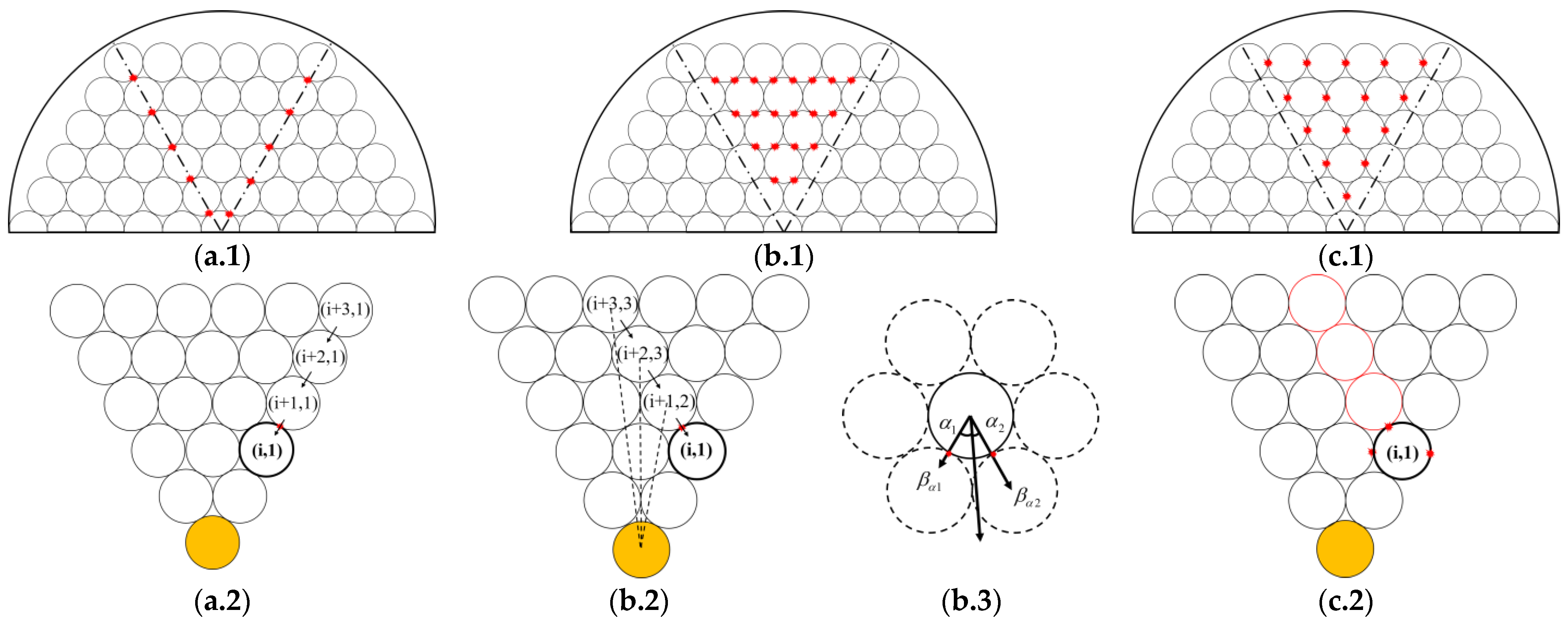
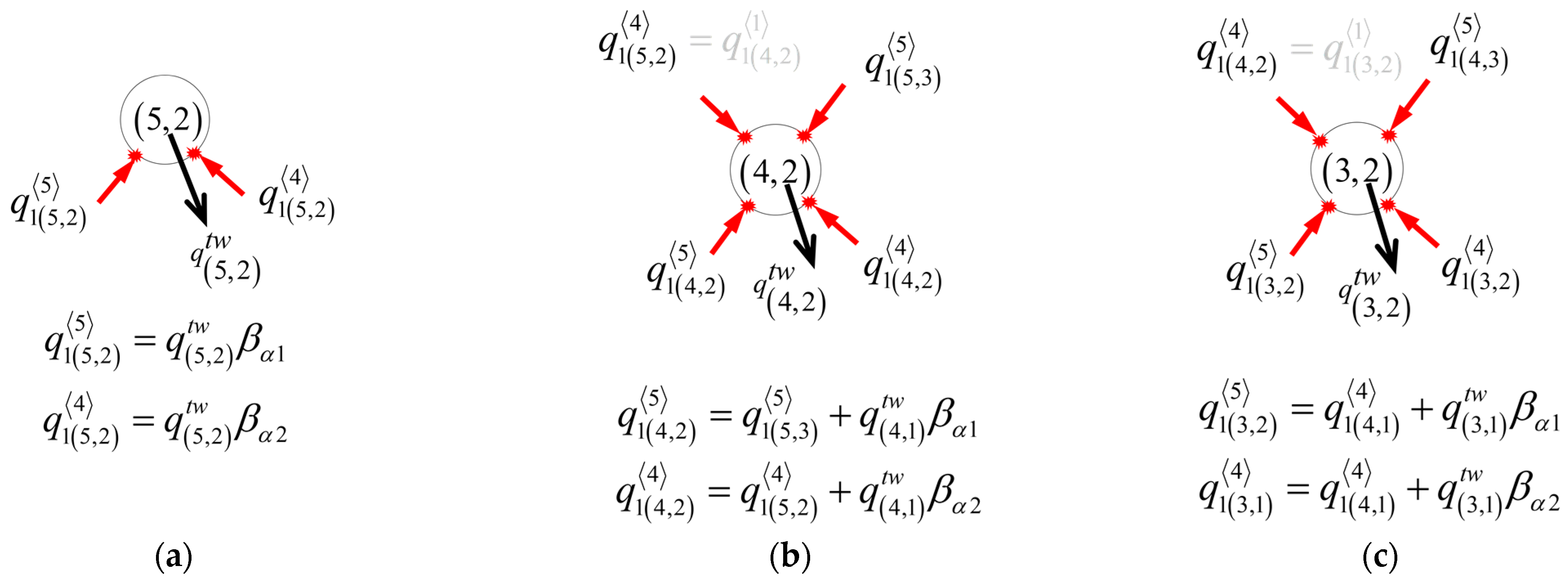
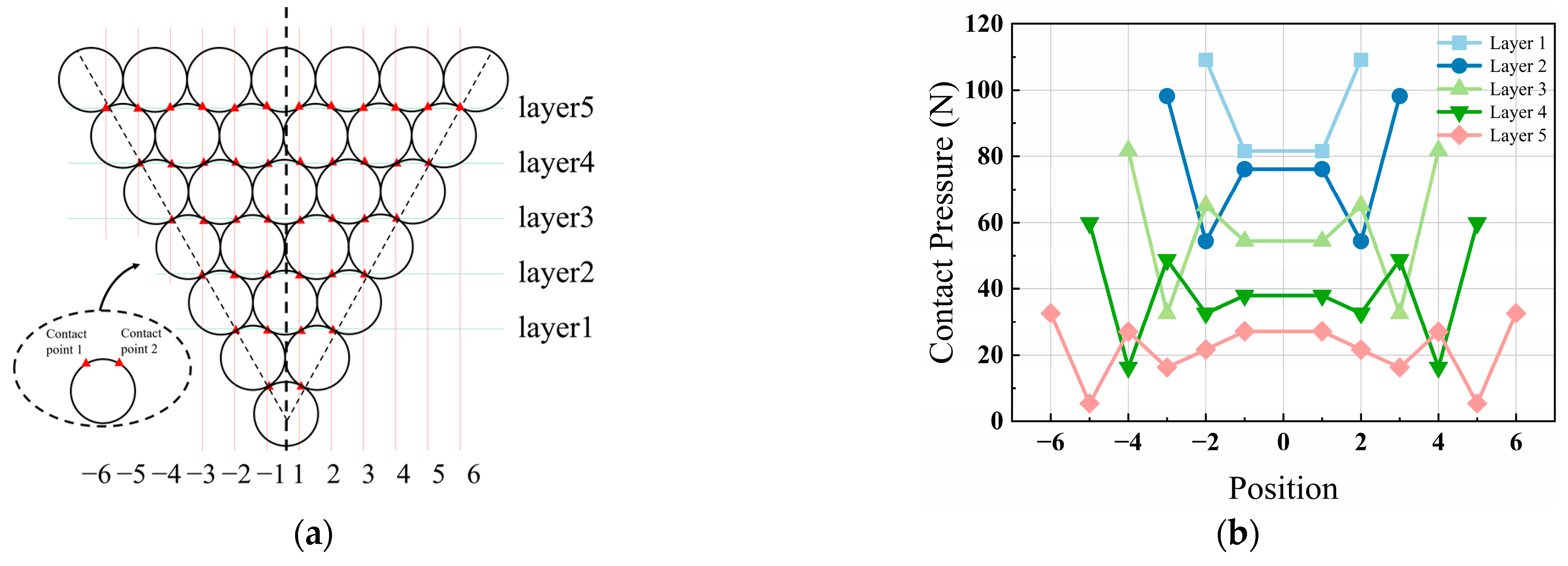
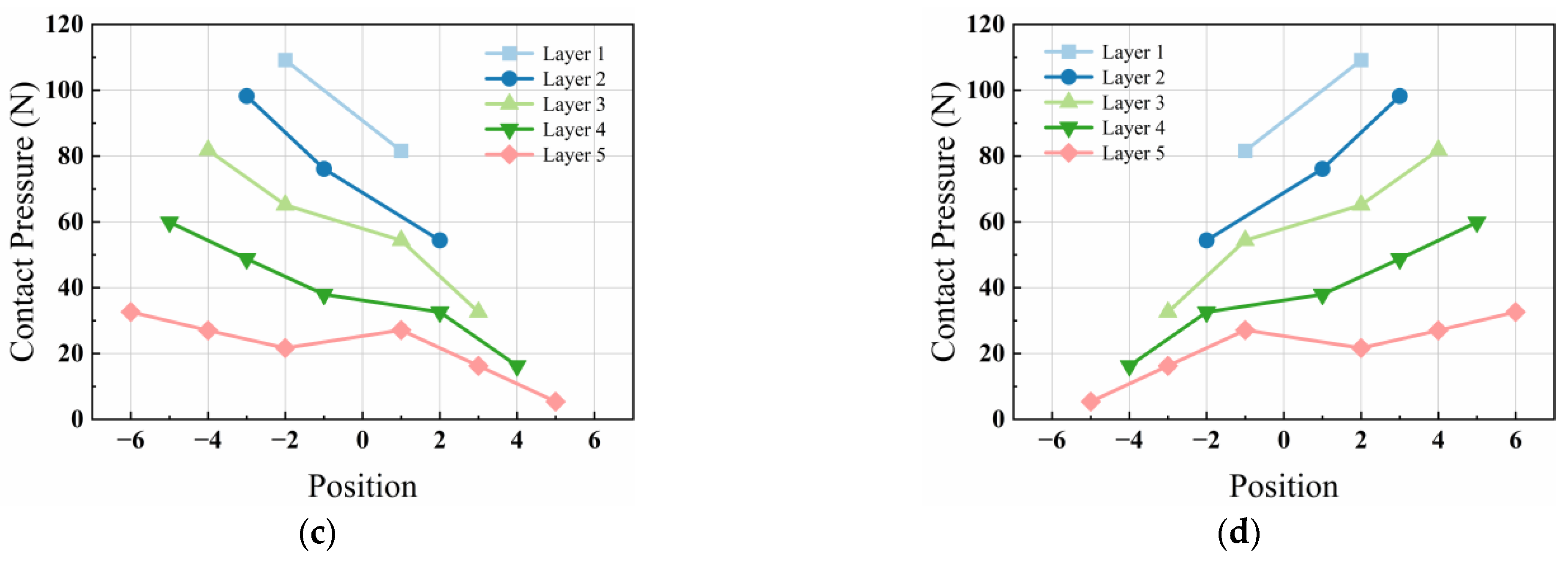
2.2.1. Diagonal Contact Points
2.2.2. Non-Diagonal Contact Points in Different Layers
2.2.3. Non-Diagonal Contact Points in Same Layer
2.3. Contact Pressure Caused by Sheath Compression
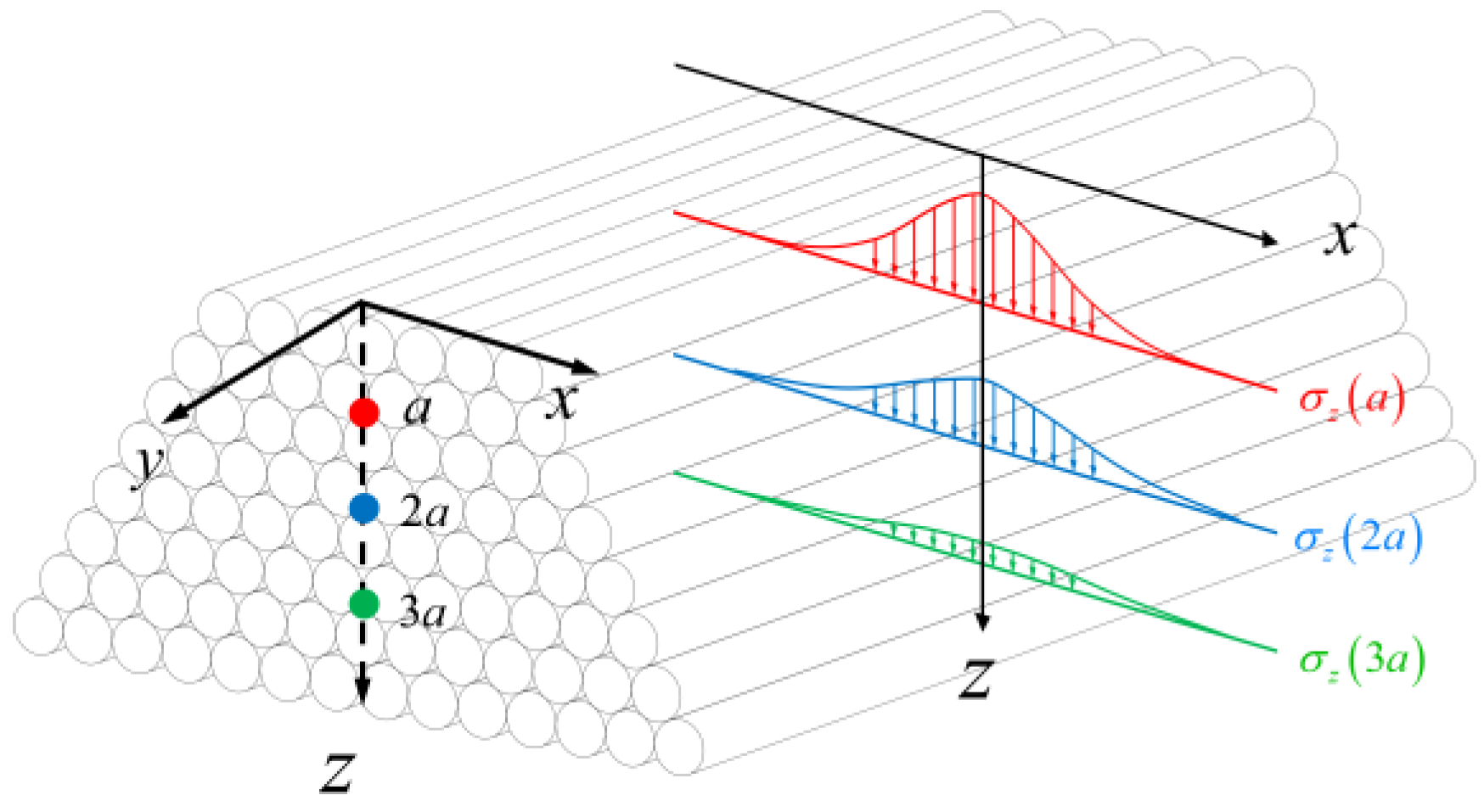
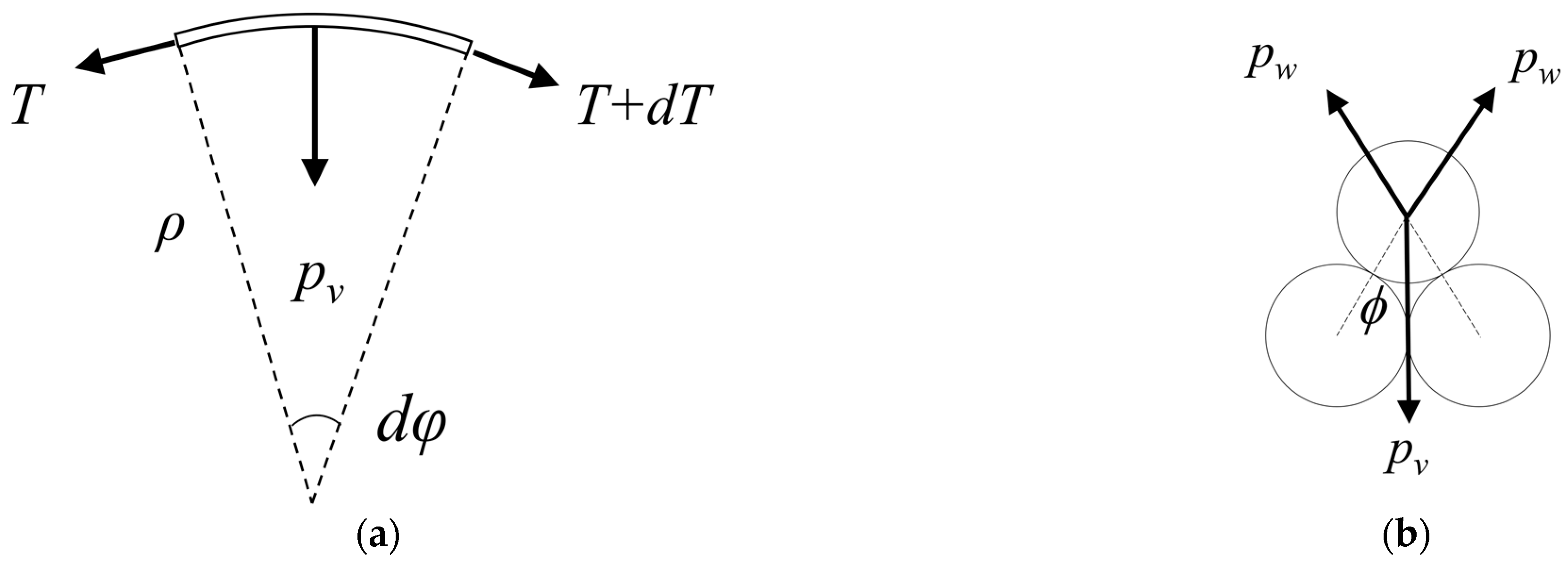
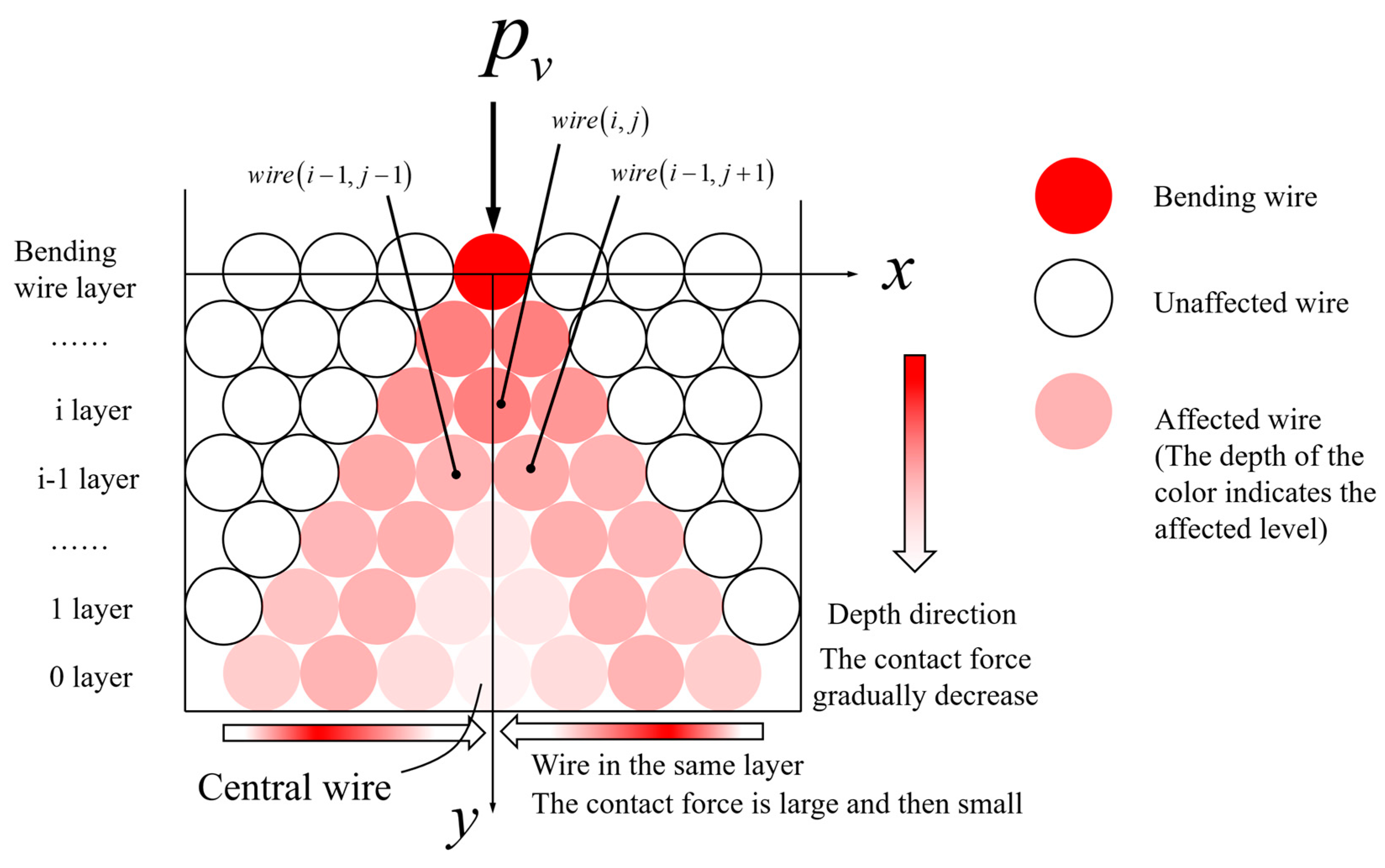
2.4. Contact Pressure Caused by Cable Bending
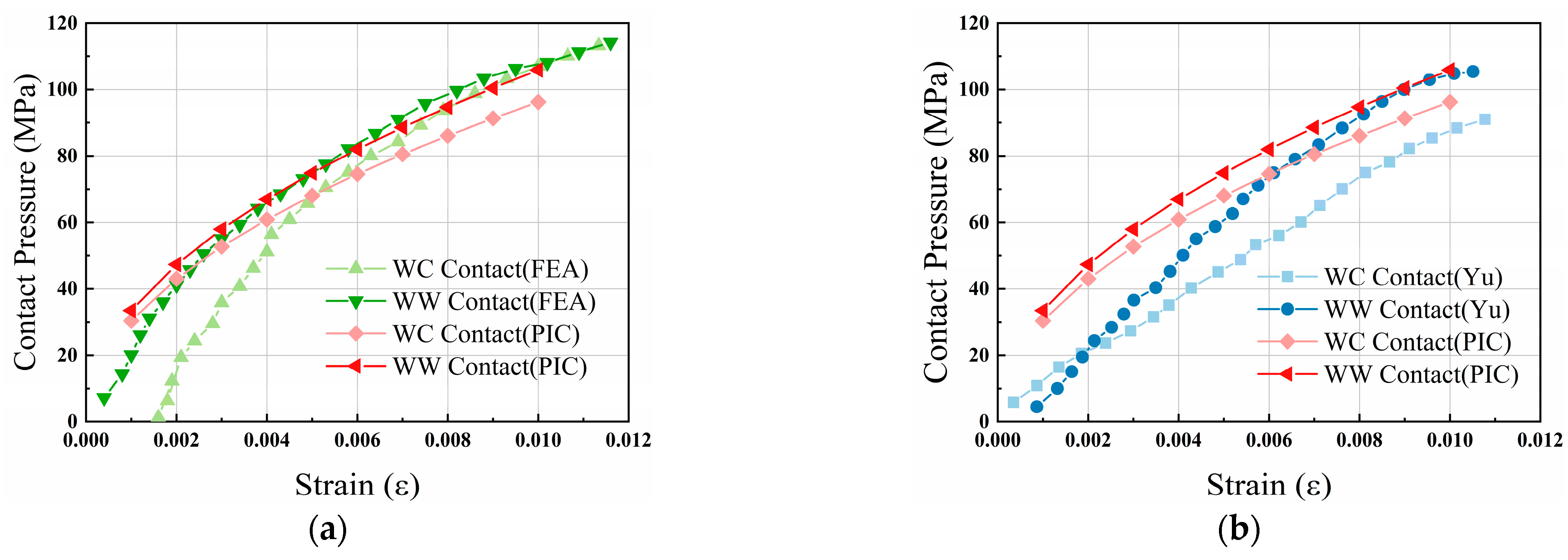
3. Internal Contact Pressure Model Validation
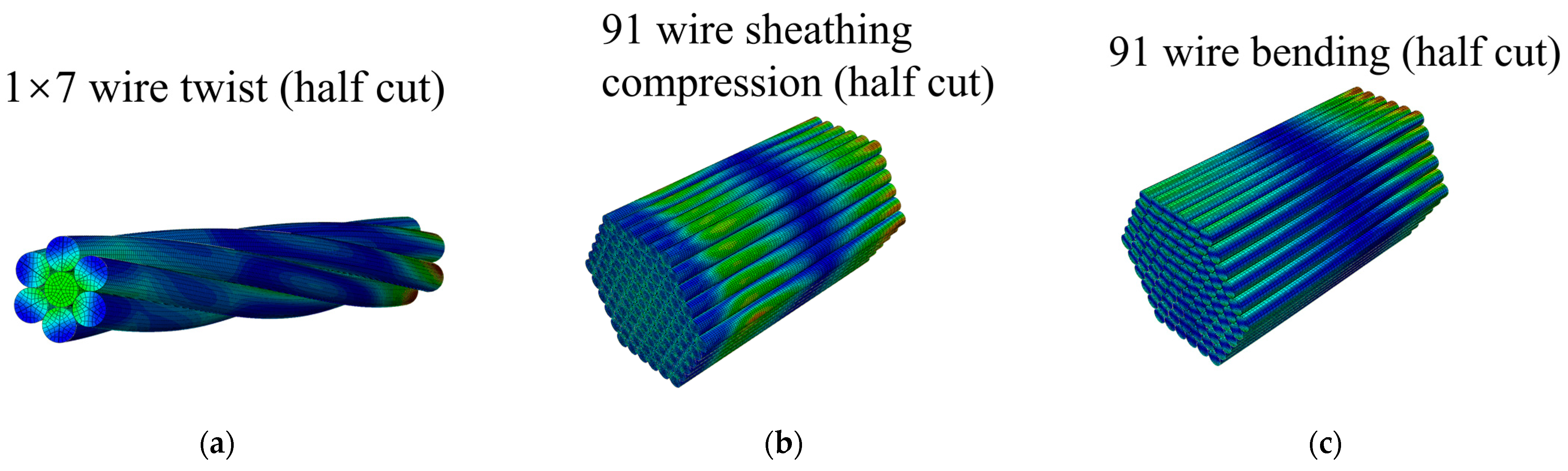
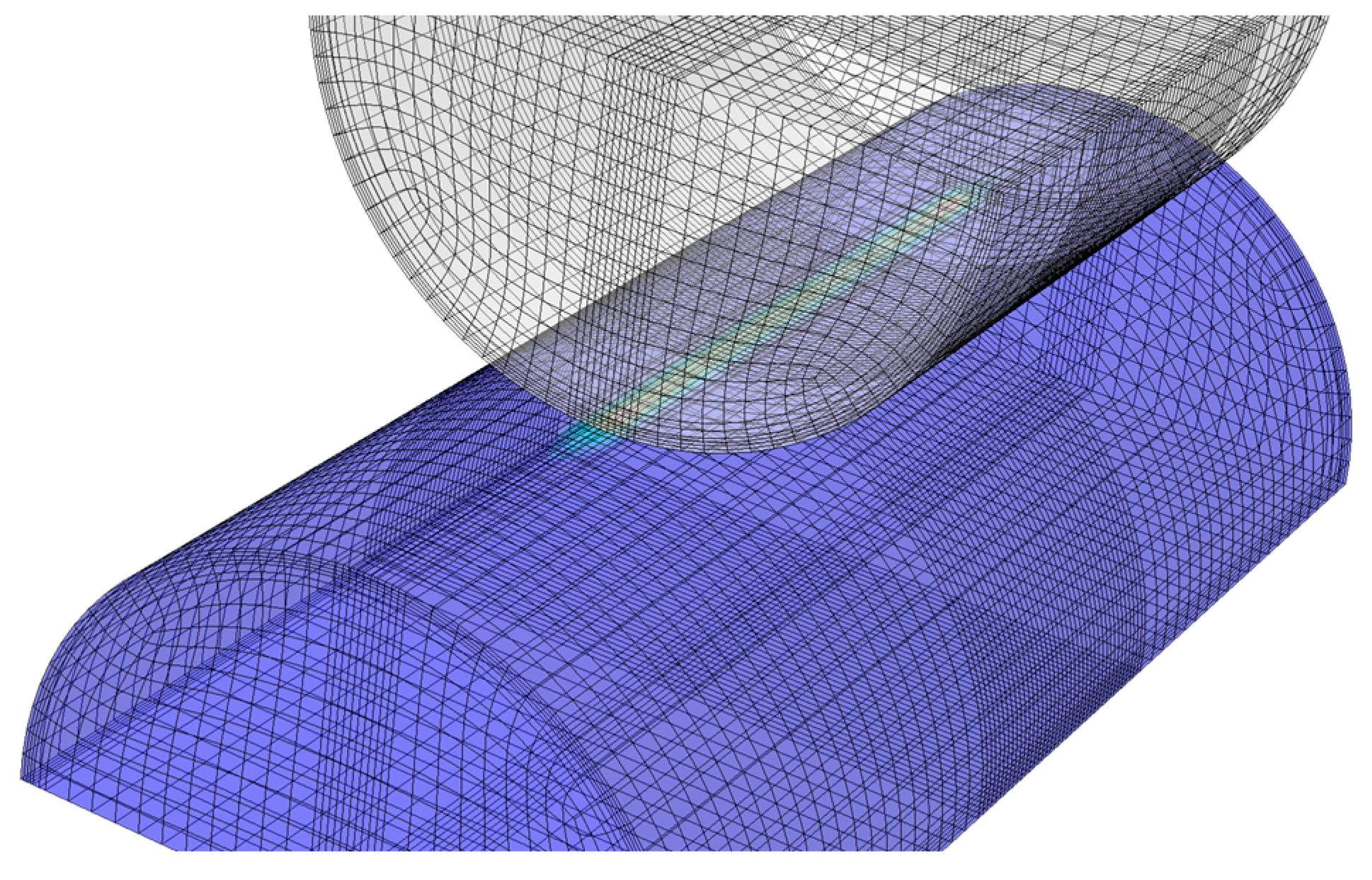
3.1. Formulation of the Finite Element Model
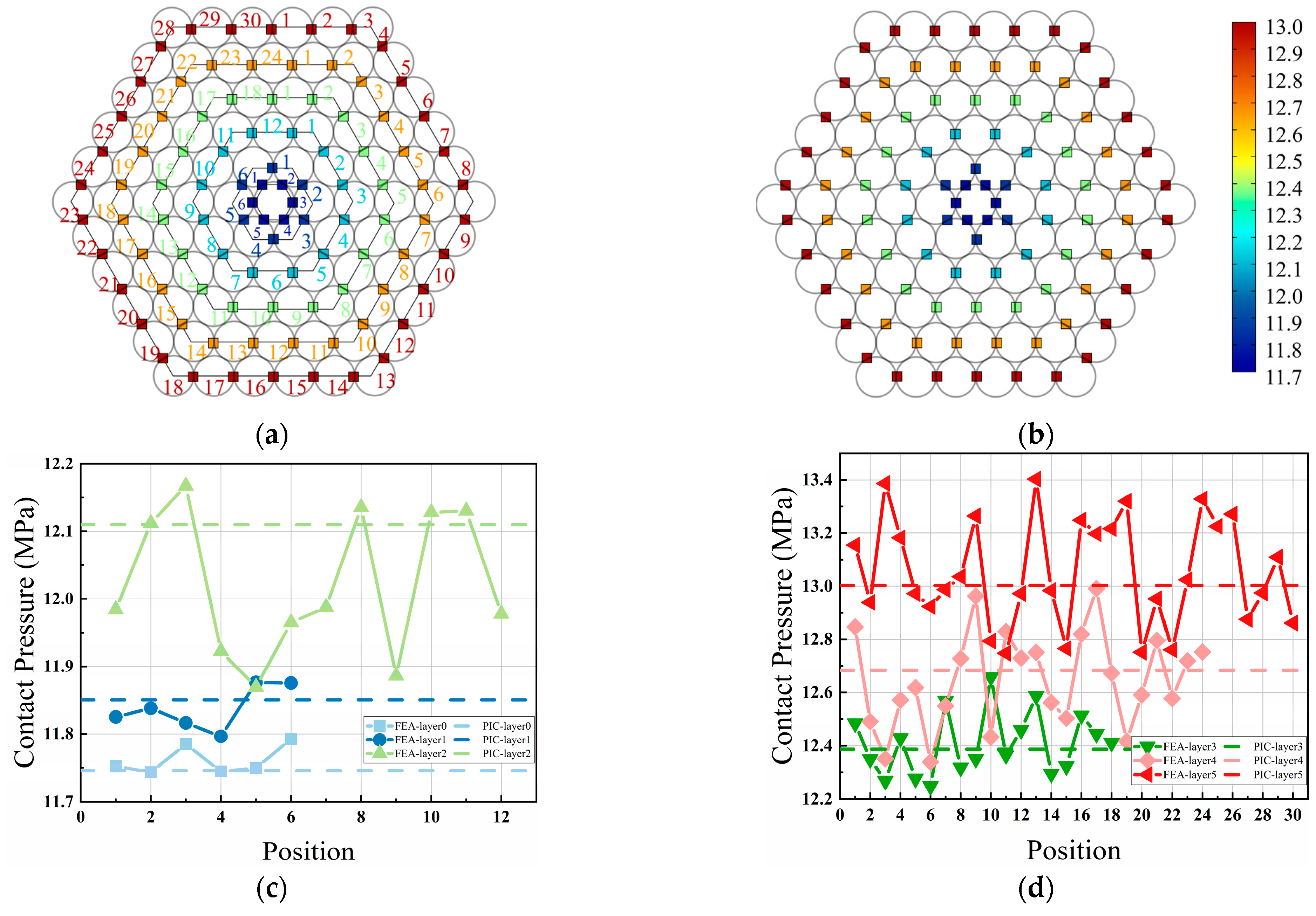
3.2. Validation for Twist Model
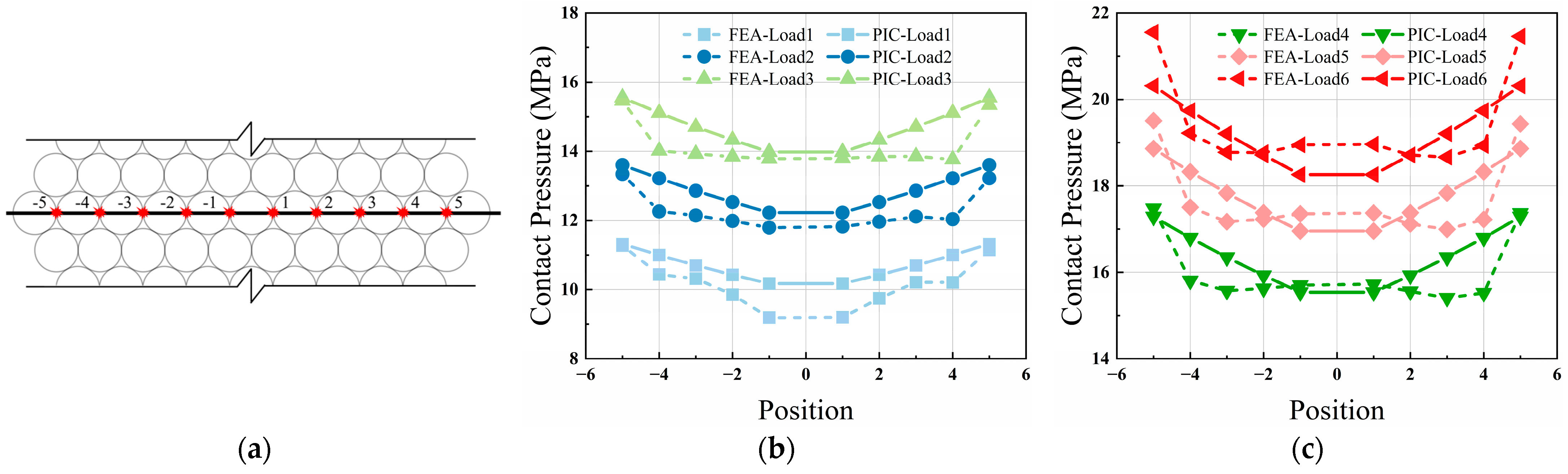
3.3. Validation for Sheathing Compression
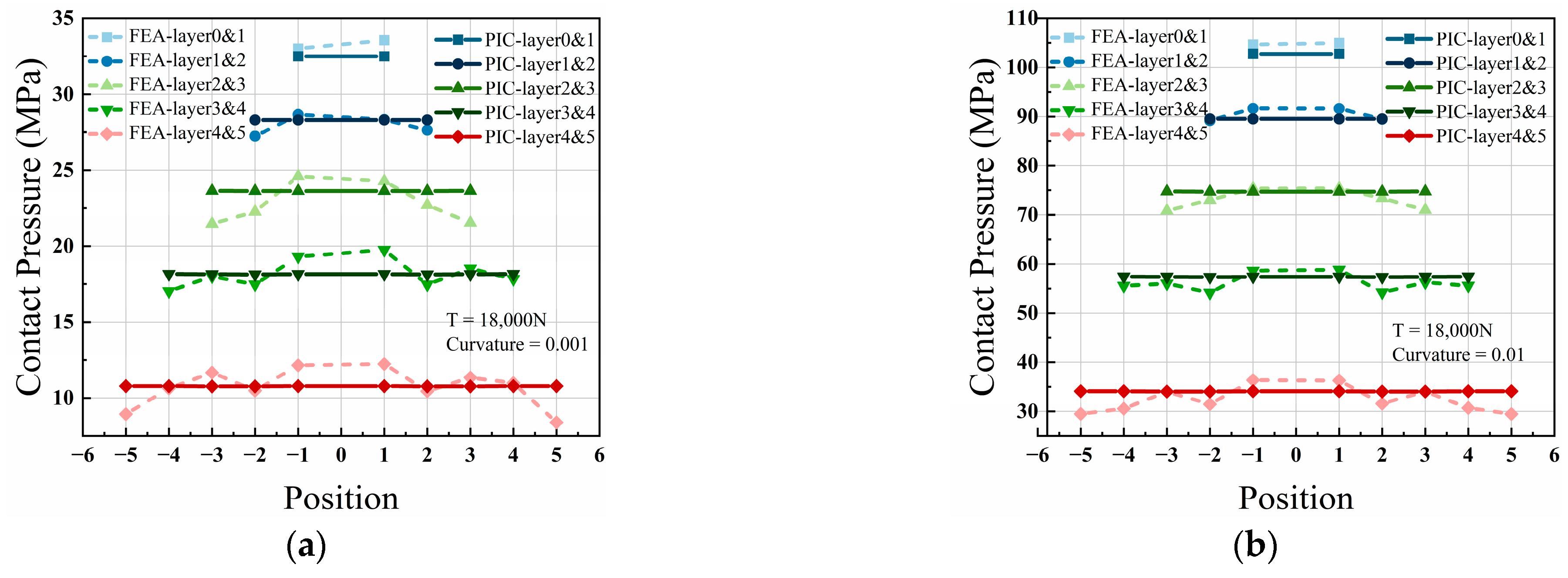
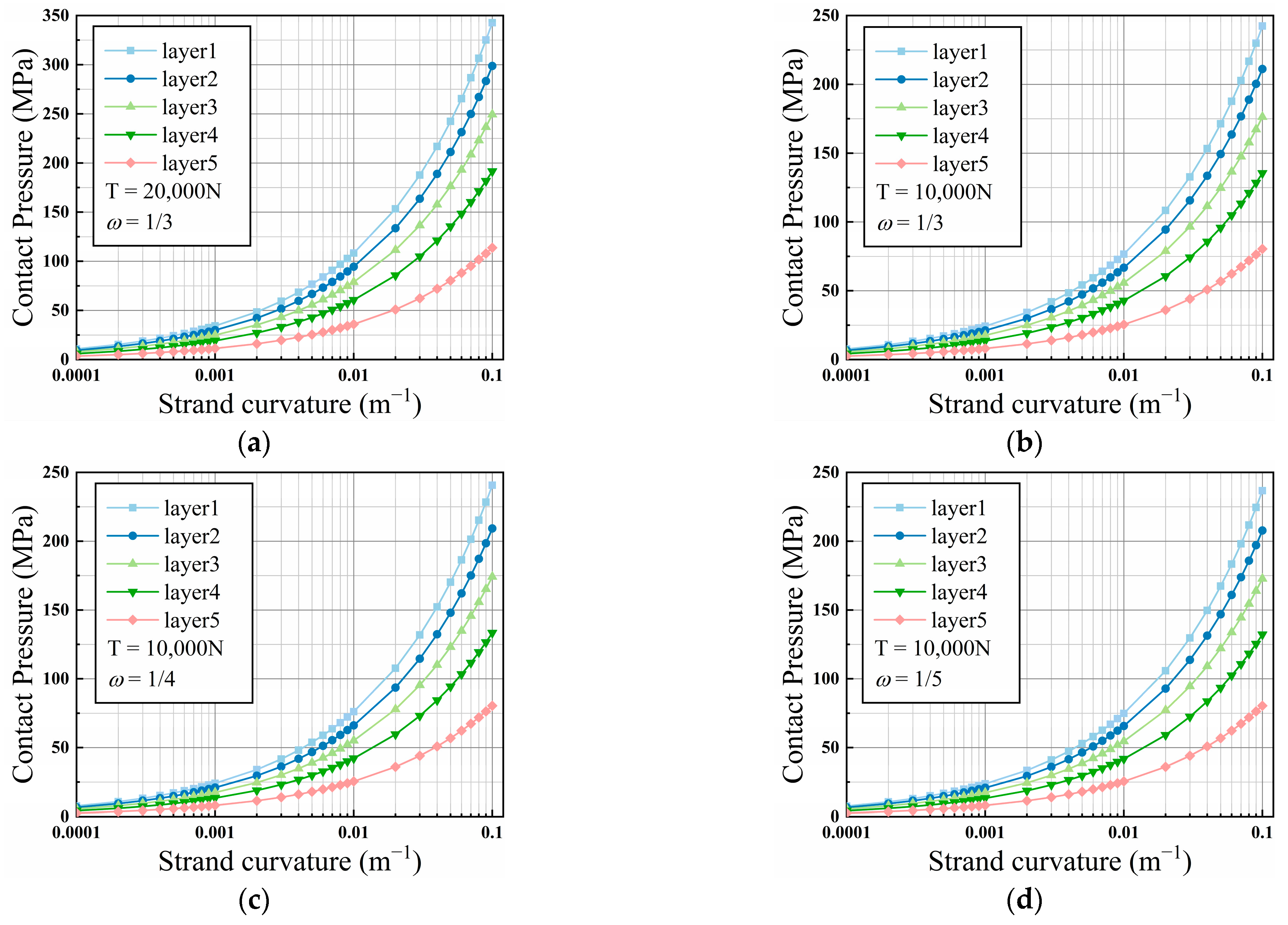
3.4. Validation for Wire Bending Model
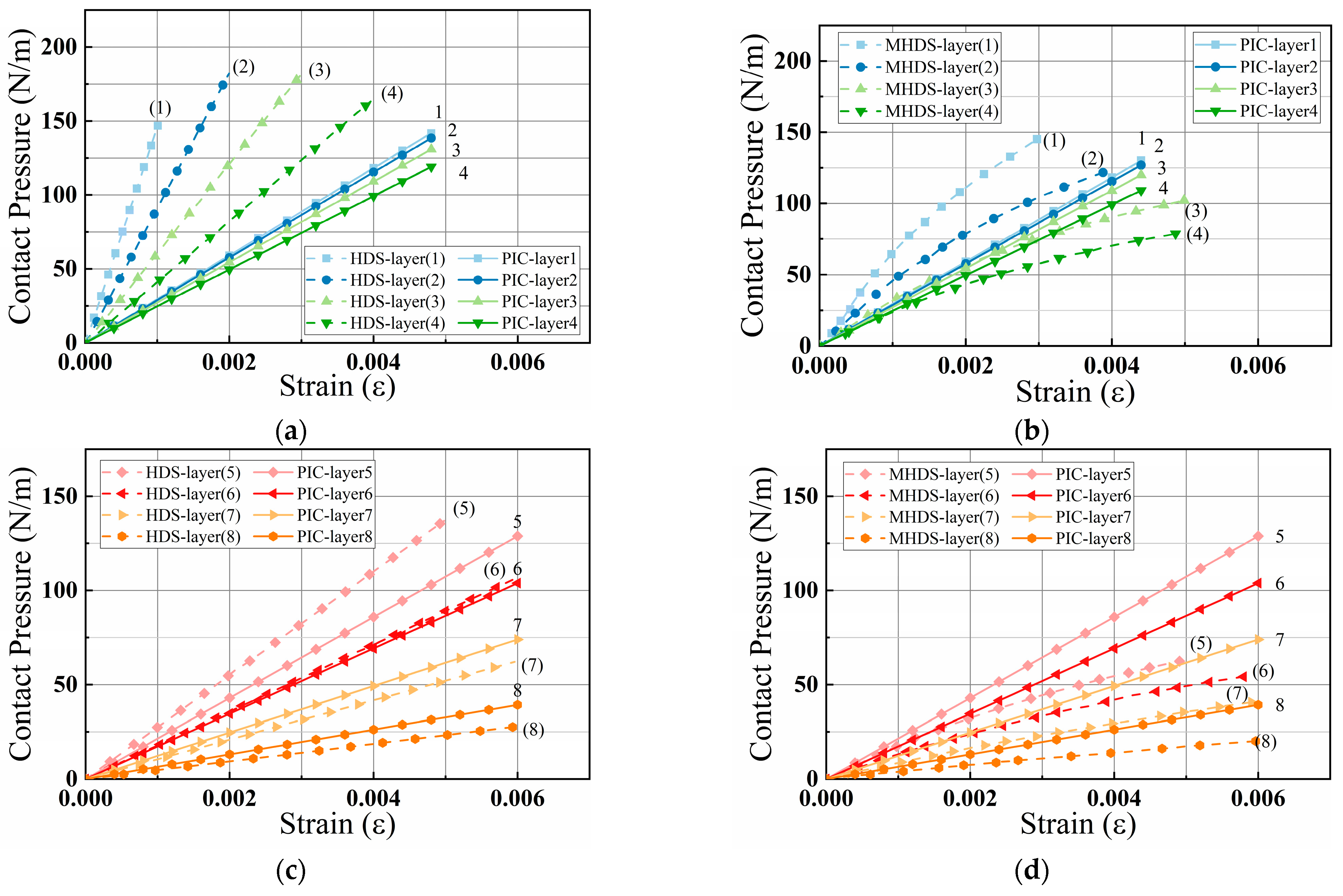
4. Fretting Wear Analysis Considering Internal Contact Pressure
4.1. Archard Wearing Model
4.2. Finite Element Model of Fretting Wear
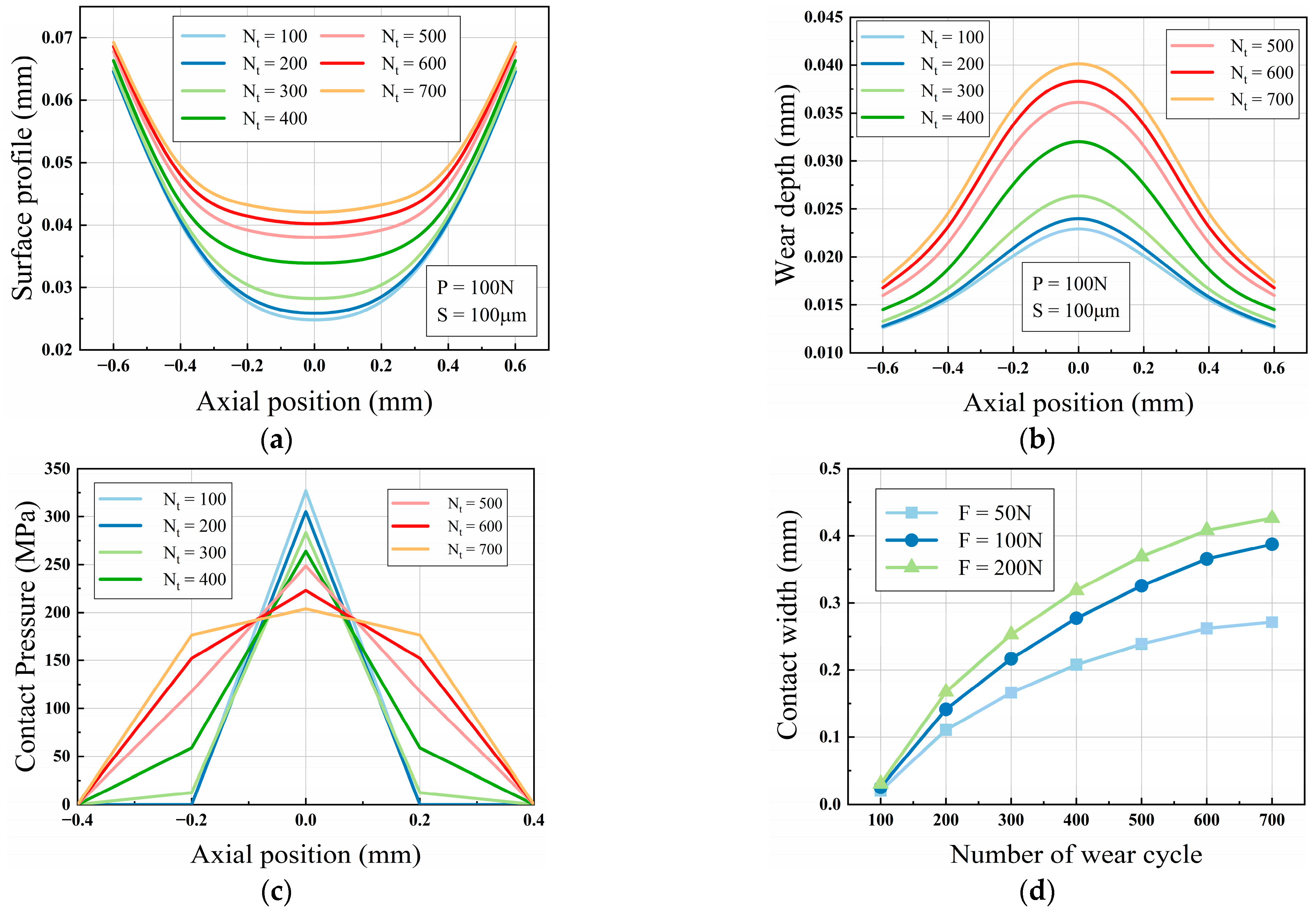
4.3. Result and Discussion
5. Conclusions
- For parallel wires, although the helix angle is relatively small, the contact pressure caused by twisting is still significant. Due to the different axial tension and twist angle, the magnitude of the contact pressure from twisting provided to the inner wire is mainly related to the position of the outer wire. The transmission of contact pressure has a cumulative effect, resulting in greater contact pressure for wires closer to the inner side. Within the same layer, the contact pressure is maximized at the points along the diagonal.
- The distribution of contact pressure between wires caused by sheath temperature shrinkage can be calculated according to the Boussinesq distribution. This assumption is reasonable when not considering variations in force chains caused by manufacturing errors. The results of calculations under this assumption show that the contact pressure between wires exhibits distinct layering, which is consistent with the results of finite element simulations.
- The contact pressure caused by the bending of the wire fluctuates with the variation in wire curvature during the vibration process of the stay cable and is also related to the axial tension of the wire. The cable exhibits distinct layering during the bending process, with relatively minor variations in contact pressure within the same layer. The wire curvature is the most significant factor influencing the contact pressure, showing an exponential relationship between the two. For cables with higher axial tension, the contact pressure is also greater, providing a lateral explanation for the delayed occurrence of slipping in stay cables with higher tensile forces. The location of the initial slipping within the cable cannot be determined to occur at the neutral axis or the outermost layer, owing to the different distributions of tangential force and interlayer frictional resistance within the stay cable.
- Based on the existing calculation results, fretting wear between two wires was simulated in finite element analysis. According to Archard’s theory of wear, it is possible to make certain estimations regarding the development of wear depth. Finite element analysis indicates that with an increase in cycle count, wear at the contact interface gradually becomes more uniform. The main reason for the averaging effect is the reduction in the disparity of contact pressure at various points. In addition, the width of the contact area at the interface increases in proportion to the increase in contact pressure. However, such an increase is not unlimited, as excessively high contact loads can change the contact mode from gross slip to partial slip, which complicates the wear analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Xie, X.; Zhao, J.L. Parametric vibration of carbon fiber reinforced plastic cables with damping effects in long-span cable-stayed bridges. J. Vib. Control 2011, 17, 2117–2130. [Google Scholar] [CrossRef]
- Zhuojie, Z. Mechanism and Mechanical Behavior of Delamination and Slippage between Wires or Strands of Cables for Large-Span Bridges; South China University of Technology: Guangzhou, China, 2016. [Google Scholar]
- Zhou, Z.; Leo, V. Fretting Wear; Science Press: Beijing, China, 2002. [Google Scholar]
- Cruzado, A.; Hartelt, M.; Wäsche, R.; Urchegui, M.A.; Gómez, X. Fretting wear of thin steel wires. Part 1: Influence of contact pressure. Wear 2010, 268, 1409–1416. [Google Scholar] [CrossRef]
- Chen, Y.P.; Meng, F.M. Numerical study on wear evolution and mechanical behavior of steel wires based on semi-analytical method. Int. J. Mech. Sci. 2018, 148, 684–697. [Google Scholar] [CrossRef]
- Zhang, D.; Ge, S.; Zhu, Z. Friction and Wear Performance on Fretting Wear of Steel Wires in Hoisting Ropes. J. China Univ. Min. Technol. 2002, 31, 367–370. [Google Scholar]
- Zhang, D.; ShiRong, G.E. Research on the contact mechanisms in the process of fretting wear between steel wires. J. Mech. Strength 2007, 29, 148–151. [Google Scholar]
- Yue, T.Y.; Wahab, M.A. A Review on Fretting Wear Mechanisms, Models and Numerical Analyses. Comput. Mater. Contin. 2019, 59, 405–432. [Google Scholar] [CrossRef]
- Wang, L.; Shen, R.L.; Zhang, S.H.; Bai, L.H.; Zhen, X.X.; Wang, R.H. Strand element analysis method for interaction between cable and saddle in suspension bridges. Eng. Struct. 2021, 242, 112283. [Google Scholar] [CrossRef]
- Wang, D.; Zhu, H.; Gao, W.; Zhang, D.; Tan, D.; Zhao, X. Research on Dynamic Contact and Slip Mechanisms of Parallel Steel Wires in the Main Cable of Suspension Bridge. J. Mech. Eng. 2021, 57, 228–242. [Google Scholar]
- Zhang, H.; Yao, L.J.; Zheng, X.L.; Shen, M.J.; Xie, X. Corrosion-Fatigue Analysis of Wires in Bridge Cables Considering Time-Dependent Electrochemical Corrosion Process. J. Eng. Mech. 2023, 149. [Google Scholar] [CrossRef]
- Zhongxiang, L. Study on Damage Mechanism and Life Assessment of Bridge Suspenders under Coupled Corrosion-Fretting Fatigue; Southeast University: Nanjing, China, 2019. [Google Scholar]
- Wang, D.; Zhang, J. Prediction of Fretting Fatigue Crack Propagation Life of Steel Wire Considering Fretting Wear. Tribology 2021, 41, 710–722. [Google Scholar] [CrossRef]
- Llavori, I.; Zabala, A.; Urchegui, M.A.; Tato, W.; Gómez, X. A coupled crack initiation and propagation numerical procedure for combined fretting wear and fretting fatigue lifetime assessment. Theor. Appl. Fract. Mech. 2019, 101, 294–305. [Google Scholar] [CrossRef]
- Starkey, W.L.; Cress, H.A. An Analysis of Critical Stresses and Mode of Failure of a Wire Rope. J. Manuf. Sci. Eng. 1959, 81, 307–311. [Google Scholar] [CrossRef]
- Utting, W.S.; Jones, N. The response of wire rope strands to axial tensile loads—Part II. Comparison of experimental results and theoretical predictions. Int. J. Mech. Sci. 1987, 29, 621–636. [Google Scholar] [CrossRef]
- Utting, W.S.; Jones, N. The response of wire rope strands to axial tensile loads—Part I. Experimental results and theoretical predictions. Int. J. Mech. Sci. 1987, 29, 605–619. [Google Scholar] [CrossRef]
- McColl, I.R.; Ding, J.; Leen, S.B. Finite element simulation and experimental validation of fretting wear. Wear 2004, 256, 1114–1127. [Google Scholar] [CrossRef]
- Ghoreishi, S.R.; Messager, T.; Cartraud, P.; Davies, P. Validity and limitations of linear analytical models for steel wire strands under axial loading, using a 3D FE model. Int. J. Mech. Sci. 2007, 49, 1251–1261. [Google Scholar] [CrossRef]
- Meng, F.M.; Chen, Y.P.; Du, M.G.; Gong, X.S. Study on effect of inter-wire contact on mechanical performance of wire rope strand based on semi-analytical method. Int. J. Mech. Sci. 2016, 115, 416–427. [Google Scholar] [CrossRef]
- Chen, Y.P.; Meng, F.M.; Gong, X.S. Full contact analysis of wire rope strand subjected to varying loads based on semi-analytical method. Int. J. Solids Struct. 2017, 117, 51–66. [Google Scholar] [CrossRef]
- Huang, N.C. Finite extension of an elastic strand with a central core. J. Appl. Mech.-Trans. Asme 1978, 45, 852–858. [Google Scholar] [CrossRef]
- Gnanavel, B.K.; Parthasarathy, N.S. Effect of interfacial contact forces in radial contact wire strand. Arch. Appl. Mech. 2011, 81, 303–317. [Google Scholar] [CrossRef]
- Leclair, R.A. Axial response of multilayered strands with compliant layers. J. Eng. Mech.-Asce 1991, 117, 2884–2903. [Google Scholar] [CrossRef]
- Johansson, L. Numerical Simulation of Contact Pressure Evolution in Fretting. J. Tribol. 1994, 116, 247–254. [Google Scholar] [CrossRef]
- Yu, Y. Semi-Refined Finite Element Model of Cable and Its Application on Bending Behavior and Wire Break; Tianjin University: Tianjin, China, 2015. [Google Scholar]
- Waisman, H.; Montoya, A.; Betti, R.; Noyan, I.C. Load Transfer and Recovery Length in Parallel Wires of Suspension Bridge Cables. J. Eng. Mech. 2011, 137, 227–237. [Google Scholar] [CrossRef]
- Montoya, A.; Waisman, H.; Betti, R. A simplified contact-friction methodology for modeling wire breaks in parallel wire strands. Comput. Struct. 2012, 100, 39–53. [Google Scholar] [CrossRef]
- Zheng, G.; Li, H. Normal Stress between Steel Wires in the Stay-cable. In Proceedings of the International Conference on Intelligent Structure and Vibration Control (ISVC 2011), Chongqing, China, 14–16 January 2011; pp. 541–546. [Google Scholar]
- Brügger, A.; Lee, S.Y.; Mills, J.A.A.; Betti, R.; Noyan, I.C. Partitioning of Clamping Strains in a Nineteen Parallel Wire Strand. Exp. Mech. 2017, 57, 921–937. [Google Scholar] [CrossRef]
- Brügger, A.; Lee, S.Y.; Robinson, J.; Morgantini, M.; Betti, R.; Noyan, I.C. Internal Contact Mechanics of 61-Wire Cable Strands. Exp. Mech. 2022, 62, 1475–1488. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, J.Q.; Mutoh, Y. Evaluation of fretting wear based on the frictional work and cyclic saturation concepts. Int. J. Mech. Sci. 2008, 50, 897–904. [Google Scholar] [CrossRef]
- Argatov, I.; Chai, Y.S. Contact Geometry Adaptation in Fretting Wear: A Constructive Review. Front. Mech. Eng. 2020, 6, 51. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, Z.H.; Liu, H.B. Advanced approaches to calculate recovery length and force redistribution in semi-parallel wire cables with broken wires. Eng. Struct. 2017, 131, 44–56. [Google Scholar] [CrossRef]
- Sun, G.; Chen, Z.; Liu, Z. Analytical and Experimental Investigation of Thermal Expansion Mechanism of Steel Cables. 2011, 23, 1017–1027. J. Mater. Civ. Eng. [CrossRef]
- Hongying, J.; Tiande, M.; Jingbu, L.U. A probabilistic model for force transmission in two dimensional granular packs. Chin. J. Geotech. Eng. 2006, 28, 881–885. [Google Scholar]
- Liu, Y.; Miao, F.; Miao, T. Force distributions in two dimensional granular packs. Chin. J. Geotech. Eng. 2005, 27, 468–473. [Google Scholar]
- Hong, K.J.; Kiureghian, A.D.; Sackman, J.L. Bending behavior of helically wrapped cables. J. Eng. Mech.-Asce 2005, 131, 500–511. [Google Scholar] [CrossRef]
- Khan, S.W.; Gencturk, B.; Shahzada, K.; Ullah, A. Bending Behavior of Axially Preloaded Multilayered Spiral Strands. J. Eng. Mech. 2018, 144. [Google Scholar] [CrossRef]
- Wensrich, C.M.; Kisi, E.H.; Zhang, J.F.; Kirstein, O. Measurement and analysis of the stress distribution during die compaction using neutron diffraction. Granul. Matter 2012, 14, 671–680. [Google Scholar] [CrossRef]




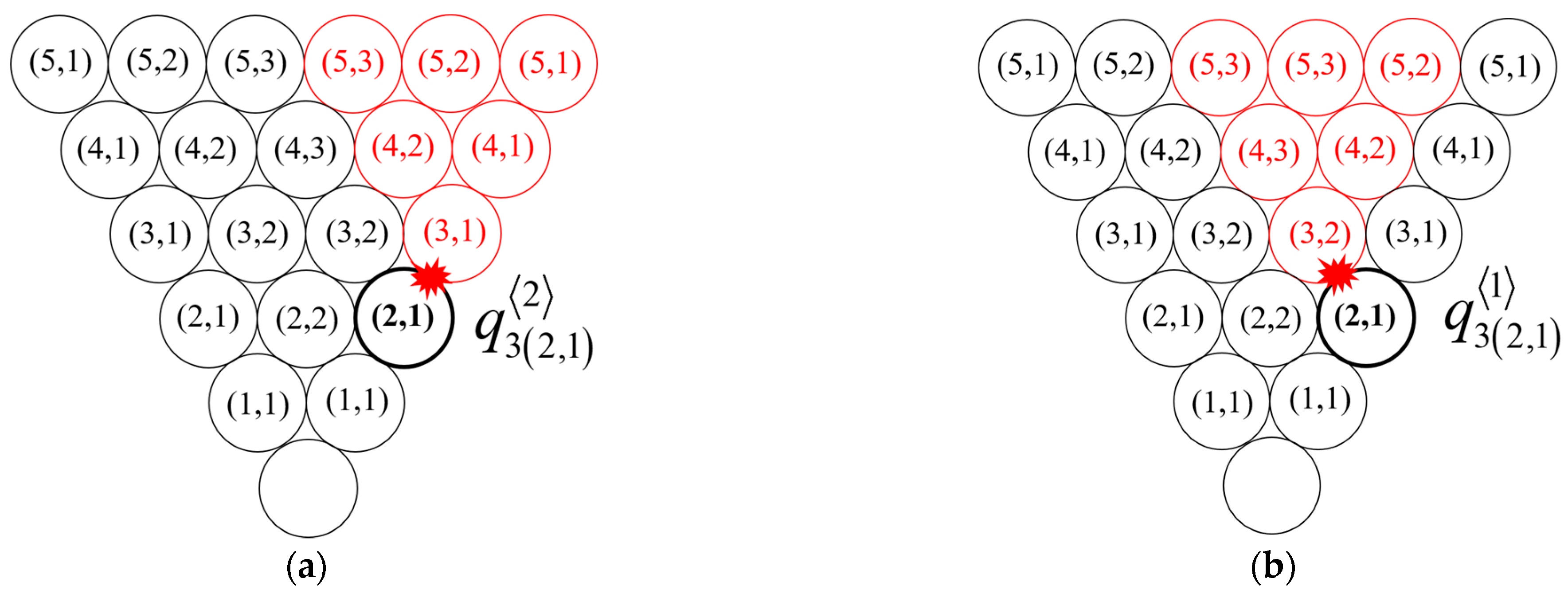

| Layer | x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|
| 1 | y | 1.000 | —— | —— | —— | —— | —— | —— |
| 2 | —— | 0.500 | —— | —— | —— | —— | —— | |
| 3 | 0.500 | —— | 0.417 | —— | —— | —— | —— | |
| 4 | —— | 0.319 | —— | 0.347 | —— | —— | —— | |
| 5 | 0.106 | —— | 0.324 | —— | 0.289 | —— | —— | |
| 6 | —— | 0.107 | —— | 0.318 | —— | 0.241 | —— | |
| 7 | 0.036 | —— | 0.142 | —— | 0.305 | —— | 0.201 |
| Wire radius | 3.5 | |||
| Young modulus | 210 | |||
| Poisson’s ratio | 0.3 | |||
| Positive pressure | 50 | 100 | 200 | |
| Wear coefficient | 8.2 × 10−8 | |||
| Wire displacement | 100 | |||
| Cycle number | 100~700 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Fan, T. A Theoretical Method for Calculating the Internal Contact Pressure of Parallel Wire Cable during Fretting Wear. Appl. Sci. 2024, 14, 1401. https://doi.org/10.3390/app14041401
Zhang Z, Fan T. A Theoretical Method for Calculating the Internal Contact Pressure of Parallel Wire Cable during Fretting Wear. Applied Sciences. 2024; 14(4):1401. https://doi.org/10.3390/app14041401
Chicago/Turabian StyleZhang, Zhicheng, and Taiheng Fan. 2024. "A Theoretical Method for Calculating the Internal Contact Pressure of Parallel Wire Cable during Fretting Wear" Applied Sciences 14, no. 4: 1401. https://doi.org/10.3390/app14041401
APA StyleZhang, Z., & Fan, T. (2024). A Theoretical Method for Calculating the Internal Contact Pressure of Parallel Wire Cable during Fretting Wear. Applied Sciences, 14(4), 1401. https://doi.org/10.3390/app14041401






