Critically Leveraging Theory for Optimal Control of Quadrotor Unmanned Aircraft Systems
Abstract
:1. Introduction
2. The Structure and Mathematical Model of the Quadrotor
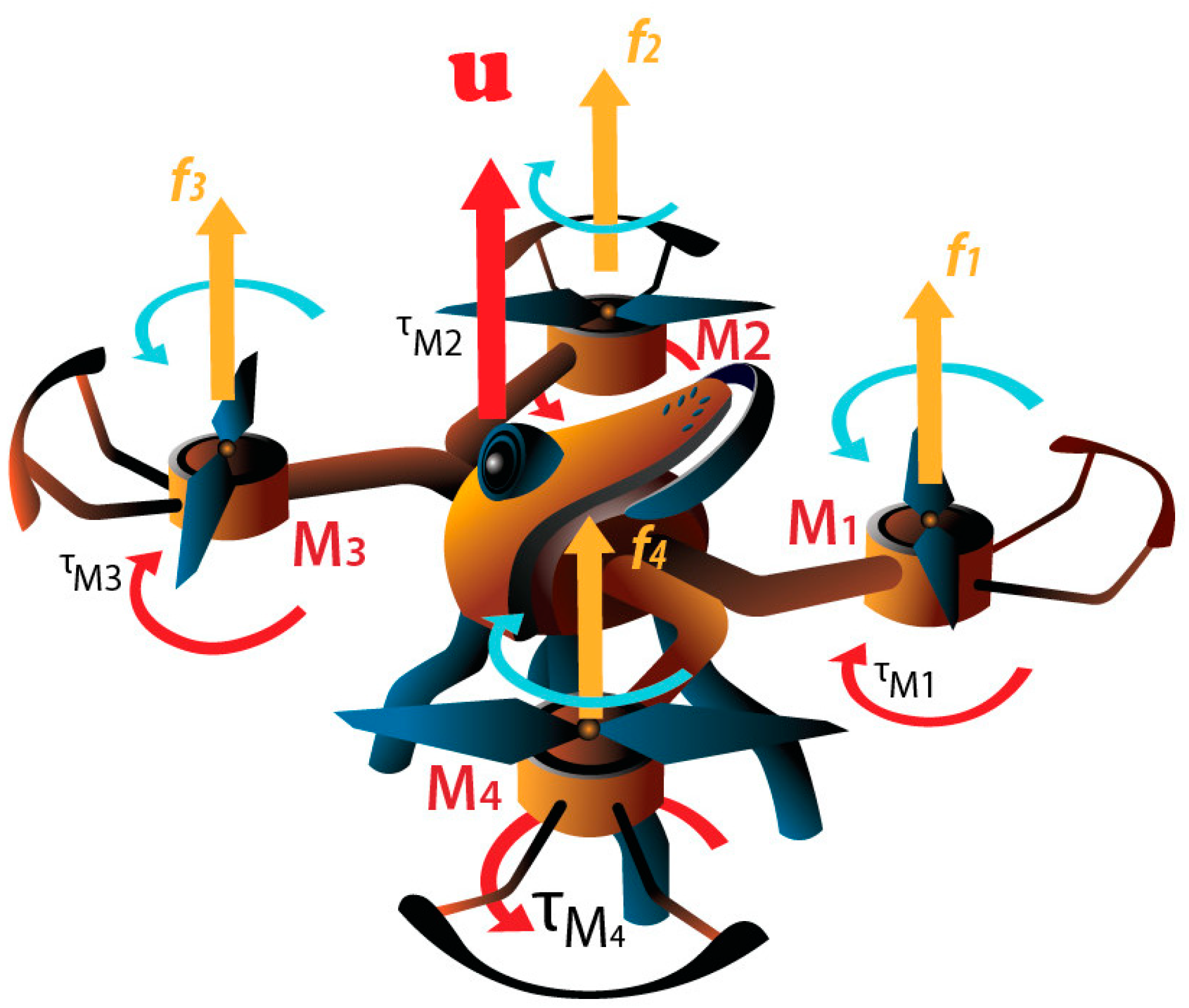
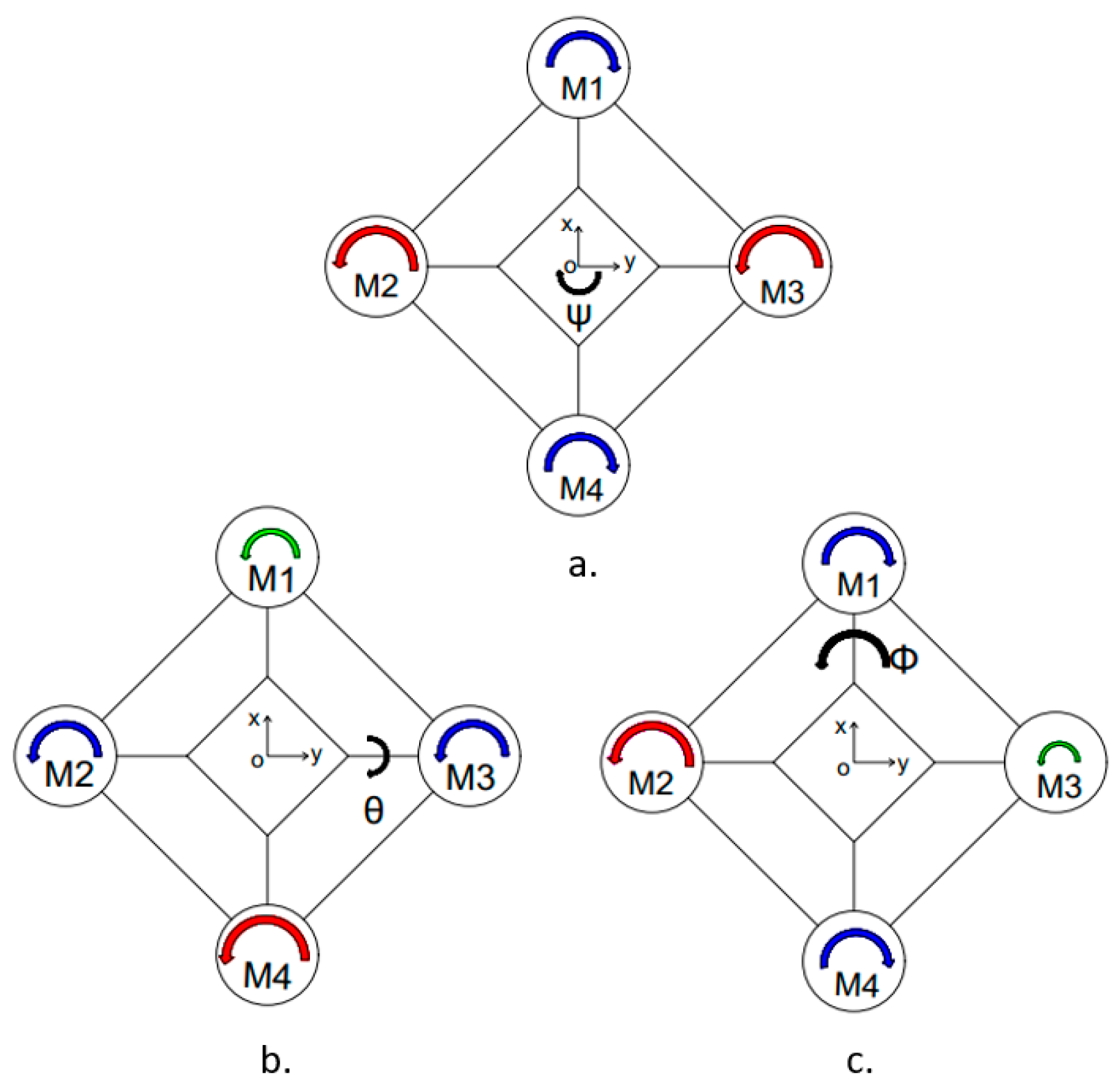
2.1. Structure and Working Principle
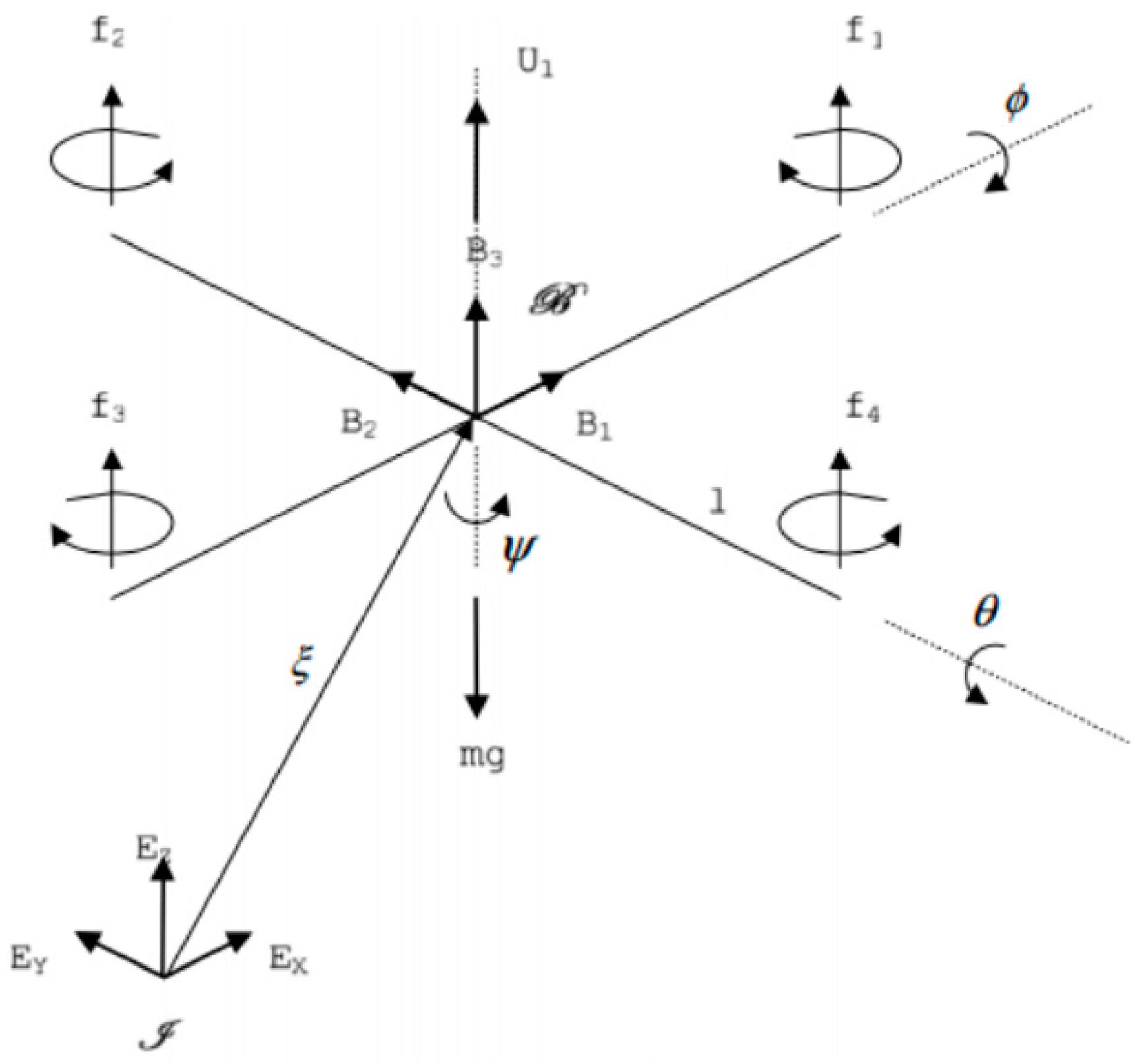
2.2. Drone Kinematics
2.3. Euler–Lagrange Equation
3. Optimized Controller Design for Quadrotor
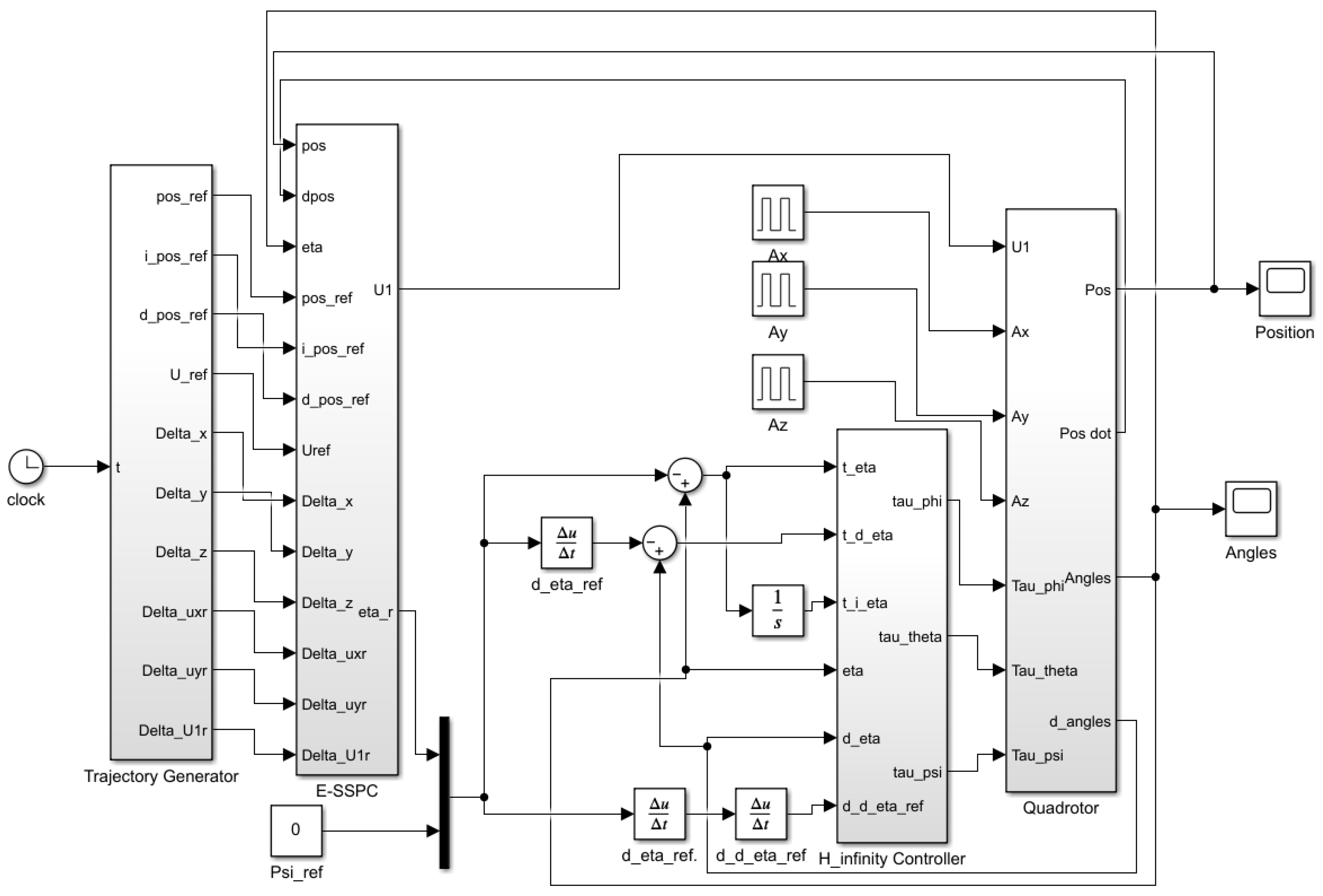
3.1. Controller Design
3.2. E-SSPC for Orbital Tracking
- are the set states and control inputs, respectively. Assume there are no external disturbances in the virtual device. This virtual device allows us to obtain set control inputs for translational motions, assuming that the Quadrotor’s height is stable. Therefore, in this case, the set values are:
3.3. Nonlinear Control for Rotational Subsystem
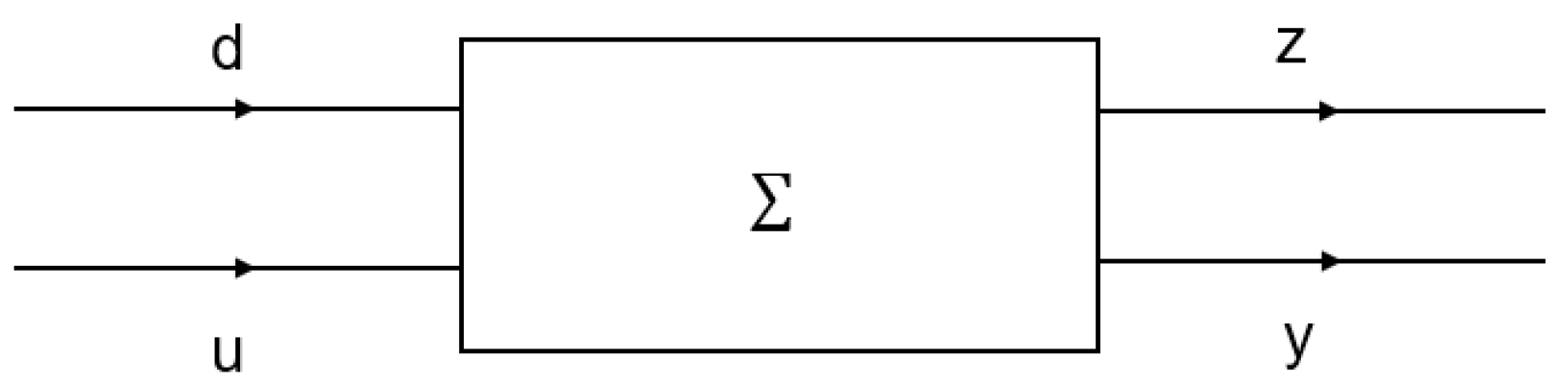
- where u is the control vector, d is the input noise (noise to be suppressed or the signal to be tracked), y is the metering output, and z is the control lever output (tracking error, cost function). The optimal control problem , roughly speaking, is to find a controller C that handles the output y and modulates the input u so that it is a closed loop:
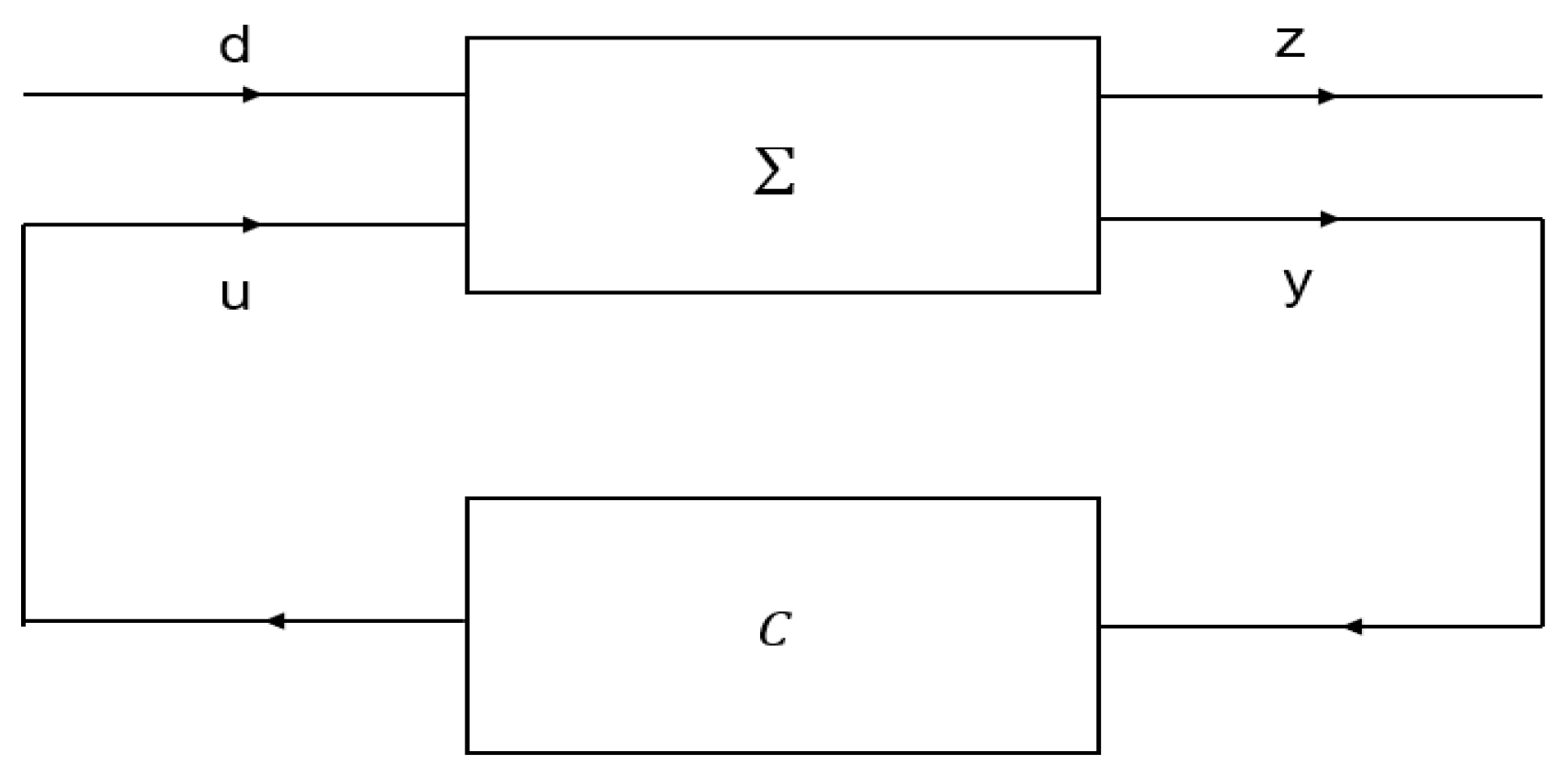
3.4. Kalman Filter
- -
- Prediction:
- -
- Update:
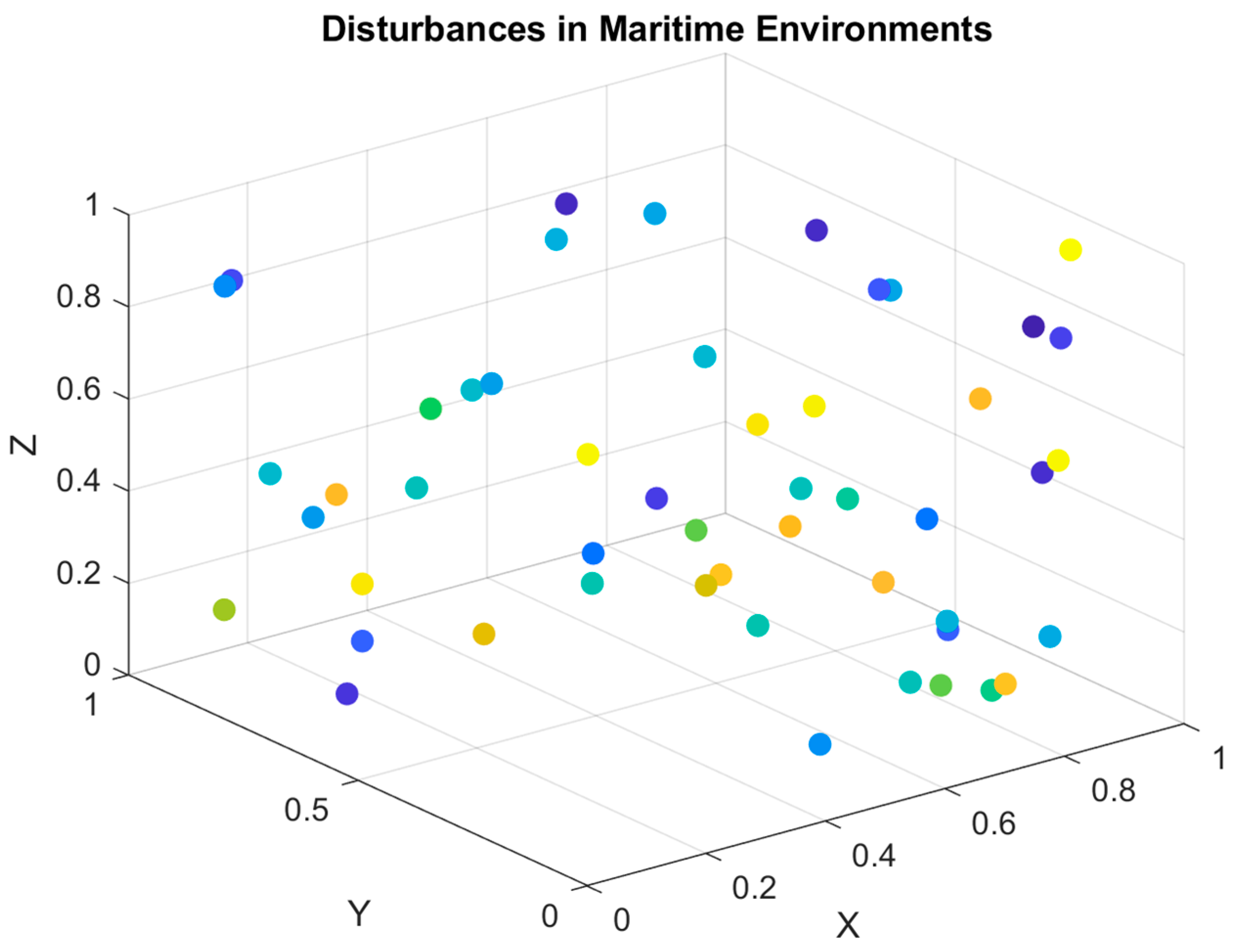
3.5. Evaluating Quadrotor Controller Robustness to Disturbances in Maritime Environments
4. Optimized Controller Design for Quadrotor
4.1. Nonlinear Control for Rotational Subsystem
4.2. Control Parameters
4.3. Kalman Filter
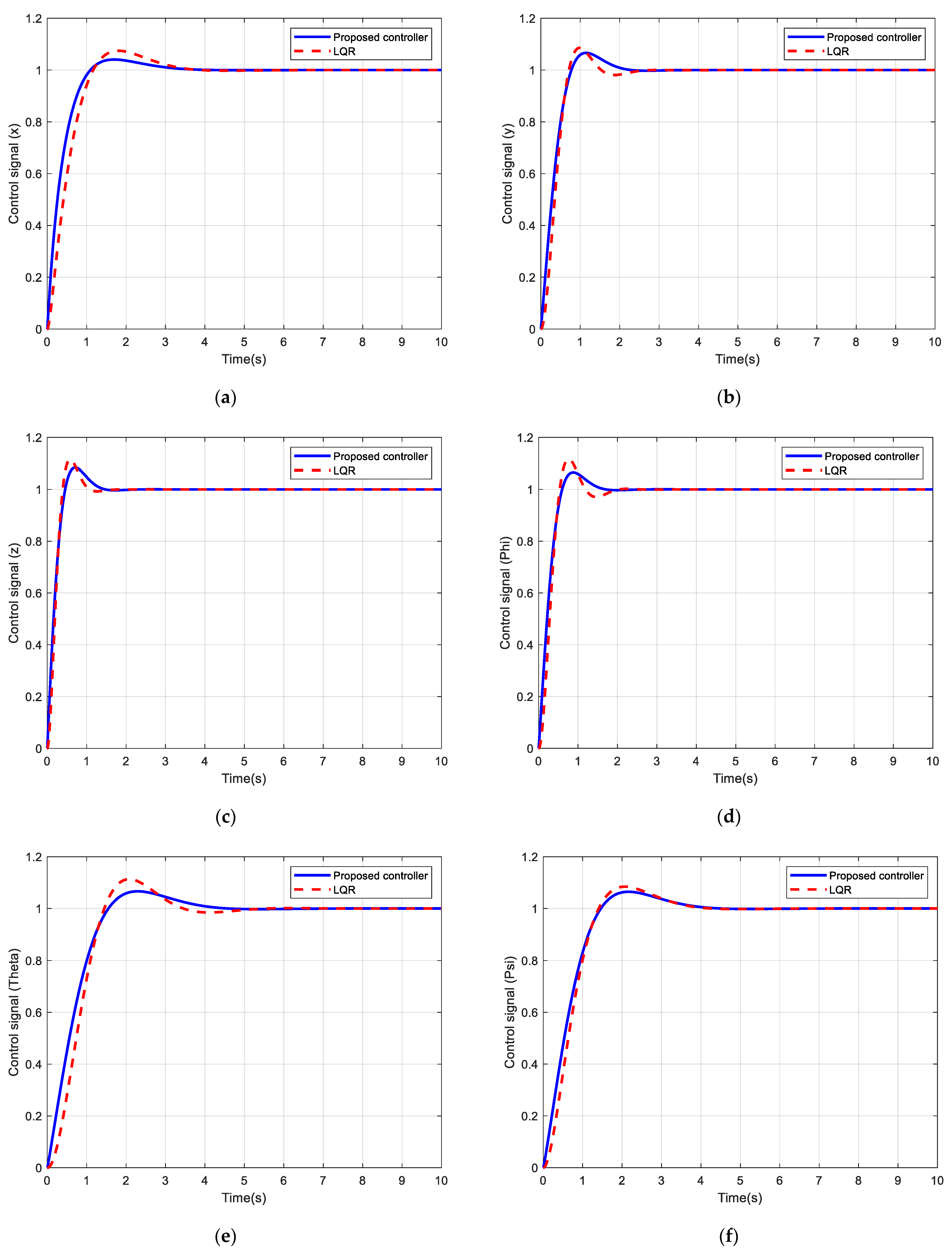
4.4. Results
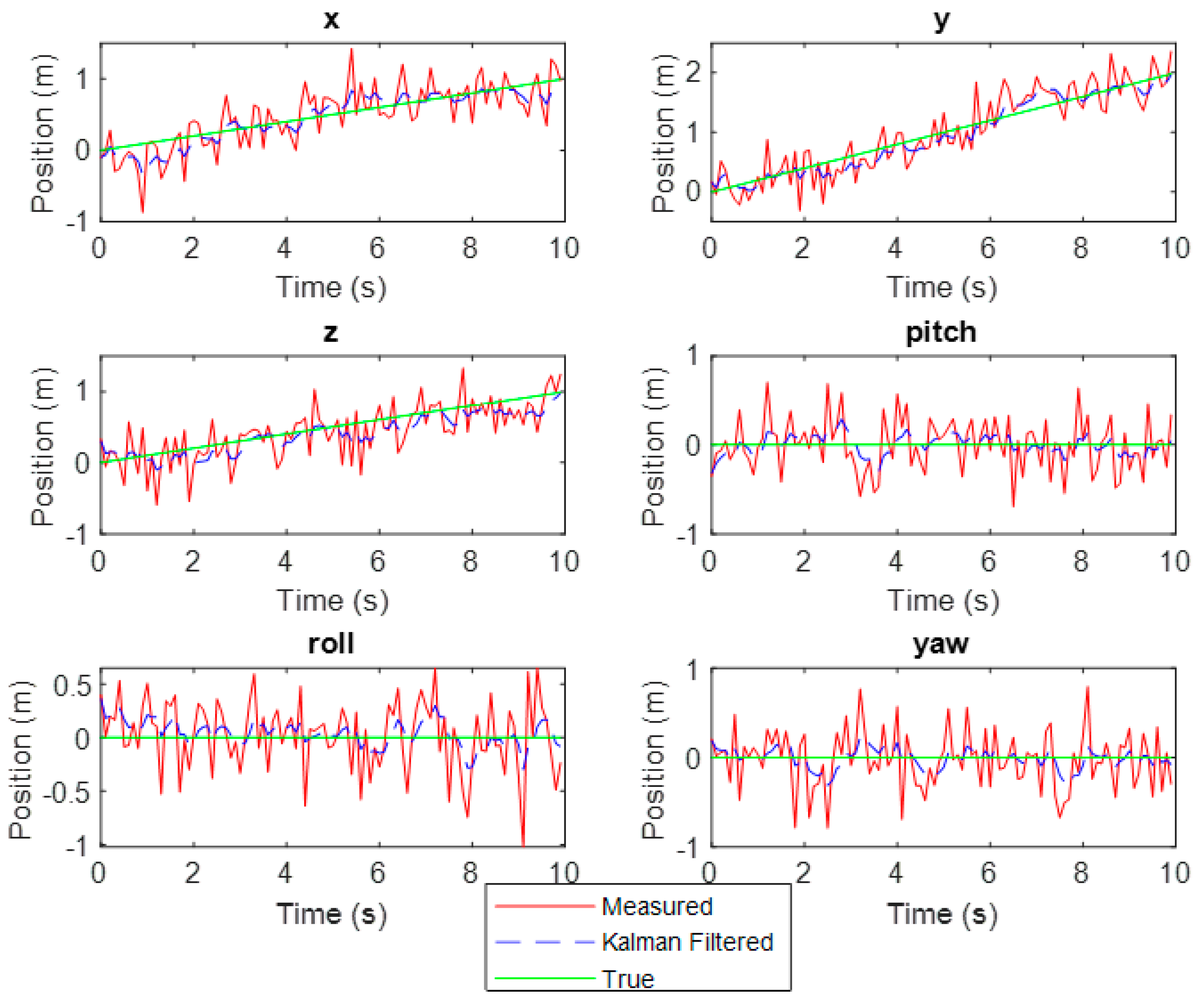
- -
- For position variables x, y, z, the transient time is 0.3 s, 0.2 s, and 0.3 s, respectively.
- -
- For rotation angle variables, transient time < 0.2 s.
- -
- In the case of noise affecting the object during operation.
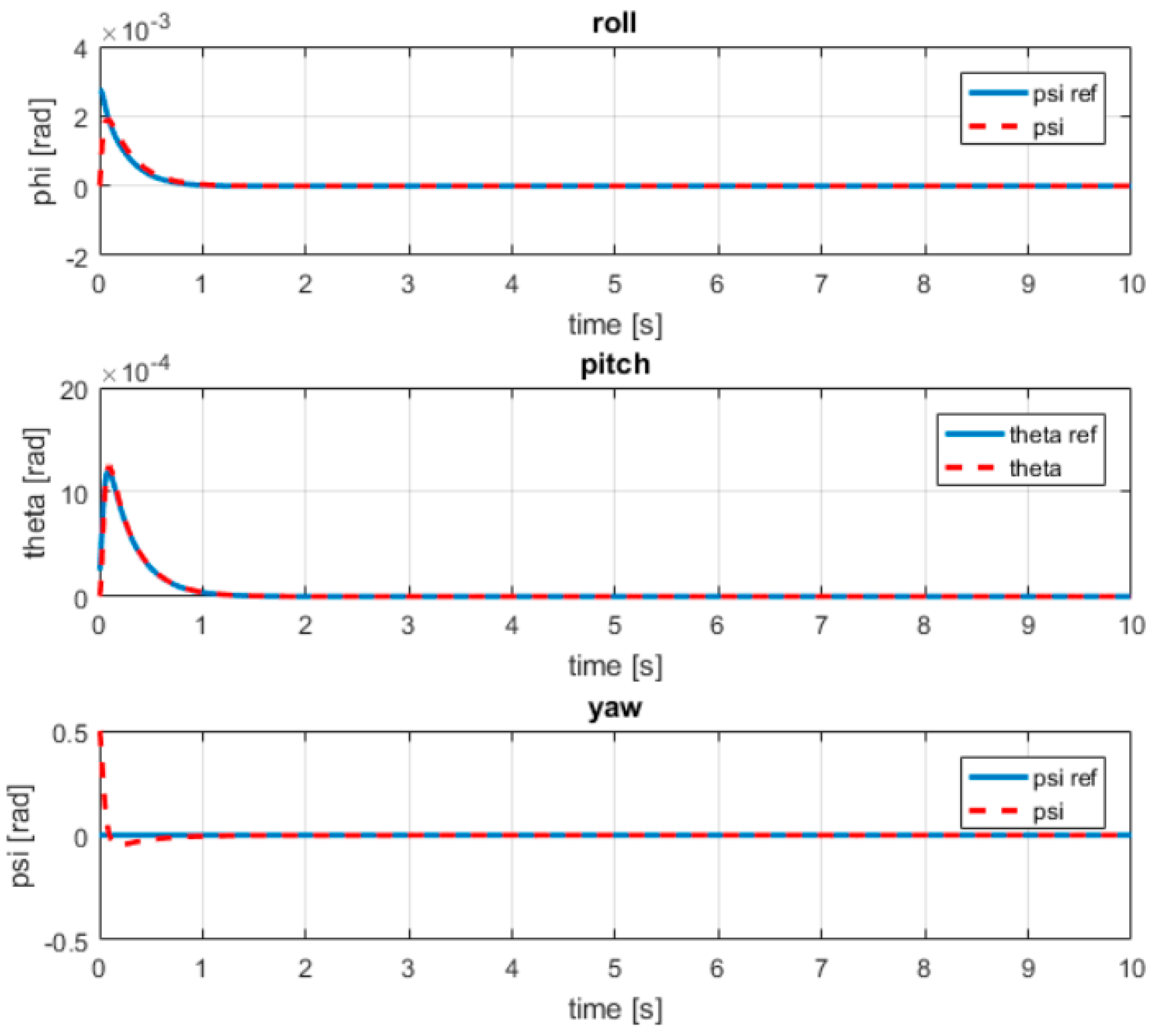
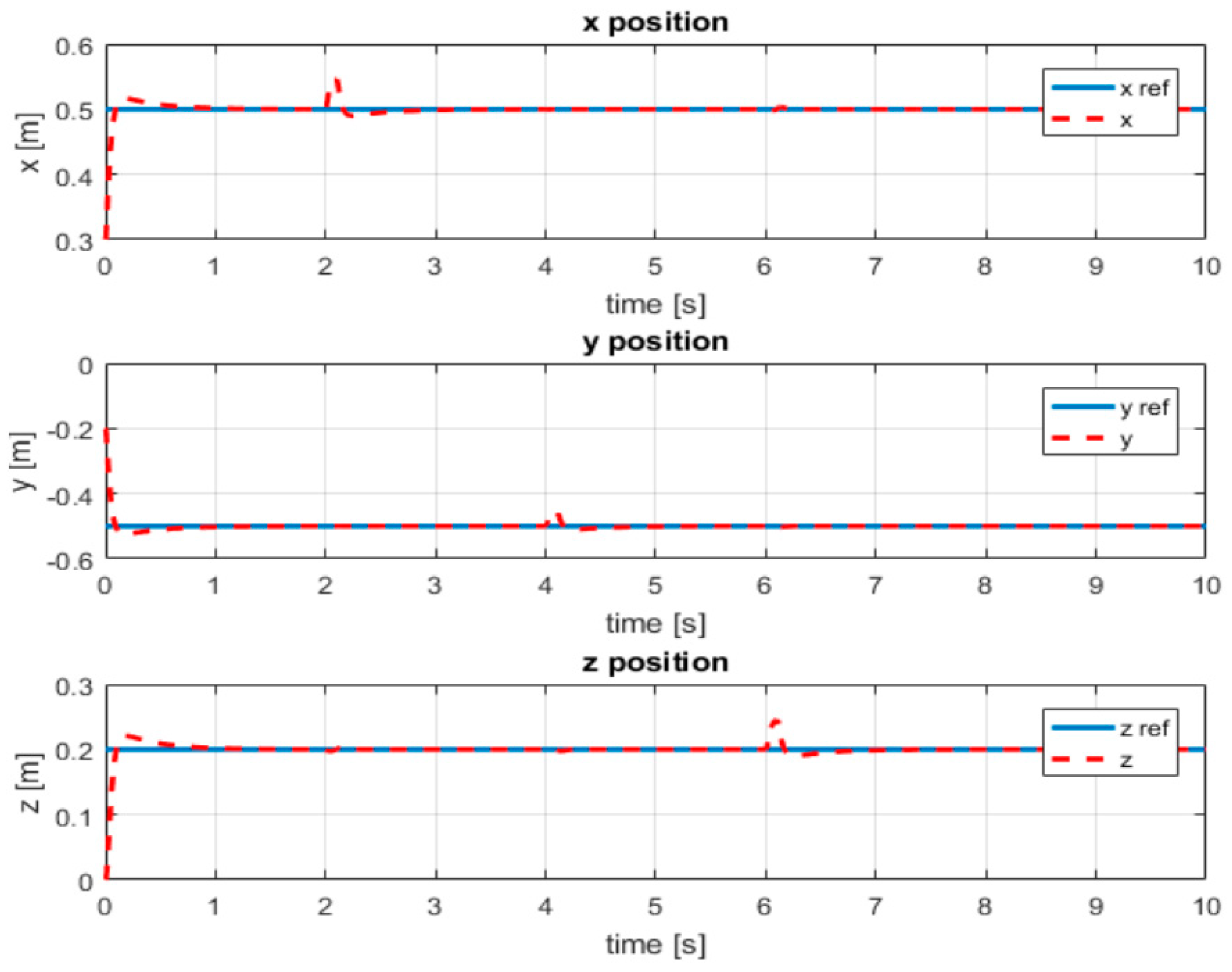
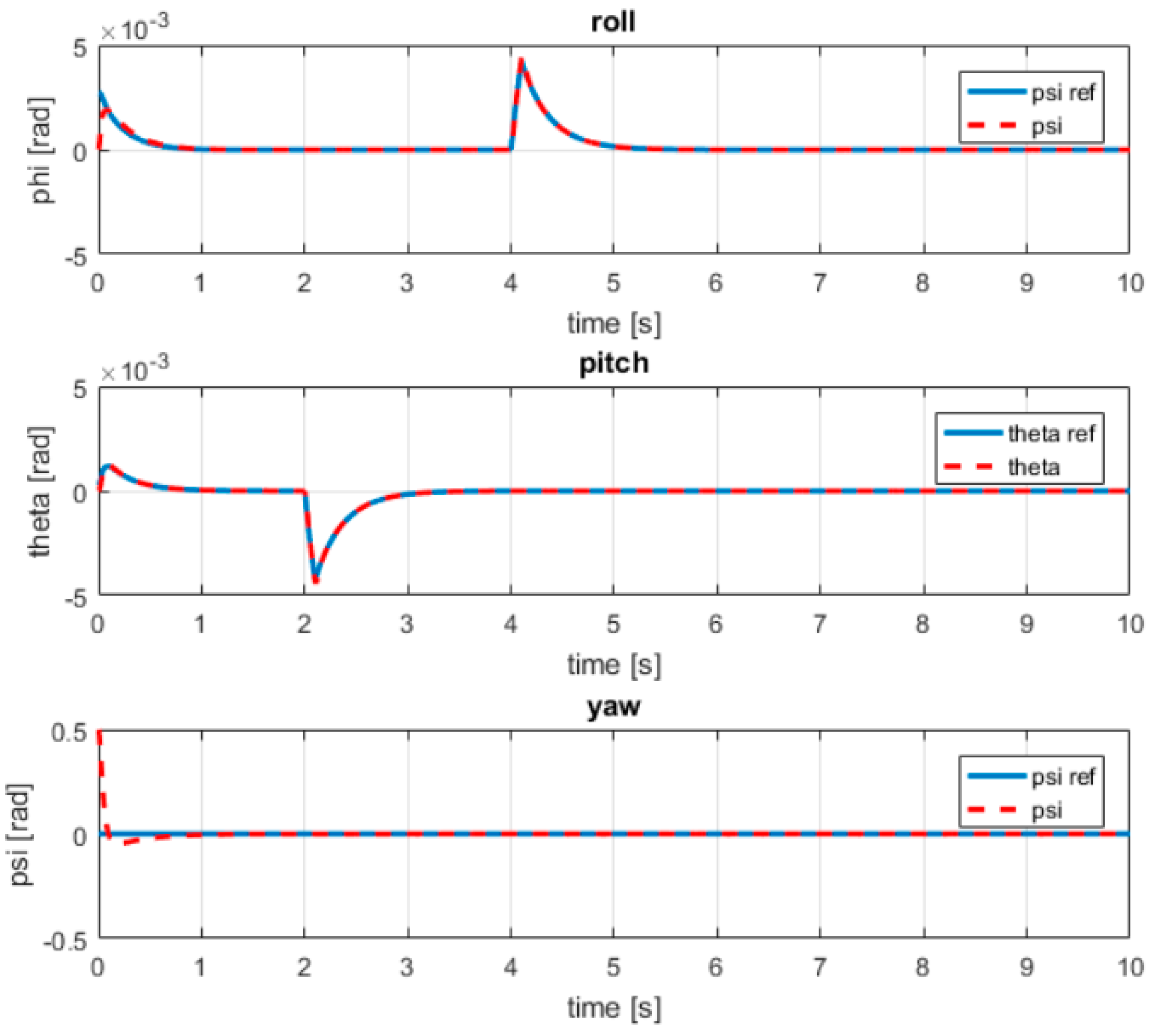
4.5. Evaluating Quadrotor Controller Robustness to Disturbances in Maritime Environments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| UAV | Unmanned Aerial Vehicle |
| E-SSPC | Error model State Space Predictive Controller |
| MPC | Energy of a system |
| AI | Artificial Intelligence |
References
- Moon, J.S.; Kim, C.; Youm, Y.; Bae, J. UNI-Copter: A portable single-rotor-powered spherical unmanned aerial vehicle (UAV) with an easy-to-assemble and flexible structure. J. Mech. Sci. Technol. 2018, 32, 2289–2298. [Google Scholar] [CrossRef]
- Cheng, E. Aerial Photography and Videography Using Drones; Peachpit Press: Berkeley, CA, USA, 2015. [Google Scholar]
- Shah, T.A.; Ullah, I.; Khan, M.A.; Lorenz, P.; Innab, N. An Efficient Certificateless Forward-Secure Signature Scheme for Secure Deployments of the Internet of Things. J. Sens. Actuator Netw. 2023, 12, 10. [Google Scholar] [CrossRef]
- Choi, C.H.; Jang, H.J.; Lim, S.G.; Lim, H.C.; Cho, S.H.; Gaponov, I. Automatic wireless drone charging station creating essential environment for continuous drone operation. In Proceedings of the 2016 International Conference on Control, Automation and Information Sciences (ICCAIS), Ansan, Republic of Korea, 27–29 October 2016. [Google Scholar]
- Ganji, E.; Grenzdörffer, G.; Andert, S. Estimating the Reduction in Cover Crop Vitality Followed by Pelargonic Acid Application Using Drone Imagery. Agronomy 2023, 13, 354. [Google Scholar] [CrossRef]
- Li, J.; Lan, Y.; Shi, Y. Research progress on airflow characteristics and field pesticide application system of rotary-wing UAV. Trans. Chin. Soc. Agric. Eng. 2018, 34, 104–118. [Google Scholar]
- Pirker, D.; Fischer, T.; Lesjak, C.; Steger, C. Global and secured uav authentication system based on hardware-security. In Proceedings of the 2020 8th IEEE International Conference on Mobile Cloud Computing, Services, and Engineering (MobileCloud), Oxford, UK, 3–6 August 2020. [Google Scholar]
- Yang, G.; Lin, X.; Li, Y.; Cui, H.; Xu, M.; Wu, D.; Rydén, H.; Redhwan, S.B. A telecom perspective on the internet of drones: From LTE-advanced to 5G. arXiv 2018, arXiv:1803.11048. [Google Scholar]
- Mo, H.; Ghulam, F. Nonlinear and adaptive intelligent control techniques for quadrotor uav—A survey. Asian J. Control 2019, 21, 989–1008. [Google Scholar] [CrossRef]
- Ducard, G.J.J.; Allenspach, M. Review of designs and flight control techniques of hybrid and convertible VTOL UAVs. Aerosp. Sci. Technol. 2021, 118, 107035. [Google Scholar] [CrossRef]
- Liu, Z.; He, Y.; Yang, L.; Han, J. Control techniques of tilt rotor unmanned aerial vehicle systems: A review. Chin. J. Aeronaut. 2017, 30, 135–148. [Google Scholar] [CrossRef]
- Pham, D.-A.; Han, S.-H. Design of Combined Neural Network and Fuzzy Logic Controller for Marine Rescue Drone Trajectory-Tracking. J. Mar. Sci. Eng. 2022, 10, 1716. [Google Scholar] [CrossRef]
- Qian, L.; Liu, H.H.T. Path-Following Control of A Quadrotor UAV With A Cable-Suspended Payload Under Wind Disturbances. IEEE Trans. Ind. Electron. 2020, 67, 2021–2029. [Google Scholar] [CrossRef]
- Welch, G.F. Kalman filter. In Computer Vision: A Reference Guide; Springer: Boston, MA, USA, 2020; pp. 1–3. [Google Scholar]
- Maybeck, P.S. The Kalman filter: An introduction to concepts. In Autonomous Robot Vehicles; Springer: New York, NY, USA, 1990; pp. 194–204. [Google Scholar]
- Kim, K.J. Dynamic virtual work principle versus virtual power principle for systems with non-holonomic constraints. J. Mech. Sci. Technol. 2022, 36, 2239–2257. [Google Scholar] [CrossRef]
- Yan, J.; Wang, X.; Yu, Y. Distance-based Formation Control for Fixed-wing UAVs Subject to Positive Minimum Linear Velocity Constraints. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022. [Google Scholar]
- Nascimento, T.P.; Dórea, C.E.T.; Gonçalves, L.M.G. Nonholonomic mobile robots’ trajectory tracking model predictive control: A survey. Robotica 2018, 36, 676–696. [Google Scholar] [CrossRef]
- Elijah, T.; Jamisola, R.S., Jr.; Tjiparuro, Z.; Namoshe, M. A review on control and maneuvering of cooperative fixed-wing drones. Int. J. Dyn. Control 2021, 9, 1332–1349. [Google Scholar] [CrossRef]
- Gul, F.; Alhady, S.S.N.; Rahiman, W. A review of controller approach for autonomous guided vehicle system. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 552–562. [Google Scholar]
- Castillo, R.L.G.; Lospez, A.E.D.; Lozano, R.; Pégard, C. Quadrotorcraft Control; Springer: London, UK, 2013. [Google Scholar]
- Fantoni, I.; Lozano, R. Non-Linear Control for Underactuated Mechanical Systems; Springer: London, UK, 2002. [Google Scholar]
- Omar, H.M.; Mukras, S.M.S. Integrating anti-swing controller with px4 autopilot for quadrotor with suspended load. J. Mech. Sci. Technol. 2022, 36, 1511–1519. [Google Scholar] [CrossRef]
- Lee, C.; An, D. Reinforcement learning and neural network-based artificial intelligence control algorithm for self-balancing quadruped robot. J. Mech. Sci. Technol. 2021, 35, 307–322. [Google Scholar] [CrossRef]
- Castillo, P.; Lozano, R.; Dzul, A. Stabilization of a mini rotorcraft with four rotors. IEEE Control Syst. Mag. 2005, 25, 45–55. [Google Scholar]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. Backstepping/nonlinear H∞ control for path tracking of a quadrotor unmanned aerial vehicle. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 3356–3361. [Google Scholar]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An integral predictive/nonlinear H∞ control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Rossiter, J.A. Model-Based Predictive Control: A Practical Approach; CRC Press: New York, NY, USA, 2003. [Google Scholar]
- Yang, G.-H.; Wang, J.L.; Soh, Y.C. Reliable H∞ controller design for linear systems. Automatica 2001, 37, 717–725. [Google Scholar] [CrossRef]
- Van der Schaft, A. L2-Gain and Passivity Techniques in Nonlinear Control; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Kühne, F.; Lages, W.F.; Mahony, R. Point stabilization of mobile robots with nonlinear model predictive control. In Proceedings of the IEEE International Conference Mechatronics and Automation, Niagara Falls, ON, Canada, 29 July–1 August 2005; Volume 3, pp. 1163–1168. [Google Scholar]
- van der Schaft, A. L2-gain analysis of nonlinear systems and nonlinear state feedback HI control. IEEE Trans. Autom. Control. 1992, 37, 770–784. [Google Scholar] [CrossRef]
- Beng, W.F.; Postlethwaite, I. Robust non-linnear H∞/adaptive control of robot manipulator motion. Sage J. 1994, 208. [Google Scholar] [CrossRef]
- Ortega, M.G.; Vargas, M.; Vivas, C.; Rubio, F.R. Robustness Improvement of a Non-linear H∞ Controller for Robot Manipulatiors via Saturation Function. J. Robot. Syst. 2005, 22, 421–437. [Google Scholar] [CrossRef]
- Camacho, E.; Bordons, C. Model Predictive Control; Springer: New York, NY, USA, 1998. [Google Scholar]
- Olfati-Saber, R. Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Ezequiel, C.A.F.; Cua, M.; Libatique, N.C.; Tangonan, G.L.; Alampay, R.; Labuguen, R.T.; Favila, C.M.; Honrado, J.L.E.; Caños, V.; Devaney, C.; et al. UAV aerial imaging applications for post-disaster assessment, environmental management and infrastructure development. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014. [Google Scholar]
- Huang, T.; Huang, D.; Wang, Z.; Shah, A. Robust tracking control of a quadrotor UAV based on adaptive sliding mode controller. Complexity 2019, 2019, 7931632. [Google Scholar] [CrossRef]
- Mann, J. The spatial structure of neutral atmospheric surface-layer turbulence. J. Fluid Mech. 1994, 273, 141–168. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ Numbers. Dokl. Akad. Nauk SSSR 1941, 30, 301. [Google Scholar]
- Bhumralkar, C.M. Parameterization of the planetary boundary layer in atmospheric general circulation models. Rev. Geophys. 1976, 14, 215–226. [Google Scholar] [CrossRef]
- Isaac, O.; Atkins, E.M. Qualitative failure analysis for a small quadrotor unmanned aircraft system. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Fakharzadeh J., A. Finding the optimum domain of a nonlinear wave optimal control system by measures. J. Appl. Math. Comput. 2003, 13, 183–194. [Google Scholar] [CrossRef]
- Ujević, N. Error inequalities for an optimal quadrature formula. J. Appl. Math. Comput. 2007, 24, 65–79. [Google Scholar] [CrossRef]
- Okasha, M.; Kralev, J.; Islam, M. Design and Experimental Comparison of PID, LQR and MPC Stabilizing Controllers for Parrot Mambo Mini-Drone. Aerospace 2022, 9, 298. [Google Scholar] [CrossRef]
- Massé, C.; Gougeon, O.; Nguyen, D.-T.; Saussié, D. Modeling and control of a quadcopter flying in a wind field: A comparison between LQR and structured H∞ control techniques. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018. [Google Scholar]
- Walt, M.; Butterfield, S. Future for Offshore Wind Energy in the United States; No. NREL/CP-500-36313; National Renewable Energy Lab.: Golden, CO, USA, 2004. [Google Scholar]
- Kiernozek, J.M. Controlling a Drone Using the LQR Method; Instytut Techniki Lotniczej i Mechaniki Stosowanej: Warsaw, Poland, 2023. [Google Scholar]


| Parameters | Value | Unit |
|---|---|---|
| Mass (m) | 1.74 | kg |
| Length from wing to center (l) | 0.21 | m |
| Second-level heading | 9.81 | m/s2 |
| Ixx | 0.004 | kgm2 |
| Iyy | 0.004 | kgm2 |
| Izz | 0.0084 | kgm2 |
| Sea State | Turbulence Intensity (%) | Gust Scales (m/s) |
|---|---|---|
| Calm | 5 | ±1 |
| Moderate | 10 | ±2 |
| Rough | 15 | ±3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, D.-A.; Han, S.-H. Critically Leveraging Theory for Optimal Control of Quadrotor Unmanned Aircraft Systems. Appl. Sci. 2024, 14, 2414. https://doi.org/10.3390/app14062414
Pham D-A, Han S-H. Critically Leveraging Theory for Optimal Control of Quadrotor Unmanned Aircraft Systems. Applied Sciences. 2024; 14(6):2414. https://doi.org/10.3390/app14062414
Chicago/Turabian StylePham, Duc-Anh, and Seung-Hun Han. 2024. "Critically Leveraging Theory for Optimal Control of Quadrotor Unmanned Aircraft Systems" Applied Sciences 14, no. 6: 2414. https://doi.org/10.3390/app14062414
APA StylePham, D.-A., & Han, S.-H. (2024). Critically Leveraging Theory for Optimal Control of Quadrotor Unmanned Aircraft Systems. Applied Sciences, 14(6), 2414. https://doi.org/10.3390/app14062414







