A Wavelet Extraction Method of Attenuation Media for Direct Acoustic Impedance Inversion in Depth Domain
Abstract
1. Introduction
2. Methodology
2.1. Influence of Attenuation Media on Depth-Domain Source Wavelets
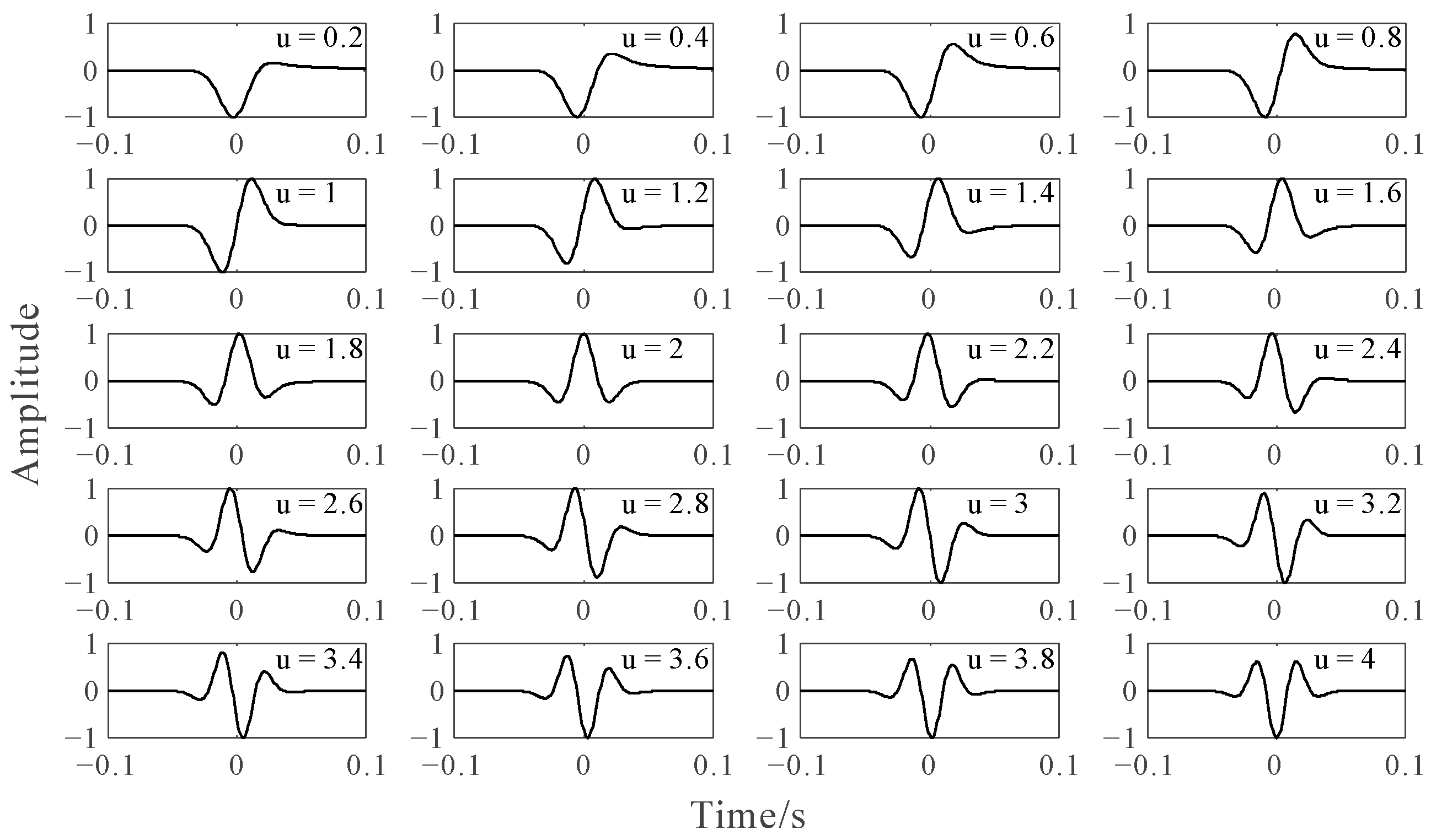
2.2. Concept of Depth-Domain Generalized Seismic Wavelet
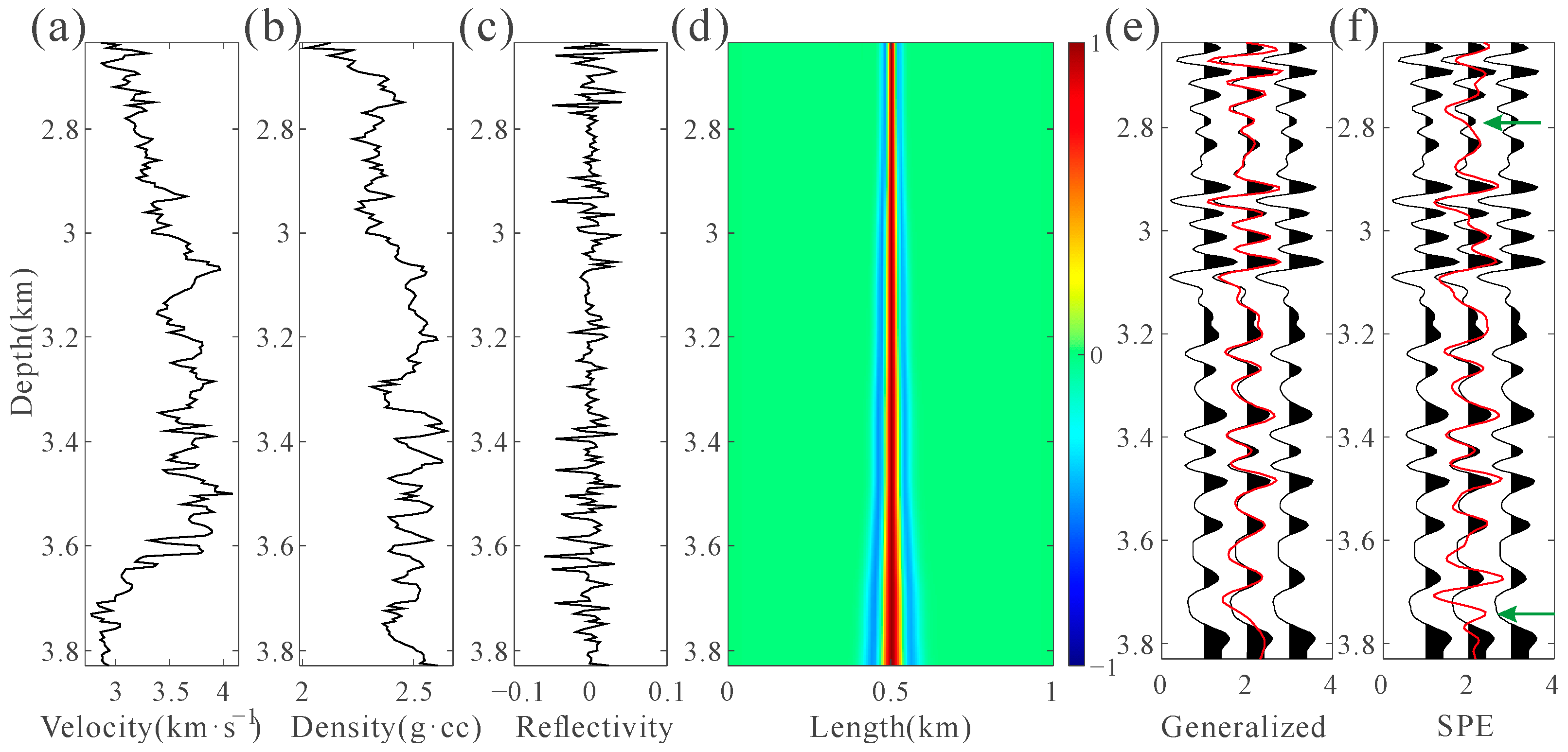
2.3. Extraction Approach of the Depth-Domain Generalized Seismic Wavelet
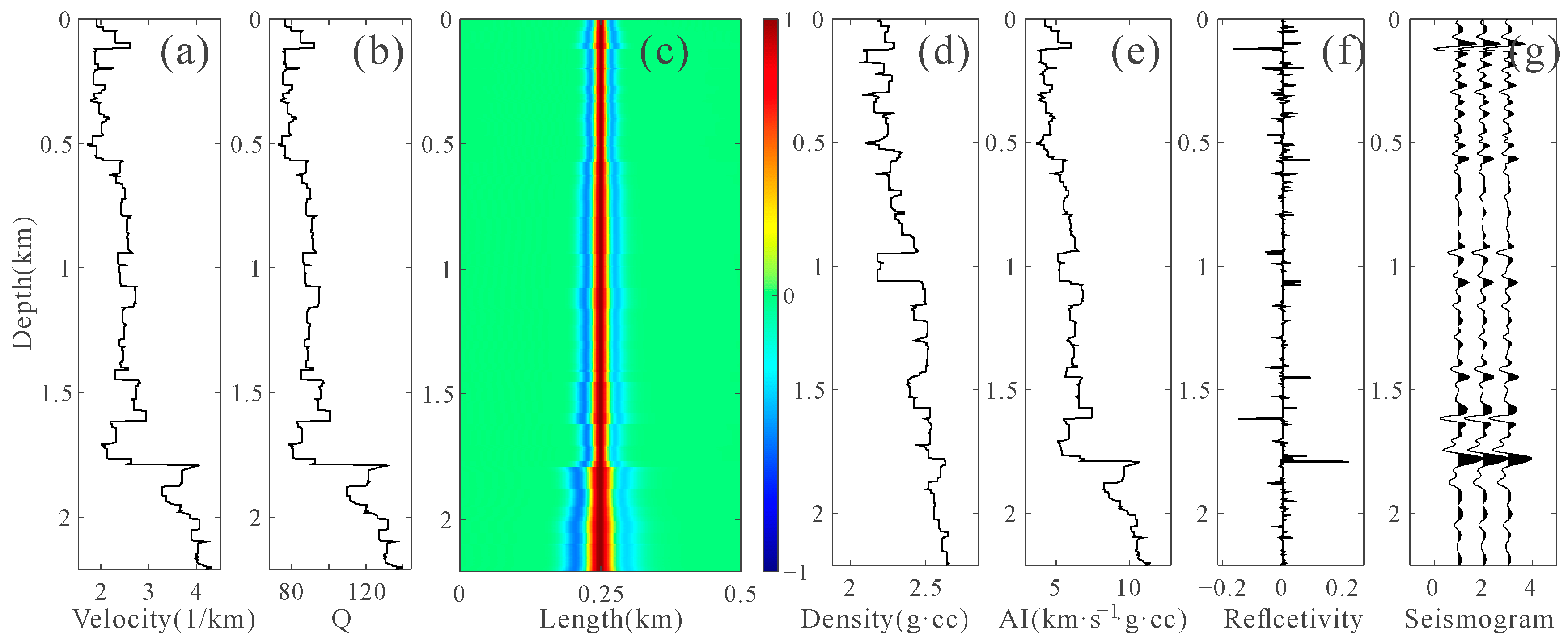
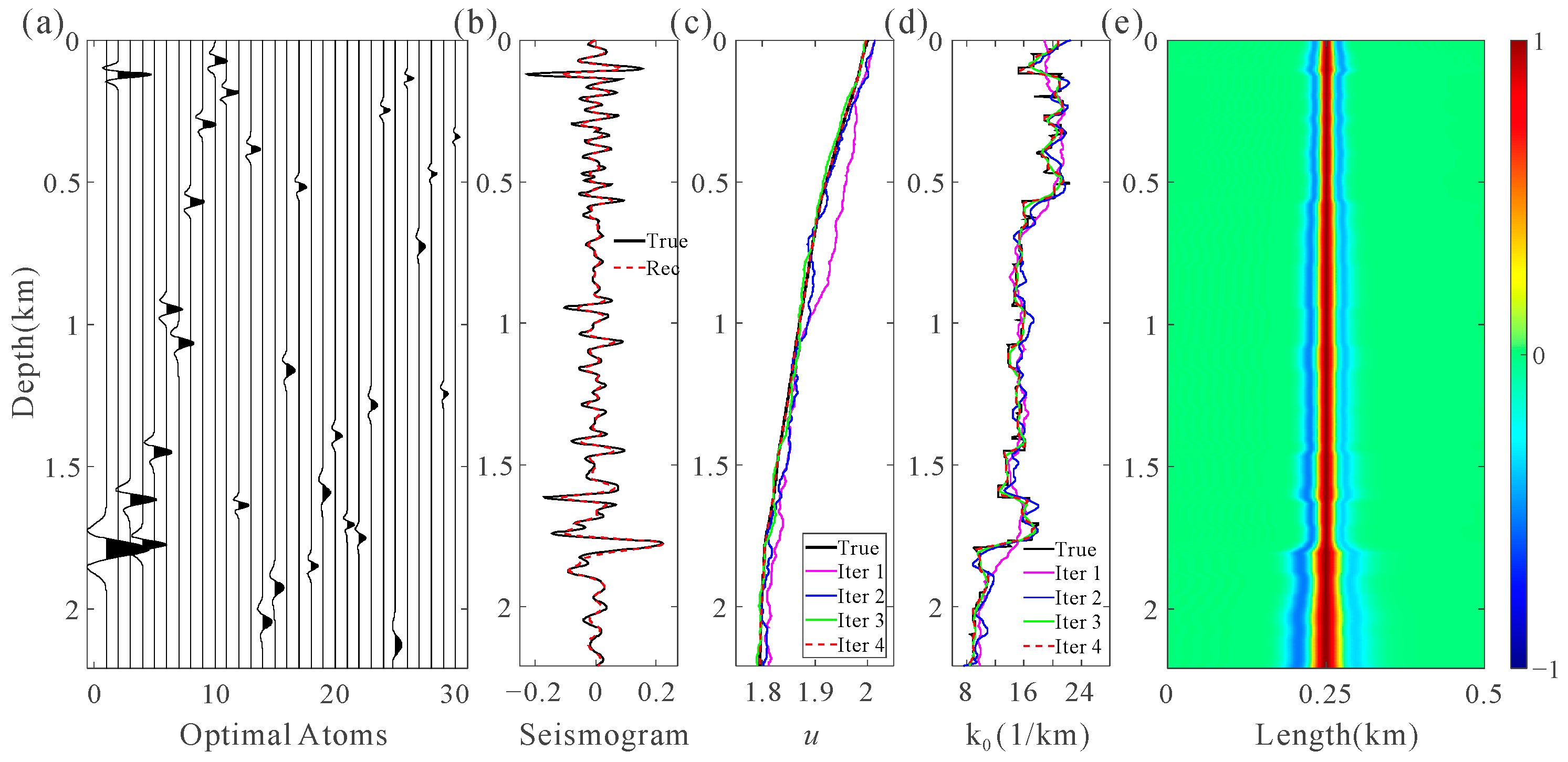
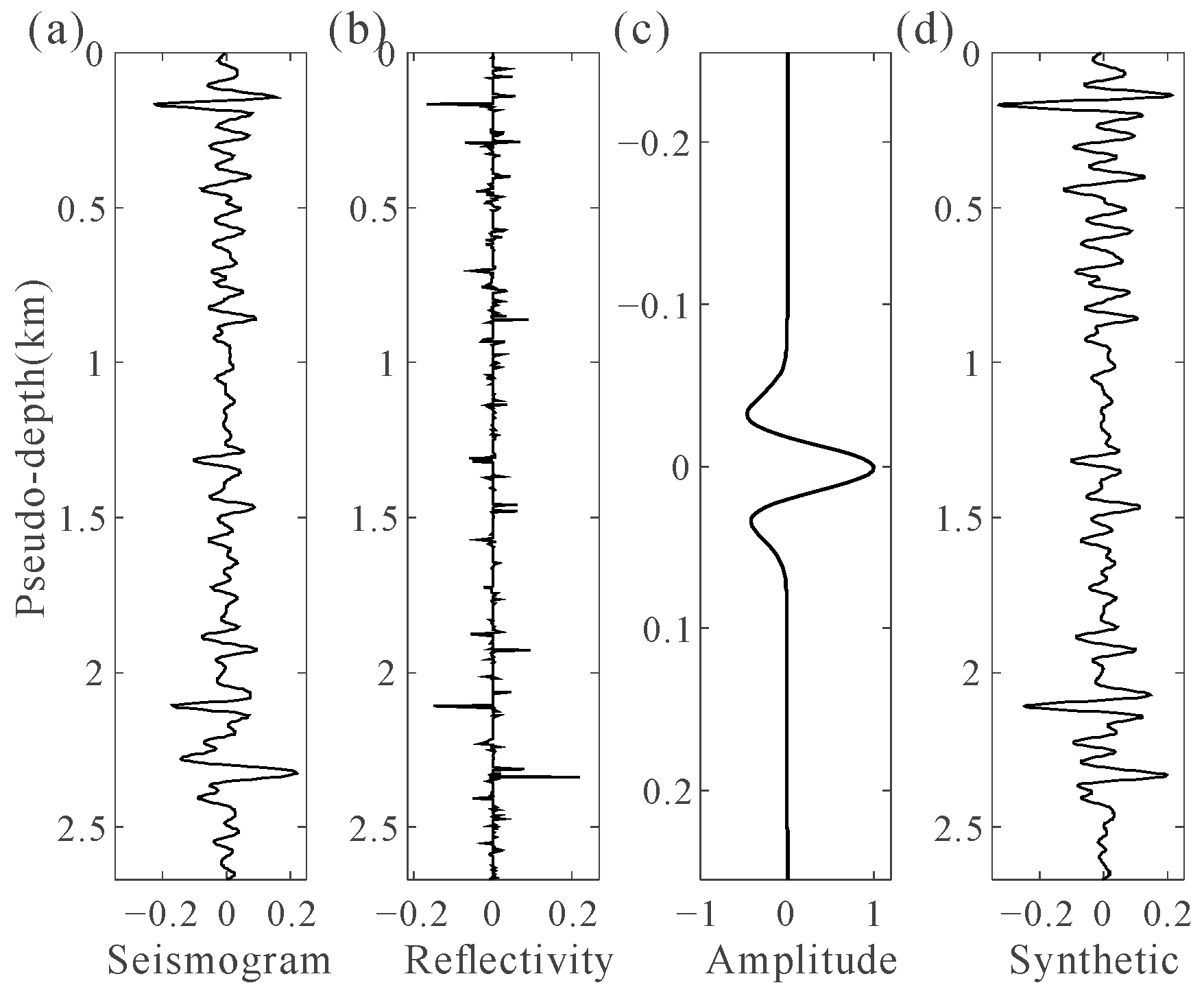
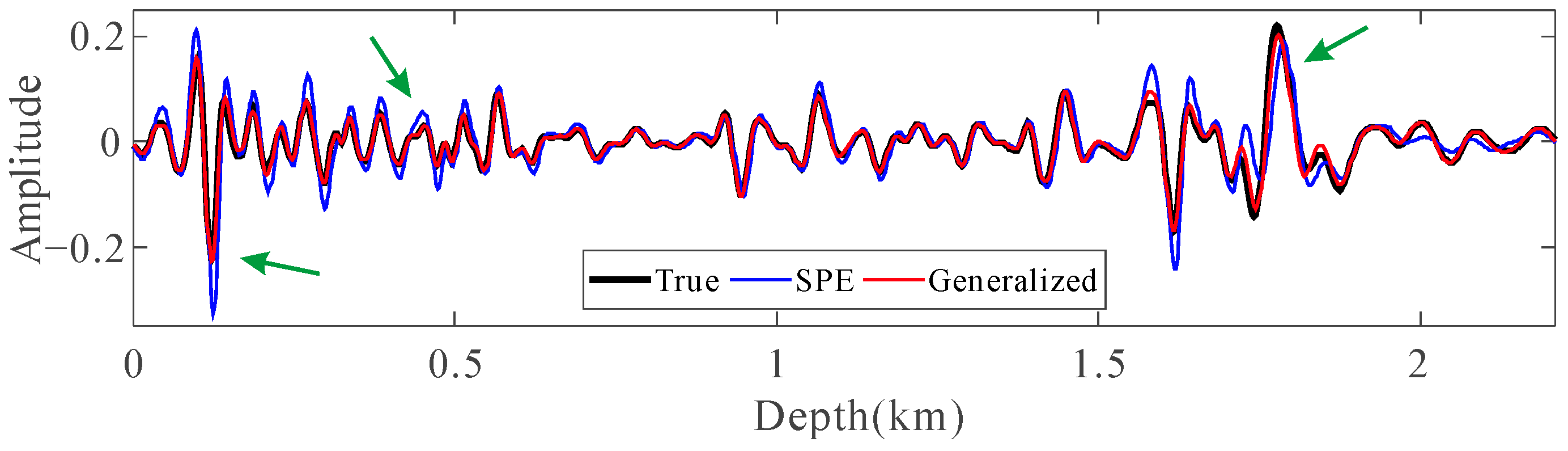
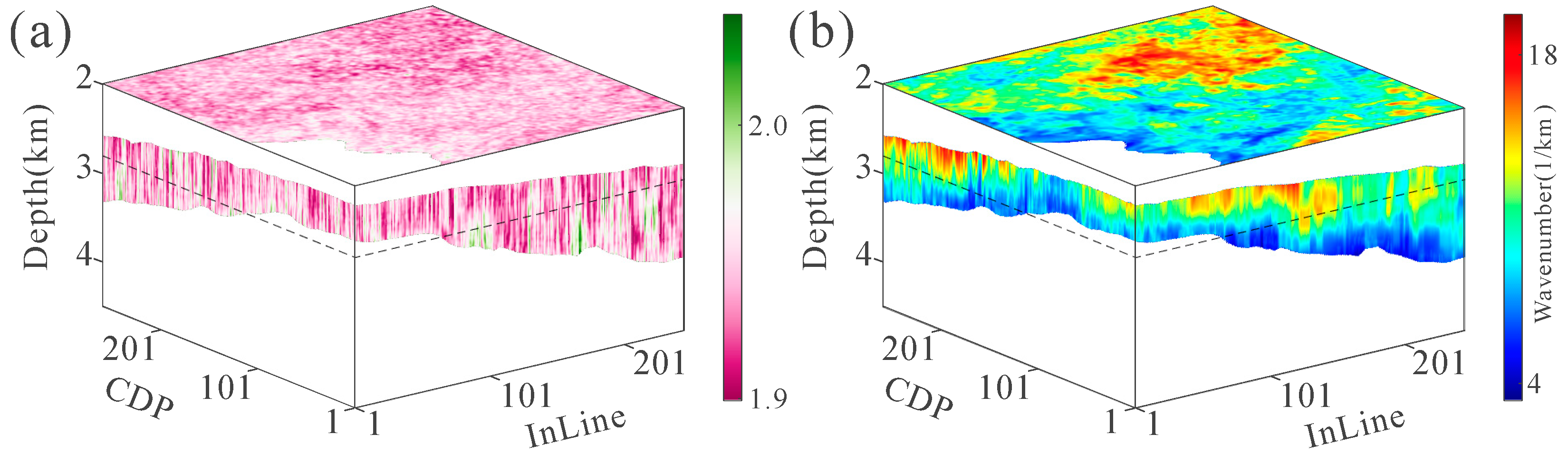
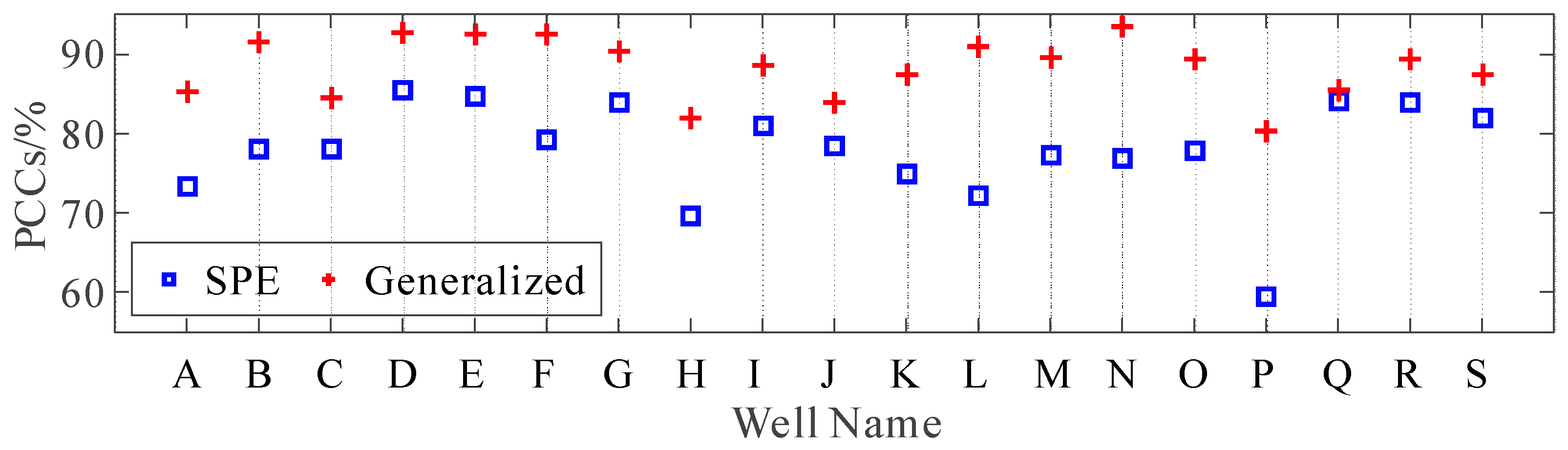
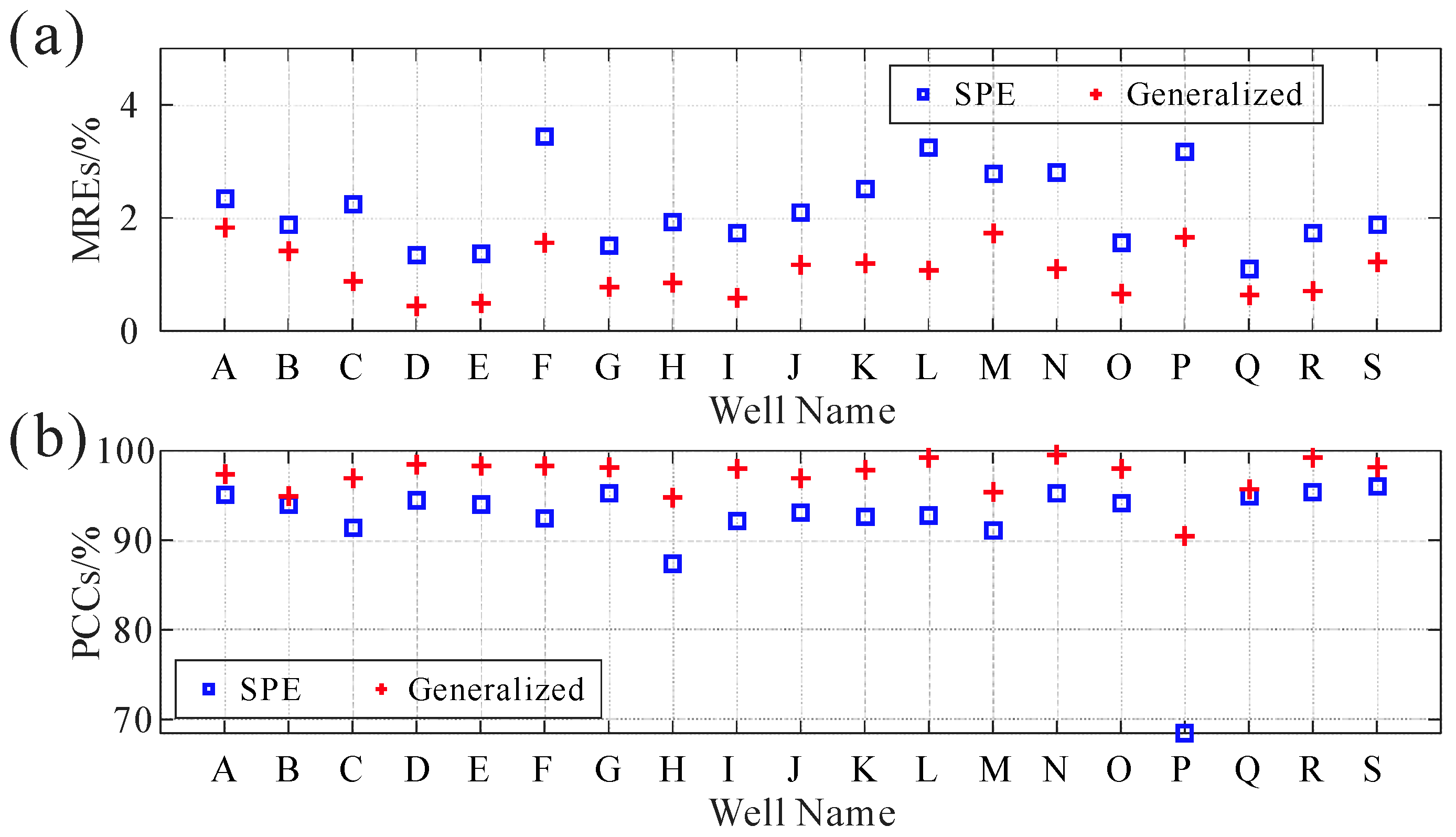
3. Examples
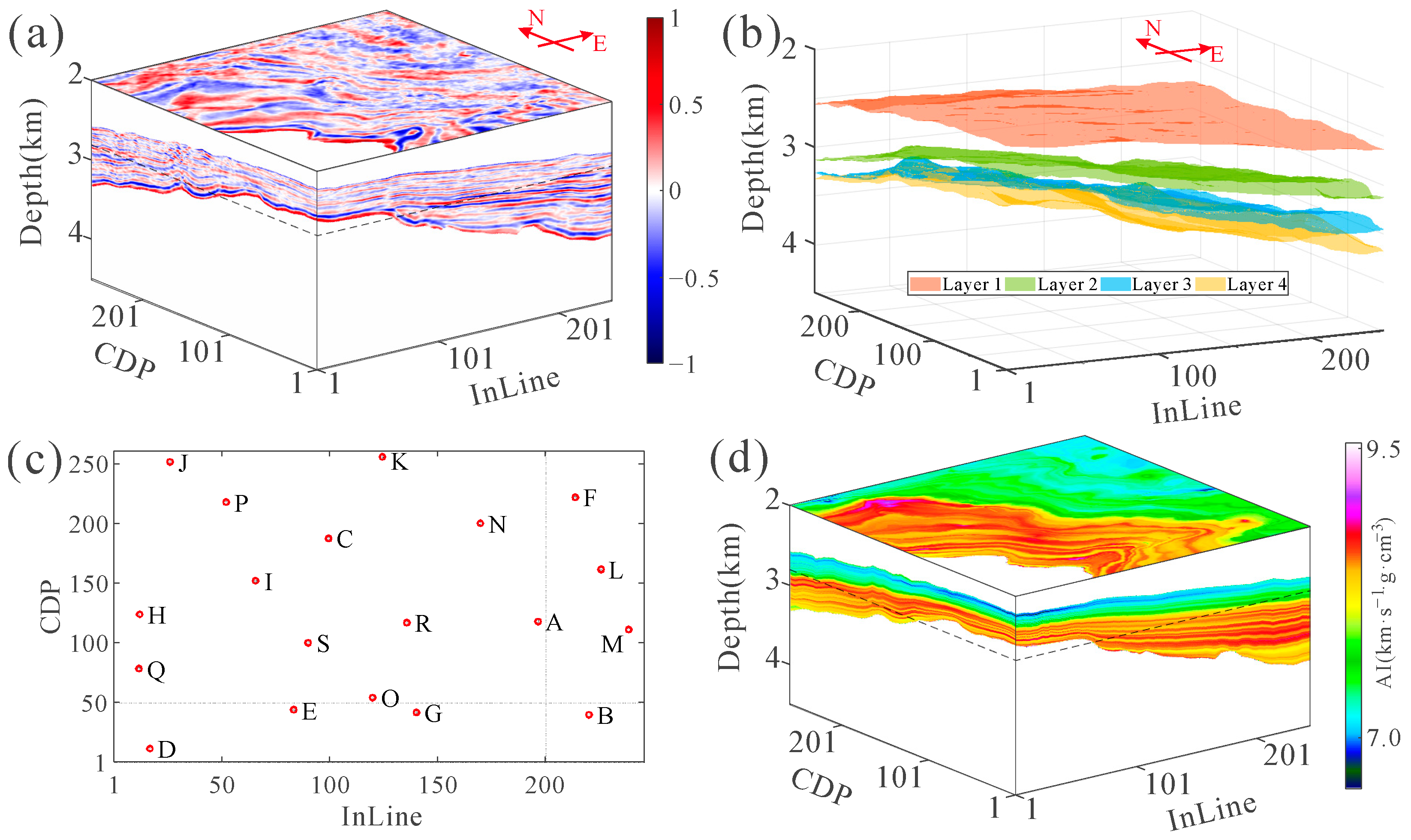
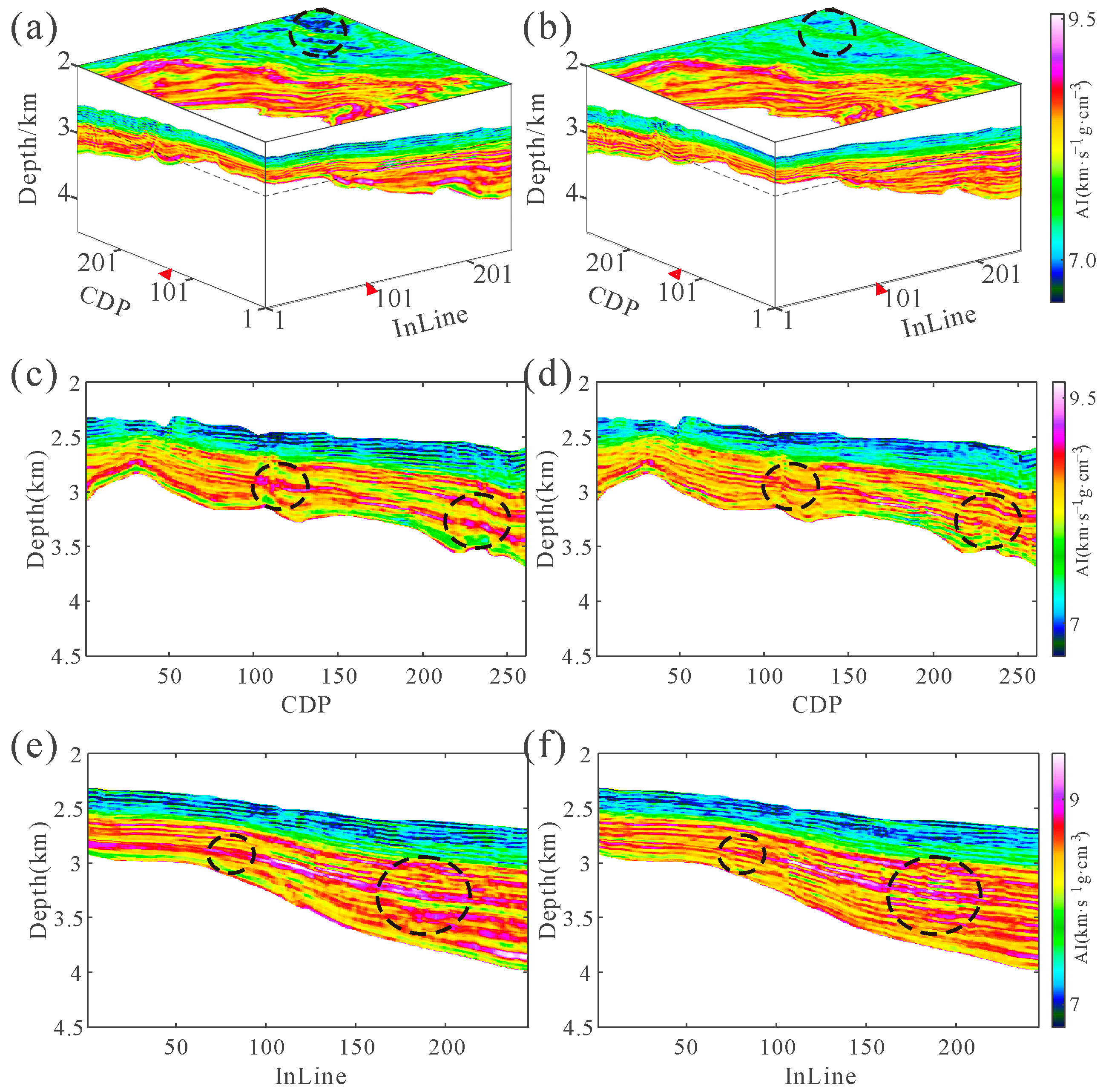
4. Inversion on a 3D Field Dataset
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Etgen, J.T.; Kumar, C. What really is the difference between Time and Depth Migration? A tutorial. In Proceedings of the 82nd Annual International Meeting, SEG, Expanded Abstracts, Salt Lake City, UT, USA, 6–11 October 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Cai, R.; Sun, C.; Li, S. A strategy for acoustic impedance direct inversion in depth domain. In Proceedings of the Second International Meeting for Applied Geoscience & Energy, SEG, Expanded Abstracts, Houston, TA, USA, 28 August–2 September 2022; pp. 228–232. [Google Scholar] [CrossRef]
- Li, B.; Sun, M.; Xiang, C.; Bai, Y. Least-Squares Reverse Time Migration in Imaging Domain Based on Global Space-Varying Deconvolution. Appl. Sci. 2022, 12, 2361. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, H.; Liu, H. Estimation of Relative Acoustic Impedance Perturbation from Reverse Time Migration Using a Modified Inverse Scattering Imaging Condition. Appl. Sci. 2023, 13, 5291. [Google Scholar] [CrossRef]
- Li, S.; Peng, G.; Wang, J.; Tian, T. Advantages and applications of seismic data interpretation in depth domain. In Proceedings of the 90nd Annual International Meeting, SEG, Expanded Abstracts, Houston, TX, USA, 11–16 October 2020; pp. 1053–1057. [Google Scholar] [CrossRef]
- Lin, T.; Zhang, B.; Guo, S.; Marfurt, K.; Wan, Z.; Guo, Y. Spectral decomposition of time-versus depth-migrated data. In Proceedings of the 82nd Annual International Meeting, SEG, Expanded Abstracts, Salt Lake City, UT, USA, 6–11 October 2012; pp. 1384–1388. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, K.; Alekhue, J.E. Depth-domain seismic reflectivity inversion with compressed sensing technique. Interpretation 2017, 5, T1–T9. [Google Scholar] [CrossRef]
- Mustafa, A.; Alfarraj, M.; AIRegib, G. Joint Learning for Spatial Context-based Seismic Inversion of Multiple Datasets for Improved Generalizability and Robustness. Geophysics 2021, 86, O37–O48. [Google Scholar] [CrossRef]
- Niu, X.; Zhang, J.; Liu, J. Seismic impedance inversion in depth domain based on deep learning. Unconv. Resour. 2023, 3, 72–83. [Google Scholar] [CrossRef]
- Hao, J.; Zhang, Y.; Wang, Y.; Zhou, L.V. Application of Seismic Motion Inversion Method in Depth Domain at the Early Stage of Development. In Proceedings of the International Field Exploration and Development Conference 2021, Qingdao, China, 11–16 October 2021; pp. 843–851. [Google Scholar] [CrossRef]
- Hao, J.; Wu, S.; Yang, J.; Zhang, Y.; Sha, X. Application of Seismic Waveform Indicator Inversion in the Depth Domain: A Case Study of Pre-Salt Thin Carbonate Reservoir Prediction. Energies 2023, 16, 3073. [Google Scholar] [CrossRef]
- Meza Ramses, G. Colored inversion in depth domain. In Proceedings of the First International Meeting for Applied Geoscience & Energy, SEG, Expanded Abstracts, Denver, CO, USA, 26 September–1 October 2021; pp. 246–250. [Google Scholar] [CrossRef]
- Waters, K.; Kemper, M. Improved seismic characterization through facies based inversion in the depth domain. In Proceedings of the 89th Annual International Meeting, SEG, Expanded Abstracts, San Antonio, TA, USA, 15–20 September 2019; pp. 600–604. [Google Scholar] [CrossRef]
- Hu, Z.; Zhu, H.; Lin, B.; Xu, S. Wavelet analysis and convolution in depth domain. In Proceedings of the 77th Annual International Meeting, SEG, Expanded Abstracts, San Antonio, TA, USA, 23–28 September 2007; pp. 2733–2737. [Google Scholar] [CrossRef]
- Singh, Y. Deterministic inversion of seismic data in the depth domain. Lead. Edge 2012, 31, 538–545. [Google Scholar] [CrossRef]
- Jiang, W.; Chen, X.; Zhang, J.; Luo, X.; Dan, Z.; Xiao, W. Impedance inversion of pre-stack seismic data in the depth domain. Appl. Geophys. 2019, 16, 427–437. [Google Scholar] [CrossRef]
- Sun, Q.; Zong, Z.; Yin, X.; Meng, X. Amplitude variation with incident angle inversion for fluid factor in the depth domain. In Proceedings of the 88th Annual International Meeting, SEG, Expanded Abstracts, Anaheim, CA, USA, 11–16 October 2018; pp. 605–609. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Luo, X.; Li, J. Seismic wavelet estimation in depth domain using Gibbs sampling-based Bayesian method. In Proceedings of the 2018 CPS/SEG International Geophysical Conference, Beijing, China, 24–27 April 2018; pp. 1180–1184. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Jiang, W.; Liu, Y.; Xu, H. Estimation of the depth-domain seismic wavelet based on velocity substitution and a generalized seismic wavelet model. Geophysics 2022, 87, R213–R222. [Google Scholar] [CrossRef]
- Sengupta, M.; Zhang, H.; Zhao, Y.; Jervis, M.; Grana, D. Direct depth domain Bayesian amplitude-variation-with-offset inversion. Geophysics 2021, 86, M167–M176. [Google Scholar] [CrossRef]
- Fletcher, R.P.; Archer, S.; Nichols, D.; Mao, W. Inversion after depth imaging. In Proceedings of the 82nd Annual International Meeting, SEG, Expanded Abstracts, Salt Lake City, UT, USA, 6–11 October 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Fletcher, R.P.; Nichols, D.; Bloor, R.; Coates, R.T. Least-squares migration? Data domain versus image domain using point spread functions. Lead. Edge 2016, 35, 157–162. [Google Scholar] [CrossRef]
- Zhang, R.; Deng, Z. A depth variant seismic wavelet extraction method for inversion of post-stack depth-domain seismic data. Geophysics 2018, 83, R569–R579. [Google Scholar] [CrossRef]
- Zhang, R.; Deng, Z. Depth-domain angle and depth variant seismic wavelets extraction for prestack seismic inversion. Geophysics 2023, 88, R1–R10. [Google Scholar] [CrossRef]
- Letki, L.; Tang, J.; Du, X. Depth domain inversion case study in complex subsalt area. In Proceedings of the 77th EAGE Conference and Exhibition 2015, Madrid, Spain, 1–4 June 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Letki, L.; Tang, J.; Inyang, C.; Du, X.; Fletcher, R.P. Depth domain inversion to improve the fidelity of subsalt imaging: A Gulf of Mexico case study. First Break 2015, 33, 81–85. [Google Scholar] [CrossRef]
- Letki, L.; Darke, K.; Borges, Y.A. A comparison between time domain and depth domain inversion to acoustic impedance. In Proceedings of the 85th Annual International Meeting, SEG, Expanded Abstracts, New Orleans, LA, USA, 18–23 October 2015; pp. 3376–3380. [Google Scholar] [CrossRef]
- Leon, L.; Inyang, C.; Hegazy, M.; Hydal, S. Least-squares migration in the image domain and depth-domain inversion: A Gulf of Mexico case study. In Proceedings of the 88th Annual International Meeting, SEG, Expanded Abstracts, Anaheim, CA, USA, 11–16 October 2018; pp. 4146–4150. [Google Scholar] [CrossRef]
- Cavalca, M.; Fletcher, R.P.; Du, X. Q-compensation through depth domain inversion. In Proceedings of the 77th EAGE Conference and Exhibition 2015, Madrid, Spain, 1–4 June 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Caprioli, P.; Du, X.; Fletcher, R.P. Deghosting through depth domain inversion. In Proceedings of the 77th EAGE Conference and Exhibition 2015, Madrid, Spain, 1–4 June 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Du, X.; Fletcher, R.P.; Cavalca, M. Prestack depth-domain inversion after reverse time migration. In Proceedings of the 78th EAGE Conference and Exhibition 2016, Vienna, Austria, 1–4 June 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Sengupta, M.; Zhang, H. Direct depth domain elastic inversion. In Proceedings of the 88th Annual International Meeting, SEG, Expanded Abstracts, Anaheim, CA, USA, 11–16 October 2018; pp. 506–510. [Google Scholar] [CrossRef]
- Paxton, A.; Kholiq, A.; Zhang, L.; Shadlow, J.; Shadrina, M. Large-scale pre-stack seismic depth-domain inversion: A case study from the Northern Carnarvon basin, Offshore Austria. In Proceedings of the 83rd EAGE Conference and Exhibition 2022, Madrid, Spain, 6–9 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Shadrina, M.; Leone, C.; Cavalca, M.; Fletcher, R.; Gherasim, M. 4D Depth-domain inversion: Recovering time-lapse signal from non-repeatable surveys. In Proceedings of the Second EAGE Workshop Practical Reservoir Monitoring 2019, Amsterdam, The Netherlands, 1–4 April 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Cavalca, M.; Fletcher, R.P.; Shadrina, M.; Leone, C.; Leon, L. Depth-domain inversion for enhanced quantitative interpretation. In Proceedings of the First EAGE Conference on Seismic Inversion 2020, Online, 11–16 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, Y. Generalized seismic wavelets. Geophys. J. Int. 2015, 203, 1172–1178. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Expanded Abstracts, Pacific Grove, CA, USA, 1–3 November 1993; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, H. Reducing computation cost by Lax-Wendroff methods with fourth-order temporal accuracy. Geophysics 2019, 84, T109–T119. [Google Scholar] [CrossRef]
- Liu, H.; Luo, Y. An analytic signal-based accurate time-domain viscoacoustic wave equation from the constant-Q theory. Geophysics 2021, 86, T117–T126. [Google Scholar] [CrossRef]
- Ricker, N. The form and laws of propagation of seismic wavelets. Geophysics 1953, 18, 10–40. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaie-Zadeh, M.; Jutten, C. Learning overcomplete dictionaries based on atom-by-atom updating. IEEE Trans. Signal Process. 2014, 62, 883–891. [Google Scholar] [CrossRef]
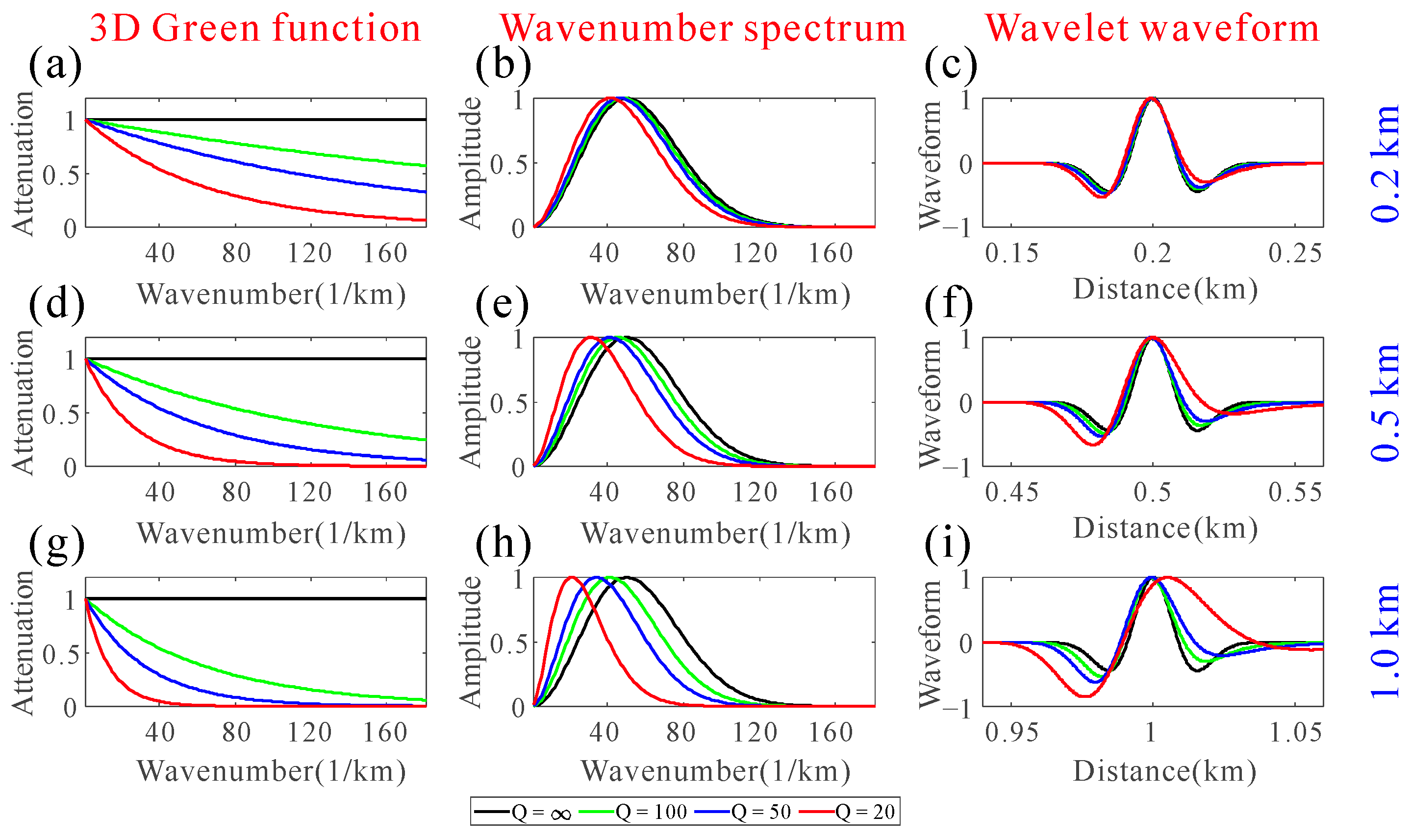
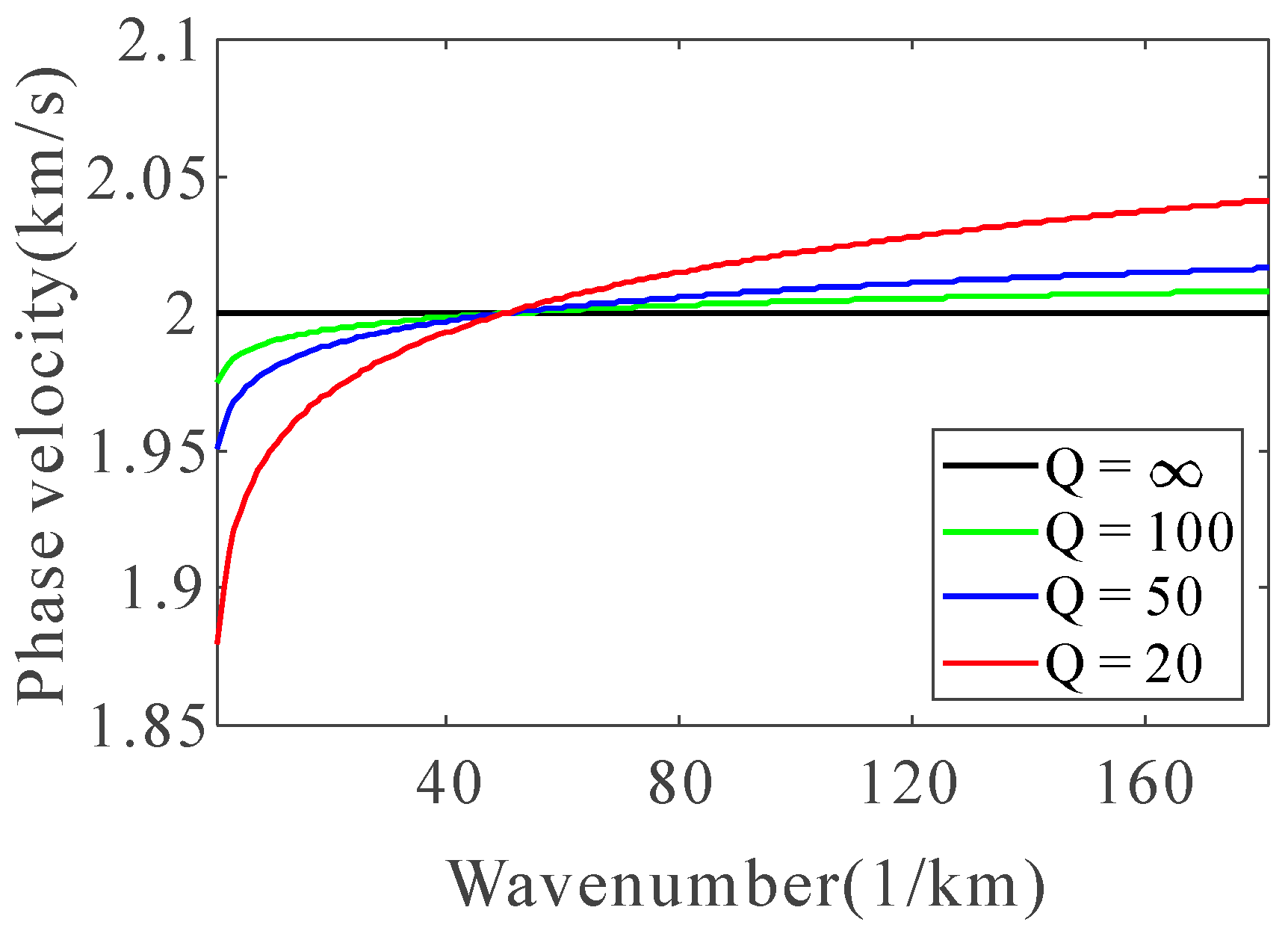







| Q = ∞ | Q = 100 | Q = 50 | Q = 20 | |
|---|---|---|---|---|
| Distance = 0.2 km | (2.00, 50.0 km−1) | (1.95, 49.0 km−1) | (1.88, 48.2 km−1) | (1.72, 25.6 km−1) |
| Distance = 0.5 km | (2.00, 50.0 km−1) | (1.84, 47.6 km−1) | (1.71, 45.2 km−1) | (1.42, 39.6 km−1) |
| Distance = 1.0 km | (2.00, 50.0 km−1) | (1.72, 45.4 km−1) | (1.51, 39.6 km−1) | (1.15, 28.6 km−1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Cai, R.; Yao, Z. A Wavelet Extraction Method of Attenuation Media for Direct Acoustic Impedance Inversion in Depth Domain. Appl. Sci. 2024, 14, 2478. https://doi.org/10.3390/app14062478
Sun C, Cai R, Yao Z. A Wavelet Extraction Method of Attenuation Media for Direct Acoustic Impedance Inversion in Depth Domain. Applied Sciences. 2024; 14(6):2478. https://doi.org/10.3390/app14062478
Chicago/Turabian StyleSun, Chengyu, Ruiqian Cai, and Zhen’an Yao. 2024. "A Wavelet Extraction Method of Attenuation Media for Direct Acoustic Impedance Inversion in Depth Domain" Applied Sciences 14, no. 6: 2478. https://doi.org/10.3390/app14062478
APA StyleSun, C., Cai, R., & Yao, Z. (2024). A Wavelet Extraction Method of Attenuation Media for Direct Acoustic Impedance Inversion in Depth Domain. Applied Sciences, 14(6), 2478. https://doi.org/10.3390/app14062478






