Dynamic Response of the Tunnel Lining with a Circumferential Crack Subjected to a Harmonic Point Load

Abstract

Cracks are one of the most common diseases of tunnel lining, and the structural dynamic response can be used to assess the health of a tunnel. Hence, this paper investigates the dynamic response of shield tunnel lining with a partly circumferential crack. The shield tunnel lining is regarded as a thin cylindrical shell and analyzed independently. The research methodology integrates the wave propagation method, the local flexibility matrix, the line spring model and the wave superposition principle. The results show that the position and depth of a partly circumferential crack can influence the natural frequency of the shield tunnel lining. Under the fixed-position load, as the distance from the monitoring point to the crack increases, the difference in displacement response amplitude between the undamaged and cracked linings diminishes. Moreover, deepening cracks enlarge the magnitude of amplitude differences. When the load approaches the crack, the radial amplitude difference first increases and then decreases as the monitor moves away from the crack. This finding helps determine the required monitor position. The displacement response of the selected monitor indicates that the closer the load position is to the crack, the larger the amplitude difference. The results aid in identifying the crack position and selecting corresponding load and monitor locations.

1. Introduction

Tunnel lining cracks are one of the most common diseases threatening shield tunnels [1,2]. The circumferential crack is one of lining crack types [3,4,5]. The orientation of circumferential cracks is perpendicular to the tunnel axial direction. These cracks mainly occur due to uneven loads acting on the tunnel structure and uneven tunnel settlement. Improper handling of settlement joints during construction can also lead to the appearance of circumferential cracks, affecting the regular use of the tunnel structure [6]. The presence of circumferential cracks is often accompanied by issues such as water leakage, highlighting the importance of addressing them promptly. Furthermore, many studies utilize structural dynamic response for monitoring and assessing tunnel health [7,8,9]. Hence, exploring the dynamic response of a shield tunnel with and without a partly circumferential crack is necessary. This paper approaches the shield tunnel lining as a thin cylindrical shell and analyzes it independently. Moreover, a superposition of point-load cases with suitable translations and rotations can determine the response to a complicated load [10]. Therefore, the response of the shield tunnel lining to a point load is meaningful. Then, this paper delves into the dynamic response of the shield tunnel lining with a partly circumferential crack subjected to a harmonic point load.

The vibration characteristics of a thin cylindrical shell are complex due to the coupling effect of circumferential and axial modes [11]. The wave propagation method is one of the tools to study the vibration characteristics of cylindrical shells. The wave propagation method assumes that the displacement solution of the structural vibration is in the form of waves. The equations of motion use the displacement waveform to solve for the coefficients in terms of the structure’s boundary conditions and internal continuity conditions. The method adapts well to these complex conditions [12]. Flügge [13] established the free vibration displacement equations of thin cylindrical shells and proposed a wave propagation method to solve these equations. The study investigates the relationship between dimensionless frequency and energy distribution. It analyzes the propagation properties of complex waves in low-order circumferential modes [14]. Zhang et al. [15,16] used the wave propagation method to solve for the natural frequencies of cylindrical shells in a vacuum and in fluid-filled conditions. The validation of the result compared the outcome from wave propagation and finite element methods. Li [17] studied the effectiveness and accuracy of the wave propagation method based on the Flügge shell theory and discussed the results under various boundary conditions. In the study, the wave propagation method had reliable solutions for long shells and cylindrical shells supported by sheared diaphragms. In addition, the wave propagation method is accurate when dealing with short shells because it considers the coupling effect of the circumferential and axial vibration modes. Iqbal et al. [18] applied the wave propagation method to explore the vibration characteristics of functionally graded cylindrical shells, and the comparison with authoritative results verified the correctness of the method. Furthermore, Gan et al. [19] employed the wave propagation method to study the free vibration characteristics of ring-ribbed cylindrical shells under initial static pressure. The research extends the scope of the application for the wave propagation method. The wave propagation method exhibits adaptability to complex boundary conditions and has wide applications. The displacement solution of the wave propagation method can be integrated with the crack model utilized in this paper.

Cracks influence the thin cylindrical shell’s structural parameters and vibration characteristics [20]. This causes local stiffness reduction and increases the damping of the damaged position [21,22]. The line spring model (LSM) can describe the problem of internal and surface cracks in plates and shells. Rice and Levy [23] first used distributed line springs to simulate cracks. The study obtained local flexibility at the crack position according to fracture mechanics’ strain energy release rate. Delale et al. [24,25] improved LSM in a flat plate. The research also used the model to describe cylindrical shells’ circumferential or axial partial penetration cracks. After that, Parks et al. [26] optimized LSM and brought it into the finite element models to explore the elastic–plastic response. Mohan [27] modeled surface cracks in pipes and elbows by LSM. The validation of the model applied finite elements and experimental results. Nikpour [28] investigated the effect of a circumferential surface crack on the axisymmetric vibration of an anisotropic cylindrical shell. The crack modelled by LSM increases the flexibility of the cylindrical shell. Zhu and Li et al. [29,30] combined LSM and the wave propagation method to analyze the vibration power flow of infinitely long cylindrical shells. Moreover, the study evaluated the effect of crack location and depth on the vibration characteristics of the shell. Moazze et al. [31] simulated the cylindrical shell’s semi-elliptical surface cracks by LSM. The results indicated the effect of crack parameters on a cylindrical shell’s natural frequency. In addition, the length of the cracks was smaller than the radius of the cylindrical shell, and the distribution was in any direction. Wang et al. [11] adopted the wave propagation method and LSM to analyze the nonlinear vibration response of the thin cylindrical shell with a straight crack. This illustrates that the cooperation of these two methods is reliable. Overall, LSM effectively presents the stiffness reduction caused by cracks, thereby reflecting displacement changes in their vicinity. This model can integrate with the wave propagation method.

The achievements above support the results of the dynamic analysis of a thin cylindrical shell with a crack. This facilitates the exploration of the dynamic response of the shield tunnel lining with a partly circumferential crack subjected to a normal point load. This paper introduces four innovative aspects. First, it focuses on displacement as the primary parameter for analysis, integrating methods for solving free and forced vibrations mentioned in the literature and elucidating the response mechanism in the crack-affected lining region using the LSM model. Second, it uses harmonic point loading, which differs from the commonly used loading methods in the current dynamic response research of thin cylindrical shells. Third, it addresses the crack morphology by establishing an analytical model for a partly circumferential crack located inside shield tunnels, aligning with the characteristics of tunnel damage. Lastly, it innovates in the setup of loading and monitoring positions, introducing varying loading and monitoring positions and analyzing their effects on the dynamic response monitoring of tunnel structures. In addition, this paper presents finite element models to validate the dynamic model considered with and without a partly circumferential crack.

The remaining part of the paper proceeds as follows. Section 2 describes the methodology for the dynamic simulation of the shield tunnel lining with a partly circumferential crack. Then, Section 3 uses the literature and the finite element model (FEM) to validate the proposed analytical approach. After that, Section 4 shows the vibration response of the shield tunnel lining without or with a partly circumferential crack. The analysis reveals the evolution of the natural frequency and forced vibration displacement response under different crack morphologies. Section 5 proposes the main conclusion.

2. Methodology

The research methodology of this paper incorporates referencing and integrating multiple methods and techniques. First, the dynamic model for free vibration is established using the wave propagation method described by Li [17], which is applied to a circular cylindrical shell. Subsequently, the modeling for forced vibration follows Wang [11] using the residue theorem. The state of a harmonic point load is expressed as reported previously [10]. The crack model is developed employing LSM depicted by Wang [11], which is used for a straight crack. The parameters of a partly circumferential crack are adjusted as in Hu [32]. After that, the displacement responses are shipped to the superposition principle for analyzing the variation in displacement around the crack.

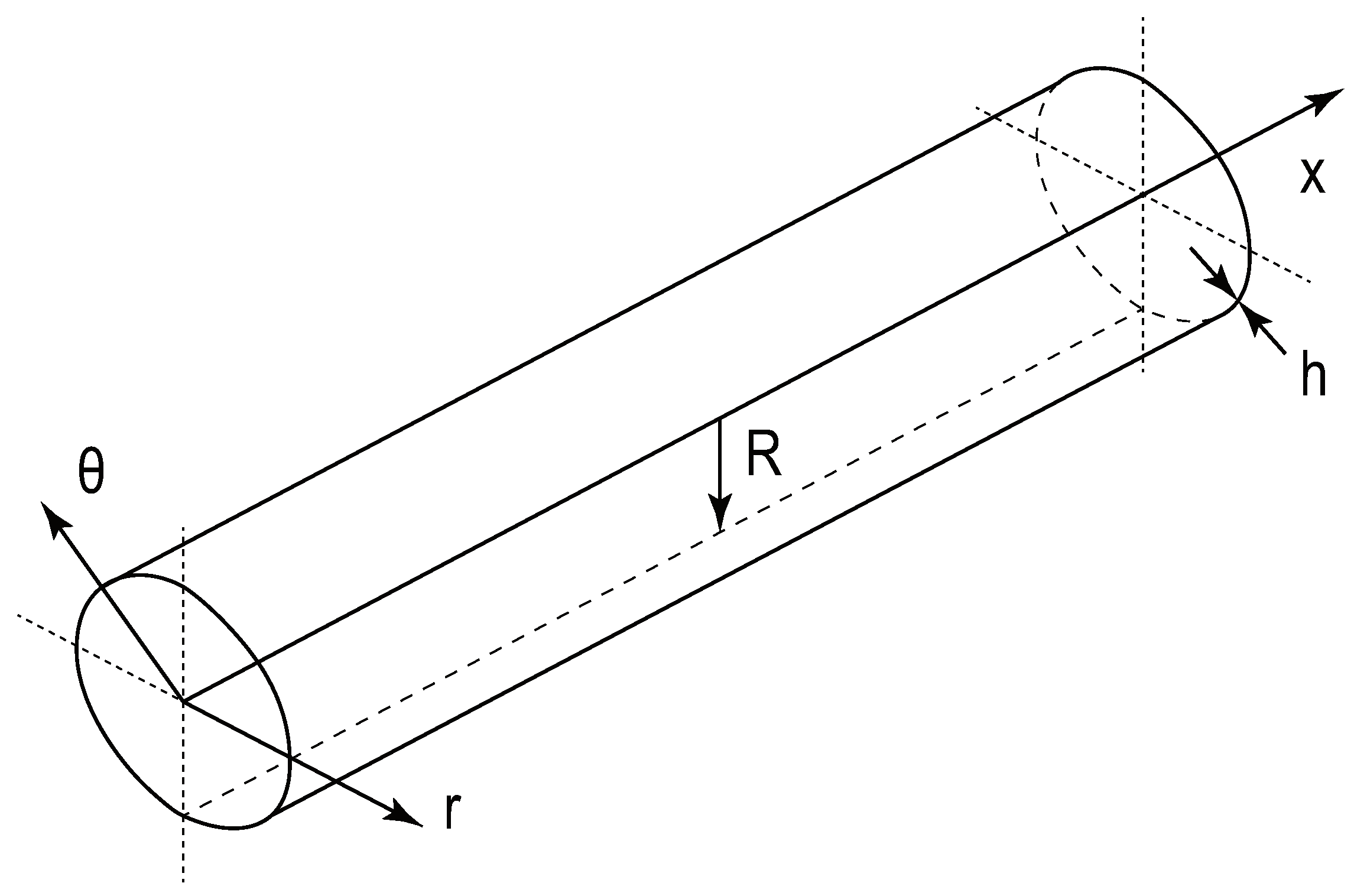
2.1. Dynamic Model for Free Vibration

Flügge shell theory provides a basis for the dynamic model of the shield tunnel lining [13]. The governing differential equations of the shield tunnel lining are as follows. Each equation represents one of the three principal directions.

$$\begin{array}{c}R\frac{{\partial }^{2}u}{\partial x^2}+\frac{1-\mu }{2R}\frac{{\partial }^{2}u}{\partial {\theta }^2}+\frac{1+\mu }{2}\frac{{\partial }^{2}v}{\partial x\partial \theta }-\mu \frac{\partial w}{\partial x}+\frac{h^2}{12}\left(\frac{1-\mu }{2R^3}\frac{{\partial }^{2}u}{\partial {\theta }^2}+\frac{{\partial }^{3}w}{\partial x^3}-\frac{1-\mu }{2R^2}\frac{{\partial }^{3}w}{\partial x\partial {\theta }^2}\right)\\ -\rho R\frac{\left(1-{\mu }^2\right)}{E}\frac{{\partial }^{2}u}{\partial t^2}=0\end{array}$$

(1)

$$\begin{array}{c}R\frac{1+\mu }{2}\frac{{\partial }^{2}u}{\partial x\partial \theta }+R^2\frac{1-\mu }{2}\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial {\theta }^2}-\frac{\partial w}{\partial \theta }+\frac{h^2}{12}\left[\frac{3(1-\mu )}{2}\frac{{\partial }^{2}v}{\partial x^2}+\frac{3-\mu }{2}\frac{{\partial }^{3}w}{\partial x^2\partial \theta }\right]\\ -\rho R^2\frac{\left(1-{\mu }^2\right)}{E}\frac{{\partial }^{2}v}{\partial t^2}=0\end{array}$$

(2)

$$\begin{array}{c}R\mu \frac{\partial u}{\partial x}+\frac{\partial v}{\partial \theta }-w-\frac{h^2}{12}\left(R^2\frac{{\partial }^{4}w}{\partial x^4}+\frac{2{\partial }^{4}w}{\partial x^2\partial {\theta }^2}+\frac{{\partial }^{4}w}{R^2\partial {\theta }^4}\right)\\ -\frac{h^2}{12}\left(R\frac{{\partial }^{3}u}{\partial x^3}-\frac{1-\mu }{2R}\frac{{\partial }^{3}u}{\partial x\partial {\theta }^2}+\frac{3-\mu }{2}\frac{{\partial }^{3}v}{\partial x^2\partial \theta }+\frac{w}{R^2}+\frac{2{\partial }^{2}w}{R^2\partial {\theta }^2}\right)\\ +\rho R^2\frac{\left(1-{\mu }^2\right)}{E}\frac{{\partial }^{2}w}{\partial t^2}=0\end{array}$$

(3)

Symbols u, v and w represent the axial x, circumferential $\theta$, and radial r displacements, as shown in Figure 1. The radius of the midplane is R, the lining thickness is h, the material density is $\rho$, Poisson’s ratio is $\mu$, and the Young modulus is E. The displacements of the shell have the following forms of wave propagation [33].

$$\begin{array}{cc}\hfill u& \hfill =\sum _{n=0}^{\infty }\sum _{m=1}^{\infty }\tilde{U}cosn\theta e^{i\left(\omega t-k_{nm}x\right)}\hfill \\ \hfill v& \hfill =\sum _{n=0}^{\infty }\sum _{m=1}^{\infty }\tilde{V}sinn\theta e^{i\left(\omega t-k_{nm}x\right)}\hfill \\ \hfill w& \hfill =\sum _{n=0}^{\infty }\sum _{m=1}^{\infty }\tilde{W}cosn\theta e^{i\left(\omega t-k_{nm}x\right)}\hfill \end{array}$$

(4)

Symbols $k_{nm}$ and $\omega$ represent the axial wavenumber and circular frequency. The circumferential mode number is n, the half-wavenumber in the axial direction is m, the time factor is $e^{i\omega t}$. Symbols $\tilde{U}$, $\tilde{V}$, and $\tilde{W}$ represent the axial, circumferential, and radial displacement amplitudes. Furthermore, the clamped–clamped boundary condition provides the axial wavenumber as $k_{nm}=\frac{(2m+1)\pi }{2L}$, and L is the lining length [34]. After that, substituting the waveform solution into Equations (1)–(3) provides three equations in the amplitudes of $\tilde{U}$, $\tilde{V}$, and $\tilde{W}$, which can be presented in matrix form.

$$\left[\begin{array}{ccc}\hfill A_{11}\hfill & \hfill A_{12}\hfill & \hfill A_{13}\hfill \\ \hfill A_{21}\hfill & \hfill A_{22}\hfill & \hfill A_{23}\hfill \\ \hfill A_{31}\hfill & \hfill A_{32}\hfill & \hfill A_{33}\hfill \end{array}\right]\left[\begin{array}{c}\tilde{U}\\ \tilde{V}\\ \tilde{W}\end{array}\right]=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]$$

(5)

This study sets the dimensionless frequency to $\mathsf{\Omega }=\omega R\sqrt{\frac{\rho \left(1-{\mu }^2\right)}{E}}$, and the dimensionless axial wavenumber to $\lambda =k_{nm}R$. Then, the components of the matrix $\left[A_{3\times 3}\right]$ are

$$\begin{array}{c}{A}_{11}={\lambda }^2-{\mathsf{\Omega }}^2+\frac{1-\mu }{2}\left(1+\frac{h^2}{12R^2}\right)n^2,A_{12}=-in\lambda \frac{1+\mu }{2},\\ A_{13}=i{n}^2\lambda \frac{1-\mu }{2}\frac{h^2}{12R^2}-i\mu \lambda -i{\lambda }^3\frac{h^2}{12R^2},A_{21}=in\lambda \frac{1+\mu }{2},\\ A_{22}=n^2-{\mathsf{\Omega }}^2+\frac{1-\mu }{2}\left(1+\frac{h^2}{4R^2}\right){\lambda }^2,A_{23}=n+n{\lambda }^2\frac{h^2}{12R^2}\frac{3-\mu }{2},\\ A_{31}=i{n}^2\lambda \frac{h^2}{12R^2}\frac{1-\mu }{2}-i\lambda \mu -i{\lambda }^3\frac{h^2}{12R^2},A_{32}=-n-n{\lambda }^2\frac{h^2}{12R^2}\frac{3-\mu }{2},\\ A_{33}={\mathsf{\Omega }}^2-\frac{h^2}{12R^2}{\left(n^2-1\right)}^2-{\lambda }^2\frac{h^2}{12R^2}\left(2n^2+{\lambda }^2\right)-1\end{array}$$

(6)

The non-trivial solutions of Equation (5) indicate the determinant of the characteristic matrix $\left[A_{3\times 3}\right]$ is zero.

$$det\left(\left[A_{3\times 3}\right]\right)=0$$

(7)

The expansion of Equation (7) offers a characteristic equation with dimensionless frequency $\mathsf{\Omega }$ and wavenumber $\lambda$. The characteristic equation below can calculate the natural frequencies after selecting the dimensionless wavenumber based on the clamped–clamped boundary condition [17].

$$a_6{\mathsf{\Omega }}^6+a_4{\mathsf{\Omega }}^4+a_2{\mathsf{\Omega }}^2+a_0=0$$

(8)

Symbols $a_i$ ($i=0,2,4,6$) are the coefficients of Equation (8). The smallest of the three roots represents the flexural vibration, and the other two are in-plane vibrations [15]. Furthermore, the eighth-order algebraic equation for the dimensionless axial wavenumber $\lambda$ can be obtained when dimensionless frequency $\mathsf{\Omega }$ is known.

$$b_8{\lambda }^8+b_6{\lambda }^6+b_4{\lambda }^4+b_2{\lambda }^2+b_0=0$$

(9)

Symbols $b_j$ ($j=0,2,4,6,8$) are the coefficients of Equation (9). The four pairs of roots for the polynomial function are of three types: pure real, pure imaginary, and conjugate complex. Moreover, the real, pure, imaginary, and complex roots correspond to propagating, near-field, and attenuating standing waves [17]. The basic properties of three vibrating waves explain the generation and propagation mechanism of the dynamic response of the shield tunnel lining.

2.2. Dynamic Model for Forced Vibration

Equation (10) shows the state of external excitation p for time-harmonic normal point load. Symbols $\delta \left(x\right)$ and $\delta \left(\theta \right)$ are Dirac delta functions. Symbol F represents the normal harmonic point load amplitude.

$$p(x,\theta ,t)=F\frac{\delta \left(x\right)\delta \left(\theta \right)}{R}{e}^{i\omega t}$$

(10)

Fourier transformation on the axial, circumferential, radial displacement and excitation changes the positive and negative relationship between axial wavenumber and the time factor. Its matrix form is as follows. The linear combination of these spatially harmonic components offers the total displacements resulting from the harmonic point load,

$$\left[\begin{array}{ccc}\hfill A_{11}\hfill & \hfill A_{12}\hfill & \hfill A_{13}\hfill \\ \hfill A_{21}\hfill & \hfill A_{22}\hfill & \hfill A_{23}\hfill \\ \hfill A_{31}\hfill & \hfill A_{32}\hfill & \hfill A_{33}\hfill \end{array}\right]\left[\begin{array}{c}\tilde{U}\\ \tilde{V}\\ \tilde{W}\end{array}\right]=\frac{\left(1-{\mu }^2\right)R^2}{Eh}\left[\begin{array}{c}0\\ 0\\ \tilde{P}\end{array}\right]$$

(11)

where harmonic stress $\tilde{P}$ for particular circumferential mode number n is to be deduced from Equation (10) as

$$\tilde{P}=\left\{\begin{array}{c}F/2\pi R,n=0\\ F/\pi R,n\ge 1\end{array}\right.$$

(12)

This study sets matrix $\left[C_{3\times 3}\right]$ to be the inverse of matrix $\left[A_{3\times 3}\right]$. Equation (11) becomes

$$\left[\begin{array}{c}\tilde{U}\\ \tilde{V}\\ \tilde{W}\end{array}\right]=\frac{\tilde{P}\left(1-{\mu }^2\right)R^2}{Eh}\left[\begin{array}{c}\hfill C_{13}\hfill \\ \hfill C_{23}\hfill \\ \hfill C_{33}\hfill \end{array}\right]$$

(13)

The inverse Fourier transformation can produce spatial-domain axial $u_x$, circumferential $v_x$, and radial $w_x$ displacement as follows:

$$\left[\begin{array}{c}\hfill u_x\hfill \\ \hfill v_x\hfill \\ \hfill w_x\hfill \end{array}\right]=\frac{\tilde{P}\left(1-{\mu }^2\right)R^2}{Eh}\left[\begin{array}{c}\hfill {\int }_{-\infty }^{+\infty }{C}_{13}{e}^{i\frac{\lambda }{R}t}d\lambda \hfill \\ \hfill {\int }_{-\infty }^{+\infty }{C}_{23}{e}^{i\frac{\lambda }{R}t}d\lambda \hfill \\ \hfill {\int }_{-\infty }^{+\infty }{C}_{33}{e}^{i\frac{\lambda }{R}t}d\lambda \hfill \end{array}\right]$$

(14)

Equation (14) can be calculated using the residue theorem [11]. It can compute the integral form of Equation (14) by finding the singularity of the function. Then, the equations for the displacements of the coupled system in the form of the residual method are

$$\left[\begin{array}{c}\hfill u_x\hfill \\ \hfill v_x\hfill \\ \hfill w_x\hfill \end{array}\right]=\frac{\tilde{P}\left(1-{\mu }^2\right)R^2}{Eh}\left[\begin{array}{c}\hfill \sum _{s=1}^{k}Res\left[C_{13}\left({\lambda }_s\right)\right]\hfill \\ \hfill \sum _{s=1}^{k}Res\left[C_{23}\left({\lambda }_s\right)\right]\hfill \\ \hfill \sum _{s=1}^{k}Res\left[C_{33}\left({\lambda }_s\right)\right]\hfill \end{array}\right]$$

(15)

Symbol k is the roots’ number of Equation (9) and $Res\left[C_{3\times 1}\left({\lambda }_s\right)\right]$ is the residue of the integrand. The linear combination of spatially harmonic components yields the total displacements induced by a harmonic point load. The summation of an infinite number of circumferential modes is impossible. Therefore, achieving satisfactory convergence becomes the determining criterion for the number of modes. Also, the time-harmonic displacement response can be obtained through the inverse Fourier transform of the summation of circumferential modes in the wavenumber domain. The total time-harmonic displacements are as follows. Displacements ${\tilde{U}}_n$, ${\tilde{V}}_n$, and ${\tilde{W}}_n$ correspond to a circumferential mode n from Equation (11) by applying the harmonic point load as in Equation (12).

$$\left[\begin{array}{c}\hfill u\hfill \\ \hfill v\hfill \\ \hfill w\hfill \end{array}\right]=\frac{1}{2\pi R}{\int }_{-\infty }^{+\infty }\left(\left[\begin{array}{c}{\tilde{U}}_0\\ 0\\ {\tilde{W}}_0\end{array}\right]+\sum _{n=1}^{\infty }\left[\begin{array}{c}{\tilde{U}}_{n}cosn\theta \\ {\tilde{V}}_{n}sinn\theta \\ {\tilde{W}}_{n}cosn\theta \end{array}\right]\right)e^{i\frac{\lambda }{R}t}d\lambda e^{i\omega t}$$

(16)

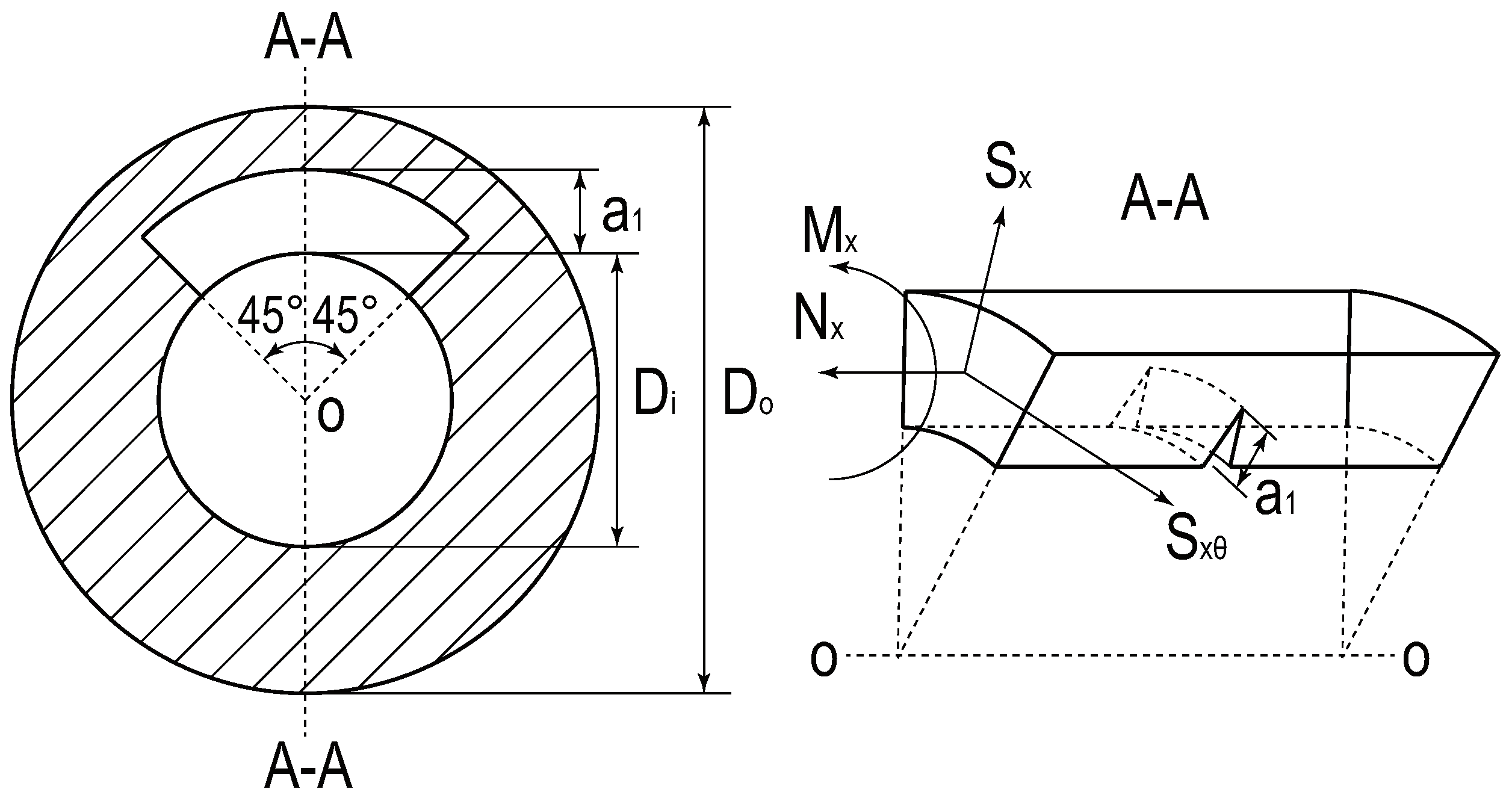
2.3. Crack Simulation

There is a section of circumferential surface crack in the wall of the shield tunnel lining. Its depth $a_1$ is uniform along the circumferential direction, and the crack is always open during vibration. Figure 2 illustrates the crack morphology in a longitudinal element of unit width from the lining and the crack’s location in the annular cross-section of the tunnel lining. The outer diameter of the tube is $D_o$, and the inner diameter is $D_i$. Meanwhile, the cracked lining unit is subjected to axial force $N_x$, bending moment $M_x$, effective radial shear $S_x$, and effective circumferential shear $S_{x\theta }$. The crack is symmetric about the lining tube axis A-A, and the crack distribution angle is $45°$ on both sides of the axis.

The crack simulation uses LSM. It weakens the stiffness over a localized region. In addition, the local flexibility due to the crack results in discontinuities in the generalized displacements on both sides of the crack. The deformation on both sides of the crack attributed to the local flexibility is shown below [28].

$${\delta }^R-{\delta }^L=M_{i\times i}P$$

(17)

The generalized displacements on the left and right sides of the crack are ${\delta }^R$ and ${\delta }^L$, respectively. The local flexibility is $M_{i\times i}$, and the generalized force is P. The coupling among the bending moment, the axial shear force, the transverse shear force, and the corresponding bending and axial deformations provide information on the individual components in the local flexibility matrix of the cracked area. The local flexibility matrix and the relevant equations are presented below [32].

$$\begin{array}{c}{F}_1\left(a\right)=\sqrt{tan\frac{\pi a}{2h}/\frac{\pi a}{2h}}\left(0.751+2.02\frac{a}{h}+0.37{\left(1-sin\frac{\pi a}{2h}\right)}^3\right)/cos\frac{\pi a}{2h}\\ F_2\left(a\right)=\sqrt{tan\frac{\pi a}{2h}/\frac{\pi a}{2h}}\left(0.923+0.199{\left(1-sin\frac{\pi a}{2h}\right)}^4\right)/cos\frac{\pi a}{2h}\\ F_{II}\left(a\right)=\left(1.122-0.561\frac{a}{h}+0.085{\left(\frac{a}{h}\right)}^2+0.18{\left(\frac{a}{h}\right)}^3\right)/\sqrt{1-\frac{a}{h}}\end{array}$$

(18)

Symbols $F_1$, $F_2$ and $F_{II}$ are the correction factors of stress intensity. Symbol a is the variable for depth, and ${\theta }_1$ is the variable for crack angle. For the plane stress, $E^{\prime }=E$, and for the plane strain, $E^{\prime }=E/\left(1-{\mu }^2\right)$. The elements of the local flexibility matrix are

$$\begin{array}{c}{M}_{11}=\frac{16R}{E^{\prime }{D}_o^4{\left(1-{\eta }^2\right)}^2}{\int }_0^{a_1}a{F}_1^2\left(a\right)da,\\ M_{12}=\frac{128RL}{\pi E^{\prime }{D}_o^5\left({\eta }^6-{\eta }^4-{\eta }^2+1\right)}{\int }_0^{\pi /4}{cos}^2{\theta }_{1}d{\theta }_1{\int }_0^{a_1}a{F}_1\left(a\right)F_2\left(a\right)da,\\ M_{13}=\frac{256R}{\pi E^{\prime }{D}_o^5\left({\eta }^6-{\eta }^4-{\eta }^2+1\right)}{\int }_0^{\pi /4}{cos}^2{\theta }_{1}d{\theta }_1{\int }_0^{a_1}a{F}_1\left(a\right)F_2\left(a\right)da,\\ M_{22}=\frac{64R}{\pi E^{\prime }{D}_o^4{\left(1-{\eta }^2\right)}^2}{\int }_0^{\pi /4}{cos}^2{\theta }_{1}d{\theta }_1{\int }_0^{a_1}a{F}_{II}^2\left(a\right)da\\ +\frac{257R{L}^2}{\pi E^{\prime }{D}_o^6{\left(1-{\eta }^4\right)}^2}{\int }_0^{\pi /4}{cos}^4{\theta }_{1}d{\theta }_1{\int }_0^{a_1}a{F}_2^2\left(a\right)da,\\ M_{23}=\frac{514RL}{\pi E^{\prime }{D}_o^6{\left(1-{\eta }^4\right)}^2}{\int }_0^{\pi /4}{cos}^4{\theta }_{1}d{\theta }_1{\int }_0^{a_1}a{F}_2^2\left(a\right)da,\\ M_{33}=\frac{1028R}{\pi E^{\prime }{D}_o^6{\left(1-{\eta }^4\right)}^2}{\int }_0^{\pi /4}{cos}^4{\theta }_{1}d{\theta }_1{\int }_0^{a_1}a{F}_2^2\left(a\right)da,\\ M_{44}=\frac{4(1+\mu )}{E^{\prime }h}{\int }_0^{a_1}tan\frac{\pi a}{2h}da,\\ M_{12}=M_{21},M_{13}=M_{31},M_{23}=M_{32},M_{14}=M_{41},M_{24}=M_{42},\\ M_{34}=M_{43},M_{14}=M_{24}=M_{34}=0,\eta =D_i/D_o\end{array}$$

(19)

The additional displacement in the region around the crack can be decomposed in axial u, angular $\partial w/\partial x$, radial w, and circumferential v directions. The generalized force contains axial force $N_x$, bending moment $M_x$, effective radial shear $S_x$, and effective circumferential shear $S_{x\theta }$. Then, the expanded Equation (17) is shown below.

$$\left[\begin{array}{c}{u}^R-u^L\\ \partial w^R/\partial x-\partial w^L/\partial x\\ w^R-w^L\\ v^R-v^L\end{array}\right]=\left[M_{4\times 4}\right]\left[\begin{array}{c}{N}_x\\ M_x\\ S_x\\ S_{x\theta }\end{array}\right]$$

(20)

In Equation (20), the symbols $u^R$ and $u^L$ indicate the axial displacement to the left and right of the crack, respectively. Other symbols of similar form indicate displacements and angles in the corresponding directions and sides. Moreover, solving the stiffness matrix of the cracked lining requires the additional local flexibility matrix, which is crucial in obtaining the free vibration characteristics of the shield tunnel lining with a circumferential crack.

2.4. Displacement Response of a Circumferential Crack

When an incident wave encounters a discontinuity at the boundary between two different media, it generates a transmitted wave and a reflected wave. The cracks do not induce a phase change in reflected, transmitted, or incident waves [35]. The external excitation position is set as the origin of axial coordinate x, and the distance between this external excitation point and the section containing the crack is $L_1$. In each mode n, four waves are in the positive direction and four in the negative direction in the axial coordinate. Therefore, four incident waves and four reflected waves are in the crack’s left region ($0\le x\le L_1$). The superposition of these eight waves for circumferential mode n yields axial displacement $u_1$ in the area, given by the following equation. Symbol $U_{nm}$ ($m=1,2,3,\dots ,16$) represents the wave amplitude.

$$\begin{array}{c}{u}_1={\displaystyle \sum _{m=1}^4}{U}_{nm}cosn\theta e^{i\left(\omega t-k_{nm}x\right)}\\ +{\displaystyle \sum _{m=5}^8}{U}_{nm}cosn\theta e^{i\left(\omega t-k_{n(m-4)}\left(x-L_1\right)\right)}\end{array}$$

(21)

On the right side ($x\ge L_1$) of the crack, the displacement response is generated by the superposition of four transmitted waves. In addition, the displacement response due to the crack occurs in the angular range ($0°\le \theta \le 45°$) in which the crack is distributed, as shown in Figure 2. Then, axial displacement $u_2$ at circumferential mode n is shown below.

$$u_2=\sum _{m=9}^{12}{U}_{nm}cosn\theta e^{i\left(\omega t+k_{n(m-8)}\left(x-L_1\right)\right)}$$

(22)

In the angular range ($45°\le \theta \le 180°$) of the non-crack part on the crack’s location cross-section, its right-side displacement response is the superposition of four waves generated by the excitation and remains unchanged. Axial displacement $u_3$ of circumferential mode n in this region is as follows:

$$u_3=\sum _{m=1}^4{U}_{nm}cosn\theta e^{i\left(\omega t-k_{nm}x\right)}$$

(23)

The displacement response in the area ($x\le 0$) to the right of the excitation point is the superposition of four waves. The area’s axial displacement $u_4$ at circumferential mode n is shown below.

$$u_4=\sum _{m=13}^{16}{U}_{nm}cosn\theta e^{i\left(\omega t+k_{n(m-12)}x\right)}$$

(24)

The displacement, force, and moment are equal on either side of the section containing the excitation point ($x=0$). Also, the force and moment are identical on either side of the section containing the crack ($x=L_1$). Equation (20) presents the difference between the displacements on the two sides of the area where the crack is located ($x=L_1$ and $0°\le \theta \le 45°$). The details of these equivalence conditions are

at $x=0$,

$$u^R=u^L,\partial w^R/\partial x=\partial w^L/\partial x,w^R=w^L,v^R=v^L,$$

(25)

$$N_x^R=N_x^L,M_x^R=M_x^L,S_{x\theta }^R=S_{x\theta }^L,S_x^R=S_x^L+F,$$

(26)

at $x=L_1$,

$$N_x^R=N_x^L,M_x^R=M_x^L,S_x^R=S_x^L,S_{x\theta }^R=S_{x\theta }^L$$

(27)

The wave amplitudes can be obtained by substituting Equations (21), (22) and (24) into the displacement and stress conditions above. Calculating displacements in the circumferential and radial directions is similar to the equations and methods of axial direction.

2.5. Load and Monitor Location

This paper explores the vibration response of the shield tunnel lining with a partly circumferential crack under a harmonic point load. Figure 3 presents the location of the load, crack, and monitors. Relative position $\phi$ is the ratio of the axial distance from the specified point to the left end of the tunnel lining to the total length. The crack’s relative depth $\gamma$ is the crack depth ratio to the thickness of the shield tunnel lining. The amplitude and frequency of the harmonic point excitation force are set at 100 N and 100 Hz, respectively. In this study, 6 load positions are arranged along the axial direction, and each is assigned its relative position: $0.2$, $0.25$, $0.3$, $0.35$, $0.4$, and $0.45$. Meanwhile, monitoring points are at axial relative positions of $0.55$, $0.6$, $0.65$, $0.7$, $0.75$, and $0.8$. In the circumferential section, each axial position has 12 monitoring points, with a $30°$ angle between adjacent monitoring points, as shown in Figure 3. Additionally, the partly circumferential crack is located at a relative position of $0.5$. The simulation considers the individual impacts of alterations in the load position and the monitoring point position on the displacement response.

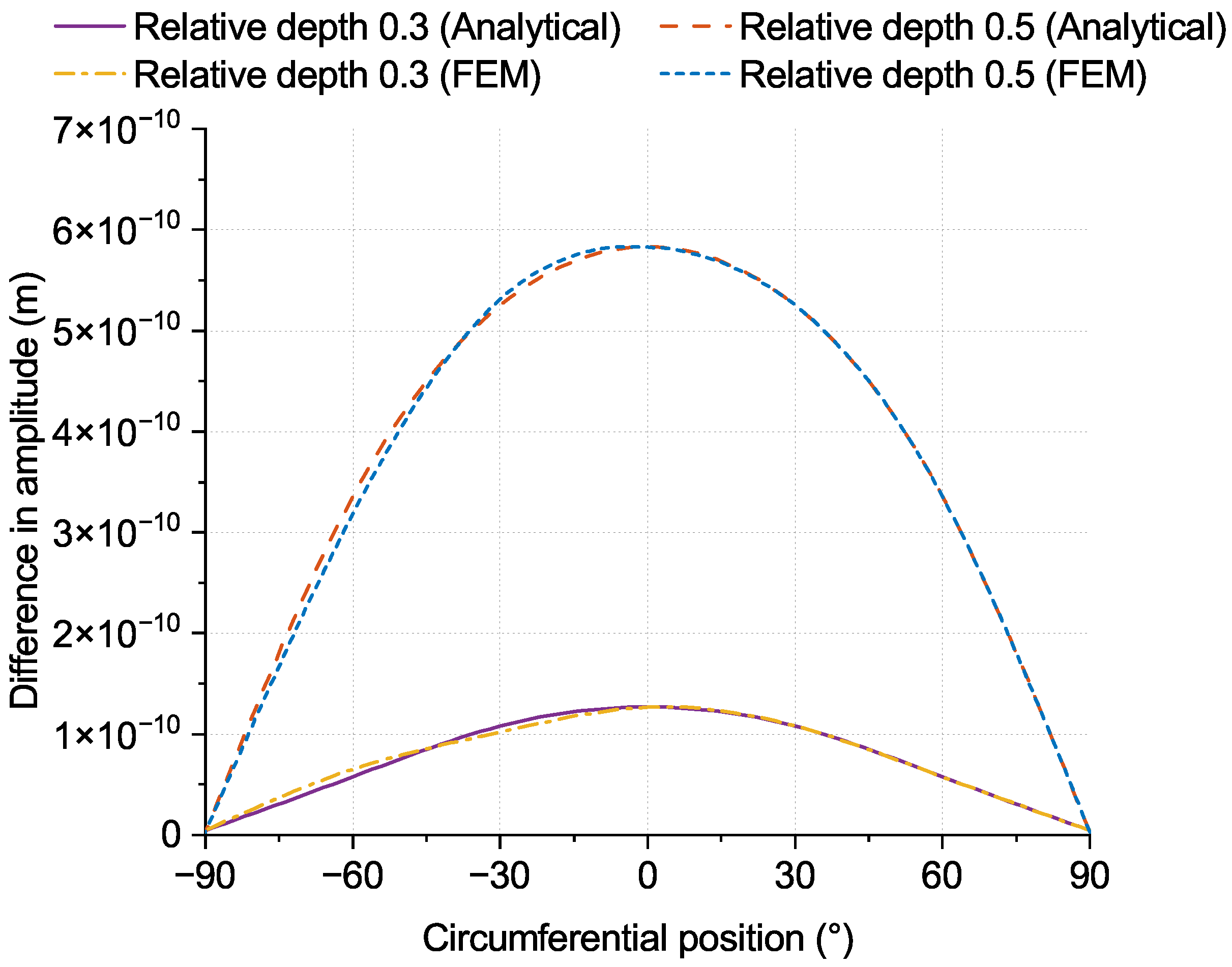
3. Model Validation

The model validation process involves three steps. First, validation of the dynamic model for free vibration of the undamaged shield tunnel lining is conducted based on the literature [11,34]. The properties and dimensions of the shell are $R=1$ m, $L/R=20$, $h=0.01$ m, $\mu =0.3$, $\rho =7850$ kg/m³, and $E=210$ GPa. The boundary condition is clamped−clamped. The natural frequencies of the analytical results, as presented in

Table 1. Comparison of the natural frequencies of the analytical and corresponding reference results.

Analytical	Reference [11]	Reference [34]	Mode (n,m)
12.14 Hz	12.13 Hz	12.17 Hz	(2,1)
28.06 Hz	28.06 Hz	28.06 Hz	(2,2)
19.61 Hz	19.61 Hz	19.61 Hz	(3,1)
23.28 Hz	23.28 Hz	23.28 Hz	(3,2)
31.97 Hz	31.97 Hz	31.98 Hz	(3,3)
36.47 Hz	36.48 Hz	36.47 Hz	(4,1)
37.37 Hz	37.38 Hz	37.37 Hz	(4,2)
39.77 Hz	39.77 Hz	39.78 Hz	(4,3)

, are compared with corresponding reference values. The maximum difference between the analytical and reference results is less than $1\%$, affirming the accuracy of both the model and the natural frequency solution method.

Second, no comparable literature is available to provide data for validating the effectiveness and precision of the proposed method. Consequently, this paper establishes the FEM of the shield tunnel lining with a partly circumferential crack. The FEM is utilized to ensure the accuracy of the results. Literature [34] serves as the basis for validating the FEM of the undamaged shield tunnel lining. Moreover, the FEM incorporates a cohesive element for modeling the partly circumferential crack. As shown in Figure 4, the shield tunnel lining is simulated using ABAQUS. The length-to-radius ratio $L/R$ of the model is 20. The tunnel lining material is concrete, which has a density $\rho$ of 2500 kg/m³, Young’s modulus E of $34.5$ GPa, and Poisson’s ratio $\mu$ of $0.2$. The lining is considered circular, with radius R of $2.85$ m and lining thickness h of $0.3$ m. The elements are 8-node linear brick elements ($C3D8$). As the mesh number increases, the first-order natural frequency can gradually converge, enabling the determination of the mesh configuration [11]. For mesh configurations exceeding 276,552 meshes, the natural frequencies remain virtually unchanged and are consistent with the analytical solution. Consequently, the 276,552 meshes configuration addresses the vibration response of the shield tunnel lining featuring a partly circumferential crack.

Table 2. Comparison of the first three-order natural frequencies with different crack depths of the analytical and corresponding FEM results.

Order	Crack Relative Depth 0.4			Crack Relative Depth 0.6
	1	2	3	1	2	3
Natural frequency (FEM)	1.980 Hz	5.239 Hz	9.758 Hz	1.978 Hz	5.239 Hz	9.749 Hz
Natural frequency (Analytical)	1.996 Hz	5.240 Hz	9.894 Hz	1.982 Hz	5.239 Hz	9.750 Hz

shows the natural frequencies of the analytical and corresponding FEM results. Extracting the first three orders of the natural frequency and setting two relative depths, with the crack positioned in the middle of the shield tunnel lining, the maximum difference between the analytical and FEM results is less than $1.5\%$. This verification confirms the appropriateness of the adopted lining model with a circumferential crack.

Lastly, to enhance the applicability of the proposed approach, it is essential to validate the results of the forced vibration response of the shield tunnel lining with a partly circumferential crack. The properties and dimensions of the lining remain unchanged. Figure 5 displays one example of the validation procedure. The point load’s frequency and amplitude are set at 100 Hz and 100 N. The load, crack, and monitor relative positions are 0.25, 0.5, and 0.55, respectively. Additionally, seven monitors are spaced at a circumferential angle of $30°$ between neighboring points. The figure indicates the amplitude difference in radial displacements obtained through both FEM and the proposed method across two relative depths. The vertical axis denotes the difference in displacement response amplitudes between undamaged and cracked tunnel linings. Meanwhile, the horizontal axis represents the angular distribution of monitoring points along the circumferential section. The comparison of analytical and related FEM results reveals a good agreement, irrespective of crack depth variations. This alignment attests to the correctness and accuracy of the analytical approach for the vibration response of the shield tunnel lining with a partly circumferential crack.

4. Results and Discussion

This paper utilizes wave propagation, LSM, and analytical methods to investigate the vibration response of the shield tunnel lining with a partly circumferential crack. The shield tunnel lining material is concrete, with $R=2.85$ m, $L/R=40$, $h=0.3$ m, $\mu =0.2$, $\rho =2500$ kg/m³, and $E=34.5$ GPa. The vibration response analysis of the shield tunnel lining with a partly circumferential crack has three components. The first segment explores the natural frequencies of shield tunnel lining. It describes the depth and location influence of the partly circumferential crack on these frequencies. The following part extracts the displacement response of the shield tunnel lining with a partly circumferential crack, revealing the displacement variation law at different positions and directions. Section 5 establishes different point load positions, observing the displacement changes across different positions and directions.

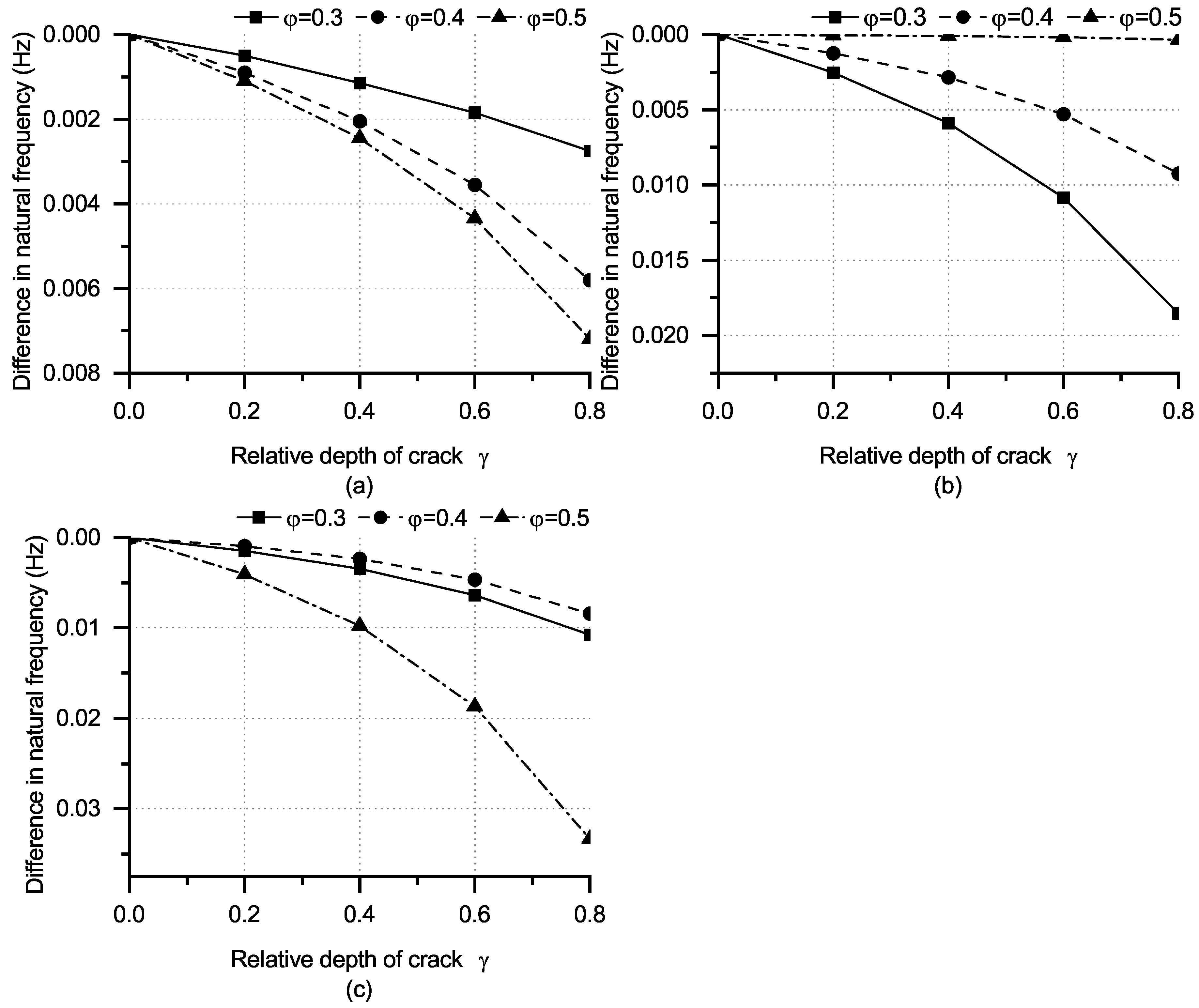
4.1. Natural Frequency Characteristics

Cracks cause a reduction in the stiffness of the structure. Decreasing stiffness can reduce the natural frequency of the structural system. This section shows and discusses the effects of crack depth and position on the natural frequencies of the shield tunnel lining. The natural frequencies of the cracked lining in the results are smaller than those of the ideal lining. Moreover, the shield tunnel lining is a symmetrical structure. Hence, locating the cracks only in the left or right half of the lining is a reasonable method.

Figure 6 illustrates the relationship between the first three orders of natural frequency and crack relative depth for a partly circumferential crack. The vertical coordinate is the difference between the natural frequencies of the ideal and cracked linings. The crack’s three relative positions, $0.3$, $0.4$ and $0.5$, correspond to the three curves in the figure. In Figure 6a, as the crack’s relative depth increases, the tunnel lining’s first-order natural frequency shows a downward trend. The natural frequency with a relative position of $0.5$ decreases the fastest among them. When the crack position moves from the middle to both ends of the lining, the trend of the first-order natural frequency changing with the relative depth slows down. Figure 6b presents the results for second-order natural frequency. In contrast to the first-order one, as the crack position approaches either end, the trend of the second-order natural frequency accelerates concerning the crack’s relative depth. Notably, the second-order natural frequency of the tunnel lining, when the crack is at a relative position of $0.5$, is almost unchanged as the relative depth increases. In the third-order mode, as illustrated in Figure 6c, all such frequencies decline as the crack depth increases. The natural frequency experiences the most significant reduction when the relative crack position is at $0.5$. Conversely, the natural frequency gradually decreases as the crack position approaches either end of the tunnel lining. Additionally, the third-order natural frequency curves for relative positions of $0.3$ and $0.4$ closely resemble each other.

Figure 7 demonstrates the correlation between the initial three orders of natural frequency and the relative position of a partly circumferential crack. The four curves in the graph represent the relative depths of $0.2$, $0.4$, $0.6$, and $0.8$. In Figure 7a, the curves of first-order natural frequency all exhibit a parabolic shape. A reduced relative depth of the crack leads to a gentle curve and decreases effects on first-order natural frequency. Meanwhile, all four curves reach their maximum values when the crack is positioned in the central section of the tunnel lining. As the crack approaches either end of the lining, the rate of decrease in the first-order natural frequency becomes gradual. In Figure 7b, the middle position of the tunnel lining is a second-order mode node. Consequently, the second-order natural frequency remains consistent at a relative position of $0.5$, regardless of varying crack depths. Furthermore, there is a maximum value on either side of the tunnel lining. This placement of the crack results in the most pronounced variation in the second-order natural frequency. Figure 7c reveals two nodes corresponding to the third-order mode, exhibiting similar characteristics to the second-order mode node. Moreover, there are maximum values on either side of each node. These peak values pinpoint the most sensitive crack positions for the third-order natural frequency. Also, as the crack depth increases, the sensitivity of the natural frequency intensifies.

This section delves into the impact of a partly circumferential crack’s relative depth and position on the first three orders of natural frequencies of the tunnel lining. The growing crack depth accelerates the rate of decline in the first three orders of natural frequencies. Remarkably, variations in crack depth have minimal influence on the natural frequencies when the crack position aligns with a modal node. In addition, when the crack position falls midway between two nodes of one mode, the corresponding natural frequency is most responsive to changes in crack depth. These findings are consistent with prior research [11], reinforcing the reliability of the results presented in this section.

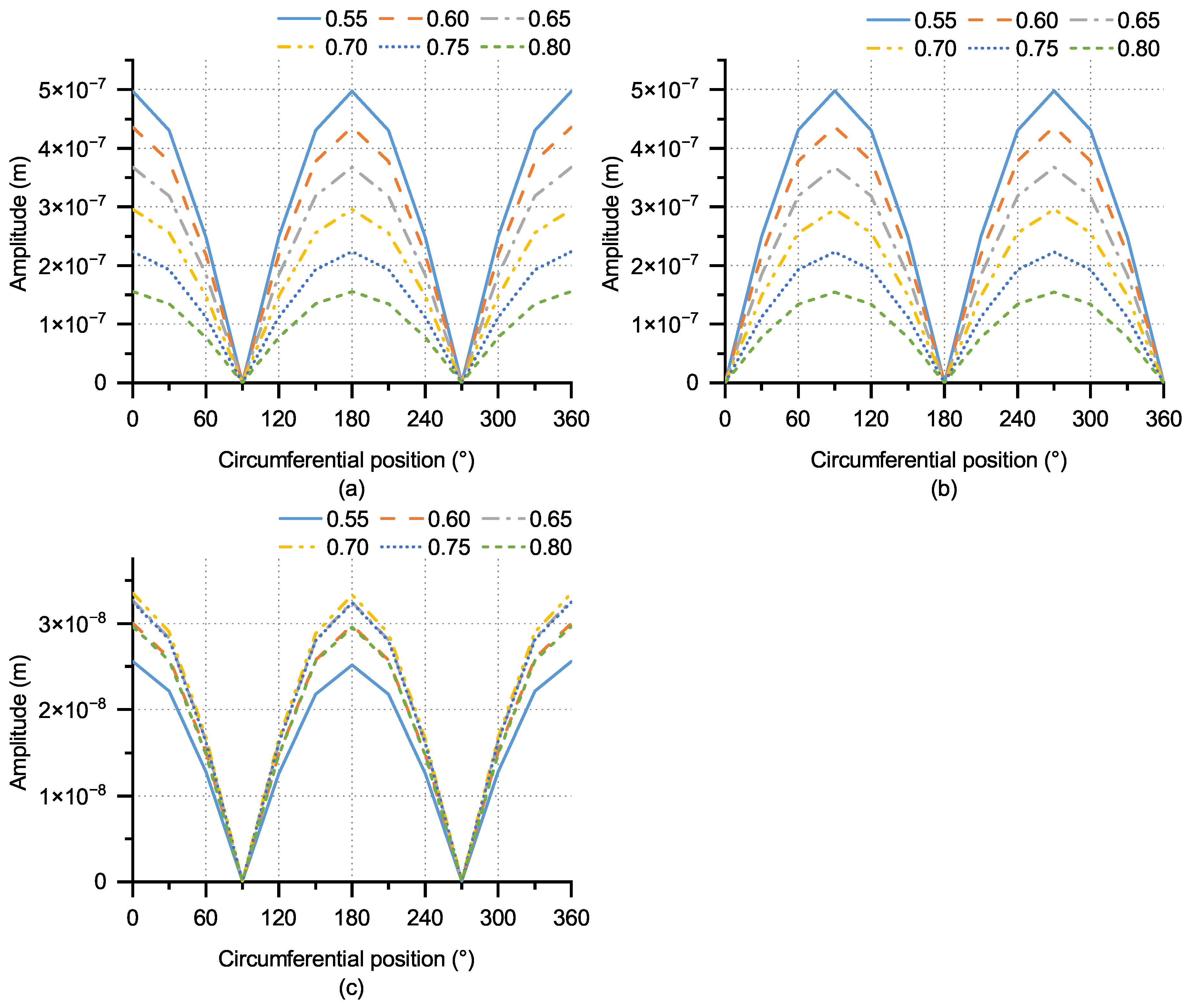
4.2. Forced Vibration with Different Monitoring Positions

This section explores the displacement response of different monitoring points under a position-fixed harmonic point load. The model parameters and boundary conditions are the same as in Section 4.1. The relative position of the load point is $0.25$. The location of the crack and monitoring points are mentioned in Section 2.5. Figure 8 depicts the displacement response of the undamaged tunnel lining subjected to harmonic point excitation. Figure 8a, b, and c represent the radial, circumferential, and axial displacement responses. The vertical axis represents the amplitude of the displacement response. The horizontal axis represents the angular distribution of monitoring points along the circumferential section. Each curve within the figure corresponds to the monitoring points’ specific axial relative position.

In Figure 8a, the radial displacement’s maximum amplitude at monitoring points is $0°$ and $180°$ in the circumferential angle. Figure 8c reveals that the maximum amplitude of axial displacement occurs at the same location. Meanwhile, in Figure 8b, the circumferential displacement response differs from the other two directions, exhibiting the minimum value at the corresponding monitoring position. The displacement response of the cracked lining is consistent with the shape and maximum amplitude position in Figure 8. Therefore, this section does not present similar results for cracked tunnel linings. According to the displacement response and the crack’s location, the radial and axial displacements are suitable results for further analysis.

Figure 9 illustrates the impact of cracks on the displacement response at the monitoring point at a circumferential angle of $0°$. Figure 9a and b depict the radial and axial displacement responses, respectively. The figure displays three distinct relative crack depths: $0.3$, $0.4$, and $0.5$, each corresponding to a different curve. The vertical axis represents the difference between the displacement response amplitudes of intact and cracked tunnel linings. Notably, the displacement response amplitudes of the cracked tunnel lining in this section are greater than those of the undamaged tunnel lining. Meantime, the horizontal axis denotes the axial relative position. In Figure 9a, the difference in axial displacement amplitudes corresponding to each axial relative position expands with increasing crack depth. Moreover, as the relative position increases, the amplitude difference diminishes, and this diminishing trend becomes more prominent with increasing crack depth. While the trends in amplitude differences between the axial and radial directions are similar, the extent of change in the axial direction is smaller when compared to the radial direction. The findings presented in this section reveal that cracks diminish the local stiffness of the tunnel lining, leading to an increase in the displacement response. As a result, differences in the displacement response amplitudes emerge between the undamaged and cracked linings. These discrepancies progressively diminish with increasing distance from the crack. The variance in displacement between the cracked and undamaged regions helps identify the crack’s circumferential location, with the circumferential position displacement becoming more pronounced as the monitoring point approaches the crack location.

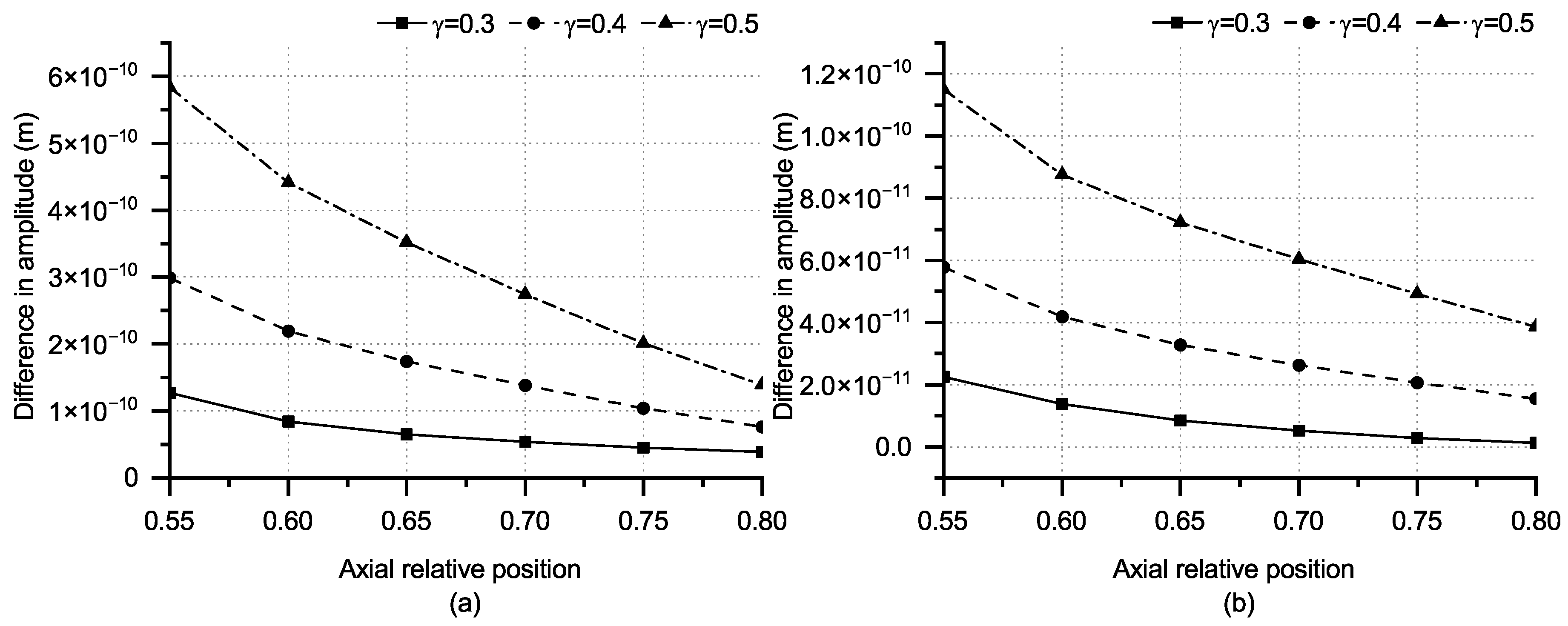
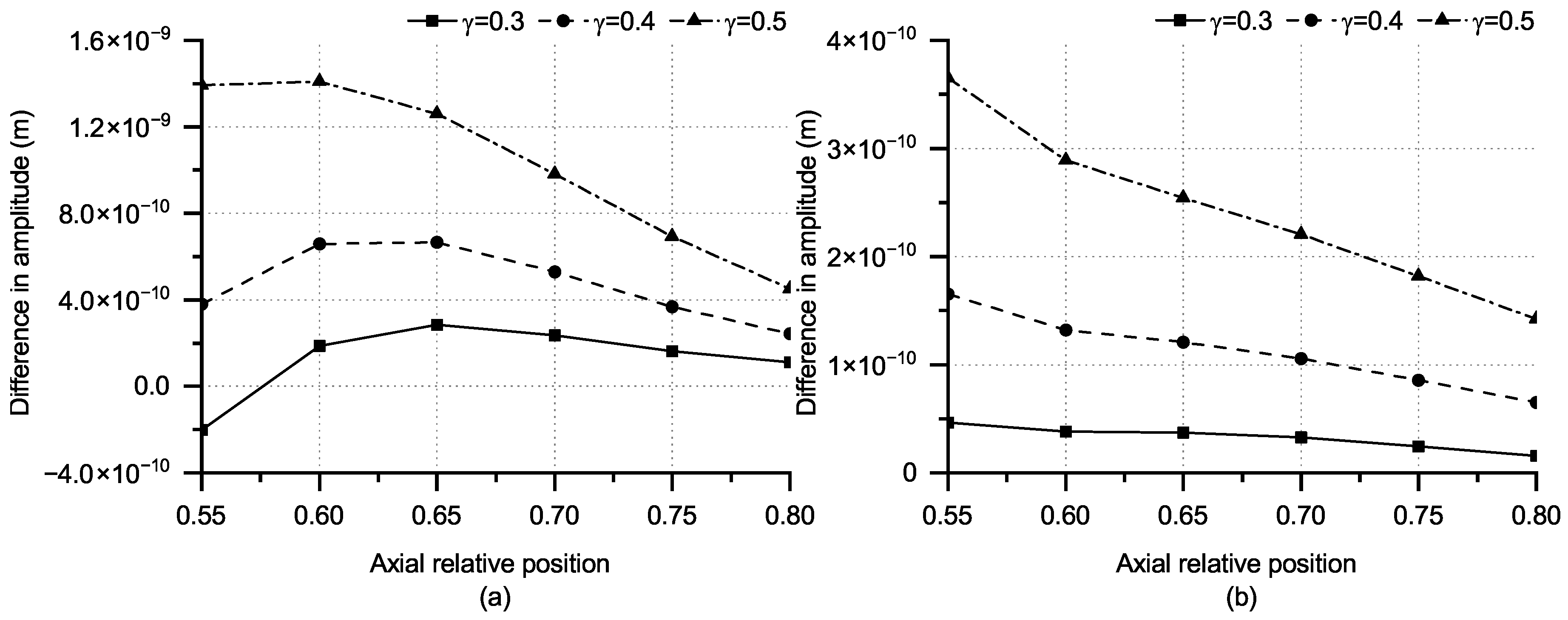
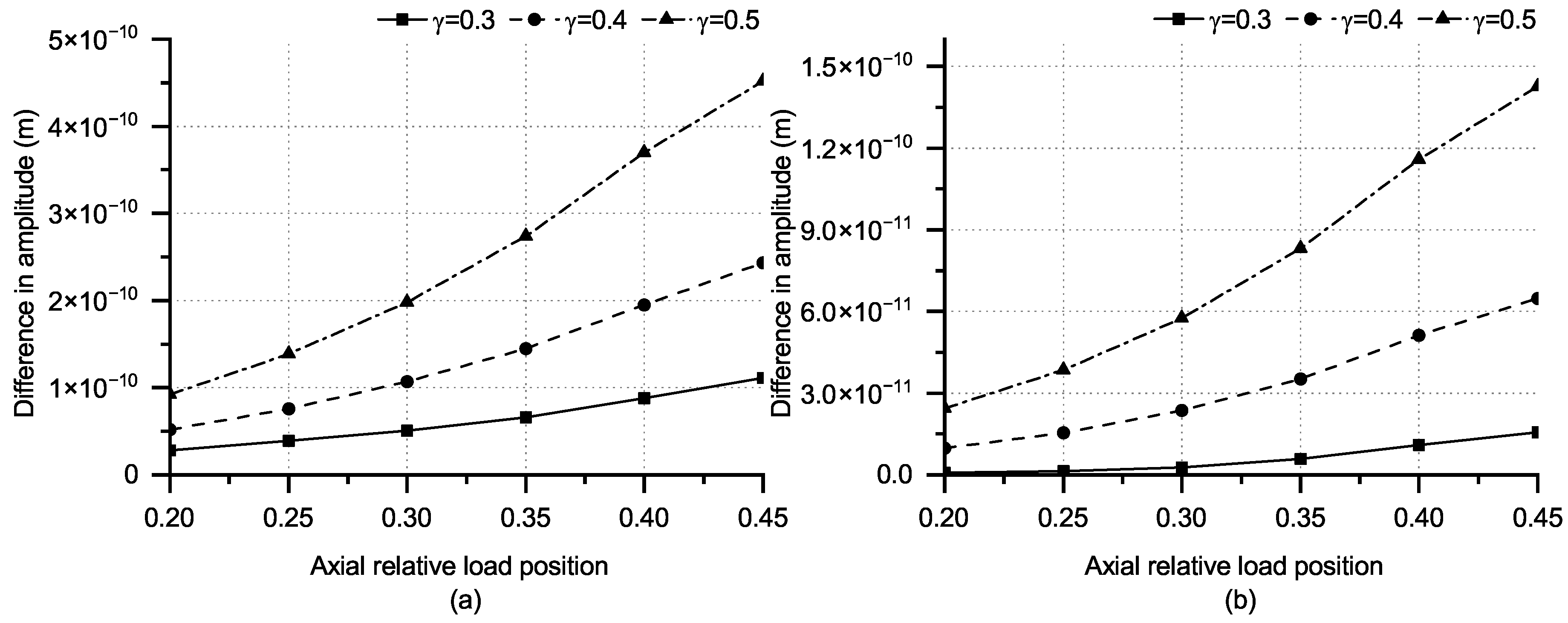
4.3. Forced Vibration under Different Load Positions

This section investigates the influence of varying load locations on the displacement response surrounding the crack. The model parameters and boundary conditions are consistent with the previous section. The locations of the crack and load points are mentioned in Section 2.5. The analysis concentrates on variations in displacement response within the crack’s impact region. Accordingly, six monitoring positions are distributed along the axial direction, with each section housing a corresponding monitoring point set at a circumferential angle of $0°$.

Figure 10a indicates the crack’s influence on the radial displacement response of the $0°$ circumferential angle monitoring point at a relative load position of $0.45$. The curves correspond to the three relative crack depths of $0.3$, $0.4$, and $0.5$, respectively. The ordinate is the displacement amplitude difference between the cracked and undamaged lines. Meanwhile, the horizontal axis is the axial relative position. All curves increase first and then decrease. The shallower the crack depth, the lower the initial point of the respective curve and the more apparent the upward trend. This phenomenon occurs due to the interaction and superposition of the four transmitted waveforms [11]. As the distance between the monitor and the crack increases, the radial displacement amplitude of the cracked lining first increases and then decreases. Meanwhile, the amplitude difference is the amplitude of the undamaged lining minus that of the cracked lining. Therefore, the amplitude difference curve shows an initial rising and then falling trend. In addition, as the distance between the load position and the crack increases, this initially rising and then decreasing trend gradually disappears, transitioning into a trend of complete decline. Figure 10b shows the impact of the crack on the axial displacement response of the $0°$ circumferential angle monitoring point at a relative load position of $0.45$. This demonstrates that the phenomena observed in the radial displacement response are absent in the axial direction. All curves exhibit a descending trend, which becomes increasingly evident as the relative depth of the crack rises. Furthermore, Figure 10 reveals that monitoring points with axial relative positions of $0.65$, $0.7$, $0.75$, and $0.8$ provide regular amplitude difference outcomes. This section analyzes the monitoring point results with axial relative positions of $0.65$ and $0.8$.

Figure 11 displays the effect of load points at different locations on the displacement response of the monitoring point for the cracked tunnel lining. The monitoring point is at a circumferential angle of $0°$ and an axial relative position of $0.65$. The vertical coordinate is the difference between the displacement response amplitudes of the ideal and cracked linings. The horizontal coordinate is the axial relative load position. The three relative crack depths, $0.3$, $0.4$ and $0.5$, correspond to the three curves in the figure. In Figure 11a, as the load point approaches the crack, the amplitude differences show an increasing trend regardless of the crack’s relative depth. This upward trend intensifies with the growing relative crack depth. However, the rising trend of amplitude differences weakens when the load moves from an axial relative position of $0.4$ to $0.45$. Figure 11b shows that the amplitude difference in the axial direction follows a similar trend to that observed in the radial direction. The distinction is that the variation range in the cracked lining’s amplitude differences in the axial direction is smaller than the variation range in the radial direction.

Figure 12 shows the impact of the load position on another monitor’s displacement response. The monitoring point’s axial relative position is $0.8$, keeping other parameters consistent with those in Figure 11. The general trend in the variation of displacement amplitude difference depicted in Figure 11 and Figure 12 is similar. Otherwise, there are some minor differences. In Figure 12, the upward trend of the radial and axial amplitude differences does not weaken when the load moves from the axial relative position of $0.4$ to $0.45$. In addition, the ranges of amplitude difference change for both radial and axial directions in Figure 12 and are smaller than those of corresponding directions in Figure 11.

In summary, this section studies the influence of various point load positions on the displacement response around the crack. First, as the load point nears the crack, the amplitude differences of the monitoring points exhibit an initial increase followed by a decrease as the distance between the monitoring point and the crack grows. This phenomenon vanishes gradually with the increasing distance between the load position and the crack, ultimately becoming a consistent downward trend in the amplitude difference. According to prior results, the subsequent analysis chooses monitoring points with regular amplitude difference variations. Then, the amplitude differences are analyzed under different load positions for the monitoring points. The results indicate that the corresponding amplitude differences experience an upward trend as the load point approaches the crack. In addition, the rise in crack depth intensifies this trend. These results can provide a basis for determining the optimal locations of excitation and monitoring points when identifying crack circumferential position.

5. Conclusions

This paper explores the dynamic response of a shield tunnel lining with a partly circumferential crack under a harmonic point load. The dynamic model is established based on the Flügge shell theory. The wave propagation method is employed to solve the dynamic model and obtain the free vibration characteristics of the tunnel lining. Subsequently, the residue theorem is applied to acquire the forced vibration response. Additionally, the simulation of a partly circumferential crack utilizes the LSM. The displacement response around the crack is ultimately determined by employing the wave superposition principle. The methodology enables the investigation of the evolution law of vibration responses in shield tunnel linings with various crack morphologies. The conclusion has three parts:

• The partly circumferential crack reduces the natural frequency of the shield tunnel lining because it causes local flexibility in the lining. Moreover, the rise in crack depth accelerates the decrease in natural frequency. Meanwhile, when the partly circumferential crack is positioned at a modal node, the crack minimally impacts the natural frequency of this mode. In contrast, when the crack is located in the middle of two nodes, the natural frequency of this mode undergoes the most significant variation. Therefore, the partly circumferential crack intensifies the fluctuation of natural frequency changes in high-order modes. This finding can aid in identifying the axial location of the crack and evaluating its depth;
• The monitoring point at $0°$ circumferentially experiences the highest amplitudes of displacement response in both radial and axial directions under a time-harmonic normal point load. Hence, the displacement response in both directions can be used to analyze a partly circumferential crack at the $0°$ circumferential position. The radial and axial amplitude differences show a downward trend on the other side of the crack as the distance from the monitoring point to the partly circumferential crack increases. In the meantime, the difference in radial displacement amplitudes exceeds that of axial displacement amplitudes. Furthermore, as the crack deepens, the scope in displacement amplitude difference increases. The variation in displacement response occurs in the region affected by the partly circumferential crack. Consequently, the alteration in radial and axial displacement amplitudes helps identify the crack’s circumferential position, and the radial displacement is more effective than the axial one;
• When the time-harmonic normal point load is near the crack, the radial amplitude difference on the other side of the crack initially increases and subsequently decreases. This phenomenon diminishes progressively as the load position moves away from the crack. Since the amplitude difference of the required monitoring points needs to have evolution laws, the axial relative positions of the monitor should be $0.65$, $0.7$, $0.75$, and $0.8$. As the distance between the load point and the crack decreases, the radial and axial amplitude differences of the selected monitoring points show a downward trend. Moreover, as the monitoring point relocates away from the crack, the range of variation in amplitude differences gradually decreases. Meanwhile, the deepening crack exhibits an enlarged variation range in radial and axial displacements. The results contribute to the identification of the crack’s circumferential position, providing a basis for selecting the load point and corresponding monitoring point locations.

This paper explores the dynamic response of the independent shield tunnel lining. Future research could integrate soil into the model to investigate the dynamic response of the lining structure within the tunnel–soil system. The analysis should consider both intact and cracked lining structures. Moreover, further study could concentrate on various external excitations, exploring the corresponding vibration response of the shield tunnel lining, with and without cracks. In addition, the practical utility of such small-scale displacement variations may pose challenges for direct application in real-world scenarios. Therefore, further investigation into methods is needed to bridge the gap between the observed small-scale variations and their practical applications.