Influence of Monolith Length on Temperature Field of Concrete Gravity Dams
Abstract
:1. Introduction
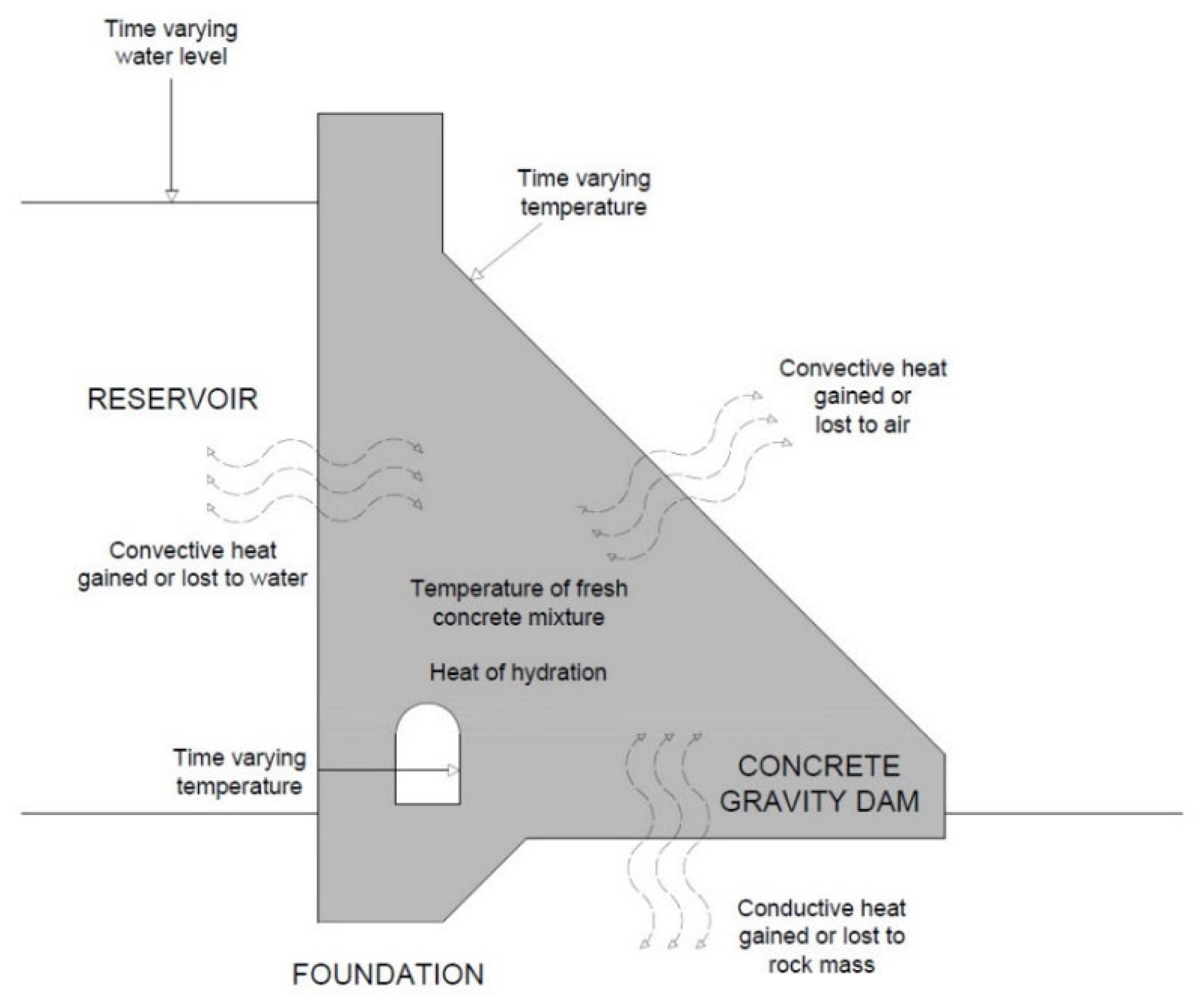
2. Theoretical Framework
2.1. Concrete Hydration Process
2.2. Heat Transfer on Surfaces of Concrete Blocks
2.3. Temperature of Fresh Concrete Mixture
2.4. Temperature of the Surrounding Rock Mass
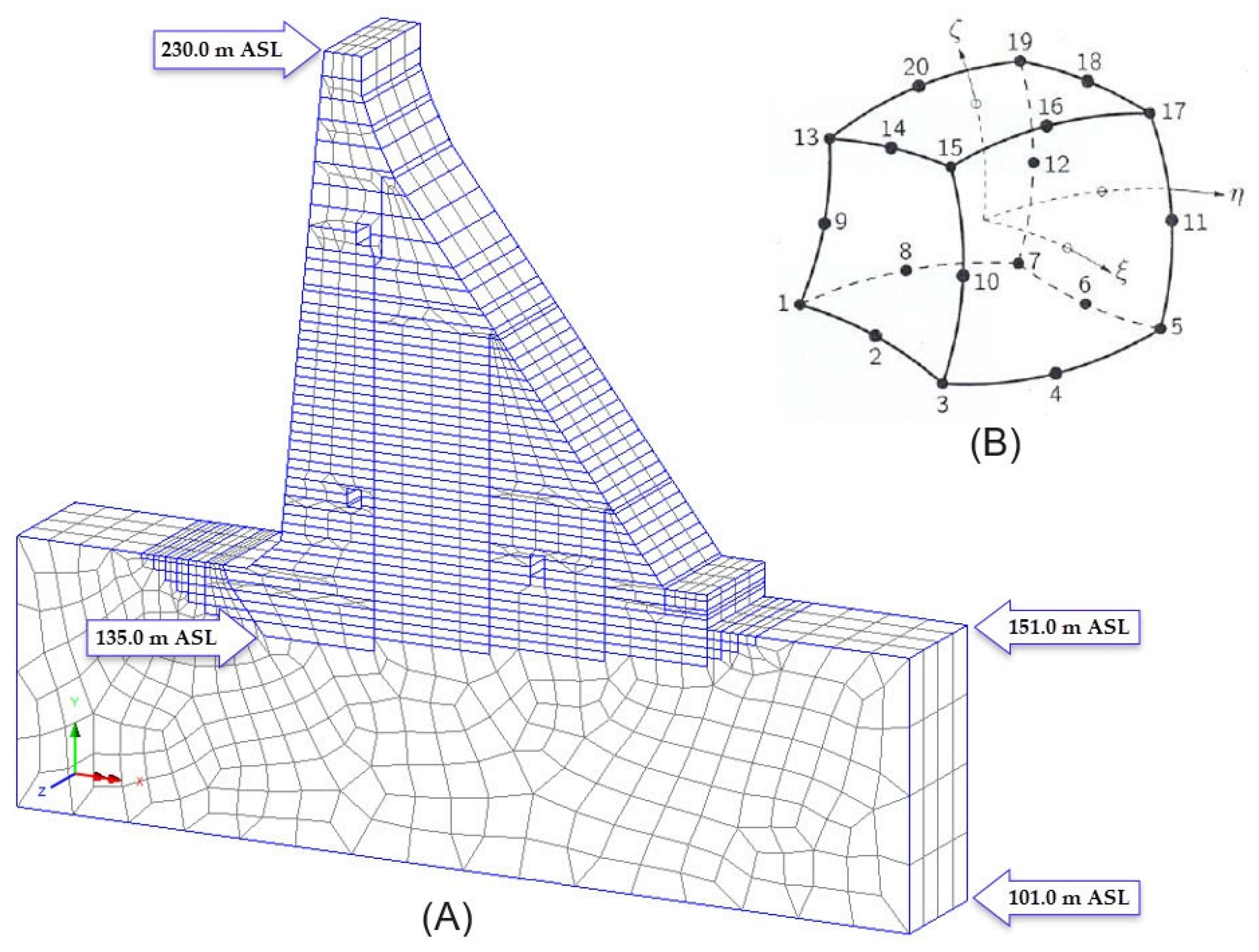
3. Numerical Models for Thermal Analysis
3.1. Model Description
3.2. Thermal Material Parameters
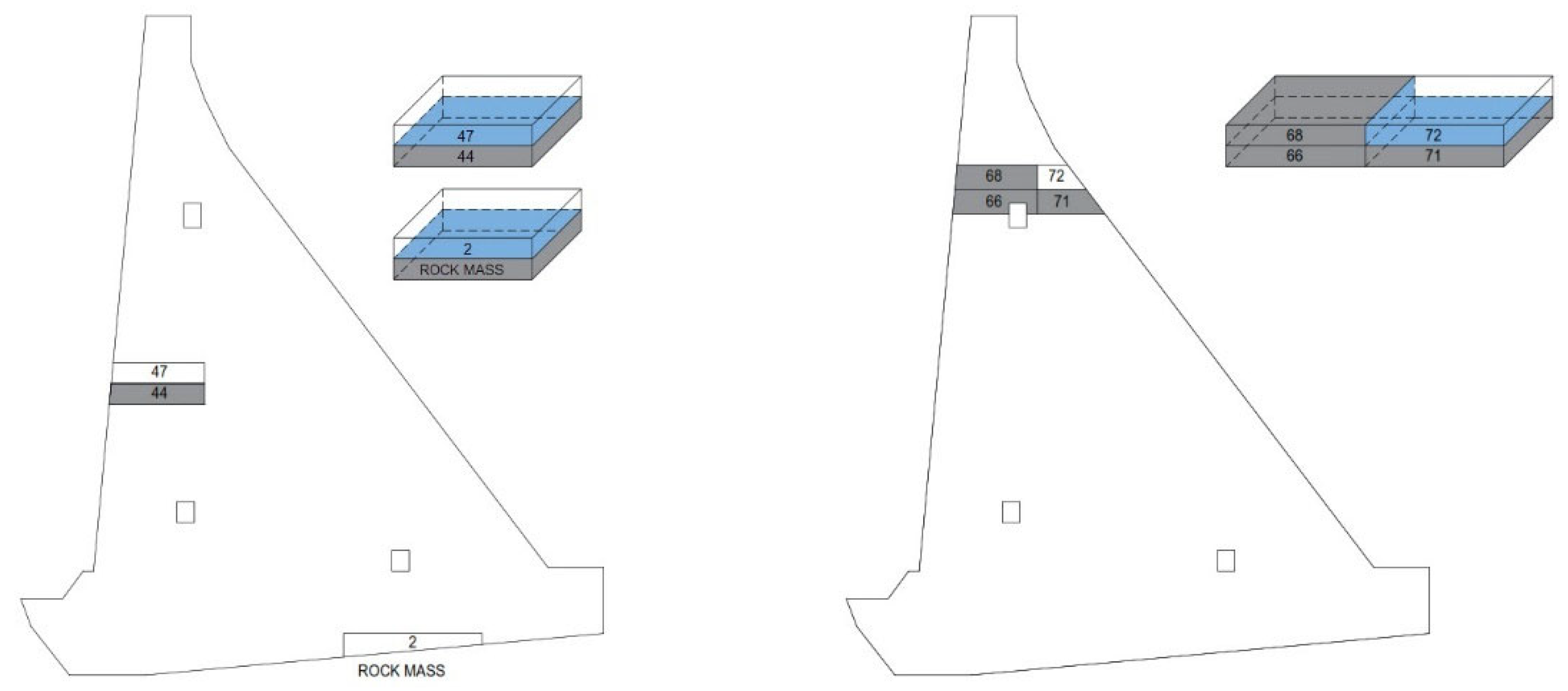
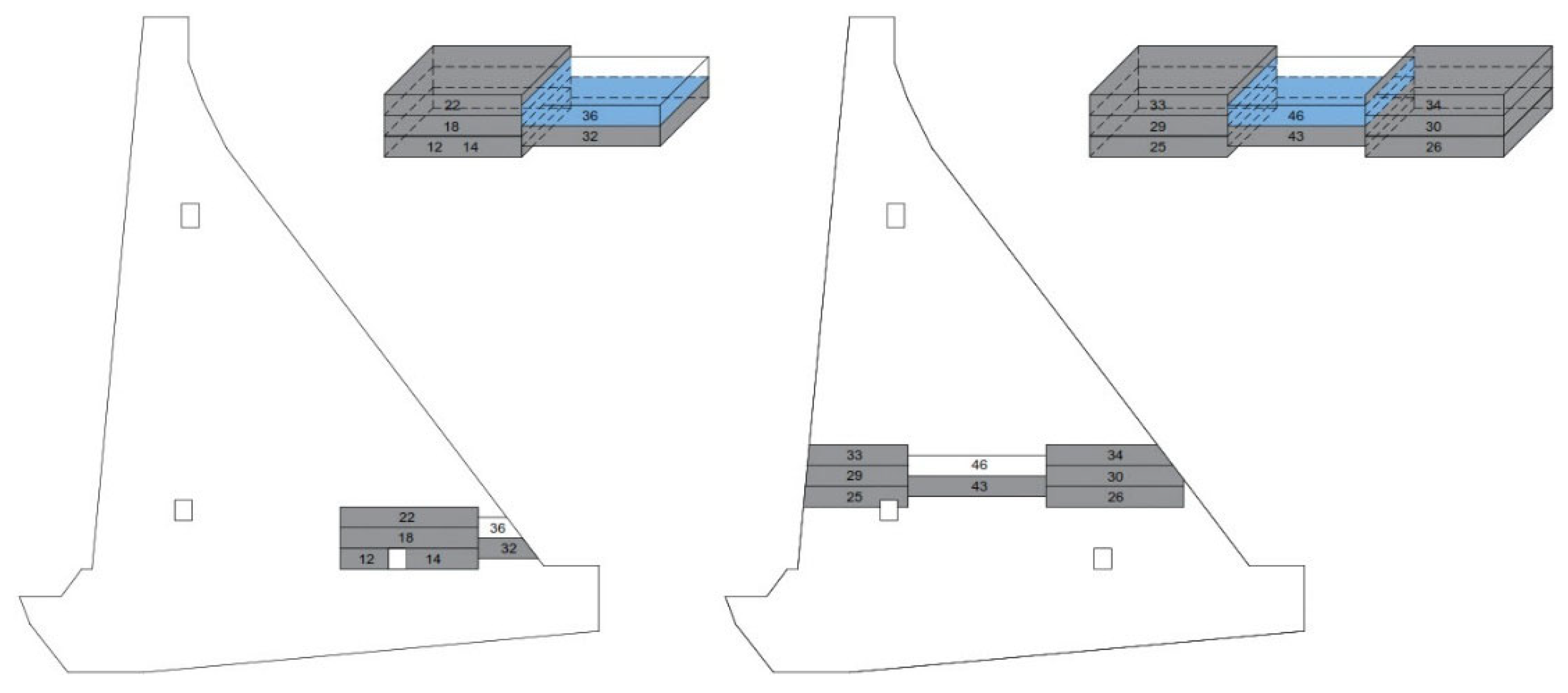
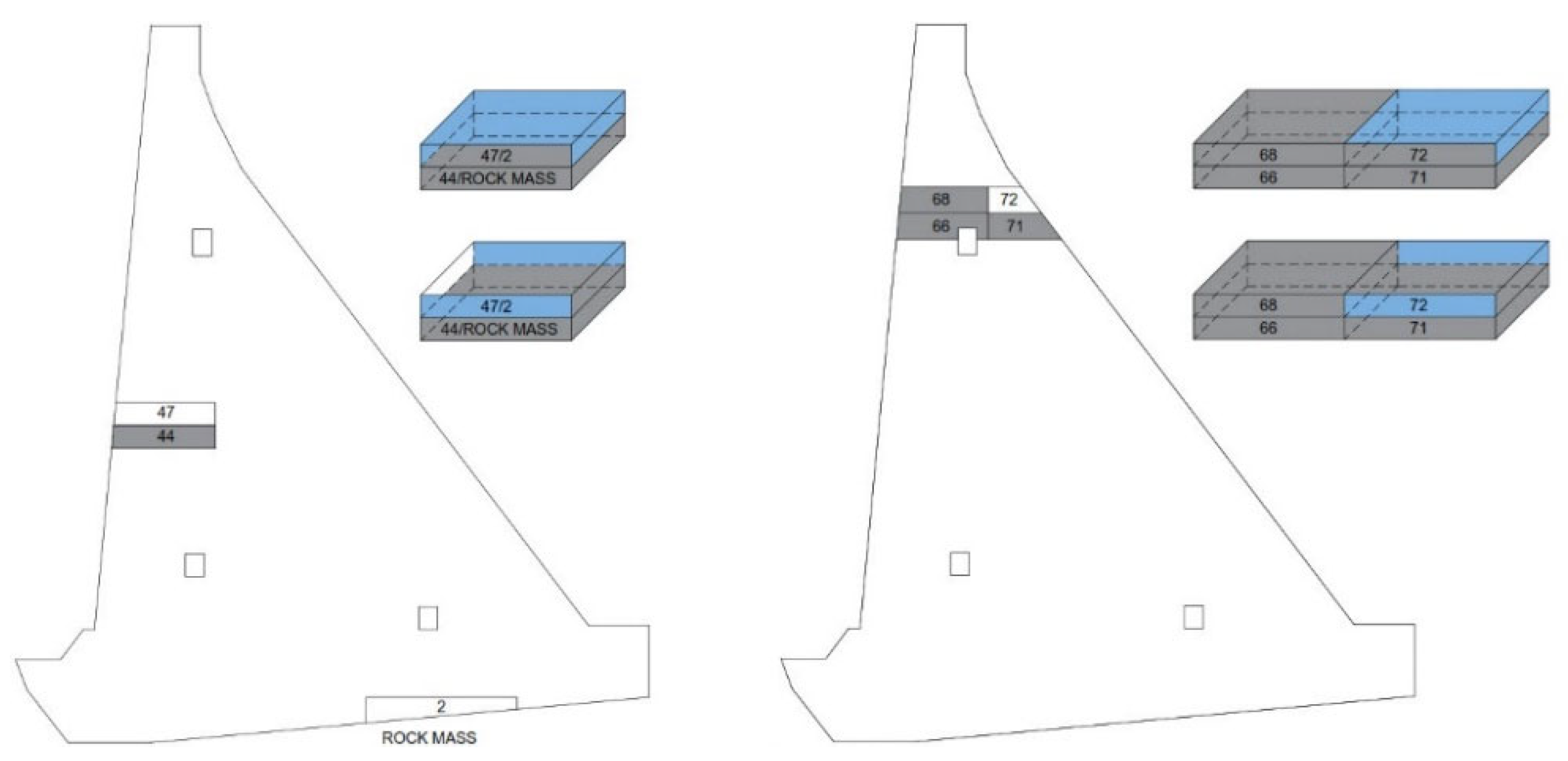
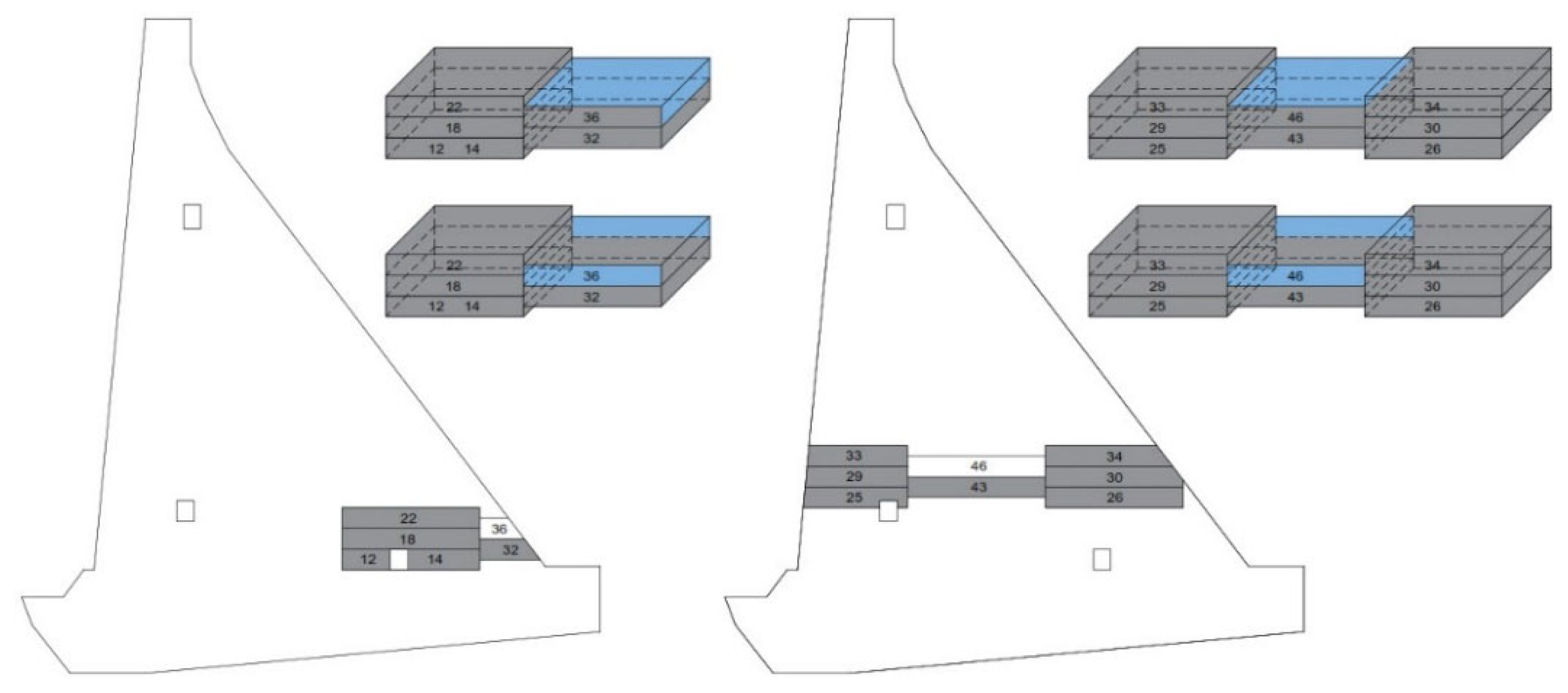
3.3. Boundary Conditions for Thermal Analysis
- The interface between the blocks and the rock mass;
- The interface between the old and fresh concrete blocks;
- The contact of the block’s surface with air;
- The contact of the block’s surface with water;
- The temperature of the fresh concrete mixture (the initial condition).
4. Analysis Results
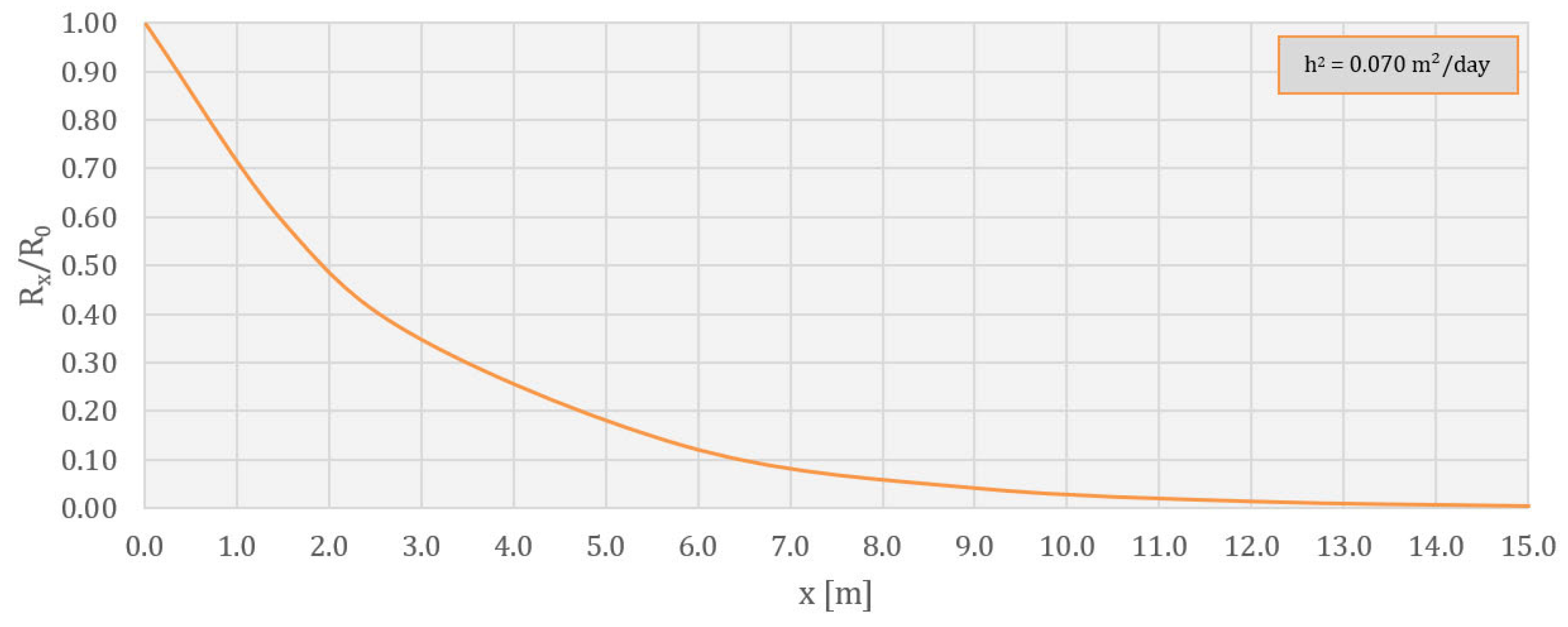
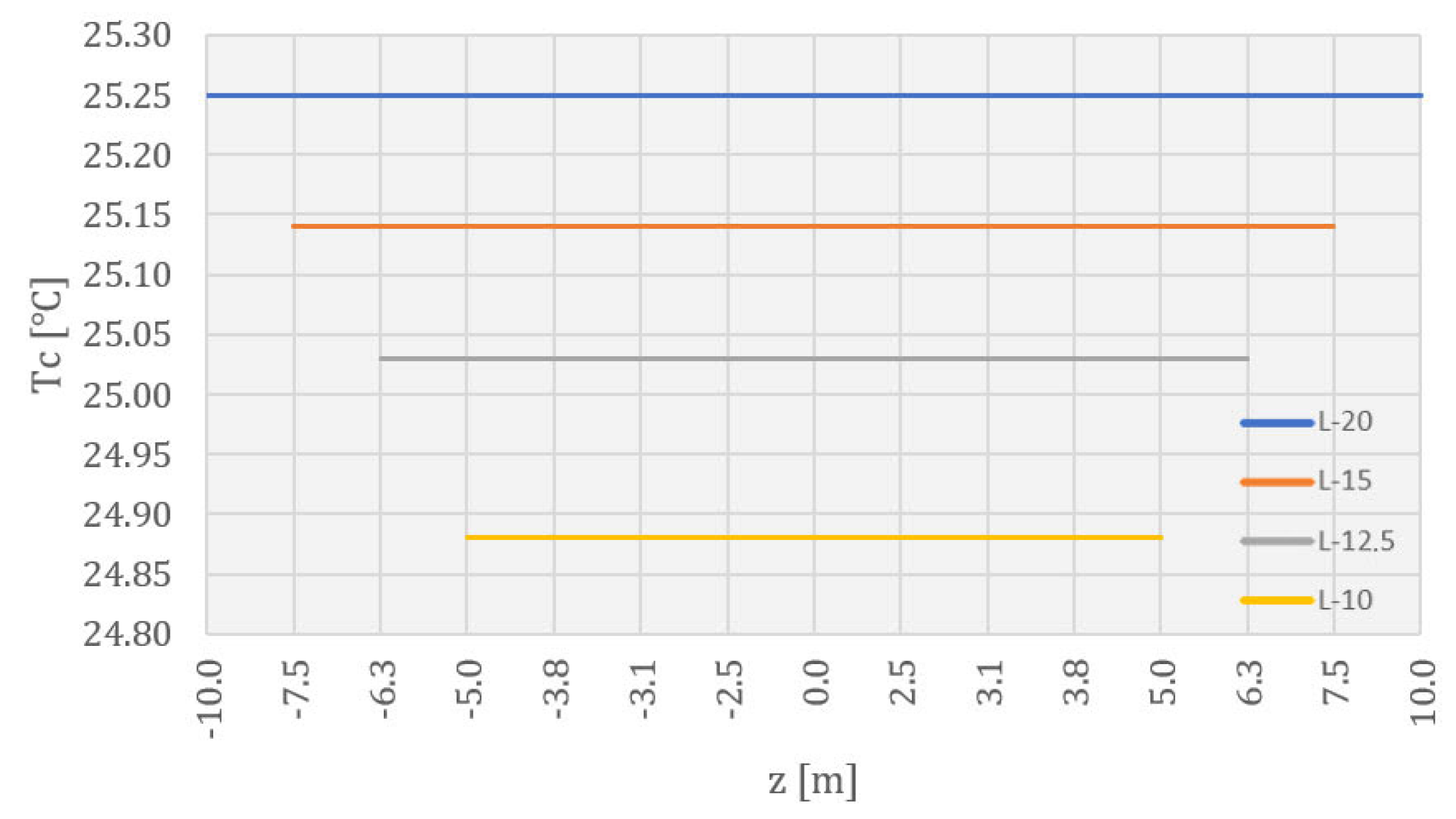
4.1. Verification of the Model
- is the value of the concrete temperature oscillation amplitude at the selected point inside the structure [°C];
- is the value of the concrete temperature oscillation amplitude at a point on the surface of the structure [°C];
- x is the distance of the observed point from the outer surface of the concrete structure [m];
- is the diffusivity of the concrete [m2/day];
- is the air temperature oscillation period (365 days);
- is the thermal conductivity coefficient [J/day m K];
- is the specific heat capacity of the concrete [J/kg/K];
- is the concrete density [kg/m3].
- Based on the results presented for the control nodes and the performed verification, it can be concluded that the numerical model simulated the thermal behavior of the analyzed CGD well.
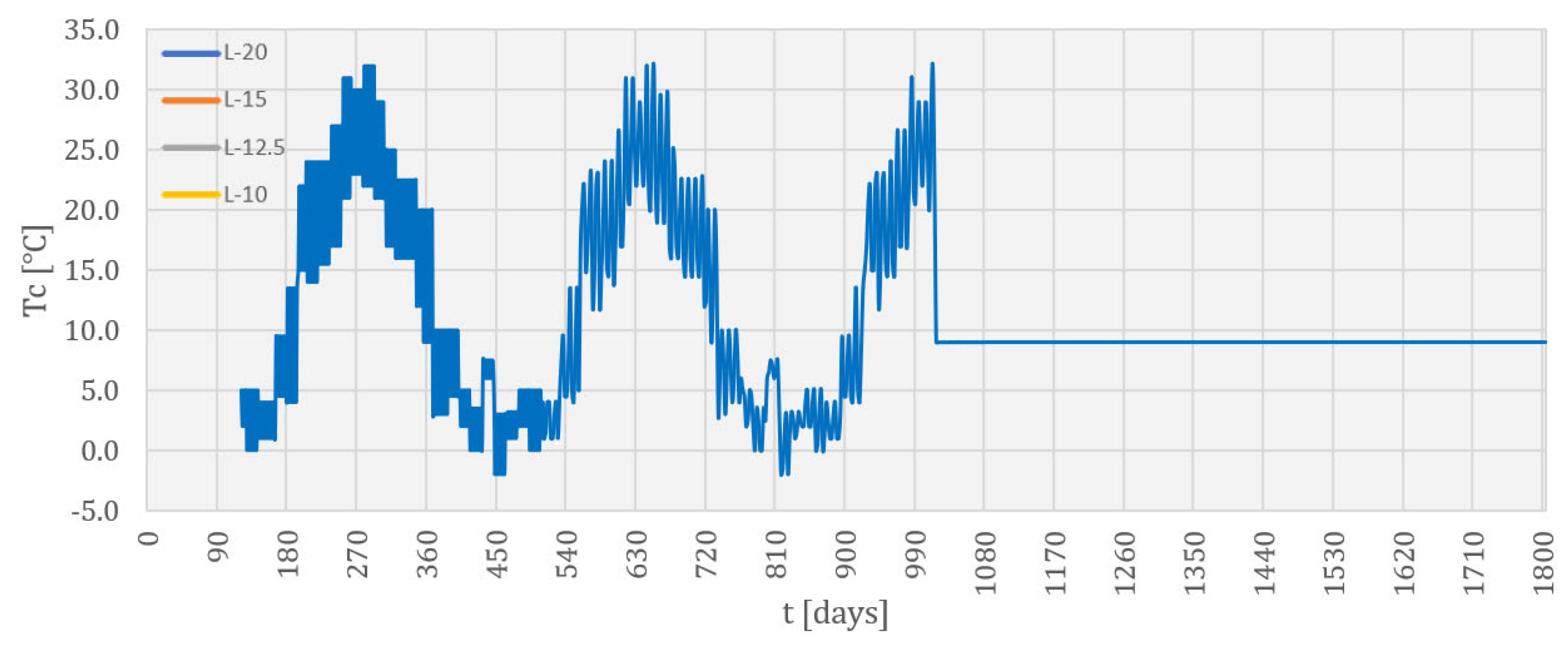
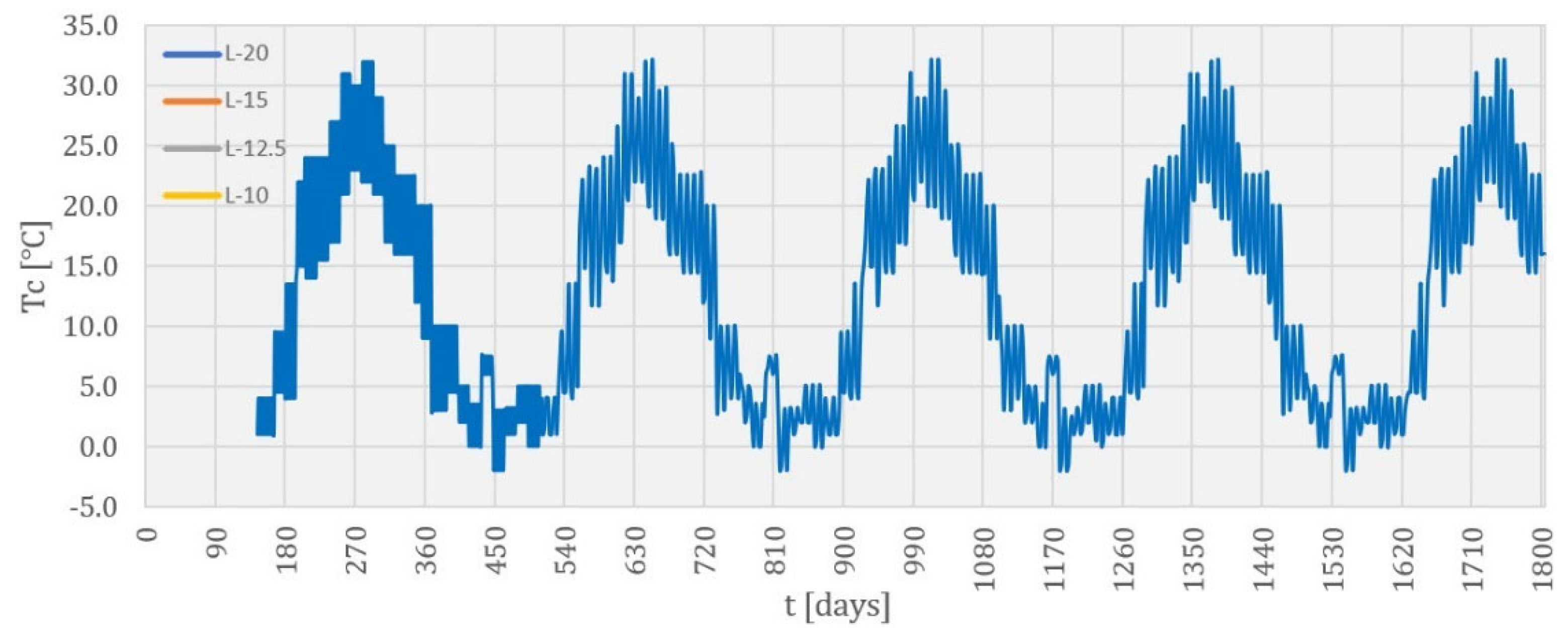
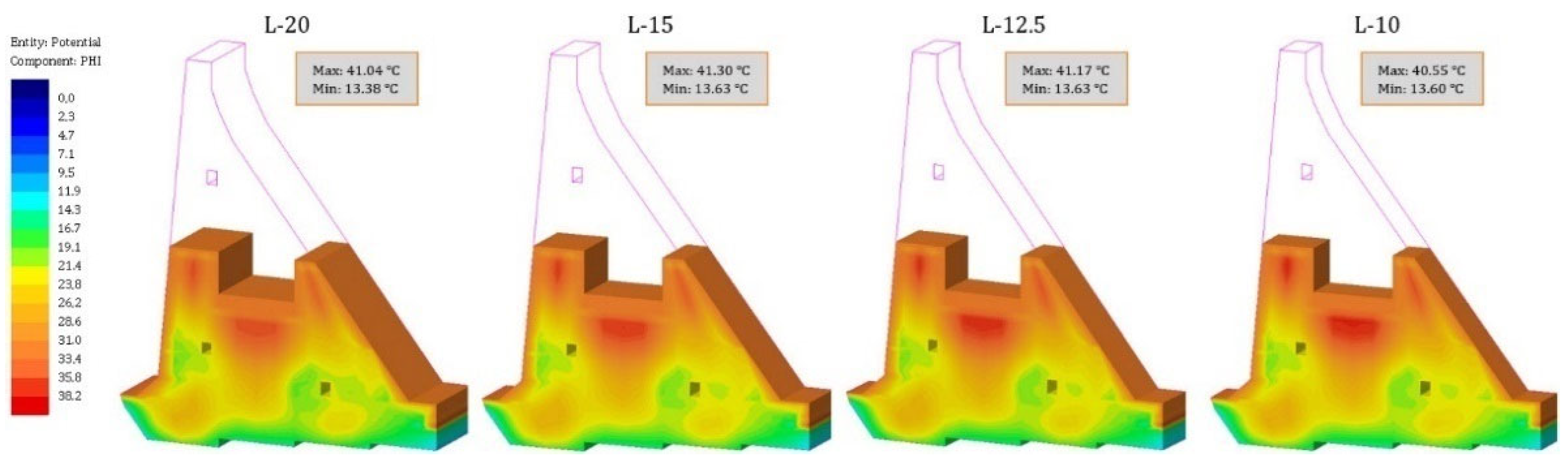
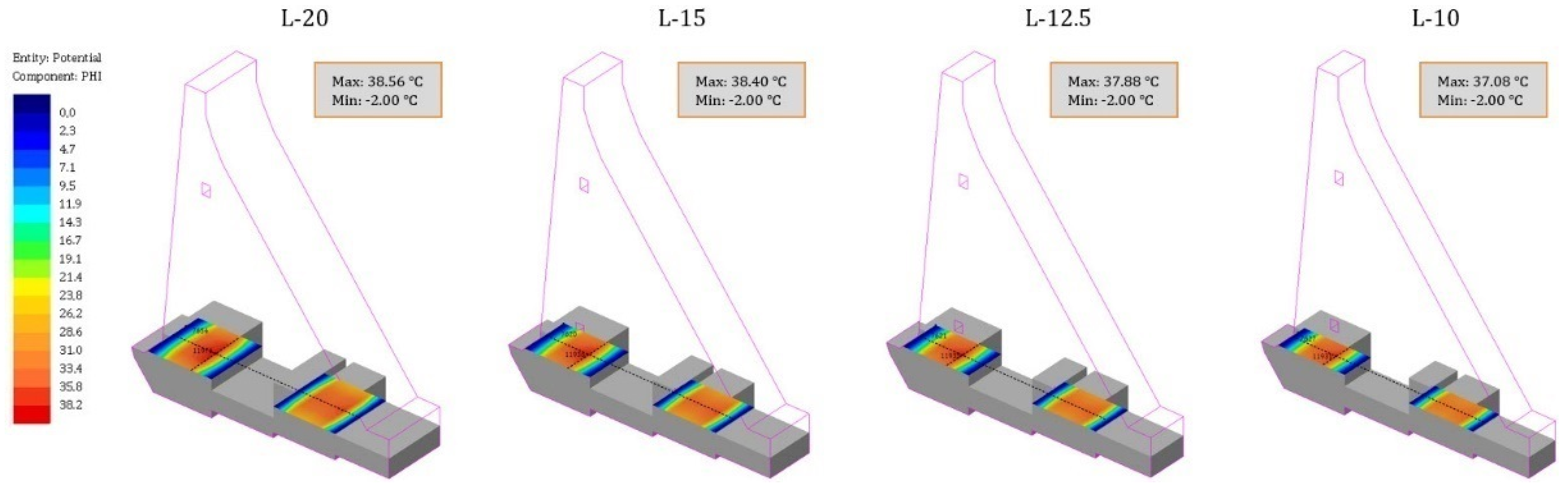
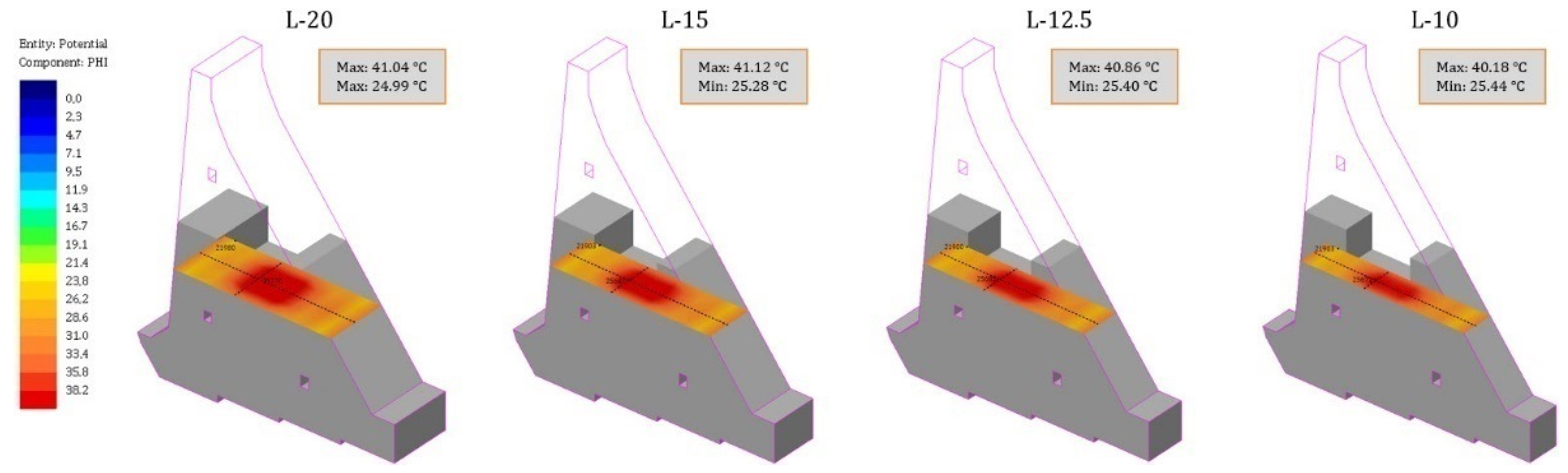
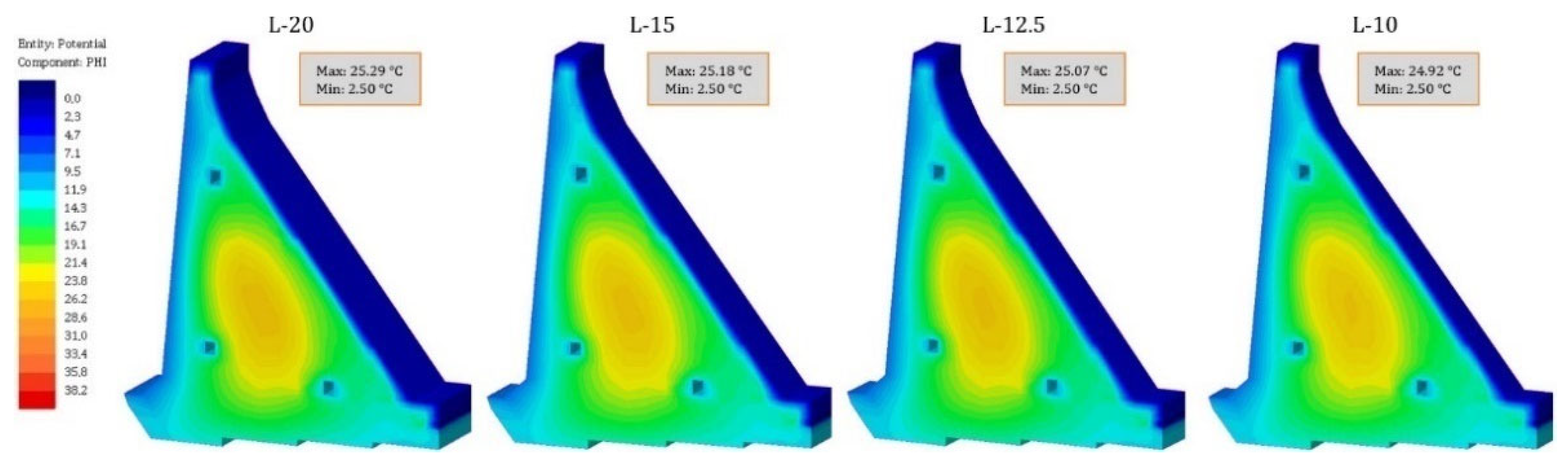
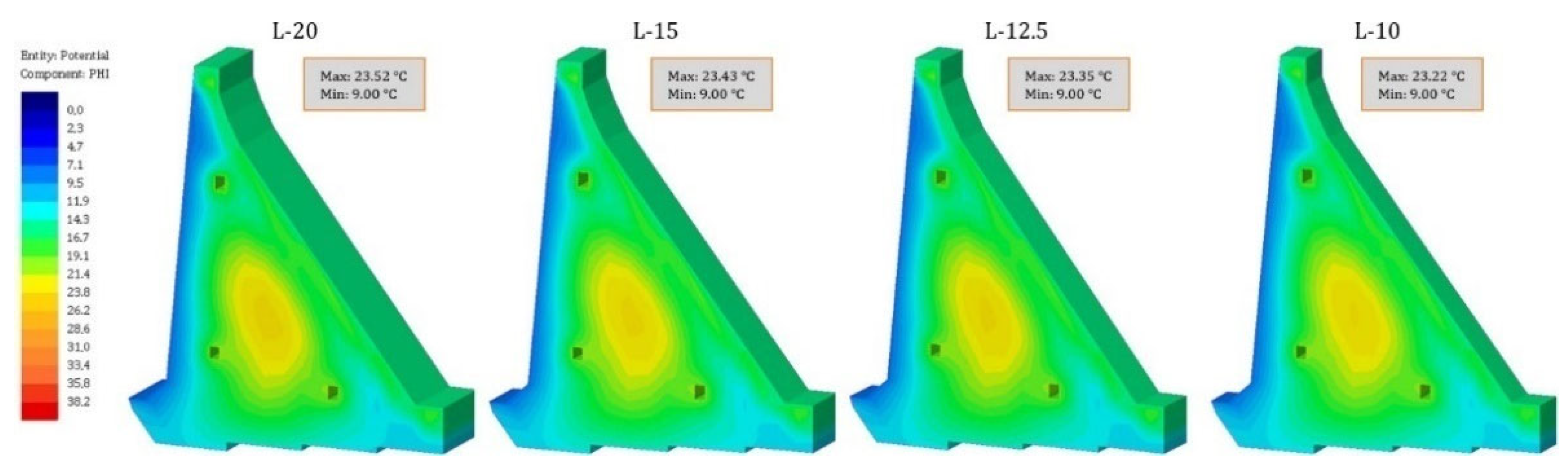
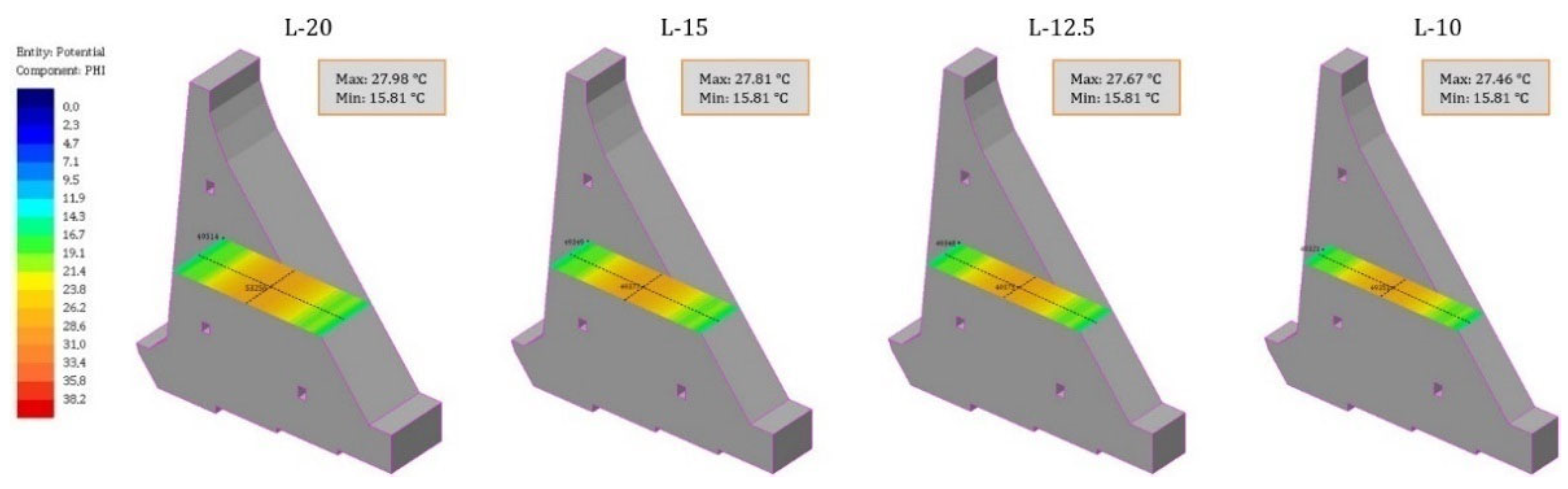
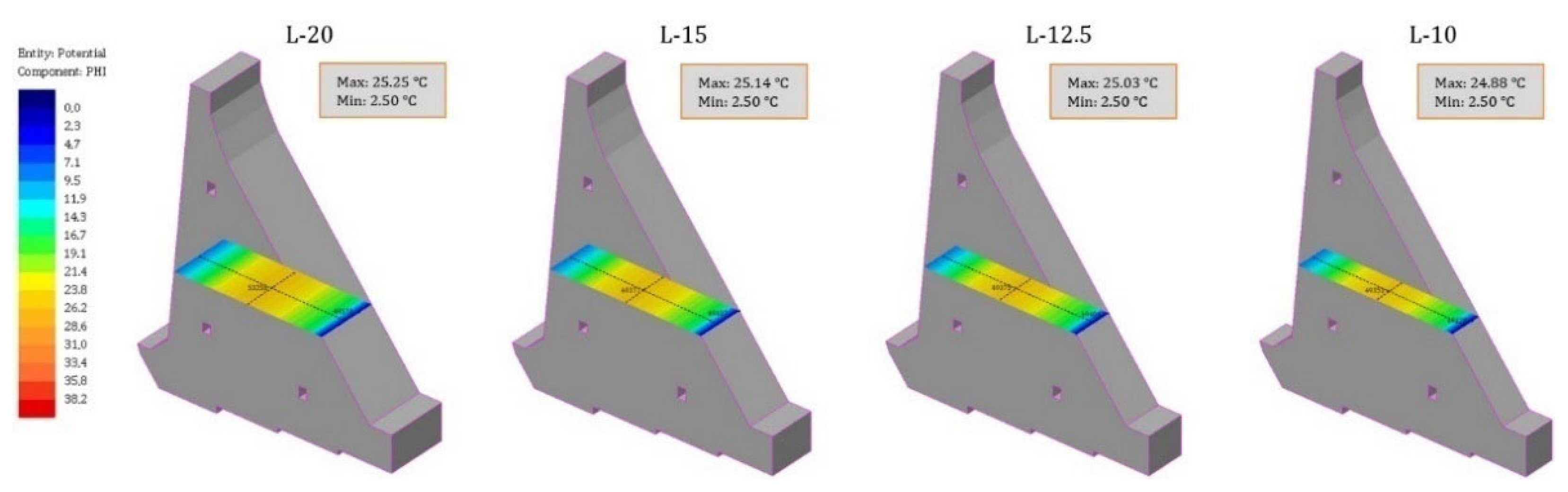
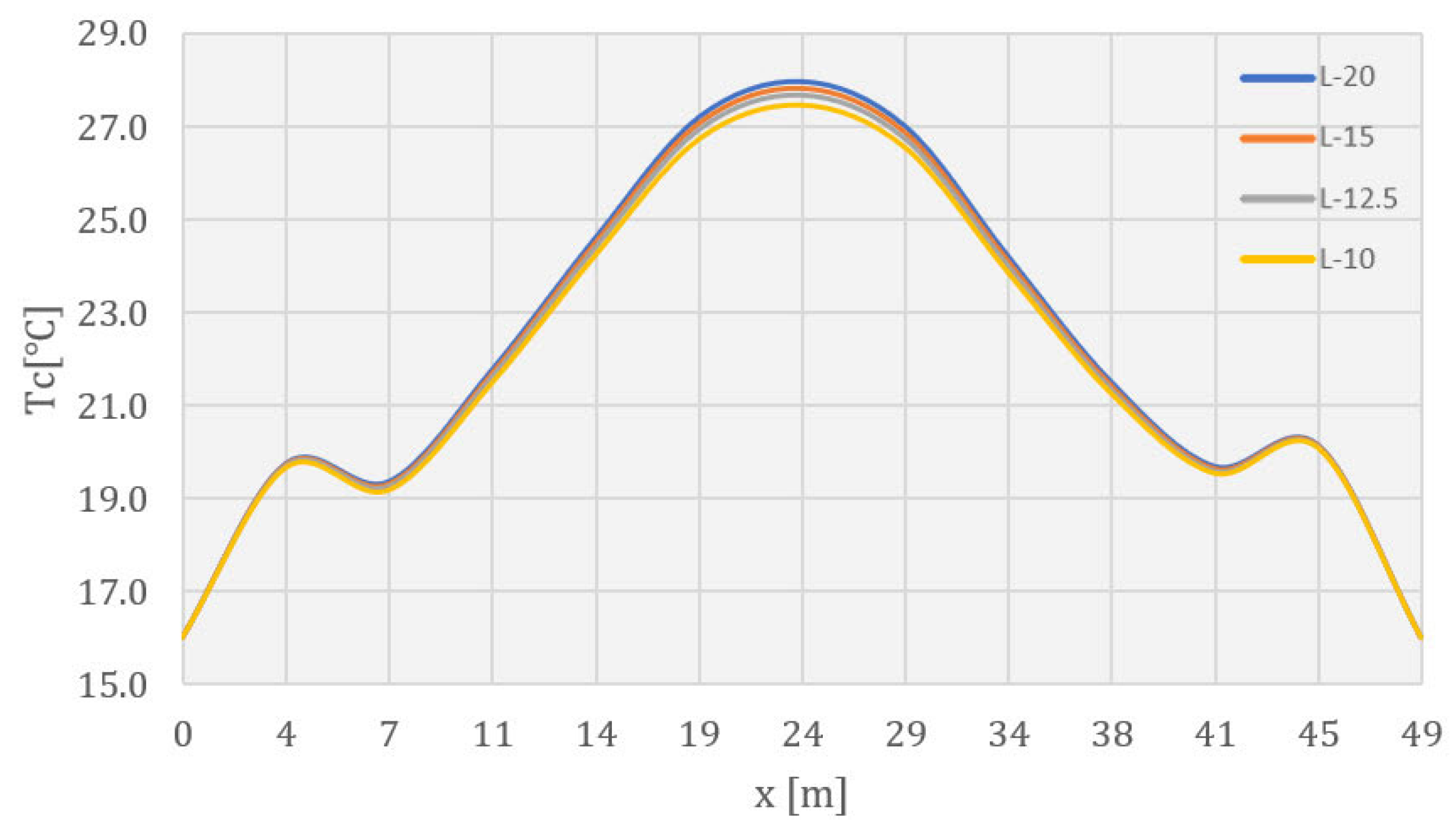
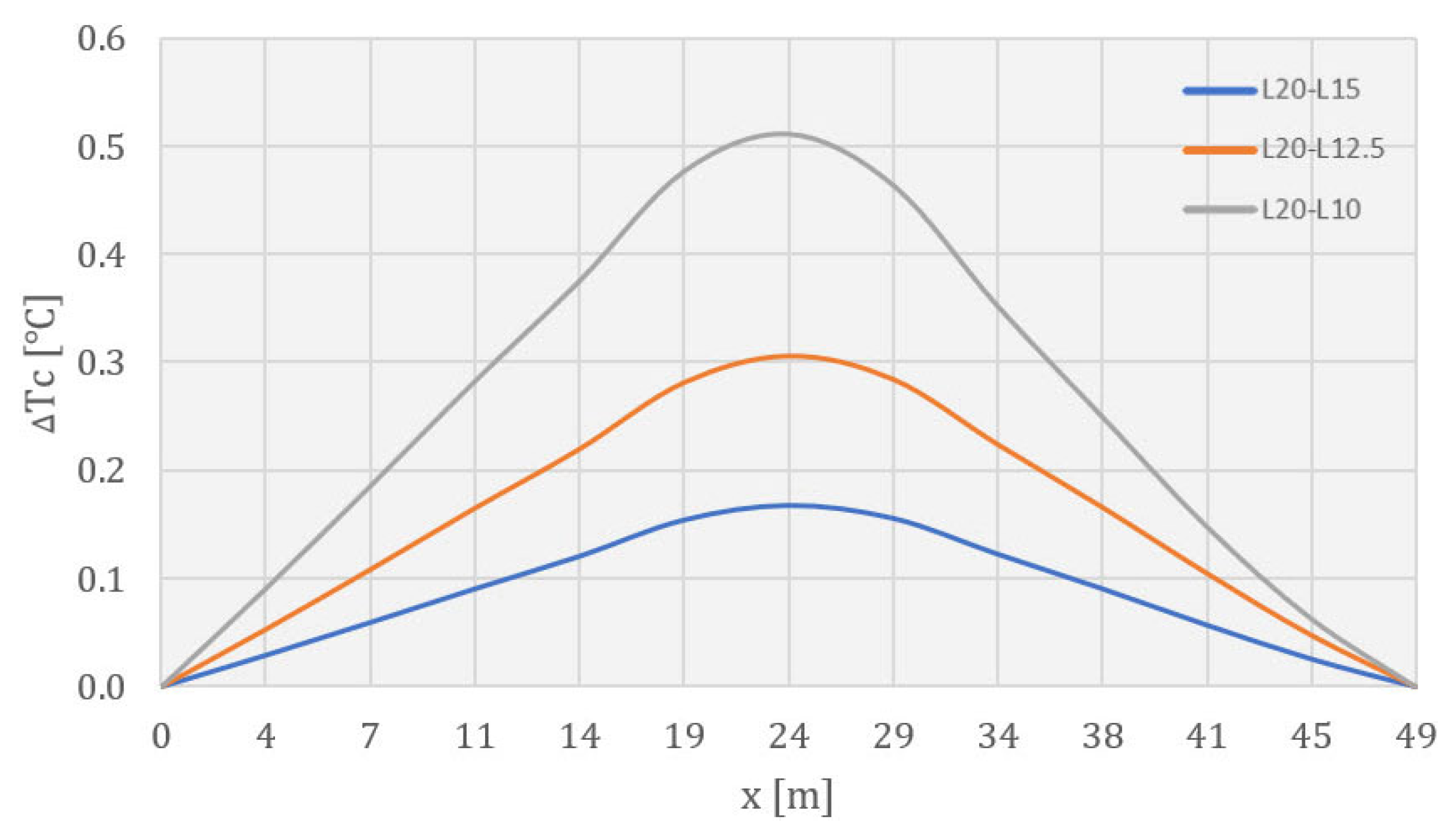
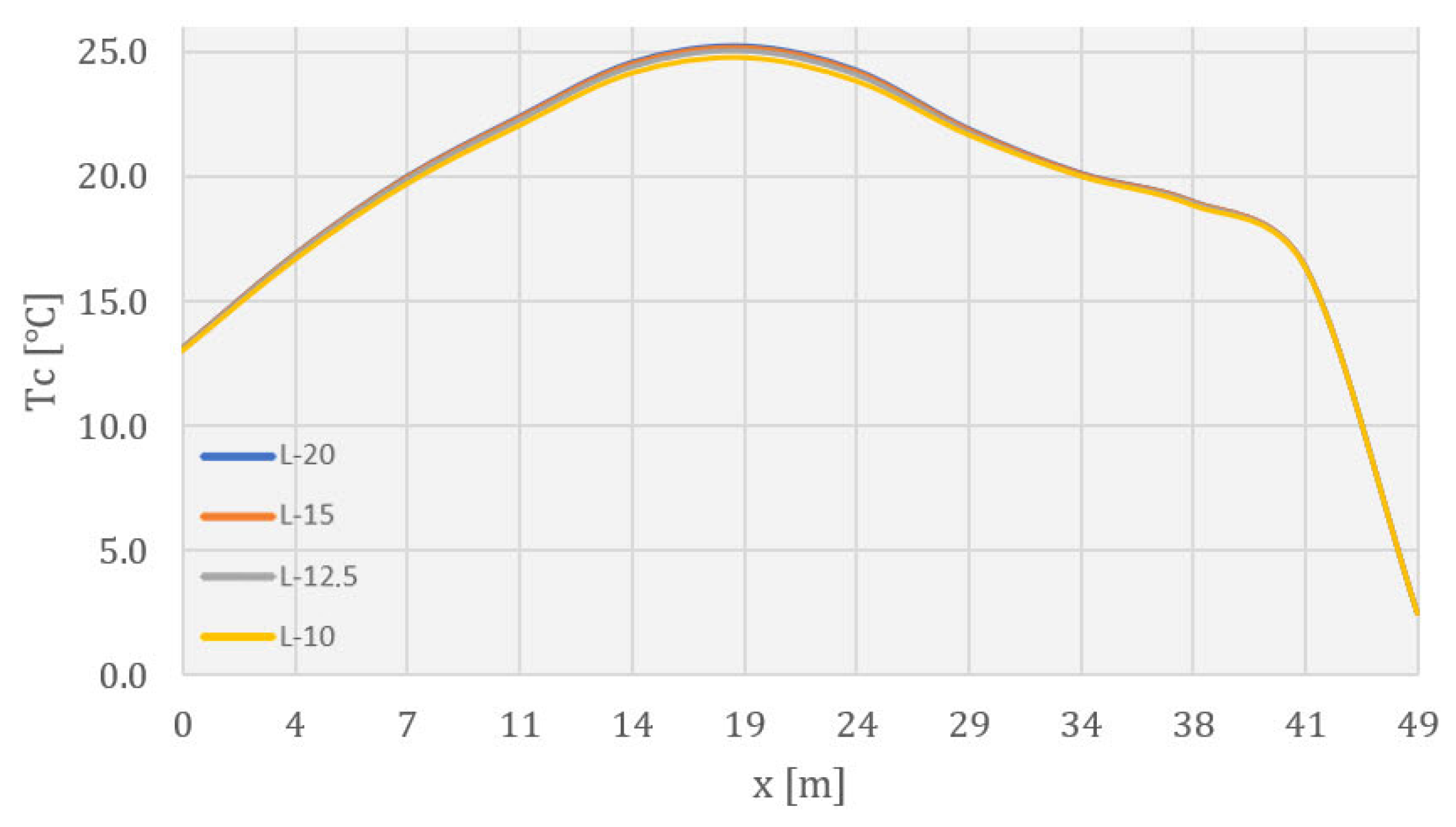
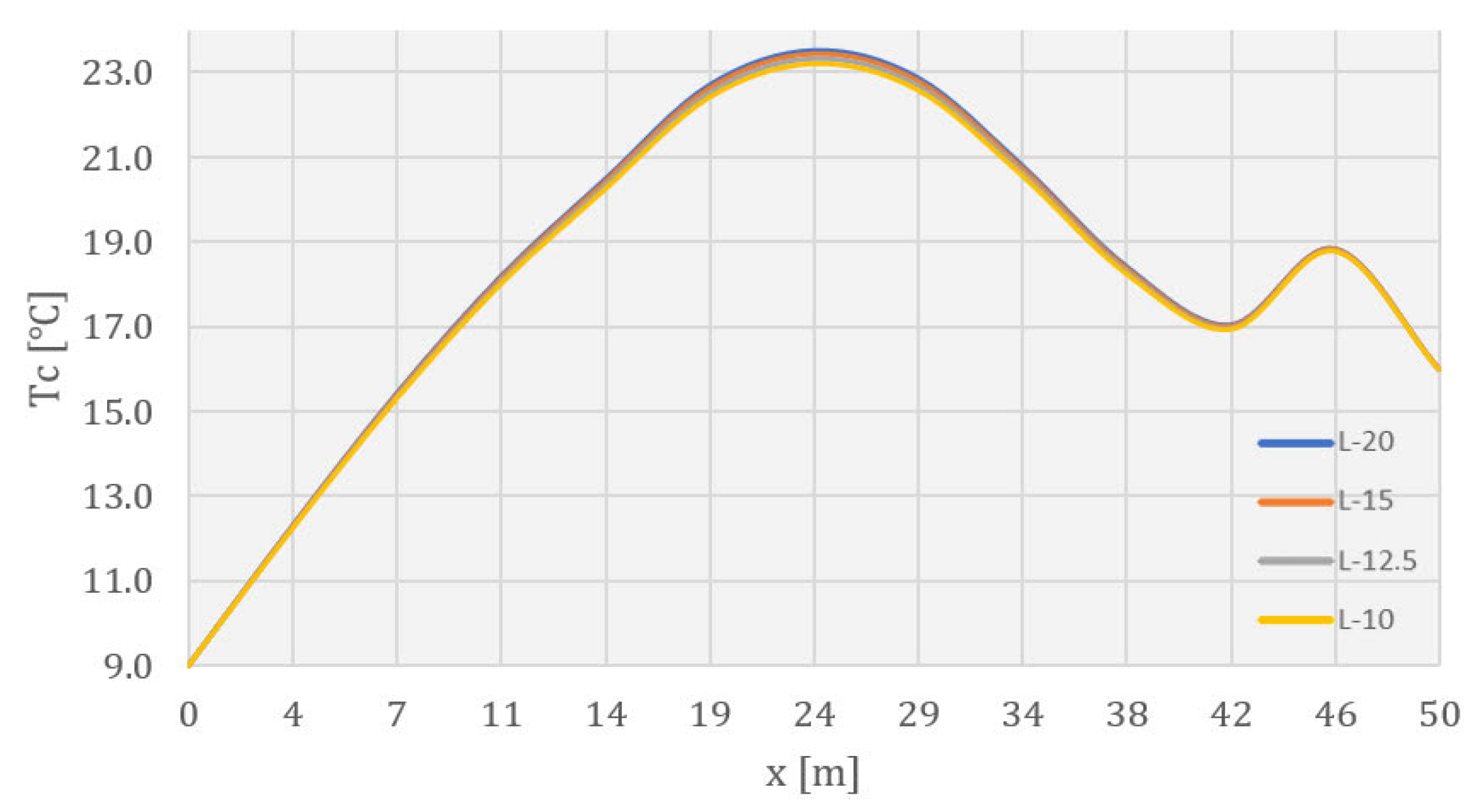
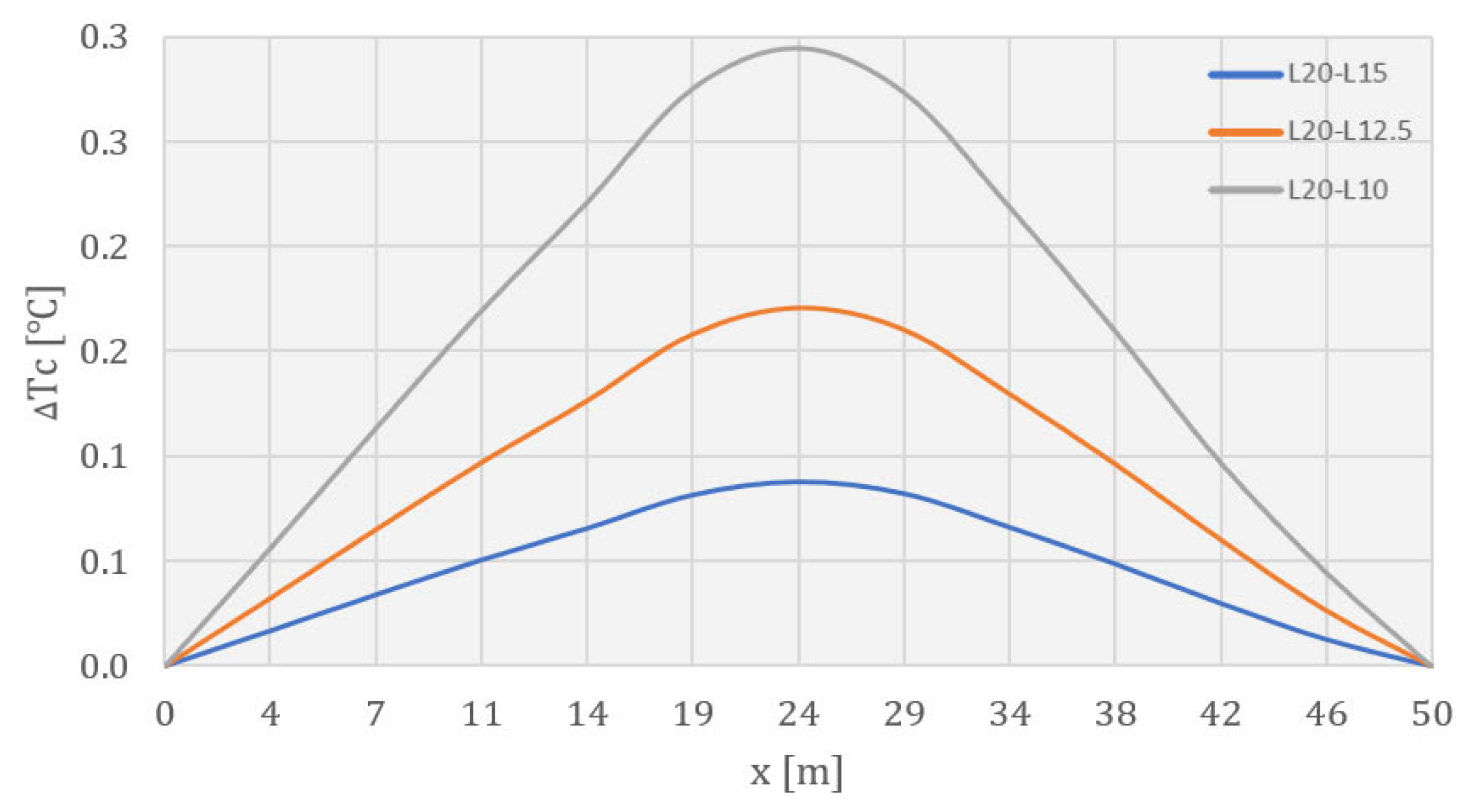
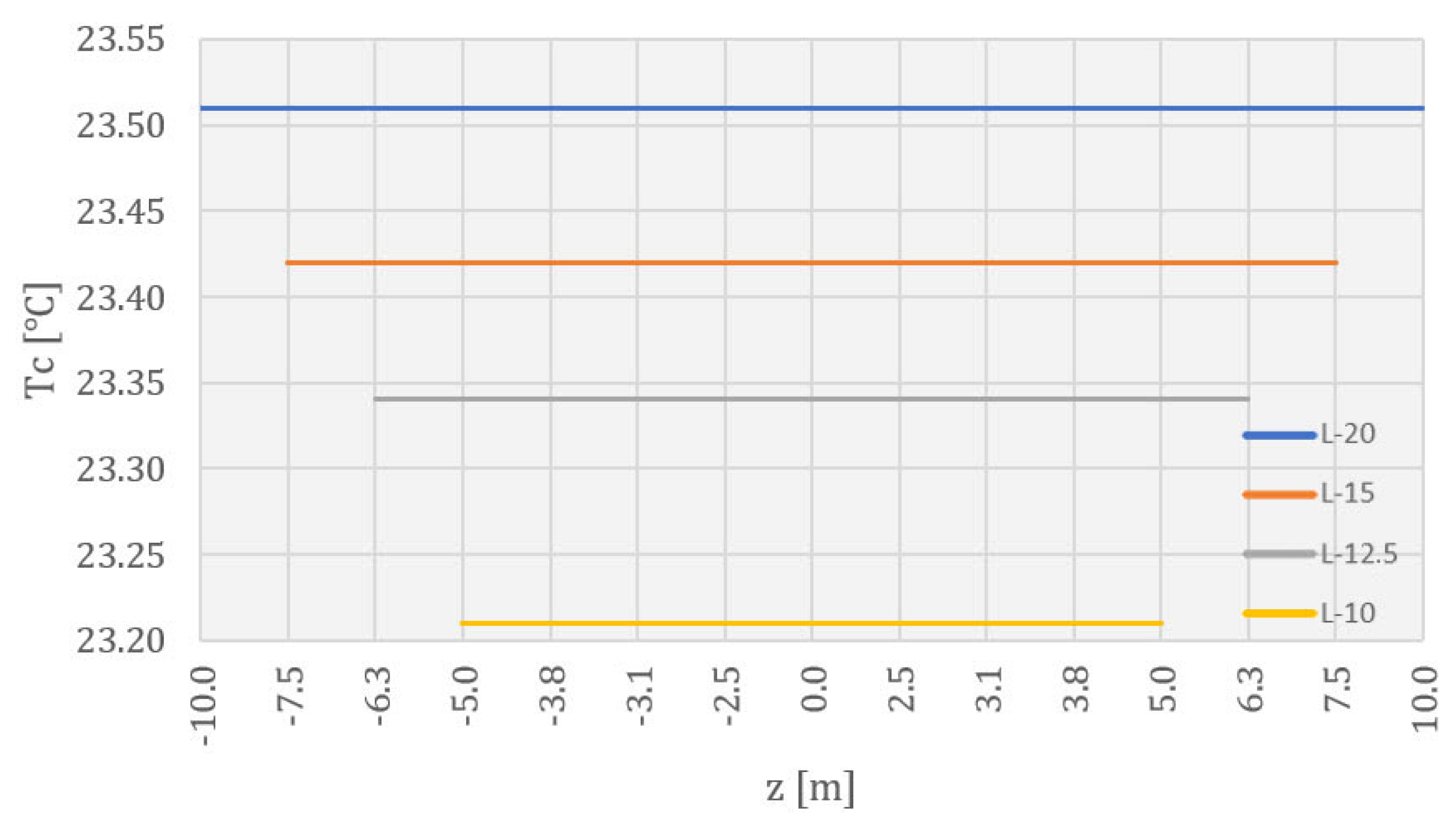
- The results of the temperature field calculation in the dam’s body are presented in selected characteristic time sections. As the rock mass was not the subject of this work, this part of the model has been omitted from the following results. The selected characteristic time sections were as follows: the 84th day (10 January of the second year), the 283rd day (27 July of the second year), the 512th day (13 March of the third year), the 1080th day (2 October of the fourth year), the 1505th day (1 December of the fifth year), and the 1804th day (25 September of the sixth year). The first three sections show the period of construction, while the remaining three show the period of the service life.
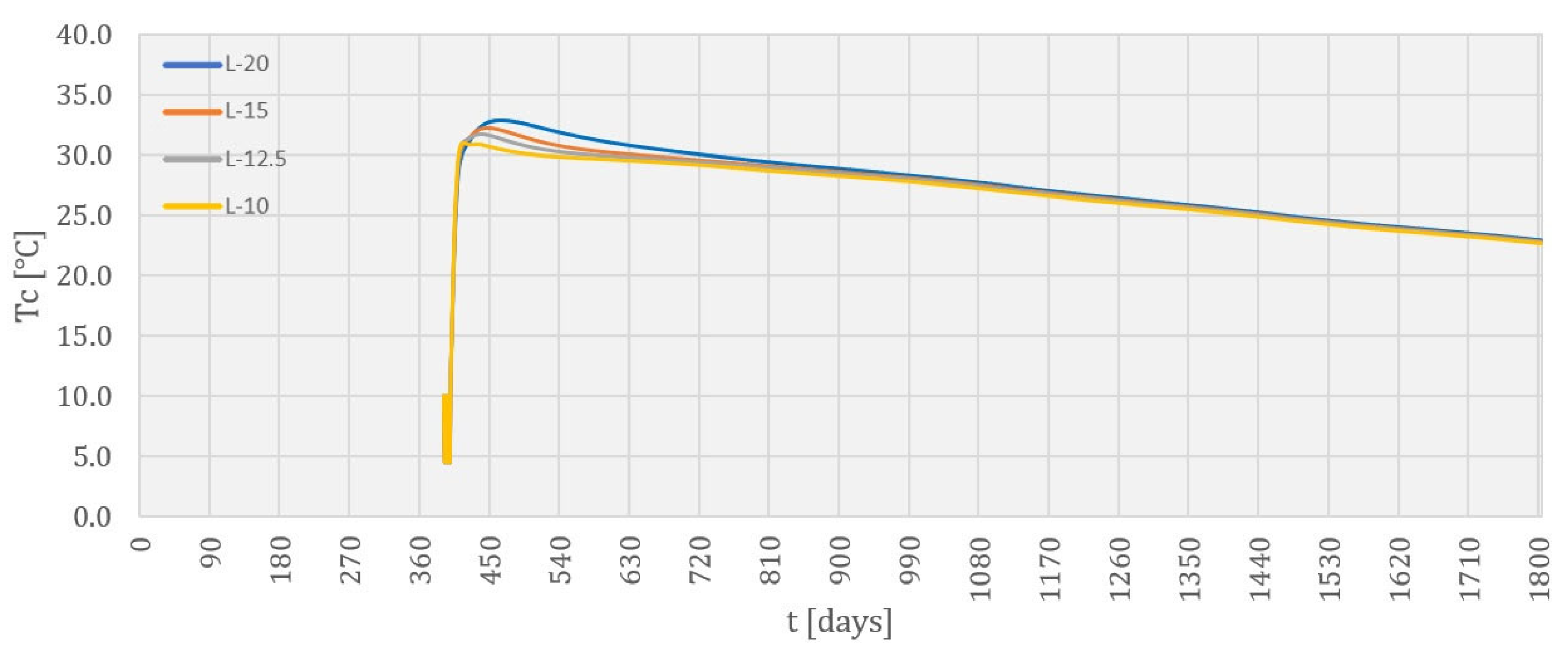
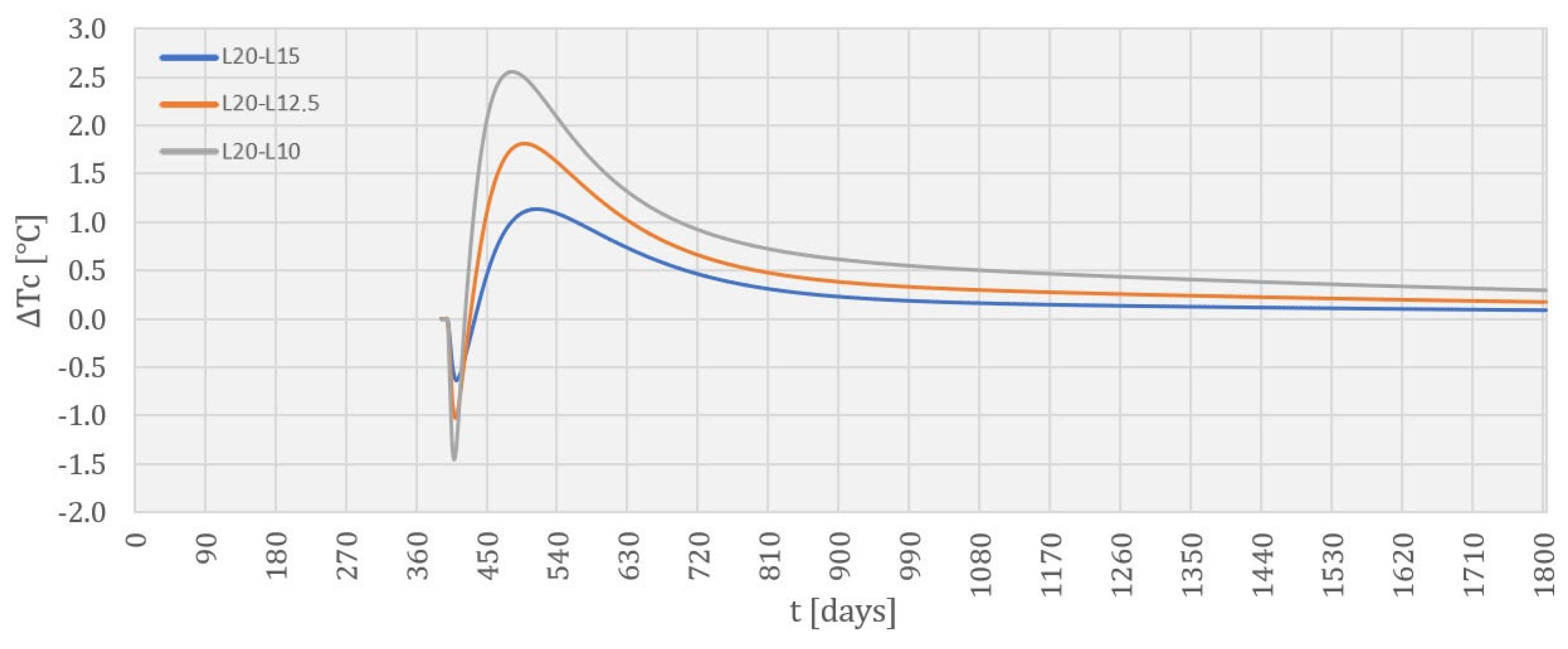
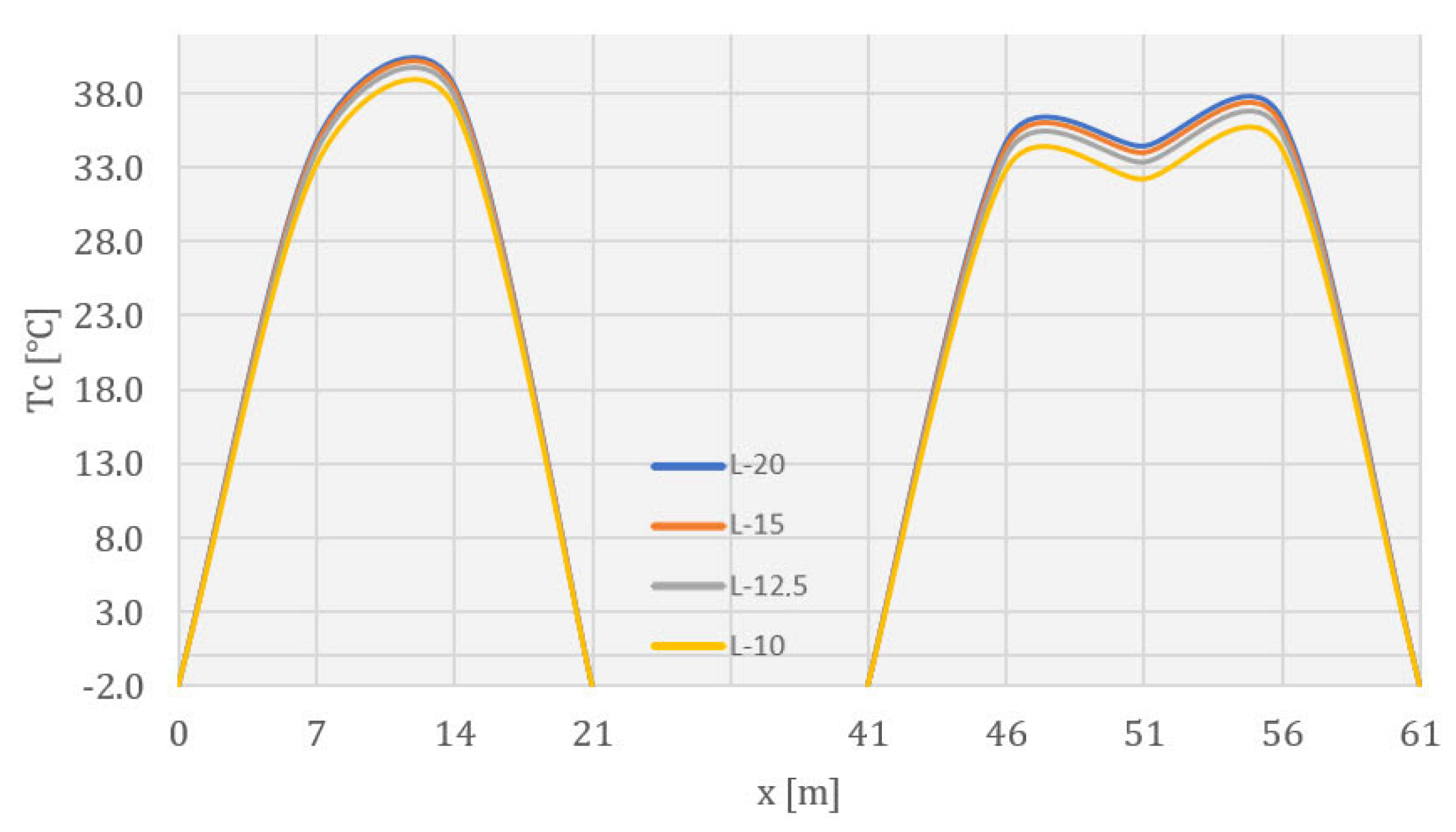
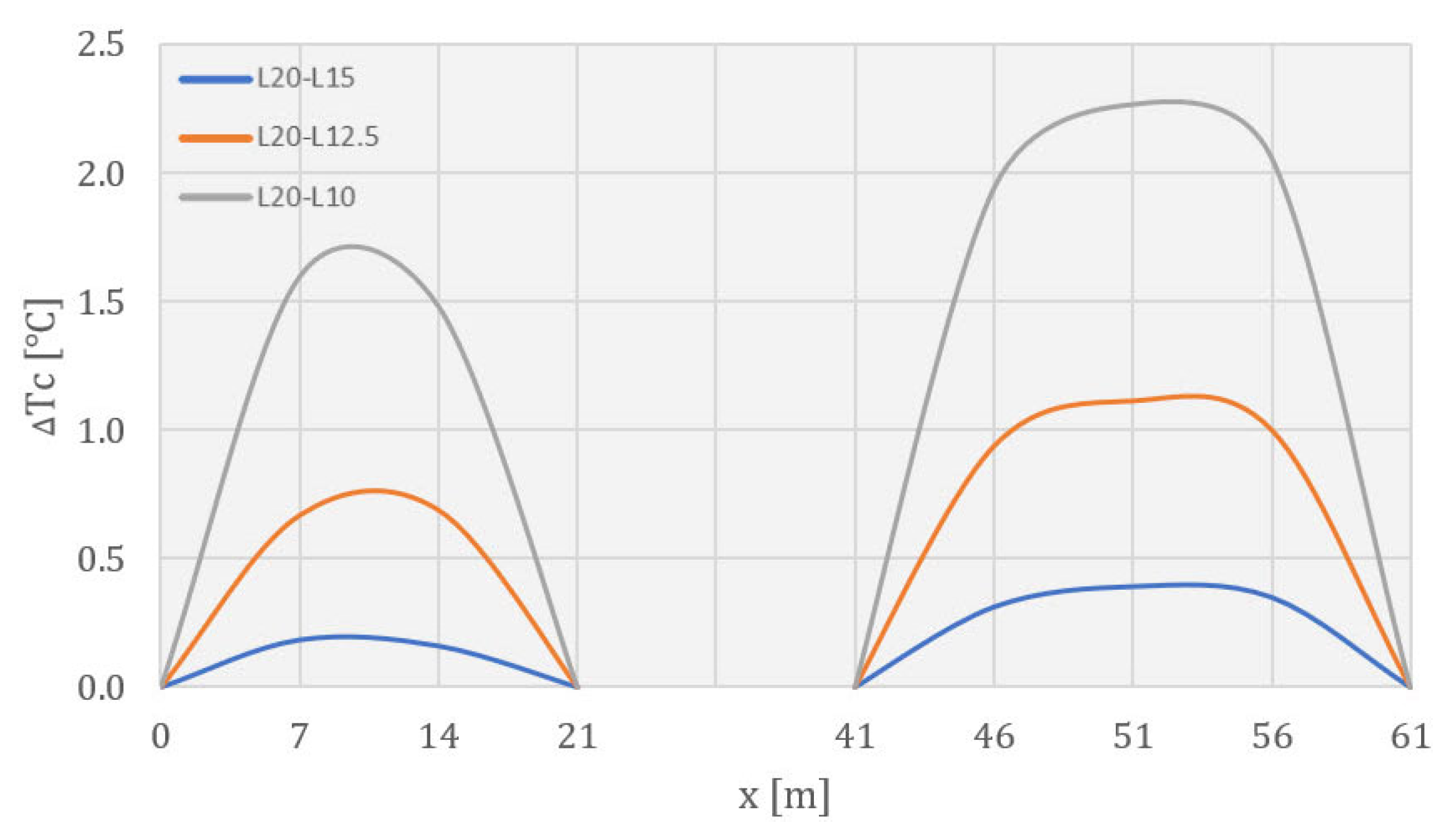
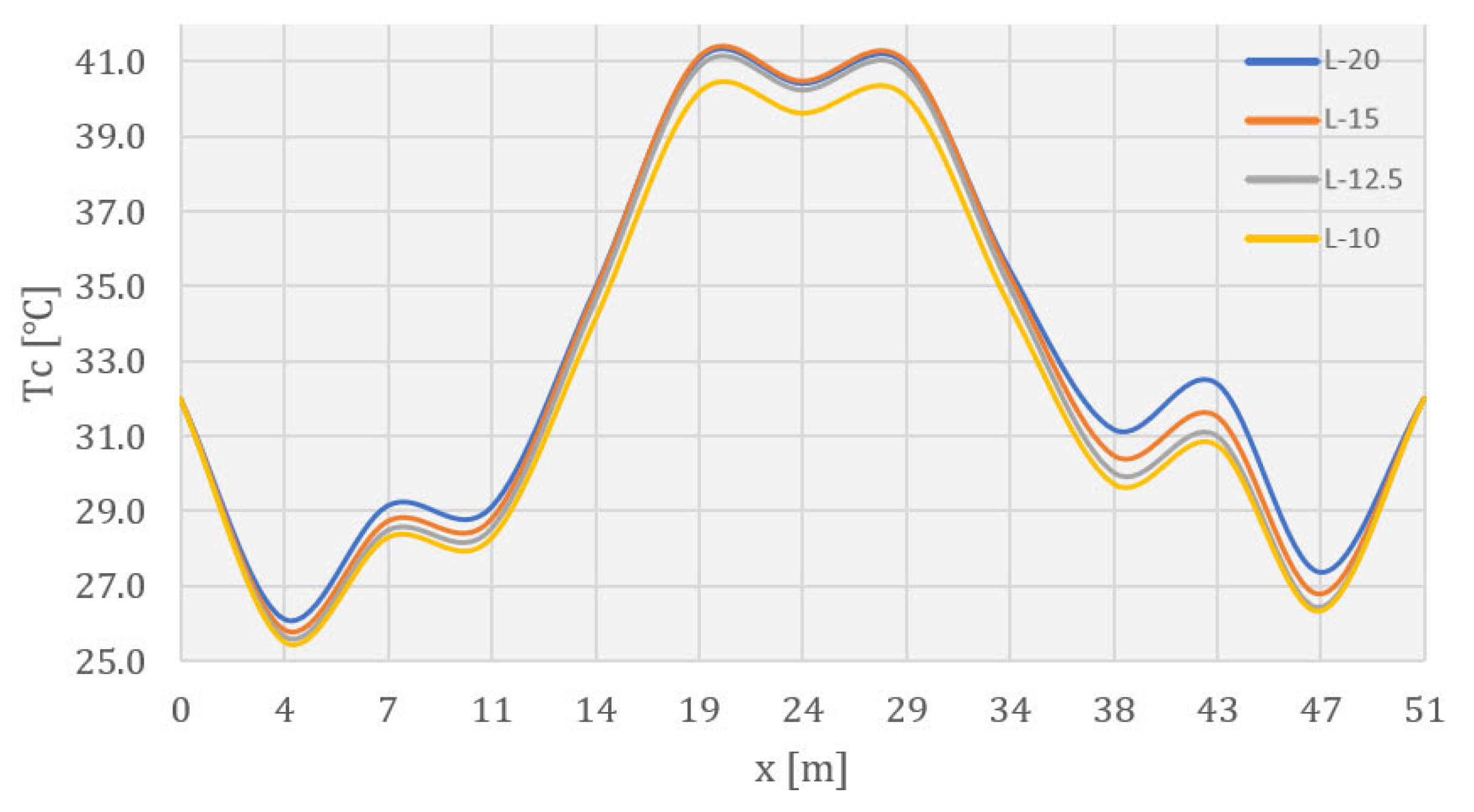
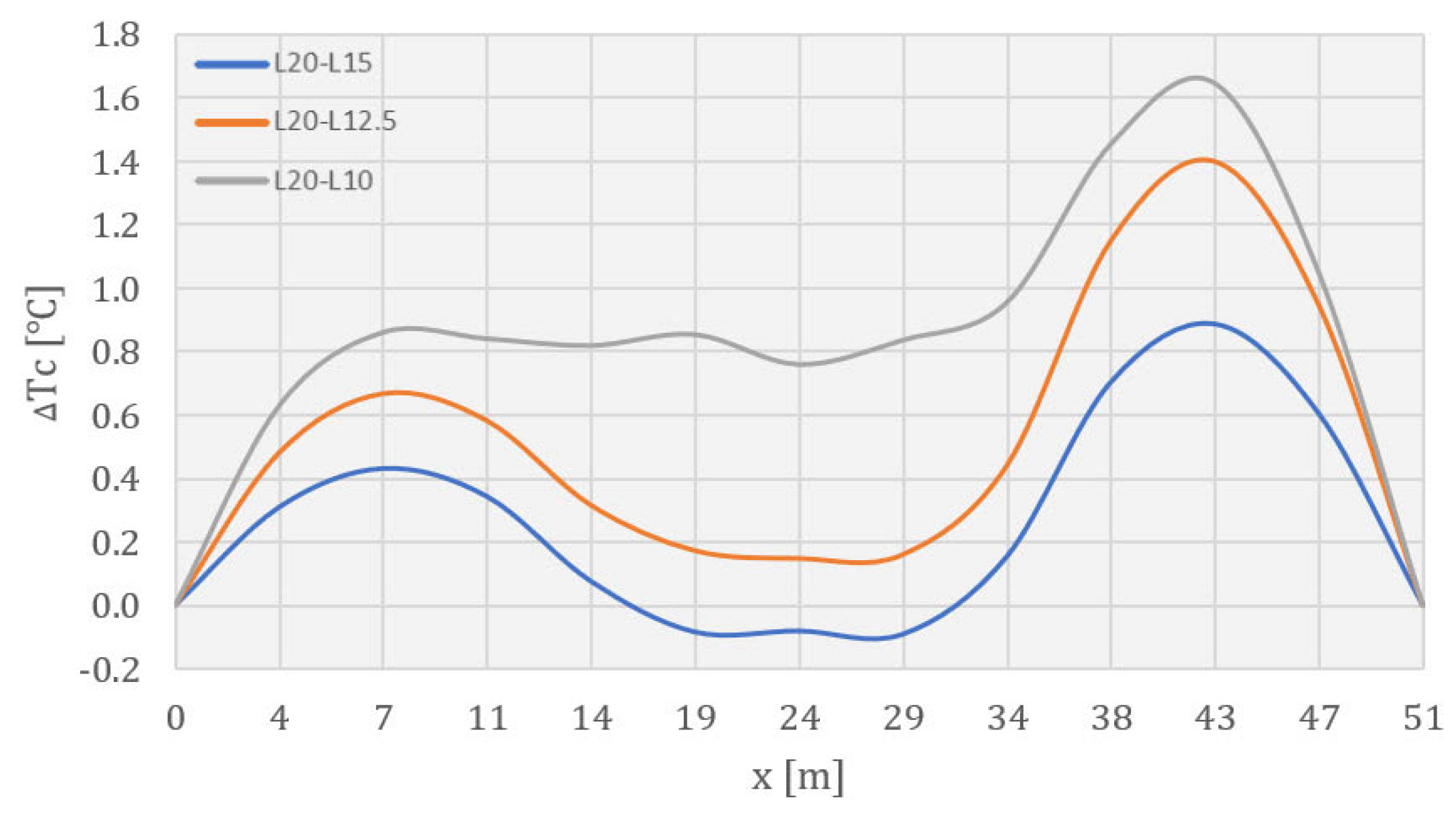
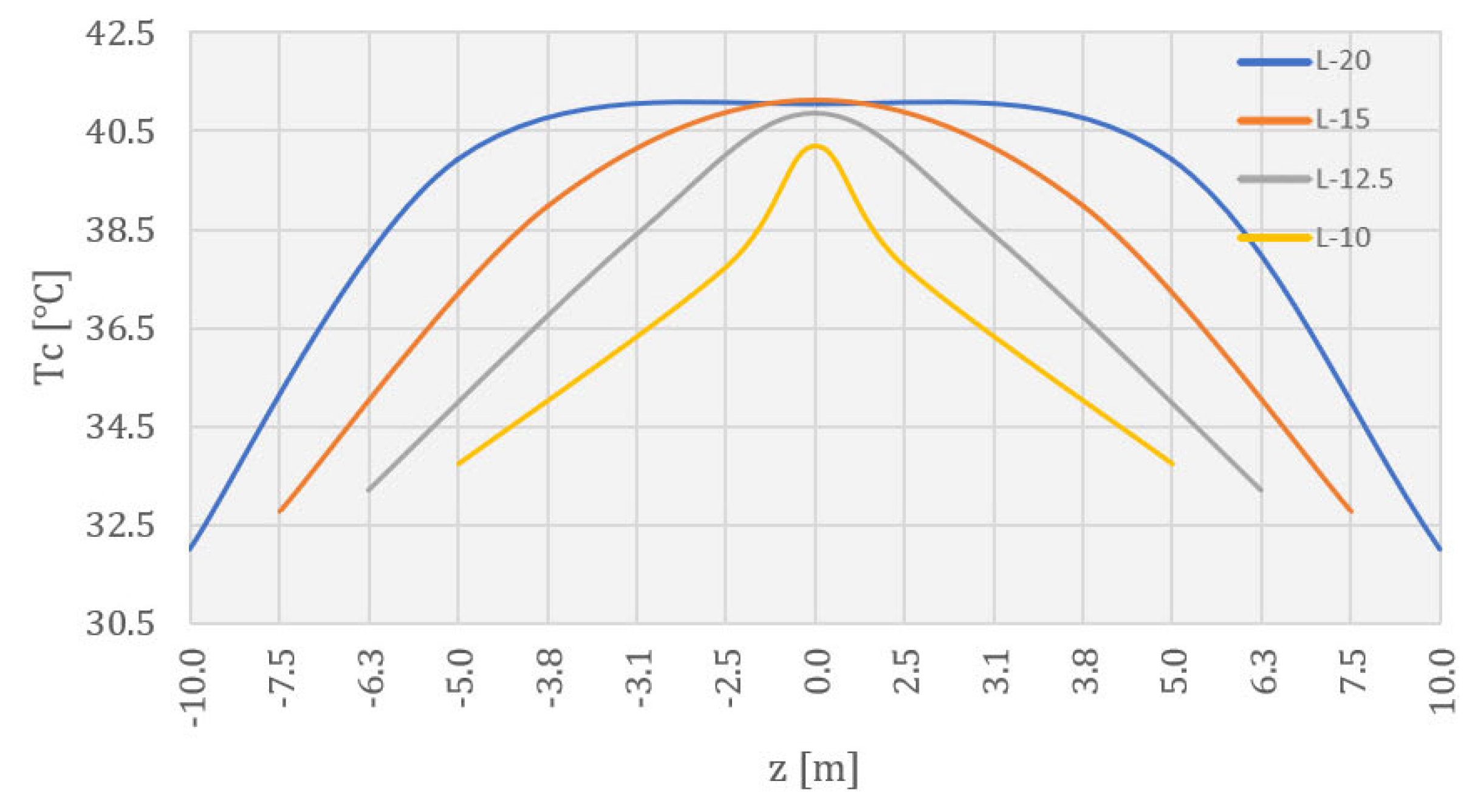
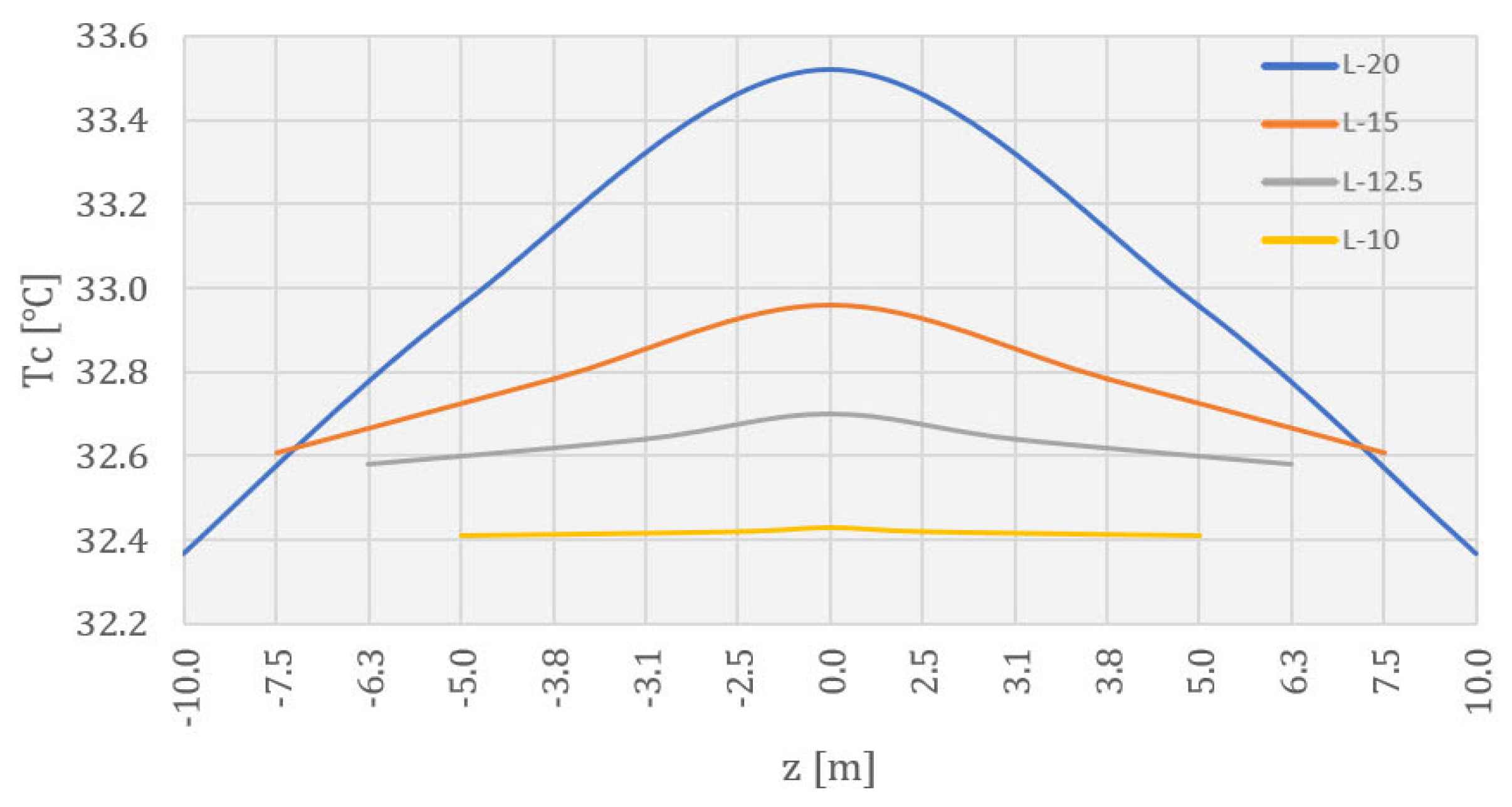
4.2. Temperature Field during Construction
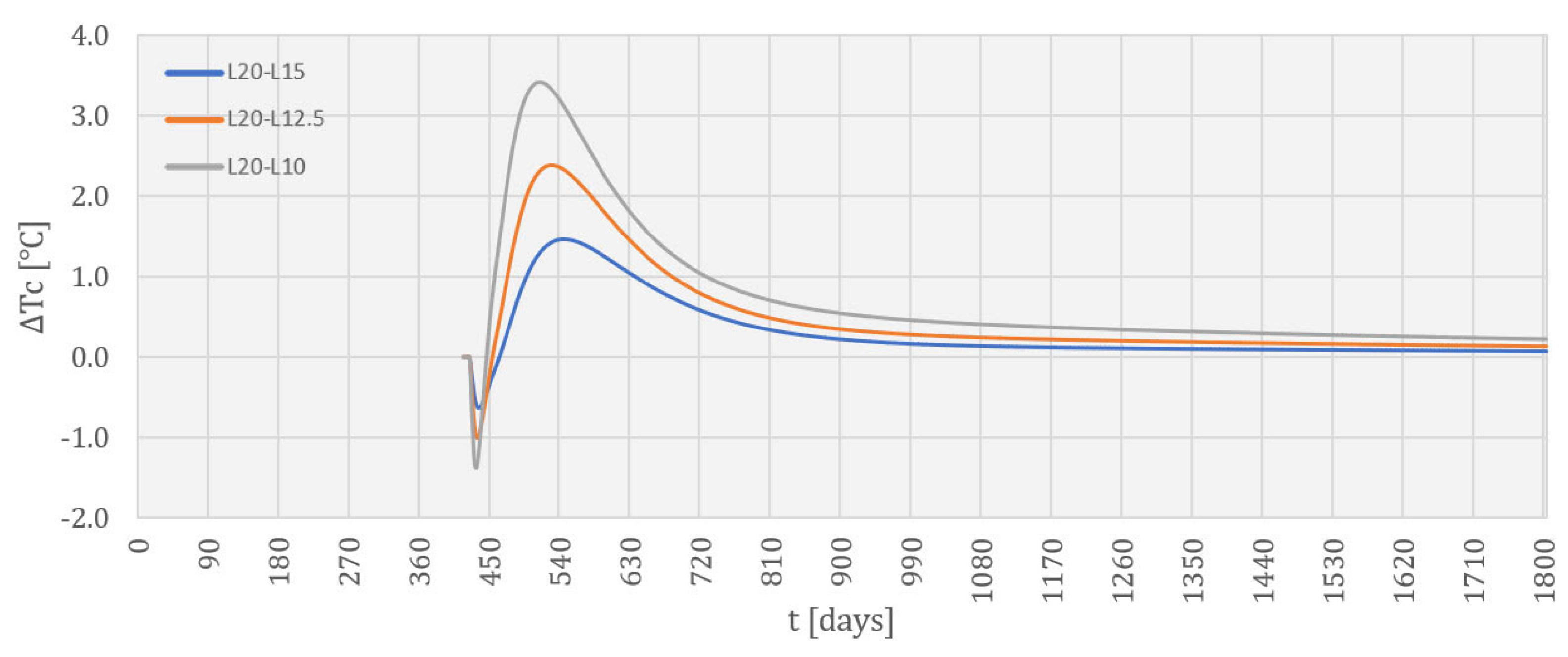
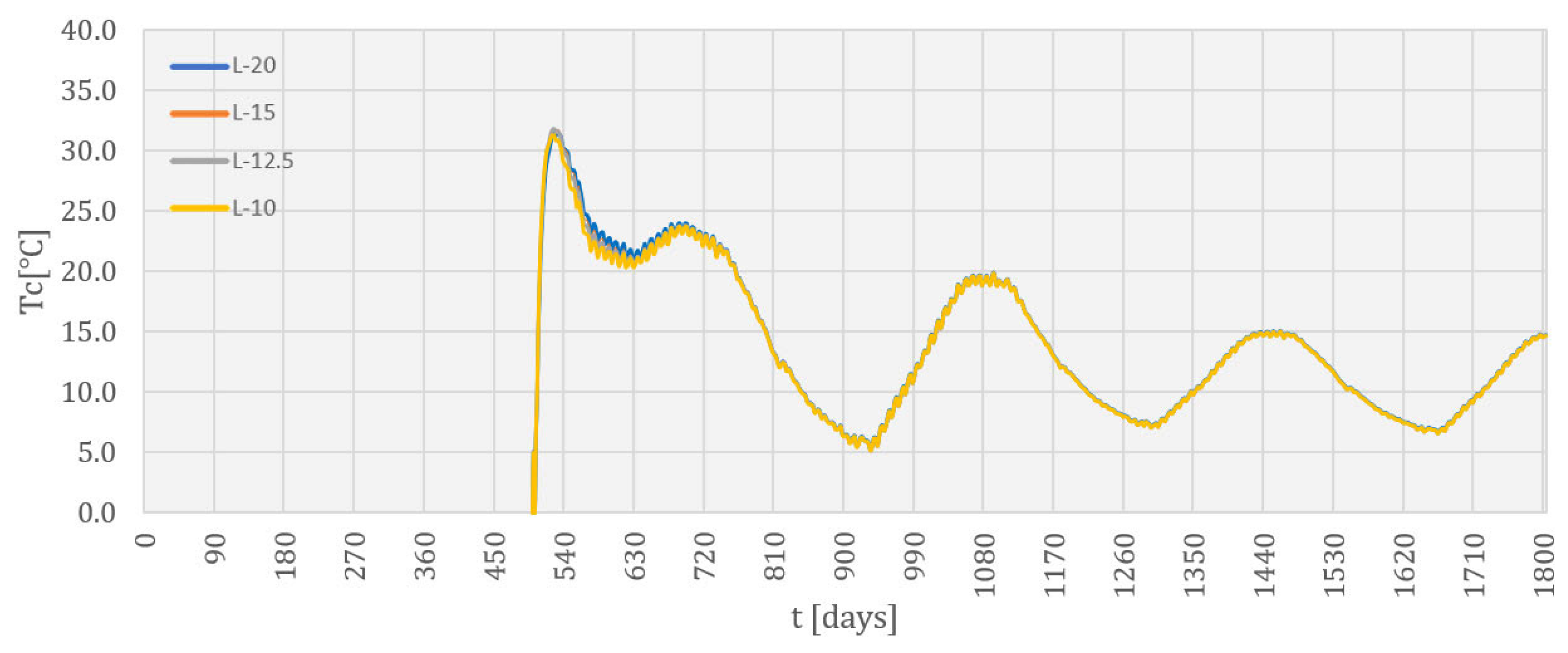
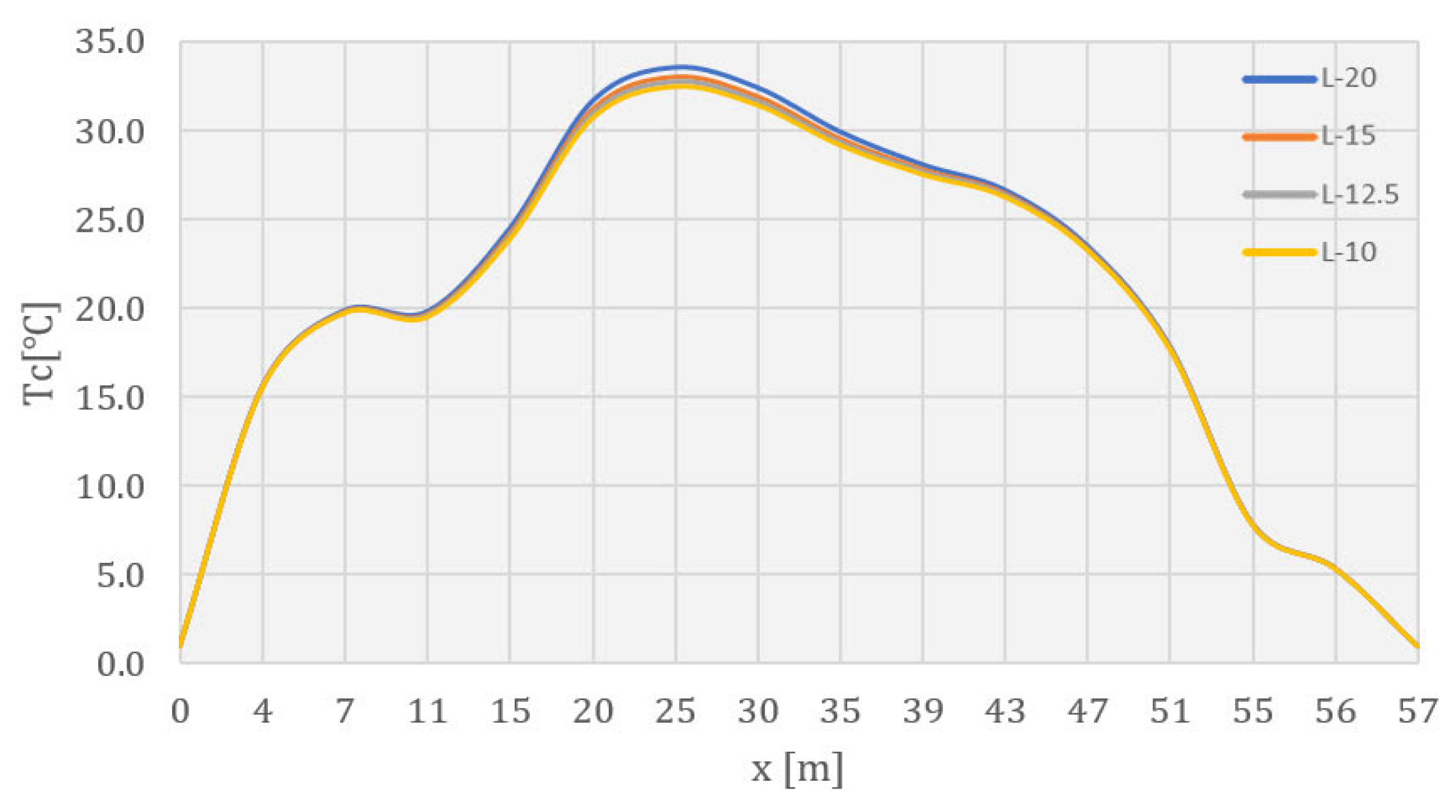
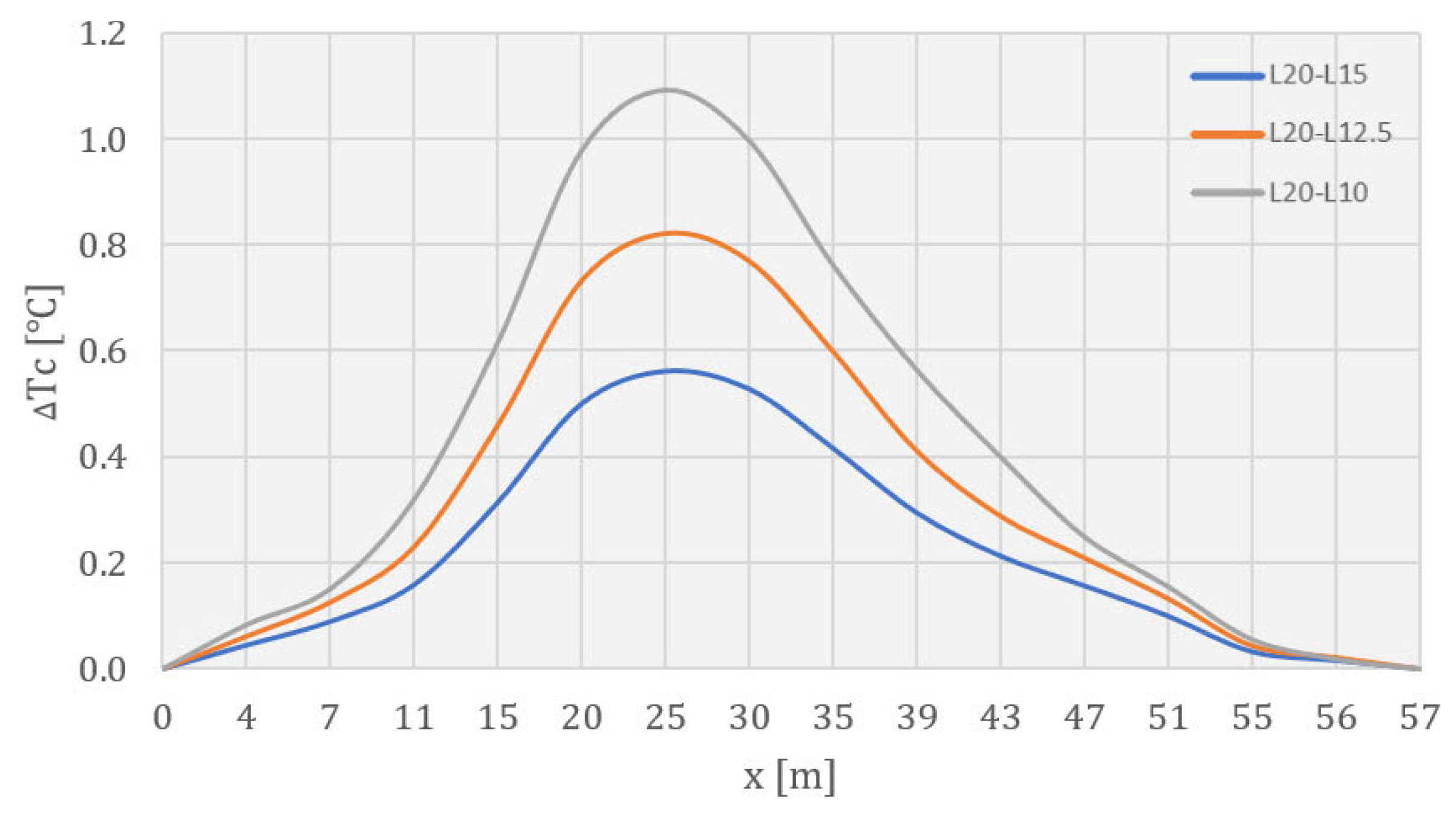
4.3. Temperature Field during Service Life
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Malm, R. Guideline for FE Analyses of Concrete Dams; Energiforsk: Stockholm, Sweden, 2016. [Google Scholar]
- Ishikawa, M. Thermal stress analysis of a concrete dam. Comput. Struct. 1991, 40, 347–352. [Google Scholar] [CrossRef]
- Léger, P.; Venturelli, J.; Bhattacharjee, S.S. Seasonal temperature and stress distributions in concrete gravity dams. Part 1: Modeling. Can. J. Civ. Eng. 1993, 20, 999–1017. [Google Scholar] [CrossRef]
- Léger, P.; Venturelli, J.; Bhattacharjee, S.S. Seasonal temperature and stress distributions in concrete gravity dams. Part 2: Behavior. Can. J. Civ. Eng. 1993, 20, 1018–1029. [Google Scholar] [CrossRef]
- Daoud, M.; Galanis, N.; Ballivy, G. Calculation of the periodic temperature field in a concrete dam. Can. J. Civ. Eng. 1997, 24, 772–784. [Google Scholar] [CrossRef]
- Ganelli, F.; Beko, A.; Mordini, A. Structural assessment of the Mignano solid-gravity dam based on the monitoring data. Struct. Eng. Int. 2012, 22, 130–138. [Google Scholar] [CrossRef]
- Embaby, R.A.; Abdelrahman, A.A.; Sayed-Ahmed, E.Y. Concrete gravity dams: Coupled thermal-stress numerical analysis. In IABSE Symposium Report, Proceedings of the International Association for Bridge and Structural Engineering, Madrid, Spain, 3–5 September 2014; Taylor & Francis: Boca Raton, FL, USA, 2014; Volume 102, pp. 467–474. [Google Scholar]
- Sayed-Ahmed, E.Y.; Abdelrahman, A.A.; Embaby, R.A. Concrete dams: Thermal-stress and construction stage analysis. Dams Reserv. 2018, 28, 12–30. [Google Scholar] [CrossRef]
- Ayotte, E.; Massicotte, B.; Houde, J.; Gocevski, V. Modeling the thermal stresses at early ages in a concrete monolith. ACI Mater. J. 1997, 94, 577–587. [Google Scholar]
- Cervera, M.; Oliver, J.; Prato, T. Simulation of construction of RCC dams-I: Temperature and aging. J. Struct. Eng. 2000, 126, 1053–1061. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Simulation of construction of RCC dams- II: Stress and damage. J. Struct. Eng. 2000, 126, 1062–1069. [Google Scholar] [CrossRef]
- Luna, R.; Wu, Y. Simulation of temperature and stress fields during RCC dam construction. J. Constr. Eng. Manag. 2000, 126, 381–388. [Google Scholar] [CrossRef]
- Amberg, F. Thermal analysis of a RCC dam during construction. In Proceedings of the 7th International Benchmark Workshop on Numerical Analysis of Dams, Bucharest, Romania, 24–26 September 2003. [Google Scholar]
- Waleed, A.M.; Jaafar, M.S.; Noorzaei, J.; Bayagoob, K.H.; Amini, R. Effect of Placement Schedule on the Thermal and Structural Response of R CC Dams, Using Finite Element Analysis. In Geo Jordan 2004, Proceedings of the Advances in Geotechnical Engineering with Emphasis on Dams, Highway Materials, and Soil Improvement Conference, Irbid, Jordan, 12–15 July 2004; ASCE Library: Lawrence, KS, USA, 2004; pp. 94–104. [Google Scholar]
- Malkawi, A.; Mutasher, S.; Qiu, T. Thermal-structural modeling and temperature control of roller compacted concrete gravity dam. Perform. Constr. Facil. 2003, 17, 177–187. [Google Scholar] [CrossRef]
- Zhang, X.F.; Li, S.Y.; Li, Y.L.; Ge, Y.; Li, H. Effect of superficial insulation on roller-compacted concrete dams in cold regions. Adv. Eng. Softw. 2011, 42, 939–943. [Google Scholar] [CrossRef]
- Kurian, T.; Kavitha, P.E.; Kuriakose, B. Numerical analysis of temperature distribution across the cross section of a concrete dam during early ages. Am. J. Eng. Res. (AJER) 2013, 1, 26–31. [Google Scholar]
- Kuzmanović, V.; Savić, L.; Mladenović, N. Computation of Thermal-Stresses and Contraction Joint Distance of RCC Dams. J. Therm. Stresses 2013, 36, 112–134. [Google Scholar] [CrossRef]
- Kuzmanović, V.; Savić, L.; Mladenović, N. Thermal-stress behaviour of RCC gravity dams. FME Trans. 2015, 43, 30–34. [Google Scholar] [CrossRef]
- Mirković, U.; Kuzmanović, V.; Todorović, G. Long-Term Thermal Stress Analysis and Optimization of Contraction Joint Distance of Concrete Gravity Dams. Appl. Sci. 2022, 12, 8163. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, J.; Sun, X.; Feng, J.; Sheng, D.; Wang, H.; Zhou, X.; He, Y.; Diao, M.; Zhan, Q. Simulation of thermal stress and control measures for rock-filled concrete dam in high-altitude and cold regions. Eng. Struct. 2021, 230, 111721. [Google Scholar] [CrossRef]
- Ijaz, N.; Weimin, Y.E.; ur Rehman, Z.; Ijaz, Z.; Junaid, M.F. Global insights into micro-macro mechanisms and environmental implications of limestone calcined clay cement (LC3) for sustainable construction applications. Sci. Total Environ. 2023, 907, 167794. [Google Scholar] [CrossRef] [PubMed]
- ACI. Manual of Concrete Practice. Part 1; American Concrete Institute: Detroit, MI, USA, 1981. [Google Scholar]
- Cervera, M.; Oliver, J.; Prato, T. Thermo-chemo-mechanical model for concrete. I: Hydration and aging. J. Eng. Mech. 1999, 125, 1018–1027. [Google Scholar] [CrossRef]
- Schindler, A.K.; Folliard, K.J. Influence of supplementary cementing materials on the heat of hydration of concrete. In Proceedings of the Advances in Cement and Concrete IX Conference, Copper Mountain Conference Resort in Colorado, Copper Mountain, CO, USA, 10–14 August 2003. [Google Scholar]
- Petrović, P. Hidrotehničke Konstrukcije, Drugi Deo; Građevinski Fakultet: Beograd, Srbija, 2002. [Google Scholar]
- Kim, S.G.; Wang, K. Effect of heat generation from cement hydration on mass concrete placement. Masters Abstr. Int. 2010, 49, 3. [Google Scholar]
- Ponce-Farfán, C.; Santillán, D.; Toledo, M.Á. Thermal Simulation of Rolled Concrete Dams: Influence of the Hydration Model and the Environmental Actions on the Thermal Field. Water 2020, 12, 858. [Google Scholar] [CrossRef]
- Bofang, Z. Prediction of Water Temperature in Deep Reservoirs. Dam Eng. 1997, 8, 13–25. [Google Scholar]
- Mirković, U.; Ivanović, J.; Pavić, M.; Radovanović, S.; Mirković, N.; Gospavić, R.; Todorović, G. A method of determining parameters of Bofang model on the example of “Bileca” reservoir. In Proceedings of the Zbornik Radova 7. Međunarodne Konferencije-Savremena Dostignuća u Građevinarstvu, Subotica, Serbia, 23–24 April 2019; pp. 695–705. [Google Scholar]
- Kuzmanović, V. Thermal-Stress Analysis of Roller Compacted Concrete Dams. Ph.D. Thesis, Faculty of Civil Engineering, University of Belgrade, Beograd, Serbia, 2007. [Google Scholar]
- Malcolm Dunstan & Associates. Available online: https://rccdams.co.uk/dams/platanovryssi (accessed on 1 March 2022).
- LUSAS. Available online: https://www.lusas.com (accessed on 1 March 2022).
- Platanovryssi Hydroelectric Project. Measurement Results; Public Power Corporation: Athens, Greece, 2004. [Google Scholar]
- Sheibany, F.; Ghaemian, M. Effects of environmental action on thermal stress analysis of Karaj concrete arch dam. J. Eng. Mech. 2006, 132, 532–544. [Google Scholar] [CrossRef]
- Bofang, Z. Introduction. In Thermal Stresses and Temperature Control of Mass Concrete; Butterworth-Heinemann: Oxford, UK, 2014; pp. 1–10. [Google Scholar] [CrossRef]
- Bofang, Z. Precooling and Surface Cooling of Mass Concrete. In Thermal Stresses and Temperature Control of Mass Concrete; Butterworth-Heinemann: Oxford, UK, 2014; pp. 401–408. [Google Scholar] [CrossRef]












| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| k | Thermal conductivity coefficient | 1.80 | W/(m × K) |
| c | Specific heat capacity | 950.0 | J/(kg × K) |
| α | Coefficient of thermal expansion | 11.5 × 10−6 | 1/°C |
| h1 | Combined convective heat-transfer coefficient (air–concrete) | 20.10 | W/(m2 × K) |
| h2 | Combined convective heat-transfer coefficient (water–concrete) | 500.0 | W/(m2 × K) |
| Parameter | Value | Unit |
|---|---|---|
| Cement ratio (type I) in the concrete mass m (for Portland cement) | 50 | kg/m3 |
| 12.5 × 10−3 | 1/h | |
| Water–cement ratio Fly ash ratio in the concrete mass | 0.47 | - |
| 225.0 | kg/m3 | |
| CaO ratio in the fly ash | 17.0 | % |
| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| k | Thermal conductivity coefficient | 2.40 | W/(m × K) |
| c | Specific heat capacity | 880.0 | J/(kg × K) |
| α | Coefficient of thermal expansion | 9.0 × 10−6 | 1/°C |
| Date/Time | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X 8–23 | 10.2 | 11.5 | 12.7 | 13.9 | 15.5 | 18.0 | 20.5 | 19.0 | 15.4 | 12.4 | 10.7 | 9.0 |
| X–XI 23–8 | 4.2 | 5.4 | 6.7 | 7.9 | 9.1 | 9.5 | 10.0 | 9.4 | 7.5 | 5.4 | 4.2 | 3.0 |
| XI 8–23 | 4.6 | 5.2 | 5.8 | 6.5 | 7.4 | 9.0 | 10.6 | 9.6 | 7.9 | 6.4 | 5.2 | 4.0 |
| XI–XII 23–8 | 2.2 | 2.4 | 2.6 | 2.8 | 3.3 | 4.5 | 5.8 | 5.4 | 4.5 | 3.7 | 2.8 | 2.0 |
| XII 8–23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.4 | 2.5 | 4.5 | 3.6 | 2.5 | 1.8 | 1.0 | 0.0 |
| XII–I 23–8 | 6.2 | 6.4 | 6.6 | 6.8 | 7.1 | 7.5 | 7.9 | 7.3 | 7.0 | 6.8 | 6.4 | 6.0 |
| I 8–23 | −1.8 | −1.6 | −1.4 | −1.2 | −0.5 | 1.5 | 3.6 | 3.3 | 2.7 | −0.4 | −1.2 | −2.0 |
| I–II 23–8 | 1.2 | 1.4 | 1.6 | 1.8 | 2.2 | 3.0 | 3.8 | 3.3 | 2.5 | 1.8 | 1.5 | 1.0 |
| II 8–23 | 2.0 | 2.0 | 2.0 | 2.0 | 2.4 | 4.0 | 5.6 | 5.4 | 4.5 | 3.6 | 2.9 | 2.0 |
| II–III 23–8 | 0.2 | 0.4 | 0.6 | 0.8 | 1.4 | 3.4 | 5.6 | 5.4 | 4.5 | 3.3 | 1.6 | 0.0 |
| III 8–18 | 1.2 | 1.4 | 1.6 | 1.8 | 2.3 | 3.5 | 4.8 | 3.7 | 2.5 | 2.0 | 1.6 | 1.0 |
| III 18–31 | 1.0 | 1.0 | 1.0 | 1.0 | 1.2 | 2.5 | 3.7 | 4.0 | 4.0 | 3.5 | 2.2 | 1.0 |
| IV 1–14 | 4.6 | 4.7 | 4.8 | 4.9 | 5.4 | 7.5 | 9.6 | 10.0 | 9.0 | 7.4 | 6.0 | 4.5 |
| IV 15–28 | 4.6 | 4.2 | 3.7 | 3.3 | 3.9 | 8.5 | 13.1 | 14.0 | 13.5 | 11.7 | 8.3 | 5.0 |
| IV–V 29–11 | 15.2 | 16.0 | 16.7 | 17.4 | 18.4 | 20.5 | 22.6 | 23.0 | 21.5 | 19.1 | 16.8 | 14.5 |
| V 12–26 | 13.0 | 14.1 | 15.1 | 16.2 | 17.7 | 21.0 | 24.3 | 24.3 | 23.0 | 20.3 | 16.2 | 12.0 |
| V–VI 27–9 | 15.2 | 14.9 | 14.6 | 14.2 | 14.9 | 19.5 | 24.1 | 25.0 | 24.0 | 21.7 | 18.6 | 15.5 |
| VI 10–24 | 17.0 | 17.0 | 17.0 | 17.0 | 17.9 | 22.5 | 27.1 | 28.0 | 26.5 | 23.7 | 20.3 | 17.0 |
| VI–VII 25–7 | 21.2 | 20.9 | 20.6 | 20.2 | 21.0 | 26.0 | 31.0 | 31.3 | 29.5 | 26.9 | 24.2 | 21.5 |
| VII 8–22 | 24.0 | 22.9 | 21.9 | 20.8 | 20.9 | 25.5 | 30.1 | 30.1 | 28.5 | 26.7 | 25.8 | 25.0 |
| VII–VIII 23–5 | 20.7 | 19.5 | 20.0 | 21.7 | 23.8 | 28.0 | 32.2 | 33.0 | 32.0 | 29.5 | 25.7 | 22.0 |
| VIII 6–19 | 20.3 | 18.7 | 19.0 | 20.7 | 22.7 | 26.0 | 29.3 | 30.7 | 29.5 | 27.0 | 24.5 | 22.0 |
| VIII–IX 20–2 | 16.2 | 15.3 | 16.0 | 17.7 | 19.6 | 22.5 | 25.4 | 24.7 | 23.5 | 22.0 | 19.5 | 17.0 |
| IX 3–9 | 15.2 | 14.3 | 14.7 | 16.0 | 17.5 | 20.0 | 22.5 | 23.0 | 22.0 | 20.2 | 18.1 | 16.0 |
| Month | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tag,mm (°C) | 10 | 10 | 12 | 14 | 16 | 20 | 22 | 22 | 20 | 16 | 12 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirković, U.; Kuzmanović, V.; Todorović, G. Influence of Monolith Length on Temperature Field of Concrete Gravity Dams. Appl. Sci. 2024, 14, 3248. https://doi.org/10.3390/app14083248
Mirković U, Kuzmanović V, Todorović G. Influence of Monolith Length on Temperature Field of Concrete Gravity Dams. Applied Sciences. 2024; 14(8):3248. https://doi.org/10.3390/app14083248
Chicago/Turabian StyleMirković, Uroš, Vladan Kuzmanović, and Goran Todorović. 2024. "Influence of Monolith Length on Temperature Field of Concrete Gravity Dams" Applied Sciences 14, no. 8: 3248. https://doi.org/10.3390/app14083248
APA StyleMirković, U., Kuzmanović, V., & Todorović, G. (2024). Influence of Monolith Length on Temperature Field of Concrete Gravity Dams. Applied Sciences, 14(8), 3248. https://doi.org/10.3390/app14083248







