Dynamic Modeling and Improved Nonlinear Model Predictive Control of a Free-Floating Dual-Arm Space Robot

Abstract

With the increasing demand for space missions, space robots have become the focus of research and attention. As a typical representative, the free-floating dual-arm space robot has the characteristics of multiple degrees of freedom, a floating base, and dynamic coupling between the manipulator and the base, so its modeling and control are very challenging. To address these challenges, a novel dynamic modeling and control method is proposed for a free-floating dual-arm space robot. First, an explicit dynamic model of a free-floating dual-arm space robot is established based on the explicit canonical multi-rigid-body dynamic modeling theory and combined with the concept of a dynamic equivalent manipulator. The establishment process of this model is not only simple and canonical to avoid the definition and calculation of many intermediate variables, but the symbolic result expression of the model also has the characteristics of iteration, which is convenient for computer automatic modeling. Next, aiming at addressing the problem of trajectory tracking and the base attitude stability of a free-floating dual-arm space robot with parameter perturbation and external disturbance, an improved nonlinear model predictive control method introducing the idea of sliding mode variable structure is proposed. Theoretical analysis shows that the proposed controller has better robustness than the traditional nonlinear model predictive controller. Then, an in-orbit service task is designed to verify the effectiveness of the proposed dynamic modeling and control strategy of the free-floating dual-arm space robot. Finally, the dynamic modeling and control methods proposed are discussed and summarized. The proposed methods can not only realize the tracking of the desired trajectory of the arms of the free-floating space robot, but can also realize the stable control of the base of the free-floating space robot. This paper provides new insights into the difficult problems regarding the dynamics and control of free-floating dual-arm space robots.

1. Introduction

Since the 1990s, space manipulators used to manipulate and capture payloads have received extensive attention [1,2,3,4,5,6]. Space manipulator can not only be installed on a space station to assist astronauts in the maintenance of the space station [7,8,9], but can also be installed on an unmanned satellite to carry out in-orbit maintenance of the satellite and capture space debris [10,11,12,13]. In 2007, the US Orbital Express project carried out capture and maintenance experiments of controlled target satellites using unmanned satellites equipped with a manipulator [14]. Unlike a manipulator with a fixed base on the ground, the base of a small space robot composed of a small unmanned satellite and manipulator is generally movable [15]. This kind of space robot with a movable base is a typical unrooted tree multibody dynamic system, which has the characteristics of many degrees of freedom (DOF), strong nonlinearity and strong coupling [16]. Its dynamic modeling and control are challenging and have attracted increasing attention from researchers in recent years [1,15].

Compared with single-arm space robots, the establishment of the dynamic model of a dual-arm space robot is more complicated. So far, according to the different expressions of dynamic equations, the dynamic modeling methods of multibody systems such as robots are mainly divided into recursive methods based on the Newton–Euler equation and explicit methods based on the Lagrange equation. Recursive methods can obtain efficient recursive equations, but they are not suitable for the derivation of a high control law [17,18]. Compared with recursive methods, the expression of the dynamic equation of explicit methods is more intuitive. The pseudo inertia matrix method [19,20] and the generalized momentum method [21] are two common explicit dynamic modeling methods. However, these two explicit methods both have the problem that many intermediate variables need to be analyzed and calculated. Recently, an explicit multi-rigid-body dynamic modeling method was proposed, which can directly obtain the final canonical expression of a multibody system [22,23].

Unlike ground robots with a fixed base, space robots have dynamic coupling between the arm and the movable base [24,25]. If this is not controlled, it will lead to accidental movement of the base and affect the performance of the space robot [7,26,27]. For example, to ensure reliable communication with the ground or receive solar energy, the base of the satellite needs to accurately point in a fixed position, but the dynamic coupling between the arm and the base will interfere with the attitude of base [7]. Dubowsky and Papadopoulos [28] divided space robots with movable bases into free-flying space robots and free-floating space robots according to the different control problems to be solved. Unlike free-flying space robots that need to control the position and attitude of the base at the same time, free-floating space robots only needs to consider the control of base attitude, which can save energy [29]. In order to simplify the kinematic analysis of free-floating space robots, Vafa and Dubowsky [30] proposed the concept of the virtual manipulator (VM). VM is a fixed base robot with the same kinematic equivalence as a free-floating space robot, and its first joint is a passive spherical joint, which represents the free-floating characteristics of the space robot [31]. Liang [32] extended the concept of VM and proposed the dynamic equivalent manipulator (DEM), which can simultaneously simplify the kinematics and dynamics analysis of free-floating space robots.

In the process of in-orbit service, a space robot will not only be subjected to unknown disturbances from the outside, but will also be constrained by the uncertainty of internal parameters of the system caused by the change in fuel quality and other factors [15]. Therefore, designing controllers for space robots is a challenge which has been studied by many researchers [33,34,35]. Papadopoulos and Dubowsky [29] noted the similarities in control between free-floating space robots and ground fixed-base robots. Since then, many control algorithms designed for ground fixed-base robots have been studied and applied in space robots. Among them, the PID control method, which has been widely studied in ground industrial robots, has also been used in space robots [36]. However, this method has the problem of parameter tuning difficulty when it is applied to control an in-orbit service space robot with complex disturbances. Sliding mode control (SMC) is widely applied in the field of nonlinear systems because of its high precision and fast response [37,38]. Slotine et al. [39] first used SMC to design the controller of a two-DOF manipulator, and then the researchers conducted much research on the SMC of robots, representing a typical nonlinear system [40,41]. In recent years, many novel SMC methods have been proposed for the in-orbit service of space robots [42,43]. Model predictive control (MPC) is an excellent control method based on a system model to obtain a control signal by minimizing the objective function [44]. Raimondo et al. [45,46] improved MPC for the control problem of nonlinear systems and obtained better control performance. In the field of space robots, compared with other control methods, there is relatively less research on MPC. When studying the control problem of dual-arm space robots, Shi [47] found that MPC can achieve higher-precision control performance than SMC when there is no system disturbance, while SMC shows better robustness than MPC when there is system disturbance. Tomasz Rybus [44] discussed the possibility of applying a nonlinear model predictive controller (NMPC) to a free-floating space robot. Tomasz Rybus [11] proposed a new concept for a free-floating space robot control system, in which the NMPC controller introduced a trajectory planning module, but the paper only carried out a numerical simulation on the planar case of the two-DOF manipulator.

In this paper, the dynamic model of a free-floating dual-arm space robot with stylization and high computational efficiency is established by using the concept of DEM and the explicit multi-rigid-body dynamic modeling theory [22,23], and a novel control method is proposed. This method can be effectively applied to the terminal trajectory tracking and base attitude stability control of free-floating space robots under the condition of parameter perturbation and external disturbance. The remainder of this paper is organized as follows: in Section 2, a free-floating dual-arm space robot is modeled and analyzed by using explicit multi-rigid-body dynamic modeling theory and DEM. In Section 3, an improved NMPC controller is designed and its stability is analyzed based on Lyapunov theory. In Section 4, an in-orbit service task is designed and a numerical simulation is performed to verify the proposed controller. In Section 5, the dynamic modeling and control methods for the free-floating space robot are discussed, while the conclusions are provided in Section 6.

2. Dynamic Modeling of Free-Floating Dual-Arm Space Robot

This section mainly introduces and analyzes the dynamic model of a free-floating dual-arm space robot based on the explicit multi-rigid-body dynamic modeling method and combined with the concept of DEM, which is used for subsequent control research. Because kinematics is the foundation of dynamics [17], the kinematic model is introduced first before the dynamic modeling.

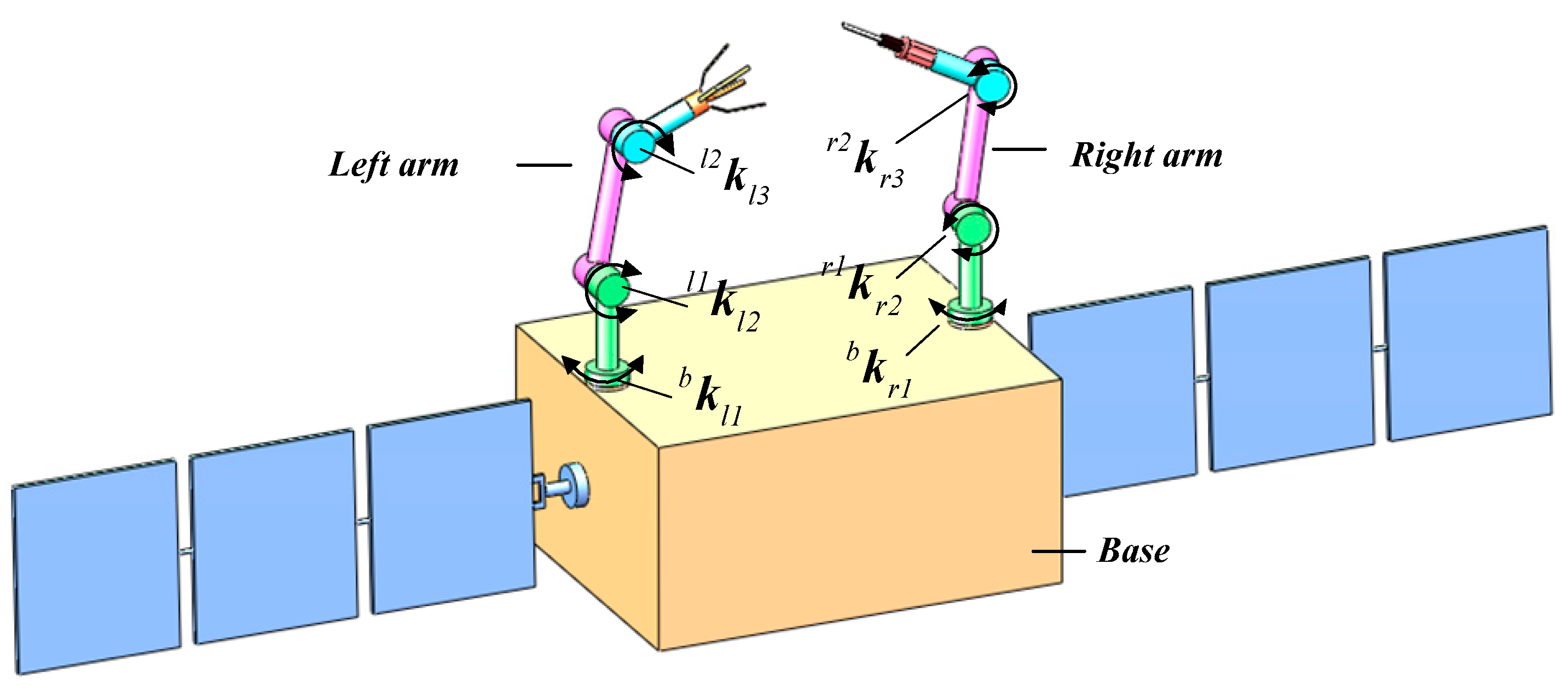
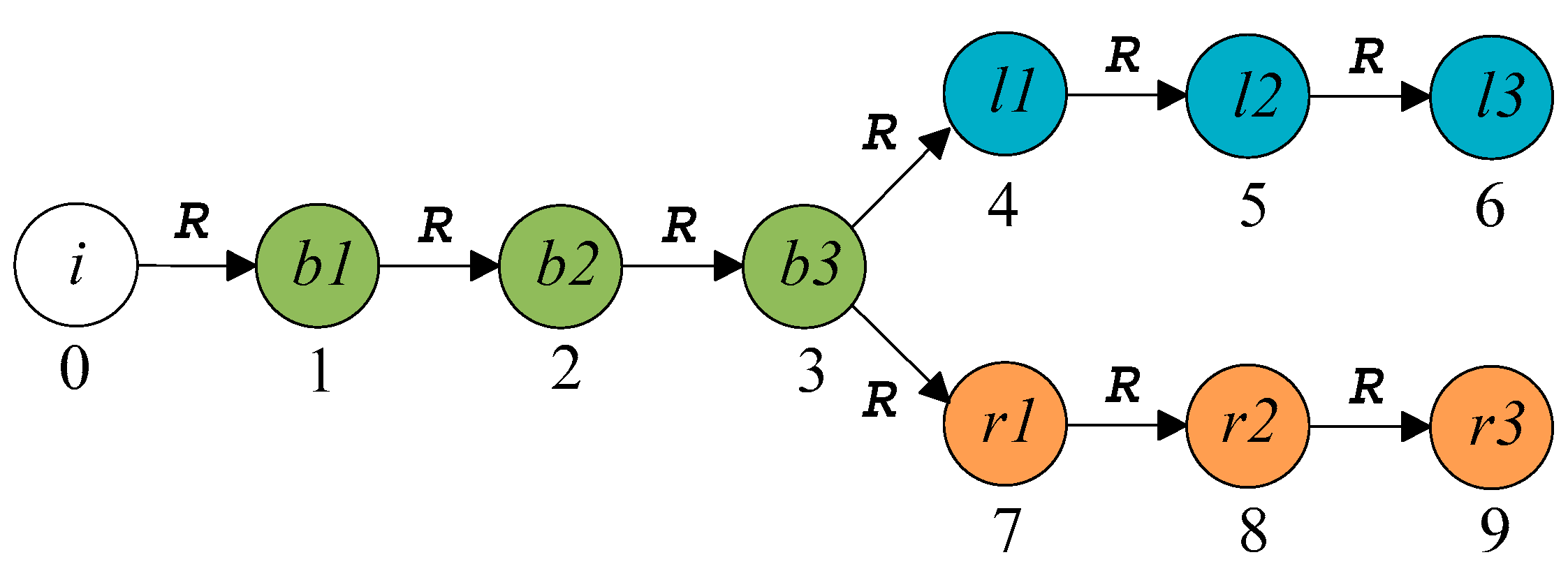
2.1. Kinematic Modeling

The free-floating dual-arm space robot used in this study is a typical unrooted tree multibody system [16]. The schematic diagram of the free-floating dual-arm space robot studied in this paper is shown in Figure 1. The topological structure analysis and the establishment of the reference frames of the space robot are introduced below.

The topology of a robot is usually composed of nodes representing the links (except the root node) and arcs representing the joints [48]. The schematic diagram of the free-floating dual-arm space robot is shown in Figure 1, where ${}^{\overline{l}}\mathit{k}_l$ represents the kinematic pair composed of parent link $\overline{l}$ and child link l. Each arm of the free-floating dual-arm space robot contains three single-DOF revolute pairs. The attitude of the base of the free-floating space robot has three rotational DOF. According to the concept of DEM, after the free-floating base of the space robot is equivalent to three single-DOF revolute pairs, the unrooted free-floating tree-chain space robot can be equivalent to a fixed-base tree-chain ground robot [31]. According to the above analysis, the topology graph of the free-floating dual-arm space robot is shown in Figure 2, where i represents the inertial space, b represents the base, l represents the left arm, r represents the right arm and R represents the revolute pair. Except for the root node, the remaining nine nodes in the topology correspond to the nine DOF of the free-floating dual-arm space robot, and these nodes are numbered in turn. In addition, unless otherwise specified, the rest of the symbols used in this article are shown in

Table A1. Symbol descriptions.

Symbols	Description	Symbols	Description
${\varphi }_l^{\overline{l}}$	Angular position along ${}^{\overline{l}}\mathit{n}_l$	${}^{\overline{l}}\varphi _l$	$\mathrm{Vector} \mathrm{form} \mathrm{of} {\varphi }_l^{\overline{l}}$
${\mathit{r}}_l^{\overline{l}}$	$\mathrm{Linear} \mathrm{position} \mathrm{along} {}^{\overline{l}}\mathit{n}_l$	${}_0{}^{\overline{l}}\mathit{r}_l$	$\mathrm{Vector} \mathrm{from} O_{\overline{l}}$$\mathrm{to} O_l$
${}^{\overline{l}}\mathit{r}_l$	$\mathrm{Vector} \mathrm{form} \mathrm{of} {\mathit{r}}_l^{\overline{l}}$	${}^{\overline{l}}\mathit{Q}_l$	$\mathrm{Rotation\; matrix\; from} \overline{l} \mathrm{to} l$
$\mathrm{u}\mathit{L}$	Closed subtree of link u	${}^i\mathsf{𝟷}_l$	Kinematic chain from i to l
${\mathrm{m}}_k$	Mass of link k	${}^{kI}\mathit{J}_{kI}$	Inertia tensor of link k
${\mathit{M}}_R^{[u][\ast ]}$	Inertial force matrix of revolute joint u	${\mathit{h}}_R^{[u]}$	Bias force vector of revolute joint u
${}^{iL}\mathit{\tau }_u$	resultant torque on axis ${}^{\overline{u}}\mathit{n}_u$ except gravity	${\mathit{M}}^{[\mathrm{u}][\mathrm{k}]}$	uth row and kth column element of inertia matrix

of Appendix A.

To improve the calibration accuracy of the robot’s structural parameters, we propose a reference system establishment method based on the Axis-Invariant [49]. The reference frames and the Axis-Invariant of the left arm of the free-floating dual-arm space robot are described in Figure 3. The origin of the inertial reference frame $O_i{x}_i{y}_i{z}_i$ is located at the center of the Earth. The origin of the base reference frame $O_b{x}_b{y}_b{z}_b$ is located at the center of mass of the base. The origins of the joint reference frames $O_l{x}_l{y}_l{z}_l$ are located on the rotation axes of the joints. At the initial moment, the directions of these reference frames are consistent. The Axis-Invariant ${}^{\overline{l}}\mathit{n}_l$ is defined as the motion axis vector direction of joint l. For more background and applications of the Axis-Invariant, refer to [22,23,49,50,51].

With the Axis-Invariant ${}^{\overline{l}}\mathit{n}_l$ as the reference axis, the rotational vector ${}^{\overline{l}}\mathit{\varphi }_l$ of the rotating joint and the translational vector ${}^{\overline{l}}\mathit{r}_l$ of the prismatic joint can be expressed as follows [22,23]:

$${}^{\overline{l}}\mathit{\varphi }_l={}^{\overline{l}}\mathit{n}_l·{\varphi }_l^{\overline{l}}$$

(1)

$${}^{\overline{l}}\mathit{r}_l={}^{\overline{l}}\mathit{n}_l·{\mathrm{r}}_l^{\overline{l}}+{}_0{}^{\overline{l}}\mathit{r}_l$$

(2)

The rotation transformation matrix ${}^{\overline{l}}\mathit{Q}_l$ based on the Axis-Invariant ${}^{\overline{l}}\mathit{n}_l$ can be expressed as follows [22,23]:

$${}^{\overline{\mathit{l}}}\mathit{Q}_l=\mathit{1}+{}^{\overline{l}}\tilde{\mathit{n}}_l·\sin ({\varphi }_l^{\overline{l}})+{}^{\overline{l}}\tilde{\mathit{n}}_{\mathit{l}}^{^2}·\left(1-\cos ({\varphi }_l^{\overline{l}})\right)$$

(3)

According to the expression of the rotation transformation matrix ${}^{\overline{l}}\mathit{Q}_l$ in Equation (3), the iterative kinematic equations of multi-joint series based on the Axis-Invariant ${}^{\overline{l}}\mathit{n}_l$ can be expressed as follows:

$${}^i\mathit{Q}_l=\underset{k}{\prod ^{{}^i\mathsf{𝟷}_l}}{}^{\overline{k}}\mathit{Q}_k$$

(4)

$${}^i\mathit{\varphi }_l={\displaystyle \sum _k^{{}^i\mathsf{𝟷}_l}{}^{i|\overline{k}}\varphi _k}={\displaystyle \sum _k^{{}^i\mathsf{𝟷}_l}{}^i\mathit{Q}_{\overline{k}}·{}^{\overline{\mathit{k}}}\mathit{\varphi }_{\mathit{k}}}$$

(5)

$${}^{\overline{\mathit{i}}}\mathit{r}_{\mathit{l}}={\displaystyle \sum _k^{{}^i\mathsf{𝟷}_l}{}^{i|\overline{k}}\mathit{r}_k}={\displaystyle \sum _k^{{}^i\mathsf{𝟷}_l}{}^i\mathit{Q}_{\overline{k}}·{}^{\overline{\mathit{k}}}\mathit{r}_{\mathit{k}}}$$

(6)

where the left superscript “i|” of the vector represents the projection of the vector under the inertial reference frame $O_i{x}_i{y}_i{z}_i$.

The velocity vector and acceleration vector are the derivative and second derivative of the displacement vector, respectively. By taking the derivative and second derivative of Equations (5) and (6), the iterative velocity and iterative acceleration of multi-joint kinematic chain ${}^{i}l_l$ can be expressed as follows:

$${}^i\dot{\varphi }_l={\displaystyle \sum _k^{{}^i\mathsf{𝟷}_l}\left({}^{i|\overline{k}}\dot{\varphi }_k\right)}$$

(7)

$${}^l\ddot{\varphi }_i={\displaystyle \sum _k^{{}^i\mathsf{𝟷}_l}\left({}^i\dot{\tilde{\varphi }}_{\overline{k}}·{}^{i|\overline{k}}\dot{\varphi }_k+{}^{i|\overline{k}}\ddot{\varphi }_k\right)}$$

(8)

$${}^i\mathit{r}\dot{}_l={\displaystyle \sum _k^{{}^i\mathsf{𝟷}_l}\left({}^i\dot{\tilde{\varphi }}_{\overline{k}}·{}^{i|\overline{k}}\mathit{r}_k+{}^{i|\overline{k}}\dot{\mathit{r}}_k\right)}$$

(9)

$${}^i\ddot{\mathit{r}}_l={\displaystyle \sum _k^{{}^i\mathsf{𝟷}_l}}\left({}^i\ddot{\tilde{\varphi }}_{\overline{k}}·{}^{i|\overline{k}}\mathit{r}_k+{}^i\dot{\tilde{\varphi }}_{\overline{k}}^{^2}·{}^{i|\overline{k}}\mathit{r}_k+2·{}^i\dot{\tilde{\varphi }}_{\overline{k}}·{}^{i|\overline{k}}\dot{\mathit{r}}_k+{}^{i|\overline{k}}\ddot{\mathit{r}}_k\right)$$

(10)

2.2. Dynamic Modeling

As a classical method of multibody system dynamics modeling, the Lagrange equation is widely used in the field of robot dynamics [52]. When the free-floating dual-arm space robot serving in orbit is running in space, the influence of gravity can be ignored, and the joint type of the robot only contains rotating joints. The Lagrange equation expression of the space robot tree-chain multibody system based on the Axis-Invariant, which only contains rotating joints and ignores gravity, is as follows [22,23]:

$$\frac{d}{dt}\left(\frac{\partial {ℰ}_{\mathit{L}}^i}{\partial {\dot{\varphi }}_u^{\overline{u}}}\right)-\frac{\partial {ℰ}_{\mathit{L}}^i}{\partial {\varphi }_u^{\overline{u}}}={ }^{i|\overline{u}}{\mathit{n}}_u^{\mathrm{T}}·{ }^{iL}{\mathit{\tau }}_u$$

(11)

where ${ℰ}_L^i$ is an energy term,

$${ℰ}_{\mathit{L}}^i={\displaystyle \sum _k^{i\mathit{L}}}\left(\frac{1}{2}·{}^i\dot{\varphi }_k^{\mathrm{T}}·{}^{i|kI}\mathit{J}_{kI}·{}^i\dot{\varphi }_k+\frac{1}{2}·{\mathrm{m}}_k·{}^i\dot{\mathit{r}}_{kI}^{\mathrm{T}}·{}^i\dot{\mathit{r}}_{kI}\right)$$

(12)

The iterative partial derivative equation based on the Axis-Invariant is [22,23]

$$\frac{\partial {}^i\mathit{r}_{nS}}{\partial {\varphi }_k^{\overline{k}}}=\frac{\partial {}^i\dot{\mathit{r}}_{nS}}{\partial {\dot{\varphi }}_k^{\overline{k}}}=\frac{\partial {}^i\ddot{\mathit{r}}_{nS}}{\partial {\ddot{\varphi }}_k^{\overline{k}}}={}^{i|\overline{k}}\tilde{\mathit{n}}_k·{}^{i|k}\mathit{r}_{nS}$$

(13)

$$\frac{\partial {}^i\dot{\varphi }_n}{\partial {\dot{\varphi }}_k^{\overline{k}}}=\frac{\partial {}^i\ddot{\varphi }_n}{\partial {\ddot{\varphi }}_k^{\overline{k}}}={}^{i|\overline{k}}\mathit{n}_k$$

(14)

Substituting Equations (1)–(10) and (13) and (14) into Equations (11) and (12), after simplifying the results, the explicit canonical dynamic expression of the space robot tree-chain multibody system that ignores gravity and only contains rotating joints can be obtained:

$${}^{i|\overline{u}}\mathit{n}_u^{\mathrm{T}}·{\mathrm{M}}_R^{[u][\ast ]}·\ddot{\mathit{q}}+{}^{i|\overline{u}}\mathit{n}_u^{\mathrm{T}}·{\mathit{h}}_R^{[u]}={}^{i|\overline{u}}\mathit{n}_u^{\mathrm{T}}·{}^{iL}\mathit{\tau }_u$$

(15)

where $M_{\mathit{R}}^{[u][\ast ]}$ is a 3 × 3 inertia matrix for revolute pairs and ${\mathit{h}}_{\mathit{R}}^{[u]}$ is a 3D bias force vector for revolute pairs,

$$\begin{array}{l}{\mathit{M}}_{\mathit{R}}^{[u][\ast ]}·\ddot{\mathit{q}}={\displaystyle \sum _l^{{}^i\mathsf{𝟷}_{\overline{u}}}}\left({\displaystyle \sum _j^{u\mathit{L}}}\left({}^{i|jI}\mathit{J}_{jI}-{\mathrm{m}}_j·{}^{i|u}\tilde{\mathit{r}}_{jI}·{}^{i|l}\tilde{\mathit{r}}_{jI}\right)·{}^{i|\overline{l}}\mathit{n}_l·{\ddot{\varphi }}_l^{\overline{l}}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \sum _k^{u\mathit{L}}}\left({\displaystyle \sum _j^{k\mathit{L}}}\left({}^{i|jI}\mathit{J}_{jI}-{\mathrm{m}}_j·{}^{i|u}\tilde{\mathit{r}}_{jI}·{}^{i|k}\tilde{\mathit{r}}_{jI}\right)·{}^{i|\overline{k}}\mathit{n}_k·{\ddot{\varphi }}_k^{\overline{k}}\right) \end{array}$$

(16)

$$\begin{array}{l}{\mathit{h}}_{\mathit{R}}^{[u]}={\displaystyle \sum _l^{{}^i\mathsf{𝟷}_{\overline{u}}}\left\{\left.\left({\displaystyle \sum _k^{u\mathit{L}}\left({}^{i|kI}\mathit{J}_{kI}-{\mathrm{m}}_k·{}^{i|u}\tilde{\mathit{r}}_{kI}·{}^{i|l}\tilde{\mathit{r}}_{kI}\right)}\right)·{}^i\dot{\tilde{\varphi }}_{\overline{l}}·{}^{i|\overline{l}}\dot{\varphi }_l\right\}\right.}\\ \hspace{1em}\hspace{1em} +{\displaystyle \sum _k^{u\mathit{L}}\left\{\left.\left({\displaystyle \sum _j^{k\mathit{L}}\left({}^{i|jI}\mathit{J}_{jI}-{\mathrm{m}}_j·{}^{i|u}\tilde{\mathit{r}}_{jI}·{}^{i|k}\tilde{\mathit{r}}_{jI}\right)}\right)·{}^i\dot{\tilde{\varphi }}_{\overline{k}}·{}^{i|\overline{k}}\dot{\varphi }_k\right\}\right.}\\ \hspace{1em}\hspace{1em} +{\displaystyle \sum _k^{u\mathit{L}}\left({\mathrm{m}}_k·{}^{i|u}\tilde{\mathit{r}}_{kI}·{\displaystyle \sum _l^{{}^i\mathsf{𝟷}_{kI}}\left({}^i\dot{\tilde{\varphi }}_{\overline{l}}^{^2}·{}^{i|\overline{l}}\mathit{r}_l+2·{}^i\dot{\tilde{\varphi }}_{\overline{l}}·{}^{i|\overline{l}}\dot{\mathit{r}}_l\right)}\right)}\\ \hspace{1em}\hspace{1em} +{\displaystyle \sum _k^{u\mathit{L}}\left({}^i\dot{\tilde{\varphi }}_k·{}^{i|kI}\mathit{J}_{kI}·{}^i\dot{\varphi }_k\right)}\end{array}$$

(17)

According to Equation (15) and the above topological analysis, the explicit canonical dynamic model of the base, left arm and right arm of the free-floating dual-arm space robot can be obtained as follows:

$$\begin{array}{cc} \mathit{base}:\hfill & \left\{\begin{array}{l}{}^i\mathit{n}_1^{\mathrm{T}}·{\mathit{M}}_{\mathit{R}}^{[1][•]}·\ddot{\mathit{q}}+{}^i\mathit{n}_1^{\mathrm{T}}·{\mathit{h}}_{\mathit{R}}^{[1]}={}^i\mathit{n}_1^{\mathrm{T}}·{}^{iL}\mathit{\tau }_1\\ {}^{i|1}\mathit{n}_2^{\mathrm{T}}·{\mathit{M}}_{\mathit{R}}^{[2][•]}·\ddot{\mathit{q}}+{}^{i|1}\mathit{n}_2^{\mathrm{T}}·{\mathit{h}}_{\mathit{R}}^{[2]}={}^{i|1}\mathit{n}_2^{\mathrm{T}}·{}^{iL}\mathit{\tau }_2\\ {}^{i|2}\mathit{n}_3^{\mathrm{T}}·{\mathit{M}}_{\mathit{R}}^{[3][•]}·\ddot{\mathit{q}}+{}^{i|2}\mathit{n}_3^{\mathrm{T}}·{\mathit{h}}_{\mathit{R}}^{[3]}={}^{i|2}\mathit{n}_3^{\mathrm{T}}·{}^{iL}\mathit{\tau }_3\end{array}\right.\hfill \\ \mathit{left} \mathit{arm}:\hfill & \left\{\begin{array}{l}{}^{i|3}\mathit{n}_4^{\mathrm{T}}·{\mathit{M}}_{\mathit{R}}^{[4][•]}·\ddot{\mathit{q}}+{}^{i|3}\mathit{n}_4^{\mathrm{T}}·{\mathit{h}}_{\mathit{R}}^{[4]}={}^{i|3}\mathit{n}_4^{\mathrm{T}}·{}^{iL}\mathit{\tau }_4 \\ {}^{i|4}\mathit{n}_5^{\mathrm{T}}·{\mathit{M}}_{\mathit{R}}^{[5][•]}·\ddot{\mathit{q}}+{}^{i|4}\mathit{n}_5^{\mathrm{T}}·{\mathit{h}}_{\mathit{R}}^{[5]}={}^{i|4}\mathit{n}_5^{\mathrm{T}}·{}^{iL}\mathit{\tau }_5\\ {}^{i|5}\mathit{n}_6^{\mathrm{T}}·{\mathit{M}}_{\mathit{R}}^{[6][•]}·\ddot{\mathit{q}}+{}^{i|5}\mathit{n}_6^{\mathrm{T}}·{\mathit{h}}_{\mathit{R}}^{[6]}={}^{i|5}\mathit{n}_6^{\mathrm{T}}·{}^{iL}\mathit{\tau }_6\end{array}\right.\hfill \\ \mathit{right} \mathit{arm}:\hfill & \left\{\begin{array}{c}{}^{i|3}\mathit{n}_7^{\mathrm{T}}·{\mathit{M}}_{\mathit{R}}^{[7][•]}·\ddot{\mathit{q}}+{}^{i|3}\mathit{n}_7^{\mathrm{T}}·{\mathit{h}}_{\mathit{R}}^{[7]}={}^{i|3}\mathit{n}_7^{\mathrm{T}}·{}^{iL}\mathit{\tau }_7 \\ {}^{i|7}\mathit{n}_8^{\mathrm{T}}·{\mathit{M}}_{\mathit{R}}^{[8][•]}·\ddot{\mathit{q}}+{}^{i|7}\mathit{n}_8^{\mathrm{T}}·{\mathit{h}}_{\mathit{R}}^{[8]}={}^{i|7}\mathit{n}_8^{\mathrm{T}}·{}^{iL}\mathit{\tau }_8\\ {}^{i|8}\mathit{n}_9^{\mathrm{T}}·{\mathit{M}}_{\mathit{R}}^{[9][•]}·\ddot{\mathit{q}}+{}^{i|8}\mathit{n}_9^{\mathrm{T}}·{\mathit{h}}_{\mathit{R}}^{[9]}={}^{i|8}\mathit{n}_9^{\mathrm{T}}·{}^{iL}\mathit{\tau }_9\end{array}\right.\hfill \end{array}$$

(18)

The above Equation (18) can be rewritten as follows:

$$\left[\begin{array}{l}{\mathit{M}}^{[1][1]} {\mathit{M}}^{[1][2]} {\mathit{M}}^{[1][3]} \cdots \cdots {\mathit{M}}^{[1][7]} {\mathit{M}}^{[1][8]} {\mathit{M}}^{[1][9]}\\ {\mathit{M}}^{[2][1]} {\mathit{M}}^{[2][2]} {\mathit{M}}^{[2][3]} \cdots \cdots {\mathit{M}}^{[2][7]} {\mathit{M}}^{[2][8]} {\mathit{M}}^{[2][9]}\\ {\mathit{M}}^{[3][1]} {\mathit{M}}^{[3][2]} {\mathit{M}}^{[3][3]} \cdots \cdots {\mathit{M}}^{[3][7]} {\mathit{M}}^{[3][8]} {\mathit{M}}^{[3][9]}\\ \hspace{1em}\hspace{1em}⋮ ⋮ ⋮\hspace{1em}\hspace{1em}\hspace{1em}\cdots \cdots \hspace{1em}\hspace{1em}\hspace{1em}⋮ ⋮ ⋮\\ \hspace{1em}\hspace{1em}⋮ ⋮ ⋮\hspace{1em}\hspace{1em}\hspace{1em}\cdots \cdots \hspace{1em}\hspace{1em}\hspace{1em}⋮ ⋮ ⋮\\ {\mathit{M}}^{[7][1]} {\mathit{M}}^{[7][2]} {\mathit{M}}^{[7][3]} \cdots \cdots {\mathit{M}}^{[7][7]} {\mathit{M}}^{[7][8]} {\mathit{M}}^{[7][9]}\\ {\mathit{M}}^{[8][1]} {\mathit{M}}^{[8][2]} {\mathit{M}}^{[8][3]} \cdots \cdots {\mathit{M}}^{[8][7]} {\mathit{M}}^{[8][8]} {\mathit{M}}^{[8][9]}\\ {\mathit{M}}^{[9][1]} {\mathit{M}}^{[9][2]} {\mathit{M}}^{[9][3]} \cdots \cdots {\mathit{M}}^{[9][7]} {\mathit{M}}^{[9][8]} {\mathit{M}}^{[9][9]}\end{array}\right]\left[\begin{array}{l}{\ddot{\varphi }}_1^i\\ {\ddot{\varphi }}_2^1\\ {\ddot{\varphi }}_3^2\\ ⋮\\ ⋮\\ {\ddot{\varphi }}_7^3\\ {\ddot{\varphi }}_8^7\\ {\ddot{\varphi }}_9^8\end{array}\right]+\left[\begin{array}{l}{\mathit{h}}^{[1]}\\ {\mathit{h}}^{[2]}\\ {\mathit{h}}^{[3]}\\ ⋮\\ ⋮\\ {\mathit{h}}^{[7]}\\ {\mathit{h}}^{[8]}\\ {\mathit{h}}^{[9]}\end{array}\right]=\left[\begin{array}{l}{\mathit{\tau }}^{[1]}\\ {\mathit{\tau }}^{[2]}\\ {\mathit{\tau }}^{[3]}\\ ⋮\\ ⋮\\ {\mathit{\tau }}^{[7]}\\ {\mathit{\tau }}^{[8]}\\ {\mathit{\tau }}^{[9]}\end{array}\right]$$

(19)

According to Equations (16) and (17), the inertia matrix M^[·][·] and the bias force vector h^[·] in Equation (19) can be defined by Equations (A1)–(A9) and Equations (A10)–(A15) in Appendix B, respectively.

3. Design of the Improved NMPC Controller

In this section, an improved NMPC controller is designed for the trajectory tracking control of a free-floating dual-arm space robot serving in orbit. The principle of the improved NMPC controller designed in this paper is shown in Figure 4. As shown in Figure 4, the controller proposed in this paper is mainly composed of a predictive control unit for the rolling optimization of a nominal dynamic model and a sliding mode variable structure control unit for the purposes of weakening the influence of disturbance. The improved NMPC controller introduced the idea of SMC control and added the sliding mode variable structure control technology to suppress the disturbance, which improved the performance of the traditional NMPC controller.

According to Figure 4, the control law of the proposed controller can be expressed as follows:

$$\mathit{u}={\mathit{u}}_{\mathrm{m}}+{\mathit{u}}_{\mathrm{c}}$$

(20)

where ${\mathit{u}}_m$ is the torque generated by the predictive control unit and ${\mathit{u}}_c$ is the torque generated by the sliding mode variable structure control unit.

3.1. Design of the NMPC Controller

The designed predictive controller refers to the classical NMPC control algorithm developed in [53]. NMPC is essentially a kind of optimal control that aims to minimize the trajectory tracking error during control. Therefore, the cost function of the NMPC is often expressed as [53,54]:

$$J_{\mathit{cost}}=\frac{1}{2}{\displaystyle {\int }_{T_1}^{T_2}\mathit{e}{(\mathit{t}+\tau )}^{\mathrm{T}}\mathit{e}(t+\tau )d\tau }$$

(21)

where $\mathit{e}(t+\tau )=\mathit{q}(t+\tau )-{\mathit{q}}_d(t+\tau )$ is the prediction error at time $t+\tau$ and $\tau$ is the prediction time. $\mathit{q}(t+\tau )$ and ${\mathit{q}}_d(t+\tau )$ represent the actual and desired joint angles of the system at time $t+\tau$, respectively.

The truncated Taylor series is applied to expand $\mathit{q}(t+\tau )$ as follows:

$$\mathit{q}(t+\tau )=\mathit{q}(t)+\tau \dot{\mathit{q}}(t)+\frac{{\tau }^2}{2}\ddot{\mathit{q}}(\mathrm{t})$$

(22)

If $\mathit{T}(t)=[{\mathit{I}}_{9\times 9}\tau ·{\mathit{I}}_{9\times 9}\frac{{\tau }^2}{2}·{\mathit{I}}_{9\times 9}]$, ${\mathit{\rho }}_{ }(t)=[\mathit{q}(t)\dot{\mathit{q}}(t)\ddot{\mathit{q}}(t){]}^{\mathrm{T}}$, and ${\mathit{\rho }}_d(t)=[{\mathit{q}}_d(t){\dot{\mathit{q}}}_d(t){\ddot{\mathit{q}}}_d(t){]}^{\mathrm{T}}$ are taken, then $\mathit{q}(t+\tau )$ and ${\mathit{q}}_d(t+\tau )$ can be expressed as:

$$\begin{array}{l}{\mathit{q}}_{ }(t+\tau )=\mathit{T}(t)·\mathit{\rho }(t)\\ {\mathit{q}}_d(t+\tau )=\mathit{T}(t)·{\mathit{\rho }}_d(t)\end{array}$$

(23)

According to Equation (23), the prediction error $\mathrm{e}(t+\mathit{\tau })$ can be re-expressed as:

$$\mathit{e}(t+\tau )=\mathit{T}(t)(\mathit{\rho }(t)-{\mathit{\rho }}_d(t))$$

(24)

The nominal dynamic model of the free-floating dual-arm space robot under ideal conditions can be expressed as follows:

$$\widehat{\mathit{M}}·\ddot{\mathit{q}}(t)+\widehat{\mathit{h}}=\mathit{u}$$

(25)

where $\widehat{\mathit{M}}$ and $\widehat{\mathit{h}}$ are the nominal inertia matrix and nominal bias force vector of the free-floating dual-arm space robot constructed in the second section of this paper under ideal conditions.

According to Equation (25), the vector $\mathit{\rho }(t)$ can be expressed as

$$\mathit{\rho }(t)=\left[\begin{array}{c}\mathit{q}(t)\\ \dot{\mathit{q}}(t)\\ \ddot{\mathit{q}}(t)\end{array}\right]=\left[\begin{array}{c}\mathit{q}(t)\\ \dot{\mathit{q}}(t)\\ -{\widehat{\mathit{M}}}^{-1}·\widehat{\mathrm{h}}\end{array}\right]+\left[\begin{array}{c}{0}_{9\times 1}\\ 0_{9\times 1}\\ {\widehat{\mathit{M}}}^{-1}·\mathit{u}\end{array}\right]$$

(26)

According to Equation (26), the cost function $J_{\mathit{cost}}$ in Equation (21) can be re-expressed as

$$J_{\cos t}=\frac{1}{2}{(\mathit{\rho }(t)-{\mathit{\rho }}_d(t))}^{\mathrm{T}}\mathit{\Pi }(\mathit{\rho }(t)-{\mathit{\rho }}_d(t))$$

(27)

The matrix $\mathit{\Pi }$ in the above formula is expressed as

$$\begin{array}{l}\mathit{\Pi }={\displaystyle {\int }_{T_1}^{T_2}\mathit{T}{(t)}^{\mathrm{T}}\mathit{T}(t)d\tau }\\ \hspace{1em}=\left[\begin{array}{l}{T}_r·{\mathit{{\rm I}}}_{9\times 9}\frac{T_r{ }^2}{2}·{\mathit{{\rm I}}}_{9\times 9}\frac{T_r{ }^3}{6}·{\mathit{{\rm I}}}_{9\times 9}\\ \frac{T_r{ }^2}{2}·{\mathit{{\rm I}}}_{9\times 9}\frac{T_r{ }^3}{3}·{\mathit{{\rm I}}}_{9\times 9}\frac{T_r{ }^4}{8}·{\mathit{{\rm I}}}_{9\times 9}\\ \frac{T_r{ }^3}{6}·{\mathit{{\rm I}}}_{9\times 9}\frac{T_r{ }^4}{8}·{\mathit{{\rm I}}}_{9\times 9}\frac{T_r{ }^5}{20}·{\mathit{{\rm I}}}_{9\times 9}\end{array}\right]\\ \end{array}$$

(28)

where the rolling period $T_r=T_2-T_1$.

The system control law ${\mathit{u}}_m$ of the predictive control unit can be solved according to $\frac{\partial J_{\mathit{cost}}}{\partial {\mathit{u}}_m}=0$:

$${\mathit{u}}_m=-\widehat{\mathit{M}}\left\{\begin{array}{l}\left[\frac{10}{3T_r{ }^2}·{\mathit{{\rm I}}}_{9\times 9}\frac{5}{2T_r}·{\mathit{{\rm I}}}_{9\times 9} {\mathit{{\rm I}}}_{9\times 9}\right]·\\ \backslash \left[\begin{array}{l}\mathit{q}(t)-{\mathit{q}}_d(t)\\ \dot{\mathit{q}}(t)-{\dot{\mathit{q}}}_d(t)\\ -{\widehat{\mathit{M}}}^{-1}·\widehat{\mathit{h}}-{\ddot{\mathit{q}}}_d(t)\end{array}\right]\end{array}\right\}$$

(29)

According to $\mathit{e}(t)=\mathit{q}(t)-{\mathit{q}}_d(t)$ and $\dot{\mathit{e}}(t)=\dot{\mathit{q}}(t)-{\dot{\mathit{q}}}_d(t)$, Equation (29) can be re-expressed as

$${\mathit{u}}_m=-\widehat{\mathit{M}}·[{\mathit{A}}_1·\mathit{e}(t)+{\mathit{A}}_2·\dot{\mathit{e}}(t)]+\widehat{\mathit{h}}+\widehat{\mathit{M}}·{\ddot{\mathit{q}}}_d(t)$$

(30)

where ${\mathit{A}}_1=\frac{10}{3T_r{ }^2}·{\mathit{{\rm I}}}_{9\times 9}$, ${\mathit{A}}_2=\frac{5}{2T_r}·{\mathit{{\rm I}}}_{9\times 9}$.

3.2. Design of an Improved NMPC Controller Based on Sliding Mode Variable Structure

During the in-orbit service of an actual space robot, the dynamic parameters will change due to factors such as fuel consumption, and the space robot will inevitably be affected by external disturbances. Therefore, considering the influence of parameter uncertainty and external disturbances, the practical dynamic model of the in-orbit service free-floating dual-arm space robot is

$$\mathit{M}·\ddot{\mathit{q}}(t)+\mathit{h}=\mathit{u}+\mathit{d}$$

(31)

where $\mathit{M}$ and $\mathit{h}$ are the actual inertia matrix and the actual bias force vector of the free-floating dual-arm space robot, respectively, and d is the external disturbance.

The sliding mode function is taken as

$$\mathit{s}=\dot{\mathit{e}}(t)+\mathit{P}·\mathit{e}(t)+\mathit{V}·{\displaystyle {\int }_0^t\mathit{e}(t)dt}$$

(32)

where $\mathit{e}(t)=\mathit{q}(t)-{\mathit{q}}_d(t)$, $\dot{\mathit{e}}(t)=\dot{\mathit{q}}(t)-{\dot{\mathit{q}}}_{\mathrm{d}}(t)$, $\mathit{P}=2\mathit{\Lambda }$, $\mathit{V}={\mathit{\Lambda }}^2$, $\mathit{\Lambda }$ is a positive definite diagonal matrix of size $9\times 9$, ${\lambda }_i$ is a diagonal element of $\mathit{\Lambda }$, and ${\mathrm{\lambda }}_i>0$.

The sliding mode hyperplane is

$$\dot{\mathit{s}}=\ddot{\mathit{e}}(t)+\mathit{P}·\dot{\mathit{e}}(t)+\mathit{V}·\mathit{e}(t)$$

(33)

According to $\ddot{\mathit{e}}(t)=\ddot{\mathit{q}}(t)-{\ddot{\mathit{q}}}_d(t)$, Equation (33) can be re-expressed as

$$\dot{\mathit{s}}=\ddot{\mathit{q}}(t)-[{\ddot{\mathit{q}}}_d(t)-\mathit{P}·\dot{\mathit{e}}(t)-\mathit{V}·\mathit{e}(t)]$$

(34)

The reference acceleration ${\ddot{\mathit{q}}}_{\mathit{r}}(t)$ is taken as

$${\ddot{\mathit{q}}}_{\mathit{r}}(t)={\ddot{\mathit{q}}}_d(t)-\mathit{P}·\dot{\mathit{e}}(t)-\mathit{V}·\mathit{e}(t)$$

(35)

Then, Equation (34) can be re-expressed as

$$\dot{\mathit{s}}=\ddot{\mathit{q}}(t)-{\ddot{\mathit{q}}}_{\mathit{r}}(t)$$

(36)

According to Equation (31), we can obtain

$$\ddot{\mathit{q}}(t)={\mathit{M}}^{-1}·\left(\mathit{u}+\mathit{d}-\mathit{h}\right)$$

(37)

According to Equation (37), Equation (36) can be re-expressed as

$$\dot{\mathit{s}}={\mathit{M}}^{-1}·[\mathit{u}+\mathit{d}-\mathit{h}-\mathit{M}·{\ddot{\mathit{q}}}_r(t)]$$

(38)

By substituting Equations (20), (30) and (35) into Equation (38), we can obtain

$$\dot{\mathit{s}}={\mathit{M}}^{-1}·({\mathit{u}}_{\mathrm{c}}+\Delta \mathit{u})$$

(39)

where $\Delta \mathit{u}$ is the uncertainty of the system.

According to Equation (39), we can obtain

$${\mathit{s}}^{\mathrm{T}}·\dot{\mathit{s}}={\mathit{s}}^{\mathrm{T}}·{\mathit{M}}^{-1}·({\mathit{u}}_c+\Delta \mathit{u})$$

(40)

Theorem 1.

Suppose there is a positive definite matrix $\mathit{B}\in {\mathcal{R}}^{\mathit{a}\times \mathit{a}}$ of $\mathit{a}\times \mathit{a}$ and there is a positive real number b > 0 such that $b·\mathit{I}>\mathit{B}$ holds, where I is the identity matrix of size $\mathit{a}\times \mathit{a}$. Suppose any vector $\mathit{y}\in {\mathcal{R}}^{\mathit{a}}$ and $‖\mathit{y}‖\le \rho$; then, for any vector $\mathit{x}\in {\mathcal{R}}^a$, the following inequality holds:

$${\mathit{x}}^{\mathrm{T}}·\mathit{B}·\mathit{y}\le b·\rho ·‖\mathit{x}‖$$

(41)

According to Theorem 1, we can obtain

$${\mathit{s}}^{\mathrm{T}}·{\mathit{M}}^{-1}·\Delta \mathit{u}\le \frac{1}{\stackrel{m}{\_}}·\rho ·‖\mathit{s}‖$$

(42)

where $\stackrel{m}{\_}$ is the infimum of M.

Because $‖\mathit{s}‖\le {\displaystyle \sum _{i=1}^9\left|s_i\right|}$, then according to Equations (40) and (42), we can obtain

$${\mathit{s}}^{\mathrm{T}}·\dot{\mathit{s}}\le \frac{1}{\stackrel{m}{\_}}·\rho ·{\displaystyle \sum _{i=1}^9\left|s_i\right|+{\mathit{s}}^{\mathrm{T}}·{\mathit{M}}^{-1}·{\mathit{u}}_c}$$

(43)

3.3. Analysis of Stability

The sliding mode boundary thickness is denoted as ${\sigma }_i$. If the control process of the closed-loop control system from the initial state to the sliding mode surface is expected to satisfy Lyapunov stability, then

$$\frac{1}{2}·\frac{d}{dt}\left({\mathit{s}}^{\mathrm{T}}·\mathit{s}\right)\le -{\displaystyle \sum _{i=1}^9\left({\eta }_i·\left(\left|s_i\right|-{\varphi }_i\right)\right)}<0$$

(44)

Because ${\mathit{s}}^{\mathrm{T}}·\dot{\mathit{s}}=\frac{1}{2}·\frac{d}{dt}\left({\mathit{s}}^{\mathrm{T}}·\mathit{s}\right)$, according to Equations (43) and (44), to ensure the stability of the system, it is necessary to select ${\mathit{u}}_c$ to meet the following conditions:

$$\frac{1}{\stackrel{m}{\_}}·\rho ·{\displaystyle \sum _{i=1}^9\left|s_i\right|}+{\mathit{s}}^{\mathrm{T}}·{\mathit{M}}^{-1}·{\mathit{u}}_c\le -{\displaystyle \sum _{i=1}^9\left({\eta }_i·\left|s_i\right|-{\eta }_i·{\varphi }_i\right)}<0$$

(45)

Equation (45) can be re-expressed as

$${\mathit{s}}^{\mathrm{T}}·{\mathit{M}}^{-1}·{\mathit{u}}_c\le -{\displaystyle \sum _{i=1}^9\left(\left(\frac{\rho }{\underset{\_}{m}}+{\eta }_i\right)·\left|s_i\right|-{\eta }_i·{\varphi }_i\right)}$$

(46)

According to Equation (46), the control law of the sliding mode variable structure control unit can be constructed as

$${\mathit{u}}_c=-\mathit{G}·\mathit{\Omega }(s_i)·\mathit{s}$$

(47)

where $\mathit{G}$ is a positive definite diagonal matrix of size $9\times 9$, $g_i\left(s_i\right)$ is a diagonal element of $\mathit{G}$ and $g_i\left(s_i\right)$ is a positive definite function; $\mathit{\Omega }$ is also a positive definite diagonal matrix of size $9\times 9$, and $1/\left|s_i\right|$ is a diagonal element of $\mathit{\Omega }$.

By substituting Equation (47) into Equation (46), we can obtain

$$\overline{m}·{\mathit{s}}^{\mathrm{T}}·{\mathit{M}}^{-1}·\mathit{G}\left(s_{\mathrm{i}}\right)·\mathit{\Omega }\left(s_{\mathrm{i}}\right)·\mathit{s}\ge \overline{m}·{\displaystyle \sum _{\mathrm{i}=1}^9\left(\left(\frac{\rho }{\underset{\_}{m}}+{\eta }_i\right)·\left|s_i\right|-{\eta }_i·{\varphi }_i\right)}$$

(48)

where $\overline{m}$ is the supremum of M.

Theorem 2.

Consider $\mathit{M}\in {\mathcal{R}}^{a\times a}$ to be a positive definite matrix of size $a\times a$ and $\mathit{K}\in {\mathcal{R}}^{a\times a}$to be a diagonal positive definite matrix of size $a\times a$. If there exists a positive real number $m>0$ and $m·\mathit{I}\ge \mathit{M}$, then for any vector $\mathit{x}\in {\mathcal{R}}^a$, the following equation holds:

$$m·{\mathit{x}}^t·{\mathit{M}}^{-1}·\mathit{K}·\mathit{x}\ge {\mathit{x}}^t·\mathit{K}·\mathit{x}$$

(49)

The proof of Theorem 2 is given in Equations (A16)–(A18) in Appendix C.

According to Theorem 2, we can obtain

$$\begin{array}{l}\overline{m}·{\mathit{s}}^{\mathrm{T}}·{\mathit{M}}^{-1}·\mathit{G}\left(s_{\mathrm{i}}\right)·\mathit{\Omega }\left(s_{\mathrm{i}}\right)·\mathit{s}\ge {\mathit{s}}^{\mathrm{T}}·\mathit{G}\left(s_{\mathrm{i}}\right)·\mathit{\Omega }\left(s_{\mathrm{i}}\right)·\mathit{s}\\ \begin{array}{cc}& \backslash ={\displaystyle \sum _{i=1}^9\left(g_i\left(s_i\right)·s_i·\mathrm{dsgn}\left(s_i\right)\right)}\ge 0\end{array}\end{array}$$

(50)

According to Equations (48) and (50), to ensure the stability of the system, the following equation needs to be satisfied:

$${\displaystyle \sum _{i=1}^9\left(g_i\left(s_i\right)·s_i·\mathrm{dsgn}\left(s_i\right)\right)}\ge \overline{m}·{\displaystyle \sum _{i=1}^9\left(\left(\frac{\rho }{\stackrel{m}{\_}}+{\eta }_i\right)·\left|s_i\right|-{\eta }_i·{\varphi }_i\right)}$$

(51)

The above Equation (51) can be re-expressed as

$$g_i\left(s_i\right)>\overline{m}·\left(\frac{\rho }{\stackrel{m}{\_}}+{\eta }_i\right)-\frac{\overline{m}·{\eta }_i·{\varphi }_i}{\left|s_i\right|}$$

(52)

The control law of the sliding mode variable structure control unit in Equation (47) is equivalent to

$$u_c^{[i]}=-g_i\left(s_i\right)·\frac{1}{\left|s_i\right|}·s_i=-g_i\left(s_i\right)·\mathrm{dsgn}\left(s_i\right)$$

(53)

Since the slope of the sign function dsgn() in Equation (53) is infinite, the control signal of the system has a serious jitter problem in the switching process. In this paper, the hyperbolic tangent function tanh() with a gentler slope is introduced to replace the sign function dsgn() to improve it. According to Equations (52) and (53), the improved $u_c^{[i]}$ can be expressed as

$$u_c^{[i]}=-g_i\left(s_i\right)·\tan \mathrm{h}\left(s_i\right)=-\overline{m}·\left(\frac{\rho }{\stackrel{m}{\_}}+{\eta }_i\right)·\tan \mathrm{h}\left(s_i\right)$$

(54)

According to Equation (54), we can obtain the control law ${\mathit{u}}_c$ of the sliding mode variable structure control unit of the system as

$${\mathit{u}}_c=-\mathit{G}·\tanh (\mathit{s})$$

(55)

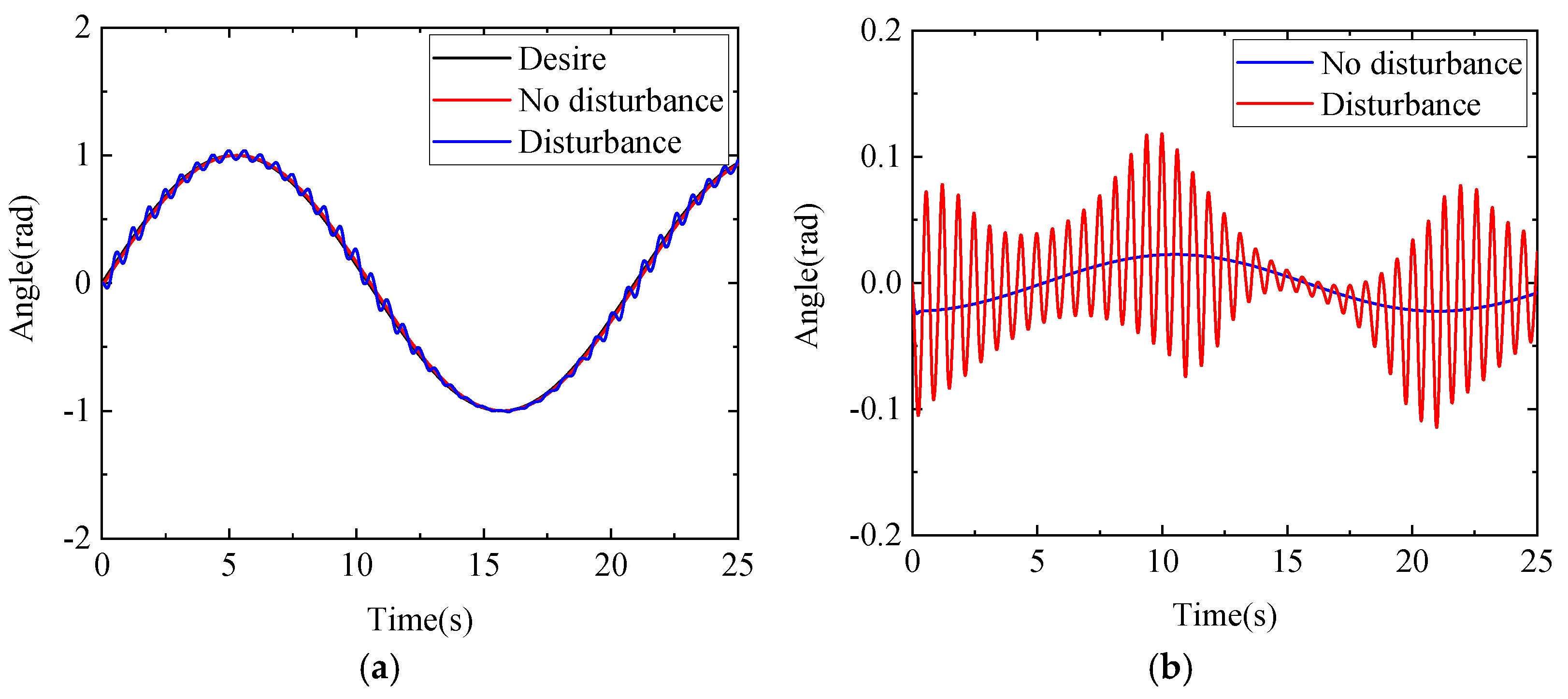
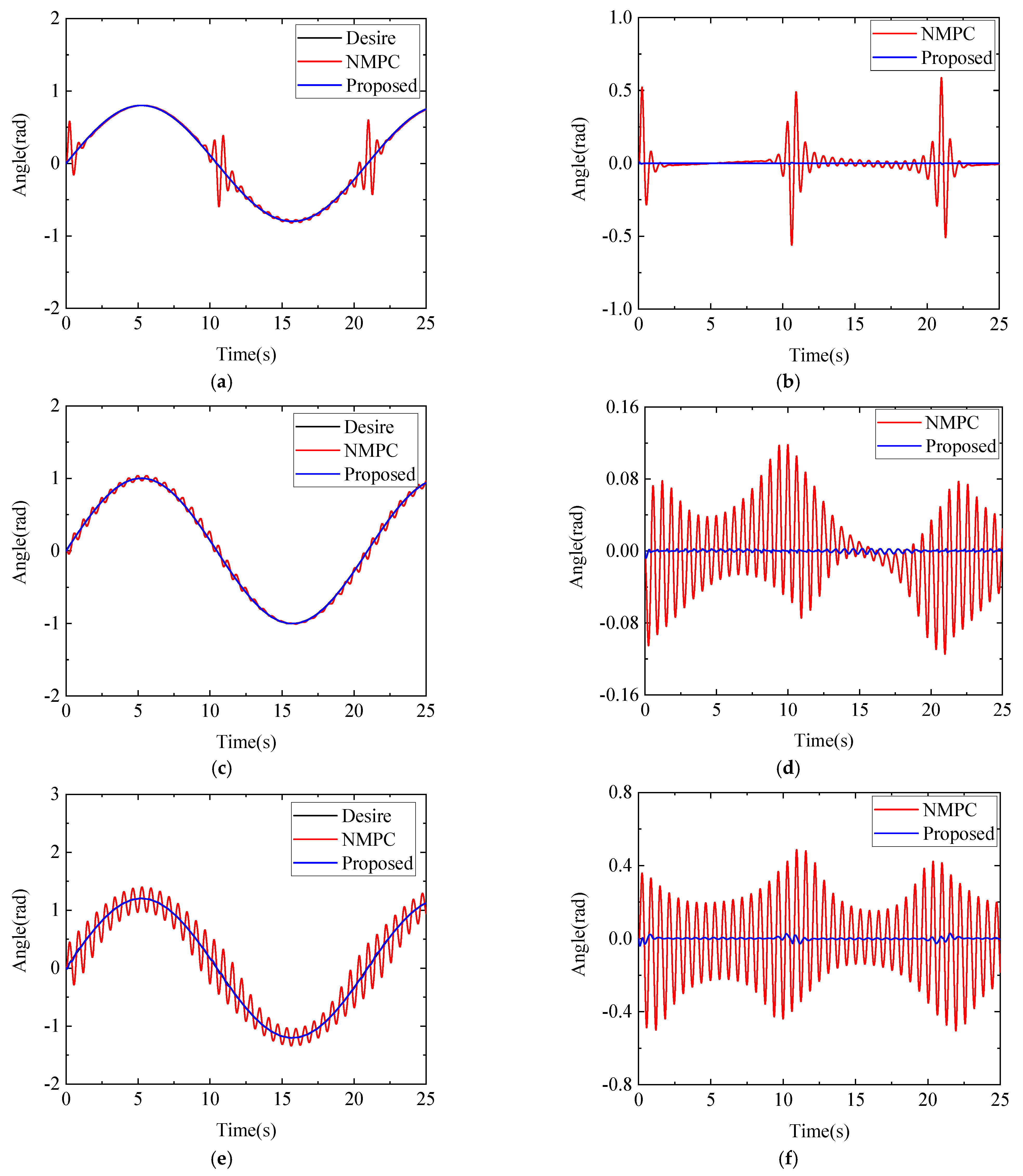
4. Simulation

In this section, an in-orbit service task as shown in Figure 5 is designed for a free-floating dual-arm space robot, in which one manipulator performs the capture operation on the target object and the other manipulator performs the maintenance operation on the captured object. The parameters of the free-floating dual-arm space robot are shown in

Table 1. Initial parameters of the free-floating dual-arm space robot.

Parameter	Symbol	Value
Axis-Invariant	${}^i\mathit{n}_1$ ${}^1\mathit{n}_2$, ${}^3\mathit{n}_4$, ${}^3\mathit{n}_7$ ${}^2\mathit{n}_3$, ${}^4\mathit{n}_5$, ${}^5\mathit{n}_6$, ${}^7\mathit{n}_8$, ${}^8\mathit{n}_9$	[1 0 0]T [0 1 0]T [0 0 1]T
Initial linear position (m)	${}_0{}^1\mathit{r}_2$; ${}_0{}^2\mathit{r}_3$; ${}_0{}^3\mathit{r}_4$; ${}_0{}^4\mathit{r}_5$; ${}_0{}^5\mathit{r}_6$; ${}_0{}^3\mathit{r}_7$; ${}_0{}^7\mathit{r}_8$; ${}_0{}^8\mathit{r}_9$	[0 0 0]T; [0 0 0]T; [−0.5 0.5 0]T; [0 0.2 0]T; [0 0.3 0]T; [0.5 0.5 0]T; [0 0.2 0]T; [0 0.3 0]T
Center position of the link mass (m)	${}^1\mathit{r}_{1I}$; ${}^2\mathit{r}_{2I}$; ${}^3\mathit{r}_{3I}$; ${}^4\mathit{r}_{4I}$; ${}^5\mathit{r}_{5I}$; ${}^6\mathit{r}_{6I}$; ${}^7\mathit{r}_{7I}$; ${}^8\mathit{r}_{8I}$; ${}^9\mathit{r}_{9I}$	[0 0 0]T; [0 0 0]T; [0 0 0.1]T; [0 0.1 0]T; [0 0.15 0]T; [0 0.1 0]T; [0 0.1 0]T; [0 0.15 0]T; [0 0.1 0]T
Link mass (kg)	$m_1$; ${\mathrm{m}}_2$; ${\mathrm{m}}_3$; ${\mathrm{m}}_4$; ${\mathrm{m}}_5$; ${\mathrm{m}}_6$; ${\mathrm{m}}_7$; ${\mathrm{m}}_8$; ${\mathrm{m}}_9$	0; 0; 300; 30; 10; 5; 30; 10; 5
Link MOI (kg·m2)	${}^{1I}\mathit{J}_{1I}$; ${}^{2I}\mathit{J}_{2I}$; ${}^{3I}\mathit{J}_{3I}$ ${}^{4I}\mathit{J}_{4I}$; ${}^{5I}\mathit{J}_{5I}$; ${}^{6I}\mathit{J}_{6I}$; ${}^{7I}\mathit{J}_{7I}$; ${}^{8I}\mathit{J}_{8I}$; ${}^{9I}\mathit{J}_{9I}$	diag(0,0,0); diag(0,0,0); diag(0.1,0.1,0.002); diag(0.03,0.006,0.03); diag(0.002,0.002,0.001); diag(0.001,0.001,0.0002); diag(0.03,0.006,0.03); diag(0.002,0.002,0.001); diag(0.001,0.001,0.0002)
Step size (s)	$\Delta t$	0.001
Steps	i	25,000
Rolling period (s)	$T_r$	0.1
Diagonal elements of $\mathit{\Lambda }$	${\lambda }_1$; ${\lambda }_2$; ${\lambda }_3$; ${\lambda }_4$; ${\lambda }_5$; ${\lambda }_6$; ${\lambda }_7$; ${\lambda }_8$; ${\lambda }_9$	20; 10; 200; 45; 20; 10; 45; 20; 10
Dynamic parameter uncertainty	$\mathit{M}$; $\mathit{h}$	1.5 $\widehat{\mathit{M}}$; 1.5 $\widehat{\mathit{h}}$
External disturbance	d1; d2; d3; d4; d5; d6; d7; d8; d9	10sin(0.01i); 40sin(0.01i); 20sin(0.01i); 2sin(0.01i); 2sin(0.01i); 2sin(0.01i); 2sin(0.01i); 2sin(0.01i); 2sin(0.01i)

.

The space robot will inevitably be affected by uncertain dynamic parameters and external disturbance when it performs the in-orbit service task. First, we use the traditional NMPC method to simulate and contrast the trajectory tracking of the space robot under the influence of dynamic parameter uncertainty and external disturbance. The relevant parameter settings of the dynamic parameter uncertainty and external disturbance of the space robot during simulation can be found in Table 1. Taking joint 5 as an example, the traditional NMPC method is used to simulate and compare the actual situation of the free-floating dual-arm space robot affected by parameter uncertainty and external disturbance with the ideal situation that is not affected. The results are shown in Figure 6. It can be seen from Figure 6 that the traditional NMPC method has a good control effect on the robot under ideal conditions, but the control effect of the robot under actual conditions with disturbances needs to be improved.

To show the advantages of the proposed improved NMPC method, we next build two controllers based on the traditional NMPC method and the proposed improved NMPC method, respectively. The relevant parameter settings of these two controllers can be found in Table 1. We use these two controllers to simulate the trajectory tracking of the two arms of the free-floating dual-arm space robot under the influence of uncertain dynamic parameters and external disturbances. Figure 7 shows the tracking comparison of each joint of the left arm based on these two controllers to the desired trajectory. As shown in Figure 7, compared with the traditional NMPC controller, the proposed improved NMPC controller is more accurate in tracking the desired trajectory, and can keep the error within the target range, showing an excellent control effect.

Unlike the ground fixed manipulator, the attitude of the base of the free-floating dual-arm space robot needs to be controlled stably; otherwise, it will seriously affect the operation accuracy of the two arms, resulting in the failure of the operation task. Therefore, we finally use these two controllers to simulate the stable control of the base attitude of the free-floating dual-arm space robot. In order to further demonstrate the advantages of the designed improved NMPC controller, we increase the amplitude of the external disturbance of the robot base attitude simulation experiment to five times the original to increase the uncertainty of the system to verify the performance of the proposed controller. Figure 8 shows the error comparison of the base attitude stabilization control of the free-floating dual-arm space robot based on these two controllers. It can be seen from Figure 8 that compared with the traditional NMPC controller, the designed improved controller obtains a more stable base attitude. The proposed controller shows excellent stability in conditions of strong disturbance.

5. Discussion

This section will discuss the proposed method from two perspectives: dynamic modeling and control.

• Dynamic modeling:

  (1)

  The free-floating dual-arm space robot studied in this paper is a complex multibody system with nine DOF. The modeling efficiency of the traditional explicit multibody system dynamic modeling method needs to be improved. For example, when the pseudo inertia matrix method [19,20] is used, the pseudo inertia matrix, the homogeneous transformation matrix, and other intermediate variables need to be calculated; when the generalized momentum method [21] is used, although the computational efficiency of the inertia matrix is higher than that of the pseudo inertia matrix method, it is also necessary to derive and calculate the intermediate variables such as the Jacobian matrix, and the generalized momentum method cannot explicitly establish the bias force vector. The space robot modeling method in this paper avoids the definition and operation of intermediate variables, and its modeling efficiency is higher than the traditional explicit modeling method. The highest computational complexity is obtained when all joint types of the robot are considered as rotational joints.

  Table 2. Comparison of computational complexity.

  Numbers		Pseudo-Inertia Matrix Method	Generalized Momentum Method	Explicit Canonical Method
  Inertia matrix	Multiplication	21n3 + 63n2 + 66n	7n3 + 12n2 + 3n	3.5n3 + 16n2 + 12.5n
  	Addition	18n3 + 49.5n2 + 43.5n	5n3 + 10n2 + 2n	3.5n3 + 10n2 + 6.5n
  Bias force vector	Multiplication	91n2 + 157n	-	16.5n2 + 43.5n
  	Addition	67n2 + 105n	-	7.5n2 + 27.5n

  shows the comparison of the computational complexity of the inertia matrix M and the bias force vector h in the calculation of an n-DOF robot with full rotational joints when the three different explicit dynamics modeling methods are adopted. Table 2 shows that the computational complexity of the explicit canonical method in this paper is significantly lower than those of the other two methods.

  (2)

  Due to the floating characteristics of the base of the free-floating space robot, it is difficult to combine the traditional explicit dynamic modeling method with DEM, because it requires tedious and complex analysis processes, such as the definition and operation of complex intermediate variables. When combined with DEM, our explicit canonical dynamic modeling method can avoid the tedious and complex analysis of intermediate variables.

  (3)

  Due to the inconvenient modeling method, most of the literature in the study of space robot dynamics and control only simulates the plane situation of the two-DOF manipulator, which makes it difficult to reflect the real working state of the complex multi-DOF space robot. When using the proposed explicit dynamic modeling method, it is easy to establish a dynamic model for complex multi-DOF space robot for control research.

• Control:

  (1)

  Compared with other traditional control methods, research on the NMPC method applied to space robots is not extensive enough. Recently, Tomasz Rybus [11,44] explored the possibility of using the NMPC method to control manipulators mounted on free-floating space robots. However, Tomasz Rybus [11,44] only considered the trajectory tracking control of the end manipulator of the free-floating space robot, and did not consider the stable control of the attitude of the base of the free-floating space robot. In addition, Tomasz Rybus [11,44] only carried out dynamic modeling and simulation verification of the NMPC method for a two-DOF planar manipulator. This paper not only considers the trajectory tracking control of the end manipulator of the free-floating space robot, but also considers the stable control of the base attitude of the free-floating space robot. In addition, the dynamic modeling and control simulation of the free-floating dual-arm space robot with nine DOF are carried out in this paper.

  (2)

  The free-floating space robot has high requirements on the accuracy of trajectory tracking and the stability of the base attitude. The traditional NMPC method has difficulty meeting these requirements. This paper innovatively introduces the idea of sliding mode variable structure to improve the traditional NMPC method. The proposed improved NMPC method has better robustness and can better meet the requirements of trajectory tracking accuracy and base attitude stability for free-floating space robots serving in orbit.

  (3)

  Inspired by the literature [15], the control system in this paper consists of a combined controller for the base and the arms, rather than two separate controllers, which can reduce the risk of failure.

6. Conclusions

Based on a new dynamic modeling theory, a novel dynamic control method is proposed for the free-floating dual-arm space robot. This method can not only realize the tracking of the desired trajectory by the two arms of the space robot, but also realize the stable control of the space robot base. The in-orbit service mission of space debris capture was designed and simulated. The main contributions of this paper are as follows:

(1)

Based on a new explicit multi-rigid-body dynamic modeling method and employing the concept of DEM, the dynamic model of a free-floating dual-arm space robot is established. The modeling process of the model is simple and standardized, which is convenient for computer programming.

(2)

After introducing the control idea of the sliding mode variable structure into the traditional NMPC method, a novel NMPC controller is designed, which effectively solves the problem of tracking the desired trajectory and stabilizing the base attitude of the free-floating dual-arm space robot under unknown model uncertainty and external disturbance.

This article focuses on the challenging problem of dynamic modeling and control of free-floating space robots. The proposed new dynamic modeling and control method can be effectively applied to the on-orbit service tasks of free-floating dual-arm space robots, providing new insights into the challenging problems regarding the dynamics and control of complex multi-DOF space robots. In order to fully verify the method proposed in this paper, a prototype platform of a free-floating dual-arm space robot will be built in the future, and the development and test of hardware system will be carried out. At the same time, in the future, factors such as link flexibility, joint friction and contact collision will be considered to study the dynamic modeling, control and planning of multi-arm space robots.