Numerical Simulation of a Submerged Floating Tunnel: Validation and Analysis
Abstract
:1. Introduction
2. CEL Method for One- and Two-Way Fluid–Structure Coupling Validation
2.1. CEL Method
- (1)
- Partitioning Eulerian regions: Divide the computational domain into several small Eulerian regions.
- (2)
- Constructing Lagrangian functions: For each physical quantity within each Eulerian region, construct a corresponding Lagrangian function.
- (3)
- Solving Euler equations: For each physical quantity within each Eulerian region, use the Euler method to solve its corresponding Euler equation.
- (4)
- Interpolation transfer: Use interpolation methods to transfer physical quantities within Eulerian regions to adjacent Eulerian regions, forming a complete Lagrangian description of the computational domain.
- (5)
- Time stepping: Repeat steps 3 and 4 to perform time-stepping calculations.
2.1.1. Fluid Motion Equations (Eulerian Equations)
2.1.2. Solid Motion Equations (Lagrangian Equations)
2.1.3. Coupling
2.2. Numerical Simulation of Circular Cylinder Flow
2.3. Verification of Round-Rod Dragging Results
3. Numerical Study of Shaking Table Model for Scaled-Down SFT
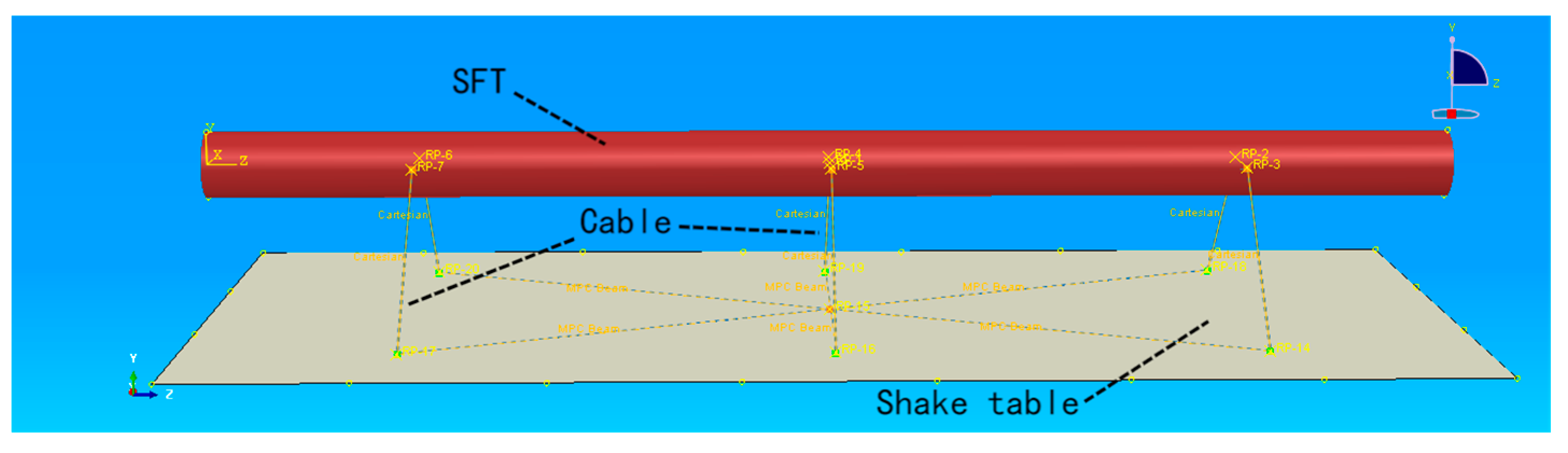
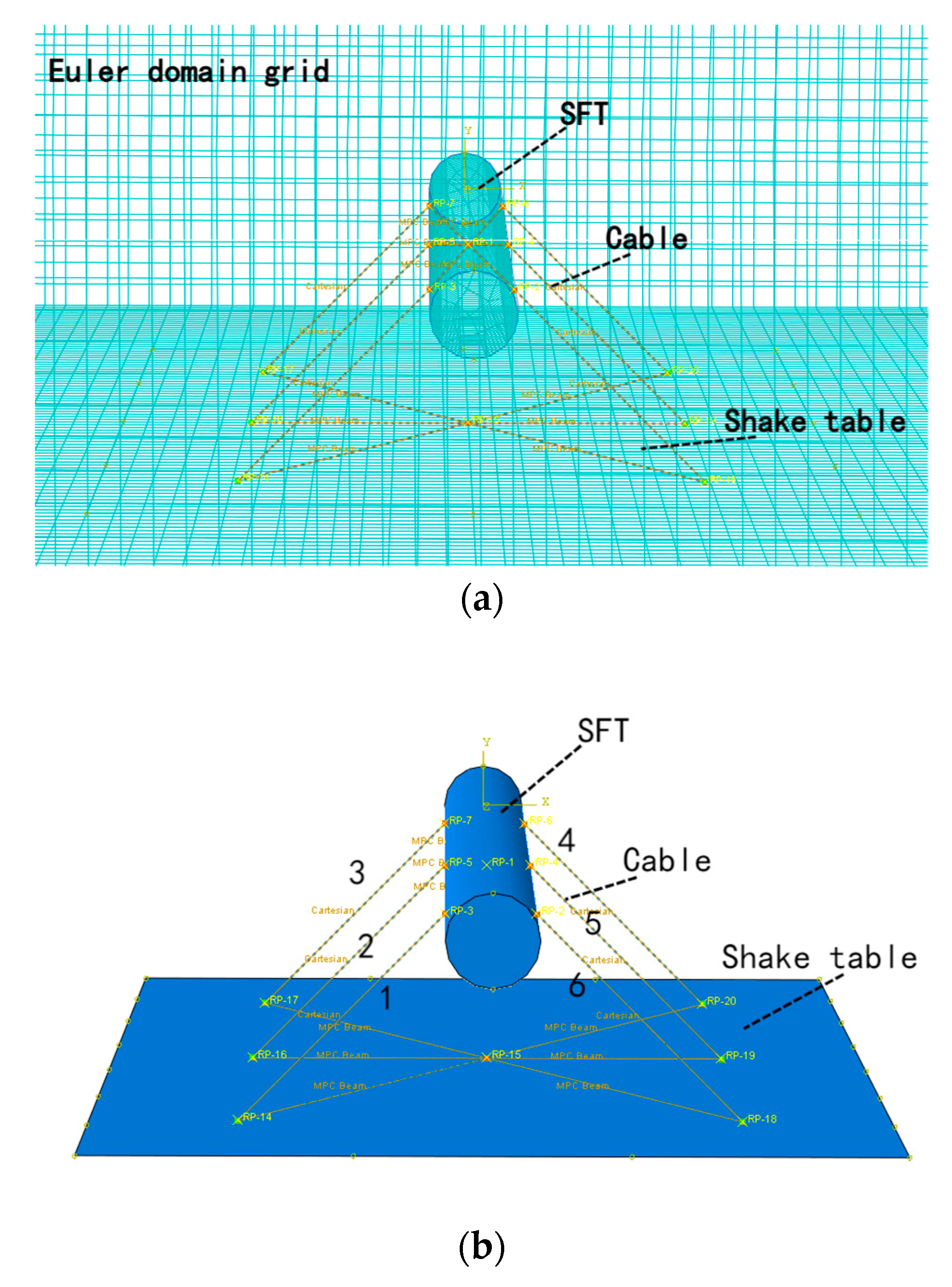
3.1. Experimental Overview
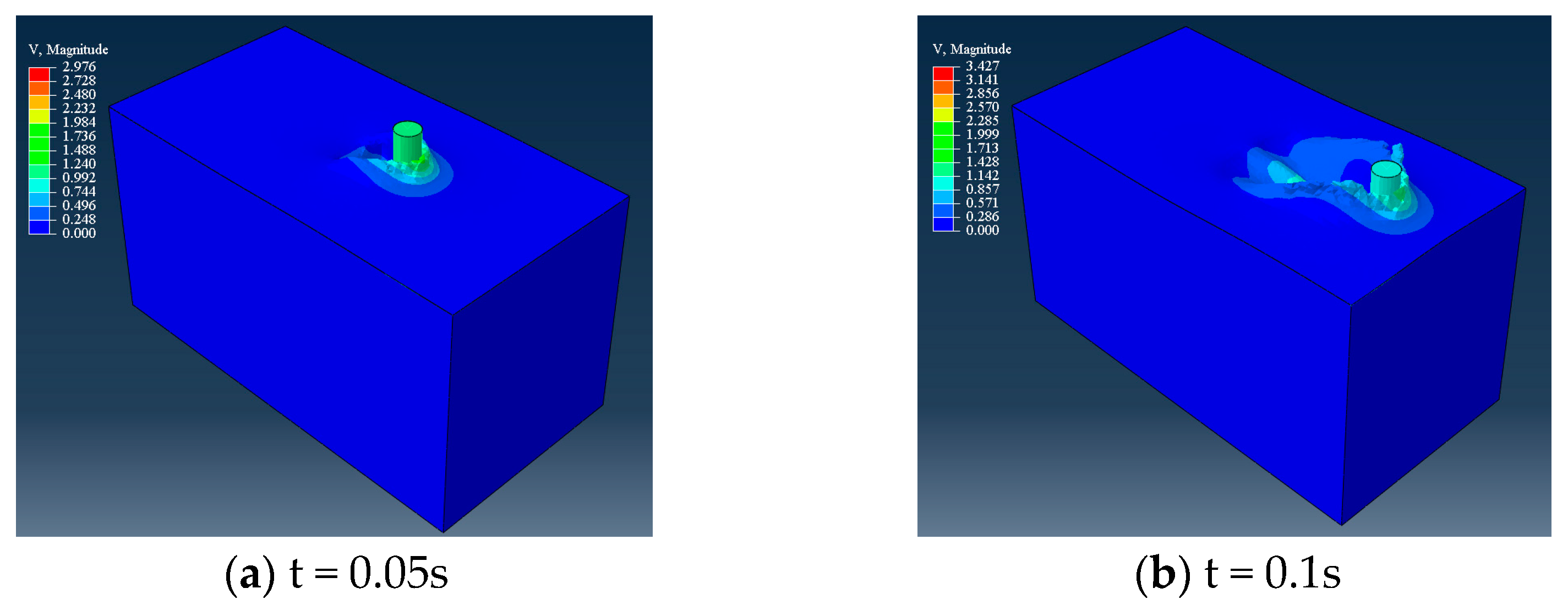
3.2. Numerical Modelling
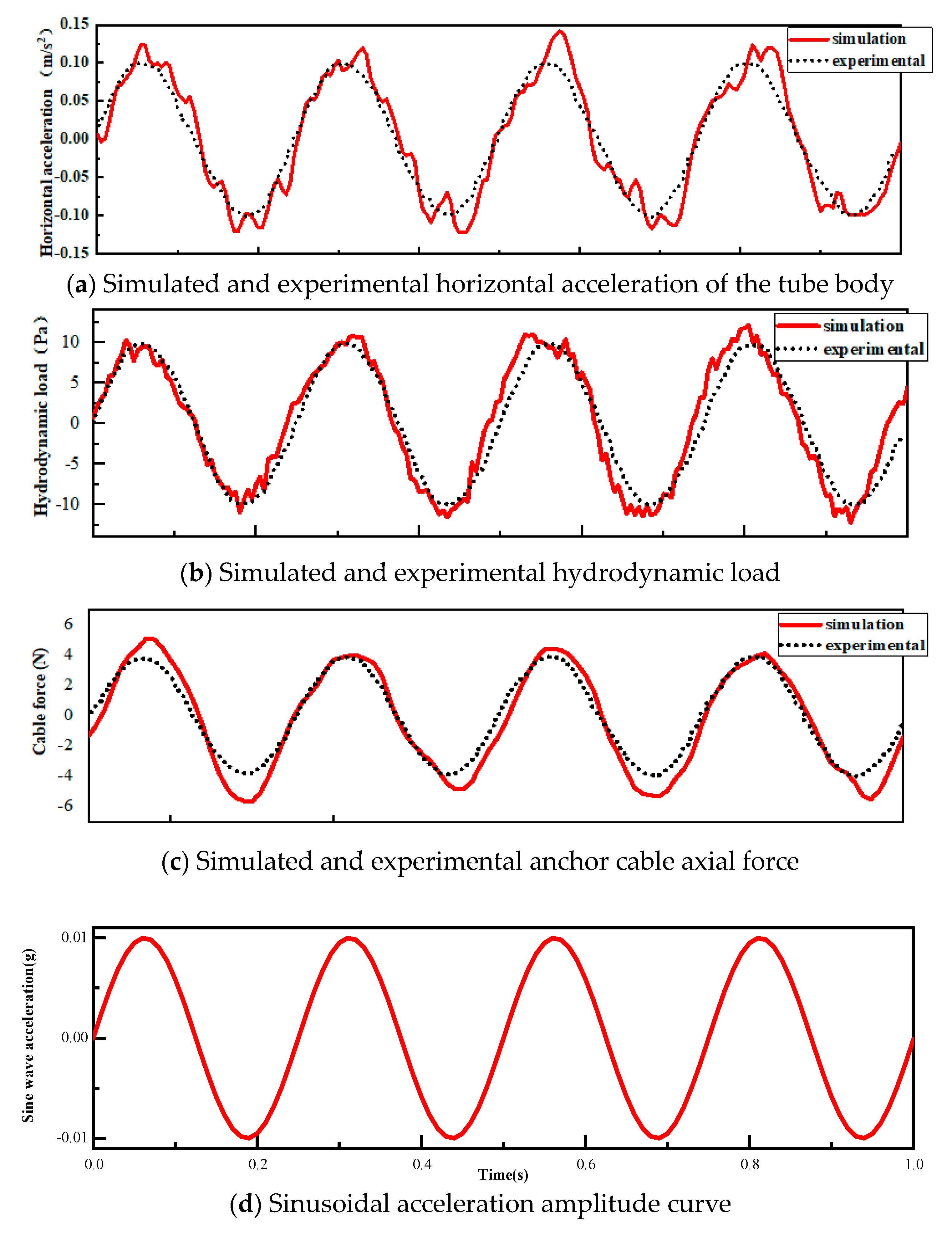
3.3. Results Analysis
4. SFT Dynamic Frequency Response Analysis
5. Conclusions
- (1)
- The verification of the CEL method in two hypothetical cylindrical flow calculations and a comparison of the results with those of experimental model SFT tests demonstrated that the CEL method is capable of effectively simulating the seismic dynamic response of SFTs.
- (2)
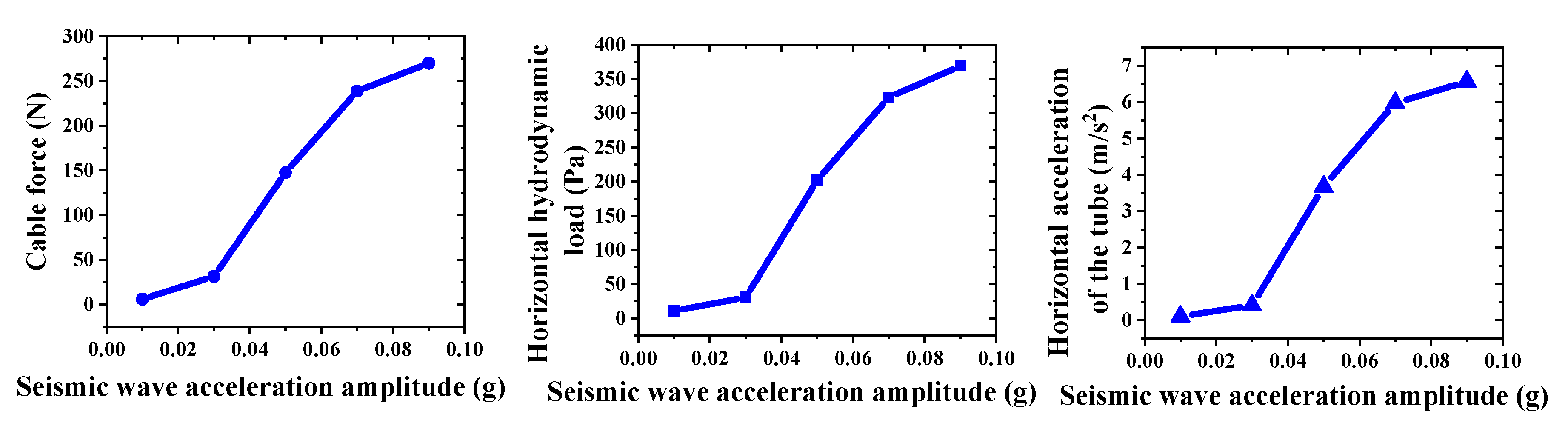
- The natural frequency of an SFT prototype in a water environment was found to be 1.5 Hz. Thus, when conducting the seismic design of the SFT, the response of the structure under earthquake action should be evaluated. In the analysis, it is necessary to consider the matching relationship between the natural frequency of the structure and the frequency of the earthquake wave motion in order to determine the resonance condition of the structure and its corresponding seismic response characteristics.
- (3)
- The seismic warning threshold for the prototype SFT was 0.03× g. Thus, if an SFT based on this prototype is applied in a real-life setting, an earthquake early warning alarm would need to be issued once the ground motion acceleration reached this level. This would ensure that the anchor cable had a sufficient level of safety redundancy, and it would allow the operating company ample time to implement earthquake response measures.
- (4)
- Under seismic conditions, the peak acceleration of the prototype SFT tube body significantly increased, leading to amplification effects. Therefore, in the seismic design of SFTs, the interaction between the tube body, anchor cable, and seabed should be the foremost consideration.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- China Association for Science and Technology publishes 60 major scientific problems and engineering and technical problems in 12 fields. J. China Railw. Soc. 2018, 40, 24, 53, 87, 135.
- Wu, Z.; Wang, D.; Ke, W. Experimental investigation for the dynamic behavior of submerged floating tunnel subjected to the combined action of earthquake, wave, and current. Ocean Eng. 2021, 239, 109911. [Google Scholar] [CrossRef]
- Li, H.; Cheng, X.; Yu, H.; Fu, D. Seismic response simulation of submerged floating tunnel with tension legs: A case study on the Qiongzhou Strait Crossing Tunnel Project. Mod. Tunnel. Technol. 2022, 59, 146–154. [Google Scholar]
- Xiang, Y.; Yang, Y.; Bai, B. Methods for Analyzing Seismic Response of Submerged Floating Tunnel and Research Development. In Proceedings of the 14th International Conference on Vibration Problems, Crete, Greece, 1–4 September 2019; Springer Nature: Singapore, 2019. [Google Scholar]
- Wu, Z.; Ni, P.; Mei, G. Vibration response of cable for submerged floating tunnel under simultaneous hydrodynamic force and earthquake excitations. Adv. Struct. Eng. 2018, 21, 1761–1773. [Google Scholar] [CrossRef]
- Fogazzi, P.; Perotti, F. The dynamic response of seabed anchored floating tunnels under seismic excitation. Earthq. Eng. Struct. Dyn. 2000, 29, 273–295. [Google Scholar] [CrossRef]
- Martinelli, L.; Barbella, G.; Feriani, A. Modeling of Qiandao Lake submerged floating tunnel subject to multi-support seismic input. Procedia Eng. 2010, 4, 311–318. [Google Scholar] [CrossRef]
- Martinelli, L.; Barbella, G.; Feriani, A. A numerical procedure for simulating the muti-support seismic response of SFT anchored by cables. Eng. Struct. 2011, 33, 2850–2860. [Google Scholar] [CrossRef]
- Brancaleoni, F.; Castellani, A.; D’Asdia, P. The response of submerged tunnels to their environment. Eng. Struct. 1989, 11, 47–56. [Google Scholar] [CrossRef]
- Martire, G.; Faggianoa, B.; Mazzolani, F.M.; Zollo, A.; Stabile, T. Seismic analysis of an SFT solution for the Messina Strait crossing. Procedia Eng. 2010, 4, 303–310. [Google Scholar] [CrossRef]
- Xiao, J.; Huang, G. Transverse earthquake response and design analysis of SFT with various shore connections. Procedia Eng. 2010, 4, 233–242. [Google Scholar] [CrossRef]
- Chen, W.; Huang, G. Seismic wave passage effect on the dynamic response of SFT. Procedia Eng. 2010, 4, 217–224. [Google Scholar] [CrossRef]
- Chao, C.F.; Xiang, Y.Q.; Lin, J.P. Patterns of cable VIV suppression based on the fluid-structure interaction. Mech. Eng. 2015, 37, 725–730. (In Chinese) [Google Scholar]
- Chao, C.F.; Xiang, Y.Q.; Yang, C. Experiments on dynamic fluid-structure coupled responses of anchor cables of submerged floating tunnel. J. Vib. Shock 2016, 3, 158–163. (In Chinese) [Google Scholar]
- Sun, S.; Chen, J. Study on hydrodynamic pressure of SFT under earthquake-SV wave. J. Disast. Prev. Mitig. Eng. 2006, 4, 425–430. (In Chinese) [Google Scholar]
- Sun, S.; Chen, J. Study on dynamic water pressure of undersea anchorage SFT-P wave. J. Harbin Inst. Technol. 2008, 8, 1292–1296. (In Chinese) [Google Scholar]
- Chen, J.; Li, J.; Sun, S. Experimental and numerical analysis of submerged floating tunnel. J. Cent. South Univ. 2012, 19, 2949–2957. [Google Scholar] [CrossRef]
- Sun, S.; Chen, J. Dynamic Response Analysis of SFT. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2008. (In Chinese). [Google Scholar]
- Zhang, H.; Yang, Z. A global review for the hydrodynamic response investigation method of submerged foating tunnels. Ocean Eng. 2021, 225, 108825. [Google Scholar] [CrossRef]
- Zhu, Y. Wave Mechanics in Ocean Engineering; Tianjin University Press: Tianjin, China, 1991. [Google Scholar]
- Matsui, T.; San, K.C. Finite element slope stability analysis by shear strength reduction technique. Soils Found. 1992, 32, 59–70. [Google Scholar] [CrossRef]
- Shiau, J.S.; Lyamin, A.V.; Sloan, S.W. Bearing capacity of a sand layer on clay by finite element limit analysis. Can. Geotech. J. 2003, 40, 900–915. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Noh, W.F. CEL: A Time-Dependent Two Space-Dimensional, Coupled Eulerian-Lagrangian Code; Lawrence Radiation Laboratory: Livermore, CA, USA, 1964. [Google Scholar]
- Hajivalie, F.; Yeganeh-Bakhtiary, A.; Houshanghi, H.; Gotoh, H. Euler–Lagrange model for scour in front of vertical breakwater. Appl. Ocean Res. 2012, 34, 96–106. [Google Scholar] [CrossRef]
- Mittal, V.; Chakraborty, T.; Matsagar, V. Dynamic analysis of liquid storage tank under blast using coupled Euler–Lagrange formulation. Thin-Walled Struct. 2014, 84, 91–111. [Google Scholar] [CrossRef]
- Cheng, Z.; Chauchat, J.; Hsu, T.J.; Calantoni, J. Eddy interaction model for turbulent suspension in Reynolds-averaged Euler–Lagrange simulations of steady sheet flow. Adv. Water Resour. 2017, 111, 435–451. [Google Scholar] [CrossRef]
- ABAQUS, Version 2016. EF Documentation. Dassault Systèmes: Vélizy-Villacoublay, France, 2016.
- Roshko, A. On the Development of Turbulent Wakes from Vortex Streets; NASA: Washington, DC, USA, 1953. [Google Scholar]
- Taneda, S. Downstream development of the wakes behind cylinders. J. Phys. Soc. Jpn. 1959, 14, 843–848. [Google Scholar] [CrossRef]
- Sarpkaya, T. Vortex-induced oscillations: A selective review. J. Appl. Mech. 1979, 46, 241–258. [Google Scholar] [CrossRef]
- Xiao, S. Research on Constitutive Model and Numerical Simulation of Sand Rheology under Low Effective Stress; Tsinghua University: Beijing, China, 2020. (In Chinese) [Google Scholar]
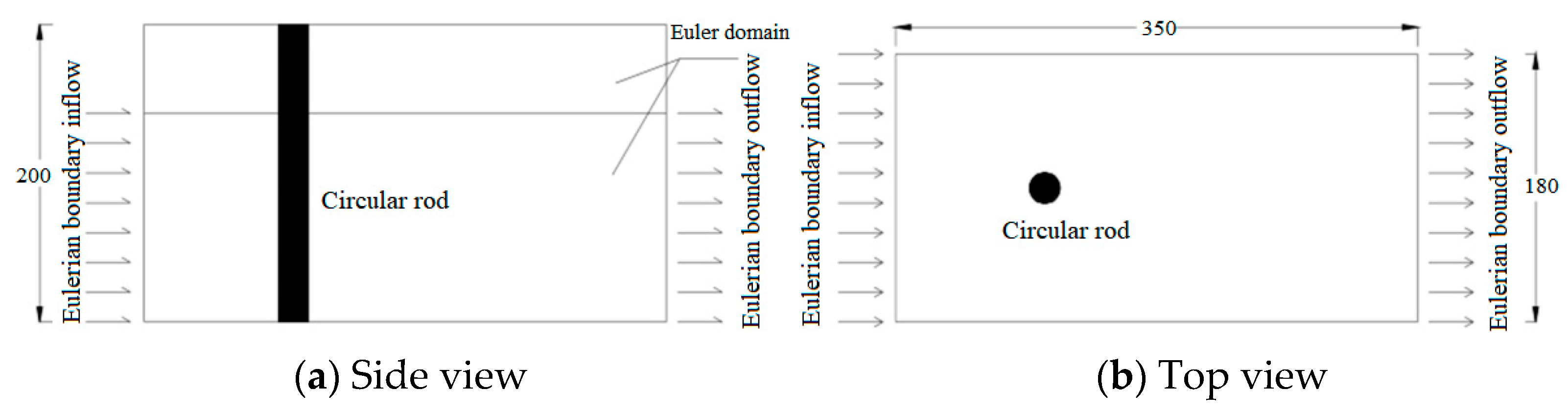
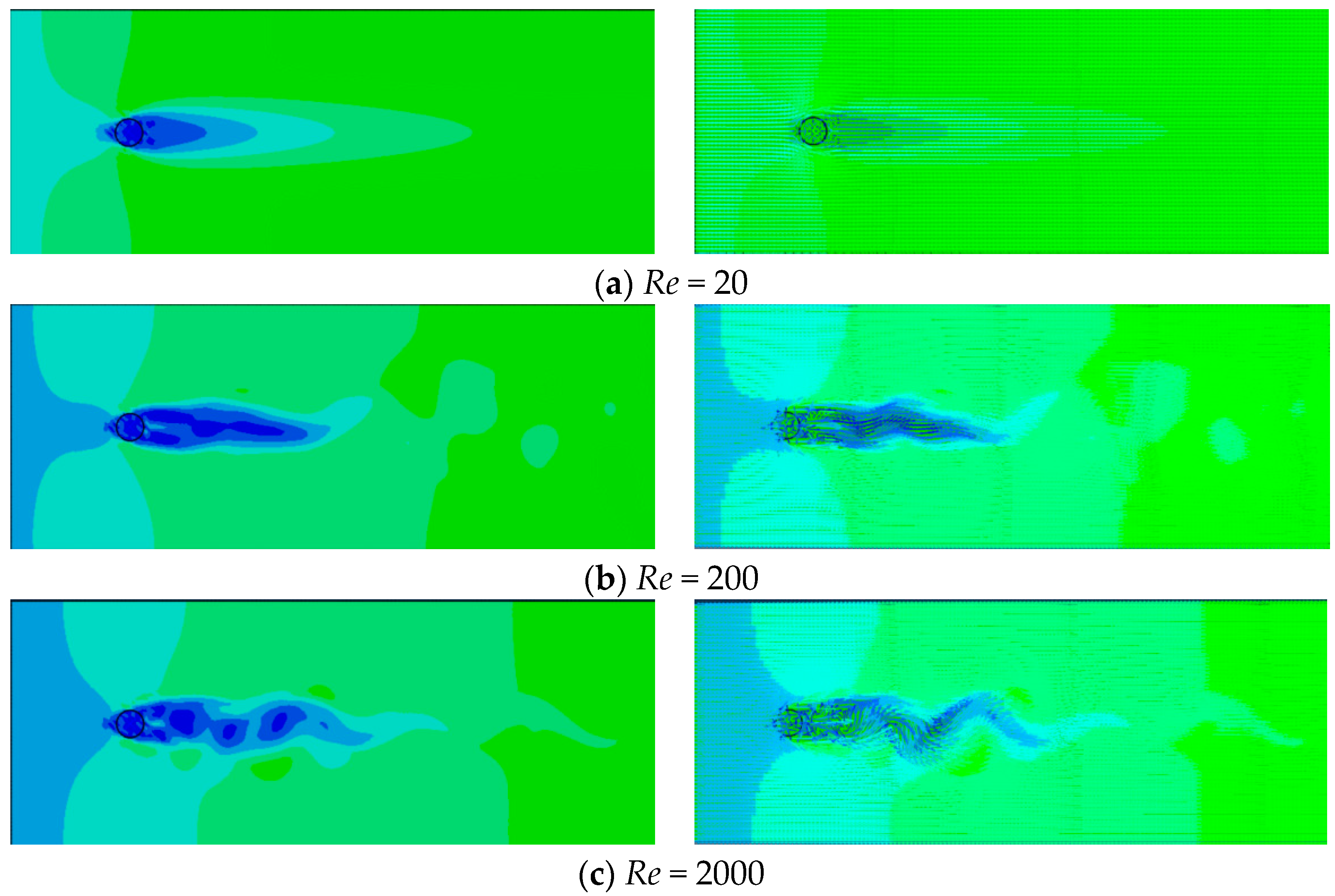
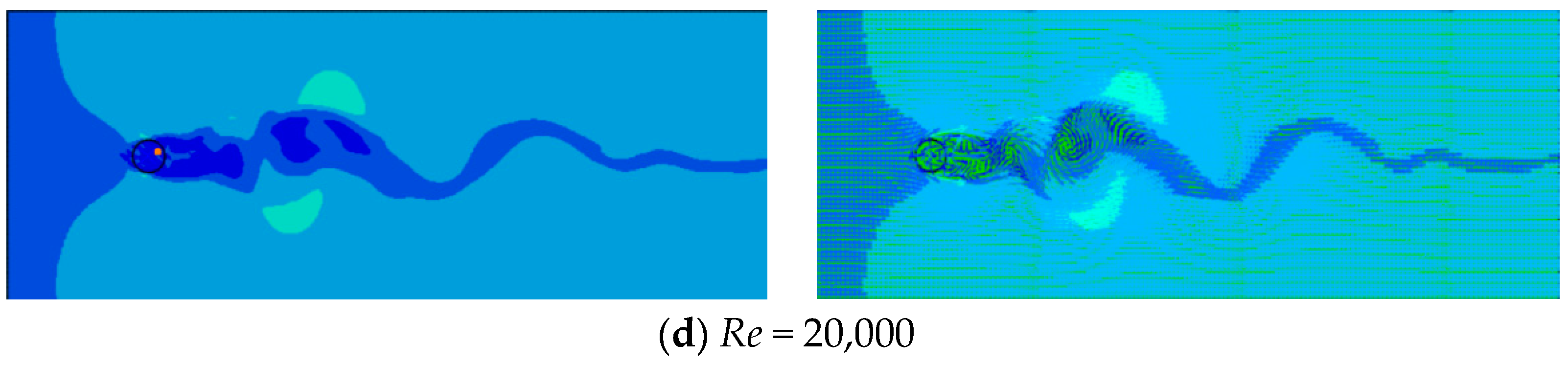
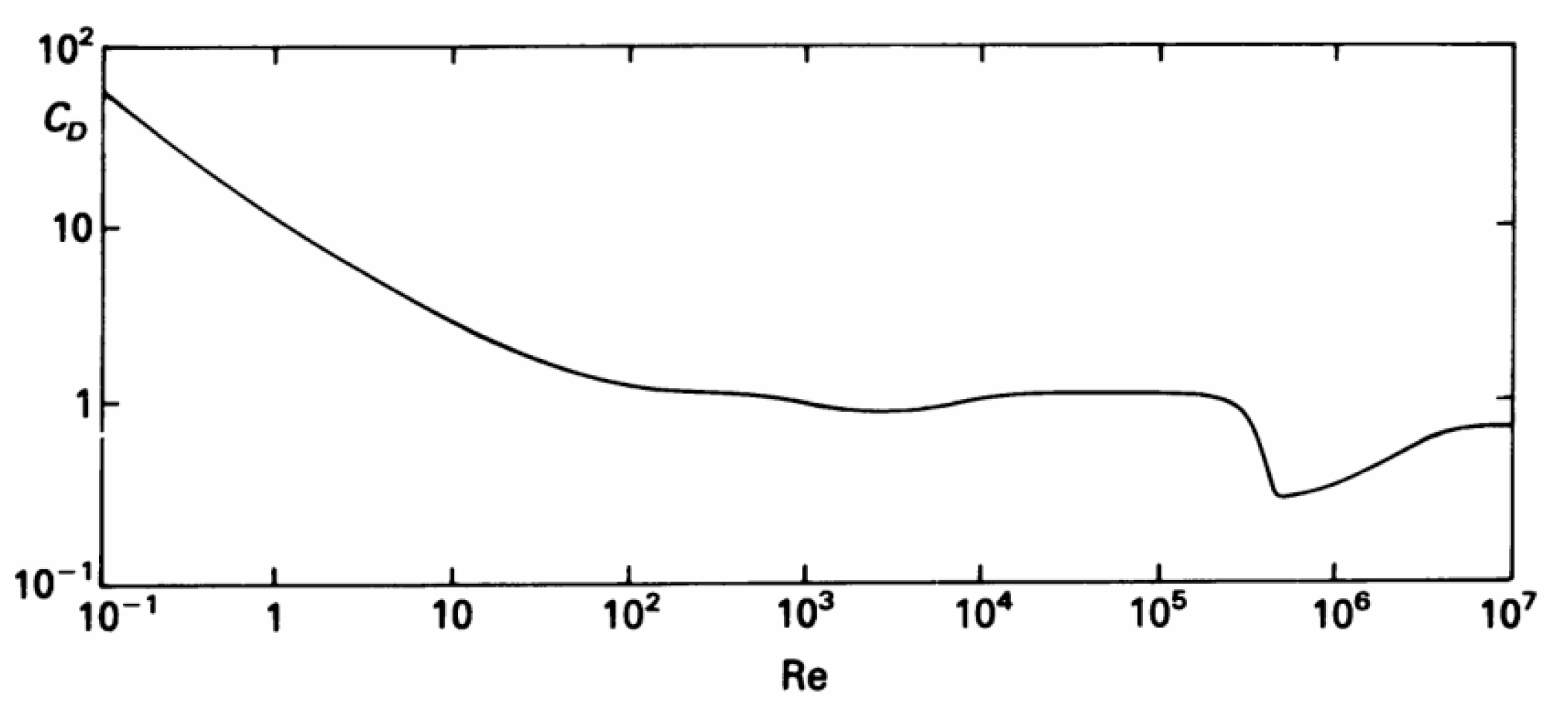

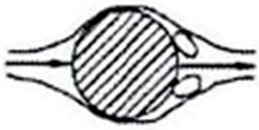 | 15 < Re < 40: A group of small, fixed vortices appeared after a cylinder |
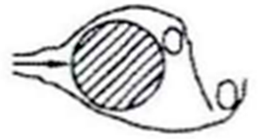 | 150 < Re < 300,000 Periodic alternating turbulent vortex discharge occurred |
| V (m/s) | CD | Re | Drag Force: Empirical Value (N) | Drag Force: Simulated Value (N) | Relative Error % |
|---|---|---|---|---|---|
| 0.5 | 1.08 | 10,000 | 2.7 | 2.9 | 7.4 |
| 1 | 1.12 | 20,000 | 11.2 | 10.5 | 6.3 |
| 2 | 1.13 | 40,000 | 45.2 | 44.4 | 1.77 |
| 5 | 1.1 | 100,000 | 275 | 256.2 | 6.8 |
| Physical Indicators | Dimensional System [L][ρ][ε][g] | Similarity Constant (N = 50) | |
|---|---|---|---|
| Geometric features | Geometric dimension | [L] | 1/N |
| Area | [L]2 | 1/N2 | |
| Inertia moment | [L]4 | 1/N4 | |
| Material behavior | Density | [ρ] | 1 |
| Elasticity modulus | [L][ρ][g][ε]−1 | 1 | |
| Mass | [ρ][L]3 | 1/N3 | |
| Dynamic characteristics | Input vibration acceleration | [g] | 1 |
| Field acceleration | [g] | 1 | |
| Force | [ρ][L]3[g] | 1/N3 | |
| Input vibration time | [L]0.5[ε]0.5[g]−0.5 | 1/N0.5 | |
| Vibrational frequency | [L]−0.5[ε]−0.5[g]0.5 | N0.5 | |
| Dynamic response acceleration | [g] | 1 | |
| Dynamic response stress | [ρ][L][g] | 1/N | |
| Dynamic response strain | [ε] | 1 |
| Seismic Wave Acceleration (× g) | Cable Force (MPa) | Horizontal Hydrodynamic Load (Pa) | Horizontal Acceleration of the Tube (m/s2) | |||
|---|---|---|---|---|---|---|
| σm | σp | Pm | Pp | ap | am | |
| 0.01 | 3.40 | 169.85 | 11 | 550 | 0.11 | 0.11 |
| 0.03 | 10.70 | 535.03 | 30.5 | 1525 | 0.41 | 0.41 |
| 0.05 | 83.51 | 4175.51 | 202 | 10,100 | 3.68 | 3.68 |
| 0.07 | 135.20 | 6760.08 | 322.8 | 16,140 | 5.98 | 5.98 |
| 0.09 | 152.92 | 7646.14 | 369.2 | 18,460 | 6.57 | 6.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Cheng, X.; Pan, H. Numerical Simulation of a Submerged Floating Tunnel: Validation and Analysis. Appl. Sci. 2024, 14, 3589. https://doi.org/10.3390/app14093589
Li H, Cheng X, Pan H. Numerical Simulation of a Submerged Floating Tunnel: Validation and Analysis. Applied Sciences. 2024; 14(9):3589. https://doi.org/10.3390/app14093589
Chicago/Turabian StyleLi, Hao, Xiaohui Cheng, and Hua Pan. 2024. "Numerical Simulation of a Submerged Floating Tunnel: Validation and Analysis" Applied Sciences 14, no. 9: 3589. https://doi.org/10.3390/app14093589
APA StyleLi, H., Cheng, X., & Pan, H. (2024). Numerical Simulation of a Submerged Floating Tunnel: Validation and Analysis. Applied Sciences, 14(9), 3589. https://doi.org/10.3390/app14093589






