Investigation of the Effects of Vortex Isolation Plates with Different Opening Ratios and Sizes on Vortex-Induced Vibration
Abstract
:Featured Application
Abstract
1. Introduction
2. Introduction to Experiments
2.1. Test Equipment and Parameters
2.2. Test Cases
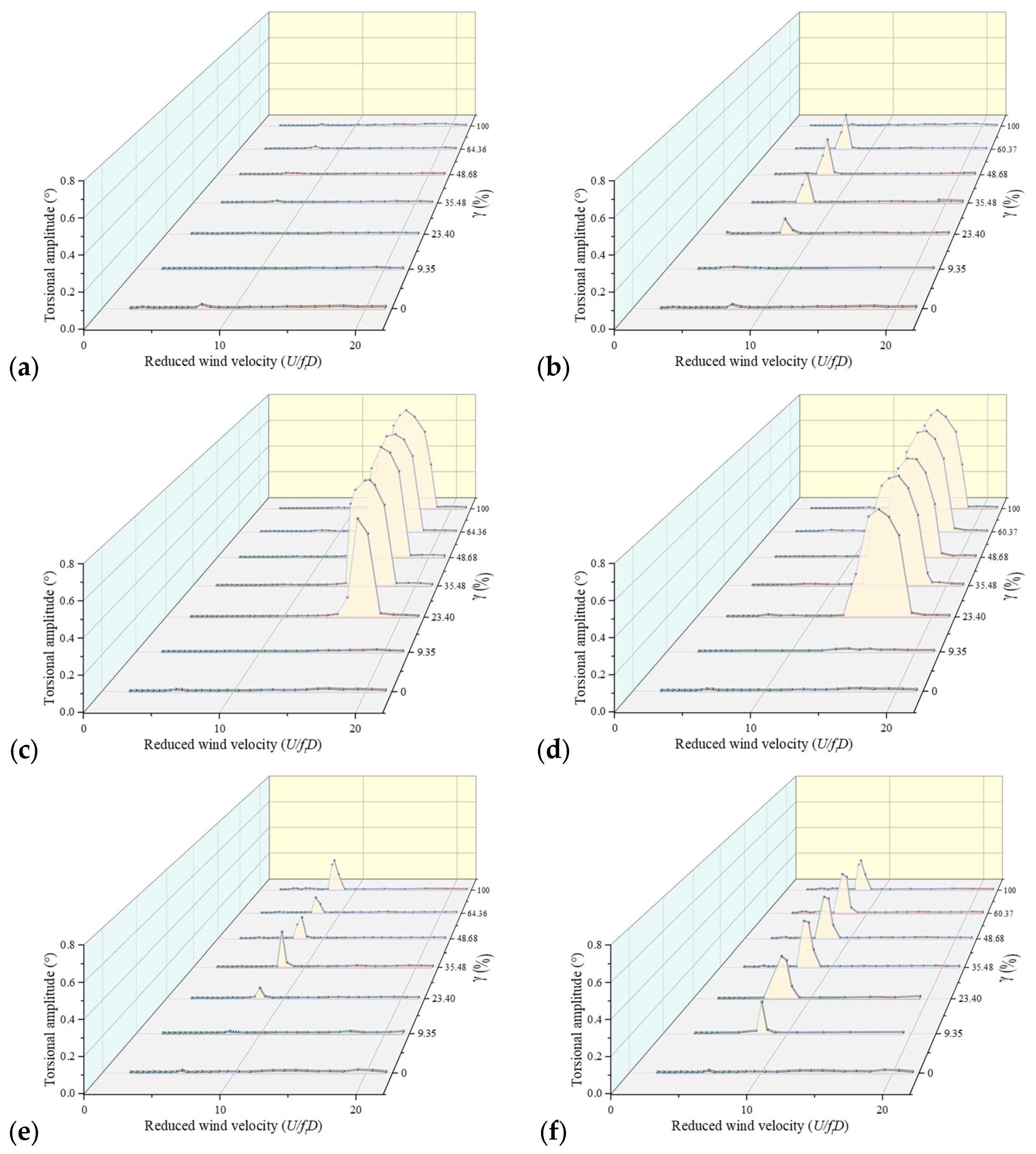
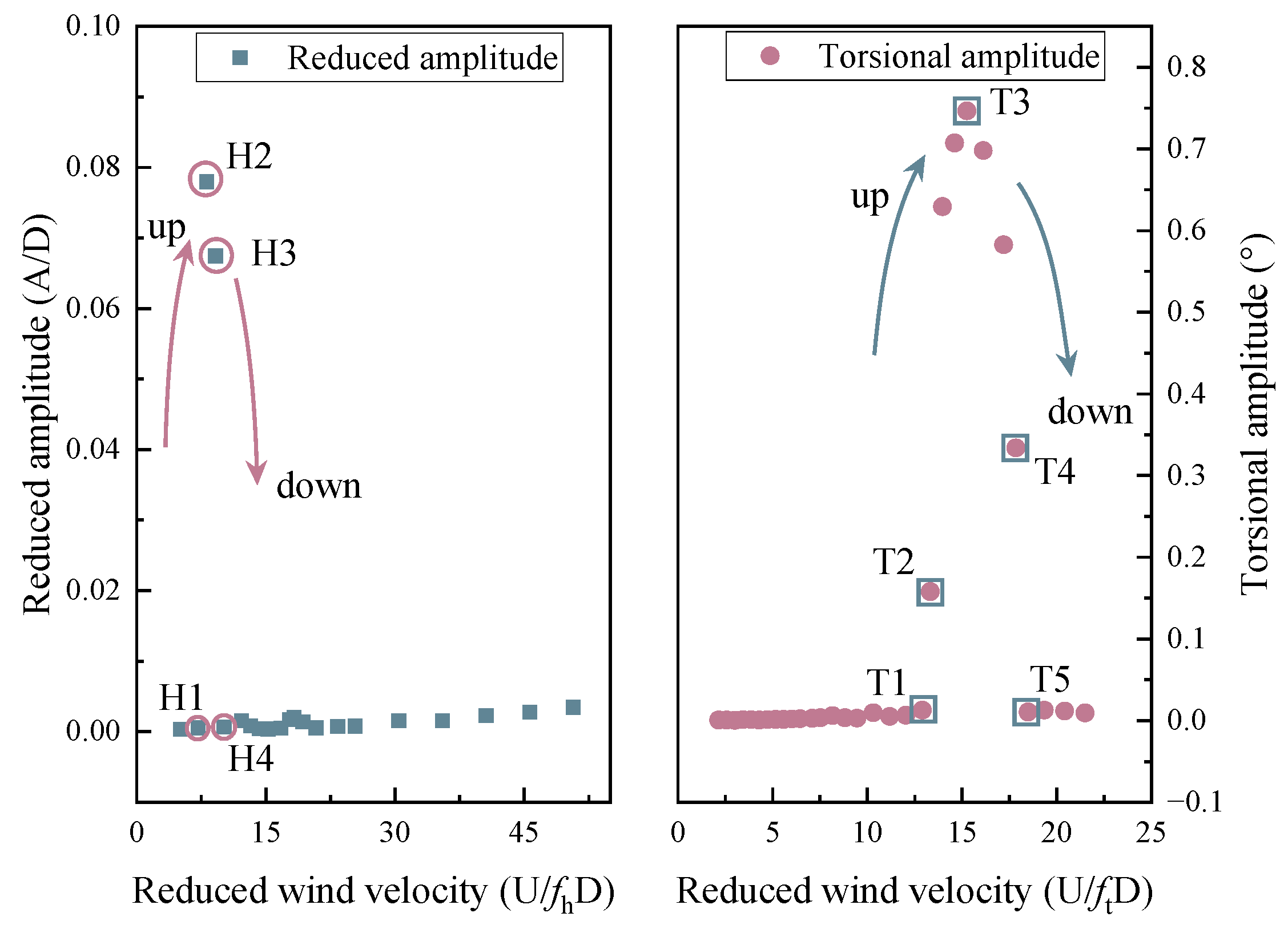
3. Vortex-Induced Vibration Performance with Different Vortex Isolation Plates
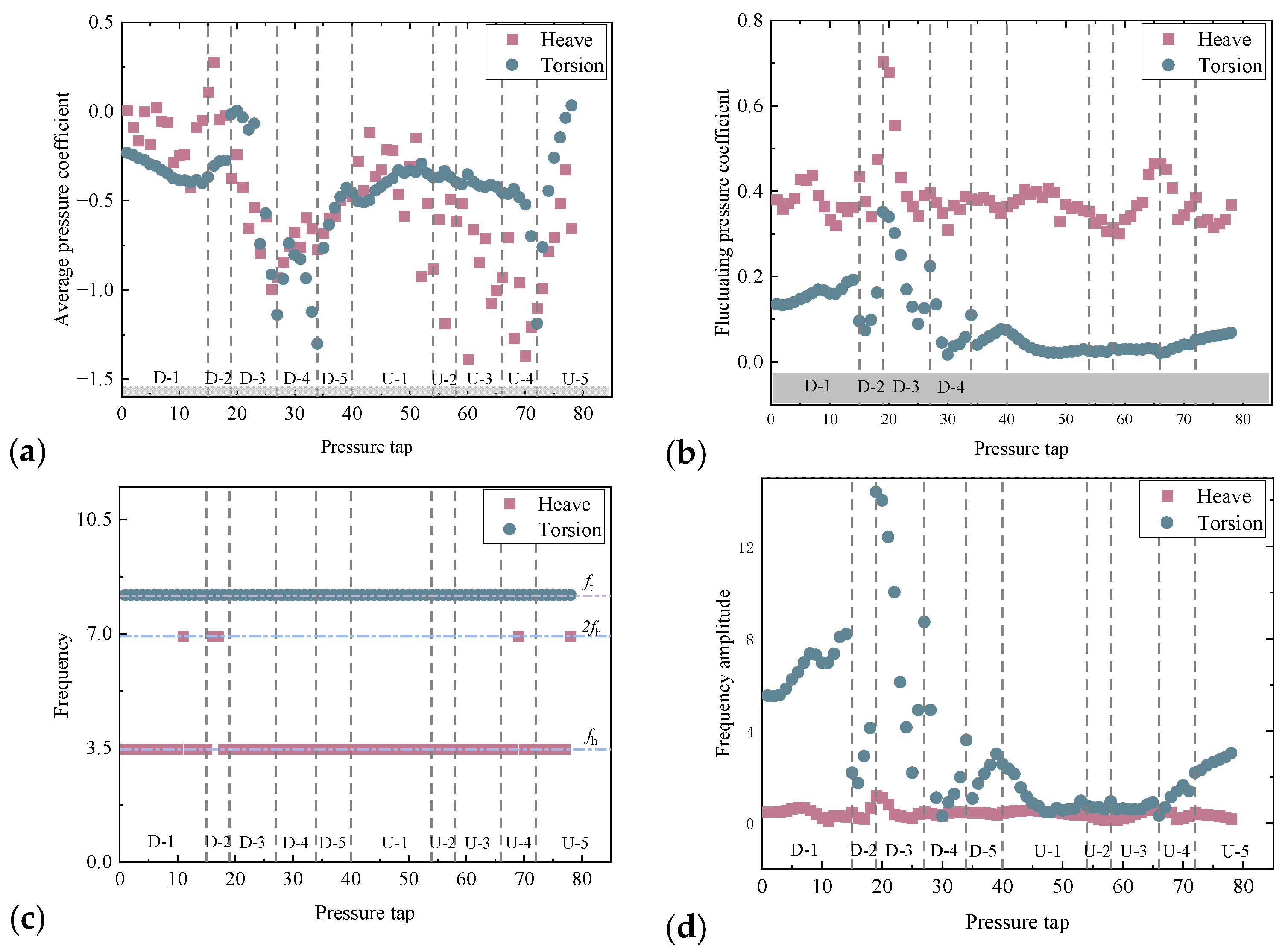
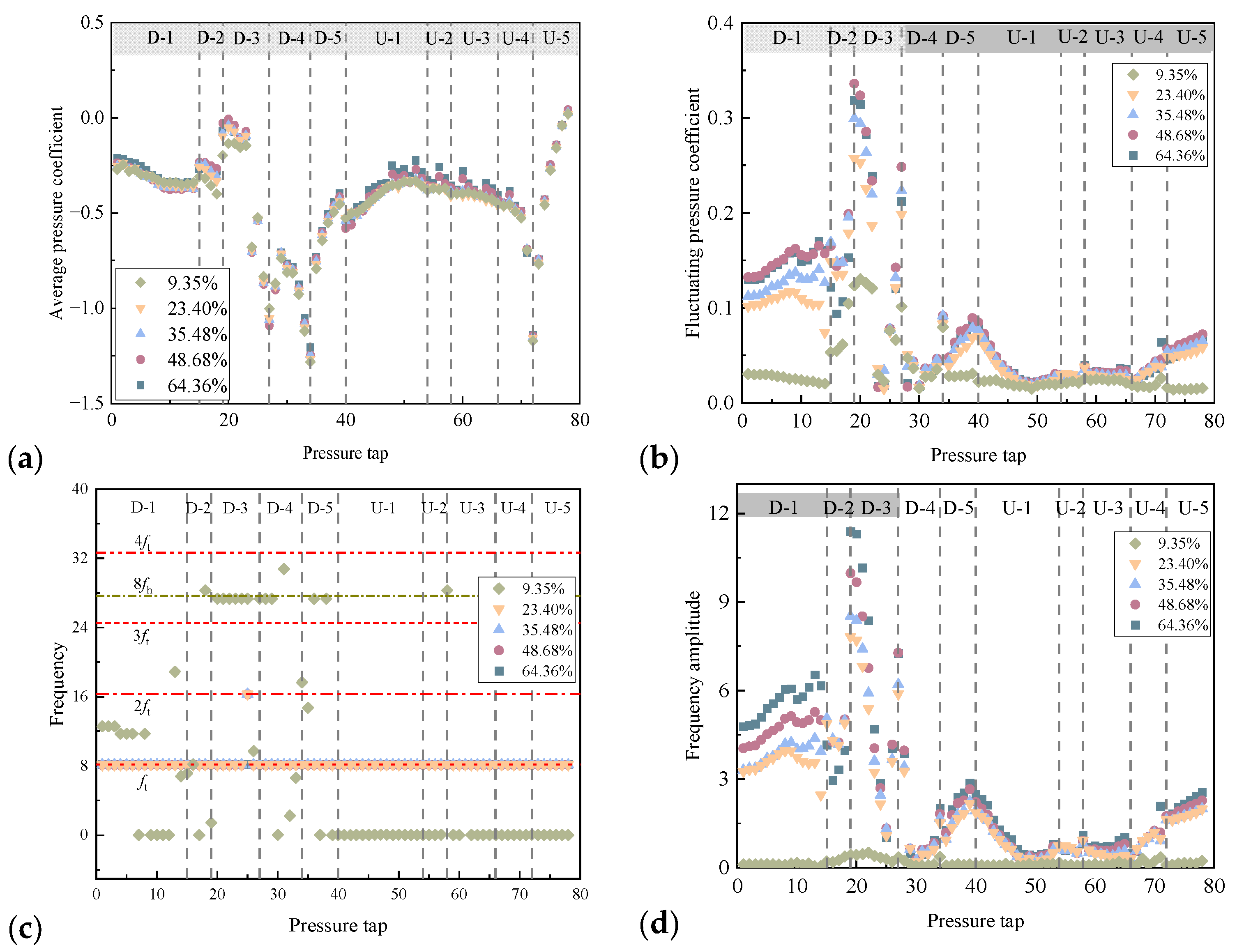
4. Wind Pressure Characteristics with Different Vortex Isolation Plates
5. Conclusions
6. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, M.; Wang, X.; Cai, J.; Brazhenko, V.; Tan, J.; Xu, Z. Analysis on flow-induced vibration of square cylinders with different vibration forms and the flow energy harvesting capacity. Phys. Fluids 2023, 35, 095124. [Google Scholar] [CrossRef]
- Hu, P.; Wang, S.; Han, Y.; Cai, C.S.; Yuan, B.; Ding, S. Numerical simulations on flow control of the long hanger around a bridge tower based on active suction and blowing method. Phys. Fluids 2023, 35, 115145. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Z.; Zhou, S.; Wang, Y.; Chen, Z. Monitoring-based identification of nonlinear aerodynamic damping in multi-mode vortex-induced vibrations of a stay cable. J. Wind Eng. Ind. Aerodyn. 2024, 247, 105703. [Google Scholar] [CrossRef]
- Bai, H.; Li, R.; Xu, G.J.; Kareem, A. Aerodynamic performance of Π-shaped composite deck cable-stayed bridges including VIV mitigation measures. J. Wind Eng. Ind. Aerodyn. 2021, 208, 104451. [Google Scholar] [CrossRef]
- Li, J.W.; Wu, P.; Hao, J.M.; Pan, H. Experimental and numerical studies on the two “lock-in” regions characteristic of vertical vortex-induced vibration of Π-shaped composite bridge deck. J. Wind Eng. Ind. Aerodyn. 2022, 228, 105122. [Google Scholar] [CrossRef]
- Wang, J.Y.; Wang, F.; He, R.; Li, J.W.; Hao, J.M.; Zhang, J.P.; Huang, X.M. Investigation of the intrinsic characteristics of two lock-in regions in a 10:1 π-shaped deck. Ocean. Eng. 2024, 293, 116607. [Google Scholar] [CrossRef]
- Yang, Y.X.; Zhou, R.; Ge, Y.J. Vortex-induced vibration and its control for long-span bridges with twin-box girder. China Civ. Eng. J. 2014, 47, 107–114. [Google Scholar] [CrossRef]
- Larose, G.L.; Larsen, S.V.; Larsen, A.; Hui, M.; Jensen, A. Sectional model experiments at high Reynolds number for the deck of a 1018 m span cable-stayed bridge. In Proceedings of the 11th International Conference on Wind Engineering, Lubbock, TX, USA, 2–5 June 2003; pp. 373–800. [Google Scholar]
- Ma, C.M.; Wang, J.X.; LI, Q.S.; ASCE, M.; Qin, H.; Liao, H.L. Vortex-Induced Vibration Performance and Suppression Mechanism for a Long Suspension Bridge with Wide Twin-Box Girder. J. Struct. Eng. 2018, 144, 04018202–04018214. [Google Scholar] [CrossRef]
- Laima, S.J.; Li, H.; Chen, W.L.; Li, F.C. Investigation and control of vortex-induced vibration of twin-box girders. J. Fluids Struct. 2013, 39, 205–221. [Google Scholar] [CrossRef]
- Kwok, K.C.S.; Qin, X.R.; Fok, C.H.; Hitchcock, P.A. Wind-induced pressures around a sectional twin-deck bridge model: Effects of gap-width on the aerodynamic forces and vortex shedding mechanisms. J. Wind Eng. Ind. Aerodyn. 2012, 110, 50–61. [Google Scholar] [CrossRef]
- de Miranda, S.; Patruno, L.; Ricci, M.; Ubertini, F. Numerical study of a twin box bridge deck with increasing gap ratio by using RANS and LES approaches. Eng. Struct. 2015, 99, 546–558. [Google Scholar] [CrossRef]
- Yang, Y.X.; Zhou, R.; Ge, Y.J.; Zhang, L.H. Experimental studies on VIV performance and countermeasures for twin-box girder bridges with various slot width ratios. J. Fluids Struct. 2016, 66, 476–489. [Google Scholar] [CrossRef]
- Jeong, W.M.; Liu, S.N.; Jakobsen, J.B.; Ong, M.C. Unsteady RANS simulation of flow around a twin-box bridge girder cross section. Energies 2019, 12, 2670. [Google Scholar] [CrossRef]
- Liu, S.Y.; Hu, C.X.; Zhao, L.; Ge, Y.J. Aerodynamic force evolution characteristics around the central-slotting box girder during the whole trosional vortex-induced vibration process. Eng. Mech. 2020, 37, 196–205. [Google Scholar] [CrossRef]
- Li, H.; Laima, S.J.; Ou, J.P.; Zhao, X.F.; Zhou, W.S.; Yu, Y.; Li, N.; Liu, Z.Q. Investigation of vortex-induced vibration of a suspension bridge with two separated steel box girders based on field measurements. Eng. Struct. 2011, 33, 1894–1907. [Google Scholar] [CrossRef]
- Li, H.; Laima, S.J.; Zhang, Q.Q.; Li, N.; Liu, Z.Q. Field monitoring and validation of vortex-induced vibrations of a long-span suspension bridge. J. Wind Eng. Ind. Aerodyn. 2014, 124, 54–67. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, R.; Yang, Y.X.; Ge, Y.J. Vortex-induced vibration control for twin box girder bridges with vertical central stabilzers. J. Tongji Univ. (Nat. Sci.) 2019, 47, 617–626. [Google Scholar] [CrossRef]
- Ma, C.M.; Wang, J.X.; Luo, N.; Li, H.J.; Liao, H.L. Vortex-induced vibration performance and control measures of wide twin-box girder. J. Southwest Jiaotong Univ. 2019, 54, 724–730. [Google Scholar] [CrossRef]
- Li, Z.G.; Zhou, Q.; Ma, C.M.; Liao, H.L. Mechanism of suppressing vortex-induced vibration of twin-box girder using central grids. Bridge Constr. 2018, 48, 19–24. [Google Scholar]
- He, H.X.; Li, J.W.; Zhou, J.L. Testing and analysis of vortex-excited vibration of central slotted box section cable-stayed bridge. Bridge Constr. 2012, 42, 34–40. [Google Scholar]
- Wang, Q.; Lin, D.J.; Liao, H.L.; Sun, Y.G. Investigation on the vortex-induced vibration and aerodynamic countermeasures of twin box bridge by wind tunnel tests. Highway 2013, 7, 294–299. [Google Scholar]
- Ouyang, K.J.; Chen, Z.Q.; Han, Y.; Li, H.L. Vortex-induced vibration of a suspension bridge with central-slotted box section and its control test study. J. Vib. Shock. 2009, 28, 199–202+233. [Google Scholar] [CrossRef]

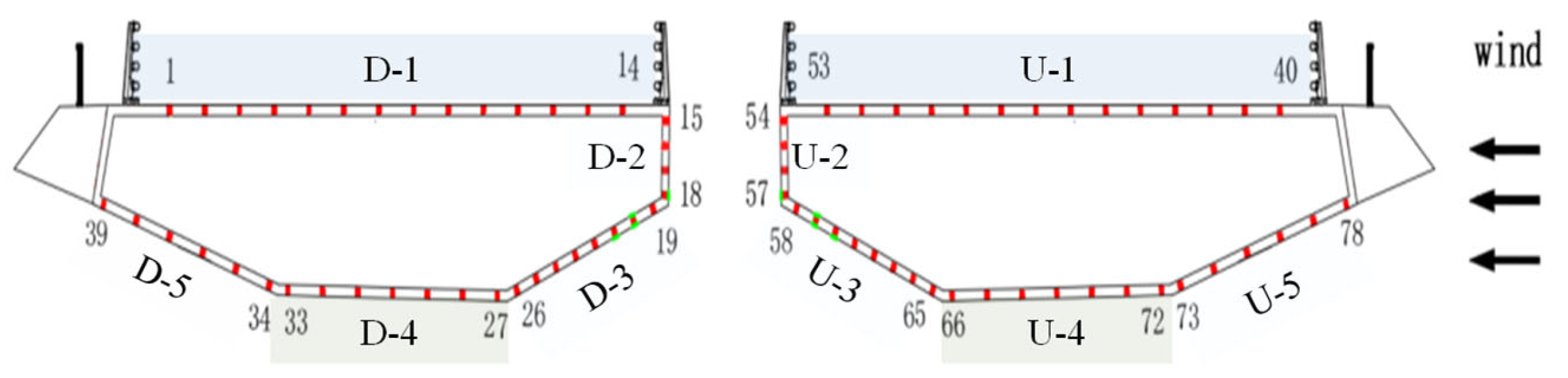

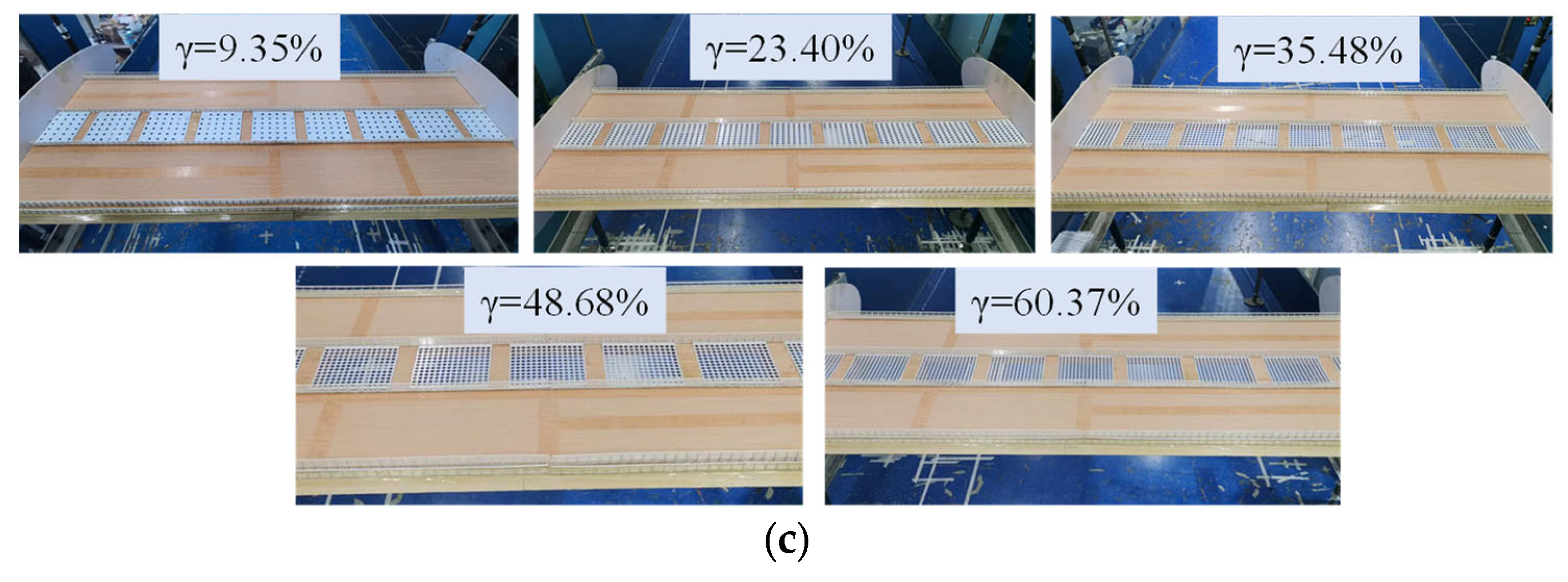
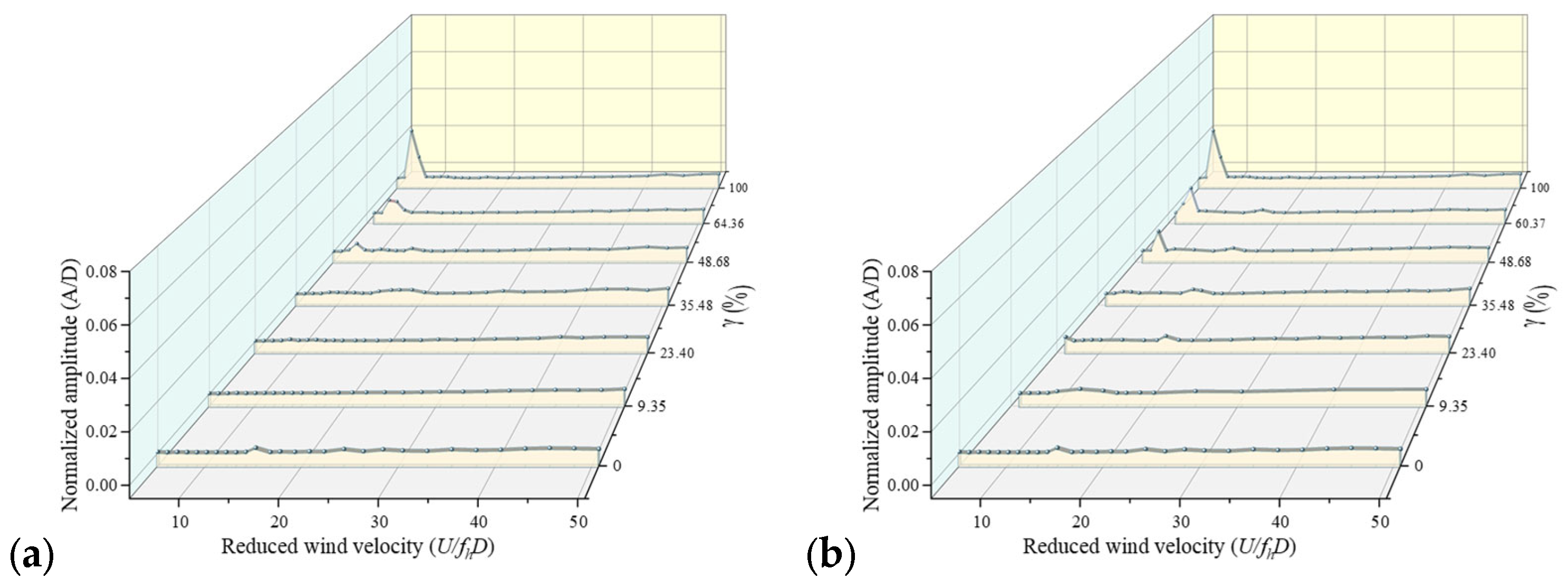
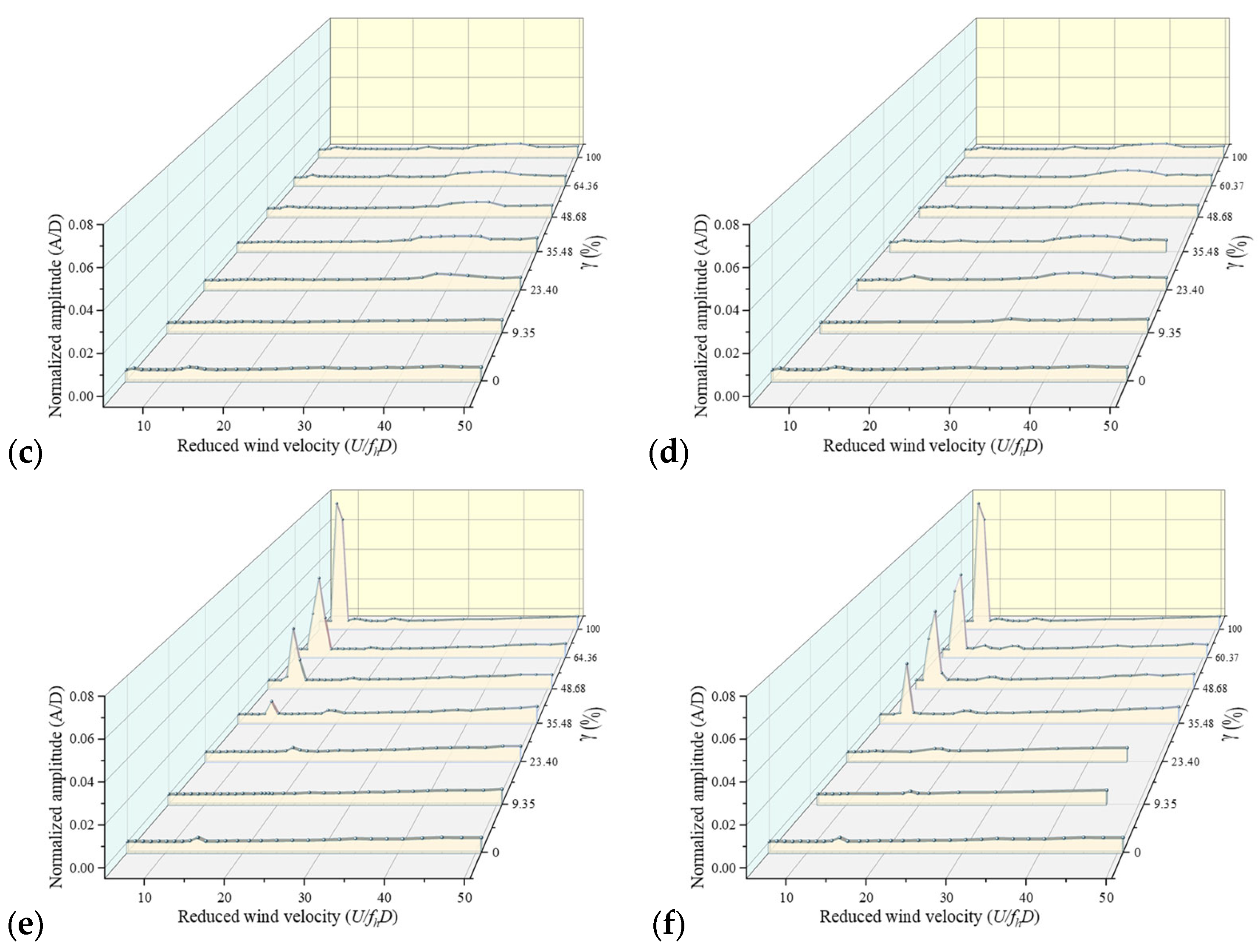

| Parameter | Symbol | Unit | Real Bridge Value | Scale Ratio | Test Value | Error (%) |
|---|---|---|---|---|---|---|
| Width | B | m | 50.4 | 1/70 | 0.72 | - |
| Height | H | m | 4 | 1/70 | 0.057 | - |
| Length | L | m | - | - | 1.80 | - |
| Mass per unit length | m | kg/m | 37,000 | 1/702 | 7.72 | −2.2 |
| Mass moment of inertia per unit | Jm | kg·m2/m | 8,490,000 | 1/704 | 0.34 | 2.9 |
| Heaving frequency | fb | Hz | 0.1432 | — | 3.42 | 1.2 |
| Torsional frequency | ft | Hz | 0.6295 | — | 8.30 | −1.7 |
| Heaving damping | ξb | % | — | — | 0.3 | - |
| Torsional damping | ξt | % | — | — | 0.21 | - |
| Cases | Type of Vortex Isolation Plates | Opening Ratio (%) | AOA | Opening Number | Single Opening Area (mm2) |
|---|---|---|---|---|---|
| 1 | No plate | 100% | 0° +3° −3° | - | - |
| 2 | No opening | 0% | 0 | 0 | |
| 3–5 | Plate with 20 mm opening diameter | 9.35% | 68 | 314.16 | |
| 6–8 | 23.40% | 170 | |||
| 9–11 | 35.48% | 258 | |||
| 12–14 | 48.68% | 354 | |||
| 15–17 | 64.36% | 468 | |||
| 18–20 | Plate with 10 mm opening diameter | 9.35% | 272 | 78.54 | |
| 21–23 | 23.40% | 680 | |||
| 24–26 | 35.48% | 1032 | |||
| 27–29 | 48.68% | 1416 | |||
| 30–32 | 60.37% | 1756 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Wang, J.; Wang, F. Investigation of the Effects of Vortex Isolation Plates with Different Opening Ratios and Sizes on Vortex-Induced Vibration. Appl. Sci. 2024, 14, 3863. https://doi.org/10.3390/app14093863
He H, Wang J, Wang F. Investigation of the Effects of Vortex Isolation Plates with Different Opening Ratios and Sizes on Vortex-Induced Vibration. Applied Sciences. 2024; 14(9):3863. https://doi.org/10.3390/app14093863
Chicago/Turabian StyleHe, Hanxin, Jiaying Wang, and Feng Wang. 2024. "Investigation of the Effects of Vortex Isolation Plates with Different Opening Ratios and Sizes on Vortex-Induced Vibration" Applied Sciences 14, no. 9: 3863. https://doi.org/10.3390/app14093863
APA StyleHe, H., Wang, J., & Wang, F. (2024). Investigation of the Effects of Vortex Isolation Plates with Different Opening Ratios and Sizes on Vortex-Induced Vibration. Applied Sciences, 14(9), 3863. https://doi.org/10.3390/app14093863






