Next Article in Journal
A LeViT–EfficientNet-Based Feature Fusion Technique for Alzheimer’s Disease Diagnosis
Next Article in Special Issue
Effects of Materials and Riblets on Erosion Mitigation Induced by Multiple Collapses of Cavitation Bubbles
Previous Article in Journal
New Methods of Series Expansions between Three Anomalies
Previous Article in Special Issue
Beacon, a Lightweight Deep Reinforcement Learning Benchmark Library for Flow Control
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 14
Issue 9
10.3390/app14093878
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Numerical Modeling of Venous Outflow from the Cranial Cavity in the Supine Body Position

by
Marian Simka
1,*,
Joanna Czaja
1,
Agata Kawalec
1,
Paweł Latacz
2 and
Uliana Kovalko
1
1
Institute of Medical Sciences, University of Opole, 45-040 Opole, Poland
2
Department of Vascular Surgery and Angiology, Brothers of Mercy St. John of God Hospital, 31-061 Krakow, Poland
*
Author to whom correspondence should be addressed.
Appl. Sci. 2024, 14(9), 3878; https://doi.org/10.3390/app14093878
Submission received: 20 March 2024 / Revised: 25 April 2024 / Accepted: 27 April 2024 / Published: 30 April 2024
(This article belongs to the Special Issue Advances in Active and Passive Techniques for Fluid Flow Manipulation)
Browse Figures
Versions Notes

Abstract

:
The hemodynamic relevance of differently located stenoses of the internal jugular veins remains undetermined. It particularly concerns nozzle-like strictures in the upper parts of these veins and stenotic jugular valves located at the end of these veins. This study was aimed at understanding flow disturbances caused by such stenoses. The computational fluid dynamics software Flowsquare+ was used. We constructed 3-dimensional models of the venous outflow, comprising two alternative routes: the tube representing the internal jugular vein and an irregular network representing the vertebral veins. At the beginning of the tube representing the internal jugular vein, differently shaped and sized short strictures representing nozzle-like strictures were built in. At the end of this tube, differently shaped membranes representing the jugular valve were built in. With the use of computational fluid dynamics modeling, we studied how these two obstacles influenced the outflow. We found that the most relevant outflow disturbances were evoked by the nozzle-like strictures in the upper part of the internal jugular vein that were small, long, or asymmetrically positioned. Very tight stenotic valves and septum-like malformed valve were equally hemodynamically relevant. These findings suggest that both upper and lower strictures of the internal jugular vein can be of clinical significance.

1. Introduction

The internal jugular veins (IJVs), the paired veins located in the neck, constitute the primary blood outflow route from the brain. Still, actual outflow routes from the head, particularly from the cranial cavity, depend on the body posture. While in the horizontal (supine, prone, and lateral decubitus) body positions, at least one of the IJVs is open, enabling an unrestricted venous outflow; however, in the upright (sitting and standing) body positions, the IJVs collapse due to the gravitational effects (negative transmural pressure). Consequently, a substantial part of the outflow is shifted towards alternative routes, primarily to the vertebral venous plexus and vertebral veins, which are situated alongside the cervical part of vertebral column [1,2,3,4,5,6,7]. This outflow pathway is composed of the vertebral veins, the epidural venous plexus, and other adjacent tiny veins. Since the veins in the vertebral outflow route are of smaller diameter, even if their total cross-sectional area is comparable to that of the IJVs, flow resistance in this pathway is much higher in comparison with the non-collapsed IJVs. Therefore, a majority of cerebral venous outflow utilizes the jugular route. This situation changes when the head is elevated (in the standing or sitting individuals). In this body position, about 80–90% of blood flows out through the vertebral veins and adjacent venous plexuses, contrasting with approximately 30% or even less in the horizontal position. Of note, venous outflow in the upright body position is facilitated by the gravity. Therefore, a high flow resistance in the vertebral route does not substantially affect the cerebral venous outflow. On the other hand, at least theoretically, pathological strictures in the IJVs should compromise cerebral venous outflow in the horizontal body positions, even if the vertebral outflow route is not narrowed.
Currently, it remains controversial if such a compromised cerebral venous outflow is of any clinical relevance considering the abundance of collateral venous channels in the neck. Still, several studies have claimed impaired venous outflow as a cause of neurodegenerative and neuroinflammatory diseases [8,9,10,11,12,13,14,15]. Therefore, understanding the physical background of the compromised venous outflow from the brain is important. A majority of the strictures in the IJV are either found in the upper part of this vein, at the level of the jugular foramen, or in the lower part, where stenosis is usually caused by abnormal morphology of the jugular valve (the only valve of this vein, located just above junction of the IJV with the brachiocephalic vein) [16,17,18]. There is an ongoing debate regarding which of these strictures are more relevant. Since the investigations on blood vessel flow in living subjects are difficult to perform, are invasive, and are often not possible to conduct due to bioethical aspects, computational flow modeling (CFM) can provide a surrogate insight into the biomechanics of blood flow. Our previous research, utilizing computational flow simulations, suggested that strictures located at the level of the jugular foramen are probably more hemodynamically relevant [19]. This is in line with the results of clinical studies that evaluated flow and morphology of the IJVs with the use of magnetic resonance (MR) imaging [20,21]. Yet, in this in silico study [19], we used 3D models of the IJVs, still without alternative outflow pathways. Furthermore, we evaluated the flow only qualitatively. In the current paper, we used more reliable models comprising both jugular and vertebral outflow pathways and quantitative assessments of the flow. Models comprising both jugular and vertebral outflow pathways have already been validated and described in another paper published by our team [22]. Here, we present the results of next step of this research, which evaluated flow disturbances caused by strictures of different shapes, positions, and sizes in the upper and lower parts of the IJV. The main goal of the current study was to evaluate quantitatively the flow in narrowed IJVs in order to determine which types of stenoses are hemodynamically more relevant. Potentially, it could help properly design the diagnostic and therapeutic clinical trials for neurological patients.

2. Materials and Methods

For the purpose of this study, CFM software, the Flowsquare+ (Nora Scientific, City, Japan), was used. All the computations were executed in the Intel BOXNUC8i7BEH2 mini PC (Intel, Santa Clara, CF, USA) equipped with the Intel® CoreTM i7 processor and the Intel® Iris® Plus Graphics 655 graphic card. In Flowsquare+, transport equations are discretized by using a first order upwind difference scheme for the advection terms, and second order central difference scheme for the other terms, which allows for a straightforward boundary specification and less computational costs. The time advancement is performed by the explicit Euler method. Mathematical details of this software can be found at: https://fsp.norasci.com/math_en.html.
The 3-dimensional models were 180 mm long along the axis of flow, and 60 mm and 30 mm along the other axes. The mesh size of the models in any direction was 0.25 mm and contained about 7 million of active cells. The grid independency study was constructed for the velocity in the outflow field at 2500 steps. The study was conducted in a stepwise fashion, starting with a coarser mesh, and then reducing the mesh until the velocity became constant. Figure 1 shows the mesh independence study graph, in which the mesh size was optimized at the size of 0.31 mm. We also found that the maximum mesh size that enabled modeling of the vertebral pathway (consisting of tiny channels) was 0.5 mm. In order to better simulate the flow, we chose the size of cell to be 0.25 mm, since with reduced mesh the computations became too long.
The models comprised the initial inflow field representing the cerebral circulation, which branched into two alternative outflow routes: the tube representing the internal jugular vein and the irregular network representing the vertebral veins and the epidural venous plexus that forms the vertebral outflow route in humans. Then, these two alternative pathways joined together again to form the outflow field. To facilitate the simulations, we modeled only one side of the cerebral venous outflow: one internal jugular vein and one side of the vertebral venous pathway. The tubular-shaped model of the internal jugular vein was 125 mm long and at the outflow had the cross-sectional diameters of 10 mm and 12 mm (cross-sectional area of 0.94 cm2). The model of the vertebral venous pathway had a similar length as the model of the internal jugular vein and had the cross-sectional area at the outflow of about 0.75 cm2; however, the main part of the vertebral pathway was divided into many thin irregular parallel channels (Figure 2, Figure 3, Figure 4 and Figure 5).
During the simulations, 10 probes measuring flow parameters were positioned inside the models: two probes in the inflow field; two probes in the middle part of the IJV; three probes in the terminal part of the IJV, just above the jugular valve; and three probes in the terminal part of the vertebral pathway (Figure 6). Details of the validation of this model were presented in our previous paper [22].
The flow was simulated using 2500 consecutive steps, each of them lasting 0.28 ms, which in total was equivalent to 0.7 s of the real-time flow. Using our computer, it took around 24 h of computational time for each case. The parameters of the fluid were set up to be similar to those observed during blood flow in the IJV. The velocity component along the long axis of the model for the initial field, of which the area was 2.08 cm2, was set up at 8 cm/s, which enabled the inflow of fluid into the model without strictures in the jugular route at the level of 400 mL/min, which was equal to approximately 50% of the physiological cerebral blood flow [22]. The velocity profile in the initial field was flat and constant. The walls of all models were rigid. The initial pressure was 750 Pa (equivalent to 7.65 cm H2O; a physiological pressure in the IJV in the supine body position). The dynamic viscosity of the fluid was set to 2.78 × 10−3 kg/m/s (which is the dynamic viscosity of whole blood at 37 °C). The density of the modeled fluid was constant and set at 1055 kg/m3, which is the density of blood at room temperature [23,24].
We augmented the model of cerebral venous outflow in the supine body position, which has been validated in our previous study [22], with two strictures (Figure 7). The first one was positioned at the beginning of the IJV, mimicking the nozzle-like stenosis evoked by a narrow jugular foramen, an enlarged transverse process of the atlas, or an elongated styloid process of the temporal bone. Such pathological strictures can be seen in some patients, particularly those presenting with neurological symptoms [12]. The second stricture was positioned at the end of the IJV, mimicking a stenotic jugular valve. Such aberrant jugular valves are also found in some patients [14].
We constructed models with following types of upper IJV strictures:
  • No stenosis in the upper part of the IJV (cross-sectional area of 0.94 cm2);
  • Minor elliptically shaped stenosis in the upper part of the IJV (cross-sectional area of 0.42 cm2);
  • Minor irregularly shaped stenosis in the upper part of the IJV (cross-sectional area of 0.60 cm2);
  • Major elliptically shaped stenosis in the upper part of the IJV (cross-sectional area of 0.24 cm2);
  • Major elliptically shaped stenosis in the upper part of the IJV (cross-sectional area of 0.24 cm2) with opening positioned eccentrically;
  • Major elliptically shaped stenosis in the upper part of the IJV (cross-sectional area of 0.24 cm2) with a longer narrowed segment (12 mm instead of 2.5 mm);
  • Very narrow elliptically shaped stenosis in the upper part of the IJV (cross-sectional area of 0.07 cm2);
  • Very narrow elliptically shaped stenosis in the upper part of the IJV (cross-sectional area of 0.07 cm2) with opening positioned eccentrically;
  • Major stenosis in the upper part of the IJV comprising 2 eccentrically positioned openings (cross-sectional area of 0.48 cm2);
  • Major stenosis in the upper part of the IJV comprising eccentrically positioned short flattening (cross-sectional area of 0.48 cm2).
We also constructed different types of valves in the lower part of the IJV:
  • No valve;
  • Bicuspid valve, distance between leaflets set to 4.3 mm (opening located centrally, 4.3 mm × 8.5 mm);
  • Bicuspid valve, distance between leaflets set to 1.5 mm (opening located centrally, 1.5 mm × 8.5 mm);
  • Septum instead of a valve, almost completely obstructing the IJV (opening located next to the wall, 1.5 mm × 8.5 mm).
Of note, in our study, the valve leaflets and the septum, unlike actual intraluminal structures located in the IJVs, were immobile, since the CFD software used did not allow for the building of a mobile and elastic material. In total, we examined 10 models exhibiting different types and shapes of the strictures; the morphologies of these strictures are presented in Table 1. The total flow in the jugular and vertebral channels were measured with the above-described probes. The model with the collapsed IJV, which has been validated in our previous paper, was used as the reference (Model 11 in Table 1).

3. Results

In total, we performed flow simulations in 14 models of the cerebral venous outflow. The geometry of these models, particularly the cross-sectional area and length of the upper stenosis, morphology of the valve located downstream, flow volumes, and the degree of shift from the jugular to the vertebral pathway, is presented in Table 1.
Our previous flow simulations in the model, in which the IJV did not exhibit any strictures, revealed that 84% of the fluid flew through the IJV. In the current study, with a longer time of simulated flow, we obtained a similar result (90%). In our 3-dimensional models with two alternative outflow pathways, a shift from the jugular to the vertebral pathway was interpreted as the sign of hemodynamically relevant flow resistances evoked by stenotic lesions in the IJV (nozzle-like upper stricture or stenotic abnormal valve located downstream). We also interpreted the degree of such a shift as the level of hemodynamic relevance of the stenosis. Quantitative results of the simulations are presented in Table 1.
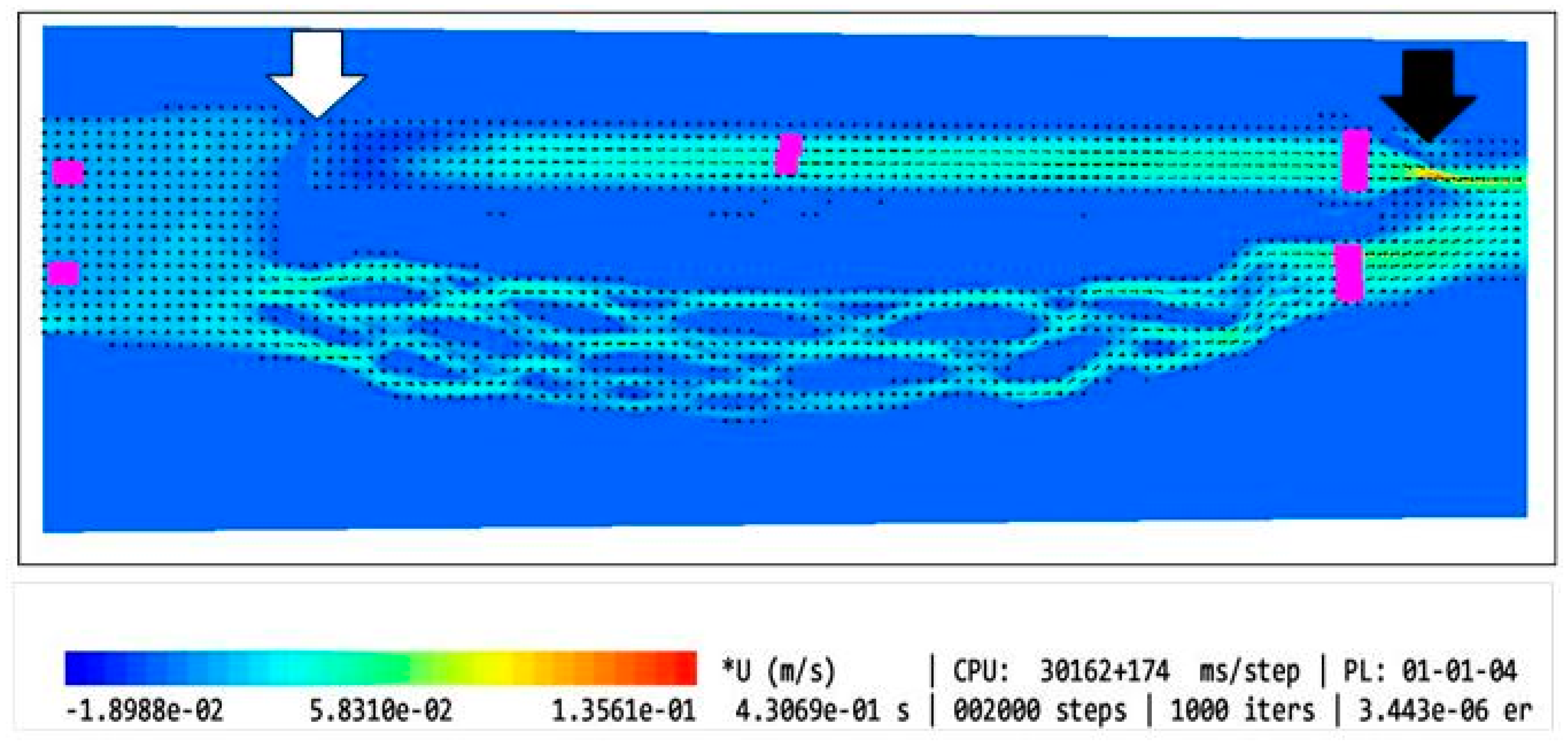
We found that a significant shift from the jugular to the vertebral pathway can be evoked by both upper and lower lesions (Table 1). Regarding the nozzle-like strictures located upstream, flow resistance resulting in the shift of the flow towards the vertebral outflow route seemed to be more significant if such a stenosis was shaped in the following ways:
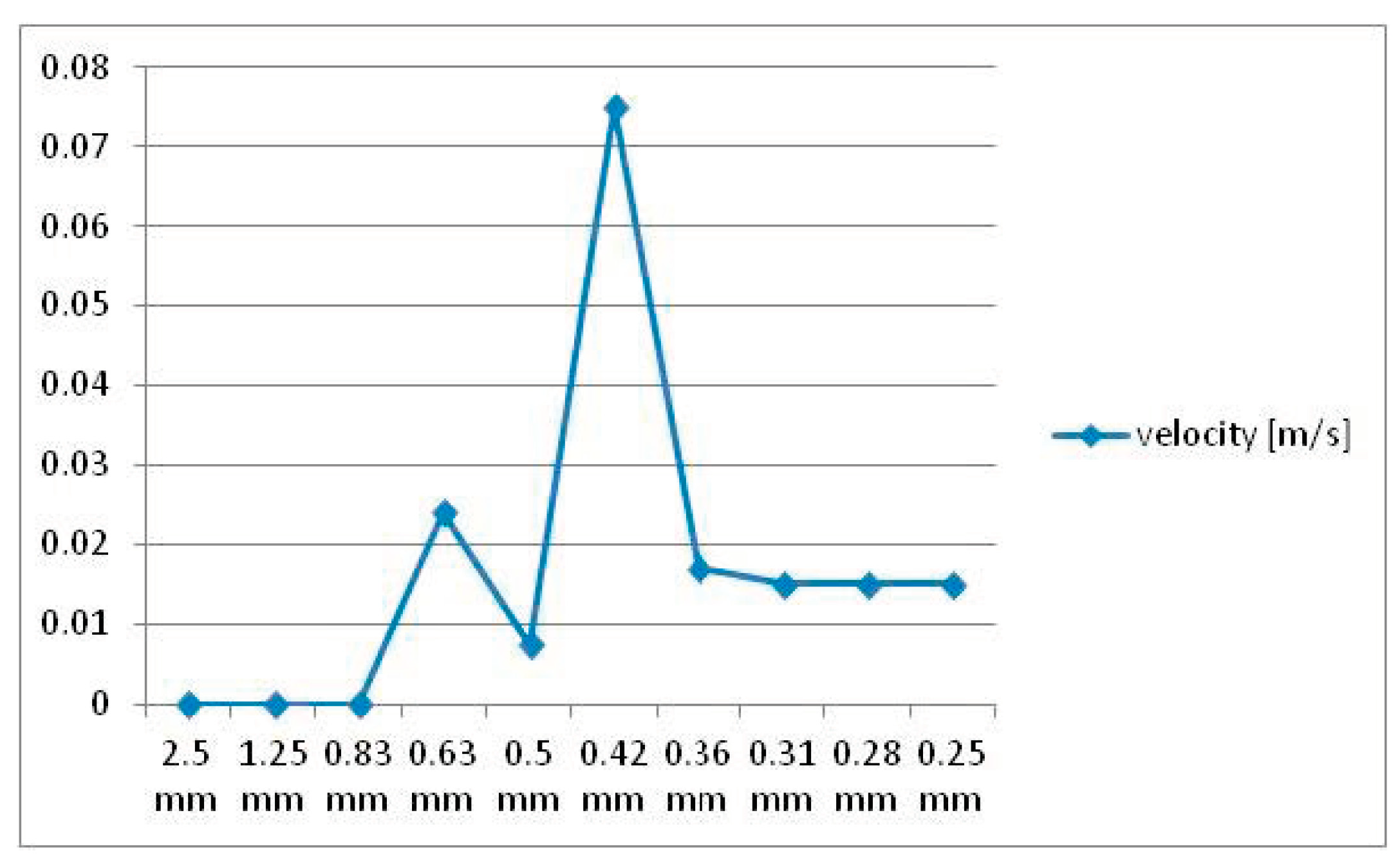
  • Narrower (Models 6 and 9);
  • Longer (Model 8);
  • Eccentrically positioned (Models 7, 10, and 13);
  • Irregularly shaped (Models 5 and 12).
Regarding stenoses of the jugular valve located downstream, the shift was more pronounced if the distance between stiff valve leaflets was smaller (Model 3 vs. Model 4). Abnormally shaped valve forming a septum (Model 11) resulted in the most significant flow disturbances. Some qualitative examples of the flow pattern in the settings of different strictures are shown in Figure 8, Figure 9, Figure 10 and Figure 11.

4. Discussion

In this in silico study, we demonstrated that both upper and lower strictures in the IJV can be hemodynamically significant and potentially clinically relevant. Besides, some types of these strictures, e.g., asymmetrically positioned nozzle-like stenoses located at the level of the jugular foramen or a membrane-shaped jugular valve particularly compromising the flow through the IJV, shift the outflow towards the vertebral pathway. Our results can, at least partially, resolve some clinical dilemmas, which will be further discussed.
Of note, in the past, some papers describing the numerical simulations of flow in the IJV were published. Yet, these models did not investigate vein morphologies with the nozzle-like strictures in the proximal part of this vein [25,26]. In our previous paper, based on the results of computational flow simulations using the same CFD package, we suggested that strictures located at the level of the jugular foramen are more clinically relevant than pathological jugular valves [19]. Yet, in this study, we evaluated the flow only in models without alternative outflows through the vertebral pathway. Also, flow disturbances evoked by the stenoses were evaluated qualitatively by an assessment of flow characteristics. In the current study, we evaluated the flow quantitatively and with an alternative outflow route, and thus they are more similar to real patients. In contrast to the former study, the present study found that both types of the strictures—located upstream and downstream—can significantly compromise the outflow. Importantly, since severe flow impairments were caused by the short nozzle-like stenoses, especially those located eccentrically, it is probable that flow separation and flow reversal were the main causes of an increased flow resistance and a shift in the outflow towards the vertebral pathway (Figure 8 and Figure 9). But stenotic jugular valves (Figure 10 and Figure 11), especially membrane-shaped, could equally evoke significant flow impairments.
Usually, albeit in living humans, the IJVs exhibit slightly irregular shapes and there is an asymmetry regarding their size (typically the right IJV is wider than the left one), there are no strictures in these veins that significantly alter the cerebral venous outflow. Of note, the IJVs represent the major outflow route from the brain in the horizontal body position, including during sleep. Recently, it has been hypothesized that an impaired cerebral venous outflow can affect function of the glymphatic system, which is responsible for cleansing the brain from noxious metabolites, including pathological proteins [27,28]. Importantly, the glymphatic system is mainly active during sleep; therefore, an unrestricted venous outflow from the brain during sleep is potentially indispensable. Although, for the time being, direct observations proving that there is indeed a causative association between venous abnormalities and neurological pathologies are lacking, it is known that malformed IJVs are more often seen in neurological patients in comparison with healthy controls [13,15].
Interestingly, a decade ago, many multiple sclerosis patients were managed using endovascular angioplasty of their narrowed IJVs. Unfortunately, although early results of such a treatment were encouraging, positive outcomes in a long run were seen only in some subgroups of these patients [29,30,31]. Therefore, this treatment modality is no longer the standard one. However, a majority of the aforementioned endovascular procedures comprised balloon angioplasties of pathological jugular valves. External compressions at the level of the jugular foramen were not addressed, while it is known that such strictures are quite common in these patients [13,20]. This may account for the unfavorable results of the clinical trials in multiple sclerosis patients. In addition, stenotic lesions of the IJVs are found in other neurological pathologies, including Alzheimer’s and Parkinson’s diseases, Ménière disease, and lateral amyotrophic sclerosis. Thus, addressing these venous abnormalities may have a prophylactic or therapeutic potential.
Yet, the hemodynamic relevance of different types of strictures in the IJVs is difficult to assess in living subjects. Firstly, all investigations aimed at such an evaluation are more or less invasive and not free from severe side effects. Therefore, clinical investigations are very difficult to conduct, considering bioethical issues. Secondly, proper interpretation of these investigations (catheter venography, Doppler ultrasonography, or magnetic resonance imaging) is not obvious [32]. Therefore, in silico flow modeling can provide a surrogate evaluation of the hemodynamic significance of particular types of these strictures. This was the primary aim of our current CFD study.
From the physical point of view, it may seem obvious that a narrow or eccentrically positions stricture should evoke flow impairment. Still, from the clinical perspective, this problem is not so straightforward. In the neck, there are many alternative outflow routes, and some of the veins can be temporarily squeezed by adjacent bones, muscles, and ligaments without clinical consequences. There is a general thinking among clinicians that irrespective of these narrowings, there are still enough veins to provide adequate cerebral venous drainage. In the case of a suspected clinically relevant stenosis, doctors either perform non-invasive MR imaging or invasive catheter angiography, while color Doppler ultrasonography primarily serves the purpose of a screening test. Still, there are problems with interpretations of all these diagnostic modalities. While MR can reveal decreased flow velocity and reduced vein diameter (e.g., caused by external compression), this diagnostic method poorly shows abnormal valves. On the contrary, standard catheter angiography cannot demonstrate flow abnormalities caused by stenoses located at the level of the jugular foramen, unless the diagnostic catheter is advanced to the intracranial venous sinuses, which is associated with a risk of life-threatening bleeding; therefore, it is not performed routinely. Moreover, during catheter venography, doctors actually assess the flow of the contrast and not the whole blood stream. Consequently, such phenomena as flow separation or flow reversal can remain undetected. Theoretically, these flow phenomena could be detected non-invasively using color Doppler ultrasonography; yet, for the time being, no clinically validated criteria exist that can be used for such a purpose [32]. Moreover, usually color Doppler ultrasonography cannot be used at the level of the jugular foramen because of the bones in this area. This lack of understanding of relevant vs. irrelevant flow disturbances in the IJV is probably responsible for discordant results of the diagnostic studies in these veins [33].
Currently, the significance of irregular flow in blood vessels in the medical literature is not adequately understood. Doctors acknowledge that in most of blood vessels, the energy losses resulting in a drop of pressure come from friction. But in some blood vessels, frictional energy losses are accompanied by other types of losses, in physics commonly referred to as minor losses [34,35]. These energy losses primarily result from flow separation that typically develops when a blood vessel bends or suddenly expands. Except for aneurysms (pathologically enlarged arteries), the significance of flow separation and their associated minor losses has been largely ignored by medical research. In the case of abdominal aortic aneurysms, numerical simulations explained that flow separation and stagnation inside the aneurysm, and not an increased tension of the aneurysmatic wall, are primarily responsible for ruptures [36,37,38,39,40]. Similarly, CFD studies on cerebral artery aneurysms helped in the proper understanding of flow phenomena occurring in these pathological dilatations. It subsequently resulted in designing special stents that currently are routinely used for the treatment of cerebral aneurysms [41,42,43,44]. Flow abnormalities resulting in flow separation can severely impair blood flow, and IJVs are probably one of those blood vessels where these phenomena are of clinical consequence [45]. Still, it should be emphasized that unlike cerebral and aortic aneurysms, we are very far from comprehending these flow phenomena. Our study could be seen as one of the earliest initial steps in this process.
We acknowledge that there are limitations to our study. Firstly, to facilitate simulations, we built models comprising only one side of the cerebral outflow. Models with two IJVs could provide further insight into this problem, especially if only one IJV is affected. Secondly, valve leaflets in our models were stiff and immobile. In reality, they exhibit different levels of elasticity and movability. In our other in silico study, we demonstrated that there is a dynamic interplay between stenoses located upstream and valves located downstream, and that a relevant stenosis changes the valve geometry to the unfavorable one [46]. Thirdly, flow volume measurements using the “probes” were not very precise. Yet, even such an approximate assessment could provide useful insight into the problem studied. Besides, flow modeling using our CFD package was probably prone to developing significant errors when the flow resistances in the studied fields were high; thus, we obtained very different total flow volumes in particular models (see Table 1).
Other limitations of this study are associated with the use of simplified models instead of the real morphology-based ones. Besides, the interplay between the veins and surrounding tissues should also be modeled. Also, in living subjects, the vertebral veins dilate when they become the primary outflow route from the brain (e.g., in the sitting or standing humans, but also in a case of IJV stenosis). In our simulations, the morphology of the vertebral outflow route remained unchanged, which probably accounted for decreased flow volumes in the models with stenoses (see Table 1).
It should also be mentioned that in this study, the fluid was considered Newtonian. In reality, blood is a non-Newtonian fluid. Since blood is a shear-thinning fluid, slowing down its flow is associated with a higher flow resistance than that of a Newtonian fluid, which probably resulted in non-adequate flow modeling. However, the level of errors associated with non-Newtonian characteristics of blood is difficult to estimate. Of note, flow modeling of a non-Newtonian fluid cannot be conducted using such a simple CFD package, such as the one used in our study. Besides, non-Newtonian characteristics of blood is not linear, it depends on multiple factors, such as hematocrit, flow velocity, turbulences, blood plasma composition, and interactions with the endothelium. Therefore, even more powerful CFD software and computers would not solve all these variables. Yet, at least regarding the problem studied in this paper, all these shortcomings do not seem very relevant. Since this study was aimed at understanding the clinical relevance of the strictures in the IJV, despite a lack of precise flow estimations (like in the engineering studies) and alongside comparisons of these simulations to the body of current medical evidence, any resulting inaccuracies from the use of Newtonian fluid do not seem substantial.
Some uncertainties regarding the interpretation of imaging studies could be explained by our CFD modeling. For example, morphological abnormalities of the IJV in the form of flattening of its upper part at the level of the first cervical vertebra were found in MR examination more frequently in multiple sclerosis patients than in healthy controls [20,21,47,48,49]. Still, in a majority of such patients, both color Doppler sonographic and catheter venography examinations were unable to reveal any hemodynamically significant stenoses at this level. Our numerical simulations provide an explanation of this discordance. In the current diagnostic recommendations [18], bidirectional flow detected in the IJV is interpreted as the reflux (a completely reversed flow), indicating the jugular valve failure. Our numerical simulations suggest that such a bidirectional Doppler spectrum rather reflects the flow separation, with the areas characterized by flow reversal. These abnormalities result from flow disturbances evoked by the strictures in the upper part of IJV, not the valve. Of note, catheter venography may fail to demonstrate a hemodynamically relevant stenosis in this area, especially if the tip of the catheter is positioned at the level of the upper stenosis or lower. Considering our findings, should a relevant stenosis be diagnosed, MR imaging should demonstrate a narrowed IJV (e.g., due to compression by an enlarged transverse process of the first vertebra) and color Doppler sonography should reveal an abnormal spectrum in the middle and lower segments of this vein. Similarly, a hemodynamically relevant pathological jugular valve should be diagnosed if an abnormal morphology is demonstrated by ultrasonography and the flow above such a valve is slowed down but it is not “bidirectional”. Of course, in many patients, both upper and lower strictures can coexist and abnormalities found in imaging examinations in such patients can be more complex. Nonetheless, this study can serve the purpose of being a framework for future research in this field.

5. Conclusions

Numerical flow simulations of the flow in the IJVs suggest that both upper and lower strictures of these veins can be of clinical significance. Therefore, clinical studies on these veins, especially in the context of neurological pathologies, should comprise morphological and functional assessments of the entire course of the IJVs, from their origin in the cranial cavity to their junction with the brachiocephalic veins in the neck. It particularly regards possible stenoses at the level of the jugular foramen, as well as the jugular valve and other intraluminal structures located in the lower part of the IJV.

Author Contributions

Conceptualization, M.S.; methodology, M.S. and J.C.; software, M.S.; validation, M.S. and P.L.; formal analysis, M.S. and A.K.; investigation, J.C. and U.K.; resources, M.S.; data curation, M.S., A.K. and P.L; writing—original draft preparation, M.S.; writing—review and editing, P.L.; supervision, M.S.; project administration, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by research grant of the University of Opole.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Source data presented in this study are available on request from the corresponding author. Preprint version of this paper is available at: https://doi.org/10.20944/preprints202403.1639.v1.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Cirovic, S.; Walsh, C.; Fraser, W.D.; Gulino, A. The effect of posture and positive pressure breathing on the hemodynamics of the internal jugular vein. Aviat Space Environ. Med. 2003, 74, 125–131. [Google Scholar] [PubMed]
  2. Ciuti, G.; Righi, D.; Forzoni, L.; Fabbri, A.; Pignone, A.M. differences between internal jugular vein and vertebral vein flow examined in real time with the use of multigate ultrasound color doppler. Am. J. Neuroradiol. 2013, 34, 2000–2004. [Google Scholar] [CrossRef] [PubMed]
  3. Doepp, F.; Schreiber, S.J.; von Műnster, T.; Rademacher, J.; Klingebiel, R.; Valdueza, J.M. How does the blood leave the brain? A systematic ultrasound analysis of cerebral venous drainage patterns. Neuroradiology 2004, 46, 565–570. [Google Scholar] [CrossRef]
  4. Schaller, B. Physiology of cerebral venous blood flow: From experimental data in animals to normal function in humans. Brain Res. Rev. 2004, 46, 243–260. [Google Scholar] [CrossRef] [PubMed]
  5. Schreiber, S.J.; Lürtzing, F.; Götze, R.; Doepp, F.; Klingbiel, R.; Valdueza, J.M. Extrajugular pathways of human cerebral venous blood drainage assessed by duplex ultrasound. J. Appl. Physiol. 2003, 94, 1802–1805. [Google Scholar] [CrossRef] [PubMed]
  6. Simka, M.; Czaja, J.; Kowalczyk, D. Collapsibility of the internal jugular veins in the lateral decubitus body position: A potential role of the cerebral venous outflow against neurodegeneration. Med. Hypotheses 2019, 133, 109397. [Google Scholar] [CrossRef] [PubMed]
  7. Zaniewski, M.; Simka, M. Biophysics of venous return from the brain from the perspective of the pathophysiology of chronic cerebrospinal venous insufficiency. Rev. Recent Clin. Trials 2012, 7, 88–92. [Google Scholar] [CrossRef]
  8. Alpini, D.C.; Bavera, P.M.; Hahn, A.; Mattei, V. Chronic cerebrospinal venous insufficiency (CCSVI) in Meniere disease: Case or cause? Sci. Med. 2013, 4, 9–15. [Google Scholar]
  9. Beggs, C.; Chung, C.P.; Bergsland, N.; Wang, P.-N.; Shepherd, S.; Cheng, C.-Y.; Dwyer, M.G.; Hu, H.-H.; Zivadinov, R. Jugular venous reflux and brain parenchyma volumes in elderly patients with mild cognitive impairment and Alzheimer’s disease. BMC Neurol. 2013, 13, 157. [Google Scholar] [CrossRef] [PubMed]
  10. Cheng, C.Y.; Chang, F.C.; Chao, A.C.; Chung, C.-P.; Hu, H.-H. Internal jugular venous abnormalities in transient monocular blindness. BMC Neurol. 2013, 13, 94. [Google Scholar] [CrossRef] [PubMed]
  11. Chung, C.P.; Beggs, C.; Wang, P.N.; Bergsland, N.; Shepherd, S.; Cheng, C.Y.; Ramasamy, D.P.; Dwyer, M.G.; Hu, H.H.; Zivadinov, R. Jugular venous reflux and white matter abnormalities in Alzheimer’s disease: A pilot study. J. Alzheimer Dis. 2014, 39, 601–609. [Google Scholar] [CrossRef] [PubMed]
  12. Ding, J.Y.; Zhou, D.; Pan, L.Q.; Ya, J.; Liu, C.; Yan, F.; Fan, C.; Ding, Y.; Ji, X.; Meng, R. Cervical spondylotic internal jugular venous compression syndrome. CNS Neurosci. Ther. 2020, 26, 47–54. [Google Scholar] [CrossRef] [PubMed]
  13. Sethi, S.K.; Utriainen, D.T.; Daugherty, A.M.; Feng, W.; Hewett, J.J.; Raz, N.; Haacke, E.M. Jugular venous flow abnormalities in multiple sclerosis patients compared to normal controls. J. Neuroimaging 2015, 25, 600–607. [Google Scholar] [CrossRef] [PubMed]
  14. Simka, M.; Latacz, P.; Ludyga, T.; Kazibudzki, M.; Świerad, M.; Janas, P.; Piegza, J. Prevalence of extracranial venous abnormalities: Results from a sample of 586 multiple sclerosis patients. Funct. Neurol. 2011, 26, 197–203. [Google Scholar] [PubMed]
  15. Zivadinov, R.; Marr, K.; Cutter, G.; Ramanathan, M.; Benedict, R.H.; Kennedy, C.; Elfadil, M.; Yeh, A.E.; Reuther, J.; Brooks, C.; et al. Prevalence, sensitivity, and specificity of chronic cerebrospinal venous insufficiency in MS. Neurology 2011, 77, 38–44. [Google Scholar] [CrossRef] [PubMed]
  16. Simka, M.; Hubbard, D.; Siddiqui, A.H.; Dake, M.D.; Sclafani, S.J.; Al-Omari, M.; Eisele, C.G.; Haskal, Z.J.; Ludyga, T.; Miloševič, Z.V.; et al. Catheter venography for the assessment of internal jugular veins and azygous vein: Position statement by expert panel of the International Society for Neurovascular Disease. Vasa 2013, 42, 168–176. [Google Scholar] [CrossRef] [PubMed]
  17. Zamboni, P.; Morovic, P.; Menegatti, E.; Viselner, G.; Nicolaides, A.N. Screening for chronic cerebrospinal venous insufficiency (CCSVI) using ultrasound—Recommendations for a protocol. Int. Angiol. 2011, 30, 571–597. [Google Scholar] [PubMed]
  18. Zivadinov, R.; Bastianello, S.; Dake, M.D.; Ferral, H.; Haacke, E.M.; Haskal, Z.J.; Hubbard, D.; Liasis, N.; Mandato, K.; Sclafani, S.; et al. Recommendations for multimodal noninvasive and invasive screening for detection of extracranial venous abnormalities indicative of chronic cerebrospinal venous insufficiency: A position statement of the International Society for Neurovascular Disease. J. Vasc. Interv. Radiol. 2014, 25, 1785–1794.e17. [Google Scholar] [CrossRef]
  19. Simka, M.; Latacz, P. Numerical modeling of blood flow in the internal jugular vein with the use of computational fluid mechanics software. Phlebology 2021, 36, 541–548. [Google Scholar] [CrossRef] [PubMed]
  20. Feng, W.; Utriainen, D.; Trifan, G.; Elias, S.; Sethi, S.; Hewett, J.; Haacke, E.M. Characteristics of flow through the internal jugular veins at cervical C2/C3 and C5/C6 levels for multiple sclerosis patients using MR phase contrast imaging. Neurol. Res. 2012, 34, 802–809. [Google Scholar] [CrossRef] [PubMed]
  21. Haacke, E.M.; Feng, W.; Utriainen, D.; Trifan, G.; Wu, Z.; Latif, Z.; Katkuri, Y.; Hewett, J.; Hubbard, D. Patients with multiple sclerosis with structural venous abnormalities on MR Imaging exhibit an abnormal flow distribution of the internal jugular veins. J. Vasc. Interv. Radiol. 2012, 23, 60–68. [Google Scholar] [CrossRef] [PubMed]
  22. Simka, M.; Skuła, M.; Bielaczyc, G. Validation of models of venous outflow from the cranial cavity in the supine and upright body positions. Phlebol. Rev. 2022, 30, 8–12. [Google Scholar] [CrossRef]
  23. Phillips, R.A.; Van Slyke, D.D.; Hamilton, P.B.; Dole, V.P.; Emerson, K.; Archibald, R.M. Measurement of specific gravities of whole blood and plasma by standard copper sulfate solutions. J. Biol. Chem. 1950, 183, 305–330. [Google Scholar] [CrossRef]
  24. Trudnowski, R.J.; Rico, R.C. Specific gravity of blood and plasma at 4 and 37 °C. Clin. Chem. 1974, 20, 615–616. [Google Scholar] [CrossRef] [PubMed]
  25. Caiazzo, A.; Montecinos, G.; Müller, L.O.; Haacke, E.M.; Toro, E.F. Computational haemodynamics in stenotic internal jugular veins. J. Math. Biol. 2015, 70, 745–772. [Google Scholar] [CrossRef]
  26. Carini, V. A Computational Fluid Structure Interaction Study in Internal Jugular Veins Subjected to Gravity. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 2017. [Google Scholar]
  27. Zivadinov, R.; Chung, C.P. Potential involvement of the extracranial venous system in central nervous system disorders and aging. BMC Med. 2013, 11, 60. [Google Scholar] [CrossRef] [PubMed]
  28. Simka, M. Activation of the glymphatic system during sleep—Is the cerebral venous outflow a missing piece of the puzzle? Phlebol. Rev. 2019, 7, 1–2. [Google Scholar] [CrossRef]
  29. Zamboni, P.; Tesio, L.; Galimberti, S.; Massacesi, L.; Salvi, F.; D’alessandro, R.; Cenni, P.; Galeotti, R.; Papini, D.; D’amico, R.; et al. Efficacy and safety of extracranial vein angioplasty in multiple sclerosis. JAMA Neurol. 2018, 75, 35–43. [Google Scholar] [CrossRef] [PubMed]
  30. Zamboni, P.; Galeotti, R.; Salvi, F.; Giaquinta, A.; Setacci, C.; Alborino, S.; Guzzardi, G.; Sclafani, S.J.; Maietti, E.; Veroux, P.; et al. Effects of Venous Angioplasty on Cerebral Lesions in Multiple Sclerosis: Expanded Analysis of the Brave Dreams Double-Blind, Sham-Controlled Randomized Trial. J. Endovasc. Ther. 2020, 27, 1526602819890110. [Google Scholar] [CrossRef] [PubMed]
  31. Simka, M. An overview of randomized controlled trials on endovascular treatment for chronic cerebrospinal venous insufficiency in multiple sclerosis patients. Phlebologie 2021, 50, 76–80. [Google Scholar] [CrossRef]
  32. Simka, M.; Ludyga, T.; Latacz, P.; Kazibudzki, M. Diagnostic accuracy of current sonographic criteria for the detection of outflow abnormalities in the internal jugular veins. Phlebology 2013, 28, 285–292. [Google Scholar] [CrossRef] [PubMed]
  33. Simka, M. Chronic cerebrospinal venous insufficiency: Current perspectives. J. Vasc. Diagn. 2014, 2, 1–13. [Google Scholar] [CrossRef]
  34. Rend, R.R.; Sparrow, E.M.; Bettenhausen, D.W.; Abraham, J. Parasitic pressure losses in diffusers and in their downstream piping systems for fluid flow and heat transfer. Int. J. Heat Mass Transf. 2013, 61, 56–61. [Google Scholar] [CrossRef]
  35. Li, L.; Walker, A.M.; Rival, D.E. The characterization of a non-Newtonian blood analog in natural- and shear-layer-induced transitional flow. Biorheology 2014, 51, 275–291. [Google Scholar] [CrossRef] [PubMed]
  36. Mariotti, A.A.; Boccadifuoco, A.; Celi, S.; Salvetti, M.V. Hemodynamics and stresses in numerical simulations of the thoracic aorta: Stochastic sensitivity analysis to inlet flow-rate waveform. Comput. Fluids 2021, 230, 105123. [Google Scholar] [CrossRef]
  37. Morbiducci, U.; Ponzini, R.; Gallo, D.; Bignardi, C.; Rizzo, G. Inflow boundary conditions for image-based computational hemodynamics: Impact of idealized versus measured velocity profiles in the human aorta. J. Biomech. 2013, 46, 102–109. [Google Scholar] [CrossRef] [PubMed]
  38. Bhagavan, D.; Di Achille, P.; Humphre, Y.D. Strongly coupled morphological features of aortic aneurysms drive intraluminal thrombus. Sci. Rep. 2018, 8, 13273. [Google Scholar] [CrossRef] [PubMed]
  39. Joly, F.; Soulez, G.; Garcia, D.; Lessard, S.; Kauffmann, C. Flow stagnation volume and abdominal aortic aneurysm growth: Insights from patient-specific computational flow dynamics of Lagrangian-coherent structures. Comput. Biol. Med. 2018, 92, 98–109. [Google Scholar] [CrossRef] [PubMed]
  40. Lozowy, R.J.; Kuhn, D.C.; Ducas, A.A.; Boyd, A.J. The relationship between pulsatile flow impingement and intraluminal thrombus deposition in abdominal aortic aneurysms. Cardiovasc. Eng. Technol. 2017, 8, 57–69. [Google Scholar] [CrossRef] [PubMed]
  41. Wang, C.; Tian, Z.; Liu, J.; Jing, L.; Paliwal, N.; Wang, S.; Zhang, Y.; Xiang, J.; Siddiqui, A.H.; Meng, H.; et al. Flow diverter effect of LVIS stent on cerebral aneurysm hemodynamics: A comparison with Enterprise stents and the Pipeline device. J. Transl. Med. 2016, 14, 199. [Google Scholar] [CrossRef]
  42. Li, G.; Song, X.; Wang, H.; Liu, S.; Ji, J.; Guo, Y.; Qiao, A.; Liu, Y.; Wang, X. Prediction of cerebral aneurysm hemodynamics with porous-medium models of flow-diverting stents via deep learning. Front. Physiol. 2021, 12, 733444. [Google Scholar] [CrossRef] [PubMed]
  43. Kim, S.; Yang, H.; Hong, I.; Oh, J.H.; Kim, Y.B. computational study of hemodynamic changes induced by overlapping and compacting of stents and flow diverter in cerebral aneurysms. Front. Neurol. 2021, 12, 705841. [Google Scholar] [CrossRef] [PubMed]
  44. Satoh, T.; Sugiu, K.; Hiramatsu, M.; Haruma, J.; Date, I. Evaluation of the shrinkage process of a neck remnant after stent-coil treatment of a cerebral aneurysm using silent magnetic resonance angiography and computational fluid dynamics analysis: Illustrative case. J. Neurosurg. Case Lessons 2024, 7, CASE24141. [Google Scholar] [CrossRef] [PubMed]
  45. Simka, M.; Latacz, P.; Redelbach, W. Blood flow in the internal jugular veins during the spaceflight—Is it actually bidirectional? Life Sci. Space Res. 2020, 25, 103–106. [Google Scholar] [CrossRef] [PubMed]
  46. Rashid, A.; Iqrar, S.A.; Rashid, A.; Simka, M. Results of numerical modeling of blood flow in the internal jugular vein exhibiting different types of strictures. Diagnostics 2022, 12, 2862. [Google Scholar] [CrossRef] [PubMed]
  47. Zivadinov, R.; Karmon, Y.; Dolic, K.; Hagemeier, J.; Marr, K.; Valnarov, V.; Kennedy, C.L.; Hojnacki, D.; Carl, E.M.; Hopkins, L.N.; et al. Multimodal noninvasive and invasive imaging of extracranial venous abnormalities indicative of CCSVI: Results of the PREMiSe pilot study. BMC Neurol. 2013, 13, 151. [Google Scholar] [CrossRef] [PubMed]
  48. Rahman, M.T.; Sethi, S.K.; Utriainen, D.T.; Hewett, J.J.; Haacke, E.M. A comparative study of magnetic resonance venography techniques for the evaluation of the internal jugular veins in multiple sclerosis patients. Magn. Reson. Imaging 2013, 31, 1668–1676. [Google Scholar] [CrossRef] [PubMed]
  49. Zaharchuk, G.; Fischbein, N.J.; Rosenberg, J.; Herfkens, R.J.; Dake, M.D. Comparison of MR and contrast venography of the cervical venous system in multiple sclerosis. Am. J. Neuroradiol. 2011, 32, 1482–1489. [Google Scholar] [CrossRef] [PubMed]
Applsci 14 03878 g001
Figure 1. Mesh independence study graph.
Figure 1. Mesh independence study graph.
Applsci 14 03878 g001
Applsci 14 03878 g002
Figure 2. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below). In this particular model, the valve-shaped stricture is at the end of the model of the internal jugular vein, and flow was from the left to the right but the simulation has not yet started. The deep blue color represents no flow.
Figure 2. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below). In this particular model, the valve-shaped stricture is at the end of the model of the internal jugular vein, and flow was from the left to the right but the simulation has not yet started. The deep blue color represents no flow.
Applsci 14 03878 g002
Applsci 14 03878 g003
Figure 3. The view from inside the model without strictures. The green arrow is pointing at the beginning of jugular vein, and the blue arrow is pointing at the network of channels in the vertebral outflow route.
Figure 3. The view from inside the model without strictures. The green arrow is pointing at the beginning of jugular vein, and the blue arrow is pointing at the network of channels in the vertebral outflow route.
Applsci 14 03878 g003
Applsci 14 03878 g004
Figure 4. Stenosis at the beginning of the internal jugular vein (arrow) seen from outside (A) and inside (B).
Figure 4. Stenosis at the beginning of the internal jugular vein (arrow) seen from outside (A) and inside (B).
Applsci 14 03878 g004
Applsci 14 03878 g005
Figure 5. Stenotic jugular valve (arrow) seen from outside (A) and inside (B).
Figure 5. Stenotic jugular valve (arrow) seen from outside (A) and inside (B).
Applsci 14 03878 g005
Applsci 14 03878 g006
Figure 6. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below). Magenta squares represent the probes—in these areas flow characteristics was measured. Flow is from the left to the right. In this model, there are no stenoses in the internal jugular vein; consequently, most of the outflow utilizes the jugular pathway.
Figure 6. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below). Magenta squares represent the probes—in these areas flow characteristics was measured. Flow is from the left to the right. In this model, there are no stenoses in the internal jugular vein; consequently, most of the outflow utilizes the jugular pathway.
Applsci 14 03878 g006
Applsci 14 03878 g007
Figure 7. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below); magenta squares represent the probes. Flow is from the left to the right. There are 2 strictures in the internal jugular vein: in the beginning (white arrow) and at its end (black arrow). In the model with stenoses, part of the flow is shifted towards the vertebral pathway.
Figure 7. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below); magenta squares represent the probes. Flow is from the left to the right. There are 2 strictures in the internal jugular vein: in the beginning (white arrow) and at its end (black arrow). In the model with stenoses, part of the flow is shifted towards the vertebral pathway.
Applsci 14 03878 g007
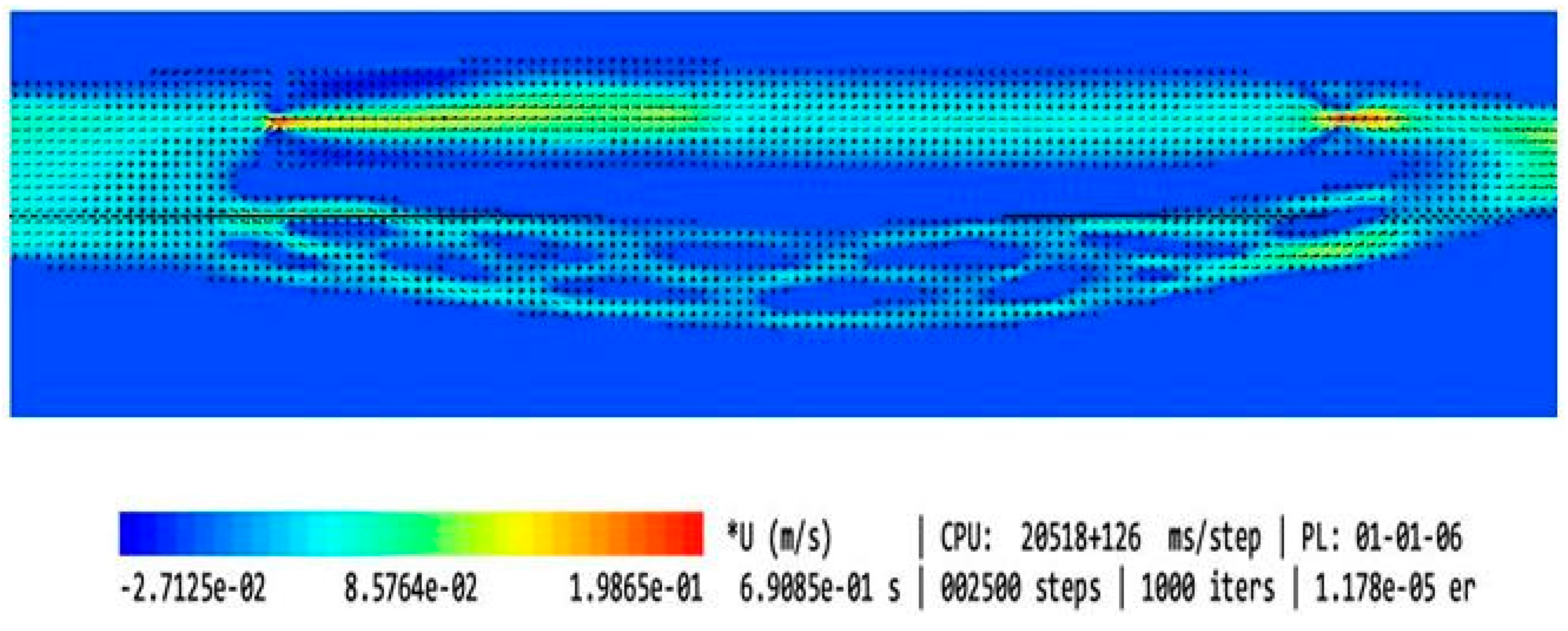
Applsci 14 03878 g008
Figure 8. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below); flow is from the left to the right. There is a significant stenosis at the beginning of the jugular pathway and stenotic valve downstream.
Figure 8. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below); flow is from the left to the right. There is a significant stenosis at the beginning of the jugular pathway and stenotic valve downstream.
Applsci 14 03878 g008
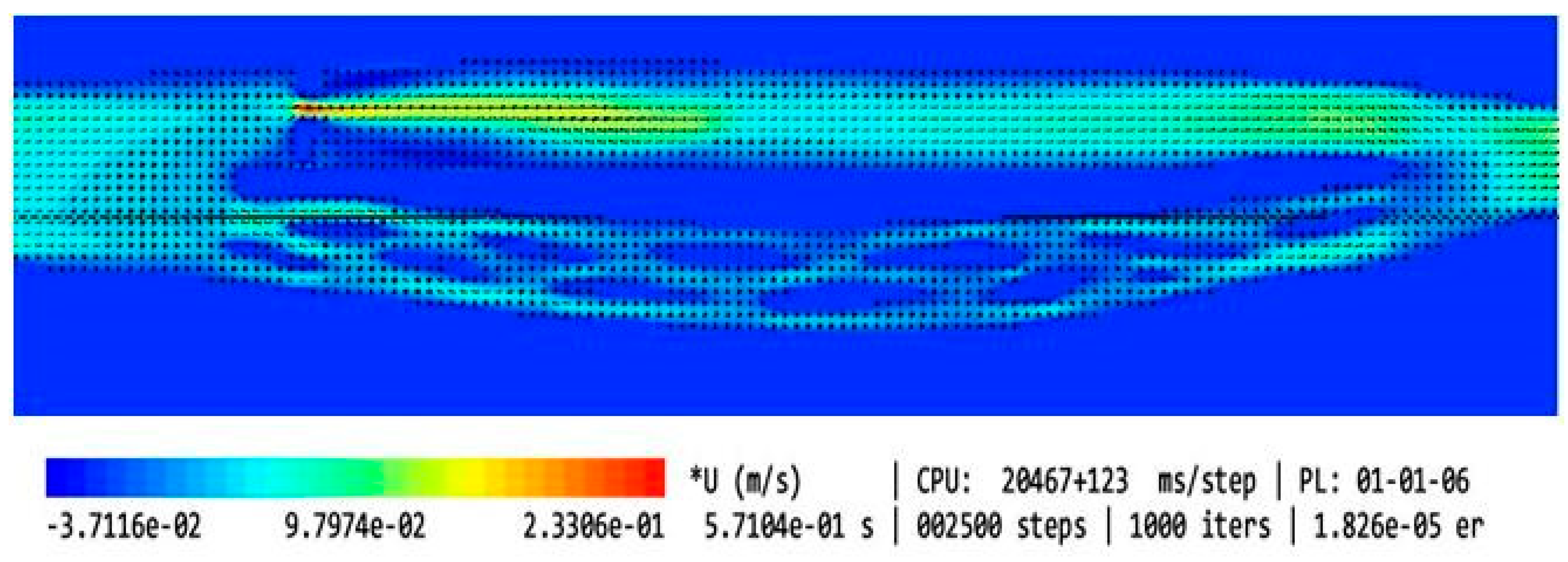
Applsci 14 03878 g009
Figure 9. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below); flow is from the left to the right. There is a significant stenosis at the beginning of the jugular pathway and no valve downstream.
Figure 9. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below); flow is from the left to the right. There is a significant stenosis at the beginning of the jugular pathway and no valve downstream.
Applsci 14 03878 g009
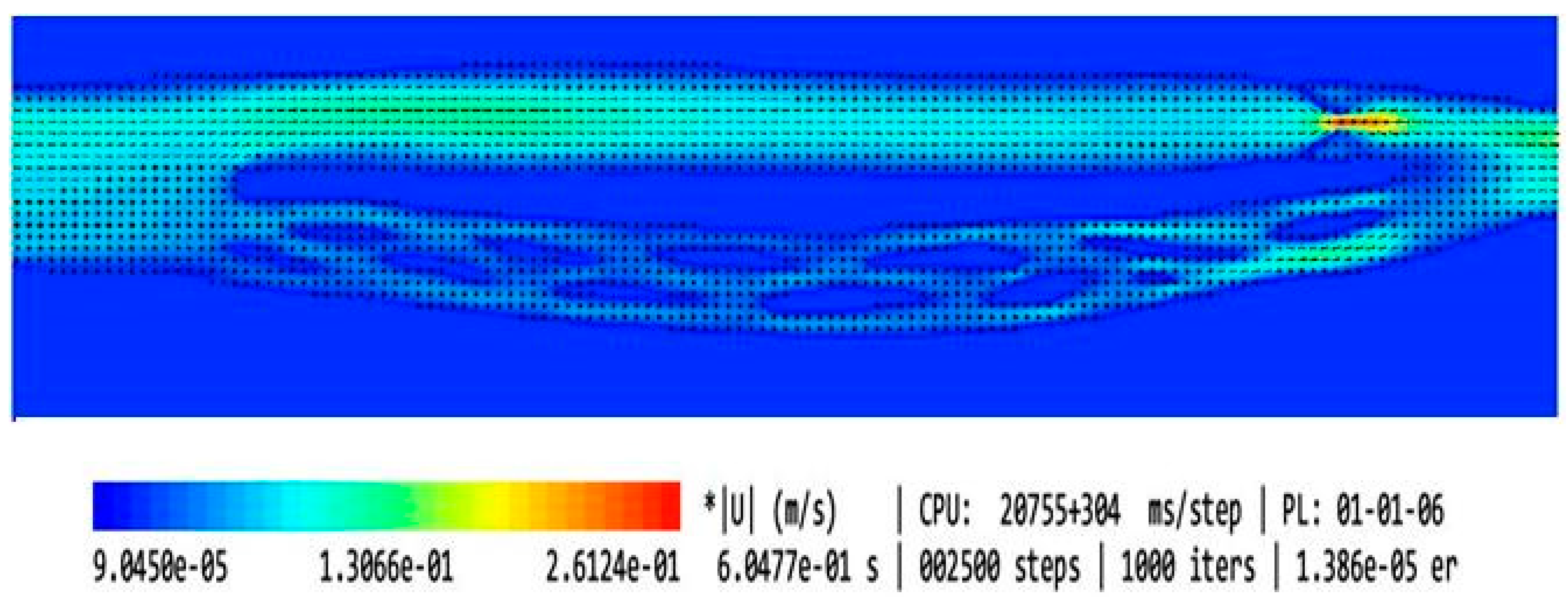
Applsci 14 03878 g010
Figure 10. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below); flow is from the left to the right. Upper part of the jugular pathway is unrestricted and there is a stenotic valve downstream.
Figure 10. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below); flow is from the left to the right. Upper part of the jugular pathway is unrestricted and there is a stenotic valve downstream.
Applsci 14 03878 g010
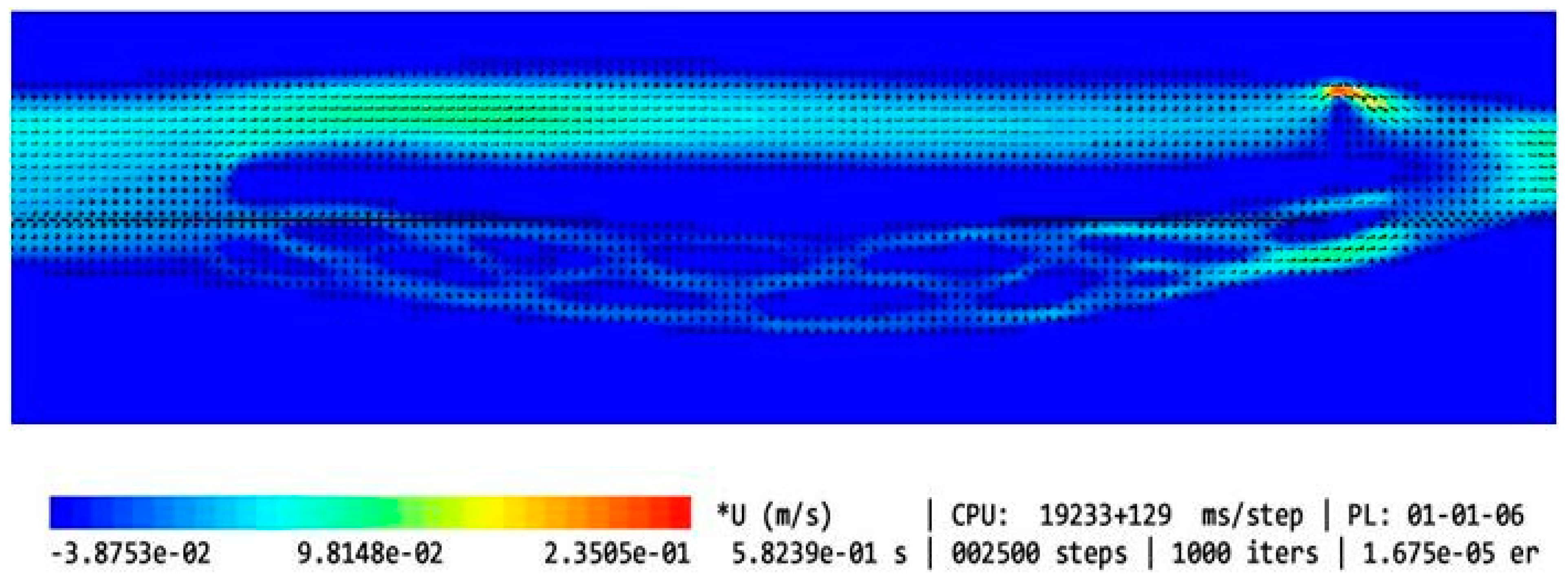
Applsci 14 03878 g011
Figure 11. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below); flow is from the left to the right. Upper part of the jugular pathway is unrestricted, while downstream there is a septum nearly completely obstructing the outflow.
Figure 11. Model of the cerebral venous outflow comprising the internal jugular vein (above) and the vertebral venous plexus (below); flow is from the left to the right. Upper part of the jugular pathway is unrestricted, while downstream there is a septum nearly completely obstructing the outflow.
Applsci 14 03878 g011
Table 1. Characteristic of the strictures in the modeled internal jugular vein, flow volumes in the jugular, and vertebral pathways.
Table 1. Characteristic of the strictures in the modeled internal jugular vein, flow volumes in the jugular, and vertebral pathways.
Type of the ModelShape of the Upper Nozzle-like Stricture Cross-Sectional Area at the Level of Upper StenosisLength of the Upper StrictureValve in the Lower Part of IJVFlow Volume in the Internal Jugular
Vein
[mL/min]		Flow Volume in the Vertebral Plexus [mL/min]Total Flow in the Outflow Field [mL/min]Jugular/
Vertebral Flows
[%/%]
1Model without upper stenosis and no valveno stricture0.94 cm2no strictureno valve3213535690/10
2Model with minor upper stenosis and no valveApplsci 14 03878 i0010.42 cm22.5 mmno valve66417083480/20
3Model without upper stenosis and wide valveno stricture0.94 cm2no stricturebicuspid valve, distance between leaflets: 4.3 mm


579


187


766


76/24
4Model without upper stenosis, and narrow valveno stricture0.94 cm2no stricturebicuspid valve, distance between leaflets: 1.5 mm


446


339


785


57/43
5Model with irregularly shaped minor stenosis, and narrow valveApplsci 14 03878 i0020.60 cm32.5 mmbicuspid valve, distance between leaflets: 1.5 mm


398


301


699


57/42
6Model with elliptically shaped, centrally positioned stenosis, and narrow valveApplsci 14 03878 i0030.24 cm3 2.5 mmbicuspid valve, distance between leaflets: 1.5 mm28229457649/51
7Model with elliptically shaped, eccentrically positioned stenosis, and narrow valveApplsci 14 03878 i0040.24 cm32.5 mmbicuspid valve, distance between leaflets: 1.5 mm25029554546/54
8Model with elliptically shaped, centrally positioned long stenosis, and narrow valveApplsci 14 03878 i0050.24 cm3 12 mmbicuspid valve, distance between leaflets: 1.5 mm39644884447/53
9Model with elliptically shaped, centrally positioned severe stenosis, and narrow valveApplsci 14 03878 i0060.07 cm3 2.5 mmbicuspid valve, distance between leaflets: 1.5 mm28033761745/55
10Model with elliptically shaped, eccentrically positioned severe stenosis, and narrow valveApplsci 14 03878 i0070.07 cm3 2.5 mmbicuspid valve, distance between leaflets: 1.5 mm12616729343/57
11Model without upper stenosis, and septum instead of valveno stricture0.94 cm2no strictureseptum26356143/57
12Model with two elliptically shaped, eccentrically positioned stenoses, and narrow valveApplsci 14 03878 i0080.48 cm3 (2 × 0.24 cm3)2.5 mmbicuspid valve, distance between leaflets: 1.5 mm25029554546/54
13Model with eccentrically positioned short flattening, and normal valveApplsci 14 03878 i0090.48 cm32.5 mmbicuspid valve, distance between leaflets: 1.5 mm12115827943/57
14Model with collapsed IJVno stricturecollapsed internal jugular veinno strictureno valve498713636/64
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Simka, M.; Czaja, J.; Kawalec, A.; Latacz, P.; Kovalko, U. Numerical Modeling of Venous Outflow from the Cranial Cavity in the Supine Body Position. Appl. Sci. 2024, 14, 3878. https://doi.org/10.3390/app14093878

AMA Style

Simka M, Czaja J, Kawalec A, Latacz P, Kovalko U. Numerical Modeling of Venous Outflow from the Cranial Cavity in the Supine Body Position. Applied Sciences. 2024; 14(9):3878. https://doi.org/10.3390/app14093878

Chicago/Turabian Style

Simka, Marian, Joanna Czaja, Agata Kawalec, Paweł Latacz, and Uliana Kovalko. 2024. "Numerical Modeling of Venous Outflow from the Cranial Cavity in the Supine Body Position" Applied Sciences 14, no. 9: 3878. https://doi.org/10.3390/app14093878

APA Style

Simka, M., Czaja, J., Kawalec, A., Latacz, P., & Kovalko, U. (2024). Numerical Modeling of Venous Outflow from the Cranial Cavity in the Supine Body Position. Applied Sciences, 14(9), 3878. https://doi.org/10.3390/app14093878

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop