Bayesian Hyperparameter Optimization of Machine Learning Models for Predicting Biomass Gasification Gases
Abstract
:1. Introduction
- Optimum hyperparameter combinations for predicting biomass gas composition using machine learning were determined through Bayesian optimization.
- Machine learning model performance was analyzed under both optimal and suboptimal conditions to identify the most accurate and robust model.
- The predictive capability of the models was generalized using a comprehensive dataset aggregated from various studies.
- The statistical significance of model performance under optimal and suboptimal conditions was evaluated using t-tests and Cohen’s d.
2. Materials and Methods
2.1. Dataset Description
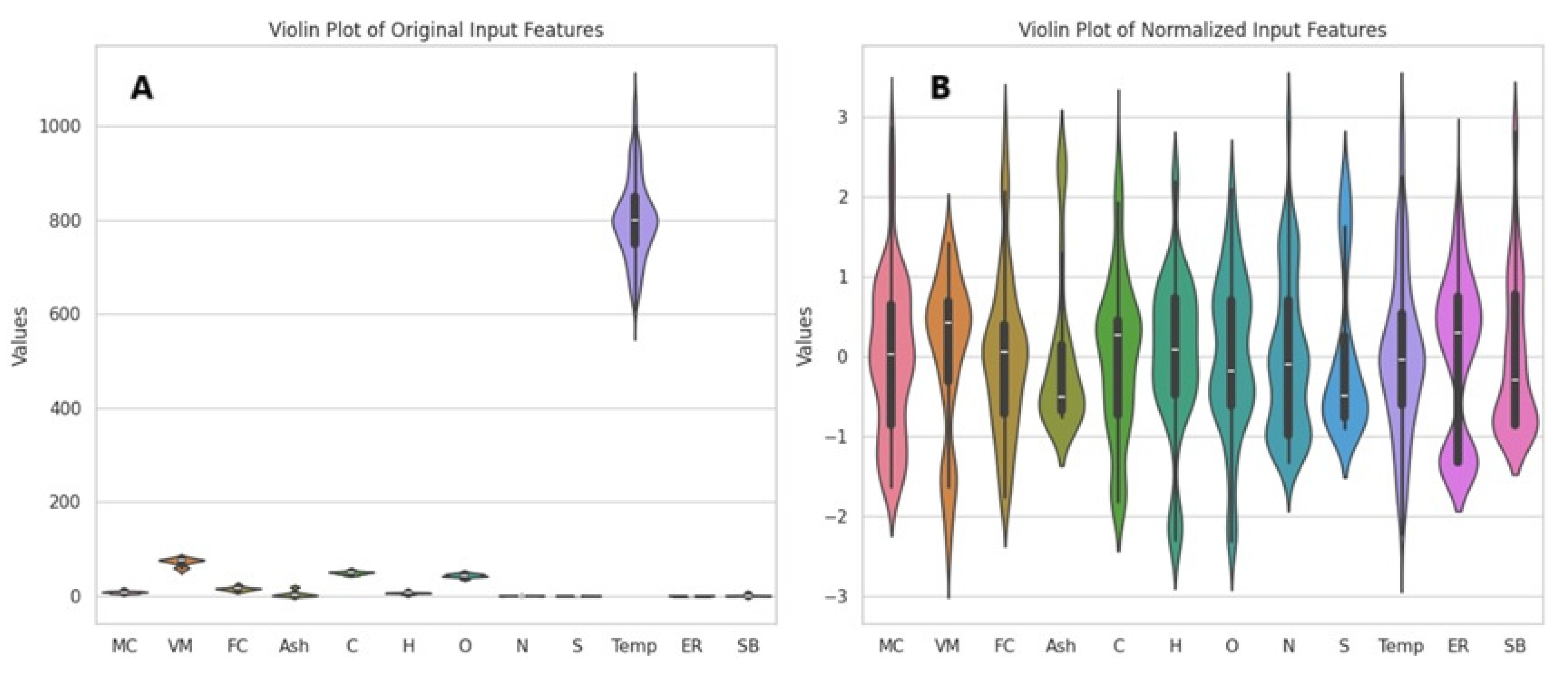
2.2. Pre-Processing Step
2.3. Machine Learning Methods
2.4. Hyperparameter Optimization
- Selection of Initial Points: Several random combinations of parameters are initially selected.
- Model Training: The model is trained with the selected hyperparameters, and predictions are made on the test data.
- Acquisition Function Maximization: The acquisition function selects new hyperparameters.
- Iteration: These steps are repeated until the optimal set of parameters is found.
2.5. Model Performance Evaluation
3. Results
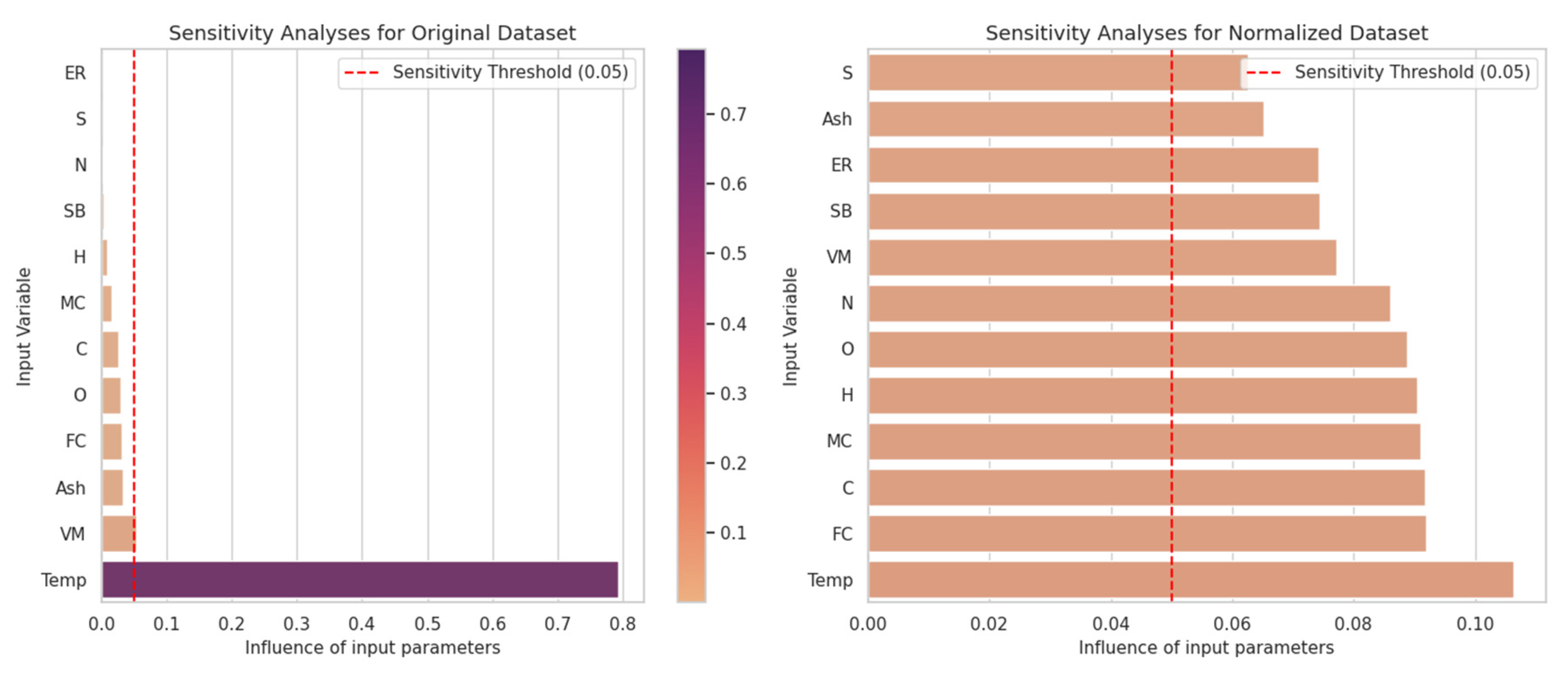
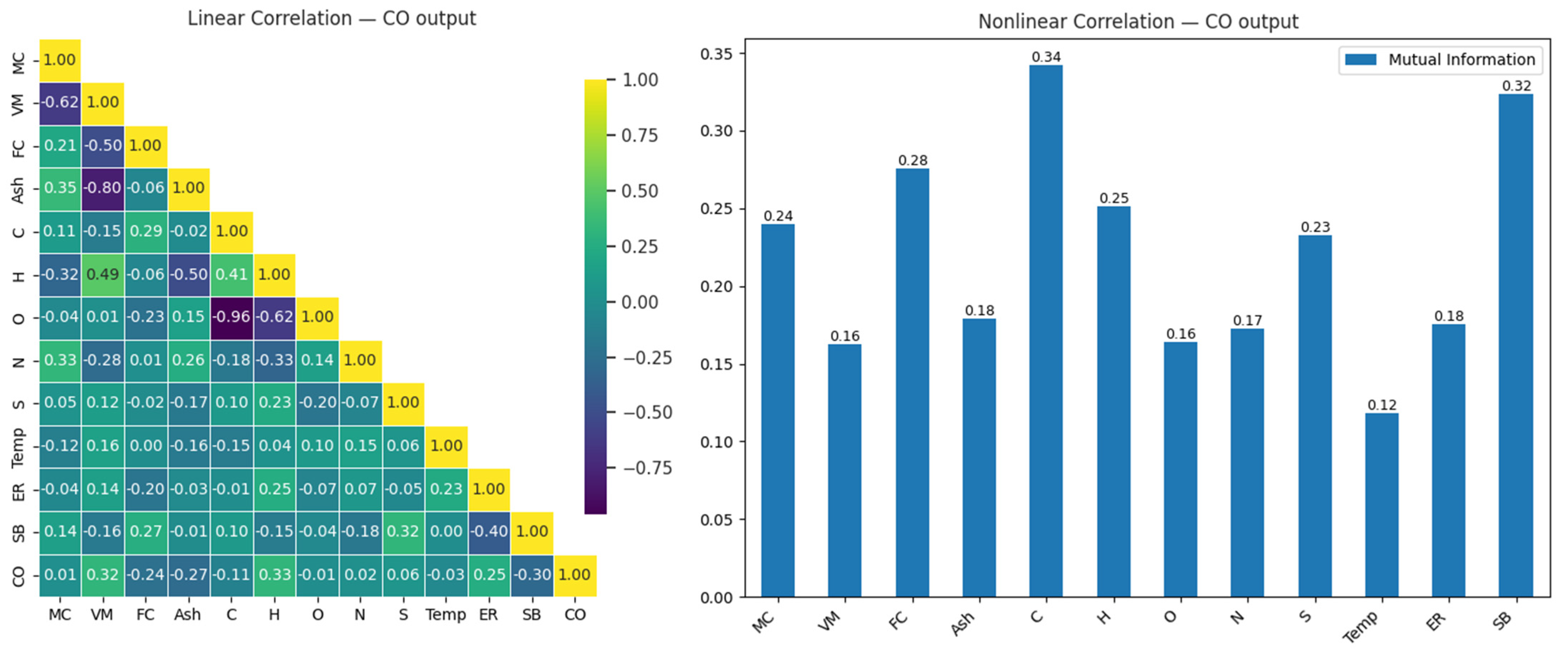
3.1. Prediction of Carbon Monoxide (CO) Gas Levels
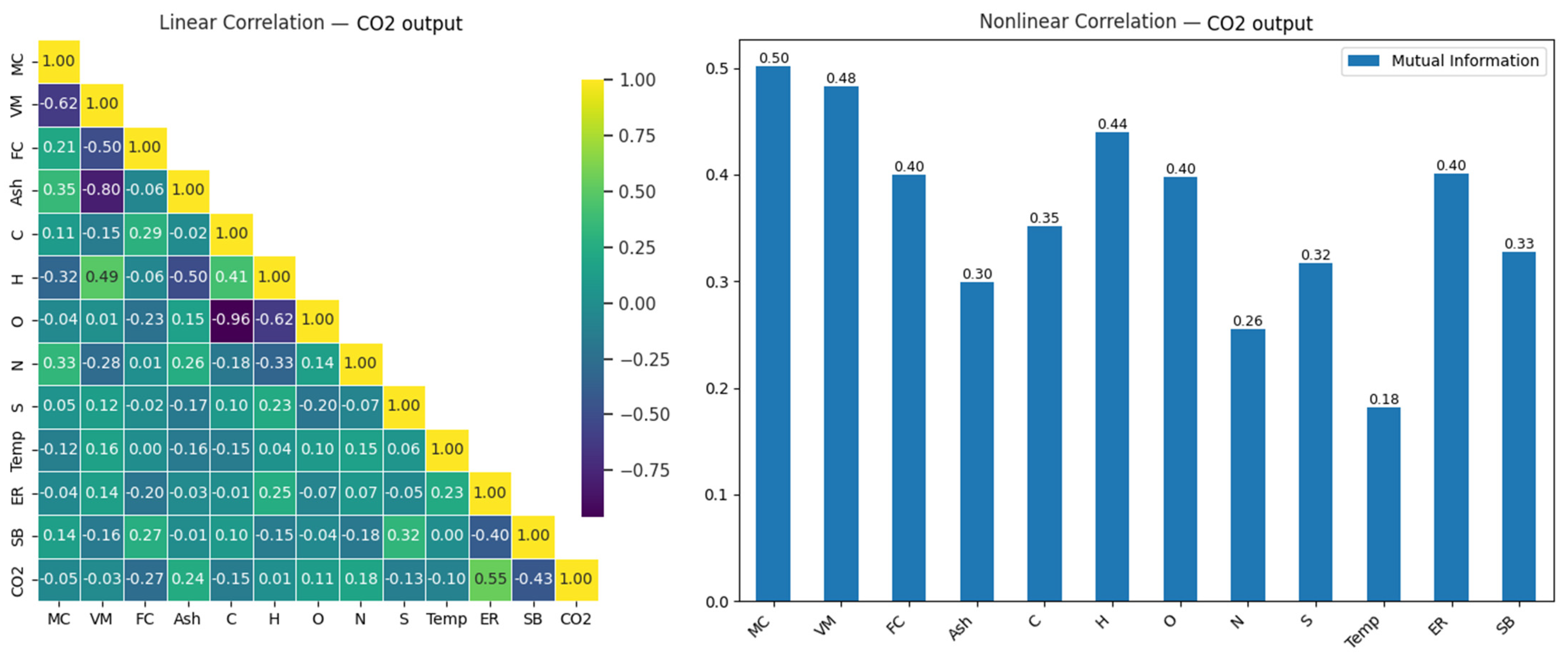
3.2. Prediction of Carbon Dioxide (CO2) Gas Levels
3.3. Prediction of Hydrogen (H2) Gas Levels
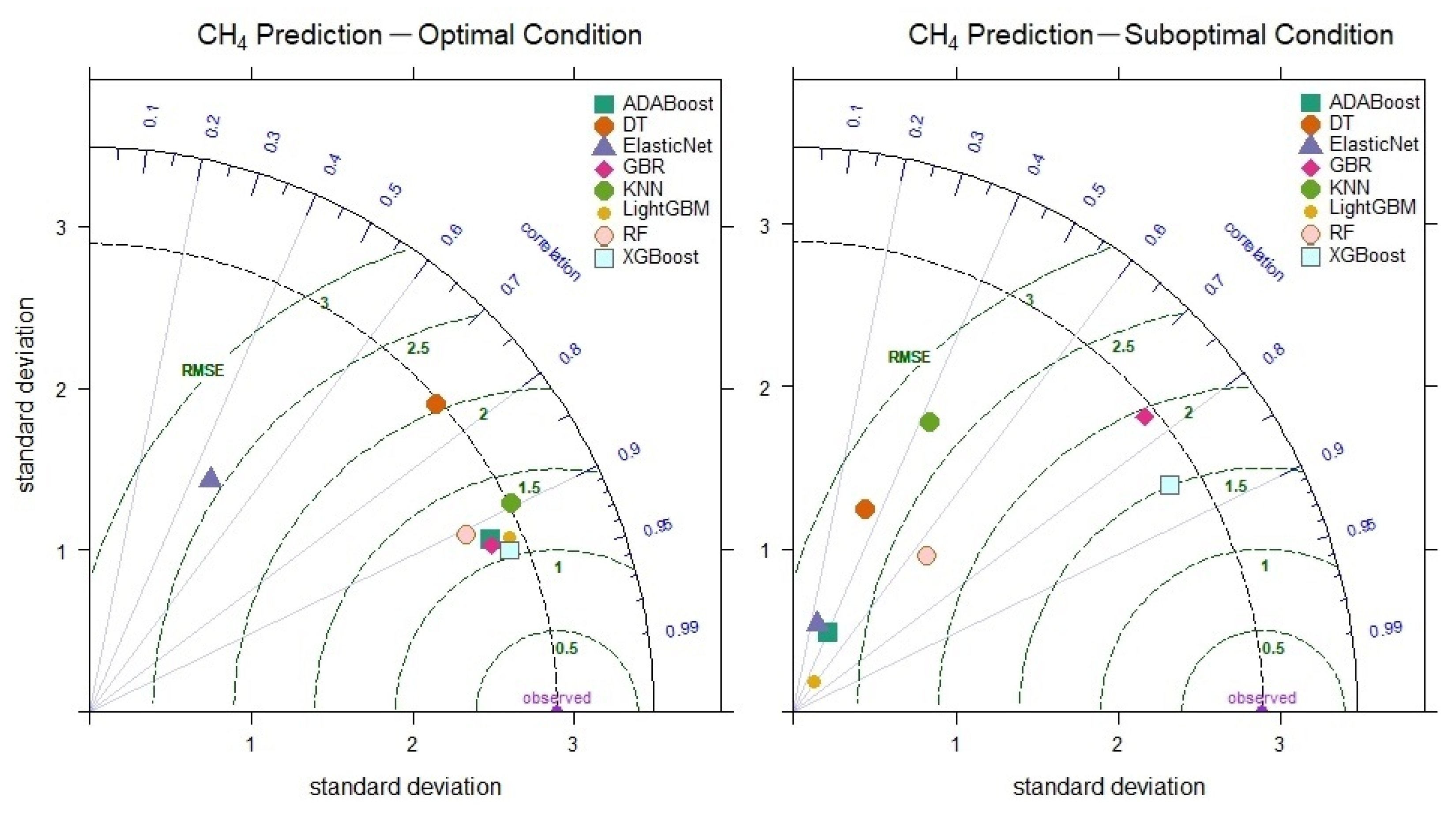
3.4. Prediction of Methane (CH4) Gas Levels
4. Discussion
- Accurate predictions of gas levels through machine learning optimize the ratios of gases to be used as fuel, thereby enhancing energy efficiency. This ensures that the biomass gasification process operates in a more efficient and energy-saving manner.
- The accurate prediction of CO, CO2, H2, and CH4 levels allows for developing environmentally friendly strategies to reduce their emissions. This, in turn, enhances the environmental sustainability of biomass gasification processes.
- Machine learning models allow for rapidly predicting gas levels in biomass gasification processes. This contributes to the process’s time efficiency and enables operators to make faster decisions.
- Instead of relying on prolonged experimental testing, machine learning allows for rapid and accurate predictions, thereby increasing the cost-effectiveness of the processes and providing significant time savings.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AdaBoost | Adaptive Boosting |
| AFR | Air Fuel Ratio |
| BAG | Bagging |
| BFB | Bubbling Fluidized Bed |
| BFR | Biomass Feed Rate |
| BM | Bed Material |
| BLS-SVM | Binary Least Squares Support Vector Machine |
| C | Carbon |
| CCE | Carbon Conversion Efficiency |
| CFR | Coal Feed Rate |
| CGE | Cold Gas Efficiency |
| R | Correlation Coefficient |
| CU | Catalyst Usage |
| DT | Devolatilization Temperature |
| DTR | Decision Tree Regression |
| Elastic Net | Elastic Net |
| ER | Equivalence Ratio |
| FC | Fixed Carbon |
| GA | Gasifying Agent |
| GB | Gradient Boosting |
| GY | Gas Yield |
| GOP | Gasifier Operation Mode |
| GBR | Gradient-Boosting Regressor |
| GS | Gasifier Scale |
| H | Hydrogen |
| KNN | K-Nearest Neighbors |
| LARS | Least-Angle Regression |
| LightGBM | Light Gradient-Boosting Machine |
| LR | Linear Regression |
| LHV | Lower Heating Value |
| MAPE | Mean Absolute Percentage Error (MAPE) |
| MC | Moisture Content |
| MC-RF | Multi-Class Random Forest Classifiers |
| MW | Molecular Weight |
| MLP | Multilayer Perceptron |
| O | Oxygen |
| PS | Particle Size |
| PR | Polynomial Regression |
| RF | Random Forest |
| RAE | Relative Absolute Error |
| RR | Ridge Regression |
| RMSE | Root Mean Squared Error |
| RT | Reactor Type |
| SA | Sensitivity Analysis |
| SB | Steam Biomass Ratio |
| SCWG | Supercritical Water Gasification |
| SFR | Steam Flow Rate |
| SVR | Support Vector Regression |
| T | Time |
| Temp | Temperature |
| VM | Volatile Matter |
| W | Catalyst Loading Amount |
| X | Carbon Conversion |
| XGBoost | Extreme Gradient Boosting |
References
- Fang, Y.; Ma, L.; Yao, Z.; Li, W.; You, S. Process optimization of biomass gasification with a Monte Carlo approach and random forest algorithm. Energy Convers. Manag. 2022, 264, 115734. [Google Scholar] [CrossRef]
- Ismail, T.M.; Shi, M.; Xu, J.; Chen, X.; Wang, F.; El-Salam, M.A. Assessment of coal gasification in a pressurized fixed bed gasifier using an ASPEN plus and Euler–Euler model. Int. J. Coal Sci. Technol. 2020, 7, 516–535. [Google Scholar] [CrossRef]
- Ozbas, E.E.; Aksu, D.; Ongen, A.; Aydin, M.A.; Ozcan, H.K. Hydrogen production via biomass gasification, and modeling by supervised machine learning algorithms. Int. J. Hydrogen Energy 2019, 44, 17260–17268. [Google Scholar] [CrossRef]
- Nguyen, T.L.T.; Hermansen, J.E.; Nielsen, R.G. Environmental assessment of gasification technology for biomass conversion to energy in comparison with other alternatives: The case of wheat straw. J. Clean. Prod. 2013, 53, 138–148. [Google Scholar] [CrossRef]
- ASEAN. ASEAN Strategy on Sustainable Biomass Energy for Agriculture Communities and Rural Development in 2020–2030. 2019. Available online: https://www.fao.org/faolex/results/details/en/c/LEX-FAOC216870/ (accessed on 10 October 2024).
- Hossain, M.R.; Rana, M.J.; Saha, S.M.; Haseeb, M.; Islam, M.S.; Amin, M.R.; Hossain, M.E. Role of energy mix and eco-innovation in achieving environmental sustainability in the USA using the dynamic ARDL approach: Accounting the supply side of the ecosystem. Renew. Energy 2023, 215, 118925. [Google Scholar] [CrossRef]
- Alfarra, F.; Ozcan, H.K.; Cihan, P.; Ongen, A.; Guvenc, S.Y.; Ciner, M.N. Artificial intelligence methods for modeling gasification of waste biomass: A review. Environ. Monit. Assess. 2024, 196, 309. [Google Scholar] [CrossRef] [PubMed]
- Kushwah, A.; Reina, T.; Short, M. Modelling approaches for biomass gasifiers: A comprehensive overview. Sci. Total Environ. 2022, 834, 155243. [Google Scholar] [CrossRef]
- Li, J.; Yao, X.; Xu, K. A comprehensive model integrating BP neural network and RSM for the prediction and optimization of syngas quality. Biomass Bioenergy 2021, 155, 106278. [Google Scholar] [CrossRef]
- Devasahayam, S.; Albijanic, B. Predicting hydrogen production from co-gasification of biomass and plastics using tree based machine learning algorithms. Renew. Energy 2024, 222, 119883. [Google Scholar] [CrossRef]
- Sison, A.E.; Etchieson, S.A.; Güleç, F.; Epelle, E.I.; Okolie, J.A. Process modelling integrated with interpretable machine learning for predicting hydrogen and char yield during chemical looping gasification. J. Clean. Prod. 2023, 414, 137579. [Google Scholar] [CrossRef]
- Elmaz, F.; Yücel, Ö.; Mutlu, A.Y. Predictive modeling of biomass gasification with machine learning-based regression methods. Energy 2020, 191, 116541. [Google Scholar] [CrossRef]
- Mutlu, A.Y.; Yucel, O. An artificial intelligence based approach to predicting syngas composition for downdraft biomass gasification. Energy 2018, 165, 895–901. [Google Scholar] [CrossRef]
- Wen, H.-T.; Lu, J.-H.; Phuc, M.-X. Applying artificial intelligence to predict the composition of syngas using rice husks: A comparison of artificial neural networks and gradient boosting regression. Energies 2021, 14, 2932. [Google Scholar] [CrossRef]
- Yucel, O.; Aydin, E.S.; Sadikoglu, H. Comparison of the different artificial neural networks in prediction of biomass gasification products. Int. J. Energy Res. 2019, 43, 5992–6003. [Google Scholar] [CrossRef]
- Serrano, D.; Golpour, I.; Sánchez-Delgado, S. Predicting the effect of bed materials in bubbling fluidized bed gasification using artificial neural networks (ANNs) modeling approach. Fuel 2020, 266, 117021. [Google Scholar]
- Ozonoh, M.; Oboirien, B.; Higginson, A.; Daramola, M. Performance evaluation of gasification system efficiency using artificial neural network. Renew. Energy 2020, 145, 2253–2270. [Google Scholar] [CrossRef]
- Shahbaz, M.; Taqvi, S.A.; Loy, A.C.M.; Inayat, A.; Uddin, F.; Bokhari, A.; Naqvi, S.R. Artificial neural network approach for the steam gasification of palm oil waste using bottom ash and CaO. Renew. Energy 2019, 132, 243–254. [Google Scholar]
- Baruah, D.; Baruah, D.C.; Hazarika, M.K. Artificial neural network based modeling of biomass gasification in fixed bed downdraft gasifiers. Biomass Bioenergy 2017, 98, 264–271. [Google Scholar] [CrossRef]
- Zhao, S.; Li, J.; Chen, C.; Yan, B.; Tao, J.; Chen, G. Interpretable machine learning for predicting and evaluating hydrogen production via supercritical water gasification of biomass. J. Clean. Prod. 2021, 316, 128244. [Google Scholar] [CrossRef]
- Ascher, S.; Sloan, W.; Watson, I.; You, S. A comprehensive artificial neural network model for gasification process prediction. Appl. Energy 2022, 320, 119289. [Google Scholar]
- Li, W.; Song, Y. Artificial neural network model of catalytic coal gasification in fixed bed. J. Energy Inst. 2022, 105, 176–183. [Google Scholar] [CrossRef]
- Pandey, D.S.; Raza, H.; Bhattacharyya, S. Development of explainable AI-based predictive models for bubbling fluidised bed gasification process. Fuel 2023, 351, 128971. [Google Scholar] [CrossRef]
- Kargbo, H.O.; Zhang, J.; Phan, A.N. Robust modelling development for optimisation of hydrogen production from biomass gasification process using bootstrap aggregated neural network. Int. J. Hydrogen Energy 2023, 48, 10812–10828. [Google Scholar] [CrossRef]
- Elmaz, F.; Yücel, Ö.; Mutlu, A.Y. Evaluating the effect of blending ratio on the co-gasification of high ash coal and biomass in a fluidized bed gasifier using machine learning. Mugla J. Sci. Technol. 2019, 5, 1–12. [Google Scholar] [CrossRef]
- Ayub, H.M.U.; Rafiq, M.; Qyyum, M.A.; Rafiq, G.; Choi, G.S.; Lee, M. Prediction of process parameters for the integrated biomass gasification power plant using artificial neural network. Front. Energy Res. 2022, 10, 894875. [Google Scholar] [CrossRef]
- Pei, A.; Zhang, L.; Jiang, B.; Guo, L.; Zhang, X.; Lv, Y.; Jin, H. Hydrogen production by biomass gasification in supercritical or subcritical water with Raney-Ni and other catalysts. Front. Energy Power Eng. China 2009, 3, 456–464. [Google Scholar] [CrossRef]
- Liu, H.; Hu, J.; Wang, H.; Wang, C.; Li, J. Experimental studies of biomass gasification with air. J. Nat. Gas Chem. 2012, 21, 374–380. [Google Scholar] [CrossRef]
- Ge, H.; Guo, W.; Shen, L.; Song, T.; Xiao, J. Experimental investigation on biomass gasification using chemical looping in a batch reactor and a continuous dual reactor. Chem. Eng. J. 2016, 286, 689–700. [Google Scholar] [CrossRef]
- Lv, P.; Xiong, Z.; Chang, J.; Wu, C.; Chen, Y.; Zhu, J. An experimental study on biomass air–steam gasification in a fluidized bed. Bioresour. Technol. 2004, 95, 95–101. [Google Scholar] [CrossRef]
- Carpenter, D.L.; Bain, R.L.; Davis, R.E.; Dutta, A.; Feik, C.J.; Gaston, K.R.; Jablonski, W.; Phillips, S.D.; Nimlos, M.R. Pilot-scale gasification of corn stover, switchgrass, wheat straw, and wood: 1. Parametric study and comparison with literature. Ind. Eng. Chem. Res. 2010, 49, 1859–1871. [Google Scholar] [CrossRef]
- Sui, M.; Li, G.-y.; Guan, Y.-l.; Li, C.-m.; Zhou, R.-q.; Zarnegar, A.-M. Hydrogen and syngas production from steam gasification of biomass using cement as catalyst. Biomass Convers. Biorefin. 2020, 10, 119–124. [Google Scholar] [CrossRef]
- Gai, C.; Dong, Y. Experimental study on non-woody biomass gasification in a downdraft gasifier. Int. J. Hydrogen Energy 2012, 37, 4935–4944. [Google Scholar] [CrossRef]
- Chen, H.; Li, B.; Yang, H.; Yang, G.; Zhang, S. Experimental investigation of biomass gasification in a fluidized bed reactor. Energy Fuels 2008, 22, 3493–3498. [Google Scholar]
- Fan, X.; Yang, L.; Jiang, J. Experimental study on industrial-scale CFB biomass gasification. Renew. Energy 2020, 158, 32–36. [Google Scholar] [CrossRef]
- Liu, L.; Huang, Y.; Cao, J.; Liu, C.; Dong, L.; Xu, L.; Zha, J. Experimental study of biomass gasification with oxygen-enriched air in fluidized bed gasifier. Sci. Total Environ. 2018, 626, 423–433. [Google Scholar] [CrossRef]
- Loha, C.; Chatterjee, P.K.; Chattopadhyay, H. Performance of fluidized bed steam gasification of biomass–modeling and experiment. Energy Convers. Manag. 2011, 52, 1583–1588. [Google Scholar] [CrossRef]
- Lan, W.; Chen, G.; Zhu, X.; Wang, X.; Wang, X.; Xu, B. Research on the characteristics of biomass gasification in a fluidized bed. J. Energy Inst. 2019, 92, 613–620. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Ngo, S.I.; Lim, Y.-I.; Lee, J.W.; Lee, U.-D.; Song, B.-H. Three-stage steady-state model for biomass gasification in a dual circulating fluidized-bed. Energy Convers. Manag. 2012, 54, 100–112. [Google Scholar] [CrossRef]
- Pang, Y.; Shen, S.; Chen, Y. High temperature steam gasification of corn straw pellets in downdraft gasifier: Preparation of hydrogen-rich gas. Waste Biomass Valorization 2019, 10, 1333–1341. [Google Scholar] [CrossRef]
- Chang, J.; Fu, Y.; Luo, Z. Experimental study for dimethyl ether production from biomass gasification and simulation on dimethyl ether production. Biomass Bioenergy 2012, 39, 67–72. [Google Scholar] [CrossRef]
- Khan, M.M.; Xu, S.; Wang, C. Catalytic biomass gasification in decoupled dual loop gasification system over alkali-feldspar for hydrogen rich-gas production. Biomass Bioenergy 2022, 161, 106472. [Google Scholar] [CrossRef]
- Ge, H.; Shen, L.; Feng, F.; Jiang, S. Experiments on biomass gasification using chemical looping with nickel-based oxygen carrier in a 25 kWth reactor. Appl. Therm. Eng. 2015, 85, 52–60. [Google Scholar]
- Khan, Z.; Kamble, P.; Check, G.R.; DiLallo, T.; O’Sullivan, W.; Turner, E.D.; Mackay, A.; Blanco-Sanchez, P.; Yu, X.; Bridgwater, A. Design, instrumentation, and operation of a standard downdraft, laboratory-scale gasification testbed utilising novel seed-propagated hybrid Miscanthus pellets. Appl. Energy 2022, 315, 118864. [Google Scholar] [CrossRef]
- Turn, S.; Kinoshita, C.; Zhang, Z.; Ishimura, D.; Zhou, J. An experimental investigation of hydrogen production from biomass gasification. Int. J. Hydrogen Energy 1998, 23, 641–648. [Google Scholar] [CrossRef]
- Kim, J.-W.; Jeong, Y.-S.; Kim, J.-S. Bubbling fluidized bed biomass gasification using a two-stage process at 600 °C: A way to avoid bed agglomeration. Energy 2022, 250, 123882. [Google Scholar] [CrossRef]
- Moghadam, R.A.; Yusup, S.; Azlina, W.; Nehzati, S.; Tavasoli, A. Investigation on syngas production via biomass conversion through the integration of pyrolysis and air–steam gasification processes. Energy Convers. Manag. 2014, 87, 670–675. [Google Scholar] [CrossRef]
- Karmakar, M.; Datta, A. Generation of hydrogen rich gas through fluidized bed gasification of biomass. Bioresour. Technol. 2011, 102, 1907–1913. [Google Scholar] [CrossRef]
- Kurkela, E.; Ståhlberg, P. Air gasification of peat, wood and brown coal in a pressurized fluidized-bed reactor. I. Carbon conversion, gas yields and tar formation. Fuel Process. Technol. 1992, 31, 1–21. [Google Scholar] [CrossRef]
- Lv, P.; Chang, J.; Xiong, Z.; Huang, H.; Wu, C.; Chen, Y.; Zhu, J. Biomass air−steam gasification in a fluidized bed to produce hydrogen-rich gas. Energy Fuels 2003, 17, 677–682. [Google Scholar] [CrossRef]
- Kallis, K.X.; Susini, G.A.P.; Oakey, J.E. A comparison between Miscanthus and bioethanol waste pellets and their performance in a downdraft gasifier. Appl. Energy 2013, 101, 333–340. [Google Scholar] [CrossRef]
- Wei, L.; Xu, S.; Liu, J.; Liu, C.; Liu, S. Hydrogen production in steam gasification of biomass with CaO as a CO2 absorbent. Energy Fuels 2008, 22, 1997–2004. [Google Scholar] [CrossRef]
- Wei, L.; Xu, S.; Liu, J.; Lu, C.; Liu, S.; Liu, C. A novel process of biomass gasification for hydrogen-rich gas with solid heat carrier: Preliminary experimental results. Energy Fuels 2006, 20, 2266–2273. [Google Scholar] [CrossRef]
- Lin, C.-L.; Weng, W.-C. Effects of different operating parameters on the syngas composition in a two-stage gasification process. Renew. Energy 2017, 109, 135–143. [Google Scholar] [CrossRef]
- Kim, Y.D.; Yang, C.W.; Kim, B.J.; Kim, K.S.; Lee, J.W.; Moon, J.H.; Yang, W.; Yu, T.U.; Lee, U.D. Air-blown gasification of woody biomass in a bubbling fluidized bed gasifier. Appl. Energy 2013, 112, 414–420. [Google Scholar] [CrossRef]
- Gómez-Barea, A.; Arjona, R.; Ollero, P. Pilot-plant gasification of olive stone: A technical assessment. Energy Fuels 2005, 19, 598–605. [Google Scholar] [CrossRef]
- Skoulou, V.; Zabaniotou, A.; Stavropoulos, G.; Sakelaropoulos, G. Syngas production from olive tree cuttings and olive kernels in a downdraft fixed-bed gasifier. Int. J. Hydrogen Energy 2008, 33, 1185–1194. [Google Scholar] [CrossRef]
- Franco, C.; Pinto, F.; Gulyurtlu, I.; Cabrita, I. The study of reactions influencing the biomass steam gasification process. Fuel 2003, 82, 835–842. [Google Scholar] [CrossRef]
- Robinson, T.; Bronson, B.; Gogolek, P.; Mehrani, P. Comparison of the air-blown bubbling fluidized bed gasification of wood and wood–PET pellets. Fuel 2016, 178, 263–271. [Google Scholar] [CrossRef]
- Li, J.; Yin, Y.; Zhang, X.; Liu, J.; Yan, R. Hydrogen-rich gas production by steam gasification of palm oil wastes over supported tri-metallic catalyst. Int. J. Hydrogen Energy 2009, 34, 9108–9115. [Google Scholar] [CrossRef]
- Mohammed, M.; Salmiaton, A.; Azlina, W.W.; Amran, M.M.; Fakhru’l-Razi, A. Air gasification of empty fruit bunch for hydrogen-rich gas production in a fluidized-bed reactor. Energy Convers. Manag. 2011, 52, 1555–1561. [Google Scholar] [CrossRef]
- Pandey, D.S.; Kwapinska, M.; Gómez-Barea, A.; Horvat, A.; Fryda, L.E.; Rabou, L.P.L.M.; Leahy, J.J.; Kwapinski, W. Poultry litter gasification in a fluidized bed reactor: Effects of gasifying agent and limestone addition. Energy Fuels 2016, 30, 3085–3096. [Google Scholar] [CrossRef]
- Kaewluan, S.; Pipatmanomai, S. Potential of synthesis gas production from rubber wood chip gasification in a bubbling fluidised bed gasifier. Energy Convers. Manag. 2011, 52, 75–84. [Google Scholar] [CrossRef]
- Narvaez, I.; Orio, A.; Aznar, M.P.; Corella, J. Biomass gasification with air in an atmospheric bubbling fluidized bed. Effect of six operational variables on the quality of the produced raw gas. Ind. Eng. Chem. Res. 1996, 35, 2110–2120. [Google Scholar] [CrossRef]
- Mansaray, K.G.; Ghaly, A.; Al-Taweel, A.; Hamdullahpur, F.; Ugursal, V. Air gasification of rice husk in a dual distributor type fluidized bed gasifier. Biomass Bioenergy 1999, 17, 315–332. [Google Scholar] [CrossRef]
- Loha, C.; Chattopadhyay, H.; Chatterjee, P.K. Energy generation from fluidized bed gasification of rice husk. J. Renew. Sustain. Energy 2013, 5, 043111. [Google Scholar] [CrossRef]
- Kaewluan, S.; Pipatmanomai, S. Gasification of high moisture rubber woodchip with rubber waste in a bubbling fluidized bed. Fuel Process. Technol. 2011, 92, 671–677. [Google Scholar] [CrossRef]
- Christodoulou, C.; Grimekis, D.; Panopoulos, K.; Pachatouridou, E.; Iliopoulou, E.; Kakaras, E. Comparing calcined and un-treated olivine as bed materials for tar reduction in fluidized bed gasification. Fuel Process. Technol. 2014, 124, 275–285. [Google Scholar] [CrossRef]
- Serrano, D.; Sánchez-Delgado, S.; Horvat, A. Effect of sepiolite bed material on gas composition and tar mitigation during C. cardunculus L. gasification. Chem. Eng. J. 2017, 317, 1037–1046. [Google Scholar] [CrossRef]
- Lahijani, P.; Zainal, Z.A. Gasification of palm empty fruit bunch in a bubbling fluidized bed: A performance and agglomeration study. Bioresour. Technol. 2011, 102, 2068–2076. [Google Scholar] [CrossRef]
- Miccio, F.; Piriou, B.; Ruoppolo, G.; Chirone, R. Biomass gasification in a catalytic fluidized reactor with beds of different materials. Chem. Eng. J. 2009, 154, 369–374. [Google Scholar] [CrossRef]
- Jamshidi, E.J.; Yusup, Y.; Kayode, J.S.; Kamaruddin, M.A. Detecting outliers in a univariate time series dataset using unsupervised combined statistical methods: A case study on surface water temperature. Ecol. Inform. 2022, 69, 101672. [Google Scholar] [CrossRef]
- Cihan, P.; Kalıpsız, O.; Gökçe, E. Hayvan hastaliği teşhisinde normalizasyon tekniklerinin yapay sinir aği ve özellik seçim performansina etkisi. Turk. Stud. 2017, 12, 59–70. [Google Scholar] [CrossRef]
- Engelbrecht, A.P.; Cloete, I.; Zurada, J.M. Determining the significance of input parameters using sensitivity analysis. In From Natural to Artificial Neural Computation, Proceedings of the International Workshop on Artificial Neural Networks, Torremolinos, Spain, 7–9 June 1995; Springer: Berlin/Heidelberg, Fermany, 1995; pp. 382–388. [Google Scholar]
- Ahmad, A.; Chaiyasarn, K.; Farooq, F.; Ahmad, W.; Suparp, S.; Aslam, F. Compressive strength prediction via gene expression programming (GEP) and artificial neural network (ANN) for concrete containing RCA. Buildings 2021, 11, 324. [Google Scholar] [CrossRef]
- Huynh, A.T.; Nguyen, Q.D.; Xuan, Q.L.; Magee, B.; Chung, T.; Tran, K.T.; Nguyen, K.T. A machine learning-assisted numerical predictor for compressive strength of geopolymer concrete based on experimental data and sensitivity analysis. Appl. Sci. 2020, 10, 7726. [Google Scholar] [CrossRef]
- Chu, H.-H.; Khan, M.A.; Javed, M.; Zafar, A.; Khan, M.I.; Alabduljabbar, H.; Qayyum, S. Sustainable use of fly-ash: Use of gene-expression programming (GEP) and multi-expression programming (MEP) for forecasting the compressive strength geopolymer concrete. Ain Shams Eng. J. 2021, 12, 3603–3617. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. In Ensemble Machine Learning: Methods and Applications; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar]
- Cihan, P.; Özcan, H.K.; Öngen, A. Prediction of tropospheric ozone concentration with Bagging-MLP method. Gazi Mühendislik Bilim. Derg. 2023, 9, 557–573. [Google Scholar] [CrossRef]
- Cihan, P. Horse Surgery and Survival Prediction with Artificial Intelligence Models: Performance Comparison of Original, Imputed, Balanced, and Feature-Selected Datasets. Kafkas Univ. Vet. Fak. Derg. 2024, 30, 233–241. [Google Scholar] [CrossRef]
- Santos, M. Bayesian Optimization for Hyperparameter Tuning. J. Bioinform. Artif. Intell. 2022, 2, 1–13. [Google Scholar]

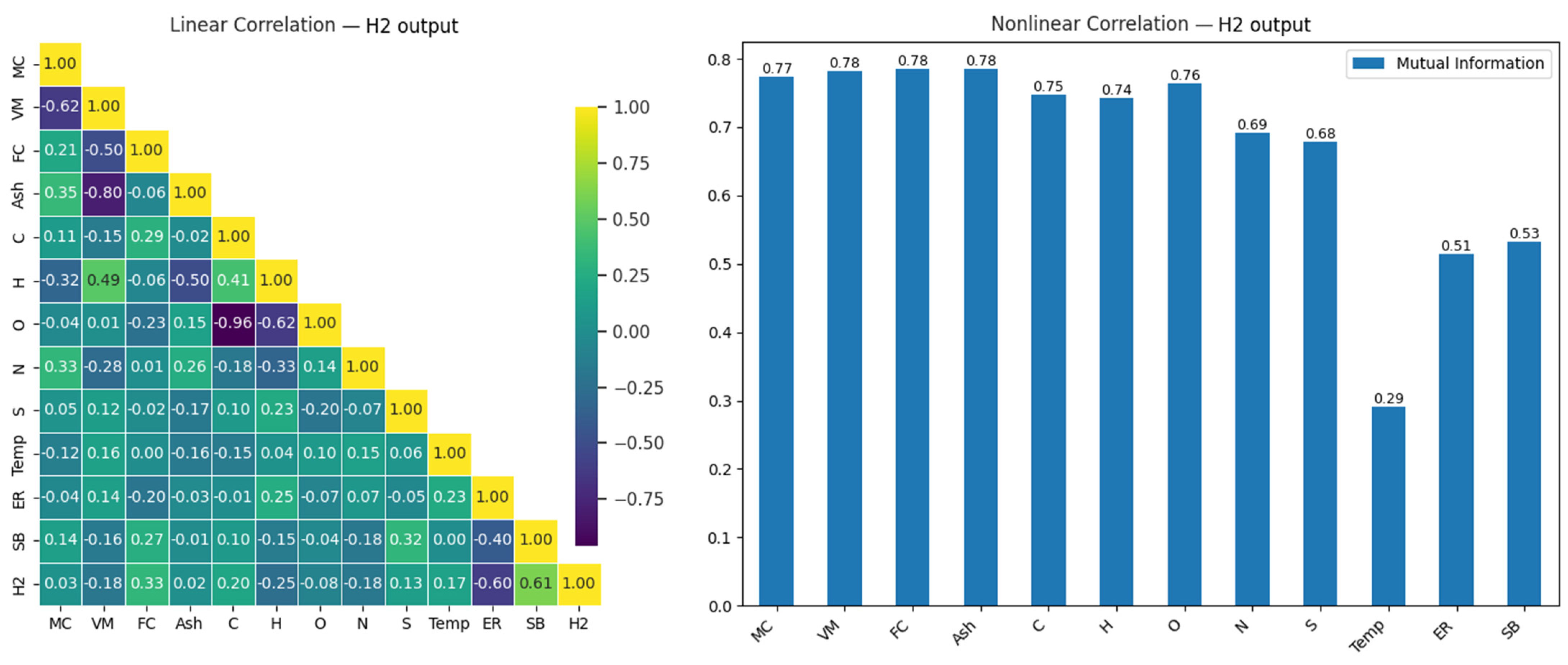
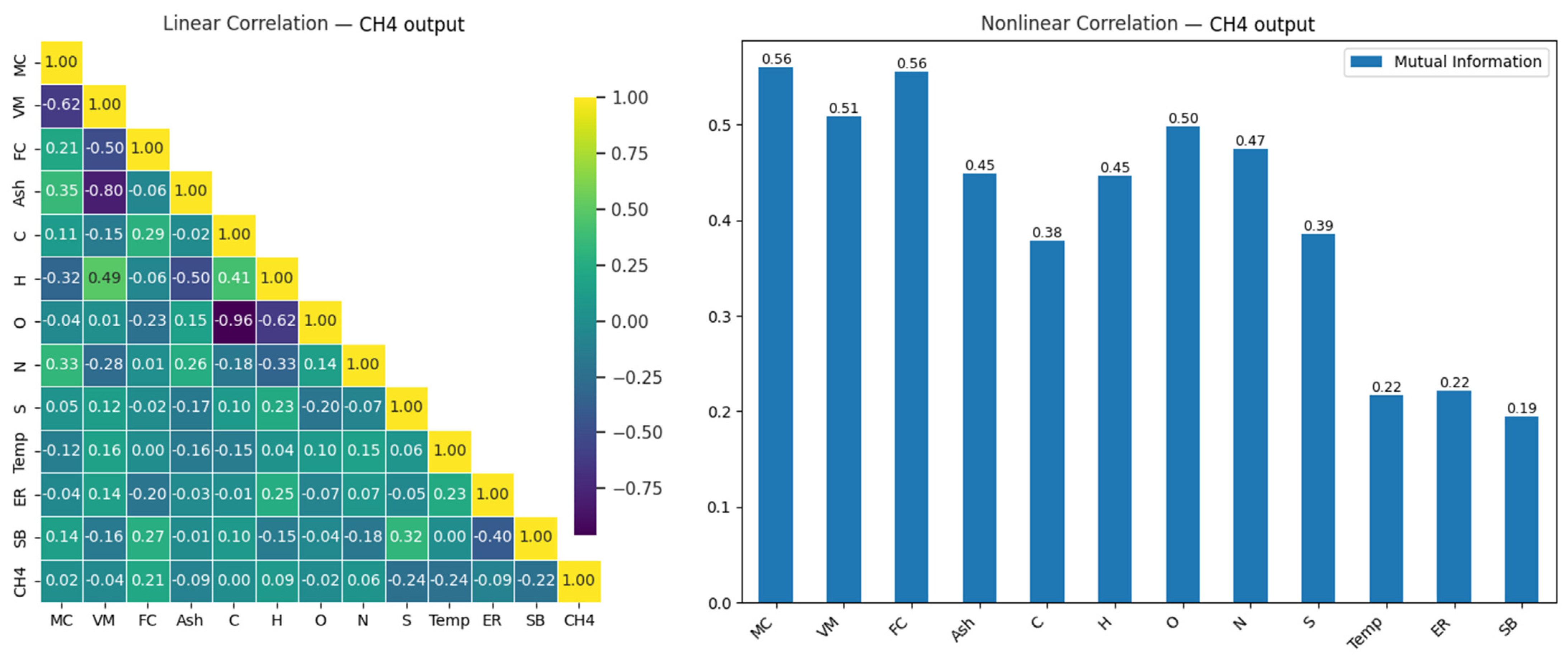
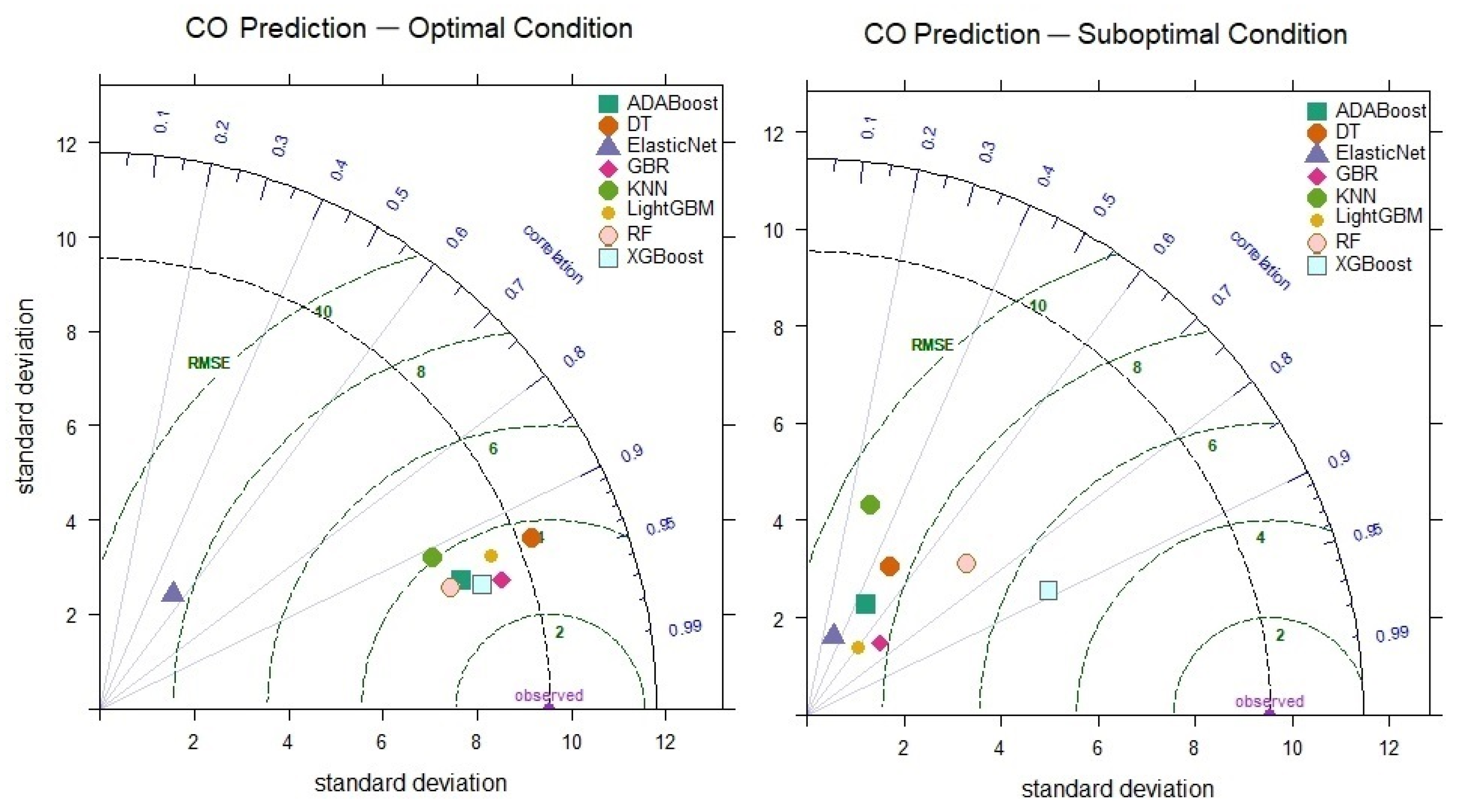
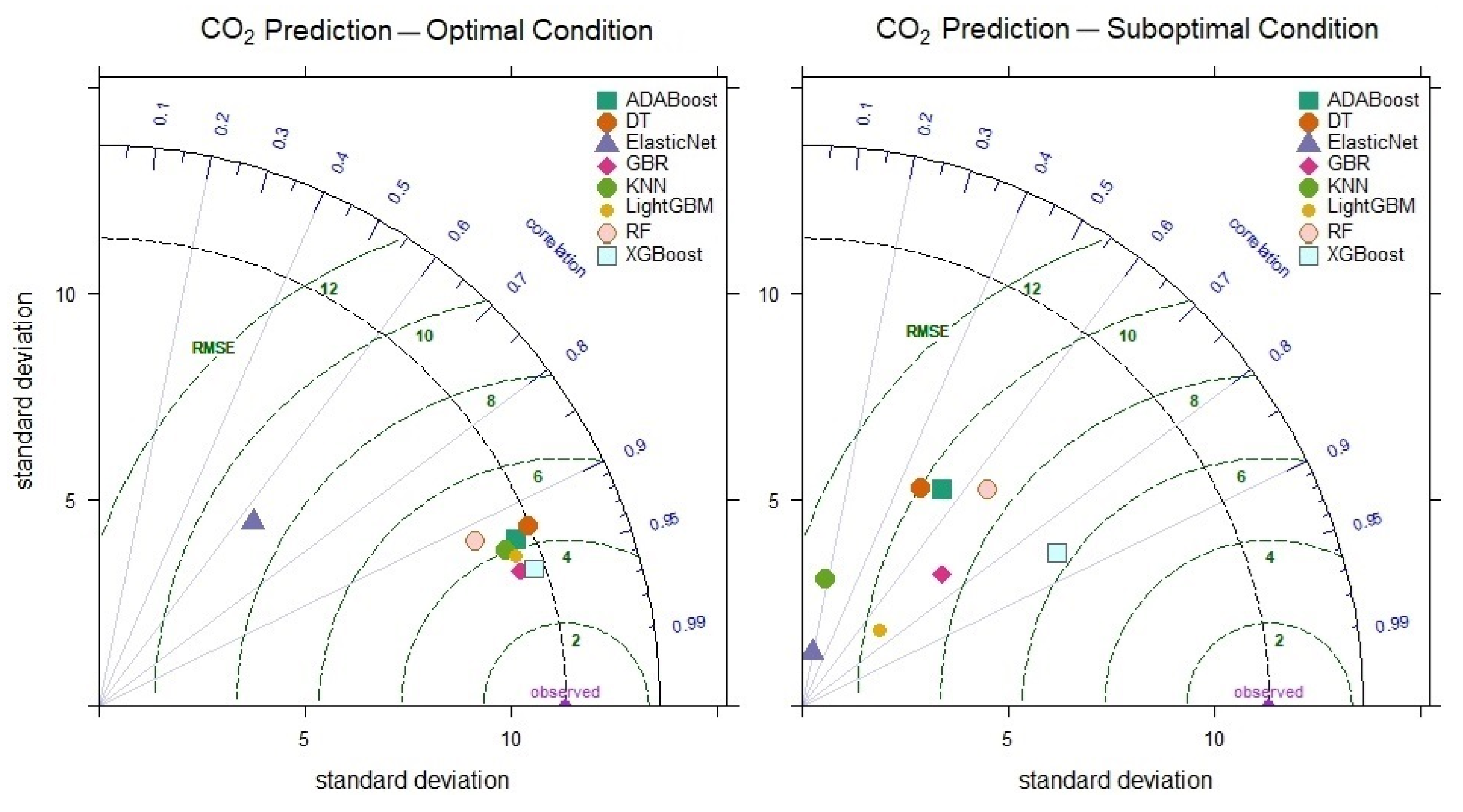

| ML Models | Input Feature | Output Feature | Reactor Type | Feedstock | Ref. |
|---|---|---|---|---|---|
| KNN, LR, SVR, DTR | T, Temp, CH4, CO, O2, CO2, HHV | H2 | Fixed bed | Olive pit | [3] |
| PR, SVR, DTR, MLP | TD (T0–T5), ER, FR | CO, CO2, CH4, H2, HHV | Downdraft | Woody biomass | [12] |
| BLS-SVM, MC-RF | TD (T0–T5), ER, FR, MC, C, H, O, N, ash, FC | CH4, H2, CO, CO2, HHV | Downdraft | Woody biomass | [13] |
| ANN, GBR | R, T, SFR, C, ash, MC, VM, LHV, H, N, S, O, ER, Temp | CH4, H2, CO, CO2, N2 | Updraft | Rice husks | [14] |
| ANN, NARX | TD (T0–T5), ER, AF, N, S, O, C, H, ash, MC, VM, LHV | CH4, H2, CO, CO2, LHV | Downdraft | Pinecone particles, wood pellet | [15] |
| ANN | O, MC, C, H, ash, ER, Temp, SB, BM | CH4, H2, CO, CO2, GY | Lab-scale BFB | Woody biomass | [16] |
| ANN | C, H, ash, MC, VM, N, S, O, LHV, ER, Temp | CGE, CCE, GY, CH4, H2, CO, CO2, LHV | Downdraft, updraft, fluidized bed, entrained bed | Biomass, coal, blends of biomass, and coal. | [17] |
| ANN | SB, Temp, coal bottom ash, CaO/biomass | CH4, H2, CO, CO2 | Integrated fixed and circulating bed | Palm oil waste | [18] |
| ANN | C, H, O, ash, M, Temp | CH4, H2, CO, CO2 | Downdraft | Various woody biomass | [19] |
| GPR, ANN, SVR, RF | C, H, O, ash | H2 yield | SCWG | Agricultural waste, municipal solid waste | [20] |
| ANN | GOP, RT, GA, GS, CU, BM, C, H, S, ash, MC, PS, Temp, ER | CH4, H2, CO, CO2, N2, C2Hn, LHV, Tar, GY, char yield | General gasifier types | Variety of feedstocks | [21] |
| CFBP, FFBP, CFBP-GA | C, H, O, ash, VM, FC, W, Temp, MW, SFR | H2, CO, CO2, X | Various gasifier types | Food waste, sludge, mixed biomass waste | [22] |
| LR, GB, LARS, RR, RF, BAG, MLP | T, BM, SB, C, H, O, MC, ash, ER | GY, H2, CO, CO2, CH4 | BFB | Variety of biomass feedstock | [23] |
| BANN, ANN | DT, Temp, SB, carrier gas flow rate, C, H, O | GY, residue, tar, H2, CO, CO2, CH4 | Two-stage gasifier | Waste wood | [24] |
| LR, PR, GR, SVR, DTR, ANN | Temp, CFR, BFR, FC, VM, ash, MC, AFR, SFR, C, H, O, rate constant | GY, CCE, HHV, CGE | Fluidized bed gasifier | High-ash coal and biomass | [25] |
| ANN | C, O, H, MC, VM, FC, ash, N, S; required power (kW) | Temp, AFR | Downdraft | 86 biomasses | [26] |
| Variable | Abbr. | Unit | Min | Max | Avg | Direction |
|---|---|---|---|---|---|---|
| Moisture content | MC | wt% | 4.6 | 27.0 | 8.7 | Input |
| Volatile matter | VM | wt% | 52.6 | 83.7 | 71.8 | Input |
| Fixed carbon | FC | wt% | 6.9 | 26.4 | 15.1 | Input |
| Ash | Ash | wt% | 0.0 | 19.5 | 4.5 | Input |
| Carbon | C | wt% | 43.3 | 58.3 | 49.2 | Input |
| Hydrogen | H | wt% | 3.6 | 8.7 | 6.1 | Input |
| Oxygen | O | wt% | 31.0 | 51.8 | 43.6 | Input |
| Nitrogen | N | wt% | 0.0 | 6.6 | 0.7 | Input |
| Sulfur | S | wt% | 0.0 | 4.2 | 0.4 | Input |
| Temperature | Temp | °C | 599.0 | 1108.0 | 801.7 | Input |
| Equivalence ratio | ER | Weight basis | 0.0 | 0.5 | 0.2 | Input |
| Steam to biomass ratio | SB | Weight basis | 0.0 | 4.7 | 0.6 | Input |
| Carbon monoxide composition | CO | Vol% | 7.4 | 50.6 | 31.0 | Output |
| Carbon dioxide composition | CO2 | Vol% | 5.0 | 59.0 | 28.9 | Output |
| Hydrogen composition | H2 | Vol% | 6.4 | 65.7 | 32.2 | Output |
| Methane composition | CH4 | Vol% | 0.4 | 22.0 | 8.0 | Output |
| Feature | Statistic | p-Value | Normal Distribution |
|---|---|---|---|
| MC | 0.9596 | <0.0001 | False |
| VM | 0.8876 | <0.0001 | False |
| FC | 0.9546 | <0.0001 | False |
| Ash | 0.7069 | <0.0001 | False |
| C | 0.9679 | <0.0001 | False |
| H | 0.9374 | <0.0001 | False |
| O | 0.9693 | <0.0001 | False |
| N | 0.9071 | <0.0001 | False |
| S | 0.7743 | <0.0001 | False |
| Temp | 0.9660 | <0.0001 | False |
| ER | 0.8717 | <0.0001 | False |
| SB | 0.8229 | <0.0001 | False |
| Model | Parameters | Test Value Range | CO | CO2 | H2 | CH4 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Optimal | Suboptimal | Optimal | Suboptimal | Optimal | Suboptimal | Optimal | Suboptimal | |||
| RF | n_estimators | 10–500 | 10 | 497 | 33 | 11 | 91 | 125 | 485 | 290 |
| max_depth | 2–100 | 75 | 2 | 73 | 2 | 23 | 2 | 71 | 2 | |
| min_samples_split | 2–50 | 4 | 4 | 2 | 43 | 2 | 7 | 2 | 40 | |
| XGBoost | n_estimators | 10–500 | 193 | 114 | 347 | 114 | 383 | 114 | 277 | 463 |
| max_depth | 2–100 | 6 | 97 | 4 | 97 | 9 | 97 | 7 | 12 | |
| learning_rate | 0.01–0.3 | 0.1641 | 0.0159 | 0.2570 | 0.0159 | 0.0743 | 0.0159 | 0.1135 | 0.2177 | |
| subsample | 0.5–1.0 | 0.9799 | 0.5909 | 0.5082 | 0.5909 | 0.6566 | 0.5909 | 0.5545 | 0.9948 | |
| min_child_weight | 1–10 | 7 | 7 | 43 | 43 | 7 | 7 | 7 | 2 | |
| Light GBM | learning_rate | 0.01–0.3 | 0.2774 | 0.0132 | 0.187 | 0.0132 | 0.2642 | 0.0174 | 0.1563 | 0.0101 |
| n_estimators | 10–500 | 395 | 26 | 229 | 26 | 269 | 24 | 222 | 15 | |
| max_depth | 2–10 | 3 | 6 | 7 | 6 | 9 | 2 | 5 | 2 | |
| num_leaves | 20–50 | 49 | 46 | 31 | 46 | 42 | 49 | 20 | 34 | |
| subsample | 0.5–1.0 | 0.8624 | 0.573 | 0.6985 | 0.573 | 0.7196 | 0.5506 | 0.8095 | 0.9037 | |
| Elastic Net | alpha | 0.001–10.0 | 0.9334 | 9.9955 | 0.3274 | 9.8627 | 0.001 | 5.2821 | 0.0011 | 8.1478 |
| l1_ratio | 0.0–1.0 | 0.82 | 0.9989 | 0.0063 | 0.9943 | 0.8718 | 0.9983 | 0.0142 | 0.9998 | |
| Ada Boost | learning_rate | 0.01–0.3 | 0.6042 | 0.0235 | 0.3807 | 0.9087 | 0.4615 | 0.8469 | 0.5191 | 0.4249 |
| n_estimators | 10–500 | 51 | 10 | 368 | 455 | 107 | 499 | 32 | 432 | |
| max_depth | 1–10 | 9 | 1 | 9 | 1 | 8 | 1 | 6 | 1 | |
| GBR | learning_rate | 0.01–0.3 | 0.0574 | 0.0147 | 0.0589 | 0.0230 | 0.217 | 0.0112 | 0.1818 | 0.047 |
| n_estimators | 10–500 | 242 | 42 | 353 | 47 | 31 | 238 | 307 | 20 | |
| max_depth | 2–10 | 9 | 2 | 5 | 2 | 7 | 2 | 2 | 7 | |
| subsample | 0.5–1.0 | 0.8074 | 0.7761 | 0.6263 | 0.7907 | 0.7013 | 0.676 | 0.5853 | 0.9981 | |
| KNN | n_neighbors | 1–50 | 3 | 20 | 2 | 43 | 3 | 23 | 2 | 59 |
| weights | Uniform, distance | distance | uniform | distance | uniform | distance | uniform | distance | Uniform | |
| algorithm | ball_tree, kd_tree, brute | ball_tree | ball_tree | kd_tree | brute | brute | kd_tree | brute | kd_tree | |
| DT | max_depth | 1–20 | 9 | 1 | 15 | 1 | 17 | 1 | 17 | 1 |
| min_samples_split | 2–20 | 3 | 2 | 4 | 3 | 2 | 2 | 19 | 3 | |
| min_samples_leaf | 1–20 | 1 | 6 | 1 | 4 | 1 | 15 | 1 | 17 | |
| Model | Optimal | Suboptimal | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | RAE (%) | MAPE (%) | Exe. (s) | RMSE | RAE (%) | MAPE (%) | Exe. (s) | |
| RF | 3.540 | 8.508 | 8.615 | 85.37 | 6.985 | 17.581 | 19.897 | 75.76 |
| XGBoost | 3.109 | 7.003 | 7.447 | 45.68 | 5.291 | 12.804 | 14.286 | 32.04 |
| LightGBM | 3.613 | 8.170 | 8.716 | 32.81 | 8.565 | 22.611 | 26.649 | 16.14 |
| ElasticNet | 8.335 | 21.378 | 24.961 | 24.50 | 9.144 | 24.171 | 28.144 | 14.79 |
| AdaBoost | 3.504 | 8.312 | 8.561 | 48.41 | 8.570 | 22.069 | 26.406 | 46.17 |
| GBR | 3.174 | 7.142 | 7.334 | 44.66 | 8.137 | 21.355 | 24.890 | 26.80 |
| KNN | 4.199 | 9.162 | 9.499 | 17.12 | 9.244 | 23.445 | 27.594 | 15.47 |
| DT | 3.786 | 8.860 | 9.180 | 34.04 | 8.386 | 22.009 | 25.326 | 20.09 |
| Model | Optimal | Suboptimal | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | RAE (%) | MAPE (%) | Exe. (s) | RMSE | RAE (%) | MAPE (%) | Exe. (s) | |
| RF | 4.711 | 12.454 | 16.895 | 107.02 | 8.637 | 24.828 | 38.337 | 48.79 |
| XGBoost | 3.590 | 8.667 | 11.616 | 33.34 | 6.432 | 17.752 | 28.253 | 37.76 |
| LightGBM | 4.048 | 10.605 | 12.669 | 35.27 | 9.611 | 26.294 | 41.801 | 16.96 |
| ElasticNet | 8.911 | 24.923 | 43.798 | 14.09 | 11.121 | 31.058 | 50.149 | 13.21 |
| AdaBoost | 4.370 | 11.624 | 13.462 | 53.87 | 9.576 | 27.028 | 43.340 | 40.37 |
| GBR | 3.599 | 9.282 | 11.606 | 47.20 | 8.546 | 24.057 | 39.029 | 43.80 |
| KNN | 4.175 | 10.662 | 12.429 | 12.95 | 11.156 | 32.576 | 47.798 | 16.56 |
| DT | 4.597 | 11.892 | 13.614 | 20.70 | 10.028 | 28.434 | 43.934 | 17.05 |
| Model | Optimal | Suboptimal | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | RAE (%) | MAPE (%) | Exe. (s) | RMSE | RAE (%) | MAPE (%) | Exe. (s) | |
| RF | 3.717 | 8.258 | 9.378 | 79.05 | 7.951 | 18.687 | 21.065 | 48.18 |
| XGBoost | 2.774 | 6.471 | 7.542 | 37.50 | 5.707 | 13.230 | 16.290 | 32.08 |
| LightGBM | 3.329 | 8.062 | 9.582 | 26.90 | 11.453 | 27.069 | 34.179 | 16.68 |
| ElasticNet | 7.256 | 17.975 | 20.556 | 24.39 | 12.695 | 30.808 | 35.267 | 28.24 |
| AdaBoost | 3.144 | 7.975 | 9.551 | 47.46 | 9.709 | 24.406 | 29.441 | 30.22 |
| GBR | 3.248 | 7.122 | 8.170 | 58.79 | 5.736 | 13.928 | 17.470 | 38.64 |
| KNN | 2.870 | 6.835 | 8.120 | 16.98 | 13.323 | 33.220 | 42.218 | 15.01 |
| DT | 4.851 | 10.316 | 12.334 | 19.21 | 9.949 | 24.914 | 29.033 | 18.94 |
| Model | Optimal | Suboptimal | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | RAE (%) | MAPE (%) | Exe. (s) | RMSE | RAE (%) | MAPE (%) | Exe. (s) | |
| RF | 1.248 | 11.954 | 19.119 | 104.16 | 2.311 | 23.016 | 45.116 | 66.62 |
| XGBoost | 1.040 | 10.547 | 14.338 | 52.11 | 1.503 | 14.018 | 16.786 | 52.36 |
| LightGBM | 1.126 | 11.612 | 15.363 | 32.42 | 2.861 | 29.946 | 56.48 | 16.01 |
| ElasticNet | 2.608 | 27.164 | 48.455 | 12.77 | 2.931 | 31.067 | 56.61 | 17.05 |
| AdaBoost | 1.186 | 12.338 | 17.431 | 59.97 | 2.994 | 31.411 | 60.675 | 36.05 |
| GBR | 1.116 | 10.746 | 15.56 | 40.93 | 1.957 | 15.745 | 16.371 | 40.17 |
| KNN | 1.318 | 11.443 | 12.254 | 15.85 | 2.833 | 29.771 | 45.336 | 24.92 |
| DT | 2.038 | 17.182 | 23.369 | 19.49 | 2.774 | 28.865 | 53.494 | 19.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cihan, P. Bayesian Hyperparameter Optimization of Machine Learning Models for Predicting Biomass Gasification Gases. Appl. Sci. 2025, 15, 1018. https://doi.org/10.3390/app15031018
Cihan P. Bayesian Hyperparameter Optimization of Machine Learning Models for Predicting Biomass Gasification Gases. Applied Sciences. 2025; 15(3):1018. https://doi.org/10.3390/app15031018
Chicago/Turabian StyleCihan, Pınar. 2025. "Bayesian Hyperparameter Optimization of Machine Learning Models for Predicting Biomass Gasification Gases" Applied Sciences 15, no. 3: 1018. https://doi.org/10.3390/app15031018
APA StyleCihan, P. (2025). Bayesian Hyperparameter Optimization of Machine Learning Models for Predicting Biomass Gasification Gases. Applied Sciences, 15(3), 1018. https://doi.org/10.3390/app15031018






