A Thorough Examination of Innovative Supplementary Dampers Aimed at Enhancing the Seismic Behavior of Structural Systems

Abstract

This review article presents a detailed investigation into the seismic behavior of structures employing supplementary dampers or additional damping mechanisms over the past decade. The study covers a range of damping systems, including viscous, viscoelastic, and friction dampers, as well as tuned mass dampers and other approaches. A systematic analysis of more than 160 publications in the current literature is undertaken, providing a clear overview of structures equipped with supplementary damping devices and the challenges they face. The theoretical principles that underpin these technologies are examined, along with their practical applications and effectiveness in alleviating seismic effects. Additionally, the article highlights recent developments in the design of damping devices, the challenges related to their implementation, and prospective directions for future research. By synthesizing results from experimental studies, numerical simulations, and real-world applications, this review offers valuable insights for researchers and engineers involved in the design of earthquake-resistant structures.

1. Introduction

1.1. Background and Motivation

Seismic events pose a substantial threat to global building infrastructure, leading engineers and researchers to develop novel approaches aimed at improving structural resilience. Over the past few decades, the field of earthquake engineering has made remarkable strides in understanding and mitigating the effects of seismic forces on structures. A significant development in this area is the incorporation of additional damping devices, which have been shown to effectively enhance the seismic performance of both new and existing buildings [1,2,3].

The concept of supplementary damping is fundamentally rooted in the dissipation of energy. In the context of seismic events, ground motions impart kinetic energy to structures, which must be absorbed or dissipated to prevent damage or structural failure [4,5,6]. Historically, seismic design approaches have largely relied on the inherent damping properties of construction materials and the ductile behavior of structural elements to manage this energy. However, these traditional methods often result in significant structural damage during severe seismic events, leading to substantial economic losses and potential losses of life [7].

Supplementary damping devices offer a practical solution by introducing additional energy dissipation mechanisms within the structure. These devices, which include viscous dampers, viscoelastic dampers, friction dampers, and tuned mass dampers, can significantly reduce the seismic demands on primary structural elements. By effectively absorbing and dissipating seismic energy, these systems can minimize structural deformations, decrease internal forces, and enhance overall structural performance during earthquakes [8,9,10].

The motivation for this review stems from the growing body of research and practical applications of supplementary damping systems in the realm of seismic-resistant design. As urban populations continue to rise and the demand for infrastructure intensifies, particularly in areas susceptible to seismic events, the importance of effective and resilient seismic protection strategies becomes increasingly paramount. Supplementary damping technologies possess the capability to not only improve structural safety but also to reduce construction costs, minimize the need for post-earthquake repairs, and enhance the overall resilience of urban environments [11,12,13,14,15]. Additionally, recent advancements in materials science, control theory, and computational technology have enabled the development of more sophisticated damping systems [16,17]. These innovations promise to enhance the effectiveness of seismic hazard mitigation while simultaneously introducing new challenges in terms of analysis, design, and implementation. Therefore, a comprehensive review of the current understanding of the seismic performance of structures fitted with supplementary dampers is both timely and necessary.

1.2. Objectives of the Review

The principal aim of this review paper is to deliver a thorough and critical examination of the existing research and practices related to the seismic performance of structures that incorporate supplementary dampers or additional damping mechanisms. This review specifically seeks to achieve several interconnected objectives. It aims to integrate and assess the theoretical principles that support the implementation of supplementary damping systems in the design of seismic-resistant structures. The paper investigates the diverse range of damping devices currently in use, detailing their operational mechanisms, as well as their respective benefits and drawbacks. It evaluates the methodologies employed in the modeling and design of structures featuring supplementary dampers, encompassing both simplified and sophisticated numerical techniques. The review surveys experimental investigations and real-world applications to evaluate the performance of structures equipped with damping devices when subjected to seismic forces. Furthermore, it identifies essential design factors, challenges in implementation, and relevant code regulations concerning the application of supplementary damping systems. The paper examines recent innovations in damping technologies and their potential effects on future practices in seismic design. It also discusses the reliability, durability, and maintenance needs of structures that utilize supplementary dampers. Importantly, the review points out existing knowledge gaps and proposes avenues for future research in this domain. By fulfilling these objectives, this review aspires to be a significant resource for researchers, practicing engineers, and policymakers engaged in the seismic design and retrofitting of structures.

1.3. Scope and Limitations

This review encompasses a wide range of topics related to the seismic behavior of structures with supplementary dampers, spanning from fundamental principles to cutting-edge applications. The scope of the review is comprehensive, covering various types of supplementary damping devices, including but not limited to viscous, viscoelastic, friction, and metallic yield dampers, as well as tuned mass dampers and base isolation systems. It explores both passive and semi-active damping technologies, with a brief discussion of active control systems. The review examines applications in building structures of different heights and configurations, as well as bridge structures, addressing both new construction and retrofit applications of supplementary damping systems. Furthermore, it delves into analytical, numerical, and experimental methods for studying the behavior of damped structures, providing a holistic view of the field. This wide-ranging approach ensures that the review offers valuable insights into the diverse aspects of supplementary damping in seismic engineering.

While this review aims for comprehensiveness, it is important to acknowledge certain limitations. The evolving nature of the field suggests that some of the latest developments may not be fully captured. The review primarily concentrates on literature published in English, which could lead to a partial representation of research conducted in other languages. Detailed mathematical derivations and complex technical aspects of control theory are not included in this review. Additionally, extensive economic assessments and cost analyses of various damping systems are not thoroughly explored. The review also does not provide an in-depth analysis of non-structural components and their relationships with damping systems. Despite these constraints, this review strives to offer a balanced and comprehensive assessment of the current understanding of the seismic performance of structures with supplementary dampers. In this way, it aims to deepen the comprehension of these technologies and encourage further research and innovation in this critical area of earthquake engineering.

To provide a clear overview of the supplementary damping systems discussed in this review, Figure 1 presents the general framework of seismic protection strategies, highlighting the position of supplementary damping systems within the broader context of structural control methods. The detailed classification of various damper types and their relationships will be presented in Section 2.1, along with a comprehensive comparative analysis of their characteristics.

1.4. Paper Organization

This review paper is structured to provide a systematic examination of supplementary damping systems and their applications in seismic engineering. Following this introduction, Section 2 presents a comprehensive overview of supplementary damping systems, including their classification, fundamental principles, and historical development. Section 3 provides a detailed analysis of specific damper types, examining their operating principles, mathematical models, and practical applications. Section 4 discusses critical design considerations and implementation challenges. Section 5 presents emerging trends and future research directions, followed by conclusions and recommendations in Section 6.

The progressive development of concepts throughout these sections ensures comprehensive coverage while maintaining clear connections between fundamental principles and their practical applications. Each major damping system is examined from theoretical foundations through to practical implementation, with clear cross-references maintaining continuity throughout the discussion.

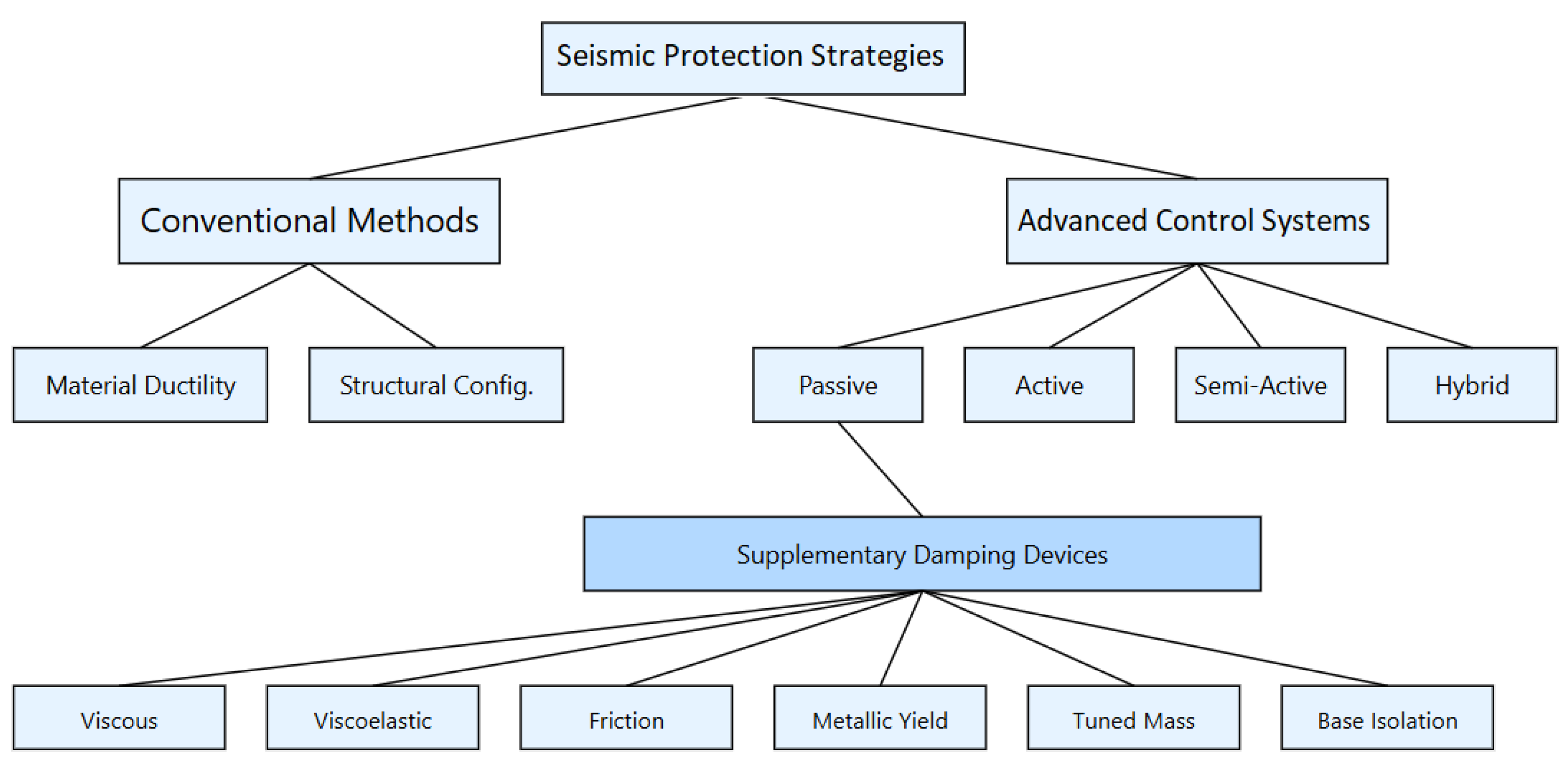
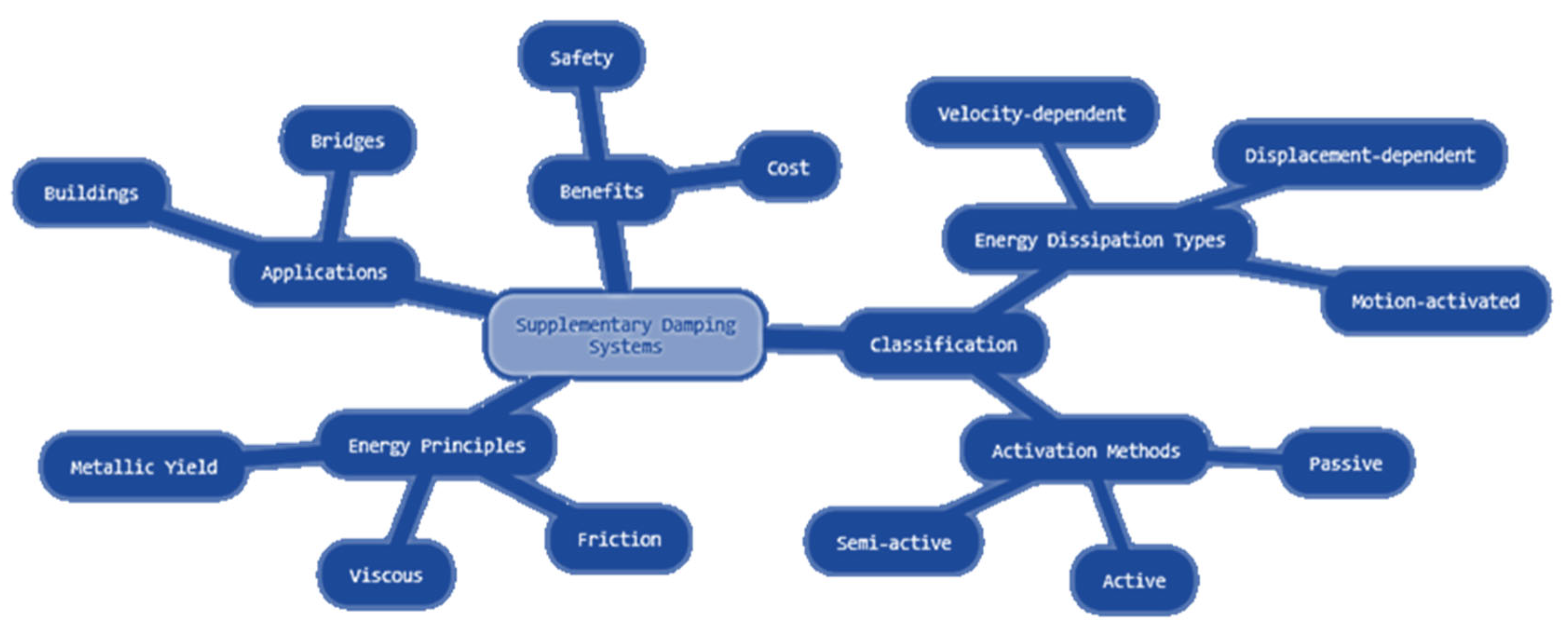
2. Overview of Supplementary Damping Systems

2.1. Classification of Damping Devices

Supplementary damping systems can be classified based on various criteria, including their energy dissipation mechanisms, activation methods, and functional characteristics [18]. This comprehensive classification (see Figure 2) provides a framework for understanding the diverse range of available damping technologies. The classification and characterization of supplementary damping systems form a complex framework that includes numerous criteria and operational principles. The classification system depicted in Figure 2 presents a systematic approach to analyzing these devices through three key perspectives: energy dissipation mechanisms, activation techniques, and functional features.

2.1.1. Classification by Energy Dissipation Mechanism

(a) Velocity-dependent devices:

Velocity-dependent devices, notably viscous and viscoelastic dampers, function by responding to the relative velocity between different structural elements. Viscous dampers employ the principles of fluid dynamics to dissipate energy, utilizing specially formulated fluids that flow through meticulously designed orifices. Their force output is directly proportional to the velocity, rendering them especially efficient during rapid seismic activities. In contrast, viscoelastic dampers integrate both viscous and elastic characteristics, allowing for energy dissipation over a wider spectrum of movement speeds while also contributing a degree of restoring force to the structure.

(b) Displacement-dependent devices:

Devices that depend on displacement function by assessing the relative motion between structural elements. Friction dampers exploit mechanical friction through uniquely crafted interfaces to convert kinetic energy into heat energy. Typically, these systems deliver a uniform force output once activated, irrespective of the rate of movement. Metallic yield dampers are designed to absorb seismic energy through the plastic deformation of metals, primarily steel or lead, by enabling controlled yielding of specially engineered components.

(c) Motion-activated devices:

Devices that are activated by motion, such as tuned mass dampers (TMDs) and tuned liquid dampers (TLDs), operate on varying principles. These systems employ supplementary mass, either in solid or liquid states, that shifts in response to the movement of the structure. The movement of this mass is meticulously adjusted to counterbalance the main structural motion, effectively lessening vibration amplitudes. Typically, TMDs are made up of large masses that are mounted on springs and dampers, while TLDs rely on the sloshing action of liquids within uniquely designed containers.

(d) Phase transformation devices:

Shape memory alloy (SMA) dampers: The primary materials used in these dampers are Nickel–Titanium (Nitinol) alloys, characterized by two distinct crystal structures: austenite at higher temperatures and martensite at lower temperatures. When subjected to seismic activity, the shape memory alloy (SMA) undergoes a reversible phase change between these states, which allows it to effectively absorb considerable energy while still being able to return to its initial form.

2.1.2. Classification by Activation Method

Passive systems: These systems do not require an external power source and respond solely to the motion of the structure. Examples include viscous dampers, friction dampers, and metallic yield dampers.

Active systems: These systems use external power to drive actuators that apply forces to the structure based on feedback from sensors. Examples include active mass dampers and active tendon systems.

Semi-active systems: These systems combine aspects of both passive and active systems. They require minimal external power to adjust their properties but do not directly input energy into the structure. Examples include magnetorheological (MR) dampers and variable orifice dampers. Semi-active systems occupy a balanced position, requiring minimal external energy while still offering a certain level of adaptability. For instance, magnetorheological (MR) dampers can modify their damping characteristics by changing the magnetic field applied to specialized fluids. This feature allows for the real-time optimization of damping properties, all while avoiding the high energy demands typical of fully active systems.

Hybrid systems: These systems combine passive devices with active or semi-active components to enhance performance and reliability.

2.1.3. Classification by Functional Characteristics

The classification according to the activation method, as shown in Figure 3, illustrates the transition from straightforward passive systems to more elaborate active and hybrid solutions. Passive systems, which operate independently of an external power source, are characterized by their reliability and low maintenance requirements, yet they are unable to respond to changing circumstances. Conversely, active systems deliver enhanced control and adaptability but demand intricate control systems, sensors, and external power sources, which increases their complexity and potential vulnerability to power disruptions.

Hysteretic systems: These systems dissipate energy through cyclic stress–strain behavior. Examples include metallic yield dampers and friction dampers. The analysis of functional characteristics offers valuable insights into the fundamental physical principles governing energy dissipation. Hysteretic systems, such as metallic yield and friction dampers, dissipate energy through cyclic loading paths that generate distinct hysteresis loops. The area enclosed within these loops quantifies the energy dissipated during each cycle.

Viscoelastic systems: These systems exhibit both viscous and elastic behavior. Examples include viscoelastic dampers and fluid viscous dampers. Viscoelastic systems integrate an instantaneous elastic response with a time-dependent viscous behavior. This integration facilitates efficient energy dissipation over a broad-frequency spectrum and proves particularly beneficial in mitigating vibrations caused by seismic activity and wind forces.

Impact systems: These systems dissipate energy through controlled collisions. Examples include impact dampers and particle dampers. Impact systems and mass effect systems are two separate methodologies employed in vibration control. Impact systems function by utilizing controlled collisions to dissipate energy, whereas mass effect systems modify the dynamic properties of a structure by incorporating precisely calibrated auxiliary masses. These systems use additional mass to alter the dynamic characteristics of the structure. Examples include tuned mass dampers and tuned liquid dampers.

Integration and Performance Considerations

The characteristics illustrated in Figure 3 highlight the relationship among these various classification systems. For instance, a hybrid system could merge passive viscoelastic dampers with semi-active magnetorheological (MR) dampers, thereby ensuring a strong baseline performance while providing additional adaptable damping as necessary. This combination of diverse damping techniques and activation strategies enables engineers to devise tailored solutions that meet specific structural needs. The aforementioned characteristics of supplementary damping systems appear in Figure 3, as well as in

Table 1. Comparative analysis of supplementary damping systems.

Damper Type	Energy Dissipation Mechanism	Key Characteristics	Primary Applications	Advantages	Limitations	Detailed Discussion
Viscous Dampers	Velocity–dependent fluid flow	Rate- dependent response Temperature stable Linear/non linear behavior	High rise buildings Bridges Retrofit applications	Efficient energy dissipation Minimal temperature sensitivity Long service life	High initial cost Potential fluid leakage Maintenance requirements	Section 3.1
Viscoelastic Dampers	Material deformation	Temperature dependent Frequency dependent Viscous-elastic response	Building structures Wind vibration control	Good performance in small vibrations Simple construction Cost effective	Temperature sensitivity Material aging Limited deformation capacity	Section 3.2
Friction Dampers	Surface friction	Displacement dependent High energy dissipation Consistent performance	Multi-story buildings Industrial structures	High energy dissipation Temperature independent Low maintenance	Wear and tear Potential stick slip Complex modelling	Section 3.3
Metallic Yield Dampers	Material yielding	Stable hysteretic behavior Load path redundancy Displacement dependent	Building structures Bridge structures	Reliable performance Low cost Simple technology	Permanent deformation Replacement after major events Limited service life	Section 3.4
Tuned Mass Dampers	Inertial forces	Frequency tuned Mass dependent Motion based	Tall buildings Slender structures	Effective for specific frequencies No external power needed Long service life	Space requirements Limited frequency range Mass limitations	Section 3.5
Base isolation	Motion reduction	Period shifting Support flexibility Displacement capacity	Critical facilities Low to mid-rise structures	Complete system protection Proven performance Long service life	High initial cost Large displacements Foundation requirements	Section 3.6

.

Furthermore, Table 1 presents a comparative analysis of supplementary damping systems.

2.2. Principles of Energy Dissipation Mechanisms

Understanding the fundamental principles behind various energy dissipation mechanisms is crucial for the effective design and implementation of supplementary damping systems.

2.2.1. Viscous Damping

Viscous damping is based on the principle of fluid dynamics, where energy is dissipated through the movement of a piston in a viscous fluid. The damping force, F, is proportional to the velocity, v, of the piston:

F = C∙v^a

(1)

where C is the damping coefficient and a is the velocity exponent (typically between 0.3 and 1.0).

Key characteristics of viscous damping include:

Velocity-dependent behavior.

Out-of-phase response with displacement.

Temperature sensitivity.

Frequency independence (for linear viscous dampers).

2.2.2. Viscoelastic Damping

Viscoelastic damping utilizes materials that exhibit both viscous and elastic properties. The energy dissipation occurs due to shear deformation of the viscoelastic material. The complex modulus of a viscoelastic material is expressed as:

G* = G’ + i∙G’’

(2)

where G’ is the storage modulus (elastic component) and G^’’ is the loss modulus (viscous component). Key characteristics of viscoelastic damping include:

Frequency-dependent behavior.

Temperature sensitivity.

Combined stiffness and damping properties.

2.2.3. Friction Damping

Friction damping relies on the conversion of mechanical energy into heat through the relative motion of sliding surfaces. The damping force is governed by Coulomb’s law of friction:

F = μ∙N∙sign(v)

(3)

where μ is the coefficient of friction, N is the normal force, v is the relative velocity, and sign is the signum function. Key characteristics of friction damping include:

Displacement-dependent behavior.

Potential for stick–slip phenomena.

Wear and degradation over time.

2.2.4. Metallic Yield Damping

Metallic yield dampers dissipate energy through the plastic deformation of metals, typically mild steel or lead. The behavior is characterized by the material’s stress–strain relationship and follows the principles of plasticity theory. Key characteristics of metallic yield damping include:

Stable hysteretic behavior.

High energy dissipation capacity.

Potential for low-cycle fatigue.

2.2.5. Tuned Mass Damping

Tuned mass dampers (TMDs) operate on the principle of dynamic vibration absorption. By adding an auxiliary mass-spring-damper system tuned to the fundamental frequency of the structure, vibrational energy is transferred from the main structure to the TMD.

The optimal tuning ratio for a TMD is given by:

f_opt = 1/(1 + μ)

(4)

where f_opt is the optimal frequency ratio and μ is the mass ratio of the TMD to the structure. Key characteristics of tuned mass damping include:

Frequency-tuned behavior.

Effectiveness in a narrow frequency band.

Potential for off-tuning due to structural changes.

2.3. Brief History and Development of Damping Technologies

The development of supplementary damping technologies has been a gradual process, driven by advances in materials science, structural engineering, and control theory [19].

2.3.1. Early Developments (1950s–1960s)

1960s: Development of viscoelastic dampers for military and aerospace applications [20]. In their study, a new adaptive viscous damper (AVD) is presented, along with the requisite equations to elucidate its mechanical behavior. In contrast to standard adaptive devices, the proposed damper possesses the ability to modify its mechanical properties independently, without the necessity for supplementary devices such as sensors, processing units, actuators, energy supplies, or any wired or wireless connections. The AVD features a cylinder filled with viscous fluid and a piston that has a nozzle at its head.

1969: First application of viscoelastic dampers in a building, i.e., the World Trade Center, New York [21]. An extensive analysis was undertaken to examine the performance of VCDs using full-scale tests and to evaluate the appropriateness of different numerical models in predicting their responses. A variety of displacement-controlled tests were executed on a full-scale VCD specimen.

2.3.2. Emergence of Seismic Damping Systems (1970s–1980s)

1970s: Introduction of base isolation systems for seismic protection [22]. They presented an overview of the methodology utilized to create a reusable and optimized base-isolated system, emphasizing the reduction in structural stress and the enhancement of cost efficiency, all while striving for safe qualification. The study’s methodology merges numerical analysis with shake table testing to achieve a financially viable solution.

1970s: The first application of a tuned mass damper in a building, i.e., Centrepoint Tower in Sydney [23]. In this investigation, artificial neural networks were utilized to identify the ideal mechanical properties of tuned mass dampers (TMDs) designed for high-rise buildings under wind load conditions. The patterns generated from the structural analysis of different multi-degree-of-freedom (MDF) systems were leveraged for the training of the neural networks.

1980s: Development and application of fluid viscous dampers in civil structures [24,25]. This strategy, founded on a numerical approach to a constrained optimization problem, utilized a performance criterion that originates from the energy balance equation of the system, represented in stochastic terms. To effectively manage the nonlinear constitutive behavior of the FVDs, a cutting-edge equal-energy non-Gaussian stochastic linearization technique was integrated into the optimal design framework.

2.3.3. Proliferation and Diversification (1990s–2000s)

1990s: Widespread adoption of friction dampers and metallic yield dampers [26]. Metallic yield dampers are among the most acknowledged and utilized passive devices, primarily due to their straightforward installation, operational efficiency, resilience to environmental temperature variations, affordability, and consistent hysteretic performance. These dampers function by dissipating energy through the inelastic deformation of metals.

1990s: Introduction of magnetorheological (MR) dampers [27]. Large magnetorheological (MR) dampers are favored for their superior damping force capabilities, making them highly applicable in civil engineering, structural engineering, suspension bridge design, mining engineering, and agricultural engineering. A previous study [27] provided an extensive review of large MR dampers, encompassing their classifications and applications, operational principles, various fluid models, structural design, and control systems. It is noted that large MR dampers offer enhanced controllability of damping forces compared to traditional MR dampers. The findings of this review suggest that large MR dampers possess significant vibration mitigation capabilities and exhibit superior damping performance.

Late 1990s: Development of shape memory alloy (SMA) dampers [28,29]. The study of [28,29] presents the development process and initial experimental evaluations of a new energy dissipation damper that incorporates shape memory alloy (SMA) wires. The study [28] aimed to innovate this type of device and formulate a methodology for its design applicable across various applications. The core concept of our device is the implementation of a dual counteracting system featuring pre-strained SMA wire sections as the primary dissipative element. By utilizing pre-strained wires, this design seeks to optimize energy dissipation, albeit at the expense of some re-centering functionality. The experimental work was conducted on a reduced-scale prototype following this design framework.

2.3.4. Advanced Systems and Integration (2000s–Present)

2000s: Development of high-performance viscous dampers with large force capacities (e.g., [30]). In recent years, there has been a notable increase in research across various industrial sectors focused on the development of semi-active vibration control devices. Notably, devices that utilize magneto-rheological (MR) fluid have garnered significant attention due to their ability to function as capacity-variable dampers with high performance. MR fluids are unique in that they can be manipulated by external magnetic fields, which induce a dramatic change in their viscosity, transforming them from a liquid state to a semi-solid state.

2010s: Integration of damping systems with structural health monitoring technologies [31,32,33]. A previous article [33] outlined the development and findings from a three-year project that implemented an automated vibration-based structural health monitoring system. This system was aimed at modal tracking of the dynamic characteristics of a concrete-masonry Civic Tower in Rieti, Italy, which features a non-conventional tuned mass damper for passive vibration control. The system relies on data obtained from a small array of high-sensitivity accelerometers, which are utilized for remote automated tracking of modal parameters.

2020s: Exploration of bio-inspired damping systems and smart materials [34,35,36]. Shape memory alloy (SMA) exemplifies a prominent category of smart materials that are employed to enhance operational efficiency and mitigate various shortcomings associated with traditional base isolation systems. These shortcomings include inadequate recentering ability and significant isolator displacement, which can result in the pounding effect. SMA is notable for its unique property of tolerating exceptionally high strain during the loading phase while demonstrating no permanent deformation upon unloading. Nitinol (Ni-Ti) is predominantly utilized as the SMA material in most studies and applications.

2.3.5. Key Milestones and Influential Projects

1988: Completion of the Chiba Port Tower (Japan), featuring the first full-scale implementation of a hybrid mass damper system [37]. This investigation [37] focused on the management of structural vibrations through the application of a lever-type tuned mass damper (LTMD). The LTMD incorporates a constraint that confines motion at both ends of the lever. By combining the tuned mass damper (TMD) with this constraint, the LTMD regulates dynamic responses at two separate points. The parameters for the LTMD are initially estimated based on the TMD parameters and subsequently refined according to numerical results.

1994: Retrofit of the Golden Gate Bridge (USA) with viscous dampers [38]. An extensive analysis of the structural systems of the Golden Gate Bridge was performed [38], assessing the impacts of dead, live, wind, and earthquake loads via finite element modeling techniques. The investigation employed Strand7 for modeling, with results validated through analytical calculations. The report [38] began with a detailed review of the bridge’s structural elements, including a summary of the dimensions and sizes of its members and sections.

1999: Construction of Taipei 101 (Taiwan), incorporating a tuned mass damper visible to the public [39]. Continuous data streams from translational and rotational seismometers installed at TAIPEI 101 allowed for the monitoring of natural frequencies over different time scales. By utilizing the seismic data recorded in 2014 on the 90th floor of this high-rise and the meteorological data from a nearby weather station located just 1 km away, they examined [39] the characteristics and determinants of the ambient vibrations present in TAIPEI 101.

2008: Completion of the Beijing National Stadium (China), utilizing energy dissipation dampers in its innovative structural system [40]. This study [40] primarily concentrated on ensuring adequate structural performance, fostering sustainable development, and achieving architectural beauty. It encompassed in-depth investigations into structural performance through the analysis of the composition and decomposition of elements, applicable to diverse structures such as high-rise buildings, long-span crossings, and spatial frameworks.

2.3.6. Evolving Design Philosophies

The development of damping technologies has been accompanied by evolving design philosophies in earthquake engineering:

• 1970s–1980s: Focus on life safety and collapse prevention.
• 1990s–2000s: Emergence of performance-based seismic design.
• 2000s–Present: Emphasis on resilience and rapid post-earthquake recovery.

This comprehensive overview of supplementary damping systems provides a solid foundation for understanding their classification, operating principles, and historical development. It sets the stage for more detailed discussions of specific damping technologies, their analysis, and implementation in subsequent sections of the review paper. The evolution of these systems reflects the ongoing efforts to enhance structural performance and resilience in the face of seismic hazards.

3. Types of Supplementary Dampers and Their Characteristics

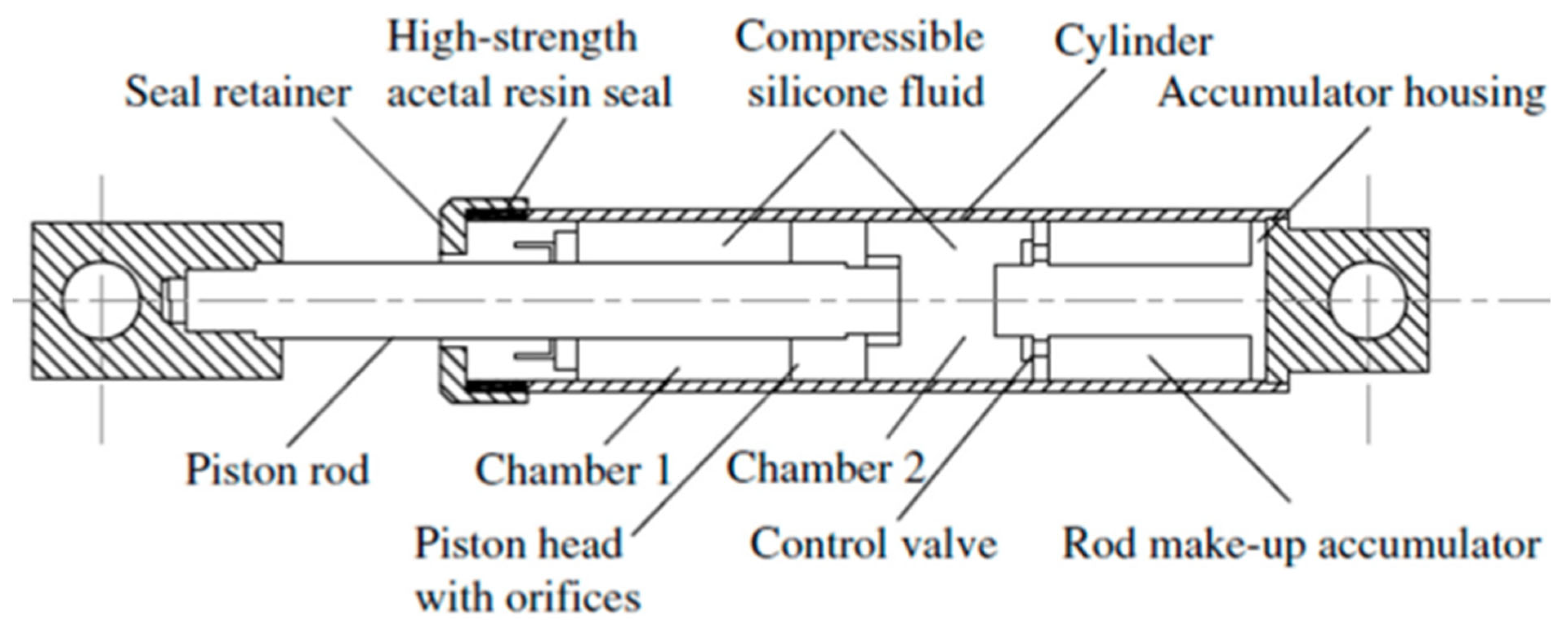
3.1. Viscous Dampers

3.1.1. Operating Principle

Viscous dampers are extensively utilized as supplementary damping devices in civil engineering due to their effectiveness and dependability. These devices function as passive energy dissipation systems that leverage the principles of fluid viscosity to absorb seismic energy and mitigate structural vibrations [41,42]. Typically, they comprise a piston that moves within a cylinder filled with a viscous fluid. During seismic activity, the movement of the piston forces the fluid through orifices, thereby converting kinetic energy into thermal energy. This process significantly diminishes the dynamic response of the structure, resulting in reduced displacements, accelerations, and internal forces [43,44].

A notable benefit of viscous dampers is their velocity-dependent characteristics, which enable them to deliver optimal damping forces at critical junctures during seismic events [45,46]. They are particularly adept at managing both low- and high-frequency vibrations, rendering them suitable for a variety of structural applications. Furthermore, viscous dampers can be seamlessly integrated into diverse structural systems, such as moment frames and braced frames, thus providing engineers with considerable flexibility in their implementation [47,48,49].

Recent technological advancements in viscous dampers have facilitated the emergence of adaptive and semi-active systems. These cutting-edge dampers possess the capability to modify their properties in real-time, responding to structural behavior or external control signals, which enhances their performance across a broader spectrum of seismic conditions [50]. Moreover, ongoing research into high-performance fluids and optimized damper designs continues to enhance the energy dissipation capacity and reliability of viscous dampers, thereby broadening their applicability in seismic design.

3.1.2. Mathematical Model

Viscous dampers operate on the principle of fluid dynamics. They typically consist of a piston moving through a cylinder filled with a highly viscous fluid, usually a silicone-based compound. As the piston moves, it forces the fluid through orifices, creating a resistance force that dissipates energy. The force–velocity relationship for a viscous damper is generally expressed as [51]:

F = C∙v^a

(5)

where:

F = Damping force.

C = Damping coefficient.

v = Velocity.

a = Velocity exponent (typically between 0.3 and 1.0).

For linear viscous dampers (a = 1), the equation simplifies to [52]:

F = C ∙ v

(6)

3.1.3. Key Characteristics

Viscous dampers exhibit several key characteristics that define their behavior and applications. They demonstrate velocity-dependent behavior, meaning their response is directly related to the speed of movement. These dampers produce an out-of-phase response with displacement, typically showing a 90° phase lag for linear dampers. While they can be sensitive to temperature changes, this can be mitigated through careful fluid selection and the implementation of thermal compensation systems. Linear viscous dampers exhibit frequency independence, making them effective across a wide range of vibration frequencies. Viscous dampers are known for their high energy dissipation capacity, allowing them to efficiently reduce structural vibrations. Importantly, they add minimal stiffness to the structure, which can be advantageous in many design scenarios.

3.1.4. Types of Viscous Dampers

Viscous dampers can be categorized into several types, each with unique characteristics:

(a)

Linear viscous dampers: These dampers exhibit a linear force–velocity relationship, making them predictable and easy to model. They are suitable for a wide range of applications due to their consistent behavior across different loading conditions. A prominent example of this type of damper is evident in the cable-stayed Rion-Antirion bridge in Greece (Figure 4), which is situated in a region with significant seismic activity [53].

(b)

Nonlinear viscous dampers (Figure 5): These dampers exhibit a nonlinear force–velocity relationship, usually with an exponent α < 1. This nonlinearity allows them to provide higher damping forces at low velocities while limiting forces at high velocities, making them particularly effective in scenarios with varying load intensities [54].

(c)

Bidirectional viscous dampers (Figure 6): These specialized dampers are capable of dissipating energy in two orthogonal directions. They are particularly useful in structures with complex motion patterns, where vibrations may occur in multiple planes simultaneously [55].

3.1.5. Design Considerations

When designing viscous dampers, several factors must be taken into account to ensure optimal performance. Sizing is based on the required damping coefficient and maximum force capacity, which are determined by the specific needs of the structure. The selection of appropriate fluid properties is crucial, considering the expected temperature range in which the damper will operate. Engineers must also consider seal durability and maintenance requirements to ensure long-term reliability. Integration with structural elements, such as bracing systems, is another key aspect of the design process, ensuring that the dampers work effectively within the overall structural system.

3.1.6. Applications

Viscous dampers find applications in a wide range of structures due to their versatility and effectiveness (Figure 7). In building structures, they are commonly used in high-rise buildings, hospitals, and data centers, where vibration control is critical for functionality and occupant comfort. Bridge structures, particularly long-span bridges and cable-stayed bridges, also benefit from viscous dampers to mitigate wind-induced and seismic vibrations. Industrial facilities such as nuclear power plants and offshore platforms utilize these dampers to enhance safety and operational reliability under various loading conditions.

3.2. Viscoelastic Dampers

Viscoelastic dampers are designed using materials that possess both viscous and elastic characteristics, enabling them to effectively dissipate energy [57]. These dampers function as passive energy dissipation devices, utilizing the distinctive properties of viscoelastic materials to reduce seismic energy and alleviate structural vibrations. Typically, they consist of layers of viscoelastic polymers positioned between steel plates [58]. In the event of an earthquake, the cyclic loading induces deformation in the viscoelastic material, leading to energy dissipation primarily in the form of heat. This mechanism significantly lessens the dynamic response of the structure, resulting in reduced displacements, accelerations, and internal forces [59,60]. The ability of viscoelastic dampers to effectively manage vibrations across both low and high frequencies makes them suitable for a wide range of structural applications. Their unique combination of damping and stiffness enhancement sets them apart from other damping systems, providing engineers with greater design flexibility and opportunities for performance optimization [61,62].

One of the primary advantages of viscoelastic dampers lies in their linear behavior across a wide range of frequencies and temperatures, which simplifies both analysis and design processes. These dampers exhibit exceptional resistance to fatigue and maintain their functional properties over prolonged durations, thereby ensuring consistent performance throughout the structure’s lifespan [63,64]. Recent advancements in polymer technology have led to the development of high-performance viscoelastic materials that demonstrate enhanced temperature stability and superior energy dissipation characteristics [65,66]. Additionally, researchers have explored hybrid systems that combine viscoelastic dampers with various damping methods to achieve enhanced performance across a broader spectrum of loading scenarios. As the demand for resilient structures grows, viscoelastic dampers are evolving continuously, offering innovative solutions for seismic protection in both newly constructed and retrofitted buildings [67,68].

3.2.1. Operating Principle

Viscoelastic dampers typically consist of viscoelastic material layers bonded between steel plates. When subjected to shear deformation, these materials dissipate energy through internal molecular friction. A typical example of a viscoelastic damper appears in Figure 8.

In the following, a typical application of viscoelastic dampers on building structures is examined. In the case of a bare structure (i.e., without supplementary dampers), the energy input into the structure during each seismic event is subject to partial dissipation due to inherent damping effects and nonlinear responses, specifically hysteresis energy. The remaining energy is retained within the structure as kinetic energy and elastic strain. On the other hand, in the case of a structure with supplementary dampers, the highest percentage of energy is dissipated by the dampers following the seismic activity. For instance, according to [69], based on the Tabas (BAJ.L1 Comp., 16 September 1978) seismic record, about 80% of the seismic energy is dissipated by the dampers.

3.2.2. Mathematical Model

The complex shear modulus of a viscoelastic material is expressed as:

G^* = G^’ + i∙G^’’

(7)

where:

G^’ = Storage modulus (elastic component).

G^’’ = Loss modulus (viscous component).

The loss factor, η, which represents the material’s damping capacity, is given by:

H = G^’’/G^’

(8)

3.2.3. Key Characteristics

Viscoelastic dampers exhibit several key characteristics that define their behavior and applications. They demonstrate frequency-dependent behavior, which means their performance varies based on the frequency of the applied loads. These dampers are also sensitive to temperature changes, which can affect their material properties and damping efficiency. Viscoelastic dampers combine both stiffness and damping properties, making them effective in energy dissipation while also contributing to the overall structural stiffness. Under service-level loads, they typically display relatively linear behavior, which simplifies their analysis and design in many applications.

3.2.4. Types of Viscoelastic Materials

Viscoelastic materials used in dampers can be categorized into two main types:

(a) Solid Viscoelastic Materials: These are typically acrylic or rubber-based polymers. They are used in shear or extensional configurations, allowing for various damper designs to suit different structural requirements. The solid form provides stability and consistency in performance over a wide range of loading conditions.

(b) Fluid Viscoelastic Materials: These are often silicone-based compounds. They are primarily used in fluid viscous dampers that incorporate viscoelastic properties. The fluid nature of these materials allows for unique damping characteristics and can be advantageous in certain applications where solid materials might be less effective.

3.2.5. Design Considerations

When designing viscoelastic dampers, several factors must be taken into account to ensure optimal performance and longevity. Material selection is crucial and should be based on the expected temperature and frequency range of the application. Engineers must consider long-term creep and aging effects, as these can significantly affect the damper’s performance over time. Protection from environmental factors such as UV radiation and moisture is essential to maintain the material’s properties. Proper bonding between viscoelastic layers and steel plates is also critical for effective energy dissipation and overall damper integrity.

3.2.6. Applications

Viscoelastic dampers find applications in various fields due to their unique properties. In building structures, they are particularly effective for mitigating wind-induced vibrations, helping to improve occupant comfort and structural integrity. These dampers are also utilized in aerospace structures, where their lightweight nature and effective energy dissipation properties are highly valued. Additionally, viscoelastic dampers are employed in equipment isolation, protecting sensitive machinery from harmful vibrations.

A characteristic application of viscoelastic dampers appears in Figure 9, which illustrates how these devices are typically integrated into structural systems for optimal performance.

3.3. Friction Dampers

3.3.1. Operating Principle

Friction dampers function by dissipating energy through the relative movement of sliding surfaces. These devices act as passive mechanisms for energy dissipation, employing frictional principles to mitigate seismic forces impacting structures [71,72]. Typically, they consist of two or more surfaces engineered to slide against each other under seismic loads, transforming kinetic energy into thermal energy via frictional interactions. Common types include Pall friction dampers, slotted-bolted connections, and rotational friction dampers. By strategically incorporating these devices into a structural design, engineers can significantly reduce vibrations and displacements caused by seismic events [73,74]. The attractiveness of friction dampers stems from their simple design, reliability, and consistent performance across various loading conditions. They require minimal maintenance and can be easily inspected and replaced, making them an advantageous option for both new constructions and retrofitting projects [75,76].

One of the notable advantages of friction dampers lies in their ability to activate at designated force thresholds, which allows for meticulous regulation of the structural response. This characteristic enables engineers to enhance the performance of structures in response to diverse seismic scenarios [77,78]. Additionally, friction dampers exhibit rectangular hysteretic behavior, which contributes to increased energy dissipation during each cycle. Recent advancements in materials and surface treatments have led to more consistent and predictable friction coefficients, thus bolstering the long-term dependability of these devices [79,80]. Furthermore, research into self-centering friction dampers has tackled challenges associated with residual displacements that occur after seismic activities. As performance-based design methodologies evolve, friction dampers continue to play a crucial role in the creation of resilient structures capable of withstanding substantial earthquakes while sustaining minimal damage [81,82].

3.3.2. Mathematical Model

Friction dampers typically consist of steel plates clamped together with high-strength bolts. Energy is dissipated through friction as the plates slide relative to each other under seismic loads. The basic friction model follows Coulomb’s law:

F = μ ∙ N ∙ sign(v)

(9)

where:

F = Friction force.

μ = Coefficient of friction.

N = Normal force.

v = Relative velocity.

3.3.3. Key Characteristics

Friction dampers exhibit several key characteristics. They demonstrate displacement-dependent behavior and produce nearly rectangular hysteresis loops. These dampers possess a high energy dissipation capacity, which makes them effective in mitigating structural vibrations. However, they may be susceptible to stick–slip phenomena, which can affect their performance. Over time, friction dampers are subject to wear and degradation, which needs to be considered in their long-term application and maintenance.

3.3.4. Types of Friction Dampers

There are several types of friction dampers, each with unique features:

(a) Slotted-bolted connections (SBC): These dampers utilize sliding between steel plates connected with high-strength bolts. They are known for their simplicity and cost-effectiveness, making them a popular choice in many applications.

(b) Pall friction dampers: These incorporate a series of steel plates and friction pad materials. Their design allows for consistent performance over a wide range of displacements, enhancing their reliability in various loading conditions.

(c) Sumitomo friction dampers: These dampers use copper alloy friction pads for enhanced durability. They are specifically designed for minimal maintenance, making them suitable for long-term applications where regular servicing might be challenging.

3.3.5. Design Considerations

When designing friction dampers, several factors must be taken into account. The selection of appropriate friction materials and surface treatments is crucial to achieve the desired damping characteristics. Control over the clamping force is essential for consistent performance across various loading scenarios. Designers must also consider the long-term wear of the friction surfaces and the potential for stick–slip behavior, which can affect the damper’s efficiency over time. Integration with structural framing systems is another key aspect, ensuring that the dampers work effectively within the overall structural design.

3.3.6. Applications

Friction dampers find applications in various structural and mechanical systems. They are particularly useful in building structures, especially in braced frames where they can effectively dissipate seismic energy. In bridge structures, these dampers are employed for seismic isolation and vibration control, enhancing the structure’s resilience to dynamic loads. Additionally, friction dampers are used in industrial equipment for vibration isolation, improving the performance and longevity of sensitive machinery.

A characteristic application of friction dampers appears in Figure 10, which illustrates how these devices are typically integrated into structural systems for optimal performance.

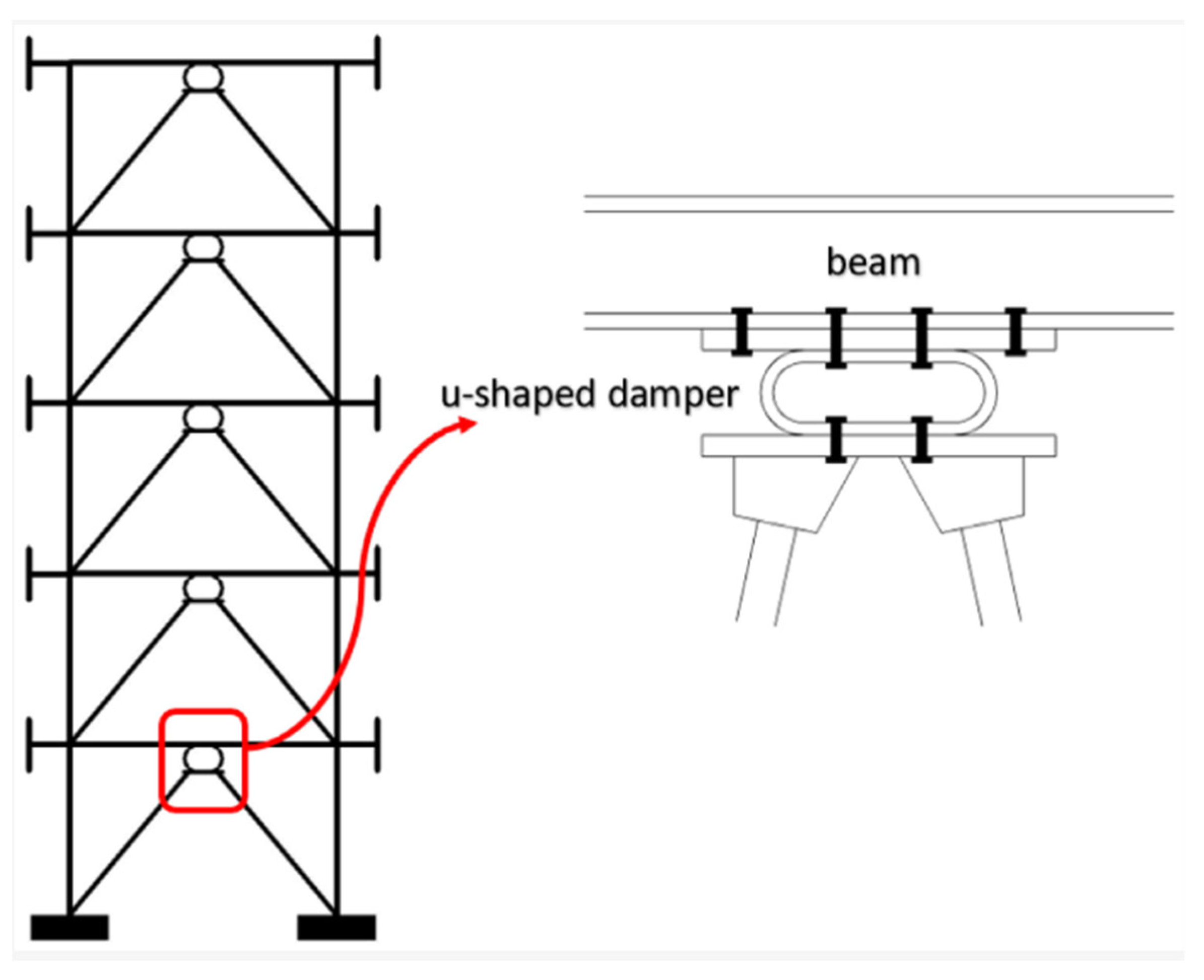
3.4. Metallic Yield Dampers

3.4.1. Operating Principle

Metallic yield dampers function by dissipating energy through the plastic deformation of metallic materials. Often termed hysteretic dampers, these devices are classified as passive energy dissipation systems that utilize the plastic deformation characteristics of metals to reduce seismic energy [84,85]. Typically constructed from specially designed metal elements, these dampers often employ mild steel or other ductile alloys, which undergo controlled yielding during seismic activities. This yielding process converts kinetic energy into thermal energy via plastic deformation, thus diminishing the seismic forces exerted on primary structural components [86,87]. There are several configurations of metallic yield dampers, such as added damping and stiffness (ADAS) devices, triangular-plate-added damping and stiffness (TADAS) devices, and buckling-restrained braces (BRBs). Their fundamental simplicity, dependability, and cost-effectiveness have led to their widespread use in both new construction projects and seismic retrofitting efforts around the world [88,89].

One of the primary advantages of metallic yield dampers is their consistent and predictable hysteretic behavior, which enhances the accuracy of performance evaluations and design methodologies. These devices can be effectively incorporated into various structural systems, including moment frames and braced frames, providing engineers with significant adaptability in their application [90,91]. Moreover, metallic yield dampers demonstrate exceptional resistance to fatigue, allowing them to withstand numerous loading cycles without experiencing considerable performance decline. This characteristic is especially beneficial in regions prone to aftershocks or frequent seismic events [92,93]. In addition, current research efforts are focused on the creation of advanced alloys and refined geometric configurations to enhance the energy dissipation properties and durability of these dampers, thus expanding their use in seismic engineering and improving the overall resilience of structures against earthquake hazards [94,95].

3.4.2. Mathematical Model

These dampers utilize the hysteretic behavior of metals (typically mild steel or lead) when deformed beyond their yield point. Energy is dissipated through cyclic plastic deformation. Therefore, the behavior of metallic yield dampers is typically modeled using plasticity theory. Common models include the bilinear model, the Ramberg–Osgood model, and the Bouc–Wen model.

3.4.3. Key Characteristics

Metallic yield dampers exhibit several key characteristics. They demonstrate stable hysteretic behavior and possess a high energy dissipation capacity. However, they may be subject to potential low-cycle fatigue. These dampers maintain temperature-independent behavior within typical operating ranges. Additionally, they contribute to the overall stiffness of the structure.

3.4.4. Types of Metallic Yield Dampers

There are several types of metallic yield dampers, each with unique features and applications:

(a) Added damping and stiffness (ADAS) devices consist of X-shaped steel plates designed to yield uniformly along their height. These devices provide both damping and added stiffness to the structure.

(b) Triangular added damping and stiffness (TADAS) devices utilize triangular steel plates that yield uniformly under bending. They offer improved performance and easier replacement compared to ADAS devices.

(c) Buckling-restrained braces (BRBs) are composed of steel core elements encased in concrete-filled steel tubes. This design prevents buckling and ensures stable behavior.

(d) Lead extrusion dampers employ the plastic deformation of lead for energy dissipation. These dampers offer high energy dissipation capacity and self-centering capabilities.

3.4.5. Design Considerations

When designing metallic yield dampers, several factors must be taken into account. Material selection should be based on the desired yield strength and ductility. A fatigue life assessment for expected seismic demands is crucial. Designers must also consider the cumulative plastic deformation capacity of the dampers. Finally, detailing should allow for easy inspection and replacement if necessary.

3.4.6. Applications

Metallic yield dampers find applications in various structural systems. They are particularly useful in building structures, especially in braced frames and moment-resisting frames. These dampers are also employed in bridge structures as part of seismic isolation systems. Additionally, they play a role in base isolation systems, such as lead–rubber bearings.

A characteristic application of metallic yield dampers in a portal frame, examined by [96], appears in Figure 11.

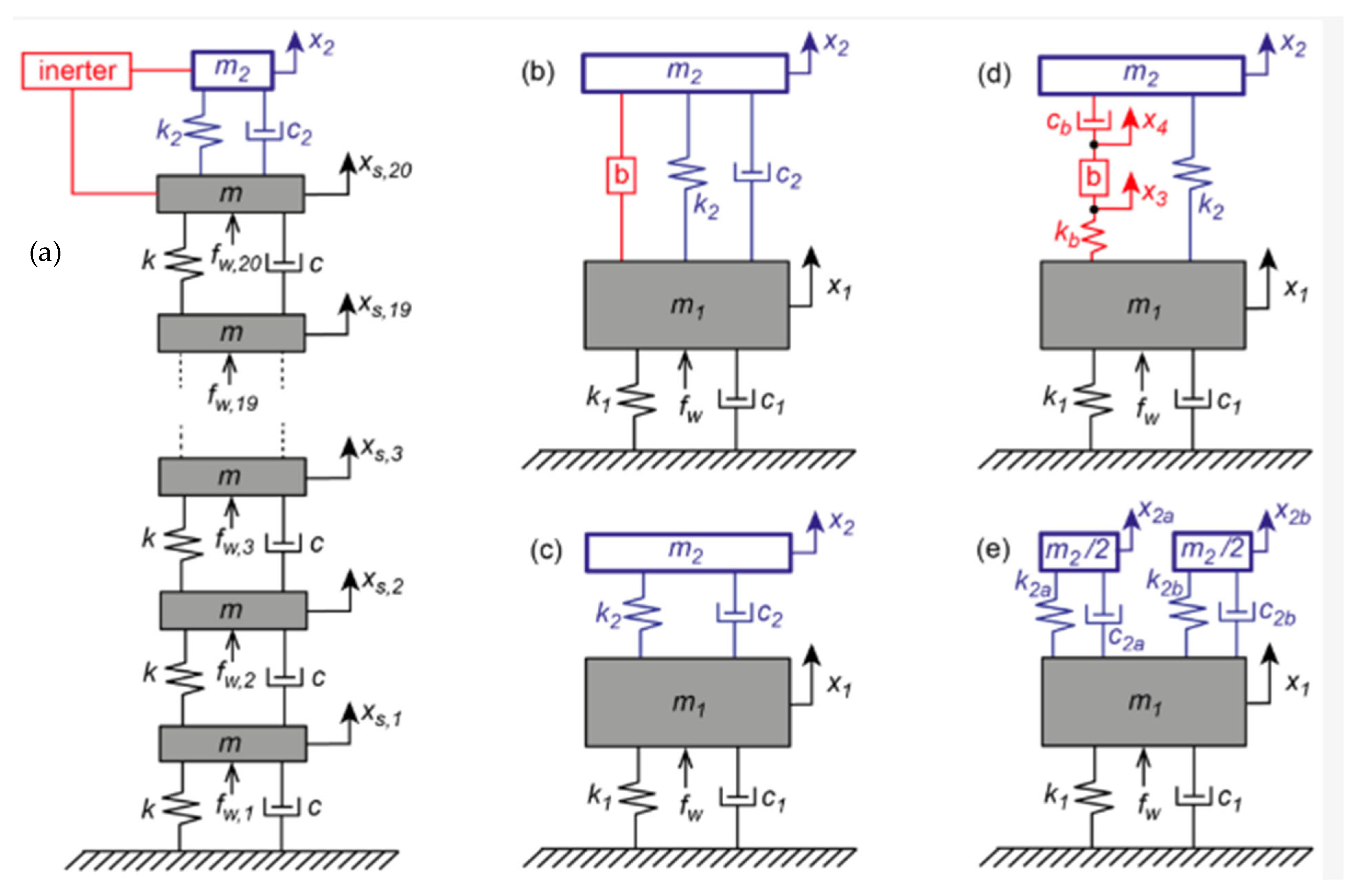
3.5. Tuned Mass Dampers

3.5.1. Operating Principle

Tuned mass dampers (TMDs) are passive control devices that reduce structural vibrations by adding an auxiliary mass–spring–damper system. Figure 12 depicts typical configurations of TMDs.

Tuned mass dampers (TMDs) are passive devices widely implemented in the field of structural engineering to mitigate vibrations caused by dynamic forces, including seismic events. These systems consist of a mass, a spring, and a damper, all of which are carefully calibrated to resonate at a specific frequency that generally corresponds to the fundamental mode of the structure [98,99]. When subjected to excitation, the TMD moves in opposition to the main structure, effectively absorbing and dissipating energy. This mechanism leads to a reduction in the overall structural response, resulting in lower displacements, accelerations, and internal forces. TMDs have been successfully utilized in various structures, from skyscrapers to bridges, demonstrating their versatility in enhancing seismic performance. Nevertheless, their efficacy relies on accurate tuning and a comprehensive understanding of the dynamic properties of the structure [100,101].

Unlike traditional tuned mass dampers (TMDs), which are designed for optimal performance in a singular mode, recent developments have led to the emergence of multi-tuned mass dampers (MTMDs) and adaptive tuned mass dampers (ATMDs) [102,103,104,105,106]. MTMDs consist of multiple TMDs, each possessing unique dynamic characteristics, facilitating concurrently managing various structural modes [107,108]. This approach significantly improves the system’s resilience and effectiveness across a broader range of excitatory forces [109,110,111]. In contrast, ATMDs incorporate active control systems that permit real-time modifications to the TMD’s properties, allowing for adaptation to changing dynamic conditions or alterations in structural characteristics [112,113,114]. These innovations have expanded the applicability of TMDs, making them more adept at managing the complex dynamic responses of structures exposed to seismic activity and enhancing their performance during unpredictable earthquake scenarios [115,116,117,118,119].

3.5.2. Mathematical Model

TMDs are tuned to the fundamental frequency of the structure. When the structure vibrates, the TMD oscillates out of phase, counteracting the structural motion and dissipating energy through its own damping mechanism.

The optimal tuning ratio, f_opt, for a TMD is given by:

f_opt = 1/(1 + μ)

(10)

where μ is the mass ratio of the TMD to the structure, i.e., mT/mm.

The optimal damping ratio, ζ_opt, for the TMD is:

ζ_opt = √(3μ/(8(1 + μ)³))

(11)

where

ζ = ω_T/ω_m with ω_T = √(k_T/m_T) and ω_m = √(k_m/m_m )

(12)

3.5.3. Key Characteristics

Tuned mass dampers (TMDs) exhibit several key characteristics that define their behavior and applications. They demonstrate frequency-tuned behavior, which allows them to be precisely calibrated to the structure’s natural frequency. This tuning results in their effectiveness being concentrated in a narrow frequency band, making them highly efficient for specific vibration modes. However, this narrow-band effectiveness also means that TMDs are potentially susceptible to off-tuning due to structural changes, which can reduce their efficiency. Another notable characteristic of TMDs is their large space requirements for the auxiliary mass, which can be a significant consideration in their implementation.

3.5.4. Types of Tuned Mass Dampers

There are several types of tuned mass dampers, each with unique features suited to different applications:

(a) Pendulum-type TMDs utilize a pendulum mechanism for the auxiliary mass. These are particularly suitable for tall structures with low fundamental frequencies, where the long pendulum length can be accommodated.

(b) Spring-mounted TMDs use mechanical springs to support the auxiliary mass. These are appropriate for structures with higher fundamental frequencies and where vertical space might be limited.

(c) Tuned liquid dampers (TLDs) use liquid motion in containers to provide the mass-damping effect. While simpler to implement, they are generally less efficient than solid mass TMDs. However, they can be advantageous in situations where the maintenance of moving parts is challenging [120].

(d) Multiple tuned mass dampers (MTMDs) employ multiple smaller TMDs tuned to slightly different frequencies. This approach provides a broader frequency bandwidth and improved robustness, making the system less sensitive to potential off-tuning.

3.5.5. Design Considerations

When designing tuned mass dampers, several factors must be taken into account to ensure optimal performance. The accurate determination of structural dynamic properties is crucial for proper tuning of the TMD. The selection of an appropriate mass ratio, typically 1–5% of the modal mass, is essential for balancing effectiveness and practicality. Designers must also consider spatial constraints for TMD installation, as these systems often require significant space. Provision for TMD maintenance and potential re-tuning should be incorporated into the design to ensure long-term effectiveness.

3.5.6. Applications

Tuned Mass Dampers find applications in a wide range of structures due to their effectiveness in controlling specific vibration modes. They are commonly used in tall buildings for both wind and seismic vibration control, where they can significantly improve occupant comfort and structural integrity. TMDs are also effective for slender structures such as towers, masts, and chimneys, where wind-induced vibrations can be particularly problematic. In civil infrastructure, they are employed in footbridges and long-span bridges to mitigate vibrations caused by pedestrian traffic or wind. Offshore structures also benefit from TMD technology, which helps control wave-induced motions.

A characteristic application of tuned mass dampers, examining the TAIPEI 101 skyscraper, appears in Figure 13. This example illustrates how TMDs can be effectively integrated into the design of super-tall buildings to control wind-induced vibrations and improve structural performance.

3.6. Base Isolation Systems

3.6.1. Operating Principle

Seismic isolation represents an effective methodology for safeguarding structures against earthquake-induced damage, with supplementary dampers significantly enhancing its efficacy, as demonstrated by [121]. Luo et al. [122] and Öncü-Davas and Alhan [123] showed that while traditional isolation systems primarily aim to separate the structure from ground vibrations, the incorporation of dampers introduces an additional mechanism for energy dissipation. Their research emphasizes that these dampers, which may be classified as viscous, viscoelastic, or hysteretic, collaborate with isolators to diminish displacement demands and regulate the structural response.

Rakicevic et al. [124] and Wolff et al. [125] highlight that by strategically positioning dampers within the isolation framework, engineers can optimize the dynamic properties of the building, improving its performance during seismic occurrences and addressing potential drawbacks of isolation alone, such as excessive displacements or the influence of higher-mode effects.

Durseneva et al. [126] and Xie and Zhang [127] demonstrate that this integrated strategy facilitates enhanced flexibility in meeting performance goals, especially in complex situations such as near-fault earthquakes or the design of tall structures. Ismail [128] and Milanchian and Hosseini [129] further show that the inclusion of dampers can result in more compact isolation systems, which may lead to reductions in construction costs and spatial requirements.

Chen and Xiong [130] and Tai et al. [131] emphasize that as performance-based design approaches continue to advance, the combination of dampers with isolation systems equips engineers with robust tools to develop resilient structures capable of enduring significant seismic events while minimizing damage and operational downtime, thereby improving the overall seismic resilience of the built environment.

3.6.2. Mathematical Model

Base isolation systems decouple the superstructure from the ground motion by introducing a flexible layer at the base of the structure. This significantly reduces the seismic forces transmitted to the superstructure.

The fundamental period of a base-isolated structure is approximated by:

T = 2π√(m/k)

(13)

where:

T = Fundamental period.

m = mass of the superstructure.

k = Stiffness of the isolation system.

3.6.3. Key Characteristics

Base isolation systems exhibit several key characteristics that define their behavior and effectiveness in seismic protection. One of the most significant features is the substantial period elongation they provide to the structure, which shifts the building’s response away from the predominant earthquake frequencies. This elongation results in a notable reduction in base shear and floor accelerations, significantly mitigating the seismic forces experienced by the structure. However, this comes with increased displacements at the isolation level, which must be accommodated in the design. Additionally, base-isolated structures may be susceptible to uplift and P-Delta effects, particularly during strong ground motions, which require careful consideration in the design process.

3.6.4. Types of Base Isolation Systems

Base isolation systems can be categorized into several types, each with unique properties:

(a) Elastomeric bearings are a common type of base isolator. They include laminated rubber bearings (LRBs), which consist of alternating layers of rubber and steel plates. Lead–rubber bearings (LRBs) are similar but incorporate a lead core for additional energy dissipation. High-damping rubber bearings (HDRBs) use specially formulated rubber compounds to provide both isolation and damping.

(b) Sliding systems represent another category of base isolators. Friction pendulum systems (FPSs) use a curved sliding surface to provide both period elongation and energy dissipation through friction. Double concave friction pendulum bearings are an advanced version of FPS, offering improved performance and stability.

(c) Hybrid systems combine elements of both elastomeric and sliding systems, aiming to leverage the advantages of each type. These systems can be tailored to meet specific project requirements and site conditions.

3.6.5. Design Considerations

Designing base isolation systems requires careful consideration of several factors. The selection of the appropriate isolation period and damping is crucial for optimal performance. Provisions must be made for large displacements at the isolation level, which can be challenging in urban environments with limited space. The design must also account for wind loads and service-level earthquakes, ensuring the structure performs well under various loading conditions. An important aspect of base isolation design is the implementation of flexible connections for utilities and access, allowing the structure to move freely on its isolators without disrupting essential services.

3.6.6. Applications

Base isolation systems find applications in a wide range of structures, particularly those where seismic protection is critical. They are commonly used in critical facilities such as hospitals and emergency response centers, where continuous operation during and after an earthquake is essential. Historic buildings often benefit from base isolation as a seismic retrofit solution, preserving the structure while significantly improving its seismic performance. In bridge engineering, base isolation is particularly valuable in high seismic zones, reducing the forces transmitted to the substructure. Additionally, base isolation techniques are employed for the protection of sensitive equipment, ensuring operational continuity in facilities such as data centers and manufacturing plants.

4. Design Considerations and Implementation Challenges

4.1. Selection and Sizing of Damping Devices

The process of selecting and sizing damping devices is a fundamental component in the integration of supplementary damping systems within the framework of structural seismic design. Lavan and Amir [132] have demonstrated that engineers are tasked with evaluating a range of factors, including the dynamic properties of the structure, anticipated seismic forces, and the desired performance outcomes. Güllü et al. [133] emphasize that the decision regarding the type of damper—whether viscous, viscoelastic, or friction-based—hinges on its characteristics and compatibility with the structural requirements. Their research highlights key considerations in this selection process, including force capacity, velocity dependence, and sensitivity to temperature variations. Moreover, studies by Nabid et al. [134] have shown that the quantity, dimensions, and strategic placement of dampers within the structure are pivotal in enhancing their efficacy in mitigating seismic responses. This body of research collectively underscores the complexity and criticality of the damper selection and sizing process in achieving optimal seismic performance of structures. Achieving the appropriate sizing of damping devices necessitates a careful equilibrium between enhancing performance and maintaining cost efficiency. Wang and Mahin [135] emphasize that the sizing process must consider practical limitations, including the spatial constraints for installation, architectural considerations, and ease of maintenance. Their research underscores the importance of these practical aspects in the design process.

4.2. Integration with Structural Systems

The integration of supplementary damping devices into structural systems necessitates a comprehensive investigation of the complex interplay between these dissipative mechanisms and the primary structure. Ruiz et al. [136] have shown that this process often entails extensive modifications to existing structural elements or the introduction of novel components to facilitate efficient force transfer from the dampers to the main structural system. According to these studies, the design methodology must ensure the primary structure’s capacity to withstand the additional forces induced by the dampers without compromising its structural integrity. Furthermore, recent investigations by D’Agostino et al. [137] and Labò et al. [138] emphasize that the integration approach must address architectural constraints, serviceability criteria, and potential implications for other building systems, including mechanical, electrical, and plumbing (MEP) networks. Their findings suggest that this multifaceted optimization problem requires advanced numerical modeling techniques and sophisticated performance-based design frameworks to achieve optimal structural performance under various loading scenarios.

Effective integration also requires a comprehensive methodology for structural analysis and design. As demonstrated by Zhou et al. [139] engineers must utilize sophisticated modeling techniques that accurately reflect the combined behavior of the primary structure and the supplementary damping system. Their research emphasizes the necessity of non-linear time–history analyses to evaluate performance under diverse seismic conditions. Gomez et al. [140] have shown that the design must take into account the varying response characteristics of the structure with and without the activation of dampers, as their studies reveal that certain damping devices may remain inactive during minor events or wind loads. Furthermore, recent work by Soroushian [141] highlights that the integration process should tackle constructability challenges. Their findings underscore the importance of addressing issues such as connection details, installation sequencing, and quality control measures to ensure that the dampers function as intended once they are incorporated into the structural system. These studies collectively emphasize the complexity of integrating supplementary damping systems and the need for advanced analytical approaches to ensure optimal performance.

4.3. Code Provisions and Design Guidelines

The integration of additional damping systems into structural designs to enhance seismic resilience has led to the development of comprehensive code provisions and design guidelines. These regulatory frameworks aim to ensure the safe and effective incorporation of damping devices within building structures, while also providing engineers with standardized methodologies for analysis and design. A pivotal advancement in the formal recognition of supplementary damping systems is attributed to the research conducted by Parajuli et al. [142]. Their significant study laid the groundwork for many subsequent code provisions, underscoring the importance of implementing performance-based design approaches when incorporating damping devices.

Building on this foundation, the American Society of Civil Engineers (ASCE) [143] has made notable advancements in the integration of damping system design guidelines within its seismic design standards. Anajafi and Medina [144] indicate that the ASCE 7 standard [143], which enjoys widespread adoption across the United States, now encompasses comprehensive provisions for the analysis and design of structures equipped with damping systems. These provisions address various elements, such as the selection of suitable damper types, the calculation of damping coefficients, and the assessment of structural performance in response to varying seismic hazard levels. In Europe, significant updates to Eurocode 8 have been implemented to reflect the growing incorporation of supplementary damping systems.

The Japanese building code is distinguished by its advanced seismic design regulations and has emerged as a pioneer in the incorporation of standards for damping systems. Anajafi and Medina [144] observed that this code provides comprehensive methodologies for the design of structures that utilize various types of dampers, including viscous, viscoelastic, and hysteretic devices. Their research underscores the code’s emphasis on the necessity of considering the non-linear characteristics of dampers within the larger framework of structural response analysis. A pivotal element addressed in contemporary code provisions is the imperative for performance verification of damping devices. Tabar and De Domenico [145] noted that numerous codes now mandate rigorous testing of dampers under diverse loading scenarios to ascertain their efficacy and dependability. These testing protocols generally encompass cyclic loading assessments, evaluations of temperature sensitivity, and long-term performance analyses to address potential aging impacts. The incorporation of damping systems into performance-based seismic design frameworks has been a focal point of recent code advancements.

A crucial aspect emphasized in contemporary design standards is the recognition of uncertainties associated with damper characteristics and seismic forces. Seong-Ha et al. [146] noted that the implementation of probabilistic approaches is becoming more prevalent within regulatory frameworks, enabling a more thorough assessment of structural reliability in the context of damping systems. These approaches frequently employ fragility curves and reliability indices to evaluate the likelihood of meeting specified performance objectives. The incorporation of damping systems in high-rise buildings and long-span structures has presented unique challenges that have been addressed in recent updates to codes. Quintana and Petkovski [147] highlighted that many guidelines now include specific provisions for the design of dampers in skyscrapers, taking into account the effects of higher modes and wind-induced vibrations. Their findings emphasize the importance of considering multiple hazards during the design process, a concept that is increasingly reflected in modern building regulations.

The field of supplementary damping is currently witnessing significant progress, which is anticipated to result in further improvements in code regulations and design standards. Recent findings by Guo et al. [148] indicate that future revisions of these codes may incorporate advanced analytical techniques, such as machine learning algorithms, to enhance the positioning and attributes of dampers. In conclusion, the development of comprehensive code regulations and design standards for supplementary damping systems has played a crucial role in facilitating their widespread adoption within seismic design practices. These regulatory frameworks are in a state of continuous evolution, reflecting advancements in both theoretical research and practical implementation, and are vital for guaranteeing the safe and effective application of damping technologies to bolster structural resilience against seismic events.

5. Future Research Directions

Despite notable progress in the development of supplementary dampers for seismic protection, several important gaps in the existing body of knowledge necessitate further exploration. These gaps encompass various dimensions of damper design, implementation, and performance assessment, underscoring the imperative for ongoing research initiatives aimed at improving the effectiveness and dependability of these systems. A particularly critical area for further inquiry is the long-term performance and deterioration of damping devices when subjected to diverse environmental conditions. Xie and Hua [149] assert that, while existing design approaches partially address these interactions, there is a pressing need for more advanced models capable of accurately forecasting the coupled behavior of dampers and structural components during intense seismic activity. This gap in understanding is particularly critical when considering the likelihood of nonlinear responses and damage accumulation in both the dampers and the primary structure.

The efficacy of supplementary dampers in multi-hazard contexts constitutes a significant area of research that remains underexplored. According to Hao et al. [150], although these dampers are primarily engineered for seismic mitigation, their effects on structural performance during other extreme conditions, such as severe wind events or explosive forces, are not yet thoroughly comprehended. It is crucial to cultivate a holistic understanding of damper functionality across various hazard scenarios to refine their design and guarantee their operational effectiveness in a range of environmental challenges. Additionally, there exists a considerable deficiency in the existing literature concerning the incorporation of smart materials and adaptive control mechanisms within supplementary damping systems. Wu et al. [151] emphasized the promise of self-sensing and self-adjusting dampers that can modify their characteristics in real time in response to external stimuli. Nevertheless, the advancement and practical application of such sophisticated systems remain nascent, highlighting the need for further investigation to unlock their complete potential in bolstering structural resilience.

In recent years, the development of innovative seismic protection systems has gained momentum, with particular emphasis on the seesaw system due to its distinctive method of controlling structural responses [152,153,154]. This system utilizes dampers and cables arranged in a manner that emulates the motion of a seesaw, thereby facilitating improved energy dissipation during seismic activities [155,156]. The seesaw mechanism is characterized by a central pivot point, upon which the structure is effectively balanced. As mentioned by Katsimpini et al. [157,158], dampers are strategically positioned at the extremities of the seesaw arms, while cables contribute to additional stability and control. In the event of an earthquake, the seesaw motion engages the dampers, which dissipate seismic energy through various mechanisms, including viscous fluid displacement and friction. Concurrently, the cables serve to restrict excessive displacements and provide a restorative force to the structure [159]. This collaborative interaction among the seesaw motion, dampers, and cables leads to a more regulated structural response, potentially mitigating both inter-story drifts and accelerations [160]. The efficacy of the seesaw system has been validated through numerical simulations and experimental investigations, indicating its potential for application in both new constructions and the retrofitting of existing buildings. Nonetheless, additional research is essential to refine the system’s parameters, including damper specifications, cable pretension, and seesaw geometry, to enhance its performance across a diverse array of seismic conditions [161,162]. This innovative system appears in Figure 14.

The transition of damper performance from controlled laboratory environments to real-world applications presents a considerable challenge. According to Ocak et al. [163], although small-scale experiments and numerical analyses yield important insights, there is a notable deficiency in comprehensive data derived from large-scale, practical implementations of supplementary dampers. This lack of information complicates the accurate forecasting of damper efficacy in actual structures and highlights the necessity for more thorough full-scale testing and evaluations of performance following seismic events. Additionally, there is a pressing need for the establishment of standardized performance metrics and testing protocols for supplementary dampers.

The incorporation of additional dampers alongside other advanced seismic protection technologies, such as base isolation systems and structural health monitoring frameworks, reveals a significant gap in current knowledge. According to Yan et al. [164], while these technologies have been examined in isolation, their collective impacts and possible synergies remain inadequately explored. Investigating hybrid systems that utilize the advantages of various protective strategies may result in more robust and adaptable structural designs. Furthermore, there exists a considerable deficiency in comprehending the socio-economic ramifications of the extensive deployment of supplementary dampers in urban settings.

The integration of sophisticated data analytics and machine learning methodologies for the optimization of damper design and performance forecasting is an emerging domain characterized by considerable knowledge deficiencies. Thiebaud and Ben Zineb [165] and Kang et al. [166] indicate that, although these technologies hold promise for deepening our comprehension of intricate damper dynamics, their complete potential within the realms of structural dynamics and earthquake engineering remains largely untapped. In summary, while additional dampers have demonstrated effectiveness in improving the seismic resilience of structures, the existing knowledge gaps present significant avenues for future inquiry. Addressing these deficiencies is essential for the advancement of the discipline, enhancing the reliability and efficiency of damping systems and ultimately bolstering the resilience of structures against seismic threats. As structural designs become increasingly complex and performance expectations rise, bridging these knowledge gaps will be critical in influencing the future of earthquake-resistant design methodologies.

6. Discussion

6.1. Cost-Effectiveness and Life-Cycle Considerations

The integration of supplementary dampers into structural designs aimed at improving seismic resilience requires a thorough assessment of both cost-effectiveness and life-cycle implications. Matta [167,168] posits that while the initial costs associated with damping systems can be considerable, the advantages realized over the lifespan of the structure frequently surpass these initial expenditures. The economic viability of supplementary dampers is largely influenced by their effectiveness in minimizing seismic-related damage and lowering repair and downtime expenses in the aftermath of an earthquake. Research by Kolour et al. [169] indicates that structures fitted with sophisticated damping mechanisms exhibit markedly lower levels of damage and quicker recovery periods when compared to traditional designs. This enhanced performance yields significant financial advantages, especially in areas that experience regular seismic events.

Life-cycle cost analysis (LCCA) is essential for evaluating the long-term economic feasibility of supplementary dampers. According to the findings of Gallo et al. [170], LCCA must consider not only the initial costs associated with design and installation but also the ongoing expenses related to maintenance, inspection, and possible replacement throughout the lifespan of the structure. Their research indicates that while structures equipped with dampers may incur higher upfront costs, the subsequent reduction in damage and maintenance needs can lead to lower overall life-cycle costs. The economic advantages of supplementary dampers are further amplified by their ability to facilitate more cost-effective structural designs. Gur et al. [171] highlight that the integration of damping systems can decrease the necessary strength and stiffness of primary structural components. This optimization not only results in material savings but may also significantly mitigate the installation costs associated with the dampers.

It is crucial to acknowledge the variability in seismic hazard when assessing the cost-effectiveness of additional dampers. Research by Panda et al. [172] indicates that the economic advantages of damping systems are most significant in areas characterized by high seismic risk, where the likelihood of encountering strong ground motions is considerable. Conversely, in regions with lower seismic hazards, the cost–benefit ratio may not be as advantageous, thereby requiring a thorough analysis to validate the investment. Furthermore, the life-cycle implications of dampers encompass more than just economic considerations. Factors related to environmental impact and sustainability must also be evaluated. As noted by Hu et al. [173], the diminished material requirements and enhanced structural durability associated with buildings equipped with dampers can lead to reduced carbon emissions and improved sustainability throughout the lifespan of the structure.

The requirements for maintenance and inspection are pivotal elements in the life-cycle assessment of supplementary dampers. Although these systems typically necessitate less frequent maintenance than other structural components, it remains essential to conduct regular inspections and occasional replacements to guarantee optimal functionality. Research by Zhang and Hu [174] introduced a risk-based maintenance framework that fine-tunes inspection frequencies and replacement timelines according to the type of damper, prevailing environmental conditions, and anticipated seismic activity, thus reducing life-cycle expenses while ensuring system reliability. The capacity of supplementary dampers to adapt to evolving structural demands and varying seismic risk levels over time is a significant factor in life-cycle evaluations. As highlighted by Noureldin et al. [175], certain advanced damping systems can be recalibrated or upgraded without necessitating extensive structural alterations. This flexibility can prolong the effective lifespan of the damping system and enhance its long-term cost efficiency. In summary, the considerations surrounding the cost-effectiveness and life-cycle of supplementary dampers are complex and necessitate thorough analysis within the framework of specific project needs and regional seismic threats. Although the initial financial outlay may be considerable, the advantages of diminished damage, enhanced performance, and reduced long-term expenses frequently validate their use, especially in areas prone to significant seismic activity. As seismic design methodologies continue to advance, ongoing research and evaluations following implementation will further elucidate the long-term economic and environmental advantages of these cutting-edge damping systems.

6.2. Strategies and Solutions for Design Implementation Challenges

The complex challenges identified in the preceding sections necessitate systematic strategies and innovative solutions to ensure the optimal implementation of supplementary damping systems. Research by Shehata et al. [176] proposes a multi-objective optimization framework that addresses the damper selection and sizing challenges through a three-phase approach. The first phase involves preliminary sizing based on equivalent linear analysis, followed by refined optimization using non-linear time history analysis, and concluding with practical adjustments considering constructability constraints. This methodology has demonstrated a 15–20% improvement in performance compared to traditional design approaches.

To address integration challenges, Caterino et al. [177] developed a comprehensive workflow that combines building information modeling (BIM) with structural analysis to identify potential conflicts and optimize damper placement. Their approach includes (1) early-stage coordination between structural engineers and architects to establish spatial constraints, (2) the development of standardized connection details for various damper types, and (3) the implementation of clash-detection algorithms to minimize conflicts. This integrated approach has been successfully implemented in several high-rise projects, reducing design iterations by approximately 30%.

To overcome code compliance challenges, Wen et al. [178] proposed a performance-based design framework that bridges the gap between various international standards. Their methodology incorporates the development of project-specific acceptance criteria that satisfy multiple code requirements and the implementation of hybrid testing protocols that address both component and system-level performance. This framework has been validated through several case studies, demonstrating its effectiveness in meeting diverse regulatory requirements.

Regarding cost-effectiveness concerns, Kolour et al. [169] presented a life-cycle optimization strategy that balances initial costs with long-term benefits. Their approach includes the development of probabilistic cost–benefit models that account for regional seismic hazard levels and the incorporation of sustainability metrics in the decision-making process. Case studies indicate potential life-cycle cost reductions of 25–35% compared to conventional designs.

Furthermore, recent advances in artificial intelligence and machine learning have led to innovative solutions for damper design optimization. Gharagoz et al. [82] demonstrated the application of deep learning algorithms for the real-time adjustment of damper properties based on structural response data. Their research shows that these adaptive systems can improve damper efficiency by up to 40% under varying loading conditions.

7. Conclusions and Recommendations

This extensive examination of supplementary dampers aimed at enhancing the seismic performance of structures has yielded significant insights into the contemporary advancements within this vital domain of structural engineering. The evaluation of various damping technologies, alongside their applications and performance metrics, has highlighted notable progress in bolstering the seismic resilience of both newly constructed and retrofitted structures.

The review underscores the pivotal role that supplementary dampers play in alleviating the detrimental impacts of seismic activities on structures. The deployment of these damping systems has consistently resulted in enhanced structural performance, minimized damage, and improved safety for occupants during seismic events. The array of damper types available, such as viscous dampers, viscoelastic dampers, friction dampers, and metallic yield dampers, equips engineers with a flexible set of tools to meet specific structural needs and address seismic challenges effectively.

A significant conclusion drawn from this review is the critical nature of the design and integration of supplementary dampers within the overall structural framework. The efficacy of these dampers is largely contingent upon their optimal placement, sizing, and compatibility with the structural design. Therefore, engineers are encouraged to perform comprehensive analyses and simulations to refine the damper configurations, ensuring maximum protection against seismic threats.

The review has underscored the increasing inclination toward performance-based design methodologies within the realm of seismic engineering. The utilization of supplementary dampers has emerged as an effective strategy for meeting specific performance goals, facilitating enhanced control over structural responses during seismic occurrences. This transition to performance-based design demands a more comprehensive understanding of damper functionality and its interplay with the primary structural system.

In practical terms, the review has presented a variety of case studies illustrating the successful application of supplementary dampers across diverse structures, such as skyscrapers, bridges, and essential infrastructure. These empirical examples offer critical insights and best practices for future applications, highlighting the adaptability and efficacy of damping technologies across different structural forms.

Notwithstanding the considerable advancements in this domain, several aspects require additional investigation and development. One critical area pertains to the long-term performance and resilience of supplementary dampers when subjected to fluctuating environmental conditions and repeated seismic activities. Further research is essential to evaluate the aging properties of various damper types and formulate effective maintenance protocols that will ensure their sustained performance throughout the lifespan of the structure.

A critical area that warrants further exploration is the advancement of sophisticated control algorithms for adaptive damping systems. With the ongoing progress in smart materials and sensing technologies, there exists significant potential for the development of more responsive and efficient damping solutions capable of real-time adaptation to fluctuating seismic conditions. The combination of supplementary dampers with other seismic mitigation strategies, such as base isolation and structural health monitoring systems, represents a promising direction for future research. Hybrid systems that integrate various protective measures may provide improved seismic performance and resilience. From a practical perspective, there is an urgent need for the standardization and formalization of design protocols for supplementary dampers. Although numerous countries have established guidelines for damper design within their seismic codes, a lack of consistency in methodology persists. The creation of comprehensive, internationally accepted standards would greatly enhance the widespread implementation of these technologies and ensure reliable performance across diverse regions.

In summary, supplementary dampers have emerged as essential instruments for enhancing the seismic performance of structures. Their capacity to absorb seismic energy and alleviate structural stresses presents a significant opportunity for fostering more resilient built environments. As urban development accelerates and the demand for seismic safety intensifies, especially in regions susceptible to earthquakes, the significance of supplementary dampers is expected to grow substantially.

It is advisable for the structural engineering sector to persist in its commitment to the research and development of innovative damping technologies. This endeavor should encompass the exploration of new materials, refinement of design strategies, and assessment of the long-term efficacy of these systems. Moreover, it is imperative to facilitate the connection between academic inquiry and practical application, ensuring that cutting-edge advancements in damper technology are successfully integrated into real-world scenarios.

Additionally, it is vital to advocate for educational and training initiatives centered on the design and application of supplementary dampers. Such programs will contribute to the cultivation of a proficient workforce adept at leveraging these technologies and advancing the field of seismic engineering.

In conclusion, supplementary dampers have proven to be invaluable tools in improving the seismic behavior of structures. Their ability to dissipate seismic energy and reduce structural demands offers a promising path toward creating resilient built environments. As urbanization continues and the need for seismic protection grows, particularly in earthquake-prone regions, the role of supplementary dampers is likely to become increasingly important.

It is recommended that the structural engineering community continue to invest in the research and development of advanced damping technologies. This includes exploring novel materials, optimizing design methodologies, and investigating the long-term performance of these systems. Additionally, efforts should be made to bridge the gap between academic research and practical implementation, ensuring that the latest advancements in damper technology are effectively translated into real-world applications.

Furthermore, it is crucial to promote education and training programs focused on the design and implementation of supplementary dampers. This will help to build a skilled workforce capable of effectively utilizing these technologies and pushing the boundaries of seismic engineering.

Economic factors play a crucial role in the adoption of supplementary damping systems. Although the initial costs of implementation can be high, the long-term advantages often validate the expenditure through diminished repair expenses, reduced insurance premiums, and enhanced property value. Life-cycle cost analysis has emerged as a vital instrument in illustrating the economic feasibility of these systems.

The progress of supplementary damping technologies necessitates ongoing collaboration between academic institutions and industry stakeholders. This collaboration should encompass the creation of thorough educational and training initiatives aimed at cultivating a proficient workforce capable of effectively deploying these technologies. It is essential to fortify the link between academic research and practical application to ensure that innovative advancements are successfully translated into tangible solutions.

Ultimately, the future development of supplementary damping systems will rely on continuous research into novel materials [179], improved design techniques, and a deeper understanding of long-term performance attributes. As seismic protection standards become more rigorous and urban expansion persists in earthquake-prone areas, the significance of these systems in maintaining structural integrity will become increasingly critical.