Study of Reynolds Number Effects on Aerodynamic Forces and Vortex-Induced Vibration Characteristics of a Streamlined Box Girder
Abstract
:1. Introduction
2. Wind Tunnel Test Setup
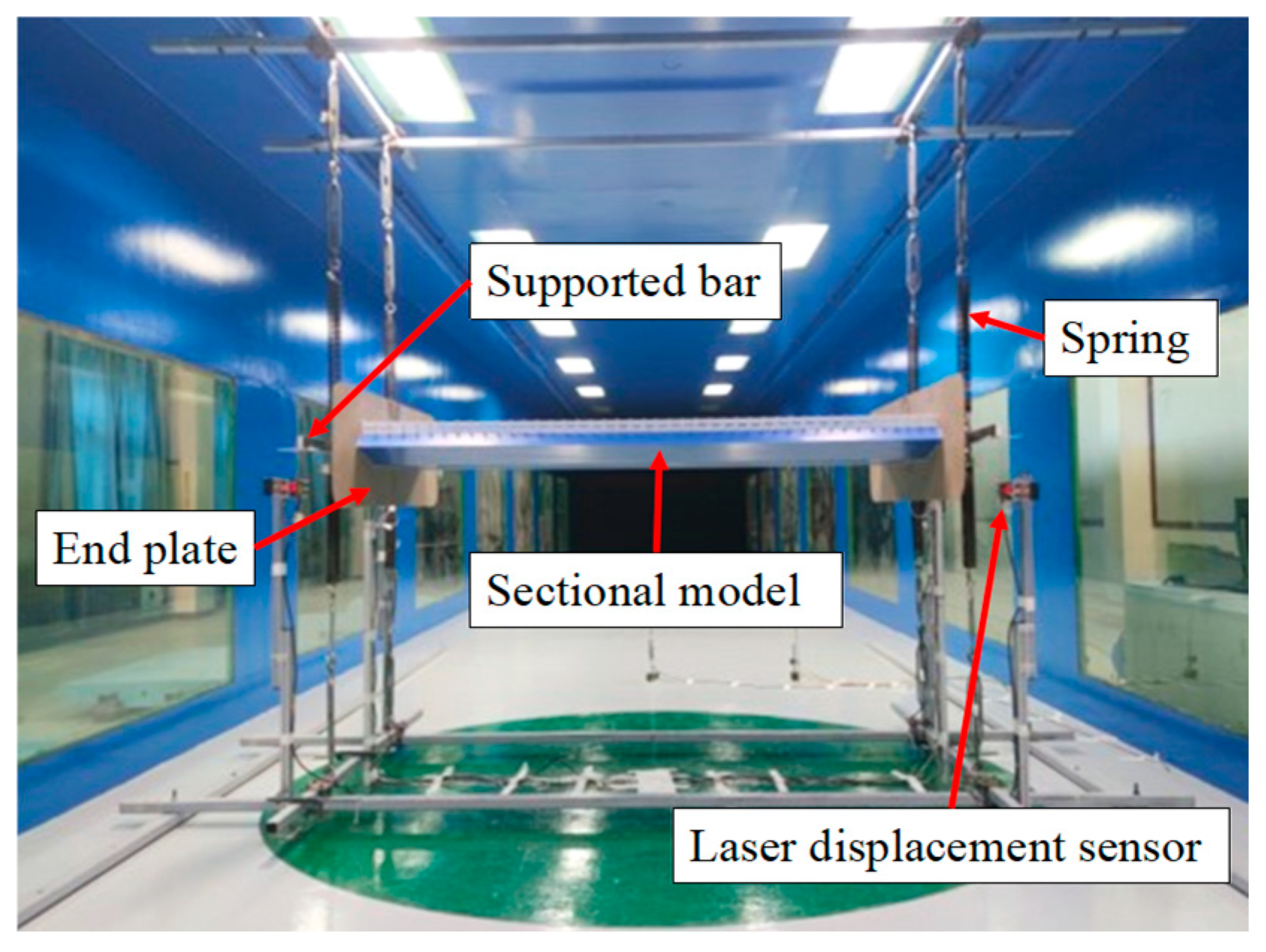
2.1. Wind Tunnel
2.2. Model Setup
2.3. Test Conditions
3. Reynolds Number Effects on Static Aerodynamic Characteristics
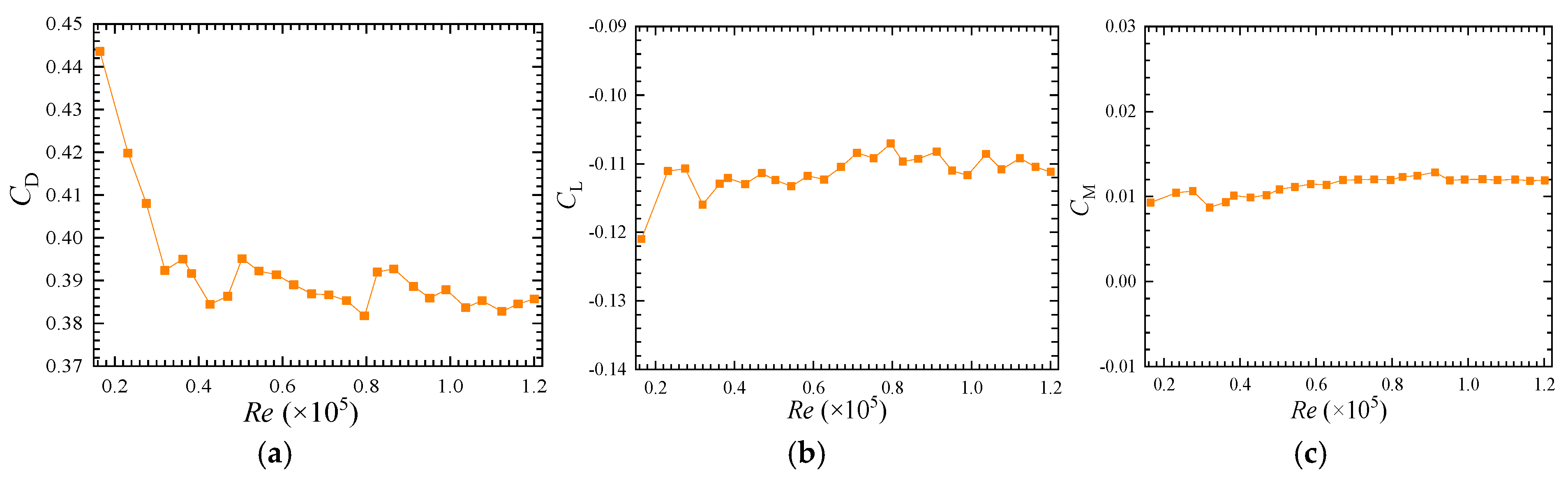
3.1. Mean Aerodynamic Force Coefficients
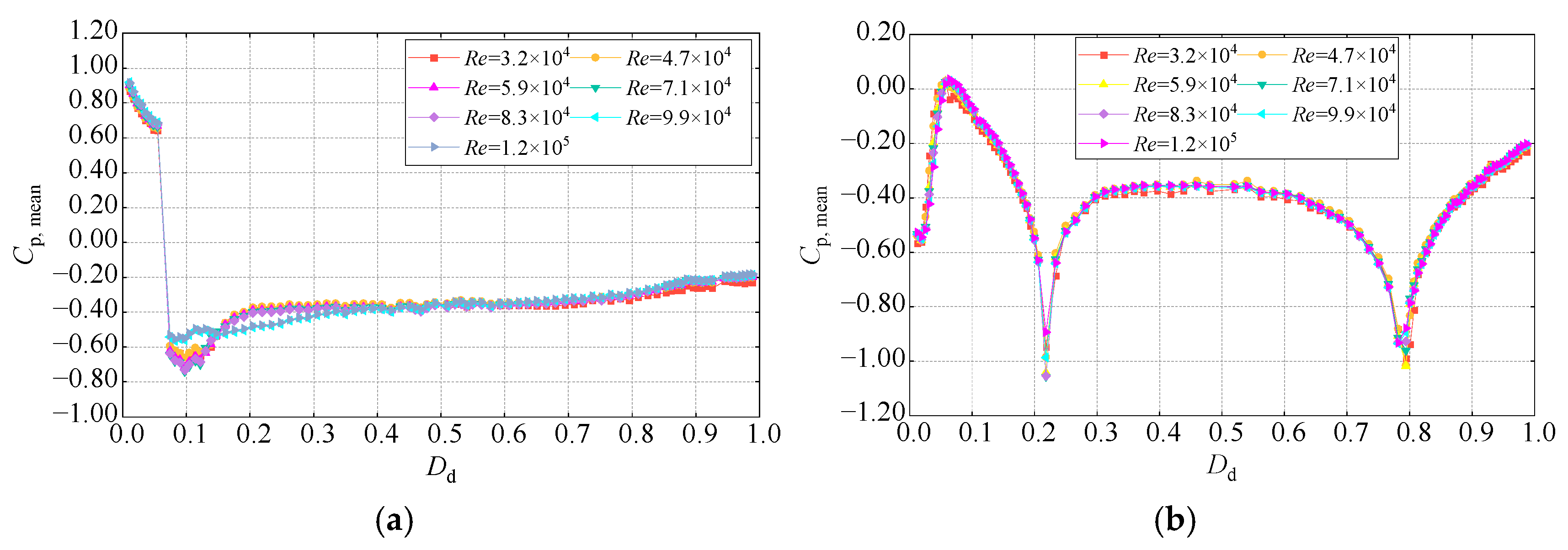
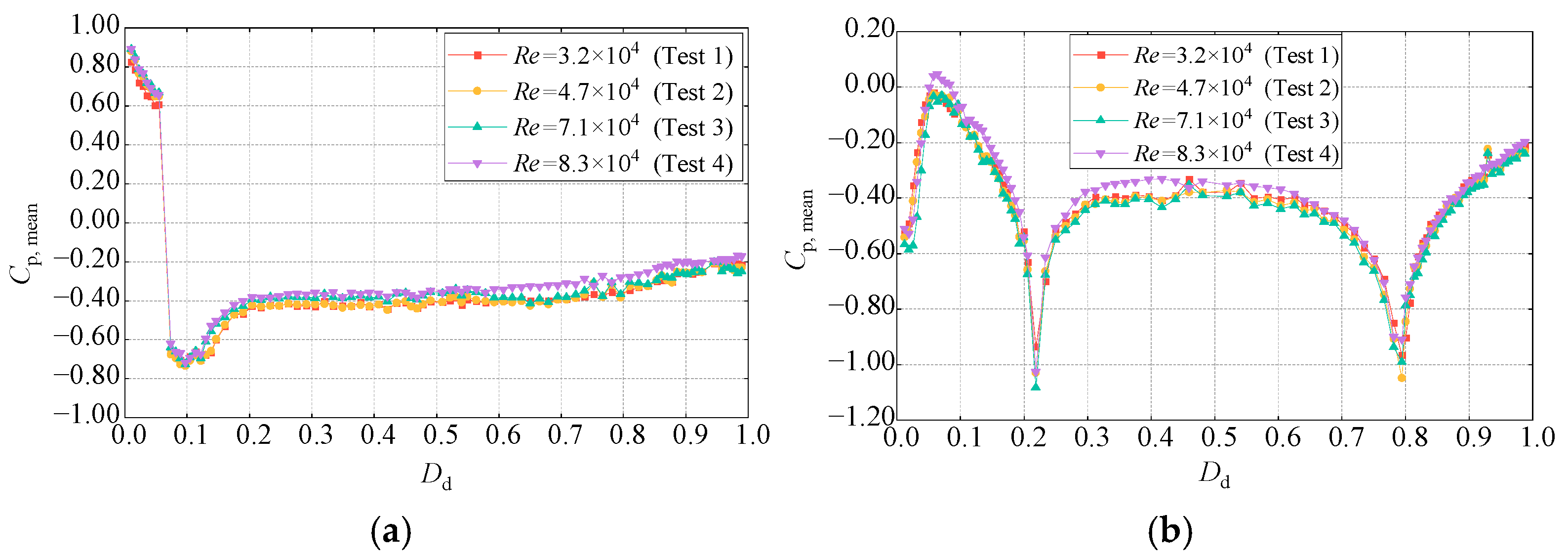
3.2. Mean Values of the Wind Pressure Coefficients
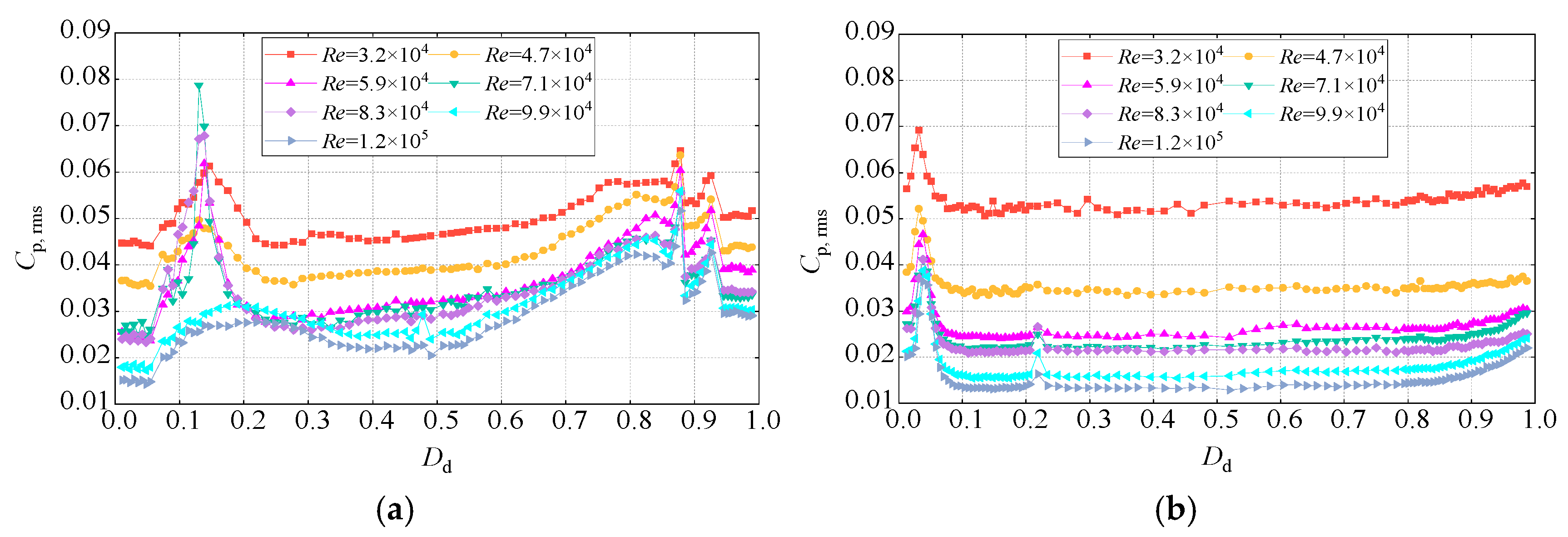
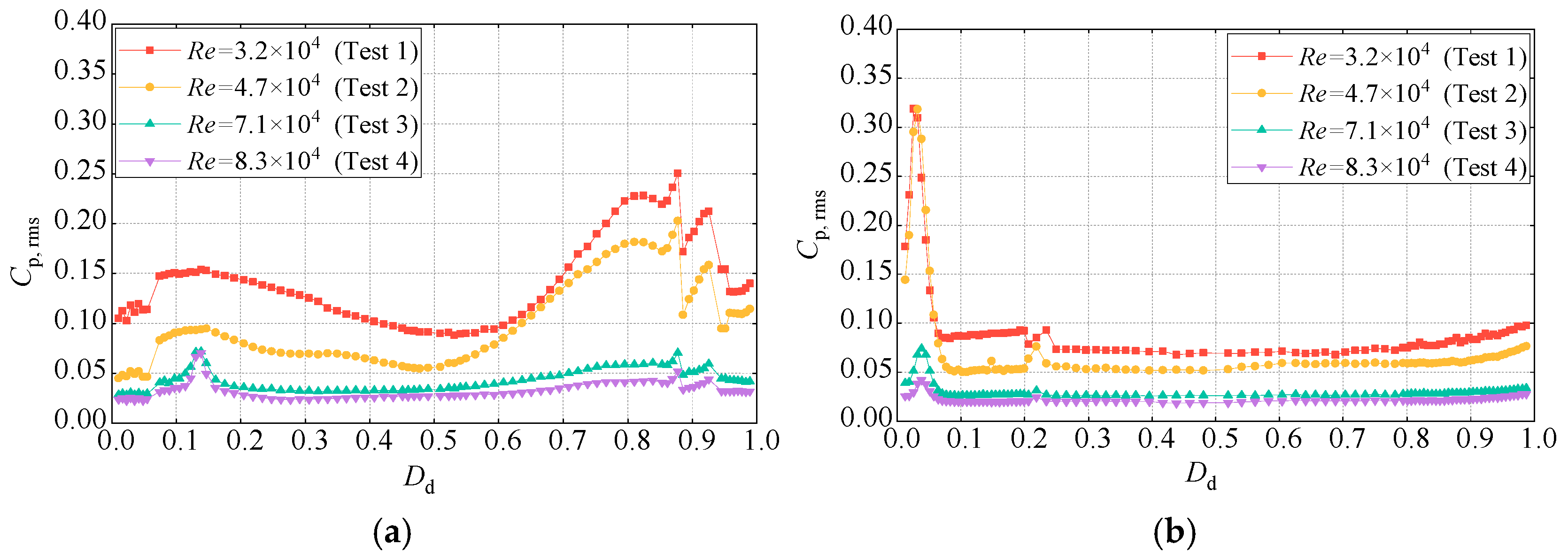
3.3. RMS Values of the Wind Pressure Coefficients
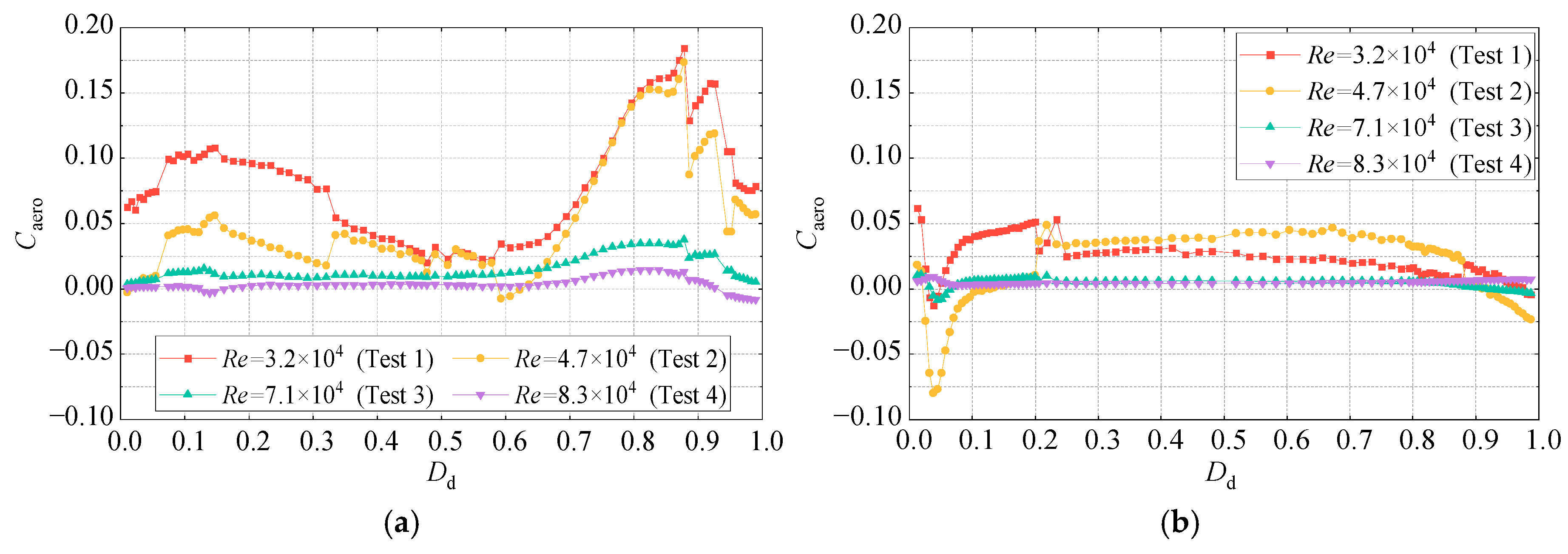
4. Reynolds Number Effect on VIV Characteristics and the Underlying Mechanism
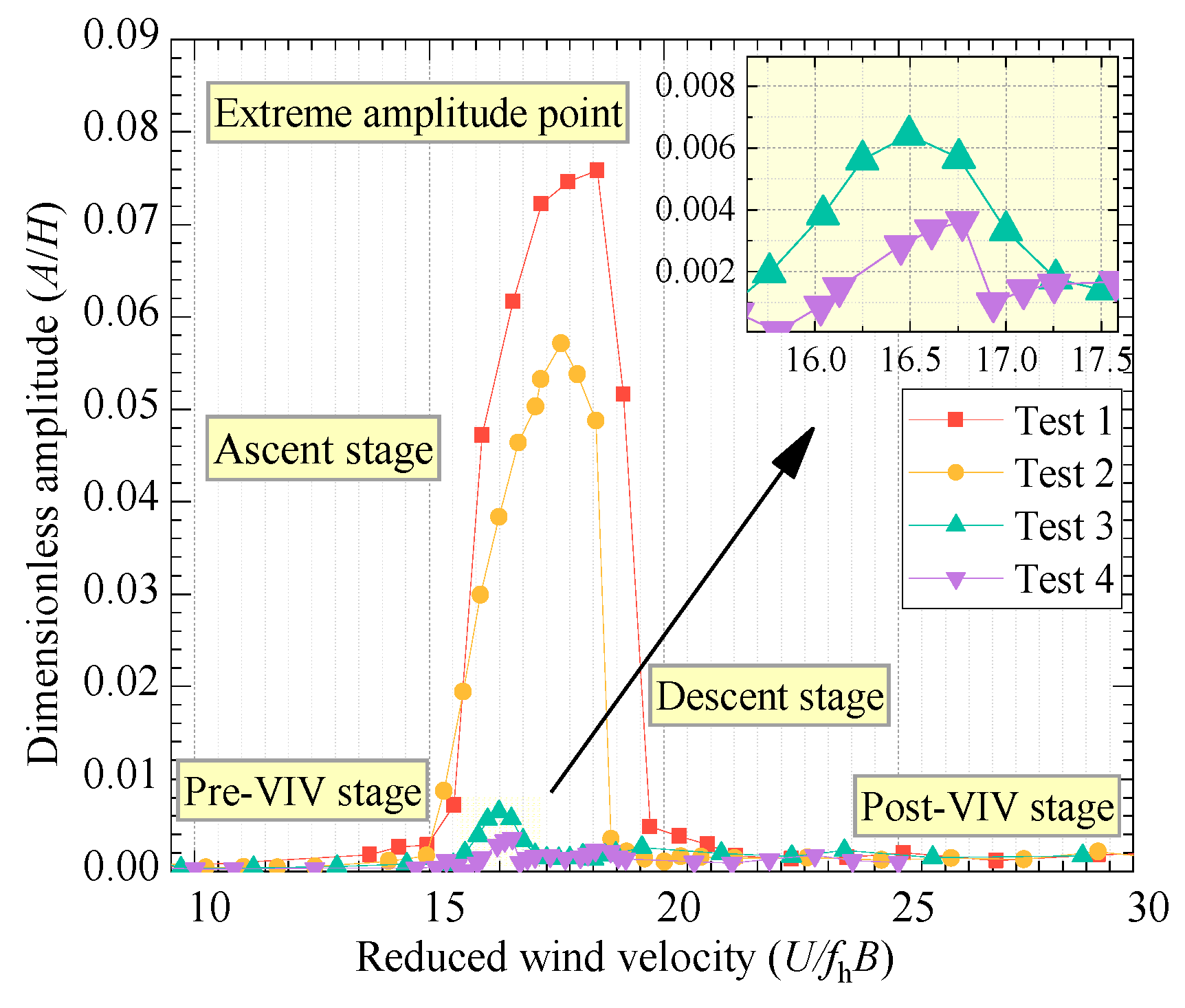
4.1. VIV Response
4.2. Time–Frequency Characteristics of Dynamic Aerodynamic Forces
4.2.1. Mean Values of the Wind Pressure Coefficients
4.2.2. RMS Values of the Wind Pressure Coefficients
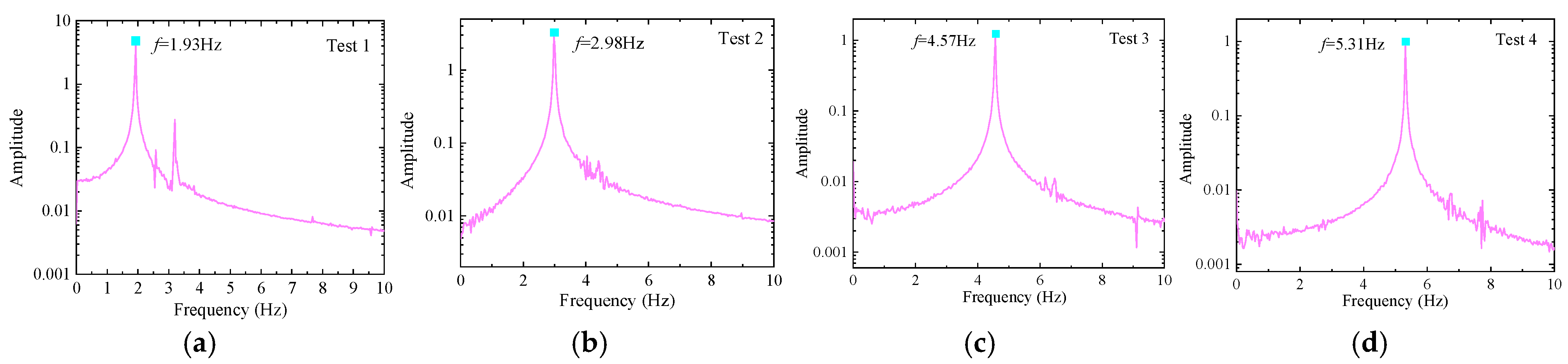
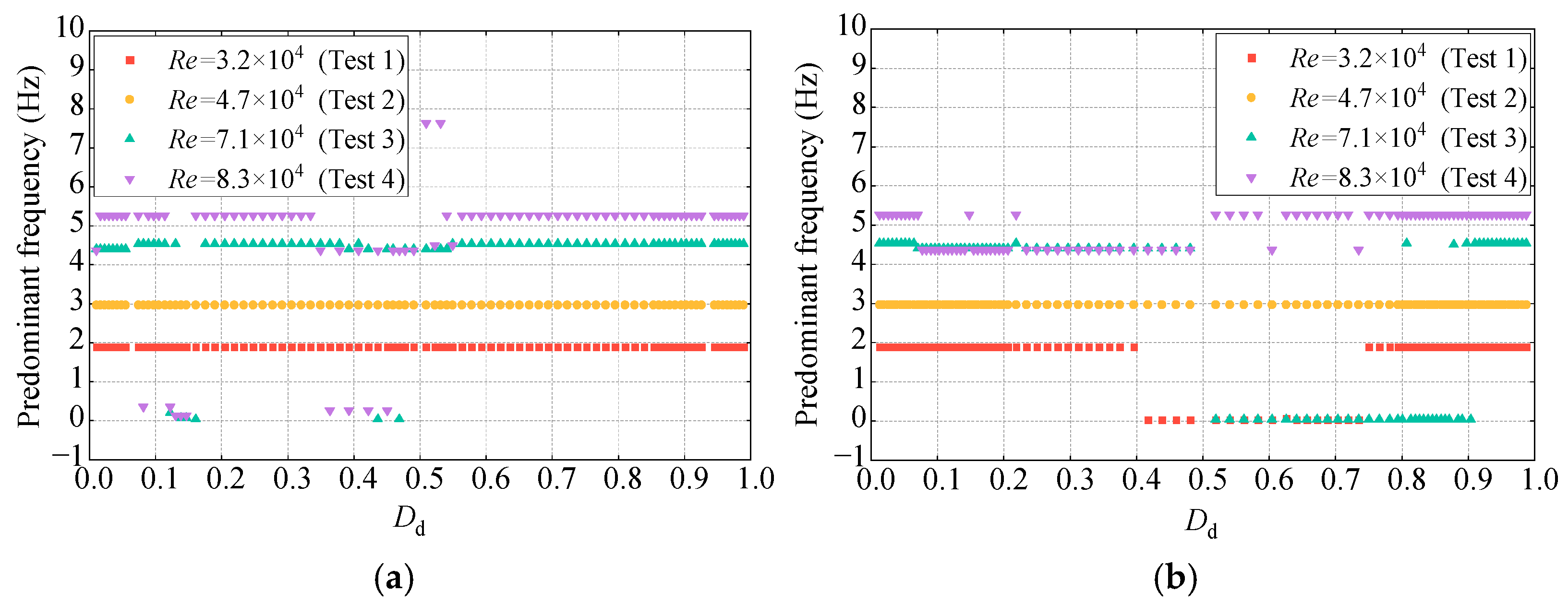
4.2.3. Dominant Frequency of Fluctuating Pressure
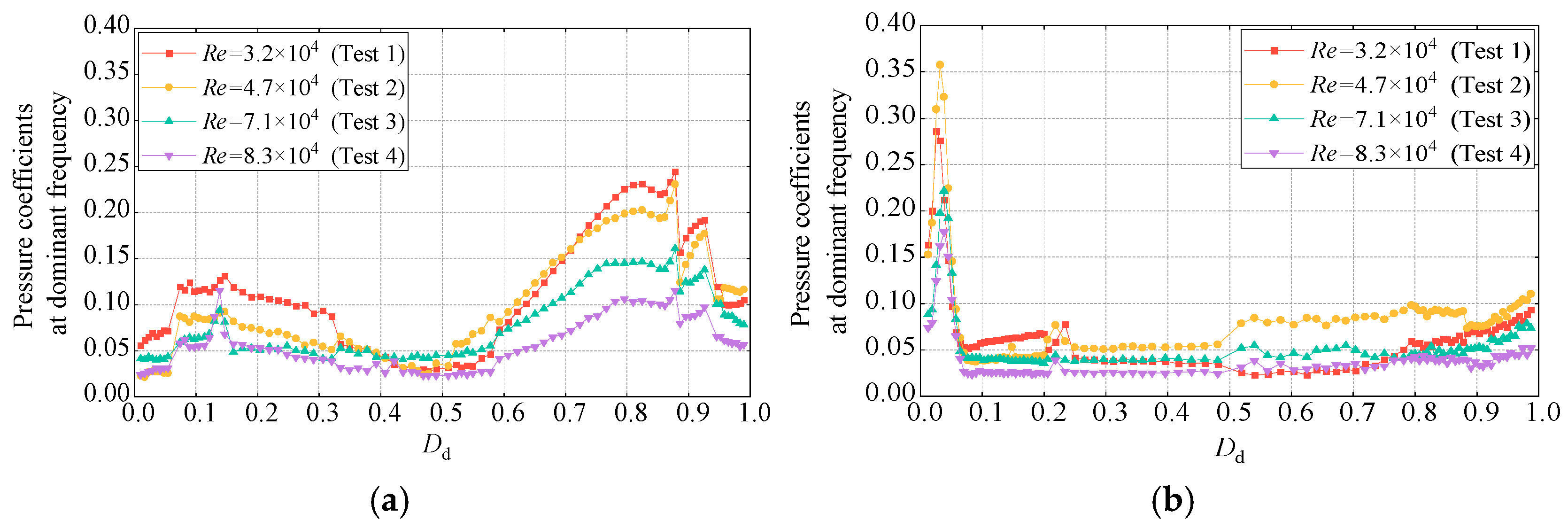
4.2.4. Distribution Characteristics of the Wind Pressure Coefficient at the Dominant Frequency
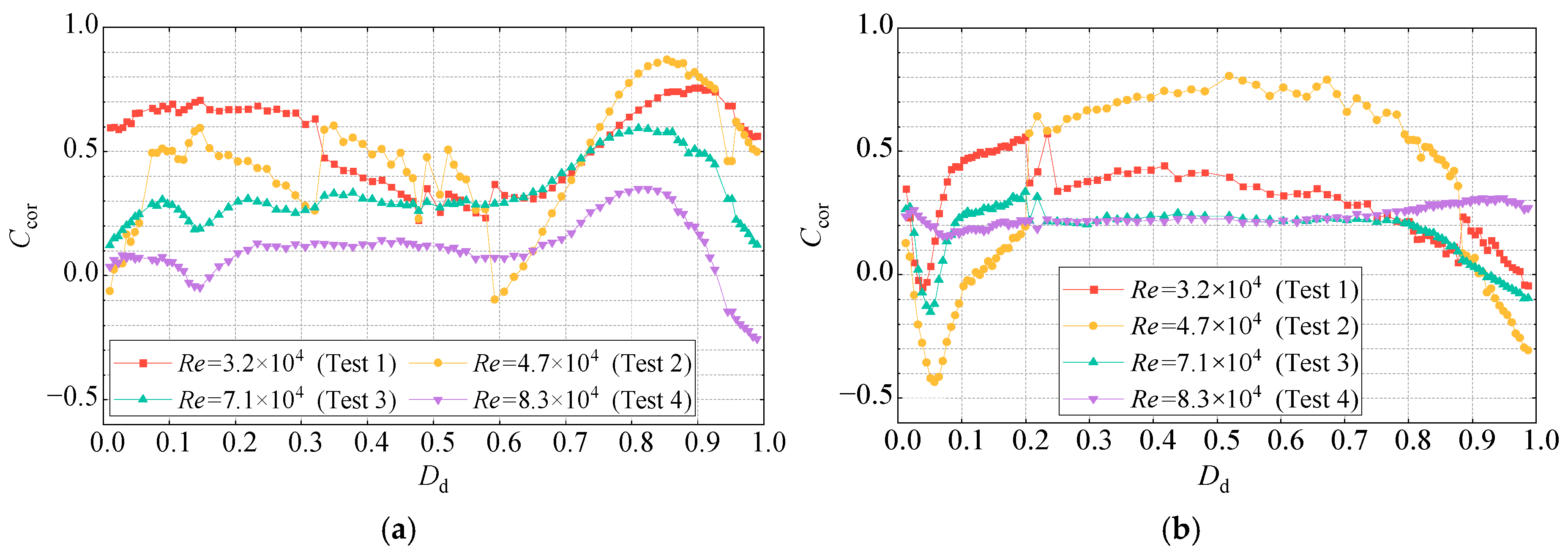
4.2.5. Correlation Coefficient Between the Local Aerodynamic Forces and the Total VIF
4.2.6. Contribution Coefficients of the Local Aerodynamic Forces to the Overall VIF
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.W.; Wu, P.; Hao, J.M.; Pan, H. Experimental and numerical studies on the two “lock-in” regions characteristic of vertical vortex-induced vibration of Π-shaped composite bridge deck. J. Wind Eng. Ind. Aerodyn. 2022, 228, 105122. [Google Scholar] [CrossRef]
- Ge, Y.J.; Zhao, L.; Cao, J.X. Case study of vortex-induced vibration and mitigation mechanism for a long-span suspension bridge. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104866. [Google Scholar] [CrossRef]
- Duan, Q.S.; Ma, C.M.; Zhang, T.; Li, Z.G. Vortex-induced vibration characteristic and trigger mechanism of semi-closed streamlined box girder trans-sea bridges. Ocean Eng. 2024, 312, 119053. [Google Scholar] [CrossRef]
- Larsen, A. Aerodynamic aspects of the final design of the 1624 m suspension bridge across the great belt. J. Wind Eng. Ind. Aerodyn. 1993, 48, 261–285. [Google Scholar] [CrossRef]
- Li, H.; Laima, S.; Ou, J.; Zhao, X.; Zhou, W.; Yu, Y.; Li, N.; Liu, Z. Investigation of vortex-induced vibration of a suspension bridge with two separated steel box girders based on field measurements. Eng. Struct. 2011, 33, 1894–1907. [Google Scholar] [CrossRef]
- Hu, C.X.; Zhao, L.; Wang, X.L.; Ge, Y.J. Spatio-temporal distribution of aerodynamic forces and their associated vortex drift patterns around a closed-box girder during torsional vortex-induced vibration. Eng. Struct. 2024, 302, 117459. [Google Scholar] [CrossRef]
- Chang, Q.; Fu, Z.; Zhang, S.; Wang, M.; Pan, X. Experimental Investigation of Reynolds Number and Spring Stiffness Effects on Vortex-Induced Vibration Driven Wind Energy Harvesting Triboelectric Nanogenerator. J. Nanomater. 2022, 12, 3595. [Google Scholar] [CrossRef]
- Fujino, Y.; Yoshida, Y. Wind-Induced Vibration and Control of Trans-Tokyo Bay Crossing Bridge. J. Struct. Eng. 2002, 128, 1012–1025. [Google Scholar] [CrossRef]
- Schewe, G.; Larsen, A. Reynolds number effects in the flow around a bluff bridge deck cross section. J. Wind Eng. Ind. Aerodyn. 1998, 74–76, 829–838. [Google Scholar] [CrossRef]
- Corriols, A.S.; Morgenthal, G. Computational Analysis of VIV Observed on Existing Bridges. In Proceedings of the Seventh International Colloquium on Bluff Body Aerodynamics and Applications (BBAA7), Shanghai, China, 2–6 September 2012. [Google Scholar]
- Zhao, L.; Cui, W.; Shen, X.; Xu, S.; Ding, Y.; Ge, Y. A fast on-site measure-analyze-suppress response to control vortex-induced-vibration of a long-span bridge. Structures 2022, 35, 192–201. [Google Scholar] [CrossRef]
- Li, H.; Laima, S.J.; Jing, H.Q. Reynolds number effects on aerodynamic characteristics and vortex-induced vibration of a twin-box girder. J. Fluids Struct. 2014, 50, 358–375. [Google Scholar] [CrossRef]
- Larose, G.; D’auteuil, A. On the Reynolds number sensitivity of the aerodynamics of bluff bodies with sharp edges. J. Wind Eng. Ind. Aerodyn. 2006, 94, 365–376. [Google Scholar] [CrossRef]
- Matsuda, K.; Cooper, K.; Tanaka, H.; Tokushige, M.; Iwasaki, T. An investigation of Reynolds number effects on the steady and unsteady aerodynamic forces on a 1:10 scale bridge deck section model. J. Wind Eng. Ind. Aerodyn. 2001, 89, 619–632. [Google Scholar] [CrossRef]
- Larsen, A.; Larose, G.L. Dynamic wind effects on suspension and cable-stayed bridges. J. Sound Vib. 2015, 334, 2–28. [Google Scholar] [CrossRef]
- Larsen, A.; Wall, A. Shaping of bridge box girders to avoid vortex shedding response. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 159–165. [Google Scholar] [CrossRef]
- Liu, Q.K.; Ma, W.Y.; Liu, X.B. Reynolds number effect on bridge wind engineering. J. Wind Eng. 2014, 39, 340–343. [Google Scholar] [CrossRef]
- Schewe, G. Reynolds-number effects in flow around more-or-less bluff bodies. J. Wind. Eng. Ind. Aerodyn. 2001, 89, 1267–1289. [Google Scholar] [CrossRef]
- Larose, G.; D’auteuil, A. Experiments on 2D rectangular prisms at high Reynolds numbers in a pressurised wind tunnel. J. Wind Eng. Ind. Aerodyn. 2008, 96, 923–933. [Google Scholar] [CrossRef]
- Pires, O.; Munduate, X.; Ceyhan, O.; Jacobs, M.; Snel, H. Analysis of high Reynolds numbers effects on a wind turbine airfoil using 2D wind tunnel test data. J. Phys. Conf. Ser. 2016, 753, 022047. [Google Scholar] [CrossRef]
- Lee, S.; Kwon, S.-D.; Yoon, J. Reynolds number sensitivity to aerodynamic forces of twin box bridge girder. J. Wind Eng. Ind. Aerodyn. 2014, 127, 59–68. [Google Scholar] [CrossRef]
- Kargarmoakhar, R.; Chowdhury, G.A.; Irwin, A.P. Reynolds number effects on twin box girder long span bridge aerodynamics. Wind Struct. 2015, 20, 327–347. [Google Scholar] [CrossRef]
- Laima, S.; Wu, B.; Jiang, C.; Chen, W.; Li, H. Numerical study on Reynolds number effects on the aerodynamic characteristics of a twin-box girder. Wind Struct. 2019, 28, 285–298. [Google Scholar]
- Ran, Y.; Chen, W.-L.; Jin, Y.; Li, H.; Gao, D. Reynolds number sensitivity of the aerostatic characteristics of a long-span rail-cum-road bridge girder with three separated boxes. J. Wind Eng. Ind. Aerodyn. 2024, 250, 105776. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, Y.; Zhang, Y.; Li, W. Simulation Research on the Effect of Reynolds Number on the Aerodynamic Characteristics of High Lift Device. J. Phys. Conf. Ser. 2022, 2280, 012010. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, D.; Xu, X.; Li, G. Investigation of Reynolds Number Effects on Aerodynamic Characteristics of a Transport Aircraft. Aerospace 2021, 8, 177. [Google Scholar] [CrossRef]
- Alireza MNavid, G. Experimental investigation of Reynolds number and spring stiffness effects on vortex induced vibrations of a rigid circular cylinder. Eur. J. Mech. B Fluids 2018, 74, 34–40. [Google Scholar]
- Wang, R.; Zhang, M. An analytical study on vortex-induced vibrations of cylinders with variable cross-section in the range of low Reynolds numbers. Int. J. Comput. Methods Eng. Sci. Mech. 2024, 25, 45–55. [Google Scholar] [CrossRef]
- Kang, Z.; Zhang, C.; Chang, R.; Ma, G. A Numerical Investigation of the Effects of Reynolds Number on Vortex-Induced Vibration of the Cylinders with Different Mass Ratios and Frequency Ratios. Int. J. Nav. Archit. Ocean. Eng. 2019, 11, 835–850. [Google Scholar] [CrossRef]
- Gu, J.; Fernandes, A.C.; Sales, J.S. Alternative insight to understand the Reynolds number effects in vortex-induced vibration. Mar. Struct. 2020, 69, 102686. [Google Scholar] [CrossRef]
- Zhao, H.; Ding, H.; Wang, C.; Li, K.; Wang, G.; Ren, B. Vortex-induced vibration at low Reynolds numbers: Vortex shedding modes transitions. Ocean Eng. 2023, 288, 115931. [Google Scholar] [CrossRef]
- Liu, G.; Song, Z.; Xu, W.; Sha, M. Numerical study on the VIVs of two side-by-side elastically coupled cylinders under different Re and natural frequencies. Ocean Eng. 2023, 284, 115261. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Chen, D.; Peng, X.; Xu, X. Numerical Investigation on the Reynolds Number Effects of Supercritical Airfoil. Procedia Eng. 2012, 31, 103–109. [Google Scholar] [CrossRef]
- Ran, Y.; Chen, W.-L.; Jin, Y.; Li, H.; Gao, D. Reynolds number sensitivity of the vortex dynamics around a long-span rail-cum-road bridge girder with three separated boxes. J. Wind Eng. Ind. Aerodyn. 2024, 250, 105785. [Google Scholar] [CrossRef]
- Laima, S.; Jiang, C.; Li, H.; Chen, W.; Ou, J. A numerical investigation of Reynolds number sensitivity of flow characteristics around a twin-box girder. J. Wind Eng. Ind. Aerodyn. 2018, 172, 298–316. [Google Scholar] [CrossRef]
- Wang, C.; Hua, X.; Feng, Z.; Xiao, H.; Chen, Z.; Zhang, J. Experimental investigation on vortex-induced vibrations of a triple-box girder with web modification. J. Wind Eng. Ind. Aerodyn. 2021, 218, 104783. [Google Scholar] [CrossRef]
- Hu, C.; Zhao, L.; Chen, H.; Zhou, Z.; Ge, Y. Reynolds number effects on aerodynamic forces of a streamlined closed-box girder during vortex-induced vibrations. J. Vib. Shock 2019, 38, 118–125. (In Chinese) [Google Scholar]
- Hu, C.; Zhao, L.; Ge, Y. Time-frequency evolutionary characteristics of aerodynamic forces around a streamlined closed-box girder during vortex-induced vibration. J. Wind Eng. Ind. Aerodyn. 2018, 182, 330–343. [Google Scholar] [CrossRef]
- Xu, F.; Ying, X.; Li, Y.; Zhang, M. Experimental Explorations of the Torsional Vortex-Induced Vibrations of a Bridge Deck. J. Bridg. Eng. 2016, 21, 04016093. [Google Scholar] [CrossRef]
- Cui, X.; Li, J.W.; Chen, F.; Liu, J.X. Reynolds number effect on vortex resonance of streamline-like bridge deck section. J. Changan Univ. 2011, 31, 47–51+62. (In Chinese) [Google Scholar]
- Lee, B.E. The susceptibility of tests on two-dimensional bluff bodies to incident flow variations. J. Wind Eng. Ind. Aerodyn. 1977, 2, 133–148. [Google Scholar] [CrossRef]
- Zheng, Y.F.; Liu, Q.K.; Liu, X.B.; Ma, W.Y. Influence of end state on aerodynamic characteristics of cable segment model. Eng. Mech. 2017, 34 (Suppl. S1), 192–196. (In Chinese) [Google Scholar]
- Kubo, Y.; Miyazaki, M.; Kato, K. Effects of end plates and blockage of structural members on drag forces. J. Wind Eng. Ind. Aerodyn. 1989, 32, 329–342. [Google Scholar] [CrossRef]
- Bai, H.; Liu, B.X.; Ji, N.C.; Li, J.W. Reasonable size estimation of the binary and plates of a segmental model. J. Vib. Shock 2023, 42, 312–320. (In Chinese) [Google Scholar]
- Gabbai, R.; Benaroya, H. An overview of modeling and experiments of vortex-induced vibration of circular cylinders. J. Sound Vib. 2004, 282, 575–616. [Google Scholar] [CrossRef]
- Duranay, A.; Demirhan, A.E.; Dobrucali, E.; Kinaci, O.K. A review on vortex-induced vibrations in confined flows. Ocean Eng. 2023, 285, 115309. [Google Scholar] [CrossRef]
- Sarpkaya, T. Hydrodynamic damping, flow-induced oscillations, and biharmonic response. J. Offshore Mech. Arctic. Eng. 1995, 117, 232–238. [Google Scholar] [CrossRef]

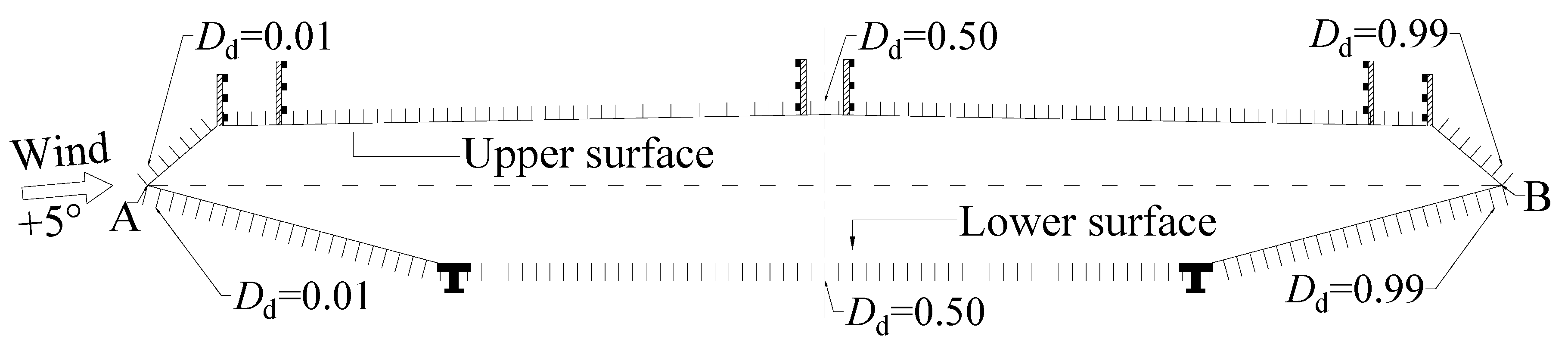
| Parameter Name | Prototype Value | Similitude Ratio | Model Value |
|---|---|---|---|
| Length, L [m] | 96.8 | -- | 2.140 |
| Width, B [m] | 32.0 | 1:30 | 1.070 |
| Height, H [m] | 3.5 | 1:30 | 0.117 |
| Mass, m [kg·m−1] | 2.56 × 104 | 1:302 | 28.545 |
| Frequency, f [Hz] | 0.245 | 1:7.837 | 1.920 |
| Damping ratio, ζ | -- | -- | 0.22% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Sun, Y.; Liu, Q.; Li, Z.; Han, Y.; Li, K. Study of Reynolds Number Effects on Aerodynamic Forces and Vortex-Induced Vibration Characteristics of a Streamlined Box Girder. Appl. Sci. 2025, 15, 2202. https://doi.org/10.3390/app15042202
Wang B, Sun Y, Liu Q, Li Z, Han Y, Li K. Study of Reynolds Number Effects on Aerodynamic Forces and Vortex-Induced Vibration Characteristics of a Streamlined Box Girder. Applied Sciences. 2025; 15(4):2202. https://doi.org/10.3390/app15042202
Chicago/Turabian StyleWang, Binxuan, Yifei Sun, Qingkuan Liu, Zhen Li, Yuan Han, and Kaiwen Li. 2025. "Study of Reynolds Number Effects on Aerodynamic Forces and Vortex-Induced Vibration Characteristics of a Streamlined Box Girder" Applied Sciences 15, no. 4: 2202. https://doi.org/10.3390/app15042202
APA StyleWang, B., Sun, Y., Liu, Q., Li, Z., Han, Y., & Li, K. (2025). Study of Reynolds Number Effects on Aerodynamic Forces and Vortex-Induced Vibration Characteristics of a Streamlined Box Girder. Applied Sciences, 15(4), 2202. https://doi.org/10.3390/app15042202





