Three-Band Spectral Camera Structure Design Based on the Topology Optimization Method
Abstract
:1. Introduction
2. Design of Three-Band Structural Components
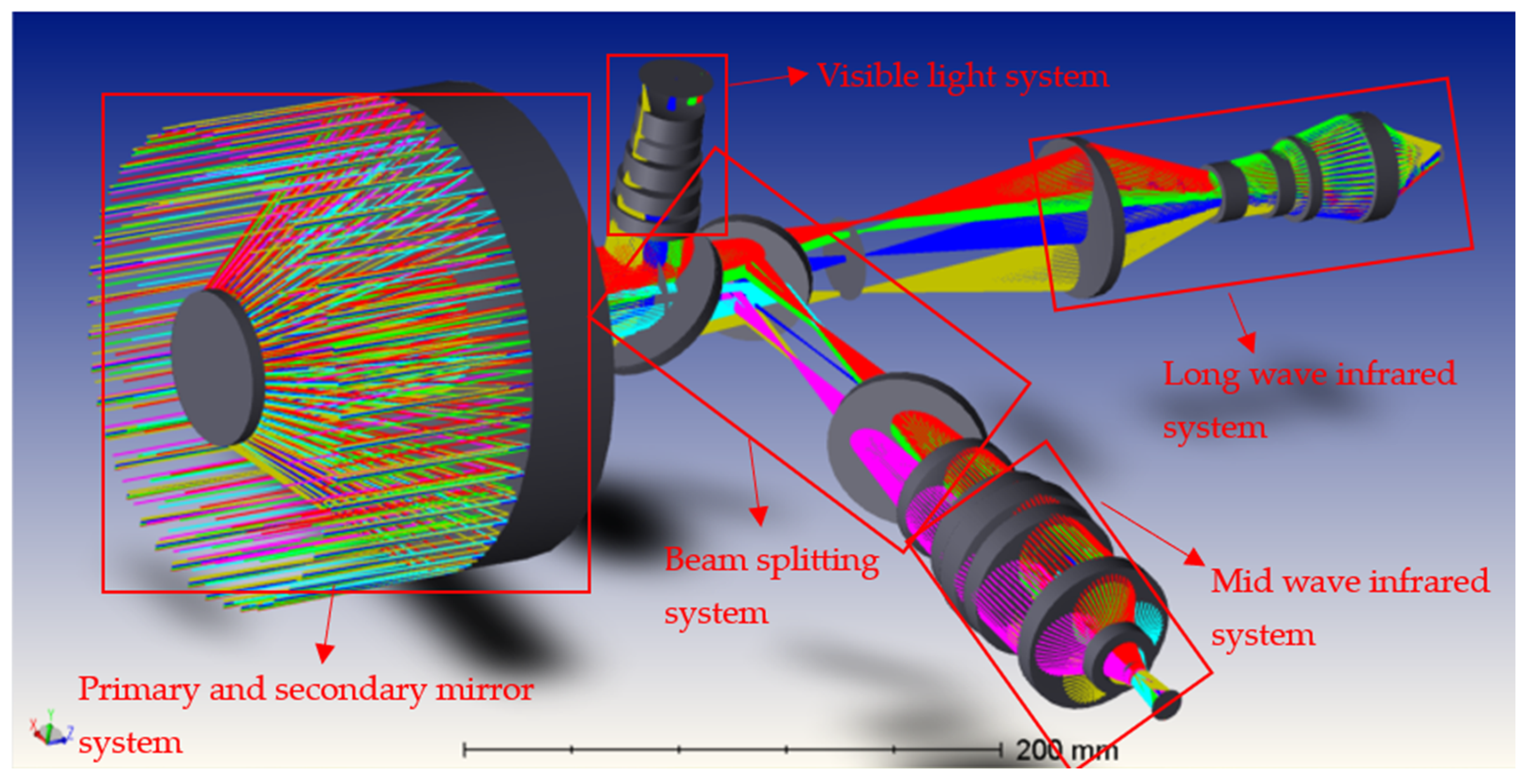
2.1. Structural Design Requirements
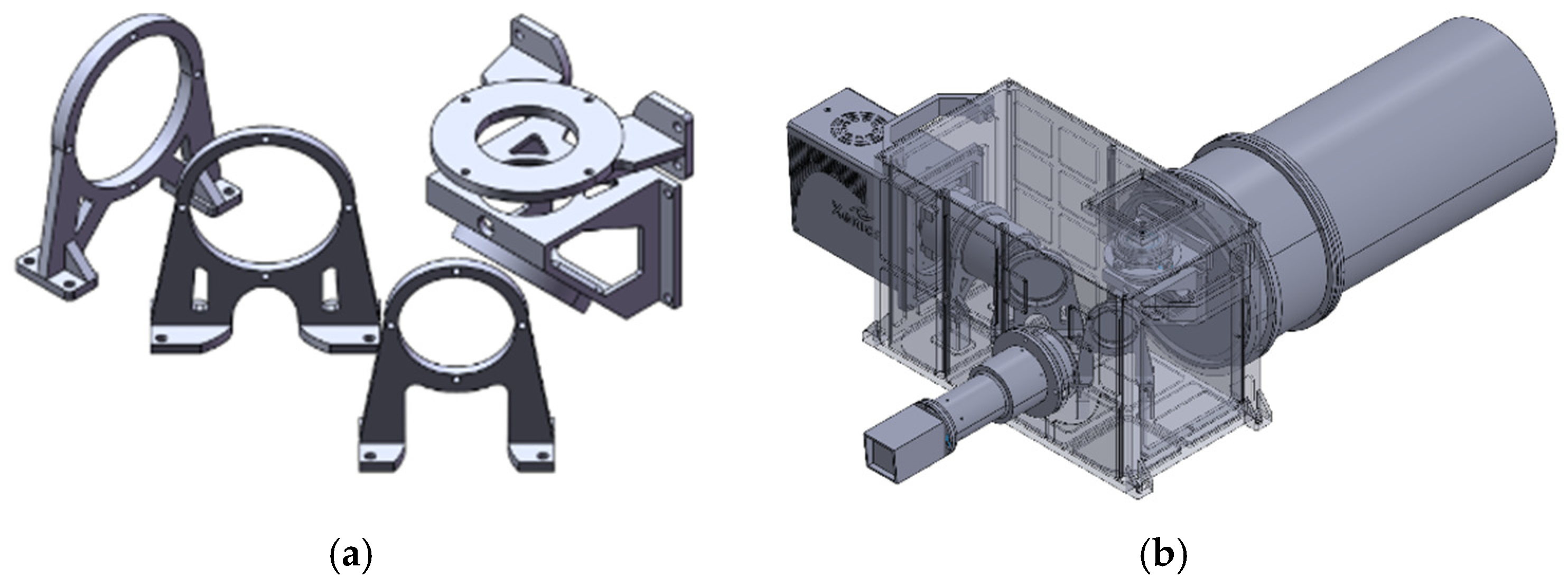
2.2. Initial Structural Design
2.3. Optimization Method of the Structure
2.3.1. Topology Optimization Method
2.3.2. Parameter Optimization Method
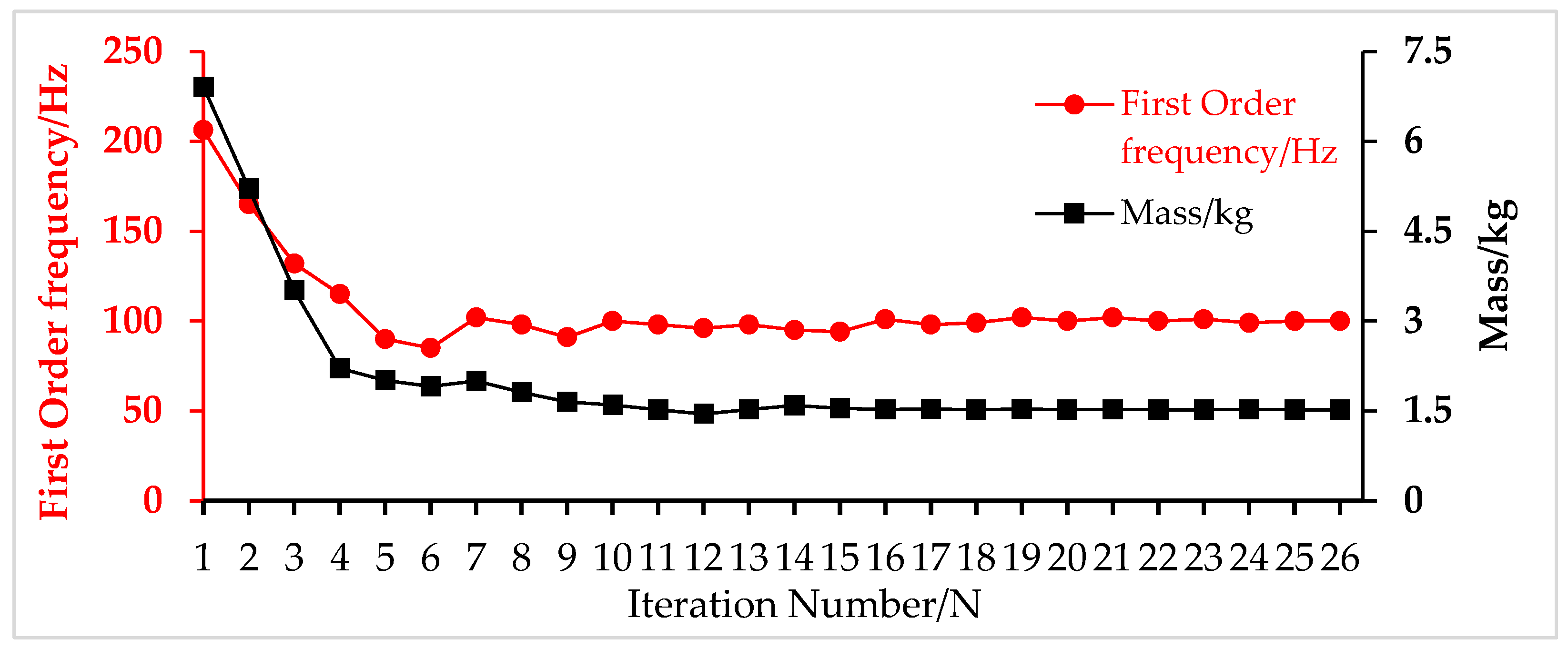
2.4. Optimization Process
3. Three-Band Optimization Results
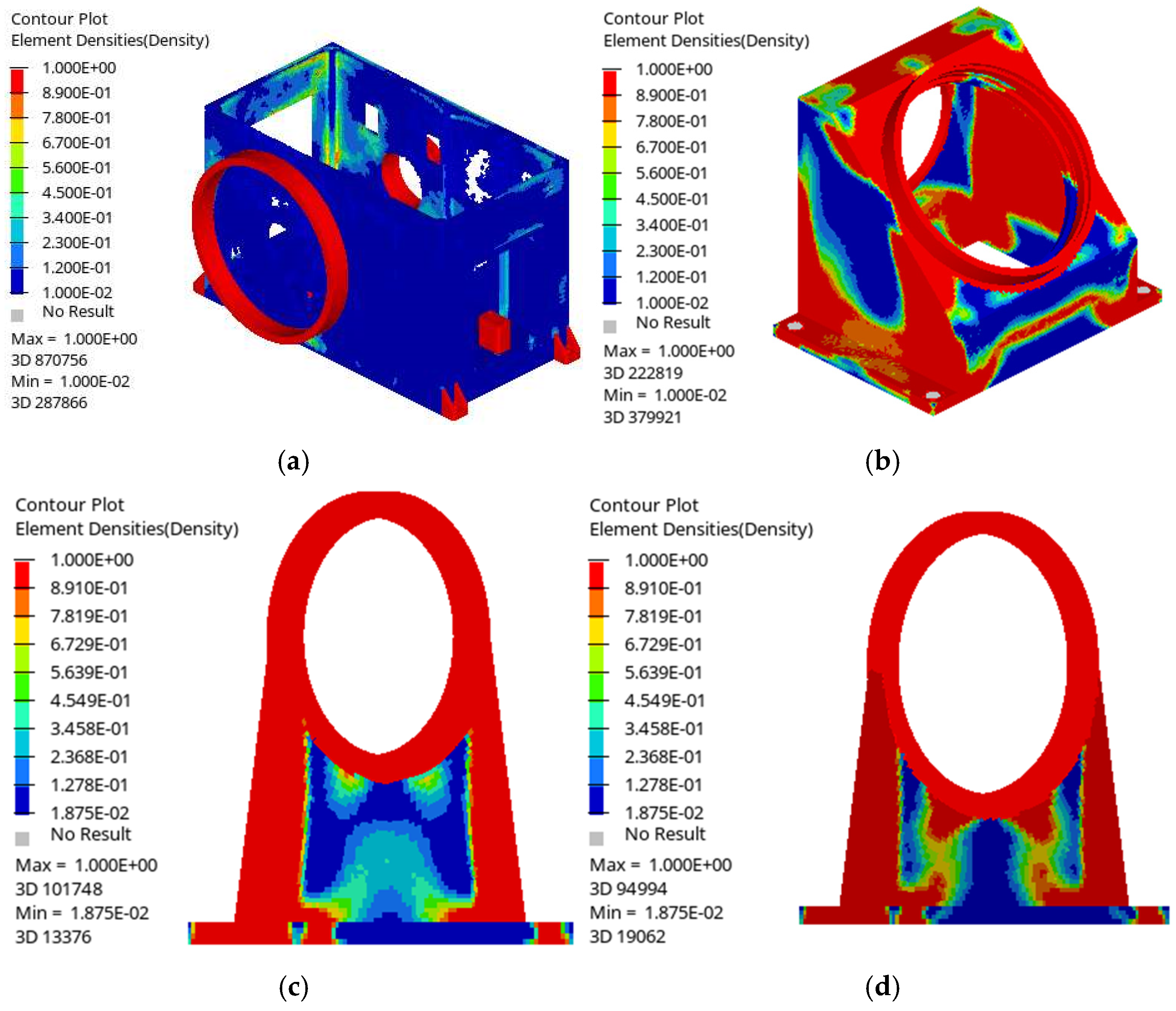
3.1. Topology Optimization Results
3.2. Parameter Optimization Results
3.3. Final Optimization Results
4. Performance Analysis
4.1. Modal Analysis
4.2. Dynamic Analysis
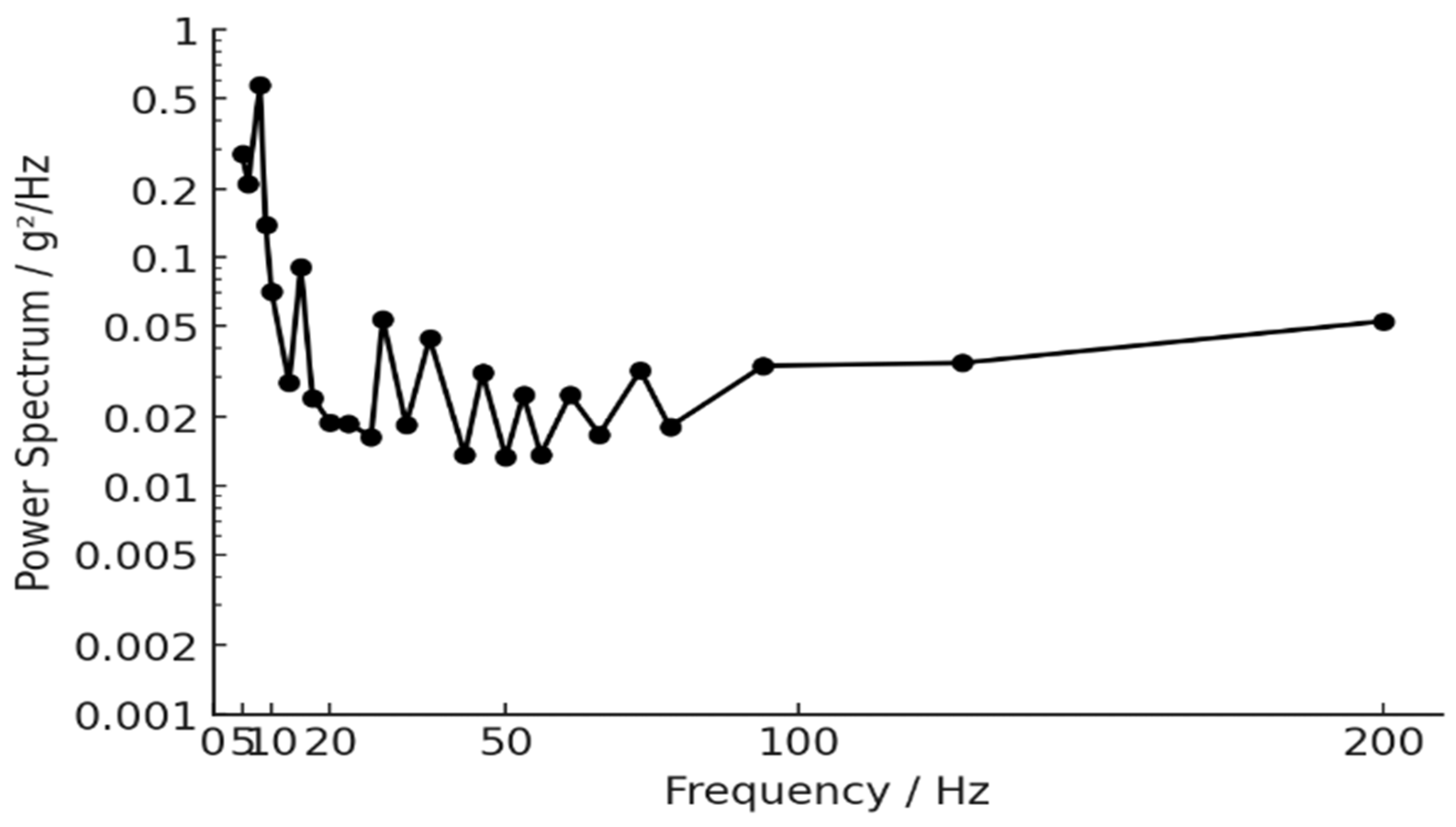
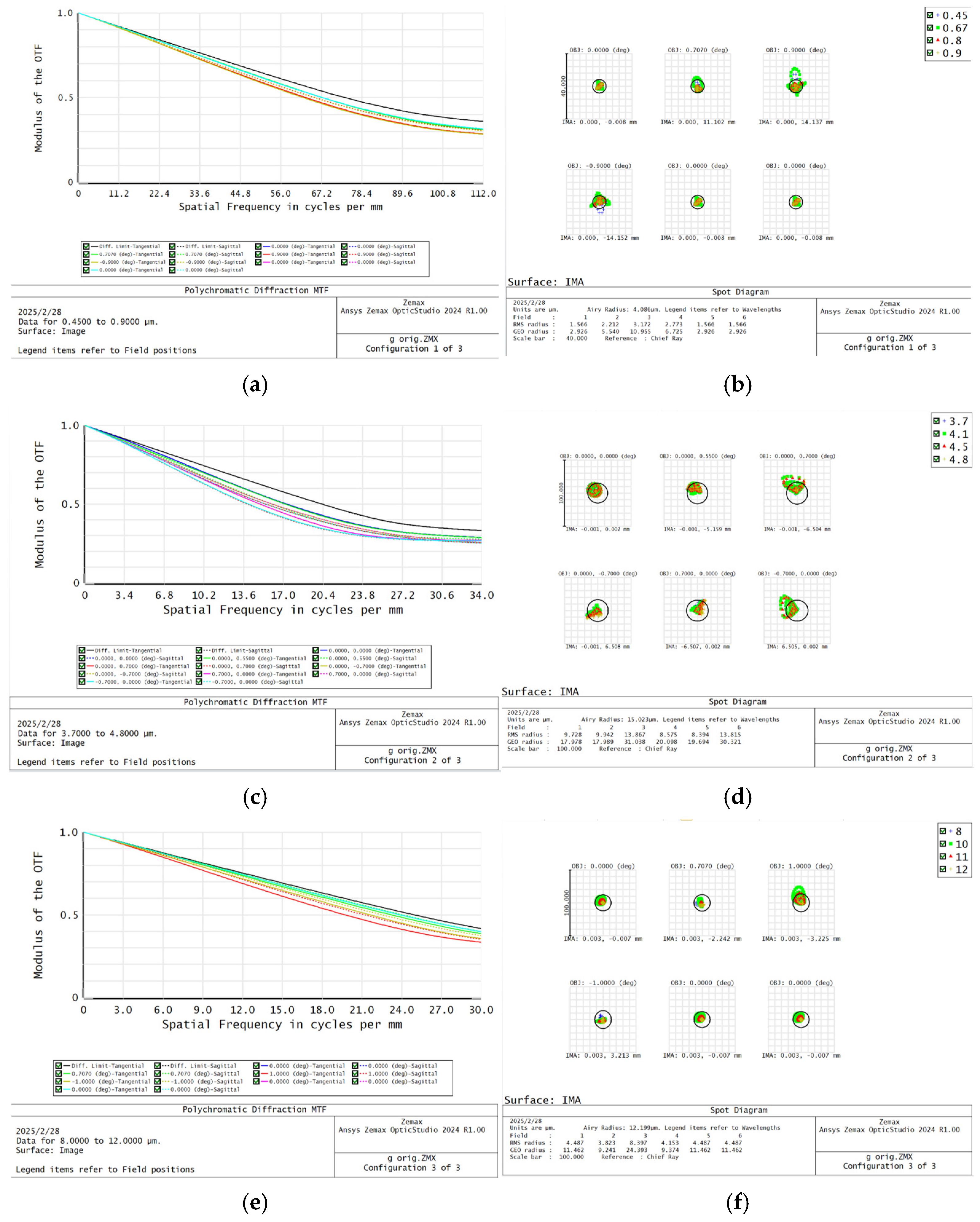
4.3. Optical Analysis
5. Three-Band Multispectral Camera Testing
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.J.; Liu, J.; Chen, Y. Design of dual-band, high zoom ratio and continuous co-focal optical system. Acta Photonica Sin. 2016, 45, 1022003. [Google Scholar]
- Liu, K.; Chen, R.L.; Chang, L.Y.; Lei, G.Z.; Zou, G.Y. Common-aperture dual channel infrared scanning imaging optical system. J. Appl. Opt. 2012, 33, 395–401. [Google Scholar]
- Wu, H.B.; Zhang, X.; Wang, L.J.; Yan, L.; Shi, G.W. Common aperture optical system of single photon laser and medium wave infrared. Opt. Precis. Eng. 2021, 29, 1260–1269. [Google Scholar] [CrossRef]
- Guo, Y.L.; Yu, X.; Cai, K.J.; Yang, L. Optical design of TV/IR dual-band common-aperture system. Infrared Technol. 2018, 40, 125–132. [Google Scholar]
- Yu, H.; Fei, J.D.; Zhang, Y.; Gao, Y.; Kang, W.M. Common aperture combination simulation technology for multi-spectral scene. Infrared Laser Eng. 2011, 40, 1629–1633. [Google Scholar]
- Smeesters, L.; Belay, G.Y.; Ottevaere, H.; Meuret, Y.; Vervaeke, M.; Erps, V.J.; Thienpont, H. Two-channel multiresolution refocusing imaging system using a tunable liquid lens. Appl. Opt. 2014, 53, 4002–4010. [Google Scholar] [CrossRef]
- Cheng, Z.F.; Liu, F.H.; Xun, X.C. Opto-mechanical design and analysis of dual-band sharing aperture imaging system. Infrared Laser Eng. 2015, 44, 3366–3372. [Google Scholar]
- Yue, B.Y.; Liu, J.; Guo, J.; Chen, Y.; Li, H. Optical system design of folded/diffractive co-aperture infrared dual-band beam positioner. Infrared Laser Eng. 2019, 48, 418003. [Google Scholar]
- Chen, X.Y.; Gao, M. Design of airborne dual-band common aperture photoelectric aiming optical system. Infrared Laser Eng. 2021, 50, 20200322. [Google Scholar]
- Ma, Z.P.; Xue, Y.K.; Shen, Y.; Zhao, X.H.; Zhou, C.L. Design and realization of visible/LWIR dual-color common aperture optical system. Acta Photonica Sin. 2021, 50, 24–32. [Google Scholar]
- Shao, M.Q. Research of the Integrated Optimization Design Method for the Optomechanical Structure of Space Cameras. Doctor’s Thesis, University of Chinese Academy of Sciences, Changchun, China, 2021. [Google Scholar]
- Wang, Z.S. Structure Optimization Design and Mechanical Properties Research of a Space Ultraviolet Large Field Scanning Imager. Master’s Thesis, University of Chinese Academy of Sciences, Changchun, China, 2021. [Google Scholar]
- Tyflopoulos, E.; Steinert, M. Topology and Parametric Optimization-Based Design Processes for Lightweight Structures. Appl. Sci. 2020, 10, 4496. [Google Scholar] [CrossRef]
- Hassani, V.; Mehrabi, H.A.; Ibrahim, Z.; Ibrahim, Z.; Ituarte, I. A Comparison between parametric structural optimization methods and software-based topology optimization of a rectangular sample under tensile load for additive manufacturing processes. Int. J. Eng. Res. Appl. 2021, 11, 37–58. [Google Scholar]
- Ravichandran, K.; Masoudi, N.; Fadel, G.M.; Wiecek, M.M. Parametric Optimization for Structural Design Problems. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2019. [Google Scholar]
- Zhang, M.Q. Optimization design of optical lens structure for large field of view in space TOF cameras. China New Technol. Prod. 2022, 20, 79–82. [Google Scholar]
- Sun, B.Y.; Guo, X.W.; Zhang, Z.L.; Jiang, Z.H.; Wang, C. Structural optimization design of wide-format array scanning cameras. J. Nanjing Univ. Aeronaut. Astronaut. 2020, 52, 191–198. [Google Scholar]
- Wang, P.P.; Xin, H.W.; Zhu, J.Q.; Wang, Y.X. Optimization design of lightweight long-strip reflective mirror structures. Opto-Electron. Eng. 2020, 47, 101–107. [Google Scholar]
- Song, W.Y. Design of a Novel All-Carbon Support Structure for Space Cameras and Research on Mechanical and Thermal Stability of the Entire System. Doctor’s Thesis, University of Chinese Academy of Sciences, Changchun, China, 2022. [Google Scholar]
- Tyflopoulos, E.; Flem, D.T.; Steinert, M.; Olsen, A. State of the art of generative design and topology optimization and potential research needs. In Proceedings of the DS 91: Proceedings of NordDesign 2018, Linköping, Sweden, 14–17 August 2018. [Google Scholar]
- Li, L.; Wang, D.; Yang, H.B.; Tan, L.Y.; Sun, Z.L. Optimization design of flexible vibration damping support structure for space cameras. Opt. Precis. Eng. 2016, 24, 1677–1684. [Google Scholar]
- Jia, X.Z.; Jin, G.; Jia, J.Q.; Ang, Y.; Xu, Z. Topology optimization design of the main load-bearing substrate structure for lightweight space cameras. J. Space Sci. 2011, 31, 395–400. [Google Scholar]
- Guan, Y.J.; Xin, H.W.; Zhao, G.J.; Liu, J.; Ren, J.Y. Topology optimization design of the main supporting structure for space cameras. Opt. Precis. Eng. 2007, 8, 1157–1163. [Google Scholar]
- Qu, H.D. Design and Mechanical Characteristics Research of Optomechanical Structures for Space Telescopes. Master’s Thesis, Changchun University of Technology, Changchun, China, 2021. [Google Scholar]
- Lazarov, B.S.; Wang, F.W.; Sigmund, O. Length scale and manufacturability in density-based topology optimization. Arch. Appl. Mech. 2016, 86, 189. [Google Scholar] [CrossRef]
- Fu, X.J. Key Technology Research on Topology and Shape Integrated Optimization Algorithms. Doctor’s Thesis, University of Technology, Hangzhou, China, 2008. [Google Scholar]
- Yang, J.Y.; Yang, X.; Zheng, J.H. Structure Components Optimization Design of Ultraviolet Imaging Spectrometer. Acta Photonica Sin. 2023, 52, 0930004. [Google Scholar]
- Owen, A.B. Orthogonal arrays for computer experiments, integration and visualization. Stat. Sin. 1992, 2, 439–452. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, Y. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Fonseca, C.M.; Fleming, P.J. An overview of evolutionary algorithms in multiobjective optimization. Evol. Comput. 1995, 3, 1–16. [Google Scholar] [CrossRef]
- Fonsenca, C.M.; Fleming, P.J. Genetic algorithms for multiobjective optimization: Formulation, discussion and generalization. In Proceedings of the 5th International Conference on Genetic Algorithms, Urbana-Champaign, IL, USA, 1 June 1993; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Sun, Y.; Li, F.; Yang, J.F.; Qian, C.S. Optimum design and experiment verification of space coaxial reflective secondary mirror support structure. Acta Photonica Sin. 2018, 47, 722003. [Google Scholar] [CrossRef]
- Jiang, R.K. Dynamic analysis and optimization of astronomical survey camera. Master’s Thesis, University of Chinese Academy of Sciences, Chengdu, China, 2018. [Google Scholar]
- National Military Standard GJB 150.6-1986. Available online: https://www.doc88.com/p-7374950707990.html (accessed on 1 January 2025).
- Zernike, F. Beugungstheorie des Schneidenver-fahrens und Seiner Verbesserten Form, der Phasenkontrastmethode. Physica 1934, 1, 689–704. [Google Scholar] [CrossRef]
- Bhatia, A.B.; Wolf, E. On the circle polynomials of Zernike and related orthogonal sets. Math. Proc. Camb. Philos. Soc. 1954, 50, 40–48. [Google Scholar] [CrossRef]













| Housing | A, B, C, D, E | ||
|---|---|---|---|
| Mass/kg | Initial | ||
| Optimization | |||
| First Modal/Hz | Initial | ||
| Optimization | |||
| Z-Deformation/nm | Initial | ||
| Optimization | |||
| L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | |
|---|---|---|---|---|---|---|---|---|
| Upper/mm | 4.0 | 6.0 | 3.0 | 36.0 | 44.0 | 5.5 | 48.0 | 7.5 |
| Lower/mm | 1.5 | 4.0 | 3.5 | 32.0 | 40.0 | 3.5 | 44.0 | 3.0 |
| Initial/mm | 3.0 | 5.0 | 5.0 | 33.0 | 41.0 | 5.0 | 45.0 | 6.0 |
| Parameter optimization/mm |
| Mass/kg | Frequency/Hz | |
|---|---|---|
| Initial | ||
| Topology optimization | ||
| Parameter optimization | ||
| Z-Deformation for topology optimization | ||
| Z-Deformation for parameter optimization | ||
| Direction | X | Y | Z |
|---|---|---|---|
| Result/RMS | 3.64 | 0.512 | 3.97 |
| Magnification | 1.3 | 0.18 | 1.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Wan, Y.; Guo, J.; Zou, C.; Zheng, X. Three-Band Spectral Camera Structure Design Based on the Topology Optimization Method. Appl. Sci. 2025, 15, 2974. https://doi.org/10.3390/app15062974
Hu K, Wan Y, Guo J, Zou C, Zheng X. Three-Band Spectral Camera Structure Design Based on the Topology Optimization Method. Applied Sciences. 2025; 15(6):2974. https://doi.org/10.3390/app15062974
Chicago/Turabian StyleHu, Kai, Yuzhu Wan, Jialong Guo, Chunbo Zou, and Xiangtao Zheng. 2025. "Three-Band Spectral Camera Structure Design Based on the Topology Optimization Method" Applied Sciences 15, no. 6: 2974. https://doi.org/10.3390/app15062974
APA StyleHu, K., Wan, Y., Guo, J., Zou, C., & Zheng, X. (2025). Three-Band Spectral Camera Structure Design Based on the Topology Optimization Method. Applied Sciences, 15(6), 2974. https://doi.org/10.3390/app15062974





