A Novel Optimal Control Strategy of Four Drive Motors for an Electric Vehicle
Abstract
1. Introduction
2. Simulation Platform and Optimal Energy Management
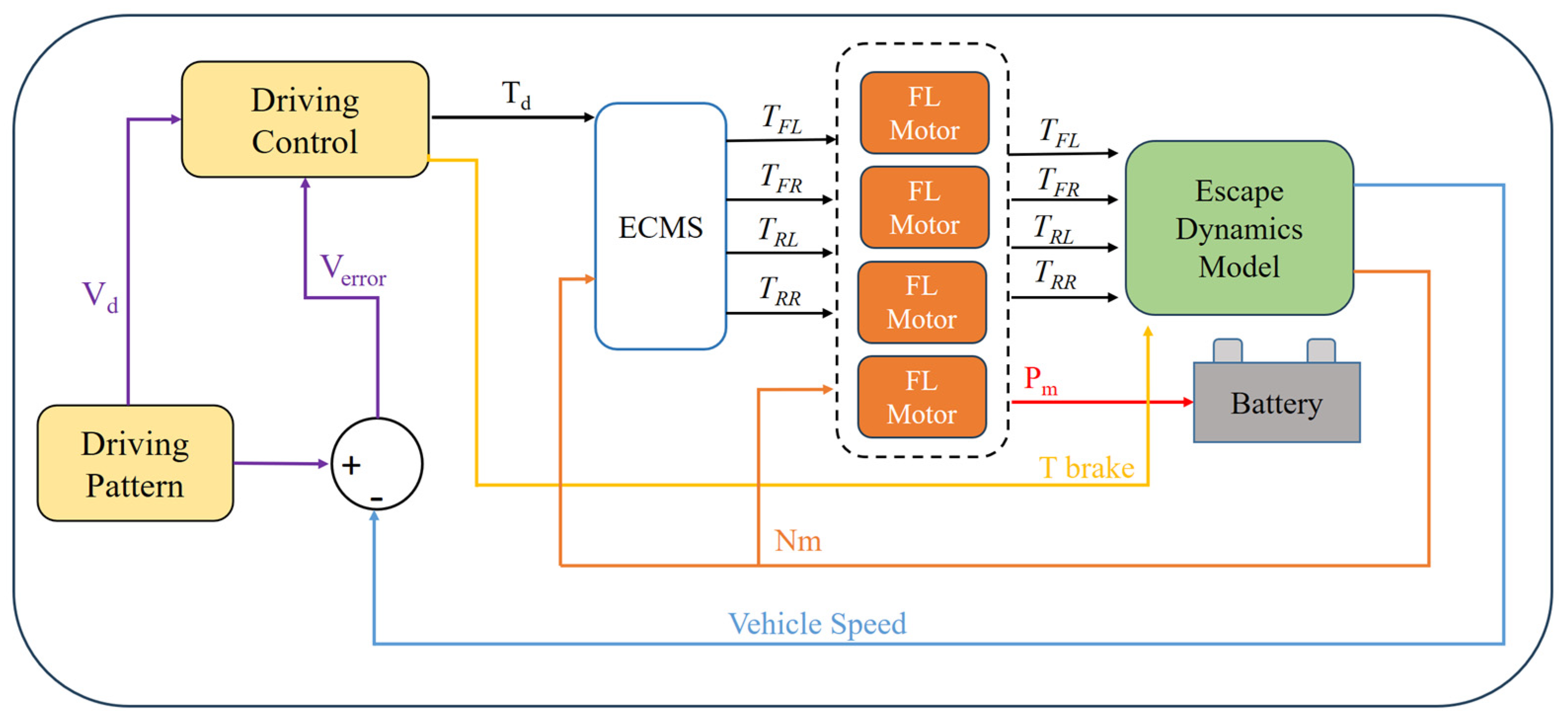
2.1. Electric Vehicle Simulation Platform
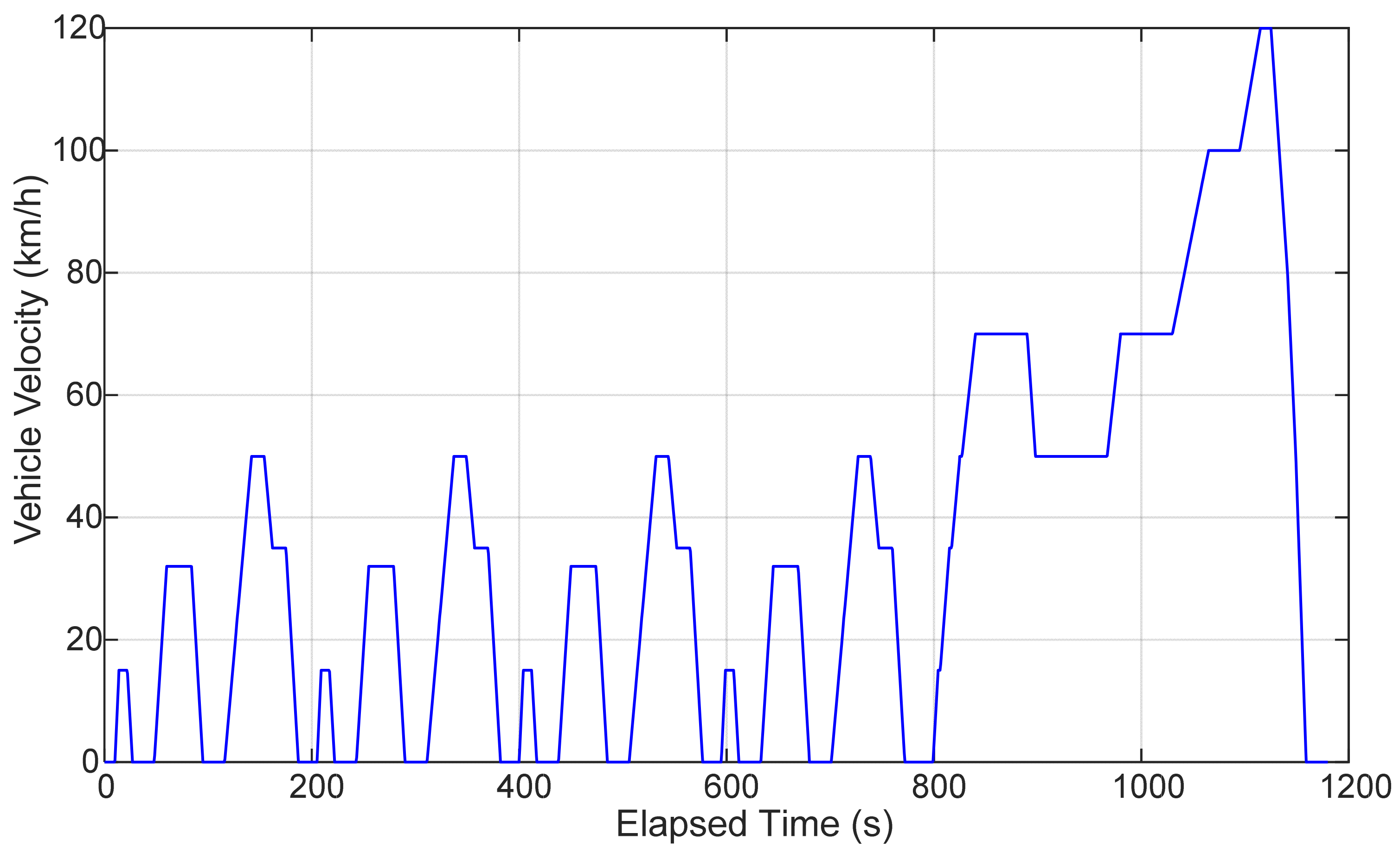
2.1.1. Driving Cycle Model
2.1.2. Driver Model
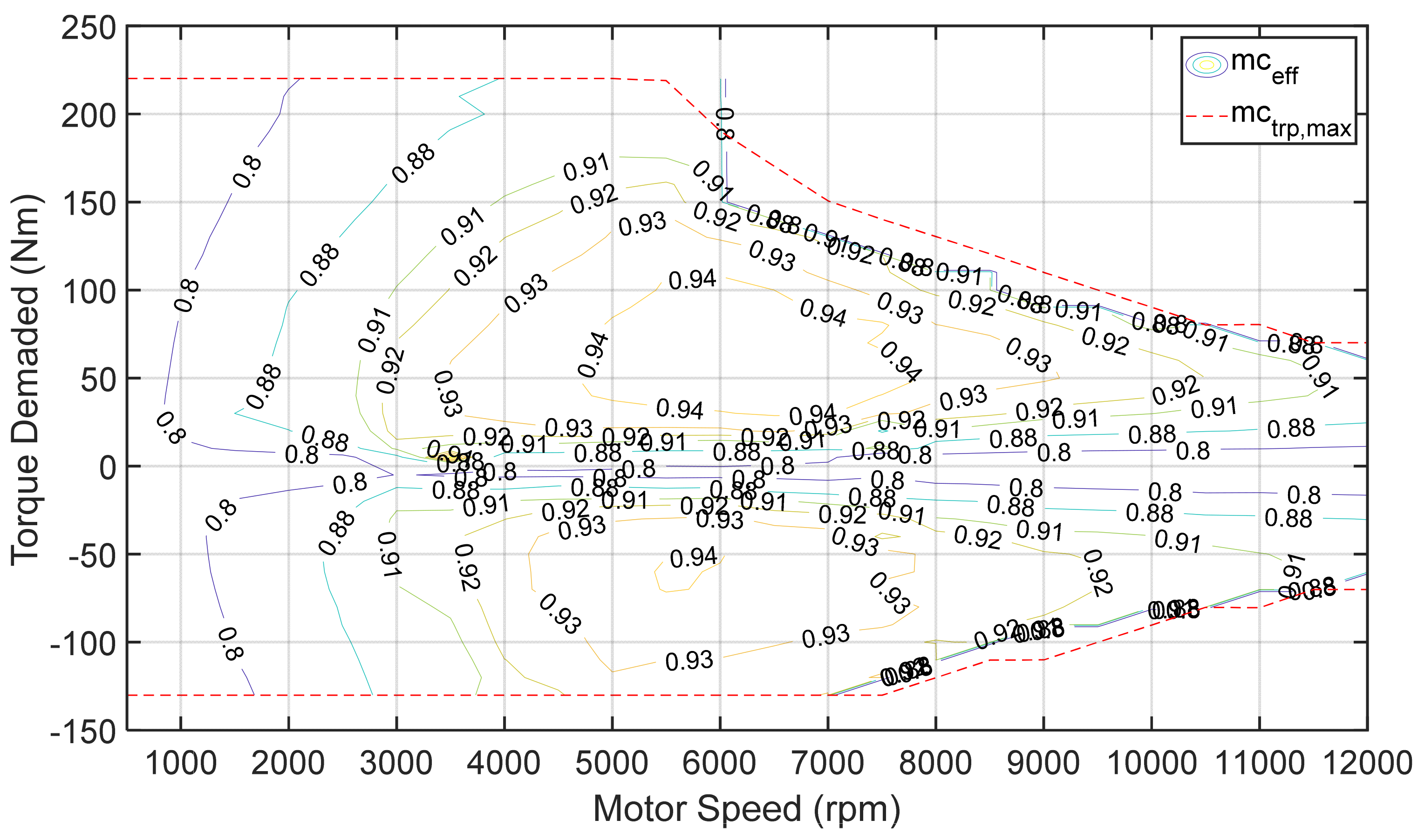
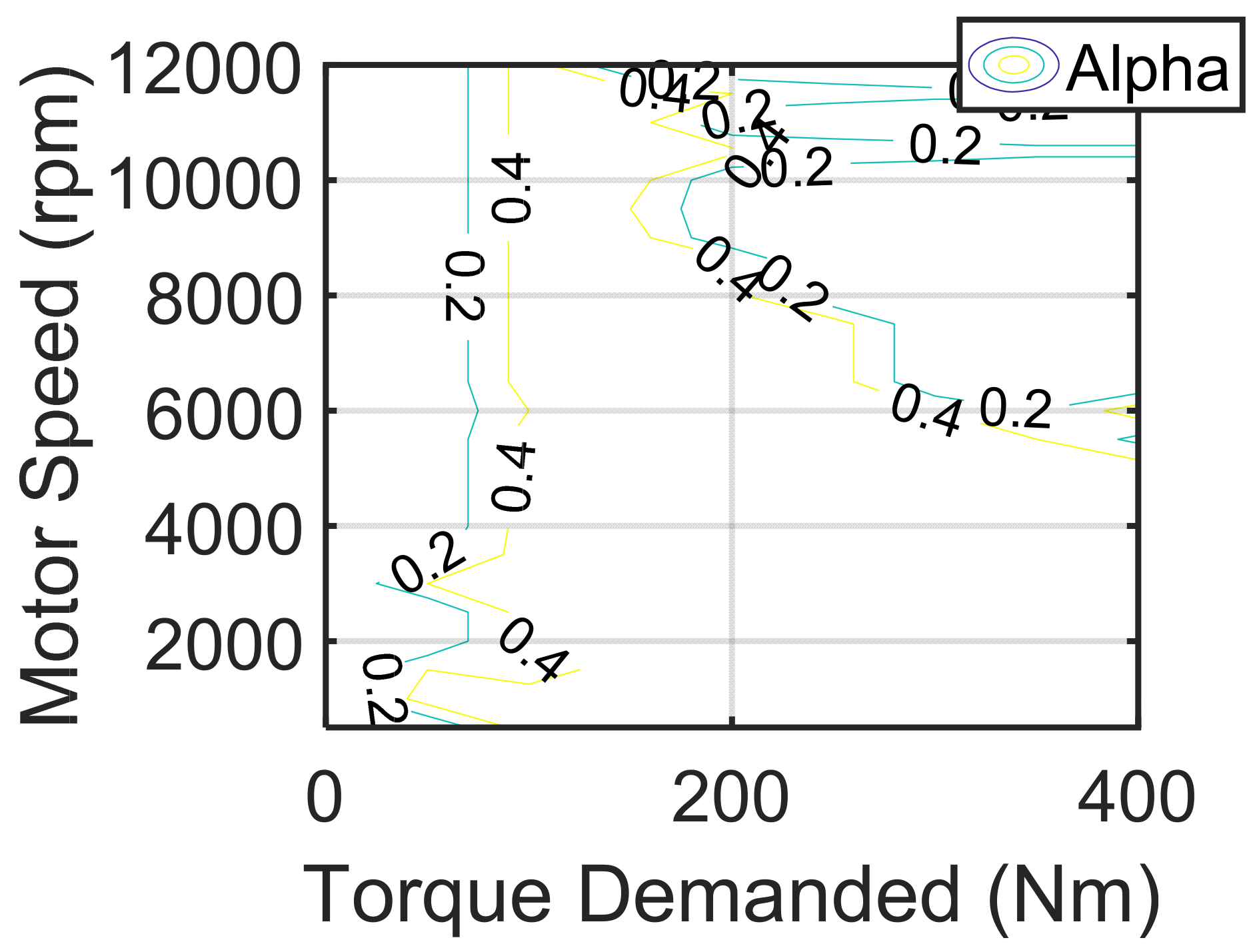
2.1.3. Drive Motor Model
2.1.4. Lithium Battery Model
2.1.5. Vehicle Dynamics Model
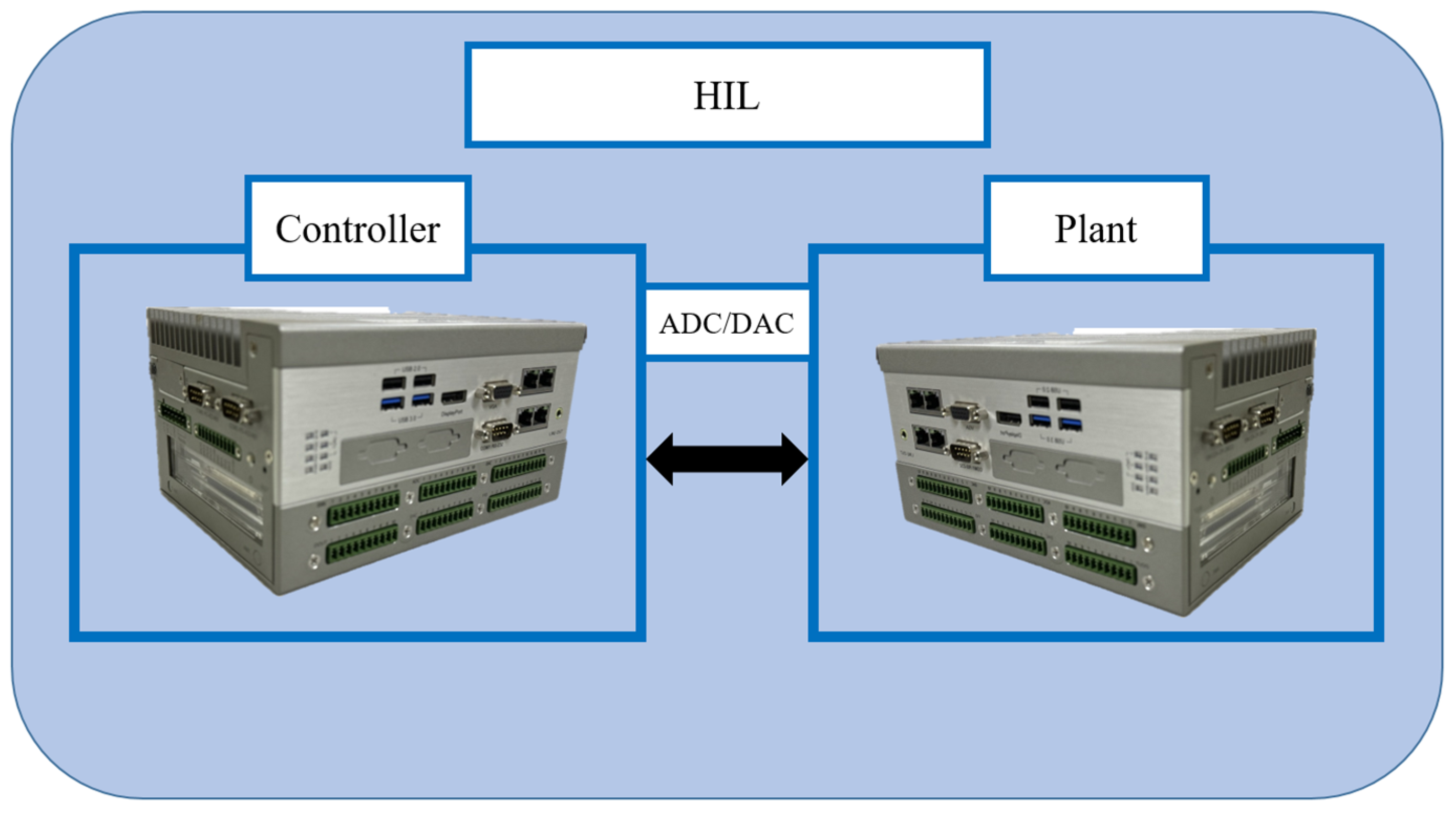
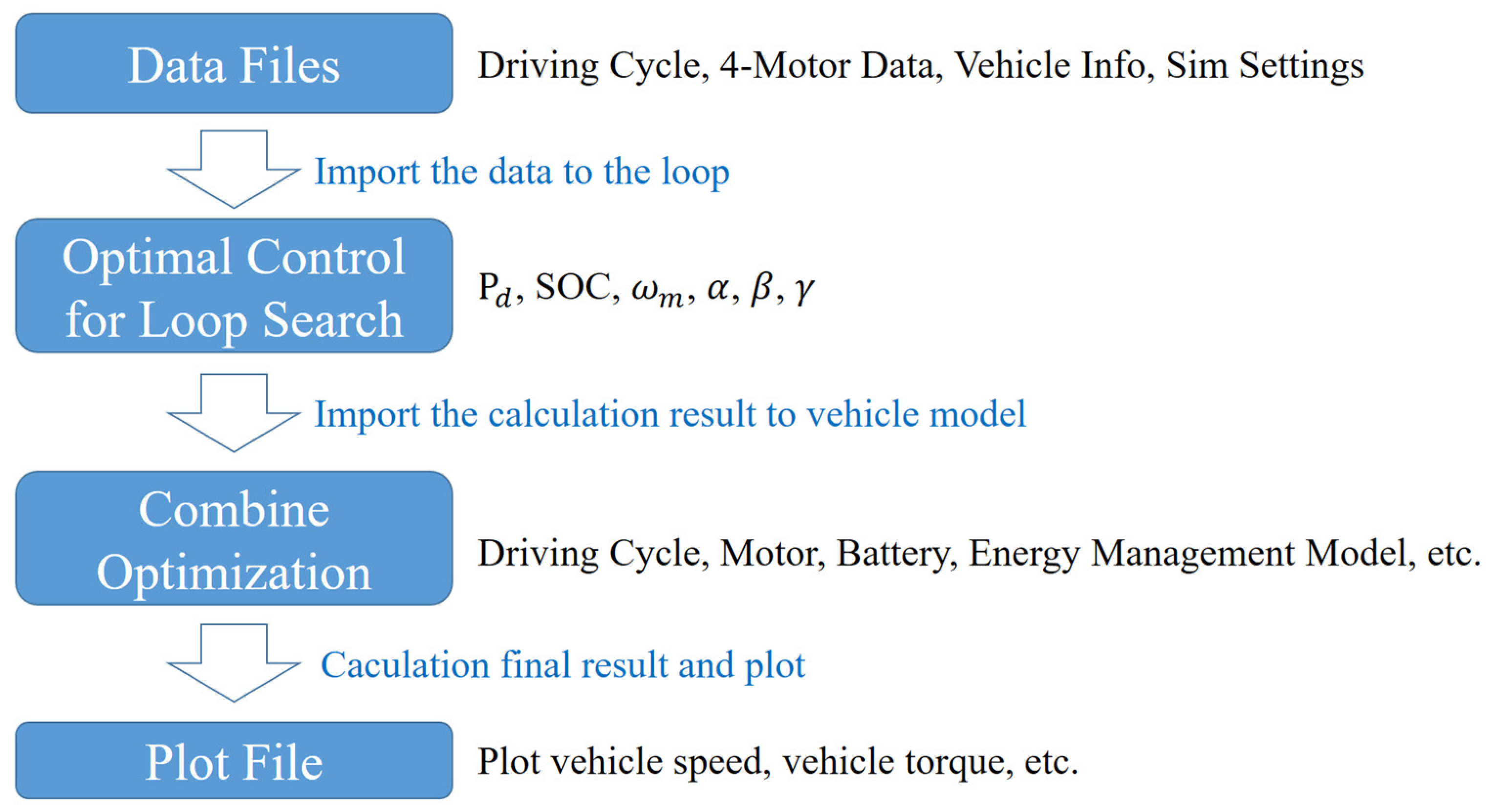
2.1.6. Hardware-in-the-Loop System Architecture
2.2. Optimal Energy Management of the Four-Wheel-Side Motors
2.3. Optimal Energy Management of the Front and Rear Axle Motors
3. Discussion of Simulation Results
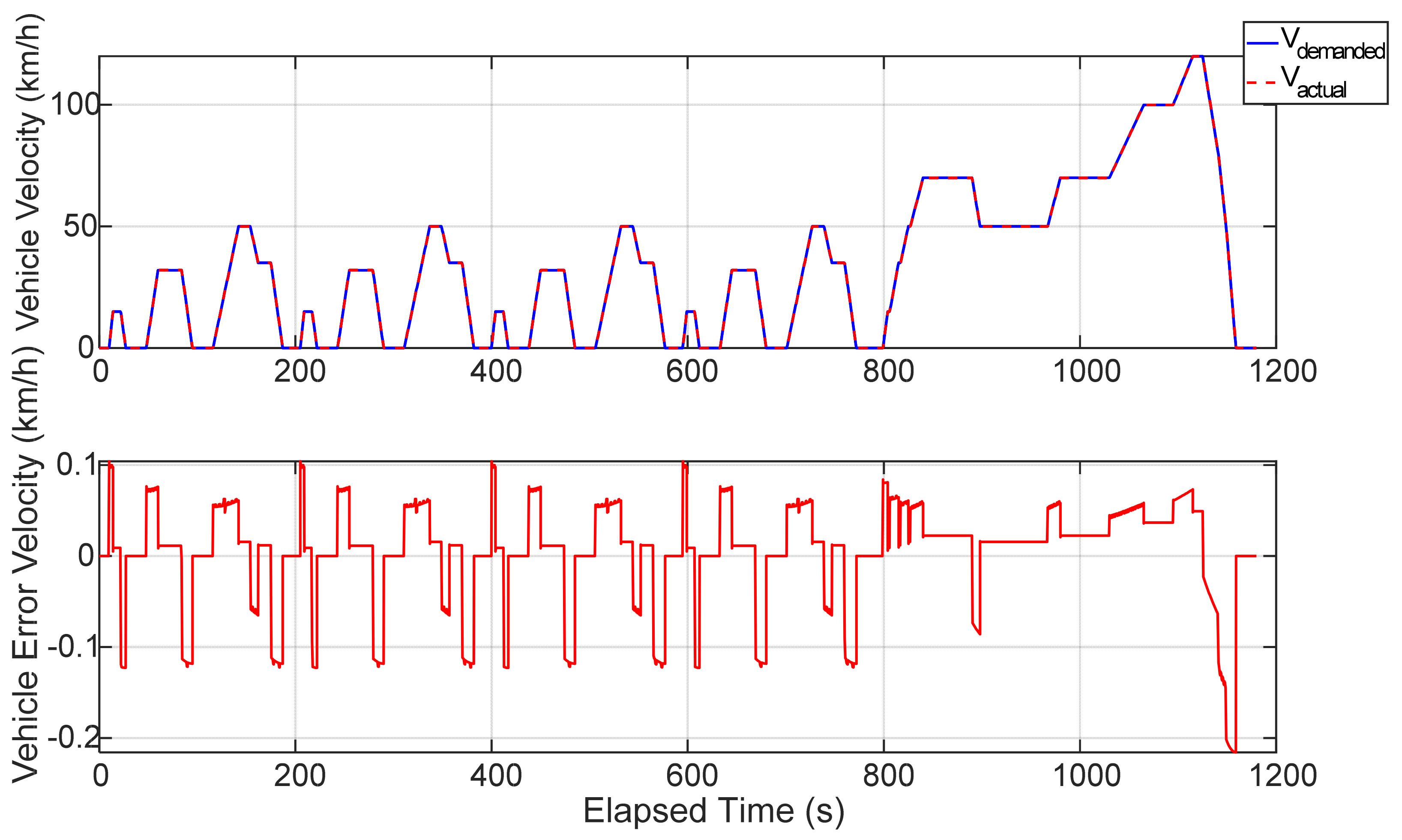
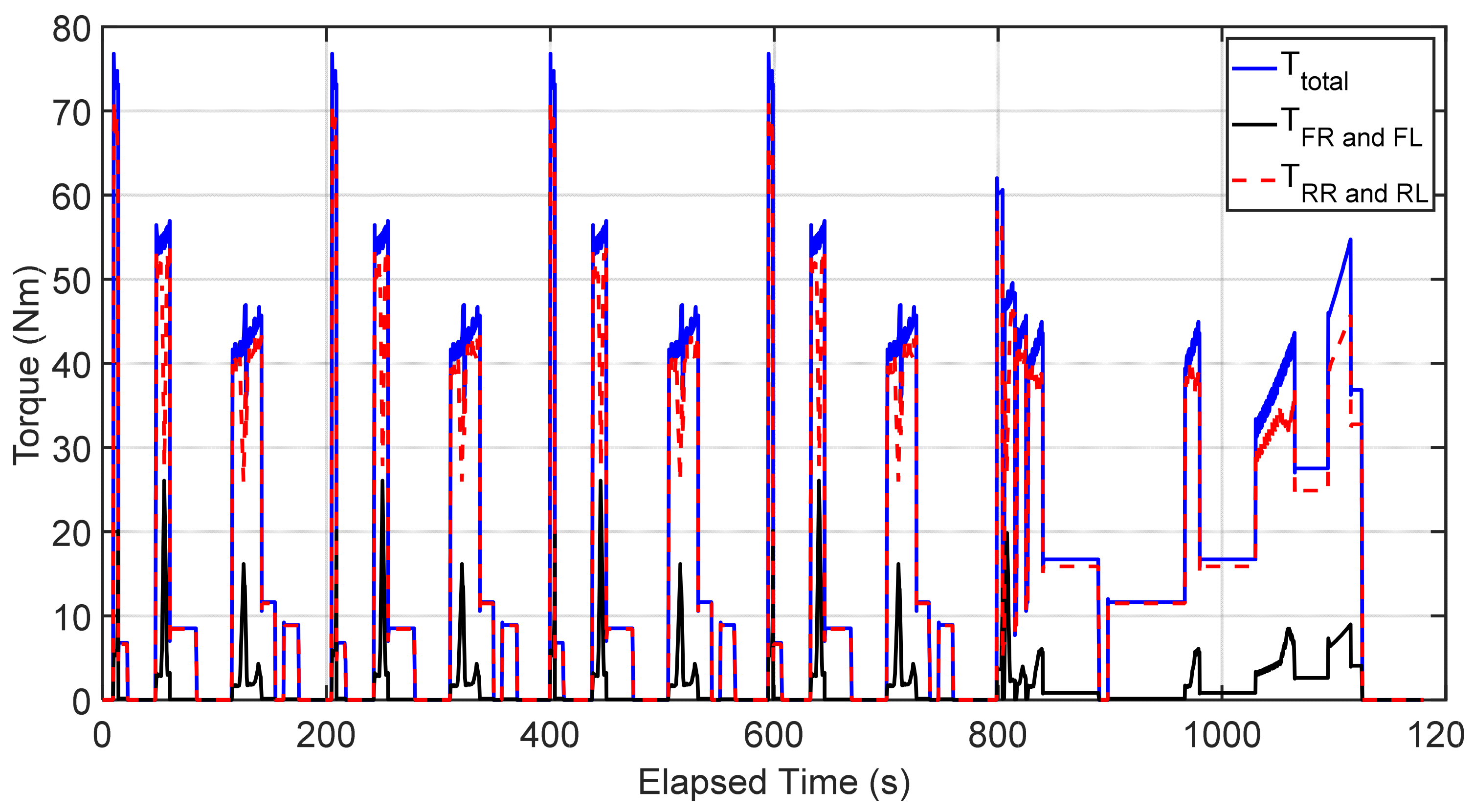
3.1. Performance Analysis of the Optimal Energy Management for the Electric Vehicle
3.2. Energy Efficiency and Equivalent Fuel Economy Analysis of the Optimal Energy Management for the Electric Vehicle
- ⮚
- Algorithms were established for four-wheel average torque mode, rule-based control, front and rear axle motor optimization, and four-wheel motor optimization. These optimizations were developed based on the ECMS method.
- ⮚
- Compared to the four-wheel average torque mode, rule-based control and the optimized system achieved significant improvements in a pure simulation environment, with increases in pure electric efficiency of 0.096 0.096%/0.535559%/1.261334% and 0.169%/1.50289%/3.917369%, respectively, as shown in Table 7 and Table 8; in a HIL environment, the increases were 0.070%/1.560%/5.054% and 0.424%/1.288%/4.770%, respectively, as shown in Table 9 and Table 10.
4. Conclusions
- (a)
- Established algorithms for the average torque mode, rule-based control, optimization of the front and rear axle motors, and four-wheel motors optimization. The optimization uses the ECMS method for development.
- (b)
- Compared to the average torque mode and rule-based control under the UDDS driving cycle, in a pure simulation environment, the enhancement rates for pure electric energy efficiency are 3.9%/6.8%/10.7% and 0.8%/4.8%/5.6%, respectively. In the hardware-in-the-loop (HIL) simulation comparison, the enhancement rates for pure electric energy efficiency are 3.6%/5.8%/6.1% and 0.6%/4.8%/6.0%, respectively. (These four improvement rates are based on 45 kW/95 kW and two control strategies.)
- (c)
- Compared to the average torque mode and rule-based control under the FTP-75 driving cycle, in a pure simulation environment, the enhancement rates for pure electric energy efficiency are 0.1%/0.5%/1.3% and 0.2%/1.5%/3.9%, respectively. In the hardware-in-the-loop (HIL) simulation comparison, the enhancement rates for pure electric energy efficiency are 0.1%/1.6%/5.1% and 0.4%/1.3%/4.8%, respectively. (These four improvement rate are based on 45 kW/95 kW and two control strategies.)
- (d)
- The four-wheel optimization algorithm showed a higher improvement rate compared to the front and rear axle optimization algorithm, mainly due to the four-wheel optimization algorithm’s ability to more delicately control the output of each motor, reducing losses in the energy distribution process, thereby significantly enhancing overall efficiency.
- (e)
- The ECMS method considers all factors in its search, allowing it to find the global optimum solution.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| power distribution ratio of the first gear | |
| power distribution ratio of the second gear | |
| power distribution ratio of the third gear | |
| represents the relationship between battery | |
| rolling resistance coefficient | |
| air density | |
| gradient angle | |
| efficiency of the battery charge and discharge | |
| overall efficiency of the final drive | |
| efficiency of the drive motor | |
| efficiency of the left front wheel motor | |
| efficiency of the right front wheel motor | |
| efficiency of the left rear wheel motor | |
| efficiency of the right rear wheel motor | |
| frontal area of the EV | |
| drag coefficient | |
| input power of the left front wheel motor | |
| input power of the right front wheel motor | |
| input power of the left rear wheel motor | |
| input power of the right rear wheel motor | |
| braking force | |
| gravitational acceleration | |
| charge and discharge current of the battery | |
| optimal objective function | |
| integral gain of the PI controller | |
| proportional gain of the PI controller | |
| total vehicle mass | |
| wheel speed of the drive motor | |
| discharge power of the battery | |
| rated capacity of the lithium battery | |
| air resistance | |
| equivalent internal resistance of the lithium battery gradient resistance | |
| gradient resistance | |
| rolling resistance | |
| tire radius | |
| state of charge for lithium battery | |
| state of charge initial value of lithium battery | |
| total demanded torque | |
| output torque of the final drive | |
| output torque of the drive motor | |
| output torque of the left front wheel motor | |
| output torque of the right front wheel motor | |
| output torque of the left rear wheel motor | |
| output torque of the right rear wheel motor | |
| battery temperature | |
| voltage of the lithium battery | |
| vehicle velocity | |
| open circuit voltage of the lithium battery | |
| the error between the demanded vehicle velocity and the actual vehicle velocity |
References
- Alhajeri, N.S.; Dannoun, M.; Alrashed, A.; Aly, A.Z. Environmental and Economic Impacts of Increased Utilization of Natural Gas in the Electric Power Generation Sector: Evaluating the Benefits and Trade−offs of Fuel Switching. J. Nat. Gas Sci. Eng. 2019, 71, 102969. [Google Scholar] [CrossRef]
- Aljarrah, R.; Al-Omary, M.; Salem, Q.; Abu-Hamad, J.; Karimi, M.; Al-Rousan, W. Relationship Between Fault Level and System Strength in Future Renewable-rich Power Grids. Appl. Sci. 2023, 13, 142. [Google Scholar] [CrossRef]
- Ozgen, S.; Cernuschi, S.; Caserini, S. An Overview of Nitrogen Oxides Emissions from Biomass Combustion for Domestic Heat Production. Renew. Sustain. Energy Rev. 2021, 135, 110113. [Google Scholar]
- Donskoy, I. Techno-Economic Efficiency Estimation of Promising Integrated Oxyfuel Gasification Combined-Cycle Power Plants with Carbon Capture. Clean Technol. 2023, 5, 215–232. [Google Scholar] [CrossRef]
- Ram, M.; Child, M.; Aghahosseini, A.; Bogdanov, D.; Lohrmann, A.; Breyer, C. A Comparative Analysis of Electricity Generation Costs from Renewable, Fossil Fuel and Nuclear Sources in G20 Countries for the Period 2015–2030. J. Clean. Prod. 2018, 199, 687–704. [Google Scholar] [CrossRef]
- Alanazi, F. Electric Vehicles: Benefits, Challenges, and Potential Solutions for Widespread Adaptation. Appl. Sci. 2023, 13, 6016. [Google Scholar] [CrossRef]
- Kumar, M.; Panda, K.P.; Naayagi, R.T.; Thakur, R.; Panda, G. Comprehensive Review of Electric Vehicle Technology and Its Impacts: Detailed Investigation of Charging Infrastructure, Power Management, and Control Techniques. Appl. Sci. 2023, 13, 8919. [Google Scholar] [CrossRef]
- Chifu, V.R.; Cioara, T.; Pop, C.B.; Rusu, H.G.; Anghel, I. Deep Q-Learning-Based Smart Scheduling of EVs for Demand Response in Smart Grids. Appl. Sci. 2024, 14, 1421. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Sawle, Y.; Lala, H. A Comprehensive Review on Optimization of Hybrid Renewable Energy Systems Using Various Optimization Techniques. Renew. Sustain. Energy Rev. 2023, 176, 113192. [Google Scholar] [CrossRef]
- Sheu, K.B. Simulation for the Analysis of a Hybrid Electric Scooter Powertrain. Appl. Energy 2008, 85, 589–606. [Google Scholar] [CrossRef]
- Şen, M.; Özcan, M.; Eker, Y.R. Fuzzy Logic-Based Energy Management System for Regenerative Braking of Electric Vehicles with Hybrid Energy Storage System. Appl. Sci. 2024, 14, 3077. [Google Scholar] [CrossRef]
- Farhadi Gharibeh, H.; Farrokhifar, M. Online Multi-Level Energy Management Strategy Based on Rule-Based and Optimization-Based Approaches for Fuel Cell Hybrid Electric Vehicles. Appl. Sci. 2021, 11, 3849. [Google Scholar] [CrossRef]
- Milićević, S.; Blagojević, I.; Milojević, S.; Bukvić, M.; Stojanović, B. Numerical Analysis of Optimal Hybridization in Parallel Hybrid Electric Powertrains for Tracked Vehicles. Energies 2024, 17, 3531. [Google Scholar] [CrossRef]
- An, S.; Gan, Y.; Peng, X.; Dian, S. Charging Optimization with an Improved Dynamic Programming for Electro-Gasoline Hybrid Powered Compound-Wing Unmanned Aerial Vehicle. Energies 2025, 18, 30. [Google Scholar]
- Katrašnik, T. Analytical Method to Evaluate Fuel Consumption of Hybrid Electric Vehicles at Balanced Energy Content of the Electric Storage Devices. Appl. Energy 2010, 87, 3330–3339. [Google Scholar]
- Xu, W.; Chen, H.; Zhao, H.Y.; Ren, B.T. Torque Optimization Control for Electric Vehicles with Four in-wheel Motors Equipped with Regenerative Braking System. Mechatronics 2019, 57, 95–108. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, X.; Zhou, M.; Liu, L.; Niu, S.; Zhou, C.; Wang, Y. Multi-Temporal Energy Management Strategy for Fuel Cell Ships Considering Power Source Lifespan Decay Synergy. J. Mar. Sci. Eng. 2025, 13, 34. [Google Scholar]
- Xue, D.; Wang, H.; Wang, J.; Guan, C.; Xia, Y. Equivalent Cost Minimization Strategy for Plug-In Hybrid Electric Bus with Consideration of an Inhomogeneous Energy Price and Battery Lifespan. Sustainability 2025, 17, 460. [Google Scholar]
- Zhang, S.; Wang, H.; Yang, C.; Ouyang, Z.; Wen, X. Optimization of Energy Management Strategy for Series Hybrid Electric Vehicle Equipped with Dual-Mode Combustion Engine Under NVH Constraints. Appl. Sci. 2024, 14, 12021. [Google Scholar] [CrossRef]
- Puma-Benavides, D.S.; Calderon-Najera, J.d.D.; Izquierdo-Reyes, J.; Galluzzi, R.; Llanes-Cedeño, E.A. Methodology to Improve an Extended-Range Electric Vehicle Module and Control Integration Based on Equivalent Consumption Minimization Strategy. World Electr. Veh. J. 2024, 15, 439. [Google Scholar] [CrossRef]
- Tang, Q.S.; Yang, Y.; Luo, C.; Yang, Z.; Fu, C.Y. A Novel Electro-hydraulic Compound Braking System Coordinated Control Strategy for a Four-wheel-drive Pure Electric Vehicle Driven by Dual Motors. Energy 2022, 241, 122750. [Google Scholar]
- Guo, J.; Guo, Z.; Chu, L.; Zhao, D.; Hu, J.; Hou, Z. A Dual-Adaptive Equivalent Consumption Minimization Strategy for 4WD Plug-In Hybrid Electric Vehicles. Sensors 2022, 22, 6256. [Google Scholar] [CrossRef]
- Guo, Z.; Chu, L.; Hou, Z.; Wang, Y.; Hu, J.; Sun, W. A Dual Distribution Control Method for Multi-Power Components Energy Output of 4WD Electric Vehicles. Sensors 2022, 22, 9597. [Google Scholar] [CrossRef] [PubMed]
- Pradeep, D.J.; Kumar, Y.V.P.; Siddharth, B.R.; Reddy, C.P.; Amir, M.; Khalid, H.M. Critical Performance Analysis of Four-wheel Drive Hybrid Electric Vehicles Subjected to Dynamic Operating Conditions. World Electr. Veh. J. 2023, 14, 138. [Google Scholar] [CrossRef]
- Hung, Y.H.; Wu, C.H. A Combined Optimal Sizing and Energy Management Approach for Hybrid in-wheel Motors of EVs. Appl. Energy 2015, 139, 260–271. [Google Scholar]
- Li, S.B.; Chu, L.; Hu, J.C.; Pu, S.L.; Li, J.H.; Hou, Z.R.; Sun, W. A Novel A-ECMS Energy Management Strategy Based on Dragonfly Algorithm for Plug-in FCEVs. Sensors 2023, 23, 1192. [Google Scholar] [CrossRef]
- EDM—S. Available online: https://www.zept.com.tw/edm1-s-p95 (accessed on 17 December 2024).
- Ji, P.; Nie, W.W.; Liu, J.L. Research on Magnetic Coupling Flywheel Energy Storage Device for Vehicles. Appl. Sci. 2024, 14, 7951. [Google Scholar]
- Kozak, M.; Merkisz, J. Oxygenated Diesel Fuels and Their Effect on PM Emissions. Appl. Sci. 2022, 12, 7709. [Google Scholar] [CrossRef]
- Wu, C.H.; Xu, Y.X. The Optimal Control of Fuel Consumption for a Heavy-Duty Motorcycle with Three Power Sources Using Hardware-in-the-Loop Simulation. Energies 2019, 13, 22. [Google Scholar] [CrossRef]
- Liu, J.; Liu, C.; Zong, C.F.; Zheng, H. Fault-tolerant Control of 4WID/4WIS Electric Vehicles Based on Reconfigurable Control Allocation. J. South China Univ. Technol. 2013, 41, 125–131. [Google Scholar]
- Zhang, B.; Lu, S. Fault-tolerant Control for Four-wheel Independent Actuated Electric Vehicle Using Feedback Linearization and Cooperative Game Theory. Control Eng. Pract. 2020, 101, 104510. [Google Scholar] [CrossRef]






| Item | Specification | |
|---|---|---|
| Drive Motor | Type | Permanent Magnet Synchronous |
| Maximum Output Power | 95 kW (Single)/380 kW (Four Units) | |
| Maximum Output Torque | 210 Nm@4125 rpm | |
| Energy Storage Battery | Type | Lithium-ion Ternary Battery |
| Rated voltage | 288 V | |
| Maximum Capacity | 64.58 Ah (8.6 kWh) | |
| Vehicle Parameters | Vehicle Mass | 1728 kg |
| Gravitational Acceleration | 9.81 m/s2 | |
| Aerodynamic Drag Coefficient | 0.35 | |
| Density of Air | 1.2 kg/m3 | |
| Frontal Area | 3.5 m2 | |
| Tire Radius | 0.329 | |
| Rolling Resistance Coefficient | 0.01 | |
| Road Grade | 0% | |
| Final Drive Ratio | 9.78 | |
| Drive Friction Coefficient | 0.95 | |
| Mode | Condition | Power Distribution |
|---|---|---|
| Mode1 | and | ; |
| Mode2 | ; | |
| Mode3 | and | ; |
| Average Torque (Four-Wheel) | Rule-Based Control (Front-Rear Axle) | Optimal (Front-Rear Axle) | Optimal (Four-Wheel) | |
|---|---|---|---|---|
| Energy Efficiency (km/kWh) | 4.7862 | 4.9749 | 5.1122 | 5.2985 |
| Improvement Rate (%) | 3.9 | 6.8 | 10.7 |
| Average Torque (Four-Wheel) | Rule-Based Control (Front-Rear Axle) | Optimal (Front-Rear Axle) | Optimal (Four-Wheel) | |
|---|---|---|---|---|
| Energy Efficiency (km/kWh) | 4.8028 | 4.8245 | 5.0319 | 5.0710 |
| Improvement Rate (%) | -- | 0.8 | 4.8 | 5.6 |
| Average Torque (Four-Wheel) | Rule-Based Control (Front-Rear Axle) | Optimal (Front-Rear Axle) | Optimal (Four-Wheel) | |
|---|---|---|---|---|
| Energy Efficiency (km/kWh) | 4.8517 | 5.0261 | 5.1319 | 5.1467 |
| Improvement Rate (%) | -- | 3.6 | 5.8 | 6.1 |
| Average Torque (Four-Wheel) | Rule-Based Control (Front-Rear Axle) | Optimal (Front-Rear Axle) | Optimal (Four-Wheel) | |
|---|---|---|---|---|
| Energy Efficiency (km/kWh) | 4.7966 | 4.8252 | 5.0285 | 5.0856 |
| Improvement Rate (%) | -- | 0.6 | 4.8 | 6.0 |
| Average Torque (Four-Wheel) | Rule-Based Control (Front-Rear Axle) | Optimal (Front-Rear Axle) | Optimal (Four-Wheel) | |
|---|---|---|---|---|
| Energy Efficiency (km/kWh) | 5.4149 | 5.4201 | 5.4439 | 5.4832 |
| Improvement Rate (%) | -- | 0.1 | 0.5 | 1.3 |
| Average Torque (Four-Wheel) | Rule-Based Control (Front-Rear Axle) | Optimal (Front-Rear Axle) | Optimal (Four-Wheel) | |
|---|---|---|---|---|
| Energy Efficiency (km/kWh) | 5.2765 | 5.2854 | 5.3558 | 5.4833 |
| Improvement Rate (%) | -- | 0.2 | 1.5 | 3.9 |
| Average Torque (Four-Wheel) | Rule-Based Control (Front-Rear Axle) | Optimal (Front-Rear Axle) | Optimal (Four-Wheel) | |
|---|---|---|---|---|
| Energy Efficiency (km/kWh) | 5.1401 | 5.1468 | 5.2203 | 5.3999 |
| Improvement Rate (%) | -- | 0.1 | 1.6 | 5.1 |
| Average Torque (Four-Wheel) | Rule-Based Control (Front-Rear Axle) | Optimal (Front-Rear Axle) | Optimal (Four-Wheel) | |
|---|---|---|---|---|
| Energy Efficiency (km/kWh) | 5.1546 | 5.1765 | 5.2210 | 5.4005 |
| Improvement Rate (%) | -- | 0.4 | 1.3 | 4.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-H.; Gao, W.-Z.; Yang, J.-M. A Novel Optimal Control Strategy of Four Drive Motors for an Electric Vehicle. Appl. Sci. 2025, 15, 3505. https://doi.org/10.3390/app15073505
Wu C-H, Gao W-Z, Yang J-M. A Novel Optimal Control Strategy of Four Drive Motors for an Electric Vehicle. Applied Sciences. 2025; 15(7):3505. https://doi.org/10.3390/app15073505
Chicago/Turabian StyleWu, Chien-Hsun, Wei-Zhe Gao, and Jie-Ming Yang. 2025. "A Novel Optimal Control Strategy of Four Drive Motors for an Electric Vehicle" Applied Sciences 15, no. 7: 3505. https://doi.org/10.3390/app15073505
APA StyleWu, C.-H., Gao, W.-Z., & Yang, J.-M. (2025). A Novel Optimal Control Strategy of Four Drive Motors for an Electric Vehicle. Applied Sciences, 15(7), 3505. https://doi.org/10.3390/app15073505






