Hypergraph Analysis of Functional Brain Connectivity During Figurative Attention
Abstract
:1. Introduction
2. Mathematical Basis
2.1. Main Definitions
2.2. Summarization
2.3. Coherence
2.4. Cross-Correlation
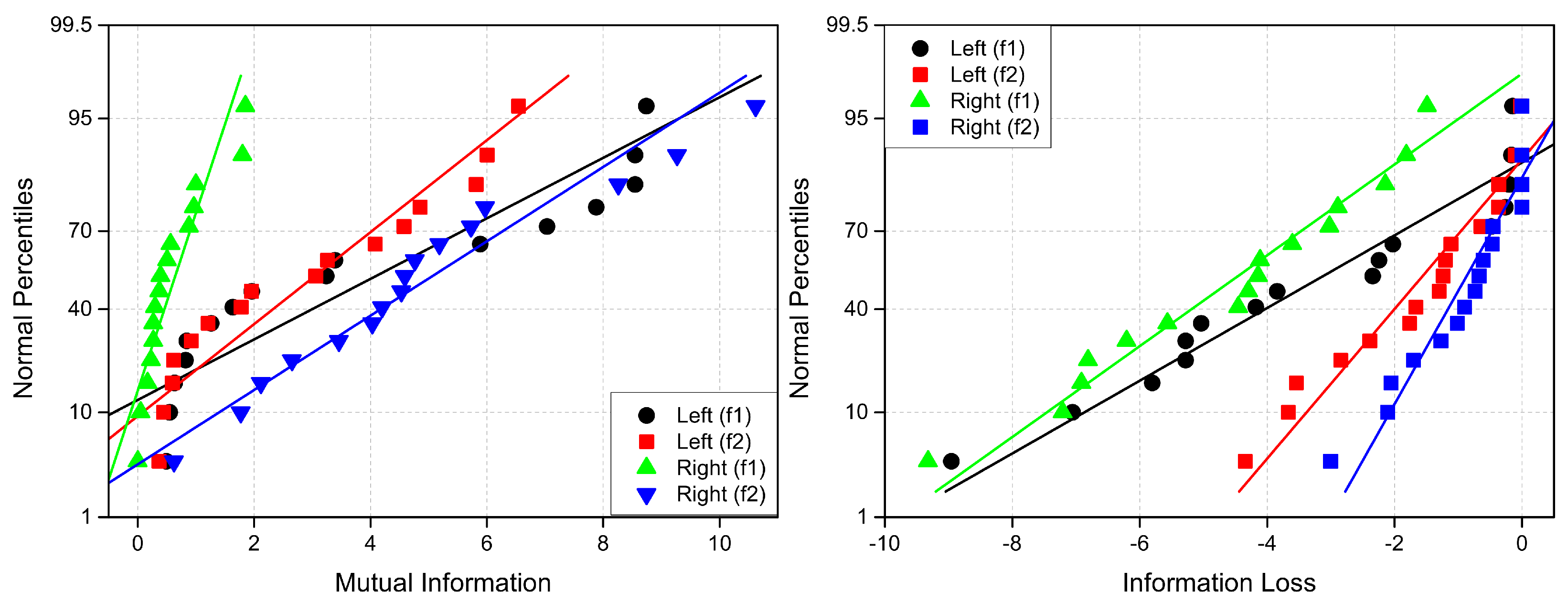
2.5. Mutual Information
3. Materials and Experimental Methods
3.1. Participant
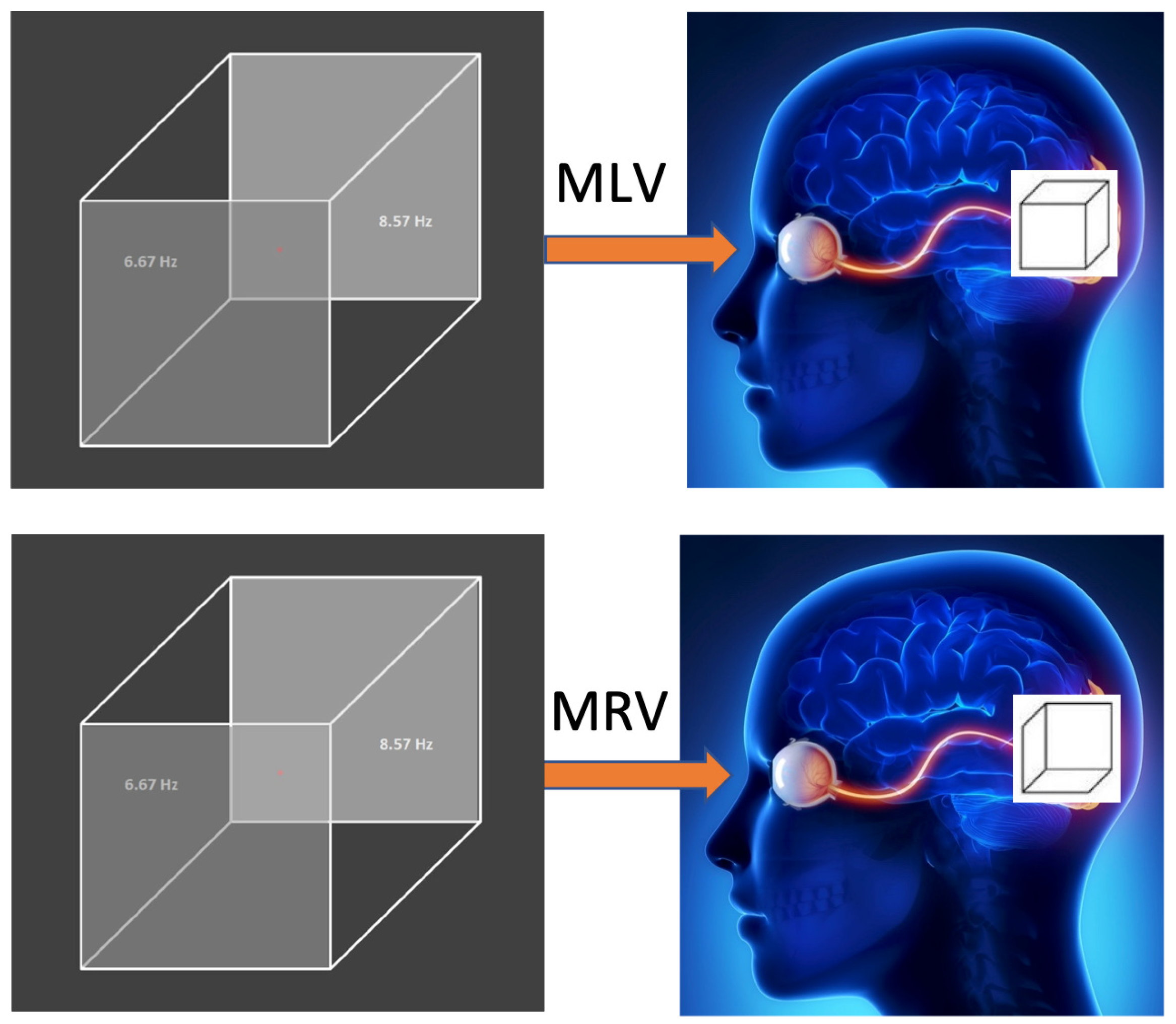
3.2. Stimulus
3.3. Experimental Setup
3.4. Experimental Paradigm
4. Experimental Data Analysis
4.1. Artifact Removal
- (i)
- Reference to frontal channels: Since our EEG equipment did not include electro-oculography electrodes, we used frontal channels (F7 and F8) as references for the ocular correction ICA. Cumulative quadratic correlation allows the precise removal of relevant components without losing neuronal information. The FP1 channel served as a common VEOG reference to detect vertical artifacts.
- (ii)
- Infomax Extended ICA algorithm: This algorithm improves the efficiency of artifact correction compared to standard ICA while preserving the neuronal signal of interest. Additionally, a Quality Control process is incorporated to ensure the validity of the obtained results. This approach enables the effective identification and reduction of ocular artifacts in EEG signals, thus facilitating the subsequent analysis of cortical responses associated with the visual stimulus by eliminating or mitigating interference from eye movements and blinks.
- (iii)
- Value trigger algorithm: This algorithm facilitated the detection of characteristic patterns, such as blinks. Blinks were identified on the basis of their absolute magnitude, with definitive blink movements determined using the correlation method. The blink detection threshold (blink value trigger) was set at 97%, which means that any value above this threshold was recognized as a blink. The selection of the 97% activation threshold for blink detection was based on experimental analysis using data from 28 participants. During threshold optimization, lower values significantly increased the rate of false positives, compromising the integrity of the neuronal signal. The 97% threshold was identified as the optimal balance between sensitivity and specificity, allowing robust identification of ocular artifacts without affecting the underlying signal. The signal correlation was established at 70% relative to a predefined blink template. This algorithm enhances detection accuracy by ensuring that triggers are only activated for signals with a high morphological similarity to a characteristic blink pattern, thereby reducing the erroneous detection of other artifacts. Additionally, a visual analysis using back-projection (Inverse ICA) was implemented as a validation method. This technique allowed the eliminated components to be projected back into the original domain, facilitating a visual inspection of the processed data. This procedure confirmed that ocular artifact suppression was performed selectively, preserving relevant neuronal activity while minimizing EEG signal distortion.These values were experimentally determined by considering their influence on attenuating the signal of interest in the spectral regions of and in the occipital lobes (O1, Oz, O2 channels).
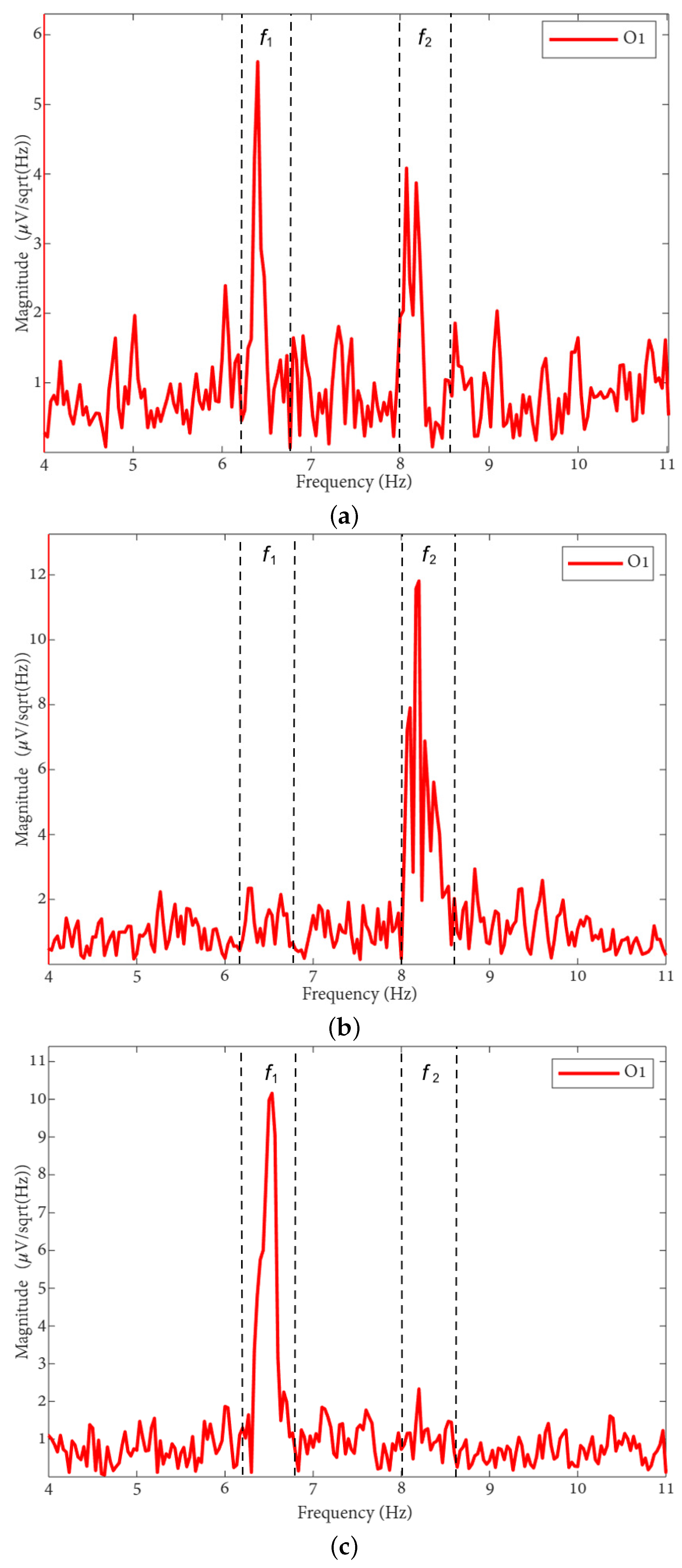
4.2. Spectral Analysis
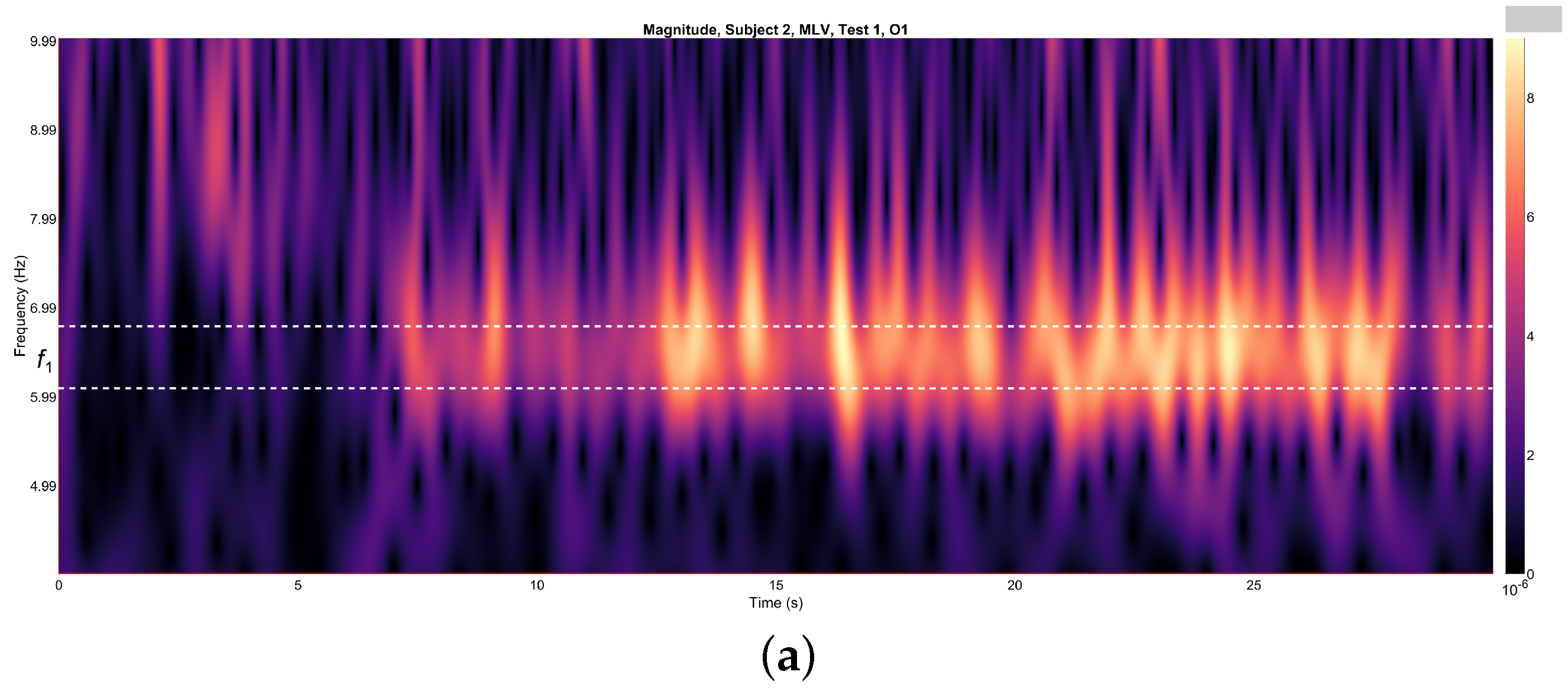
4.3. Wavelet Analysis
5. Graph Construction
5.1. Connectivity Graphs Based on Coherence
5.2. Connectivity Graphs Based on Cross-Correlation
5.3. Connectivity Graphs Based on Mutual Information
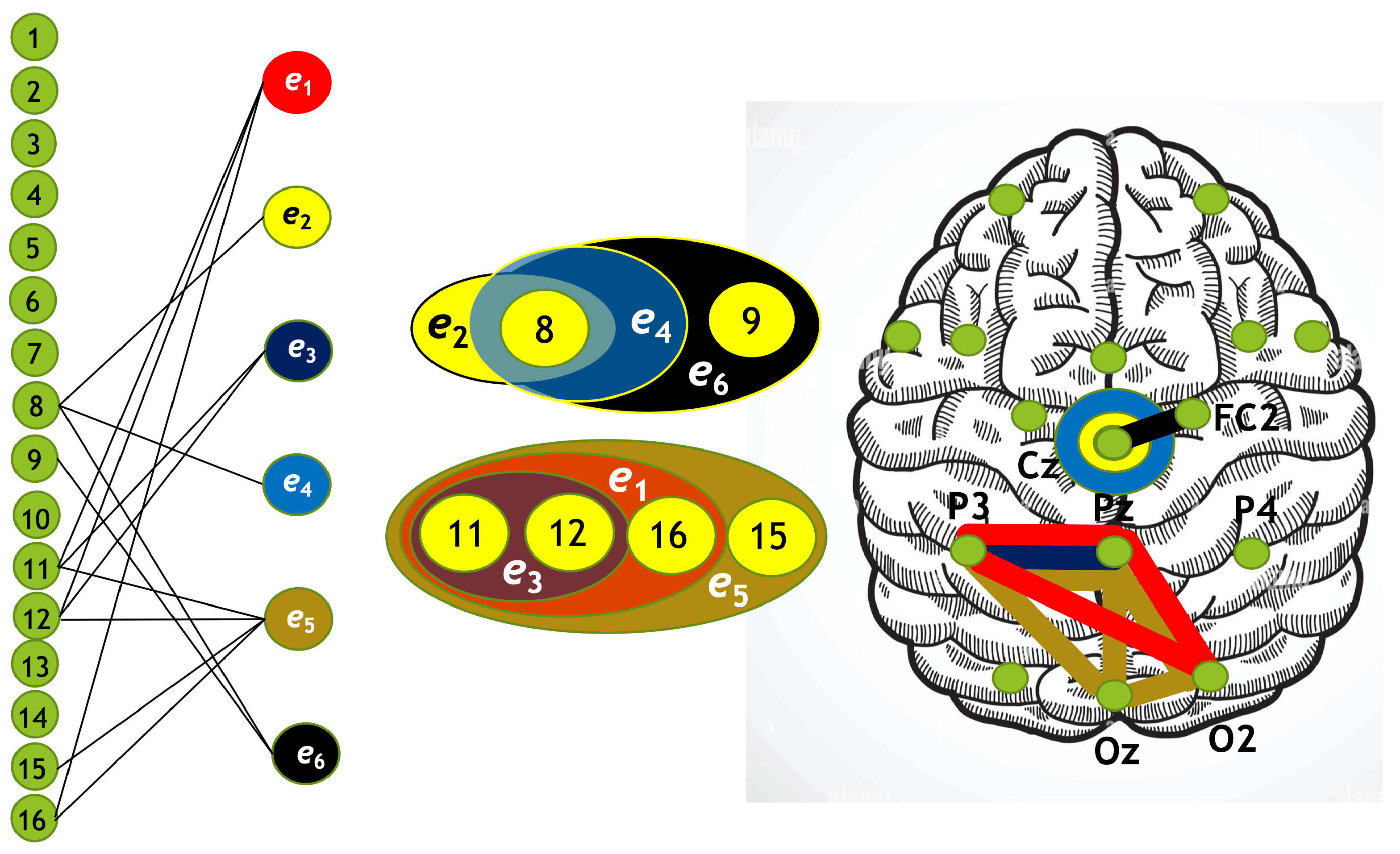
6. Hypergraph Construction
- (1)
- Compute the label of every node i for each connectivity measure using Equation (2) (Lab ).
- (2)
- From the probability distribution of all n labels for each connectivity measure found the mean and standard deviation .
- (3)
- Calculate threshold value for each connectivity measure (“+” for , “−” for ).
- (4)
- Using the threshold value, determine whether a change in connectivity is significant or not. The change is significant if the label .
- (5)
- Using the summarization technique described in Section 2.2 remove insignificant nodes whose labels are smaller than the threshold value. Weak changes in connectivity are considered as brain noise and are not related to attention.
- (6)
- Construct incident matrices using Equation (5).
6.1. Simple Hypergraphs
6.2. Multilayer Hypergraphs
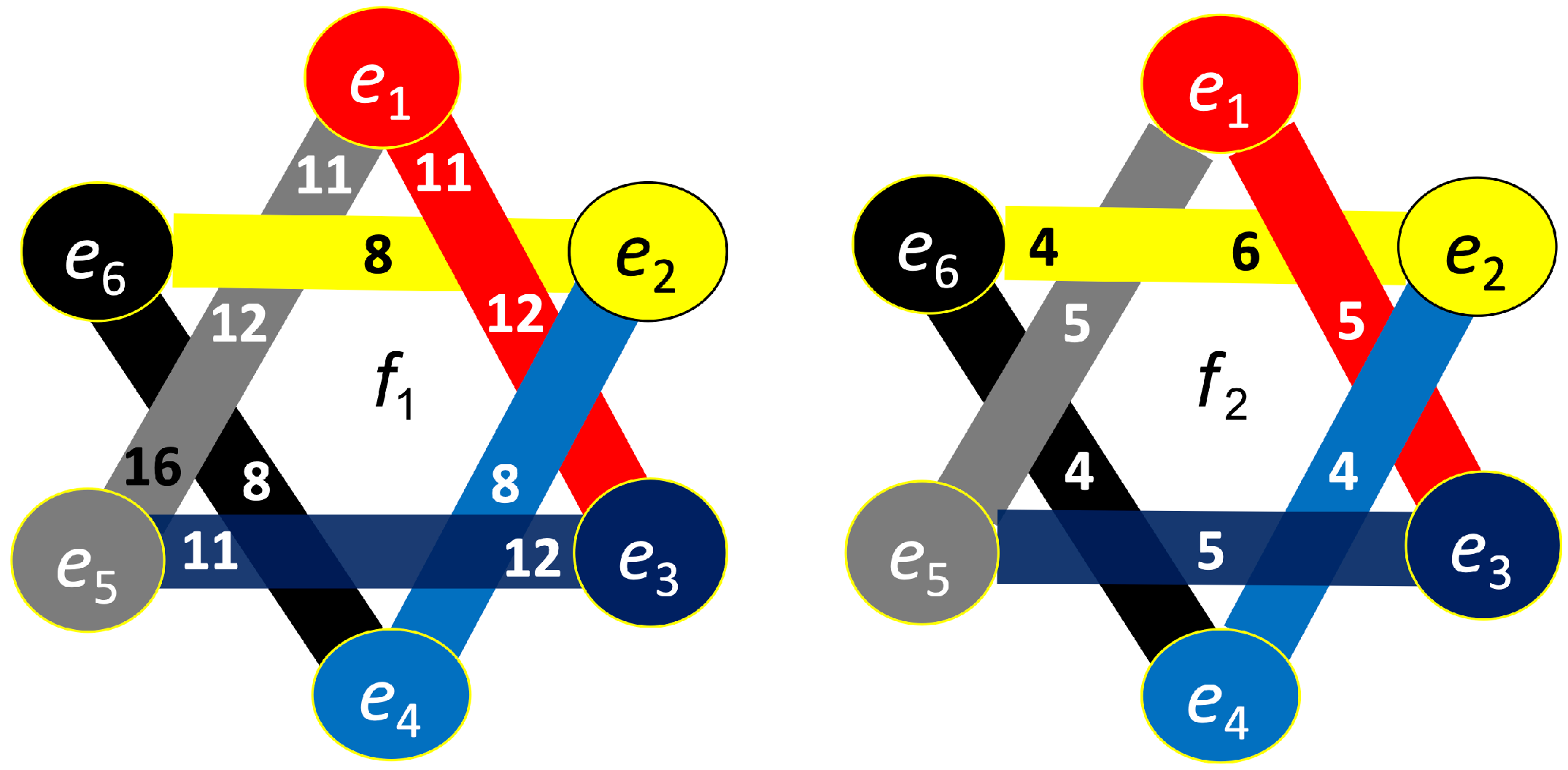
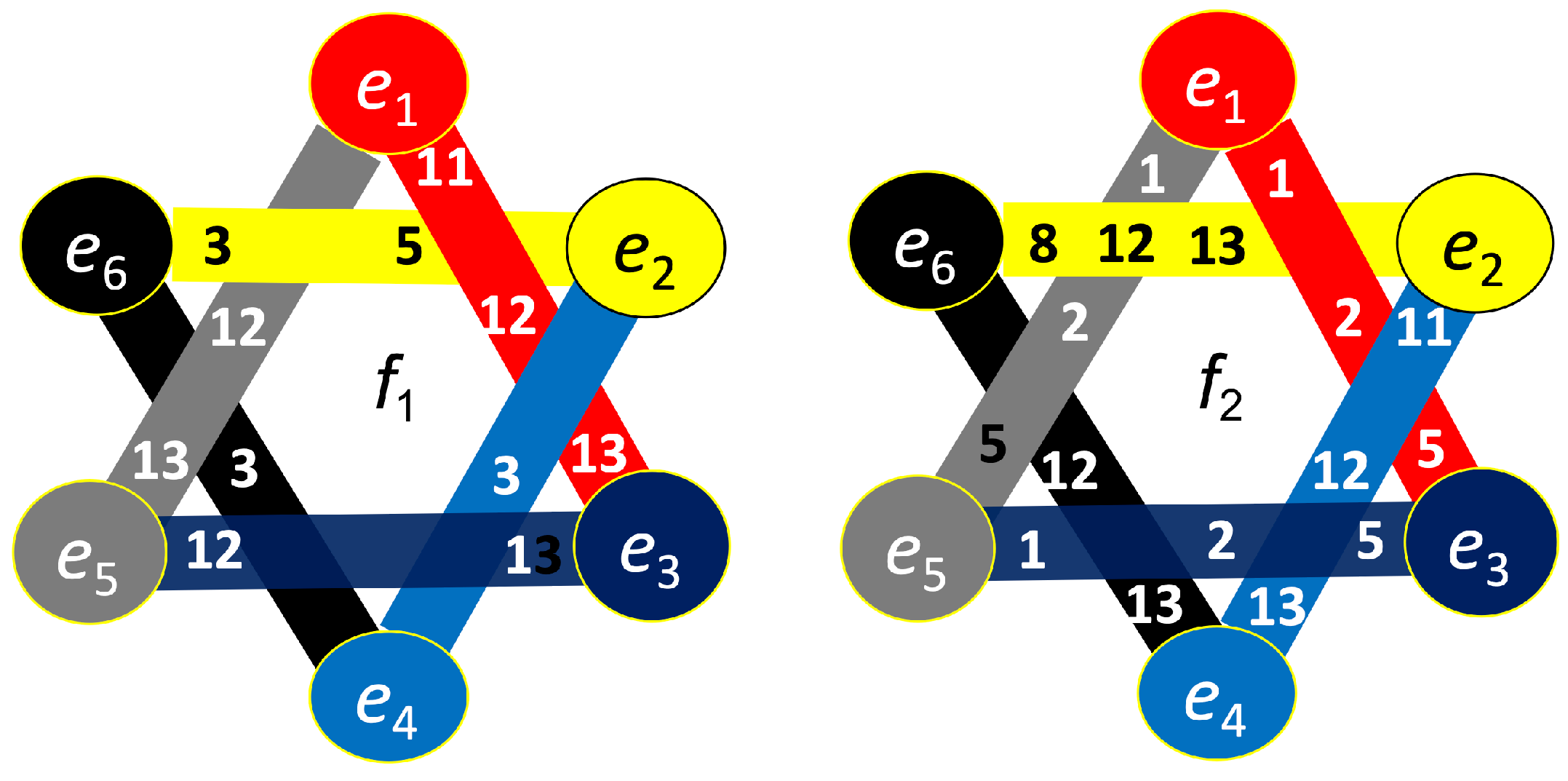
6.3. Dual Clique Expansions
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Data Acquisition Details
- (1)
- Recording (triggers): Triggers were configured within the BrainVision Recorder program, manually activated by the researcher through keypresses at the start and end of each recording. These triggers were labeled in the raw EEG signals, allowing for later identification of the analysis window.
- (2)
- Start and End Margins: The recording included a 3 s margin before the start and 3 s after the end, resulting in a total window of 36 s, of which 30 s corresponded to the experimental period of interest.
- (3)
- Justification for Temporal Margins: The implementation of these temporal margins aimed to minimize artifacts associated with the initiation and termination instructions of the task. The participant took approximately 3 s to process the start instruction, which could introduce transient artifacts in the signal. Similarly, the recording automatically stopped at 36 s with the trigger, reducing the variability associated with manual intervention in the recording termination.
- (4)
- Preprocessing Segmentation: During preprocessing, the 30 s window was extracted, discarding the first and last 3 s to eliminate transient artifacts and ensure that the analysis was performed on stationary data, free from transient influences.This methodological approach reduced variability and increased data reliability without requiring additional hardware for event activation.
Appendix B. Connectivity Matrices
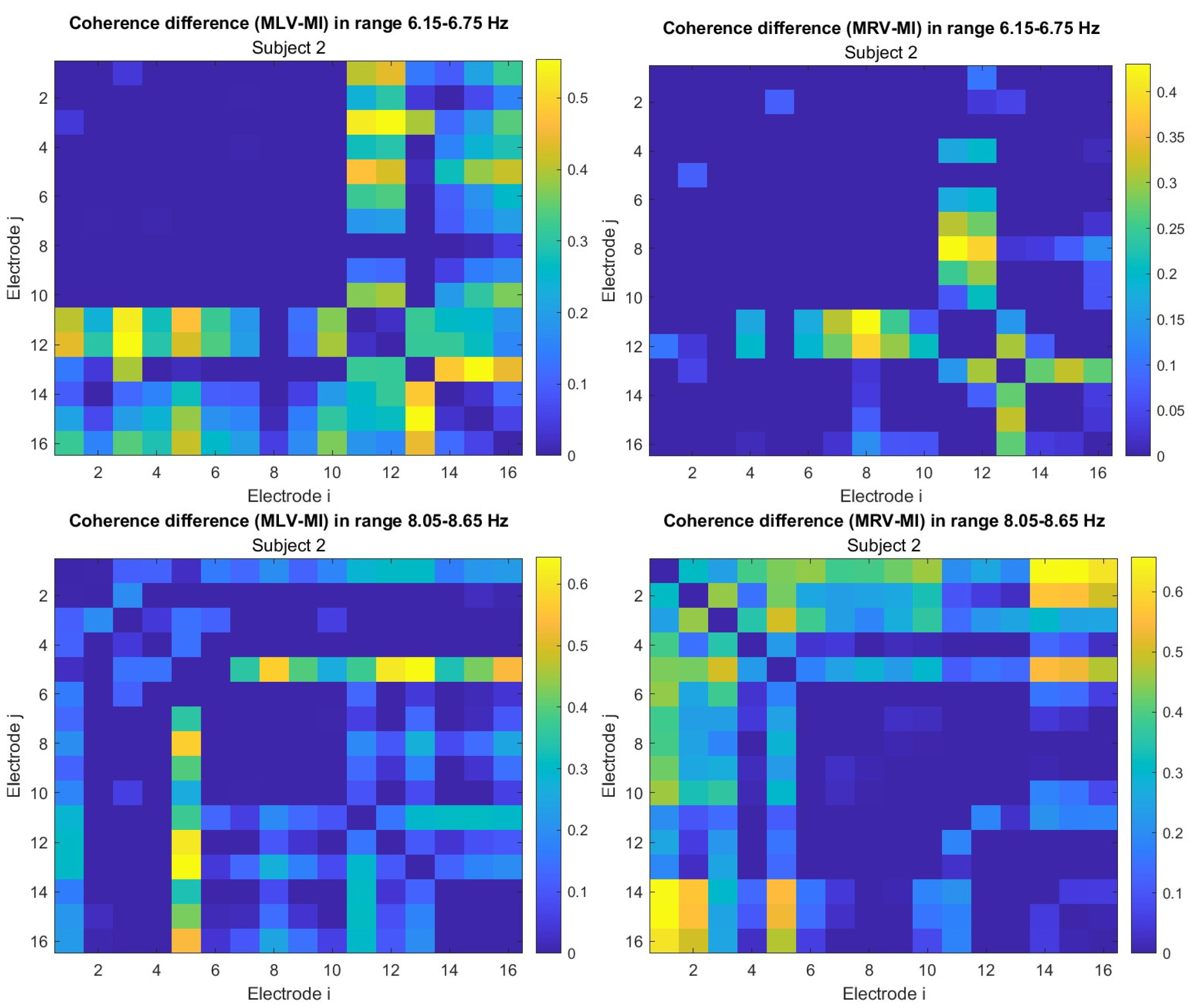



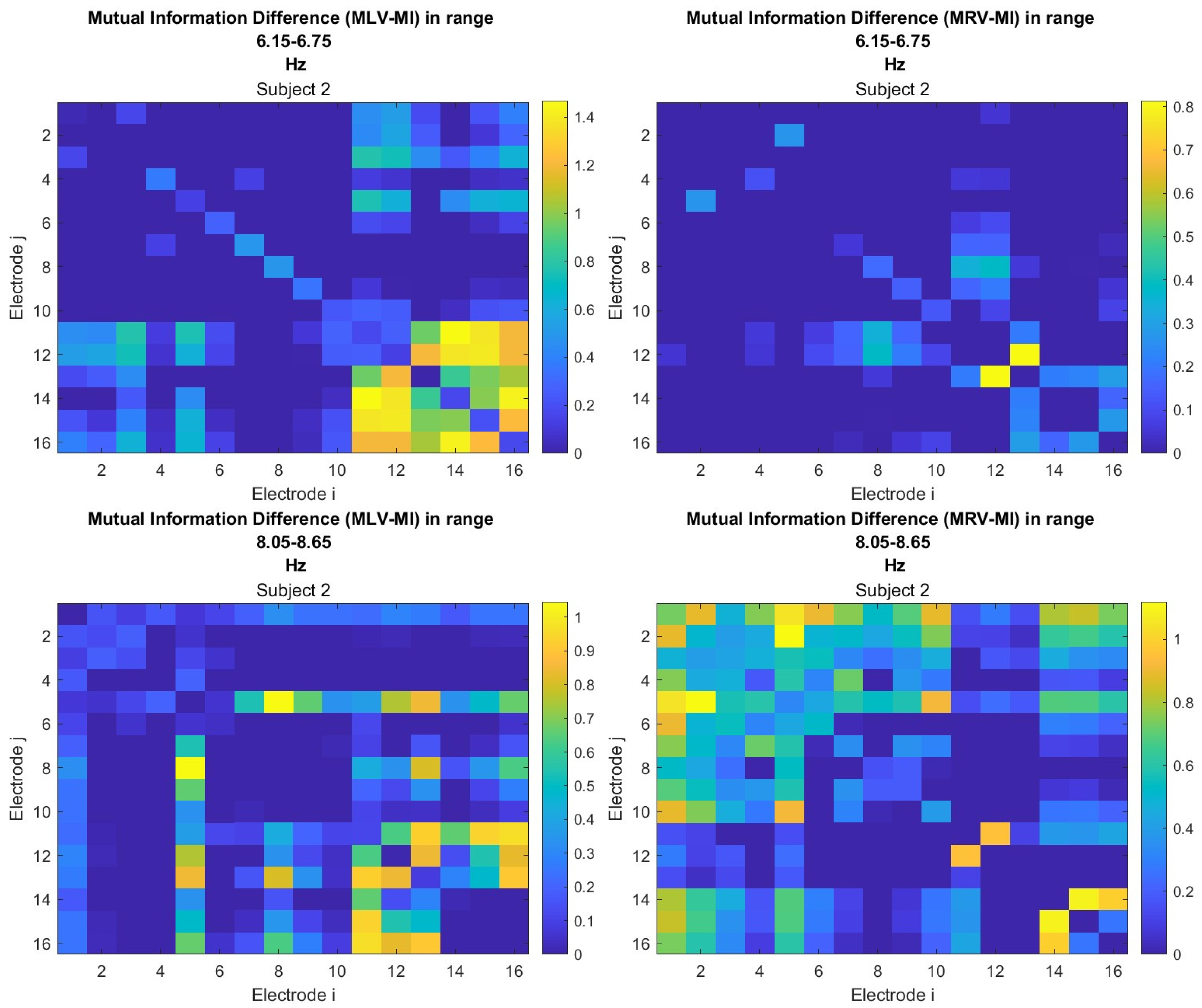
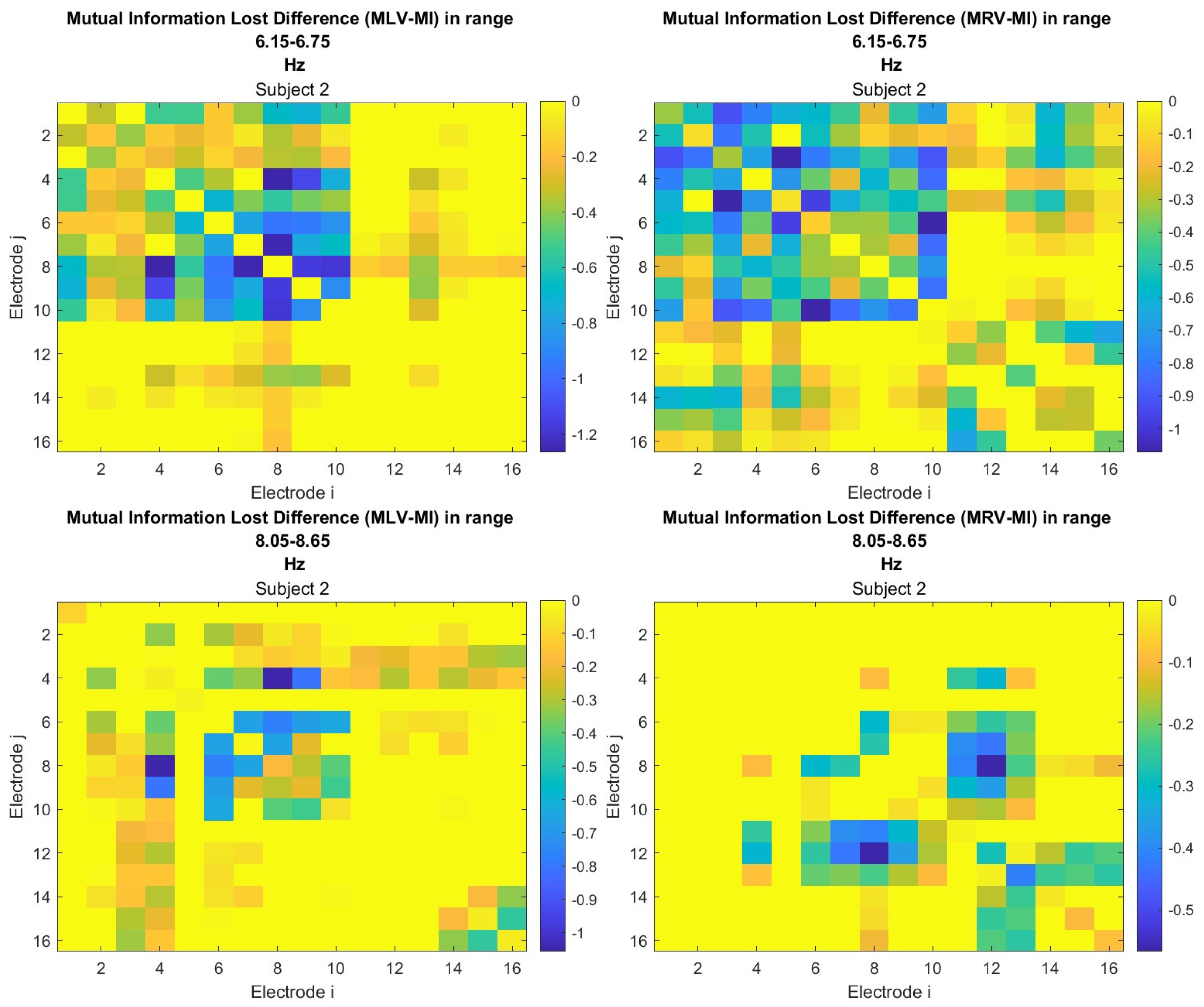
Appendix C. Probability Measures
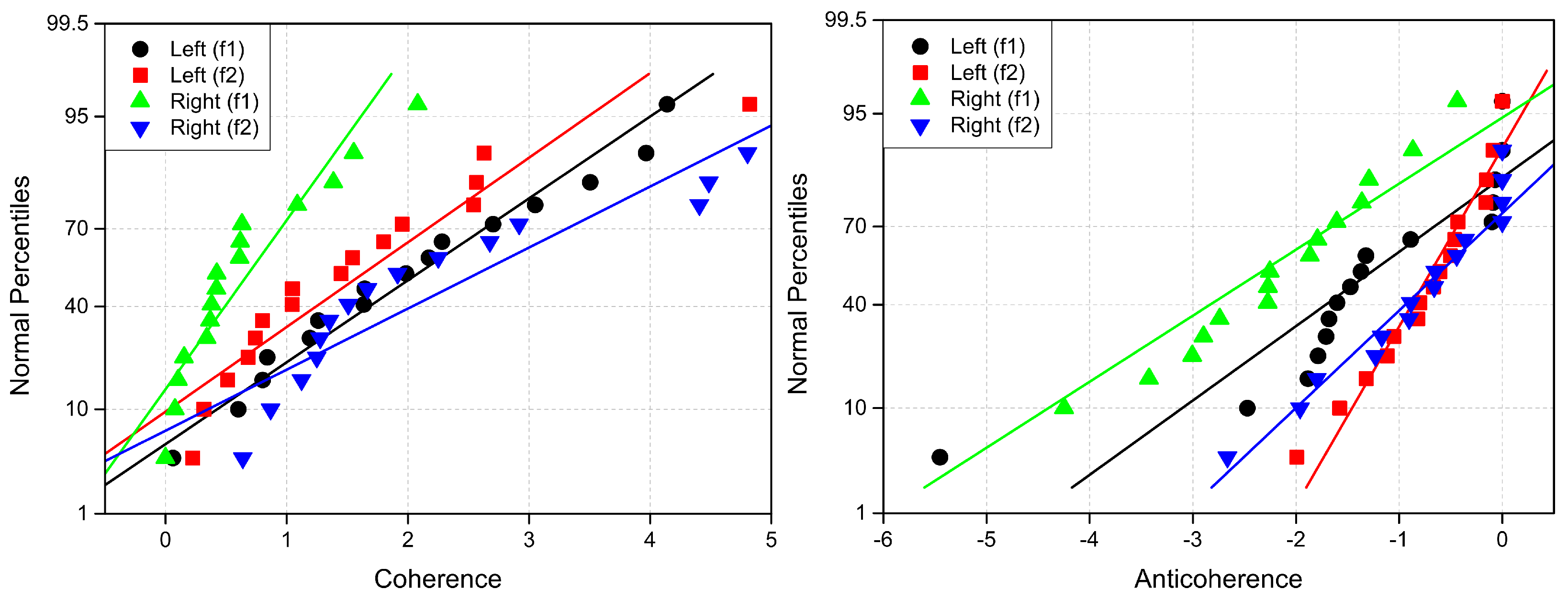

| Measure | Left | Left | Right | Right | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coh | 1.99 | 1.18 | 3.17 | 1.54 | 1.14 | 2.69 | 0.64 | 0.57 | 1.21 | 2.45 | 1.59 | 4.04 |
| ACoh | 1.31 | 0.55 | 1.48 | 0.55 | ||||||||
| Corr | 0.98 | 0.70 | 1.68 | 1.15 | 0.85 | 2.00 | 0.37 | 0.36 | 0.73 | 1.95 | 1.16 | 3.11 |
| ACorr | 0.92 | 0.47 | 0.91 | 0.37 | ||||||||
| MInf | 3.84 | 3.21 | 7.05 | 2.88 | 2.11 | 4.99 | 0.60 | 0.55 | 1.15 | 4.86 | 2.62 | 7.48 |
| ILoss | 2.67 | 1.30 | 2.14 | 0.86 |
References
- Towle, V.L.; Hunter, J.D.; Edgar, J.C.; Chkhenkeli, S.A.; Castelle, M.C.; Frim, D.M.; Kohrman, M.; Hecox, K. Frequency domain analysis of human subdural recordings. J. Clin. Neurophysiol. 2007, 24, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Hramov, A.E.; Frolov, N.S.; Maksimenko, V.A.; Kurkin, S.A.; Kazantsev, V.B.; Pisarchik, A.N. Functional networks of the brain: From connectivity restoration to dynamic integration. Phys. Uspekhi 2021, 64, 584–616. [Google Scholar]
- Boccaletti, S.; De Lellis, P.; del Genio, C.; Alfaro-Bittner, K.; Criado, R.; Jalan, S.; Romance, M. The structure and dynamics of networks with higher order interactions. Phys. Rep. 2023, 1018, 1–64. [Google Scholar]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Friston, K.J. Functional and effective connectivity: A review. Brain Connect. 2011, 1, 13–36. [Google Scholar]
- Tavor, I.; Jones, O.P.; Mars, R.; Smith, S.; Behrens, T.; Jbabdi, S. Task-free MRI predicts individual differences in brain activity during task performance. Science 2016, 352, 216–220. [Google Scholar]
- Greicius, M. Resting-state functional connectivity in neuropsychiatric disorders. Curr. Opin. Neurol. 2008, 21, 424–430. [Google Scholar] [CrossRef]
- Zhang D, R.M. Disease and the brain’s dark energy. Nat. Rev. Neurol. 2010, 6, 15–28. [Google Scholar]
- Dennis, E.L.; Thompson, P.M. Functional brain connectivity using fMRI in aging and Alzheimer’s disease. Neuropsychol. Rev. 2014, 24, 49–62. [Google Scholar]
- Tomasi, D.; Volkow, N.D. Aging and functional brain networks. Mol. Psychiatry 2012, 17, 549–558. [Google Scholar]
- Sala-Llonch, R.; Bartrés-Faz, D.; Junqué, C. Reorganization of brain networks in aging: A review of functional connectivity studies. Front. Psychol. 2015, 6, 663. [Google Scholar]
- Contreras, J.A.; Goñi, J.; Risacher, S.L.; Sporns, O.; Saykin, A.J. The structural and functional connectome and prediction of risk for cognitive impairment in older adults. Curr. Behav. Neurosci. Rep. 2015, 2, 234–245. [Google Scholar] [PubMed]
- Davison, E.N.; Turner, B.O.; Schlesinger, K.J.; Miller, M.B.; Grafton, S.T.; Bassett, D.S.; Carlson, J.M. Individual differences in dynamic functional brain connectivity across the human lifespan. PLoS Comput. Biol. 2016, 12, e1005178. [Google Scholar]
- Zuo, X.N.; Ehmke, R.; Mennes, M.; Imperati, B.; Castellanos, F.X.; Sporns, O.; Milham, M.P. Network centrality in the human functional connectome. Cereb. Cortex 2012, 22, 1862–1875. [Google Scholar]
- Greene, A.S.; Gao, S.; Scheinost, D.; Constable, R.T. Task-induced brain state manipulation improves prediction of individual traits. Nat. Commun. 2018, 9, 2807. [Google Scholar]
- Gu, S.; Yang, M.; Medaglia, J.D.; Gur, R.C.; Gur, R.E.; Satterthwaite, T.D.; Bassett, D.S. Functional hypergraph uncovers novel covariant structures over neurodevelopment. Hum. Brain Mapp. 2017, 38, 3823–3835. [Google Scholar]
- Xiao, L.; Wang, J.; Kassani, P.H.; Zhang, Y.; Bai, Y.; Stephen, J.M.; Wilson, T.W.; Calhoun, V.D.; Wang, Y.P. Multi-hypergraph learning based brain functional connectivity analysis in fMRI data. IEEE Trans. Med. Imaging 2020, 39, 1746–1758. [Google Scholar]
- Ji, Y.; Zhang, Y.; Shi, H.; Jiao, Z.; Wang, S.H.; Wang, C. Constructing dynamic brain functional networks via hyper-graph manifold regularization for mild cognitive impairment classification. Front. Neurosci. 2021, 15, 669345. [Google Scholar]
- Ji, J.; Ren, Y.; Lei, M. FC–HAT: Hypergraph attention network for functional brain network classification. Inf. Sci. 2022, 608, 1301–1316. [Google Scholar]
- Wu, K.; Song, X.; Chai, L. Graph metrics based brain hypergraph learning in schizophrenia patients. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 3251–3256. [Google Scholar]
- Xi, Z.; Liu, T.; Shi, H.; Jiao, Z. Hypergraph representation of multimodal brain networks for patients with end-stage renal disease associated with mild cognitive impairment. Math. Biosci. Eng. 2023, 20, 1882–1902. [Google Scholar]
- Wang, J.; Li, H.; Qu, G.; Cecil, K.M.; Dillman, J.R.; Parikh, N.A.; He, L. Dynamic weighted hypergraph convolutional network for brain functional connectome analysist. Med. Image Anal. 2023, 87, 102828. [Google Scholar] [CrossRef] [PubMed]
- Niua, J.; Dua, Y. Applications of hypergraph-based methods in classifying and subtyping psychiatric disorders: A survey. Radiol. Sci. 2023, 2, 83–95. [Google Scholar] [CrossRef]
- Yang, J.; Hu, M.; Hu, Y.; Zhang, Z.; Zhong, J. Diagnosis of autism spectrum disorder (ASD) using recursive feature elimination-graph neural network (RFE-GNN) and phenotypic feature extractor (PFE). Sensors 2023, 23, 9647. [Google Scholar] [CrossRef] [PubMed]
- Hao, X.; Li, J.; Ma, M.; Qin, J.; Zhang, D.; Liu, F.; for Alzheimer’s Disease Neuroimaging Initiative. Hypergraph convolutional network for longitudinal data analysis in Alzheimer’s disease. Comput. Biol. Med. 2024, 168, 107765. [Google Scholar] [CrossRef]
- Gao, X.; Zhu, Y.; Yang, Y.; Zhang, F.; Zhou, F.; Tian, X.; Xu, K.; Chen, Y. A seizure detection method based on hypergraph features and machine learning. Biomed. Signal Process. Control 2022, 77, 103769. [Google Scholar] [CrossRef]
- Li, M.; Qiu, M.; Zhu, L.; Kong, W. Feature hypergraph representation learning on spatial-temporal correlations for EEG emotion recognition. Cogn. Neurodyn. 2023, 17, 1271–1281. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, Y.; Liu, R.; Peng, Y.; Cao, J.; Li, J.; Kong, W. Decoding multi-brain motor imagery from EEG using coupling feature extraction and few-shot learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 4683–4692. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, J.; Yap, P.T.; Shen, D. View-aligned hypergraph learning for Alzheimer’s disease diagnosis with incomplete multi-modality data. Med. Image Anal. 2017, 36, 123–134. [Google Scholar]
- Peña Serrano, N.; Jaimes-Reátegui, R.; Pisarchik, A.N. Hypergraph of functional connectivity based on event-related coherence: Magnetoencephalography data analysis. Appl. Sci. 2024, 14, 2343. [Google Scholar] [CrossRef]
- Bretto, A. Hypergraph Theory: An Introduction; Mathematical Engineering Series; Springer: Cham, Switzerland, 2013.
- Dai, Q.; Gao, Y. Hypergraph Computation; Springer: Singapore, 2023. [Google Scholar]
- Wang, Z.; Liu, J.; Zhong, N.; Qin, Y.; Zhou, H.; Yang, J.; Li, K. A naïve hypergraph model of brain networks. In Brain Informatics. BI 2012. Lecture Notes in Computer Science; Zanzotto, F.M., Tsumoto, S., Taatgen, N., Yao, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7670, pp. 119–129. [Google Scholar]
- Caetano e Souza, R.H.; Martins Naves, E.L. Attention detection in virtual environments using EEG signals: A Scoping review. Front. Physiol. 2021, 12, 727840. [Google Scholar]
- Esqueda-Elizondo, J.J.; Juárez-Ramírez, R.; López-Bonilla, O.R.; García-Guerrero, E.E.; Galindo-Aldana, G.M.; Jiménez-Beristáin, L.; Serrano-Trujillo, A.; Tlelo-Cuautle, E.; Inzunza-González, E. Attention measurement of an autism spectrum disorder user using EEG signals: A case study. Math. Comput. Appl. 2022, 27, 21. [Google Scholar] [CrossRef]
- Mateos, D.M.; Krumm, G.; Arán Filippetti, V.; Gutierrez, M. Power spectrum and connectivity analysis in EEG recording during attention and creativity performance in children. NeuroSci 2022, 3, 347–365. [Google Scholar] [CrossRef]
- Al-Nafjan, A.; Aldayel, M. Predict students’ attention in online learning using EEG data. Sustainability 2022, 14, 6553. [Google Scholar] [CrossRef]
- Escalante Puente de la Vega, W.; Imbert Paredes, R.; Villalba Mora, E.; Pisarchik, A.N. Figurative attention: EEG-based assessment using ambiguous stimuli. Prepr. (Res. Sq.). [CrossRef]
- Bowyer, S.M. Coherence a measure of the brain networks: Past and present. Neuropsychiatr. Electrophysiol. 2016, 2, 1. [Google Scholar]
- Chiarion, G.; Sparacino, L.; Antonacci, Y.; Faes, L.; Mesin, L. Connectivity analysis in EEG data: A tutorial review of the state of the art and emerging trends. Bioengineering 2023, 10, 372. [Google Scholar] [CrossRef]
- Jeong, J.; Gore, J.C.; Peterson, B.S. Mutual information analysis of the EEG in patients with Alzheimer’s disease. Clin. Neurophysiol. 2001, 112, 827–835. [Google Scholar] [CrossRef]
- Zien, J.Y.; Schlag, M.D.F.; Chan, P.K. Multilevel spectral hypergraph partitioning with arbitrary vertex sizes. IEEE Trans. Comput.-Aided Des. Integr. 1999, 18, 1389–1399. [Google Scholar]
- Chholak, P.; Maksimenko, V.A.; Hramov, A.E.; Pisarchik, A.N. Voluntary and involuntary attention in bistable visual perception: A MEG study. Front. Hum. Neurosci. 2020, 14, 597895. [Google Scholar] [CrossRef]
- Liu, Y.; Safavi, T.; Dighe, A.; Koutra, D. Graph summarization methods and applications: A survey. ACM Comput. Surv. 2018, 51, 62. [Google Scholar]
- Maccioni, A.; Abadi, D.J. Scalable pattern matching over compressed graphs via dedensification. In Proceedings of the ACM Conference on Knowledge Discovery and Data Mining (KDD’16), San Francisco, CA, USA, 13–17 August 2016; ACM Press: Cambridge, MA, USA, 2016; pp. 1755–1764. [Google Scholar]
- Andrew, C.; Pfurtscheller, G. Event-related coherence as a tool for studying dynamic interaction of brain regions. Electroencephalogr. Clin. Neurophysiol. 1996, 98, 144–148. [Google Scholar] [PubMed]
- Pisarchik, A.; Hramov, A. Coherence resonance in neural networks: Theory and experiments. Phys. Rep. 2023, 1000, 1–57. [Google Scholar]
- Gross, J.; Schmitz, F.; Schnitzler, I.; Kessler, K.; Shapiro, K.; Hommel, B.; Schnitzler, A. Modulation of long-range neural synchrony reflects temporal limitations of visual attention in humans. Proc. Natl. Acad. Sci. USA 2004, 101, 13050–13055. [Google Scholar] [PubMed]
- Guggisberg, A.G.; Honma, S.M.; Findlay, A.M.; Dalal, S.S.; Kirsch, H.E.; Berger, M.S.; Nagarajan, S.S. Mapping functional connectivity in patients with brain lesions. Ann. Neurol. 2008, 63, 193–203. [Google Scholar]
- Belardinelli, P.; Ciancetta, L.; Staudt, M.; Pizzella, V.; Londei, A.; Birbaumer, N.; Romani, G.L.; Braun, C. Cerebro-muscular and cerebro-cerebral coherence in patients with pre- and perinatally acquired unilateral brain lesions. NeuroImage 2007, 37, 1301–1314. [Google Scholar]
- de Pasquale, F.; Della Penna, S.; Snyder, A.Z.; Lewis, C.; Mantini, D.; Marzetti, L.; Belardinelli, P.; Ciancetta, L.; Pizzella, V.; Romani, G.L.; et al. Temporal dynamics of spontaneous MEG activity in brain networks. Proc. Natl. Acad. Sci. USA 2010, 107, 6040–6045. [Google Scholar] [CrossRef]
- Kim, J.S.; Shin, K.S.; Jung, W.H.; Kim, S.N.; Kwon, J.S.; Chung, C.K. Power spectral aspects of the default mode network in schizophrenia: An MEG study. BMC Neurosci. 2014, 15, 104. [Google Scholar]
- Bowyer, S.M.; Gjini, K.; Zhu, X.; Kim, L.; Moran, J.E.; Rizvi, S.U.; Gumenyuk, N.T.; Tepley, N.; Boutros, N.N. Potential biomarkers of schizophrenia from MEG resting-state functional connectivity networks: Preliminary data. J. Behav. Brain Sci. 2015, 5, 1. [Google Scholar]
- Boutros, N.N.; Galloway, M.P.; Ghosh, S.; Gjini, K.; Bowyer, S.M. Abnormal coherence imaging in panic disorder: A magnetoencephalography investigation. Neuroreport 2013, 24, 487–491. [Google Scholar]
- Chholak, P.; Niso, G.; Maksimenko, V.A.; Kurkin, S.A.; Frolov, N.S.; Pitsik, E.N.; Hramov, A.E.; Pisarchik, A.N. Visual and kinesthetic modes affect motor imagery classification in untrained subjects. Sci. Rep. 2019, 9, 9838. [Google Scholar]
- Pisarchik, A.N.; Chholak, P.; Hramov, A.E. Brain noise estimation from MEG response to flickering visual stimulation. Chaos Solitons Fractals X 2019, 1, 100005. [Google Scholar] [CrossRef]
- Baldassarre, A.; Lewis, C.M.; Committeri, G.; Snyder, A.Z.; Luca Romani, G.; Corbetta, M. Individual variability in functional connectivity predicts performance of a perceptual task. Proc. Natl. Acad. Sci. USA 2012, 109, 3516–3521. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, R.; Kong, R.; Bhattacharjee, S.; Li, J.; Zhou, J.; Thomas Yeo, B.T. Individual-specific fMRI-Subspaces improve functional connectivity prediction of behavior. NeuroImage 2019, 189, 804–812. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Tadel, F.; Baillet, S.; Mosher, J.C.; Pantazis, D.; Leahy, R.M. Brainstorm: A user-friendly application for MEG/EEG analysis. Comput. Intell. Neurosci. 2011, 2011, 879716. [Google Scholar] [CrossRef]
- GitLab.com. Available online: https://gitlab.com/bci_project/visual_stimulation_codes/datas_eeg (accessed on 10 January 2025).
- Hennighausen, E.; Heil, M.; Rösler, F. A correction method for DC drift artifacts. Electroencephalogr. Clin. Neurophysiol. 1993, 86, 199–204. [Google Scholar] [CrossRef]
- Kim, H.; Luo, J.; Chu, S.; Cannard, C.; Hoffmann, S.; Miyakoshi, M. ICA’s bug: How ghost ICs emerge from effective rank deficiency caused by EEG electrode interpolation and incorrect re-referencing. Front. Signal Process. 2023, 3, 1064138. [Google Scholar] [CrossRef]
- Isoglu-Alkaç, U.; Basar-Eroglu, C.; Ademoglu, A.; Demiralp, T.; Miener, M.; Stadler, M. Alpha activity decreases during the perception of necker cube reversals: An application of wavelet transform. Biol. Cybern. 2000, 82, 313–320. [Google Scholar] [CrossRef]
- Adeli, H.; Zhou, Z.; Dadmehr, N. Analysis of EEG records in an epileptic patient using wavelet transform. J. Neurosci. Methods 2003, 123, 69–87. [Google Scholar] [CrossRef]
- Ghuman, A.S.; McDaniel, J.R.; Martin, A. A wavelet-based method for measuring the oscillatory dynamics of resting-state functional connectivity in MEG. Neuroimage 2011, 56, 69–77. [Google Scholar] [CrossRef]
- Maksimenko, V.A.; Hramov, A.E.; Grubov, V.V.; Nedaivozov, V.O.; Makarov, V.V.; Pisarchik, A.N. Nonlinear effect of biological feedback on brain attentional state. Nonlin. Dyn. 2019, 95, 1923–1939. [Google Scholar] [CrossRef]
- Maksimenko, V.A.; Frolov, N.S.; Hramov, A.E.; Runnova, A.E.; Grubov, V.V.; Kurths, J.; Pisarchik, A.N. Neural interactions in a spatially-distributed cortical network during attentional tasks. Front. Behav. Neurosci. 2019, 13, 220. [Google Scholar] [CrossRef] [PubMed]
- Khramova, M.V.; Kuc, A.K.; Maksimenko, V.A.; Frolov, N.S.; Grubov, V.V.; Kurkin, S.A.; Pisarchik, A.N.; Shusharina, N.N.; Fedorov, A.A.; Hramov, A.E. Monitoring the cortical activity of children and adults during cognitive task completion. Sensors 2021, 21, 6021. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Sang, J.; Xu, C.; Rui, Y. Topic-sensitive influencer mining in interest-based social media networks via hypergraph learning. IEEE Trans. Multimed. 2014, 16, 796–812. [Google Scholar]
- Martinet, L.E.; Kramer, M.; Viles, W.; Perkins, L.; Spencer, E.; Chu, C.J.; Cash, S.S.; Kolaczyk, E.D. Robust dynamic community detection with applications to human brain functional networks. Nat. Commun. 2020, 11, 2785. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, K.; Guo, J. Link prediction with hypergraphs via network embedding. Appl. Sci. 2023, 13, 523. [Google Scholar] [CrossRef]
- Berge, C. Graphs and Hypergraphs; North-Holland: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Bi, X.A.; Wang, Y.; Luo, S.; Chen, K.; Xing, Z.; Xu, L. Hypergraph structural information aggregation generative adversarial networks for diagnosis and pathogenetic factors identification of Alzheimer’s disease with imaging genetic data. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 7420–7434. [Google Scholar]
- Harmony, T.; Fernández, T.; Silva, J.; Bernal, J.; Díaz-Comas, L.; Reyes, A.; Marosi, E.; Rodríguez, M.; Rodríguez, M. EEG delta activity an indicator of attention to internal processing during performance of mental tasks. Int. J. Psychophysiol. 1996, 24, 161–171. [Google Scholar]
- Li, X.; Hu, B.; Zhu, T.; Yan, J.; Zheng, F. Towards affective learning with an EEG feedback approach. In Proceedings of the First ACM International Workshop on Multimedia Technologies for Distance Learning, Beijing, China, 23 October 2009; pp. 33–38. [Google Scholar]
- Zhou, S.; Gao, T. Brain activity recognition method based on attention-based RNN mode. Appl. Sci. 2011, 11, 425. [Google Scholar]
- Fahimi, F.; Goh, W.B.; Lee, T.S.; Guan, C. Neural indexes of attention extracted from EEG correlate with elderly reaction time in response to an attentional task. In Proceedings of the 3rd International Conference on Crowd Science and Engineering, Singapore, 28–31 July 2018; pp. 1–6. [Google Scholar]
- Wan, W.; Cui, X.; Gao, Z.; Gu, Z. Frontal EEG-based multi-level attention states recognition using dynamical complexity and extreme gradient boosting. Int. J. Psychophysiol. 2021, 15, 673955. [Google Scholar]
- Myrden, A.; Chau, T. A passive EEG-BCI for single-trial detection of changes in mental state. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 345–356. [Google Scholar]
- Alirezaei, M.; Hajipour Sardouie, S. Detection of human attention using EEG signals. In Proceedings of the 24th Iranian Conference on Biomedical Engineering and 2nd International Iranian Conference on Biomedical Engineering, Tehran, Iran, 30 November–1 December 2017; pp. 1–5. [Google Scholar]
- Nuamah, J.K.; Seong, Y. Support vector machine (SVM) classification of cognitive tasks based on electroencephalography (EEG) engagement index. Brain-Comput. Interfaces 2018, 5, 1–12. [Google Scholar]
- Aci, c.I.; Kaya, M.; Mishchenko, Y. Distinguishing mental attention states of humans via an EEG-based passive BCI using machine learning methods. Expert Syst. Appl. 2019, 134, 153–166. [Google Scholar] [CrossRef]

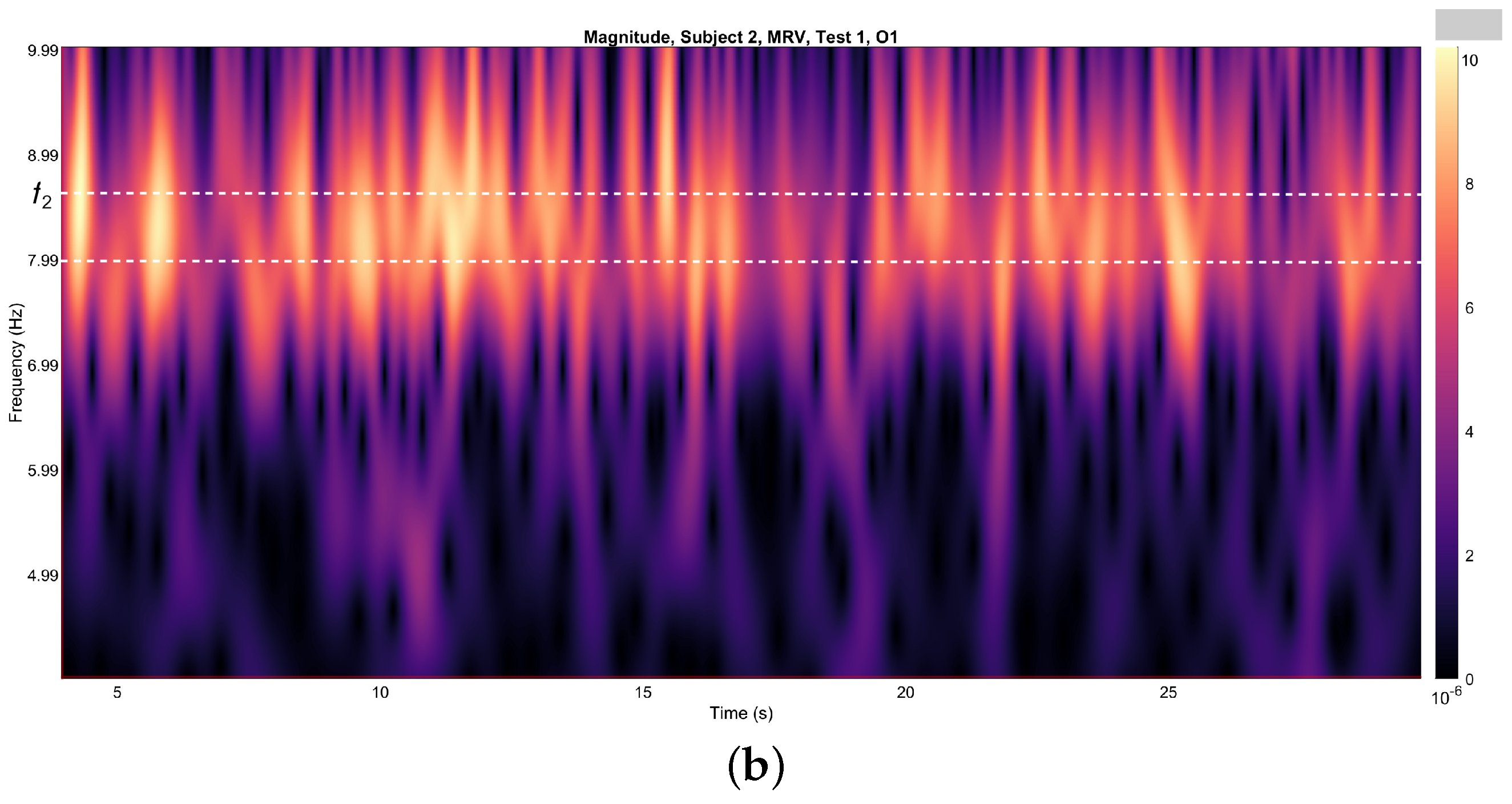



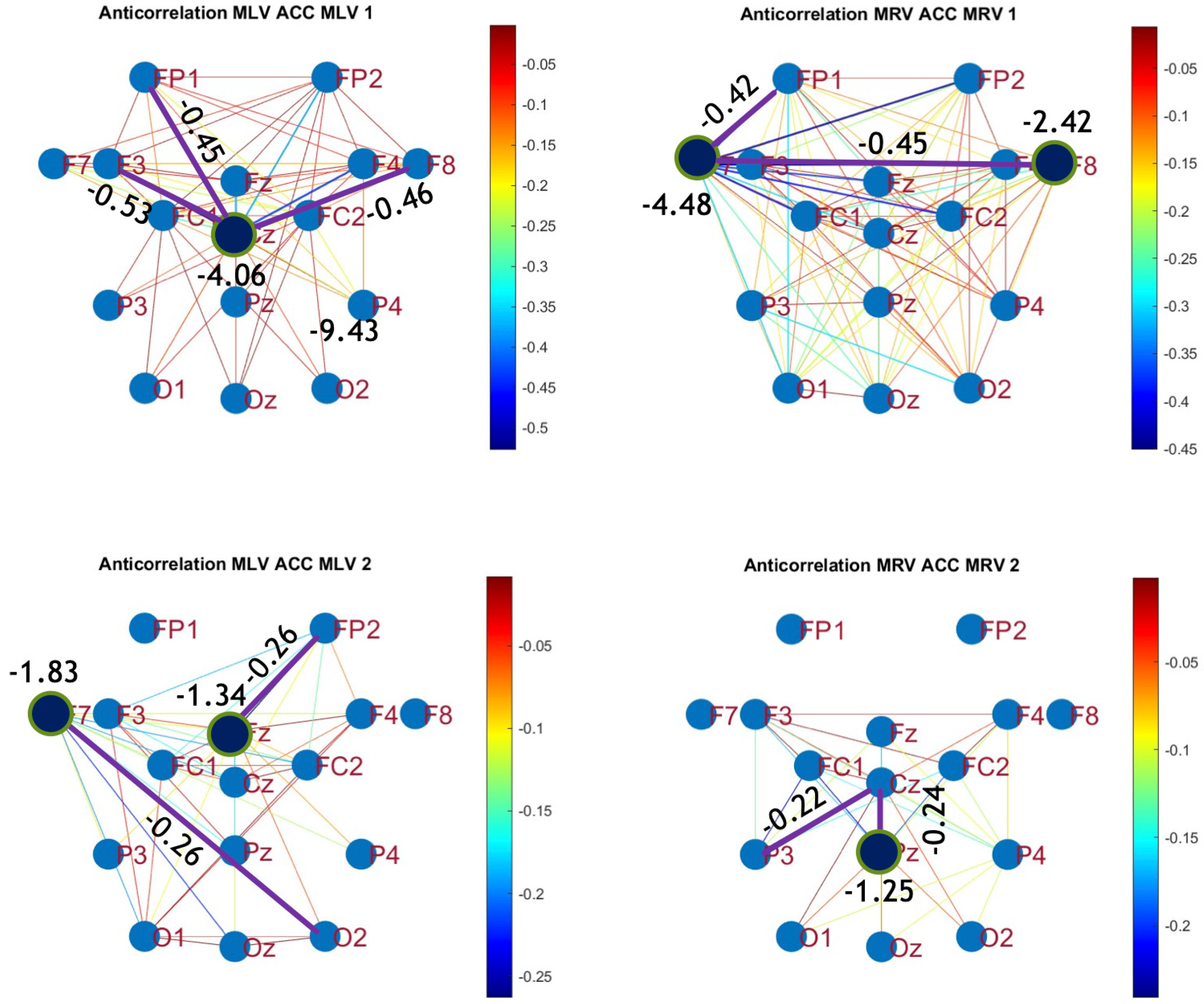
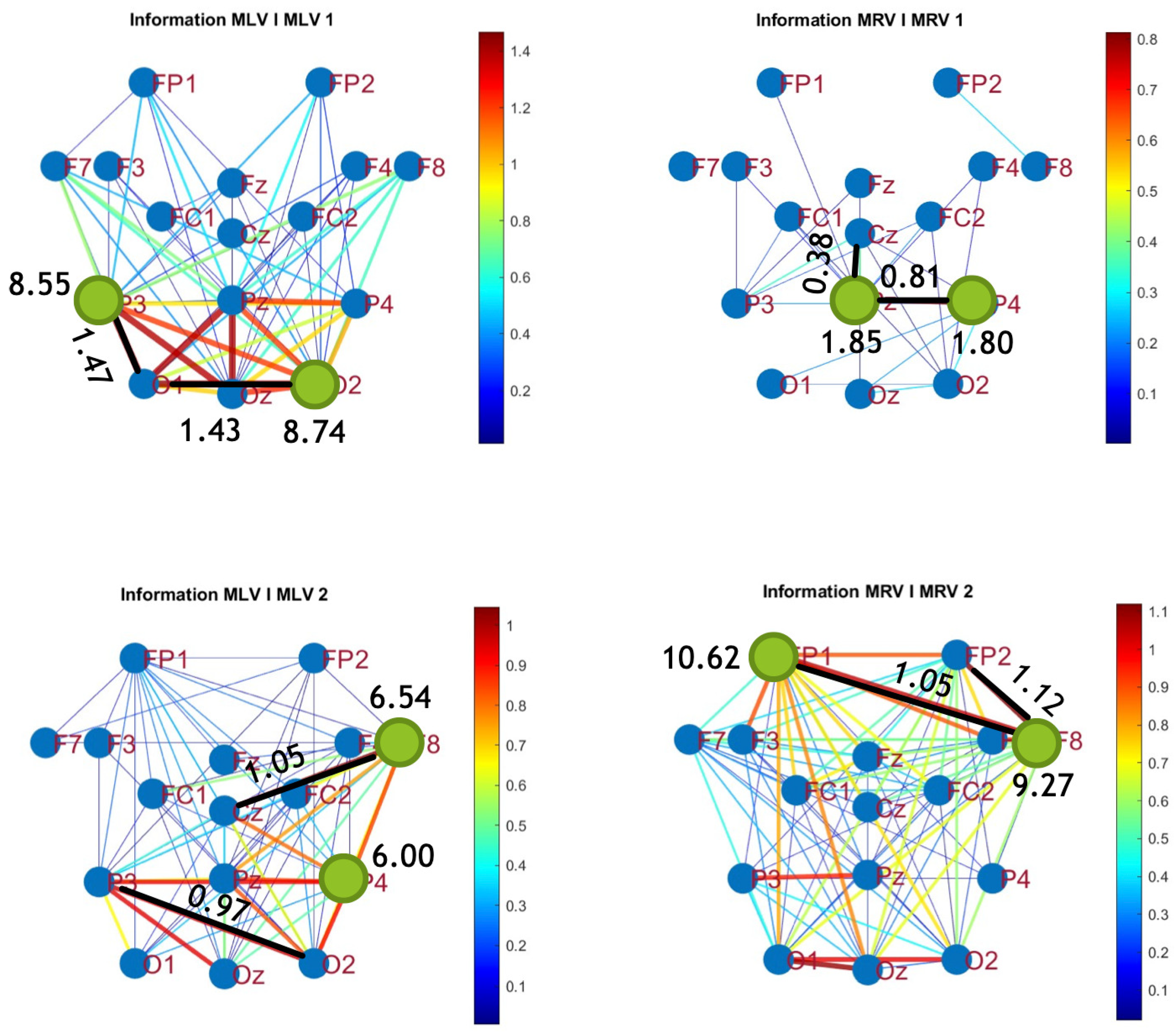
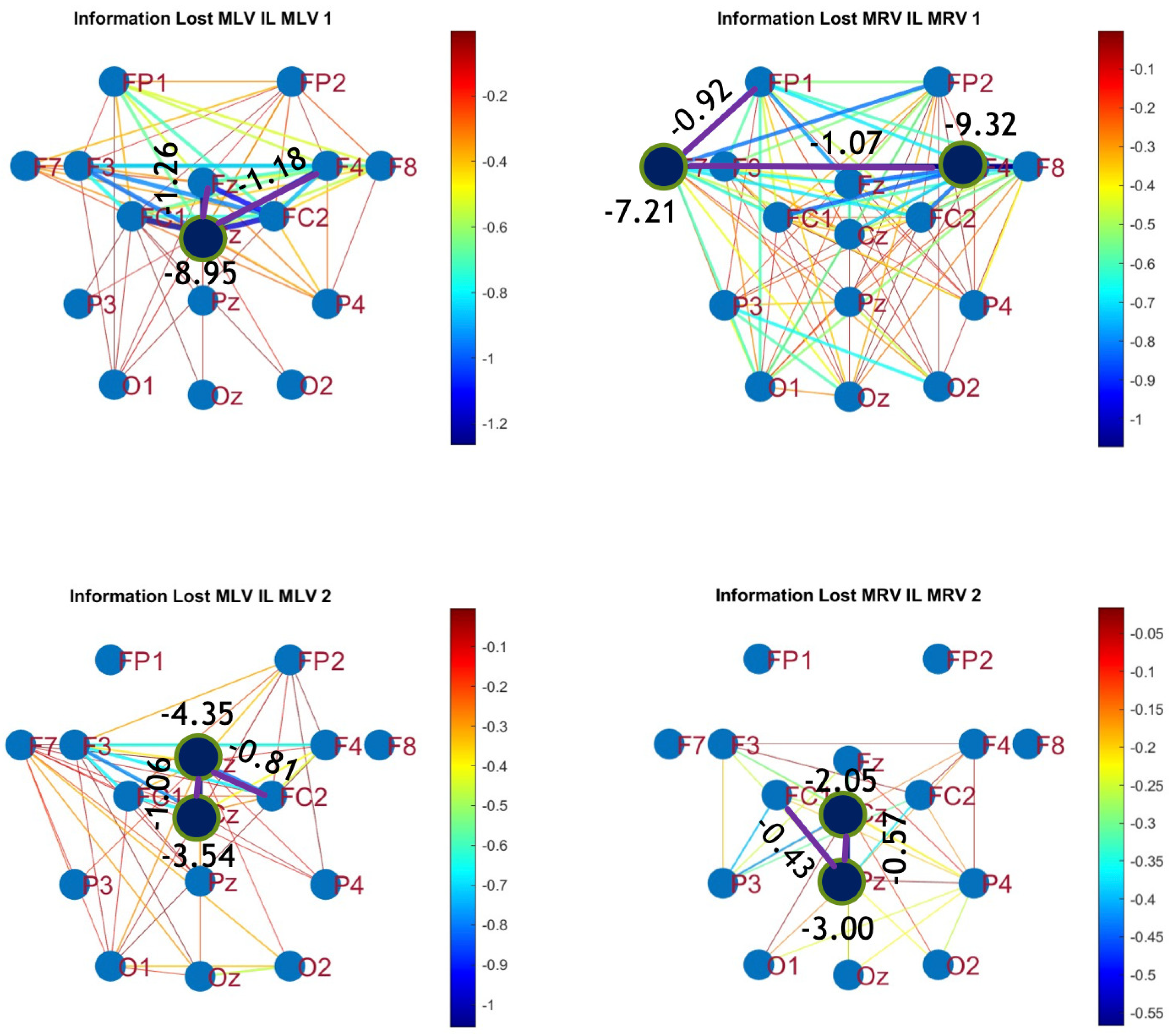





| Measure | Value | Lobes | Value | Lobes |
|---|---|---|---|---|
| Max | 0.55 | F7–Pz | 0.53 | F7–P3 |
| Max | 0.64 | F8–P4 | 0.61 | F8–Pz |
| Max | 0.43 | Cz–P3 | 0.39 | Cz–Pz |
| Max | 0.66 | Oz–FP1 | 0.65 | O1–FP1 |
| Min | Cz–FP1 | Cz–F3 | ||
| Min | Fz–FP2 | F3–FP2 | ||
| Min | F7–F8 | F7–F4 | ||
| Min | Pz–Cz | P3–Cz |
| Measure | Value | Lobes | Value | Lobes |
|---|---|---|---|---|
| Max | 0.40 | F7–Pz | 0.37 | F7–P3 |
| Max | 0.49 | F8–Pz | 0.46 | F8–P4 |
| Max | 0.28 | P3–Cz | 0.28 | Pz–Cz |
| Max | 0.51 | Oz–FP1 | 0.51 | O2–FP1 |
| Min | Cz–F3 | Cz–FP1 | ||
| Min | Fz–FP2 | O2–F7 | ||
| Min | F7–F8 | F7–FP1 | ||
| Min | Pz–Cz | P3–Cz |
| Measure | Value | Lobes | Value | Lobes |
|---|---|---|---|---|
| Max | 1.41 | O1–P3 | 1.43 | O1– O2 |
| Max | 1.05 | Cz–F3 | 0.97 | O2–P3 |
| Max | 0.81 | P4–Pz | 0.38 | Pz–Cz |
| Max | 1.12 | F8–FP2 | 1.05 | F8–FP1 |
| Min | Cz–Fz | Cz–F4 | ||
| Min | Cz–Fz | Cz–FC2 | ||
| Min | F7–F4 | F7–FP1 | ||
| Min | Pz–Cz | Pz–FC1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| FP1 | FP2 | F7 | Fz | F8 | F3 | FC1 | Cz | FC2 | F4 | P3 | Pz | P4 | O1 | Oz | O2 |
| Measure | Hyperedge | (Left ) | (Left ) | (Right ) | (Right ) |
|---|---|---|---|---|---|
| Coherence | 3 | 1 | 3 | 4 | |
| Anticoherence | 1 | 3 | 2 | 4 | |
| Correlation | 2 | 2 | 3 | 4 | |
| Anticorrelation | 1 | 2 | 1 | 3 | |
| Mut. Inform. | 4 | 3 | 1 | 3 | |
| Inform. Loss | 2 | 3 | 2 | 2 | |
| Order | 6 | 9 | 7 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pisarchik, A.N.; Peña Serrano, N.; Escalante Puente de la Vega, W.; Jaimes-Reátegui, R. Hypergraph Analysis of Functional Brain Connectivity During Figurative Attention. Appl. Sci. 2025, 15, 3833. https://doi.org/10.3390/app15073833
Pisarchik AN, Peña Serrano N, Escalante Puente de la Vega W, Jaimes-Reátegui R. Hypergraph Analysis of Functional Brain Connectivity During Figurative Attention. Applied Sciences. 2025; 15(7):3833. https://doi.org/10.3390/app15073833
Chicago/Turabian StylePisarchik, Alexander N., Natalia Peña Serrano, Walter Escalante Puente de la Vega, and Rider Jaimes-Reátegui. 2025. "Hypergraph Analysis of Functional Brain Connectivity During Figurative Attention" Applied Sciences 15, no. 7: 3833. https://doi.org/10.3390/app15073833
APA StylePisarchik, A. N., Peña Serrano, N., Escalante Puente de la Vega, W., & Jaimes-Reátegui, R. (2025). Hypergraph Analysis of Functional Brain Connectivity During Figurative Attention. Applied Sciences, 15(7), 3833. https://doi.org/10.3390/app15073833








