Dimensional Accuracy Analysis of Splined Shafts and Hubs Obtained by Fused-Deposition Modeling 3D Printing Using a Genetic Algorithm and Artificial Neural Network
Abstract
1. Introduction
Objectives of the Study
- To analyze the influence of printing parameters on the dimensional accuracy of splined shafts and hubs manufactured using FDM.
- To identify the dominant factors contributing to significant dimensional deviations.
- To evaluate measurement methods for dimensional deviations and validate them through statistical analysis techniques.
2. Literature Review
3. Materials and Methods
3.1. Materials Used
3.2. Printing Parameters
- Layer thickness: 0.09 mm, 0.14 mm, and 0.19 mm.
- Infill density: 20%, 50%, and 80%.
- Nozzle temperature: 210 °C.
- Printing speed: 50 mm/s.
- Build plate temperature: 60 °C.
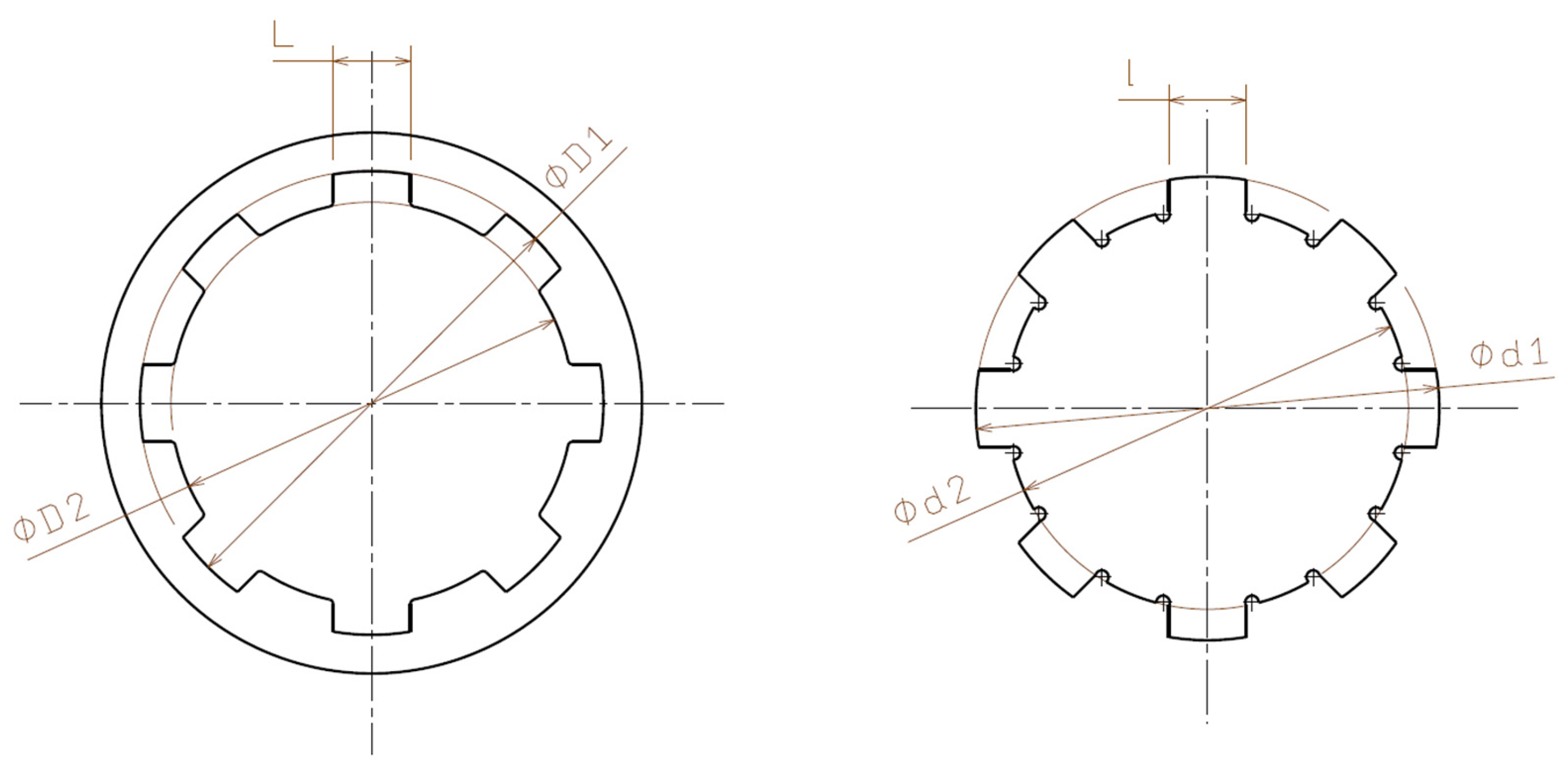
3.3. Part Geometry
3.4. Measurement Procedure
- Model: Tesa Micro-Hite 3D.
- Accuracy: ±0.001 mm.
- Measuring range: 400 × 500 × 450 mm.
- Probing method: Tactile system with an interchangeable probe head.
- Software used: TESA Reflex v.2022, Renens, Switzerland and TESA Power-Inspect v.2022, Renens, Switzerland for dimensional analysis.
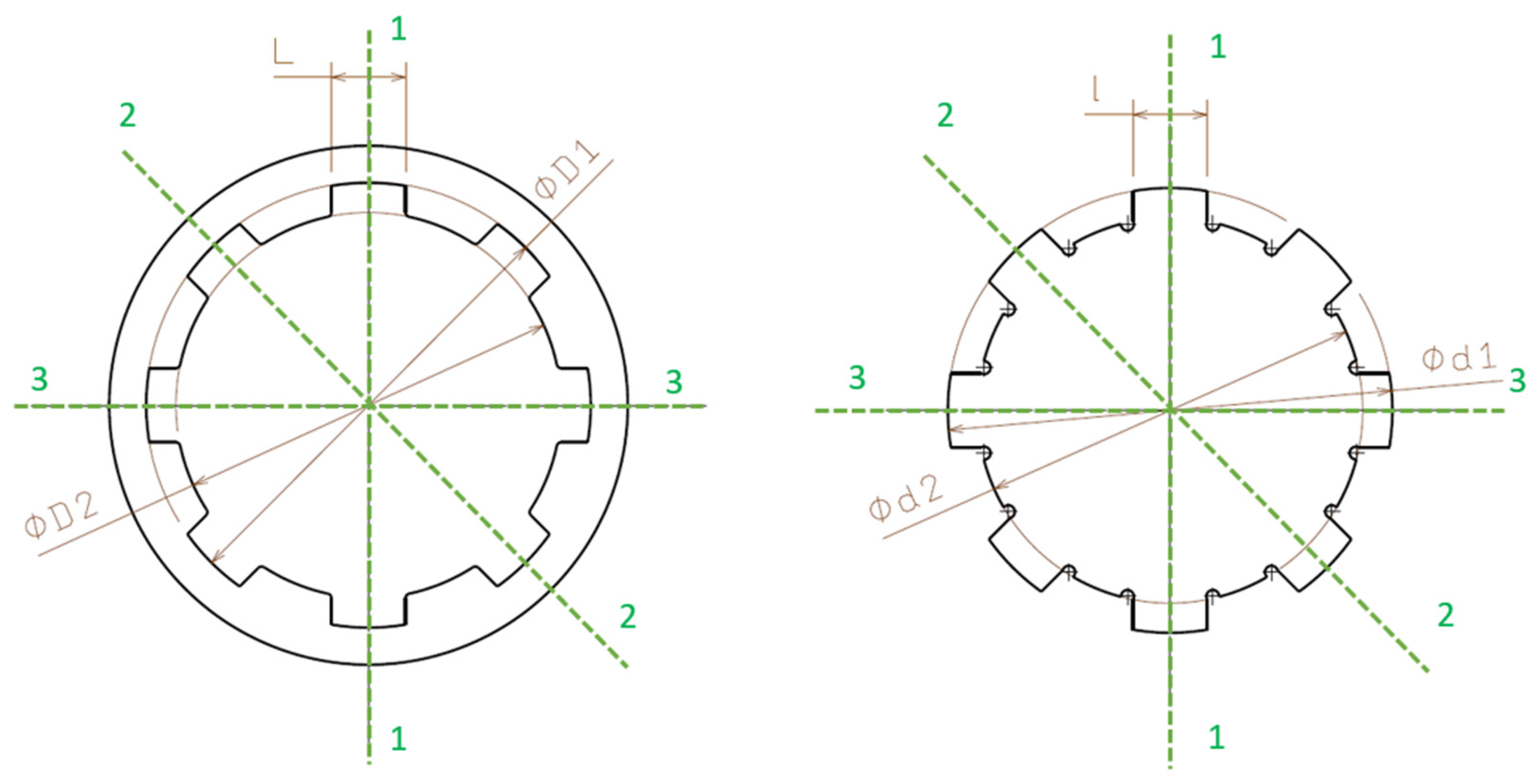
- 0°—Axis 1-1: The primary longitudinal direction, corresponding to the alignment of the part on the printing platform.
- 45°—Axis 2-2: A diagonal direction, used to identify irregular shrinkage variations.
- 90°—Axis 3-3: A direction perpendicular to the primary longitudinal axis.
4. Dimensional Deviations Study
4.1. Experimental Plan
- Layer thickness (A): 0.09 mm, 0.14 mm, and 0.19 mm;
- Infill density (B): 20%, 50%, and 80%;
- Nominal diameter, Ød1n, ØD1n (C): 48 mm, 54 mm, and 60 mm.
4.2. Measurements
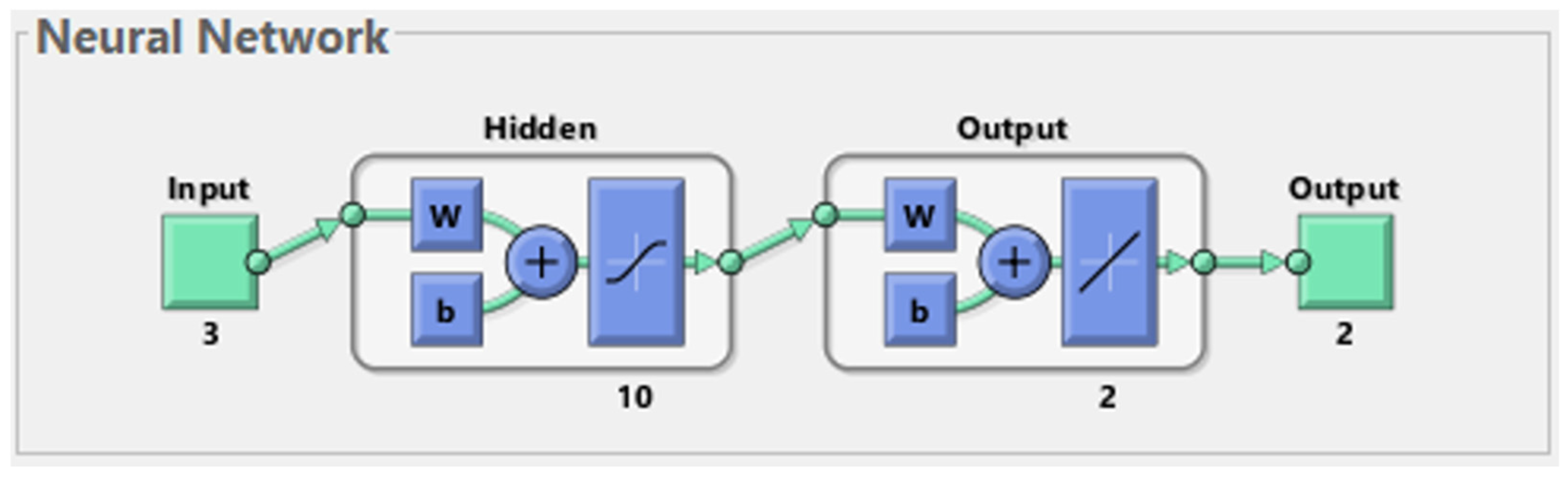
4.3. Data Processing
- Input matrix: (27 × 3).
- Output matrix: (27 × 2).
- Absolute relative deviation for the shaft (ard Ød1), defined as a ratio in Equation (1).
- Absolute relative deviation for the hole (ard ØD1), defined similarly.
4.4. Identified Patterns and Trends in Dimensional Deviations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies. In 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Stojković, J.R.; Turudija, R.; Vitković, N.; Górski, F.; Păcurar, A.; Pleşa, A.; Ianoşi-Andreeva-Dimitrova, A.; Păcurar, R. An Experimental Study on the Impact of Layer Height and Annealing Parameters on the Tensile Strength and Dimensional Accuracy of FDM 3D Printed Parts. Materials 2023, 16, 4574. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Modeling, analysis, and optimization of dimensional accuracy of FDM-fabricated parts using definitive screening design and deep learning feedforward artificial neural network. Adv. Manuf. 2021, 9, 115–129. [Google Scholar] [CrossRef]
- Karad, A.S.; Sonawwanay, P.D.; Naik, M.; Thakur, D.G. Experimental study of effect of infill density on tensile and flexural strength of 3D printed parts. J. Eng. Appl. Sci. 2023, 70, 104. [Google Scholar]
- Vora, H.D.; Sanyal, S. A comprehensive review: Metrology in additive manufacturing and 3D printing technology. Prog. Addit. Manuf. 2020, 5, 319–353. [Google Scholar] [CrossRef]
- Boschetto, A.; Bottini, L. Accuracy prediction in fused deposition modeling. Int. J. Adv. Manuf. Technol. 2014, 73, 913–928. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Mathematical modeling and FDM process parameters optimization using response surface methodology based on Q-optimal design. Appl. Math. Model. 2016, 40, 10052–10073. [Google Scholar]
- Eryıldız, M. Effect of build orientation on mechanical behaviour and build time of FDM 3D-printed PLA parts: An experimental investigation. Eur. Mech. Sci. 2021, 5, 116–120. [Google Scholar]
- Pant, M.; Singari, R.M.; Arora, P.K.; Moona, G.; Kumar, H. Wear assessment of 3–D printed parts of PLA (polylactic acid) using Taguchi design and Artificial Neural Network (ANN) technique. Mater. Res. Express 2020, 7, 115307. [Google Scholar] [CrossRef]
- Darbar, R.; Patel, P.M. Optimization of fused deposition modeling process parameter for better mechanical strength and surface roughness. Int. J. Mech. Eng. 2017, 6, 7–18. [Google Scholar]
- Camposeco-Negrete, C. Optimization of FDM parameters for improving part quality, productivity and sustainability of the process using Taguchi methodology and desirability approach. Prog. Addit. Manuf. 2020, 5, 59–65. [Google Scholar] [CrossRef]
- Anghel, D.C.; Iordache, D.M.; Rizea, A.D.; Stanescu, N.D. A New Approach to Optimize the Relative Clearance for Cylindrical Joints Manufactured by FDM 3D Printing Using a Hybrid Genetic Algorithm Artificial Neural Network and Rational Function. Processes 2021, 9, 925. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Parametric appraisal of fused deposition modelling process using the grey Taguchi method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 135–145. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Parametric appraisal of mechanical property of fused deposition modelling processed parts. Mater. Des. 2010, 31, 287–295. [Google Scholar] [CrossRef]
- Sood, A.K.; Chaturvedi, V.; Datta, S.; Mahapatra, S.S. Optimization of process parameters in fused deposition modeling using weighted principal component analysis. J. Adv. Manuf. Syst. 2011, 10, 241–259. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Experimental investigation and empirical modelling of FDM process for compressive strength improvement. J. Adv. Res. 2012, 3, 81–90. [Google Scholar] [CrossRef]
- Sood, A.K.; Equbal, A.; Toppo, V.; Ohdar, R.K.; Mahapatra, S.S. An investigation on sliding wear of FDM built parts. CIRP J. Manuf. Sci. Technol. 2012, 5, 48–54. [Google Scholar] [CrossRef]
- Equbal, A.; Sood, A.K.; Toppo, V.; Ohdar, R.K.; Mahapatra, S.S. Prediction and analysis of sliding wear performance of fused deposition modelling-processed ABS plastic parts. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 1261–1271. [Google Scholar] [CrossRef]
- Sahu, R.K.; Mahapatra, S.S.; Sood, A.K. A study on dimensional accuracy of fused deposition modeling (FDM) processed parts using fuzzy logic. J. Manuf. Sci. Prod. 2013, 13, 183–197. [Google Scholar] [CrossRef]
- Padhi, S.K.; Sahu, R.K.; Mahapatra, S.S.; Das, H.C.; Sood, A.K.; Patro, B.; Mondal, A.K. Optimization of fused deposition modeling process parameters using a fuzzy inference system coupled with Taguchi philosophy. Adv. Manuf. 2017, 5, 231–242. [Google Scholar] [CrossRef]
- Mohanty, A.; Nag, K.S.; Bagal, D.K.; Barua, A.; Jeet, S.; Mahapatra, S.S.; Cherkia, H. Parametric optimization of parameters affecting dimension precision of FDM printed part using hybrid Taguchi-MARCOS-nature inspired heuristic optimization technique. Mater. Proc. 2022, 50, 893–903. [Google Scholar] [CrossRef]
- Haghighi, A.; Li, L. Study of the relationship between dimensional performance and manufacturing cost in fused deposition modeling. Rapid Prototyp. J. 2018, 24, 395–408. [Google Scholar] [CrossRef]
- Dey, A.; Yodo, N. A Systematic Survey of FDM Process Parameter Optimization and Their Influence on Part Characteristics. J. Manuf. Mater. Process. 2019, 3, 64. [Google Scholar] [CrossRef]
- Asadollahi-Yazdi, E.; Gardan, J.; Lafon, P. Toward integrated design of additive manufacturing through a process development model and multi-objective optimization. Int. J. Adv. Manuf. Technol. 2018, 96, 4145–4164. [Google Scholar] [CrossRef]
- Mahmood, S.; Qureshi, A.; Talamona, D. Taguchi based process optimization for dimension and tolerance control for fused deposition modelling. Addit. Manuf. 2018, 21, 183–190. [Google Scholar] [CrossRef]
- Wang, Y.; Jun-Tong, X.; Jin, Y. A model research for prototype warp deformation in the FDM process. Int. J. Adv. Manuf. Technol. 2007, 33, 1087–1096. [Google Scholar] [CrossRef]
- Bahnini, I.; Anghel, D.C.; Rizea, A.D.; Zaman, U.K.; Siadat, A. Accuracy Investigation of Fused Deposition Modelling (FDM) Processed ABS and ULTRAT Parts. Int. J. Manuf. Mater. Mech. Eng. 2022, 12, 1–19. [Google Scholar] [CrossRef]
- Petruse, R.E.; Simion, C.; Bondrea, I. Geometrical and Dimensional Deviations of Fused Deposition Modelling (FDM) Additive-Manufactured Parts. Metrology 2024, 4, 411–429. [Google Scholar] [CrossRef]
- Sawant, D.A.; Shinde, B.M.; Raykar, S.J. Post processing techniques used to improve the quality of 3D printed parts using FDM: State of art review and experimental work. Mater. Today Proc. 2023, in press. [CrossRef]
- Gradinaru, S.; Tabaras, D.; Gheorghe, D.; Gheorghita, D.; Zamfir, R.; Vasilescu, M.; Dobrescu, M.; Grigorescu, G.; Cristescu, I. Analysis of the anisotropy for 3D printed pla parts usable in medicine. Univ. Politech. Buchar. Sci. Bull. Ser. B Chem. Mater. Sci. 2019, 81, 313–324. [Google Scholar]
- Simion, I.; Arion, A.F. Dimensioning rules for 3D printed parts using additive technologies (FDM). Univ. Politech. Buchar. Sci. Bull. Ser. D 2016, 78, 79–92. [Google Scholar]
- Maurya, A.K.; Kumar, A. Study the microhardness and surface roughness of as-built and heat-treated additive manufactured IN718 alloy. Univ. Politech. Buchar. Sci. Bull. Ser. D 2022, 84, 211–224. [Google Scholar]



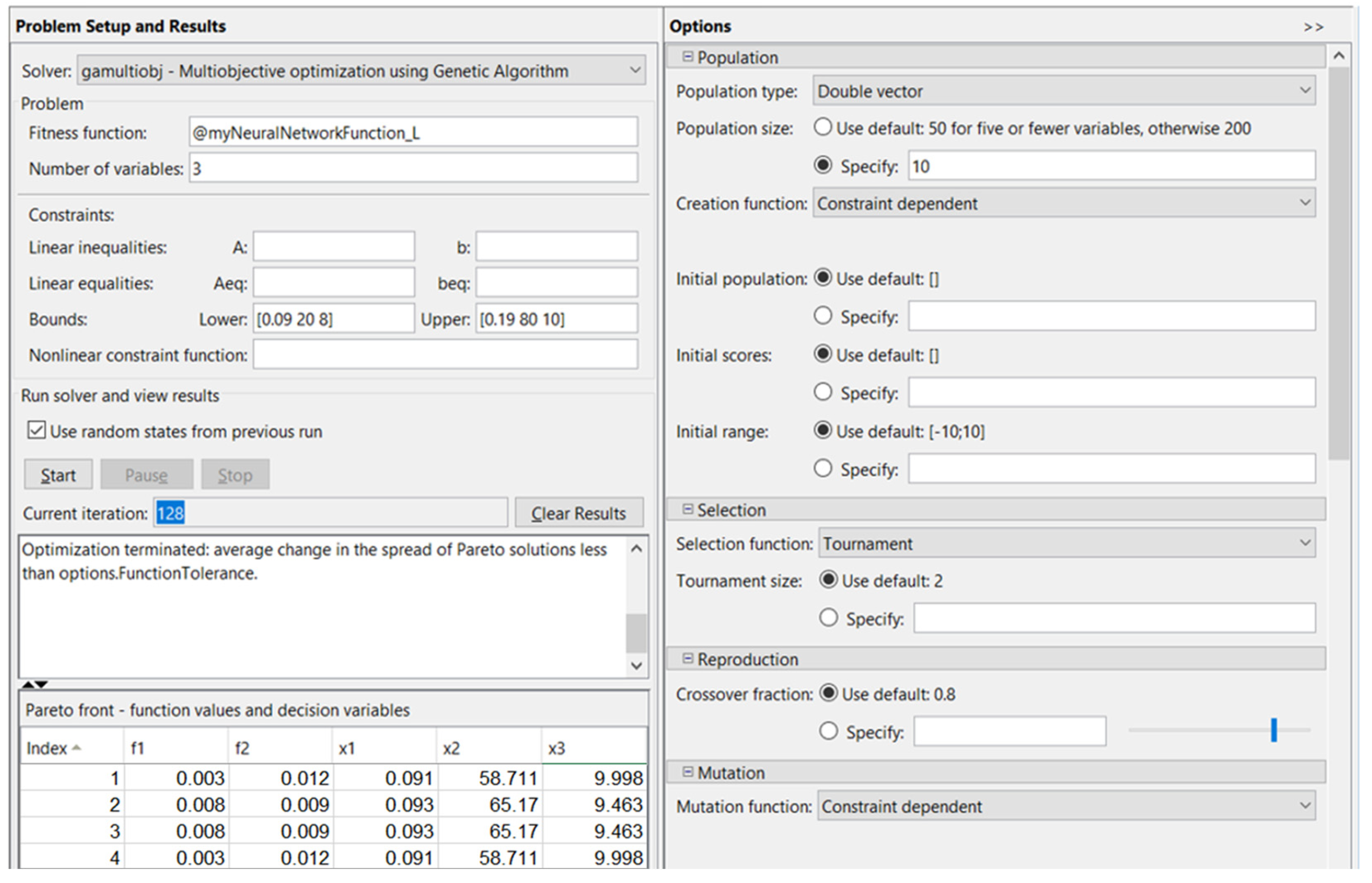

| No. | Layer Thickness | Infill Density | Nominal Diameter Ød1n, ØD1n |
|---|---|---|---|
| 1. | 0.09 | 20 | 48 |
| 2. | 0.09 | 50 | 54 |
| 3. | 0.09 | 80 | 60 |
| 4. | 0.14 | 50 | 48 |
| 5. | 0.14 | 80 | 54 |
| 6. | 0.14 | 20 | 60 |
| 7. | 0.19 | 80 | 48 |
| 8. | 0.19 | 20 | 54 |
| 9. | 0.19 | 50 | 60 |
| No. | Layer Thickness | Infill Density | Ød1n, ØD1n (mm) | Ød1m (mm) | ØD1m (mm) |
|---|---|---|---|---|---|
| 1. | 0.09 | 20 | 48 | 47.772 | 47.669 |
| 2. | 0.09 | 20 | 48 | 47.82 | 47.631 |
| 3. | 0.09 | 20 | 48 | 47.822 | 47.66 |
| 4. | 0.09 | 50 | 54 | 53.775 | 53.688 |
| 5. | 0.09 | 50 | 54 | 53.78 | 53.697 |
| 6. | 0.09 | 50 | 54 | 53.81 | 53.74 |
| 7. | 0.09 | 80 | 60 | 59.812 | 59.68 |
| 8. | 0.09 | 80 | 60 | 59.789 | 59.655 |
| 9. | 0.09 | 80 | 60 | 59.798 | 59.705 |
| 10. | 0.14 | 20 | 48 | 47.816 | 47.63 |
| 11. | 0.14 | 20 | 48 | 47.81 | 47.659 |
| 12. | 0.14 | 20 | 48 | 47.843 | 47.634 |
| 13. | 0.14 | 50 | 54 | 53.783 | 53.663 |
| 14. | 0.14 | 50 | 54 | 53.785 | 53.599 |
| 15. | 0.14 | 50 | 54 | 53.825 | 53,675 |
| 16. | 0.14 | 80 | 60 | 59.722 | 59.593 |
| 17. | 0.14 | 80 | 60 | 59.756 | 59.604 |
| 18. | 0.14 | 80 | 60 | 59.811 | 59.68 |
| 19. | 0.19 | 20 | 48 | 47.89 | 47.602 |
| 20. | 0.19 | 20 | 48 | 47.845 | 47.618 |
| 21. | 0.19 | 20 | 48 | 47.878 | 47.647 |
| 22. | 0.19 | 50 | 54 | 53.767 | 53.564 |
| 23. | 0.19 | 50 | 54 | 53.774 | 53.584 |
| 24. | 0.19 | 50 | 54 | 53.83 | 53.658 |
| 25. | 0.19 | 80 | 60 | 59.78 | 59.554 |
| 26. | 0.19 | 80 | 60 | 59.867 | 59.568 |
| 27. | 0.19 | 80 | 60 | 59.809 | 59.604 |
| No. | Layer Thickness | Infill Density | Ød2n, ØD2n (mm) | Ød2m (mm) | ØD2m (mm) |
|---|---|---|---|---|---|
| 1. | 0.09 | 20 | 42 | 41.838 | 41.687 |
| 2. | 0.09 | 20 | 42 | 41.839 | 41.697 |
| 3. | 0.09 | 20 | 42 | 41.881 | 41.711 |
| 4. | 0.09 | 50 | 46 | 45.842 | 45.751 |
| 5. | 0.09 | 50 | 46 | 45.846 | 45.777 |
| 6. | 0.09 | 50 | 46 | 45.878 | 45.813 |
| 7. | 0.09 | 80 | 52 | 51.884 | 51.742 |
| 8. | 0.09 | 80 | 52 | 51.868 | 51.734 |
| 9. | 0.09 | 80 | 52 | 51.873 | 51.801 |
| 10. | 0.14 | 20 | 42 | 41.88 | 41.699 |
| 11. | 0.14 | 20 | 42 | 41.879 | 41.704 |
| 12. | 0.14 | 20 | 42 | 41.883 | 41.73 |
| 13. | 0.14 | 50 | 46 | 45.847 | 45.706 |
| 14. | 0.14 | 50 | 46 | 45.871 | 45.691 |
| 15. | 0.14 | 50 | 46 | 45.874 | 45.746 |
| 16. | 0.14 | 80 | 52 | 51.789 | 51.68 |
| 17. | 0.14 | 80 | 52 | 51.849 | 51.721 |
| 18. | 0.14 | 80 | 52 | 51.889 | 51.756 |
| 19. | 0.19 | 20 | 42 | 41.826 | 41.676 |
| 20. | 0.19 | 20 | 42 | 41.875 | 41.697 |
| 21. | 0.19 | 20 | 42 | 41.885 | 41.743 |
| 22. | 0.19 | 50 | 46 | 45.85 | 45.667 |
| 23. | 0.19 | 50 | 46 | 45.856 | 45.681 |
| 24. | 0.19 | 50 | 46 | 45.898 | 45.746 |
| 25. | 0.19 | 80 | 52 | 51.839 | 51.576 |
| 26. | 0.19 | 80 | 52 | 51.847 | 51.652 |
| 27. | 0.19 | 80 | 52 | 51.872 | 51.709 |
| No. | Layer Thickness | Infill Density | ln, Ln (mm) | lm (mm) | Lm (mm) |
|---|---|---|---|---|---|
| 1. | 0.09 | 20 | 8 | 8.071 | 7.907 |
| 2. | 0.09 | 20 | 8 | 8.004 | 7.862 |
| 3. | 0.09 | 20 | 8 | 8.063 | 7.843 |
| 4. | 0.09 | 50 | 9 | 9.063 | 8.94 |
| 5. | 0.09 | 50 | 9 | 9.012 | 8.872 |
| 6. | 0.09 | 50 | 9 | 9.073 | 8.921 |
| 7. | 0.09 | 80 | 10 | 10.074 | 9.898 |
| 8. | 0.09 | 80 | 10 | 10.022 | 9.871 |
| 9. | 0.09 | 80 | 10 | 10.082 | 9.91 |
| 10. | 0.14 | 20 | 8 | 8.033 | 7.871 |
| 11. | 0.14 | 20 | 8 | 8.082 | 7.83 |
| 12. | 0.14 | 20 | 8 | 8.081 | 7.852 |
| 13. | 0.14 | 50 | 9 | 9.099 | 8.829 |
| 14. | 0.14 | 50 | 9 | 9.081 | 8.839 |
| 15. | 0.14 | 50 | 9 | 9.067 | 8.869 |
| 16. | 0.14 | 80 | 10 | 10.065 | 9.845 |
| 17. | 0.14 | 80 | 10 | 10.084 | 9.896 |
| 18. | 0.14 | 80 | 10 | 10.096 | 9.896 |
| 19. | 0.19 | 20 | 8 | 8.082 | 7.834 |
| 20. | 0.19 | 20 | 8 | 8.062 | 7.867 |
| 21. | 0.19 | 20 | 8 | 8.081 | 7.9 |
| 22. | 0.19 | 50 | 9 | 9.059 | 8.848 |
| 23. | 0.19 | 50 | 9 | 9.08 | 8.849 |
| 24. | 0.19 | 50 | 9 | 9.078 | 8.794 |
| 25. | 0.19 | 80 | 10 | 10.065 | 9.858 |
| 26. | 0.19 | 80 | 10 | 10.082 | 9.845 |
| 27. | 0.19 | 80 | 10 | 10.076 | 9.858 |
| No. | Layer Thickness | Infill Density | Ød1, ØD1n (mm) | ard Ød1 | ard ØD1 |
|---|---|---|---|---|---|
| 1. | 0.09 | 20 | 48 | 0.0048 | 0.0069 |
| 2. | 0.09 | 20 | 48 | 0.0038 | 0.0077 |
| 3. | 0.09 | 20 | 48 | 0.0037 | 0.0071 |
| 4. | 0.09 | 50 | 54 | 0.0042 | 0.0058 |
| 5. | 0.09 | 50 | 54 | 0.0041 | 0.0056 |
| 6. | 0.09 | 50 | 54 | 0.0035 | 0.0048 |
| 7. | 0.09 | 80 | 60 | 0.0031 | 0.0053 |
| 8. | 0.09 | 80 | 60 | 0.0035 | 0.0058 |
| 9. | 0.09 | 80 | 60 | 0.0034 | 0.0049 |
| 10. | 0.14 | 20 | 48 | 0.0038 | 0.0077 |
| 11. | 0.14 | 20 | 48 | 0.0040 | 0.0071 |
| 12. | 0.14 | 20 | 48 | 0.0033 | 0.0076 |
| 13. | 0.14 | 50 | 54 | 0.0040 | 0.0062 |
| 14. | 0.14 | 50 | 54 | 0.0040 | 0.0074 |
| 15. | 0.14 | 50 | 54 | 0.0032 | 0.0060 |
| 16. | 0.14 | 80 | 60 | 0.0046 | 0.0068 |
| 17. | 0.14 | 80 | 60 | 0.0041 | 0.0066 |
| 18. | 0.14 | 80 | 60 | 0.0032 | 0.0053 |
| 19. | 0.19 | 20 | 48 | 0.0023 | 0.0083 |
| 20. | 0.19 | 20 | 48 | 0.0032 | 0.0080 |
| 21. | 0.19 | 20 | 48 | 0.0025 | 0.0074 |
| 22. | 0.19 | 50 | 54 | 0.0043 | 0.0081 |
| 23. | 0.19 | 50 | 54 | 0.0042 | 0.0077 |
| 24. | 0.19 | 50 | 54 | 0.0031 | 0.0063 |
| 25. | 0.19 | 80 | 60 | 0.0037 | 0.0074 |
| 26. | 0.19 | 80 | 60 | 0.0022 | 0.0072 |
| 27. | 0.19 | 80 | 60 | 0.0032 | 0.0066 |
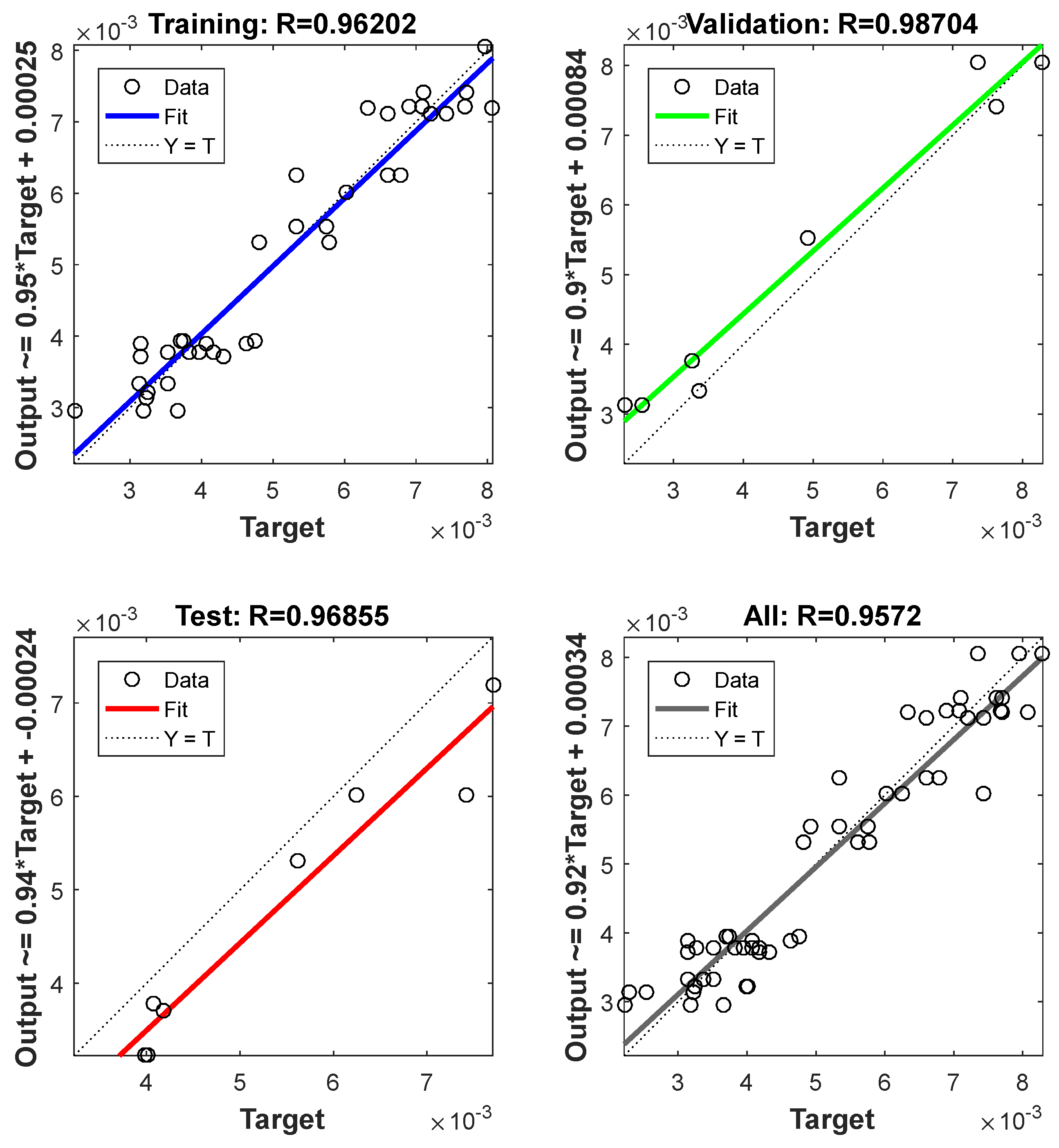
| Dataset | Number of Samples | MSE (Mean Squared Error) | R2 (Correlation Coefficient) |
|---|---|---|---|
| Training | 19 | 2.16272 × 10−7 | 0.962024 |
| Validation | 4 | 2.84401 × 10−7 | 0.987041 |
| Testing | 4 | 4.87121 × 10−7 | 0.968548 |
| No. | Layer Thickness | Infill Density | Ød2n, ØD2n (mm) | ard Ød2 | ard ØD2 |
|---|---|---|---|---|---|
| 1. | 0.09 | 20 | 42 | 0.0039 | 0.0075 |
| 2. | 0.09 | 20 | 42 | 0.0038 | 0.0072 |
| 3. | 0.09 | 20 | 42 | 0.0028 | 0.0069 |
| 4. | 0.09 | 50 | 46 | 0.0034 | 0.0054 |
| 5. | 0.09 | 50 | 46 | 0.0033 | 0.0048 |
| 6. | 0.09 | 50 | 46 | 0.0027 | 0.0041 |
| 7. | 0.09 | 80 | 52 | 0.0022 | 0.0050 |
| 8. | 0.09 | 80 | 52 | 0.0025 | 0.0051 |
| 9. | 0.09 | 80 | 52 | 0.0024 | 0.0038 |
| 10. | 0.14 | 20 | 42 | 0.0029 | 0.0072 |
| 11. | 0.14 | 20 | 42 | 0.0029 | 0.0070 |
| 12. | 0.14 | 20 | 42 | 0.0028 | 0.0064 |
| 13. | 0.14 | 50 | 46 | 0.0033 | 0.0064 |
| 14. | 0.14 | 50 | 46 | 0.0028 | 0.0067 |
| 15. | 0.14 | 50 | 46 | 0.0027 | 0.0055 |
| 16. | 0.14 | 80 | 52 | 0.0041 | 0.0062 |
| 17. | 0.14 | 80 | 52 | 0.0029 | 0.0054 |
| 18. | 0.14 | 80 | 52 | 0.0021 | 0.0047 |
| 19. | 0.19 | 20 | 42 | 0.0041 | 0.0077 |
| 20. | 0.19 | 20 | 42 | 0.0030 | 0.0072 |
| 21. | 0.19 | 20 | 42 | 0.0027 | 0.0061 |
| 22. | 0.19 | 50 | 46 | 0.0033 | 0.0072 |
| 23. | 0.19 | 50 | 46 | 0.0031 | 0.0069 |
| 24. | 0.19 | 50 | 46 | 0.0022 | 0.0055 |
| 25. | 0.19 | 80 | 52 | 0.0031 | 0.0082 |
| 26. | 0.19 | 80 | 52 | 0.0029 | 0.0067 |
| 27. | 0.19 | 80 | 52 | 0.0025 | 0.0056 |
| No. | Layer Thickness | Infill Density | ln, Ln (mm) | ard l | ard L |
|---|---|---|---|---|---|
| 1. | 0.09 | 20 | 8 | 0.0089 | 0.0116 |
| 2. | 0.09 | 20 | 8 | 0.0050 | 0.0173 |
| 3. | 0.09 | 20 | 8 | 0.0079 | 0.0196 |
| 4. | 0.09 | 50 | 9 | 0.0070 | 0.0111 |
| 5. | 0.09 | 50 | 9 | 0.0013 | 0.0142 |
| 6. | 0.09 | 50 | 9 | 0.0081 | 0.0088 |
| 7. | 0.09 | 80 | 10 | 0.0074 | 0.0102 |
| 8. | 0.09 | 80 | 10 | 0.0022 | 0.0129 |
| 9. | 0.09 | 80 | 10 | 0.0082 | 0.0090 |
| 10. | 0.14 | 20 | 8 | 0.0041 | 0.0161 |
| 11. | 0.14 | 20 | 8 | 0.0103 | 0.0213 |
| 12. | 0.14 | 20 | 8 | 0.0101 | 0.0185 |
| 13. | 0.14 | 50 | 9 | 0.0110 | 0.0190 |
| 14. | 0.14 | 50 | 9 | 0.0090 | 0.0179 |
| 15. | 0.14 | 50 | 9 | 0.0074 | 0.0146 |
| 16. | 0.14 | 80 | 10 | 0.0065 | 0.0155 |
| 17. | 0.14 | 80 | 10 | 0.0084 | 0.0104 |
| 18. | 0.14 | 80 | 10 | 0.0096 | 0.0104 |
| 19. | 0.19 | 20 | 8 | 0.0103 | 0.0208 |
| 20. | 0.19 | 20 | 8 | 0.0078 | 0.0166 |
| 21. | 0.19 | 20 | 8 | 0.0101 | 0.0125 |
| 22. | 0.19 | 50 | 9 | 0.0066 | 0.0169 |
| 23. | 0.19 | 50 | 9 | 0.0089 | 0.0168 |
| 24. | 0.19 | 50 | 9 | 0.0087 | 0.0229 |
| 25. | 0.19 | 80 | 10 | 0.0065 | 0.0142 |
| 26. | 0.19 | 80 | 10 | 0.0082 | 0.0155 |
| 27. | 0.19 | 80 | 10 | 0.0076 | 0.0142 |
| Nominal Values | ard_Shaft | ard_Hub |
|---|---|---|
| Ød1n, D1n | ard_Ød1p = 0.0036 | ard_ØD1p = 0.0061 |
| Ød2n, D2n | ard_Ød2p = 0.0022 | ard_ØD2p = 0.0019 |
| ln, Ln | ard_lp = 0.0038 | ard_Lp = 0.0116 |
| Measured Values | ard_Shaft | ard_Hub |
|---|---|---|
| Ød1n = 50.12; D1n = 49.91 | ard_Ød1e = 0.0024 | ard_ØD1e = 0.0018 |
| Ød2n = 42.06. D2n = 42.07 | ard_Ød2e = 0.0014 | ard_ØD2e = 0.0017 |
| ln = 10.04. Ln = 9.95 | ard_le = 0.004 | ard_Le = 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rizea, A.-D.; Banică, C.-F.; Georgescu, T.; Sover, A.; Anghel, D.-C. Dimensional Accuracy Analysis of Splined Shafts and Hubs Obtained by Fused-Deposition Modeling 3D Printing Using a Genetic Algorithm and Artificial Neural Network. Appl. Sci. 2025, 15, 3958. https://doi.org/10.3390/app15073958
Rizea A-D, Banică C-F, Georgescu T, Sover A, Anghel D-C. Dimensional Accuracy Analysis of Splined Shafts and Hubs Obtained by Fused-Deposition Modeling 3D Printing Using a Genetic Algorithm and Artificial Neural Network. Applied Sciences. 2025; 15(7):3958. https://doi.org/10.3390/app15073958
Chicago/Turabian StyleRizea, Alin-Daniel, Cristina-Florena Banică, Tatiana Georgescu, Alexandru Sover, and Daniel-Constantin Anghel. 2025. "Dimensional Accuracy Analysis of Splined Shafts and Hubs Obtained by Fused-Deposition Modeling 3D Printing Using a Genetic Algorithm and Artificial Neural Network" Applied Sciences 15, no. 7: 3958. https://doi.org/10.3390/app15073958
APA StyleRizea, A.-D., Banică, C.-F., Georgescu, T., Sover, A., & Anghel, D.-C. (2025). Dimensional Accuracy Analysis of Splined Shafts and Hubs Obtained by Fused-Deposition Modeling 3D Printing Using a Genetic Algorithm and Artificial Neural Network. Applied Sciences, 15(7), 3958. https://doi.org/10.3390/app15073958






