Key Issues in Using the Freezing Method in Power Tunnel Rehabilitation Projects
Abstract
1. Introduction
2. Vertical Freezing Program Design
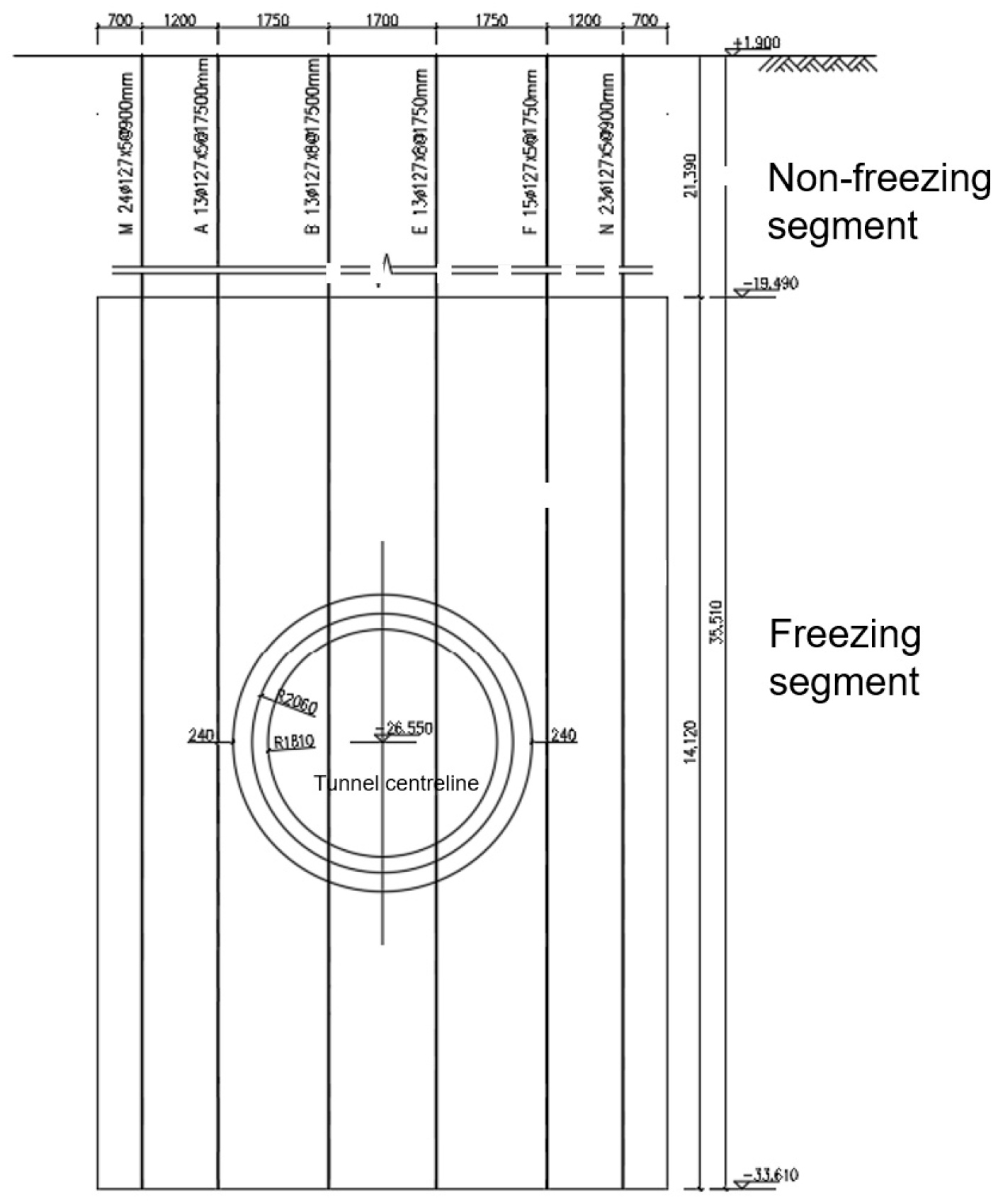
2.1. Project Overview
2.2. Arrangement of Freezing Pipes
3. Establishment of Finite Element Numerical Simulations
3.1. Fundamental Assumption
- 1.
- The analysis herein neglects the influence of stress and displacement fields on the temperature field, focusing solely on the hydrothermal interaction between seepage and temperature fields.
- 2.
- It is assumed that the soil constitutes a saturated, homogeneous, isotropic porous medium with a constant total porosity.
- 3.
- Thermal-physical properties within the soil layers are considered constant across layers.
- 4.
- The impact of solute concentration on the freezing point is negligible, and ice is assumed to be stationary, without deformation.
- 5.
- It is assumed that the initial temperature of the stratum is 18 °C, the soil is a porous saturated medium, and the soil is homogeneously distributed and homogeneous.
3.2. Model Calculation Theory
3.2.1. Temperature Field Theory
3.2.2. Percolation Field Theory
3.2.3. Theory of Coupled Temperature and Seepage Fields
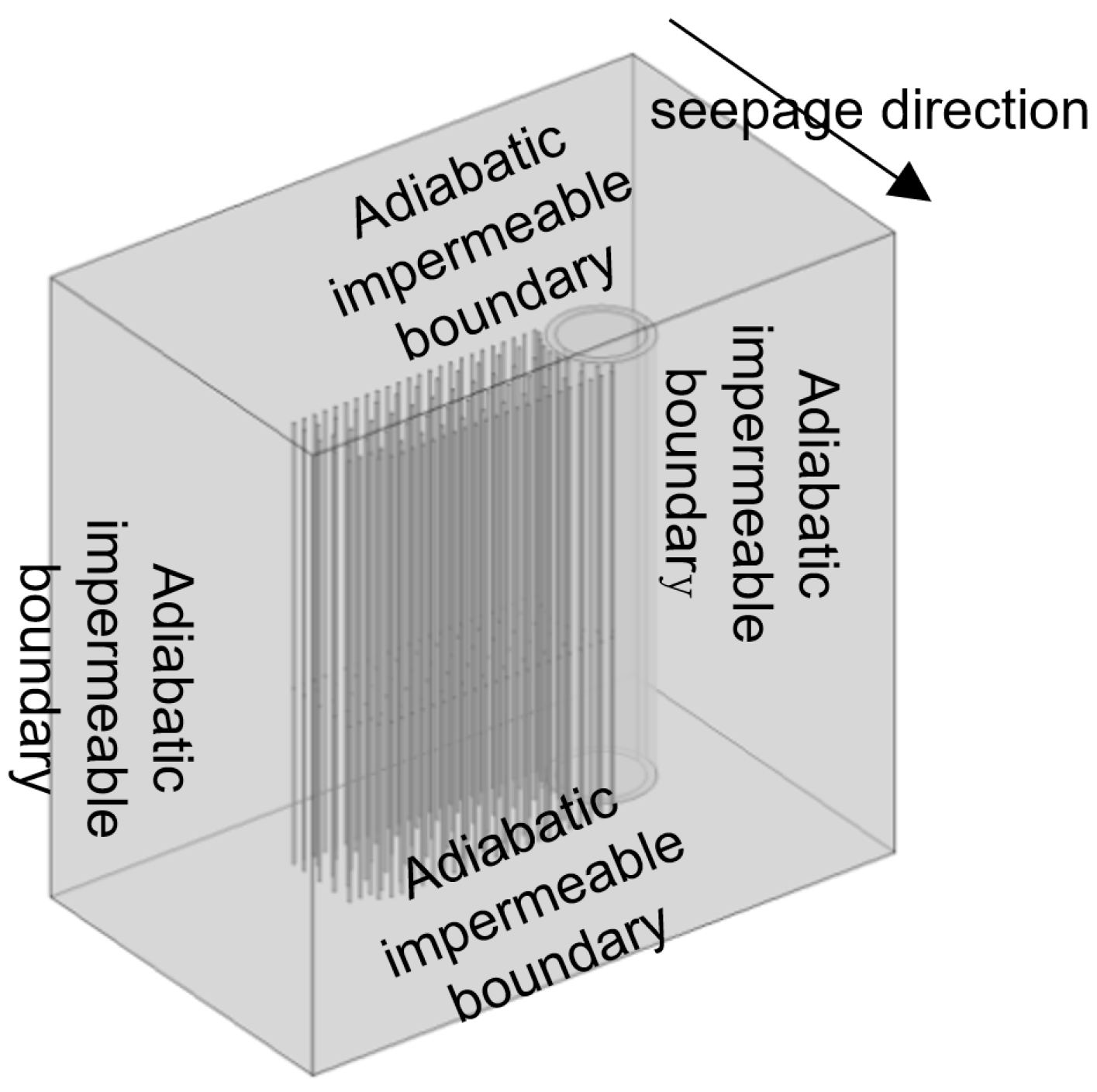
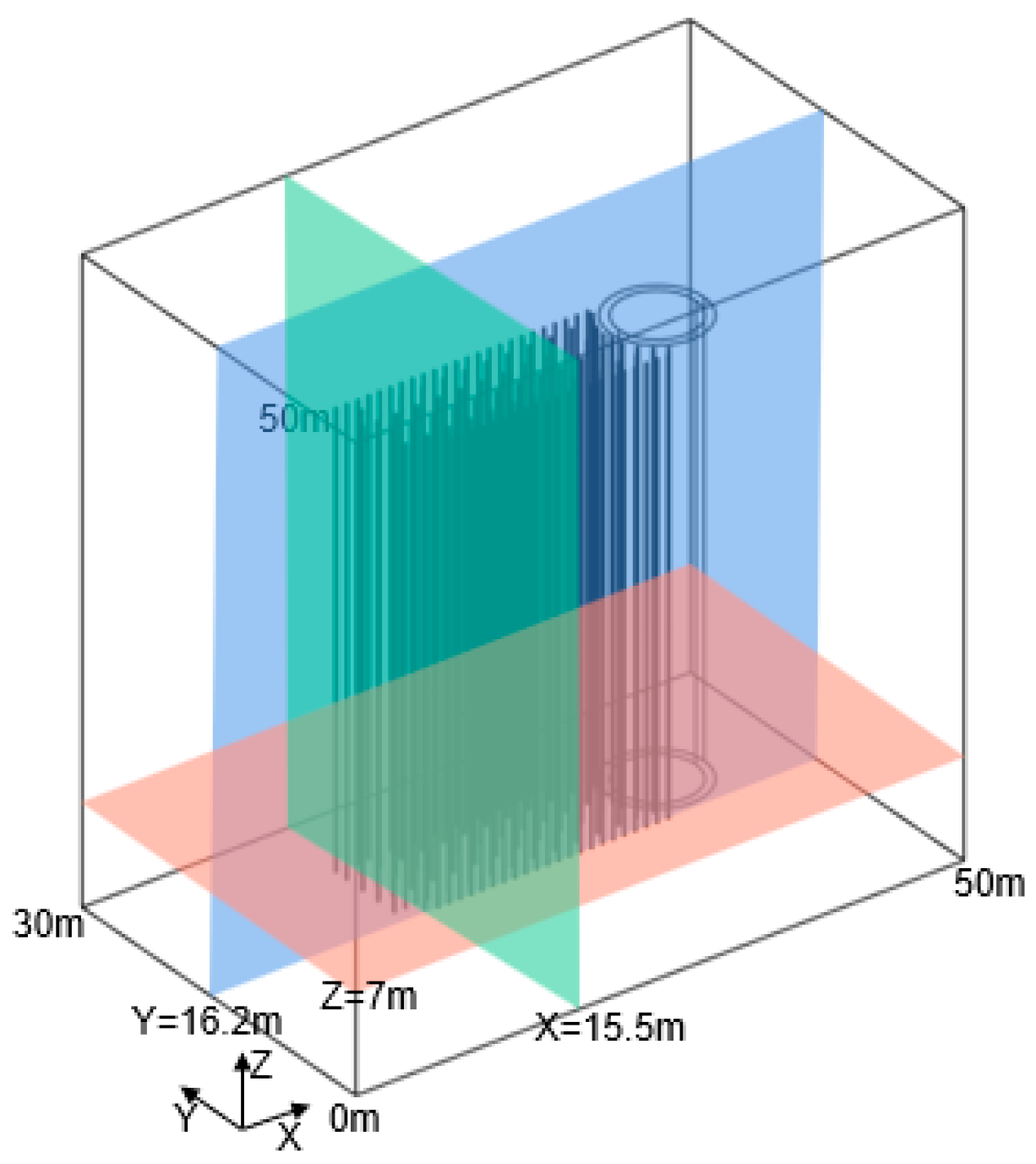
3.3. Geometric Modeling and Parameter Selection
4. Analysis of Numerical Simulation Results
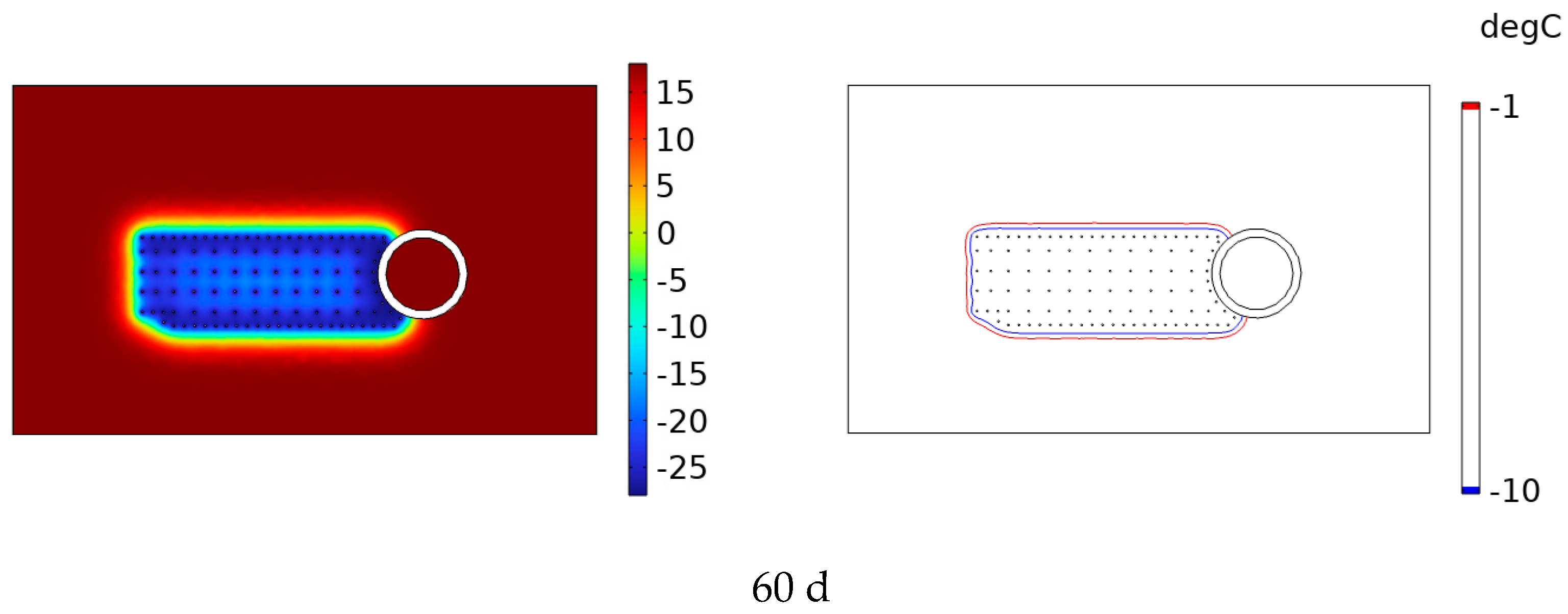
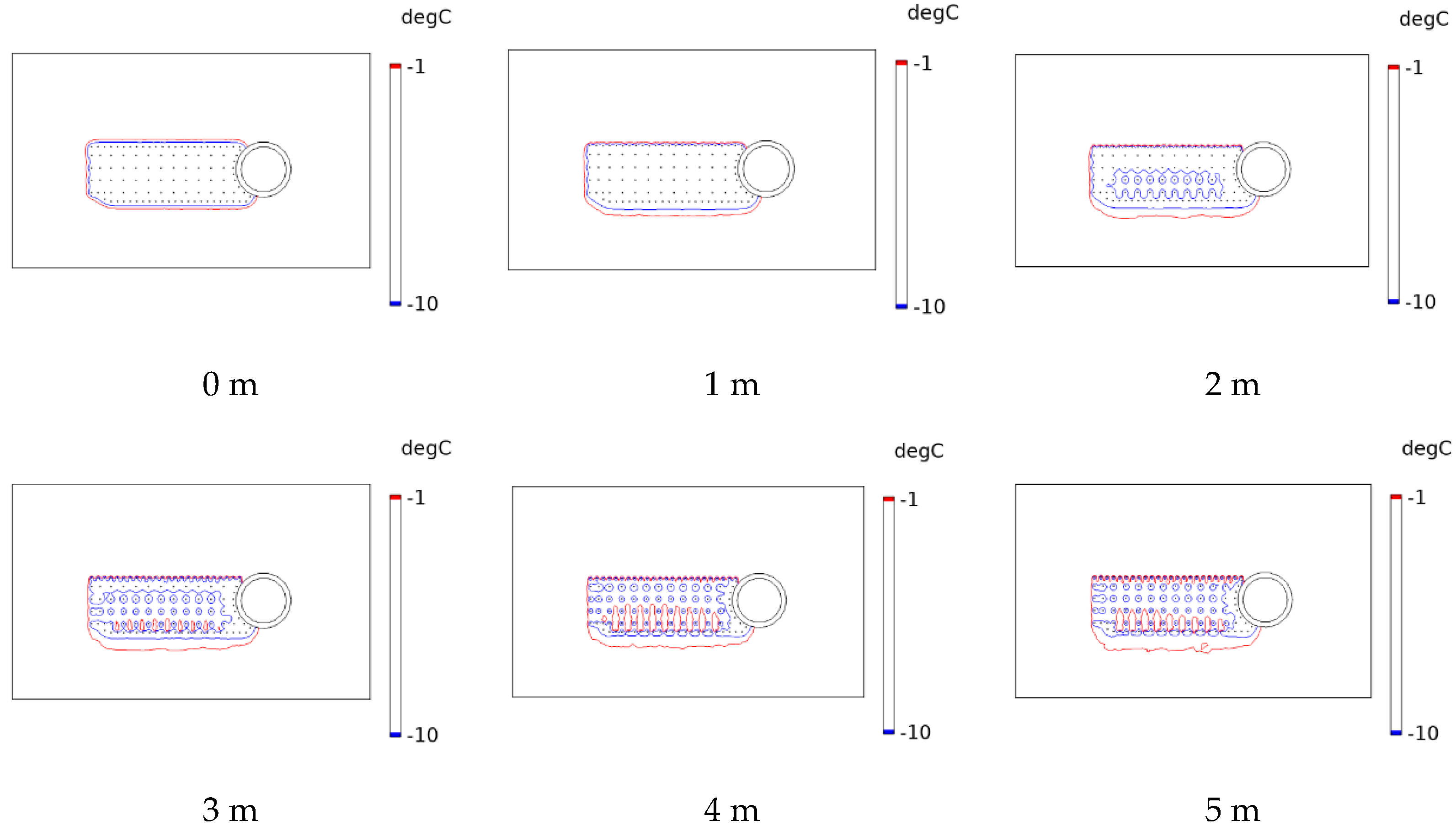
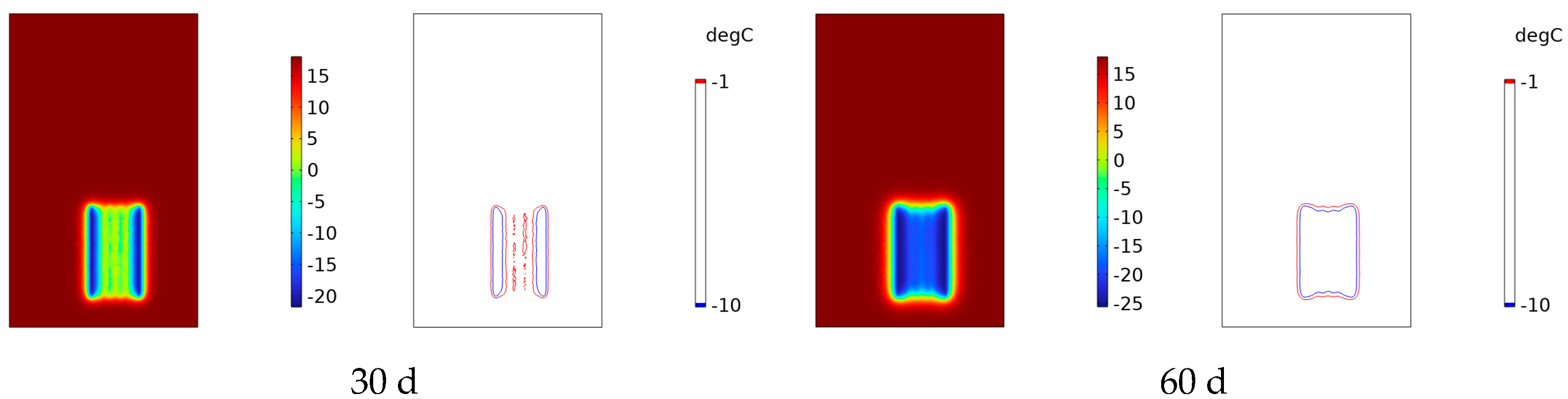
4.1. Freezing Temperature Field and Permafrost Curtain Development Pattern in the Z-Section
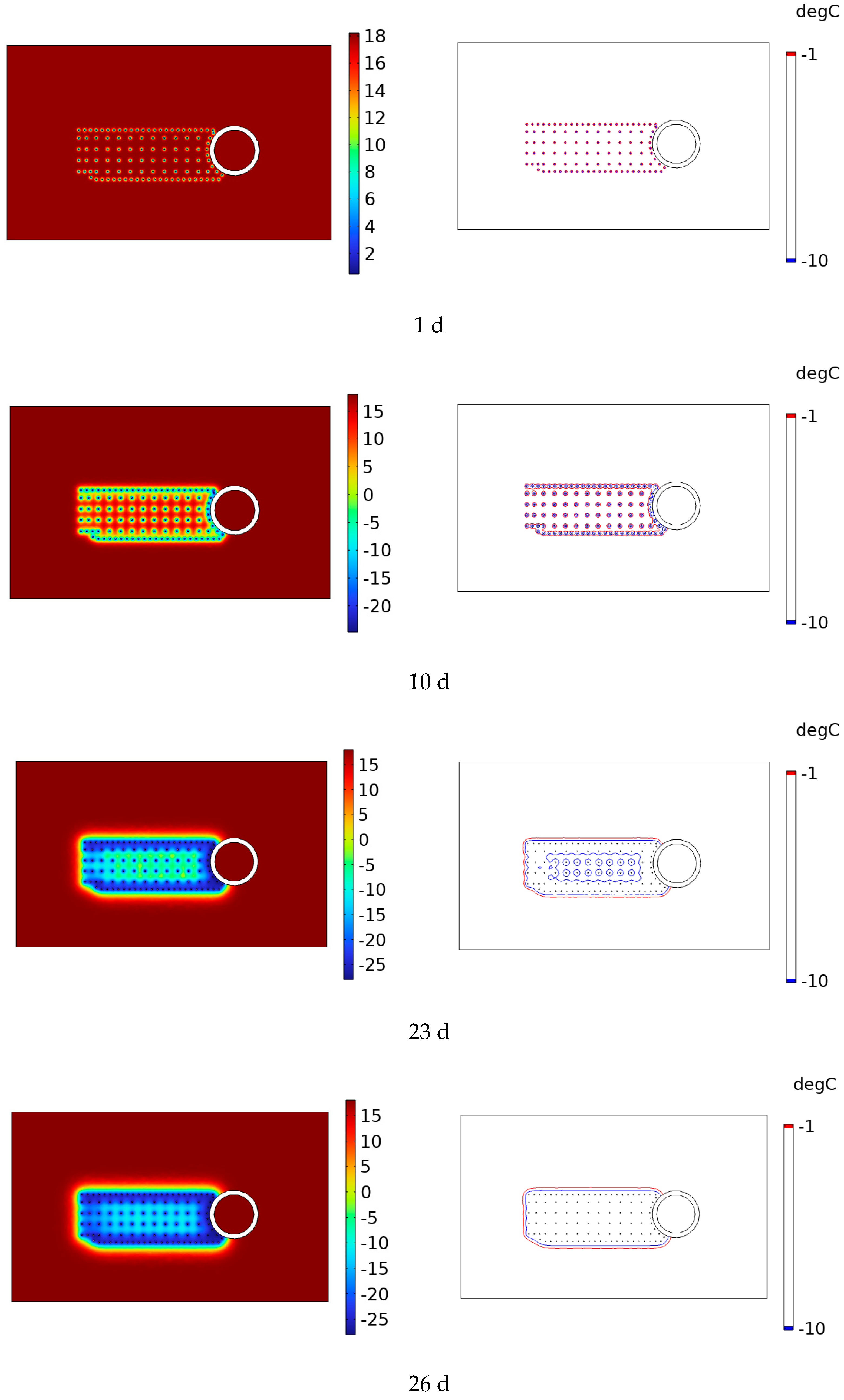
4.1.1. Z-Section Without Considering the Seepage Flow Scenario
4.1.2. Z-Section Considering Seepage Flow
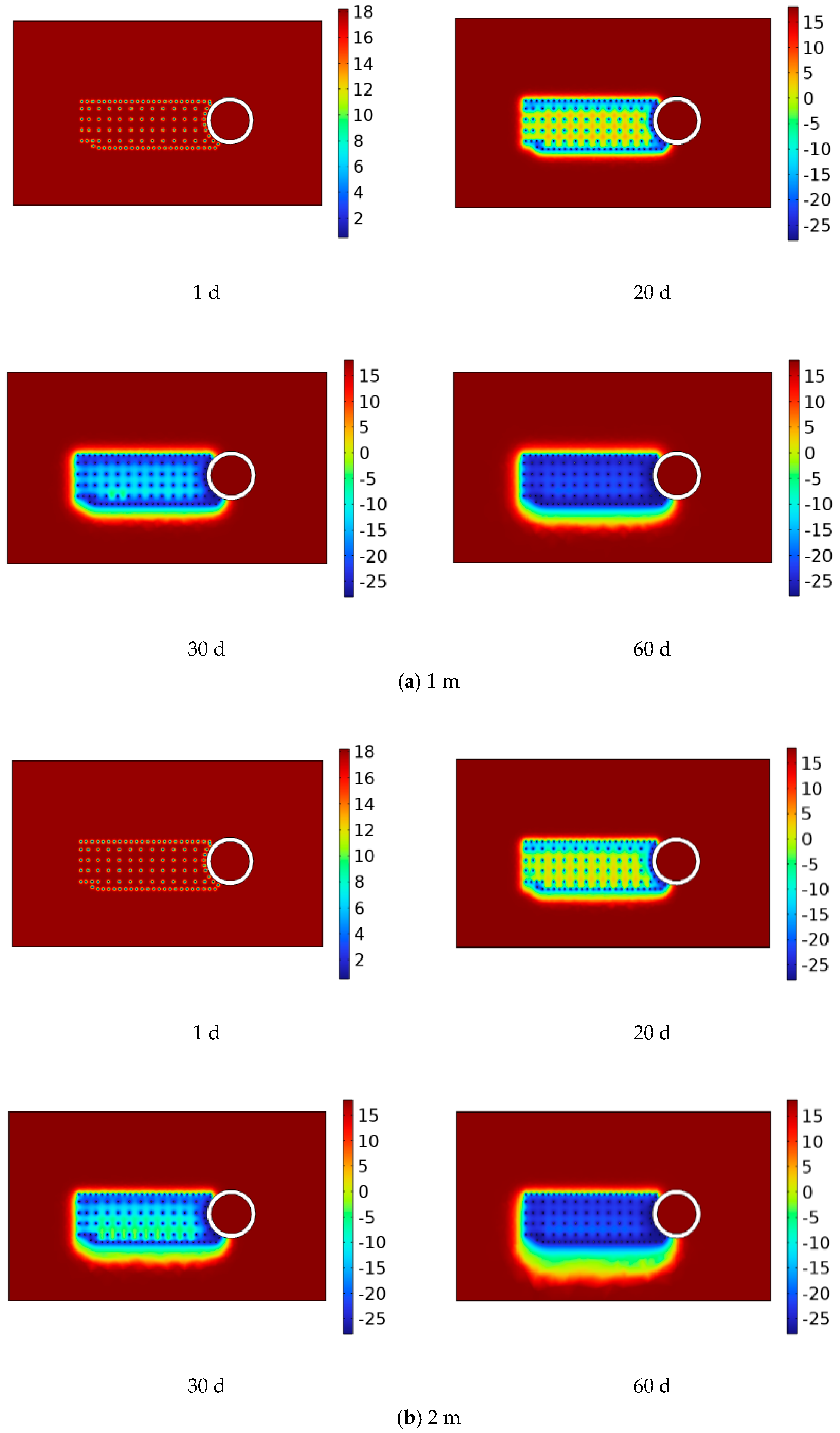
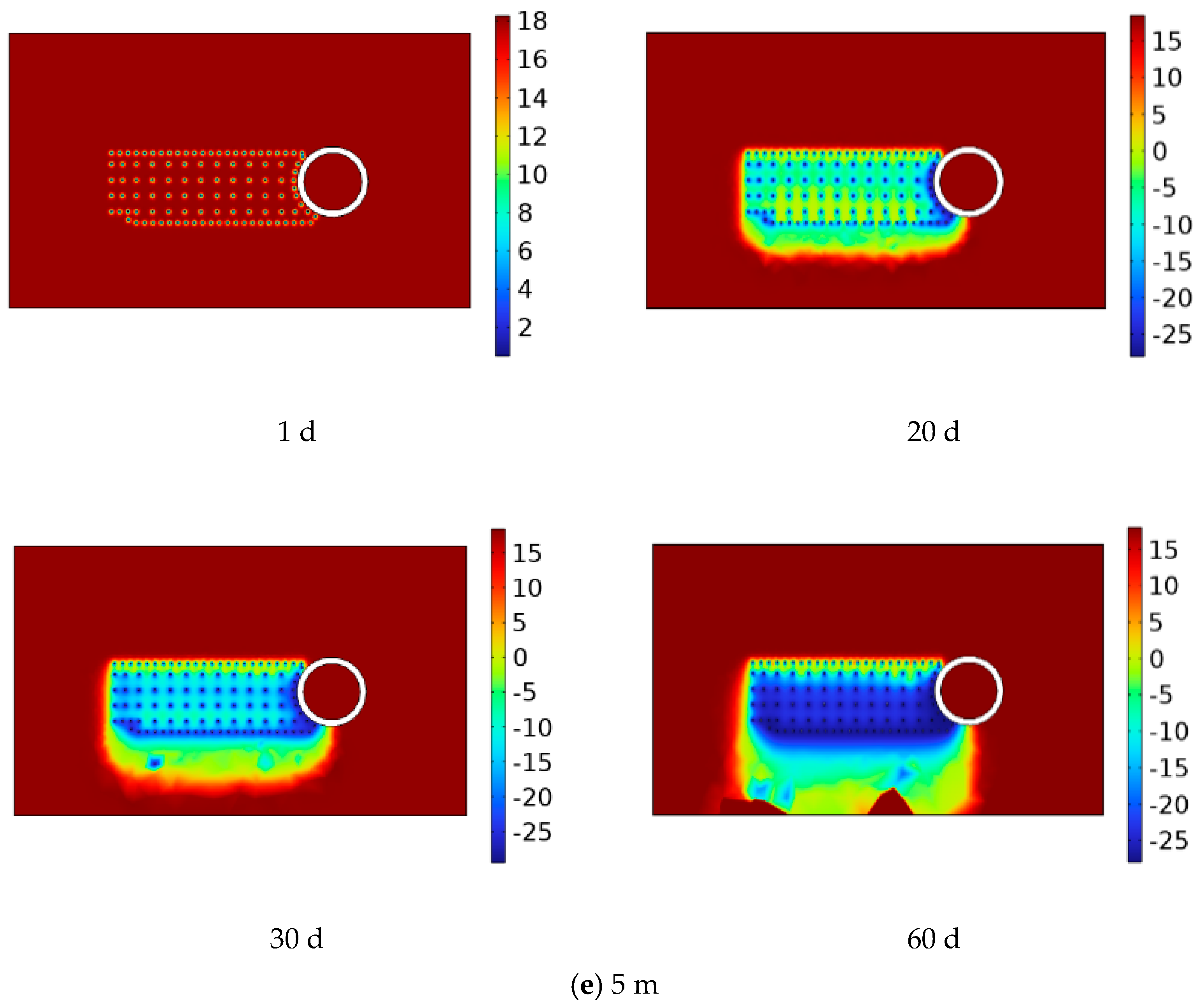
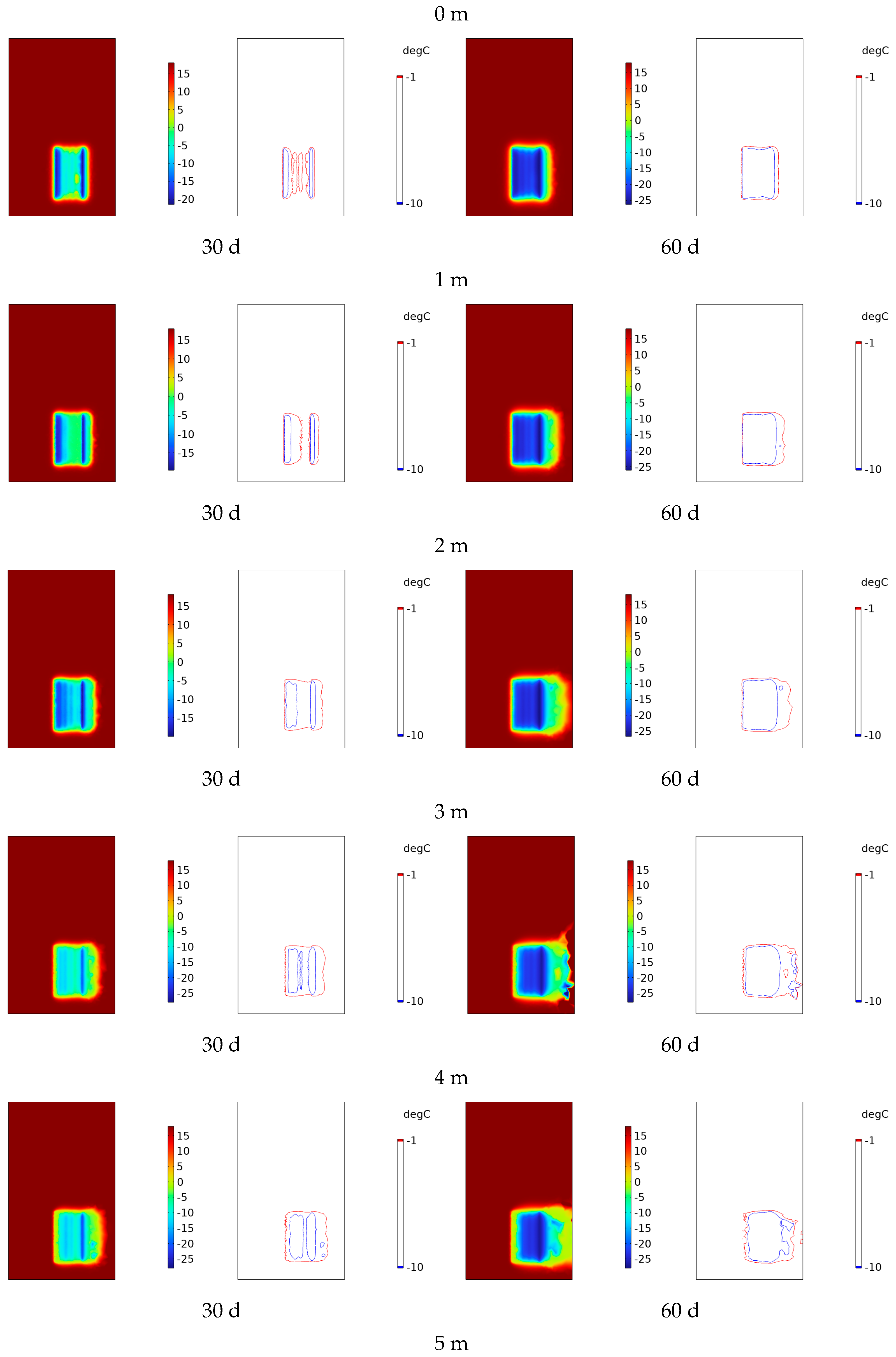
4.2. X-Section Permafrost Curtain Development Law
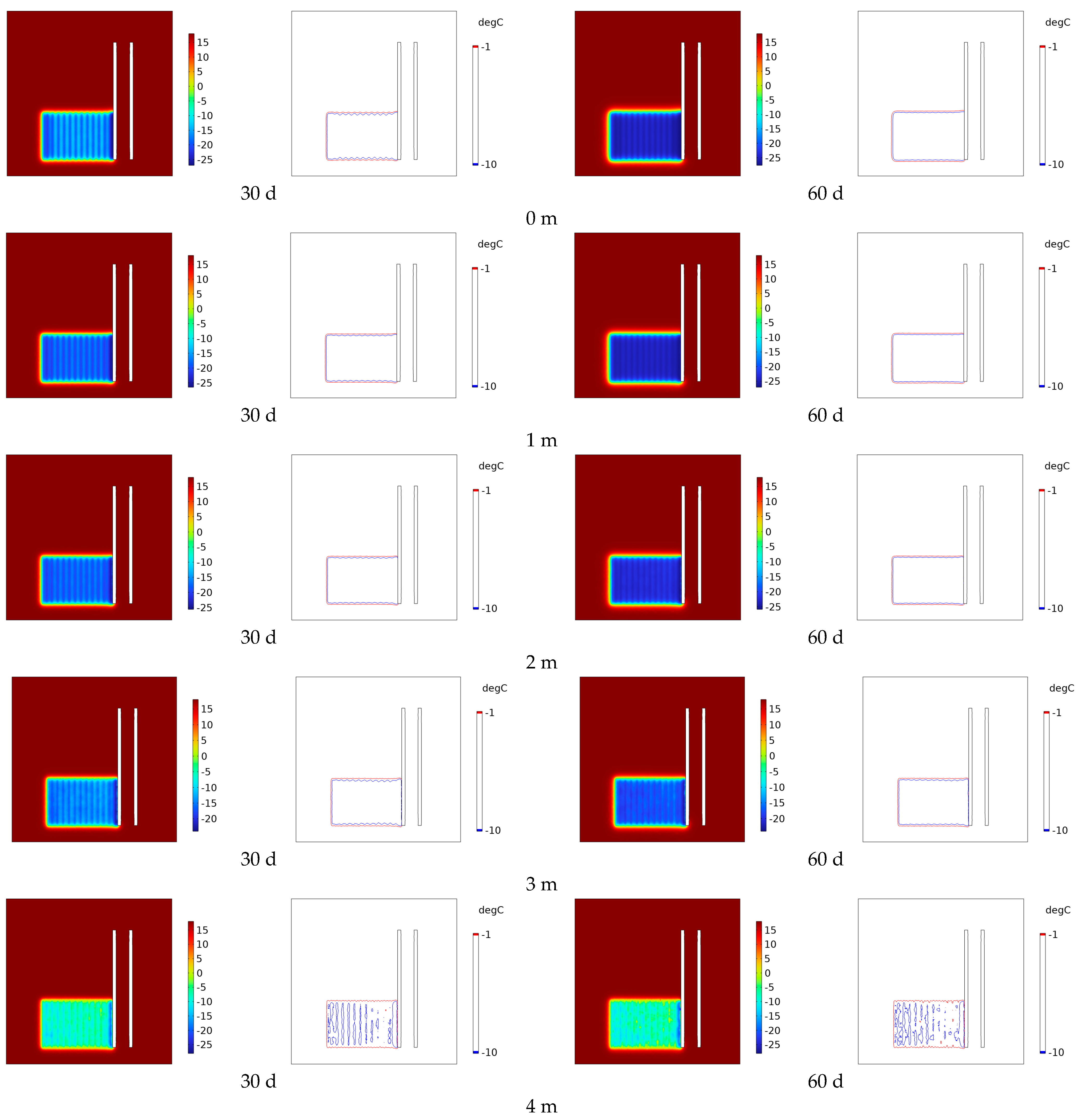
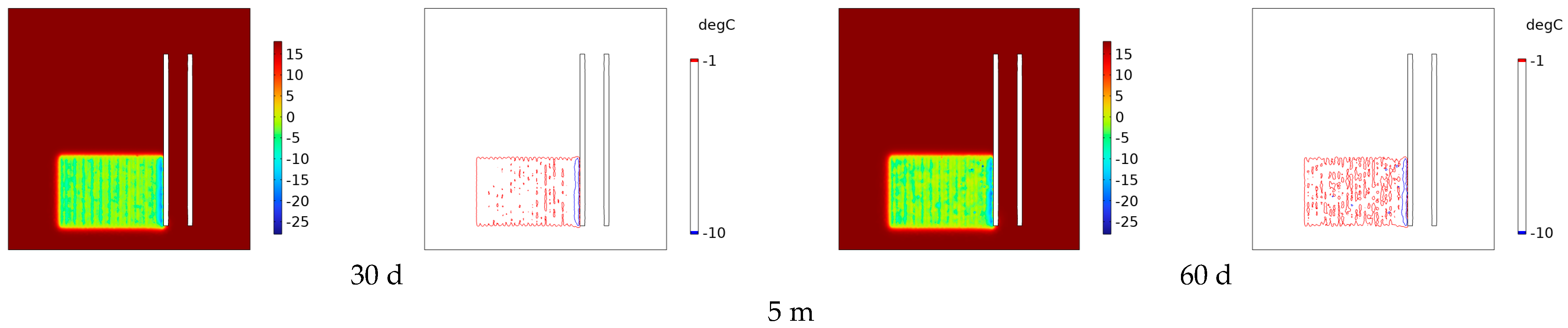
4.3. Y-Section Permafrost Curtain Development Law
5. Analysis of Pathway Observation Points
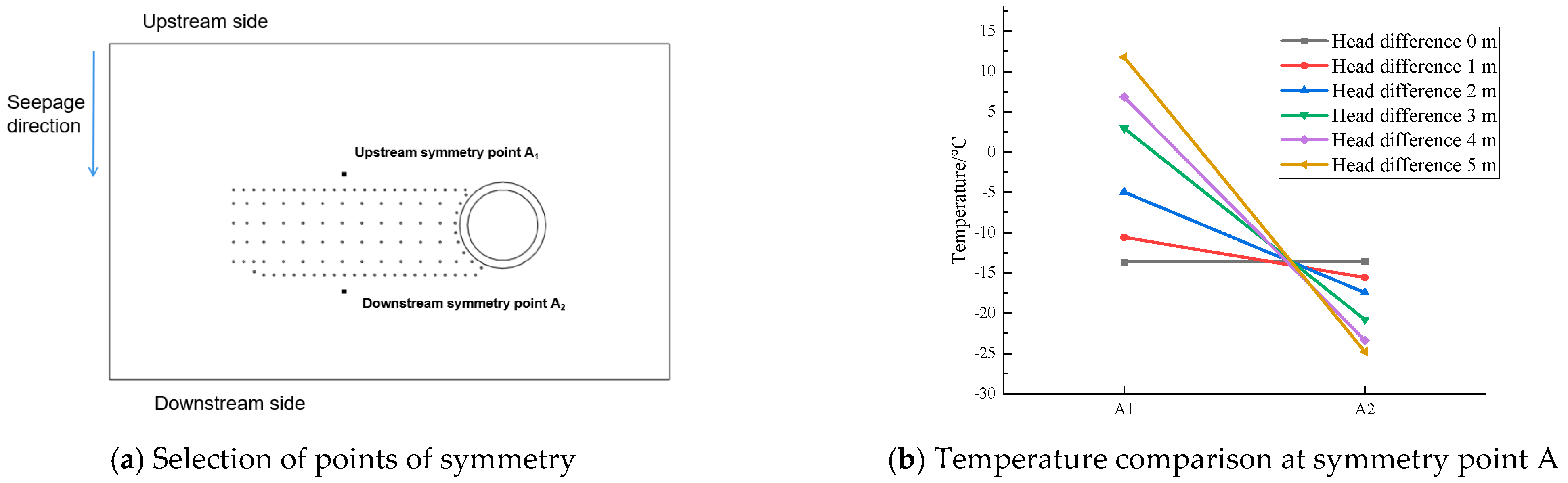
5.1. Temperature Comparison of Upstream and Downstream Symmetry Points Under Seepage Conditions
5.2. Analysis of Pathway Observation Points
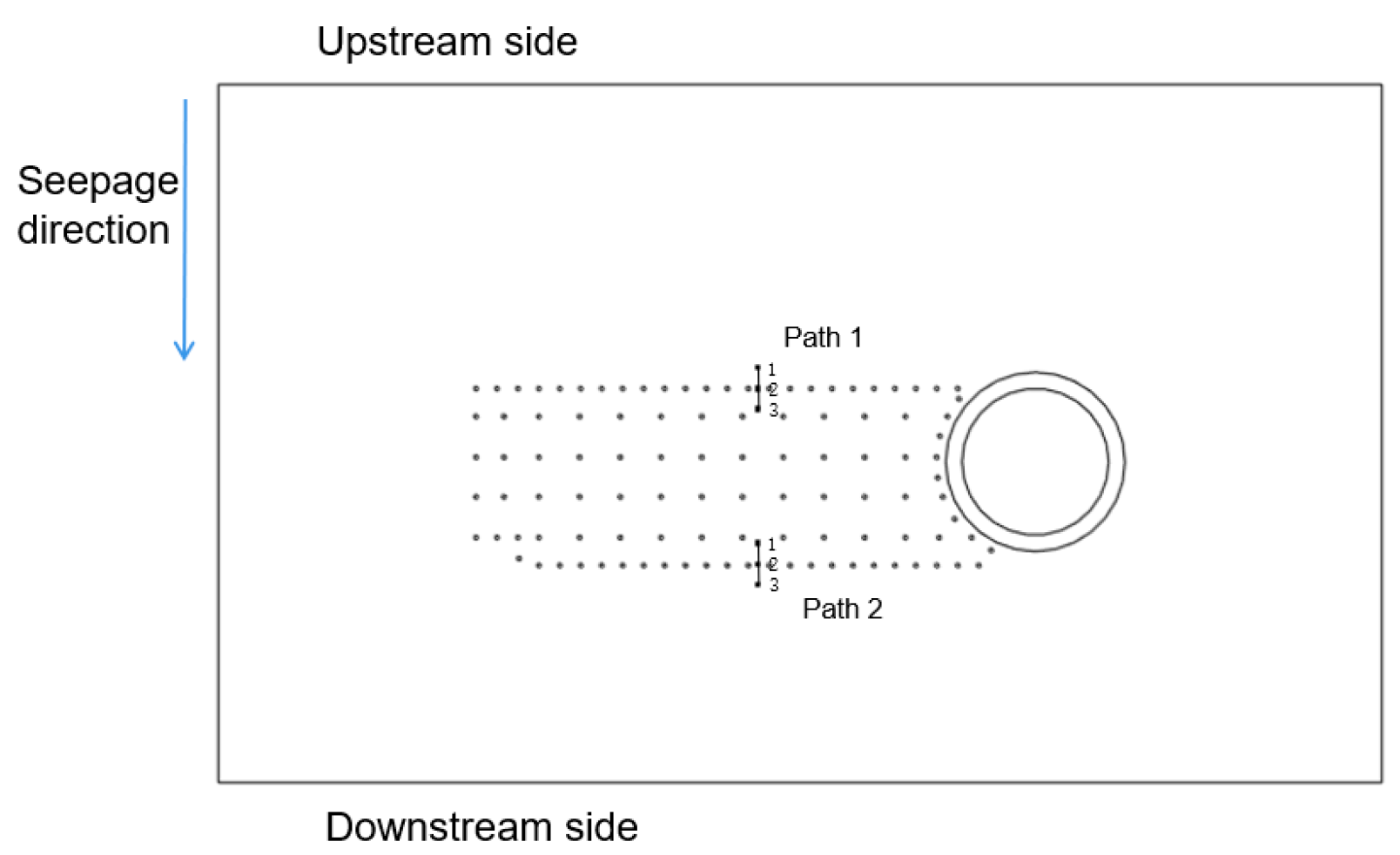
5.2.1. Path Selection
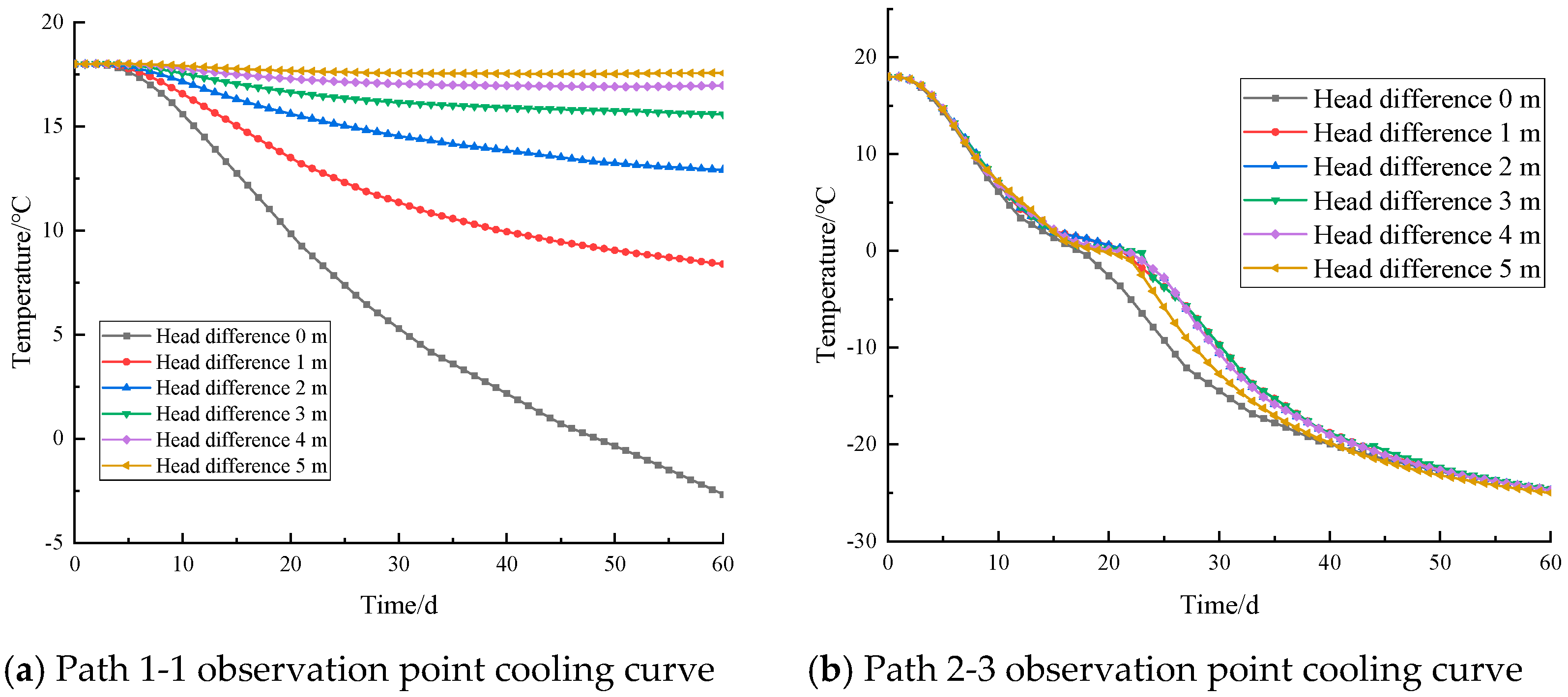
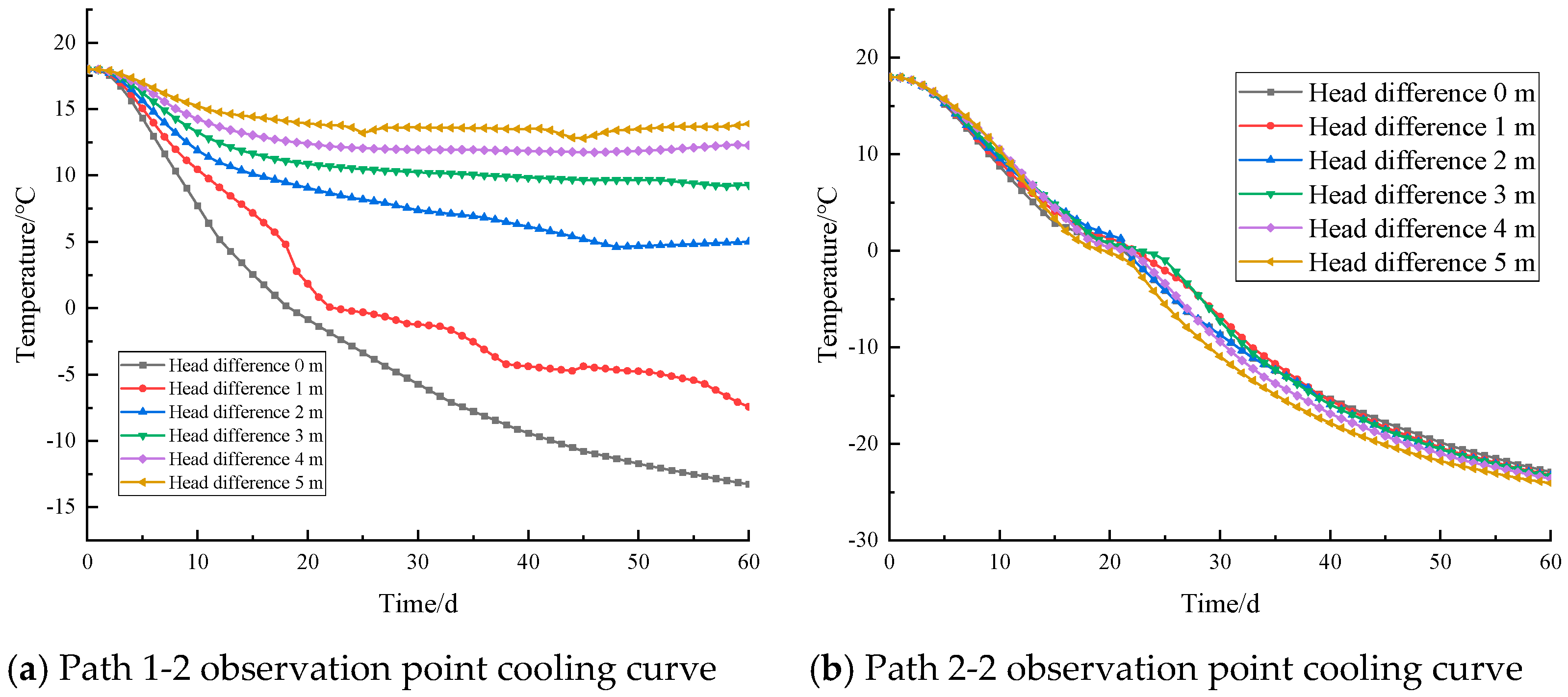
5.2.2. Analysis of Cooling Patterns at Temperature Observation Points
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhan, Y.; Lu, Z.; Yao, H. Numerical analysis of thermo-hydro-mechanical coupling of diversion tunnels in a seasonally frozen region. J. Cold Reg. Eng. 2020, 34, 04020018. [Google Scholar] [CrossRef]
- Williams, R.J.; Alsahly, M.A.; Meschke, G. Computational modelling of artificial ground freezing in mechanized tunnelling. In Expanding Underground-Knowledge and Passion to Make a Positive Impact on the World; CRC Press: Boca Raton, FL, USA, 2023; pp. 1510–1514. [Google Scholar]
- Jin, H.; Lee, J.; Ryu, B.H.; Go, G.H. Experimental and numerical study on hydro-thermal behaviour of artificial freezing system with water flow. J. Korean Geotech. Soc. 2020, 36, 17–25. [Google Scholar]
- Zhelnin, M.; Kostina, A.; Plekhov, O.; Panteleev, I.; Levin, L. Numerical simulation of soil stability during artificial freezing. Procedia Struct. Integr. 2019, 17, 316–323. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Z.; Wan, P.; Tang, Y.; Zhao, W. Effects of seepage in clay-sand composite strata on artificial ground freezing and surrounding engineering environment. Chin. J. Geotech. Eng. 2021, 43, 471–480. [Google Scholar]
- Mauro, A.; Normino, G.; Cavuoto, F.; Marotta, P.; Massarotti, N. Modeling artificial ground freezing for construction of two tunnels of a metro station in Napoli (Italy). Energies 2020, 13, 1272. [Google Scholar] [CrossRef]
- Niu, Y.; Hong, Z.Q.; Zhang, J.; Han, L. Frozen curtain characteristics during excavation of submerged shallow tunnel using Freeze-Sealing Pipe-Roof method. Res. Cold Arid. Reg. 2022, 14, 267–273. [Google Scholar] [CrossRef]
- Hong, Z.; Zhang, J.; Han, L.; Wu, Y. Numerical Study on Water Sealing Effect of Freeze-Sealing Pipe-Roof Method Applied in Underwater Shallow-Buried Tunnel. Front. Phys. 2022, 9, 794374. [Google Scholar] [CrossRef]
- Cui, Z.D.; Zhang, L.J.; Xu, C. Numerical simulation of freezing temperature field and frost heave deformation for deep foundation pit by AGF. Cold Reg. Sci. Technol. 2023, 213, 103908. [Google Scholar] [CrossRef]
- Alzoubi, M.A.; Xu, M.; Hassani, F.P.; Poncet, S.; Sasmito, A.P. Artificial ground freezing: A review of thermal and hydraulic aspects. Tunn. Undergr. Space Technol. 2020, 104, 103534. [Google Scholar] [CrossRef]
- Pang, C.; Cai, H.; Hong, R.; Li, M.; Yang, Z. Evolution law of three-dimensional non-uniform temperature field of tunnel construction using local horizontal freezing technique. Appl. Sci. 2022, 12, 8093. [Google Scholar] [CrossRef]
- Afshani, A.; Akagi, H. Artificial ground freezing application in shield tunneling. Jpn. Geotech. Soc. Spec. Publ. 2015, 3, 71–75. [Google Scholar] [CrossRef]
- Li, M.; Cai, H.; Liu, Z.; Pang, C.; Hong, R. Research on frost heaving distribution of seepage stratum in tunnel construction using horizontal freezing technique. Appl. Sci. 2022, 12, 11696. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, W.; Qi, J.; Zhang, T. Analytic computation on the forcible thawing temperature field formed by a single heat transfer pipe with unsteady outer surface temperature. J. Coal Sci. Eng. 2012, 18, 18–24. [Google Scholar] [CrossRef]
- Zhou, X.; Jiang, G.; Li, F.; Gao, W.; Han, Y.; Wu, T.; Ma, W. Comprehensive review of artificial ground freezing applications to urban tunnel and underground space engineering in China in the last 20 years. J. Cold Reg. Eng. 2022, 36, 04022002. [Google Scholar] [CrossRef]
- Kang, Y.; Hou, C.; Li, K.; Liu, B.; Sang, H. Evolution of temperature field and frozen wall in sandy cobble stratum using LN2 freezing method. Appl. Therm. Eng. 2021, 185, 116334. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, Q.; Hu, X.; Tan, L. Application of Horizontal Ground Freezing Method in Shanghai Metro Rehabilitation Project. J. Anhui Univ. Archit. Technol. (Nat. Sci. Ed.) 2008, 3, 21–25. [Google Scholar]
- Hu, X.; Long, L. Submarine Shield Repair Freeze Reinforcement Technology. J. Undergr. Space Eng. 2010, 6, 537–542. [Google Scholar]
- Hao, M.; Shi, Z. Application of Freezing Method in the Rehabilitation of River Bottom Intake Tunnels. Well Constr. Technol. 2014, 35, 12–16. [Google Scholar] [CrossRef]
- Xiao, Z.; Hu, X.; Zhang, Q. Design of Freezing Method in Subway Rehabilitation Works. J. Geotech. Eng. 2006, 1716–1719. [Google Scholar]
- Chu, Y.; Zhu, B.; Zhang, Y. Application of Freezing Method in Rehabilitation Works of Cross River Tunnel. Tunn. Constr. 2010, 30, 596–599. [Google Scholar]
- Xiao, Z.; Hu, X.; Zhang, Q. Application of four-row local freezing method in Shanghai metro repair project. Geotechnics 2006, 27, 300–304. [Google Scholar] [CrossRef]
- Fu, Y.; Hu, J.; Wu, Y. Finite element study on temperature field of subway connection aisle construction via artificial ground freezing method. Cold Reg. Sci. Technol. 2021, 189, 103327. [Google Scholar] [CrossRef]
- Liu, P.; Hu, J.; Dong, Q.; Chen, Y. Studying the Freezing Law of Reinforcement by Using the Artificial Ground Freezing Method in Shallow Buried Tunnels. Appl. Sci. 2024, 14, 7106. [Google Scholar] [CrossRef]
- Hu, J. Experimental Study on Freezing Temperature and Mechanical Properties of Soil Before and After Cement Improvement. Railw. Constr. 2013, 18, 156–159. [Google Scholar]
- Jun, H.; Ping, Y.; Zhao-wen, D.; Rong, C. Study on numerical simulation of cup-shaped horizontal freezing reinforcement project near shield launching. In Proceedings of the International Conference on Electric Technology and Civil Engineering (ICETCE), Lushan, China, 22–24 April 2011; pp. 5522–5525. [Google Scholar]
- Liu, W.B. Research on Freezing and Reinforcement Technology of Large-Diameter Shield Tunneling in Heyan Road Cross-River Channel in Nanjing; Hainan University: Haikou, China, 2021. [Google Scholar]
- Wu, Y.W. Research on the Evolution of Construction Temperature Field of Freezing Method of Dongbin Section of Nanning Metro; Hainan University: Haikou, China, 2019. [Google Scholar]






| Parameter Name | Parameter Value |
|---|---|
| Soil density (kg/m3) | Unfrozen ground 1920 Frozen ground 1880 |
| Soil thermal conductivity (W/(m·K)) | Unfrozen ground 1.18 Frozen ground 1.79 |
| Specific heat of soil (J/(kg·K)) | Unfrozen ground 1.53 Frozen ground 1.61 |
| Soil permeability coefficient (m/s) | Unfrozen ground 0.56 × 10−4 Frozen ground 1.91 × 10−30 |
| Soil porosity | 0.4 |
| Density of ice (kg/m3) | 920 |
| Thermal conductivity of water (W/(m·K)) | 0.55 |
| Thermal conductivity of ice (W/(m·K)) | 2.14 |
| Specific heat of water (J/(kg·K)) | 4180 |
| Specific heat of ice (J/(kg·K)) | 2100 |
| Latent heat of phase transition of water ice (KJ/(kg·K)) | 334 |
| Time/d | 0 | 5 | 10 | 20 | 30 | 40 | 50 | 60 |
| Temperature/°C | 18 | −15 | −28 | −28 | −28 | −28 | −28 | −28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Gan, H.; Zhou, J.; Ye, T.; Huang, L.; Shang, X. Key Issues in Using the Freezing Method in Power Tunnel Rehabilitation Projects. Appl. Sci. 2025, 15, 4200. https://doi.org/10.3390/app15084200
Hu J, Gan H, Zhou J, Ye T, Huang L, Shang X. Key Issues in Using the Freezing Method in Power Tunnel Rehabilitation Projects. Applied Sciences. 2025; 15(8):4200. https://doi.org/10.3390/app15084200
Chicago/Turabian StyleHu, Jun, Huajing Gan, Jie Zhou, Tingfen Ye, Lei Huang, and Xinming Shang. 2025. "Key Issues in Using the Freezing Method in Power Tunnel Rehabilitation Projects" Applied Sciences 15, no. 8: 4200. https://doi.org/10.3390/app15084200
APA StyleHu, J., Gan, H., Zhou, J., Ye, T., Huang, L., & Shang, X. (2025). Key Issues in Using the Freezing Method in Power Tunnel Rehabilitation Projects. Applied Sciences, 15(8), 4200. https://doi.org/10.3390/app15084200








