A Comparative Study of Kinetic Reaction Schemes for the Isomerization Process of the C6 Series
Abstract
1. Introduction
2. Methodology
2.1. Chemical Equilibrium Modeling
2.2. Mathematical Model of the Isomerization Process
3. Results and Discussion
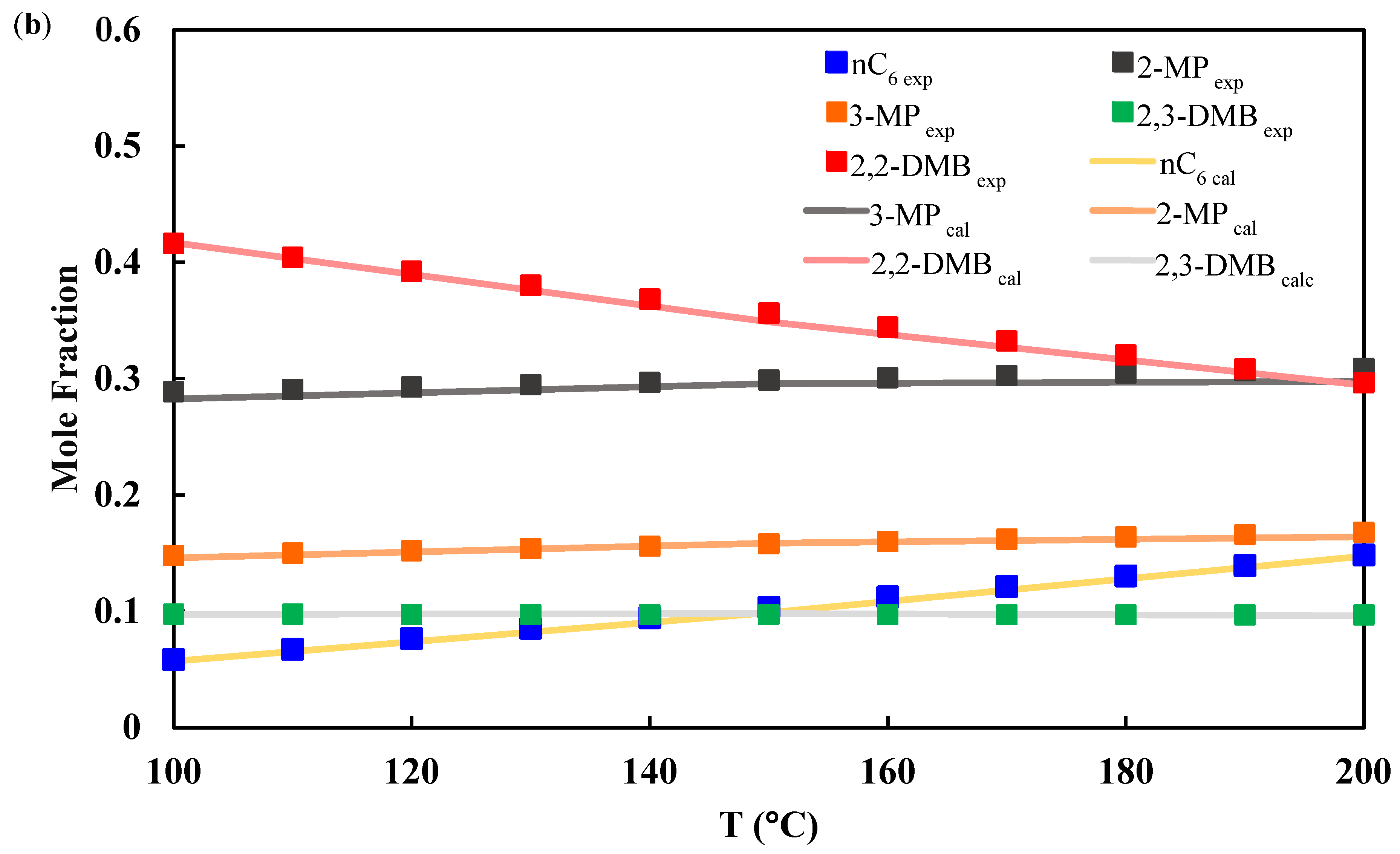
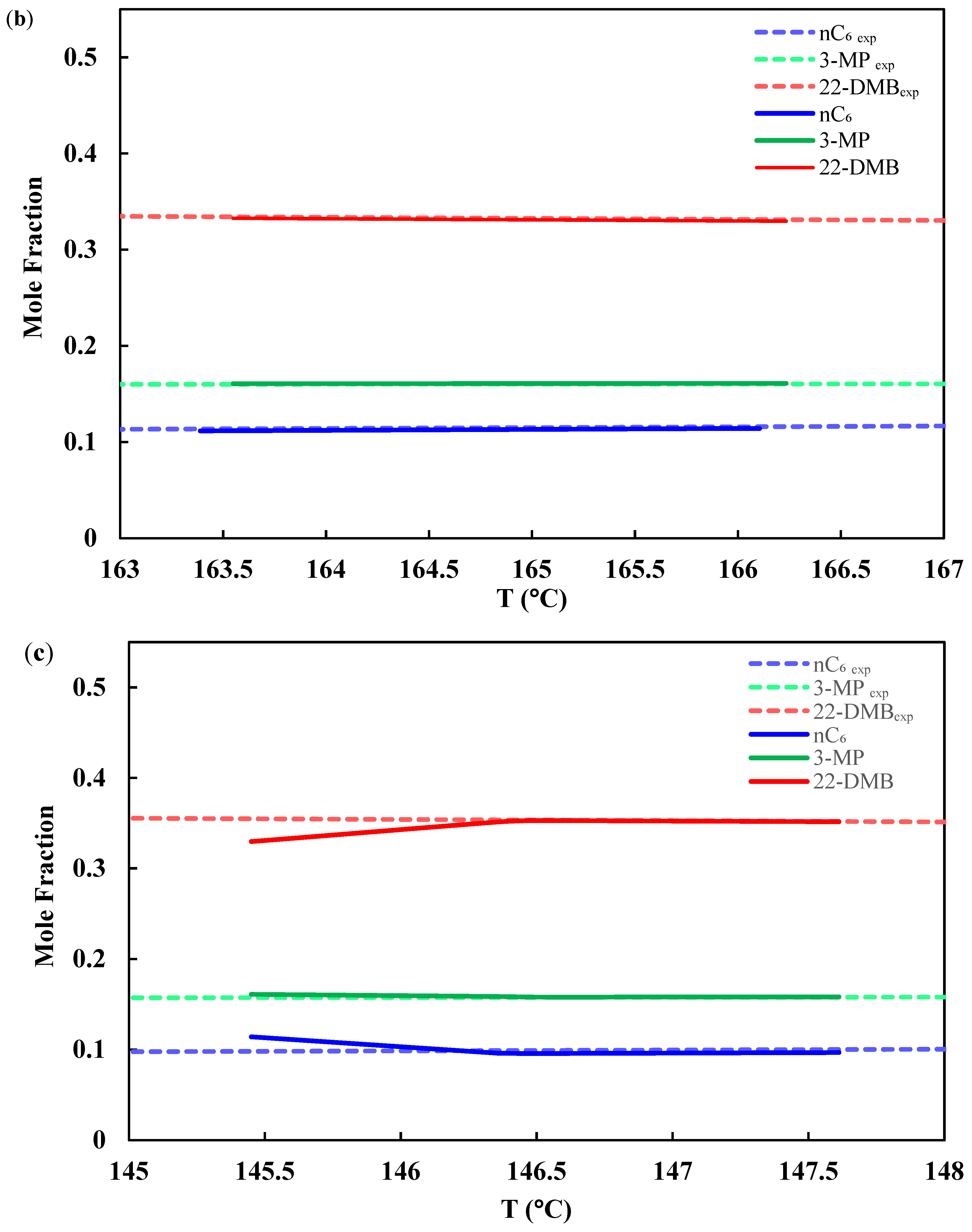
3.1. Chemical Equilibrium
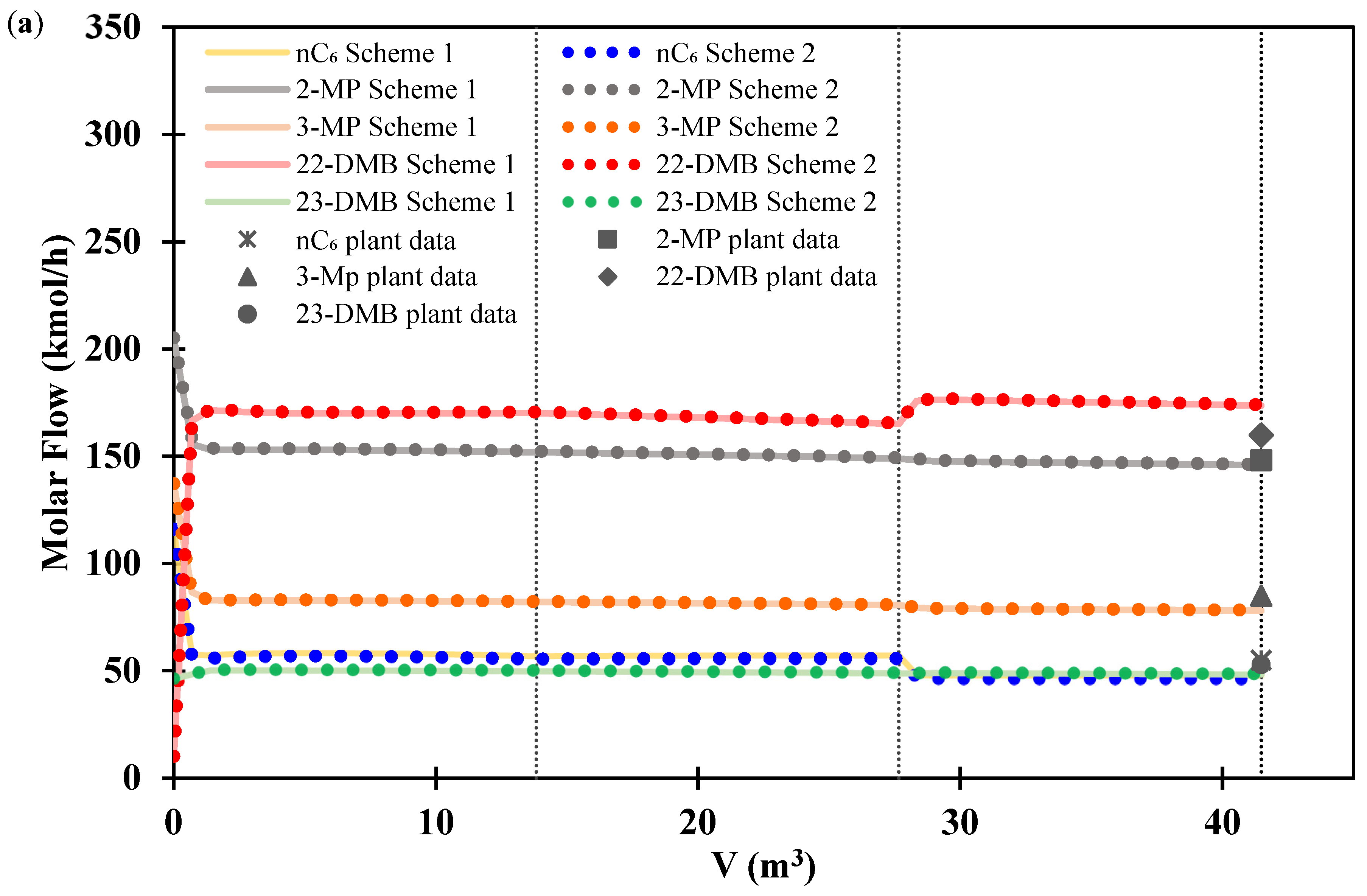
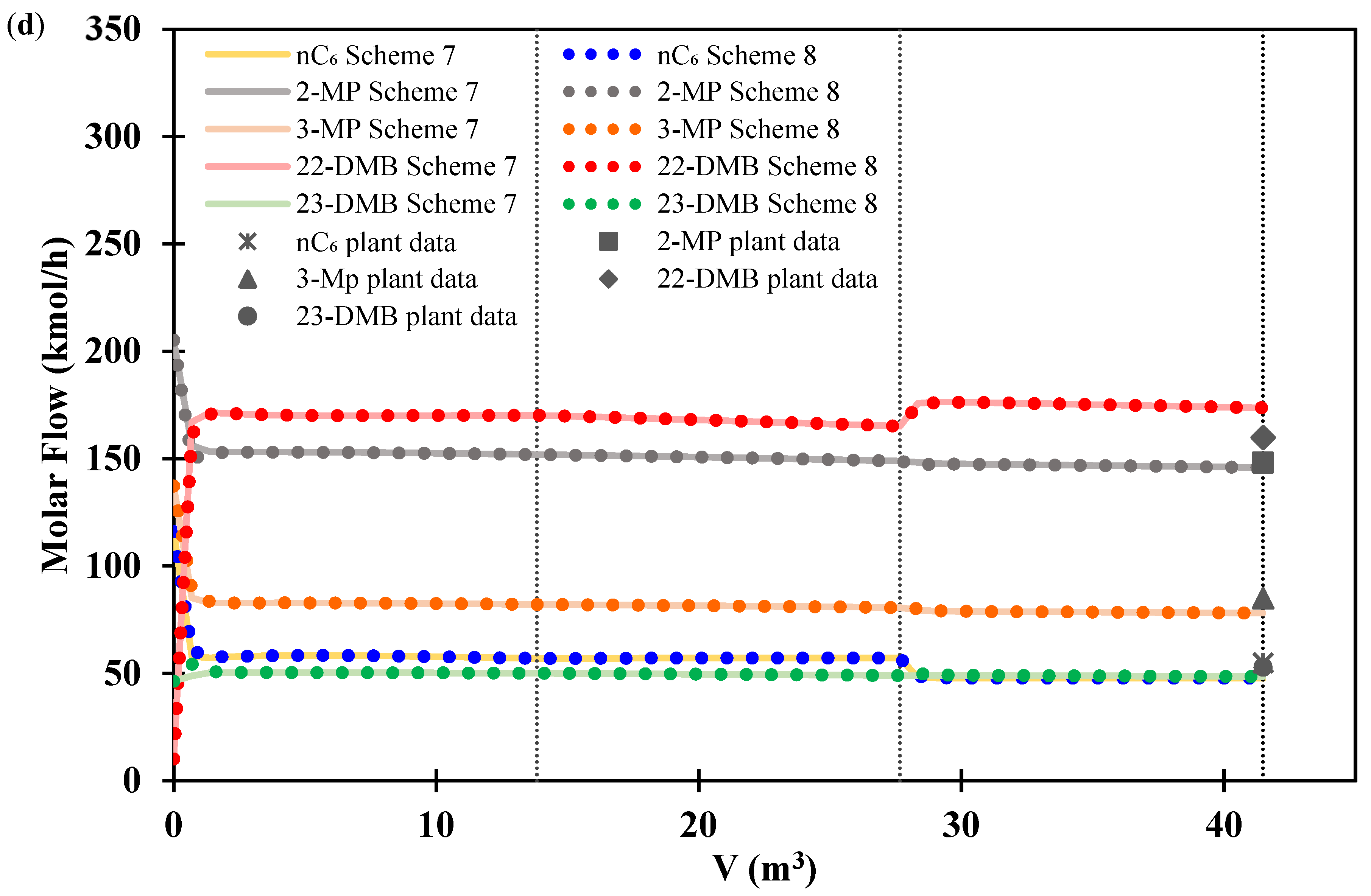
3.2. Isomerization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
| nC4 | n-Butane |
| iC4 | Isobutane |
| nC5 | n-Pentane |
| iC5 | Isopentane |
| B | Benzene |
| H2 | Hydrogen |
| CH | Cyclohexane |
| MCP | Methylcyclopentane |
| C3H8 | Propane |
| C2H6 | Ethane |
| CH4 | Methane |
References
- Mammadova, M.; Isayeva, Y.; Agayeva, S.; Zarbaliev, R.; Iskenderova, A.; Imanova, A.; Abasov, S. Isomerization conversion of straight run gasoline, gas gasoline and their mixture on Co/HZSM-5/ZrO2/SO4 composite catalyst. Process. Petrochem. Oil Refin. 2024, 25, 343–352. [Google Scholar] [CrossRef]
- Awadh, A.; Ammar, S. Synthesis of efficient bifunctional Pt/PWA-Nb2O5 nanocatalysts for catalytic isomerization of n-hexane: Experimental and optimization studies. Case Stud. Chem. Environ. Eng. 2024, 10, 100898. [Google Scholar] [CrossRef]
- Hassan, N.; Jalil, A.; Twu, L.; Fatah, N.; Hambali, H.; Hussain, I.; Firmansyah, M. Hydroisomerization of n-hexane over metal oxides-loaded fibrous silica catalyst for cleaner fuel production. Int. J. Hydrogen Energy 2023, 48, 20525–20537. [Google Scholar] [CrossRef]
- Song, Y.; Peng, B.; Wang, R.; Han, L.; Zhao, W.; Wang, L.; Lin, W. One-step desilication-recrystallization towards enhanced diffusion for Ni/ZSM-5-catalyzed n-hexane hydrogenative isomerization. J. Chem. Eng. 2023, 476, 1385–8947. [Google Scholar] [CrossRef]
- Dzhikiya, O.; Smolikov, M.; Belopukhov, E.; Yablokova, S.; Doronin, A.; Gulyaeva, T.; Belyi, A. A study of fluorine-containing catalysts based on MOR and BEA zeolites in isomerization of n-hexane. AIP Conf. Proc. 2020, 2285, 020005. [Google Scholar]
- Bolton, A.; Lanewala, M. A mechanism for the isomerization of the hexanes using zeolite catalysts. J. Catal. 1970, 18, 1–11. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Jarullah, A.T.; Abed, F.; Mujtaba, I. Modeling of an industrial naphtha isomerization reactor and development and assessment of a new isomerization process. Chem. Eng. Res. Des. 2018, 137, 33–46. [Google Scholar] [CrossRef]
- Said, M.; Ahmed, T.; Moustafa, T. Predictive Modeling and Optimization for an Industrial Penex Isomerization Unit: A Case Study. Energy Fuels 2014, 28, 7726–7741. [Google Scholar] [CrossRef]
- Cull, N.; Brenner, H. Applying Nonlinear Regression to Kinetics of Hexane Isomerization. Ind. Eng. Chem. 1961, 53, 833–836. [Google Scholar] [CrossRef]
- Evering, B.; Waugh, R. Catalytic Isomerization of Isomeric Hexanes. Ind. Eng. Chem. 1951, 43, 1820–1823. [Google Scholar] [CrossRef]
- Volkova, G.; Reshetnikov, S.; Shkuratova, L.; Budneva, A.; Paukshtis, E. n-Hexane skeletal isomerization over sulfated zirconia catalysts with different Lewis acidity. Chem. Eng. J. 2007, 134, 106–110. [Google Scholar] [CrossRef]
- Koncsag, C.; Tutun, I.; Safta, C. Study of C5/C6 isomerization on Pt/H-zeolite catalyst in industrial conditions. Ovidius Univ. Annal. Chem. 2013, 22, 102–106. [Google Scholar]
- Adžamić, T.; Mužic, M.; Adžamić, Z.; Sertić Biond, K. Isomerization of n-Hexane on Pt/SO4-ZrO2. GOMABN 2011, 50, 12–21. [Google Scholar]
- Chekantsev, N.; Gyngazova, M.; Ivanchina, E. Mathematical modeling of light naphtha (C5, C6) isomerization process. Chem. Eng. J. 2014, 238, 120–128. [Google Scholar] [CrossRef]
- Enikeeva, L.; Faskhutdinov, A.; Koledina, K.; Faskhutdinova, R.; Gubaydullin, I. Modeling and optimization of the catalytic isomerization of the pentane hexane fraction with maximization of individual high-octane components yield. React. Kinet. Mech. Catal. 2021, 133, 879–895. [Google Scholar] [CrossRef]
- Faskhutdinov, A.; Faskhutdinova, R.; Arefyev, I.; Enikeeva, L. Numerical simulation of the catalytic process of isomerization of pentane-hexane cut. J. Phys. Conf. Ser. 2019, 1368, 042016. [Google Scholar] [CrossRef]
- Diaz-Cervantes, D.K.; Castro-Agüero, A.; López-Medina, F.; Ortíz-Arroyo, A.; Pérez-Villaseñor, F.; Medina-Velázquez, D.Y.; Elías-Domínguez, A. A short reaction kinetic set for modeling the isomerization process considering rigorous chemical equilibrium. Next Res. 2025, 2, 100173. [Google Scholar] [CrossRef]
- Strang, G. Introduction to Linear Algebra, 5th ed.; Wellesley-Cambridge Press: Wellesley, MA, USA, 2022. [Google Scholar]
- Pines, H.; Kvetinskas, B.; Kassel, L.; Ipatieff, V. Determination of Equilibrium Constants for Butanes and Pentanes. J. Am. Chem. Soc. 1975, 67, 631–637. [Google Scholar] [CrossRef]
- PENEX UOP, Operation Manual. 1995.
- Smith, J.; Van Ness, H.; Abbott, M.; Swihart, M. Introduction to Chemical Engineering Thermodynamics, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2018. [Google Scholar]
- Tiscareño, L.F. ABC Para Comprender Reactores Químicos con Multireacción, 1st ed.; Reverté: Tampico, Mexico, 2008. [Google Scholar]
- Walas, S. Phase Equilibria in Chemical Engineering, 1st ed.; Butterworth: Boston, MA, USA, 1985. [Google Scholar]
- Fogler, S.H. Elements of Chemical Reaction Engineering; Michigan Prentice Hall: Boston, MA, USA, 2020. [Google Scholar]
- Honeywell. UniSim Design Suite R500TM; Honeywell: Charlotte, NC, USA, 2024. [Google Scholar]
- Stewart, W.; Caracotsios, M.; Sorensen, J. Non-Linear Estimation Parameters Using the GREG Program; Department of Chemical Engineering, University of Wisconsin-Madison: Madison, WI, USA, 1990. [Google Scholar]
- Chuzlov, V.A.; Chekantsev, N.V.; Ivanchina, E.D. Development of Complex Mathematical Model of Light Naphtha Isomerization and Rectification Processes. Procedia Chem. 2014, 10, 236–243. [Google Scholar] [CrossRef]
- Chuzlov, V.A.; Ivanchina, E.D.; Chekantsev, N.V.; Molotov, K.V. Efficiency improvement of the light gasoline fractions isomerization by mathematical modeling. Procedia Eng. 2025, 113, 131–137. [Google Scholar] [CrossRef]
- Padmavath, G.; Chaudhuri, K.K. Modelling and Simulation of Commercial Catalytic Naphtha Reformers. Can. J. Chem. Eng. 1997, 75, 930–937. [Google Scholar]
- Ancheyta-Jufirez, J.; Villafuerte-Macias, E. Experimental validation of a kinetic model for naphtha reforming. Stud. Surf. Sci. Catal. 2001, 133, 615–618. [Google Scholar]




| Reaction Schemes | |||
|---|---|---|---|
| 1 [8] | 2 [9] | 3 [12] | 4 [13] |
| 5 [14] | 6 | 7 | 8 |
| No. | Reaction |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 |
| No. | ||||
|---|---|---|---|---|
| 1 | 2.1404 × 1015 | 79,100.00 | −2.1384 | 1166.4 |
| 2 | 3.3047 × 1015 | 79,411.60 | −0.6308 | 745.10 |
| 3 | Values of the respective C6 series scheme | |||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | 7.8288 × 1014 | 87,250.67 | ||
| 9 | 3.3698 × 108 | 54,405.67 | ||
| 10 | 1.2296 × 106 | 31,903.05 | ||
| 11 | 9.5595 × 1012 | 80,522.16 | ||
| 12 | 2.3764 × 1013 | 75,961.05 | ||
| 13 | 3.2298 × 109 | 62,673.40 | ||
| 14 | 9.3115 × 104 | 29,091.70 | ||
| 15 | 1.6746 × 1010 | 71,126.52 | ||
| 16 | 7.4853 × 1011 | 71,437.13 | ||
| 17 | 3.3165 × 109 | 71,546.33 | ||
| Reaction | ||||
|---|---|---|---|---|
| 2.0911 × 1016 | 78,300.00 | −2.6386 | 1580.30 | |
| 2.2400 × 1017 | 86,300.00 | −2.9883 | 1464.30 | |
| 4.8600 × 1019 | 80,600.00 | −5.6357 | 3073.50 | |
| 2.9142 × 1013 | 74,921.73 | −4.0006 | 1690.20 | |
| 3.4772 × 1015 | 79,357.62 | −4.1394 | 2285.10 | |
| 9.3100 × 1015 | 86,300.00 | −0.3496 | −116.09 | |
| 5.2100 × 1015 | 81,800.00 | −1.3620 | 109.86 | |
| 6.8600 × 1016 | 81,600.00 | −2.3747 | 335.96 | |
| 9.1100 × 1016 | 91,800.00 | −1.5014 | 705.26 | |
| 2.2400 × 1017 | 86,300.00 | −1.0125 | 226.02 | |
| 5.5137 × 1018 | 89,900.00 | −0.1388 | 594.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Cervantes, D.K.; Elías-Domínguez, A.; Castro-Agüero, Á.; Pérez-Villaseñor, F.; Ortíz-Arroyo, A.; López-Medina, F.; López-López, E.; Osorio-de-la-Rosa, E. A Comparative Study of Kinetic Reaction Schemes for the Isomerization Process of the C6 Series. Appl. Sci. 2025, 15, 4429. https://doi.org/10.3390/app15084429
Díaz-Cervantes DK, Elías-Domínguez A, Castro-Agüero Á, Pérez-Villaseñor F, Ortíz-Arroyo A, López-Medina F, López-López E, Osorio-de-la-Rosa E. A Comparative Study of Kinetic Reaction Schemes for the Isomerization Process of the C6 Series. Applied Sciences. 2025; 15(8):4429. https://doi.org/10.3390/app15084429
Chicago/Turabian StyleDíaz-Cervantes, Diana K., Arturo Elías-Domínguez, Ángel Castro-Agüero, Fernando Pérez-Villaseñor, Arturo Ortíz-Arroyo, Friné López-Medina, Eduardo López-López, and Edith Osorio-de-la-Rosa. 2025. "A Comparative Study of Kinetic Reaction Schemes for the Isomerization Process of the C6 Series" Applied Sciences 15, no. 8: 4429. https://doi.org/10.3390/app15084429
APA StyleDíaz-Cervantes, D. K., Elías-Domínguez, A., Castro-Agüero, Á., Pérez-Villaseñor, F., Ortíz-Arroyo, A., López-Medina, F., López-López, E., & Osorio-de-la-Rosa, E. (2025). A Comparative Study of Kinetic Reaction Schemes for the Isomerization Process of the C6 Series. Applied Sciences, 15(8), 4429. https://doi.org/10.3390/app15084429







