Design of a Double-Matched Cross-Polar Single Antenna Harmonic Tag
Abstract
:1. Introduction
- A new concept of a one-port harmonic transponder matched at both frequencies;
- A new exploitation of the modal behavior of annular ring antenna that allows dual polarization using only one compact antenna;
- The insensitivity of the tag to the object on which it will be placed (e.g., it can be wearable) thanks to the use of microstrip technology.
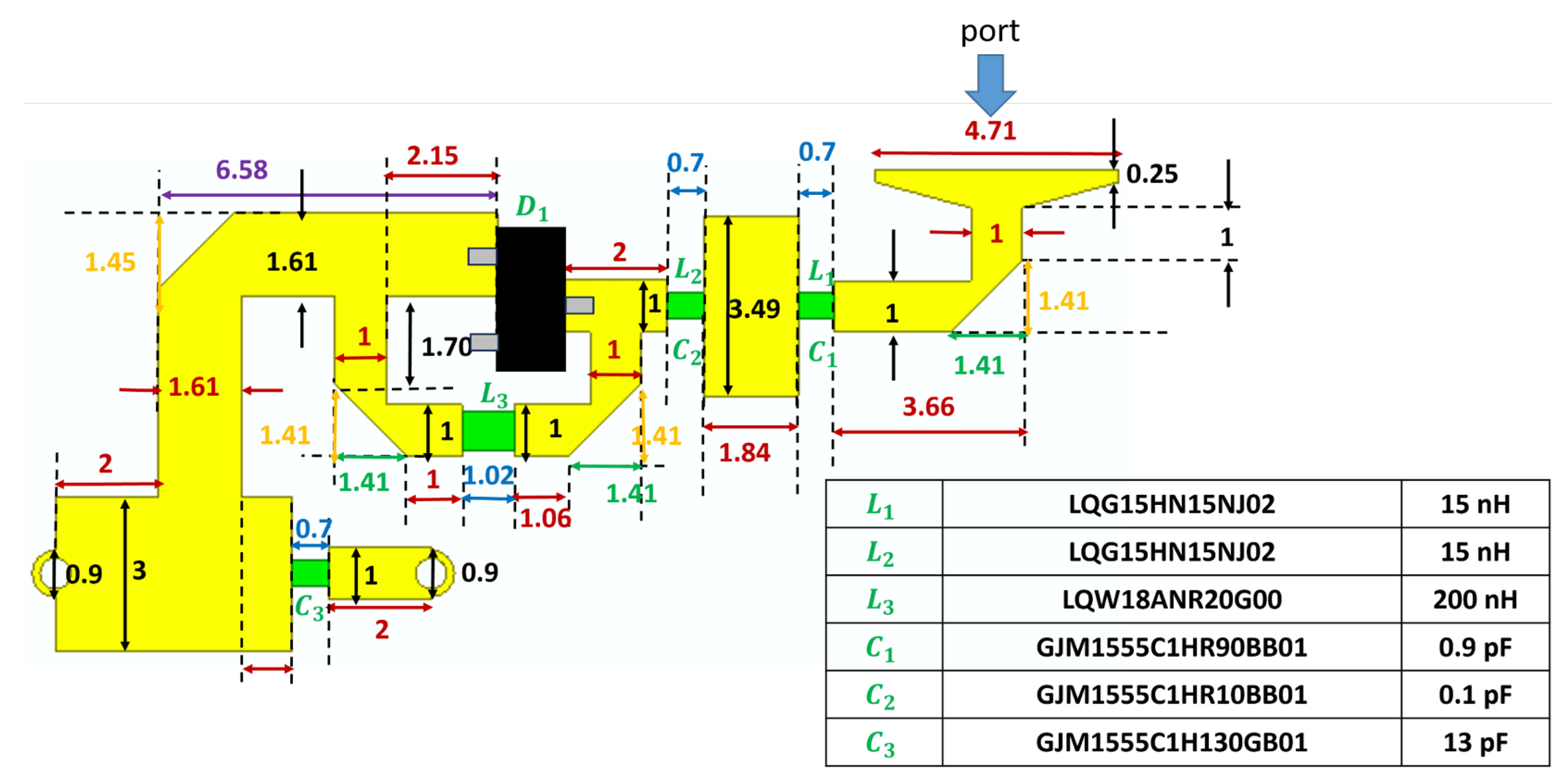
2. Doubled-Matched Doubler Circuit
3. Antenna Design
3.1. Rationale of the Antenna Design Procedure
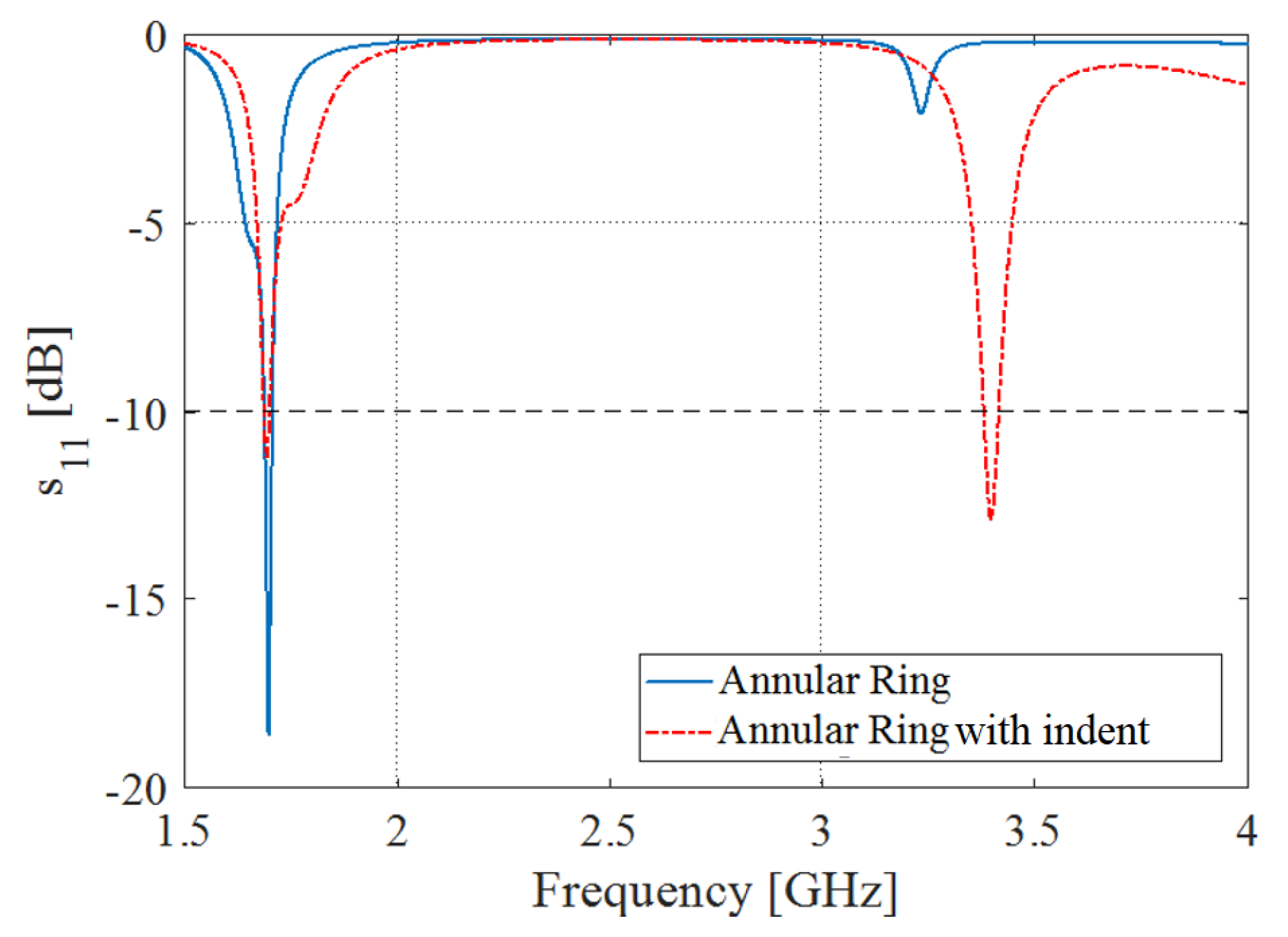
3.2. Antenna Design Procedure
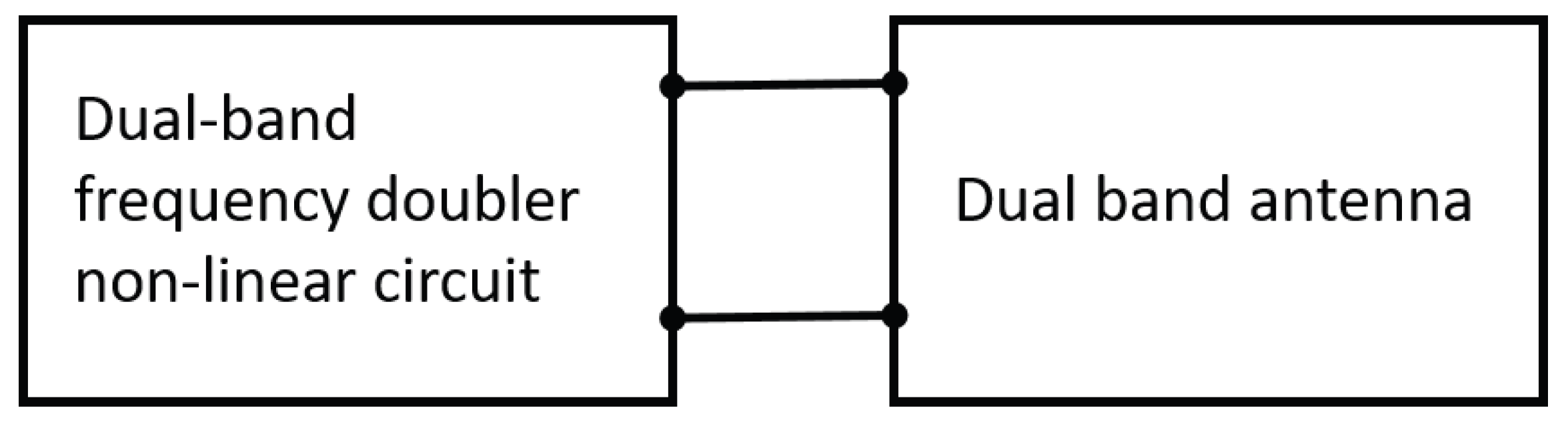
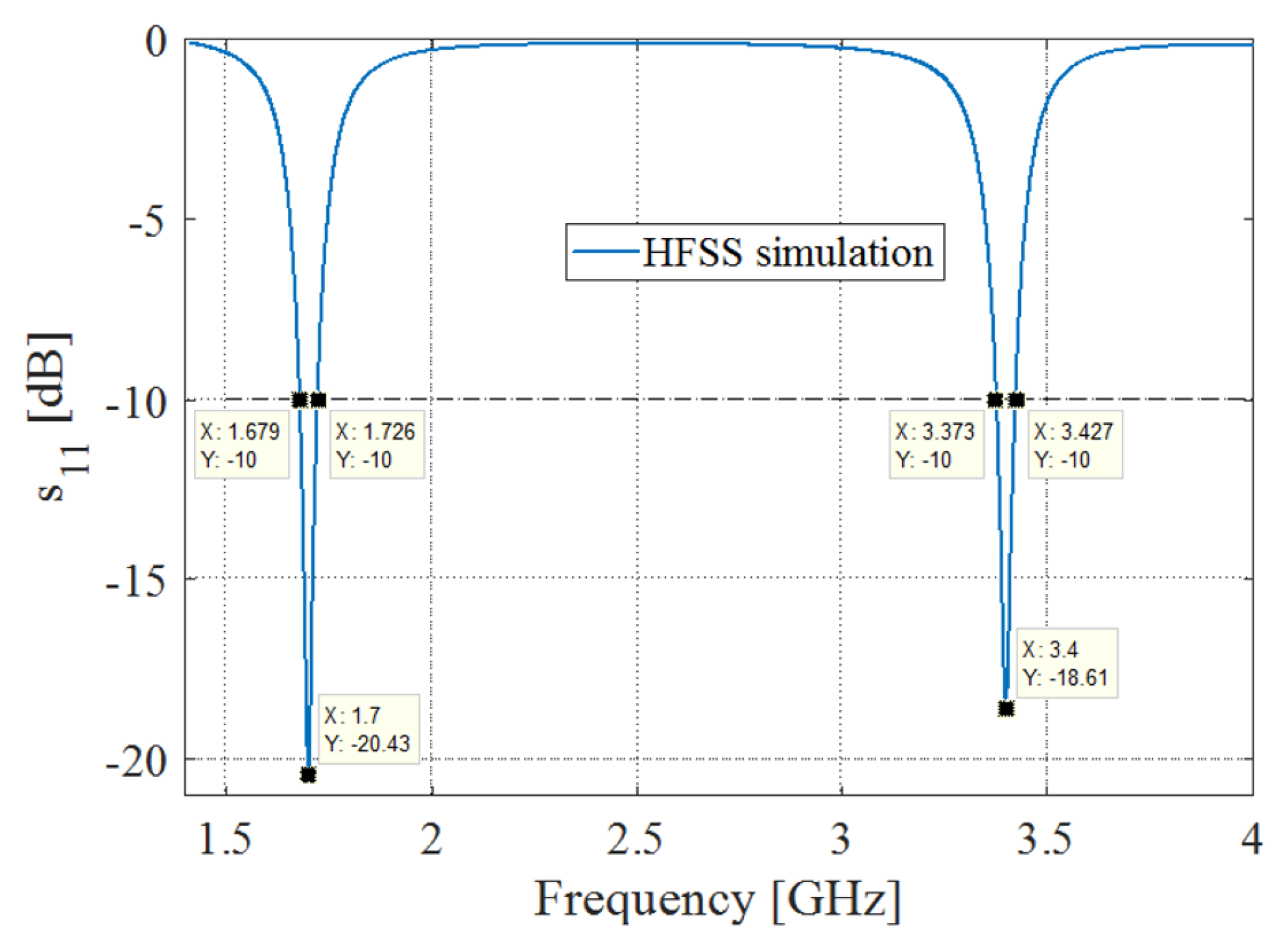
4. Electromagnetic Analysis of Assembled Doubler Network and Antenna
5. Prototype Realization and Measurements
5.1. Measurements of the Realized Doubler Circuit
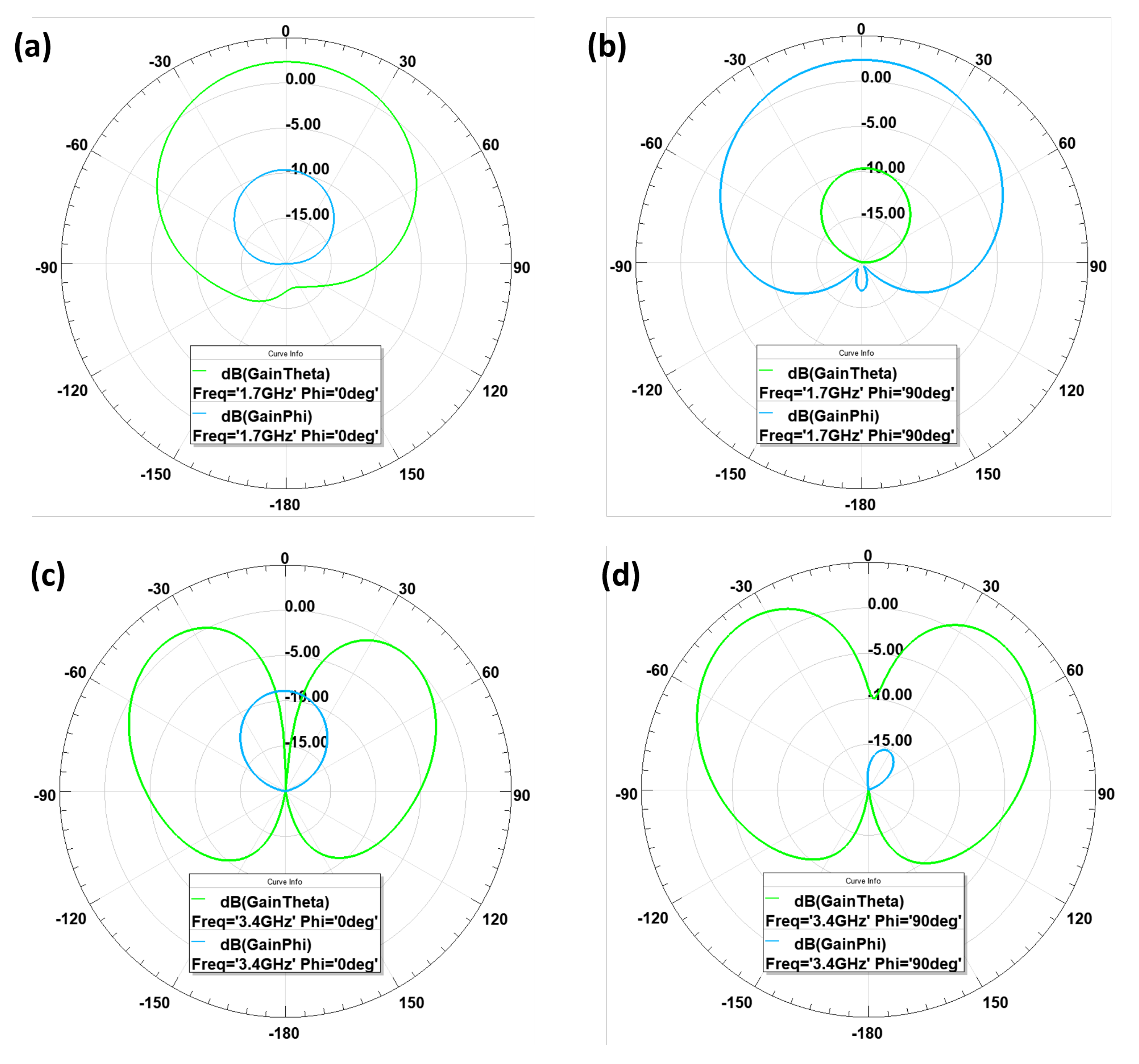
5.2. Measurements of the Realized Antenna
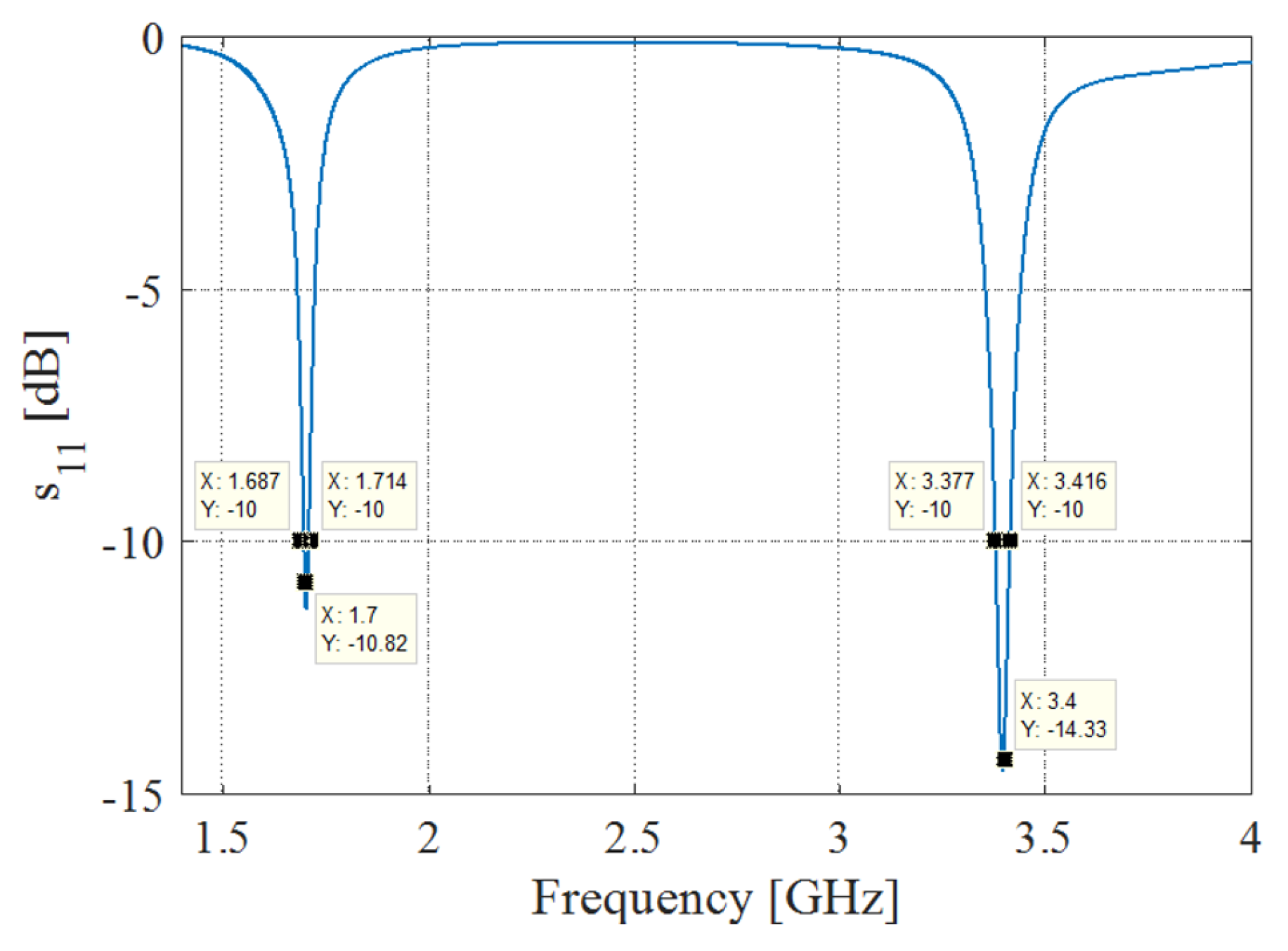
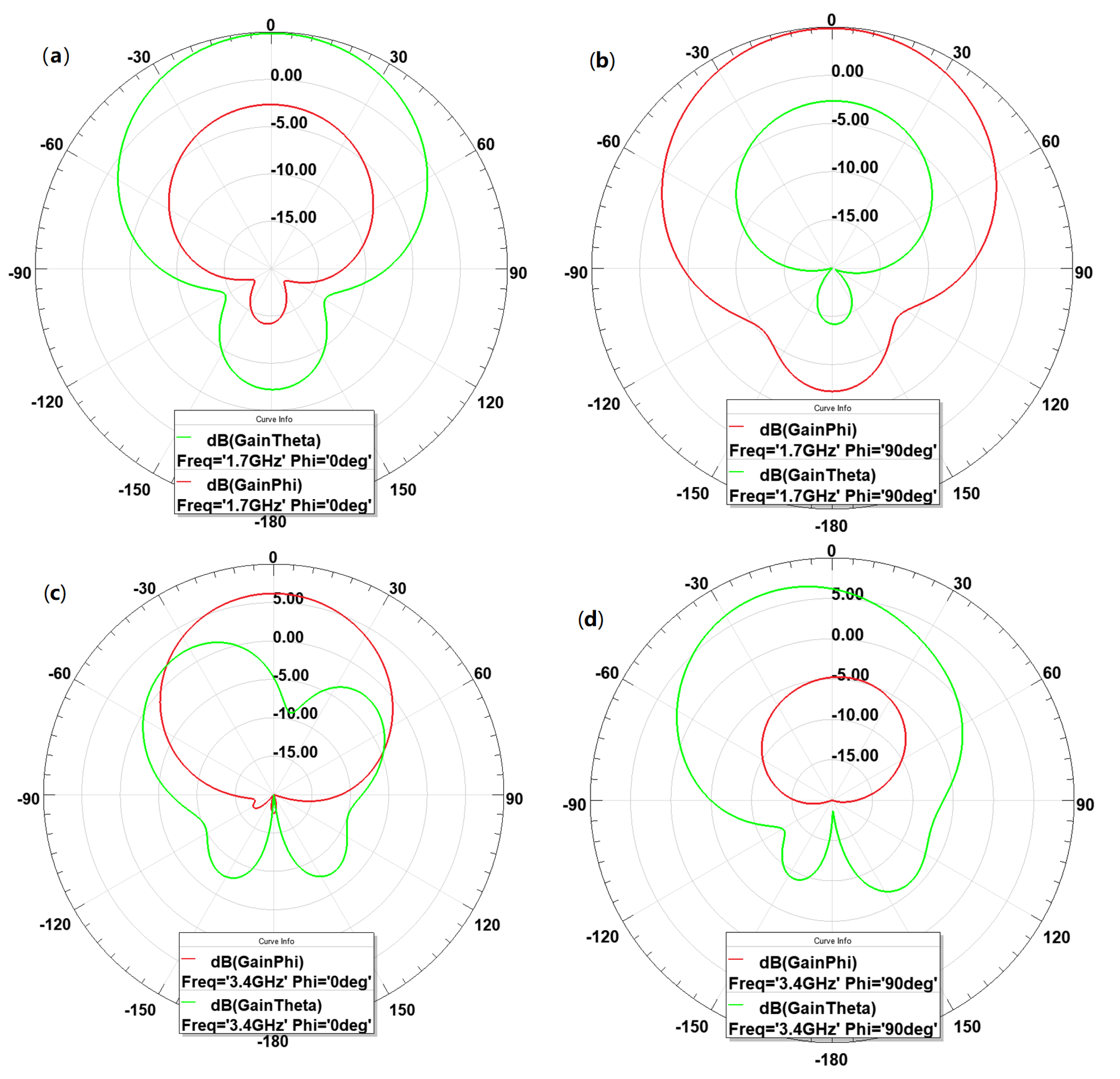
5.3. Measurements of the Complete Tag
6. Discussion of Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- DiNatale, A.; DiCarlofelice, A.; DiGiampaolo, E. A Crack Mouth Opening Displacement Gauge Made with Passive UHF RFID Technology. IEEE Sensors J. 2022, 22, 174–181. [Google Scholar] [CrossRef]
- Zhang, D.; Yang, L.T.; Chen, M.; Zhao, S.; Guo, M.; Zhang, Y. Real-Time Locating Systems Using Active RFID for Internet of Things. IEEE Syst. J. 2016, 10, 1226–1235. [Google Scholar] [CrossRef]
- Casella, G.; Bigliardi, B.; Bottani, E. The evolution of RFID technology in the logistics field: A review. Procedia Comput. Sci. 2022, 200, 1582–1592. [Google Scholar] [CrossRef]
- Potyrailo, R.A.; Nagraj, N.; Tang, Z.; Mondello, F.J.; Surman, C.; Morris, W. Battery-free Radio Frequency Identification (RFID) Sensors for Food Quality and Safety. J. Agric. Food Chem. 2012, 60, 8535–8543. [Google Scholar] [CrossRef]
- Hughes, J.D.; Occhiuzzi, C.; Batchelor, J.; Marrocco, G. Twin-Grid Array as 3.6 GHz Epidermal Antenna for Potential Backscattering 5G Communication. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 2092–2096. [Google Scholar] [CrossRef]
- Lavric, A.; Popa, V. A LoRaWAN: Long range wide area networks study. In Proceedings of the 2017 International Conference on Electromechanical and Power Systems (SIELMEN), Iasi, Romania, 11–13 October 2017; pp. 417–420. [Google Scholar] [CrossRef]
- Nikitin, P.; Rao, K. Performance limitations of passive UHF RFID systems. In Proceedings of the 2006 IEEE Antennas and Propagation Society International Symposium, Albuquerque, NM, USA, 9–14 July 2006; pp. 1011–1014. [Google Scholar] [CrossRef]
- Di Carlofelice, A.; Di Giampaolo, E.; Tognolatti, P. A Van-Atta UWB Cross-Polar Chipless Tag to be Used as a Sensor. In Proceedings of the 2023 Photonics & Electromagnetics Research Symposium (PIERS), Prague, Czech Republic, 3–6 July 2023; pp. 698–702. [Google Scholar] [CrossRef]
- Athauda, T.; Karmakar, N. Chipped Versus Chipless RF Identification: A Comprehensive Review. IEEE Microw. Mag. 2019, 20, 47–57. [Google Scholar] [CrossRef]
- Mondal, S.; Kumar, D.; Chahal, P. Recent Advances and Applications of Passive Harmonic RFID Systems: A Review. Micromachines 2021, 12, 420. [Google Scholar] [CrossRef]
- Lach, M.; Hani, M.; Looschen, C.; Buchberger, C.; Biebl, E. Evaluation of UHF-RFID Tag Performance Considering Near-Field and Detuning Effects on Various Dielectric and Inhomogeneous Application Surfaces. In Proceedings of the 2021 Kleinheubach Conference, Miltenberg, Germany, 28–30 September 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Mei, L.H.; Yue, W.J.; Kun, X.L.; Xin, Y.T. Influence of UHF tags in the different material surface to RFID system. In Proceedings of the 2014 3rd Asia-Pacific Conference on Antennas and Propagation, Harbin, China, 26–29 July 2014; pp. 713–715. [Google Scholar] [CrossRef]
- Zhu, J.; Li, Y.; Jin, C.; Liu, X.; Liu, H. Optimum Separation for Performance Improvement of RFID Solenoid Coil Antenna in Metallic Environments. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1611–1615. [Google Scholar] [CrossRef]
- Faudzi, N.M.; Ali, M.T.; Ismail, I.; Jumaat, H.; Sukaimi, N.H.M. Compact microstrip patch UHF-RFID tag antenna for metal object. In Proceedings of the 2014 IEEE Symposium on Wireless Technology and Applications (ISWTA), Kuala Lumpur, Malaysia, 28 September–1 October 2014; pp. 160–164. [Google Scholar] [CrossRef]
- Li, B.; He, Y.; Zuo, L.; Long, Y. Metric of the Application Environment Impact to the Passive UHF RFID System. IEEE Trans. Instrum. Meas. 2014, 63, 2387–2395. [Google Scholar] [CrossRef]
- Jouali, R.; Aoutoul, M.; Ouahmane, H.; Ahmad, S.; Had, A.; El Moukhtafi, F.; Parchin, N.O.; See, C.H.; Abd-Alhameed, R. Design of an Analog RFID-Based Tag Antenna with Opened Circuited L-Shaped Stubs for Applications in Localization. Electronics 2022, 11, 1027. [Google Scholar] [CrossRef]
- Balog, M.; Szilagyi, E.; Dupláková, D.; Mindas, M. Effect Verification of External Factor to Readability of RFID Transponder Using Least Square Method. Measurement 2016. [Google Scholar] [CrossRef]
- Dupláková, D.; Knapčíková, L.; Hatala, M.; Szilagyi, E. Mathematical Modeling of Temperature Characteristics of RFID Tags with their Subsequent Application in Engineering Production. TEM Journa 2016. [Google Scholar] [CrossRef]
- Colpitts, B.; Boiteau, G. Harmonic radar transceiver design: Miniature tags for insect tracking. IEEE Trans. Antennas Propag. 2004, 52, 2825–2832. [Google Scholar] [CrossRef]
- Recco. Available online: https://recco.com/technology/ (accessed on 7 November 2023).
- Palazzi, V.; Alimenti, F.; Kalialakis, C.; Mezzanotte, P.; Georgiadis, A.; Roselli, L. Highly Integrable Paper-Based Harmonic Transponder for Low-Power and Long-Range IoT Applications. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3196–3199. [Google Scholar] [CrossRef]
- Rasilainen, K.; Ilvonen, J.; Lehtovuori, A.; Hannula, J.M.; Viikari, V. On Design and Evaluation of Harmonic Transponders. IEEE Trans. Antennas Propag. 2015, 63, 15–23. [Google Scholar] [CrossRef]
- Gu, X.; Srinaga, N.N.; Guo, L.; Hemour, S.; Wu, K. Diplexer-Based Fully Passive Harmonic Transponder for Sub-6-GHz 5G-Compatible IoT Applications. IEEE Trans. Microw. Theory Tech. 2019, 67, 1675–1687. [Google Scholar] [CrossRef]
- Pisa, S.; Trifiletti, A.; Tommasino, P.; Monsurrò, P.; Tognolatti, P.; Leuzzi, G.; Di Carlofelice, A.; Di Giampaolo, E. An Intermodulation Radar for Non-Linear Target and Transceiver Detection. Sensors 2024, 24, 1433. [Google Scholar] [CrossRef]
- Palazzi, V.; Alimenti, F.; Virili, M.; Mariotti, C.; Orecchini, G.; Mezzanotte, P.; Roselli, L. A novel compact harmonic RFID sensor in paper substrate based on a variable attenuator and nested antennas. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Ghazali, M.I.M.; Karuppuswami, S.; Chahal, P. Embedded Passive RF Tags towards Intrinsically Locatable Buried Plastic Materials. In Proceedings of the 2016 IEEE 66th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 31 May–3 June 2016; pp. 2575–2580. [Google Scholar] [CrossRef]
- Mondal, S.; Chahal, P. A Passive Harmonic RFID Tag and Interrogator Development. IEEE J. Radio Freq. Identif. 2019, 3, 98–107. [Google Scholar] [CrossRef]
- Yu, F.; Lyon, K.G.; Kan, E.C. A Novel Passive RFID Transponder Using Harmonic Generation of Nonlinear Transmission Lines. IEEE Trans. Microw. Theory Tech. 2010, 58, 4121–4127. [Google Scholar] [CrossRef]
- Zhang, L.; Karasiewicz, D.; Cifctioglu, B.; Wu, H. A 1.6-to-3.2/4.8 GHz dual-modulus injection-locked frequency multiplier in 0.18μm digital CMOS. In Proceedings of the 2008 IEEE Radio Frequency Integrated Circuits Symposium, Atlanta, GA, USA, 15–17 June 2008; pp. 427–430. [Google Scholar] [CrossRef]
- Wang, C.C.; She, H.C.; Hu, R. A 1.2 GHz programmable DLL-based frequency multiplier for wireless applications. In Proceedings of the 9th International Conference on Electronics, Circuits and Systems, Dubrovnik, Croatia, 15–18 September 2002; Volume 1, pp. 69–72. [Google Scholar] [CrossRef]
- ERC Report 025: The European Table of Frequency Allocations and Applications in the Frequency Range 8.3 kHz to 3000 GHz. Available online: https://docdb.cept.org/document/593 (accessed on 4 April 2025).
- Murata Manufacturing Co., Ltd. Available online: https://www.murata.com/en-eu (accessed on 7 November 2023).
- DiCarlofelice, A.; DiGiampaolo, E.; Tognolatti, P. A Procedure to Design Feasible Dual Band Matching Networks with Minimum Complexity. Electronics 2022, 11, 3569. [Google Scholar] [CrossRef]
- AWR Microwave Office Software. Available online: https://www.cadence.com/ko_KR/home/tools/system-analysis/rf-microwave-design/awr-microwave-office.html (accessed on 7 November 2023).
- Broadcom Inc. Available online: https://www.broadcom.com/ (accessed on 13 April 2025).
- Kubina, B.; Romeu, J.; Mandel, C.; Schüßler, M.; Jakoby, R. Quasi-chipless wireless temperature sensor based on harmonic radar. Electron. Lett. 2014, 50, 86–88. [Google Scholar] [CrossRef]
- Ansys HFSS—3D High Frequency Simulation Software. Available online: https://www.ansys.com/products/electronics/ansys-hfss (accessed on 7 November 2023).
- Row, J.S. Dual-frequency circularly polarised annular-ring microstrip antenna. Electron. Lett. 2004, 40, 153–154. [Google Scholar] [CrossRef]
- James, J.R.; Hall, P.S. Handbook of Microstrip Antennas; Peter Peregrinus Ltd.: London, UK, 1989. [Google Scholar]


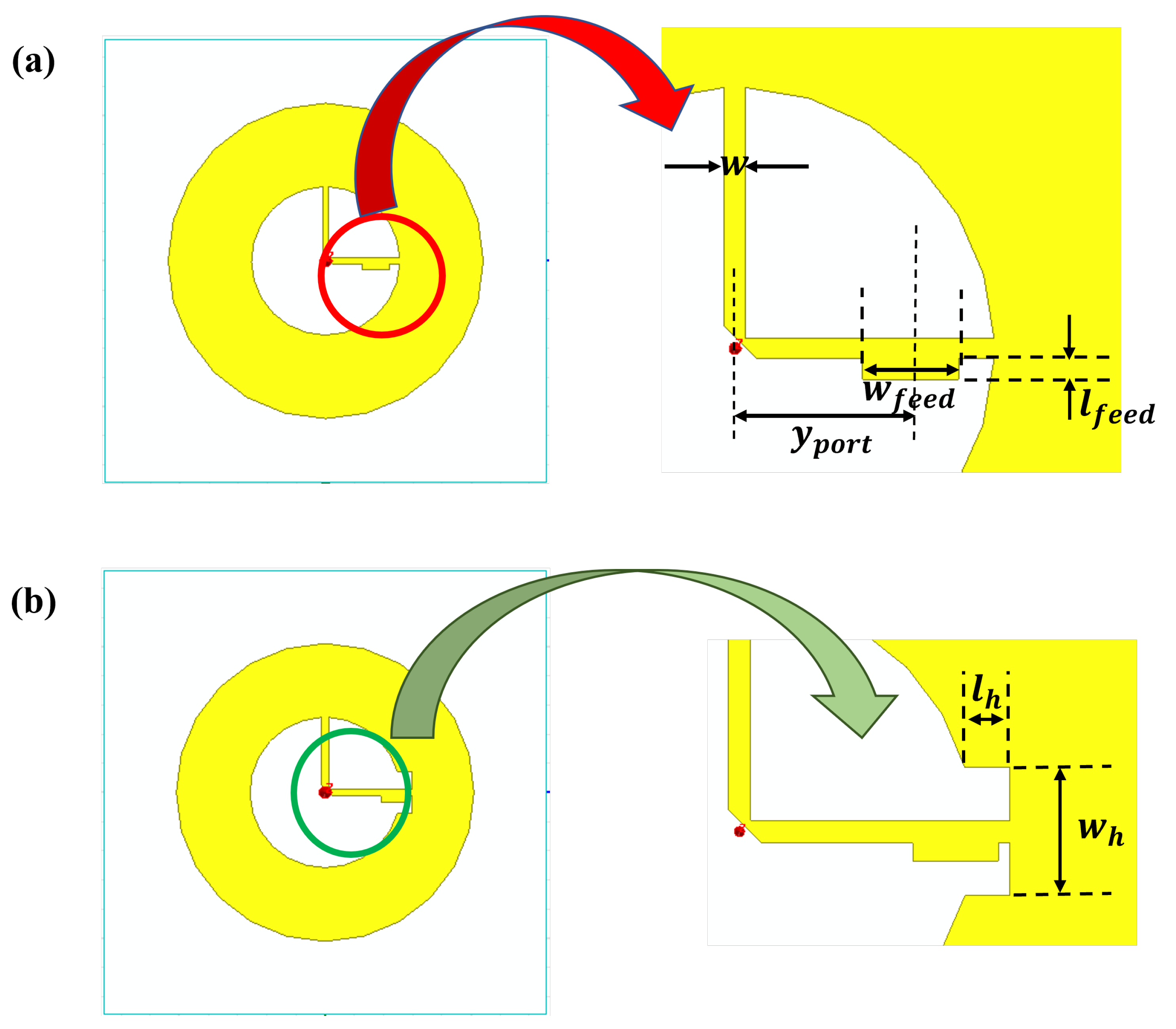

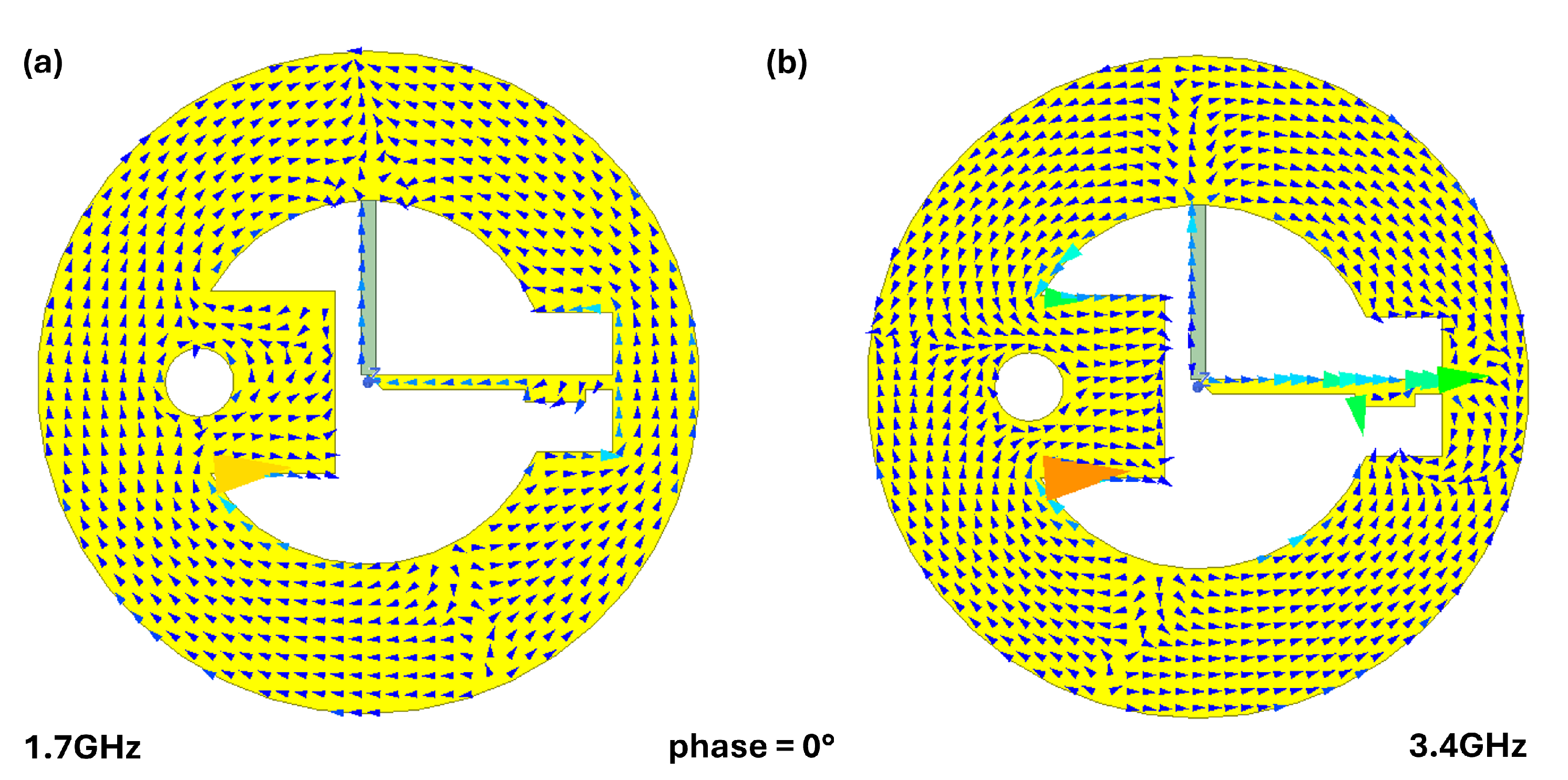
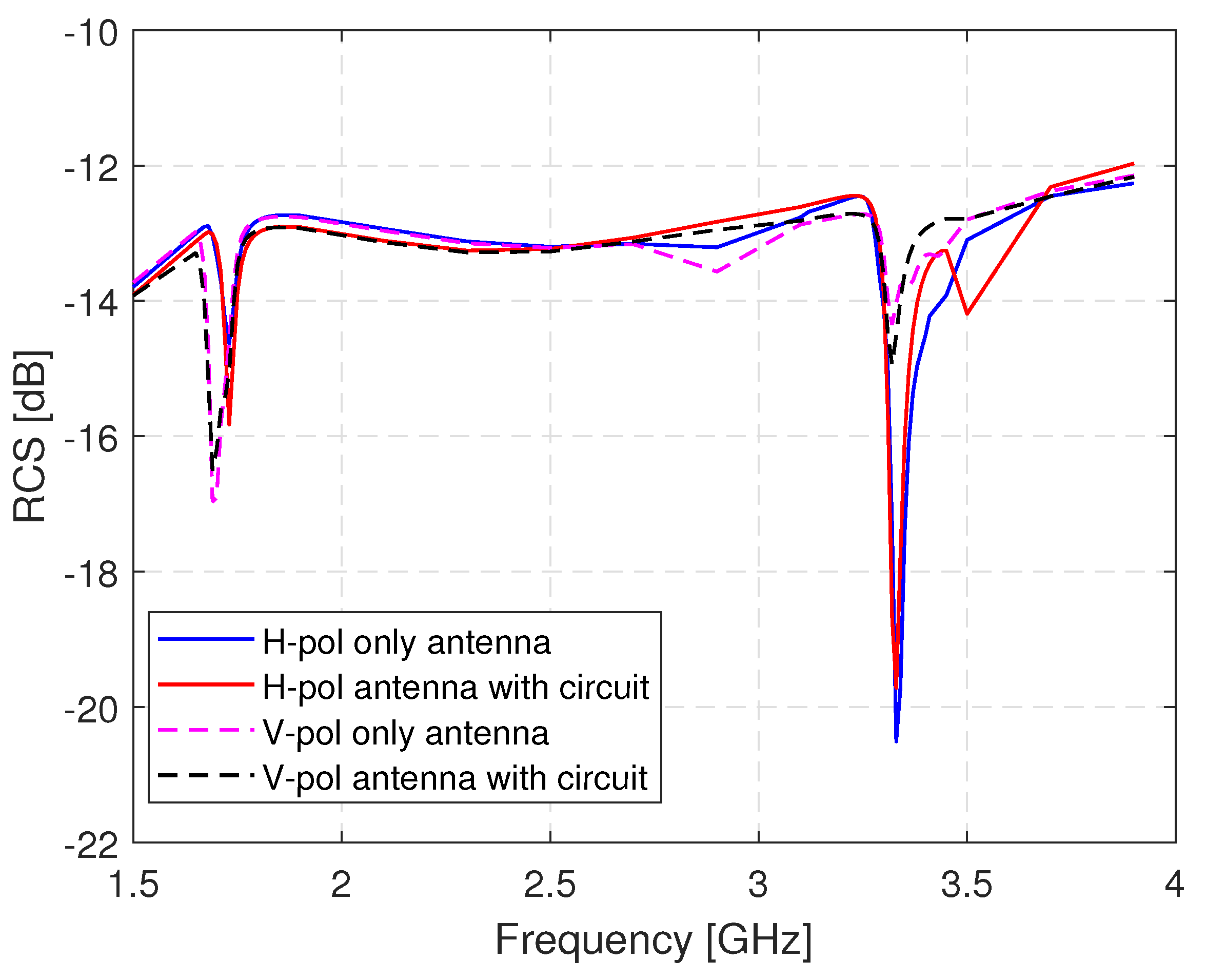

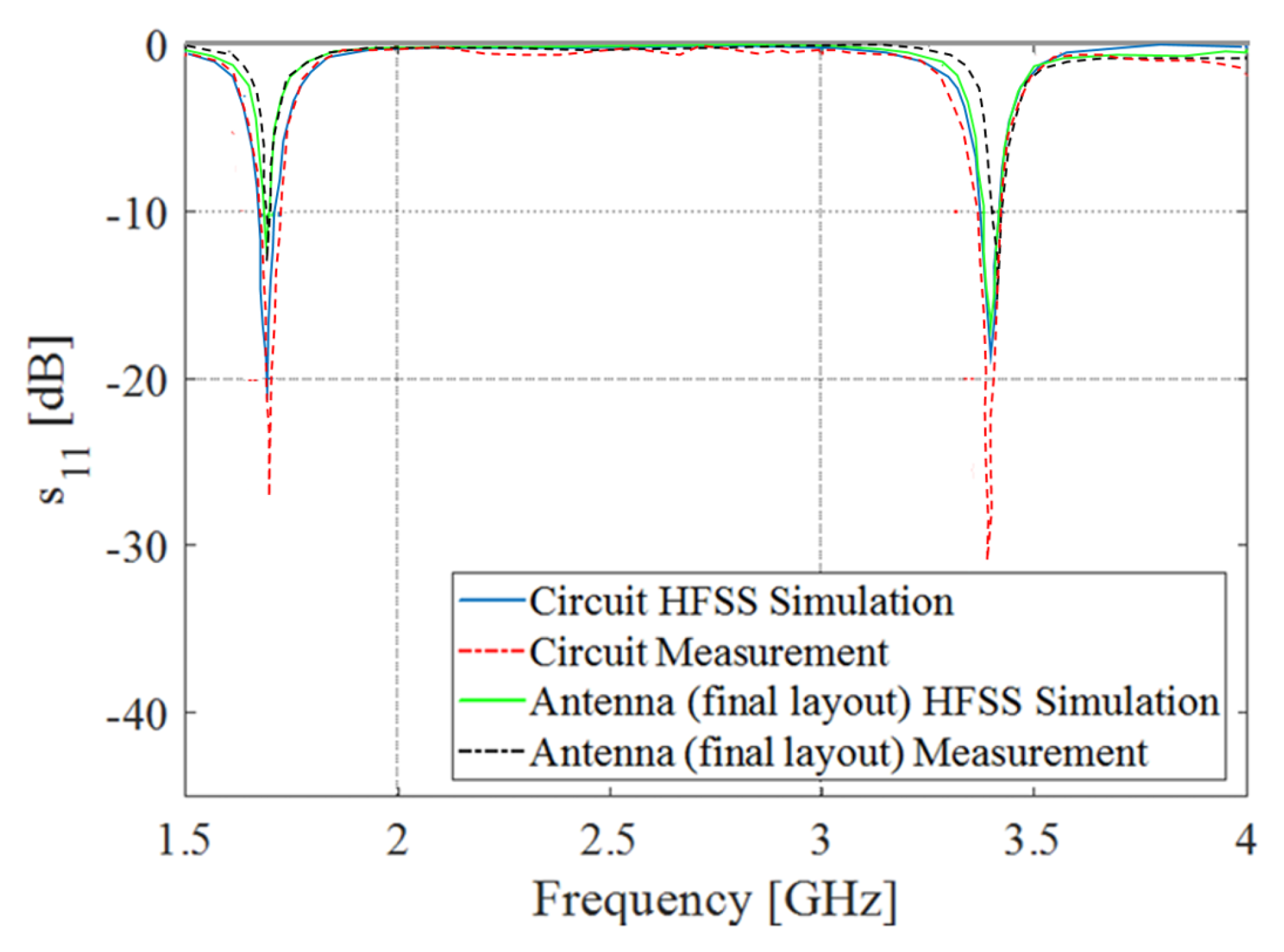
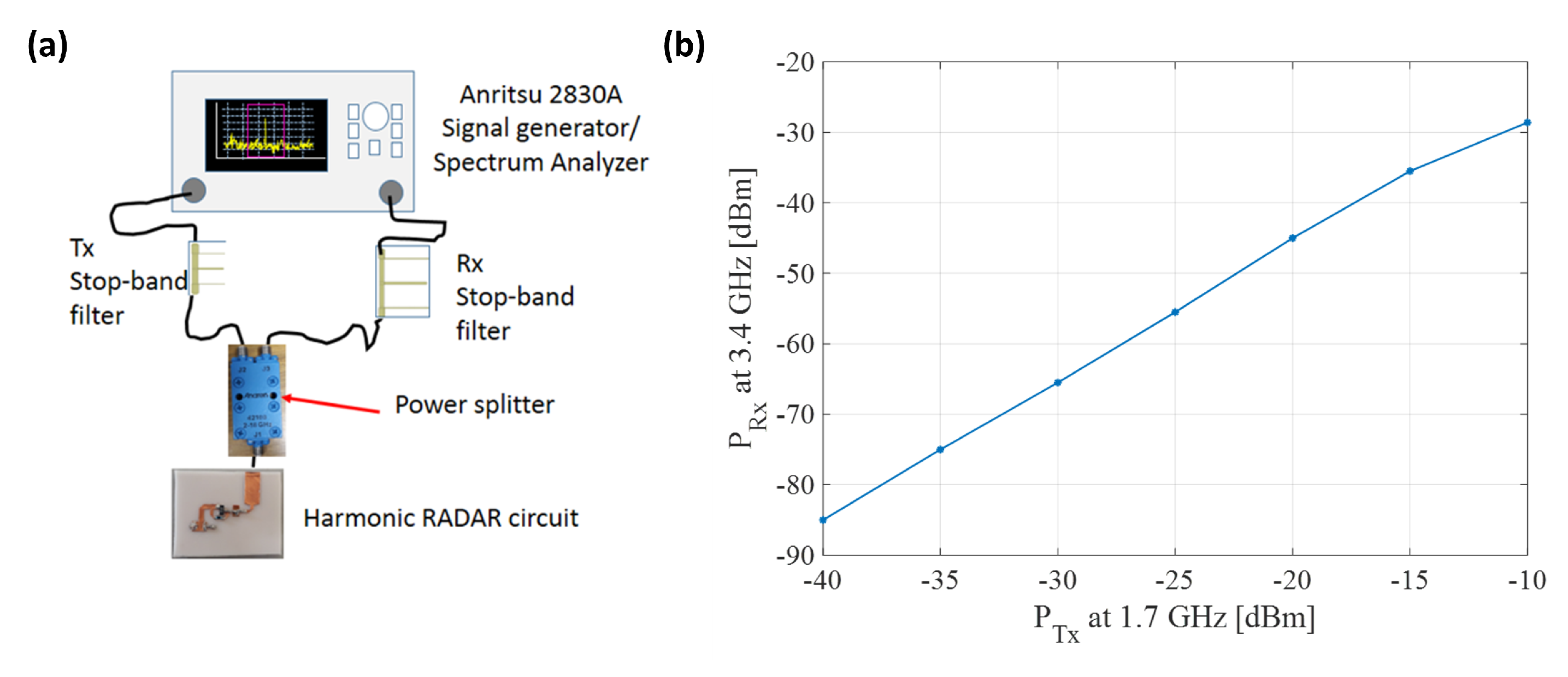
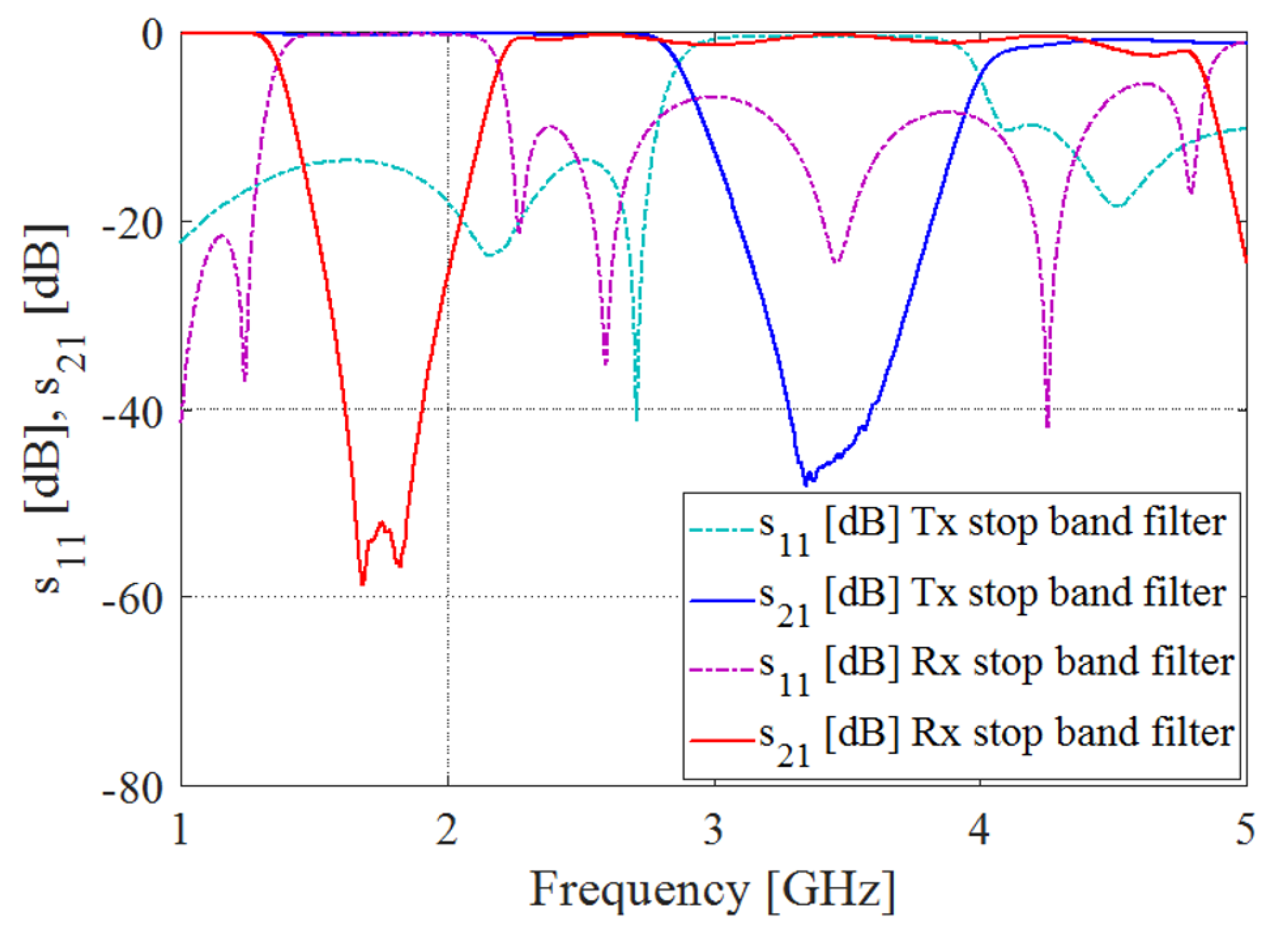


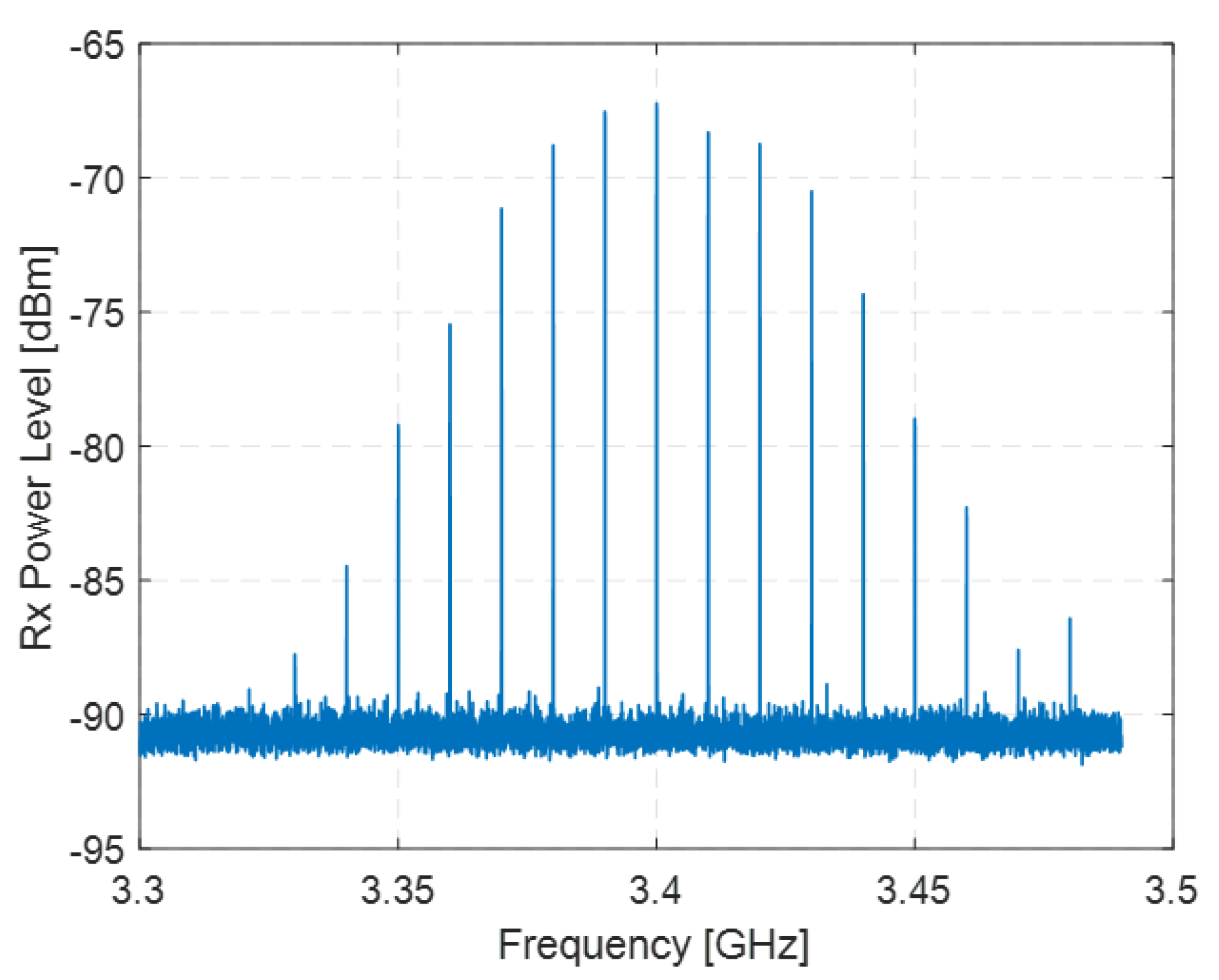
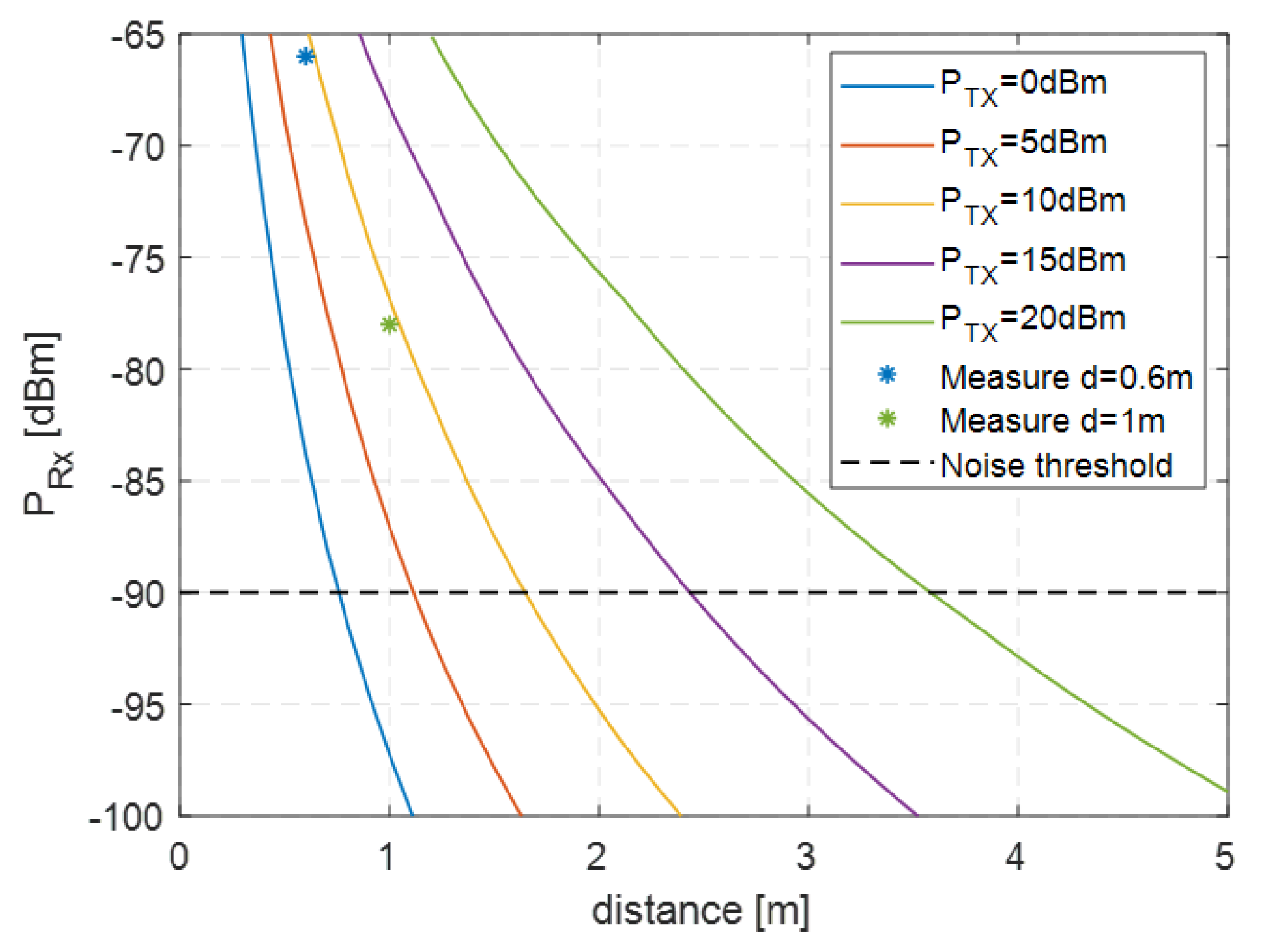
| Parameters | [mm] |
|---|---|
| 14.52 | |
| 27.07 | |
| lfeed | 1 |
| wfeed | 4.71 |
| w | 1.14 |
| yport | 14.9 |
| lh | 4.91 |
| wh | 11.1 |
| lstub | 12.12 |
| wstub | 15 |
| rcirc-slot | 2.81 |
| ycirc-slot | 4.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
DiCarlofelice, A.; DiNatale, A.; DiGiampaolo, E.; Tognolatti, P. Design of a Double-Matched Cross-Polar Single Antenna Harmonic Tag. Appl. Sci. 2025, 15, 4590. https://doi.org/10.3390/app15084590
DiCarlofelice A, DiNatale A, DiGiampaolo E, Tognolatti P. Design of a Double-Matched Cross-Polar Single Antenna Harmonic Tag. Applied Sciences. 2025; 15(8):4590. https://doi.org/10.3390/app15084590
Chicago/Turabian StyleDiCarlofelice, Alessandro, Antonio DiNatale, Emidio DiGiampaolo, and Piero Tognolatti. 2025. "Design of a Double-Matched Cross-Polar Single Antenna Harmonic Tag" Applied Sciences 15, no. 8: 4590. https://doi.org/10.3390/app15084590
APA StyleDiCarlofelice, A., DiNatale, A., DiGiampaolo, E., & Tognolatti, P. (2025). Design of a Double-Matched Cross-Polar Single Antenna Harmonic Tag. Applied Sciences, 15(8), 4590. https://doi.org/10.3390/app15084590







