Service Management of Employee Shuttle Service Under Inhomogeneous Fleet Constraints Using Dynamic Linear Programming: A Case Study
Abstract
1. Introduction
- Reduce fleet operational costs by optimizing the number and type of service vehicles.
- Improve vehicle utilization rates by adjusting routes and schedules based on demand fluctuations.
- Enhance environmental sustainability by decreasing fuel consumption and lowering emissions.
- Provide a flexible, scalable transport model applicable to other industrial and corporate mobility networks.
2. Literature Review
2.1. Impact of Demand and Service Management on Traffic Density
2.2. Overview of Previous Studies
2.3. Study Objective and Expectations
3. Materials and Methods
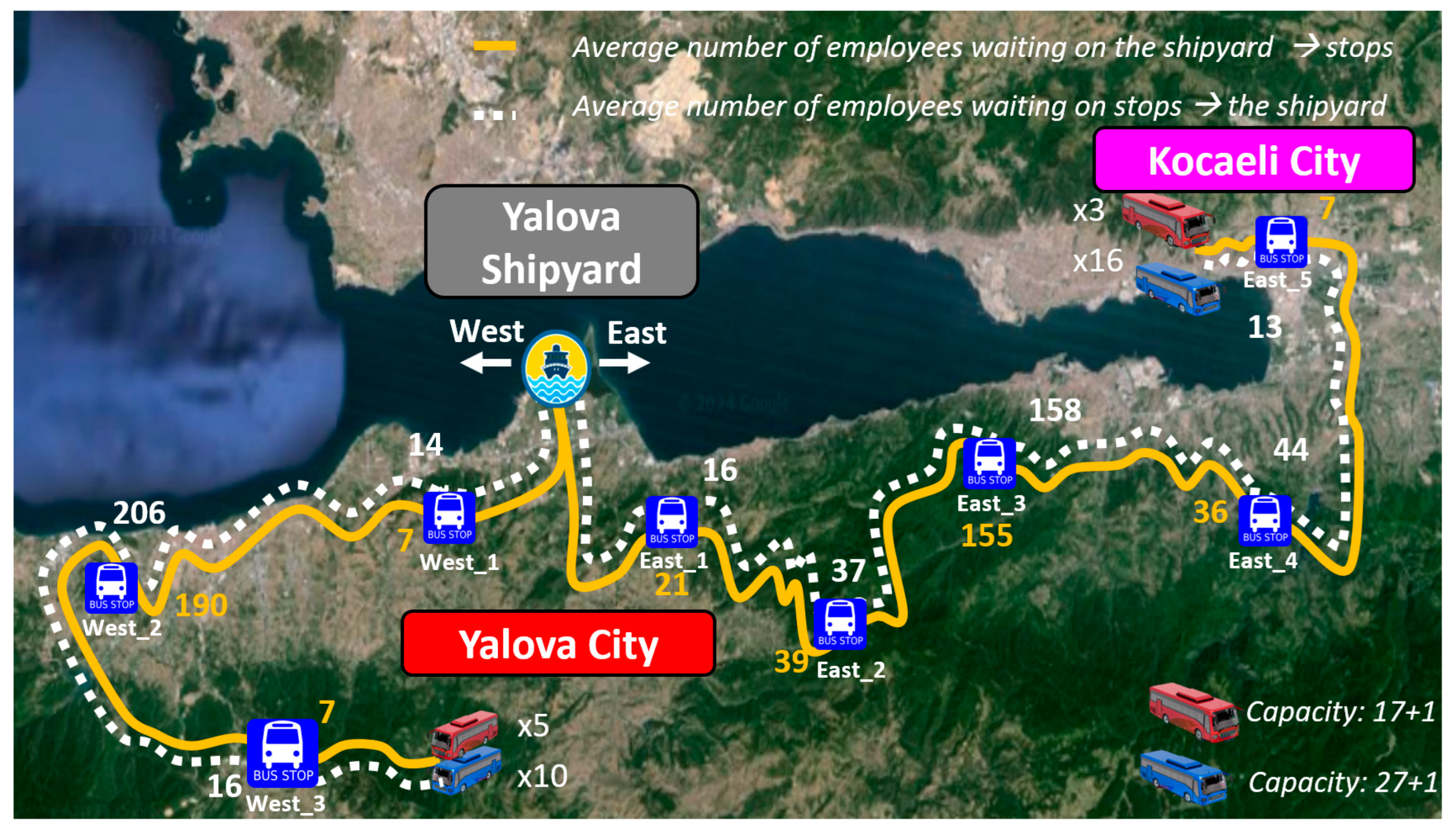
3.1. Study Site: Yalova Shipyard
3.2. Present Shuttle System
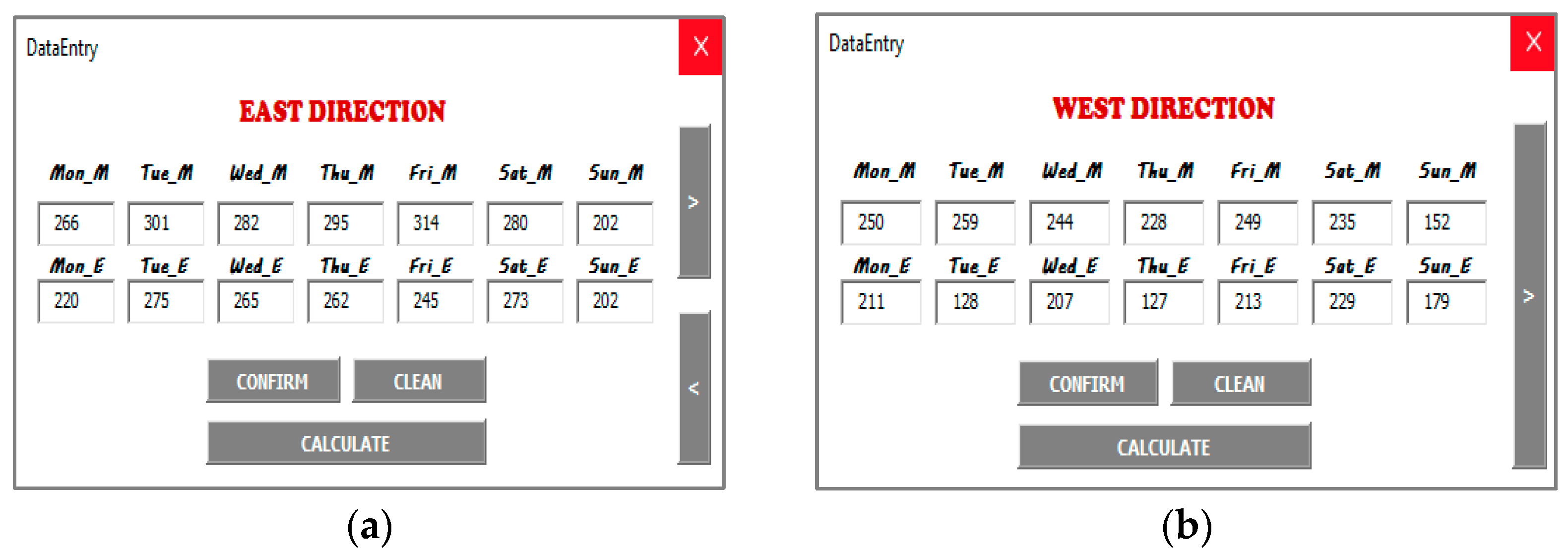
3.3. Data Collection and Extraction
- Analysis Results
4. Model Selection and Development
4.1. Model Selection
4.2. Model Development
- where
- : The objective function (either maximization or minimization).
- : The coefficients of decision variables .
- : The coefficients in the constraints.
- : The right-hand-side values of constraints.
- : The non-negativity constraints.
- where
- : The number of time periods (stages).
- : The vector of decision variables at time .
- : The cost/reward vector at time .
- : The constraints matrix at time .
- : Captures the inter-period dependencies between decisions at different stages.
- : The resource availability vector at time .
- where
- : Day ().
- : Time (.
- : day time. The number of employees going west.
- : day time. The number of employees going east.
- : day time. The number of vehicles with 17 capacity required for east direction.
- : day time. The number of vehicles with 27 capacity required for east direction.
- : day time. The number of vehicles with 17 capacity required for west direction.
- : day time. The number of vehicles with 27 capacity required for west direction.
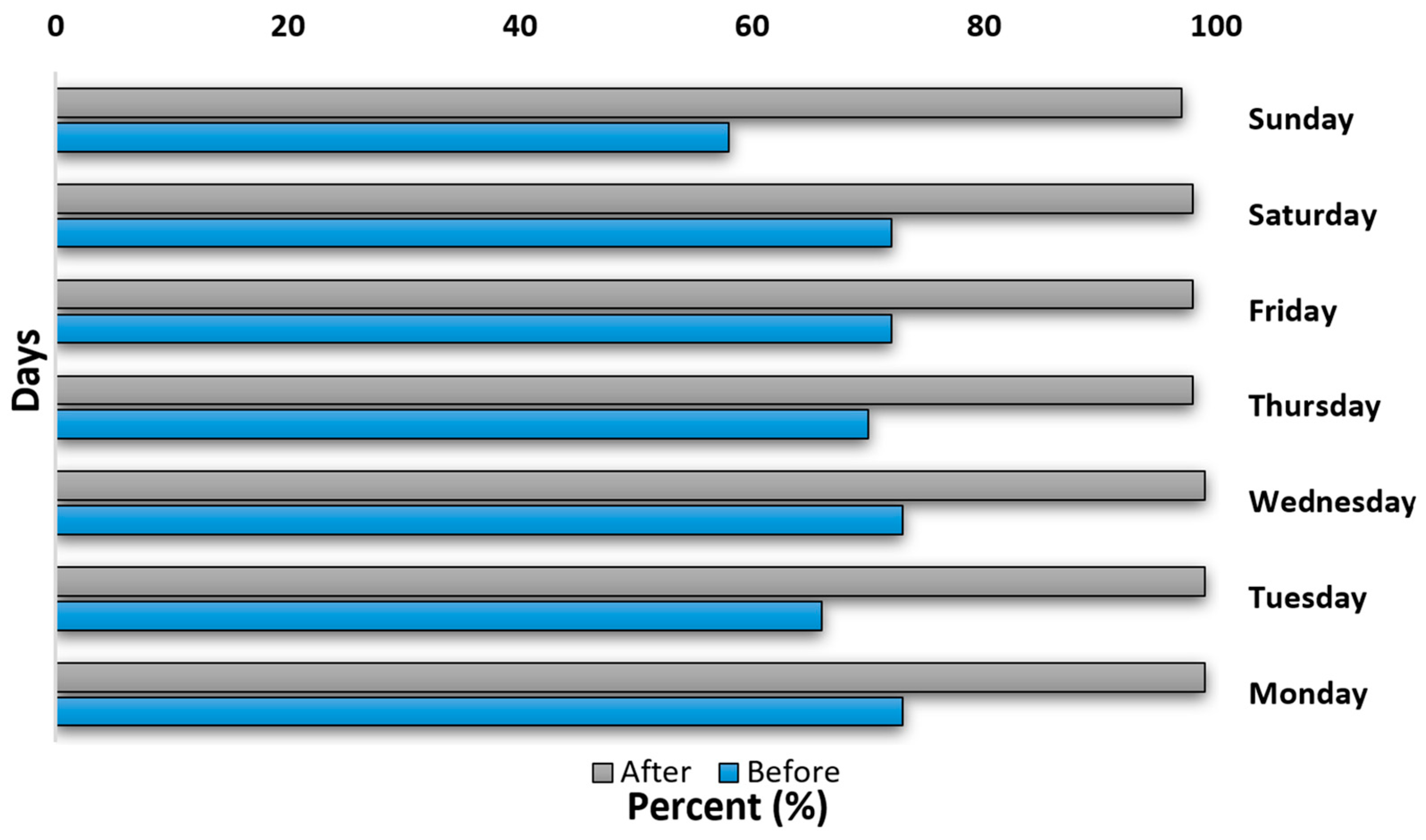
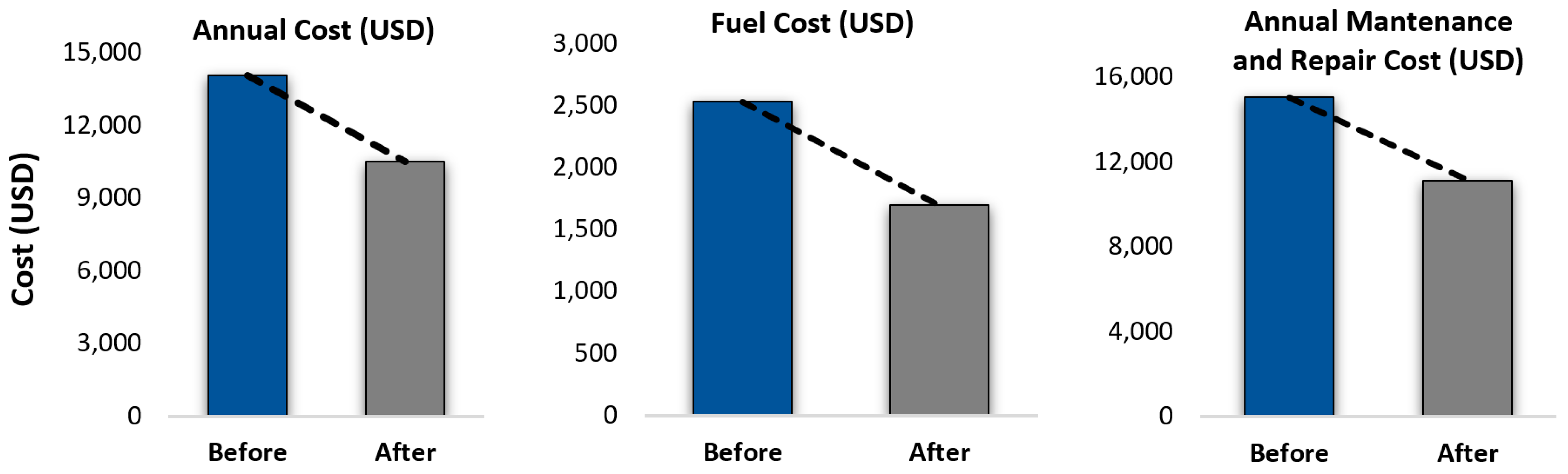
5. Model Results and Discussion
6. Conclusions and Suggestions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization (WHO). Available online: https://www.who.int (accessed on 28 January 2025).
- Türkiye Raporu. Toplumsal Bir Yara: Türkiye’de Trafik Kazaları Raporu 2022. Available online: https://turkiyeraporu.com/arastirma/toplumsal-bir-yara-turkiyede-trafik-kazalari-8929 (accessed on 19 November 2024).
- Alzard, M.H.; Maraqa, M.A.; Chowdhury, R.; Khan, Q.; Albuquerque, F.D.B.; Mauga, T.I.; Aljunadi, K.N. Estimation of Greenhouse Gas Emissions Produced by Road Projects in Abu Dhabi, United Arab Emirates. Sustainability 2019, 11, 2367. [Google Scholar] [CrossRef]
- Naess, B.; Seppanen, C.; Arunachalam, S.; Dowling, R.G.; Wu, Z.; Fordham, D.; Rouphail, N.M.; Zamurs, J.; The Cadmus Group, Inc. Evaluation of Methods for Modeling Vehicle Activity at Signalized Intersections for Air Quality Hot-Spot Analyses; Federal Highway Administration, Office of Natural Environment: Washington, DC, USA, 2020.
- Cui, H.; Qiu, J.; Cao, J.; Guo, M.; Chen, X.; Gorbachev, S. Route Optimization in Township Logistics Distribution Considering Customer Satisfaction Based on Adaptive Genetic Algorithm. Math. Comput. Simul. 2023, 204, 28–42. [Google Scholar] [CrossRef]
- Jiang, H.; Yao, Z.; Zhang, Y.; Jiang, Y.; He, Z. Pedestrian Shuttle Service Optimization for Autonomous Intersection Management. Transp. Res. Part C Emerg. Technol. 2024, 163, 104623. [Google Scholar] [CrossRef]
- Wu, M.; Yu, C.; Ma, W.; An, K.; Zhong, Z. Joint Optimization of Timetabling, Vehicle Scheduling, and Ride-Matching in a Flexible Multi-Type Shuttle Bus System. Transp. Res. Part C Emerg. Technol. 2022, 139, 103657. [Google Scholar] [CrossRef]
- Dai, Z.; Cathy Liu, X.; Li, H.; Wang, M.; Ma, X. Semi-Autonomous Bus Platooning Service Optimization with Surrogate Modeling. Comput. Ind. Eng. 2023, 175, 108838. [Google Scholar] [CrossRef]
- Oikonomou, M.; Sekadakis, M.; Katrakazas, C.; Hillebrand, J.; Vlahogianni, E.; Yannis, G. Traffic & Environmental Impact Assessment under Distinct Operational Speeds for Automated Shuttle Bus Services. Transp. Res. Procedia 2023, 72, 517–524. [Google Scholar] [CrossRef]
- Lv, D.; Zhang, W.; Wang, K.; Hao, H.; Yang, Y. Urban Aerial Mobility for Airport Shuttle Service. Transp. Res. Part A Policy Pract. 2024, 188, 104202. [Google Scholar] [CrossRef]
- Xu, Z.; Zheng, N. Integrating Connected Autonomous Shuttle Buses as an Alternative for Public Transport—A Simulation-Based Study. Multimodal Transp. 2024, 3, 100133. [Google Scholar] [CrossRef]
- Jędrzejczyk, W. Sharing Economy—Access Is Better Than Ownership: Owning a Car vs. Using the Services of Companies Providing Passenger Transport. Procedia Comput. Sci. 2024, 246, 5205–5213. [Google Scholar] [CrossRef]
- Anund, A.; Ludovic, R.; Caroleo, B.; Hardestam, H.; Dahlman, A.; Skogsmo, I.; Nicaise, M.; Arnone, M. Lessons Learned from Setting up a Demonstration Site with Autonomous Shuttle Operation—Based on Experience from Three Cities in Europe. J. Urban Mobil. 2022, 2, 100021. [Google Scholar] [CrossRef]
- Solaymani, S. CO2 Emissions Patterns in 7 Top Carbon Emitter Economies: The Case of Transport Sector. Energy 2019, 168, 989–1001. [Google Scholar] [CrossRef]
- Caban, J.; Vrabel, J.; Górnicka, D.; Nowak, R.; Jankiewicz, M.; Matijošius, J.; Palka, M. Overview of Energy Harvesting Technologies Used in Road Vehicles. Energies 2023, 16, 3787. [Google Scholar] [CrossRef]
- Characterizing CO2 and NOx Emission of Vehicles Crossing Toll Stations in Highway. Available online: https://colab.ws/articles/10.1016%2Fj.trd.2023.104024 (accessed on 28 January 2025).
- Lu, C.; Xie, D.-F.; Zhao, X.-M.; Qu, X. The Role of Alternative Fuel Buses in the Transition Period of Public Transport Electrification in Europe: A Lifecycle Perspective. Int. J. Sustain. Transp. 2022, 17, 626–638. [Google Scholar] [CrossRef]
- Caban, J.; Małek, A.; Šarkan, B. Strategic Model for Charging a Fleet of Electric Vehicles with Energy from Renewable Energy Sources. Energies 2024, 17, 1264. [Google Scholar] [CrossRef]
- Roy, A.; McCabe, B.Y.; Saxe, S.; Posen, I.D. Review of Factors Affecting Earthworks Greenhouse Gas Emissions and Fuel Use. Renew. Sustain. Energy Rev. 2024, 194, 114290. [Google Scholar] [CrossRef]
- Downs, A. Still Stuck in Traffic: Coping with Peak-Hour Traffic Congestion; Brookings Institution Press: Washington, DC, USA, 2005; ISBN 978-0-8157-9655-8. [Google Scholar]
- Wu, X.; Zhang, Y.; Chen, Y. A Dynamic Programming Model for Joint Optimization of Electric Drayage Truck Operations and Charging Stations Planning at Ports. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11710–11719. [Google Scholar] [CrossRef]
- Kim, S.; Kwak, M. Customer Complaint Analysis via Review-Based Control Charts and Dynamic Importance–Performance Analysis. Appl. Sci. 2023, 13, 5991. [Google Scholar] [CrossRef]
- Rotaris, L.; Danielis, R. Commuting to College: The Effectiveness and Social Efficiency of Transportation Demand Management Policies. Transp. Policy 2015, 44, 158–168. [Google Scholar] [CrossRef]
- Batur, I.; Koç, M. A Review of System Dynamics Applications in Sustainable Urban Transportation. In Proceedings of the European Conference on Sustainability, Energy & the Environment 2017 Official Conference Proceedings, Brighton, UK, 7–9 July 2017; pp. 1–11. [Google Scholar]
- Piras, F.; Sottile, E.; Meloni, I. Modal Share Change Following Implementation of Travel Demand Management Strategies. Transp. Res. Rec. 2018, 2672, 731–741. [Google Scholar] [CrossRef]
- Cumming, I.; Weal, Z.; Afzali, R.; Rezaei, S.; Idris, A.O. The Impacts of Office Relocation on Commuting Mode Shift Behaviour in the Context of Transportation Demand Management (TDM). Case Stud. Transp. Policy 2019, 7, 346–356. [Google Scholar] [CrossRef]
- Rosenfield, A.; Attanucci, J.P.; Zhao, J. A Randomized Controlled Trial in Travel Demand Management. Transportation 2020, 47, 1907–1932. [Google Scholar] [CrossRef]
- Bahrami, S.; Vignon, D.; Yin, Y.; Laberteaux, K. Parking Management of Automated Vehicles in Downtown Areas. Transp. Res. Part C Emerg. Technol. 2021, 126, 103001. [Google Scholar] [CrossRef]
- Ku Do Kim, J.; Yu, Y.; Kim, S.; Lee, S.; Lee, S. Assessment of Eco-Friendly Effects on Green Transportation Demand Management. Chem. Eng. Trans. 2021, 89, 121–126. [Google Scholar] [CrossRef]
- Farahmand, Z.H.; Gkiotsalitis, K.; Geurs, K.T. Mobility-as-a-Service as a Transport Demand Management Tool: A Case Study among Employees in the Netherlands. Case Stud. Transp. Policy 2021, 9, 1615–1629. [Google Scholar] [CrossRef]
- Bucchiarone, A.; Bassanelli, S.; Luca, M.; Centellegher, S.; Cipriano, P.; Giovannini, L.; Lepri, B.; Marconi, A. An End-to-End Solution for Facilitating Urban Cyclability. Trans. Intell. Transport. Syst. 2023, 24, 15830–15843. [Google Scholar] [CrossRef]
- Ghafelebashi, A.; Razaviyayn, M.; Dessouky, M. Congestion Reduction via Personalized Incentives. Transp. Res. Part C Emerg. Technol. 2023, 152, 104153. [Google Scholar] [CrossRef]
- Vega-Gonzalo, M.; Gomez, J.; Christidis, P.; Manuel Vassallo, J. The Role of Shared Mobility in Reducing Perceived Private Car Dependency. Transp. Res. Part D Transp. Environ. 2024, 126, 104023. [Google Scholar] [CrossRef]
- Zong, F.; Zeng, M.; Yu, P. A Parking Pricing Scheme Considering Parking Dynamics. Transportation 2024, 51, 1349–1371. [Google Scholar] [CrossRef]
- Maghrour Zefreh, M.; Torok, A. Theoretical Comparison of the Effects of Different Traffic Conditions on Urban Road Traffic Noise. J. Adv. Transp. 2018, 2018, 7949574. [Google Scholar] [CrossRef]
- Maghrour Zefreh, M.; Torok, A. Single Loop Detector Data Validation and Imputation of Missing Data. Measurement 2018, 116, 193–198. [Google Scholar] [CrossRef]
- Ribeiro, P.J.G.; Dias, G.; Mendes, J.F.G. Public Transport Decarbonization: An Exploratory Approach to Bus Electrification. World Electr. Veh. J. 2024, 15, 81. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, Q.; He, Q.; Shi, Y.; Wang, B.; Dong, R.; Sun, Y.; Zhang, X.; Xu, Z.; Liu, B. Unveiling the Heterogeneity of Commuters’ Travel Mode Change in Different Cities and Their Sensitivity to Incentives. ATS 2024, 62, 139–158. [Google Scholar]
- Petrunoff, N.; Wen, L.M.; Rissel, C. Effects of a Workplace Travel Plan Intervention Encouraging Active Travel to Work: Outcomes from a Three-Year Time-Series Study. Public Health 2016, 135, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, L.; Friman, M.; Gärling, T. Perceived Attributes of Bus and Car Mediating Satisfaction with the Work Commute. Transp. Res. Part A Policy Pract. 2013, 47, 87–96. [Google Scholar] [CrossRef]
- Carapellucci, F.; Conti, V.; Lelli, M.; Liberto, C.; Orchi, S.; Valenti, G.; Valentini, M.P. Tools and Methodologies for the Analysis of Home-to-Work Shuttle Service Impacts: The ENEA “Casaccia” Case Study. Future Transp. 2023, 3, 901–917. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Zhong, N. Omnichannel Retail Operations with Mixed Fulfillment Strategies. Int. J. Prod. Econ. 2022, 254, 108608. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, H.; Zhou, A. A Particle Swarm Optimization Algorithm for Mixed-Variable Optimization Problems. Swarm Evol. Comput. 2021, 60, 100808. [Google Scholar] [CrossRef]
- Alimoradi, M.; Azgomi, H.; Asghari, A. Trees Social Relations Optimization Algorithm: A New Swarm-Based Metaheuristic Technique to Solve Continuous and Discrete Optimization Problems. Math. Comput. Simul. 2022, 194, 629–664. [Google Scholar] [CrossRef]
- Altekin, F.T.; Bukchin, Y. A Multi-Objective Optimization Approach for Exploring the Cost and Makespan Trade-off in Additive Manufacturing. Eur. J. Oper. Res. 2022, 301, 235–253. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hà, M.H. On the Min-Cost Traveling Salesman Problem with Drone. Transp. Res. Part C Emerg. Technol. 2018, 86, 597–621. [Google Scholar] [CrossRef]
- Islam, M.R.; Mahmud, M.R.; Pritom, R.M. Transportation Scheduling Optimization by a Collaborative Strategy in Supply Chain Management with TPL Using Chemical Reaction Optimization. Neural Comput. Appl. 2020, 32, 3649–3674. [Google Scholar] [CrossRef]
- Mirzahossein, H.; Zargari, S.A. A Combined Model of Congestion Toll Pricing Based on System Optimization with Minimum Toll. Teh. Vjesn. 2018, 25, 1162–1168. [Google Scholar] [CrossRef]
- Gibson, E.; Deo, S.; Jónasson, J.O.; Kachule, M.; Palamountain, K. Redesigning Sample Transportation in Malawi Through Improved Data Sharing and Daily Route Optimization. Manuf. Serv. Oper. Manag. 2023, 25, 1209–1226. [Google Scholar] [CrossRef]
- Aydın, M.M. The Modeling of Effective Parameters on Public Bus Passengers’ Boarding Time Prediction. J. Eng. Res. 2021, 10, 1–16. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, Y.; Li, X.; Li, B. A Heuristic Optimization Approach for Multi-Vehicle and One-Cargo Green Transportation Scheduling in Shipbuilding. Adv. Eng. Inform. 2021, 49, 101306. [Google Scholar] [CrossRef]
- Zhao, C.; Tang, J.; Gao, W.; Zeng, Y.; Li, Z. Many-Objective Optimization of Multi-Mode Public Transportation under Carbon Emission Reduction. Energy 2024, 286, 129627. [Google Scholar] [CrossRef]
- Dantzig, G.B. Linear Programming and Extensions; Princeton University Press: Princeton, NJ, USA, 1998; 656p, ISBN 978-0-691-05913-6. Available online: https://press.princeton.edu/books/paperback/9780691059136/linear-programming-and-extensions?srsltid=AfmBOooXVS9g5koilVcXR-1vM3eLID5k8XvnnDd0letMo7fulNB3g0qO (accessed on 19 April 2025).
- Panneerselvam, R. Operations Research, 3rd ed.; PHI Learning: Delhi, India, 2023; 640p, ISBN 978-93-5443-789-2. Available online: https://www.phindia.com/Books/BookDetail/9789354437892/operations-research-panneerselvam?srsltid=AfmBOoo5gWZgZWArNULm_Y3wGmGxBmhvPn2G-52Zoue8rO1yLTqiwXrC (accessed on 19 April 2025).
- Lähdeaho, O.; Hilmola, O.-P. An Exploration of Quantitative Models and Algorithms for Vehicle Routing Optimization and Traveling Salesman Problems. Supply Chain Anal. 2024, 5, 100056. [Google Scholar] [CrossRef]
- Yalçındağ, S. Employee shuttle bus routing problem. Mugla J. Sci. Technol. 2020, 6, 105–111. [Google Scholar] [CrossRef]
- Xiong, J.; Chen, B.; Li, X.; He, Z.; Chen, Y. Demand responsive service-based optimization on flexible routes and departure time of community shuttles. Sustainability 2020, 12, 897. [Google Scholar] [CrossRef]
- Yan, S.; Tseng, C.H. A passenger demand model for airline flight scheduling and fleet routing. Comput. Oper. Res. 2002, 29, 1559–1581. [Google Scholar] [CrossRef]
- Federal Highway Administration (FHWA). Mitigating Traffic Congestion-The Role of Demand-Side Strategies; Report No. FHWA-HOP-05-001; The Association for Commuter Transportation: Washington, DC, USA, October 2004. Available online: https://ops.fhwa.dot.gov/publications/mitig_traf_cong/index.htm (accessed on 19 April 2025).
- Frieß, N.M.; Pferschy, U. Planning a zero-emission mixed-fleet public bus system with minimal life cycle cost. Public Transp. 2024, 16, 39–79. [Google Scholar] [CrossRef]
- Wei, M.; Yang, C.; Liu, T. An integrated multi-objective optimization for dynamic airport shuttle bus location, route design and departure frequency setting problem. Int. J. Environ. Res. Public Health 2022, 19, 14469. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, X.; Wei, X.; Yu, Y.; Tang, J. Robust optimization model for single line dynamic bus dispatching. Sustainability 2021, 14, 73. [Google Scholar] [CrossRef]
- Čižiūnienė, K.; Matijošius, J.; Liebuvienė, J.; Sokolovskij, E. Comparison of the Relative Importance of Factors Affecting the Conveyance of Bulk and Liquid Cargo. Appl. Sci. 2024, 14, 1151. [Google Scholar] [CrossRef]
- Matijošius, J.; Čižiūnienė, K.; Liebuvienė, J.; Sokolovskij, E. Research Determining the Priority Order of Forces Acting on a Vehicle Transporting Logs. Appl. Sci. 2023, 13, 6174. [Google Scholar] [CrossRef]
- Bertsekas, D. Dynamic Programming and Optimal Control: Volume I; Athena Scientific: Nashua, NH, USA, 2012; Volume 4. [Google Scholar]
- Toth, P.; Vigo, D. (Eds.) Vehicle Routing: Problems, Methods, and Applications, 2nd ed.; SIAM: Philadelphia, PA, USA, 2014; Available online: https://epubs.siam.org/doi/book/10.1137/1.9781611973594 (accessed on 19 April 2025).
- Ghaemi, Z.; Tran, T.T.; Smith, A.D. Comparing classical and metaheuristic methods to optimize multi-objective operation planning of district energy systems considering uncertainties. Appl. Energy 2022, 321, 119400. [Google Scholar] [CrossRef]
- Kozłowski, E.; Antosz, K.; Sęp, J.; Prucnal, S. Integrating Sensor Systems and Signal Processing for Sustainable Production: Analysis of Cutting Tool Condition. Electronics 2023, 13, 185. [Google Scholar] [CrossRef]
- Majerek, D.; Rymarczyk, T.; Wójcik, D.; Kozłowski, E.; Rzemieniak, M.; Gudowski, J.; Gauda, K. Machine Learning and Deterministic Approach to the Reflective Ultrasound Tomography. Energies 2021, 14, 7549. [Google Scholar] [CrossRef]
- Gill, A. Optimisation of the Technical Object Maintenance System Taking Account of Risk Analysis Results. EiN 2017, 19, 420–431. [Google Scholar] [CrossRef]






| Reference | Content of the Study | Strategy |
|---|---|---|
| Rotaris and Danielis [23] | Reducing private car use at university using transport demand management |
|
| Batur and Koç [24] | Simulation of the change in traffic density with the implementation of selected travel management strategies |
|
| Piras et al. [25] | Developing voluntary travel behavior change programs for urban mobility using transport demand management |
|
| Cumming et al. [26] | Reducing traffic congestion and parking pressure caused by commuting to work |
|
| Rosenfield et al. [27] | Aims to reduce parking demand in an urban workplace |
|
| Wu et al. [21] | Dynamic optimization strategies for ride services |
|
| Bahrami et al. [28] | Parking management of automated vehicles in downtown areas |
|
| Ku et al. [29] | A public-transport-focused study for an environmentally friendly city |
|
| Farahmand et al. [30] | A case study in transport demand management policy for employees in the Netherlands |
|
| Bucchiarone et al. [31] | A study on sustainable mobility from home to work targeting public and private employees |
|
| Ghafelebashi et al. [32] | Congestion reduction via personalized incentives |
|
| Vega-Gonzalo et al. [33] | Examining the role of shared mobility in reducing private vehicle dependency |
|
| Data Registration Number | Observed Date | Observed Time | Licensed Plate No | Bus Stop ID | Bus Capacity |
|---|---|---|---|---|---|
| 1 | 1 December 2023 | Morning | 0034 | West_1 | 27 |
| 2 | Morning | 4268 | East_4 | 27 | |
| 3 | Morning | 4052 | East_4 | 27 | |
| 4 | Morning | 0034 | West_1 | 27 | |
| 5 | Morning | 4052 | East_4 | 27 | |
| 6 | Morning | 4052 | East_4 | 27 | |
| 7 | Morning | 0034 | West_1 | 27 | |
| 8 | Morning | 0034 | West_1 | 27 | |
| 9 | Morning | 4132 | East_2 | 27 | |
| 10 | Morning | 4090 | East_2 | 27 | |
| 11 | Morning | 4100 | East_3 | 27 | |
| 12 | Morning | 4262 | East_5 | 27 | |
| 13 | Morning | 4100 | East_3 | 27 | |
| 14 | Morning | 4090 | East_2 | 27 | |
| 15 | Morning | 4013 | East_3 | 27 | |
| 16 | Morning | 4125 | West_3 | 17 | |
| 17 | Morning | 4048 | East_1 | 27 | |
| 18 | Morning | 4125 | West_3 | 17 | |
| 19 | Morning | 4187 | East_3 | 27 | |
| 20 | Morning | 4054 | East_3 | 17 | |
| 21 | Morning | 0111 | West_3 | 27 | |
| 22 | Morning | 4048 | East_1 | 27 | |
| 23 | Morning | 4268 | West_3 | 27 | |
| 24 | Morning | 4262 | East_5 | 27 | |
| 771 | 1 December 2023 | Evening | 0034 | West_1 | 27 |
| 772 | Evening | 4217 | East_3 | 27 | |
| 773 | Evening | 4052 | East_5 | 27 | |
| 774 | Evening | 0102 | West_2 | 27 | |
| 775 | Evening | 0034 | West_1 | 27 | |
| 776 | Evening | 0208 | West_2 | 27 | |
| 777 | Evening | 4098 | East_1 | 27 | |
| 778 | Evening | 4025 | East_1 | 17 | |
| 779 | Evening | 0034 | West_1 | 27 | |
| 780 | Evening | 4052 | East_1 | 27 | |
| 781 | Evening | 4262 | East_4 | 27 | |
| 782 | Evening | 4098 | East_1 | 27 | |
| 783 | Evening | 0250 | West_2 | 27 | |
| 784 | Evening | 4268 | East_4 | 27 | |
| 785 | Evening | 4013 | East_3 | 27 | |
| 786 | Evening | 4100 | East_3 | 27 | |
| 787 | Evening | 4013 | East_3 | 27 |
| Time of Day | West Direction | East Direction | ||||
|---|---|---|---|---|---|---|
| Plate No | Bus Capacity | Occupancy/(%) | Plate No | Bus Capacity | Occupancy/(%) | |
| Morning | 0034 | 27 | 14/(52) | 4025 | 17 | 14/(52) |
| 0002 | 27 | 17/(63) | 4054 | 17 | 7/(41) | |
| 0020 | 27 | 28/(104) | 4090 | 27 | 16/(59) | |
| 0082 | 17 | 16/(94) | 4132 | 27 | 15/(56) | |
| 0102 | 27 | 27/(100) | 4289 | 17 | 12/(71) | |
| 0111 | 27 | 22/(81) | 4013 | 27 | 27/(100) | |
| 0208 | 27 | 23/(85) | 4022 | 27 | 5/(19) | |
| 0250 | 27 | 9/(33) | 4048 | 27 | 16/(59) | |
| 0298 | 17 | 12/(71) | 4052 | 27 | 19/(70) | |
| 0326 | 27 | 26/(96) | 4098 | 27 | 18/(67) | |
| 0370 | 17 | 17/(100) | 4100 | 27 | 26/(96) | |
| 5090 | 17 | 17/(100) | 4168 | 27 | 5/(19) | |
| 4125 | 17 | 16/(94) | 4187 | 27 | 16/(59) | |
| ― | ― | ― | 4217 | 27 | 10/(37) | |
| ― | ― | ― | 4262 | 27 | 17/(63) | |
| ― | ― | ― | 4268 | 27 | 20/(74) | |
| Evening | 0034 | 27 | 12/(71) | 4025 | 17 | 11/(65) |
| 0002 | 27 | 12/(71) | 4054 | 17 | 5/(29) | |
| 0020 | 27 | 24/(89) | 4090 | 27 | 21/(78) | |
| 0082 | 17 | 14/(82) | 4132 | 27 | 10/(37) | |
| 0102 | 27 | 27/(100) | 4289 | 17 | 16/(94) | |
| 0111 | 27 | 27/(100) | 4013 | 27 | 20/(74) | |
| 0208 | 27 | 28/(104) | 4022 | 27 | 17/(63) | |
| 0250 | 27 | 17/(63) | 4048 | 27 | 20/(74) | |
| 0298 | 17 | 15/(88) | 4098 | 27 | 22/(81) | |
| 0326 | 27 | 17/(63) | 4100 | 27 | 25/(93) | |
| 0370 | 17 | 10/(59) | 4168 | 27 | 24/(89) | |
| 5090 | 17 | 17/(100) | 4187 | 27 | 12/(44) | |
| 4125 | 17 | 3/(18) | 4217 | 27 | 18/(67) | |
| ― | ― | ― | 4262 | 27 | 7/(26) | |
| ― | ― | ― | 4052 | 27 | 20/(74) | |
| ― | ― | ― | 4268 | 27 | 25/(93) | |
| Vehicle Type | Fuel Consumption (per km) | Monthly Maintenance and Repair Expenses (TL) | All Other Annual Expenses (TL) |
|---|---|---|---|
| 17 + 1 | USD 0.13 | USD 71.5 | USD 668.3 |
| 27 + 1 | USD 0.16 | USD 92.7 | USD 899.4 |
| Criteria | Method | |
|---|---|---|
| Dynamic Linear Programming | Optimization Methods | |
| Optimality | Excellent | Approximate |
| Sequential decision-making suitability | Excellent | Moderate |
| Handling linear/structured constraints | Excellent | Limited |
| Robustness in fleet allocation problems | High | Moderate |
| Computational predictability | High | Medium/low |
| Ease of parameter tuning | Simple | Moderate/complex |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aydin, M.M.; Sokolovskij, E.; Jaskowski, P.; Matijošius, J. Service Management of Employee Shuttle Service Under Inhomogeneous Fleet Constraints Using Dynamic Linear Programming: A Case Study. Appl. Sci. 2025, 15, 4604. https://doi.org/10.3390/app15094604
Aydin MM, Sokolovskij E, Jaskowski P, Matijošius J. Service Management of Employee Shuttle Service Under Inhomogeneous Fleet Constraints Using Dynamic Linear Programming: A Case Study. Applied Sciences. 2025; 15(9):4604. https://doi.org/10.3390/app15094604
Chicago/Turabian StyleAydin, Metin Mutlu, Edgar Sokolovskij, Piotr Jaskowski, and Jonas Matijošius. 2025. "Service Management of Employee Shuttle Service Under Inhomogeneous Fleet Constraints Using Dynamic Linear Programming: A Case Study" Applied Sciences 15, no. 9: 4604. https://doi.org/10.3390/app15094604
APA StyleAydin, M. M., Sokolovskij, E., Jaskowski, P., & Matijošius, J. (2025). Service Management of Employee Shuttle Service Under Inhomogeneous Fleet Constraints Using Dynamic Linear Programming: A Case Study. Applied Sciences, 15(9), 4604. https://doi.org/10.3390/app15094604










