Investigation into the Fracture Evolution Law of Overlying Strata Roof in Shallowly Buried “Three-Soft” Coal Seam Fully Mechanized Mining Faces and Its Influence on the Feasibility of Gob-Side Entry Retaining
Abstract
:1. Introduction
2. General Situation of the Project
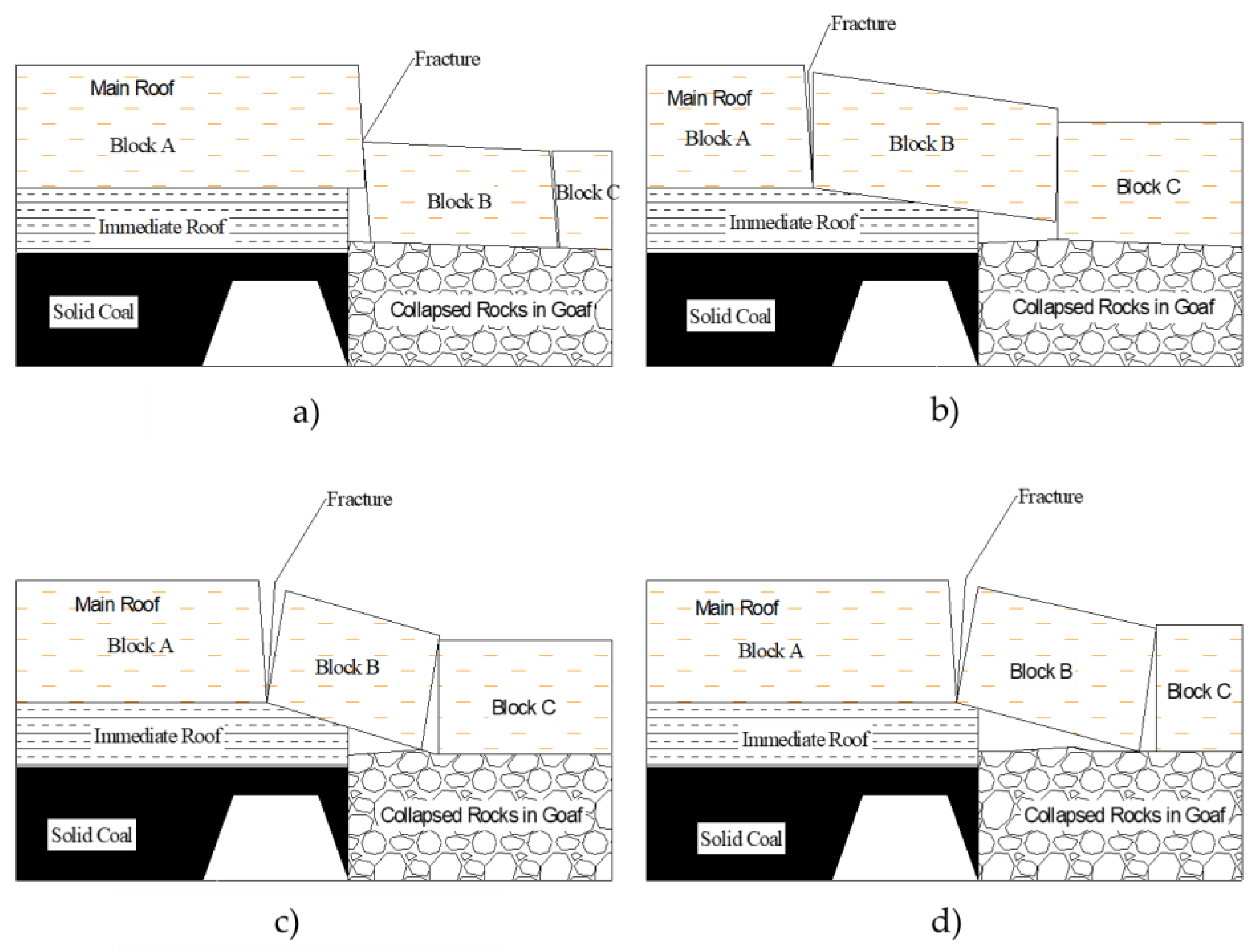
3. Characteristics of Roof Fracture Positions in Gob-Side Entry Retaining
3.1. Main Roof Fracture Location Analysis
3.2. The Influence of Coal Seam Thickness on Main Roof Fracture
4. Theoretical Analysis of Roof Influence on Underlying Coal and Rock Strata After Coal Seam Mining
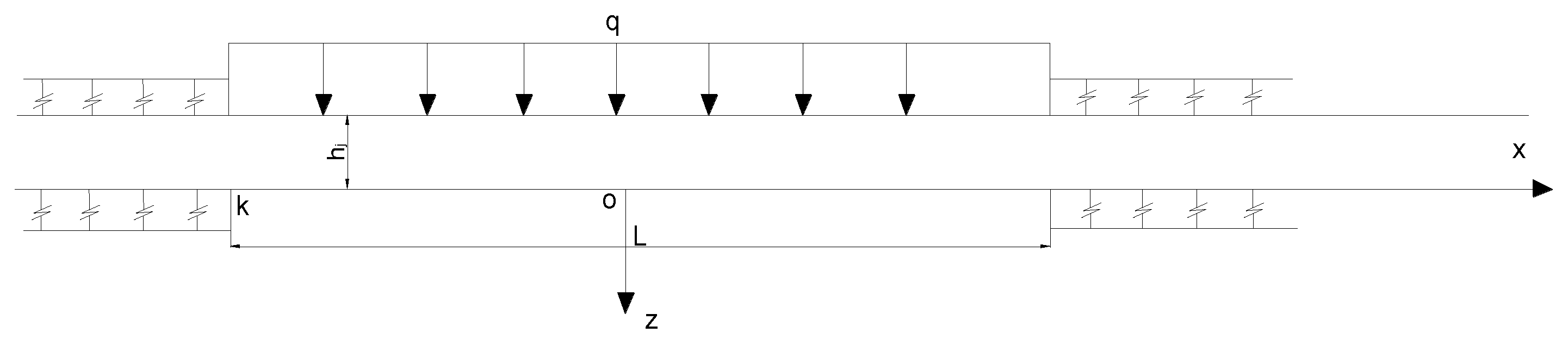
4.1. Analysis of the Mechanical Model
4.1.1. Basic Assumptions
4.1.2. Establishment and Solution of the Mechanical Model
4.2. Fracture Laws of Overburden Roof
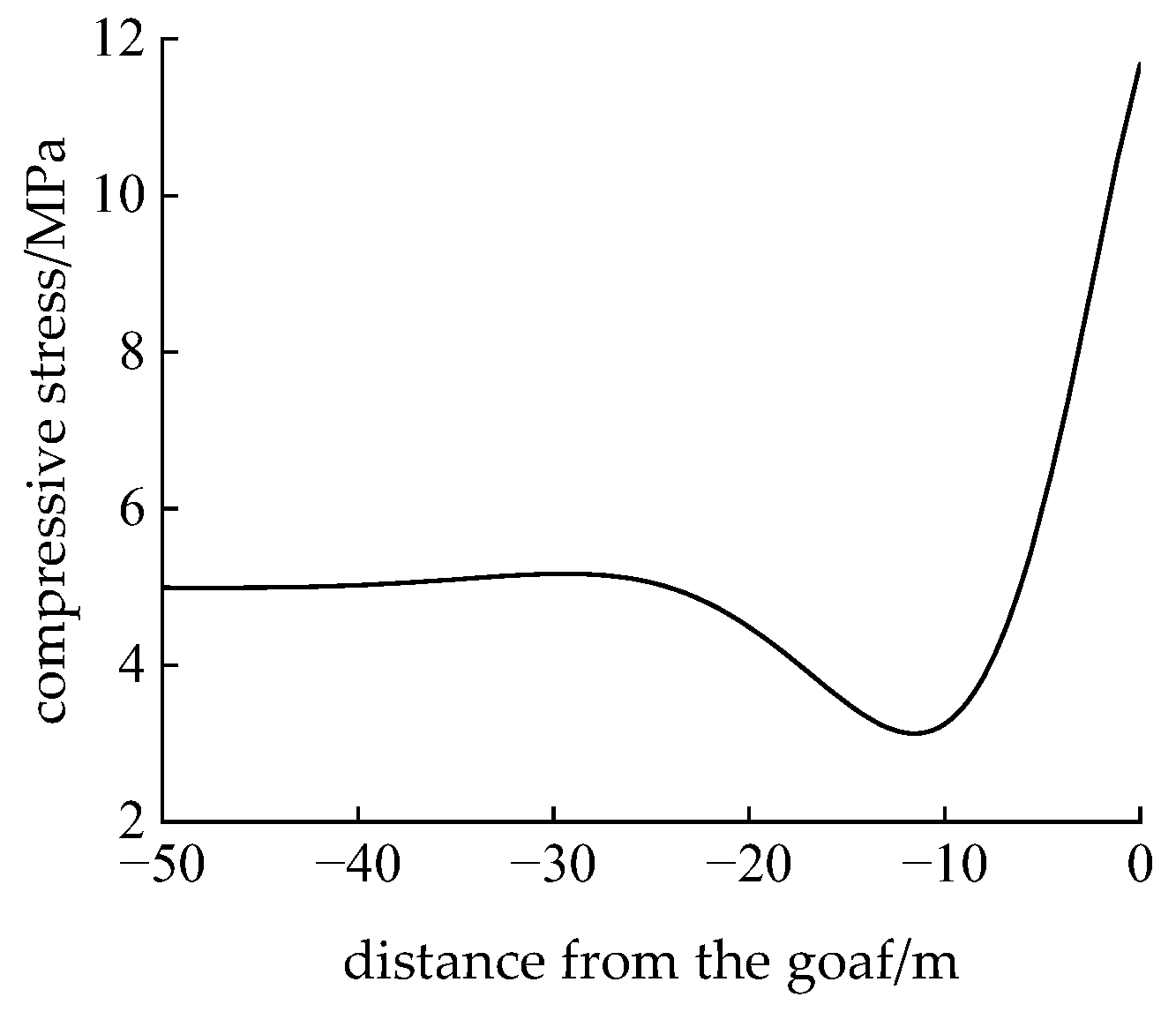
4.2.1. The Acting Force of the Main Roof on the Underlying Coal and Rock Strata
4.2.2. Analysis of Roof Fracture Characteristics
4.3. The Effect of Horizontal Stress on Roadway Stability
5. Numerical Simulation of Stope Overburden
5.1. Numerical Model Development
5.2. Post-Mining Roof Fracture Characteristics of Gob-Side Entry Retaining for No. 2-1 Coal Seam
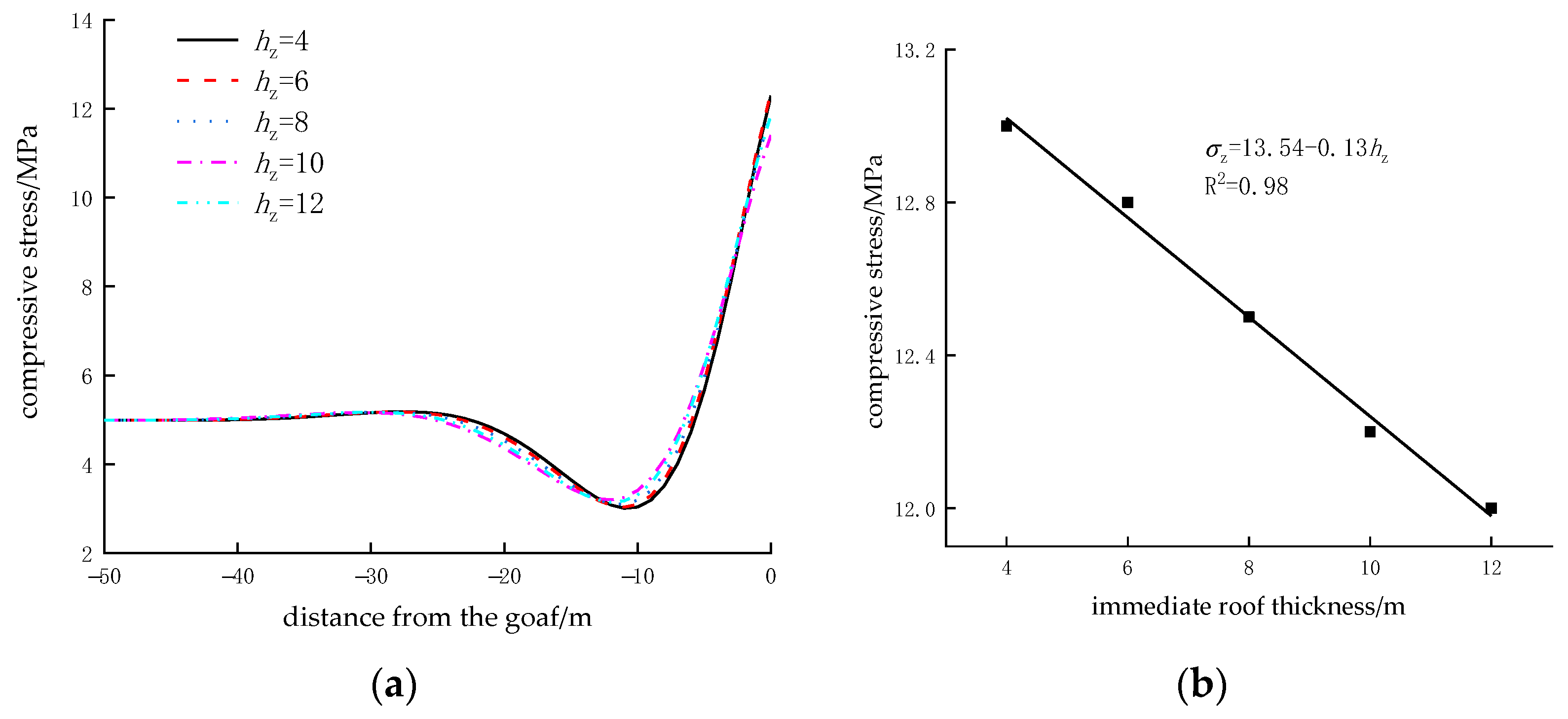
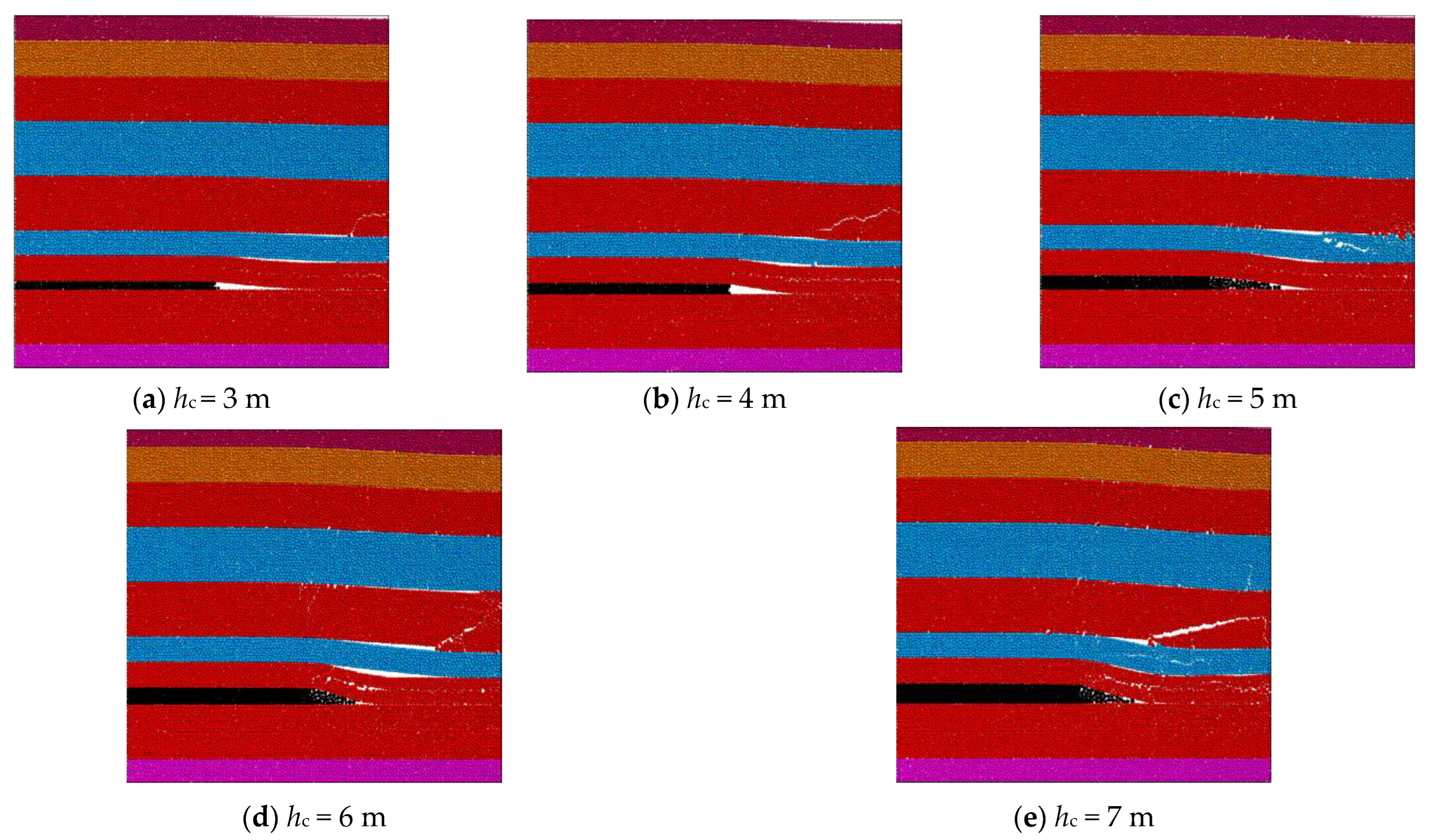
5.2.1. Influence of Coal Seam Thickness
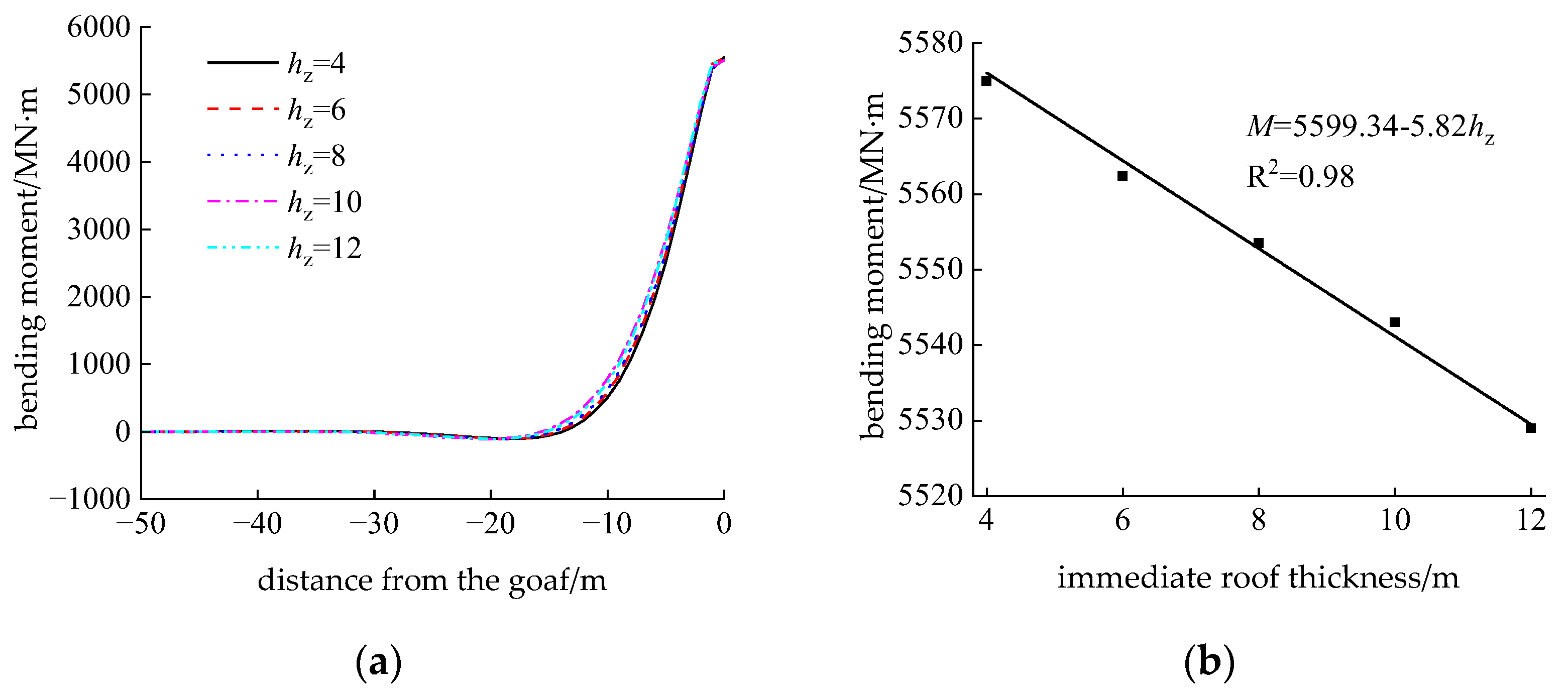
5.2.2. Influence of Immediate Roof Thickness
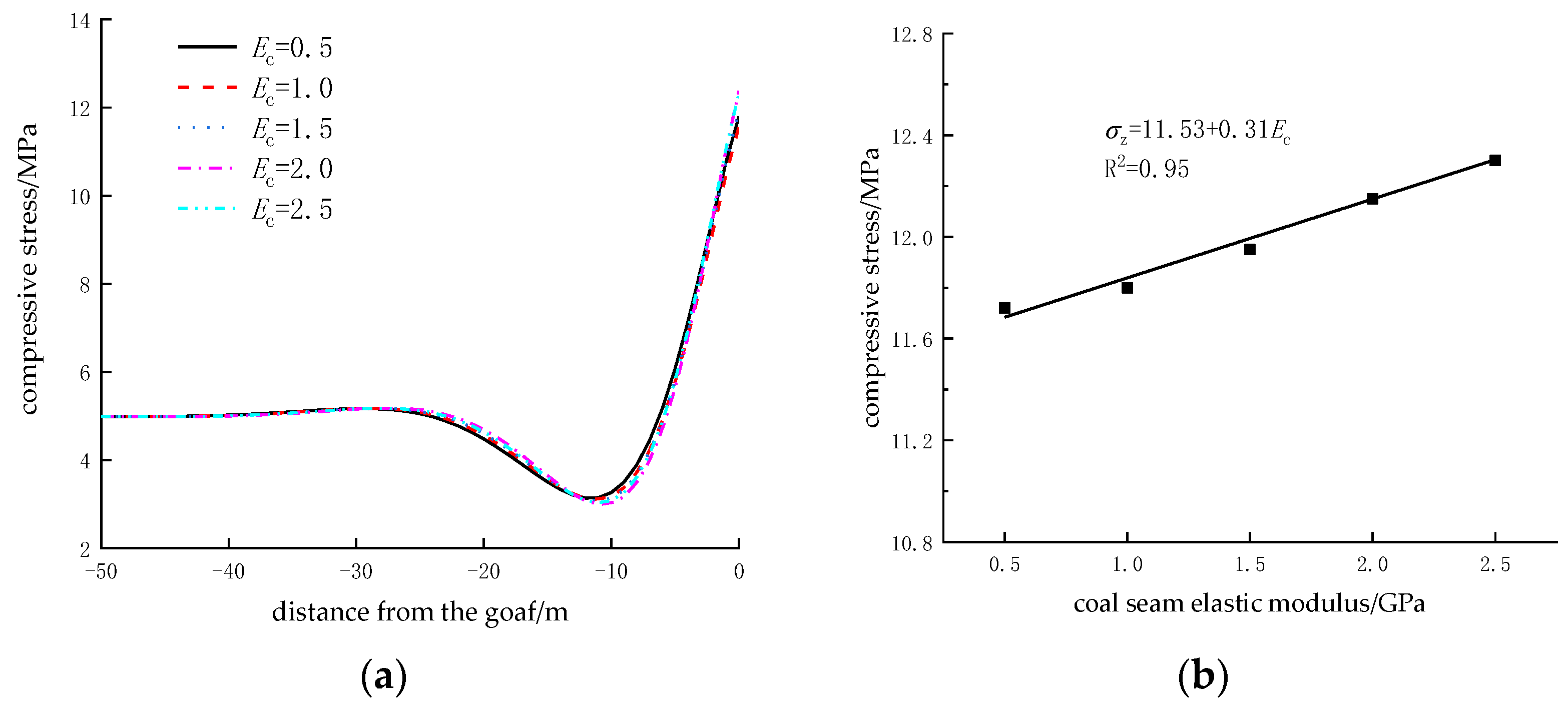
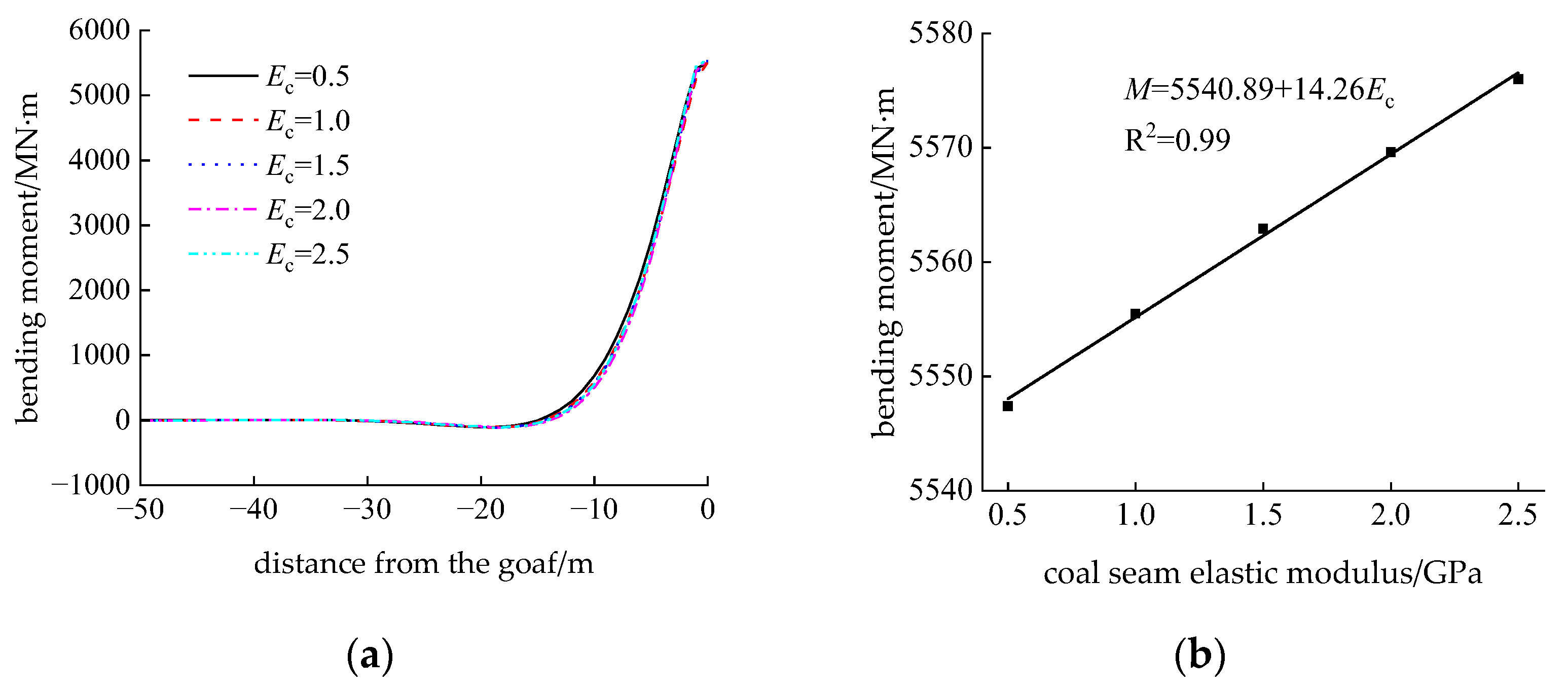
5.2.3. Influence of Coal Seam Elastic Modulus
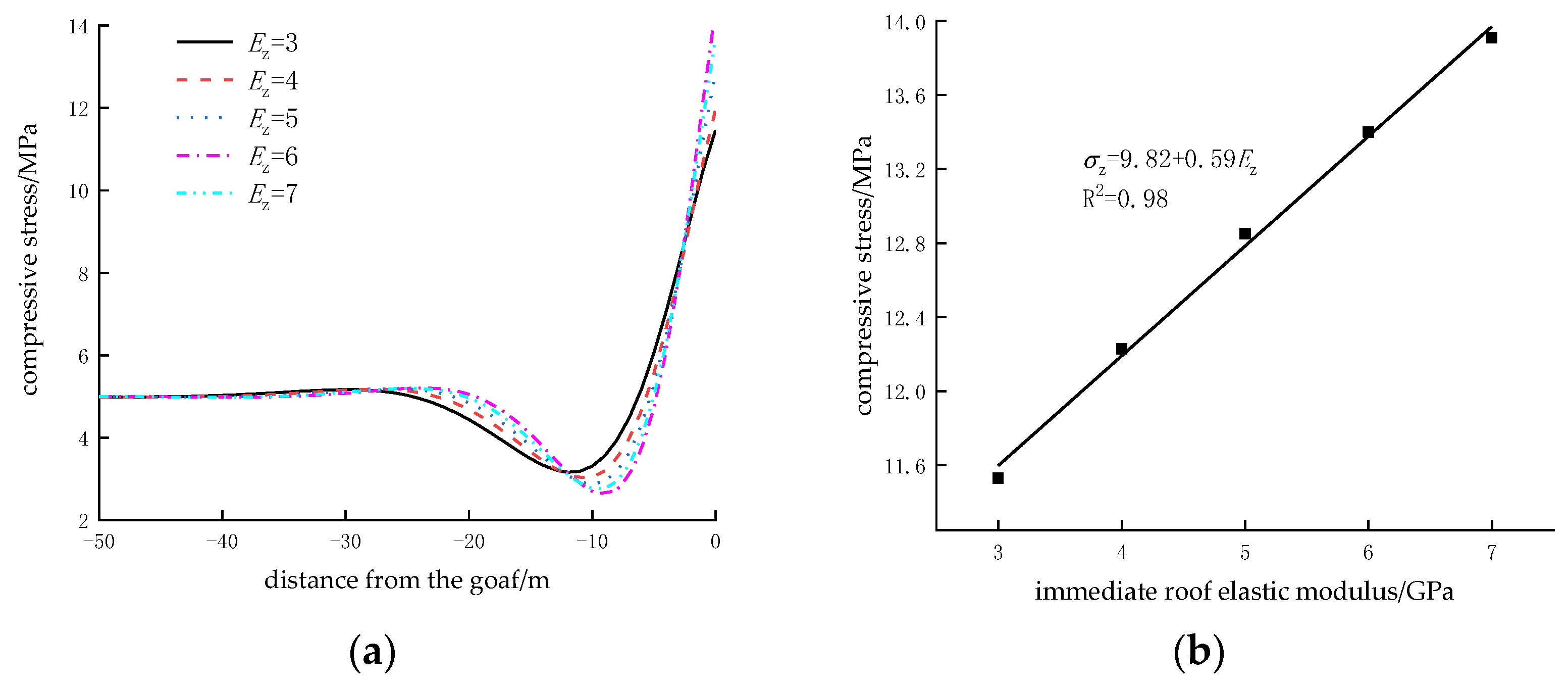
5.2.4. Influence of Immediate Roof Elastic Modulus
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, Z.Q.; Cui, Z.D.; Xia, H.C.; Tang, J.Q.; Wen, Z.J. The fundamental theoretical and engineering research on the green safe no coal pillar mining model by mainly using coal gangue backfill. J. China Coal Soc. 2010, 35, 705–710. [Google Scholar] [CrossRef]
- He, M.; Zhu, G.; Guo, Z. Longwall mining “cutting cantilever beam theory” and 110 mining method in China: The third mining science innovation. J. Rock Mech. Geotech. Eng. 2015, 7, 483–492. [Google Scholar] [CrossRef]
- Zhang, Z.; Bai, J.; Wang, X.; Xu, Y.; Yan, S.; Liu, H.; Wu, W.; Zhang, W. Research Progress and Prospects of Surrounding Rock Control Technology for Gob-Side Entry Retaining in China. J. China Coal Soc. 2023, 48, 3979–4000. [Google Scholar] [CrossRef]
- He, M.C.; Gao, Y.B.; Yang, J.; Guo, Z.B.; Wang, E.Y.; Wang, Y.J. An energy-gathered roof cutting technique in no-pillar mining and its impact on stress variation in surrounding rocks. J. Rock Mech. Eng. 2017, 36, 1314–1325. [Google Scholar] [CrossRef]
- Kang, H.; Zhang, X.; Wang, D.; Tian, J.; Yi, Z.; Jiang, W. Surrounding Rock Control Technology and Its Application in Non-Pillar Mining. J. China Coal Soc. 2022, 47, 16–44. [Google Scholar] [CrossRef]
- Wang, Y.J.; He, M.C.; Zhang, K.X.; Yang, J.; Zhen, E.Z.; Zhu, Z.; Gao, Y.; Ma, Z.M. Strata behavior characteristics and control countermeasures for the gateroad surroundings in innovative non-pillar mining method with gateroad formed automatically. J. Min. Saf. Eng. 2018, 35, 677–685. [Google Scholar] [CrossRef]
- Wang, J.; Xu, J.; Yang, S.; Wang, Z. Development of strata movement and its control in underground mining: In memory of 40 years of Voussoir Beam Theory proposed by Academician Minggao Qian. Coal Sci. Technol. 2023, 51, 80–94. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, Y.; Bai, J.; Tian, Z.; Zhang, Z.; Wang, R.; Fu, H.; Liu, S.; Deng, M.; Zhu, Q.; et al. Dynamic Stability Mechanism and Control of Surrounding Rock in Abandoned Roadways under Masonry Beam Structure. J. China Coal Soc. 2025, 1–18. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, L.; Zhang, D.; Hu, Y.; Chang, J.; Zhang, Z. Deformation and Fracture Mechanisms of Thick Hard Roofs in Upward Mining Coalfaces: A Mechanical Model and Its Validation. Appl. Sci. 2024, 14, 10278. [Google Scholar] [CrossRef]
- Gao, X.; Pan, Y.; Zhao, T.; Wang, W.; Xiao, Y.; Song, Y.; Dai, L. Interlayer Shear Sliding Behaviors during the Fracture Process of Thick Sandstone Roof and Its Mechanism Leading to Coal Mine Tremors. Appl. Sci. 2024, 14, 4323. [Google Scholar] [CrossRef]
- Li, J.; Zheng, C.; Gu, S.; Wu, B.; Wang, X.; Song, Y. Study and Application of the Fracture Mechanics Model for Stope Roof under the Coupling Effect of Immediate Roof and Main Roof. Coal Geol. Explor. 2023, 51, 123–129. [Google Scholar]
- Gao, L.; Liu, P.; Zhang, P.; Wu, G.; Kang, X. Influence of fracture types of main roof on the stability of surrounding rock of the gob-side coal-rock roadway in inclined coal seams and its engineering application. Meitiandizhi Yu Kantan/Coal Geol. Explor. 2022, 50, 73–80. [Google Scholar] [CrossRef]
- Yang, D.; Gao, M.; Cheng, Y.; Sheng, W.; Chen, J. Analysis on instability of surrounding rock in gob-side entry retaining with the character of soft rock composite roof. Adv. Mater. Res. 2012, 524–527, 396–403. [Google Scholar] [CrossRef]
- Chen, D.; Wang, X.; Li, M.; Bai, J.; Zhang, F.; Yu, Y.; Zhao, X.; Wang, G. Study on the Fracture Location of Main Roof and Stability of Surrounding Rock in the Gob-Side Entry. SSRN 2023. [Google Scholar] [CrossRef]
- Yu, B.; Kuang, T.; Yang, J.; Zhu, W. Analysis of Overlying Strata Structure and Its Evolution Characteristics for Hard Roof in Ultra-Thick Coal Seam Mining. Coal Sci. Technol. 2023, 51, 95–104. [Google Scholar] [CrossRef]
- Liu, J.; Li, C.; Shi, Y.; Zhang, Y. Stability Analysis and Fracture Patterns of Hard Main Roof in Longwall Top Coal Caving with Large Mining Height. Shock. Vib. 2021, 2021, 9930221. [Google Scholar] [CrossRef]
- Herezy, Ł.; Janik, D.; Skrzypkowski, K. Powered Roof Support—Rock Strata Interactions on the Example of an Automated Coal Plough Syste. Stud. Geotech. Mechanica 2018, 40, 46–55. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, C.; Lin, X.; Chi, G.M.; Fan, C.Z.; Yu, Y.J. Roof Pressure Evolution and Support Crushing Prediction of Fully Mechanized Caving Face Based on Zoning Support Mechanical Model. J. China Coal Soc. 2022, 47, 3622–3633. [Google Scholar] [CrossRef]
- Vu, T.T.; Do, S.A. Determination of the rock mass displacement zone by numerical modeling method when exploiting the longwall at the Nui Beo Coal Mine, Vietnam. Min. Miner. Depos. 2023, 17, 59–66. [Google Scholar] [CrossRef]
- Demin, V.; Khalikova, E.; Rabatuly, M.; Amanzholov, Z.; Zhumabekova, A.; Syzdykbaeva, D.; Bakhmagambetova, G.; Yelzhanov, Y. Research into mine working fastening technology in the zones of increased rock pressure behind the longwall face to ensure safe mining operations. Min. Miner. Depos. 2024, 18, 27–36. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, A.K.; Mishra, A.K.; Singh, R. Underground mining of thick coal seams. Int. J. Min. Sci. Technol. 2015, 25, 885–896. [Google Scholar] [CrossRef]
- Shen, J. Study on the Mechanism of Overburden Movement and Retaining Strategies for Gob-Side Entry Retaining in Three-Soft Thick Coal Seams. Ph.D. Thesis, Henan Polytechnic University, Jiaozuo, China, 2022. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, S.; Zhang, C. Deformation Characteristics and Response Factors of Rock Bolt Body in Roadway with Layered Composite Roof. Appl. Sci. 2024, 14, 6694. [Google Scholar] [CrossRef]
- Lv, K.; He, F.; Xu, X.; Zhai, W.; Qin, B. Fracture characteristics and stability analysis of the main roof structure with special—Shaped load—Elastic foundation. Chin. J. Rock Mech. Eng. 2023, 42, 930–947. [Google Scholar] [CrossRef]






| Lithology | Elastic Modulus /103 MPa | Tensile Strength /MPa | Cohesion /MPa | Internal Friction Angle /° | Poisson Ratio |
|---|---|---|---|---|---|
| sandy mudstone | 3.2 | 2.1 | 3.5 | 25 | 0.31 |
| packsand | 4.2 | 2.3 | 4.4 | 22 | 0.24 |
| mudstone | 2.5 | 1.3 | 2.2 | 24 | 0.17 |
| medium sandstone | 4.2 | 2.9 | 5.9 | 26 | 0.27 |
| No. 2-1 coal | 0.5 | 0.1 | 1.5 | 22 | 0.24 |
| limestone | 27.7 | 6.2 | 45.8 | 12.6 | 0.3 |
| Coal Seam Thickness/m | 3 | 4 | 5 | 6 | 7 |
| Fracture Position/m | +0.5 | 0 | −0.4 | −4.5 | −7.7 |
| Immediate Roof Thickness/m | 4 | 6 | 8 | 10 | 12 |
| Fracture Position/m | +1.4 | +0.5 | 0 | −1.5 | −3.5 |
| Coal Seam Elastic Modulus/ 103 MPa | 0.5 | 1 | 1.5 | 2 | 2.5 |
| Fracture Position/m | 0 | 0 | +1.4 | +1.4 | +1.4 |
| Immediate Roof Elastic Modulus/103 MPa | 3 | 4 | 5 | 6 | 7 |
| Fracture Position /m | 0 | +1.4 | +1.4 | +1.5 | +1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Yang, Y.; Li, S.; Zhu, K. Investigation into the Fracture Evolution Law of Overlying Strata Roof in Shallowly Buried “Three-Soft” Coal Seam Fully Mechanized Mining Faces and Its Influence on the Feasibility of Gob-Side Entry Retaining. Appl. Sci. 2025, 15, 4607. https://doi.org/10.3390/app15094607
Hu G, Yang Y, Li S, Zhu K. Investigation into the Fracture Evolution Law of Overlying Strata Roof in Shallowly Buried “Three-Soft” Coal Seam Fully Mechanized Mining Faces and Its Influence on the Feasibility of Gob-Side Entry Retaining. Applied Sciences. 2025; 15(9):4607. https://doi.org/10.3390/app15094607
Chicago/Turabian StyleHu, Guoyou, Yongkang Yang, Shuai Li, and Konghao Zhu. 2025. "Investigation into the Fracture Evolution Law of Overlying Strata Roof in Shallowly Buried “Three-Soft” Coal Seam Fully Mechanized Mining Faces and Its Influence on the Feasibility of Gob-Side Entry Retaining" Applied Sciences 15, no. 9: 4607. https://doi.org/10.3390/app15094607
APA StyleHu, G., Yang, Y., Li, S., & Zhu, K. (2025). Investigation into the Fracture Evolution Law of Overlying Strata Roof in Shallowly Buried “Three-Soft” Coal Seam Fully Mechanized Mining Faces and Its Influence on the Feasibility of Gob-Side Entry Retaining. Applied Sciences, 15(9), 4607. https://doi.org/10.3390/app15094607






