A Deep Learning Framework for High-Frequency Signal Forecasting Based on Graph and Temporal-Macro Fusion
Abstract
1. Introduction
- We propose a deep quantitative modeling framework that integrates asset graph learning, cross-scale temporal modeling, and macro-semantic embedding to jointly capture structural dependencies, temporal dynamics, and external disturbances in signal data, thereby improving the accuracy and robustness of predictive models.
- We introduce the use of large language models (LLMs) to extract macroeconomic policy semantics for strategy construction, aligning textual sentiment embeddings with system signals to improve interpretability and sensitivity to exogenous changes.
- We conduct extensive empirical evaluations on real-world large-scale datasets, assessing performance from multiple dimensions, including classification accuracy, return prediction error, and backtesting outcomes. Results show that our approach achieved superior robustness under varying conditions.
- We implement an end-to-end prototype system for signal generation, enabling full-cycle automation from data ingestion to strategy execution, demonstrating scalability and deployment feasibility.
2. Related Work
2.1. Applications of Deep Learning in Data-Driven Strategy Modeling
2.2. Graph Neural Networks for Modeling Inter-Entity Relationships
2.3. Macro-Factor Driven Strategy Modeling
3. Materials and Method
3.1. Data Collection
3.2. Data Preprocessing and Augmentation
3.3. Proposed Method
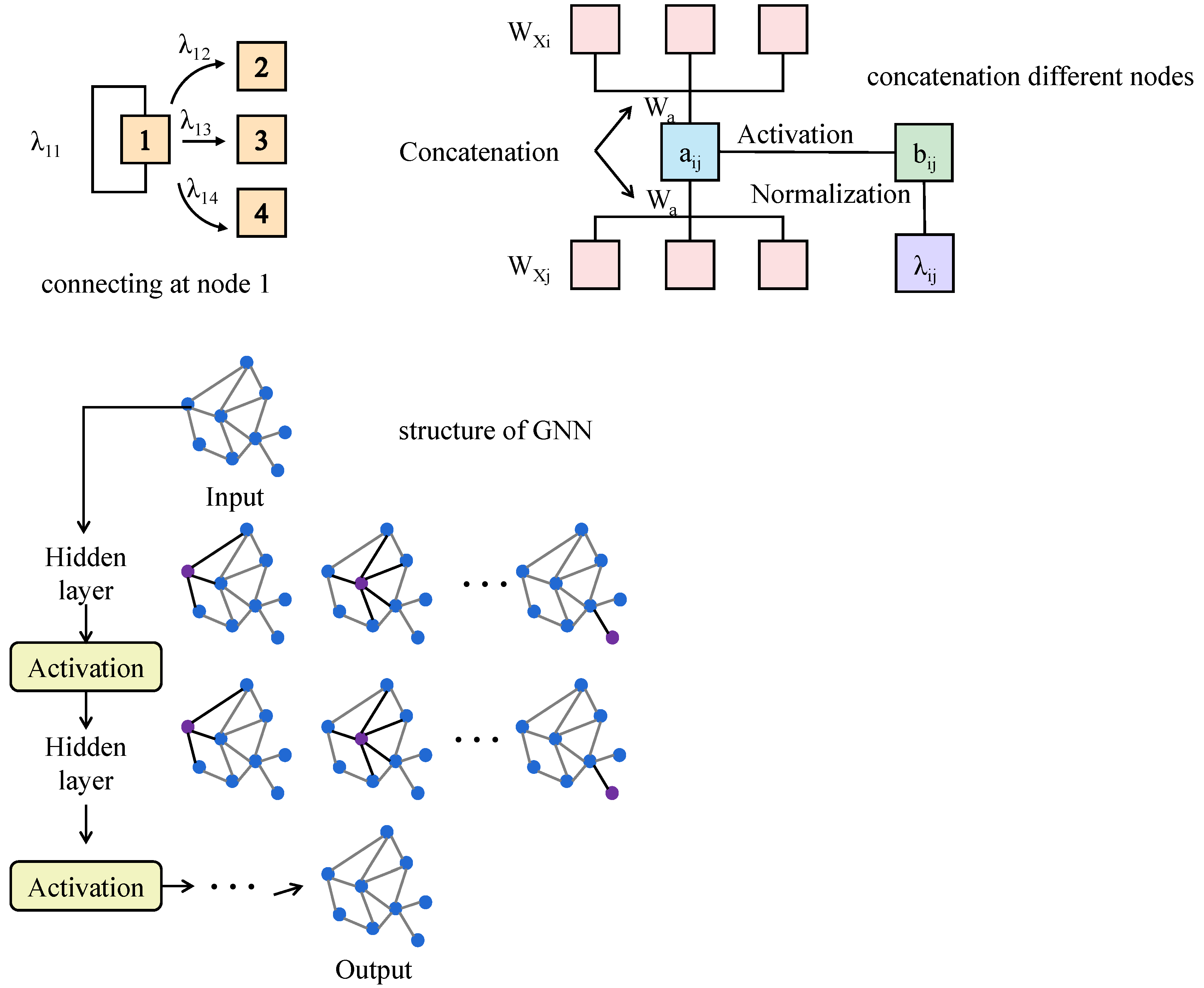
3.3.1. Graph Modeling and Graph Attention Module
3.3.2. Multi-Scale Transformer Module (Revised)
3.3.3. Macroeconomic Factor Fusion Module
3.3.4. Unified Optimization Objective for Multi-Module Coordination
4. Results and Discussion
4.1. Experimental Design
4.2. Evaluation Metrics
4.3. Baseline Models
4.4. Classification and Regression Results on Signal Sequences
4.5. Performance Comparison Under Module Removal Settings
4.6. Strategy Performance Comparison Under Different Data Environments
4.7. Impact of Input Frequency Features on Model Performance
4.8. Parameter and Activation Sensitivity Analysis
4.9. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goldstein, I. Information in financial markets and its real effects. Rev. Financ. 2023, 27, 1–32. [Google Scholar] [CrossRef]
- Eaton, G.W.; Green, T.C.; Roseman, B.; Wu, Y. Zero-Commission Individual Investors, High Frequency Traders, and Stock Market Quality. 2021. Available online: https://pages.stern.nyu.edu/~jhasbrou/SternMicroMtg/Old/SternMicroMtg2021/Papers/Zero-commission%20individual%20traders.pdf (accessed on 19 March 2021).
- Fu, Y. GM (1,1) and Quantitative Trading Decision Model. In Financial Engineering and Risk Management; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Lin, Z.F.; Zhao, H.H.; Sun, Z. Nonlinear modeling of financial state variables and multiscale numerical analysis. Eur. Phys. J. Spec. Top. 2025, 7, 1–15. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, Y.; Wang, M.; Liu, Z. Quantamental Trading: Fundamental and Quantitative Analysis with Multi-factor Regression Model Strategy. In Proceedings of the International Conference on Business and Policy Studies; Springer: Singapore, 2023; pp. 1455–1470. [Google Scholar]
- Eti, S. The use of quantitative methods in investment decisions: A literature review. Res. Anthol. Pers. Financ. Improv. Financ. Lit. 2021, 1–20. [Google Scholar] [CrossRef]
- Olukoya, O. Time series-based quantitative risk models: Enhancing accuracy in forecasting and risk assessment. Int. J. Comput. Appl. Technol. Res. 2023, 12, 29–41. [Google Scholar]
- Zhang, J.; Huang, Y.; Huang, C.; Huang, W. Research on arima based quantitative investment model. Acad. J. Bus. Manag. 2022, 4, 54–62. [Google Scholar]
- Diqi, M.; Utami, E.; Wibowo, F.W. A Study on Methods, Challenges, and Future Directions of Generative Adversarial Networks in Stock Market Prediction. In Proceedings of the 2024 IEEE International Conference on Technology, Informatics, Management, Engineering and Environment (TIME-E), Bali, Indonesia, 7–9 August 2024; Volume 5, pp. 148–153. [Google Scholar]
- Sahu, S.K.; Mokhade, A.; Bokde, N.D. An overview of machine learning, deep learning, and reinforcement learning-based techniques in quantitative finance: Recent progress and challenges. Appl. Sci. 2023, 13, 1956. [Google Scholar] [CrossRef]
- Ludkovski, M. Statistical machine learning for quantitative finance. Annu. Rev. Stat. Its Appl. 2023, 10, 271–295. [Google Scholar] [CrossRef]
- Liu, X.Y.; Yang, H.; Gao, J.; Wang, C.D. FinRL: Deep reinforcement learning framework to automate trading in quantitative finance. In Proceedings of the Second ACM International Conference on AI in Finance, Virtual Event, 3–5 November 2021; pp. 1–9. [Google Scholar]
- Horvath, B.; Muguruza, A.; Tomas, M. Deep learning volatility: A deep neural network perspective on pricing and calibration in (rough) volatility models. Quant. Financ. 2021, 21, 11–27. [Google Scholar] [CrossRef]
- Khunger, A. Learning for financial stress testing: A data-driven approach to risk management. Int. J. Innov. Stud. 2022, 3, 97–113. [Google Scholar] [CrossRef]
- Sirignano, J.; Cont, R. Universal features of price formation in financial markets: Perspectives from deep learning. In Machine Learning and AI in Finance; Routledge: London, UK, 2021; pp. 5–15. [Google Scholar]
- Nguyen, D.K.; Sermpinis, G.; Stasinakis, C. Big data, artificial intelligence and machine learning: A transformative symbiosis in favour of financial technology. Eur. Financ. Manag. 2023, 29, 517–548. [Google Scholar] [CrossRef]
- Khuwaja, P.; Khowaja, S.A.; Dev, K. Adversarial learning networks for FinTech applications using heterogeneous data sources. IEEE Internet Things J. 2021, 10, 2194–2201. [Google Scholar] [CrossRef]
- Borisov, V.; Broelemann, K.; Kasneci, E.; Kasneci, G. DeepTLF: Robust deep neural networks for heterogeneous tabular data. Int. J. Data Sci. Anal. 2023, 16, 85–100. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Y.; Wei, J.; Wu, H.; Deng, M. HLSTM: Heterogeneous long short-term memory network for large-scale InSAR ground subsidence prediction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8679–8688. [Google Scholar] [CrossRef]
- Ahmed, I.; Ahmad, M.; Chehri, A.; Jeon, G. A heterogeneous network embedded medicine recommendation system based on LSTM. Future Gener. Comput. Syst. 2023, 149, 1–11. [Google Scholar] [CrossRef]
- Qu, L.; Zhou, Y.; Liang, P.P.; Xia, Y.; Wang, F.; Adeli, E.; Fei-Fei, L.; Rubin, D. Rethinking architecture design for tackling data heterogeneity in federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10061–10071. [Google Scholar]
- Corso, G.; Stark, H.; Jegelka, S.; Jaakkola, T.; Barzilay, R. Graph neural networks. Nat. Rev. Methods Prim. 2024, 4, 17. [Google Scholar] [CrossRef]
- Brody, S.; Alon, U.; Yahav, E. How attentive are graph attention networks? arXiv 2021, arXiv:2105.14491. [Google Scholar]
- Tumiran, M.A. Constructing a framework from quantitative data analysis: Advantages, types and innovative approaches. Quantum J. Soc. Sci. Humanit. 2024, 5, 198–212. [Google Scholar] [CrossRef]
- Peng, R.; Liu, K.; Yang, P.; Yuan, Z.; Li, S. Embedding-based retrieval with llm for effective agriculture information extracting from unstructured data. arXiv 2023, arXiv:2308.03107. [Google Scholar]
- De Bellis, A. Structuring the Unstructured: An LLM-Guided Transition. In Proceedings of the Doctoral Consortium at ISWC 2023 Co-Located with 22nd International Semantic Web Conference (ISWC 2023), Athens, Greece, 7 November 2023. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 193–209. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Araci, D. Finbert: Financial sentiment analysis with pre-trained language models. arXiv 2019, arXiv:1908.10063. [Google Scholar]
- Xin, C.; Han, Q.; Pan, G. Correlation Matters: A Stock Price Predication Model Based on the Graph Convolutional Network. In International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2024; pp. 228–239. [Google Scholar]
- Vladov, S.; Scislo, L.; Sokurenko, V.; Muzychuk, O.; Vysotska, V.; Osadchy, S.; Sachenko, A. Neural Network Signal Integration from Thermogas-Dynamic Parameter Sensors for Helicopters Turboshaft Engines at Flight Operation Conditions. Sensors 2024, 24, 4246. [Google Scholar] [CrossRef]


| Data Type | Source | Sample Size |
|---|---|---|
| Stock Trading Data | Wind/Tushare | 300 stocks × 2400 days |
| Technical Indicators | Self-calculated | 300 stocks × 13 × 2400 days |
| Asset Graph Matrix | Constructed | 300 × 300 × 2400 graphs |
| Macroeconomic Indicators | Wind | 120 time points per indicator |
| Policy News Summaries | Caixin, NBS, Sina Finance | 21,483 texts |
| Language Model Output | ChatGPT API | One-to-one with policy texts |
| Model | Precision (%) | Recall (%) | F1-Score (%) | MSE (×) | MAE (×) |
|---|---|---|---|---|---|
| SVM | 81.4 | 80.9 | 81.1 | 3.12 | 1.42 |
| XGBoost | 82.7 | 81.9 | 82.3 | 2.78 | 1.33 |
| LightGBM | 83.5 | 82.6 | 83.0 | 2.65 | 1.28 |
| LSTM | 85.8 | 85.1 | 85.4 | 2.39 | 1.19 |
| TCN | 86.9 | 86.4 | 86.6 | 2.21 | 1.12 |
| FinBERT | 87.1 | 86.5 | 86.8 | 2.18 | 1.10 |
| StockGCN | 89.3 | 88.0 | 88.6 | 2.04 | 1.07 |
| Proposed Method | 92.4 | 91.6 | 92.0 | 1.76 | 0.96 |
| Configuration | Precision (%) | Recall (%) | F1-Score (%) | MSE (×) | MAE (×) |
|---|---|---|---|---|---|
| w/o Temporal | 87.5 | 86.9 | 87.2 | 2.46 | 1.22 |
| w/o Macro | 88.1 | 87.3 | 87.7 | 2.42 | 1.19 |
| w/o Graph | 89.2 | 88.7 | 88.9 | 2.31 | 1.14 |
| Proposed | 92.4 | 91.6 | 92.0 | 1.76 | 0.96 |
| Market Condition | Precision (%) | Recall (%) | F1-Score (%) | MSE | MAE |
|---|---|---|---|---|---|
| Stable Growth | 93.5 | 92.7 | 93.1 | 1.52 | 0.89 |
| High-Frequency Volatility | 91.6 | 90.8 | 91.2 | 1.83 | 0.99 |
| Overall Declining | 90.2 | 89.3 | 89.7 | 1.94 | 1.06 |
| Feature Type | Precision (%) | Recall (%) | F1-Score (%) | MSE (×) | MAE (×) |
|---|---|---|---|---|---|
| Low-Freq Only | 88.3 | 87.5 | 87.9 | 2.47 | 1.23 |
| High-Freq Only | 89.6 | 88.9 | 89.2 | 2.34 | 1.15 |
| Multi-Freq | 92.4 | 91.6 | 92.0 | 1.76 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, L.; He, S.; Li, T.; Huang, Y.; Jiang, Y.; Yang, H.; Lv, C. A Deep Learning Framework for High-Frequency Signal Forecasting Based on Graph and Temporal-Macro Fusion. Appl. Sci. 2025, 15, 4605. https://doi.org/10.3390/app15094605
Zhang X, Zhang L, He S, Li T, Huang Y, Jiang Y, Yang H, Lv C. A Deep Learning Framework for High-Frequency Signal Forecasting Based on Graph and Temporal-Macro Fusion. Applied Sciences. 2025; 15(9):4605. https://doi.org/10.3390/app15094605
Chicago/Turabian StyleZhang, Xijue, Liman Zhang, Siyang He, Tianyue Li, Yinke Huang, Yaqi Jiang, Haoxiang Yang, and Chunli Lv. 2025. "A Deep Learning Framework for High-Frequency Signal Forecasting Based on Graph and Temporal-Macro Fusion" Applied Sciences 15, no. 9: 4605. https://doi.org/10.3390/app15094605
APA StyleZhang, X., Zhang, L., He, S., Li, T., Huang, Y., Jiang, Y., Yang, H., & Lv, C. (2025). A Deep Learning Framework for High-Frequency Signal Forecasting Based on Graph and Temporal-Macro Fusion. Applied Sciences, 15(9), 4605. https://doi.org/10.3390/app15094605





