Comprehensive Mechanical Analysis Model for Stability of Thin Sidewalls Under Localized Complex Loads
Abstract
:1. Introduction
2. Mechanical Analysis Model for TSWs
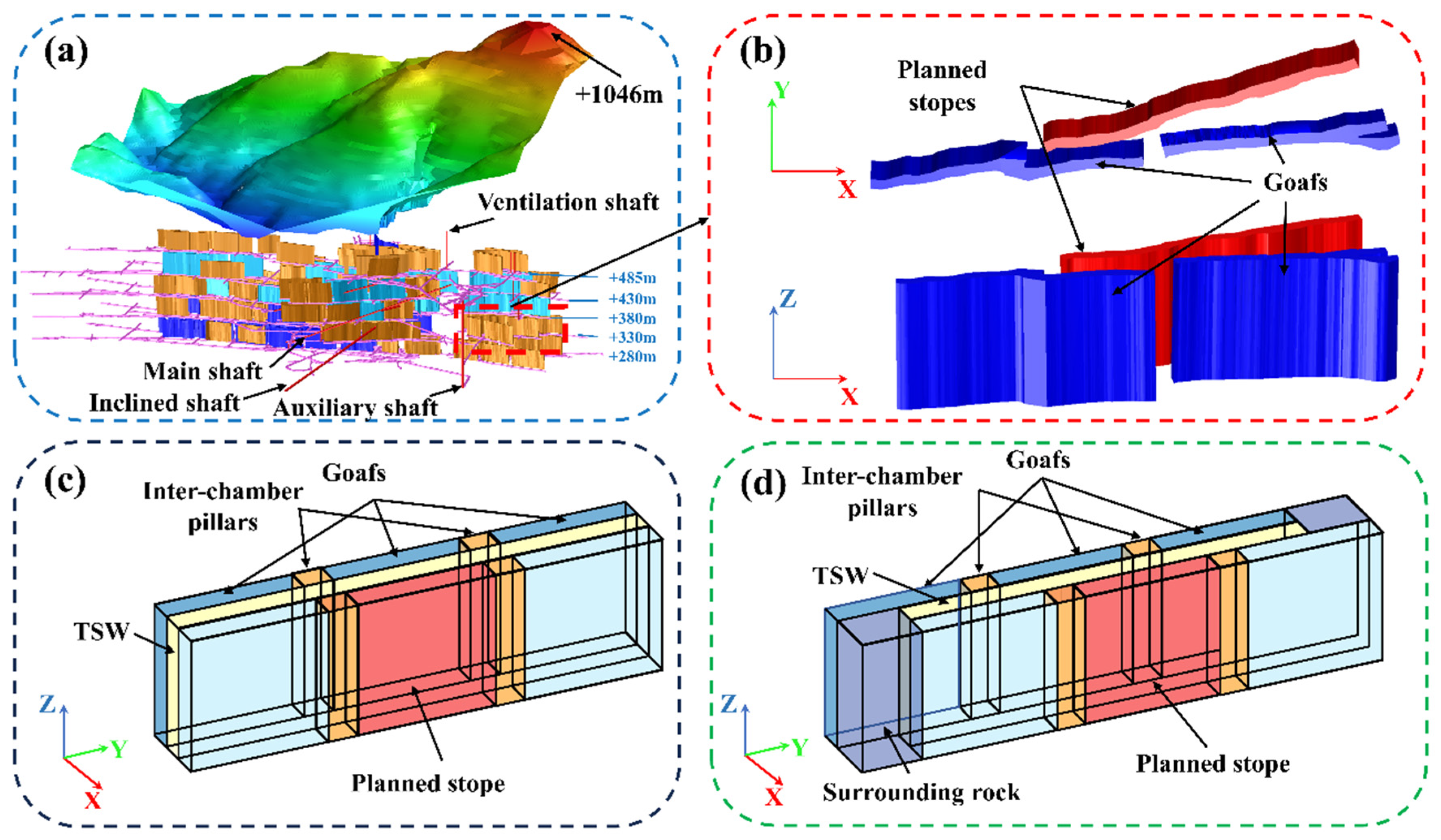
2.1. Background
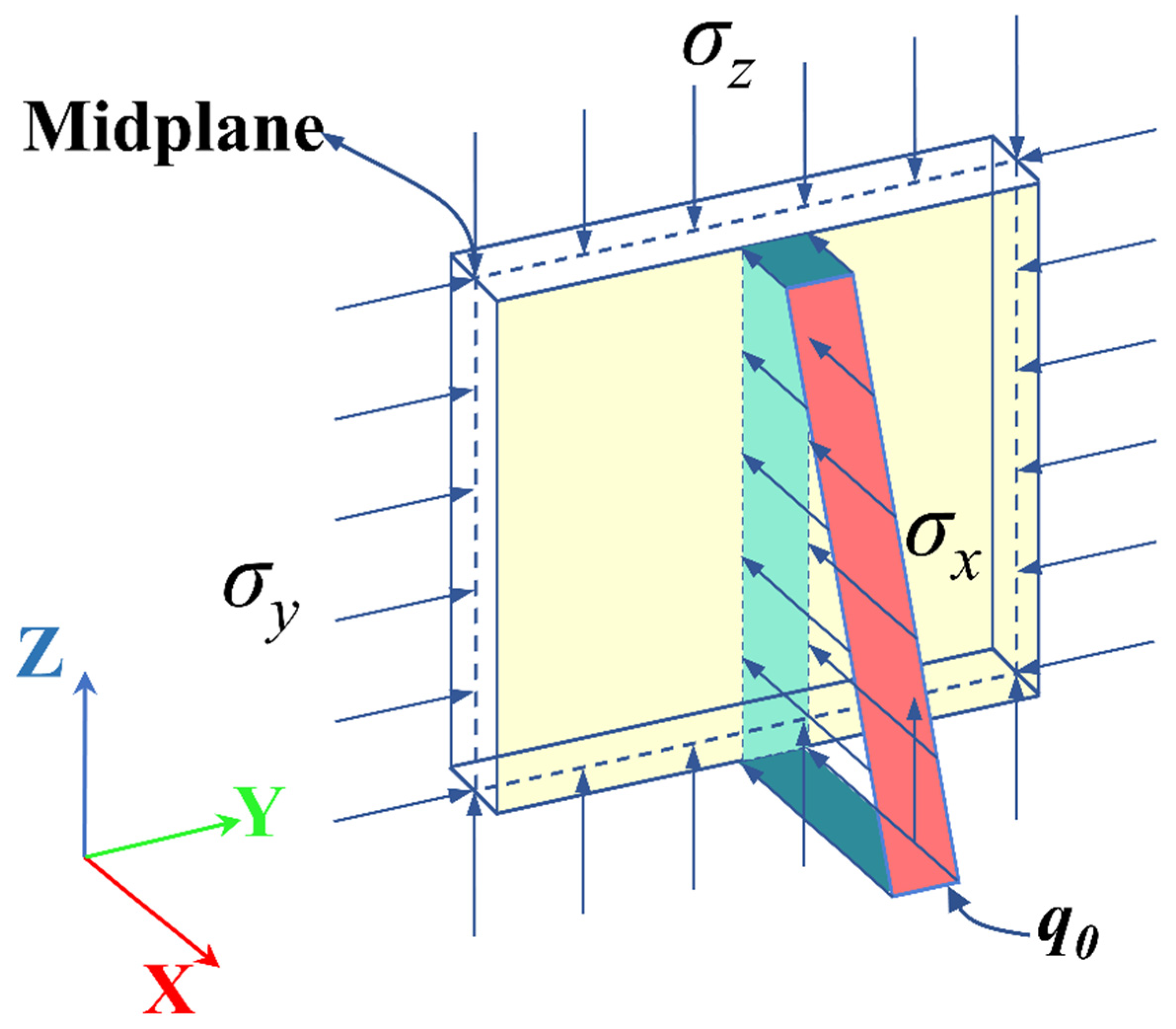
2.2. Mechanical Model
- (1)
- The TSW is considered a continuous, homogeneous material after discounting the in situ rock strength.
- (2)
- The TSW surface is smooth and uniform in width, which is represented by the average actual width in the model. Dynamic disturbances from blasting are neglected.
- (3)
- Displacements induced by loading are small, and boundary displacements are minimal due to the relatively large TSW size.
- (4)
- Once plastic damage initiates, the load-bearing capacity of the TSW drops significantly, and even minor stress variations can result in large lateral deflections. This assumption is valid in hard rock mining environments.
- (5)
- There is negligible plastic deformation at the contact interfaces between the TSW and the surrounding rock, consistent with conditions in hard rock mines.
- (6)
- Stress analysis conforms to the standard sign conventions of elastic mechanics.
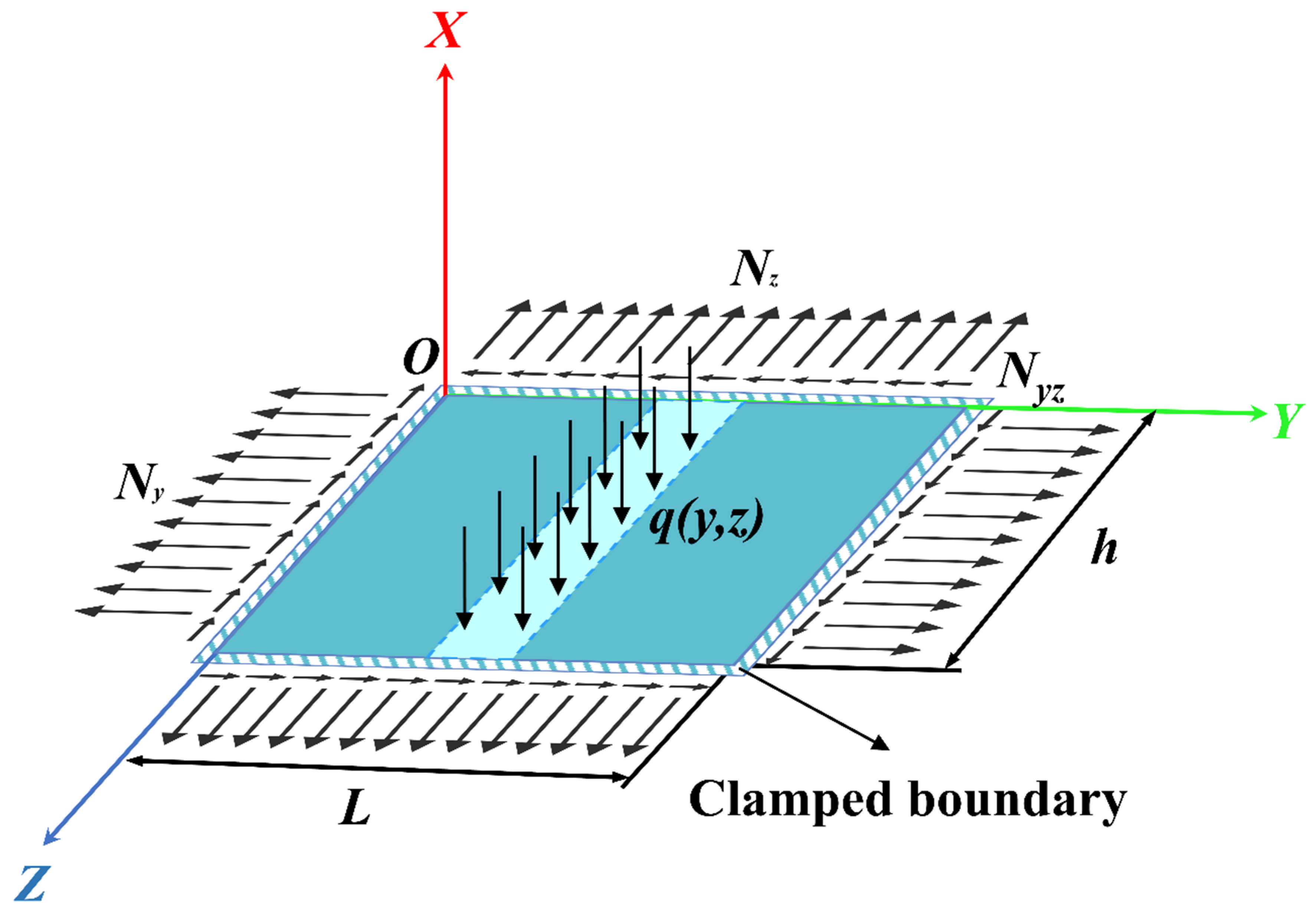
3. Analysis of Mechanical Model of Rectangular Plate Supported on Four Edges Under Local Lateral Load, Longitudinal and Transverse Load
3.1. Thin Plate Differential Equilibrium Equation
3.2. Determining Coefficients for Deflection Expressions with Additional Terms
3.3. Calculation of Bending Moments, and Internal Forces in Thin Plates
3.4. TSWs Yield Judgment Method
4. Calculation and Analysis of Mechanical Models
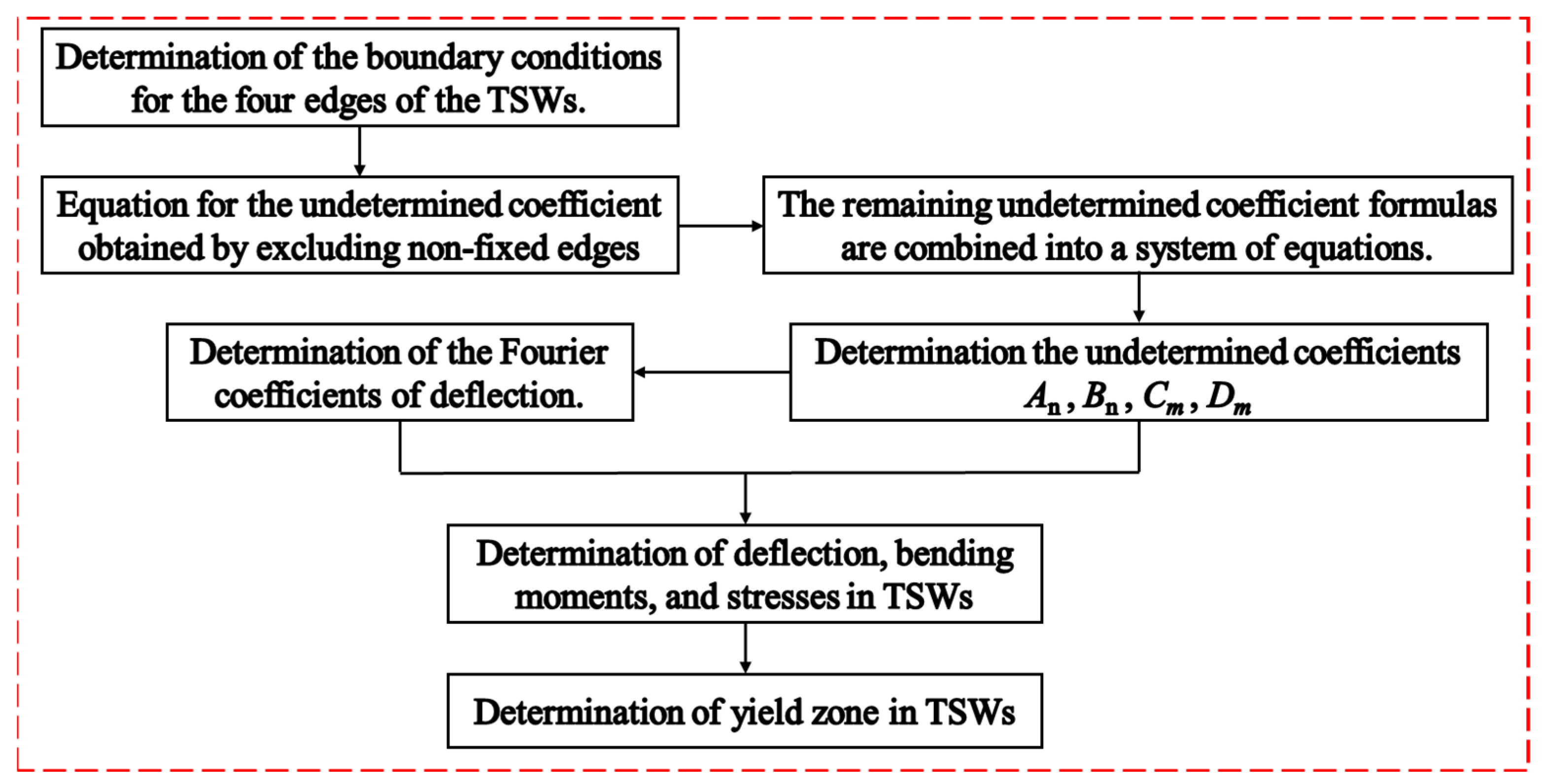
4.1. Calculation Procedure
4.2. Determining Calculation Parameters
4.3. Determining the Number of Convergent Series Terms in the Mechanical Model
4.4. Comparative Study of Computational Results with Existing Method
5. Stability Analysis of TSWs
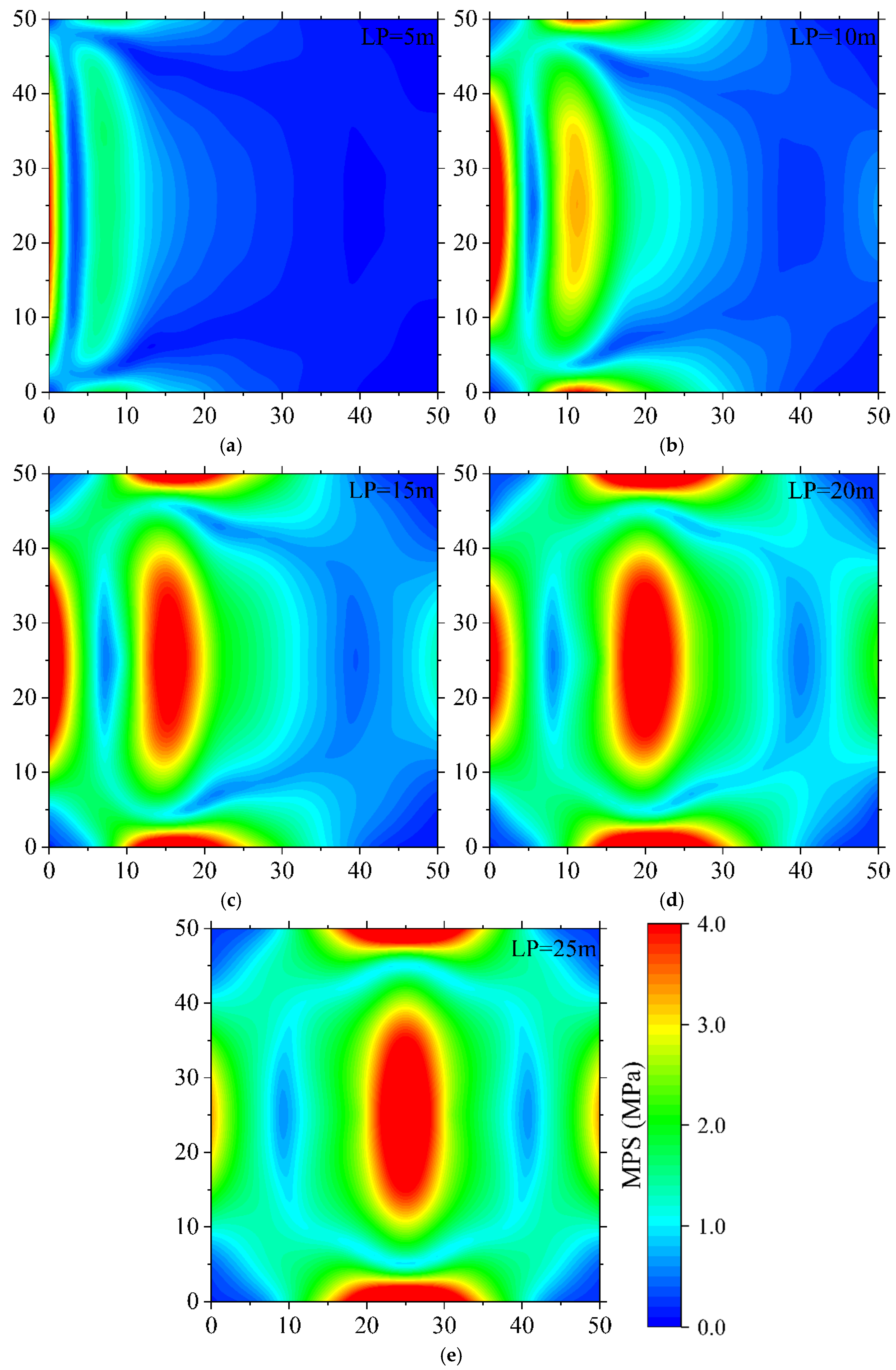
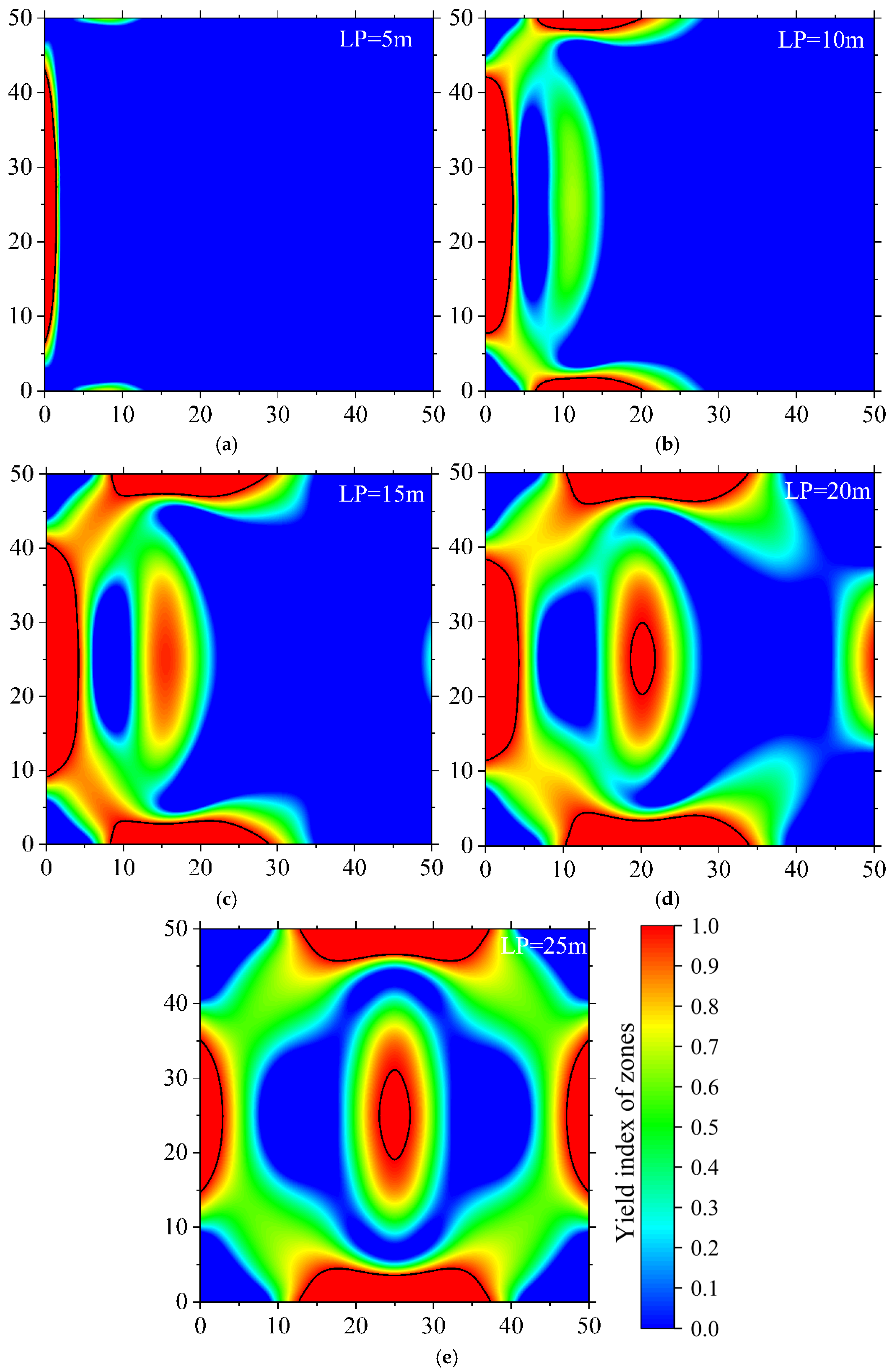
5.1. Stress Distribution and Yield Zone Analysis of TSWs
5.2. Analysis of Influencing Factors
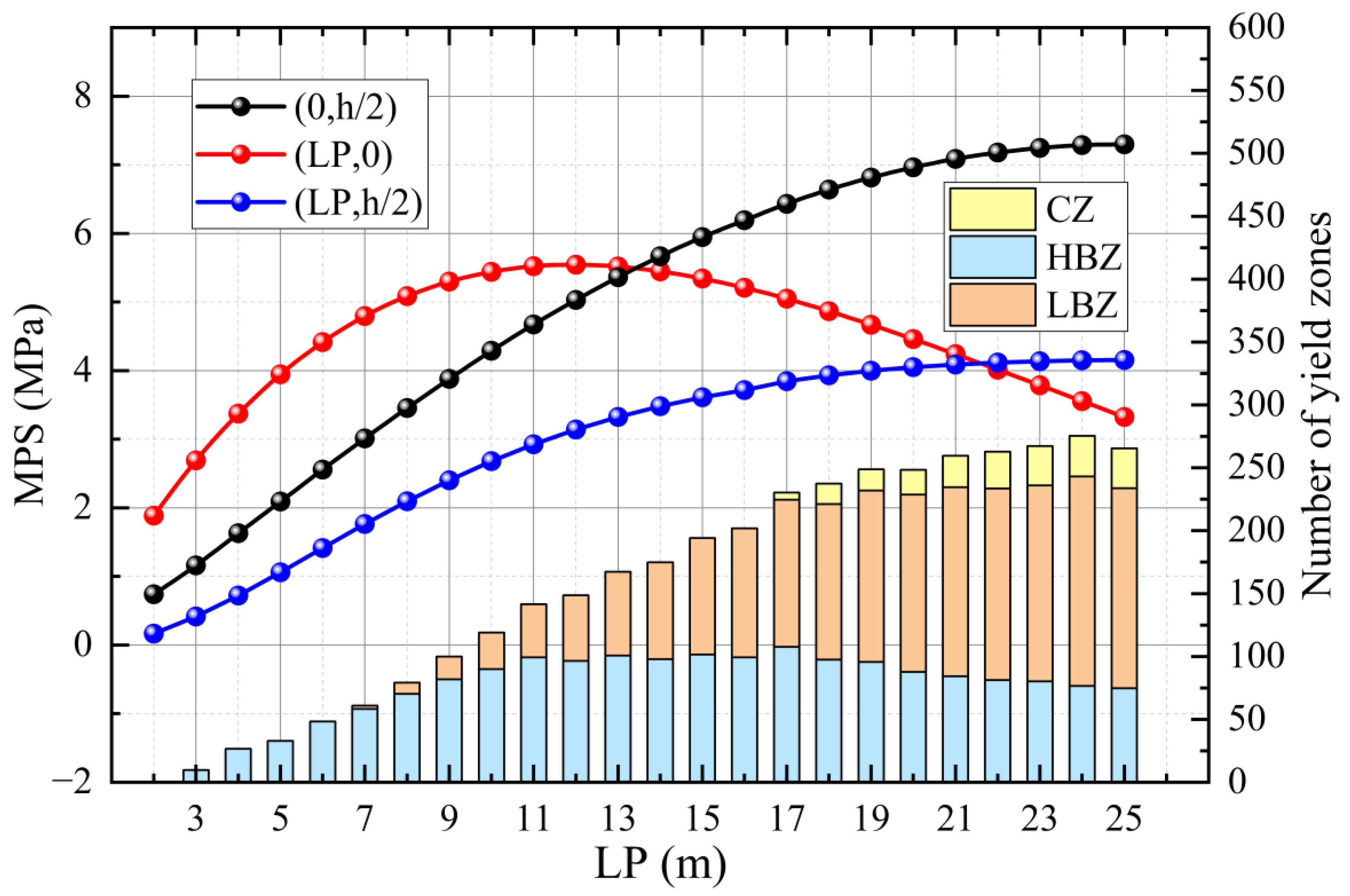
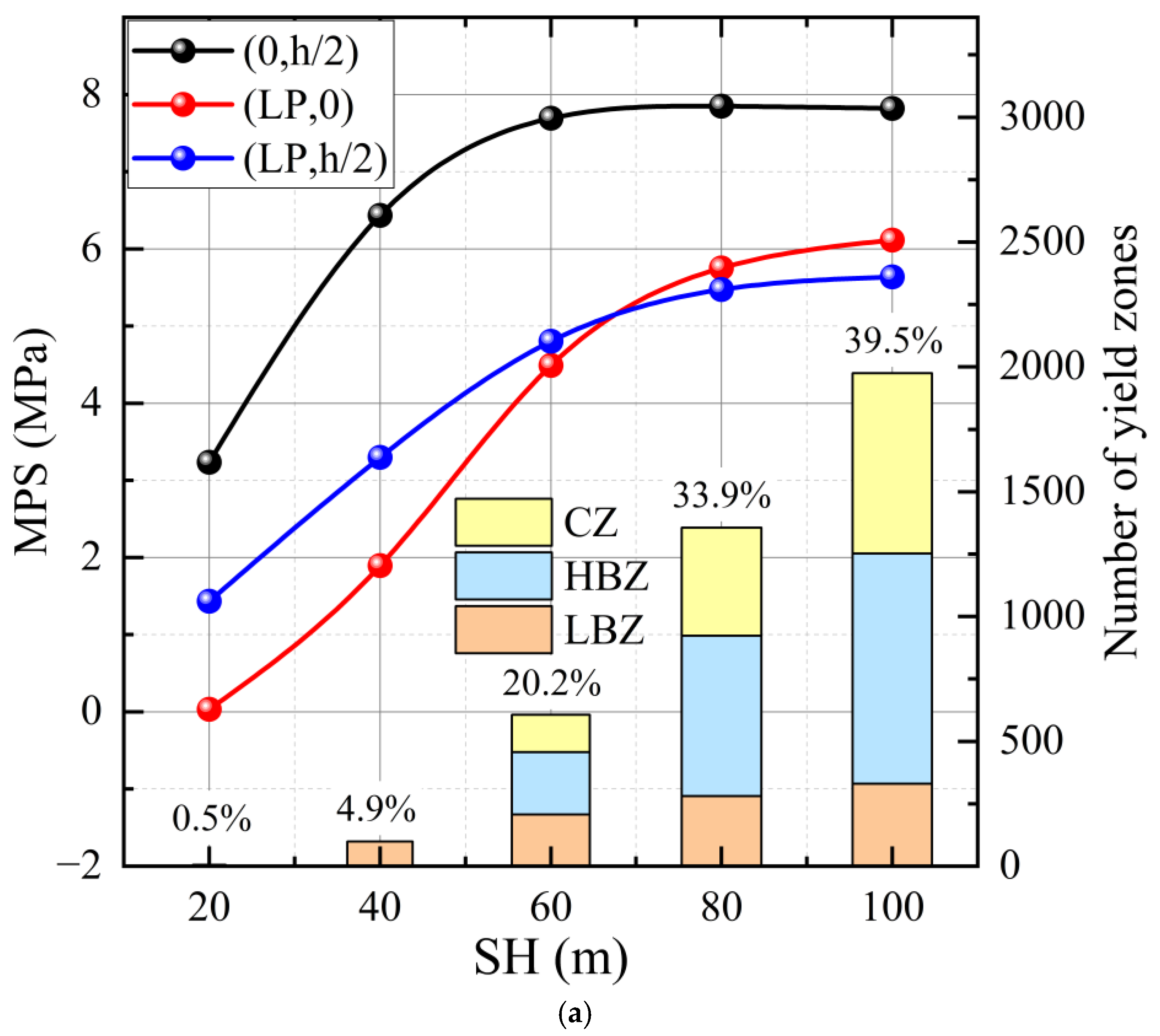
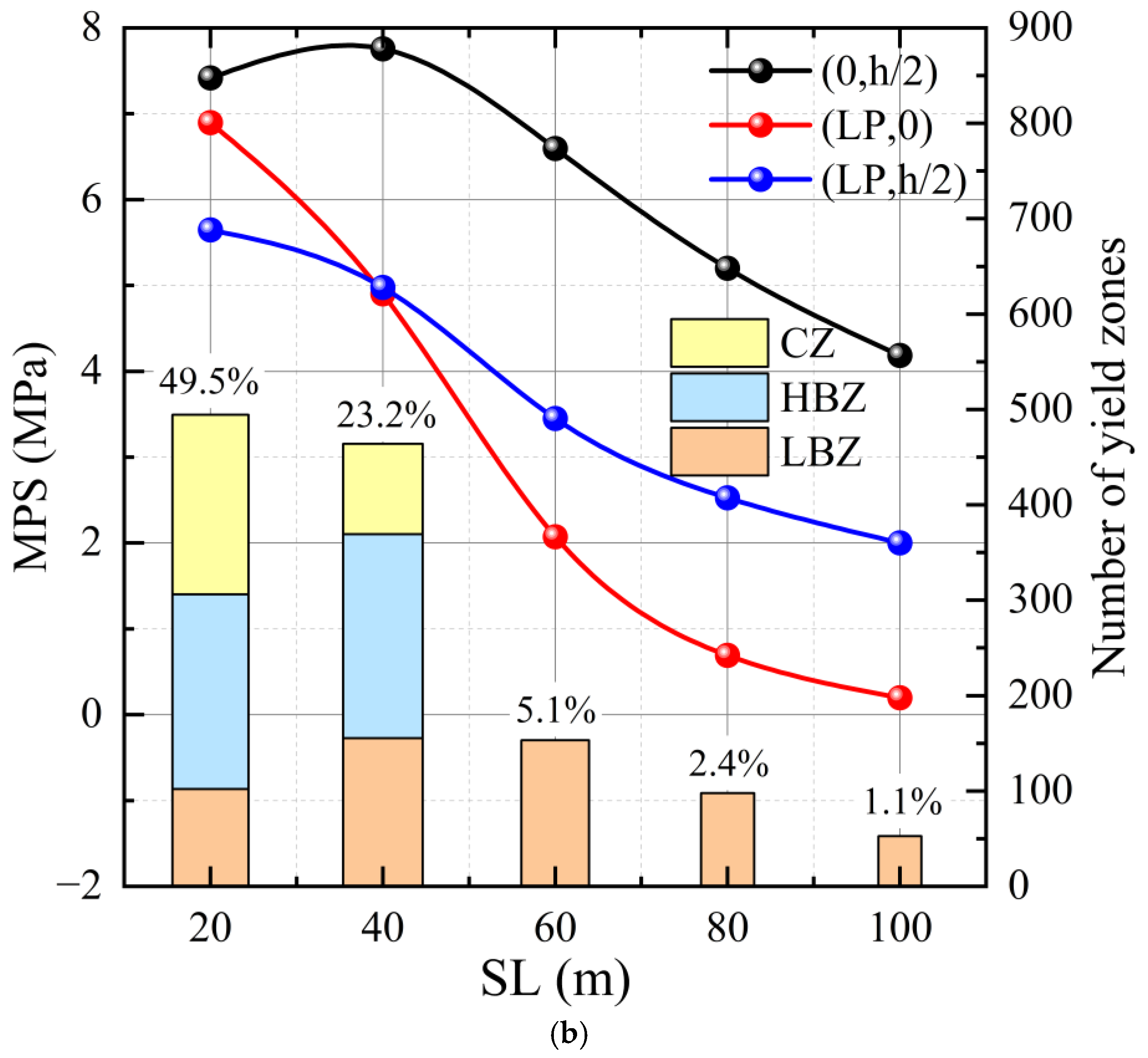
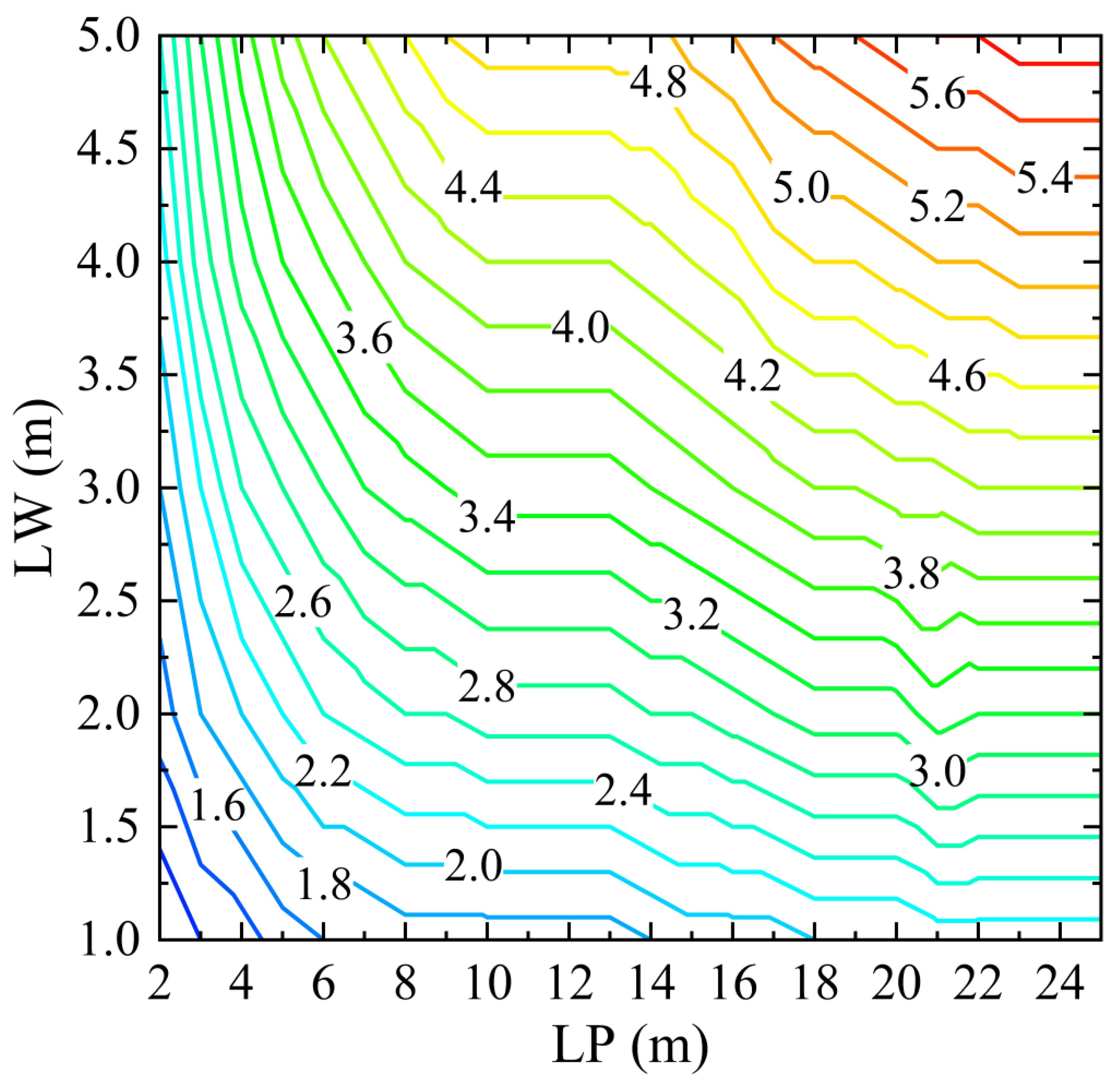
5.2.1. Influence of Lateral Load Center Position on TSW Stability
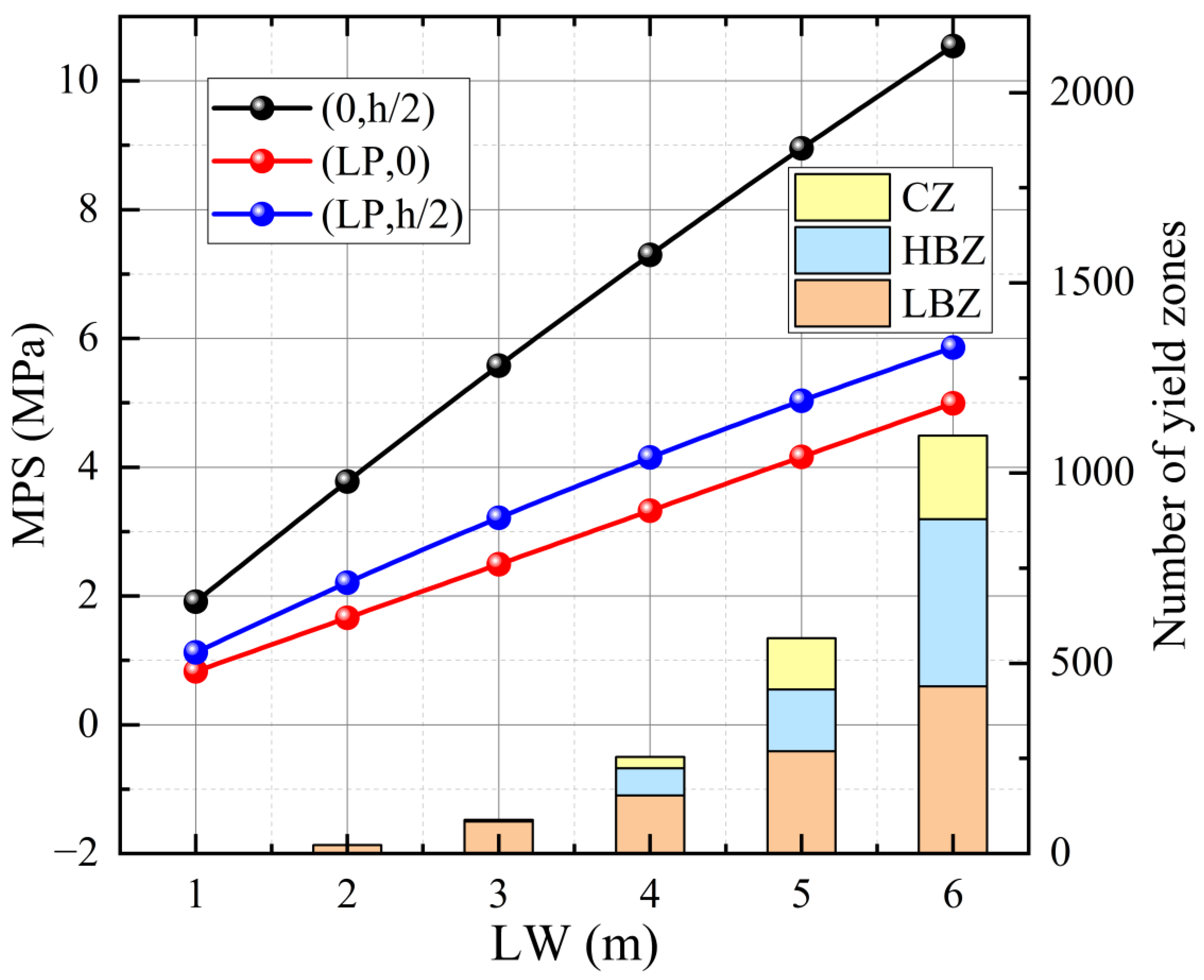
5.2.2. Influence of Lateral Load Width on TSW Stability
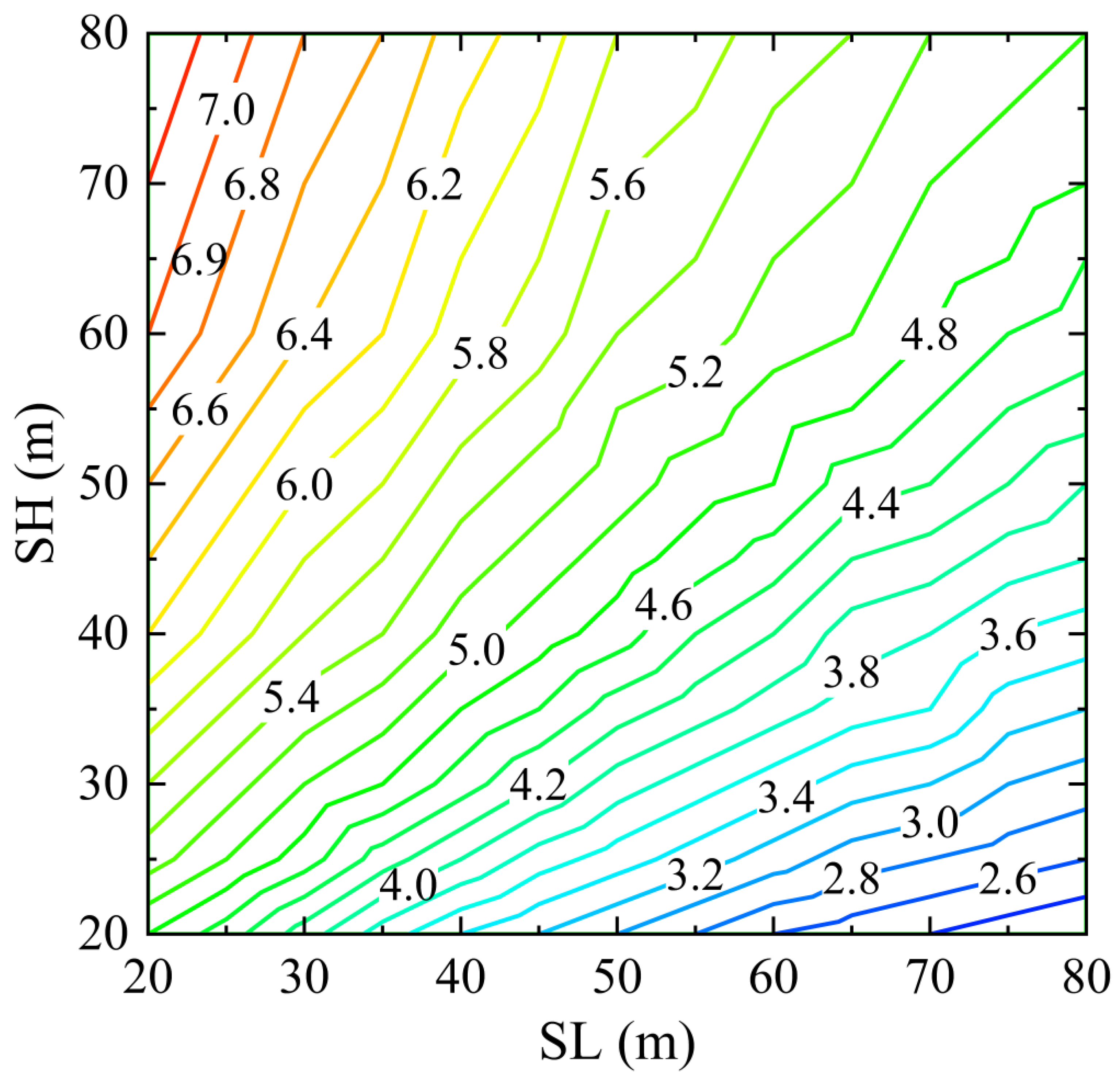
5.2.3. Influence of Sidewall Length and Height on TSW Stability
5.3. Variation in Critical Thickness with TSW Structural Parameters and Lateral Load Conditions
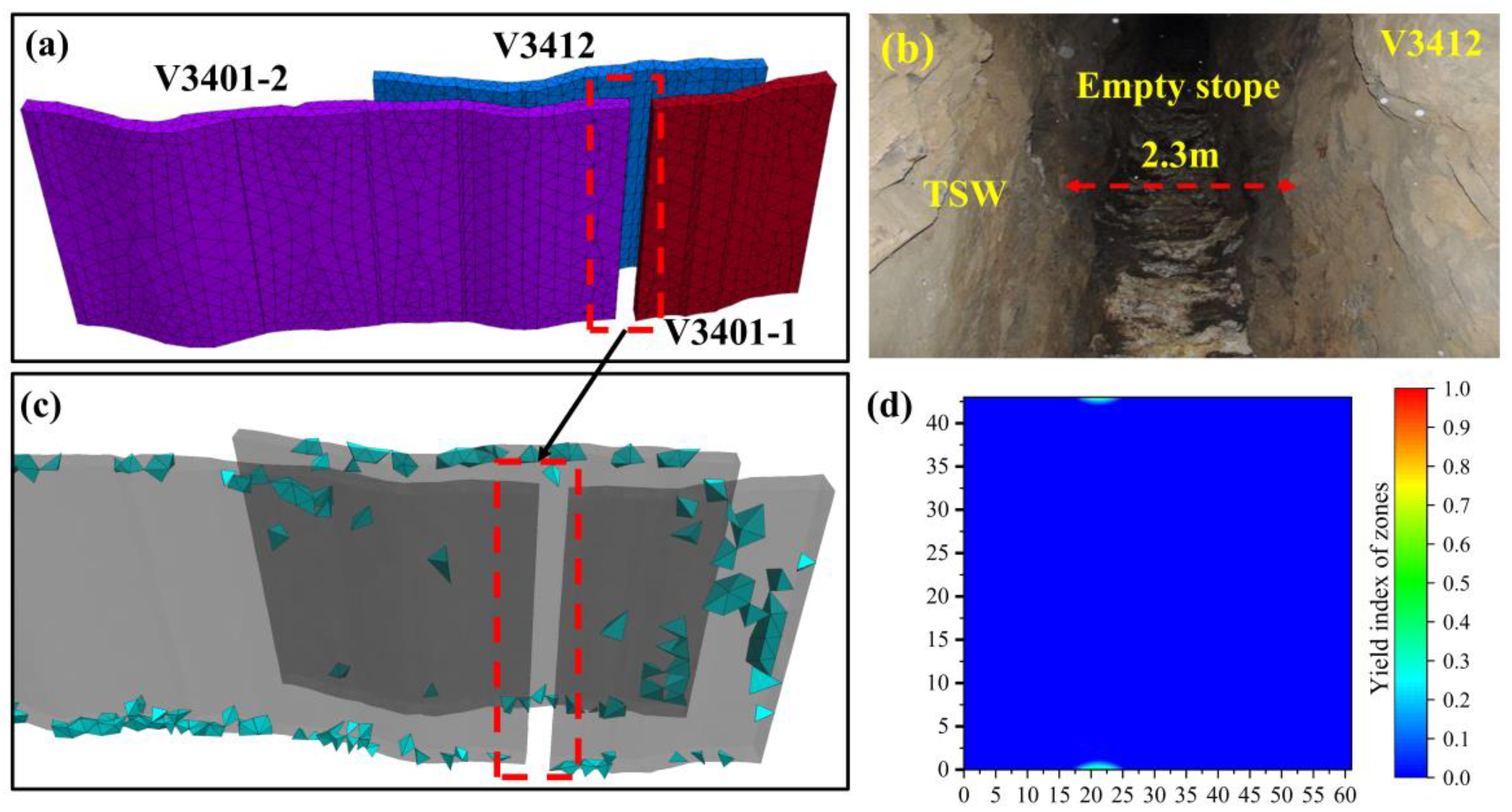
5.4. Engineering Application of the Model and Its Reliability Verification
6. Discussion
7. Conclusions
- (1)
- This study proposes a mechanical model for calculating the stability of TSWs under local complex loads. The model computes the stress distribution of TSWs under different operational conditions and determines the yield state of TSWs using the D-P yield criterion.
- (2)
- A comparison with the results of two existing theoretical models reveals that the accuracy of the mechanical model in this study improves by 5% and 53%, respectively. This indicates that the proposed model more effectively accounts for the influence of in situ stresses and boundary conditions.
- (3)
- Based on the analysis of the mechanical model, it is shown that the maximum principal stress (MPS) on the TSW occurs at the midpoint of the left boundary (0, h/2), the center of the lateral load on the lower boundary (LP, 0), or the center of the lateral load (LP, h/2).
- (4)
- Taking the residual ore recovery project at the Sawtooth Pit as a case study, this research investigates the changes in stress distribution, yield zone quantity, and critical thickness of TSWs under various parameters. The results indicate that to meet the mining company’s requirements for residual ore recovery, it is advisable to maximize SL and minimize LP, LW, and SH.
- (5)
- Using the theoretical model presented in this study, the critical thickness of four TSWs in the residual ore recovery project was calculated as 4.6 m, 4.2 m, 2.6 m, and 11.9 m. Additionally, stability analyses of TSWs at the V3412 and V3301 mining sites, based on calculations of maximum principal stress and stability, further validate the accuracy of the mechanical model for engineering applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| D | Flexural rigidity (N/m) |
| Deflection (m) | |
| E | Elastic modulus (GPa) |
| Poisson ratio | |
| Thickness of the thin plate (m) | |
| Y-direction in-plane force unit width (MPa) | |
| Z-direction in-plane force unit width (MPa) | |
| YZ-direction in-plane shear force unit width (MPa) | |
| Localized lateral force per unit area (MPa) | |
| Vertical stress in the z-direction (MPa) | |
| Transverse stress in the y-direction (MPa) | |
| Lateral stress in the x-direction (MPa) | |
| Localized lateral force Fourier coefficient | |
| Linear load (MPa) | |
| Stope length (m) | |
| B | Stope width (m) |
| Stope height (m) | |
| Coordinates of the localized lateral load center (m) | |
| a | Width of inter-chamber pillar (m) |
| Maximum value of lateral load (MPa) | |
| k | Lateral load per unit (MPa) |
| Deflection Fourier coefficient | |
| , , , | Undetermined coefficients |
| Axial bending moment in the z-direction (KNm) | |
| Axial bending moment in the y-direction (KNm) | |
| Tangent bending moment in the yz-direction (KNm) | |
| Maximum principal stress (MPa) | |
| Minimum principal stress (MPa) | |
| Second deviatoric invariant (MPa) | |
| Deviatoric stress tensor (MPa) | |
| First stress invariant (MPa) | |
| Material constant | |
| K | Material constant |
| C | Cohesion (MPa) |
| Internal friction angle (°) | |
| Lateral stress factor | |
| Rock capacity (KN·m−3) | |
| SF | Safety coefficient |
References
- Zhao, X.D.; Zhou, X. Design Method and Application of Stope Structure Parameters in Deep Metal Mines Based on an Improved Stability Graph. Minerals 2023, 13, 2. [Google Scholar] [CrossRef]
- Dubiński, J. Sustainable Development of Mining Mineral Resources. J. Sustain. Min. 2013, 12, 1–6. [Google Scholar] [CrossRef]
- Wang, H.X.; Chen, H.; Sun, Z.M.; Yu, B.; Liu, J.D. Application of bunch-hole blasting in recovering residual ore in irregular goaf groups. In Blasting in Mining-New Trends; CRC Press: Boca Raton, FL, USA, 2012; p. 101. [Google Scholar]
- Zhao, X.C.; Hong, Y. Application of open-pit and underground mining technology for residual coal of end slopes. Min. Sci. Technol. 2010, 20, 266–270. [Google Scholar] [CrossRef]
- Wright, G.; Czelusta, J. Mineral resources and economic development. In Proceedings of the Conference on Sector Reform in Latin America, Stanford Center for International Development, Stanford, CA, USA, 13–15 November 2003; pp. 13–15. [Google Scholar]
- Yang, S.L.; Yue, H.; Li, Q.; Chen, Y.S. Study on failure behaviors of roofs with varying thicknesses in longwall coal mining working face. Rock Mech. Rock Eng. 2024, 57, 6259–6282. [Google Scholar] [CrossRef]
- Wang, W.; Luo, Z.Q.; Qi, F.X.; Cao, S.X. Safe roof blasting thickness of VCR stope under complex boundary condition. J. Northeast. Univ. (Nat. Sci.) 2016, 37, 721–725. [Google Scholar] [CrossRef]
- Alejano, L.R.; Taboada, J.; García-Bastante, F.; Rodriguez, P. Multi-approach back-analysis of a roof bed collapse in a mining room excavated in stratified rock. Int. J. Rock Mech. Min. Sci. 2008, 45, 899–913. [Google Scholar] [CrossRef]
- Wang, H.W.; Jiang, Y.D.; Zhao, Y.X.; Zhu, J.; Liu, S. Numerical investigation of the dynamic mechanical state of a coal pillar during longwall mining panel extraction. Rock Mech. Rock Eng. 2013, 46, 1211–1221. [Google Scholar] [CrossRef]
- Guo, J.; Cheng, X.; Lu, J.J.; Zhao, Y.; Xie, X.B. Research on Factors Affecting Mine Wall Stability in Isolated Pillar Mining in Deep Mines. Minerals 2022, 12, 623. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, Y.; Zhang, W.X.; Dai, X.G.; Xie, X.B. Stress analysis of mine wall in panel barrier pillar-stope under multi-directional loads. J. Cent. South Univ. 2018, 49, 3020–3028. [Google Scholar] [CrossRef]
- Wang, L.M.; Zhang, X.Q.; Yin, S.H.; Zhang, X.L.; Jia, Y.F.; Kong, H.L. Evaluation of Stope Stability and Displacement in a Subsidence Area Using 3Dmine–Rhino3D–FLAC3D Coupling. Minerals 2022, 12, 1202. [Google Scholar] [CrossRef]
- Huang, Z.G.; Dai, X.G.; Dong, L.J. Buckling failures of reserved thin pillars under the combined action of in-plane and lateral hydrostatic compressive forces. Comput. Geotech. 2017, 87, 128–138. [Google Scholar] [CrossRef]
- Jiang, L.C.; Jiao, H.Z.; Wang, Y.D.; Wang, G.G. Comprehensive safety factor of roof in goaf underdeep high stress. J. Cent. South Univ. 2021, 28, 595–603. [Google Scholar] [CrossRef]
- Jiang, L.C.; Xu, A.J.; Yu, H. Safety thickness of goaf roof under different pillar overlapping ratio. Chin. J. Nonferrous Met. 2022, 32, 3505–3516. [Google Scholar]
- Xie, X.B.; Deng, R.N.; Dong, X.J.; Yan, Z.Z. Stability of goaf group system based on catastrophe theory and rheological theory. Rock Soil Mech. 2018, 39, 1963–1972. [Google Scholar] [CrossRef]
- Xie, X.B.; Li, D.X.; Kong, L.Y. Stability analysis model of ore wall based on elastic thin plate theory and its application. J. Min. Saf. Eng. 2020, 37, 698–706. [Google Scholar] [CrossRef]
- Brown, T.; Pitfield, P. Tungsten. In Critical Metals Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 385–413. [Google Scholar] [CrossRef]
- Kumah, A. Sustainability and gold mining in the developing world. J. Clean. Prod. 2006, 14, 315–323. [Google Scholar] [CrossRef]
- Beatty, M.F. A theory of elastic stability for incompressible, hyperelastic bodies. Int. J. Solids Struct. 1967, 3, 23–37. [Google Scholar] [CrossRef]
- Green, A.E.; Zerna, W. Theoretical Elasticity; Courier Corporation: North Chelmsford, MA, USA, 1992. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-hill: New York, NY, USA, 1959; pp. 240–246. [Google Scholar]
- Ventsel, E.; Krauthammer, T.; Carrera, E. Thin plates and shells: Theory, analysis, and applications. Appl. Mech. Rev. 2002, 55, 72–73. [Google Scholar] [CrossRef]
- Lu, P.; He, L.H.; Lee, H.P.; Lu, C. Thin plate theory including surface effects. Int. J. Solids Struct. 2006, 43, 4631–4647. [Google Scholar] [CrossRef]
- Szilard, R. Theories and applications of plate analysis: Classical, numerical and engineering methods. Appl. Mech. Rev. 2004, 57, 32–33. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Roque, C.; Ferreira, A.; Reddy, J. Analysis of Mindlin micro plates with a modified couple stress theory and a meshless method. Appl. Math. Model. 2013, 37, 4626–4633. [Google Scholar] [CrossRef]
- Zhang, F.F. Elastic Thin Plates; Beijing Science Press: Beijing, China, 1984; pp. 58–62. [Google Scholar]
- Yan, Z.D. Fourier Series Solutions in Structural Mechanics; Tianjin University Press: Tianjin, China, 1989; pp. 150–197. [Google Scholar]
- Luo, B.Y.; Ye, Y.C.; Cao, Z.; Wang, Q.H.; Li, Y.F.; Chen, H. Estimation of pillar strength and effect of inclination under gently inclined layered deposits based on Mohr-Coulomb criterion. Rock Soil Mech. 2019, 40, 1940–1946. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Working Group of Handbook of Building Structural Statics. Handbook of Building Structural Statics; Architecture and Building Press in Chinese: Beijing, China, 1998; pp. 227–228. (In Chinese) [Google Scholar]
- Pu, H.; Huang, Y.G.; Chen, R.H. Mechanical analysis for X-O type fracture morphology of stope roof. J. China Univ. Min. Technol. 2011, 40, 835–840. [Google Scholar]
- Grimstad, E.; Bhasin, R. Stress strength relationships and stability in hard rock. Proc. Conf. Recent Adv. Tunneling Technol. 1996, 1, 3–8. [Google Scholar]
- Huo, X.F.; Shi, X.Z.; Qiu, X.Y.; Zhou, J.; Gou, Y.G.; Yu, Z.; Ke, W.Y. Rock damage control for large-diameter-hole lateral blasting excavation based on charge structure optimization. Tunn. Undergr. Space Technol. 2020, 106, 103569. [Google Scholar] [CrossRef]
- He, L.; Zhang, Q.B. Numerical investigation of arching mechanism to underground excavation in jointed rock mass. Tunn. Undergr. Space Technol. 2015, 50, 54–67. [Google Scholar] [CrossRef]
- Qiu, X.Y.; Shi, X.Z.; Gou, Y.G.; Zhou, J.; Chen, H.; Huo, X.F. Short-delay blasting with single free surface: Results of experimental tests. Tunn. Undergr. Space Technol. 2018, 74, 119–130. [Google Scholar] [CrossRef]
- Jia, H.W.; Yan, B.X.; Yilmaz, E. A large goaf group treatment by means of mine backfill technology. Adv. Civ. Eng. 2021, 1, 1–19. [Google Scholar] [CrossRef]
- Qian, D.Y.; Zhang, N.; Shimada, H.; Wang, C.; Sasaoka, T.; Zhang, N.C. Stability of goaf-side entry driving in 800-m-deep island longwall coal face in underground coal mine. Arabian J. Geosci. 2016, 9, 1–28. [Google Scholar] [CrossRef]


| Parameters | Value | Units |
|---|---|---|
| Stope length (L) | 50 | m |
| Stope width (B) | 4 | m |
| Stope height (h) | 50 | m |
| Sidewall thickness (Wb) | 3 | m |
| Inter-chamber pillar width (a) | 4 | m |
| In-plane force in the y-direction (Ny) | 47.2 | MN·m−1 |
| In-plane force in the z-direction (Nz) | 78.8 | MN·m−1 |
| maximum value of lateral load (q0) | 22.1 | MPa |
| lateral load per unit (k) | 0.044 | MPa·m−1 |
| Rock Type | Orebody | Surrounding Rock | Units |
|---|---|---|---|
| Density | 2800 | 2500 | kg·m−3 |
| Elastic modulus | 32.5 | 20.0 | GPa |
| Cohesion | 5.2 | 4.9 | MPa |
| Internal friction angle | 50.0 | 36.0 | ° |
| Tensile strength | 5.0 | 4.6 | MPa |
| Poisson ratio | 0.26 | 0.3 | N/A |
| Number of Term in Series | (L/2,h/2) | (L/2,h/2) | (0,h/2) |
|---|---|---|---|
| 5 | 0.00016991734 | 0.003578805 | −0.001246028 |
| 10 | 0.00016982046 | 0.003574659 | −0.001247692 |
| 20 | 0.00016976138 | 0.003537642 | −0.001247242 |
| 30 | 0.00016973226 | 0.003562551 | −0.001247599 |
| 40 | 0.00016972079 | 0.003550222 | −0.001247482 |
| 50 | 0.00016971889 | 0.003552966 | −0.001247585 |
| 60 | 0.00016971786 | 0.003551420 | −0.001247520 |
| 70 | 0.00016971715 | 0.003553237 | −0.001247567 |
| 80 | 0.00016971682 | 0.003552425 | −0.001247539 |
| Calculation Method | (L/2,h/2) | (L/2,h/2) | (L/2,h/2) | (0,h/2) |
|---|---|---|---|---|
| This paper | 0.0013246 | 0.024199 | 0.024209 | −0.052965 |
| Theory of Plates and Shells | 0.00126 | 0.0231 | 0.0231 | −0.0513 |
| Error (%) | +4.88% | +4.54% | +4.58% | −3.14% |
| Working Group of Handbook of Building Structural Statics | - | 0.0368 | 0.0368 | - |
| Error (%) | - | −52.07% | −52.01% | - |
| Stope Number | V3412 | V3429 | V32010 | V3301 | Units |
|---|---|---|---|---|---|
| SL | 61 | 71 | 118 | 56 | m |
| Stope span | 2.3 | 2.6 | 3.0 | 1.9 | m |
| SH | 43 | 42 | 45 | 48 | m |
| Stope Inclination angle | 83 | 85 | 84 | 85 | ° |
| LP | (20.7, 21.5) | (22, 21) | (72, 22.5) | (10.3, 24) | m |
| LW | 3.3 | 3.6 | 2.9 | 11 | m |
| ST | 9 | 6 | 10.7 | 6.4 | m |
| Stope Number | V3412 | V3429 | V32010 | V3301 | Units |
|---|---|---|---|---|---|
| MPS | 1.46 | 2.05 | 0.49 | 6.94 | MPa |
| extremal point | (20.7, 0) | (22, 0) | (72, 0) | (0, 24) | m |
| critical thickness | 4.6 | 4.2 | 2.6 | 11.9 | m |
| yield or not | Not | Not | Not | Yes | N/A |
| Stope Number | V3412 | V3301 | Units |
|---|---|---|---|
| Mechanical model | 1.46 | 6.94 | MPa |
| Numerical simulation | 1.41 | 7.12 | MPa |
| Errors | 3.55% | −2.53% | N/A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Li, Y.; Lu, Y.; Qiu, X. Comprehensive Mechanical Analysis Model for Stability of Thin Sidewalls Under Localized Complex Loads. Appl. Sci. 2025, 15, 4665. https://doi.org/10.3390/app15094665
Shi X, Li Y, Lu Y, Qiu X. Comprehensive Mechanical Analysis Model for Stability of Thin Sidewalls Under Localized Complex Loads. Applied Sciences. 2025; 15(9):4665. https://doi.org/10.3390/app15094665
Chicago/Turabian StyleShi, Xiuzhi, Yixin Li, Yuran Lu, and Xianyang Qiu. 2025. "Comprehensive Mechanical Analysis Model for Stability of Thin Sidewalls Under Localized Complex Loads" Applied Sciences 15, no. 9: 4665. https://doi.org/10.3390/app15094665
APA StyleShi, X., Li, Y., Lu, Y., & Qiu, X. (2025). Comprehensive Mechanical Analysis Model for Stability of Thin Sidewalls Under Localized Complex Loads. Applied Sciences, 15(9), 4665. https://doi.org/10.3390/app15094665






