Numerical Analysis of Passive, Compound, and Active Augmented Heat Transfer Methods for Concentric Tube Heat Exchanger
Abstract
1. Introduction
2. Methods
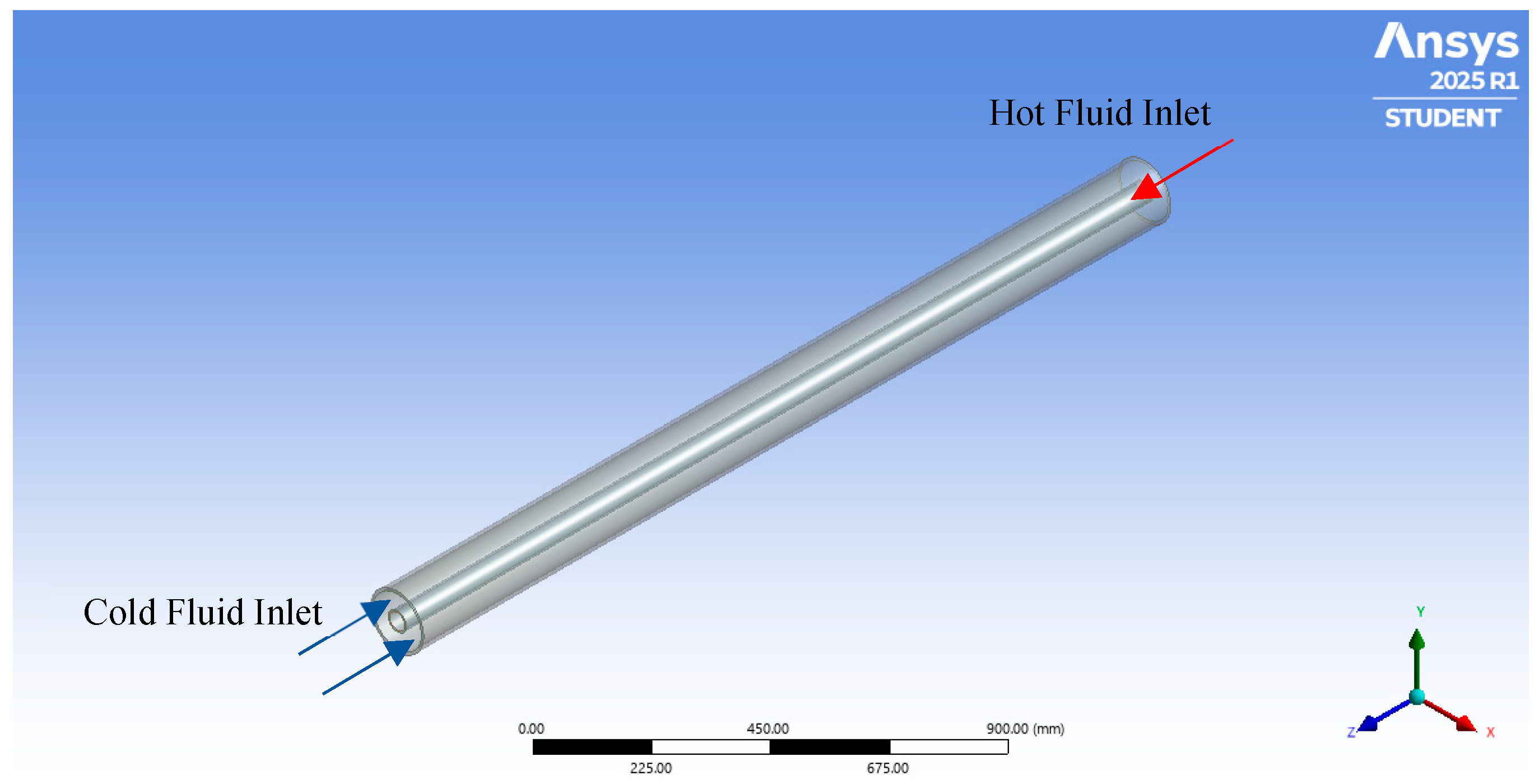
2.1. Description of the Problem
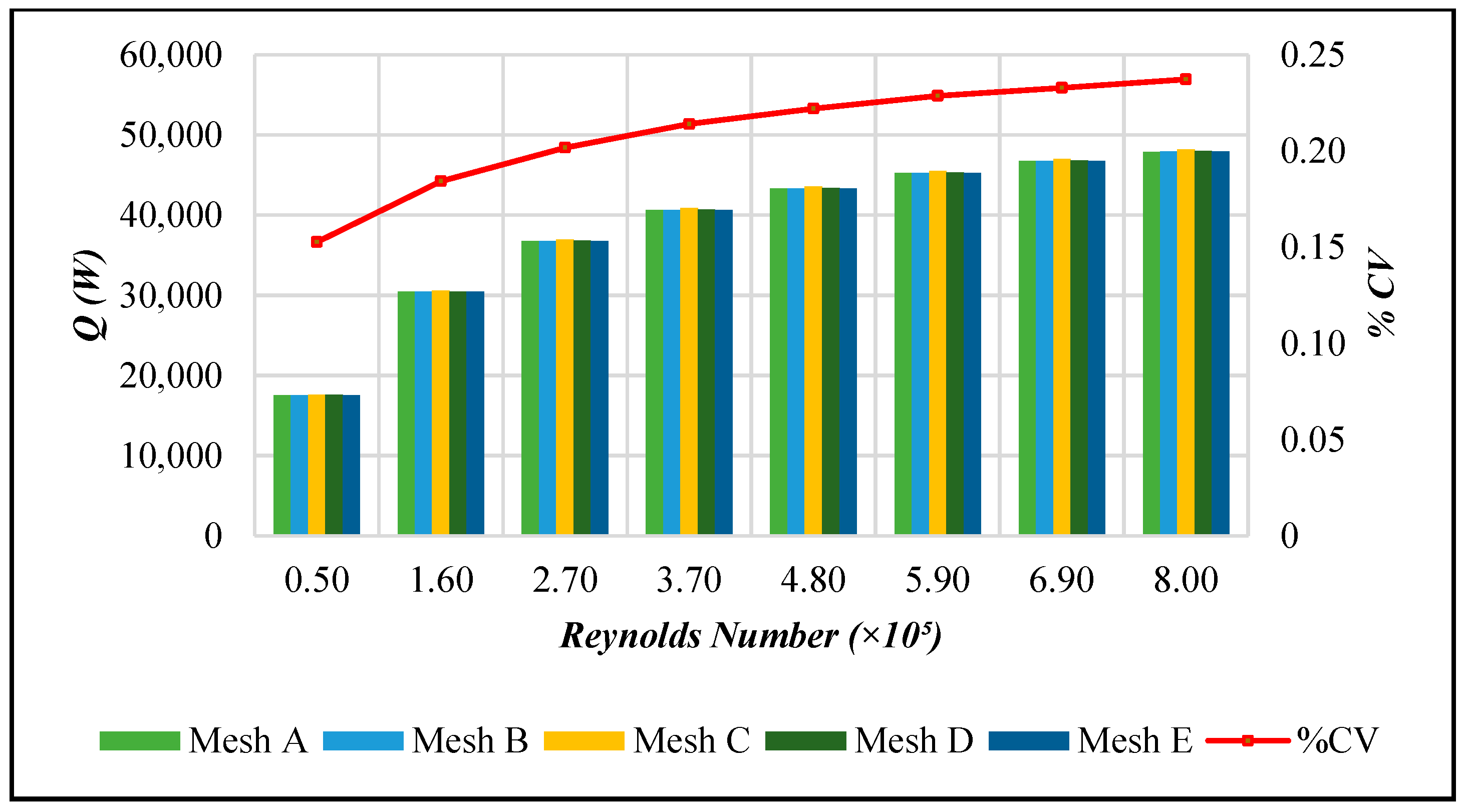
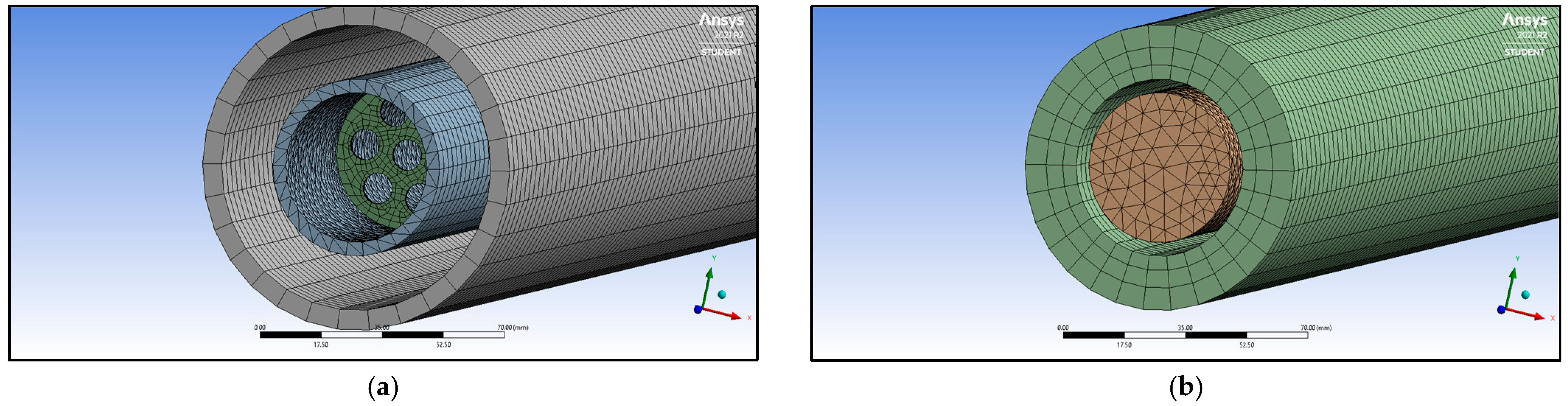
2.1.1. Study on Grid Dependence and Parameter Sensitivity Analysis
2.1.2. Numerical Model Validation Approach
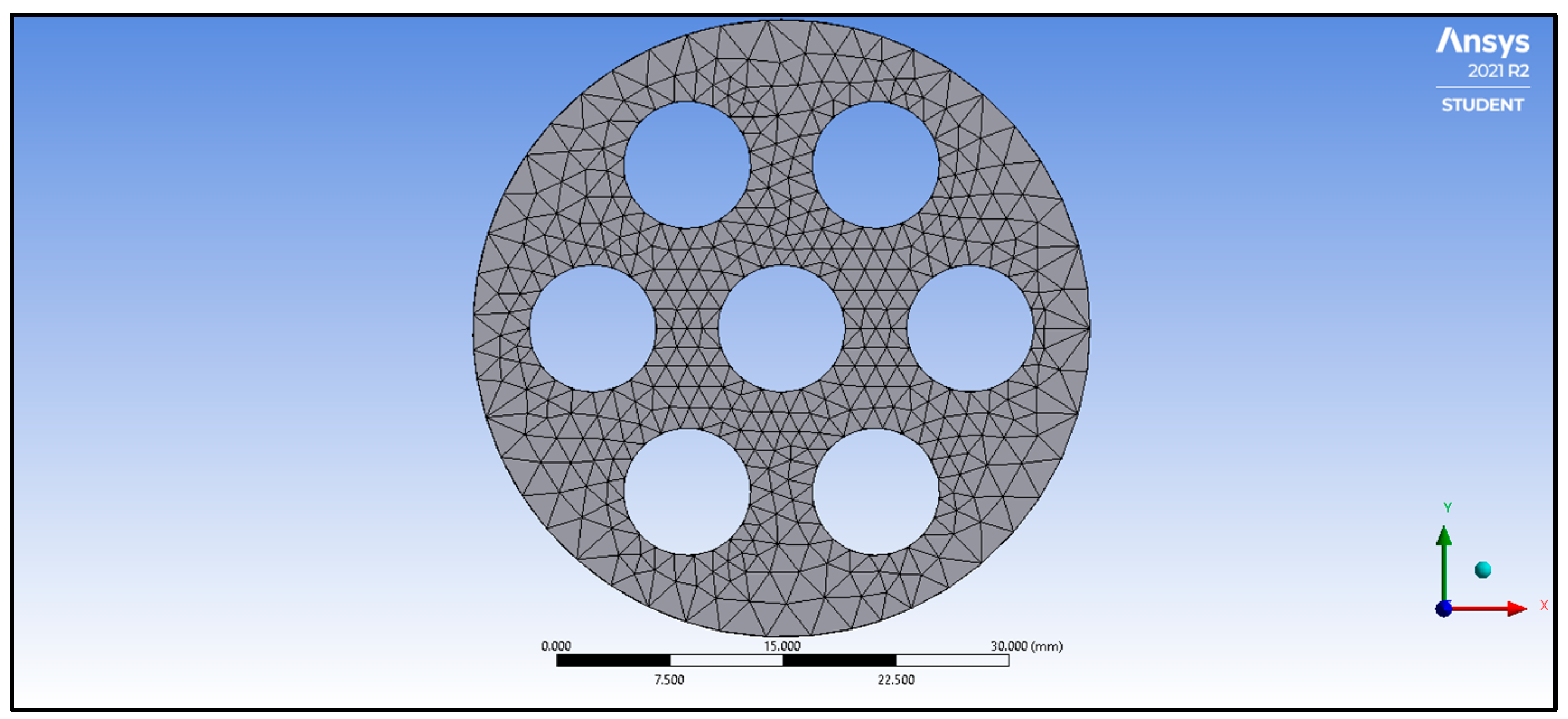
2.1.3. Passive AHT Study
2.1.4. Active AHT Study
2.1.5. Compound AHT Study
2.2. Governing Equations
2.3. Numerical Model and Boundary Conditions
3. Results
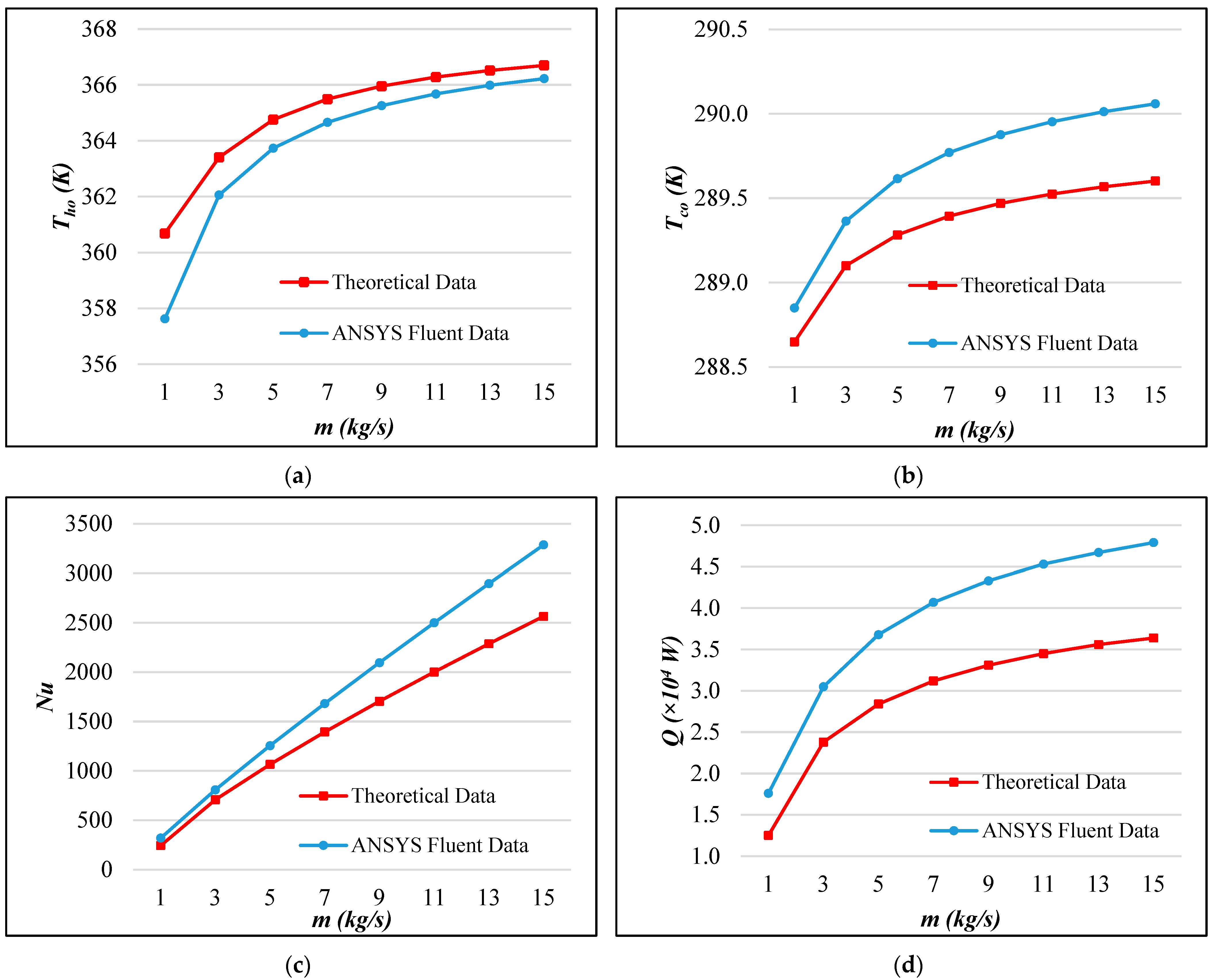
3.1. Validation of Numerical Model
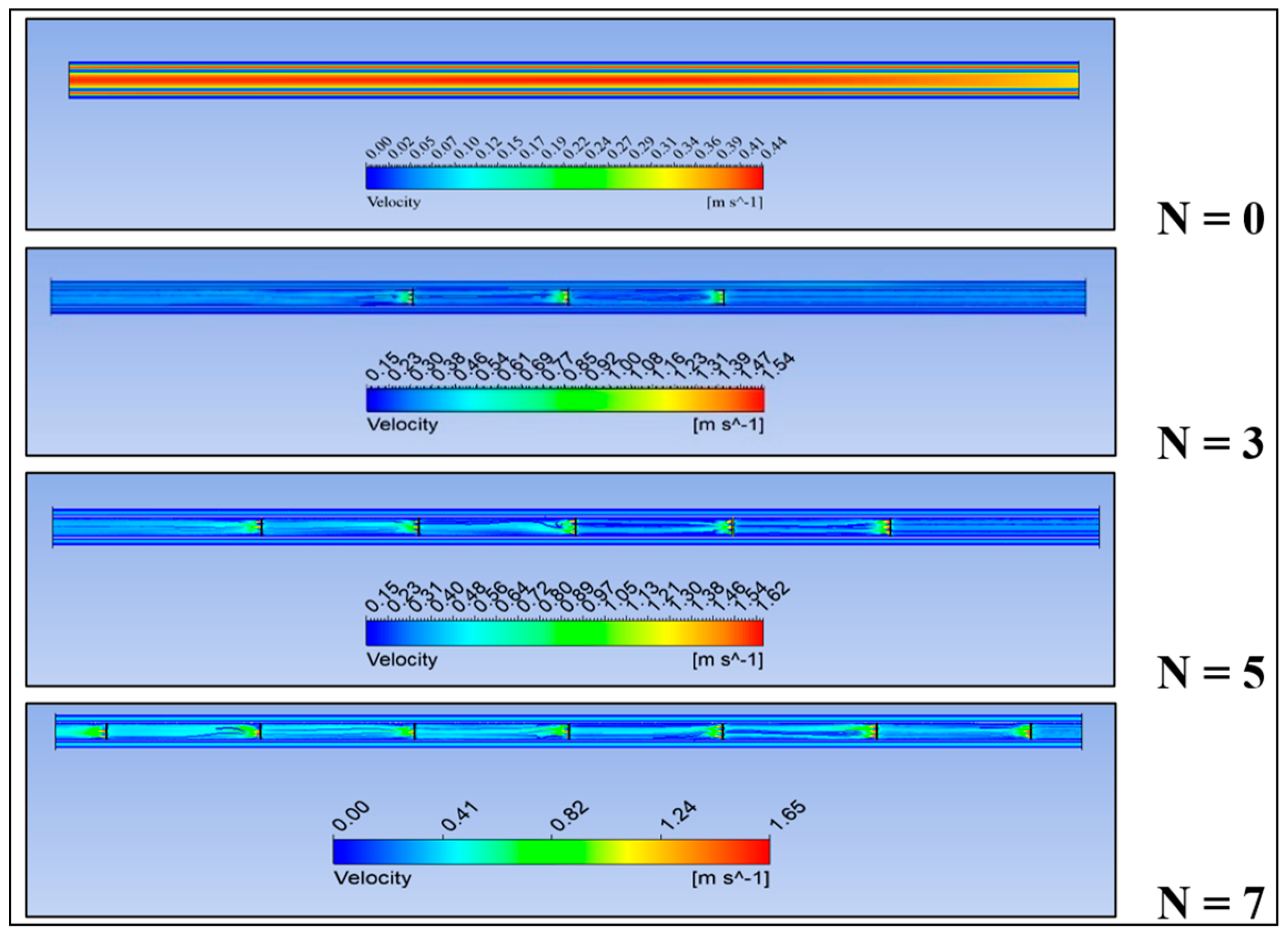
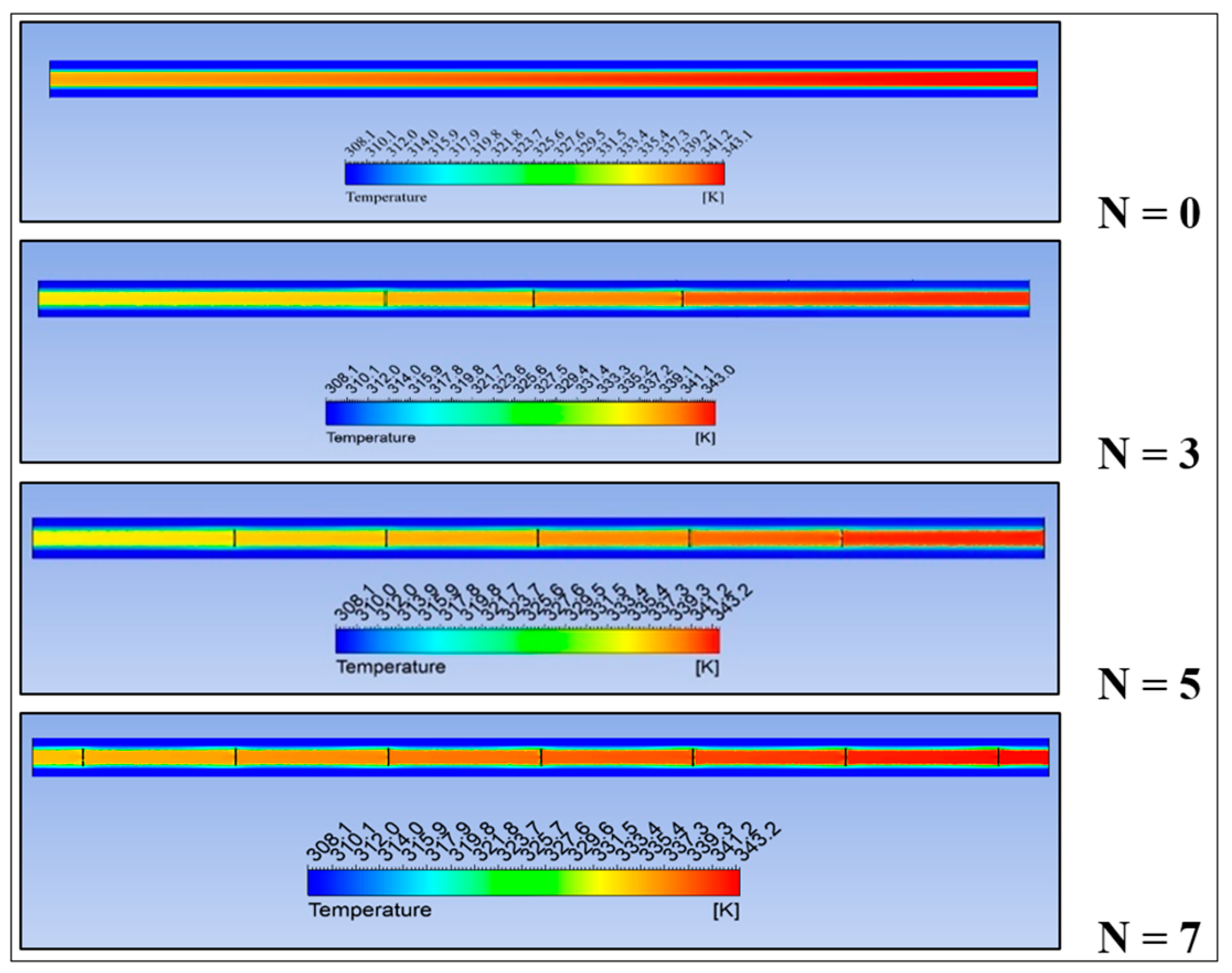
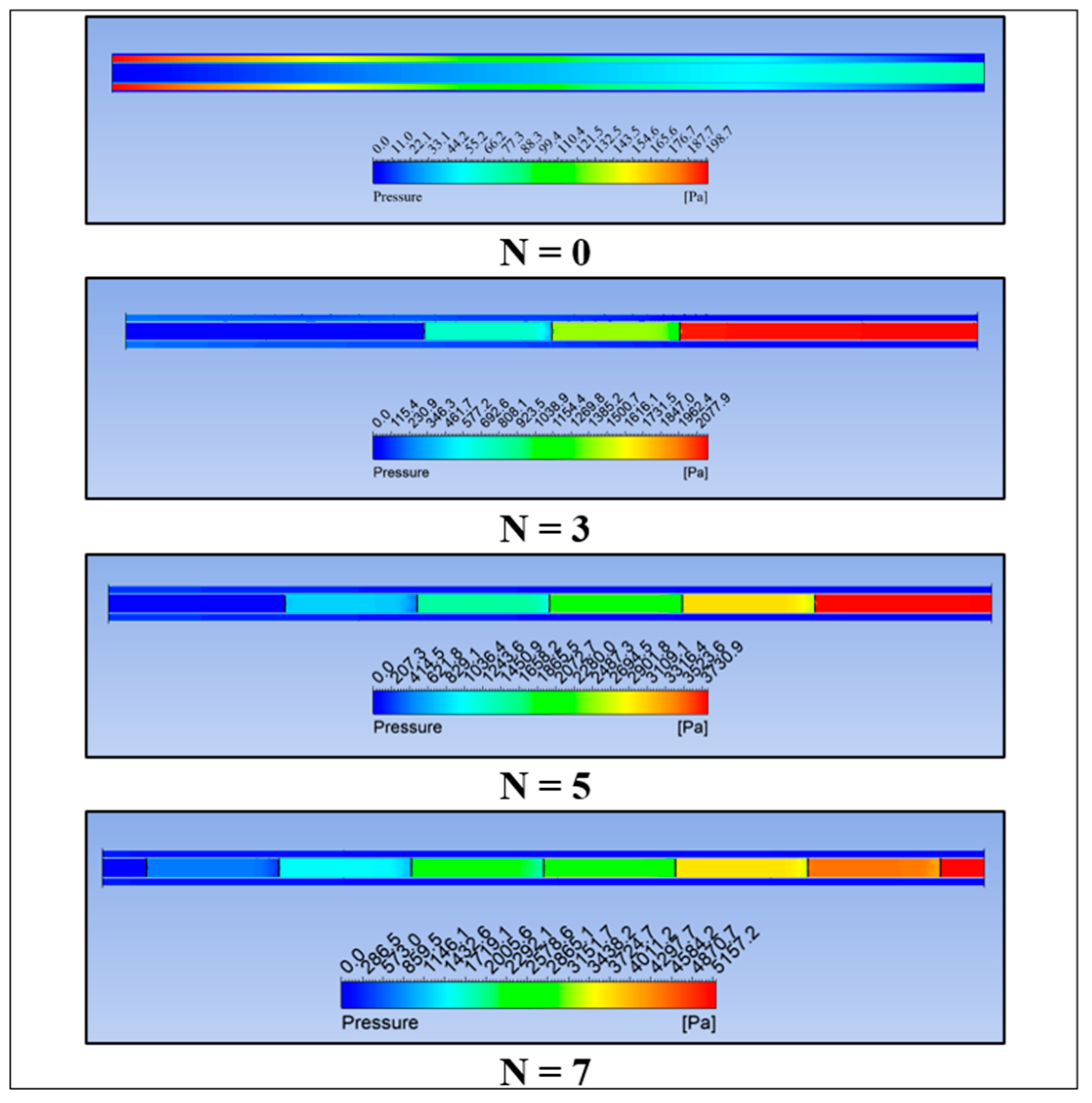
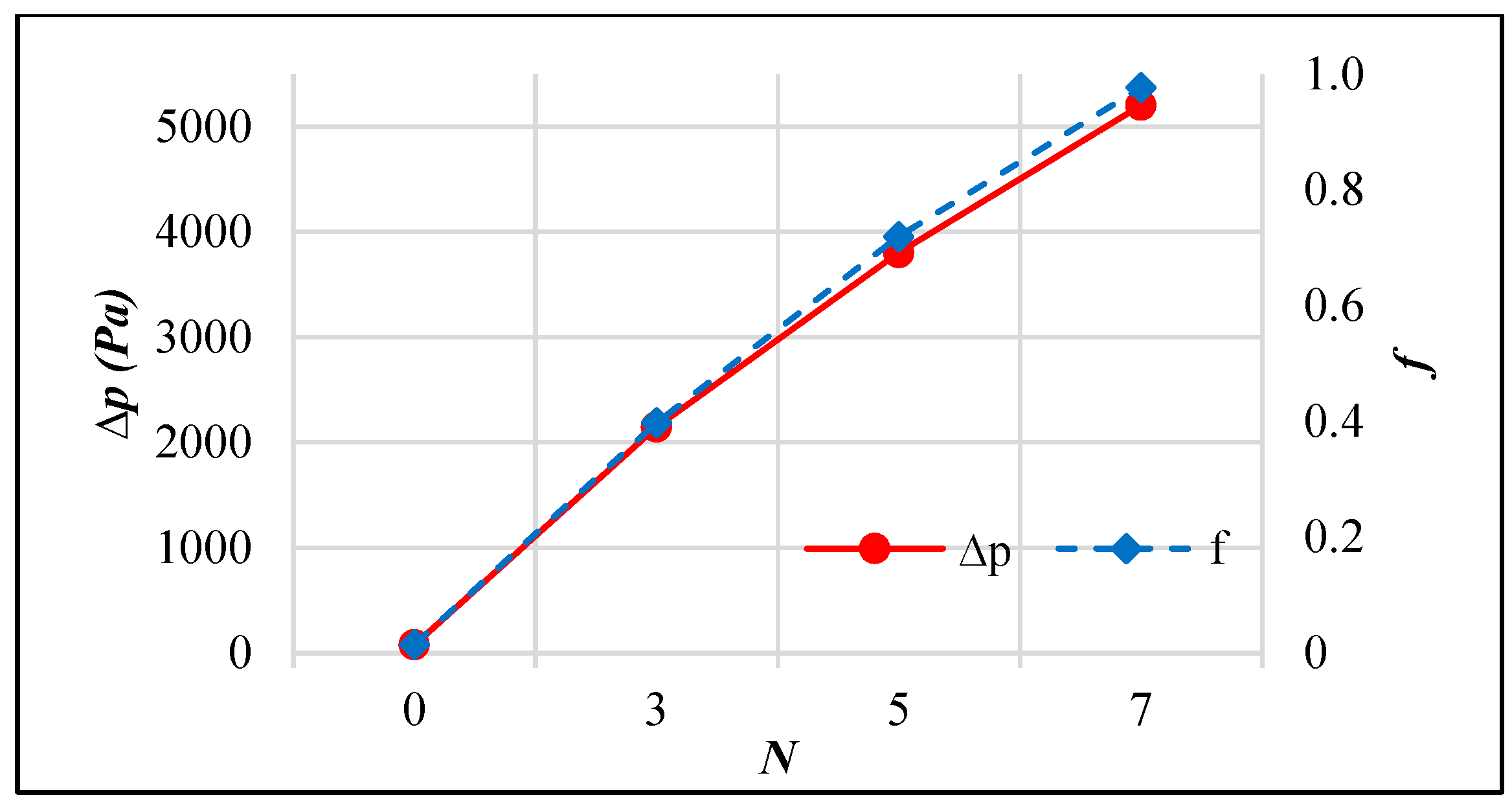
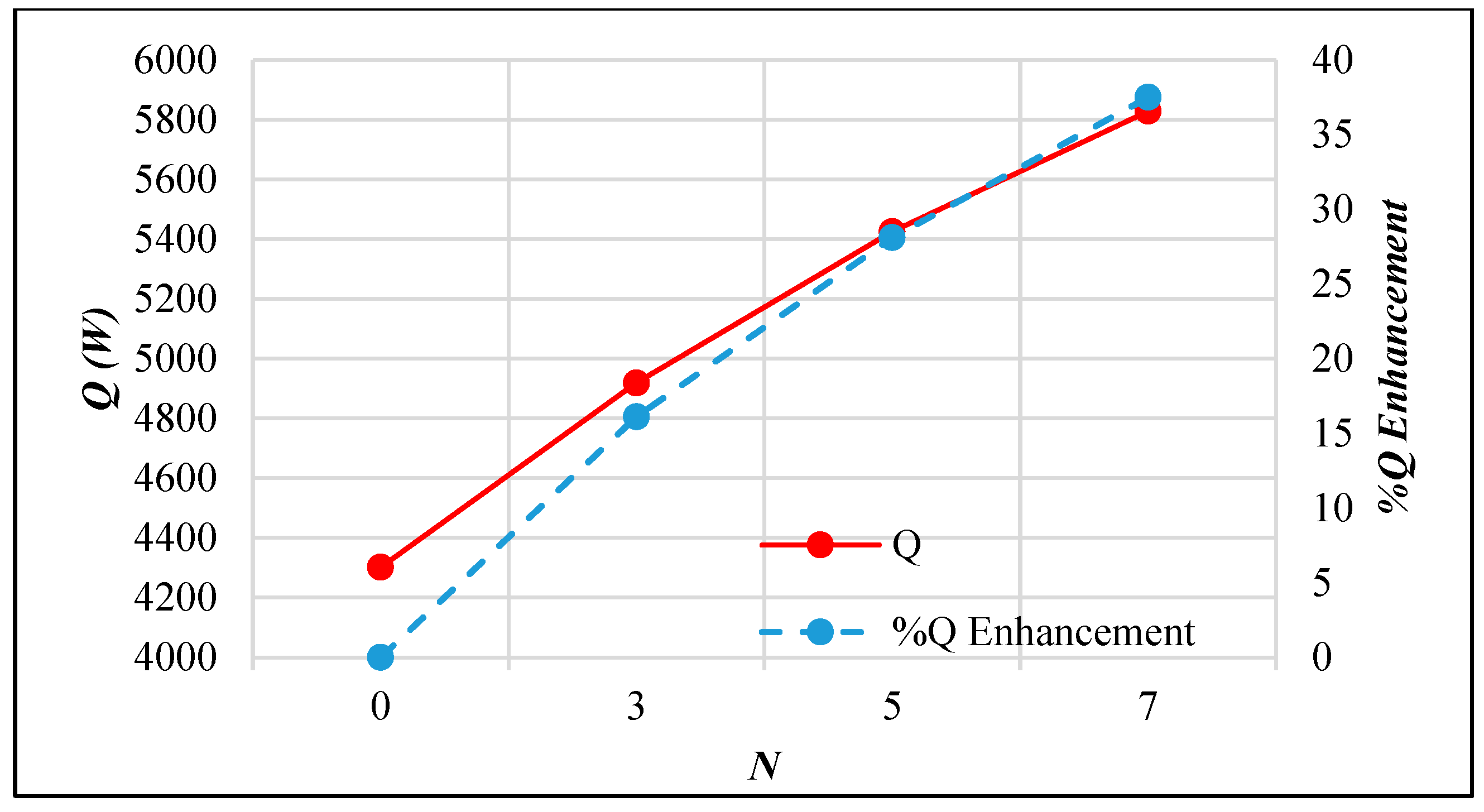
3.2. Passive AHT Study
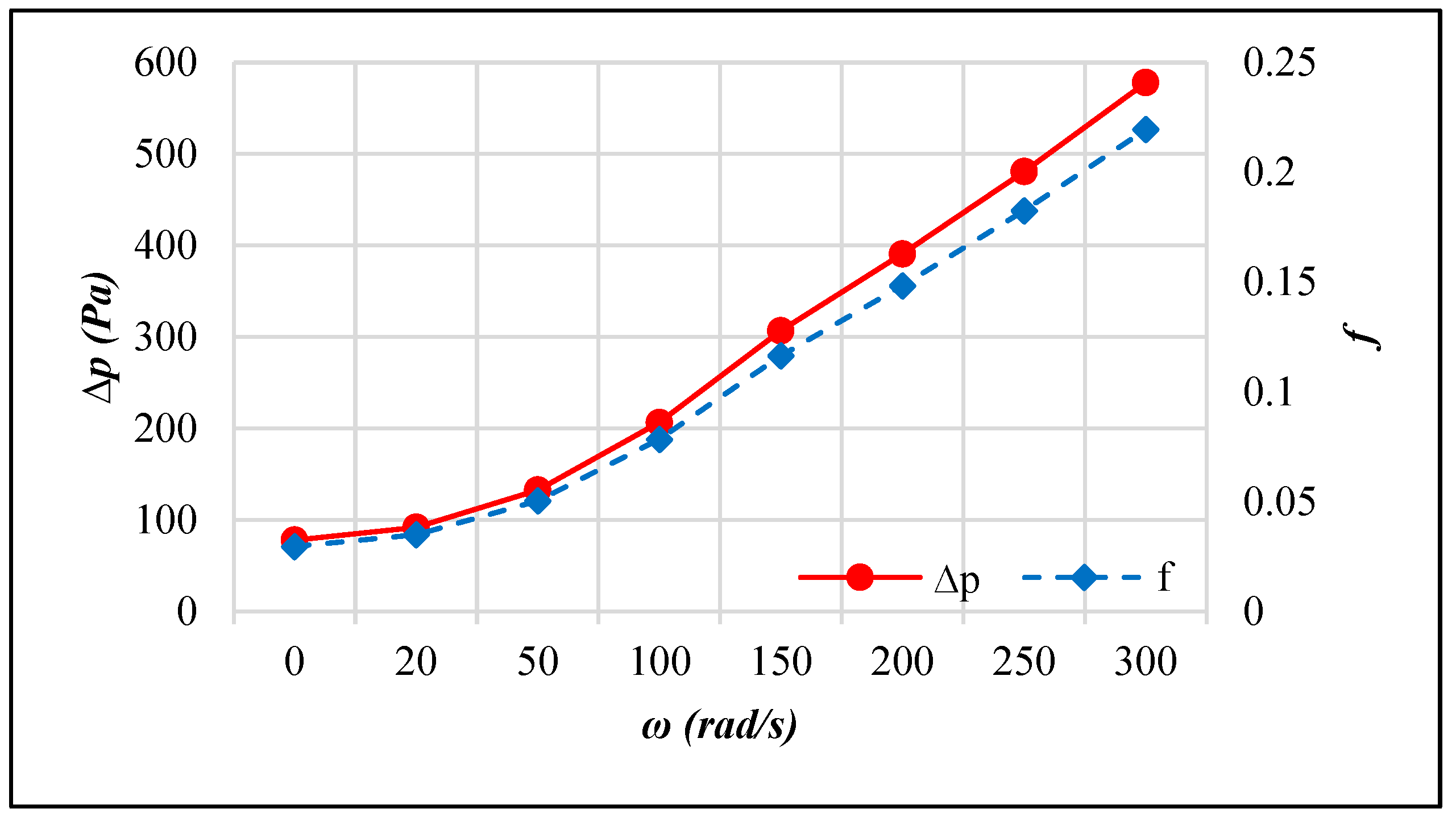
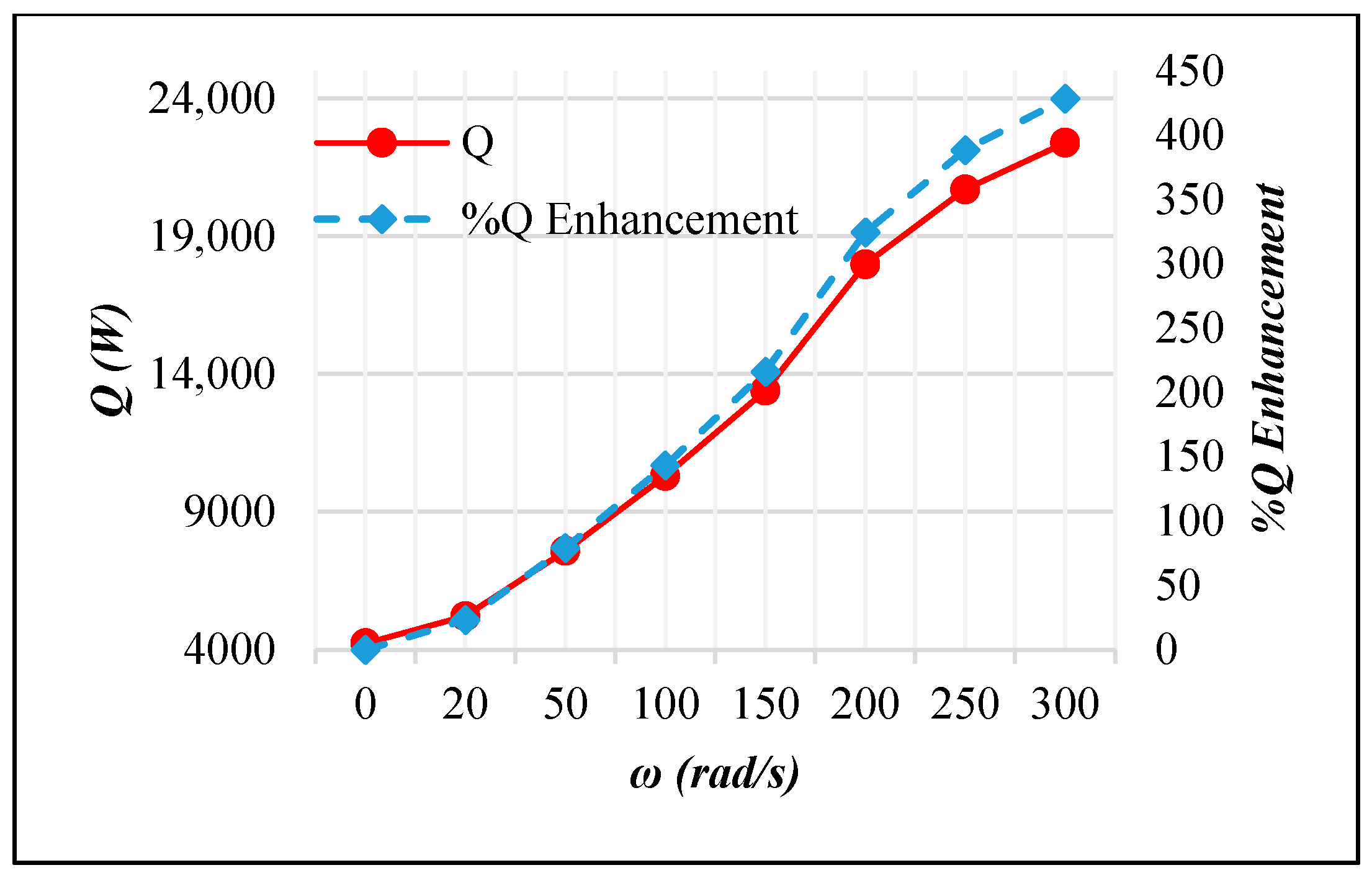
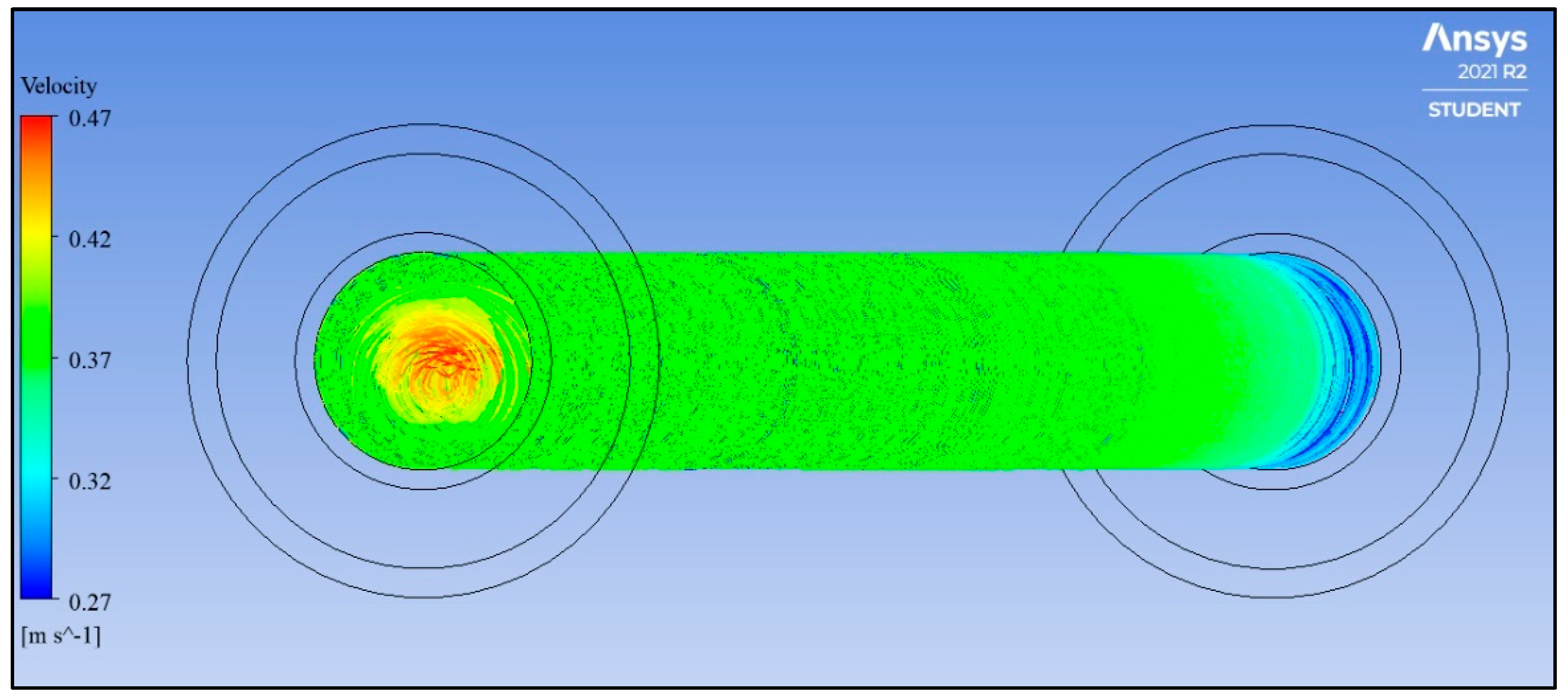
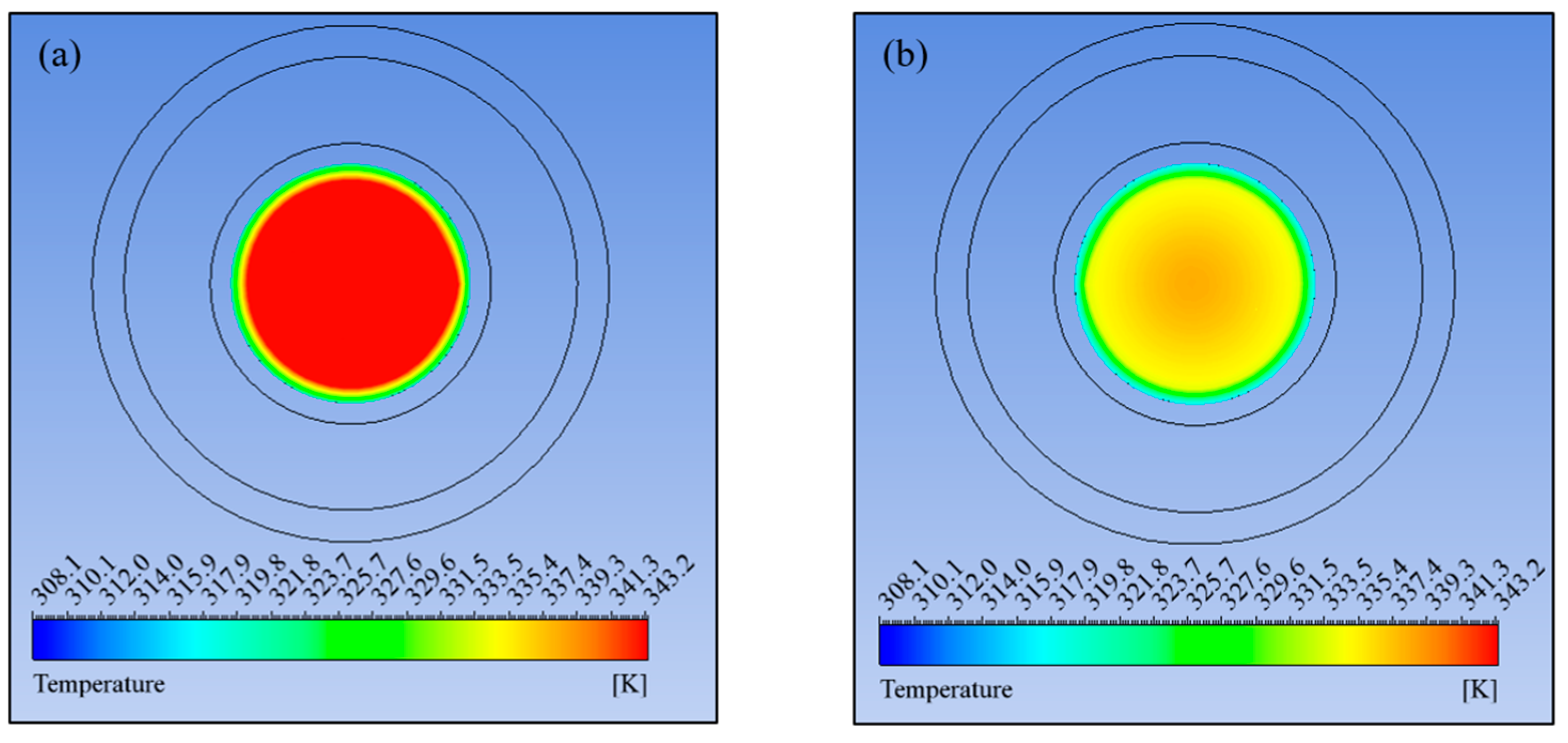
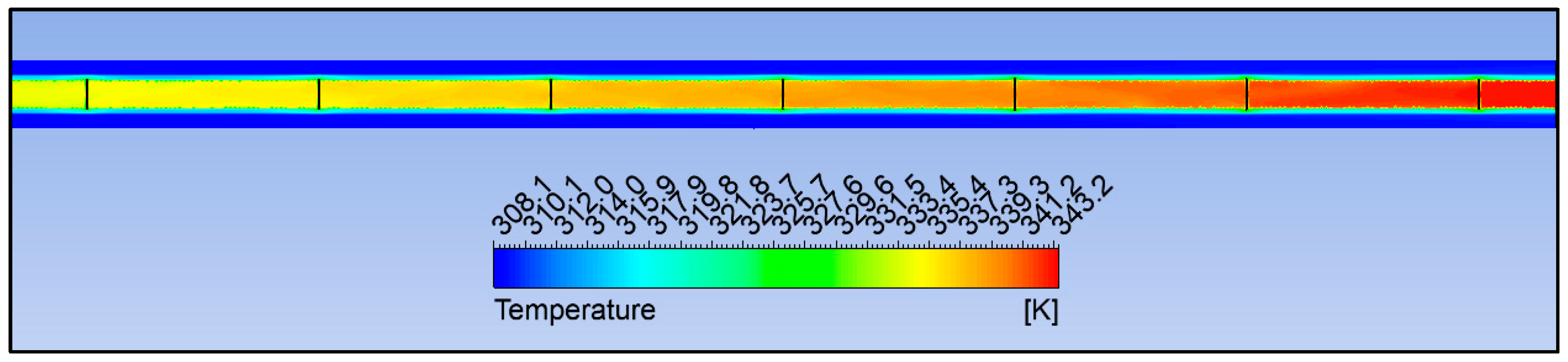
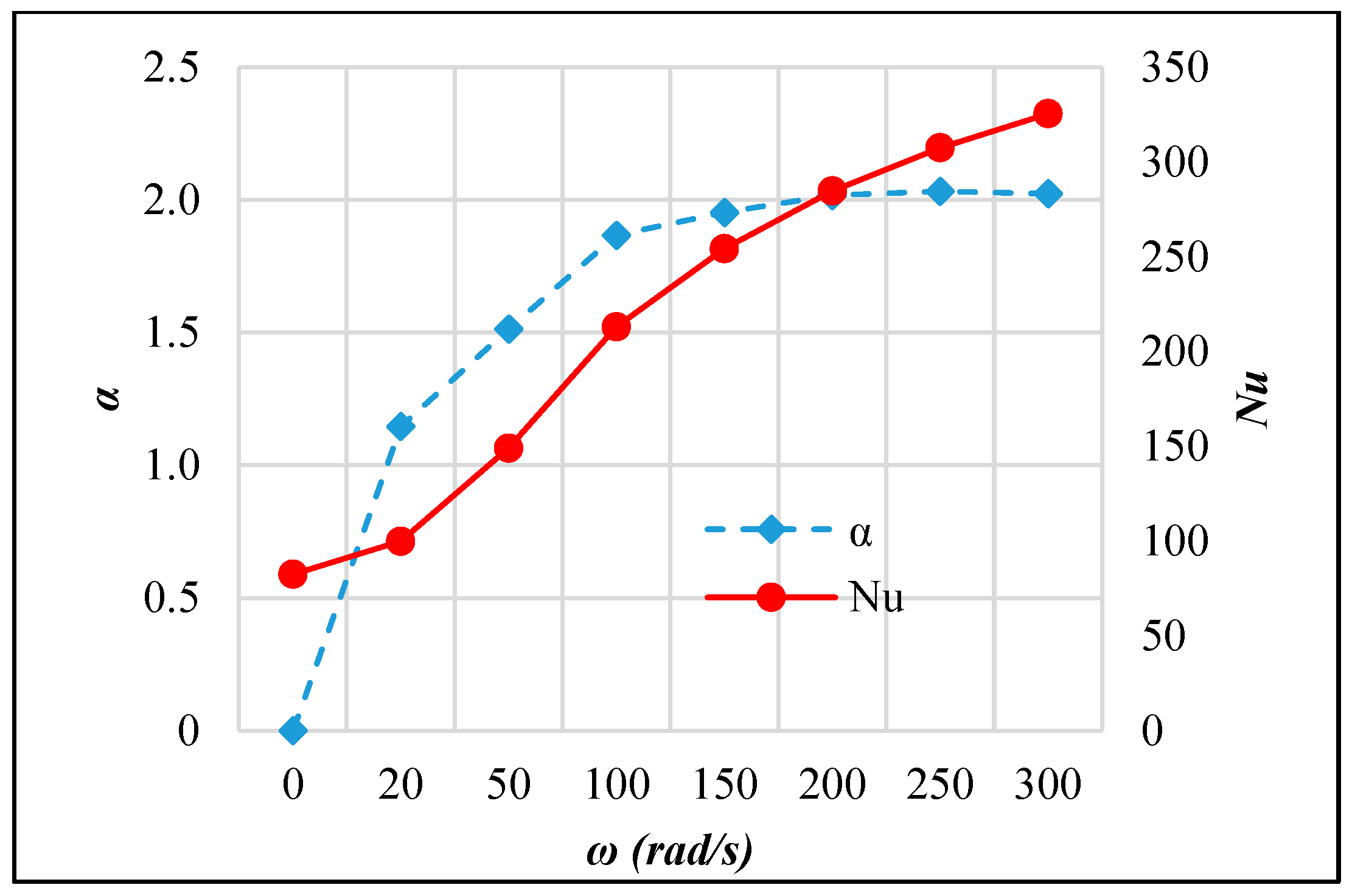
3.3. Active AHT Study
3.4. Compound AHT Study
4. Conclusions
- Passive AHT: At N = 7, the heat transfer rate of the static circular perforated pipe increased by 41.8%. However, the thermal performance factor of 0.72 was relatively low due to the abrupt increase in pressure drop, which is not well-balanced with the convective heat transfer improvement.
- Active AHT: Rotating the inner pipe up to 300 rad/s enhanced the heat transfer rate by 4.28 times. The thermal performance factor at this speed is 2.02, which was indicative of the AHT efficiency. Moreover, the pressure drop recorded was comparatively lower than the active and compound AHT methods performed.
- Compound AHT: The rotation of inserts intensified swirls and vortices, resulting in rapid thermal mixing and a 47.5% improvement in heat transfer rate at 300 rad/s. The thermal performance factor is recorded at 0.80, indicating a better CCTHE effectiveness than the passive AHT.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Begag, A.; Saim, R.; Abboudi, S.; Öztop, H.F. Effect of internal and external corrugated surfaces on the characteristics of heat transfer and pressure drop in a concentric tube heat exchanger. Int. J. Therm. Sci. 2021, 165, 106930. [Google Scholar]
- Kumar, V.; Sahoo, R.R. 4 E’s (Energy, Exergy, Economic, Environmental) performance analysis of air heat exchanger equipped with various twisted turbulator inserts utilizing ternary hybrid nanofluids. Alex. Eng. J. 2022, 61, 5033–5050. [Google Scholar] [CrossRef]
- Li, H.; Yang, X.; Wang, C.; Shi, S.; Ma, R.; Yuan, Y. Research and Application of Steam Condensation Heat Transfer Model Containing Noncondensable Gas on a Wall Surface. Appl. Sci. 2023, 13, 10520. [Google Scholar] [CrossRef]
- Li, H.; You, Z.; Zhang, H. Experimental investigation on the heat transfer enhancement of steam condensation on tube with hydrophilic-hydrophobic hybrid surface. J. Phys. Conf. Ser. 2022, 2280, 012059. [Google Scholar]
- Brodov, Y.M.; Aronson, K.E.; Ryabchikov, A.Y.; Nirenstein, M.A. Heat transfer augmentation during water steam condensation on twisted profile tubes. WIT Trans. Ecol. Environ. 2014, 190, 479–490. [Google Scholar]
- Ahmadi, S.; Eraghubi, M.; Akhavan-Behabadi, M.A.; Hanafizadeh, P.; Sayadian, S.; Robinson, A.J. EHD augmented heat transfer during upward bubbly flow boiling for low to medium frequency AC electric fields. Int. J. Therm. Sci. 2023, 191, 108346. [Google Scholar]
- Suri, A.R.S.; Pun, A.K.; Al Haque, M.S. Review of heat transfer augmentation methods and effect of using dimpled ribs and nanofluids. Mater Today Proc. 2022, 50, 830–836. [Google Scholar] [CrossRef]
- Nakhchi, M.E.; Hatami, M.; Rahmati, M. Experimental investigation of performance improvement of double-pipe heat exchangers with novel perforated elliptic turbulators. Int. J. Therm. Sci. 2021, 168, 107057. [Google Scholar]
- Nakhchi, M.E.; Esfahani, J.A.; Kim, K.C. Numerical study of turbulent flow inside heat exchangers using perforated louvered strip inserts. Int. J. Heat Mass. Transf. 2020, 148, 119143. [Google Scholar]
- Liu, P.; Zheng, N.; Shan, F.; Liu, Z.; Liu, W. Heat transfer enhancement for laminar flow in a tube using bidirectional conical strip inserts. Int. J. Heat Mass. Transf. 2018, 127, 1064–1076. [Google Scholar] [CrossRef]
- Keklikcioglu, O.; Ozceyhan, V. Experimental investigation on heat transfer enhancement in a circular tube with equilateral triangle cross sectioned coiled-wire inserts. Appl. Therm. Eng. 2018, 131, 686–695. [Google Scholar]
- Padmanabhan, S.; Yuvatejeswar Reddy, O.; Venkata Ajith Kumar Yadav, K.; Bupesh Raja, V.K.; Palanikumar, K. Heat transfer analysis of double tube heat exchanger with helical inserts. Mater. Today Proc. 2021, 46, 3588–3595. [Google Scholar] [CrossRef]
- Pandey, L.; Prajapati, H.; Singh, S. CFD study for enhancement of heat transfer and flow characteristics of circular tube heat exchanger using Y-shaped insert. Mater. Today Proc. 2021, 46, 9827–9836. [Google Scholar]
- Alam, T.; Kim, M.H. A comprehensive review on single phase heat transfer enhancement techniques in heat exchanger applications. Renew. Sustain. Energy Rev. 2018, 81, 813–839. [Google Scholar] [CrossRef]
- Thapa, S.; Samir, S.; Kumar, K.; Singh, S. A review study on the active methods of heat transfer enhancement in heat exchangers using electroactive and magnetic materials. Mater. Today Proc. 2021, 45, 4942–4947. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Aissa, A.; Suriya Uma Devi, S.; Prakash, M.; Kolsi, L.; Moria, H.; Jamshed, W.; Younis, O. Effect of a rotating cylinder on the 3D MHD mixed convection in a phase change material filled cubic enclosure. Sustain. Energy Technol. Assess. 2022, 51, 101879. [Google Scholar]
- Tombrink, J.; Jockenhöfer, H.; Bauer, D. Experimental investigation of a rotating drum heat exchanger for latent heat storage. Appl. Therm. Eng. 2021, 183, 116221. [Google Scholar]
- Hosseinian, A.; Meghdadi Isfahani, A.H. Experimental study of heat transfer enhancement due to the surface vibrations in a flexible double pipe heat exchanger. Heat Mass Transf./Waerme- Und Stoffuebertragung 2018, 54, 1113–1120. [Google Scholar]
- Promvonge, P.; Eiamsa-ard, S. Heat transfer behaviors in a tube with combined conical-ring and twisted-tape insert. Int. Commun. Heat Mass Transf. 2007, 34, 849–859. [Google Scholar]
- Afsharpanah, F.; Ajarostaghi, S.S.M.; Hamedani, F.A.; Pour, M.S. Compound Heat Transfer Augmentation of a Shell-and-Coil Ice Storage Unit with Metal-Oxide Nano Additives and Connecting Plates. Nanomaterials 2022, 12, 1010. [Google Scholar] [CrossRef] [PubMed]
- Louahdi, M.; Salhi, J.E.; Essaouini, H.; Zarrouk, T.; Lahlaouti, M.L. Three-dimensional analysis for optimizing thermo-hydrodynamic performance of heat exchangers with perforated semi-circular inserts. Case Stud. Therm. Eng. 2024, 60, 104611. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Evaluation of empirical models for predicting monthly mean horizontal diffuse solar radiation. Renew. Sustain. Energy Rev. 2016, 56, 246–260. [Google Scholar] [CrossRef]
- Hangi, M.; Rahbari, A.; Lipiński, W. Design improvement of compact double-pipe heat exchangers equipped with tube-side helical insert and annulus-side helical strip: Hydrothermal and exergy analyses. Appl. Therm. Eng. 2021, 190, 116805. [Google Scholar] [CrossRef]
- Pourahmad, S.; Pesteei, S.M.; Ravaeei, H.; Khorasani, S. Experimental study of heat transfer and pressure drop analysis of the air/water two-phase flow in a double tube heat exchanger equipped with dual twisted tape turbulator: Simultaneous usage of active and passive methods. J. Energy Storage 2021, 44, 103408. [Google Scholar] [CrossRef]
- Maradiya, C.; Vadher, J.; Agarwal, R. The heat transfer enhancement techniques and their Thermal Performance Factor. Beni-Suef Univ. J. Basic Appl. Sci. 2018, 7, 1–21. [Google Scholar] [CrossRef]
- Ali, M.A.M.; El-Maghlany, W.M.; Eldrainy, Y.A.; Attia, A. Heat transfer enhancement of double pipe heat exchanger using rotating of variable eccentricity inner pipe. Alex. Eng. J. 2018, 57, 3709–3725. [Google Scholar] [CrossRef]










| Author | Insert Type | Effect on Heat Transfer Rate | Reference |
|---|---|---|---|
| Nakhchi et al. (2021) | Double-perforated inclined elliptic insert | Increase by 39.4% in heat transfer rate | [8] |
| Nakhchi et al. (2020) | Louvered Strip Insert | A stronger axial velocity near the pipe wall, thereby increased the heat transfer rate by 45.8%. | [9] |
| Liu et al. (2018) | Bidirectional conical strip insert | Increased in Nusselt number (Nu) by 2.35–9.85 times | [10] |
| Keklikcioglu and Ozceyhan (2018) | Equilateral triangle cross-sectioned coiled-wire insert | A maximum increase of 1.67 times in thermal performance | [11] |
| Padmanabhan et al. (2021) | Helical insert of 5 mm and 15 mm pitch | Increase by 63.91% and 31.39% in heat transfer rate, respectively | [12] |
| Pandey et al. (2021) | Y-shaped insert | Increase by 5.05 times in heat transfer rate | [13] |
| Author | Method | Type | Effect on Heat Transfer Rate | Reference |
|---|---|---|---|---|
| Al-Kouz et al. (2022) | Active | Rotating cylinder | Increase by 21.2% in heat transfer rate | [16] |
| Tombrink et al. (2021) | Active | Decanoic acid phase change material coupled with rotation | Increase by 142% in heat transfer rate | [17] |
| Hosseinian and Isfahani (2018) | Active | Surface vibration | Increase by 97% in heat transfer coefficient | [18] |
| Promvonge and Eiamsa-ard (2007) | Compound | Combined conical-ring and twisted-tape insert | Increase by 367% in heat transfer rate | [19] |
| Afsharpanah et al. (2022) | Compound | Nano-additives and connecting plates | Increase by 29.97% in heat transfer rate | [20] |
| Properties | Water | Toluene | Copper | Steel |
|---|---|---|---|---|
| Density (kg/m3) | 998.2 | 866 | - | - |
| Viscosity (kg/m-s) | 0.001003 | 0.000586 | - | - |
| Specific heat (J/kg-K) | 4182 | 1675 | - | - |
| Thermal Conductivity (W/m-K) | 0.6 | 0.151 | 387.6 | 16.27 |
| Type | Cell Zone | Condition |
|---|---|---|
| Mass Flow (kg/s) | Cold inlet | 6 |
| Hot inlet | 1, 3, 5, 7, 9, 11, 13, and 15 | |
| Temperature (K) | Cold Inlet | 288.15 |
| Hot Inlet | 368.15 | |
| Outlet Gauge Pressure (Pa) | Cold and Hot Inlet | 0 |
| Specification | Outer Tube | Inner Tube |
|---|---|---|
| Fluid | Toluene | Water |
| Diameter, in | 1½ (Sch.40 copper pipe) | 3 (Sch.40 steel pipe) |
| Length, m | 2.0 | 2.0 |
| Type | Zone | Condition |
|---|---|---|
| Mass Flow (kg/s) | Cold inlet/Hot Inlet | 1.2/0.4 |
| Temperature (K) | Cold Inlet/Hot Inlet | 308.15/343.15 |
| Outlet Gauge Pressure (Pa) | Cold and Hot Inlet | 0 |
| Heat Flux (W/m2) | Adiabatic Outer Pipe Wall | 0 |
| Shear Condition | Inner Pipe and Outer Pipe Wall | No Slip |
| Parameter | RRMSE | Agreement Indication |
|---|---|---|
| Th,o | 0.37% | Excellent |
| Tc,o | 0.13% | Excellent |
| Nu | 22.76% | Good |
| 24.34% | Fair |
| AHT Technique | Heat Transfer Enhancement | Reference |
|---|---|---|
| Circular perforated insert (N = 7) | 41.8% | This study |
| Rotating inner pipe (ω = 300 rad/s) | 428% | This study (Section 3.3) |
| Rotating circular perforated insert (N = 7, ω = 300 rad/s) | 47.5% | This study (Section 3.4) |
| 15 mm pitched helical insert | 31.39% | [12] |
| Perforated elliptic vortex generators | 39.4% | [8] |
| Perforated louvered strip insert | 45.8% | [9] |
| 5 mm pitched helical insert | 63.91% | [12] |
| Perforated Y-shaped insert | 505% | [13] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ardeta, L.G.A.; Doma, Jr., B. Numerical Analysis of Passive, Compound, and Active Augmented Heat Transfer Methods for Concentric Tube Heat Exchanger. Appl. Sci. 2025, 15, 4701. https://doi.org/10.3390/app15094701
Ardeta LGA, Doma, Jr. B. Numerical Analysis of Passive, Compound, and Active Augmented Heat Transfer Methods for Concentric Tube Heat Exchanger. Applied Sciences. 2025; 15(9):4701. https://doi.org/10.3390/app15094701
Chicago/Turabian StyleArdeta, Louise Grace Avena, and Bonifacio Doma, Jr. 2025. "Numerical Analysis of Passive, Compound, and Active Augmented Heat Transfer Methods for Concentric Tube Heat Exchanger" Applied Sciences 15, no. 9: 4701. https://doi.org/10.3390/app15094701
APA StyleArdeta, L. G. A., & Doma, Jr., B. (2025). Numerical Analysis of Passive, Compound, and Active Augmented Heat Transfer Methods for Concentric Tube Heat Exchanger. Applied Sciences, 15(9), 4701. https://doi.org/10.3390/app15094701






