Random Forest-Based Prediction of the Optimal Solid Ink Density in Offset Lithography
Abstract
:1. Introduction
2. Theory
2.1. Methods for Testing the Quality of Printed Matter
2.1.1. Density Testing
2.1.2. Colorimetry Detection
2.2. Random Forest
3. Materials and Methods
3.1. Experimental Equipment and Materials
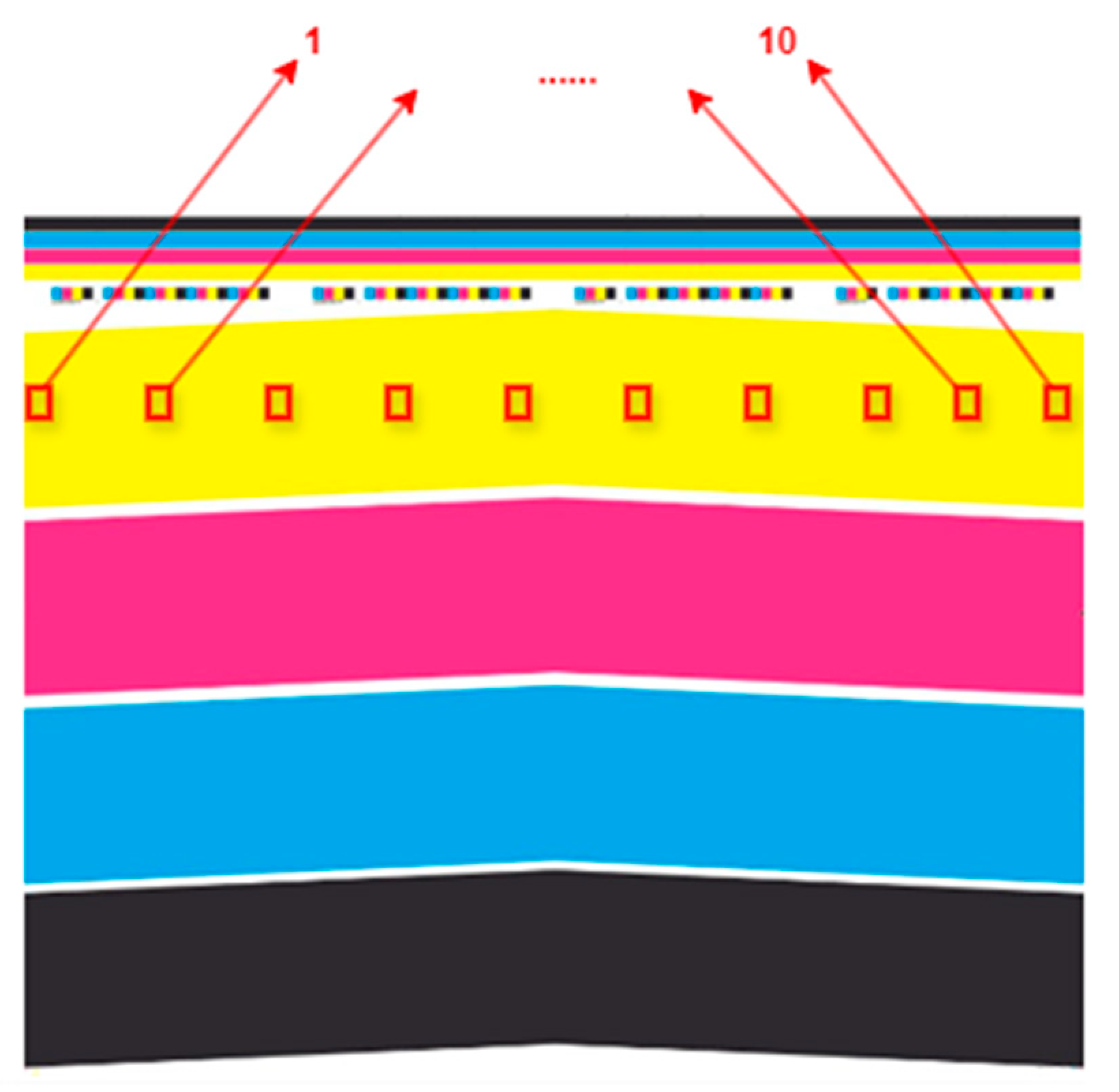
3.2. Data Acquisition
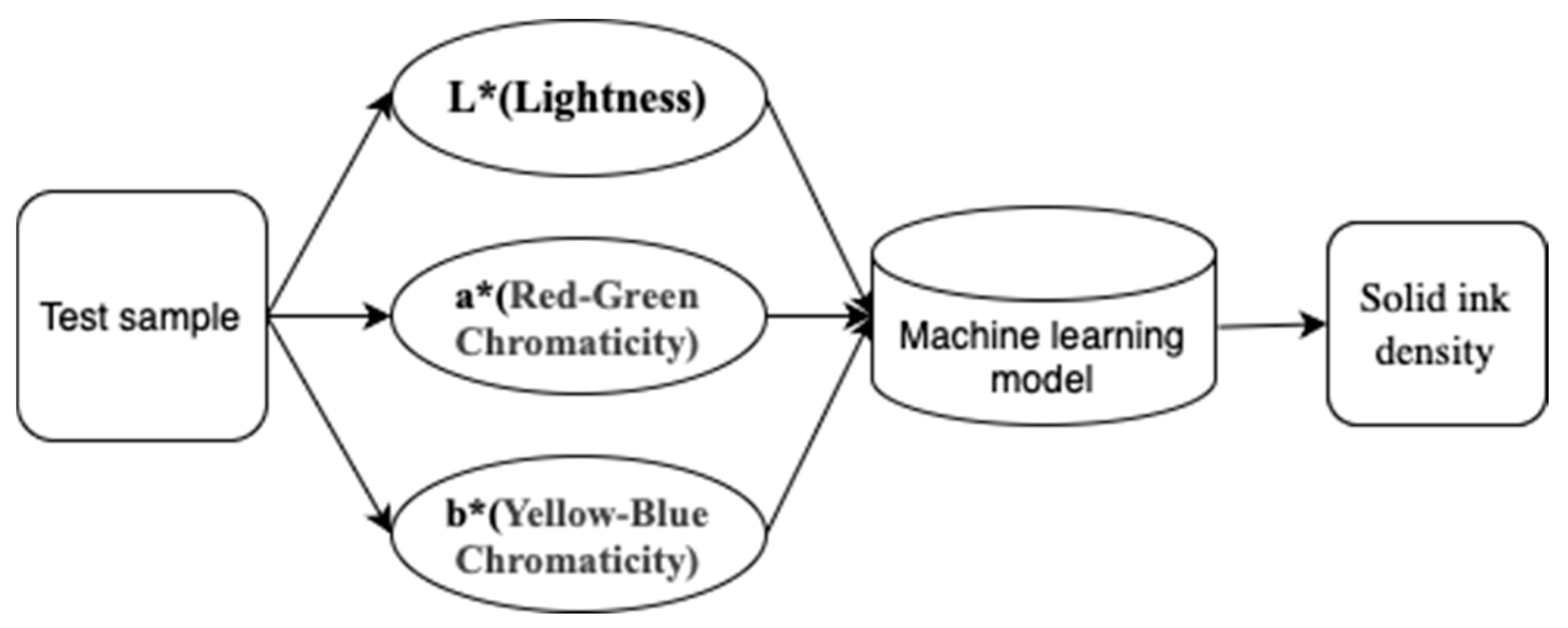
3.3. Optimal Solid Ink Density Matching Model
3.4. Data Pre-Processing
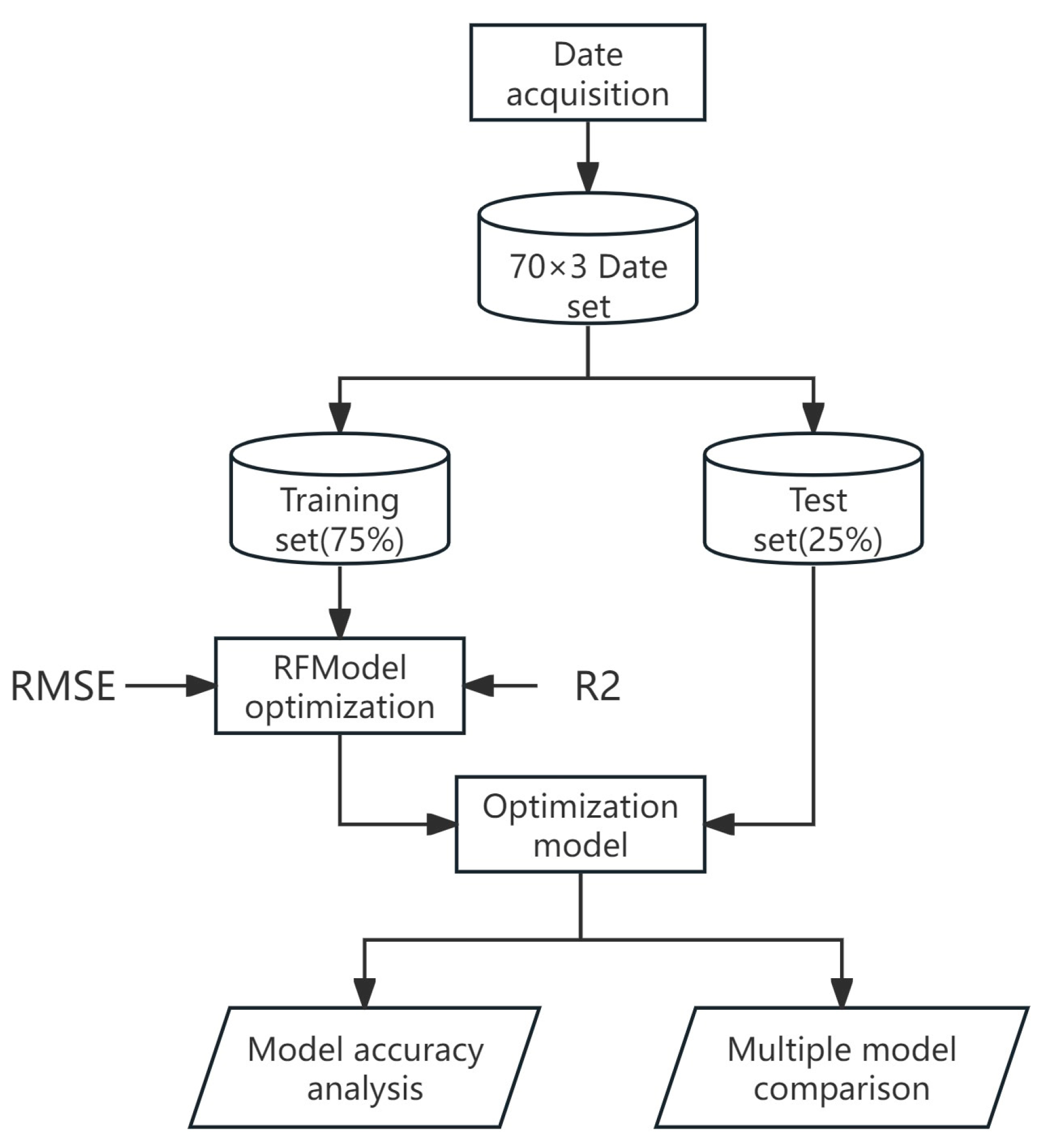
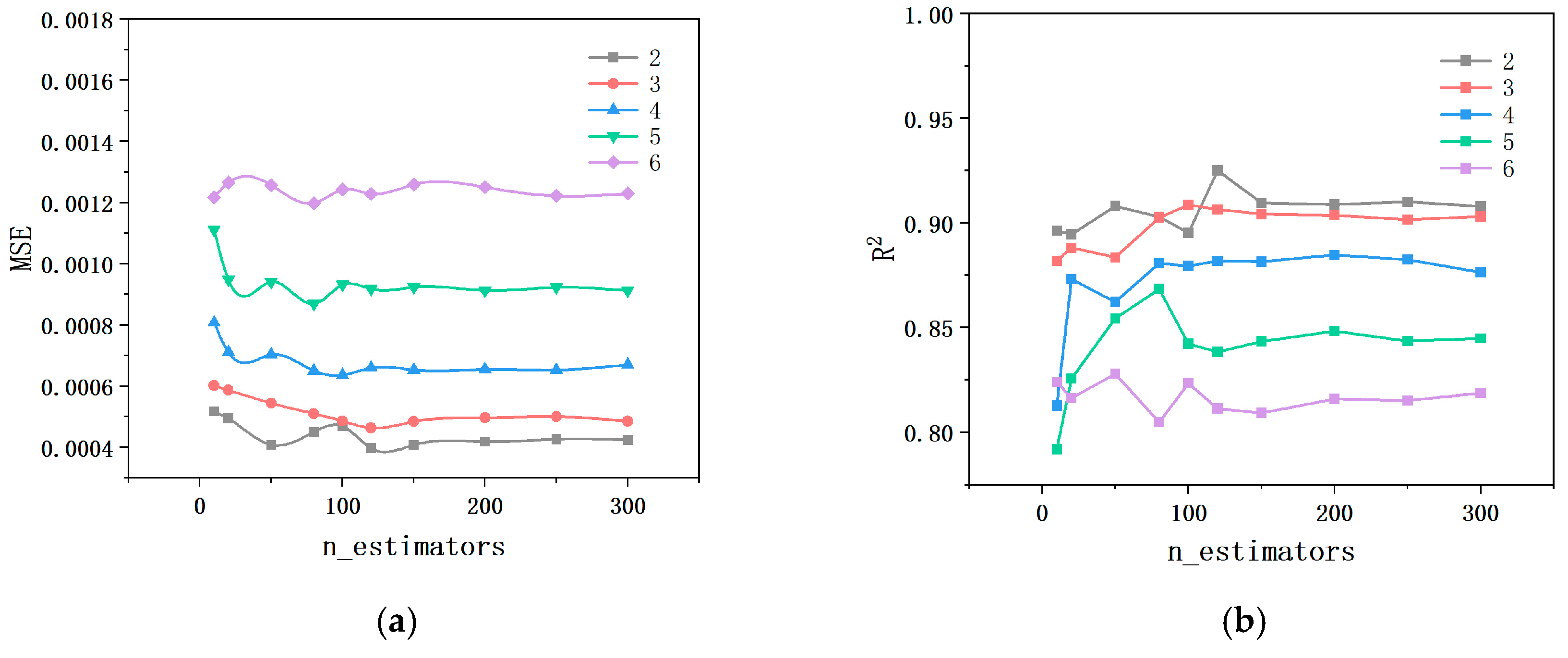
3.5. Hyperparameter Optimization in Random Forest Algorithms
3.6. Other Machine-Learning Methods for Comparison
3.7. Evaluation Indicators
4. Results
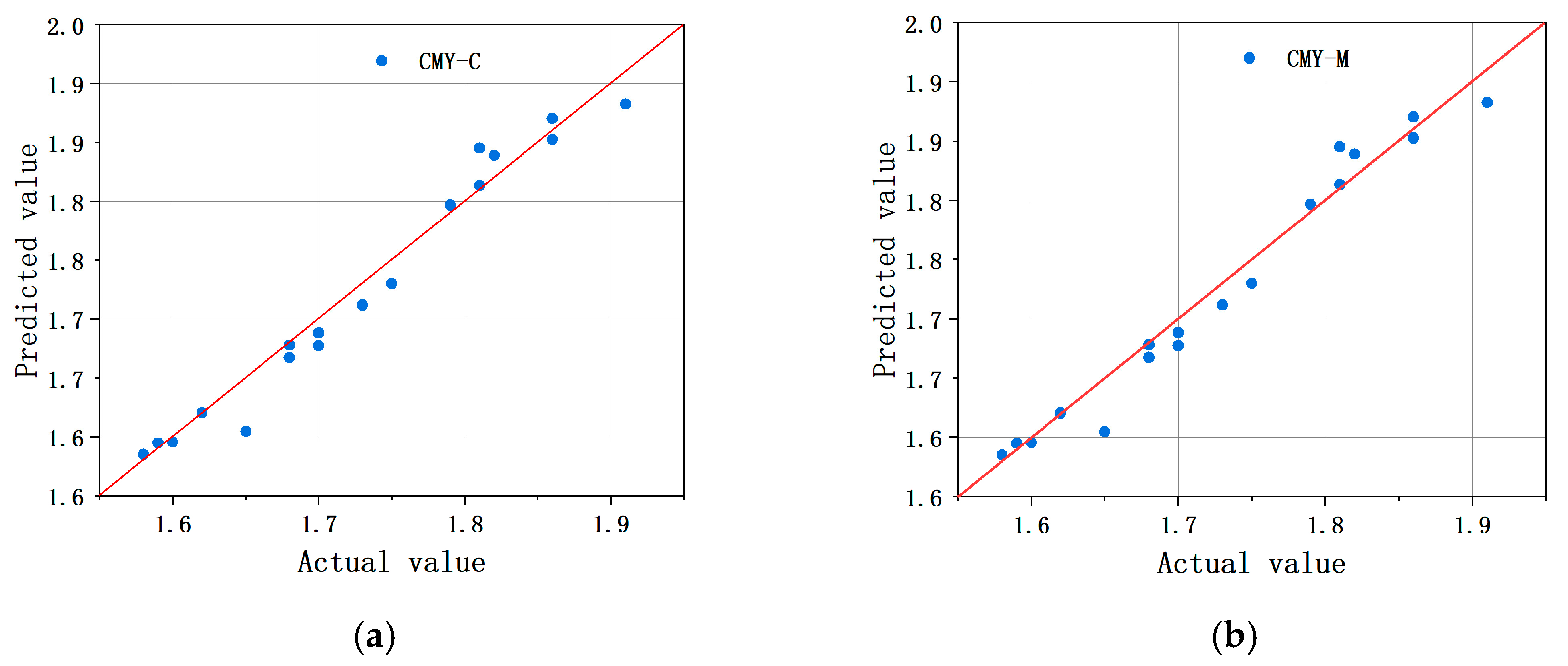
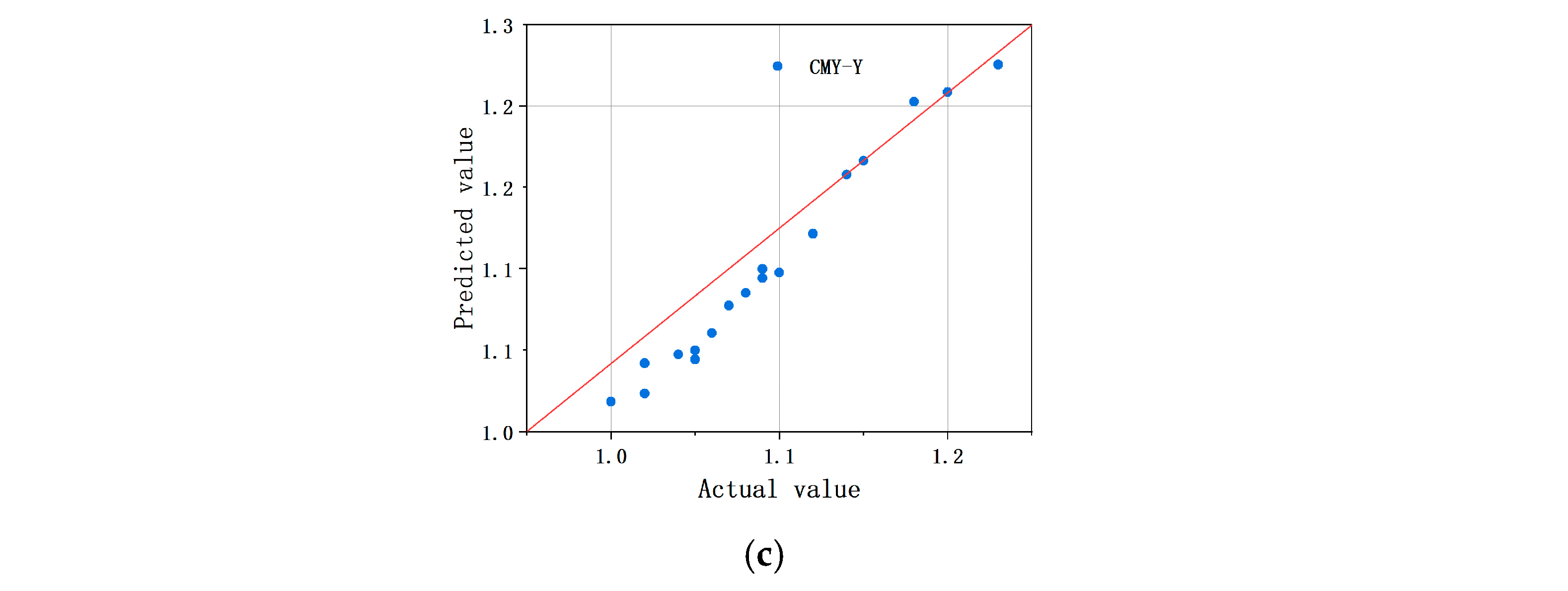
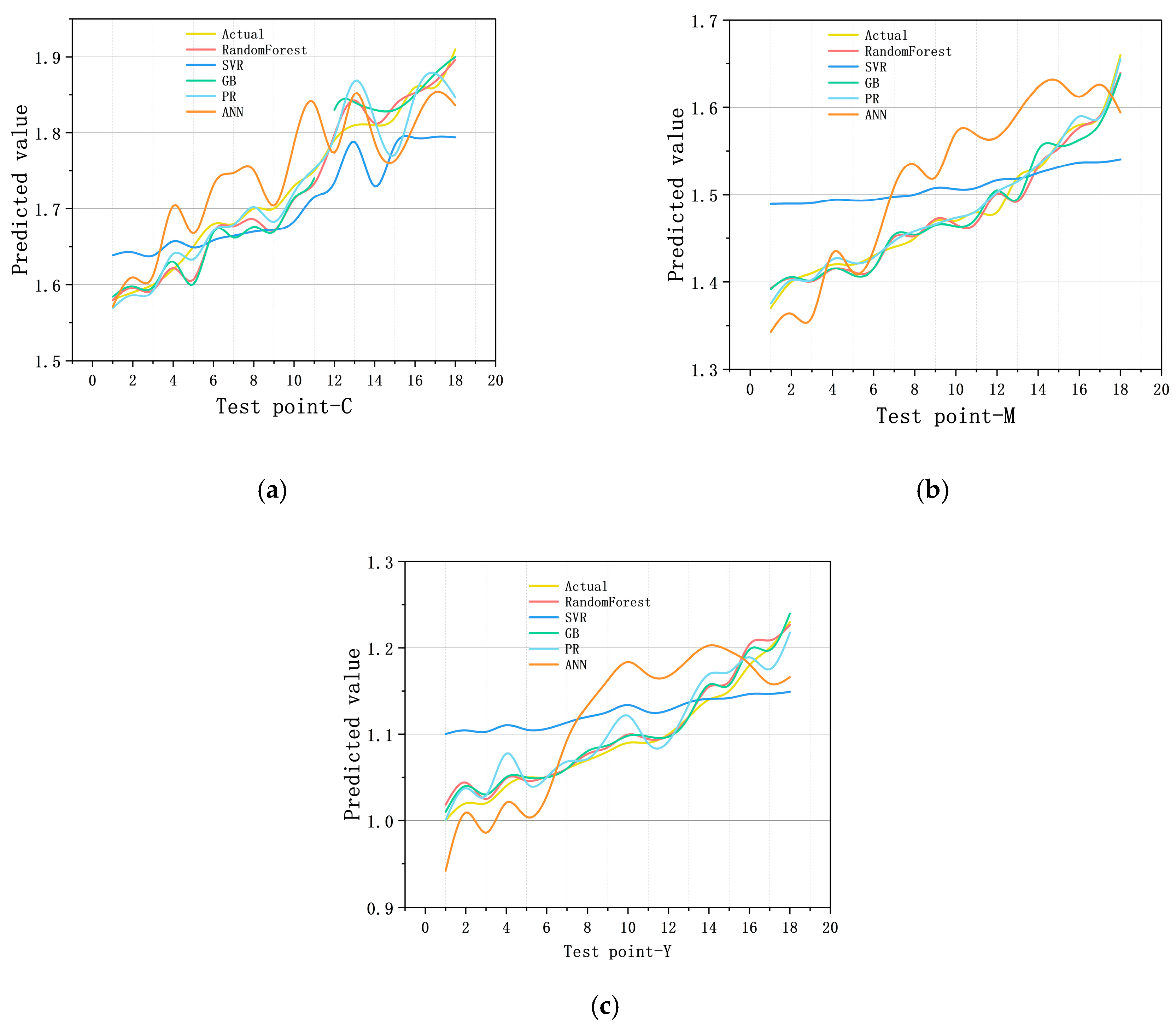
4.1. Model Training Results
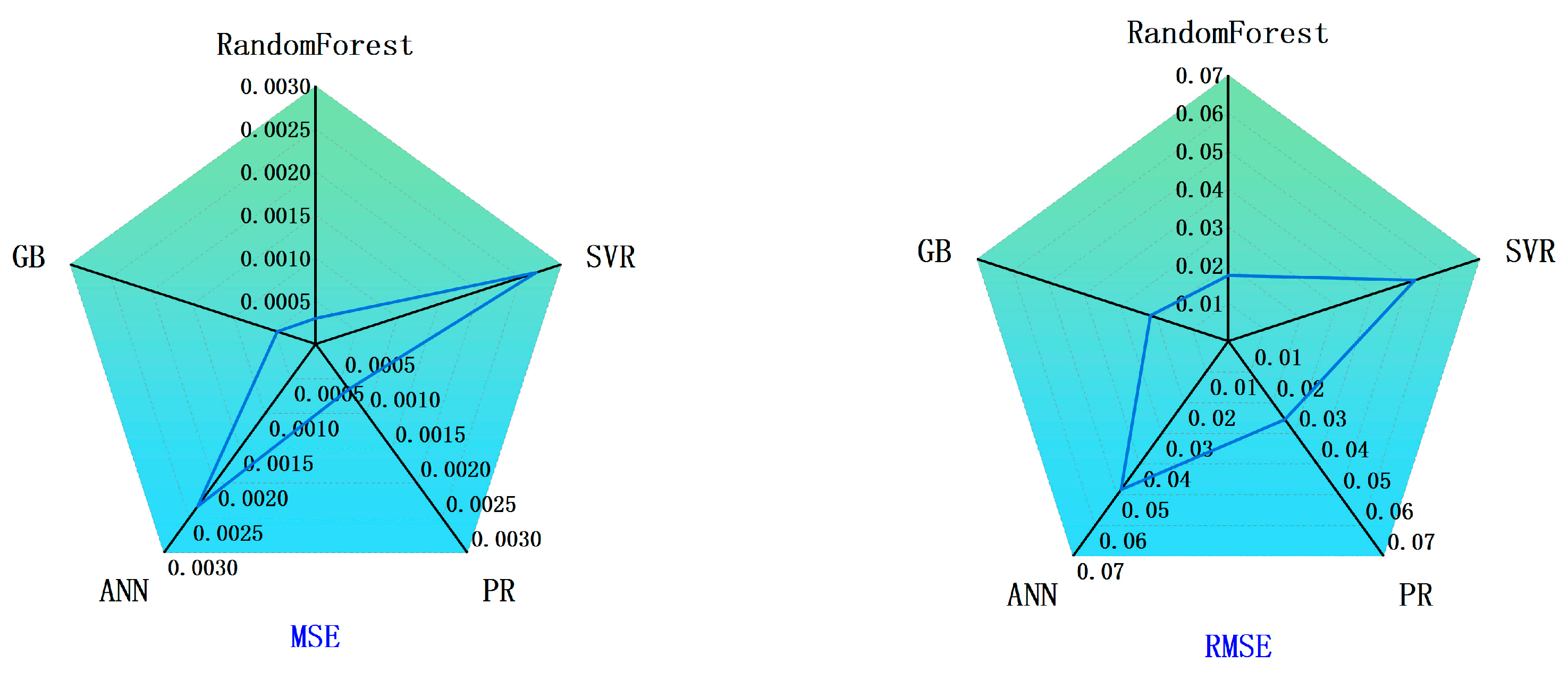
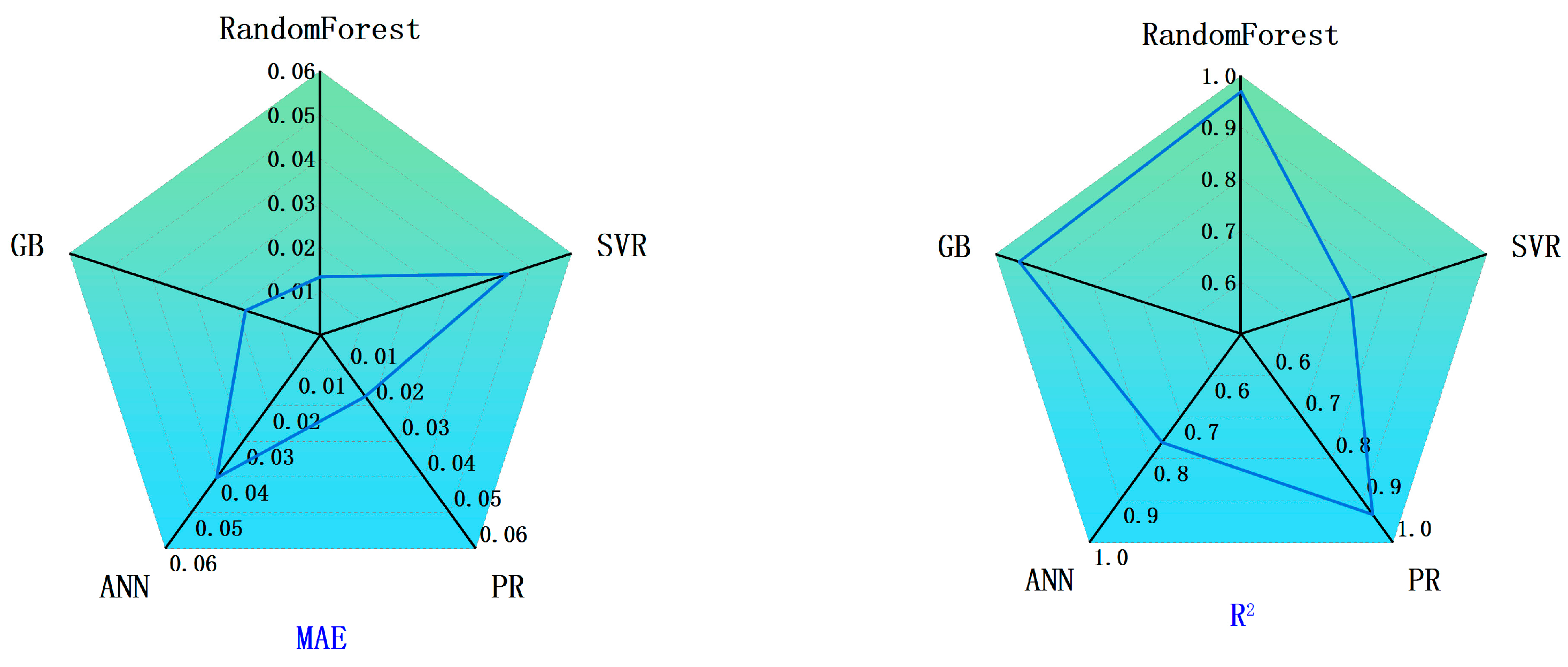
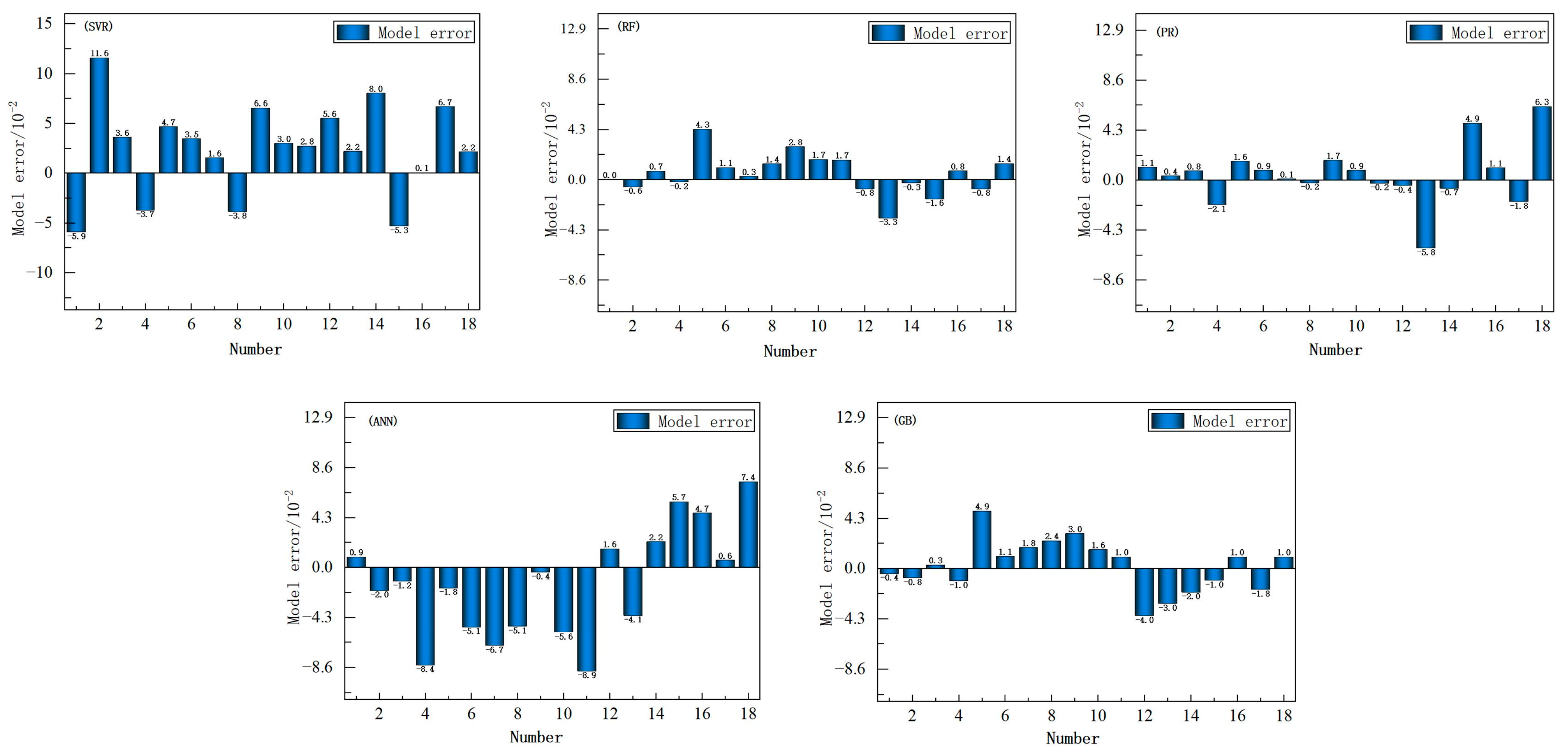
4.2. Comparative Evaluation of Model Performance
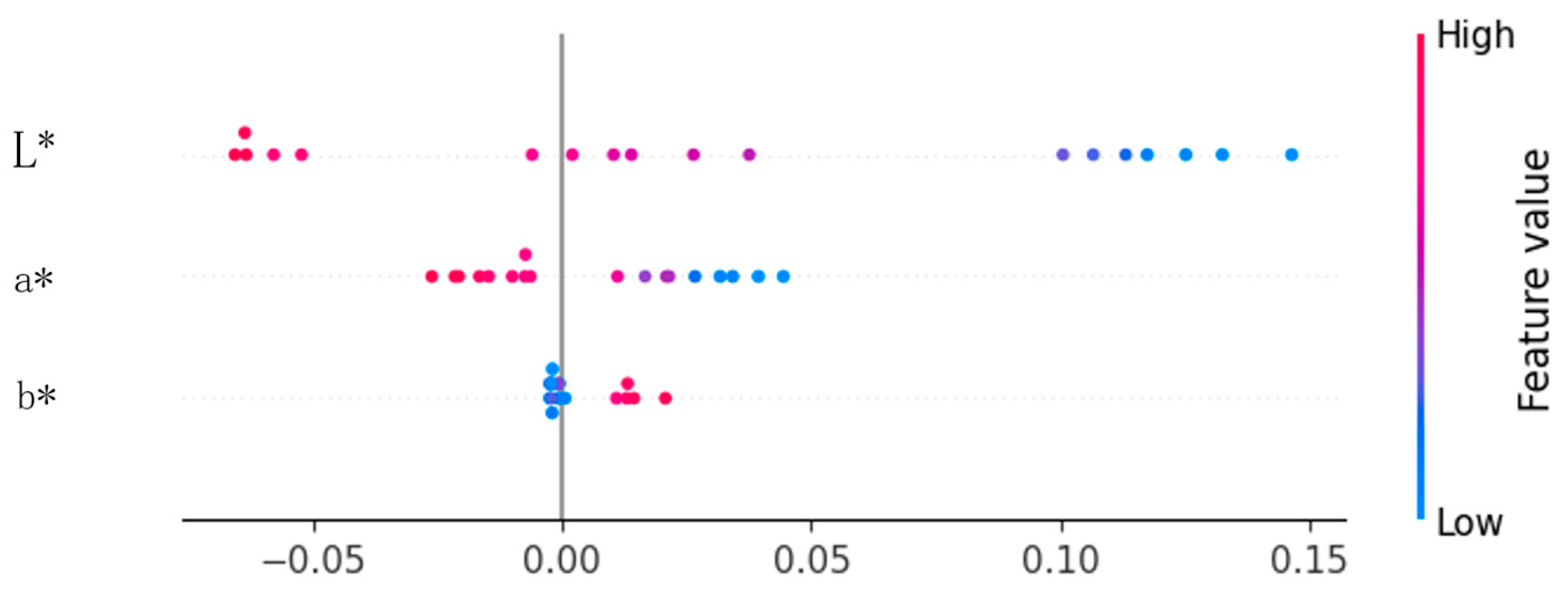
4.3. Feature Importance Analysis
4.4. Neutral Gray Chromaticity Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CMY | three colours: cyan, magenta, yellow |
| RF | Random Forest |
| SVR | Support Vector Regression |
| CIELAB | CIE 1976 (L*, a*, b*) colour space |
| MSE | Mean Squared Error |
| RMSE | Root Mean Square Error |
| ANN | Artificial neural network |
| GB | Gradient Boosting |
| MAE | Mean Absolute Error |
| MLP | Multi-Layer Perceptron |
References
- Yuan, W.; Zhao, X.; Jiang, Q. Study on Offset Printing Quality Parameter Control Method Based on Density. Packag. Eng. 2011, 32, 81–84. [Google Scholar]
- ISO 12647-2:2013; Graphic Technology—Process Control for the Production of Half-Tone Colour Separations, Proof and Production Prints—Part 2: Offset Lithographic Processes. ISO: Geneva, Switzerland, 2013.
- Chen, F.; Xiang, Z. Experimental Analysis of Optimal Solid Ink Density for Secondary Fiber Newsprint. Print. Ind. 2021, 5, 55–59. [Google Scholar]
- Yang, B.; Xu, J.; Long, H.; Guo, L. Study on the Matching Relationship Between Minimum Color Difference and Optimal Density in Print. Digit. Print. 2020, 147–151. [Google Scholar] [CrossRef]
- Guo, L.; Wang, J.; Sun, L.; Wen, L.; Dang, L. Research on Optimal Solid Ink Density of Printed Products Based on Regression Algorithms. Packag. Eng. 2018, 39, 210–215. [Google Scholar]
- Kwak, S.; Kim, J.; Ding, H.; Xu, X.; Chen, R.; Guo, J.; Fu, H. Machine Learning Prediction of the Mechanical Properties of γ-TiAl Alloys Produced Using Random Forest Regression Model. J. Mater. Res. Technol. 2022, 18, 520–530. [Google Scholar] [CrossRef]
- Alnaqeb, R.; Alrashdi, F.; Alketbi, K.; Ismail, H. Machine Learning-Based Water Potability Prediction. In Proceedings of the 2022 IEEE/ACS 19th International Conference on Computer Systems and Applications (AICCSA), Abu Dhabi, United Arab Emirates, 5–8 December 2022; IEEE: New York, NY, USA, 2022. [Google Scholar]
- Kotenko, I.V.; Saenko, I.B. Exploring Opportunities to Identify Abnormal Behavior of Data Center Users Based on Machine Learning Models. Pattern Recogn. Image Anal. 2023, 33, 368–372. [Google Scholar] [CrossRef]
- Yu, C.X.; Ying, S.; Min, Z.X.; Feng, G. Research Progress and Trend of the Machine Learning Based on Fusion. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 1–7. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine Learning and Deep Learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, L.; Huang, Y. ADAS Simulation Result Dataset Processing Based on Improved BP Neural Network. Data 2024, 9, 11. [Google Scholar] [CrossRef]
- Kumano, S.; Akutsu, T. Comparison of the Representational Power of Random Forests, Binary Decision Diagrams, and Neural Networks. Neural Comput. 2022, 34, 1019–1044. [Google Scholar] [CrossRef]
- Zhou, M. Study on Calculation Method of Overprint Density in Offset Printing Ink. Master’s Thesis, Jiangnan University, Wuxi, China, 2008. [Google Scholar]
- Fernandez-Reche, J.; Uroz, J.; Diaz, J.A.; Garcia-Beltran, A. Color Reproduction on Inkjet Printers and Paper Colorimetric Properties. 2003. Available online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?doi=10.1117/12.526511 (accessed on 12 April 2025).
- Li, B.; Zhang, J.; Zeng, Z. Detection and Evaluation of Blanket Printability. Packag. Eng. 2017, 38, 211–216. [Google Scholar]
- CIE 015:2018; CIE Recently Released a New Edition of Colorimetry Standard. China Lighting Appliance: Guangdong, China, 2018; Volume 60.
- Wei, N. Color Spaces and Color Management. China Inf. Technol. Educ. 2024, 89–94. [Google Scholar] [CrossRef]
- Simonot, L.; Hébert, M.; Dupraz, D. Goniocolorimetry: From Measurement to Representation in the CIELAB Color Space. Color Res. Appl. 2011, 36, 169–178. [Google Scholar] [CrossRef]
- Lv, Q. Research on Quality Control of Digital Proofing. Master’s Thesis, Jiangnan University, Wuxi, China, 2011. [Google Scholar]
- Fang, Y.; Lu, X.; Li, H. A Random Forest-Based Model for the Prediction of Construction-Stage Carbon Emissions at the Early Design Stage. J. Clean. Prod. 2021, 328, 129657. [Google Scholar] [CrossRef]
- Pan, M.; Xia, B.; Huang, W.; Ren, Y.; Wang, S. PM2.5 Concentration Prediction Model Based on Random Forest and SHAP. Int. J. Pattern Recognit. Artif. Intell. 2024, 38, 2452012. [Google Scholar] [CrossRef]
- Nieto, P.J.G.; Gonzalo, E.G.; García, L.A.M.; Prado, L.Á.; Sánchez, A.B. Predicting the Critical Superconducting Temperature Using the Random Forest, MLP Neural Network, M5 Model Tree and Multivariate Linear Regression. Alex. Eng. J. 2024, 86, 144–156. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J. Prediction of Nanofiltration and Reverse-Osmosis-Membrane Rejection of Organic Compounds Using Random Forest Model. J. Environ. Eng.-ASCE 2020, 146, 04020127. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z. RF_phage Virion: Classification of Phage Virion Proteins with a Random Forest Model (Vol 13, 1103783, 2023). Front. Genet. 2023, 14, 1224665. [Google Scholar]
- Wang, J.; Hou, Z.; Chen, Y.; Li, G.; Kan, G.; Xiao, P.; Li, Z.; Mo, D.; Huang, J. The Acoustic Attenuation Prediction for Seafloor Sediment Based on in-situ Data and Machine Learning Methods. J. Ocean Univ. China 2025, 24, 95–102. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Feature Wise Normalization: An Effective Way of Normalizing Data. Pattern Recognit. 2022, 122, 108307. [Google Scholar] [CrossRef]
- Li, H.; Lin, J.; Lei, X.; Wei, T. Compressive Strength Prediction of Basalt Fiber Reinforced Concrete via Random Forest Algorithm. Mater. Today Commun. 2022, 30, 103117. [Google Scholar] [CrossRef]
- Regis, R.G. Hyperparameter Tuning of Random Forests Using Radial Basis Function Models. In Machine Learning, Optimization, and Data Science, Proceedings of the 8th International Conference, LOD 2022, Certosa di Pontignano, Italy, 18–22 September 2022; Revised Selected Papers, Part I; Nicosia, G., Ojha, V., LaMalfa, E., LaMalfa, G., Pardalos, P., DiFatta, G., Giuffrida, G., Umeton, R., Eds.; Springer International Publishing Ag: Cham, Switzerland, 2023; Volume 13810, pp. 309–324. [Google Scholar]
- Ganesan, K.; Palanisamy, S.; Krishnasamy, V.; Salau, A.O.; Rathinam, V.; Seeni Nayakkar, S.G. Hybrid Photovoltaic/Thermal Performance Prediction Based on Machine Learning Algorithms with Hyper-Parameter Tuning. Int. J. Sustain. Energy 2024, 43, 2364226. [Google Scholar] [CrossRef]
- Shams, M.Y.; Elshewey, A.M.; El-kenawy, E.-S.M.; Ibrahim, A.; Talaat, F.M.; Tarek, Z. Water Quality Prediction Using Machine Learning Models Based on Grid Search Method. Multimed Tools Appl 2024, 83, 35307–35334. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, L.; Li, J.; Li, Y.; Zhou, Y.; Liu, W.; Ai, Y.; Zhang, B.; Qu, J.; Zhang, Y. Development and Optimization of an Artificial Neural Network (ANN) Model for Predicting the Cadmium Fixation Efficiency of Biochar in Soil. J. Environ. Chem. Eng. 2024, 12, 114196. [Google Scholar] [CrossRef]
- Kuehn, J.; Abadie, S.; Delpey, M.; Roeber, V. Super-Resolution on Unstructured Coastal Wave Computations with Graph Neural Networks and Polynomial Regressions. Coast. Eng. 2024, 194, 104619. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, J.; Lin, C.; Li, Z. Optimization of Low-Earth Orbit Density Model Based on Support Vector Regression. Adv. Space Res. 2025, 75, 3601–3613. [Google Scholar] [CrossRef]
- Sampath, R.; Indumathi, J. Earlier Detection of Alzheimer Disease Using N-Fold Cross Validation Approach. J. Med. Syst. 2018, 42, 217. [Google Scholar] [CrossRef]
- GB/T 17934.1-1999; Graphic Technology—Process Control for the Production of Half-Tone Colour Separations, Proof and Production Prints—Part 1: Parameters and Measurement Methods. The State Bureau of Quality and Technical Supervision: Beijing, China, 1999. Available online: https://www.chinesestandard.net/PDF/English.aspx/GBT17934.1-2021 (accessed on 22 April 2025).
- GB/T 2624-2012; Sheet-Fed Offset Ink. Ministry of Industry and Information Technology of the People’s Republic of China: Beijing, China, 2012. Available online: https://www.chinesestandard.net/PDF/English.aspx/QBT2624-2012 (accessed on 22 April 2025).
- de Queiróz Lamas, W. Algae’s Potential as a Bio-Mass Source for Bio-Fuel Production: MLR vs. ANN Models Analyses. Fuel 2025, 395, 134853. [Google Scholar] [CrossRef]


| 128 g/m2 Coated Paper | ISO 12647-2:2013 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average | Standard Value | Allowance | |
| L | 93.27 | 92.28 | 93.18 | 93.24 | 93.16 | 92.67 | 93.25 | 93.67 | 92.36 | 93.41 | 93.05 | 95 | ±3 |
| a | 0.87 | 0.86 | 0.85 | 0.85 | 0.82 | 0.83 | 0.83 | 0.79 | 0.85 | 0.88 | 0.84 | 0 | ±2 |
| b | −3.78 | −3.84 | −3.85 | −3.43 | −3.52 | −3.16 | −3.75 | −3.26 | −3.26 | −3.34 | −3.52 | −2 | ±2 |
| HangHua Ink | ISO 12647-2:2013 | |||||||
|---|---|---|---|---|---|---|---|---|
| C | M | Y | K | C | M | Y | K | |
| L | 57.26 | 47.85 | 89.85 | 18.75 | 55 | 48 | 89 | 16 |
| a | −36.84 | 74.26 | −3.75 | 0.21 | −37 | 74 | −5 | 0 |
| b | −50.89 | −3.97 | 90.86 | 0.11 | −50 | −3 | 93 | 0 |
| ΔE | 1.23 | 0.89 | 2.17 | 2.95 | ≤5 | ≤5 | ≤5 | ≤5 |
| Ink | L | a | b |
|---|---|---|---|
| C | 0.92 | −0.82 | 0.78 |
| M | 0.89 | −0.79 | 0.82 |
| Y | 0.88 | −0.86 | 0.85 |
| Name | Default Value | Description |
|---|---|---|
| n_estimators | 100 | The number of decision trees to control the complexity and stability of the model. |
| max_depth | None | The maximum depth of the tree. If the value is “none” the node will continue unless all leaves are pure. |
| min_samples_split | 2 | The minimum number of samples required to divide nodes. |
| max_leaf_num | None | Maximum number of leaf nodes. |
| Model | Best Params |
|---|---|
| Random Forest | Max features: none min samples leaf: 1 min samples split: 2 |
| SVR | c: 0.1 gamma: 0.1 |
| Polynomial Regression | Linearregression fit intercept: false Polynomial features degree: 2 |
| ANN | activation: tanh alpha: 0.01 hidden layer sizes: 100 solver: adam |
| GB | Learning rate: 0.2 Max depth: 5 Min samples leaf: 1 Min samples split: 5 n_estimators: 200 |
| Printing Ink | L* | a* | b* |
|---|---|---|---|
| C | 56 | −35 | −44 |
| M | 45 | 68 | −3 |
| Y | 83 | −5 | 87 |
| Printing Ink | Calculated Density Range | Optimum Solid Ink Density | China’s National Standard Range |
|---|---|---|---|
| C | 1.57–1.92 | 1.62 | 1.5–2.0 |
| M | 1.56–1.91 | 1.61 | 1.3–1.6 |
| Y | 1.02–1.22 | 1.08 | 0.9–1.1 |
| Model | MSE | RMSE | R2 | MAE |
|---|---|---|---|---|
| Random Forest | 0.00029 | 0.0173 | 0.9692 | 0.0131 |
| SVR | 0.00269 | 0.0518 | 0.7233 | 0.0448 |
| Polynomial Regression | 0.00065 | 0.0255 | 0.9332 | 0.0173 |
| ANN | 0.0023 | 0.0483 | 0.7605 | 0.0401 |
| GB | 0.00046 | 0.0216 | 0.9513 | 0.0178 |
| Feature Name | SHAP Value |
|---|---|
| L* | 0.0345 |
| a* | 0.0069 |
| b* | 0.0083 |
| Index | 25C19M19Y | 50C40M40Y | 75C66M66Y | ||||||
|---|---|---|---|---|---|---|---|---|---|
| L | a | b | L | a | b | L | a | b | |
| 1 | 76.1 | 0.1 | −0.3 | 58.4 | −0.5 | −0.7 | 37.6 | −1.5 | −0.7 |
| 2 | 75.9 | 0.3 | −0.5 | 57.5 | 0.8 | 0.3 | 36.5 | −1.8 | −1.3 |
| 3 | 75.3 | 0.5 | −0.6 | 57.7 | −0.3 | −0.2 | 35.7 | −1.3 | −1.2 |
| 4 | 75.7 | 0.4 | −0.2 | 58.8 | 0.9 | 0.8 | 36.8 | −0.9 | 0.8 |
| 5 | 76.1 | 0.3 | −0.4 | 57.9 | 0.8 | −0.5 | 37.9 | −1.8 | −0.5 |
| 6 | 75.3 | 0.2 | −0.3 | 59.4 | 0.6 | −0.4 | 38.4 | −1.6 | −1.4 |
| Average | 75.7 | 0.3 | −0.3 | 58.2 | 0.3 | −0.1 | 37.1 | −0.1 | −0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, L.; Fan, H.; Qi, Y.; Li, J. Random Forest-Based Prediction of the Optimal Solid Ink Density in Offset Lithography. Appl. Sci. 2025, 15, 4830. https://doi.org/10.3390/app15094830
Peng L, Fan H, Qi Y, Li J. Random Forest-Based Prediction of the Optimal Solid Ink Density in Offset Lithography. Applied Sciences. 2025; 15(9):4830. https://doi.org/10.3390/app15094830
Chicago/Turabian StylePeng, Laihu, Hao Fan, Yubao Qi, and Jianqiang Li. 2025. "Random Forest-Based Prediction of the Optimal Solid Ink Density in Offset Lithography" Applied Sciences 15, no. 9: 4830. https://doi.org/10.3390/app15094830
APA StylePeng, L., Fan, H., Qi, Y., & Li, J. (2025). Random Forest-Based Prediction of the Optimal Solid Ink Density in Offset Lithography. Applied Sciences, 15(9), 4830. https://doi.org/10.3390/app15094830





