Enhanced Rolling Bearing Fault Diagnosis Using Multimodal Deep Learning and Singular Spectrum Analysis
Abstract
:1. Introduction
- (1)
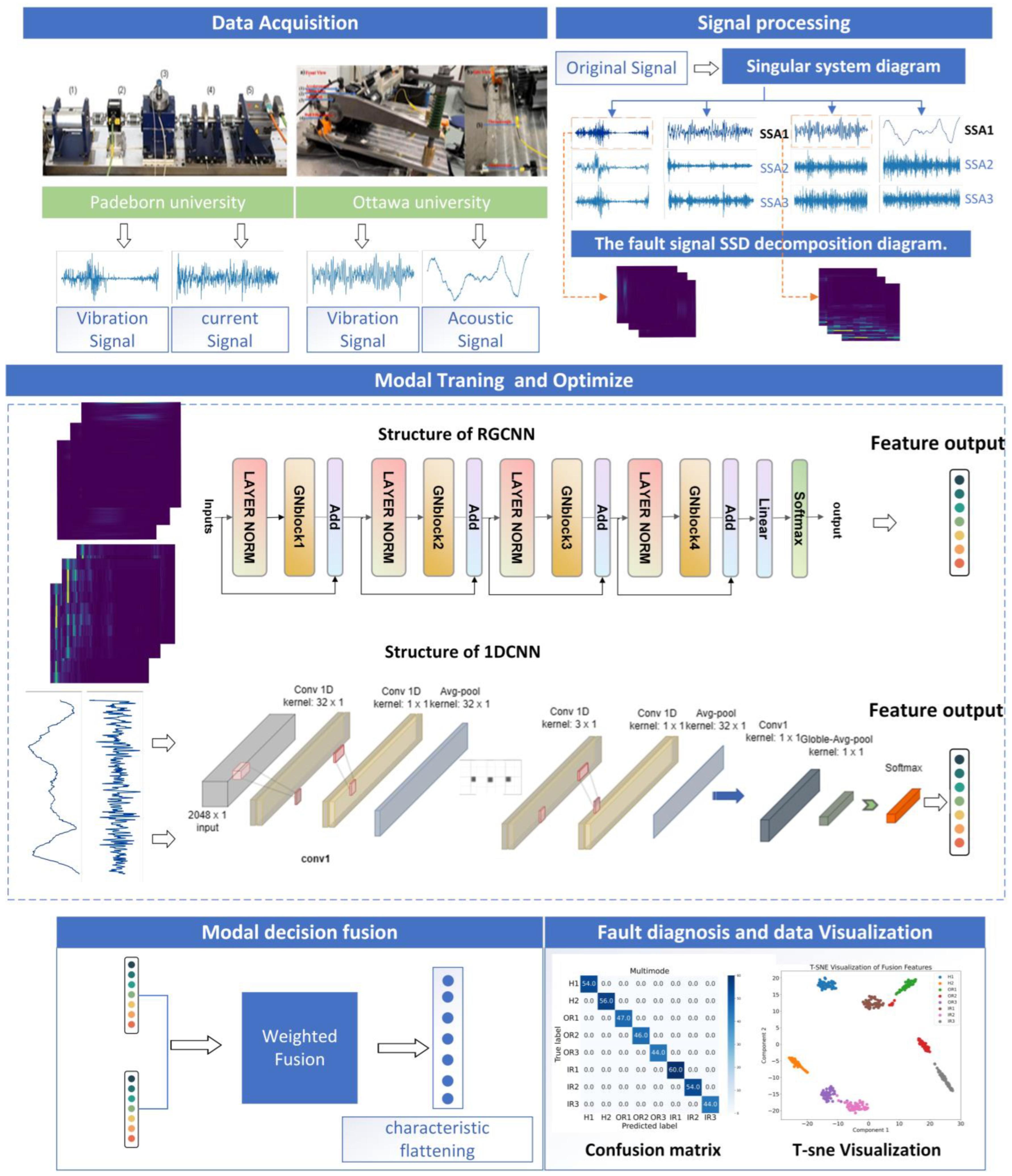
- To better represent the fault-related information of vibration and signals, singular spectrum time series analysis is used to extract signal features.
- (2)
- A novel network is constructed using recurrent gated convolution to learn and optimize two-dimensional image data.
- (3)
- The decision-level fusion method integrates different deep learning models to achieve more accurate fault diagnosis results.
- (4)
- We conducted experimental evaluations of the proposed method on a dataset of bearings with various faults and performed a comprehensive comparative study.
2. Related Work
3. Methods
3.1. Signal Preprocessing Method
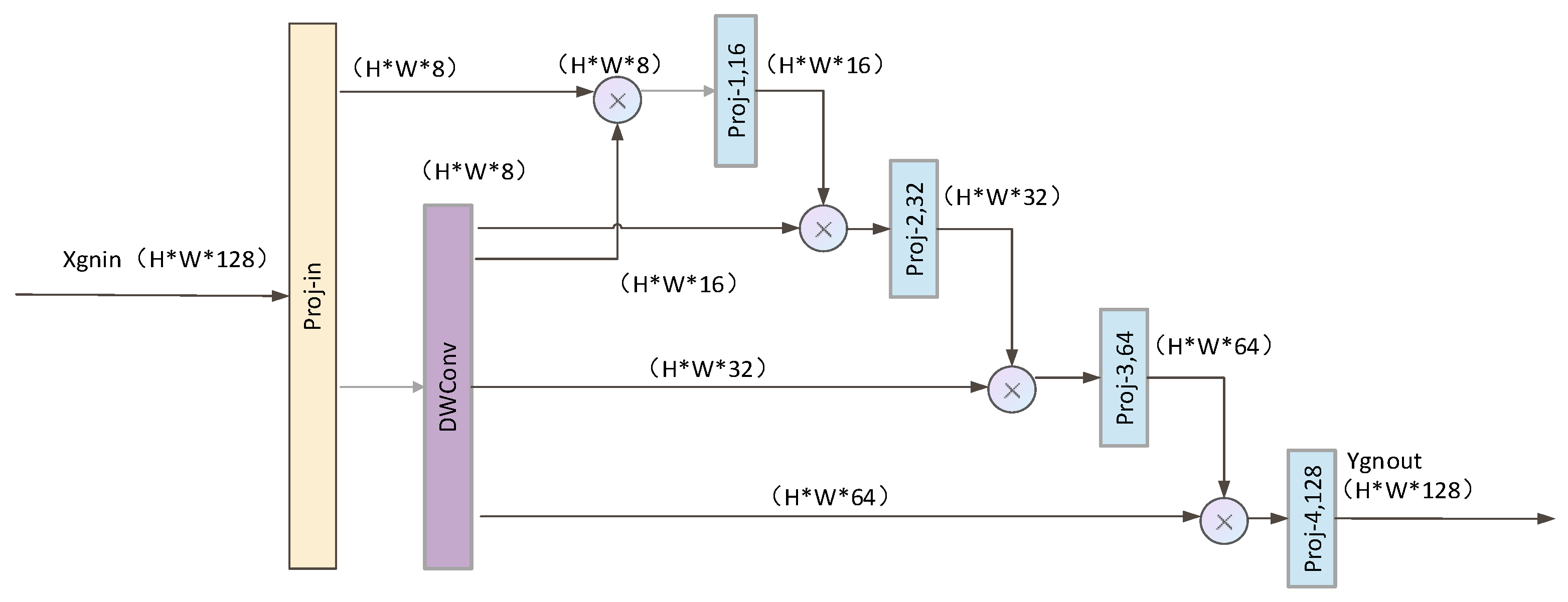
3.2. RGCNN Model
3.3. 1DCNN Model
3.4. Multimodal Fusion for Decision-Making
4. Results
4.1. Dataset
4.2. Parameter Settings
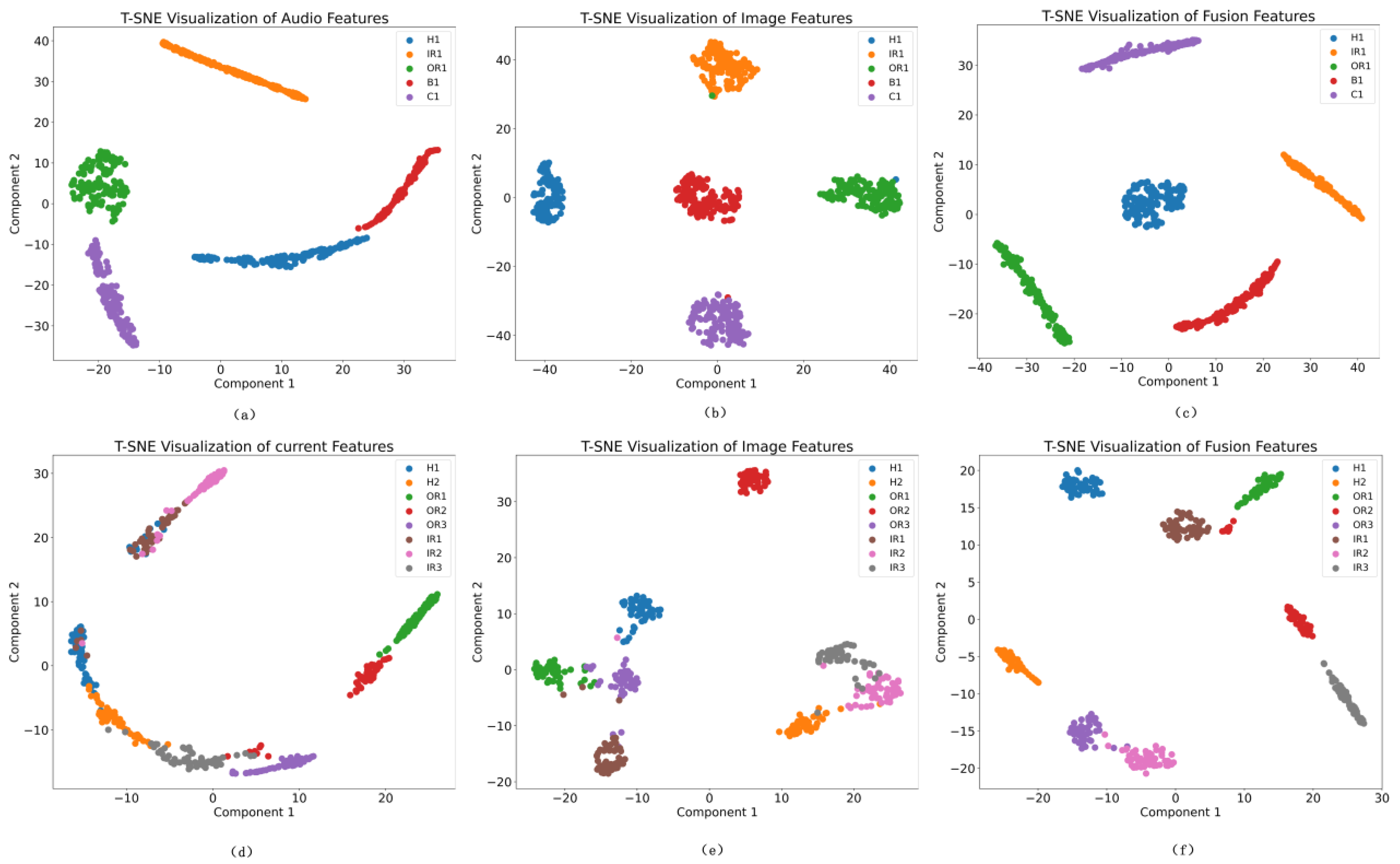
4.3. Fault Detection Results Analysis
4.4. Fault Diagnosis Based on Individual Modes
4.5. Fault Diagnosis Method Based on MFFD
4.6. Ablation Study of Singular Spectrum Analysis
4.7. Ablation Study of Order n for High Order Interactions
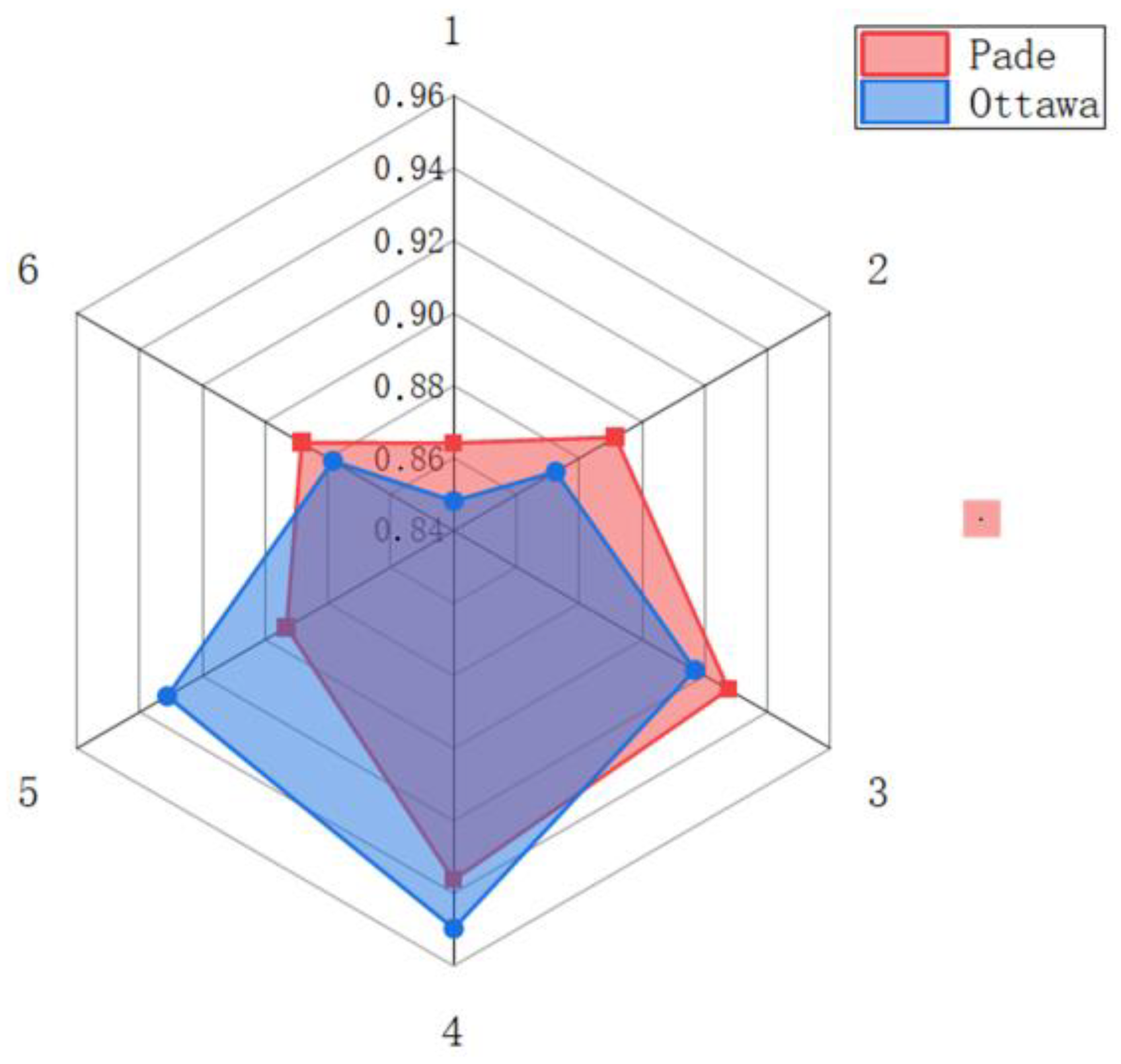
4.8. Comparison of Other Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, N.; Huang, W.; Ding, C.; Wang, J.; Zhu, Z. Physics-informed unsupervised domain adaptation framework for cross-machine bearing fault diagnosis. Adv. Eng. Inform. 2024, 62, 102774. [Google Scholar] [CrossRef]
- Cui, B.; Cheng, Y.; Jia, P.; Liu, Z.; Wang, B.; Ye, J.; Li, Y.; Chen, W.; Wang, Z. Temperature Field Analysis and Temperature Control of Vacuum Ultra High Speed Angular Contact Ball Bearings. J. Phys. Conf. Ser. 2024, 2784, 012009. [Google Scholar] [CrossRef]
- Sheng, L.; Qiubo, J.; Yadong, X.; Ke, F.; Yulin, W.; Beibei, S.; Xiaoan, Y.; Xin, S.; Ke, Z.; Qing, N. Digital twin-driven focal modulation-based convolutional network for intelligent fault diagnosis. Reliab. Eng. Syst. Saf. 2023, 240, 109590. [Google Scholar] [CrossRef]
- Lu, F.; Tong, Q.; Jiang, X.; Feng, Z.; Liu, R.; Xu, J.; Huo, J. DPICEN: Deep physical information consistency embedded network for bearing fault diagnosis under unknown domain. Reliab. Eng. Syst. Saf. 2024, 252, 110454. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Q.; Liang, S.Y. Physics-based intelligent prognosis for rolling bearing with fault feature extraction. Int. J. Adv. Manuf. Technol. 2018, 97, 611–620. [Google Scholar] [CrossRef]
- Zhao, D.; Shao, D.; Cui, L. CTNet: A data-driven time-frequency technique for wind turbines fault diagnosis under time-varying speeds. ISA Trans. 2024, 154, 335–351. [Google Scholar] [CrossRef]
- Li, Y.; Wang, T.; Xie, J.; Yang, J.; Pan, T.; Yang, B. A simulation data-driven semi-supervised framework based on MK-KNN graph and ESSGAT for bearing fault diagnosis. ISA Trans. 2024, 155, 261–273. [Google Scholar] [CrossRef]
- Hu, Y.; Li, H.; Shi, P.; Chai, Z. A prediction method for the real-time remaining useful life of wind turbine bearings based on the Wiener process. Renew. Energy 2018, 127, 452–460. [Google Scholar] [CrossRef]
- Wan, W.; Chen, J.; Xie, J. MIM-Graph: A multi-sensor network approach for fault diagnosis of HSR Bogie bearings at the IoT edge via mutual information maximization. ISA Trans. 2023, 139, 574–585. [Google Scholar] [CrossRef]
- Pan, Z.; Guan, Y.; Fan, F.; Zheng, Y.; Lin, Z.; Meng, Z. Rolling bearings fault diagnosis based on two-stage signal fusion and deep multi-scale multi-sensor network. ISA Trans. 2024, 154, 311–334. [Google Scholar] [CrossRef]
- Cheng, Y.; Lin, M.; Wu, J.; Zhu, H.; Shao, X. Intelligent fault diagnosis of rotating machinery based on continuous wavelet transform-local binary convolutional neural network. Knowl. -Based Syst. 2021, 216, 106796. [Google Scholar] [CrossRef]
- Liu, Y.; Wen, W.; Bai, Y.; Meng, Q. Self-supervised feature extraction via time–frequency contrast for intelligent fault diagnosis of rotating machinery. Measurement 2023, 210, 112551. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Qin, X.; Sun, Y. A two-stage fault diagnosis methodology for rotating machinery combining optimized support vector data description and optimized support vector machine. Measurement 2022, 200, 111651. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, Q.; Shang, M.; Gu, Y. Extreme learning Machine-based classifier for fault diagnosis of rotating Machinery using a residual network and continuous wavelet transform. Measurement 2021, 183, 109864. [Google Scholar] [CrossRef]
- Zhang, D.; Stewart, E.; Ye, J.; Entezami, M.; Roberts, C. Roller bearing degradation assessment based on a deep MLP convolution neural network considering outlier regions. IEEE Trans. Instrum. Meas. 2019, 69, 2996–3004. [Google Scholar] [CrossRef]
- Zhilin, D.; Dezun, Z.; Lingli, C. An intelligent bearing fault diagnosis framework: One-dimensional improved self-attention-enhanced CNN and empirical wavelet transform. Nonlinear Dyn. 2024, 112, 6439–6459. [Google Scholar]
- Li, F.; Wang, L.; Wang, D.; Wu, J.; Zhao, H. An adaptive multiscale fully convolutional network for bearing fault diagnosis under noisy environments. Measurement 2023, 216, 112993. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, L. Graph neural network-based bearing fault diagnosis using Granger causality test. Expert Syst. Appl. 2024, 242, 122827. [Google Scholar] [CrossRef]
- Shao, Y.; Yuan, X.; Zhang, C.; Song, Y.; Xu, Q. A novel fault diagnosis algorithm for rolling bearings based on one-dimensional convolutional neural network and INPSO-SVM. Appl. Sci. 2020, 10, 4303. [Google Scholar] [CrossRef]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-time motor fault detection by 1-D convolutional neural networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Rao, Y.; Zhao, W.; Tang, Y.; Zhou, J.; Lim, S.N.; Lu, J. Hornet: Efficient high-order spatial interactions with recursive gated convolutions. arXiv 2022, 35, 10353–10366. [Google Scholar]
- Luo, Y.; Lu, W.; Kang, S.; Tian, X.; Kang, X.; Sun, F. Enhanced Feature Extraction Network Based on Acoustic Signal Feature Learning for Bearing Fault Diagnosis. Sensors 2023, 23, 8703. [Google Scholar] [CrossRef] [PubMed]
- Kundu, P. Review of rotating machinery elements condition monitoring using acoustic emission signal. Expert Syst. Appl. 2024, 252, 124169. [Google Scholar] [CrossRef]
- Bonizzi, P.; Karel, J.M.; Meste, O.; Peeters, R.L. Singular spectrum decomposition: A new method for time series decomposition. Adv. Adapt. Data Anal. 2014, 6, 1450011. [Google Scholar] [CrossRef]
- Lin, T.; Ren, Z.; Zhu, L.; Huang, K.; Zhu, Y.; Zeng, L.; Wan, J. Neural architecture search for multi-sensor information fusion-based intelligent fault diagnosis. Adv. Eng. Inform. 2024, 62, 102776. [Google Scholar] [CrossRef]
- Wang, J.; Fu, P.; Zhang, L.; Gao, R.X.; Zhao, R. Multilevel information fusion for induction motor fault diagnosis. IEEE/ASME Trans. Mechatron. 2019, 24, 2139–2150. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Xu, L.; Liu, L.; De Silva, C.W. Fault diagnosis for rotating machinery using multiple sensors and convolutional neural networks. IEEE/ASME Trans. Mechatron. 2017, 23, 101–110. [Google Scholar] [CrossRef]
- Li, C.; Sanchez, R.-V.; Zurita, G.; Cerrada, M.; Cabrera, D.; Vásquez, R.E. Gearbox fault diagnosis based on deep random forest fusion of acoustic and vibratory signals. Mech. Syst. Signal Process. 2016, 76, 283–293. [Google Scholar] [CrossRef]
- Ma, M.; Sun, C.; Chen, X. Deep coupling autoencoder for fault diagnosis with multimodal sensory data. IEEE Trans. Ind. Inform. 2018, 14, 1137–1145. [Google Scholar] [CrossRef]
- Li, X.; Wan, S.; Liu, S.; Zhang, Y.; Hong, J.; Wang, D. Bearing fault diagnosis method based on attention mechanism and multilayer fusion network. ISA Trans. 2022, 128, 550–564. [Google Scholar] [CrossRef]
- Shao, H.; Lin, J.; Zhang, L.; Galar, D.; Kumar, U. A novel approach of multisensory fusion to collaborative fault diagnosis in maintenance. Inf. Fusion 2021, 74, 65–76. [Google Scholar] [CrossRef]
- Li, X.; Cheng, J.; Shao, H.; Liu, K.; Cai, B. A fusion CWSMM-based framework for rotating machinery fault diagnosis under strong interference and imbalanced case. IEEE Trans. Ind. Inform. 2021, 18, 5180–5189. [Google Scholar] [CrossRef]
- Peng, Y.; Qiao, W.; Cheng, F.; Qu, L. Wind turbine drivetrain gearbox fault diagnosis using information fusion on vibration and current signals. IEEE Trans. Instrum. Meas. 2021, 70, 3518011. [Google Scholar] [CrossRef]
- Huo, Z.; Martínez-García, M.; Zhang, Y.; Shu, L. A multisensor information fusion method for high-reliability fault diagnosis of rotating machinery. IEEE Trans. Instrum. Meas. 2021, 71, 3500412. [Google Scholar] [CrossRef]
- Wang, W.; McFadden, P. Early detection of gear failure by vibration analysis i. calculation of the time-frequency distribution. Mech. Syst. Signal Process. 1993, 7, 193–203. [Google Scholar] [CrossRef]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A.A. Analysis of Time Series Structure: SSA and Related Techniques; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Sehri, M.; Dumond, P.; Bouchard, M. University of Ottawa constant load and speed rolling-element bearing vibration and acoustic fault signature datasets. Data Brief 2023, 49, 109327. [Google Scholar] [CrossRef]
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification. In Proceedings of the PHM Society European Conference, Bilbao, Spain, 5–8 July 2016. [Google Scholar] [CrossRef]





| Layer | Type | Kernel | Channel | Stride | Pading | OUTPUT |
|---|---|---|---|---|---|---|
| 1 | INPUT | - | - | - | - | 2048 × 1 |
| 2 | Conv | 32 × 1 | 32 | 1 | Yes | 2048 × 32 |
| 3 | Conv | 1 × 1 | 32 | - | Yes | 2048 × 32 |
| 4 | AVP | 32 × 1 | - | - | - | 2048 × 32 |
| 5 | Conv | 16 × 1 | 32 | 2 | Yes | 1024 × 32 |
| 6 | Conv | 1 × 1 | 32 | - | Yes | 1024 × 32 |
| 7 | AVP | 32 × 1 | - | - | - | 1024 × 32 |
| 8 | Conv | 9 × 1 | 64 | 2 | Yes | 512 × 64 |
| 9 | Conv | 1 × 1 | 64 | - | Yes | 512 × 64 |
| 10 | AVP | 32 × 1 | - | - | - | 512 × 64 |
| 11 | Conv | 6 × 1 | 64 | 2 | Yes | 256 × 64 |
| 12 | Conv | 1 × 1 | 64 | - | Yes | 256 × 64 |
| 13 | AVP | 32 × 1 | - | - | - | 256 × 64 |
| 14 | Conv | 3 × 1 | 128 | 4 | Yes | 64 × 128 |
| 15 | Conv | 1 × 1 | 128 | - | Yes | 64 × 128 |
| 16 | AVP | 32 × 1 | - | - | - | 64 × 128 |
| 17 | Conv | 3 × 1 | 128 | 4 | Yes | 16 × 128 |
| Global AVP | ||||||
| SoftMax | ||||||
| Bearing Code | Bearing Name | Damage Level | Class | Characteristic of Damage |
|---|---|---|---|---|
| H-1-0 | H1 | No damage | H | Single point |
| I-1-2 | IR1 | No damage | IR | Single point |
| 0-6-2 | OR1 | Plasticdeform; indentations | OR | Single point |
| B-11-2 | B1 | Fatigue; pitting | B | Single point |
| C-16-2 | C1 | Plasticdeform | C | Single point |
| Bearing Code | Bearing Name | Damage | Class | Characteristic of Damage |
|---|---|---|---|---|
| K001 | H1 | No damage | H | - |
| K002 | H2 | No damage | H | - |
| KA15 | OR1 | Plasticdeform; indentations | OR | Single point |
| KA16 | OR2 | Fatigue; pitting | OR | Single point |
| KA30 | OR3 | Plasticdeform; indentations | OR | Distributed |
| KI16 | IR1 | Fatigue; pitting | IR | Single point |
| KI18 | IR2 | Fatigue; pitting | IR | Single point |
| KI21 | IR3 | Fatigue; pitting | IR | Single point |
| Dataset | Ottawa | Pade | ||||
|---|---|---|---|---|---|---|
| Method | 1DCNN | RGCNN | MFFD | 1DCNN | RGCNN | MFFD |
| Accuracy | 89.25 | 95.75 | 98.75 | 92.25 | 96.00 | 99.00 |
| Precision | 0.9012 | 0.9590 | 0.9887 | 0.9255 | 0. 9624 | 0.0991 |
| Recall | 0.8998 | 0.9562 | 0.9871 | 0.9240 | 0. 9590 | 0.9898 |
| F1 | 0.8992 | 0.9569 | 0.9877 | 0.9231 | 0.9598 | 0.9903 |
| Dataset | Pade | Ottawa | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
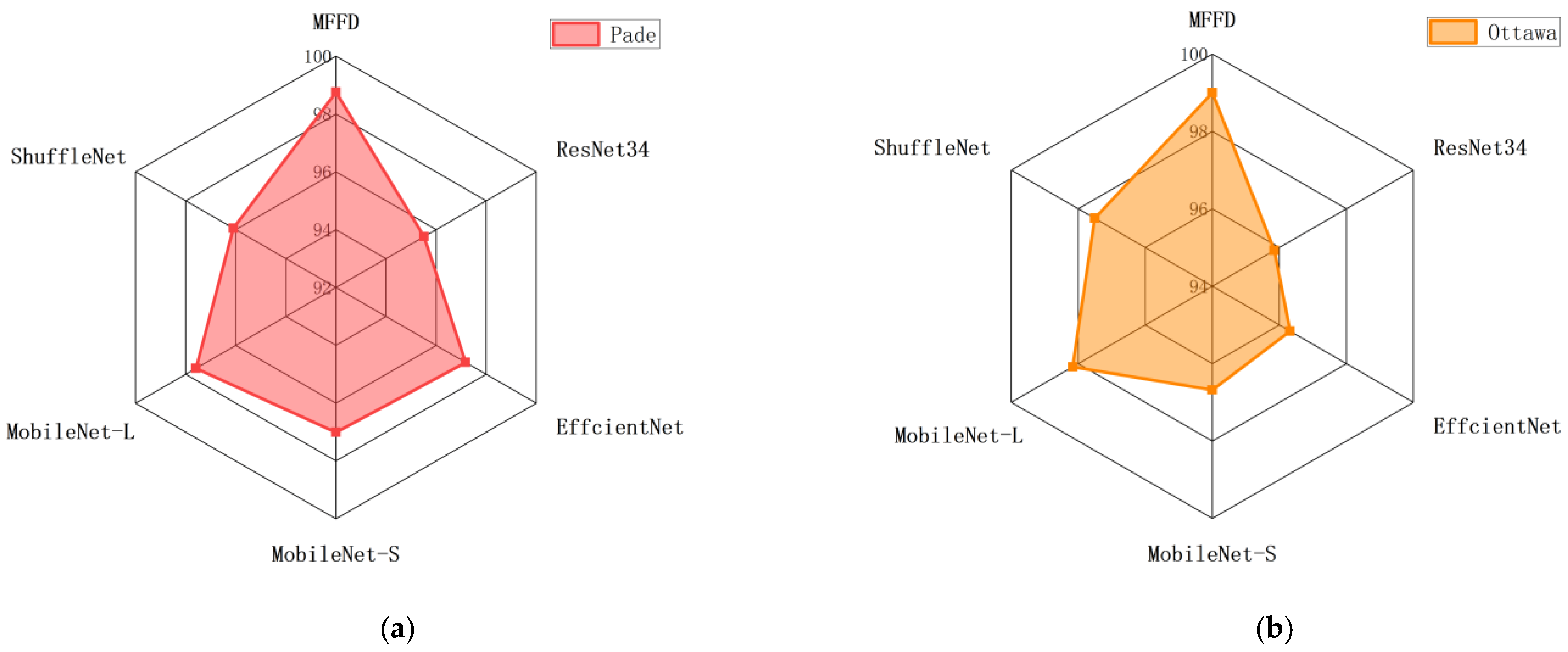
| Method | ResNet34 | Effcient Net | Mobile Net-S | Mobile Net-L | Shuffle Net | MFFD | ResNet34 | Effcient Net | Mobile Net-S | Mobile Net-L | Shuffle Net | MFFD |
| Accuracy | 95.52 | 97.18 | 97.01 | 97.59 | 96.10 | 98.75 | 95.85 | 96.32 | 96.68 | 98.17 | 97.51 | 99.00 |
| Precision | 0.9586 | 0.9722 | 0.9702 | 0.9763 | 0.9627 | 0.9887 | 0.9600 | 0.9629 | 0.9685 | 0.9821 | 0.9753 | 0.9910 |
| Recall | 0.9554 | 0.9733 | 0.9710 | 0.9755 | 0.9609 | 0.9871 | 0.9590 | 0.9733 | 0.9667 | 0.9816 | 0.9744 | 0.9898 |
| F1 | 0.9554 | 0.9718 | 0.9698 | 0.9752 | 0.9609 | 0.9877 | 0.9584 | 0.9632 | 0.9667 | 0.9816 | 0.9747 | 0.9903 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, H.; Bai, R.; Shi, Y.; Chen, X.; Xu, Q. Enhanced Rolling Bearing Fault Diagnosis Using Multimodal Deep Learning and Singular Spectrum Analysis. Appl. Sci. 2025, 15, 4828. https://doi.org/10.3390/app15094828
Wang Y, Wang H, Bai R, Shi Y, Chen X, Xu Q. Enhanced Rolling Bearing Fault Diagnosis Using Multimodal Deep Learning and Singular Spectrum Analysis. Applied Sciences. 2025; 15(9):4828. https://doi.org/10.3390/app15094828
Chicago/Turabian StyleWang, Yunhang, Hongwei Wang, Ruoyang Bai, Yuxin Shi, Xicong Chen, and Qingang Xu. 2025. "Enhanced Rolling Bearing Fault Diagnosis Using Multimodal Deep Learning and Singular Spectrum Analysis" Applied Sciences 15, no. 9: 4828. https://doi.org/10.3390/app15094828
APA StyleWang, Y., Wang, H., Bai, R., Shi, Y., Chen, X., & Xu, Q. (2025). Enhanced Rolling Bearing Fault Diagnosis Using Multimodal Deep Learning and Singular Spectrum Analysis. Applied Sciences, 15(9), 4828. https://doi.org/10.3390/app15094828






