Effects of Vibration on the Electrical Performance of Lithium-Ion Cells Based on Mathematical Statistics
Abstract
:1. Introduction
2. Experimental Method
2.1. Determination of Sample Size
2.2. Test Electrical Performance
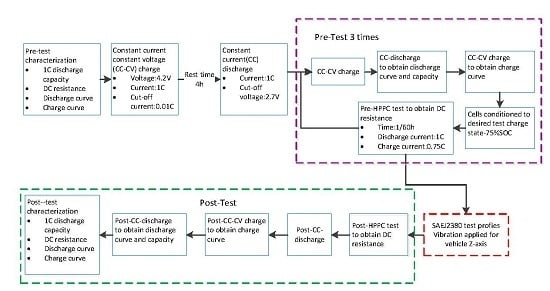
2.2.1. The Program Design of Cell Sample Test
2.2.2. Measuring the 1C Discharge Capacity
2.2.3. Measurement Uncertainty of DC Resistance
2.3. Design of Vibration Test
3. Experimental Results
3.1. Effect of Vibration on 1C Discharge Capacity
3.1.1. Probability Density Function of Capacity Samples
3.1.2. Cumulative Distribution Function of Capacity Samples
3.1.3. Kolmogorov–Smirnov (K–S) Test for 1C Capacity Distribution
3.1.4. Comparison for Capacity Distribution of Samples before and after Vibration
3.2. Effect of Vibration on DC Resistance
3.2.1. Parameters Estimation Based on Samples before Vibration
Estimation of Confidence Interval for the Population Mean
Estimation of Confidence Interval for the Population Standard Variation
3.2.2. Hypothesis Testing for Samples after Vibration
Hypothesis Testing for the Internal Resistance Mean μ after Vibration
Hypothesis Testing for the Resistance Standard Variation after Vibration
4. Consistency Analysis
4.1. Feature Extraction
4.1.1. Peaks Value of Incremental Capacity (IC) Curves Phase Transformation
4.1.2. Ratio of Potentio-Charge Capacity to Galvano-Charge Capacity
4.1.3. Discharge Curve
4.2. Feature Calculation
4.3. Consistency Analysis Based on Hierarchical Clustering Method
4.3.1. Clustering Tree
4.3.2. Inconsistent Coefficient
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, L.; Fu, X.; Guan, Y. Review of the remaining useful life prognostics of vehicle lithium-ion batteries using data-driven methodologies. Appl. Sci. 2016, 6, 166. [Google Scholar] [CrossRef]
- Saravanan, M.; Ambalavanan, S. Failure analysis of cast-on-strap in lead-acid battery subjected to vibration. Eng. Fail. Anal. 2011, 18, 2240–2249. [Google Scholar] [CrossRef]
- He, B.; Wang, H.; He, X. Vibration test methods and their experimental research on the performance of the lead-acid battery. J. Power Sources 2014, 268, 326–330. [Google Scholar] [CrossRef]
- Rajalakshmi, N.; Pandian, S.; Dhathathreyan, K.S. Vibration tests on a PEM fuel cell stack usable in transportation application. Int. J. Hydrogen Energy 2009, 34, 3833–3837. [Google Scholar] [CrossRef]
- Betournay, M.C.; Bonnell, G.; Edwardson, E.; Paktunc, D.; Kaufman, A.; Lomma, A.T. The effects of mine conditions on the performance of a PEM fuel cell. J. Power Sources 2004, 134, 80–87. [Google Scholar] [CrossRef]
- Pham, H.L.; Dietz, J.E.; Adams, D.E.; Sharp, N.D. Lithium-ion battery cell health monitoring using vibration diagnostic test. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013. [Google Scholar]
- Shevtsov, S.; Chang, S.H. Modeling of vibration energy harvesting system with power PZT stack loaded on Li-Ion battery. Int. J. Hydrogen Energy 2016, 41, 12618–12625. [Google Scholar] [CrossRef]
- Kume, M.; Murakami, T. Battery array configured to prevent vibration. U.S. Patent 8,999,555, 7 April 2015. [Google Scholar]
- Choi, Y.; Jung, D.; Ham, K.; Bae, S. A study on the accelerated vibration endurance tests for battery fixing bracket in electrically driven vehicles. Procedia Eng. 2011, 10, 851–856. [Google Scholar] [CrossRef]
- Reddy, P.R.; Reddy, P.S.; Reddy, K.V.K. Vibration analysis of a Torpedo battery tray using FEA. Int. J. Eng. Res. Technol. 2014, 03, 128–134. [Google Scholar]
- Li, J.; Tian, H.; Wu, P. Analysis of random vibration of power battery box in electric vehicles. In Proceedings of the 2014 IEEE Conference Transportation Electrification ASIA-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar]
- Hong, S.K.; Epureanu, B.I.; Castanier, M.P. Parametric reduced-order models of battery pack vibration including structural variation and prestress effects. J. Power Sources 2014, 261, 101–111. [Google Scholar] [CrossRef]
- Arora, S.; Shen, W.; Kapoor, A. Review of mechanical design and strategic placement technique of a robust battery pack for electric vehicles. Renew. Sustain. Energy Rev. 2016, 60, 1319–1331. [Google Scholar] [CrossRef]
- Lee, J.K.; Yeo, J.S.; Jang, M.C.; Yoon, J.M.; Kang, D.M. Mechanical durability and electrical durability of an aluminium-laminated lithium-ion polymer battery pack for a hybrid electric vehicle. J. Automob. Eng. 2010, 224, 765–773. [Google Scholar] [CrossRef]
- Yang, L.; Cheng, X.; Gao, Y.; Yin, G. Effect of vibration on the life of LiCoO2/MCMB battery. Battery Bimon. 2014, 04, 202–205. (In Chinese) [Google Scholar]
- An, Y.; Zhang, Z.; Chang, X.; Jiang, T.; Rong, C.; Chen, H. Resarch on vibration resistance of electric vehicle lithium-ion battery cells. In Proceedings of the China Automotive Engineering Society Annual Meeting, Beijing, China, 26 November 2013. (In Chinese). [Google Scholar]
- Brand, M.; Schuster, S.; Bach, T.; Fleder, E.; Stelz, M.; Glaser, S.; Muller, J.; Sextl, G.; Jossen, A. Effects of vibrations and shocks on lithium-ion cells. J. Power Sources 2015, 288, 62–69. [Google Scholar] [CrossRef]
- Wang, D.; Wu, X.; Wang, Z.; Chen, L. Cracking causing cyclic instability of LiFePO4 cathode material. J. Power Sources 2005, 140, 125–128. [Google Scholar] [CrossRef]
- Hooper, J.; Marco, J. Characterising the in-vehicle vibration inputs to the high voltage battery of an electric vehicle. J. Power Sources 2014, 245, 510–519. [Google Scholar] [CrossRef]
- Hooper, J.; Marco, J. Experimental modal analysis of lithium-ion pouch cells. J. Power Sources 2015, 285, 247–259. [Google Scholar] [CrossRef]
- Hooper, J.; Marco, J.; Chouchelamane, G.; Lyness, C. Vibration durability testing of nickel manganese cobalt oxide (NMC) lithium-ion 18650 battery cells. Energies 2016, 9, 52. [Google Scholar] [CrossRef]
- Bruen, T.; Hooper, J.; Marco, J.; Gama, M.; Chouchelamane, G. Analysis of a battery management system (BMS) control strategy for vibration aged nickel manganese cobalt oxide (NMC) lithium-Iion 18650 battery cells. Energies 2016, 9, 255. [Google Scholar] [CrossRef]
- Hooper, J.; Marco, J.; Chouchelamane, G.; Lyness, C.; Taylor, J. Vibration durability testing of nickel cobalt aluminum oxide (NCA) lithium-ion 18650 battery cells. Energies 2016, 9, 281. [Google Scholar] [CrossRef] [Green Version]
- Marco, J.; Hooper, J. Defining a representative vibration durability test for electric vehicle (EV) rechargeable energy storage systems (RESS). In Proceedings of the Electric Vehicle Symposium (EVS 29), Montréal, QC, Canada, 19–21 June 2016. [Google Scholar]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Ma, Z.; Jiang, Y. Lithium-ion battery aging mechanisms and life model under different charging stresses. J. Power Sources 2017, 356, 103–114. [Google Scholar] [CrossRef]
- Barai, A.; Chouchelamane, G.H.; Guo, Y.; McGordon, A.; Jennings, P. A study on the impact of lithium-ion cell relaxation on electrochemical impedance spectroscopy. J. Power Sources 2015, 280, 74–80. [Google Scholar] [CrossRef]
- Piłatowicz, G.; Marongiu, A.; Drillkens, J.; Sinhuber, P.; Sauer, D.U. A critical overview of definitions and determination techniques of the internal resistance using lithium-ion, lead-acid, nickel metal-hydride batteries and electrochemical double-layer capacitors as examples. J. Power Sources 2015, 296, 365–376. [Google Scholar] [CrossRef]
- Schweiger, H.G.; Obeidi, O.; Komesker, O.; Raschke, A.; Schiemann, M.; Zehner, C.; Birke, P. Comparison of several methods for determining the internal resistance of lithium ion cells. Sensors 2010, 10, 5604–5625. [Google Scholar] [CrossRef] [PubMed]
- Jossen, A. Fundamentals of battery dynamics. J. Power Sources 2006, 154, 530–538. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A comparative study of commercial lithium ion battery cycle life in electrical vehicle: Aging mechanism identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Tang, X.C.; Pan, C.Y.; He, L.P.; Li, L.Q.; Chen, Z.Z. A novel technique based on the ratio of potentio-charge capacity to galvano-charge capacity (RPG) for determination of the diffusion coefficient of intercalary species within insertion-host materials: Theories and experiments. Electrochim. Acta 2004, 49, 3113–3119. [Google Scholar] [CrossRef]
- Honkura, K.; Takahashi, K.; Horiba, T. Capacity-fading prediction of lithium-ion batteries based on discharge curves analysis. J. Power Sources 2011, 196, 10141–10147. [Google Scholar] [CrossRef]
- Jiang, D.; Pei, J.; Zhang, A. DHC: A density-based hierarchical clustering method for time series gene expression data. In Proceedings of the Third IEEE Symposium on BioInformatics and BioEngineering, Hongkong, China, 12–12 March 2003; pp. 393–400. [Google Scholar]














| Test Conditions Vibration Spectrum | Test Conditions State of Charge (StableOC) (%) | Normal Test Accel. (g rms) | Normal Test Time (h) | Normal Test Cumul. Time (h) |
|---|---|---|---|---|
| Vertical 1 spectrum | 75 | 1.9 | 0.15 | 0.15 |
| Vertical 1 spectrum | 75 | 0.95 | 3.5 | 3.65 |
| Vertical 2 spectrum | 75 | 1.9 | 0.15 | 3.8 |
| Vertical 2 spectrum | 75 | 0.95 | 3.5 | 7.3 |
| Vertical 3 spectrum | 75 | 1.9 | 0.15 | 7.45 |
| Vertical 3 spectrum | 75 | 0.95 | 3.5 | 10.95 |
| Test Condition | DC Internal Resistance | ||||||
|---|---|---|---|---|---|---|---|
| Pre-Test | 38.03 | 39.47 | 39.07 | 39.67 | 37.40 | 38.47 | 38.00 |
| 36.80 | 36.60 | 36.37 | 38.23 | 37.40 | 37.83 | 36.80 | |
| 37.40 | 37.12 | 36.73 | 36.92 | 36.16 | 36.64 | 36.79 | |
| 36.23 | 34.93 | 37.56 | 37.27 | 36.66 | 36.67 | 37.61 | |
| 36.10 | 36.52 | 35.69 | |||||
| Test Condition | DC Internal Resistance | ||||||
|---|---|---|---|---|---|---|---|
| Post-Test | 37.63 | 38.87 | 38.67 | 38.63 | 37.40 | 38.43 | 38.03 |
| 35.57 | 37.83 | 37.20 | 38.43 | 37.83 | 38.87 | 37.20 | |
| 38.03 | 38.23 | 37.60 | 38.83 | 36.60 | 37.43 | 37.63 | |
| 36.57 | 36.17 | 39.20 | 42.44 | 38.72 | 38.52 | 40.09 | |
| 38.43 | 38.50 | 37.13 | |||||
| Sample Number | Capacity (mAh) | DC Resistance (mΩ) | q | A (Vs) | P1 (V) | P2 (V) | P3 (V) |
|---|---|---|---|---|---|---|---|
| 1 | 2984.2 | 38.03 | 0.2073 | 12576.5 | 3.615 | 3.648 | 4.15 |
| 2 | 2967.1 | 39.47 | 0.2061 | 12498.8 | 3.624 | 3.644 | 4.126 |
| 3 | 2987.9 | 39.07 | 0.1975 | 12582.7 | 3.617 | 3.647 | 4.129 |
| 4 | 2930.4 | 39.67 | 0.2083 | 12364.4 | 3.64 | 3.66 | 4.127 |
| 5 | 2964.1 | 37.40 | 0.2021 | 12488.5 | 3.622 | 3.654 | 4.126 |
| 6 | 2965.7 | 38.47 | 0.2050 | 12491.7 | 3.622 | 3.654 | 4.128 |
| 7 | 2977.9 | 38.00 | 0.2038 | 12570.6 | 3.619 | 3.651 | 4.165 |
| 8 | 2978.7 | 36.80 | 0.1970 | 12559.1 | 3.622 | 3.656 | 4.129 |
| 9 | 2978.2 | 36.60 | 0.2070 | 12567.5 | 3.612 | 3.646 | 4.137 |
| 11 | 3002.8 | 36.37 | 0.2016 | 12666.4 | 3.606 | 3.651 | 4.129 |
| 12 | 2993.4 | 38.23 | 0.2024 | 12621.0 | 3.616 | 3.658 | 4.134 |
| 13 | 2974.7 | 37.40 | 0.2015 | 12540.5 | 3.61 | 3.655 | 4.123 |
| 14 | 3023.8 | 37.83 | 0.1953 | 12739.2 | 3.614 | 3.655 | 4.132 |
| 15 | 2982.7 | 36.80 | 0.2018 | 12582.8 | 3.606 | 3.653 | 4.134 |
| 16 | 3015.6 | 37.40 | 0.1975 | 12722.3 | 3.61 | 3.647 | 4.134 |
| 17 | 2986 | 37.12 | 0.2032 | 12584.3 | 3.6 | 3.647 | 4.147 |
| 18 | 2964.3 | 36.73 | 0.2063 | 12503.1 | 3.599 | 3.636 | 4.141 |
| 19 | 3001 | 36.92 | 0.1962 | 12637.8 | 3.596 | 3.642 | 4.123 |
| 20 | 2997.1 | 36.16 | 0.1972 | 12638.3 | 3.6 | 3.646 | 4.14 |
| 21 | 2986.2 | 36.64 | 0.1971 | 12588.7 | 3.601 | 3.635 | 4.142 |
| 22 | 2985.7 | 36.79 | 0.2003 | 12579.5 | 3.602 | 3.648 | 4.133 |
| 23 | 2980.9 | 36.23 | 0.2000 | 12577.5 | 3.596 | 3.655 | 4.134 |
| 24 | 2990.7 | 34.93 | 0.1922 | 12610.3 | 3.586 | 3.648 | 4.136 |
| 25 | 2979.1 | 37.56 | 0.2076 | 12564.5 | 3.607 | 3.644 | 4.139 |
| 26 | 2987.2 | 37.27 | 0.2033 | 12586.6 | 3.603 | 3.638 | 4.136 |
| 27 | 2988 | 36.66 | 0.1990 | 12587.7 | 3.602 | 3.648 | 4.132 |
| 28 | 3000.4 | 36.67 | 0.1950 | 12646.5 | 3.6 | 3.65 | 4.139 |
| 29 | 2997.4 | 37.61 | 0.1983 | 12626.9 | 3.607 | 3.651 | 4.141 |
| 30 | 2985.7 | 36.10 | 0.2007 | 12574.7 | 3.596 | 3.646 | 4.134 |
| 31 | 3045.4 | 36.52 | 0.1908 | 12836.2 | 3.6 | 3.636 | 4.134 |
| 32 | 3064.6 | 35.69 | 0.1852 | 12928.2 | 3.587 | 3.637 | 4.136 |
| Sample Number | Capacity (mAh) | DC Resistance (mΩ) | q | A (Vs) | P1 (V) | P2 (V) | P3 (V) |
|---|---|---|---|---|---|---|---|
| 1 | 2925.9 | 37.63 | 0.2222 | 12331.6 | 3.646 | 3.677 | 4.151 |
| 2 | 2907.4 | 38.87 | 0.2200 | 12240.2 | 3.657 | 3.685 | 4.127 |
| 3 | 2927.6 | 38.67 | 0.2117 | 12320.8 | 3.651 | 3.678 | 4.133 |
| 4 | 2854.1 | 38.63 | 0.2228 | 12036.6 | 3.689 | 3.708 | 4.143 |
| 5 | 2913.9 | 37.40 | 0.2157 | 12264.1 | 3.655 | 3.684 | 4.141 |
| 6 | 2913.4 | 38.43 | 0.2208 | 12256.3 | 3.656 | 3.686 | 4.133 |
| 7 | 2920.5 | 38.03 | 0.2190 | 12319.9 | 3.651 | 3.682 | 4.153 |
| 8 | 2930.2 | 35.57 | 0.2116 | 12340.4 | 3.643 | 3.673 | 4.12 |
| 9 | 2904.3 | 37.83 | 0.2226 | 12241.4 | 3.632 | 3.664 | 4.157 |
| 11 | 2923.8 | 37.20 | 0.2151 | 12306.2 | 3.626 | 3.655 | 4.134 |
| 12 | 2902.2 | 38.43 | 0.2189 | 12210.9 | 3.638 | 3.657 | 4.13 |
| 13 | 2890.3 | 37.83 | 0.2174 | 12160.1 | 3.631 | 3.663 | 4.124 |
| 14 | 2951.9 | 38.87 | 0.2114 | 12403.4 | 3.637 | 3.664 | 4.116 |
| 15 | 2908.9 | 37.20 | 0.2200 | 12251.6 | 3.628 | 3.662 | 4.123 |
| 16 | 2962.1 | 38.03 | 0.2134 | 12469.3 | 3.623 | 3.654 | 4.129 |
| 17 | 2927.7 | 38.23 | 0.2226 | 12328.9 | 3.634 | 3.679 | 4.144 |
| 18 | 2873.7 | 37.60 | 0.2277 | 12121.6 | 3.635 | 3.672 | 4.135 |
| 19 | 2926.9 | 38.83 | 0.2147 | 12307.9 | 3.628 | 3.661 | 4.127 |
| 20 | 2926.6 | 36.60 | 0.2157 | 12324.9 | 3.633 | 3.676 | 4.142 |
| 21 | 2912.2 | 37.43 | 0.2169 | 12260.4 | 3.635 | 3.678 | 4.131 |
| 22 | 2915.5 | 37.63 | 0.2207 | 12268.4 | 3.638 | 3.671 | 4.134 |
| 23 | 2911.3 | 36.57 | 0.2189 | 12274.7 | 3.629 | 3.663 | 4.151 |
| 24 | 2933.2 | 36.17 | 0.2089 | 12362.1 | 3.617 | 3.651 | 4.124 |
| 25 | 2890.7 | 39.20 | 0.2218 | 12189.4 | 3.621 | 3.658 | 4.138 |
| 26 | 2915.9 | 42.44 | 0.2185 | 12273.4 | 3.628 | 3.658 | 4.132 |
| 27 | 2915.2 | 38.72 | 0.2104 | 12264.9 | 3.623 | 3.654 | 4.113 |
| 28 | 2923.1 | 38.52 | 0.2059 | 12301.2 | 3.623 | 3.666 | 4.11 |
| 29 | 2907.4 | 40.09 | 0.2136 | 12227.2 | 3.636 | 3.676 | 4.144 |
| 30 | 2909.9 | 38.43 | 0.2166 | 12239.0 | 3.621 | 3.668 | 4.127 |
| 31 | 2979.8 | 38.50 | 0.2049 | 12537.5 | 3.623 | 3.659 | 4.111 |
| 32 | 3016.2 | 37.13 | 0.1977 | 12699.5 | 3.611 | 3.647 | 4.125 |
| Cell Sample Condition | The Inconsistent Coefficient of Different Classes | ||||
|---|---|---|---|---|---|
| Class 5 | Class 4 | Class 3 | Class 2 | Class 1 | |
| Pre-Test | 2.22 | 2.51 | 2.74 | 3.22 | 2.95 |
| Post-Test | 1.30 | 2.31 | 2.60 | 3.44 | 3.10 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Ning, Z.; Peng, H.; Mu, Z.; Sun, C. Effects of Vibration on the Electrical Performance of Lithium-Ion Cells Based on Mathematical Statistics. Appl. Sci. 2017, 7, 802. https://doi.org/10.3390/app7080802
Zhang L, Ning Z, Peng H, Mu Z, Sun C. Effects of Vibration on the Electrical Performance of Lithium-Ion Cells Based on Mathematical Statistics. Applied Sciences. 2017; 7(8):802. https://doi.org/10.3390/app7080802
Chicago/Turabian StyleZhang, Lijun, Zhansheng Ning, Hui Peng, Zhongqiang Mu, and Changyan Sun. 2017. "Effects of Vibration on the Electrical Performance of Lithium-Ion Cells Based on Mathematical Statistics" Applied Sciences 7, no. 8: 802. https://doi.org/10.3390/app7080802
APA StyleZhang, L., Ning, Z., Peng, H., Mu, Z., & Sun, C. (2017). Effects of Vibration on the Electrical Performance of Lithium-Ion Cells Based on Mathematical Statistics. Applied Sciences, 7(8), 802. https://doi.org/10.3390/app7080802